Chaotische Systeme. ViLab. Marian Panten

Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis

Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften

Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos

Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen

Deterministisches Chaos

Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend

Durch Simulation dynamische Systeme entdecken Labor 6

Institut für Automatik D-ITET, 2. Sem. ETH Zürich Dr. F. J. Kraus 28. Mai 2004 Durch Simulation dynamische Systeme entdecken Labor 6 In diesem Labor wollen wir einen kleinen Einblick in die Chaostheorie

Chaos Oder Mandelbrot und Peitsche

Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,

Experimente, Ideen und Entwicklung der Chaostheorie

Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment

Seltsame Attraktoren

1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?

Bedeutende Theorien des 20. Jahrhunderts

Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik

Die Darstellung nichtlinearer Bewegungsabläufe

Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren

Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Big Data Science in und außerhalb der Physik

Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut

Nichtlineare Dynamik Einführung

Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische

+ + Personalmanagement Stuff-Turnover. Simulation im Excel. Organizational Headcount. Turnover. Recruitment

Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:

Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality

Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische

11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.

11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:

Die Chaostheorie und Fraktale in der Natur

Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur

Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos. Wintersemester 2018/ M. Zaks

Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos Wintersemester 2018/19 22.01.2019 M. Zaks hintergrund Kontext: Wettervorhersage. Entstehung von Luftbewegungen infolge der thermischen

7. Systeme mit drei (und mehr) Spezies: chaotische Systeme

7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies

Veränderung in gestalteter Beziehung

Dr. Dr. Strunk Veränderung in gestalteter Beziehung 1 complexity-research.com Veränderung in gestalteter Beziehung Dipl.-Psych. Dr. Dr. Guido Strunk 1. VORTRAG... 2 2. FEEDBACKSYSTEME NICHTLINEALITÄT...

Prozessorientierte und embodimentorientierte Psychotherapieforschung (d)

Prozessorientierte und embodimentorientierte Psychotherapieforschung (d) Dynamische Invarianten, Attraktoren Wolfgang Tschacher, Vorlesung 2015 tschacher@spk.unibe.ch http://www.embodiment.ch/ dynamische

( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme

Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)

3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).

3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau

Wie lang ist die Küste Großbritanniens?

Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das

Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie

Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie Daniela Schimming, Jennifer Richter, Juliana Schmidt Gliederung 1. Grundlagen 2. Nachrichtenjournalismus und

Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:

Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...

Feigenbaum, Chaos und die RG

Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler

Nichtlineare Phänomene und Selbstorganisation

Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren

REFERAT FÜR INNOVATIVE ARCHIKETUREN

REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE

6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität

6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst

Alles kein Zufall? DI Dr. techn. Robert Pucher. Beeinflussung des Zufalls? Untersuchungen zur willentlichen Beeinflussung von zufälligen Ereignissen

Alles kein Zufall? DI Dr. techn. Robert Pucher Beeinflussung des Zufalls? Untersuchungen zur willentlichen Beeinflussung von zufälligen Ereignissen - PEAR-Experimente in Princeton, - aktuelle Versuchsplanung

Fraktale und Beispiele aus der Physik

Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien

Chaos Seminar Wetter und Klima. Dominik Fröschl

Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung

Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen

Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper

Die Entdeckung des Chaos

Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht

Deterministisches Chaos - Versuch einer neuen Begriffsbestimmung

Deterministisches Chaos - Versuch einer neuen Begriffsbestimmung Ludwig Pohlmann AdW der DDR, Zentralinstitut für physikalische Chemie, Berlin, Rudower Chaussee 5, DDR-1199 Begriffe haben ihre Dynamik,

Differentialgleichungen 2. Differentialgleichungen und Dynamische Systeme. Peter Szmolyan

Differentialgleichungen 2 Differentialgleichungen und Dynamische Systeme Peter Szmolyan Institut für Analysis und Scientific Computing TU-Wien 1 The theory of dynamical systems is one of the domains of

Achtung Nebel! Ein Komplexitäts-Crashkurs für Projektmanager*innen

complexity-research.com Achtung Nebel! Ein Komplexitäts-Crashkurs für Projektmanager*innen Priv.-Doz. Dr. Dr. Dipl.-Psych. Guido Strunk guido.strunk@complexity-research.com www.complexity-research.com

Zufall ein Auslaufmodell?

Zufall ein Auslaufmodell? SGMI-Club 13.4.2018 Markus Hertle Zufall (Wikipedia) Von Zufall spricht man dann, wenn für ein einzelnes Ereignis oder das Zusammentreffen mehrere Ereignisse keine kausale Erklärung

Chaos im getriebenen nicht-linearen Pendel

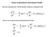Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel

Der Kosmos-Bote Mai 2017

Der Kosmos-Bote Mai 2017 Heil ge Ordnung, segensreiche Himmelstochter [... ] Friedrich Schiller Liebe Leserin, lieber Leser, kommt die Rede beiläufig auf Astronomie, denkt mancher ans Wetter! Was für eine

DYNAMISCHE SYSTEME. Hans G. Weidinger

Hans G. Weidinger Elektro-Enzephalogramm Nach H. Haken, DGNÄ Freiburg, WVG 1989 Welches EEG gehört zum gesunden Gehirn? a. EEG bei einem gesunden Menschen b. EEG bei einem epileptischem Anfall Das Gehirn

Zugänge zur nichtlinearen Dynamik. W. Oehme, Universität Leipzig

Zugänge zur nichtlinearen Dynamik W. Oehme, Universität Leipzig einfache physikalische Experimente Wirtschaft Wetter historische Bezüge Nichtlineare Dynamik Chaos und Ordnung Verkehrsstau Populationsdynamik

DAS VORHERGESAGTE CHAOS

DAS VORHERGESAGTE CHAOS Vorhersagen sind schwierig, besonders wenn sie die Zukunft betreffen, in erster Linie dann, wenn es sich um Wettervorhersagen handelt ein Zitat, das Berühmtheiten wie Nils Bohr

HARMONIK ZWISCHEN ORDNUNG UND CHAOS

HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?

GRUNDLEGENDE MODELLE. Caroline Herbek

GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)

Zuletzt zeige ich Ihnen am Beispiel von Zufallszahlengeneratoren und der künstlichen Intelligenz wie der Zufall programmiert werden kann.

Einleitung Der Zufall ist in der Vortragsreihe der Willms-Neuhaus-Stiftung schon aus vielfältiger Perspektive beleuchtet worden. Dennoch können wir weiter darüber wissenschaftlich diskutieren und wo das

Zufälle gibt s, oder gibt s die nicht? Martin Köhler Science Café Hamburg, 25. Juni 2014

Zufälle gibt s, oder gibt s die nicht? Martin Köhler Science Café Hamburg, 25. Juni 2014 Grundfrage und Gliederung Gibt es einen echten Zufall, oder wissen wir einfach nicht genug für eine exakte Vorhersage?

Ökologische Gleichungen für zwei Spezies

Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der

Thermodynamik. Wechselwirkung mit anderen Systemen Wärme, Arbeit, Teilchen

18a Temperatur 1 Thermodynamik Thermodynamik ist eine phänomenologische Wissenschaft Sie beschreibt die Wechselwirkung von Systemen mit ihrer Umgebung Aus der Erfahrung und durch zahllose Beobachtungen

8. Deterministisches Chaos

8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen

Seminar Populations- und Epidemiemodelle. Die Lorenz-Gleichungen.

Seminar Populations- und Epidemiemodelle. Die Lorenz-Gleichungen. Christian Rose 30. Juni 2013 1 1 Motivation In den sechziger Jahren des 20. Jahrhunderts fragte sich ein Meteorologe namens Lorenz, wie

Würfelt Gott oder würfelt er nicht? p.1/35

Würfelt Gott oder würfelt er nicht? Die Rolle des Zufalls im Weltbild der Physik Claus Grupen Universität Siegen Dortmund, den 21. Mai 2005 Würfelt Gott oder würfelt er nicht? p.1/35 Eine uralte Frage...

Vorwort Dynamische Systeme können durch mathematische Gleichungen modelliert werden, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Entwicklung des Systemzustandes darstellen, so daß die

Vom Algorithmus zum Chaos: Anwendungen des Computers

Vom Algorithmus zum Chaos: Anwendungen des Computers (Henner Schneider, Fb Informatik, FH Darmstadt) Die Computer verdanken ihre Entstehung den Schwierigkeiten, die das menschliche Gehirn beim Umgang mit

Der Duffing-Oszillator

11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile

Helmut Moritz. Chaostheorie und Meteorologie

Sitzungsberichte der Leibniz-Sozietät 71(2004), 37 46 Helmut Moritz Chaostheorie und Meteorologie 1. Wettervorhersage und Kausalität Die angebliche Unzuverlässigkeit der Wettervorhersage ist sprichwörtlich.

Chaos und. Alexander Mielke

Chaos und Šarkovskiǐs Anordnung der natürlichen Zahlen Alexander Mielke Die Theorie der Dynamischen Systeme geht zurück auf die bahnbrechenden Arbeiten von H. Poincaré im ausgehenden 9. Jahrhundert. Er

Grenzen der Klassischen Mechanik

Grenzen der Klassischen Mechanik M. Jakob Gymnasium Pegnitz 10. Dezember 2014 Inhaltsverzeichnis 1 Kausalität Die Fundamente der Klassischen Physik Kritik an der Klassischen Mechanik Zusammenbruch der

Stabile periodische Bewegungen (Grenzzyklen)

Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum

Nichtlinearität in der klassischen Physik

Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................

CHAOS. 1.2 Was ist deterministisches Chaos? 1.1 Einführung. 1. Deterministisches Chaos - allgemeine Vorbemerkungen. 1.1 Einführung

CHAOS 1. Deterministisches Chaos - allgemeine Vorbemerkungen 1.1 Einführung 1.2 Was ist deterministisches Chaos? 1.3 Prinzipielle "Unschärfen" 1.4 Chaotische Experimente 2. Das Magnetpendel 2.1 Versuchsaufbau

Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017

Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master

Chaos - Nichtlineare Dynamik

Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg

Fragen zu Kapitel III Seite 1 III

Fragen zu Kapitel III Seite 1 III Grundbegriffe der klassischen Mechanik Fragen 3.1 bis 3.8 Zur Beantwortung der Fragen benötigen Sie folgende Daten Masse der Erde 5,974 10 4 kg Erdradius 6371 km Erdbeschleunigung

2.7 Nichtlineare Dynamik Determinismus vs. Chaos. 2 Analytische Mechanik

Die Generatoren M i, i = x,y,z, bilden eine (Lie)- Algebra mit folgenden Eigenschaften Mi,M j M i M j M j M i = εijm k k k Wir können auch zeigen (Übung) dass ebenfalls Li,L j = ε k ij Ł k gilt. Wir überprüfen

Lineare und nichtlineare Schwingungen und Wellen

Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer

1 Nicht-lineare dynamische Systeme

1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:

Zeitreihenanalytische Verfahren für die Analyse nichtlinearer Systeme

Dipl.-Psych. Dr. Dr. Guido Strunk 2010 1 Zeitreihenanalytische Verfahren für die Analyse nichtlinearer Systeme Unterlagen zur Summer School 2010 von Dipl.-Psych. Dr. Dr. Guido Strunk guido.strunk@complexity-research.com

Die Mathematikerinnen Sonja Kowalewskaja und Amalie Emmy Noether und ihre Beiträge zur Physik

Die Mathematikerinnen Sonja Kowalewskaja und Amalie Emmy Noether und ihre Beiträge zur Physik Köln, den 26.9.2002 Ute Löw 1. Sonja Kowalewskaja 2. Der starre Körper 3.Die Bewegung von Körpern 4.Chaotische

2.2 Reversible Nichtlineare Dynamiken Determinismus

2.2 Reversible Nichtlineare Dynamiken 2.2.1 Determinismus Leukipp und Demokrit waren die Begründer des Determinismus. Dieser bedeutet, daß alle Prozesse dieser Welt nach konkreten Gesetzmäßigkeiten ablaufen

FC3 - Duffing Oszillator

FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme

COSMO-DE Ensemblevorhersagen

COSMO-DE Ensemblevorhersagen Dr. Annegret Gratzki S. Theis, C. Gebhardt, M. Buchhold, Z. Ben Bouallègue, R. Ohl, M. Paulat, C. Peralta Frankfurter Straße 135, 63067 Offenbach Email: Annegret.Gratzki@dwd.de

Die Laplace-Gleichung

http://www.flickr.com/photos/rocketdude/489565079/ Die Laplace-Gleichung 1-E1 http://img.allposters.com/6/lrg/17/1740/imj3d00z.jpg Pierre-Simon Laplace (1749-1827) war ein französischer Mathematiker und

Kinetische Theorie. Übersicht: Voraussetzungen: Verteilungsfunktionen Grundgleichungen: Kollissionen

Kinetische Theorie Übersicht: Verteilungsfunktionen Grundgleichungen: Boltzmann Vlasov Fokker-Planck Kollissionen neutral trifft neutral neutral trifft geladen geladen trifft geladen Voraussetzungen: keine

2 Modellierungsformalismen: S-Systeme und Boolesche Netze

2 Modellierungsformalismen: S-Systeme und Boolesche Netze 2.1 Potenzgesetze In der Natur sind allometrische Beziehungen der Form X i = b ij X aij j weit verbreitet. Eine solche Beziehung nennt man auch

Ordnung und Chaos, Zufall und Notwendigkeit

Ordnung und Chaos, Zufall und Notwendigkeit Von Kurt Bangert Nichts kann existieren ohne Ordnung nichts kann entstehen ohne Chaos. (Albert Einstein) Die ersten Verse der Bibel enthalten die bekannten Einleitungsworte

Einfache Modelle der Populationsdynamik

Vorlesung 4. Einfache Modelle der Populationsdynamik Wintersemester 215/16 1.11.215 M. Zaks allgemeine vorbemerkungen In kleinen Populationen schwanken die Bevolkerungszahlen stochastisch: Geburt/Tod von

Chaos & Quantenchaos SS 2009

Chaos & Quantenchaos SS 2009 H. J. Korsch FB Physik Technische Universität Kaiserslautern Einleitung Mathematisches Vorspiel : Hamiltonsche Systeme alternativ Dissipative Systeme Wege ins Chaos Quantenchaos

Theoretische Biophysik - Statistische Physik

Theoretische Biophysik - Statistische Physik 10. Vorlesung Pawel Romanczuk Wintersemester 2018 http://lab.romanczuk.de/teaching/ 1 Brownsche Bewegung Zusammenfassung letzte VL Formulierung über Newtonsche

System von Differentialgleichungen erster Ordnung

System von Differentialgleichungen erster Ordnung Die Standardform eines Systems von Differentialgleichungen ist u (t) = f (t, u(t)) mit der Anfangsbedingung u(t 0 ) = a. Dabei ist u = (u 1,..., u n )

Signalverarbeitung 2. Volker Stahl - 1 -

- 1 - Hidden Markov Modelle - 2 - Idee Zu klassifizierende Merkmalvektorfolge wurde von einem (unbekannten) System erzeugt. Nutze Referenzmerkmalvektorfolgen um ein Modell Des erzeugenden Systems zu bauen

Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:

Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:

Warum Buridans Esel nicht verhungert Gesetz und Zufall in der Physik

Warum Buridans Esel nicht verhungert Gesetz und Zufall in der Physik Prof. Dr. Peter C. Hägele, Universität Ulm peter.haegele@uni-ulm.de www.uni-ulm.de/ phaegele/ HSZ und Studium generale 31.01.2007 6.

Bloch Oszillationen. Klassisch chaotische Streuung. Klassisch chaotische Streuung

Bloch Oszillationen periodische Oszillation keine systematische Dispersion Modell der gekippten Bänder: Zwei Zeitskalen: Bloch-Zeit Antriebsperiode Annahme: mit teilerfremden ganzen Zahlen Hamilton-Operator

Chaos und Ordnung im Unternehmen

Frank Deser 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Chaos und Ordnung im Unternehmen Chaosforschung als ein

INHALTSVERZEICHNIS. FBA Physik: Chaos Chaostheoretische Anwendungen in Physik und Alltag Inhaltsverzeichnis. Dank und Widmung Seite 3.

Inhaltsverzeichnis INHALTSVERZEICHNIS Dank und Widmung Seite 3 Vorwort Seite 4 Kapitel I.: Was ist Chaos? Eine Einführung Seite 5 Vorwort Seite 5 Definition Chaos Seite 6 Grundlagen Seite 7 Philosophische

Untersuchungen am magnetischen Doppelpendel - Spaceball

Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel

Schrödingers Katze -oder- Wo ist der Übergang?

Schrödingers Katze -oder- Wo ist der Übergang? Themen Vergleich Quantenmechanik klassische Mechanik Das Gedankenexperiment Interpretationen des Messprozesses (Kopenhagener Deutung, Viele-Welten-Theorie,

Erzwungene Schwingungen

Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung

8 Dynamische Systeme. 1 Begriff und Anwendung

8 Dynamische Systeme Jörn Loviscach Versionsstand: 23. März 2013, 15:56 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html This

Poincaré-Schnitte. Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert

Poincaré-Schnitte Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert Themen 1. Was sind Poincaré-Schnitte?. Anwendung: Poincaré-Schnitte Mathematica-Beispiel: Attraktor

Zelluläre Automaten. Sommerakademie Ftan Daniel Abler

Zelluläre Automaten Sommerakademie Ftan 2004 Daniel Abler Zelluläre Automaten 1.Merkmale komplexer Systeme bzw. zellulärer Automaten 2.Grundcharakteristika - Game of Life 3.Definition 4.Eigenschaften und

Flüsse, Fixpunkte, Stabilität

1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher

Merkwürdige und chaotische Attraktoren und deren Stabilität

Merkwürdige und chaotische Attraktoren und deren Stabilität Ann-Kristin Baum Seminar Dynamische Systeme SS 06 1 Inhaltsverzeichnis 2 1 Einführung Reale Vorgänge in den Natur- oder Gesellschaftswissenschaften,

Deterministisches Chaos

Platen-Gymnasium Ansbach Kollegstufe 001/003 FACHARBEIT aus dem Fach Physik Thema: Deterministisches Chaos Verfasser: Jörg Stadlinger Leistungskurs: Physik Inhaltsverzeichnis 1. Einführung in die Chaostheorie

Wie gesetzmäßig ist der Zufall? Barbara Drossel, TU Darmstadt

1 Wie gesetzmäßig ist der Zufall? Barbara Drossel, TU Darmstadt 2 Zufall in der Physik Rechnen mit Wahrscheinlichkeiten Beispiel 1: Münzwurf 1001111010000 Zufall in der Physik 3 Zufall in der Physik 4

Chaos und Šarkovskiǐs Anordnung der natürlichen Zahlen

Chaos und Šarkovskiǐs Anordnung der natürlichen Zahlen Alexander Mielke Institut für Analysis, Dynamik und Modellierung Universität Stuttgart Die Theorie der Dynamischen Systeme geht zurück auf die bahnbrechenden

Quantenphysik. oder: Die Wissenschaft vom Geist in dermaterie

Quantenphysik oder: Die Wissenschaft vom Geist in dermaterie materiell sichtbar lokal (Ort) begreifbare Teilchen faktische Realität nicht-materiell un-sichtbar nicht-lokal (keinen Ort) nur Möglichkeiten

Chaotisches Verhalten in nichtlinearen mechanischen Modellsystemen

Bachelorarbeit im Studienfach Physik Chaotisches Verhalten in nichtlinearen mechanischen Modellsystemen Maximilian Schilcher Matrikelnummer 133957 Theoretische Physik II Universität Augsburg 17. September

Synchronisation in Natur und Technik

Am Beispiel des Kuramoto-Modells Jan Baumbach Christoph Schöler Christian Barthel 2 Inhalt 1. Einleitung 2. Kuramoto-Modell 3. Simulation und Ergebnisse 3 Die Motivation Das Phänomen Synchronisation tritt