HARMONIK ZWISCHEN ORDNUNG UND CHAOS
|
|
|
- Max Martin
- vor 5 Jahren
- Abrufe
Transkript
1 HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik? Harmonik ordnet messbaren Zahlen oder Abmessungen anhörbare Klänge zu. Denn seit Pythagoras ist bekannt, dass die ganzzahlige Teilung einer Saite (z.b. auf einem Monochord) zu Tönen führt, die zusammen mit dem Ton der ganzen Saite einfache harmonische Intervalle ergeben. Es ist wichtig, sich darüber im Klaren zu sein, dass einer Zahl oder einem Maß allein kann noch keine klingende Bedeutung zugeordnet werden kann. Diese entsteht erst in einem Intervall, also in einer Tonbeziehung, der eine Beziehungen, d.h. ein Verhältnis zwischen Zahlen oder Maßen, entspricht. In Abbildung 1 ist die Bildung der einfachsten Intervalle Oktav Quint und Terz ist dargestellt. Abbildung 1 Zahl und Klang am Beispiel der Teilung einer Monochord-Saite. Wesentlich für das harmonikale Verständnis der Natur ist die Tatsache, dass beim Schwingen jeder einzelnen Saite Obertöne mitschwingen, die mit den Tönen identisch sind, so wie sie beim einfachen ganzzahligen Teilen einer Saite entstehen. In Abbildung 2 ist die Obertonreihe auf der Basis 1=c bis zum 7. Oberton dargestellt. 1
2 Abbildung 2 Obertonreihe auf der Basis 1=c Entsprechend entsteht bei einer fortschreitend ganzzahligen Verlängerung einer schwingenden Saite eine Untertonreihe (Abbildung 3), die jedoch nicht spiegelbildlich identisch zur Obertonreihe ist. Vielmehr weist die hier erzeugte Obertonreihe einen C-Dur- Charakter, die entsprechende Untertonreihe jedoch einen f-moll-charakter auf. Abbildung 3 Untertonreihe auf der Basis 1=c Harmonik vermittelt also Entsprechungen: Grundlegenden Strukturen der Natur und der Kultur entsprechen Klänge als sinnliche Wahrnehmung. Harmonik ist somit Mittel und Weg, um auf der Basis objektiv gesicherter Erkenntnisse und ihnen zuordenbaren subjektiven Empfindungen zu einem ganzheitlichen Erlebnis der 2
3 Grundlagen der Natur und damit auch der Eingebundenheit des Menschen in eine natürlich-kosmische Ordnung zu gelangen (Abbildung 4). Abbildung 4 Der hörende Mensch 1 2. Was ist Chaostheorie? Zunächst: Es gibt keine Theorie des Chaos. Aber es gibt einen wissenschaftlichen Ansatz zum Verständnis der Beziehung zwischen Chaos und Ordnung. Was ist Ordnung? Aus bekannten Anfangsbedingungen ergeben sich stets eindeutige, reproduzierbare Ergebnisse, auch bei Änderung der Anfangsbedingungen. z.b. eine Wurfparabel aus der Anfangsrichtung und Kraft des Wurfes; oder eine ganz bestimmte Schwingung = Ton aus der Länge und Spannung einer Saite. Chaos meint in der Wissenschaft allgemein einen Zustand ohne erkennbare und reproduzierbare Gesetzmäßigkeit. In der Mathematik und Physik betrifft das heute sogenannte Dynamische Systeme, deren zeitliches Verhalten unter bestimmten Bedingungen nicht vorhergesagt, bzw. mathematisch nicht berechnet werden kann. Es liegt dann chaotisches Verhalten vor, wenn bei identischem mathematischen Ansatz selbst geringste Änderungen der Anfangswerte nach einer gewissen Zeit zu einem völlig anderen Verhalten führen. Chaos-Theorie meint deshalb eigentlich die Wissenschaft von dynamische Systemen, die fern vom Gleichgewicht stabil sind, so wie das in der Natur die lebendigen Systeme sind, also Viren, Bakterien, Pflanzen, Tiere und der Mensch. Auch Wetter und Klima und die 1 Der Begriff Der Hörende Mensch geht auf Hans Kayser zurück. Vgl. z.b. sein Buch Der Hörende Mensch- Elemente eines akustischen Weltbildes, Engel & Co., bzw. Lambert Schneider Verlag, Stuttgart 1993, ISBN
4 Populationsdynamik von ökologische Systemen gehorchen den Regeln der dynamischen Systeme. Abbildung 5 illustriert, was mit fern vom Gleichgewicht gemeint ist. Abbildung 5 Bewegung im Gleichgewicht und Wandern fern vom Gleichgewicht 2 Das Verhalten solcher Systeme hängt von geringen Veränderungen der Anfangsbedingungen ab, die nicht sicher erfassbar sind, und dabei zu chaotisch-irregulären zeitliches Abläufen führen können. Dynamische Systeme stabilisieren sich durch Rückkopplungsmechanismen und durch Verbrauch von Energie. Sie erzeugen in zeitlich begrenzten Prozessen (Lebenszeit) komplexe Strukturen durch Selbstorganisation mittels Austausch und Weitergabe von Information. Die Formen solcher Strukturen sind fraktal und (in begrenzten Bereichen) selbstähnlich. Harmonik zwischen Ordnung und Chaos. Heute verstehen wir, dass im Bereich der Begegnung von Ordnung und Chaos hochharmonische Strukturen aufleuchten. Besonders berühmt geworden ist die sogenannte Mandelbrotmenge, die populär als Apfelmännchen bekannt wurde (Abbildung 6). Abbildung 6 Die Mandelbrotmenge, auch Apfelmännchen genannt. 2 Nach Friedrich Cramer Chaos und Ordnung: Die komplexe Struktur des Lebendigen, Deutsche Verlags-Anstalt, Stuttgart
5 Ein für die Harmonik besonders bedeutungsvolles Fraktal entsteht bei der Abbildung der Gleichtonlinien aus den Teiltonkoordinaten 3, wie in Abbildung 7 dargestellt. Abbildung 7 Ein aus Gleichtonlinien erzeugtes harmonikales Fraktal Das Verhalten von dynamischen Systemen lässt sich gut an dem einfachen Beispiel der sogenannten Verhulst-Dynamik demonstrieren. Mit der von Verhulst 4 entdeckten logistischen Gleichung x n + 1 = w x n (1 - x n ) lassen sich u.a. die Entwicklung von Populationen berechnen. Es ist dabei zu beachten, dass es sich hierbei um ein iteratives Berechnungsverfahren handelt, wie es heute in der Regel in der Chaostheorie angewendet wird. Das heißt das Ergebnis x n + 1 wird iterativ weiterverwendet, indem es an die Stelle von x n eingesetzt wird. Dabei ergeben sich dann, je nach dem für die Konstante w eingesetzten Wert verschiedene Abläufe für die Population P, nämlich für 1 < w < 3 Einschwingen in quasistatische Stabilität für 3 < w < 3,45 periodisches Schwingen für 3,45 < w < 3,54 doppelperiodisches Schwingen für w = 4 chaotisches Verhalten Abbildung 8 Verschiedenes Verhalten eines dynamischen Systems 3 Nach Hans Kayser z.b. in seinem Lehrbuch der Harmonik, Occident, Zürich Pierre-François Verhulst, ) war ein belgischer Mathematiker. 5
6 Trägt man die Population P nach vielfachen Iterationen der Verhulstgleichung gegen die Wachstumskonstante w auf, erhält man das Feigenbaum Diagramm, in dem der Wechsel der Stabilitätsbereiche erkennbar wird (Abbildung 9). Abbildung 10 Feigenbaum Graphiken zeigen Strukturen im Chaos Wenn man das weiter verfolgt, zeigen sich zwischen den chaotischen Bereichen hochgeordnete Zustände, in z.b. die Vervielfältigungszahlen 2 und 3 auftauchen, wie in Abbildung 10 zu sehen ist. Abbildung 11 2er und 3er Perioden im Feigenbaumdiagramm Geht man zu noch höheren Werten der Wachstumskonstant w, so finden sich auch 4er, 5er, 6er und 7er Periodizitäten. Alle Grundzahlen der Obertonreihe finden sich zwischen den chaotischen Zuständen (Abbildung 12). 6
7 Abbildung 12 2er, 4er, 3er, 5er 6er und 7er Perioden im Feigenbaumdiagramm Es treten also die harmonikalen Obertonzahlen im Wechsel von Chaos in Erscheinung! Das berechtigt zu der Schlussfolgerung: Die Gesetze der Harmonik sind die Gesetze eines die ganze Natur durchdringenden schöpferischen Prinzips! 7
Physik & Musik. Monochord. 1 Auftrag
 Physik & Musik 2 Monochord 1 Auftrag Physik & Musik Monochord Seite 1 Monochord Bearbeitungszeit: 30 Minuten Sozialform: Einleitung Einzel- oder Partnerarbeit Das Monochord ist ein einfaches Saiteninstrument
Physik & Musik 2 Monochord 1 Auftrag Physik & Musik Monochord Seite 1 Monochord Bearbeitungszeit: 30 Minuten Sozialform: Einleitung Einzel- oder Partnerarbeit Das Monochord ist ein einfaches Saiteninstrument
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
1.) Das harmonikale Tonsystem
 atheoretische Akustik 1.) Das harmonikale Tonsystem Dieses, auf der A. v. Thimusschen Wiederentdeckung des pythagoräischen Lambdoma fussend, ist in allen meinen Werken, besonders im Lehrbuch der Harmonik
atheoretische Akustik 1.) Das harmonikale Tonsystem Dieses, auf der A. v. Thimusschen Wiederentdeckung des pythagoräischen Lambdoma fussend, ist in allen meinen Werken, besonders im Lehrbuch der Harmonik
Vortrag am 12. Januar 2015 in der aktuellen Themenreihe
 Schläft ein Lied in allen Dingen, die da träumen, fort und fort, Und die Welt hebt an zu singen, triffst du nur da Zauberwort J. v. Eichendorff Vortrag am 12. Januar 2015 in der aktuellen Themenreihe Was
Schläft ein Lied in allen Dingen, die da träumen, fort und fort, Und die Welt hebt an zu singen, triffst du nur da Zauberwort J. v. Eichendorff Vortrag am 12. Januar 2015 in der aktuellen Themenreihe Was
Vortrag auf dem Harmonik-Symposion 2015 in Nürnberg am 10. Mai 2015
 Vortrag auf dem Harmonik-Symposion 2015 in Nürnberg am 10. Mai 2015 Hans G. Weidinger http://harmonik-zentrum-deutschland.de/wpcontent/uploads/2016/01/vom-wesen-der-harmonik.pdf Was hat es uns gebracht?
Vortrag auf dem Harmonik-Symposion 2015 in Nürnberg am 10. Mai 2015 Hans G. Weidinger http://harmonik-zentrum-deutschland.de/wpcontent/uploads/2016/01/vom-wesen-der-harmonik.pdf Was hat es uns gebracht?
Wachstum mit oberer Schranke
 1 1.1 exponentielles Wir haben das eines Kontos mit festem Zinssatz untersucht. Der jährliche Zuwachs (hier die Zinsen) sind proportional zum Bestand (hier dem jeweiligen Kontostand). Die Annahme, daß
1 1.1 exponentielles Wir haben das eines Kontos mit festem Zinssatz untersucht. Der jährliche Zuwachs (hier die Zinsen) sind proportional zum Bestand (hier dem jeweiligen Kontostand). Die Annahme, daß
Anfänge in der Antike
 Akustik Eine wesentliche Grundlage der Musik ist der Schall. Seine Eigenschaften erforscht die Akustik (griechisch: ακουειν = hören). Physikalisch ist Schall definiert als mechanische Schwingungen und
Akustik Eine wesentliche Grundlage der Musik ist der Schall. Seine Eigenschaften erforscht die Akustik (griechisch: ακουειν = hören). Physikalisch ist Schall definiert als mechanische Schwingungen und
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE
 UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE Vortrag auf dem Harmonik-Symposion Nürnberg 06.05.2017 Hans G. Weidinger UNSER WELTBILD Es ist die Sehnsucht des Menschen, das Weltall und seinen eigenen
UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE Vortrag auf dem Harmonik-Symposion Nürnberg 06.05.2017 Hans G. Weidinger UNSER WELTBILD Es ist die Sehnsucht des Menschen, das Weltall und seinen eigenen
Die Mathematik der Tonleiter
 Die Mathematik der Tonleiter Jürgen Zumdick Wir betrachten eine Saite von 0 cm Länge. Wird sie in Schwingungen versetzt, so erzeugt sie einen Ton. Dessen Frequenz sei 60 Hertz. Verkürzt man die Saite um
Die Mathematik der Tonleiter Jürgen Zumdick Wir betrachten eine Saite von 0 cm Länge. Wird sie in Schwingungen versetzt, so erzeugt sie einen Ton. Dessen Frequenz sei 60 Hertz. Verkürzt man die Saite um
Die Zahl ist das Wesen aller Dinge
 Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raael 50 -gründete 5v.Chr die religiös-politische Lebensgemeinschat der Pythagoreer.
Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raael 50 -gründete 5v.Chr die religiös-politische Lebensgemeinschat der Pythagoreer.
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Jan Henrik Sylvester. 10. Februar 2003
 Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Hertz ), also 1 Schwingung pro Sekunde. Der Vorfaktor A ist die Amplitude, er misst die Lautstärke des Tons.
 1 Vorbereitungen 1.1 Was ist und wofür braucht man Fourieranalysis? Anwendungsgebiete der Fourier-Analysis sind z.b. Signalverarbeitung, Bildverarbeitung, Schaltkreisentwurf, Elektrodynamik, Optik, Akustik,
1 Vorbereitungen 1.1 Was ist und wofür braucht man Fourieranalysis? Anwendungsgebiete der Fourier-Analysis sind z.b. Signalverarbeitung, Bildverarbeitung, Schaltkreisentwurf, Elektrodynamik, Optik, Akustik,
DYNAMISCHE SYSTEME. Hans G. Weidinger
 Hans G. Weidinger Elektro-Enzephalogramm Nach H. Haken, DGNÄ Freiburg, WVG 1989 Welches EEG gehört zum gesunden Gehirn? a. EEG bei einem gesunden Menschen b. EEG bei einem epileptischem Anfall Das Gehirn
Hans G. Weidinger Elektro-Enzephalogramm Nach H. Haken, DGNÄ Freiburg, WVG 1989 Welches EEG gehört zum gesunden Gehirn? a. EEG bei einem gesunden Menschen b. EEG bei einem epileptischem Anfall Das Gehirn
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Töne, Klänge und Geräusche Arbeitsblatt
 Lehrerinformation 1/5 Arbeitsauftrag Die SuS sortieren Bilder und suchen so zuerst nach eigenen Definitionen zu Tönen, Klängen und Geräuschen, bevor sie anhand der Arbeitsblätter fachlich Klarheit erhalten.
Lehrerinformation 1/5 Arbeitsauftrag Die SuS sortieren Bilder und suchen so zuerst nach eigenen Definitionen zu Tönen, Klängen und Geräuschen, bevor sie anhand der Arbeitsblätter fachlich Klarheit erhalten.
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Wir basteln uns ein Glockenspiel
 So soll es aussehen Wir basteln uns ein Glockenspiel Wie entstehen die Töne? Würde das Glockenspiel am Kopfende angestoßen, so würden damit Logitudinalschwingungen erzeugt. Diese Schwingungen sind allerdings
So soll es aussehen Wir basteln uns ein Glockenspiel Wie entstehen die Töne? Würde das Glockenspiel am Kopfende angestoßen, so würden damit Logitudinalschwingungen erzeugt. Diese Schwingungen sind allerdings
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale?
 Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Mathematik erzeugt grafische Kunstwerke und zauberhafte Videos: Was sind Fraktale? Klaus Kusche Frühjahr 2019 Inhalt Unser Ziel Was ist ein Fraktal? Von linearen geometrischen Abbildungen zu iterierten
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I
 Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Physik & Musik. Gitarre. 1 Auftrag
 Physik & Musik 12 Gitarre 1 Auftrag Physik & Musik Gitarre Seite 1 Gitarre Voraussetzung: Bearbeitung des Postens 2 Monochord Bearbeitungszeit: 20-45 Minuten (je nach Gitarrenerfahrung) Sozialform: Einzel-
Physik & Musik 12 Gitarre 1 Auftrag Physik & Musik Gitarre Seite 1 Gitarre Voraussetzung: Bearbeitung des Postens 2 Monochord Bearbeitungszeit: 20-45 Minuten (je nach Gitarrenerfahrung) Sozialform: Einzel-
Veränderung in gestalteter Beziehung
 Dr. Dr. Strunk Veränderung in gestalteter Beziehung 1 complexity-research.com Veränderung in gestalteter Beziehung Dipl.-Psych. Dr. Dr. Guido Strunk 1. VORTRAG... 2 2. FEEDBACKSYSTEME NICHTLINEALITÄT...
Dr. Dr. Strunk Veränderung in gestalteter Beziehung 1 complexity-research.com Veränderung in gestalteter Beziehung Dipl.-Psych. Dr. Dr. Guido Strunk 1. VORTRAG... 2 2. FEEDBACKSYSTEME NICHTLINEALITÄT...
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Lösung zu Übungsblatt 12
 PN - Physik für Cheiker und Biologen Prof. J. Lipfert WS 208/9 Übungsblatt 2 Lösung zu Übungsblatt 2 Aufgabe Reinhold Messner schwingt in den Bergen: Reinhold Messner öchte den Mount Everest besteigen
PN - Physik für Cheiker und Biologen Prof. J. Lipfert WS 208/9 Übungsblatt 2 Lösung zu Übungsblatt 2 Aufgabe Reinhold Messner schwingt in den Bergen: Reinhold Messner öchte den Mount Everest besteigen
Die Zahl ist das Wesen aller Dinge
 Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raffael 50 -gründete 53v.Chr die religiös-politische Lebensgemeinschaft der Pythagoreer.
Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raffael 50 -gründete 53v.Chr die religiös-politische Lebensgemeinschaft der Pythagoreer.
Bedeutende Theorien des 20. Jahrhunderts
 Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik
Bedeutende Theorien des 20. Jahrhunderts Ein Vorstoß zu den Grenzen von Berechenbarkeit und Erkenntnis Quantenmechanik - Relativitätstheorie - Gravitation - Kosmologie - Chaostheorie - Prädikatenlogik
Lineare und nichtlineare Schwingungen und Wellen
 Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Chaotische Systeme. ViLab. Marian Panten
 Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Chaotische Systeme ViLab Marian Panten Einleitung Geschichte Übersicht Merkmale und Eigenschaften Beispiele und Anwendungen Schluss 26. November 2003 - = Marian Panten - Chaotische Systeme = - 2 Einleitung
Chaos im getriebenen nicht-linearen Pendel
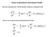 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Einführung in die Physik I. Schwingungen und Wellen 1
 Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
1. Die theoretischen Grundlagen
 Musiktheorie: Tonleitern 1 Inhaltsverzeichnis 1. Die theoretischen Grundlagen 2. Wofür braucht man Tonleitern? 1. Die theoretischen Grundlagen Tonleitern sind sozusagen das Basis-Material in der Musik.
Musiktheorie: Tonleitern 1 Inhaltsverzeichnis 1. Die theoretischen Grundlagen 2. Wofür braucht man Tonleitern? 1. Die theoretischen Grundlagen Tonleitern sind sozusagen das Basis-Material in der Musik.
Kunst und Wissenschaft
 Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
exponentielle Wachstumsphase Abbildung 1: Wachstumskurve einer Bakterienkultur
 Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
Bakterienwachstum Mathematische Schwerpunkte: Teil 1: Folgen; vollständige Induktion; rekursiv definierte Folgen Teil 2: Exponentialfunktionen Teil 3: Extremwertbestimmung; Integration einer rationalen
1 Die logistische Gleichung X t+1 = λx t (1 X t )
 1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
1 Die logistische Gleichung X t+1 = X t (1 X t ) Bisher haben wir Rekursionen mit mehr oder weniger einfachem Verhalten betrachtet; wir konnten entweder eine explizite Lösungsformel aufstellen oder ohne
Kenneth J. Falconer. Fraktale Geometrie. Mathematische Grundlagen und Anwendungen. Aus dem Englischen von Jens Meyer. Mit 98 Abbildungen
 Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
Kenneth J. Falconer Fraktale Geometrie Mathematische Grundlagen und Anwendungen Aus dem Englischen von Jens Meyer Mit 98 Abbildungen Spektrum Akademischer Verlag Heidelberg Berlin Oxford Inhalt Vorwort
1.2 Schwingungen von gekoppelten Pendeln
 0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Konstante Zu- und Abflüsse (Veränderungen)
 Konstante Zu- und Abflüsse (Veränderungen) Unser erstes Modell: Ein (großer) Eimer wird unter einen Wasserhahn gestellt. Der Wasserhahn wird geöffnet und ein konstanter Wasserstrom von 2 Litern pro Minute
Konstante Zu- und Abflüsse (Veränderungen) Unser erstes Modell: Ein (großer) Eimer wird unter einen Wasserhahn gestellt. Der Wasserhahn wird geöffnet und ein konstanter Wasserstrom von 2 Litern pro Minute
FRAKTALE. Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier
 FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
FRAKTALE Eine Dokumentation von Dominik Assmann, Philipp Gewessler und Paul Maier I. Fraktale allgemein a. Mathematischer Algorithmus i. Komplexe Zahlen b. Konvergieren und Divergieren i. Bei Mandelbrotmengen
Die Entdeckung des Chaos
 Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
AU S G A N G S P U N K T
 AU S G A N G S P U N K T Ein Buch Der Weg zum naturtönigen Kultgesang Archimandrit Johannes 2 CDs Naturtöniger Kultgesang Die 8 Kirchentonarten Herausgegeben vom Heiligen Dreifaltigkeitskloster Buchhagen
AU S G A N G S P U N K T Ein Buch Der Weg zum naturtönigen Kultgesang Archimandrit Johannes 2 CDs Naturtöniger Kultgesang Die 8 Kirchentonarten Herausgegeben vom Heiligen Dreifaltigkeitskloster Buchhagen
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Materialien zur Mathematik V
 Joachim Stiller Materialien zur Mathematik V Rekursionsgleichungen und -folgen Additionsfolgen mit f0 = 2 2 0 2 2 4 6 10 2+2-Folge 2 1 3 4 7 11 18 Lucas-Folge (1+3-Folge) 2 2 4 6 10 16 26 2+2-Folge 2 3
Joachim Stiller Materialien zur Mathematik V Rekursionsgleichungen und -folgen Additionsfolgen mit f0 = 2 2 0 2 2 4 6 10 2+2-Folge 2 1 3 4 7 11 18 Lucas-Folge (1+3-Folge) 2 2 4 6 10 16 26 2+2-Folge 2 3
Mathematik und Musik: Fourieranalyse
 Mathematik und Musik: Fourieranalyse Matheseminar JKU Linz WS2015/16 Peter Gangl Linz 5. Februar 2016 1 / 20 Outline 1 Musik mathematisch betrachtet 2 2 / 20 Outline 1 Musik mathematisch betrachtet 2 2
Mathematik und Musik: Fourieranalyse Matheseminar JKU Linz WS2015/16 Peter Gangl Linz 5. Februar 2016 1 / 20 Outline 1 Musik mathematisch betrachtet 2 2 / 20 Outline 1 Musik mathematisch betrachtet 2 2
Schnelle Fouriertransformation (FFT)
 Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Vortragsthemen. Reelle Dynamik
 Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
Vortragsthemen Jede Teilnehmende ist für ein Thema verantwortlich, das sie im Kurs vorstellen wird. Es gibt also insgesamt 15 Vorträge, 4 aus den Gebieten Reelle bzw. Komplexe Dynamik und 7 aus dem Gebiet
Erfüllt eine Funktion f für eine feste positive Zahl p und sämtliche Werte t des Definitionsbereichs die Gleichung
 34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
ZAHLEN UND TÖNE Uwe Fischer
 1 ZAHLEN UND TÖNE Uwe Fischer [Originaltext; 2006 gescannt aus Bild der kosmischen Evolution ; 1971; H. 1; S. 36-45. Leicht überarbeitet; u.a. Layout etwas geändert.] Es wird gezeigt, wie durch systematisches
1 ZAHLEN UND TÖNE Uwe Fischer [Originaltext; 2006 gescannt aus Bild der kosmischen Evolution ; 1971; H. 1; S. 36-45. Leicht überarbeitet; u.a. Layout etwas geändert.] Es wird gezeigt, wie durch systematisches
Abbildung 1: Feigenbaum-Diagramm
 Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
Kursübersicht Im folgenden findet Ihr Zusammenfassungen zu jedem der drei Teilgebiete, die wir im Kurs behandeln möchten. Die genaue Gewichtung der drei Gebiete ist noch nicht festgelegt und hängt von
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Mathematik 1 für Naturwissenschaften
 Hans Walser Mathematik 1 für Naturwissenschaften Modul 111 Systeme von Differenzialgleichungen Luchs und Hase Hans Walser: Modul 111, Systeme von Differenzialgleichungen. Luchs und Hase ii Inhalt 1 Lineare
Hans Walser Mathematik 1 für Naturwissenschaften Modul 111 Systeme von Differenzialgleichungen Luchs und Hase Hans Walser: Modul 111, Systeme von Differenzialgleichungen. Luchs und Hase ii Inhalt 1 Lineare
Das Wahre Gute Schöne in Kunst und Wissenschaft
 Das Wahre Gute Schöne in Kunst und Wissenschaft Harmonische Symmetrie oder dynamischer Symmetriebruch? Gerhard Franz 30. November 2011 Thematik: Der Begriff der Schönheit wird auf der Grundlage der Platonschen
Das Wahre Gute Schöne in Kunst und Wissenschaft Harmonische Symmetrie oder dynamischer Symmetriebruch? Gerhard Franz 30. November 2011 Thematik: Der Begriff der Schönheit wird auf der Grundlage der Platonschen
Robert Denk Proseminar Analysis WS 2016/17
 1. Inhalt des Proseminars 1 Robert Denk 21.07.2016 Proseminar Analysis WS 2016/17 1. Inhalt des Proseminars Die Grundidee einer Fourierreihe besteht darin, eine Funktion als Überlagerung von Schwingungen,
1. Inhalt des Proseminars 1 Robert Denk 21.07.2016 Proseminar Analysis WS 2016/17 1. Inhalt des Proseminars Die Grundidee einer Fourierreihe besteht darin, eine Funktion als Überlagerung von Schwingungen,
[c] = 1 m s. Erfolgt die Bewegung der Teilchen senkrecht zur Ausbreitungsrichtung der Welle, dann liegt liegt Transversalwelle vor0.
![[c] = 1 m s. Erfolgt die Bewegung der Teilchen senkrecht zur Ausbreitungsrichtung der Welle, dann liegt liegt Transversalwelle vor0. [c] = 1 m s. Erfolgt die Bewegung der Teilchen senkrecht zur Ausbreitungsrichtung der Welle, dann liegt liegt Transversalwelle vor0.](/thumbs/51/27668762.jpg) Wellen ================================================================== 1. Transversal- und Longitudinalwellen ------------------------------------------------------------------------------------------------------------------
Wellen ================================================================== 1. Transversal- und Longitudinalwellen ------------------------------------------------------------------------------------------------------------------
Lösung der harmonischen Oszillator-Gleichung
 Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
a) Anzahl Löcher für grosse Terz: 45 Anzahl Löcher für kleine Terz 43.2, das ist keine ganze Zahl, also nicht möglich. Anzahl Löcher für Quinte: 54
 Physik anwenden und verstehen: Lösungen. Akustik 4 Orell Füssli Verlag AG. Akustik Intervalle und Stimmung 4 a) Anzahl Löher ür grosse Terz: 45 Anzahl Löher ür kleine Terz 4., das ist keine ganze Zahl,
Physik anwenden und verstehen: Lösungen. Akustik 4 Orell Füssli Verlag AG. Akustik Intervalle und Stimmung 4 a) Anzahl Löher ür grosse Terz: 45 Anzahl Löher ür kleine Terz 4., das ist keine ganze Zahl,
Ökologische Gleichungen für zwei Spezies
 Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Tonhöhen in der Musik. Horst Eckardt, München 14. Juli 2013
 Tonhöhen in der Musik Horst Eckardt, München 14. Juli 2013 Inhalt Physik der Tonerzeugung (Akustik) Intervalle, Stimmung und Harmonik Besonderheiten der Musikgeschichte Tonhöhen und Solfeggio-Frequenzen
Tonhöhen in der Musik Horst Eckardt, München 14. Juli 2013 Inhalt Physik der Tonerzeugung (Akustik) Intervalle, Stimmung und Harmonik Besonderheiten der Musikgeschichte Tonhöhen und Solfeggio-Frequenzen
Differentialgleichungen I
 Differentialgleichungen I Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 5. Januar 2009 Beachtenswertes Die Veranstaltung
Differentialgleichungen I Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 5. Januar 2009 Beachtenswertes Die Veranstaltung
Systemtheorie. Vorlesung 6: Lösung linearer Differentialgleichungen. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Chaotische Systeme Der Weg ins Chaos Kontrollmethoden Probleme bei großen Systemen Zusammenfassung Quellen. Chaotische Systeme
 Der Weg ins Chaos und zurück Otto-von-Guericke- Fakultät für Informatik Institut für Simulation und Grafik Das virtuelle Labor 20.12.2007 Wo treffen wir auf chaotische Systeme Herzschlag Populationsentwicklungen
Der Weg ins Chaos und zurück Otto-von-Guericke- Fakultät für Informatik Institut für Simulation und Grafik Das virtuelle Labor 20.12.2007 Wo treffen wir auf chaotische Systeme Herzschlag Populationsentwicklungen
Differenzialgleichungen
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 30. Januar 2008 (System von) Differenzialgleichung(en) Schwingungsgleichung Newtonsche Mechanik Populationsdynamik...DGLn höherer Ordnung auf
Vorbereitung. (1) bzw. diskreten Wellenzahlen. λ n = 2L n. k n = nπ L
 Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Physik & Musik. Klavier. 1 Auftrag
 Physik & Musik 11 Klavier 1 Auftrag Physik & Musik Klavier Seite 1 Klavier Bearbeitungszeit: 45 Minuten Sozialform: Einzel- oder Partnerarbeit Einleitung: Obertöne Die meisten in der Musik verwendeten
Physik & Musik 11 Klavier 1 Auftrag Physik & Musik Klavier Seite 1 Klavier Bearbeitungszeit: 45 Minuten Sozialform: Einzel- oder Partnerarbeit Einleitung: Obertöne Die meisten in der Musik verwendeten
Inhaltsverzeichnis. I.Einführung II.Versuch III.Arbeitsblatt1 IV.Arbeitsblatt2 V.Verbesserungsvorschläge
 Inhaltsverzeichnis I.Einführung II.Versuch III.Arbeitsblatt IV.Arbeitsblatt V.Verbesserungsvorschläge I.Einführung Dauer: 0min Ziel: Vorstellung der Pythagoräer Material: Vortrag ohne Hilfsmittel In dem
Inhaltsverzeichnis I.Einführung II.Versuch III.Arbeitsblatt IV.Arbeitsblatt V.Verbesserungsvorschläge I.Einführung Dauer: 0min Ziel: Vorstellung der Pythagoräer Material: Vortrag ohne Hilfsmittel In dem
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Menge von (mindestens drei) gleichzeitig erklingenden Tönen. ein Merkmal einer Tonfunktion, mathematische Entsprechung der Tonstärke.
 GLOSSAR Akkord Amplitude äquivalente Intervalle Diesis Menge von (mindestens drei) gleichzeitig erklingenden Tönen. ein Merkmal einer Tonfunktion, mathematische Entsprechung der Tonstärke. zwei Intervalle,
GLOSSAR Akkord Amplitude äquivalente Intervalle Diesis Menge von (mindestens drei) gleichzeitig erklingenden Tönen. ein Merkmal einer Tonfunktion, mathematische Entsprechung der Tonstärke. zwei Intervalle,
Feigenbaum, Chaos und die RG
 Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
PHYSIK. Allgemeine Bildungsziele. Richtziele. Grundkenntnisse
 PHYSIK Allgemeine Bildungsziele Physik erforscht mit experimentellen und theoretischen Methoden die messend erfassbaren und mathematisch beschreibbaren Erscheinungen und Vorgänge in der Natur. Der Physikunterricht
PHYSIK Allgemeine Bildungsziele Physik erforscht mit experimentellen und theoretischen Methoden die messend erfassbaren und mathematisch beschreibbaren Erscheinungen und Vorgänge in der Natur. Der Physikunterricht
Die Blockflöte akustisch beleuchtet. Hans-Christof Maier
 Die Blockflöte akustisch beleuchtet Hans-Christof Maier Die Tonerzeugung Schneidenton Schwingungserzeugung am Labium Resonanzen Schwingungsverstärkung im Flötenrohr Der Schneidenton Ein Luftblatt wird
Die Blockflöte akustisch beleuchtet Hans-Christof Maier Die Tonerzeugung Schneidenton Schwingungserzeugung am Labium Resonanzen Schwingungsverstärkung im Flötenrohr Der Schneidenton Ein Luftblatt wird
Konjunkturtheorie. Prof. Dr. Kai Carstensen, LMU und ifo Institut Steffen Elstner, ifo Institut
 Konjunkturtheorie Prof. Dr. Kai Carstensen, LMU und ifo Institut Steffen Elstner, ifo Institut Deterministische Differenzengleichung 2. Ordnung 2 Deterministische Differenzengleichung 2. Ordnung Eine lineare
Konjunkturtheorie Prof. Dr. Kai Carstensen, LMU und ifo Institut Steffen Elstner, ifo Institut Deterministische Differenzengleichung 2. Ordnung 2 Deterministische Differenzengleichung 2. Ordnung Eine lineare
Vorlesung 1 Akustik (Fortsetzung)
 Vorlesung 1 Akustik (Fortsetzung) Zupfinstrumente Tasteninstrumente Partiturkunde Akustik Idiophone und Membranobphone Streichinstrumente Holzblasinstrumente Blechblasinstrumente 2018 Manfred Dings Wellenlänge,
Vorlesung 1 Akustik (Fortsetzung) Zupfinstrumente Tasteninstrumente Partiturkunde Akustik Idiophone und Membranobphone Streichinstrumente Holzblasinstrumente Blechblasinstrumente 2018 Manfred Dings Wellenlänge,
Seminar Akustik. Aufgaben zu Teil 1 des Skripts Uwe Reichel, Phil Hoole
 Seminar Akustik. Aufgaben zu Teil des Skripts Uwe Reichel, Phil Hoole Welche Kräfte wirken auf ein schwingendes Teilchen?! von außen angelegte Kraft (z.b. Glottisimpulse)! Rückstellkräfte (Elastizität,
Seminar Akustik. Aufgaben zu Teil des Skripts Uwe Reichel, Phil Hoole Welche Kräfte wirken auf ein schwingendes Teilchen?! von außen angelegte Kraft (z.b. Glottisimpulse)! Rückstellkräfte (Elastizität,
1.3 Zweidimensionale Systeme
 132 KAPITEL IV. QUALITATIVE THEORIE UND DYNAMISCHE SYSTEME Im Fall a 3 > 0 ist das Gleichgewicht asymptotisch stabil. Für a 2 3 > 4a 1a 2 haben wir < < 0 und es liegt ein stabiler Knoten vor (siehe den
132 KAPITEL IV. QUALITATIVE THEORIE UND DYNAMISCHE SYSTEME Im Fall a 3 > 0 ist das Gleichgewicht asymptotisch stabil. Für a 2 3 > 4a 1a 2 haben wir < < 0 und es liegt ein stabiler Knoten vor (siehe den
TAG DER MATHEMATIK. Kann man die Form einer Trommel hören? Prof. Dr. Daniel Grieser
 5. TAG DER MATHEMATIK Kann man die Form einer Trommel hören? Prof. Dr. Daniel Grieser Die 3 Grundgesetze der Schwingungen Die 3 Grundgesetze der Schwingungen 1. Es gibt gewisse elementare Schwingungsformen
5. TAG DER MATHEMATIK Kann man die Form einer Trommel hören? Prof. Dr. Daniel Grieser Die 3 Grundgesetze der Schwingungen Die 3 Grundgesetze der Schwingungen 1. Es gibt gewisse elementare Schwingungsformen
Programmierung und Angewandte Mathematik
 Programmierung und Angewandte Mathematik C++ /Scilab Programmierung und Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens SS 2012 Inhalt Steckbrief der Funktion
Programmierung und Angewandte Mathematik C++ /Scilab Programmierung und Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens SS 2012 Inhalt Steckbrief der Funktion
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
b6 6 b7 7 1 b6 6 b7 7 1 b3 3 4 #4 b6 6 b7 1 b2 2 b3 3 #4 5 b6 6 b7 7 #4 5 b6 6 b7 7
 Theorie Auszüge: Die Anordnung der Töne am Gitarrenhals sind wie der Quintenzirkel aufgebaut und macht die Gitarre dadurch mit zu dem vielseitigsten Instrument überhaupt. Durch die Quartenstimmung (Umkehrung
Theorie Auszüge: Die Anordnung der Töne am Gitarrenhals sind wie der Quintenzirkel aufgebaut und macht die Gitarre dadurch mit zu dem vielseitigsten Instrument überhaupt. Durch die Quartenstimmung (Umkehrung
Untersuchungen am magnetischen Doppelpendel - Spaceball
 Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: Ort: Geschwindigkeit:
 C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
C7 Differentgleichungen (DG) C7.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel
Fourier Reihe. Fourier Transformation. Ma 2 Lubov Vassilevskaya, SS 2008
 Fourier Reihe Fourier Transformation Entwicklung einer Funktion in eine Potenzreihe Eine beliebig oft differenzierbare Funktion f (x) kann in eine unendliche Reihe von Potenzfunktionen x n entwickelt werden
Fourier Reihe Fourier Transformation Entwicklung einer Funktion in eine Potenzreihe Eine beliebig oft differenzierbare Funktion f (x) kann in eine unendliche Reihe von Potenzfunktionen x n entwickelt werden
Höhere Mathematik III
 Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
v= f x λ 344= f x 4 f= 86 Hz (Großes F) P= 1/f 1/ , s = 0,00001ms W= F x s W= 30 x 400 W= 12000Nm 12000J
 Auflösung Wellen & Schwingungen Wenn eine Orgelpfeife für eine Wellenlänge von 4m konstruiert wird, welche Frequenz wird dann ihr Klang haben? (T = 20 ) v= f x λ 344= f x 4 f= 86 Hz (Großes F) Wenn die
Auflösung Wellen & Schwingungen Wenn eine Orgelpfeife für eine Wellenlänge von 4m konstruiert wird, welche Frequenz wird dann ihr Klang haben? (T = 20 ) v= f x λ 344= f x 4 f= 86 Hz (Großes F) Wenn die
Herbert Zeitler Wolfgang Neidhardt. Fraktale und Chaos. Eine Einführung. Wissenschaftliche Buchgesellschaft Darmstadt
 Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
Herbert Zeitler Wolfgang Neidhardt Fraktale und Chaos Eine Einführung Wissenschaftliche Buchgesellschaft Darmstadt f INHALT Einleitung 1 I. Iteration reeller Funktionen und Chaos in dynamischen Systemen.
Zufälle gibt s, oder gibt s die nicht? Martin Köhler Science Café Hamburg, 25. Juni 2014
 Zufälle gibt s, oder gibt s die nicht? Martin Köhler Science Café Hamburg, 25. Juni 2014 Grundfrage und Gliederung Gibt es einen echten Zufall, oder wissen wir einfach nicht genug für eine exakte Vorhersage?
Zufälle gibt s, oder gibt s die nicht? Martin Köhler Science Café Hamburg, 25. Juni 2014 Grundfrage und Gliederung Gibt es einen echten Zufall, oder wissen wir einfach nicht genug für eine exakte Vorhersage?
9. Akustik. I Mechanik. 12. Vorlesung EP. 7. Schwingungen 8. Wellen 9.Akustik
 12. Vorlesung EP I Mechanik 7. Schwingungen 8. Wellen 9.Akustik Versuche: Stimmgabel und Uhr ohne + mit Resonanzboden Pfeife Schallgeschwindigkeit in Luft Versuch mit Helium Streichinstrument Fourier-Analyse
12. Vorlesung EP I Mechanik 7. Schwingungen 8. Wellen 9.Akustik Versuche: Stimmgabel und Uhr ohne + mit Resonanzboden Pfeife Schallgeschwindigkeit in Luft Versuch mit Helium Streichinstrument Fourier-Analyse
