Deterministisches Chaos - Versuch einer neuen Begriffsbestimmung
|
|
|
- Gert Winkler
- vor 6 Jahren
- Abrufe
Transkript
1 Deterministisches Chaos - Versuch einer neuen Begriffsbestimmung Ludwig Pohlmann AdW der DDR, Zentralinstitut für physikalische Chemie, Berlin, Rudower Chaussee 5, DDR-1199 Begriffe haben ihre Dynamik, und diese ist um so bewegter, je mehr auch der Begriffsgegenstand und die Theorie, die mit ihm verbunden ist, im Fluß ihrer Entwicklung sind. Das trifft auch für einen Begriff zu, der eng mit der stürmischen Entwicklung der Lehre von der Selbstorganisation (Synergetik, Irreversible Thermodynamik) verbunden ist und der unter dem Namen "Deterministisches Chaos" bekannt wurde. (Für weiterführende Zitate und Originalarbeiten sei hier auf die Artikelfolge "Singuläre Determiniertheit" /Wiss. Z. d. MLU, Mat.-nat. Reihe, 1987, 1988, 1989/ verwiesen.) Geboren wurde dieser Begriff in der Mathematik, allerdings in einem Gebiet, welches über die Brücke der Modellbildung mit den Naturwissenschaften in engem Kontakt stand: in der Theorie dynamischer Systeme. So war es auch ein Mathematiker, der im Rahmen meteorologischer Forschungen versuchte, ein einfaches, berechenbares Differentialgleichungsmodell der Luftzirkulation herzuleiten und (numerisch) zu lösen (E. LORENZ /J.Atmos.Sci. 20(1963)130/). Bei der Lösung merkte Lorenz aber zu seiner Überaschung, daß die Trajektorien des Systems völlig regellos waren, also keine Periodizitäten aufwiesen. Deshalb nannte er dieses Phänomen auch erst nur eine "Deterministische nichtperiodische Strömung". Mit dem "deterministisch" unterstrich er dabei nur die Tatsache, daß es sich um normale Differentialgleichungen ohne Zufallsterme handelte, die bekanntlich für jeden Satz von Anfangsbedingungen eine eindeutige Lösung (Bahnkurve) besitzen. 1
2 Bald wurde daraus das "Deterministische Chaos", ein Begriff, der wohl weniger exakt seinen Gegenstand beschreibt, als vielmehr die Überraschung seiner Entdecker über die Existenz völlig irregulärer Lösungen von deterministischen mathematischen Gleichungen - die ihrerseits wieder als Modelle für reale Bewegungen standen - zum Ausdruck bringt. Heute wissen wir, daß diese Erscheinung, die wir der Kürze halber - bis wir zur genaueren Begriffsbestimmung kommen - einfach als "Chaos" bezeichnen wollen, kein esotherisches mathematisches Ergebnis ist, sondern daß sie in sehr vielen Prozessen in Natur, Gesellschaft und Denken (Turbulenz in der Flüssigkeitsströmung, Wetterentwicklung, Schwankungen des Erdmagnetfeldes u.a.m.) auftritt. Eine immer weiter auffächernde Forschung bringt dabei ständig neue und überraschende Eigenschaften des Chaos an den Tag. Das Chaos zeigt sich dabei strukturell und prozessual immer deutlicher als eine hochkomplizierte Form von Ordnung. Ohne auf diese Eigenschaften hier näher eingehen zu können, sei auf zwei der grundlegendsten hingewiesen: 1. Die chaotische Bewegung ist begrenzt und das Chaos-Gebiet zieht die Tajektorien aus der Umgebung an, es ist ein Attraktor. 2. Die chaotische Bewegung hängt empfindlich von den Anfangsbedingungen ab, so daß sich auch ganz eng benachbarte Bahnen im allgemeinen mit exponentieller Geschwindigkeit voneinander entfernen (Hypersensitivität). Aus disen beiden Eigenschaften, sowie aus er Tatsache, daß sich die Lösungen eines Differentialgleichungssystems niemals schneiden können, folgt zwangsläufig eine Bewegung, die zwar begrenzt ist, aber niemals zur Ruhe kommt und auch nie in eine periodische oder quasiperiodische Bahn einmünden kann. Die Bahn ist folglich völlig aperiodisch und iregulär - eben "chaotisch". Hier sind wir aber an einem Punkt angelangt, wo sich eine weitere Begriffspräzisierung als nötig erweist. Denn durch diese neuen Eigenschaften des Chaos erweist sich die übliche Praxis der mathematischphysikalischen Begriffsbildung selbst als inadäquat. Bisher war es möglich, gute mathematische Modelle bestimmter physikalischer Prozesse als idealtypische Charakteristika dieser Prozesse zu verstehen. Denn 2
3 in normalen, nichtsensitiven realen Systemen sind die kleinen Störungen von außen und innen, die prinzipiell nicht vollständig eliminierbar sind, nicht wesentlich für die Bewegung des Systems. Deshalb kann die modellierende mathematische Beschreibung, die von solchen Störungen in irgend einem Maße immer abstrahieren muß, trotzdem adäquat sein: Da die Hypersensitivität fehlt, können die reale und die mathematische Bahnkurve beliebig lange beliebig nahe beieinander bleiben, d.h. eine anfänglich gute Approximation der realen Bewegung bleibt auch eine gute Approximation. Gerade diese Korrespondenz von Modell und realem System kann in dieser Form für chaotische Systeme nicht mehr gelten, da sie ja hypersensitiv sind. Konnte man noch in der klassischen (vorchaotischen) Mechanik mit dem Begriff der Bahn eines Massenpunktes gleichzeitig sowohl den realen Prozeß (die Bahn des Schwerpunktes eines Körpers), als auch die zeitliche Lösung der entsprechenden newtonschen Bewegungsgleichung verstehen, ist dies bei der chaotischen Bewegung nicht mehr möglich. Denn hier kann jede kleine Störung einen wesentlichen Charakter bekommen, wenn sie nur im hypersensitiven Bereich auftritt. Aus dem Gesagten wird deutlich, daß in der umfangreichen Literatur zum Thema Chaos eigentlich die Rede von zwei verschiedenen Chaos-Erscheinungen ist: 1. Zum einen handelt es sich um das rein mathematische Chaos, d.h. um die entsprechenden mathematischen Gleichungen, theoretisch-mathematisch betrachtet. Da es per definitionem in den (nichtstochstischen) Differential- oder Differenzengleichungen keinen Zufall geben kann und die Existenz eindeutiger Lösungen bewiesen ist, so ist auch die "mathematische" zeitliche Bewegung streng deterministisch. Diese Bewegung ist zwar irregulär und nichtperiodisch, aber wenn sie zum zweiten Male an genau demselben mathematischen Punkt gestartet wird, so wird sie auch Punkt für Punkt die vorhergehende Bewegung wiederholen. Diese Bewegung wollen wir als ideales Chaos bezeichnen. Viele mathematische Arbeiten, in denen mit analytischen und qualitativen Methoden Sätze über das Chaos bewiesen werden, beziehen sich auf dieses idale Chaos (z.b. von SMALE, RUELLE, TAKENS, ECKMANN). 2. Zum anderen handelt es sich um das Chaos, welches wir als makroskopischen Prozeß selbst erleben, selbst sehen können, sei es in der turbulenten Flüssigkeitsbewegung oder auch beim numerischen Lösen 3
4 chaotischer Gleichungen (also des idealen Chaos!) auf dem Computer. Dieses Chaos als realer Prozeß ist notwendigerweise immer kleinen Störungen von innen (Fluktuationen, Rundungsfehler) und außen ausgesetzt. Deshalb werden in Bereichen der Hypersensitivität diese Störungen, und sind sie auch noch so klein, dazu führen, daß die Bahn wesentlich gestört wird, d.h. die ursprüngliche, nach der Störung nur noch fiktive, Bahn und die neue reale Bahn werden sich mit exponentieller Geschwindigkeit voneinander entfernen. Und dieser Störprozeß passiert immer wieder, solange nur die chaotische Bewegung anhält. Hier ist also das Rauschen, der Zufall wesentlich und untrennbar mit der realen chaotischen Bewegung verbunden. In der Realität gibt es keine chaotische (allgemeiner, keine instabile) Bewegung ohne die wesentliche Rolle des Zufalls. Das chaotische System ist hypersensitiv, es transformiert dadurch gleichsam den Zufall, das mikroskopische Rauschen auf ein makroskopisch-dynamisches Niveau hinauf. Entsprechend läuft auch ein ständiger Informationsstrom: Die ursprünglichen Anfangsbedingungen werden immer wieder vergessen und dafür schöpft das System ständig neu Information aus dem Mikroniveau für die weitere Bewegung. Aus diesen Gründen erscheint es sinnvoll, diese Bewegung als reales Chaos zu bezeichnen. Alle experimentellen Chaosforschungen einschließlich aller numerischen mathematischen Untersuchungen beziehen sich auf das reale Chaos. Diese Chaos kann man aber, im Unterschied zum idealen Chaos, nicht mehr als "deterministisch" bezeichnen, da es, wie wir betonten, intrinsich mit dem Zufall als objektiver Kategorie (Störung, Fluktuation) verbunden ist. Beide Formen des Chaos sind von wissenschaftlichem Interesse. Zwischen ihnen gibt es immer noch viele Gemeinsamkeiten, so daß die Ergebnisse, die für die eine Form des Chaos gewonnen wurden, von heuristischer Bedeutung für die andere Form sein werden. Aber jede dieser möglichen Übereinstimmungen in den Eigenschaften muß separat bewiesen werden. Denn es gibt auch wesentliche Unterschiede. Wenn diese nicht beachtet werden, kann es zu großer Konfusion kommen. Einer dieser wichtigen Unterschiede soll hier stellvertretend angeführt werden: Von einigen Chaos-Forschern (z.b. JENSEN, CHIRIKOV) wird behauptet, die Komplexität, die Irregularität einer chaotischen Trajektorie sei nichts anderes als die dynamische Umsetzung (Interpretation) der Information des Anfangspunktes, der als reelle Zahl ja im allg. eine unendliche Anzahl von Dezimalstellen enthält, in die Bewegung. So wird also eine nichtperiodische unendliche Dezimalzahl (also eine irrationale Zahl) in eine unendliche 4
5 nichtperiodische Bewegung "entrollt". Diese Behauptung stimmt - allerdings nur für das ideale Chaos. Beim realen Chaos kann es, wenn überhaupt, nur für einen endlichen Zeitraum, zwischen zwei hypersensitiven Phasen (wenn solche Lücken auftreten), gelten. Das o.g. "Vergessen" des Systems wird die Information des Startpunktes in einer endlichen Zeit für das System irrelevant werden lassen. Eine andere wichtige Eigenschaft, die jedoch nur dem realen Chaos zukommt, besteht in dem endlichen Vorhersagehorizont (LIGHTHILL, /Proc. Roy. Soc. Ser. A407 (1986)35/) bzw. in der Existenz einer makroskopischen Unbestimmtheitsrelation (NIEDERSEN u. POHLMANN 1989). Inteessant ist auch eine andere Analogie zur Quantenmechanik: Jede Messung realer chaotischer Prozesse kann diese in ihrem Verlauf wesentlich stören und damit verfälschen (KRAVCOV, /Uspekhi fis. nauk 158(1989)93/). Zusammenfassend läßt sich sagen, daß der Begriff des "deterministischen Chaos" nicht mehr als exakter wissenschaftlicher Begriff verwendet werden sollte, da er, zumindest zum Teil, nicht zutreffend ist. Man sollte deshalb der Entwicklung in der neueren Chaos-Literatur folgen und einfach von "Chaos" sprechen. Drüber hinaus macht sich aber die Unterscheidung in "ideales" und "reales" Chaos notwendig, wie oben ausgeführt werden konnte. Dabei sind die Beziehungen zwischen beiden Formen des Chaos alles andere als trivial und können noch viele Überraschungen bergen. Diese notwendig gewordene Präzisierung eines allgemeinen wissenschaftlichen Begriffes kann aber auch Rückwirkungen auf die Definition des philosophischen Begriffs des objektiven Zufalls haben, denn der geht ja unter anderem auch von den Erfahrungen der vorchaotischen Physik aus, wonach kleine Störungen unwesentlich für die Systemdynamik und deshalb zufällig sind! Was die Naturwissenschaft und die Philosophie vor allem interessieren wird, ist das reale Chaos. Das ideale Chaos ist mehr Untersuchungsgegenstand der reinen Mathematik (dynamische Systeme), aber wichtige dort gewonnene Erkenntnisse können von großer heuristischer Bedeutung für die Erforschung des realen Chaos sein. Das reale Chaos kann übrigens auch Untersuchungsgegenstand der Mathematik sein, nur handelt es sich dann zum einen um stochastisch gestörte dynamische Systeme (z.b. Langevin- Gleichung), also um keine dynamischen Systeme im engeren Sinne, zum anderen um die Theorie invarianter Maße (z.b. Wahrscheinlichkeitsmaße) auf Attraktoren dynamischer Systeme. Diese Theorien sind aber noch viel weniger entwickelt als die Theorie der dynamischen Systeme. Berlin, den
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
llya Prigogine VOM SEIN ZUM WERDEN Zeit und Komplexität in den Naturwissenschaften Überarbeitete und erweiterte Neuausgabe
 llya Prigogine VOM SEIN ZUM WERDEN Zeit und Komplexität in den Naturwissenschaften Überarbeitete und erweiterte Neuausgabe Aus dem Englischen von Friedrich Griese Piper München Zürich Inhaltsverzeichnis
llya Prigogine VOM SEIN ZUM WERDEN Zeit und Komplexität in den Naturwissenschaften Überarbeitete und erweiterte Neuausgabe Aus dem Englischen von Friedrich Griese Piper München Zürich Inhaltsverzeichnis
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Modell der Punktmasse
 Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Physik eine empirische Wissenschaft
 Experimentalphysik A 1. Einleitung Physik eine empirische Wissenschaft Die Naturerscheinungen laufen nicht regellos ab, sondern sie werden durch Naturgesetze gesteuert. Die Physik befaßt sich mit der Erforschung
Experimentalphysik A 1. Einleitung Physik eine empirische Wissenschaft Die Naturerscheinungen laufen nicht regellos ab, sondern sie werden durch Naturgesetze gesteuert. Die Physik befaßt sich mit der Erforschung
Fragen zu Kapitel III Seite 1 III
 Fragen zu Kapitel III Seite 1 III Grundbegriffe der klassischen Mechanik Fragen 3.1 bis 3.8 Zur Beantwortung der Fragen benötigen Sie folgende Daten Masse der Erde 5,974 10 4 kg Erdradius 6371 km Erdbeschleunigung
Fragen zu Kapitel III Seite 1 III Grundbegriffe der klassischen Mechanik Fragen 3.1 bis 3.8 Zur Beantwortung der Fragen benötigen Sie folgende Daten Masse der Erde 5,974 10 4 kg Erdradius 6371 km Erdbeschleunigung
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Gewöhnliche Differentialgleichungen: Einleitung
 Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Gewöhnliche Differentialgleichungen: Einleitung Die Sprache des Universums ist die Sprache der Differentialgleichungen. 1-E1 Faszinierender Anwendungsreichtum cc 1-E2 Wie verstanden die Alten das Naturgesetz?
Chaos im getriebenen nicht-linearen Pendel
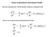 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Einführung in die Grundlagen der Theoretischen Physik
 Günther Ludwig Einführung in die Grundlagen der Theoretischen Physik Band 1: Raum, Zeit, Mechanik 2., durchgesehene und erweiterte Auflage Vieweg Inhalt Zur Einführung 1 /. Was theoretische Physik nicht
Günther Ludwig Einführung in die Grundlagen der Theoretischen Physik Band 1: Raum, Zeit, Mechanik 2., durchgesehene und erweiterte Auflage Vieweg Inhalt Zur Einführung 1 /. Was theoretische Physik nicht
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Nichtlineare Prozesse in der Elektrochemie II
 Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen:
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Westfälische Wilhelms-Universität Münster Fachbereich Physik. Quantenlogik. Martin Kohn Münster,
 Westfälische Wilhelms-Universität Münster Fachbereich Physik Quantenlogik Martin Kohn martin-kohn@gmx.de Münster, 14.09.2009 1 Einleitung Die Quantenlogik beschreibt die Anwendung der klassischen, alltäglichen
Westfälische Wilhelms-Universität Münster Fachbereich Physik Quantenlogik Martin Kohn martin-kohn@gmx.de Münster, 14.09.2009 1 Einleitung Die Quantenlogik beschreibt die Anwendung der klassischen, alltäglichen
Praktikumssemesterarbeit für Numerik Aufgabe 1 HU-Berlin, Sommersemester 2005
 Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen:
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und der Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p,
Bohm sche Mechanik. Determinismus in der Quantenmechanik. Sven Köppel Mirko Pohland. 9. Juni, Fachbereich 13, Physik
 Determinismus in Quantenmechanik Sven Köppel Mirko Pohland Fachbereich 13, Physik 9. Juni, 2011 Ergebnisse an landläufigen Quantenmechanik ähnlich wie in Thermodynamik wäre es möglich, dass die Quantenmechanik
Determinismus in Quantenmechanik Sven Köppel Mirko Pohland Fachbereich 13, Physik 9. Juni, 2011 Ergebnisse an landläufigen Quantenmechanik ähnlich wie in Thermodynamik wäre es möglich, dass die Quantenmechanik
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Interpretationen des quantenmechanischen Formalismus
 Interpretationen des quantenmechanischen Formalismus Reinhold A. Bertlmann Philipp Köhler & VO Fallstudien zur naturwissenschaftlichen Erkenntnis Quantentheorie 6. Dezember 2010 Grundlegende Fragen Warum
Interpretationen des quantenmechanischen Formalismus Reinhold A. Bertlmann Philipp Köhler & VO Fallstudien zur naturwissenschaftlichen Erkenntnis Quantentheorie 6. Dezember 2010 Grundlegende Fragen Warum
Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau)
 Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau) Vorbemerkung Die nachfolgenden Darstellungen dienen
Anwendung der Infinitesimalrechnung in der Physik (besonders geeignet für Kernfach Physik Kurshalbjahr Mechanik Anforderung auf Leistungskursniveau) Vorbemerkung Die nachfolgenden Darstellungen dienen
X.4 Elektromagnetische Wellen im Vakuum
 X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Dass die Rotation eines konservativen Kraftfeldes null ist, folgt direkt aus der Identität C 1 C 2 C 2 C 1
 I.1 Grundbegriffe der newtonschen Mechanik 11 I.1.3 c Konservative Kräfte Definition: Ein zeitunabhängiges Kraftfeld F ( r) wird konservativ genannt, wenn es ein Skalarfeld (3) V ( r) gibt, das F ( r)
I.1 Grundbegriffe der newtonschen Mechanik 11 I.1.3 c Konservative Kräfte Definition: Ein zeitunabhängiges Kraftfeld F ( r) wird konservativ genannt, wenn es ein Skalarfeld (3) V ( r) gibt, das F ( r)
Philosophische Aspekte der Modernen Physik
 Philosophische Aspekte der Modernen Physik Forum Scientiarum SS 01 Kurt Bräuer 14.06.01 www.kbraeuer.de 1 Bewusstsein und Physik Im Bewusstsein werden Weltinhalte ausgewählt exzerptiert erkannt mit Gedächtnisinhalten
Philosophische Aspekte der Modernen Physik Forum Scientiarum SS 01 Kurt Bräuer 14.06.01 www.kbraeuer.de 1 Bewusstsein und Physik Im Bewusstsein werden Weltinhalte ausgewählt exzerptiert erkannt mit Gedächtnisinhalten
Poisson-Klammern. Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G":
 Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p, q,
Poisson-Klammern Betrachte zwei physikalische Grössen, die von den Koordinaten, Impulsen und Zeit abhängen: Def: "Poisson-Klammer von F und G": Einfachste Beispiele: im Hamilton-Formalismus sind p, q,
Auffrischungskurs Physik-Kurs 20h VHS Jena. Dozent: Silvio Fuchs 22. September 2008
 Auffrischungskurs Physik-Kurs 20h VHS Jena Dozent: Silvio Fuchs 22. September 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Physik........................................... 3 1.2 Grundlegende Arbeitsweise...............................
Auffrischungskurs Physik-Kurs 20h VHS Jena Dozent: Silvio Fuchs 22. September 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Physik........................................... 3 1.2 Grundlegende Arbeitsweise...............................
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
1. Einleitung. 2. Zur Person
 Moritz Schlick: Naturgesetze und Kausalität Seminar über philosophische Aspekte in der Physik WS 2007/08 Seminarleitung: Prof. Dr. G. Münster Dr. C. Suhm Vortragender: Johannes Greber 13. 11. 2007 1. Einleitung
Moritz Schlick: Naturgesetze und Kausalität Seminar über philosophische Aspekte in der Physik WS 2007/08 Seminarleitung: Prof. Dr. G. Münster Dr. C. Suhm Vortragender: Johannes Greber 13. 11. 2007 1. Einleitung
Differentialgleichungen der Strömungsmechanik
 Differentialgleichungen der Strömungsmechanik Teil 2 Seminarvortrag: Regulär oder Singulär? Mathematische und numerische Rätsel in der Strömungsmechanik Referentin: Irena Vogel Inhalt Grundgleichungen
Differentialgleichungen der Strömungsmechanik Teil 2 Seminarvortrag: Regulär oder Singulär? Mathematische und numerische Rätsel in der Strömungsmechanik Referentin: Irena Vogel Inhalt Grundgleichungen
Inhalt. 1. Einführung in die Informatik. 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele.
 1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
Das wissen Sie: 6. Welche Möglichkeiten zur Darstellung periodischer Funktionen (Signalen) kennen Sie?
 Das wissen Sie: 1. Wann ist eine Funktion (Signal) gerade, ungerade, harmonisch, periodisch (Kombinationsbeispiele)? 2. Wie lassen sich harmonische Schwingungen mathematisch beschreiben und welche Beziehungen
Das wissen Sie: 1. Wann ist eine Funktion (Signal) gerade, ungerade, harmonisch, periodisch (Kombinationsbeispiele)? 2. Wie lassen sich harmonische Schwingungen mathematisch beschreiben und welche Beziehungen
Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser)
 2.Vorlesung Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser) P.F.: Man weiß heute, dass das Brownsche Teilchen ein Perpetuum mobile zweiter Art ist, und dass sein Vorhandensein den
2.Vorlesung Wiederholung Film Brownsche Bewegung in Milch (Fettröpfchen in Wasser) P.F.: Man weiß heute, dass das Brownsche Teilchen ein Perpetuum mobile zweiter Art ist, und dass sein Vorhandensein den
Fibonacci Zahlen: 3. Hamiltonsche Systeme. 3.1 Hamilton Dynamik. Teilverhältnis beim `goldenen Schnitt : definiert als. mit
 Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
Hamiltonsche Mechanik (Kanonische Mechanik)
 Hamiltonsche Mechanik (Kanonische Mechanik) Hamilton-Funktion und Hamiltonsche Bewegungsgleichungen Motivation: Die Hamiltonsche Formulierung der klassischen Mechanik - erweiterert Klasse der zulässigen
Hamiltonsche Mechanik (Kanonische Mechanik) Hamilton-Funktion und Hamiltonsche Bewegungsgleichungen Motivation: Die Hamiltonsche Formulierung der klassischen Mechanik - erweiterert Klasse der zulässigen
Eine transfinite Zahl als Grenzwert
 Eine transfinite Zahl als Grenzwert von Thomas Limberg, am 03.04.2010 Ist im Folgenden von reellen Zahlen, Zahlenfolgen, o.ä. die Rede, so sollen damit stets die nichtnegativen reellen Zahlen, Zahlenfolgen,
Eine transfinite Zahl als Grenzwert von Thomas Limberg, am 03.04.2010 Ist im Folgenden von reellen Zahlen, Zahlenfolgen, o.ä. die Rede, so sollen damit stets die nichtnegativen reellen Zahlen, Zahlenfolgen,
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Klassische Mechanik. Übersicht
 Klassische Mechanik WS 02/03 C. Wetterich Übersicht 0) Einführung I Newtonsche Mechanik 1) Die Newtonschen Gesetze a) Kinetik, Beschreibung durch Massenpunkte b) Kraft (i)kraftgesetze (ii)differentialgleichungen
Klassische Mechanik WS 02/03 C. Wetterich Übersicht 0) Einführung I Newtonsche Mechanik 1) Die Newtonschen Gesetze a) Kinetik, Beschreibung durch Massenpunkte b) Kraft (i)kraftgesetze (ii)differentialgleichungen
Einführung in die Quantentheorie der Atome und Photonen
 Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
beschrieben wird. B' sei ein IS das derjenigen Weltlinie folgt, die P und Q in gleichförmiger Bewegung verbindet. Aus Sicht von A folgt B' Bahn mit
 Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Statistische Kennwerte und -funktionen. Dr.-Ing. habil. H. Nobach
 Statistische Kennwerte und -funktionen Dr.-Ing. habil. H. Nobach 1. Einführung Statistische Kennwerte und -funktionen, wie Mittelwert Varianz Wahrscheinlichkeitsdichte Autokorrelation spektrale Leistungsdichte
Statistische Kennwerte und -funktionen Dr.-Ing. habil. H. Nobach 1. Einführung Statistische Kennwerte und -funktionen, wie Mittelwert Varianz Wahrscheinlichkeitsdichte Autokorrelation spektrale Leistungsdichte
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Vorlesung Theoretische Mechanik
 Julius-Maximilians-Universität Würzburg Vorlesung Theoretische Mechanik Wintersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufiges Skript 1 (Zweite Vorlesung, aufgeschrieben von Manuel Kunkel, 23. 10.
Julius-Maximilians-Universität Würzburg Vorlesung Theoretische Mechanik Wintersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufiges Skript 1 (Zweite Vorlesung, aufgeschrieben von Manuel Kunkel, 23. 10.
23. DIFFERENTIALRECHNUNG VON FUNKTIONEN VON MEHREREN VARIABLEN
 204 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
204 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
Mechanik von Quanten und Teilchen als Implikation homogener Raumzeit und Kausalität
 Mechanik von Quanten und Teilchen als Implikation homogener Raumzeit und Kausalität Seminar für theoretische Chemie Uni Tübingen, 14. Mai 2001 1 Welt der Wahrnehmung und der Physik Welterfahrung nicht
Mechanik von Quanten und Teilchen als Implikation homogener Raumzeit und Kausalität Seminar für theoretische Chemie Uni Tübingen, 14. Mai 2001 1 Welt der Wahrnehmung und der Physik Welterfahrung nicht
ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE
 ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE Von 1. FENYO Lehrstuhl für jlathelllatik, Technische Universität, Budapest (Eingegangen am 24. August, 1964.) 1. FODOR hat in einem Aufsatz [1]
ÜBER EINE TECHNISCHE ANWENDUNG DER DISTRffiUTIONENTHEORIE Von 1. FENYO Lehrstuhl für jlathelllatik, Technische Universität, Budapest (Eingegangen am 24. August, 1964.) 1. FODOR hat in einem Aufsatz [1]
beschrieben wird. B' sei ein IS das derjenigen Weltlinie folgt, die P und Q in gleichförmiger Bewegung verbindet. Aus Sicht von A folgt B' Bahn mit
 Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Minkowski-Wegelement und Eigenzeit Invariantes Wegelement entlang einer Bahnkurve einesteilchens im IS A: immer "Instantan mitlaufendes" Inertialsystem B' sei so gewählt, dass es zum Zeitpunkt t dieselbe
Einige Gedanken zur Fibonacci Folge
 Einige Gedanken zur Fibonacci Folge Im Folgenden gehe ich auf einige Aspekte von Aufgabe 4 auf Übungsblatt, d.h. auf Aufgabe 4 auf Seiten und 3 des Buches Hahn-Dzewas: Mathematik, ein. Die Aufgabe hat
Einige Gedanken zur Fibonacci Folge Im Folgenden gehe ich auf einige Aspekte von Aufgabe 4 auf Übungsblatt, d.h. auf Aufgabe 4 auf Seiten und 3 des Buches Hahn-Dzewas: Mathematik, ein. Die Aufgabe hat
Sozialwissenschaftliche Modelle und Daten SoSe 2010
 Sozialwissenschaftliche Modelle und Daten SoSe 2010 LS Sozialwissenschaftliche Methodenlehre und Sozialstatistik C. Dudel C. Dudel Sozialwissenschaftliche Modelle und Daten SoSe 2010 1 23 1 Formalia 2
Sozialwissenschaftliche Modelle und Daten SoSe 2010 LS Sozialwissenschaftliche Methodenlehre und Sozialstatistik C. Dudel C. Dudel Sozialwissenschaftliche Modelle und Daten SoSe 2010 1 23 1 Formalia 2
Lineare Differenzengleichungen und Polynome. Franz Pauer
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Synergetik. Hermann Haken. Eine Einführung. Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie
 Hermann Haken Synergetik Eine Einführung Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie Übersetzt von A. Wunderlin Dritte, erweiterte Auflage Mit 168 Abbildungen
Hermann Haken Synergetik Eine Einführung Nichtgleichgewichts-Phasenübergänge und Selbstorganisation in Physik, Chemie und Biologie Übersetzt von A. Wunderlin Dritte, erweiterte Auflage Mit 168 Abbildungen
3. Diffusion und Brechungsindex
 3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
1.2 Mengenlehre-Einführung in die reellen Zahlen
 .2 Mengenlehre-Einführung in die reellen Zahlen Inhaltsverzeichnis Repetition 2 2 Dezimalzahlen 3 3 weitere irrationale Zahlen 4 3. Zusatz: Der Beweis, dass 2 irrational ist.......................... 5
.2 Mengenlehre-Einführung in die reellen Zahlen Inhaltsverzeichnis Repetition 2 2 Dezimalzahlen 3 3 weitere irrationale Zahlen 4 3. Zusatz: Der Beweis, dass 2 irrational ist.......................... 5
3 Empirische Überstzung des Forschungsproblems (X aus 5)
 Eigene MC-Aufgaben 3 Empirische Überstzung des Forschungsproblems (X aus 5) 1. Wie kann man die Präzisierung der Aufgabenstellung (A) bezeichnen und worin soll ihr Ergebnis (B) bestehen? (A) dimensionale
Eigene MC-Aufgaben 3 Empirische Überstzung des Forschungsproblems (X aus 5) 1. Wie kann man die Präzisierung der Aufgabenstellung (A) bezeichnen und worin soll ihr Ergebnis (B) bestehen? (A) dimensionale
FILTER, ULTRAFILTER UND EINFÜHRUNG VON R
 FILTER, ULTRAFILTER UND EINFÜHRUNG VON R Im Sinne von G.W.Leibniz ist: Eine Kurve besteht aus unendlich vielen unendlich kurzen Stücken. So darf man denken, wenn man Gegenstände der Mathematik oder Physik
FILTER, ULTRAFILTER UND EINFÜHRUNG VON R Im Sinne von G.W.Leibniz ist: Eine Kurve besteht aus unendlich vielen unendlich kurzen Stücken. So darf man denken, wenn man Gegenstände der Mathematik oder Physik
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-regensburg.de/mathematik/mathematik-abels/aktuelles/index.html Schnupperstudium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-regensburg.de/mathematik/mathematik-abels/aktuelles/index.html Schnupperstudium
Dr. Wolfgang Langer - IV Methoden der empirischen Sozialforschung I - SoSe
 Dr. Wolfgang Langer - IV Methoden der empirischen Sozialforschung I - SoSe 2000 1 Wissenschaftstheorie: Begriffe und Definitionen: Quelle: Giesen,B. & Schmid, M.: Basale Soziologie: Wissenschaftstheorie.
Dr. Wolfgang Langer - IV Methoden der empirischen Sozialforschung I - SoSe 2000 1 Wissenschaftstheorie: Begriffe und Definitionen: Quelle: Giesen,B. & Schmid, M.: Basale Soziologie: Wissenschaftstheorie.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 8 2. Semester ARBEITSBLATT 8 DIE REELLEN ZAHLEN
 Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 8. Semester ARBEITSBLATT 8 DIE REELLEN ZAHLEN Bisher kennen wir bereits folgende Zahlenbereiche: N Natürliche Zahlen Z Ganze Zahlen Q Rationale Zahlen Bei
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 8. Semester ARBEITSBLATT 8 DIE REELLEN ZAHLEN Bisher kennen wir bereits folgende Zahlenbereiche: N Natürliche Zahlen Z Ganze Zahlen Q Rationale Zahlen Bei
Angewandte Stochastik
 Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Angewandte Stochastik Dr. C.J. Luchsinger 13 Allgemeine Theorie zu Markov-Prozessen (stetige Zeit, diskreter Zustandsraum) Literatur Kapitel 13 * Grimmett & Stirzaker: Kapitel 6.9 Wie am Schluss von Kapitel
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 25/6 Dörte Hansen Seminar 1 Dissipative Kräfte I Reibung Wenn wir in der theoretischen Mechanik die Bewegung eines Körpers beschreiben wollen,
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 25/6 Dörte Hansen Seminar 1 Dissipative Kräfte I Reibung Wenn wir in der theoretischen Mechanik die Bewegung eines Körpers beschreiben wollen,
heißt Exponentialreihe. Die durch = exp(1) = e (Eulersche Zahl). n! + R m+1(x) R m+1 (x) = n! m m + 2
 9 DIE EXPONENTIALREIHE 48 absolut konvergent. Beweis. Wegen x n+ n! n + )!x n = x n + < 2 für n 2 x folgt dies aus dem Quotientenkriterium 8.9). Definition. Die Reihe x n heißt Exponentialreihe. Die durch
9 DIE EXPONENTIALREIHE 48 absolut konvergent. Beweis. Wegen x n+ n! n + )!x n = x n + < 2 für n 2 x folgt dies aus dem Quotientenkriterium 8.9). Definition. Die Reihe x n heißt Exponentialreihe. Die durch
Wozu brauchen wir theoretische Physik? Ziele der Physik
 Wozu brauchen wir theoretische Physik? Wolfgang Kinzel Lehrstuhl für theoretische Physik III Universität Würzburg Ziele der Physik Die Physik sucht nach allgemeinen Naturgesetzen. Sie möchte die Natur
Wozu brauchen wir theoretische Physik? Wolfgang Kinzel Lehrstuhl für theoretische Physik III Universität Würzburg Ziele der Physik Die Physik sucht nach allgemeinen Naturgesetzen. Sie möchte die Natur
I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N
 Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
8. DIE ABLEITUNG EINER VEKTORFUNKTION
 75 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
75 Dieses Skript ist ein Auszug mit Lücken aus Einführung in die mathematische Behandlung der Naturwissenschaften I von Hans Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie das Buch auch
Aber gerade in diesem Punkt ist Newton besonders konsequent.
 2.1.Lorentz-Transformationen Aus Einstein, Mein Weltbild 1.) Trotzdem man allenthalben das Streben Newtons bemerkt, sein Gedankensystem als durch die Erfahrung notwendig bedingt hinzustellen und möglichst
2.1.Lorentz-Transformationen Aus Einstein, Mein Weltbild 1.) Trotzdem man allenthalben das Streben Newtons bemerkt, sein Gedankensystem als durch die Erfahrung notwendig bedingt hinzustellen und möglichst
Quantenmechanik& Wahrscheinlichkeit. Der liebe Gott würfelt nicht! Albert Einstein um 1923
 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Mit diesem Ausspruch
Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Mit diesem Ausspruch
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas. Thermodynamik
 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Feldbacher Markus Manipulationstechnik Kinematik. Kinetik. (Bewegungslehre) Mechanik Lehre von der Bewegung von Körpern
 Kinematik (Bewegungslehre) Mechanik Lehre von der Bewegung von Körpern Kinematik Lehre von den geo- Metrischen Bewegungsverhältnissen von Körpern. Dynamik Lehre von den Kräften Kinetik Lehre von den Bewegungen
Kinematik (Bewegungslehre) Mechanik Lehre von der Bewegung von Körpern Kinematik Lehre von den geo- Metrischen Bewegungsverhältnissen von Körpern. Dynamik Lehre von den Kräften Kinetik Lehre von den Bewegungen
Klassische Physik. PfE. Physik der Griechen. Vorgänge der materiellen Welt der Rest: Metaphysik
 Klassische Physik Physik der Griechen Vorgänge der materiellen Welt der Rest: Metaphysik Die 5 Gebiete der klass. Physik Mechanik Statistische Mechanik Thermodynamik Optik Elektrizität Elektrodynamik Magnetismus
Klassische Physik Physik der Griechen Vorgänge der materiellen Welt der Rest: Metaphysik Die 5 Gebiete der klass. Physik Mechanik Statistische Mechanik Thermodynamik Optik Elektrizität Elektrodynamik Magnetismus
Anlage zur Studienordnung des Studienganges Bachelor of Science Meteorologie Studienablaufplan/ Modulübersichtstabelle
 Bachelor of Science Meteorologie (Seite 1 von 5) Anlage zur Studienordnung des Studienganges Bachelor of Science Meteorologie Studienablaufplan/ Modulübersichtstabelle Modul und zugehörige Lehrveranstaltungen
Bachelor of Science Meteorologie (Seite 1 von 5) Anlage zur Studienordnung des Studienganges Bachelor of Science Meteorologie Studienablaufplan/ Modulübersichtstabelle Modul und zugehörige Lehrveranstaltungen
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die kontinuierlich ablaufende Zeit.
 Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
Algorithmische Mathematik und Programmieren
 Algorithmische Mathematik und Programmieren Martin Lanser Universität zu Köln WS 2016/2017 Organisatorisches M. Lanser (UzK) Alg. Math. und Programmieren WS 2016/2017 1 Ablauf der Vorlesung und der Übungen
Algorithmische Mathematik und Programmieren Martin Lanser Universität zu Köln WS 2016/2017 Organisatorisches M. Lanser (UzK) Alg. Math. und Programmieren WS 2016/2017 1 Ablauf der Vorlesung und der Übungen
Vorlesung 2: Roter Faden: Newtonsche Axiome: 1. Trägheitsgesetz 2. Bewegungsgesetz F=ma 3. Aktion=-Reaktion
 Vorlesung 2: Roter Faden: Newtonsche Axiome: 1. Trägheitsgesetz 2. Bewegungsgesetz F=ma 3. Aktion=-Reaktion Newton (1642-1727) in Philosophiae Naturalis Principia Mathematica, publiziert in 1687. Immer
Vorlesung 2: Roter Faden: Newtonsche Axiome: 1. Trägheitsgesetz 2. Bewegungsgesetz F=ma 3. Aktion=-Reaktion Newton (1642-1727) in Philosophiae Naturalis Principia Mathematica, publiziert in 1687. Immer
Rationale, irrationale und reelle Zahlen. 4-E Vorkurs, Mathematik
 Rationale, irrationale und reelle Zahlen 4-E Vorkurs, Mathematik Rationale Zahlen Der Grund für die Einführung der rationalen Zahlen ist der, dass wir mit ihnen auch Gleichungen der Form q x = p lösen
Rationale, irrationale und reelle Zahlen 4-E Vorkurs, Mathematik Rationale Zahlen Der Grund für die Einführung der rationalen Zahlen ist der, dass wir mit ihnen auch Gleichungen der Form q x = p lösen
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Die Newton'schen Axiome mit einer Farbfolie
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Newton'schen Axiome mit einer Farbfolie Das komplette Material finden Sie hier: Download bei School-Scout.de 14. Die Newton schen
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Die Newton'schen Axiome mit einer Farbfolie Das komplette Material finden Sie hier: Download bei School-Scout.de 14. Die Newton schen
1.2 Mengenlehre I-Einführung in die reellen Zahlen
 .2 Mengenlehre I-Einführung in die reellen Zahlen Inhaltsverzeichnis Checkliste 2 2 Repetition 2 3 Dezimalzahlen 3 4 Die Darstellung von Brüchen als Dezimalzahlen 3 5 irrationale Zahlen 4 6 Beispiele von
.2 Mengenlehre I-Einführung in die reellen Zahlen Inhaltsverzeichnis Checkliste 2 2 Repetition 2 3 Dezimalzahlen 3 4 Die Darstellung von Brüchen als Dezimalzahlen 3 5 irrationale Zahlen 4 6 Beispiele von
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Fey nman-vo rles u n ge n über Physik 1
 Richard P. Matthew Sands Feynman, Robert B. Leighton, Fey nman-vo rles u n ge n über Physik 1 Mechanik New Millennium-Edition DE GRUYTER Inhaltsverzeichnis 1 Atome in Bewegung 1 1.1 Einleitung 1 1.2 Materie
Richard P. Matthew Sands Feynman, Robert B. Leighton, Fey nman-vo rles u n ge n über Physik 1 Mechanik New Millennium-Edition DE GRUYTER Inhaltsverzeichnis 1 Atome in Bewegung 1 1.1 Einleitung 1 1.2 Materie
T1: Theoretische Mechanik, SoSe 2016
 T1: Theoretische Mechanik, SoSe 2016 Jan von Delft http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik Newtonsche Sätze (Originalformulierung) 1. Jeder Körper verharrt in seinem
T1: Theoretische Mechanik, SoSe 2016 Jan von Delft http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_16/t1_theor_mechanik Newtonsche Sätze (Originalformulierung) 1. Jeder Körper verharrt in seinem
Differenzengleichungen. und Polynome
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
Informatik 1. Teil 1 - Wintersemester 2012/2013. Prof. Dr.-Ing. habil. Peter Sobe Fachkultät Informatik / Mathematik
 Informatik 1 Teil 1 - Wintersemester 2012/2013 Prof. Dr.-Ing. habil. Peter Sobe Fachkultät Informatik / Mathematik Dieser Foliensatz wurde z.t. von Herrn Prof. Grossmann übernommen 0. Rechner und Programmierung
Informatik 1 Teil 1 - Wintersemester 2012/2013 Prof. Dr.-Ing. habil. Peter Sobe Fachkultät Informatik / Mathematik Dieser Foliensatz wurde z.t. von Herrn Prof. Grossmann übernommen 0. Rechner und Programmierung
Das Meßproblem in der Kopenhagener Deutung
 Das Meßproblem in der Kopenhagener Deutung Angenommen, ein quantenmechanisches System kann nur zwei Werte annehmen, z.b. Spin oben oder Spin unten... Dieses Teilchen wird in Bezug auf den Spin durch eine
Das Meßproblem in der Kopenhagener Deutung Angenommen, ein quantenmechanisches System kann nur zwei Werte annehmen, z.b. Spin oben oder Spin unten... Dieses Teilchen wird in Bezug auf den Spin durch eine
Theoretische Physik 6: Thermodynamik und Statistik
 Rainer J.Jelitto Theoretische Physik 6: Thermodynamik und Statistik Eine Einführung in die mathematische Naturbeschreibung 2. korrigierte Auflage Mit 82 Abbildungen, Aufgaben und Lösungen dulfc AU LA-Verlag
Rainer J.Jelitto Theoretische Physik 6: Thermodynamik und Statistik Eine Einführung in die mathematische Naturbeschreibung 2. korrigierte Auflage Mit 82 Abbildungen, Aufgaben und Lösungen dulfc AU LA-Verlag
Werkstatt Multiplikation Posten: Rundung im Quadrat. Informationsblatt für die Lehrkraft. Rundung im Quadrat
 Informationsblatt für die Lehrkraft Rundung im Quadrat Informationsblatt für die Lehrkraft Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Numerische Grenzen des Computers Mittelschule, technische Berufsschule,
Informationsblatt für die Lehrkraft Rundung im Quadrat Informationsblatt für die Lehrkraft Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Numerische Grenzen des Computers Mittelschule, technische Berufsschule,
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Thermodynamik un Statistische Mechanik
 Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik un Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispiele n und Aufgaben mit ausführlichen
Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik un Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispiele n und Aufgaben mit ausführlichen
Schrödingers Katze -oder- Wo ist der Übergang?
 Schrödingers Katze -oder- Wo ist der Übergang? Themen Vergleich Quantenmechanik klassische Mechanik Das Gedankenexperiment Interpretationen des Messprozesses (Kopenhagener Deutung, Viele-Welten-Theorie,
Schrödingers Katze -oder- Wo ist der Übergang? Themen Vergleich Quantenmechanik klassische Mechanik Das Gedankenexperiment Interpretationen des Messprozesses (Kopenhagener Deutung, Viele-Welten-Theorie,
Exkurs: Method of multiple scales (Mehrskalen Methode)
 Exkurs: Method of multiple scales (Mehrskalen Methode) dr. karin mora* Im folgenden betrachten wir nichtlineare dynamische Systeme (NDS) mit sogenannten kleinen nichtlinearen Termen. Viele mathematische
Exkurs: Method of multiple scales (Mehrskalen Methode) dr. karin mora* Im folgenden betrachten wir nichtlineare dynamische Systeme (NDS) mit sogenannten kleinen nichtlinearen Termen. Viele mathematische
