Aufgabe 102. Gegeben sind die folgenden Punktmengen 2 R 2 2 R M 1 D. x 2 M 2 D. x 2 W x 1 2.0;1/ ; x 2 = 0 M 3 D. x 2 W x 1 C x 2 D 0 ; x 1 x 2 D 1
|
|
|
- Dennis Hase
- vor 5 Jahren
- Abrufe
Transkript
1 Aufgabe 0 Lineare Algebra: Punktmengen (A4.5) Gegeben sind die folgenden Punktmengen R M D M D M 3 D M 4 D x x x x W R x W x N ; x D x R x W x.0;/ ; x = 0 R x W x C x D 0 ; x x D R x W x = x 3 ; x = 0 M 5 D x R W kxk = ;.; / x D 0 a) Man stelle alle Mengen graphisch dar und prüfe mit Hilfe der Zeichnung, welche der Mengen offen, abgeschlossen, beschränkt, konvex ist. b) Welche der paarweisen Durchschnitte sind leer? Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 5 von 48) a) M D x x R W x N; x D x M : abgeschlossen, nicht offen, nicht konvex, nicht beschränkt x M D R W x.0;/; x 0 x M : nicht abgeschlossen,nicht offen,konvex,nach unter beschränkt M 3 D x R W x C x D 0; x x D M 3 D ;: offen,abgeschlossen,konvex,beschränkt M 4 D x R W x x 3; x 0 M 4 : nicht offen,abgeschlossen,nicht offen,nicht konvex,nicht unten beschränkt M 5 D x R W kxk > ; x x D 0 M 5 : abgeschlossen, nicht offen, nicht konvex, nicht beschränkt b) M \ M D ; M \ M 3 D ; M \ M 3 D ; M 3 \ M 4 D ; M 3 \ M 5 D ; 5
2
3 LineareGleichungssysteme Aufgabe 07 LineareGleichungssysteme: Gozintograph (A4.7) Aus den Werkstoffen A ; A werden Zwischenprodukte A 3 ; A 4 ; A 5 und Endprodukte A 6 ; A 7 hergestellt. Die nachfolgende Graphik stellt die Verknüpfungen dar. A 3 3 A 4 A 6 A 5 A 3 4 A 7 A 4 Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 30 von 48) Die Pfeilbewertung a ij mit A i a ij! A j gibt an, wie viele Mengeneinheiten von A i zur Herstellung einer Einheit A j benötigt werden. Wie viele Einheiten von A ; A ; A 3 ; A 4 werden benötigt, wenn von A 5 ; A 6 ; A 7 genau 50, 00, 0 Einheiten verkauft werden können? Sei x i.i D ; : : : ;7/ der Gesamtbedarf (+ Verkauf) von A i. Dann ergibt sich der Reihe nach: x 7 D 0; x 6 D 00; x 5 D 490; x 4 D 460; x 3 D 840; x D 6790; x D 60 30
4 Aufgabe 08 LineareGleichungssysteme: Allgemeines zu LGS (A4.8) Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 3 von 48) a) Welche der folgenden Aussagen über lineare Gleichungssysteme sind wahr bzw. falsch? (Begründen Sie Ihre Antwort!) a.) Ein lineares Gleichungssystem mit n Gleichungen und n Variablen ist stets lösbar. a.) Ein lineares Gleichungssystem mit n Gleichungen und n Variablen ist nicht immer lösbar. a.3) Wenn ein lineares Gleichungssystem mit n Gleichungen und n Variablen lösbar ist, dann ist die Lösung eindeutig. a.4) Ein lineares Gleichungssystem mit mehr Gleichungen als Variablen ist nicht lösbar. a.5) Ein lineares Gleichungssystem mit weniger Gleichungen als Variablen kann eindeutig lösbar sein. b) Für ein lineares Gleichungssystem Ax D b sei die erweiterte Koeffizientenmatrix ( A b) durch 0 4 a mit a R 0 0 gegeben. b.) Geben Sie die allgemeine Lösung des homogenen Systems ( b = 0 ) sowie eine spezielle Lösung des inhomogenen Systems an. b.) Für welche a R ist das gegebene Gleichungssystem lösbar? b.3) Gibt es ein a R, so dass x T D.; ;;;0/ das Gleichungssystem Ax D b löst? 0 4 a 0 0 x 3 D x 4 D 0; x 5 D ; x D ; x D ; x ; x - Basis, x 3 ; x 4 ; x 5 - Nicht-Basis x x x 3 x 4 x 5./ 0 4 a./ a././ 0 0./ Spezielle Lösung des inhomogenen Systems (Startpunkt) x 3 D x 4 D x 5 D 0 ) xs T D.a 0 0 0/ Allgemeine Lösung des homogenen Systems (Richtungsvektoren): x 3 =, x 4 =0, x 5 =0 ) x T k D. 0 0/ x 3 =0, x 4 =, x 5 =0 ) xe T D / x 3 =0, x 4 =0, x 5 = ) xm T D. 0 0 /
5 8 ˆ< L D x R 5 W ˆ: 0 0 a B 0 0 A C t C 0A C t 0 B0 A C t >= 0 C 0A I t ; t ; t 3 R >; ) LGS ist für alle a R lösbar. b.3) x T D. 0/ x 5 D 0 C 0 t C 0 t C t 3 D 0 ) t 3 D 0 x 4 D 0 C 0 t C t C 0 t 3 D ) t D x 3 D 0 C t C 0 t C 0 t 3 D ) t D ) Lösungsvektor: a C. / C 0 C 0. / D ) a C. / D ) a D 4 C. / C 0 C 0. / D 0 C C 0 C 0 0 D 0 C 0 C C 0 0 D 0 C 0 C 0 C 0 D 0 Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 3 von 48) 3
6 Aufgabe 09 LineareGleichungssysteme: Neue Kostenstellen (A4.9) Die Abteilungen A ; A ; A 3 eines Betriebes sind durch mengenmäßige Leistungen a ij.i;j D ; ; 3/ von A i nach A j gegenseitig verbunden. Jede der Abteilungen gibt ferner Leistungen b i.i D ; ; 3/ an den Markt ab und hat sogenannte Primärkosten c i.i D ; ; 3/ zu tragen. Gegeben seien folgende Daten: b c 0 50 A D.a ij / 3; A A 70A A 70A a) Formulieren Sie mit den Variablen x ; x ; x 3 für die innerbetrieblichen Verrechnungspreise ein lineares Gleichungssystem für ein innerbetriebliches Kostengleichgewicht der Abteilungen A ; A ; A 3. b) Lösen Sie das Gleichungssystem von a) und interpretieren Sie das Ergebnis. b b 3 c c 3 a) Abteilung Sek.kost. Sekundärkosten für abgegebene für erhaltene Leistg. Leistungen + Primärkosten Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 33 von 48) A x.40 C 0 C 0/ D 50 C 0x C 30x 3 A x.70 C 0 C 0/ D 70 C 0x C 0x 3 A 3 x 3.60 C 30 C 0/ D 60 C 0x C 0x ) 60x 0x 30x 3 D 50 0x C 00x 0x 3 D 70 0x 0x C 00x 3 D 60 b) Gaußalgorithmus liefert: x 3 D (Verrechnungspreis Abteilung A ), x D (V.P. Abt. A ), x D (A 3 ) 33
7
8 Aufgabe 0 LineareGleichungssysteme: Zwei LGS (A5.0) Gegeben sind die beiden folgenden Gleichungssysteme:.G / x C x C x 3 D 4 x C x x 3 D 0 x x C x 3 D.G / 3x C x C x 3 D 3 x C x C x 3 D x C x 3 D a) Welches der beiden Gleichungssysteme besitzt keine Lösung, eine eindeutige Lösung, unendlich viele Lösungen? b) Wie verändert sich die Lösungsmenge von.g /, wenn die Gleichung x C x C x 3 D zusätzlich berücksichtigt werden soll? c) Wie verändert sich die Lösungsmenge von.g /, wenn die Gleichung x C x 3 D entfallen soll? d) Bestimmen Sie für.g / und.g /, falls möglich, eine Lösung mit x 3 D. Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 34 von 48) a) G : eindeutige Lösung mit x 3 D, x D, x D G : unendlich viele Lösungen, z.b. der Form: x 3 x 3 R bel., x D x 3, x D 3 b) Einsetzen: x C x C x 3 D C C D ) keine Veränderung der Lösung c) 3. Gleichung entfällt ) Keine Veränderung der Lösungsmenge d) G : x 3 D ) Widerspruch, damit G nicht lösbar. e) G : x 3 D ) X D 0; x D. Damit ist G eindeutig lösbar. 34
9 Aufgabe LineareGleichungssysteme: Marktentwicklung (A5.) Ein regionaler Markt wird von drei konkurrierenden Produkten P ;P ;P 3 beherrscht. Bezeichnet man mit a ij Œ0; den Anteil von P i -Käufern zum Zeitpunkt t N, der zum Zeitpunkt t C N das Produkt P j kauft, so charakterisiert die Matrix A D.a ij / 3;3 D 0;6 0;4 0 0; 0;6 0; 0 0; 0;8 die anteiligen Käuferfluktuationen zwischen den Produkten. Ferner beschreibt der Vektor x T D.0;5 ; 0;5 ; 0/ die Marktanteile der Produkte P ;P ;P 3 zum Zeitpunkt t D. a) Interpretieren Sie die in A und x enthaltenen Nullen. b) Berechnen Sie die Marktanteile der Produkte zu den Zeitpunkten t D ;3 und begründen Sie die Marktanteilszuwächse von P 3 mit Hilfe von A. c) Geben Sie eine stationäre Marktverteilung an, das heißt, für beliebiges t N sind xt T und xtc T D xt t A identisch. A Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 35 von 48) a) a 3 D a 3 D 0: Der Käuferanteil, der im Zeitpunkt t C gegenüber t von P nach P 3 bzw. von P 3 nach P wechselt, ist 0. x 3 D 0: Zum Zeitpunkt t D ist der Marktanteil von P 3 gleich 0. b) x T D xt A D.0;4; 0;5; 0;/ x3 T D xt A D.0;34; 0;48; 0;8/ Wachsende Marktanteile von P 3 : a 3 D a 3 D 0;: P gibt an P 3 0% seines Marktanteils ab, ebenso P 3 an P. Andererseits ist der Marktanteil von P 3 für t D ; jeweils kleiner als der Marktanteil von P. Wegen a 3 D a 3 D 0 spielt dabei P keine Rolle. c) y D x t D x tc ) y T D y T A ) y T.E A/ D 0 T mit y C y C y 3 D ) stationäre Marktverteilung y T D.0;; 0;4; 0;4/ 35
10 Aufgabe LineareGleichungssysteme: Tee (A5.) Ein Teegroßhändler führt drei Sorten Tee: Darjeeling, Nepal und Java mit den Anfangsbeständen x ;x ;x 3. Der Lagerbestand zu Beginn der ersten Woche beträgt 3 Tonnen. Nach der ersten (zweiten) Woche hat er 5 % (50 %) des Bestandes an Darjeeling und jeweils 0 % (40 %) des Bestandes an Nepal bzw. Java verkauft. Der Lagerbestand beträgt nach der ersten (zweiten) Woche 5 (8) Tonnen. Nach der dritten Woche hat er bei einem Gesamtlagerbestand von 5. Tonnen noch Vorräte von 0 % Darjeeling und jeweils 0 % Nepal bzw. Java (im Vergleich zu deren Anfangsbeständen). a) Formulieren Sie ein lineares Gleichungssystem mit den unbekannten Variablen x ;x ;x 3, das alle gegebenen Informationen angemessen wiedergibt. b) Ermitteln Sie alle ökonomisch sinnvollen Lösungen des Gleichungssystems. c) Verwerten Sie falls möglich die zusätzliche Information, dass zu Beginn der ersten Woche der Vorrat an Darjeeling um 0 % höher war als der Vorrat an Nepal. Wie verändert sich damit die Lösung von b)? Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 36 von 48) a) Lagerbestand zu Beginn: x C x C x 3 D 3 Lagerbestand nach der. Woche: 0;75x C 0;8x C 0;8x 3 D 5 Lagerbestand nach der. Woche: 0;5x C 0;6x C 0;6x 3 D 8 Lagerbestand nach der 3. Woche: 0;x C 0;x C 0;x 3 D 5; b) Gaußalgorithmus liefert: L D x R 3 C W x D ; x C x 3 D 0 c) x D ; x D ) x D 0 ) x 3 D 0 36
11 Aufgabe 3 LineareGleichungssysteme: Bier (A5.3) Eine Brauerei stellt 3 Biersorten her: Hell, Pils und Bock. Die Herstellung erfordert eine Arbeitszeit von Stunden für hl Hell, 4 Stunden für hl Pils und 5 Stunden für hl Bock, wobei insgesamt genau Z Arbeitsstunden zu leisten sind. Das für Werbung bewilligte Budget beträgt , wobei die Werbekosten je hl Hell und Bock und bei Pils betragen. Der Gewinn pro hl beträgt 0 bei Hell, 0 bei Pils und 30 bei Bock. Insgesamt soll ein Gewinn von erzielt werden. a) Formulieren Sie das gegebene Gleichungssystem. b) Ermitteln Sie die ökonomisch sinnvolle Lösungsmenge. (Hinweis: die zu produzierenden Einheiten an hl Bier sind nicht negativ). Für welchen Arbeitseinsatz Z gibt es keine Lösung, genau eine Lösung, mehrere Lösungen? c) Skizzieren Sie das in b) erhaltene Ergebnis. x ; x ; x 3 R C : Biermenge in hl für Hell (x ), Pils (x ) und Bock (x 3 ) Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 37 von 48) a) x C 4x C 5x 3 D Z (Arbeitszeit) x C x C x 3 D (Werbung) 0x C 0x C 30x 3 D (Gewinn) a) Gaußalgorithmus liefert: Keine Lösung für Z 00; für Z D 00: ) x 3 D 0000 und x C x D Damit Lösungsmenge: 8 9 < x 5000 = L D : x D x R 3 C W x D 0 C ; R ; x Ökonomisch sinnvolle Lösungen für x ; x > 0. Damit:
12 Aufgabe 4 LineareGleichungssysteme: Invertieren (A5.4) Gegeben sind die Matrizen: A D ; B D a) Zeigen Sie, dass A orthogonal ist. b) Berechnen Sie B. c) Lösen Sie das Gleichungssystem AB x D c mit unter Verwendung von b) x T D.x ; x ; x 3 ; x 4 / ; c T D.; ; 3; 4/ Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathematik Wintersemester 06/7 Aufgabensammlung (Seite 38 von 48) a) Ausmultiplizieren liefert: A 4 A D E ) A D 0 4 A b) B D B A c) Von links (!) mit B A multiplizieren ergibt: x D B A c D 38 0 ;0 ;0 C ;5A ;0
Wirtschaftsmathe für BW und IM Aufgabensammlung Wintersemester 2013/14
 Wirtschaftsmathe für BW und IM Aufgabensammlung Wintersemester 2013/14 Prof. Dr. Stefan Etschberger Hochschule Augsburg Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathe für BW und IM Wintersemester
Wirtschaftsmathe für BW und IM Aufgabensammlung Wintersemester 2013/14 Prof. Dr. Stefan Etschberger Hochschule Augsburg Prof. Dr. Stefan Etschberger Hochschule Augsburg Wirtschaftsmathe für BW und IM Wintersemester
Mathematik für International Management und Betriebswirtschaft Aufgabensammlung Wintersemester 2012/13
 Prof. Dr. Stefan Etschberger Hochschule Augsburg Mathematik fürinternational Management und Betriebswirtschaft Wintersemester 202/3 Aufgabensammlung Mathematik für International Management und Betriebswirtschaft
Prof. Dr. Stefan Etschberger Hochschule Augsburg Mathematik fürinternational Management und Betriebswirtschaft Wintersemester 202/3 Aufgabensammlung Mathematik für International Management und Betriebswirtschaft
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel
 Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 9 14 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM I (Wirtschaftsmathematik) Gleichungssysteme
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 9 14 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM I (Wirtschaftsmathematik) Gleichungssysteme
Mathematik 1 für TM Aufgabensammlung Sommersemester 2008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten
 Mathematik für TM Aufgabensammlung Sommersemester 008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten Aufgabe Lösen Sie in den nachstehenden Aufgaben die Klammern auf und fassen Sie soweit
Mathematik für TM Aufgabensammlung Sommersemester 008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten Aufgabe Lösen Sie in den nachstehenden Aufgaben die Klammern auf und fassen Sie soweit
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2012/2013
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik. 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl. C: 2 ist eine Primzahl D: 7 7. F: 3 ist Teiler von 9
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Mathematik 1 für TM Aufgabensammlung Sommersemester 2008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten
 Mathematik 1 für TM Aufgabensammlung Sommersemester 2008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten Aufgabe 1 Lösen Sie in den nachstehenden Aufgaben die Klammern auf und fassen Sie
Mathematik 1 für TM Aufgabensammlung Sommersemester 2008 Prof. Dr. Stefan Etschberger Hochschule Ravensburg-Weingarten Aufgabe 1 Lösen Sie in den nachstehenden Aufgaben die Klammern auf und fassen Sie
10 Lineare Gleichungssysteme
 ChrNelius : Lineare Algebra I (WS 2004/05) 1 10 Lineare Gleichungssysteme (101) Bezeichnungen: Ein System a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 ( ) a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a
ChrNelius : Lineare Algebra I (WS 2004/05) 1 10 Lineare Gleichungssysteme (101) Bezeichnungen: Ein System a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 ( ) a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a
Mathematik für Studierende der Biologie und des Lehramtes Chemie
 Einführung I Mathematik für Studierende der Biologie und des Lehramtes Chemie Dominik Schillo Universität des Saarlandes 007 (Stand: 007, 4:9 Uhr) Wie viel Kilogramm Salzsäure der Konzentration % muss
Einführung I Mathematik für Studierende der Biologie und des Lehramtes Chemie Dominik Schillo Universität des Saarlandes 007 (Stand: 007, 4:9 Uhr) Wie viel Kilogramm Salzsäure der Konzentration % muss
Klausurenkurs zum Staatsexamen (WS 2016/17): Lineare Algebra und analytische Geometrie 1
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Lineare Algebra und analytische Geometrie. (Herbst 2005, Thema, Aufgabe ) Bestimmen Sie alle reellen Lösungen des folgenden linearen Gleichungssystems:.2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Lineare Algebra und analytische Geometrie. (Herbst 2005, Thema, Aufgabe ) Bestimmen Sie alle reellen Lösungen des folgenden linearen Gleichungssystems:.2
Fachhochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel
 Fachhochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 9 14 jutta.arrenberg@fh-koeln.de Übungen zur Vorlesung Wirtschaftsmathematik Gleichungssysteme
Fachhochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 9 14 jutta.arrenberg@fh-koeln.de Übungen zur Vorlesung Wirtschaftsmathematik Gleichungssysteme
Klausurenkurs zum Staatsexamen (WS 2014/15): Lineare Algebra und analytische Geometrie 1
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 204/5): Lineare Algebra und analytische Geometrie. (Herbst 2005, Thema, Aufgabe ) Bestimmen Sie alle reellen Lösungen des folgenden linearen Gleichungssystems:.2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 204/5): Lineare Algebra und analytische Geometrie. (Herbst 2005, Thema, Aufgabe ) Bestimmen Sie alle reellen Lösungen des folgenden linearen Gleichungssystems:.2
Übungen zum Ferienkurs Lineare Algebra WS 14/15
 Übungen zum Ferienkurs Lineare Algebra WS 14/15 Matrizen und Vektoren, LGS, Gruppen, Vektorräume 1.1 Multiplikation von Matrizen Gegeben seien die Matrizen A := 1 1 2 0 5 1 8 7 Berechnen Sie alle möglichen
Übungen zum Ferienkurs Lineare Algebra WS 14/15 Matrizen und Vektoren, LGS, Gruppen, Vektorräume 1.1 Multiplikation von Matrizen Gegeben seien die Matrizen A := 1 1 2 0 5 1 8 7 Berechnen Sie alle möglichen
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 +
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 +
Wirtschaftsmathematik - Übungen SS 2019
 Wirtschaftsmathematik - Übungen SS 9 Blatt : Lineare Algebra. Gegeben ist eine eine 3 3 Matrix C = (c ij ) mit und eine Matrix B = ( a) Schreiben Sie die Matrix C an! j i für i < j c ij = () i j für i
Wirtschaftsmathematik - Übungen SS 9 Blatt : Lineare Algebra. Gegeben ist eine eine 3 3 Matrix C = (c ij ) mit und eine Matrix B = ( a) Schreiben Sie die Matrix C an! j i für i < j c ij = () i j für i
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Lineare Gleichungssysteme Das System a x + a x +... + a n x n = b a x + a x +... + a n x n = b. +. +... +. =. a m x + a m x +... + a mn x n = b m heißt lineares Gleichungssystem
Lineare Gleichungssysteme Lineare Gleichungssysteme Das System a x + a x +... + a n x n = b a x + a x +... + a n x n = b. +. +... +. =. a m x + a m x +... + a mn x n = b m heißt lineares Gleichungssystem
6.2. Prüfungsaufgaben zur Lösbarkeit von LGS
 6.. Prüfungsaufgaben zur Lösbarkeit von LGS Aufgabe : Lösbarkeit von LGS () Berechne mit Hilfe des Gauß-Verfahrens die Lösungsmengen der drei folgenden inhomogenen Gleichungssysteme. Gib außerdem die Lösungsmengen
6.. Prüfungsaufgaben zur Lösbarkeit von LGS Aufgabe : Lösbarkeit von LGS () Berechne mit Hilfe des Gauß-Verfahrens die Lösungsmengen der drei folgenden inhomogenen Gleichungssysteme. Gib außerdem die Lösungsmengen
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2015/2016
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik. Lehrstuhl für BWL, insb. Mathematik und Statistik Prof. Dr. Michael Merz Mathematik für Betriebswirte I Wintersemester 2018/2019
 Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
Aussagenlogik 1. Gegeben seien folgende Aussagen: A: 7 ist eine ungerade Zahl B: a + b < a + b, a, b R C: 2 ist eine Primzahl D: 7 7 E: a + 1 b, a, b R F: 3 ist Teiler von 9 Bestimmen Sie den Wahrheitswert
3 Lineare Gleichungen
 Aufgabe 3. Man löse die lineare Gleichung a 2 x b 2 a a(b ax) b + b2 a = a, a b nach der Unbekannten x auf und diskutiere die möglichen Fälle. a 2 x b 2 a a(b ax) b + b2 a = a a b a 2 bx b 3 a 2 b + a
Aufgabe 3. Man löse die lineare Gleichung a 2 x b 2 a a(b ax) b + b2 a = a, a b nach der Unbekannten x auf und diskutiere die möglichen Fälle. a 2 x b 2 a a(b ax) b + b2 a = a a b a 2 bx b 3 a 2 b + a
Aufgabe 1: Bestimmen Sie Zahlen a b. ,, für die. = b. und gleichzeitig a + b + 1 = 0 gilt. Lösung zu Aufgabe 1:
 WS 99/99 Aufgabe : Bestimmen Sie Zahlen a b,, für die 6 b a und gleichzeitig a + b + gilt. Lösung zu Aufgabe : WS 99/99 Aufgabe : Ein Unernehmen stellt aus ohstoffen (,,, ) Zwischenprodukte ( Z, Z, Z )
WS 99/99 Aufgabe : Bestimmen Sie Zahlen a b,, für die 6 b a und gleichzeitig a + b + gilt. Lösung zu Aufgabe : WS 99/99 Aufgabe : Ein Unernehmen stellt aus ohstoffen (,,, ) Zwischenprodukte ( Z, Z, Z )
Mathematik für Wirtschaftswissenschaftler I (Lineare Algebra) 2. Klausur Wintersemester 2011/
 Mathematik für Wirtschaftswissenschaftler I (Lineare Algebra) 2. Klausur Wintersemester 2011/2012 21.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN. Nachname:...................................................................
Mathematik für Wirtschaftswissenschaftler I (Lineare Algebra) 2. Klausur Wintersemester 2011/2012 21.03.2012 BITTE LESERLICH IN DRUCKBUCHSTABEN AUSFÜLLEN. Nachname:...................................................................
Die Lösungsmenge besteht aus allen n-tupeln reeller Zahlen x 1
 III. Lineare Gleichungssysteme ================================================================= 3. Einführung ---------------------------------------------------------------------------------------------------------------
III. Lineare Gleichungssysteme ================================================================= 3. Einführung ---------------------------------------------------------------------------------------------------------------
Lineare Algebra und Numerische Mathematik für D-BAUG
 R. Käppeli L. Herrmann W. Wu Herbstsemester 2016 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 6 Aufgabe 6.1 Berechnen Sie die Determinanten der beiden
R. Käppeli L. Herrmann W. Wu Herbstsemester 2016 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 6 Aufgabe 6.1 Berechnen Sie die Determinanten der beiden
Lineare Algebra und Numerische Mathematik für D-BAUG
 R Käppeli L Herrmann W Wu Herbstsemester 26 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 2 Aufgabe 2 Welche der folgenden Aussagen sind korrekt? (i) Jedes
R Käppeli L Herrmann W Wu Herbstsemester 26 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 2 Aufgabe 2 Welche der folgenden Aussagen sind korrekt? (i) Jedes
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 + x 2 =
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Lineare : Einführung Beispiele linearer a) b) c) 2x 1 3x 2 = 1 x 1 + x 2 =
Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 1
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 1 1.1 (Herbst 2005, Thema 1, Aufgabe 1) Bestimmen Sie alle reellen Lösungen des folgenden linearen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 1 1.1 (Herbst 2005, Thema 1, Aufgabe 1) Bestimmen Sie alle reellen Lösungen des folgenden linearen
5 Lineare Gleichungssysteme und Determinanten
 5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
Übungsaufgaben. Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler. Teil 1: Lineare Algebra und Optimierung.
 Übungsaufgaben Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler Teil : Lineare Algebra und Optimierung Wintersemester Matrizenrechnung Aufgabe ( 3 0 Gegeben sind die Matrizen A = 2 5 2 4 D =
Übungsaufgaben Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler Teil : Lineare Algebra und Optimierung Wintersemester Matrizenrechnung Aufgabe ( 3 0 Gegeben sind die Matrizen A = 2 5 2 4 D =
Länge eines Vektors und Abstand von zwei Punkten 2. 4 = 6. Skalarprodukt und Winkel zwischen Vektoren
 Länge eines Vektors und Abstand von zwei Punkten Aufgabe Bestimme die Länge des Vektors x. Die Länge beträgt: x ( ) =. Skalarprodukt und Winkel zwischen Vektoren Aufgabe Es sind die Eckpunkte A(; ), B(
Länge eines Vektors und Abstand von zwei Punkten Aufgabe Bestimme die Länge des Vektors x. Die Länge beträgt: x ( ) =. Skalarprodukt und Winkel zwischen Vektoren Aufgabe Es sind die Eckpunkte A(; ), B(
Lineare Gleichungssysteme. 1-E Ma 1 Lubov Vassilevskaya
 Lineare Gleichungssysteme 1-E Ma 1 Lubov Vassilevskaya Systeme linearer Funktionen und Gleichungen y = a 1 a 2... a n lineare Funktion Funktion ersten Grades,,..., unabhängige Variablen y abhängige Variable
Lineare Gleichungssysteme 1-E Ma 1 Lubov Vassilevskaya Systeme linearer Funktionen und Gleichungen y = a 1 a 2... a n lineare Funktion Funktion ersten Grades,,..., unabhängige Variablen y abhängige Variable
10. Übung zur Linearen Algebra I -
 . Übung zur Linearen Algebra I - en Kommentare an Hannes.Klarner@FU-Berlin.de FU Berlin. WS 29-. Aufgabe 37 i Für welche α R besitzt das lineare Gleichungssystem 4 αx + αx 2 = 4x + α + 2x 2 = α genau eine,
. Übung zur Linearen Algebra I - en Kommentare an Hannes.Klarner@FU-Berlin.de FU Berlin. WS 29-. Aufgabe 37 i Für welche α R besitzt das lineare Gleichungssystem 4 αx + αx 2 = 4x + α + 2x 2 = α genau eine,
Klausur Wirtschaftsmathematik VO
 Klausur Wirtschaftsmathematik VO 01. Oktober 2016 Bitte leserlich in Druckbuchstaben ausfüllen! NACHNAME: VORNAME: MATRIKELNUMMER: ERLAUBT: nur die Formelsammlung des Instituts! VERBOTEN: Taschenrechner
Klausur Wirtschaftsmathematik VO 01. Oktober 2016 Bitte leserlich in Druckbuchstaben ausfüllen! NACHNAME: VORNAME: MATRIKELNUMMER: ERLAUBT: nur die Formelsammlung des Instituts! VERBOTEN: Taschenrechner
Basistext Lineare Gleichungssysteme. Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=%
 Basistext Lineare Gleichungssysteme Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=% Mit zwei Unbekannten gibt es die allgemeine Form:! #+% '=( Gelten mehrere dieser Gleichungen
Basistext Lineare Gleichungssysteme Eine lineare Gleichung mit einer Unbekannten hat die allgemeine Form! #=% Mit zwei Unbekannten gibt es die allgemeine Form:! #+% '=( Gelten mehrere dieser Gleichungen
Kurs Grundlagen der Linearen Algebra und Analysis
 Aufgabe B0513 Lineare Optimierung Ein Unternehmen stellt drei Endprodukte P 1,P und P 3 her. Die jeweils zur Produktion einer Mengeneinheit des jeweiligen Endproduktes benötigten Mengeneinheiten des Zwischenproduktes
Aufgabe B0513 Lineare Optimierung Ein Unternehmen stellt drei Endprodukte P 1,P und P 3 her. Die jeweils zur Produktion einer Mengeneinheit des jeweiligen Endproduktes benötigten Mengeneinheiten des Zwischenproduktes
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
(Analysis und lineare Algebra) im Sommersemester 2018 15. April 2018 1/46 Die Dimension eines Vektorraums Satz 2.27 (Basisergänzungssatz) Sei V ein Vektorraum über einem Körper K. Weiter seien v 1,...,
Tutorium zur Vorlesung Lineare Algebra und analytische Geometrie I -Bearbeitungsvorschlag-
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN D Rost L Ramzews WS 18/19 Blatt 9118 Tutorium zur Vorlesung Lineare Algebra und analytische Geometrie I -Bearbeitungsvorschlag- 1 Für das in Abhängigkeit
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN D Rost L Ramzews WS 18/19 Blatt 9118 Tutorium zur Vorlesung Lineare Algebra und analytische Geometrie I -Bearbeitungsvorschlag- 1 Für das in Abhängigkeit
Lineare Algebra I (WS 12/13)
 Lineare Algebra I (WS 12/13) Bernhard Hanke Universität Augsburg 17.10.2012 Bernhard Hanke 1 / 9 Wir beschreiben den folgenden Algorithmus zur Lösung linearer Gleichungssysteme, das sogenannte Gaußsche
Lineare Algebra I (WS 12/13) Bernhard Hanke Universität Augsburg 17.10.2012 Bernhard Hanke 1 / 9 Wir beschreiben den folgenden Algorithmus zur Lösung linearer Gleichungssysteme, das sogenannte Gaußsche
Corinne Schenka Vorkurs Mathematik WiSe 2012/13
 4. Lineare Gleichungssysteme Ein lineares Gleichungssystem ist ein System aus Gleichungen mit Unbekannten, die nur linear vorkommen. Dieses kann abkürzend auch in Matrizenschreibweise 1 notiert werden:
4. Lineare Gleichungssysteme Ein lineares Gleichungssystem ist ein System aus Gleichungen mit Unbekannten, die nur linear vorkommen. Dieses kann abkürzend auch in Matrizenschreibweise 1 notiert werden:
05. Lineare Gleichungssysteme
 05 Lineare Gleichungssysteme Wir betrachten ein System von m Gleichungen in n Unbestimmten (Unbekannten) x 1,, x n von der Form a 11 x 1 + a 12 x 2 + a 13 x 3 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + a
05 Lineare Gleichungssysteme Wir betrachten ein System von m Gleichungen in n Unbestimmten (Unbekannten) x 1,, x n von der Form a 11 x 1 + a 12 x 2 + a 13 x 3 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + a
Scheinklausur zur Linearen Algebra I, WS 05/06, 1. Teil
 6.2.2005 Scheinklausur zur Linearen Algebra I, WS 05/06,. Teil Prof. Dr. G. Hiß Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und unterschreiben
6.2.2005 Scheinklausur zur Linearen Algebra I, WS 05/06,. Teil Prof. Dr. G. Hiß Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und unterschreiben
RUHR - UNIVERSITÄT BOCHUM KLAUSUR. Name. Vorname. Teilnehmer-Nr. Zur Beachtung. Bitte nicht ausfüllen
 RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 6.2.997 (WS 97/98) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 6.2.997 (WS 97/98) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
6 Lineare Gleichungssysteme
 6 LINEARE GLEICHUNGSSYSTEME 3 6 Lineare Gleichungssysteme Unter einem linearen Gleichungssystem verstehen wir ein System von Gleichungen α ξ + + α n ξ n = β α m ξ + + α mn ξ n = β m mit Koeffizienten α
6 LINEARE GLEICHUNGSSYSTEME 3 6 Lineare Gleichungssysteme Unter einem linearen Gleichungssystem verstehen wir ein System von Gleichungen α ξ + + α n ξ n = β α m ξ + + α mn ξ n = β m mit Koeffizienten α
RUHR - UNIVERSITÄT BOCHUM KLAUSUR. Name. Vorname. Teilnehmer-Nr. Zur Beachtung. Bitte nicht ausfüllen
 RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen Lineare Algebra 03.2.994 (WS 94/95) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt 9 Aufgaben;
RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen Lineare Algebra 03.2.994 (WS 94/95) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt 9 Aufgaben;
Klausur Wirtschaftsmathematik Lösungshinweise
 Klausur Wirtschaftsmathematik Lösungshinweise Prüfungsdatum: 9. Januar 05 Prüfer: Etschberger, Heiden, Jansen Studiengang: IM und BW Aufgabe Auf einem Markt konkurrieren zum Zeitpunkt t insgesamt 3 Produkte
Klausur Wirtschaftsmathematik Lösungshinweise Prüfungsdatum: 9. Januar 05 Prüfer: Etschberger, Heiden, Jansen Studiengang: IM und BW Aufgabe Auf einem Markt konkurrieren zum Zeitpunkt t insgesamt 3 Produkte
Analytische Geometrie
 Analytische Geometrie Übungsaufgaben Lineare Gleichungssysteme Oberstufe Alexander Schwarz www.mathe-aufgaben.com Oktober 05 Pflichtteilaufgaben (ohne GTR) Aufgabe : Löse die folgenden linearen Gleichungssysteme:
Analytische Geometrie Übungsaufgaben Lineare Gleichungssysteme Oberstufe Alexander Schwarz www.mathe-aufgaben.com Oktober 05 Pflichtteilaufgaben (ohne GTR) Aufgabe : Löse die folgenden linearen Gleichungssysteme:
Serie 11: Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung
 D-MATH/D-PHYS Lineare Algebra I HS 2017 Dr. Meike Akveld Serie 11: Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung 1. In dieser Aufgabe beweisen wir die Existenz der LR-Zerlegung einer quadratischen
D-MATH/D-PHYS Lineare Algebra I HS 2017 Dr. Meike Akveld Serie 11: Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung 1. In dieser Aufgabe beweisen wir die Existenz der LR-Zerlegung einer quadratischen
9 Lineare Gleichungssysteme
 9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
Eigenwerte und Eigenvektoren von Matrizen
 Eigenwerte und Eigenvektoren von Matrizen Betrachtet wird eine (n,n)-matrix A. Eine Zahl λ heißt Eigenwert von A, wenn ein Vektor v existiert, der nicht der Nullvektor ist und für den gilt: A v = λ v.
Eigenwerte und Eigenvektoren von Matrizen Betrachtet wird eine (n,n)-matrix A. Eine Zahl λ heißt Eigenwert von A, wenn ein Vektor v existiert, der nicht der Nullvektor ist und für den gilt: A v = λ v.
6. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 6. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 2/ 25..-.2. Aufgabe G (Lineare Gleichungssysteme)
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 6. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS 2/ 25..-.2. Aufgabe G (Lineare Gleichungssysteme)
Kapitel 9: Lineare Gleichungssysteme
 Kapitel 9: Lineare Gleichungssysteme Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 9: Lineare Gleichungssysteme 1 / 15 Gliederung 1 Grundbegriffe
Kapitel 9: Lineare Gleichungssysteme Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 9: Lineare Gleichungssysteme 1 / 15 Gliederung 1 Grundbegriffe
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 18. April 2016 Übersicht über die Methoden Seien v 1,..., v r Vektoren in K n. 1. Um zu prüfen, ob die Vektoren v 1,...,
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 18. April 2016 Übersicht über die Methoden Seien v 1,..., v r Vektoren in K n. 1. Um zu prüfen, ob die Vektoren v 1,...,
Tutorium/Klausurvorbereitung. Finanzmathematik
 Tutorium/Klausurvorbereitung Finanzmathematik Gesundheits- und Tourismusmanagement Hochschule für Wirtschaft und Umwelt Dozent Dipl. Mathematiker (FH) Roland Geiger Aufgabe : Folgende Matrizen sind gegeben:
Tutorium/Klausurvorbereitung Finanzmathematik Gesundheits- und Tourismusmanagement Hochschule für Wirtschaft und Umwelt Dozent Dipl. Mathematiker (FH) Roland Geiger Aufgabe : Folgende Matrizen sind gegeben:
1 Einführung Gleichungen und 2 Unbekannte Gleichungen und 3 Unbekannte... 4
 Wirtschaftswissenschaftliches Zentrum 3 Universität Basel Mathematik 2 Dr Thomas Zehrt Lineare Gleichungssysteme Inhaltsverzeichnis Einführung 2 2 Gleichungen und 2 Unbekannte 2 2 3 Gleichungen und 3 Unbekannte
Wirtschaftswissenschaftliches Zentrum 3 Universität Basel Mathematik 2 Dr Thomas Zehrt Lineare Gleichungssysteme Inhaltsverzeichnis Einführung 2 2 Gleichungen und 2 Unbekannte 2 2 3 Gleichungen und 3 Unbekannte
(c) x 2 + 3x 3 = 1 3x 1 + 6x 2 3x 3 = 2 6x 1 + 6x x 3 = 5
 Musterlösungen zu Mathematik II (Elementare Lineare Algebra) Blatt Nathan Bowler A: Präsenzaufgaben. Zeilenstufenform und reduzierte Zeilenstufenform erkennen Welche der folgenden Matrizen sind in Zeilenstufenform?
Musterlösungen zu Mathematik II (Elementare Lineare Algebra) Blatt Nathan Bowler A: Präsenzaufgaben. Zeilenstufenform und reduzierte Zeilenstufenform erkennen Welche der folgenden Matrizen sind in Zeilenstufenform?
RUHR - UNIVERSITÄT BOCHUM KLAUSUR. Name. Vorname. Teilnehmer-Nr. Zur Beachtung. Bitte nicht ausfüllen
 RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 5.2.998 (WS 998) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 5.2.998 (WS 998) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
( ) Lineare Gleichungssysteme
 102 III. LINEARE ALGEBRA Aufgabe 13.37 Berechne die Eigenwerte der folgenden Matrizen: ( ) 1 1 0 1 1 2 0 3 0 0, 2 1 1 1 2 1. 1 1 0 3 Aufgabe 13.38 Überprüfe, ob die folgenden symmetrischen Matrizen positiv
102 III. LINEARE ALGEBRA Aufgabe 13.37 Berechne die Eigenwerte der folgenden Matrizen: ( ) 1 1 0 1 1 2 0 3 0 0, 2 1 1 1 2 1. 1 1 0 3 Aufgabe 13.38 Überprüfe, ob die folgenden symmetrischen Matrizen positiv
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Berechnung von Eigenwerten und Eigenvektoren Mathematik 1 Bestimmung von Eigenwerten und Eigenvektoren Jedes λ, das det(a
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Berechnung von Eigenwerten und Eigenvektoren Mathematik 1 Bestimmung von Eigenwerten und Eigenvektoren Jedes λ, das det(a
1 Lineare Gleichungssysteme und Matrizen
 1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
1 Lineare Gleichungssysteme und Matrizen Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eines der wichtigsten Themen der linearen Algebra. Wir werden zunächst einige grundlegende Begriffe
Serie 8: Online-Test
 D-MAVT Lineare Algebra I HS 018 Prof Dr N Hungerbühler Serie 8: Online-Test Schicken Sie Ihre Lösung bis spätestens Freitag, den 3 November um 14:00 Uhr ab Diese Serie besteht nur aus Multiple-Choice-Aufgaben
D-MAVT Lineare Algebra I HS 018 Prof Dr N Hungerbühler Serie 8: Online-Test Schicken Sie Ihre Lösung bis spätestens Freitag, den 3 November um 14:00 Uhr ab Diese Serie besteht nur aus Multiple-Choice-Aufgaben
Mischungsverhältnisse: Nehmen wir an, es stehen zwei Substanzen (zum Beispiel Flüssigkeiten) mit spezifischen Gewicht a = 2 kg/l bzw.
 Kapitel 5 Lineare Algebra 51 Lineare Gleichungssysteme und Matrizen Man begegnet Systemen von linearen Gleichungen in sehr vielen verschiedenen Zusammenhängen, etwa bei Mischungsverhältnissen von Substanzen
Kapitel 5 Lineare Algebra 51 Lineare Gleichungssysteme und Matrizen Man begegnet Systemen von linearen Gleichungen in sehr vielen verschiedenen Zusammenhängen, etwa bei Mischungsverhältnissen von Substanzen
18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus
 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus Conrad Donau 8. Oktober 2010 Conrad Donau 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus 8. Oktober 2010 1 / 7 18.1 Wiederholung: Ebenen in R 3
18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus Conrad Donau 8. Oktober 2010 Conrad Donau 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus 8. Oktober 2010 1 / 7 18.1 Wiederholung: Ebenen in R 3
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 12. Übung: Woche vom (Lin.Alg.
 Übungsaufgaben 12. Übung: Woche vom 16. 1.-20. 1. 2017 (Lin.Alg. I): Heft Ü 3: 2.1.11; 2.1.8; 2.1.17; 2.2.1; 2.2.3; 1.1.1; 1.1.4; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Übungsaufgaben 12. Übung: Woche vom 16. 1.-20. 1. 2017 (Lin.Alg. I): Heft Ü 3: 2.1.11; 2.1.8; 2.1.17; 2.2.1; 2.2.3; 1.1.1; 1.1.4; Hinweis 1: 3. Test (Integration, analyt. Geom.) ist seit 9.1. freigeschalten
Serie 11: Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung
 D-MATH/D-PHYS Lineare Algebra I HS 06 Dr. Meike Akveld Serie : Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung. Gegeben seien die folgenden geordneten Basen B = (v, v, v, v ) und C = (w, w,
D-MATH/D-PHYS Lineare Algebra I HS 06 Dr. Meike Akveld Serie : Lineare Gleichungssysteme, Gauss-Elimination & LR-Zerlegung. Gegeben seien die folgenden geordneten Basen B = (v, v, v, v ) und C = (w, w,
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lineare Algebra: Lineare Gleichungssysteme und Matrizen
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare Algebra: Lineare Gleichungssysteme und Matrizen Das komplette Material finden Sie hier: School-Scout.de Thema: Lineare Algebra:
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare Algebra: Lineare Gleichungssysteme und Matrizen Das komplette Material finden Sie hier: School-Scout.de Thema: Lineare Algebra:
Hauptprüfung Abiturprüfung Baden-Württemberg
 Hauptprüfung Abiturprüfung 018 Baden-Württemberg Teil 1 (ohne Hilfsmittel) Analysis, Stochastik, Vektorgeometrie, Matrizenrechnung berufliche Gymnasien (AG, BTG, EG, SG, TG, WG) Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 018 Baden-Württemberg Teil 1 (ohne Hilfsmittel) Analysis, Stochastik, Vektorgeometrie, Matrizenrechnung berufliche Gymnasien (AG, BTG, EG, SG, TG, WG) Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüfung Fachhochschulreife 04 Baden-Württemberg Aufgabe 5 Wirtschaftliche Anwendungen Hilfsmittel: grafikfähiger Taschenrechner Berufskolleg Alexander chwarz www.mathe-aufgaben.com Januar 05 Ein Unternehmen
Hauptprüfung Fachhochschulreife 04 Baden-Württemberg Aufgabe 5 Wirtschaftliche Anwendungen Hilfsmittel: grafikfähiger Taschenrechner Berufskolleg Alexander chwarz www.mathe-aufgaben.com Januar 05 Ein Unternehmen
Lineare Algebra I (WS 12/13)
 Lineare Algebra I (WS 12/13) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 18.10.2012 Alexander Lytchak 1 / 12 Lineare Gleichungssysteme Wir untersuchen nun allgemeiner Gleichungssysteme der
Lineare Algebra I (WS 12/13) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 18.10.2012 Alexander Lytchak 1 / 12 Lineare Gleichungssysteme Wir untersuchen nun allgemeiner Gleichungssysteme der
Lineare Algebra und Numerische Mathematik D-BAUG Winter 2013 Prof. H.-R. Künsch. Regeln Multiple Choice:
 b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Winter 03 Prof. H.-R. Künsch c Alle Aufgaben haben das gleiche Gewicht. Die Lösungswege müssen, abgesehen von Aufgabe, nachvollziehbar dargestellt
b Prüfung Lineare Algebra und Numerische Mathematik D-BAUG Winter 03 Prof. H.-R. Künsch c Alle Aufgaben haben das gleiche Gewicht. Die Lösungswege müssen, abgesehen von Aufgabe, nachvollziehbar dargestellt
1 Geometrie - Lösungen von linearen Gleichungen
 Übungsmaterial Geometrie - Lösungen von linearen Gleichungen Lineare Gleichungen sind von der Form y = f(x) = 3x + oder y = g(x) = x + 3. Zwei oder mehr Gleichungen bilden ein Gleichungssystem. Ein Gleichungssystem
Übungsmaterial Geometrie - Lösungen von linearen Gleichungen Lineare Gleichungen sind von der Form y = f(x) = 3x + oder y = g(x) = x + 3. Zwei oder mehr Gleichungen bilden ein Gleichungssystem. Ein Gleichungssystem
Die simultane Anwendung des Gauß-Verfahrens zur Lösung der beiden Gleichungssysteme
 Übungsblatt Aufgabe.1 (F92 - A9-8P) a). Gegeben seien die Matrix 1 0 2 1 1 2 A = 0 1 0 0 2 0 und die Vektoren b 1 2 0 =, b = 4 2 4 4 1 2 Die simultane Anwendung des Gauß-Verfahrens zur Lösung der beiden
Übungsblatt Aufgabe.1 (F92 - A9-8P) a). Gegeben seien die Matrix 1 0 2 1 1 2 A = 0 1 0 0 2 0 und die Vektoren b 1 2 0 =, b = 4 2 4 4 1 2 Die simultane Anwendung des Gauß-Verfahrens zur Lösung der beiden
RUHR - UNIVERSITÄT BOCHUM KLAUSUR. Name. Vorname. Teilnehmer-Nr. Zur Beachtung. Bitte nicht ausfüllen
 RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 7.12.1996 (WS 96/97) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 7.12.1996 (WS 96/97) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
Wirtschafts- und Finanzmathematik
 Prof Dr Stefan Etschberger HSA Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2016/17 Determinanten: Vorüberlegung Permutationen und Inversionen
Prof Dr Stefan Etschberger HSA Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2016/17 Determinanten: Vorüberlegung Permutationen und Inversionen
2.2 Lineare Gleichungssysteme (LGS)
 2.2 Lineare Gleichungssysteme (LGS) Definition 2.2.. Ein LGS über einem Körper K von m Gleichungen in n Unbekannten x,..., x n ist ein Gleichungssystem der Form a x + a 2 x 2 +... + a n x n = b a 2 x +
2.2 Lineare Gleichungssysteme (LGS) Definition 2.2.. Ein LGS über einem Körper K von m Gleichungen in n Unbekannten x,..., x n ist ein Gleichungssystem der Form a x + a 2 x 2 +... + a n x n = b a 2 x +
Scheinklausur zur Linearen Algebra I, WS 03/04, 1. Teil
 12.12.2003 Scheinklausur zur Linearen Algebra I, WS 03/04, 1. Teil Prof. Dr. H. Pahlings Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und
12.12.2003 Scheinklausur zur Linearen Algebra I, WS 03/04, 1. Teil Prof. Dr. H. Pahlings Tragen Sie bitte auf diesem Deckblatt leserlich und in Blockbuchstaben Ihren Namen und Ihre Matrikelnummer ein und
Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix
 Inhaltsverzeichnis Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix Auf dieser Seite werden Matrizen und Vektoren fett gedruckt, um sie von Zahlen zu unterscheiden. Betrachtet wird das
Inhaltsverzeichnis Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix Auf dieser Seite werden Matrizen und Vektoren fett gedruckt, um sie von Zahlen zu unterscheiden. Betrachtet wird das
Allgemeines Gleichungssystem mit zwei Gleichungen und zwei Variablen. Der erste Index bezeichnet die Nummer der Zeile, der zweite die der Spalte.
 Lineare Gleichungssysteme. Einleitung Lineare Gleichungssysteme sind in der Theorie und in den Anwendungen ein wichtiges Thema. Theoretisch werden sie in der Linearen Algebra untersucht. Die Numerische
Lineare Gleichungssysteme. Einleitung Lineare Gleichungssysteme sind in der Theorie und in den Anwendungen ein wichtiges Thema. Theoretisch werden sie in der Linearen Algebra untersucht. Die Numerische
a) Geben Sie die zugehörigen Matrizen A RZ, A ZE und A RE. Berechnen Sie die fehlenden Werte der Rohstoff-Zwischenprodukt-Matrix.
 Lineare lgebra / nalytische Geometrie Leistungskurs ufgabe 4 Kosten und Gewinne Ein Betrieb stellt aus den Rohstoffen R 1, R 2, R 3 und R 4 die Zwischenprodukte Z 1, Z 2, Z 3 und Z 4 her und aus diesen
Lineare lgebra / nalytische Geometrie Leistungskurs ufgabe 4 Kosten und Gewinne Ein Betrieb stellt aus den Rohstoffen R 1, R 2, R 3 und R 4 die Zwischenprodukte Z 1, Z 2, Z 3 und Z 4 her und aus diesen
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
(Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
Klausur Wirtschaftsmathematik VO
 Klausur Wirtschaftsmathematik VO 08. Mai 2015 Bitte leserlich in Druckbuchstaben ausfüllen! NACHNAME: VORNAME: MATRIKELNUMMER: ERLAUBT: nur die Formelsammlung des Instituts! VERBOTEN: Taschenrechner und
Klausur Wirtschaftsmathematik VO 08. Mai 2015 Bitte leserlich in Druckbuchstaben ausfüllen! NACHNAME: VORNAME: MATRIKELNUMMER: ERLAUBT: nur die Formelsammlung des Instituts! VERBOTEN: Taschenrechner und
Abschlussprûfung Berufskolleg. Prüfungsaufgaben aus Baden-Württemberg. Matrizenrechnung. Jahrgänge 2002 bis Text Nr Stand 12.
 Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Matrizenrechnung Jahrgänge 00 bis 06 Text Nr. 733 Stand. Juli 06 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 733 Berufskolleg:
Abschlussprûfung Berufskolleg (Fachhochschulreife) Prüfungsaufgaben aus Baden-Württemberg Matrizenrechnung Jahrgänge 00 bis 06 Text Nr. 733 Stand. Juli 06 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 733 Berufskolleg:
Lineares Gleichungssystem
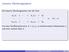 Lineares Gleichungssystem Ein lineares Gleichungssystem hat die Form a 1,1 x 1 + + a 1,n x n = b 1...... Ax = b a m,1 x 1 + + a m,n x n = b m mit einer Koeffizientenmatrix A = (a i,j ), zu bestimmenden
Lineares Gleichungssystem Ein lineares Gleichungssystem hat die Form a 1,1 x 1 + + a 1,n x n = b 1...... Ax = b a m,1 x 1 + + a m,n x n = b m mit einer Koeffizientenmatrix A = (a i,j ), zu bestimmenden
Lineare Gleichungssysteme
 Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Kapitel 16. Aufgaben. Verständnisfragen. Rechenaufgaben
 Kapitel 16 Aufgaben Verständnisfragen Aufgabe 16.1 Ist das Produkt quadratischer oberer bzw. unterer Dreiecksmatrizen wieder eine obere bzw. untere Dreiecksmatrix? Aufgabe 16.2 Bekanntlich gilt im Allgemeinen
Kapitel 16 Aufgaben Verständnisfragen Aufgabe 16.1 Ist das Produkt quadratischer oberer bzw. unterer Dreiecksmatrizen wieder eine obere bzw. untere Dreiecksmatrix? Aufgabe 16.2 Bekanntlich gilt im Allgemeinen
Aufgaben zu Kapitel 14
 Aufgaben zu Kapitel 14 1 Aufgaben zu Kapitel 14 Verständnisfragen Aufgabe 14.1 Haben (reelle) lineare Gleichungssysteme mit zwei verschiedenen Lösungen stets unendlich viele Lösungen? Aufgabe 14.2 Gibt
Aufgaben zu Kapitel 14 1 Aufgaben zu Kapitel 14 Verständnisfragen Aufgabe 14.1 Haben (reelle) lineare Gleichungssysteme mit zwei verschiedenen Lösungen stets unendlich viele Lösungen? Aufgabe 14.2 Gibt
Das Lösen linearer Gleichungssysteme
 Das Lösen linearer Gleichungssysteme Lineare Gleichungen Die Gleichung a 1 x 1 + a 2 x 2 +... + a n x n = b ist eine lineare Gleichung in den n Variablen x 1, x 2,..., x n. Die Zahlen a 1, a 2,..., a n
Das Lösen linearer Gleichungssysteme Lineare Gleichungen Die Gleichung a 1 x 1 + a 2 x 2 +... + a n x n = b ist eine lineare Gleichung in den n Variablen x 1, x 2,..., x n. Die Zahlen a 1, a 2,..., a n
D-CHAB Frühlingssemester 2018
 D-CHAB Frühlingssemester 2018 Grundlagen der Mathematik II Dr Marcel Dettling Lösung 4 1) Nur für die folgenden Wahlen kann man das Produkt bilden: A A mit Dimension (2, 2) (2, 2) (2, 2): 1 2 A Y mit Dimension
D-CHAB Frühlingssemester 2018 Grundlagen der Mathematik II Dr Marcel Dettling Lösung 4 1) Nur für die folgenden Wahlen kann man das Produkt bilden: A A mit Dimension (2, 2) (2, 2) (2, 2): 1 2 A Y mit Dimension
Aufgaben zu Kapitel 16
 Aufgaben zu Kapitel 16 1 Aufgaben zu Kapitel 16 Verständnisfragen Aufgabe 16.1 Ist das Produkt quadratischer oberer bzw. unterer Dreiecksmatrizen wieder eine obere bzw. untere Dreiecksmatrix? Aufgabe 16.2
Aufgaben zu Kapitel 16 1 Aufgaben zu Kapitel 16 Verständnisfragen Aufgabe 16.1 Ist das Produkt quadratischer oberer bzw. unterer Dreiecksmatrizen wieder eine obere bzw. untere Dreiecksmatrix? Aufgabe 16.2
Schriftliche Abiturprüfung Mathematik
 Freie und Hansestadt Hamburg Behörde für Schule und Berufsbildung Schriftliche Abiturprüfung Mathematik Beispielaufgaben für einen hilfsmittelfreien Prüfungsteil grundlegendes Anforderungsniveau Impressum
Freie und Hansestadt Hamburg Behörde für Schule und Berufsbildung Schriftliche Abiturprüfung Mathematik Beispielaufgaben für einen hilfsmittelfreien Prüfungsteil grundlegendes Anforderungsniveau Impressum
7.1 Matrizen und Vektore
 7.1 Matrizen und Vektore Lineare Gleichungssysteme bestehen aus einer Gruppe von Gleichungen, in denen alle Variablen nur in der 1. Potenz vorkommen. Beispiel Seite 340 oben: 6 x 2 = -1 + 3x 2 = 4 mit
7.1 Matrizen und Vektore Lineare Gleichungssysteme bestehen aus einer Gruppe von Gleichungen, in denen alle Variablen nur in der 1. Potenz vorkommen. Beispiel Seite 340 oben: 6 x 2 = -1 + 3x 2 = 4 mit
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker I Wintersemester 3/4 Aufgabenblatt 3 3. Januar
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathematik für Informatiker I Wintersemester 3/4 Aufgabenblatt 3 3. Januar
Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix.
 LINEARE ALGEBRA Lösbarkeit von linearen Gleichungssystemen Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix Gleichungssysteme
LINEARE ALGEBRA Lösbarkeit von linearen Gleichungssystemen Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix Gleichungssysteme
Über- und unterbestimmte
 Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Lineare Gleichungssysteme
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 5. Dezember 2007 Definition : Tomographie (Fortsetzung) : Tomographie Definition: Ein lineares Gleichungssystem (LGS) ist ein System von n
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 5. Dezember 2007 Definition : Tomographie (Fortsetzung) : Tomographie Definition: Ein lineares Gleichungssystem (LGS) ist ein System von n
