Analogfilter für Audio
|
|
|
- Oswalda Lorenz
- vor 7 Jahren
- Abrufe
Transkript
1 Analogfilter für Audio Bachelorarbeit im Rahmen des Audioelektronik Seminars verfasst von Jan Dutz Betreuer: DI David Fischer
2 Inhaltsverzeichnis Einleitung 4 2 Filtertheorie 6 2. Einführung Polkenngrößen Einfluss der Polgüte Filtertypen Phasenverzerrungen und Gruppenlaufzeit Standard-Approximationen Butterworth-Approximation Bessel-Approximation Tschebyscheff-Approximation Filterentwurf Toleranzschema Entwurf mittels Tabellen Entwurfsbeispiel Equalizer-Grundstrukturen EQ-Charakteristiken Equalizer mit invertierendem Verstärker Equalizer mit zwei Summierverstärkern Aktive Filter für Audio Sallen-Key-Tiefpass Dimensionierungsgleichungen Dimensionierungsbeispiel und Simulation Multiple-Feedback-Tiefpass Dimensionierungsgleichungen Simulation des Einflusses der begrenzten OPV-Bandbreite Vergleich der Dimensionierungsverfahren State-Variable-Filter Übertragungsfunktionen und Dimensionierung Filterstruktur mit unabhängig einstellbarer Güte Simulation der modifizierten Filterstruktur Simulation des Einflusses der begrenzten OPV-Bandbreite
3 4.4 Weitere Filtertechniken Passive RLC-Filter Aktive Filter basierend auf RLC-Strukturen Realisierungsaspekte 66 6 Schlussbetrachtungen 68 Literaturverzeichnis 70 3
4 Einleitung Das Thema Analogfilter für Audioanwendungen ist breit gefächert: Im Audiobereich gibt es vielfältige Einsatzbereiche für Filter, angefangen von der Signalaufbereitung, über die Störungsunterdrückung, bis zu Klanggestaltung und Klangsynthese. Neben den Anwendungsbereichen gibt es weitere Aspekte, welche die Vielschichtigkeit dieses Themas verdeutlichen: Es kommen verschiedenste Filtertypen und Filtercharakteristiken zum Einsatz, von einfachen Tief- und Hochpässen erster Ordnung, über Shelving- und Peakfilter in Equalizern bis hin zu Filtern höherer Ordnung in Anti-Aliasing-Filtern und Frequenzweichen. Ein weiterer Aspekt der Vielfalt ist die Steuerung der Grenzfrequenz von Filtern: In manchen Anwendungen muss die Grenzfrequenz der Filter im Betrieb nicht verändert werden; Equalizer werden zumeist manuell mit Schaltern und Potentiometern eingestellt; bei dynamischen Filtern zur Klanggestaltung wird die Grenzfrequenz elektronisch über Spannungen oder Ströme gesteuert. In vielen Anwendungen findet der Einsatz von Filtern in der digitalen Domäne statt, was die Signalaufbereitung vor und nach der Digitalwandlung als das relevanteste Teilgebiet analoger Filter erscheinen lässt. Da aber digitale Filter und Equalizer zum Teil nach analogen Vorbildern entworfen werden, besitzt auch die Theorie und Schaltungstechnik analoger Filter und Equalizer ihre Relevanz. Motivation Diese Arbeit soll einen Überblick über das Thema Analogfilter in Audioanwendungen bieten und dabei die Bereiche Filtertheorie, Filterschaltungen und deren Dimensionierung sowie Aspekte der Realisierung von Filtern, wie zum Beispiel die Wahl der Komponenten, berücksichtigen. Damit soll diese Arbeit als Grundlage für folgende Arbeiten und Projekte auf diesem Gebiet dienen. Um dies zu erreichen musste das Themengebiet sinnvoll begrenzt werden: Bei den möglichen Anwendungen liegt der Fokus dieser Arbeit auf Equalizern, manuell einstellbaren Filtern sowie Anti-Aliasing- und Rekonstruktionsfiltern. Bei den behandelten Filterschaltungen liegt der Schwerpunkt auf aktiven Filtern in Kaskadentechnik. Der Begriff Kaskadentechnik beschreibt das Zerlegen von Filtern höherer Ordnung in Teilfilter zweiter Ordnung; diese Teilfilter werden dann mit den weit verbreiteten Sallen-Key-, Multiple-Feedback-, oder State-Variable-Filterschaltungen realisiert. 4
5 Zum Inhalt Die Arbeit beginnt mit einer Zusammenfassung der Filtertheorie. Schwerpunkte liegen dabei auf den verschiedenen Charakteristiken von Filtern zweiter Ordnung sowie der Frage, wie sich diese Charakteristiken in den Übertragungsfunktionen wiederspiegeln. Das Thema Gruppenlaufzeit sowie die Filtercharakteristiken Bessel, Butterworth, und Tschebyscheff werden behandelt. In einem Beispiel zum Filterentwurf werden diese Charakteristiken miteinander verglichen. Es folgt ein Kapitel über Equalizerschaltungen. Es werden zwei Schaltungsstrukturen vorgestellt, auf deren Basis verschiedene Shelving- und Peakfilter realisiert werden können. Im Hauptteil dieser Arbeit werden die für die Kaskadentechnik wichtigen Schaltungen der Sallen-Key-, Multiple-Feedback-, und State-Variable-Filter diskutiert. Von ersteren beiden wird jeweils das Tiefpassfilter behandelt, um grundsätzliche Unterschiede zwischen beiden Schaltungsfamilien herauszuarbeiten. Es werden Beispieldimensionierungen durchgeführt und die dimensionierten Filterschaltungen werden simuliert. In den Simulationen werden die Auswirkungen von Bauteiltoleranzen sowie der Einfluss der Bandbreite der Operationsverstärker untersucht. Im Abschnitt zum State- Variable-Filter wird eine Schaltung vorgestellt, mit der sich in Verbindung mit den behandelten Equalizerschaltungen ein parametrisches Peakfilter realisieren lässt. Das Kapitel Realisierungsaspekte behandelt die Eigenschaften passiver Bauelemente und deren Einsatzmöglichkeiten in Filterschaltungen. 5
6 2 Filtertheorie 2. Einführung Die Filtertheorie beschäftigt sich mit der Beschreibung und dem Entwurf von Analogfiltern. Die Beschreibung von Analogfiltern erfolgt mittels Laplace-Übertragungsfunktionen. Die Übertragungsfunktionen werden zum Teil frequenznormiert dargestellt. Das bedeutet, dass die Variable der Übertragungsfunktion, die komplexe Frequenz s, auf die Einsatzkreisfrequenz ω D des Filters bezogen wird. Die Einsatzkreisfrequenz ist die Frequenz, bei der sich das Ende des Durchlassbereiches des Filters befindet und die Dämpfung des Filters einsetzt. Zumeist wird ω D als 3 db-grenzkreisfrequenz definiert; da dies aber nicht in allen Fällen sinnvoll ist, gibt es auch andere Definitionen der Einsatzkreisfrequenz. Die frequenznormierte Darstellung der Übertragungsfunktion ermöglicht eine einheitliche Beschreibung von Filtern unabhängig von deren Einsatzfrequenz und der verwendeten Schaltungstopologie. In der frequenznormierten Darstellung sind die Koeffizienten der Übertragungsfunktion dimensionslos. Das Prinzip der Frequenznormierung wird nun anhand des Beispiels eines RC-Tiefpasses.Ordnung verdeutlicht: Die Übertragungsfunktion des Tiefpasses lautet H(s) =, die 3 db-grenzkreisfrequenz liegt bei ω g =. In diesem Fall entspricht die Einsatzkreisfrequenz ω RC D, auf +src die normiert wird, der 3 db-grenzkreisfrequenz ω g des Filters. Bei der Frequenznormierung wird von den Frequenzvariablen ω,s auf die normierten Frequenzvariablen Ω,S übergegangen. Die Normierungsvorschrift lautet: Ω = ω bzw. S = s (2.) ω D ω D Die frequenznormierte Übertragungsfunktion des RC-Tiefpasses lautet nun: H(S) = + S Mittels der sogenannten Filtertransformationen lassen sich die verschiedenen Filtercharakteristiken (Hochpass, Bandpass, usw.) auf Tiefpassfilter in frequenznormierter Darstellung zurückführen. Die Entwurfsmethoden der Filtertheorie beziehen sich daher meist auf ein allgemeines Tiefpassfilter n-ter Ordnung der Form H(S) = + b S + b 2 S b n S n. (2.2) 6
7 Da es sich bei den in der Filtertheorie betrachteten Systemen um kausale LZI -Systeme handelt, sind Pol- und Nulstellen der Systeme entweder reell oder konjugiertkomplex. Nenner und Zähler der Übertragungsfunktionen können daher in quadratische Polynome zerlegt werden somit können die Übertragungsfunktionen durch ein Produkt biquadratischer Teilfunktionen der Form H(s) = a 0 + a s + a 2 s 2 + b s + b 2 s 2 (2.3) dargestellt werden.[0] Die Zerlegung von Übertragungsfunktionen in biquadratische Teilfunktionen hat in der Filtertheorie eine große Bedeutung: In dieser Form beschriebene Filter können durch eine Serienschaltung aktiver Filter zweiter Ordnung ohne weitere Umformungen der Übertragungsfunktion realisiert werden; in vielen Tabellenwerken zum Filterentwurf werden die Filterkoeffizienten für in Biquads zerlegte Übertragungsfunktionen angegeben. Zudem können die Koeffizienten der quadratischen Nennerpolynome durch die Polkenngrößen Polfrequenz ω P und Polgüte Q P ausgedrückt werden. Diese, den Schwingkreiskenngrößen Resonanzfrequenz und Güte äquivalenten Größen ermöglichen es, Rückschlüsse über wichtige Eigenschaften des Filters zu ziehen. I s N s-ebene s N N N R s N2 Abbildung 2.: Zur Definition der Polkenngrößen Lage des konjugiert-komplexen Polpaares s N,2 in der s-ebene 2.. Polkenngrößen Es folgt die Definition der Polkenngrößen nach v.wangenheim [0]. Die biquadratische Übertragungsfunktion besitzt zwei Polstellen s N,s N2. In der Filtertheorie ist 7
8 vor allem der Fall konjugiert-komplexer Polstellen relevant. Für das in Abbildung 2. dargestellte konjugiert-komplexe Polpaar s N,2 gelten folgende Gleichungen: s N,2 = σ N ± jω N und s N s N2 = σ N 2 + ω N 2 = s N 2 (2.4) Die Polfrequenz ω P und die Polgüte Q P sind wie folgt definiert:[0] ω P = s N = 2 σ N Q P s N = 2 cos δ (2.5) Die Polfrequenz entspricht dem Betrag der Polstellen; die Polgüte ist vom Winkel δ zwischen den komplexen Zeigern der Pole und der reellen Achse in der linken s- Halbebene abhängig. Die biquadratische Übertragungsfunktion in der Polkenngrößen- Darstellung des Nenners lautet: H(s) = a 0 + a s + a 2 s 2 + s ω P Q P + s2 ω 2 0 (2.6) Für eine Polgüte von Q P = 0, 5 fallen beide Pole zu einer doppelten Polstelle auf der negativ-reellen Achse zusammen. Dies ist der Fall der kritischen Dämpfung. Für steigende Polgüten wandert das Polpaar auf einer Kreisbahn um den Ursprung der s- Ebene in Richtung imaginäre Achse. Der Radius dieses Kreises entspricht der Polfrequenz ω P. Für Werte Q P < 0, 5 ergeben sich zwei reelle Polstellen. Obige Definition der Polgüte ist in diesem Fall nicht mehr anwendbar.[0] Mit passiven RC-Schaltungen können nur Filter mit Polgüten Q P 0, 5 realisiert werden; zur Erzeugung konjugiert-komplexer Polstellen werden aktive RC- oder passive RLC-Schaltungen benötigt. Die Polgüte bestimmt wichtige Eigenschaften eines Filters im Frequenz- sowie im Zeitbereich: Sie ist sowohl maßgeblich für das Auftreten von Resonanzüberhöhungen im Amplitudengang als auch für Überschwingen in der Sprungantwort eines Filters. In der frequenznormierten Darstellung einer Übertragungsfunktion wird die Polfrequenz auf die Einsatzfrequenz bezogen. Es entsteht die normierte Polfrequenz Ω P = ω P /ω D, die Polgüte bleibt unverändert Einfluss der Polgüte Anhand eines Tiefpassfilters zweiter Ordnung mit der Übertragungsfunktion H(s) = + s ω P Q P + s2 ω 2 P 8
9 wird nun der Einfluss der Polgüte auf den Frequenzgang eines Filters untersucht. Abbildung 2.2 stellt den Amplitudengang des Tiefpassfilters für verschiedene Polgüten Q P bei konstanter Polfrequenz ω P = rad /s dar. Aus dem Plot lässt sich entnehmen, dass eine Erhöhung der Polgüte bei gleichbleibender Polfrequenz die 3 db-grenzfrequenz des Filters erhöht. Mit steigender Polgüte setzt die Filterwirkung abrupter ein und der asymptotische Verlauf des Amplitudengangs von 40 db /Dekade wird bei niedrigeren Frequenzen erreicht. Wenn ein Tiefpassfilter zweiter Ordnung eine Polgüte von Q P = / 2 besitzt, stimmen Polfrequenz und 3 db-grenzfrequenz überein. Diese Auslegung des Filters entspricht der Butterworth-Abstimmung. In der englischsprachigen Literatur wird diese Abstimmung auch maximally flat genannt, da bei einer weiteren Erhöhung der Güte Resonanzüberhöhungen nahe der Polfrequenz auftreten. 5 Bode Diagram 0 5 Magnitude (db) Q P =0,25 Q P =0,5 Q =0,707 P Q P = Q P =,44 Q P =2 Q P =4-3dB Frequency (rad/sec) Abbildung 2.2: Amplitudengang Tiefpass 2.Ordnung für verschiedene Polgüten, bei einer Polfrequenz ω P = Eine wichtige Anforderung an Filter ist ein möglichst schmaler und steilflankiger Übergang vom Durchlass- in den Sperrbereich. Die nominelle Flankensteilheit eines Filters von n 20 db /Dekade (n ist die Filterordnung) soll möglichst schnell erreicht werden. Diese Forderung kann nur mit Polgüten größer als 0,5 erfüllt werden. Filter mit einem schmalen Übergangsbereich besitzen somit immer konjugiert-komplexe Polstellen. Im Blickfeld der Filtertheorie liegen solche Filter, die ausschließlich konjugiert-komplexe Polpaare besitzen, beziehungsweise bei ungerader Filterordnung, einen reellen Pol und ansonsten konjugiert-komplexe Polstellen. Je höher die Polgüte, desto stärker werden die Phasenänderungen im Bereich der Pol- 9
10 frequenz. Weicht der Phasengang von einem zur Frequenz proportionalem Verlauf ab, führt dies zu einer nicht konstanten Gruppenlaufzeit. Eine nicht konstante Gruppenlaufzeit hat zur Folge, dass spektrale Komponenten eines Signals beim Durchlaufen des Filters unterschiedlich stark verzögert werden. Dadurch wird die Wellenform des Signals bei gleichbleibendem harmonischen Gehalt verändert. Dies kann besonders bei transienten Audiosignalen unerwünscht sein. Phasenverzerrungen und Gruppenlaufzeit werden in Kapitel 2.3 behandelt. Die Forderung nach einem möglichst steilflankigen Filter lässt sich bei gegebener Filterordnung nicht mit der Forderung nach möglichst geringen Phasenverzerrungen vereinen. Die sogenannten Standardapproximationen ( zum Beispiel Bessel, Butterworth, Tschebyscheff ) sind Kompromisslösungen zwischen diesen konkurrierenden Zielen beim Filterentwurf. Die Standardapproximationen werden in Kapitel 2.4 behandelt. 2.2 Filtertypen Das Nennerpolynom einer biquadratischen Übertragungsfunktion gibt Auskunft über die Lage der Polstellen - und somit über die Resonanzeigenschaften eines Filters. Der Filtertyp wird durch den Zähler der Übertragungsfunktion bestimmt. Dies lässt sich auf einfache Art und Weise anhand von RLC-Filtern zweiter Ordnung veranschaulichen. In Abbildung 2.3 sind die Schaltungen der vier Grundfiltertypen Tiefpass, Hochpass, Bandpass, und Bandsperre als RLC-Vierpol dargestellt. Die Schaltungen bestehen aus einem RLC-Serienschwingkreis; die unterschiedlichen Filtercharakteristiken ergeben sich dadurch, dass die Ausgangsspannung an unterschiedlichen Punkten des Schwingkreises abgegriffen wird. Die Übertragungsfunktionen der vier Filtertypen besitzen somit das gleiche Nennerpolynom und unterscheiden sich nur in ihrem Zähler. Für die Übertragungsfunktion des RLC-Tiefpasses ergibt sich: H TP (s) = sc sc + R + sl = + src + s 2 LC = N(s) (2.7) Für Bandpass, Hochpass und Bandsperre lauten die Übertragungsfunktionen: H BP = src N(s) H HP = s2 LC N(s) H BS = + s2 LC N(s) (2.8) 0
11 R C C L L R H o c h p a s s B a n d p a s s R L R L C C T ie f p a s s B a n d s p e r r e Abbildung 2.3: Die vier Grund-Filtertypen als RLC-Vierpol Die Kenngrößen eines Serienschwingkreises sind die Resonanzfrequenz ω 0 sowie die Güte Q: ω 0 = LC Q = R L C (2.9) Diese Gleichungen lassen sich nach den in den Übertragungsfunktionen vorkommenden Koeffizienten RC und LC auflösen: ω 0 = LC = LC ω0 2 ω 0 Q = R L C LC RC = ω 0 Q Somit lassen sich die Übertragungsfunktionen in den Gleichungen 2.8 durch die Schwingkreiskenngrößen ausdrücken. In der äquivalenten Darstellung mit ω P und Q P lauten die allgemeinen Übertragungsfunktionen der vier Grundfiltertypen zweiter Ordnung (Tiefpass, Bandpass, Hochpass, Bandsperre):[0] H TP (s) = A 0 + s ω P Q P + s2 ω 2 P H BP (s) = A M s ω P Q P + s ω P Q P + s2 ω 2 P (2.0)
12 H HP (s) = A s 2 ω 2 P + s ω P Q P + s2 ω 2 P H BS (s) = + s2 ω 2 P + s ω P Q P + s2 ω 2 P (2.) Dabei sind A 0, A M, A die Grundverstärkungen der Filter. Durch die Darstellung der Filterfunktionen mit den Polkenngrößen lässt sich erkennen, welche Koeffizienten eines Filters beim Verändern der Einsatzfrequenz mit verändert werden. Dies ist in Hinblick auf durchstimmbare Filter von Bedeutung, wenn die Einsatzfrequenz unabhängig von anderen Filtereigenschaften wie der Güte oder der Grundverstärkung einstellbar sein soll. Bodediagramm Tiefpass 2.O. für variable Güten Bodediagramm Hochpass 2.O. für variable Güten Magnitude (db) Magnitude (db) Q=4 Q= Q=4 Phase (deg) Phase (deg) Q= Frequency (rad/sec) Frequency (rad/sec) Abbildung 2.4: Bodediagramme von Tiefpass und Hochpass zweiter Ordnung für verschiedene Güten In Abbildung 2.4 sind die Frequenzgänge von Tiefpass und Hochpass zweiter Ordnung für eine Polfrequenz ω P = rad /s und variablen Polgüten im Bereich zwischen 0,25 und 4 dargestellt. Man erkennt jeweils, dass die Frequenz, bei der die Dämpfung 3 db beträgt, im Allgemeinen nicht der Polfrequenz entspricht. Für hohe Güten nähert sich die 3 db-grenzfrequenz einem Endwert, und die Stelle der Resonanzüberhöhung nähert sich der Polfrequenz. Abbildung 2.5 zeigt die Bodediagramme von Bandpass- und Sperrfilter für variable Polgüten bei einer Polfrequenz von eins. Es ist ersichtlich, dass sich die Phasengänge von Tiefpass, Hochpass und Bandpass nur durch einen Offset unterscheiden. Diese Filtertypen haben die Gemeinsamkeit, dass ihre Nullstellen entweder bei Null oder im Unendlichen liegen; im Übertragungsbereich der Filter liegen somit keine Nullstellen. Aus diesem Grund werden die Filtertypen Band- Hoch- und Tiefpass als Allpolfilter bezeichnet.[8] 2
13 Bandpass Bandsperre 0 0 Magnitude (db) Q=4 Q=0.25 Magnitude (db) Q=4 Q= Q= Phase (deg) 0 45 Phase (deg) 0 45 Q= Frequency (rad/sec) Frequency (rad/sec) Abbildung 2.5: Bodediagramme von Bandpass und Bandsperre zweiter Ordnung für verschiedene Güten 2.3 Phasenverzerrungen und Gruppenlaufzeit Das Phasenverhalten und die davon abhängige Gruppenlaufzeit sind wichtige Kenngrößen von Filtern für Audioanwendungen. Im folgenden werden die Definitionen von Phasenverzerrung und Gruppenlaufzeit nach Preis [7] wiedergegeben. Ein ideales verzerrungsfreies System besitzt die Impulsantwort: h(t) = Kδ(t T ) (2.2) Es skaliert das Eingangssignal mit dem konstanten Faktor K und verzögert es um T. Der Frequenzgang eines solchen Systems lautet: H(ω) = Ke jωt (2.3) Die Verzögerung im Zeitbereich um T führt zu einer Multiplikation des Spektrums mit e jωt. Der Frequenzgang des idealen verzerrungsfreien Systems besteht aus einem konstanten Amplitudengang H(ω) = K und einem linearen, Frequenz-proportionalen Phasengang Φ(ω) = T ω. Lineare Verzerrungen treten auf, wenn der Amplitudengang nicht konstant ist ( Dämpfungsverzerrungen ), sowie wenn der Phasengang keine lineare Funktion von ω ist ( Laufzeitverzerrungen ).[8] Die Gruppenlaufzeit t G ist die negative Ableitung des Phasengangs Φ(ω) nach der Frequenz: t G (ω) = dφ (2.4) dω 3
14 Für ein ideales Verzögerungssystem ist die Gruppenlaufzeit konstant. Die Gruppenlaufzeit ist ein Maß dafür, wie lange ein Filter bei einer bestimmten Frequenz nachschwingt. Eine negative Gruppenlaufzeit verletzt nicht das Kausalitätsprinzip.[6] Der Verlauf der Gruppenlaufzeit über die Frequenz wird bei analogen Filtern mittels der normierten Gruppenlaufzeit T G beschrieben:[3] T G = t G f D = t G ωd 2π T G = 2π dφ dω (2.5) (2.6) In Gleichung 2.5 wird die Gruppenlaufzeit dabei auf die Periodendauer T D der Einsatzfrequenz f D normiert. Für T D gilt: = f D = ω D T D 2π Mit Hilfe von Plots der normierten Gruppenlaufzeit T G lässt sich der Verlauf der Gruppenlaufzeit t G für eine beliebige Einsatzfrequenz ω D eines Filters abschätzen. Dazu muss der Plot denormiert werden, das heißt die Y-Achse wird mit 2π ω D, und die X-Achse mit ω D skaliert. 0 Amplitudengang und Gruppenlaufzeit Betrag [db] Q=0.25 Q=0.707 Q=.44 Q=4 Q=8 40 Normierte Gruppenlaufzeit T G = t G ω D / 2π Q=0.25 Q=0.707 Q= Normierte Frequenz Ω = ω / ω D Q=8 Q=4 Abbildung 2.6: Amplitudengang und Gruppenlaufzeit Bandpass zweiter Ordnung Abbildung 2.6 zeigt die normierte Gruppenlaufzeit T G sowie den Amplitudengang eines Bandpassfilters zweiter Ordnung für variable Güten. Aus dem Plot kann man entnehmen, dass die Gruppenlaufzeit eines Bandpassfilters zweiter Ordnung, mit der 4
15 Mittenfrequenz f D = khz und einer Güte Q = 8 ein schmalbandiges Maximum von knapp 5 ms besitzt. Für diesen Frequenzbereich ist das ein hoher Wert, der deutlich über den in der Literatur [7] angegebenen Perzeptionsschwellen liegt. Diese bewegen sich für mittlere und hohe Frequenzen je nach Messverfahren und Programmmaterial zwischen 0,5 ms und 2 ms, für tiefe Frequenzen zwischen 3 ms und 5 ms. 2.4 Standard-Approximationen Die sogenannten Standard-Approximationen sind Verfahren zur Gewinnung der Koeffizienten von Tiefpassfiltern. Die Standard-Approximationen sind nur für Tiefpässe definiert; dank der Filtertransformationen kann aber ein mittels der Standard-Approximationen entworfenes Tiefpassfilter in ein Filter beliebiger Charakteristik umgerechnet werden. In den folgenden Abschnitten werden die Standard-Approximationen Butterworth, Bessel, Tschebyscheff beschrieben Butterworth-Approximation Die Butterworth-Approximation führt zu einem monoton fallenden Betragsfrequenzgang, der bis zum Ende des Durchgangsbereich ω D möglichst flach verläuft. Mathematisch führt dies zu der Forderung, wonach der Nenner der Betragsquadrat-Funktion H(jΩ) 2 = + k 2 Ω 2 + k 4 Ω kω 2n (2.7) nur von der höchsten vorkommenden Potenz von Ω abhängen soll:[3] H(jΩ) 2 = + kω 2n (2.8) Der Betrag des Nenners steigt somit für 0 < Ω < möglichst langsam und der Betragsfrequenzgang verläuft möglichst flach bis der Term kω 2n betragsmäßig gleich eins ist. Mit dem Faktor k kann man festlegen, wie groß die Dämpfung bei Ω = sein soll. Zur Bestimmung von k wird Ω = gesetzt: H(jΩ) 2 Ω= = + k (2.9) Für eine Betragsdämpfung von 3 db bei ω = ω D beziehungsweise Ω = folgt k =. Zur Ermittlung der Polstellen wird nun die Variable jω durch S ersetzt. 5
16 Die 2n Polstellen von H(S) 2 liegen gleichmäßig verteilt auf einem Kreis in der s- Ebene mit dem Radius 2n k : S...2n = 2n k 2n (2.20) Von diesen Polstellen ordnet man n in der linken Halbebene befindliche Polstellen H(S) zu.[0] Aus den Polstellen lassen sich mit Gleichung 2.5 die Polkenngrößen Ω P und Q P bestimmen. Für Tiefpassfilter zweiter und dritter Ordnung sind die Poldaten der Butterworth-Approximation in Tabelle 2. dargestellt. Mit der Matlab-Funktion butter lassen sich die Koeffizienten eines zeitkontinuierlichen Butterworth-Filters für eine gegebene Ordnung und 3 db-grenzfrequenz bestimmen. Ordnung konj.-kompl.-polpaar reeller Pol 2 Ω P = Q P = 0, Ω P = Q P = Ω P = Tabelle 2.: Poldaten des Butterworth-Tiefpasses, normiert auf 3 db-grenzfrequenz In Abbildung 2.7 rechts sind Amplitudengang und Gruppenlaufzeit von Butterwoth- Tiefpässen zweiter bis zehnter Ordnung dargestellt. 0 Bessel, normiert auf Grenzfrequenz der konstanten Gruppenlaufzeit 0 Butterworth, normiert auf 3dB Grenzfrequenz 0 0 Betrag [db] n=2 Betrag [db] n=2 Normierte Gruppenlaufzeit T G = t G ω D / 2π n=0 n= Normierte Frequenz Ω = ω / ω D n=0 Normierte Gruppenlaufzeit T G = t G ω D / 2π n= Normierte Frequenz Ω = ω / ω D n=0 n=2 Abbildung 2.7: Frequenzverhalten von Bessel- und Butterworth-Approximation 6
17 2.4.2 Bessel-Approximation Abbildung 2.7 links zeigt Amplitudengang und Gruppenlaufzeit von Bessel-Filtern zweiter bis zehnter Ordnung. Wie in der Abbildung ersichtlich führt die Bessel-Approximation zu Filtern mit einem maximal flachen Verlauf der Gruppenlaufzeit, bei einem im Vergleich zur Butterworth-Charakteristik weicheren Dämpfungsverlauf im Übergangsbereich. Die Plots wurden mit Hilfe der Matlab-Funktion besself erzeugt; die mittels dieser Funktion berechneten Filterkoeffizienten sind so normiert, dass bis Ω = die Gruppenlaufzeit annähernd konstant ist. Für eine Grenzfrequenz des Amplitudengangs müssen die Koeffizienten auf eine gewünschte Dämpfung bei Ω = normiert werden. Nach Tietze u. Schenk [3] können die Bessel-Koeffizienten b i=...n für einen allgemeinen Tiefpass der Form H(S) = (2.2) + b S + b 2 S b n S n mit folgender rekursiven Beziehung berechnet werden: b = b i = 2(n i + ) i(2n i + ) b i (2.22) Die so gewonnenen Koeffizienten müssen aber ebenso für eine gewünschte Dämpfung bei Ω = umgerechnet werden. In Tabelle 2.2 sind die Poldaten für Bessel-Tiefpässe zweiter und dritter Ordnung aufgeführt; die Daten sind auf eine 3 db-grenzfrequenz normiert. Ordnung konj.-kompl.-polpaar reeller Pol 2 Ω P =, 27 Q P = 0, 58-3 Ω P =, 44 Q P = 0, 69 Ω P =, 32 Tabelle 2.2: Poldaten des Bessel-Tiefpasses, normiert auf 3 db-grenzfrequenz Tschebyscheff-Approximation Während Butterworth- und Bessel-Approximationen einen monoton fallenden Amplitudengang erzeugen, besitzt der Dämpfungsverlauf von Tschebyscheff-Filtern eine Welligkeit im Durchlassbereich. Die Gruppenlaufzeit besitzt einen ausgeprägten Peak bei Ω =. Auf die Berechnung der Koeffizienten von Tschebyscheff-Tiefpässen wird hier nicht eingegangen. Die Matlab-Funktion cheby berechnet die Koeffizienten eines Tschebyscheff-Filters abhängig von der Ordnung und der angegebenen Welligkeit im Durchlassbereich in db. Tschebyscheff-Tiefpässe werden zumeist nicht auf eine 3 db-grenzfrequenz normiert, sondern auf die Frequenz, bei der die Dämpfung der 7
18 Welligkeit entspricht. In den Tabellen 2.3 und 2.4 sind die Poldaten von Tschebyscheff-Tiefpässen zweiter und dritter Ordnung für Welligkeiten von 0,5 db und db aufgeführt. Ordnung konj.-kompl.-polpaar reeller Pol 2 Ω P =, 23 Q P = 0, 86-3 Ω P =, 07 Q P =, 06 Ω P = 0, 62 Tabelle 2.3: Poldaten Tschebyscheff-Tiefpass, 0,5 db Welligkeit Ordnung konj.-kompl.-polpaar reeller Pol 2 Ω P =, 05 Q P = 0, 95-3 Ω P = Q P = 2, 02 Ω P = 0, 49 Tabelle 2.4: Poldaten Tschebyscheffl-Tiefpass, db Welligkeit In Abbildung 2.8 sind die normierten Amplitudengänge und Gruppenlaufzeiten für Tschebyscheff-Filter mit 0,5 db und db Welligkeit zu sehen. 0 Tschebyscheff 0.5dB Welligkeit, n=[2:0] 0 Tschebyscheff db Welligkeit, n=[2:0] 0 0 Betrag [db] n=2 Betrag [db] n=2 Normierte Gruppenlaufzeit T G = t G ω D / 2π n=0 n= Normierte Frequenz Ω = ω / ω D n=2 Normierte Gruppenlaufzeit T G = t G ω D / 2π n=0 n= Normierte Frequenz Ω = ω / ω D n=2 Abbildung 2.8: Frequenzverhalten Tschebyscheff mit 0.5 und db Welligkeit 8
19 2.5 Filterentwurf Die in Abschnitt 2 beschriebenen Filter zweiter Ordnung besitzen mit den Polkenngrößen Ω P und Q P, sowie einem eventuell hinzukommenden konstanten Verstärkungsfaktor A drei Kenngrößen, die beim Entwurf bestimmt werden müssen. Für Filter höherer Ordnung steigt die Anzahl der zu bestimmenden Parameter. Um die Komplexität beim Entwurf zu reduzieren, werden Filter höherer Ordnung mittels sogenannter Tiefpassprototypen entworfen. Das bedeutet, dass unabhängig von dem gewünschten Filtertyp zuerst ein Tiefpassfilter mit den gewünschten Dämpfungseigenschaften entwickelt wird. Mittels der Filtertransformationen wird der entworfene Tiefpassprototyp dann in ein Filter mit gewünschter Charakteristik umgesetzt Toleranzschema Der erste Schritt beim Filterentwurf ist das Festlegen der Anforderungen an das zu entwerfende Filter. Diese werden im sogenannten Toleranzschema formuliert. Das Toleranzschema beschreibt den zulässigen Bereich des Amplitudenganges eines normierten Tiefpassfilters. Dazu wird der Frequenzgang des Filters in drei Arbeitsbereiche unterteilt (siehe Abbildung 2.9): Im Durchlassbereich soll das Nutzsignal möglichst nicht beeinträchtigt werden; es wird die maximal erlaubte Welligkeit des Amplitudengangs angegeben. Das Verhältnis A D,min A D,max legt die Breite des Toleranzbereiches im Durchlassbereich fest. A D ist hierbei die Grundverstärkung des Filters. Der Übergangsbereich beginnt bei Ω = und endet bei Ω = Ω S. In diesem Bereich soll die Dämpfung des Filters bis auf die im Sperrbereich angegebene Mindestdämpfung anwachsen. Bei Beginn des Sperrbereiches bei Ω S wird die Mindestdämpfung des Filters spezifiziert. Sie wird mit dem Quotient A S,max A D,max angegeben.[0] Bei Tiefpässen werden Frequenzbezogene Anforderungen durch die Anwendung der Normierungsvorschrift aus Gleichung. in das Toleranzschema überführt. Für den Beginn des Sperrbereiches ergibt sich also: Ω S = ω S ω D Für die Überführung eines Hochpassfilters in ein normiertes Tiefpassfilter gilt allgemein Ω = ω D ω (2.23) 9
20 Abbildung 2.9: Toleranzschema Diese Vorschrift entspricht, neben einer Skalierung der Frequenzachse durch die Normierung, einer Spiegelung des Amplitudengangs an der Einsatzfrequenz Ω D. Somit gilt, wenn ein Hochpassfilter entworfen werden soll: Ω S = ω D ω S Anhand der im Toleranzschema formulierten Anforderungen kann nun eine geeignete Filter-Approximation gewählt werden. Mit Hilfe von Tabellen der Filterkoeffizienten oder der Poldaten kann nun die Übertragungsfunktion des entworfenen Tiefpassfilters aufgestellt werden Entwurf mittels Tabellen Je nachdem, in welcher Form die Entwurfstabellen aufbereitet sind, müssen die Tabellendaten in die passende Form der allgemeinen Tiefpassübertragungsfunktion eingesetzt werden. Im Tietze u. Schenk [3] werden die Filterdaten als Koeffizienten α i und β i eines Tiefpassfilters der Form H(S) = A 0 i + α i S + β i S 2 dargestellt. Bei ungerader Filterordnung ist b null. Grafik entnommen aus [0] 20
21 In dieser Arbeit werden die Filterdaten durch die normierte Polfrequenz Ω P und die Polgüte Q P ausgedrückt. Diese Darstellung wurde von v.wangenheim [0] übernommen. Die zugehörige Übertragungsfunktion lautet: H(S) = A 0 + S Ω P,R S i + + Ω P,i Q P,i S2 Ω P,i 2 (2.24) Dabei ist Ω P,R die Polfrequenz des bei ungerader Filterordnung auftretenden reellen Pols. Bei gerader Filterordnung fällt der Term +S/Ω P,R weg. Die normierte Übertragungsfunktion des entworfenen Tiefpassprototypen kann nun mit Gleichung 2. denormiert, oder mit Gleichung 2.23 in ein Hochpassfilter transformiert werden Entwurfsbeispiel In diesem Abschnitt wird als Beispiel zum Filterentwurf ein Tiefpassprototyp entwickelt. Das Filter soll eine Dämpfung von 0,5 db bei der Einsatzfrequenz, also bei Ω =, besitzen. Das Filter wird je einmal als Bessel-, Butterworth- und Tschebyscheff-Tiefpass ausgelegt, sodass die verschiedenen Charakteristiken verglichen werden können. Die in den Tabellen 2. und 2.2 angegebenen Poldaten für Butterworth- und Bessel- Tiefpass dritter Ordnung sind auf eine 3 db-dämpfung bei ω D normiert. Daher müssen die Filterdaten für die hier geforderte Dämpfung bei ω D neu berechnet werden. Ermittlung der Bessel-Koeffizienten Mittels der Rekursionsformel aus Gleichung 2.22 werden die Koeffizienten eines Bessel- Tiefpasses dritter Ordnung gewonnen. Es ergibt sich folgende, unskalierte Übertragungsfunktion: H(jΩ) = + jω (jω) (jω)3 Um die gewünschte Dämpfung bei Ω = zu erhalten, muss Ω skaliert werden. Zur Ermittlung des Skalierungsfaktors wird die Betragsquadratfunktion H(jΩ) 2 mit der gewünschten Leistungsdämfung bei Ω = gleichgesetzt: H(jΩ) 2 = 0,5 ( 4 0 Ω2 ) 2 + (Ω 8 20 Ω3 2 = 0 0 ) Die Lösungen dieser Gleichung wurden mit Matlab ermittelt. Als Skalierungsfaktor ist nur die positiv-reelle Lösung Ω = 0, 752 2
22 sinnvoll. Die Frequenzvariable Ω muss mit 0,752 skaliert werden, damit die Dämpfung bei Ω = 0,5 db beträgt. In die Übertragungsfunktion eingesetzt ergibt dies: H(jΩ 0, 752) = + 0, 752jΩ + 0, 225(jΩ) 2 + 0, 028(jΩ) 3 Aus dem Nennerpolynom wurden die Poldaten des entworfenen Besselfilters berechnet: Typ konj.-kompl.-polpaar reeller Pol Bessel Ω P = 3, 39 Q P = 0, 68 Ω P = 3, 8 Ermittlung der Butterworth-Poldaten Zur Ermittlung der Butterworth-Poldaten wird die Betragsquadratfunktion des Butterworth-Tiefpasses aus Gleichung 2.8 bei Ω = ausgewertet und mit der gewünschten Leistungsdämpfung gleichgesetzt: H(jΩ) 2 Ω= = + k 0,5 = 0 0 k = 0, 22 Mit Gleichung 2.20 lässt sich der Betrag der Polstellen ermitteln: S...n = 2n k Mit Gl. 2.5 folgt Ω P,...n = 2n k =, 42 Bei der Normierung des Butterworth-Filters auf die geforderte Dämpfung wird der Winkel der Polstellen, abhängig vom Term 2n in Gleichung 2.20, nicht verändert. Somit bleibt auch die Polgüte des konjugiert-komplexen Polpaares unverändert und kann aus Tabelle 2. übernommen werden. Die Poldaten des neu normierten Butterworth-Filters sind: Typ konj.-kompl.-polpaar reeller Pol Butterworth Ω P =, 42 Q P = Ω P =, 42 Vergleich der Filtercharakteristiken Die Poldaten des Tschebyscheff-Filters können aus Tabelle 2.3 übernommen werden, da der Tschebyscheff-Tiefpass mit 0,5 db Welligkeit schon auf eine 0,5 db-dämpfung bei der Durchlassgrenze normiert ist. 22
23 Abbildung 2.0 stellt den Frequenzgang sowie die normierte Gruppenlaufzeit der entworfenen Filter dar. Alle drei Filter sind auf die gleiche Dämpfung bei Ω = normiert, wie die Detailansicht des Amplitudengangs zeigt. In der Grobansicht des Amplitudenganges ist zu erkennen, dass die Dämpfung des Tschebyscheff-Filters bei bedeutend niedrigeren Frequenzen als die des Bessel-Filters einsetzt. Die normierte Gruppenlaufzeit des Tschebyscheff-Filters zeigt einen schmalen Peak bei Ω =. Für eine Einsatzfrequenz des Filters bei ω D = 20 khz würde der Zahlenwert dieses Peaks aber im 0 µs-bereich liegen, was sicher unterhalb der Perzeptionsschwelle liegt.[7] Betrag in [db] Phase in Grad Amplitudengang Tschebyscheff Bessel Butterworth Tschebyscheff Bessel Butterworth Phasengang Normierte Frequenz Ω=ω/ω D Betrag in [db] Amplitudengang (Detail) Tschebyscheff Bessel Butterworth Normierte Gruppenlaufzeit T G Tschebyscheff 0.5 Butterworth Bessel Ω=ω/ω D Abbildung 2.0: Vergleich der entworfenen Filter 23
24 3 Equalizer-Grundstrukturen In diesem Abschnitt werden zwei Equalizer-Schaltungstypen diskutiert. Beide Schaltungen enthalten als Hauptbestandteil einen Filter-Funktionsblock, der die Charakteristik des Equalizers festlegt. Je nach verwendetem Filtertyp arbeiten die Schaltungen als Shelvingfilter oder als Peakfilter. Neben Equalizerschaltungen mit eingebetteten Filtern zur Erzeugung des gewünschten Frequenzganges gibt es eine zweite Gruppe von Equalizerschaltungen, deren Frequenzabhängigkeit mit komplexen Impedanzen wie zum Beispiel Serienschwingkreisen erzeugt wird. Equalizer dieser Art werden hier nicht behandelt. Die Equalizerschaltungen werden auf die Charakteristik ihrer Anhebungs- und Absenkungskennlinien hin untersucht. Dazu wird mit beiden Schaltungen jeweils ein Peakfilter entworfen und simuliert. Die Schaltungstopologie der in den Equalizerstrukturen enthaltenen Filter wird dabei offen gelassen; in der Simulation werden die Filter mit Laplace-Funktionsblöcken modelliert. Eine Filterschaltung, welche besonders für den Einsatz in Equalizerschaltungen geeignet ist und mit der sich ein voll parametrisches Peakfilter realisieren lässt, wird in Abschnitt vorgestellt. 3. EQ-Charakteristiken Vor der Diskussion der Schaltungen werden im folgenden drei Eigenschaften von Equalizern erläutert, welche vor allem für Peakfilter relevant sind. Diese Eigenschaften werden hier nach Bohn [2] wiedergegeben. Symmetrie der Kennlinien Ein Equalizer besitzt symmetrische Kennlinien, wenn die Amplitudengänge von Anhebung und Absenkung symmetrisch zur 0 db-linie verlaufen. Diese Achsensymmetrie in der logarithmischen Darstellung wird dann erreicht, wenn die Übertragungsfunktion des Equalizers bei Anhebungen reziprok zu der Übertragungsfunktion bei Absenkungen ist. Es wird sich zeigen, dass beide vorgestellten Equalizerschaltungen symmetrische Kennlinien besitzen, da die Dämpfungsfunktion durch eine Rückkopplungsschaltung realisiert wird. Wird die Absenkungsfunktion von Equalizern durch 24
25 eine Subtraktion der unerwünschten Signalanteile ausgeführt, ergeben sich unsymmetrische Kennlinien; die Absenkungen sind in diesem Fall schmalbandiger als die Anhebungen. Proportional-Q-Charakteristik Peakfilter mit Proportional-Q-Charakteristik besitzen die Eigenschaft, dass sich bei geringen Anhebungen oder Absenkungen die Glocke der Filterkurve über ein breites Frequenzband erstreckt, jedoch für steigende Anhebungen oder Absenkungen immer schmaler wird. Mathematisch gesehen steigt die Güte des Peakfilters mit dem Betrag von Anhebung oder Absenkung. Constant-Q-Charakteristik Eine Proportional-Q-Charakteristik ist bei Peakfiltern nicht immer günstig: In einem graphischen Equalizer führt die Verwendung von Proportional-Q-Peakfiltern dazu, dass sich zwei benachbarte Bänder nur für eine bestimmte Höhe der Anhebung perfekt ergänzen, da sich die 3 db-grenzfrequenzen oberhalb und unterhalb der Centerfrequenz mit der Höhe der Anhebung verschieben. Um einen graphischen Equalizer so auszulegen, dass die Filterkurve die Faderstellung graphisch wiedergibt, müssen die 3 db-grenzfrequenzen der Peakfilter unabhängig von gewählten Anhebung sein. Dies ist der Fall bei Peakfiltern mit Constant-Q-Charakteristik. Abbildung 3. verdeutlicht die Verhältnisse bei Peakfiltern mit Proportional- und Constant-Q-Charakteristik. Bode Diagram Bode Diagram Magnitude (db) 0 8 Magnitude (db) Frequency (rad/sec) Frequency (rad/sec) (a) Constant-Q (b) Proportional-Q Abbildung 3.: Equalizer-Charakteristiken 25
26 3.2 Equalizer mit invertierendem Verstärker Die erste behandelte Equalizerschaltung besteht aus einem als invertierenden Verstärker beschalteten OPV, einem Potentiometer mit linearer Kennlinie und einem Filter-Funktionsblock. In Abbildung 3.2 ist die Schaltungsstruktur nach Self [9] dargestellt. R u _ e R - + u _ a H ( s ) lin e a r p o t Abbildung 3.2: Equalizerschaltung mit invertierendem Verstärker Mit dem Potentiometer wird zwischen dem Eingangssignal und dem Ausgangssignal übergeblendet; diese Mischung durchläuft das Filter H(s) und wird zum Eingangssignal hinzu addiert. Mit dem Potentiometer wird gleichsam zwischen einer Vorwärtskopplung und einer Rückkopplung übergeblendet. Mathematisch lässt sich das wie folgt formulieren: Wenn α die Stellung des Potentiometers in den Grenzen [0, ] ist, gilt für die die Übertragungsfunktion G(s) des Equalizers: G(s) = + 2αH(s) + ( α) 2H(s) = 2αH(s) ( α) 2H(s) (3.) Der auftretende Faktor zwei ergibt sich daraus, dass der OPV, vom positiven Eingang aus gesehen, einen nicht invertierenden Verstärker darstellt. Das Filternetzwerk H(s) kann invertierend oder nicht invertierend ausgelegt sein. Für ein nicht invertierendes Filter gilt zu beachten, dass je nach Grundverstärkung des Filters, und der Potentiometerstellung, der Nenner von G(s) zu null wird, und somit 26
27 die Schaltung instabil werden kann. Die Grundverstärkung eines nicht invertierenden Filters muss kleiner als 0,5 gewählt werden, damit die Schaltung stabil bleibt. Im folgenden wird davon ausgegangen, dass die Equalizerstruktur mit einem invertierenden Bandpassfilter bestückt wird. Auslegung als Peakfilter Die Equalizerschaltung arbeitet als Peakfilter, wenn H(s) ein Bandpassfilter darstellt. Es wird nun für H(s) das Bandpassfilter zweiter Ordnung aus Gleichung 2.0 gewählt: H(s) = H BP (s) Eingesetzt in Gleichung 3. folgt für die Übertragungsfunktion des Peakfilters: + 2αH BP (s) G(s) = + ( α) 2H BP (s) Mit der Grundverstärkung A M des Bandpassfilters lässt sich nun die maximal mögliche Anhebung und Absenkung des Peakfilters einstellen. Da die Verstärkung des Bandpassfilters bei der Mittenfrequenz der Grundverstärkung entspricht, gilt für den Betragsfrequenzgang des Peakfilters bei der Mittenfrequenz: G(s) = + 2αA M s=jωp + ( α) A M Für die beiden Endpositionen des Potentiometers bei α = und α = 0 ergibt sich: G(s) = + 2A M beziehungsweise G(s) = s=jωp s=jωp + 2A M An dieser Stelle wird die Reziprozität der Übertragungsfunktionen für Anhebung und Absenkung deutlich, die zu symmetrischen EQ-Kennlinien führt. Die maximale Anhebung / Absenkung soll nun 5 db betragen; der Verstärkungsfaktor des Peakfilters bei der Mittenfrequenz muss also G(s) = + 2A M = 0 5/20 = 5, 623 s=jωp betragen. Für die Grundverstärkung des eingebetteten Bandpassfilters ergibt sich der Wert A M = 2, 3. 27
28 Nach dem Einsetzen von Gleichung 2.0 in Gleichung 3. lautet Die Übertragungsfunktion des mit dieser Equalizerschaltung gebildeten Peakfilters: G(s) = + s [ + 2αA M ] + s2 ω P Q P ωp 2 + s [ + 2( α)a M ] + s2 ω P Q P ωp 2 max. Anhebung mit α = 0, 5 Neutralstellung 0 max. Absenkung (3.2) Simulation des Peakfilters Durch eine Simulation des Peakfilters wird die Frage geklärt, ob die Equalizerschaltung aus Abbildung 3.2 Proportional- oder Constant-Q Eigenschaften aufweist und ob die Anhebung in db linear zur Potentiometerstellung erfolgt. Die simulierte Schaltung ist in Abbildung 3.3 dargestellt. OPV und Bandpassfilter wurden in der Simulation durch Laplace-Übertragungsfunktionen modelliert. Für den OPV wurde dabei ein Einpol-Modell gewählt, mit einer Leerlaufverstärkung von 00 db und einer 3 db-grenzfrequenz der Differenzverstärkung im 0 Hz-Bereich. Das Bandpassfilter besitzt die Polgüte Q P = 2 und die Grundverstärkung A M = 2, 5. Das Potentiometer wurde mit zwei Widerständen, deren Wert als Funktion des Parameters R ausgedrückt wurde, modelliert. Es wurde eine AC-Analyse der Schaltung mit einem linearen Parametersweep für R durchgeführt. Die simulierten Frequenzgänge des Peakfilters sind in Abbildung 3.4 dargestellt. Es ist zu erkennen, dass der EQ eine Proportional-Q-Charakteristik besitzt und dass die Anhebung in db nahezu linear zur Potentiometerstellung verläuft. 28
29 5k 5k R2 R AC 0 V Freq scale=00 LAP 00000/(s+) db -2.5*(0.5*s)/(+0.5*s+s^2) LAP3 Freq scale=5k {R} {0000-R} R4 R3 Abbildung 3.3: Simulierte Equalizerschaltung R=00 R=.8k R=2.27k R=3.36k R=4.45k R=644 R=.73k R=2.82k R=3.9k db R=5k k 2k 4k 0k 20k 40k 00k Frequency / Hertz Abbildung 3.4: Simulierte Kennlinien des Peakfilters 29
30 3.3 Equalizer mit zwei Summierverstärkern Die zweite hier behandelte Equalizerschaltung wurde von Bohn [2] als Schaltung für grafische Equalizer vorgestellt und besitzt Constant-Q-Charakteristik. Die Schaltung ist in Abbildung 3.5 dargestellt. Als Besonderheit weist die Schaltung ein Potentiometer mit geerdetem Mittelabgriff auf. Ähnlich der zuvor behandelten Schaltung wird das gefilterte Signal variabel vor- oder rückgekoppelt. Bei der 2-Summierer-Schaltung wird aber nicht stufenlos zwischen Vorwärtskopplung und Rückkopplung übergeblendet. Der geerdete Mittelabgriff des Potentiometers bewirkt, dass das gefilterte Signal entweder vor- oder rückgekoppelt wird. + + u _ e R - R - u _ a R R H ( s ) R _ a c u t b o o s t p o t w it h g r o u n d e d c e n t e r t a p Abbildung 3.5: Equalizerschaltung mit Summierverstärkern Mathematisch führt dies zu einer Fallunterscheidung zwischen der Anhebungs- und Absenkungsfunktion des Equalizers. Vor der Aufstellung der Übertragungsfunktion der Schaltung wird der Verstärkungsfaktor α definiert, mit dem das mit H(s) gefilterte Signal vor- oder rückgekoppelt wird. Dieser Faktor besitzt den Wertebereich [0, R R a ]: In der Mittelposition ist weder die Vorwärts- noch die Rückkopplung wirksam, da das untere Ende von R a auf Masse liegt und somit kein Strom in die Summierverstärker fließt. In den Endpositionen des Potentiometers liegt selbiges nicht mehr im Signalweg 30
31 und der Stromfluss in einen der Summierverstärker wird nur durch R a begrenzt. G(s) = { + αh(s) Anhebung, Schleifer rechts der Mittelstellung +αh(s) Absenkung, Schleifer links der Mittelstellung (3.3) Auslegung als Peakfilter Für eine Auslegung als Peakfilter muss H(s) eine Bandpass-Charakteristik besitzen. Zur Aufstellung der Übertragungsfunktion eines auf Basis der 2-Summierer-Schaltung aufgebauten Peakfilters wird Gleichung 2.0 in Gleichung 3.3 eingesetzt. Nach Vereinfachungen ergibt sich: G(s) = + s ω P Q P [+αa M ]+ s2 ω 2 P + s ω P Q P + s2 ω 2 P + s + s2 ω P Q P ω P 2 + s [+αa ω P Q M ]+ s2 P ω P 2 Anhebung Absenkung (3.4) Der Term + αa M beschreibt den maximalen Verstärkungs- beziehungsweise Dämpfungsfaktor bei der Mittenfrequenz ω P des Peakfilters. Die Unterschiede zwischen der Proportional-Q- und der Constant-Q-Charakteristik werden in den Übertragungsfunktionen 3.4 und 3.2 deutlich: Eine Frequenzanhebung führt in beiden Fällen zur Skalierung der Koeffizienten. Bei der Funktion des Proportional-Q-Filters werden bei Anhebung und Absenkung Zähler- und Nennerpolynom verändert, wohingegen beim Constant-Q-Filter entweder das Zählerpolynom oder das Nennerpolynom beeinflusst wird. Simulation Die Simulation des Peakfilters bestätigte die Constant-Q-Charakteristik der Schaltung. Allerdings führte die Verwendung eines linearen Potentiometers mit geerdetem Mittelabgriff nicht zu einer Pegelanhebung proportional zur Potentiometerstellung. Ein interessantes Ergebnis brachte die Simulation mit einem linearen Potentiometer ohne Mittelabgriff: Die Kennlinien des Peakfilters zeigten für geringe Anhebungen Proportional-Q-Verhalten, welches in ein Constant-Q-Verhalten bei stärkeren Anhebungen überging. Das Ergebnis der Simulation ist in Abbildung 3.7 dargestellt, die simulierte Schaltung in Abbildung
32 AC 0 V 00000/(s+) LAP Freq scale= /(s+) LAP2 Freq scale=00 5k 5k db R R2 5k (0.5*s)/(+0.5*s+s^2) LAP3 Freq scale=5k 5k R3 R4 k R5 {0000-R} {R} R6 R7 Abbildung 3.6: Simulierte Equalizerschaltung R=00 R=.9k R=2.28k R=3.37k R=4.46k R=644 R=.73k R=2.82k R=3.9k R=5k k 2k 4k 0k 20k 40k 00k Frequency / Hertz Abbildung 3.7: Simulierte Anhebungskennlinien 32
33 4 Aktive Filter für Audio 4. Sallen-Key-Tiefpass Sallen-Key-Filter sind Schaltungen zur Realisierung von Filtern zweiter Ordnung. Sallen-Key-Filter werden in der Literatur auch Filter mit Einfachmitkopplung [3], oder auch Voltage Controlled Voltage Source, kurz VCVS-Filter genannt.[2] Grundlage der Sallen-Key-Schaltungen ist ein Verstärkungselement mit positiver Verstärkung v > sowie ein Filternetzwerk mit positiver Rückkopplung. In Abbildung 4. ist die Schaltung eines Sallen-Key-Tiefpasses dargestellt.[0] Sallen-Key-Tiefpässe lassen sich so auslegen, dass die Grenzfrequenz mit einem Potentiometer durchgestimmt werden kann, ohne dass andere Filterparameter mit verändert werden. Sallen-Key-Filter kommen im Audiobereich meist dann zum Einsatz, wenn eine variable Begrenzung des Audiospektrums verlangt wird. C 2 R R 2 v U _ e C U _ a Abbildung 4.: Sallen-Key-Tiefpass Das Verstärkungselement eines Sallen-Key-Tiefpasses muss nicht zwingend ein OPV sein; es können stattdessen auch diskrete oder integrierte Buffer-Verstärker, sowie Current-Feedback-Amplifier zum Einsatz kommen.[3][0] In Abbildung 4.2 ist ein Sallen- Key-Tiefpass mit OPV als Verstärker dargestellt. Eine wichtige Einschränkung besteht beim Sallen-Key-Tiefpass darin, dass die reale Schaltung ein Tiefpassverhalten nur bis in Frequenzbereiche zeigt, in denen der 33
34 C 2 R R 2 + U _ e C - R f U _ a R s Abbildung 4.2: Sallen-Key-Tiefpass mit OPV Verstärker noch als Verstärker arbeitet. Das ist maximal bis zum Erreichen der Transitfrequenz der Fall. Bereits unterhalb der Transitfrequenz wirkt sich der nicht vernachlässigbar kleine Ausgangswiderstand des Verstärkers aus, der mit der Frequenz ansteigt und mit C 2 einen Hochpass bildet. Dies wirkt der Tiefpasswirkung der Schaltung entgegen.[4] C 2 R R 2 U _ e C R _ a O L R f R s U _ a Abbildung 4.3: Ersatzschaltbild für hohe Frequenzen Abbildung 4.3 zeigt das Ersatzschaltbild eines Sallen-Key-Tiefpassfilters für Frequenzen oberhalb der Transitfrequenz des OPVs.[4] In diesem Frequenzbereich liegt die Schleifenverstärkung unter eins, sodass vom OPV nur noch der Open-Loop-Ausgangswiderstand R aol wirksam ist. Für hohe Frequenzen bleibt die Dämpfung konstant und nimmt nicht mehr mit 40 db /Dekade zu. Durch eine Kaskadierung mit einem RC- Tiefpass kann dieser Nachteil ausgeglichen werden. In Anwendungen, die eine gute Unterdrückung hoher Frequenzen erfordern, wie zum Beispiel Anti-Aliasing-Filter, werden Sallen-Key-Tiefpässe zweiter Ordnung nicht eingesetzt. 34
35 4.. Dimensionierungsgleichungen Für die Übertragungsfunktion eines Sallen-Key-Tiefpasses gilt nach [3]: H(s) = v + [C (R + R 2 ) + ( v)r C 2 ]s + R R 2 C C 2 s 2 (4.) Der Faktor v entspricht der Verstärkung des nicht-invertierenden Verstärkers: v = + R f R s. Durch vorheriges Festlegen von Relationen zwischen den Bauteilwerten ergeben sich Spezialisierungen dieser Übertragungsfunktion, die zu einfachen Dimensionierungsgleichungen führen. In der Literatur [3][0] werden meist zwei solcher Festlegungen beschrieben, die zu verschiedenen Dimensionierungen führen. Bei der ersten Herangehensweise wird festgelegt, dass beide Widerstände und beide Kondensatoren gleich groß sein sollen. Diese Dimensionierung führt dazu, dass mit der Verstärkung v die Güte festgelegt wird. Die zweite Möglichkeit liegt in der Vorgabe der Verstärkung v =. In diesem Fall wird normalerweise so vorgegangen, dass das Verhältnis der beiden Kapazitäten gewählt wird und die Widerstände davon abhängig berechnet werden. Für Audioanwendungen ist aber oft die Forderung nach gleich großen Widerständen wichtig, um Stereopotentiometer zur Einstellung der Grenzfrequenz verwenden zu können. Daher wird hier bei der Spezialisierung v = auch R = R 2 vorgegeben. Fall : R = R 2 = R, C = C 2 = C Im Fall gleich großer Widerstände und Kondensatoren vereinfacht sich H(s) zu:[3] H(s) = v + RC[3 v]s + R 2 C 2 s 2 (4.2) Nach [0] gelten folgende Dimensionierungsgleichungen, welche sich aus einem Koeffizientenvergleich mit der allgemeinen Übertragungsfunktion eines Tiefpasses zweiter Ordnung aus Gleichung 2.0 ergeben: Q P = 3 v ω P = RC (4.3) Mit der Verstärkung v kann also unabhängig von der Polfrequenz die Güte eingestellt werden. Durch Einsatz eines Doppelpotentiometers für R und R 2 kann die Polfrequenz unabhängig von Güte und Verstärkung variabel gehalten werden. Die Verstärkung wird durch die Rückkopplungswiderstände des nicht-invertierenden Verstärkers eingestellt. Je näher die Verstärkung gegen 3 geht, desto sensibler reagiert die Schaltung auf Toleranzen von R f und R s. Für Verstärkungen v = 3 wird die Schaltung instabil und schwingt. Nach v.wangenheim[0] sind Polgüten bis Q P = 4 praktikabel, was für 35
Elektronik Prof. Dr.-Ing. Heinz Schmidt-Walter
 6. Aktive Filter Filterschaltungen sind Schaltungen mit einer frequenzabhängigen Übertragungsfunktion. Man unterscheidet zwischen Tief, Hoch und Bandpässen sowie Sperrfiltern. Diesen Filtern ist gemeinsam,
6. Aktive Filter Filterschaltungen sind Schaltungen mit einer frequenzabhängigen Übertragungsfunktion. Man unterscheidet zwischen Tief, Hoch und Bandpässen sowie Sperrfiltern. Diesen Filtern ist gemeinsam,
Systemtheorie. Vorlesung 25: Butterworth-Filter. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 5: Butterworth-Filter Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übersicht Für den Filterentwurf stehen unterschiedliche Verfahren zur Verfügung Filter mit
Systemtheorie Vorlesung 5: Butterworth-Filter Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übersicht Für den Filterentwurf stehen unterschiedliche Verfahren zur Verfügung Filter mit
SV1: Aktive RC-Filter
 Signal and Information Processing Laboratory Institut für Signal- und Informationsverarbeitung. September 6 Fachpraktikum Signalverarbeitung SV: Aktive RC-Filter Einführung In diesem Versuch wird ein aktives
Signal and Information Processing Laboratory Institut für Signal- und Informationsverarbeitung. September 6 Fachpraktikum Signalverarbeitung SV: Aktive RC-Filter Einführung In diesem Versuch wird ein aktives
Systemtheorie. Vorlesung 27: Schaltungstechnische Realisierung von Filtern. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 7: Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Passive LC-Schaltungen erster Ordnung Übertragungsfunktionen, die durch die Entwurfsverfahren bestimmt werden,
Systemtheorie Vorlesung 7: Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Passive LC-Schaltungen erster Ordnung Übertragungsfunktionen, die durch die Entwurfsverfahren bestimmt werden,
Filtertypen Filter 1. Ordnung Filter 2. Ordnung Weitere Filter Idee für unser Projekt. Filter. 3. November Mateusz Grzeszkowski
 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt 3. November 2009 Mateusz Grzeszkowski / 24 Mateusz Grzeszkowski 3. November 2009 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt Motivation
typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt 3. November 2009 Mateusz Grzeszkowski / 24 Mateusz Grzeszkowski 3. November 2009 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt Motivation
Einführung in die Elektronik für Physiker
 Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE hartmut.gemmeke@kit.edu Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbandverstärker und analoge aktive Filter. HF-Verhalten von Operationsverstärkern.
Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE hartmut.gemmeke@kit.edu Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbandverstärker und analoge aktive Filter. HF-Verhalten von Operationsverstärkern.
Praktikum 2.1 Frequenzverhalten
 Elektrizitätslehre 3 Martin Schlup, Martin Weisenhorn. November 208 Praktikum 2. Frequenzverhalten Lernziele Bei diesem Versuch werden die Frequenzabhängigkeiten von elektrischen Grössenverhältnissen aus
Elektrizitätslehre 3 Martin Schlup, Martin Weisenhorn. November 208 Praktikum 2. Frequenzverhalten Lernziele Bei diesem Versuch werden die Frequenzabhängigkeiten von elektrischen Grössenverhältnissen aus
Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf
 Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf 5. Dezember 2016 Siehe begleitend: Kammeyer / Kroschel, Digitale Signalverarbeitung, 7. Auflage, Kapitel 4.2 1 Filterentwurfsstrategien 2 Diskretisierung
Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf 5. Dezember 2016 Siehe begleitend: Kammeyer / Kroschel, Digitale Signalverarbeitung, 7. Auflage, Kapitel 4.2 1 Filterentwurfsstrategien 2 Diskretisierung
Versuch 5: Filterentwurf
 Ziele In diesem Versuch lernen Sie den Entwurf digitaler Filter, ausgehend von der Festlegung eines Toleranzschemas für den Verlauf der spektralen Charakteristik des Filters, kennen. Es können Filtercharakteristiken
Ziele In diesem Versuch lernen Sie den Entwurf digitaler Filter, ausgehend von der Festlegung eines Toleranzschemas für den Verlauf der spektralen Charakteristik des Filters, kennen. Es können Filtercharakteristiken
Diskrete Folgen, z-ebene, einfache digitale Filter
 apitel 1 Diskrete Folgen, z-ebene, einfache digitale Filter 1.1 Periodische Folgen Zeitkoninuierliche Signale sind für jede Frequenz periodisch, zeitdiskrete Signale nur dann, wenn ω ein rationales Vielfaches
apitel 1 Diskrete Folgen, z-ebene, einfache digitale Filter 1.1 Periodische Folgen Zeitkoninuierliche Signale sind für jede Frequenz periodisch, zeitdiskrete Signale nur dann, wenn ω ein rationales Vielfaches
Filterentwurf. Aufgabe
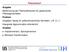 Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Einführung in die Elektronik für Physiker
 Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE gemmeke@ipe.fzk.de Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbanderstärker und analoge aktie Filter. HF-Verhalten on Operationserstärkern.
Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE gemmeke@ipe.fzk.de Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbanderstärker und analoge aktie Filter. HF-Verhalten on Operationserstärkern.
5. Laplacetransformation
 5. Laplacetransformation 5. Übersicht Laplacetransformation Die Laplacetransformation ist eine Verallgemeinerung der Fouriertransformation. Vorteile: Es können auch Transformierte für Signale angegeben
5. Laplacetransformation 5. Übersicht Laplacetransformation Die Laplacetransformation ist eine Verallgemeinerung der Fouriertransformation. Vorteile: Es können auch Transformierte für Signale angegeben
Der Tiefpass Betreuer: Daniel Triebs
 Der Tiefpass Betreuer: Daniel Triebs 1 Gliederung Definiton: Filter Ideale Tiefpass Tiefpass 1.Ordnung Frequenzgänge Grundarten des Filters Filterentwurf Tiefpass 2.Ordnung 2 Definition: Filter 3 Filter
Der Tiefpass Betreuer: Daniel Triebs 1 Gliederung Definiton: Filter Ideale Tiefpass Tiefpass 1.Ordnung Frequenzgänge Grundarten des Filters Filterentwurf Tiefpass 2.Ordnung 2 Definition: Filter 3 Filter
Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω)
 4 Systeme im Frequenzbereich (jω) 4.1 Allgemeines Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω) 1 4.2 Berechnung des Frequenzgangs Beispiel: RL-Filter
4 Systeme im Frequenzbereich (jω) 4.1 Allgemeines Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω) 1 4.2 Berechnung des Frequenzgangs Beispiel: RL-Filter
Skriptum zur 2. Laborübung. Transiente Vorgänge und Frequenzverhalten
 Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.006 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.006 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
Nachrichtentechnik [NAT] Kapitel 6: Analoge Filter. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 6: Analoge Filter. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 6: Analoge Filter. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/48/24274278.jpg) Nachrichtentechnik [NAT] Kapitel 6: Analoge Filter Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 6 Analoge Filter 3 6. Motivation..................................
Nachrichtentechnik [NAT] Kapitel 6: Analoge Filter Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 6 Analoge Filter 3 6. Motivation..................................
19. Frequenzgangkorrektur am Operationsverstärker
 9. Frequenzgangkorrektur am Operationsverstärker Aufgabe: Die Wirkung komplexer Koppelfaktoren auf den Frequenzgang eines Verstärkers ist zu untersuchen. Gegeben: Eine Schaltung für einen nichtinvertierenden
9. Frequenzgangkorrektur am Operationsverstärker Aufgabe: Die Wirkung komplexer Koppelfaktoren auf den Frequenzgang eines Verstärkers ist zu untersuchen. Gegeben: Eine Schaltung für einen nichtinvertierenden
1. Differentialgleichung der Filter zweiter Ordnung
 Prof. Dr.-Ing. F. Keller abor Elektronik 3 Filter zweiter Ordnung Info v.doc Hochschule Karlsruhe Info-Blatt: Filter zweiter Ordnung Seite /6. Differentialgleichung der Filter zweiter Ordnung Ein- und
Prof. Dr.-Ing. F. Keller abor Elektronik 3 Filter zweiter Ordnung Info v.doc Hochschule Karlsruhe Info-Blatt: Filter zweiter Ordnung Seite /6. Differentialgleichung der Filter zweiter Ordnung Ein- und
Analoge und digitale Filter
 Technische Universität Ilmenau Fakultät Elektrotechnik und Informationstechnik FG Nachrichtentechnik Übungsaufgaben zur Lehrveranstaltung Analoge und digitale Filter Filter. Ordnung. Betrachtet wird ein
Technische Universität Ilmenau Fakultät Elektrotechnik und Informationstechnik FG Nachrichtentechnik Übungsaufgaben zur Lehrveranstaltung Analoge und digitale Filter Filter. Ordnung. Betrachtet wird ein
Filterentwurf. Bernd Edler Laboratorium für Informationstechnologie DigSig - Teil 11
 Filterentwurf IIR-Filter Beispiele für die verschiedenen Filtertypen FIR-Filter Entwurf mit inv. Fouriertransformation und Fensterfunktion Filter mit Tschebyscheff-Verhalten Vorgehensweise bei Matlab /
Filterentwurf IIR-Filter Beispiele für die verschiedenen Filtertypen FIR-Filter Entwurf mit inv. Fouriertransformation und Fensterfunktion Filter mit Tschebyscheff-Verhalten Vorgehensweise bei Matlab /
Verzerrungsfreies System
 Verzerrungsfreies System x(n) y(n) n n x(n) h(n) y(n) y(n) A 0 x(n a) A 0 x(n) (n a) h(n) A 0 (n a) H(z) A 0 z a Digitale Signalverarbeitung Liedtke 8.1.1 Erzeugung einer linearen Phase bei beliebigem
Verzerrungsfreies System x(n) y(n) n n x(n) h(n) y(n) y(n) A 0 x(n a) A 0 x(n) (n a) h(n) A 0 (n a) H(z) A 0 z a Digitale Signalverarbeitung Liedtke 8.1.1 Erzeugung einer linearen Phase bei beliebigem
Referat zum Thema Frequenzweichen / Signalfilterung
 Referat zum Thema Gliederung: Einleitung I. Filter erster Ordnung 1. Tiefpass erster Ordnung 2. Hochpass erster Ordnung II. Filter zweiter Ordnung 1.Tiefpass zweiter Ordnung 2.Bandpass zweiter Ordnung
Referat zum Thema Gliederung: Einleitung I. Filter erster Ordnung 1. Tiefpass erster Ordnung 2. Hochpass erster Ordnung II. Filter zweiter Ordnung 1.Tiefpass zweiter Ordnung 2.Bandpass zweiter Ordnung
Analoge aktive Filter
 ZHAW, EK, HS009, Seite Analoge aktive Filter. Allgemeine Bemerkungen. Theoretische Grundlagen der Tiefpassfilter 3. Tiefpass-Hochpass-Transformation 4. Realisierung von Tief- und Hochpassfiltern 5. Realisierung
ZHAW, EK, HS009, Seite Analoge aktive Filter. Allgemeine Bemerkungen. Theoretische Grundlagen der Tiefpassfilter 3. Tiefpass-Hochpass-Transformation 4. Realisierung von Tief- und Hochpassfiltern 5. Realisierung
Antialiasing-Filter. Die erforderliche Dämpfung des Antialiasingfilters bei der halben Abtastfrequenz errechnet sich nach (bei N-Bit ADU): f f.
 ntialiasing-filter Bei der btastung eines auf f < fb bandbeenzten Messsignal ergibt sich, wie später gezeigt wird, für das abgetastete ignal eine periodische Wiederholung des Basisspektrums. m Überlappungen
ntialiasing-filter Bei der btastung eines auf f < fb bandbeenzten Messsignal ergibt sich, wie später gezeigt wird, für das abgetastete ignal eine periodische Wiederholung des Basisspektrums. m Überlappungen
Theorie digitaler Systeme
 Theorie digitaler Systeme Vorlesung 15: Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Entwurfsmethoden für IIR-Filtern sind für Zeitbereich und Bildbereich bekannt Finite-Impulse-Response
Theorie digitaler Systeme Vorlesung 15: Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Entwurfsmethoden für IIR-Filtern sind für Zeitbereich und Bildbereich bekannt Finite-Impulse-Response
2. Der Tiefpass. Filterschaltungen
 130 2. Der Tiefpass Wirksamkeit Schaltungsvarianten Der Tiefpass ist die in der EMV am häufigsten eingesetzte Filterschaltung. Zum besseren Verständnis und zur Abschätzung der Wirksamkeit des Filters können
130 2. Der Tiefpass Wirksamkeit Schaltungsvarianten Der Tiefpass ist die in der EMV am häufigsten eingesetzte Filterschaltung. Zum besseren Verständnis und zur Abschätzung der Wirksamkeit des Filters können
Systemtheorie Teil B
 d + d + c d + c uk d + + yk d + c d + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 8 Musterlösung Frequengang eitdiskreter Systeme...
d + d + c d + c uk d + + yk d + c d + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 8 Musterlösung Frequengang eitdiskreter Systeme...
7. Filter. Aufgabe von Filtern
 . Filter Aufgabe von Filtern Amplitude Sperren einer Frequenz oder eines Frequenzbereichs Durchlassen einer Frequenz oder eines Frequenzbereichs möglichst kleine Phasenänderung Phase Phasenverschiebung
. Filter Aufgabe von Filtern Amplitude Sperren einer Frequenz oder eines Frequenzbereichs Durchlassen einer Frequenz oder eines Frequenzbereichs möglichst kleine Phasenänderung Phase Phasenverschiebung
Betrachtetes Systemmodell
 Betrachtetes Systemmodell Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort h(t), an dessen Eingang das Signal x(t) anliegt. Das Ausgangssignal y(t) ergibt sich dann als das Faltungsprodukt
Betrachtetes Systemmodell Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort h(t), an dessen Eingang das Signal x(t) anliegt. Das Ausgangssignal y(t) ergibt sich dann als das Faltungsprodukt
Grundlagen der Signalverarbeitung
 Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
Elektronik. Aktive Filter. Andreas Zbinden. Gewerblich-Industrielle Berufsschule Bern, GIBB
 6. Semester Elektronik Aktive Filter Andreas Zbinden Gewerblich-Industrielle Berufsschule Bern, GIBB Zusammenfassung In diesem Dokument werden RC-Filter 1. Ordnung mit OPV sowie das Prinzip von Filtern
6. Semester Elektronik Aktive Filter Andreas Zbinden Gewerblich-Industrielle Berufsschule Bern, GIBB Zusammenfassung In diesem Dokument werden RC-Filter 1. Ordnung mit OPV sowie das Prinzip von Filtern
Martin Meyer. Signalverarbeitung. Analoge und digitale Signale, Systeme und Filter 5. Auflage STUDIUM VIEWEG+ TEUBNER
 Martin Meyer Signalverarbeitung Analoge und digitale Signale, Systeme und Filter 5. Auflage STUDIUM VIEWEG+ TEUBNER VII 1 Einführung 1 1.1 Das Konzept der Systemtheorie 1 1.2 Übersicht über die Methoden
Martin Meyer Signalverarbeitung Analoge und digitale Signale, Systeme und Filter 5. Auflage STUDIUM VIEWEG+ TEUBNER VII 1 Einführung 1 1.1 Das Konzept der Systemtheorie 1 1.2 Übersicht über die Methoden
Filter - Theorie und Praxis
 23.06.2016 Manuel C. Kohl, M.Sc. 1 Agenda Einführung und Motivation Analoge und digitale Übertragungssysteme Grundlegende Filtertypen Übertragungsfunktion, Impulsantwort und Faltung Filter mit endlicher
23.06.2016 Manuel C. Kohl, M.Sc. 1 Agenda Einführung und Motivation Analoge und digitale Übertragungssysteme Grundlegende Filtertypen Übertragungsfunktion, Impulsantwort und Faltung Filter mit endlicher
ELEKTRONIK 2 SCHALTUNGSTECHNIK L5-1/18 Prof. Dr.-Ing. Johann Siegl. L5 Frequenzgangdarstellung im Bodediagramm
 1 von 18 15.03.2008 11:39 ELEKTRONIK 2 SCHALTUNGSTECHNIK L5-1/18 Die Frequenzgangdarstellung mittels Bodediagramm ist ein wichtiges Hilfsmittel zur Veranschaulichung der Frequenzverläufe von Übertragungsfaktoren,
1 von 18 15.03.2008 11:39 ELEKTRONIK 2 SCHALTUNGSTECHNIK L5-1/18 Die Frequenzgangdarstellung mittels Bodediagramm ist ein wichtiges Hilfsmittel zur Veranschaulichung der Frequenzverläufe von Übertragungsfaktoren,
ÜBUNG 4: ENTWURFSMETHODEN
 Dr. Emil Matus - Digitale Signalverarbeitungssysteme I/II - Übung ÜBUNG : ENTWURFSMETHODEN 5. AUFGABE: TIEFPASS-BANDPASS-TRANSFORMATION Entwerfen Sie ein nichtrekursives digitales Filter mit Bandpasscharakteristik!
Dr. Emil Matus - Digitale Signalverarbeitungssysteme I/II - Übung ÜBUNG : ENTWURFSMETHODEN 5. AUFGABE: TIEFPASS-BANDPASS-TRANSFORMATION Entwerfen Sie ein nichtrekursives digitales Filter mit Bandpasscharakteristik!
Fourierreihen periodischer Funktionen
 Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
Übung Grundlagen der Elektrotechnik B
 Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
Kurt Diedrich Franz Peter Zantis. Filtern ohne Stress. Theorie - Konzept - Praxis. Elektor-Verlag, Aachen
 Kurt Diedrich Franz Peter Zantis Filtern ohne Stress Theorie - Konzept - Praxis Elektor-Verlag, Aachen Inhaltsverzeichnis Vorwort 7 1. Was bedeutet Filtern"? 9 1.1 Filtergrundtypen 11 1.1.1 Hochpässe 11
Kurt Diedrich Franz Peter Zantis Filtern ohne Stress Theorie - Konzept - Praxis Elektor-Verlag, Aachen Inhaltsverzeichnis Vorwort 7 1. Was bedeutet Filtern"? 9 1.1 Filtergrundtypen 11 1.1.1 Hochpässe 11
Übung 12: Bestimmung des Frequenzganges
 Übung Signale und Systeme Sommersemester Übung :Frequenzgang 5. Juli Übung : Bestimmung des Frequenzganges. Gegeben sei die Übertragungsfunktion eines diskreten Systems: (z ρe jα )(z σe jβ ) (a) Legen
Übung Signale und Systeme Sommersemester Übung :Frequenzgang 5. Juli Übung : Bestimmung des Frequenzganges. Gegeben sei die Übertragungsfunktion eines diskreten Systems: (z ρe jα )(z σe jβ ) (a) Legen
Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt
 DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
DHBW Karlsruhe Grundlagen der Elektrotechnik II Grundlagen der Elektrotechnik II Duale Hochschule Baden Württemberg Karlsruhe Dozent: Gerald Oberschmidt 5 Hoch und Tiefpässe 5. L--Hoch und Tiefpass Abbildung
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
U 2 F 2 = U r, U 2 = F a (U 1 + U r ) U 2 U 1. = V u R (337) 1 + jωτ. (1 + jωτ)(1 + jωτ) 1. Vgl. mit Gl. (317) und (322) liefert die Definition:
 Kapitel 6: Stabilität linearer Schaltungen 50 Anwendungsbeispiel (Verstärker mit SP-Kopplung) Für den dargestellten Verstärker mit einem frequenzabhängigen ückkopplungsnetzwerk läßt sich die Schleifenverstärkung
Kapitel 6: Stabilität linearer Schaltungen 50 Anwendungsbeispiel (Verstärker mit SP-Kopplung) Für den dargestellten Verstärker mit einem frequenzabhängigen ückkopplungsnetzwerk läßt sich die Schleifenverstärkung
Grundlagen der Elektrotechnik 3. Übungsaufgaben
 Campus Duisburg Grundlagen der Elektrotechnik 3 Nachrichtentechnische Systeme Prof. Dr.-Ing. Ingolf Willms Version Juli 08 Aufgabe 1: Man bestimme die Fourier-Reihenentwicklung für die folgende periodische
Campus Duisburg Grundlagen der Elektrotechnik 3 Nachrichtentechnische Systeme Prof. Dr.-Ing. Ingolf Willms Version Juli 08 Aufgabe 1: Man bestimme die Fourier-Reihenentwicklung für die folgende periodische
Bestimmung des Frequenz- und Phasenganges eines Hochpaßfilters 1. und 2. Ordnung sowie Messen der Grenzfrequenz. Verhalten als Differenzierglied.
 5. Versuch Aktive HochpaßiIter. und. Ordnung (Durchührung Seite I-7 ) ) Filter. Ordnung Bestimmung des Frequenz- und Phasenganges eines Hochpaßilters. und. Ordnung sowie Messen der Grenzrequenz. Verhalten
5. Versuch Aktive HochpaßiIter. und. Ordnung (Durchührung Seite I-7 ) ) Filter. Ordnung Bestimmung des Frequenz- und Phasenganges eines Hochpaßilters. und. Ordnung sowie Messen der Grenzrequenz. Verhalten
Allgemeine Einführung in Filter
 Allgemeine Einführung in Filter Konstantin Koslowski TU-Berlin 3. November 2009 Konstantin Koslowski (TU-Berlin) Allgemeine Einführung in Filter 3. November 2009 1 / 22 Inhalt 1 Einführung Was sind Filter
Allgemeine Einführung in Filter Konstantin Koslowski TU-Berlin 3. November 2009 Konstantin Koslowski (TU-Berlin) Allgemeine Einführung in Filter 3. November 2009 1 / 22 Inhalt 1 Einführung Was sind Filter
3. Beschreibung dynamischer Systeme im Frequenzbereich
 3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik
3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik
7.Übung Schaltungstechnik SS2009
 . Aufgabe: Aktives Filter.Ordnung Lernziele Vorteile und Nachteile aktiver Filter im Vergleich zu passiven Filter-Schaltungen. Berechnung eines einfachen Filters.Ordnung. Aufgabenstellung e d a Gegeben
. Aufgabe: Aktives Filter.Ordnung Lernziele Vorteile und Nachteile aktiver Filter im Vergleich zu passiven Filter-Schaltungen. Berechnung eines einfachen Filters.Ordnung. Aufgabenstellung e d a Gegeben
Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik. Hausaufgabe
 Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik Hausaufgabe im Fach Grundlagen der Schaltungstechnik (WS09/0) Bearbeiter Mat.-nr. Emailadresse Aufgabe erreichte Punkte
Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik Hausaufgabe im Fach Grundlagen der Schaltungstechnik (WS09/0) Bearbeiter Mat.-nr. Emailadresse Aufgabe erreichte Punkte
Eingangssignale von Verstärkern sind häufig mit hochfrequenten Störsignalen behaftet, die mit Tiefpaßfiltern unterdrückt werden können.
 4. Versuch Aktives Tiefpaßfilter. und. Ordnung Durchführung Seite H - 9 ) Filter. Ordnung Eingangssignale von Verstärkern sind häufig mit hochfrequenten Störsignalen behaftet, die mit Tiefpaßfiltern unterdrückt
4. Versuch Aktives Tiefpaßfilter. und. Ordnung Durchführung Seite H - 9 ) Filter. Ordnung Eingangssignale von Verstärkern sind häufig mit hochfrequenten Störsignalen behaftet, die mit Tiefpaßfiltern unterdrückt
Theorie digitaler Systeme
 Theorie digitaler Systeme Vorlesung 2: Fakultät für Elektro- und Informationstechnik, anfred Strohrmann Einführung Frequenzgang zeitkontinuierlicher Systeme beschreibt die Änderung eines Spektrums bei
Theorie digitaler Systeme Vorlesung 2: Fakultät für Elektro- und Informationstechnik, anfred Strohrmann Einführung Frequenzgang zeitkontinuierlicher Systeme beschreibt die Änderung eines Spektrums bei
Filterentwurf. Patrick Seiler. Präsentation im Rahmen des Projektlabors der TU Berlin im Sommersemester 2009
 Filterentwurf Patrick Seiler Präsentation im Rahmen des Projektlabors der TU Berlin im Sommersemester 2009 7. Mai 2009 1 Gliederung 1. Was sind Filter? 2. Grundlagen: Charakteristika/Kenngrößen 3. Filterentwurf
Filterentwurf Patrick Seiler Präsentation im Rahmen des Projektlabors der TU Berlin im Sommersemester 2009 7. Mai 2009 1 Gliederung 1. Was sind Filter? 2. Grundlagen: Charakteristika/Kenngrößen 3. Filterentwurf
Muster zu Kurztest Nr. 2 Fach EK 2
 Muster zu Kurztest Nr. Fach EK Auswahl von Aufgaben Prüfung Thema: OpAmp Nichtidealitäten und Filter, 3 Aufgaben, 45 Min. Aufgabe : Einfluss von Offset-Spannung und Biasstrom 9 Punkte Ein Opamp mit I Bias
Muster zu Kurztest Nr. Fach EK Auswahl von Aufgaben Prüfung Thema: OpAmp Nichtidealitäten und Filter, 3 Aufgaben, 45 Min. Aufgabe : Einfluss von Offset-Spannung und Biasstrom 9 Punkte Ein Opamp mit I Bias
Aufbau und Funktionsweise von SCF
 29. Januar 1998 by Bruno Wamister, CH- SCF s lassen sich einfach dimensionieren, mit wenigen Komponenten aufbauen, haben die Eigenschaften von Filtern höherer Ordnung und sind mit einer externen Frequenz
29. Januar 1998 by Bruno Wamister, CH- SCF s lassen sich einfach dimensionieren, mit wenigen Komponenten aufbauen, haben die Eigenschaften von Filtern höherer Ordnung und sind mit einer externen Frequenz
Labor RT Versuch RT1-1. Versuchsvorbereitung. Prof. Dr.-Ing. Gernot Freitag. FB: EuI, FH Darmstadt. Darmstadt, den
 Labor RT Versuch RT- Versuchsvorbereitung FB: EuI, Darmstadt, den 4.4.5 Elektrotechnik und Informationstechnik Rev., 4.4.5 Zu 4.Versuchvorbereitung 4. a.) Zeichnen des Bode-Diagramms und der Ortskurve
Labor RT Versuch RT- Versuchsvorbereitung FB: EuI, Darmstadt, den 4.4.5 Elektrotechnik und Informationstechnik Rev., 4.4.5 Zu 4.Versuchvorbereitung 4. a.) Zeichnen des Bode-Diagramms und der Ortskurve
4. Passive elektronische Filter
 4.1 Wiederholung über die Grundbauelemente an Wechselspannung X Cf(f) X Lf(f) Rf(f) 4.2 Einleitung Aufgabe 1: Entwickle mit deinen Kenntnissen über die Grundbauelemente an Wechselspannung die Schaltung
4.1 Wiederholung über die Grundbauelemente an Wechselspannung X Cf(f) X Lf(f) Rf(f) 4.2 Einleitung Aufgabe 1: Entwickle mit deinen Kenntnissen über die Grundbauelemente an Wechselspannung die Schaltung
SSYLB2 SS06 Daniel Schrenk, Andreas Unterweger Übung 8. Laborprotokoll SSY. Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort
 SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
7. Frequenzselektive Messungen
 Fortgeschrittenenpraktikum I Universität Rostock - Physikalisches Institut 7. Frequenzselektive Messungen Name: Daniel Schick Betreuer: Dipl. Ing. D. Bojarski Versuch ausgeführt: 1. Juni 2006 Protokoll
Fortgeschrittenenpraktikum I Universität Rostock - Physikalisches Institut 7. Frequenzselektive Messungen Name: Daniel Schick Betreuer: Dipl. Ing. D. Bojarski Versuch ausgeführt: 1. Juni 2006 Protokoll
Systemtheorie Teil B
 d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie eil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt Musterlösungen - Signalabtastung und Rekonstruktion...
d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie eil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt Musterlösungen - Signalabtastung und Rekonstruktion...
OPV Grundschaltungen. Von Philipp Scholze
 OPV Grundschaltungen Von Philipp Scholze Gliederung 1) Einleitung 1) Allgemeine Funktion eines OPVs 2) Idealer und realer OPV 3) Schaltsymbol und Kennlinie 2) Betriebsarten 3) Zusammenfassung 4) Quellen
OPV Grundschaltungen Von Philipp Scholze Gliederung 1) Einleitung 1) Allgemeine Funktion eines OPVs 2) Idealer und realer OPV 3) Schaltsymbol und Kennlinie 2) Betriebsarten 3) Zusammenfassung 4) Quellen
Aufgabensammlung. eines Filters: c) Wie stark steigen bzw. fallen die beiden Flanken des Filters?
 Aufgabensammlung Analoge Grundschaltungen 1. Aufgabe AG: Gegeben sei der Amplitudengang H(p) = a e eines Filters: a) m welchen Filtertyp handelt es sich? b) Bestimmen Sie die Mittenkreisfrequenz des Filters
Aufgabensammlung Analoge Grundschaltungen 1. Aufgabe AG: Gegeben sei der Amplitudengang H(p) = a e eines Filters: a) m welchen Filtertyp handelt es sich? b) Bestimmen Sie die Mittenkreisfrequenz des Filters
Aktiver Tiefpass mit Operationsverstärker
 Aktiver Tiefpass mit Operationsverstärker Laborbericht an der Fachhochschule Zürich vorgelegt von Samuel Benz Leiter der Arbeit: B. Obrist Fachhochschule Zürich Zürich, 17.3.2003 Samuel Benz Inhaltsverzeichnis
Aktiver Tiefpass mit Operationsverstärker Laborbericht an der Fachhochschule Zürich vorgelegt von Samuel Benz Leiter der Arbeit: B. Obrist Fachhochschule Zürich Zürich, 17.3.2003 Samuel Benz Inhaltsverzeichnis
Aktive Filter und Oszillatoren
 Aktive Filter und Oszillatoren Entwurf und Schaltungstechnik mit integrierten Bausteinen Bearbeitet von Lutz Wangenheim 1. Auflage 2007. Taschenbuch. xvi, 373 S. Paperback ISBN 978 3 540 71737 9 Format
Aktive Filter und Oszillatoren Entwurf und Schaltungstechnik mit integrierten Bausteinen Bearbeitet von Lutz Wangenheim 1. Auflage 2007. Taschenbuch. xvi, 373 S. Paperback ISBN 978 3 540 71737 9 Format
G S. p = = 1 T. =5 K R,db K R
 TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
9. Vorlesung Grundlagen der analogen Schaltungstechnik Filtersynthese
 9. Vorlesung Grundlagen der analogen Schaltungstechnik Filtersynthese 08..08 Analyse eines Filters. Ordnung (Aufgabe 7) 0 V V R C 3 0. C R v OPI 4 V.0 E.0 E.0 E0.0 E.0 E Frequency M agnitude d B P hase
9. Vorlesung Grundlagen der analogen Schaltungstechnik Filtersynthese 08..08 Analyse eines Filters. Ordnung (Aufgabe 7) 0 V V R C 3 0. C R v OPI 4 V.0 E.0 E.0 E0.0 E.0 E Frequency M agnitude d B P hase
Übungsaufgaben Digitale Signalverarbeitung
 Übungsaufgaben Digitale Signalverarbeitung Aufgabe 1: Gegeben sind folgende Zahlenfolgen: x(n) u(n) u(n N) mit x(n) 1 n 0 0 sonst. h(n) a n u(n) mit 0 a 1 a) Skizzieren Sie die Zahlenfolgen b) Berechnen
Übungsaufgaben Digitale Signalverarbeitung Aufgabe 1: Gegeben sind folgende Zahlenfolgen: x(n) u(n) u(n N) mit x(n) 1 n 0 0 sonst. h(n) a n u(n) mit 0 a 1 a) Skizzieren Sie die Zahlenfolgen b) Berechnen
Die Sprungantwort ist die Reaktion auf den Einheitssprung: G 2 (s) = 2 (s +1)(s +6) 3 (s +7)(s +2)
 Aufgabe 1: Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 1 s + (s +3) 3 (s +4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) =σ(t) W (s) = 1 s Die Übertragungsfunktion des
Aufgabe 1: Die Laplace-Transformierte der Sprungantwort ist: Y (s) = 1 s + (s +3) 3 (s +4) Die Sprungantwort ist die Reaktion auf den Einheitssprung: w(t) =σ(t) W (s) = 1 s Die Übertragungsfunktion des
5. Beispiele - Filter Seite 15
 5. Beispiele - Filter Seite 15 5.2 Entwurf digitaler Filter Zur Demonstration eines rekursiv implementierten Tiefpasses (FIR Finite Impulse Response bzw. IIR Infinite Impulse Response) soll dieses Beispiel
5. Beispiele - Filter Seite 15 5.2 Entwurf digitaler Filter Zur Demonstration eines rekursiv implementierten Tiefpasses (FIR Finite Impulse Response bzw. IIR Infinite Impulse Response) soll dieses Beispiel
KW Tiefpassfilter für 50 Watt MOSFET PA
 KW Tiefpassfilter für 50 Watt MOSFET PA Prinzip Das vorgestellte LC Tiefpassfilter arbeitet im Frequenzbereich von 0 30MHz und dient der Unterdrückung von Oberwellen (Harmonischen) der Leistungsendstufe
KW Tiefpassfilter für 50 Watt MOSFET PA Prinzip Das vorgestellte LC Tiefpassfilter arbeitet im Frequenzbereich von 0 30MHz und dient der Unterdrückung von Oberwellen (Harmonischen) der Leistungsendstufe
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.00 Uhrzeit: 09:00
INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.00 Uhrzeit: 09:00
Systemtheorie Teil B
 d 0 d c d c uk d 0 yk d c d c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 9 Musterlösungen Zeitdiskrete pproximation zeitkontinuierlicher
d 0 d c d c uk d 0 yk d c d c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 9 Musterlösungen Zeitdiskrete pproximation zeitkontinuierlicher
Bestimmung der Lage der Polstellen bei der Erweiterung von TSCHEBYSCHEFF-Tiefpässen zu CAUER-Tiefpässen. Dipl.-Ing. Leo Baumann
 Bestimmung der Lage der Polstellen bei der Erweiterung von TSCHEBYSCHEFF-Tiefpässen zu CAUER-Tiefpässen Dipl.-Ing. Leo Baumann Datum 25. Mai 2007 Inhalt 1.0 Einleitung 2.0 Synthese des CAUER Tiefpasses
Bestimmung der Lage der Polstellen bei der Erweiterung von TSCHEBYSCHEFF-Tiefpässen zu CAUER-Tiefpässen Dipl.-Ing. Leo Baumann Datum 25. Mai 2007 Inhalt 1.0 Einleitung 2.0 Synthese des CAUER Tiefpasses
ÜBUNG 2: Z-TRANSFORMATION, SYSTEMSTRUKTUREN
 ÜBUNG : Z-TRANSFORMATION, SYSTEMSTRUKTUREN 8. AUFGABE Bestimmen Sie die Systemfunktion H(z) aus den folgenden linearen Differenzengleichungen: a) b) y(n) = 3x(n) x(n ) + x(n 3) y(n ) + y(n 3) 3y(n ) y(n)
ÜBUNG : Z-TRANSFORMATION, SYSTEMSTRUKTUREN 8. AUFGABE Bestimmen Sie die Systemfunktion H(z) aus den folgenden linearen Differenzengleichungen: a) b) y(n) = 3x(n) x(n ) + x(n 3) y(n ) + y(n 3) 3y(n ) y(n)
Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik. Hausaufgabe
 Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik Hausaufgabe im Fach Grundlagen der analogen Schaltungstechnik GaST (WS 016/17) Bearbeiter Matr.-Nr. Emailadresse Aufgabe
Technische Universität Ilmenau Fakultät für Elektrotechnik und Informationstechnik Hausaufgabe im Fach Grundlagen der analogen Schaltungstechnik GaST (WS 016/17) Bearbeiter Matr.-Nr. Emailadresse Aufgabe
Entzerrung Anhebung bzw. Absenkung ausgewählter Frequenzbereiche zur Klangfarbenänderung
 Tontechnik 2 Entzerrung Audiovisuelle Medien HdM Stuttgart Entzerrung Entzerrung Anhebung bzw. Absenkung ausgewählter Frequenzbereiche zur Klangfarbenänderung Einstellung grundsätzlich nach Gehör, nicht
Tontechnik 2 Entzerrung Audiovisuelle Medien HdM Stuttgart Entzerrung Entzerrung Anhebung bzw. Absenkung ausgewählter Frequenzbereiche zur Klangfarbenänderung Einstellung grundsätzlich nach Gehör, nicht
Für einen Operationsverstärker hat sich in der Schaltungstechnik folgendes Schaltsymbol eingebürgert. (Abb. 2)
 Einführung in die Eigenschaften eines Operationsverstärkers Prof. Dr. R Schulz Für einen Operationsverstärker hat sich in der Schaltungstechnik folgendes Schaltsymbol eingebürgert. (Abb. 2) Um den Ausgang
Einführung in die Eigenschaften eines Operationsverstärkers Prof. Dr. R Schulz Für einen Operationsverstärker hat sich in der Schaltungstechnik folgendes Schaltsymbol eingebürgert. (Abb. 2) Um den Ausgang
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
Elektronik II 4. Groÿe Übung
 G. Kemnitz Institut für Informatik, Technische Universität Clausthal 9. Juni 2015 1/15 Elektronik II 4. Groÿe Übung G. Kemnitz Institut für Informatik, Technische Universität Clausthal 9. Juni 2015 G.
G. Kemnitz Institut für Informatik, Technische Universität Clausthal 9. Juni 2015 1/15 Elektronik II 4. Groÿe Übung G. Kemnitz Institut für Informatik, Technische Universität Clausthal 9. Juni 2015 G.
Tontechnik 2. Digitale Filter. Digitale Filter. Zuordnung Eingang x(t) Ausgang y(t) diskrete digitale Signale neue diskrete digitale Signale
 Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung Eingang x(t) Ausgang y(t) diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes
Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung Eingang x(t) Ausgang y(t) diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes
Praktikum Versuch Bauelemente. Versuch Bauelemente
 1 Allgemeines Seite 1 1.1 Grundlagen 1.1.1 db-echnung Da in der Elektrotechnik häufig mit sehr großen oder sehr kleinen Werten gerechnet wird, benutzt man für diese vorzugsweise die logarithmische Darstellung.
1 Allgemeines Seite 1 1.1 Grundlagen 1.1.1 db-echnung Da in der Elektrotechnik häufig mit sehr großen oder sehr kleinen Werten gerechnet wird, benutzt man für diese vorzugsweise die logarithmische Darstellung.
IX Filterschaltungen
 Praktische Elektronik 9-1 Hans-Hellmuth Cuno IX Filterschaltungen IX.1 Aktive RC-Filter Es gibt in der Elektronik viele Einsatzfälle für die Filterung von Frequenzen. Im Radiofrequenzbereich werden dazu
Praktische Elektronik 9-1 Hans-Hellmuth Cuno IX Filterschaltungen IX.1 Aktive RC-Filter Es gibt in der Elektronik viele Einsatzfälle für die Filterung von Frequenzen. Im Radiofrequenzbereich werden dazu
1 Betragsfrequenzgang
 Betragsfrequenzgang Ein vollständiges Bodediagramm besteht aus zwei Teildiagrammen. Das erste Teildiagramm wird häufig als Betragsfrequenzgang bezeichnet, das zweite Teildiagramm als Phasenfrequenzgang.
Betragsfrequenzgang Ein vollständiges Bodediagramm besteht aus zwei Teildiagrammen. Das erste Teildiagramm wird häufig als Betragsfrequenzgang bezeichnet, das zweite Teildiagramm als Phasenfrequenzgang.
Netzwerkanalyse, Netzwerksynthese und Leitungstheorie
 Netzwerkanalyse, Netzwerksynthese und Leitungstheorie Von Dipl.-Phys. G. Ulbricht Professor an der Fachhochschule München Mit 109 Bildern, 10 Tafeln und zahlreichen Beispielen und Übungsaufgaben B. G.
Netzwerkanalyse, Netzwerksynthese und Leitungstheorie Von Dipl.-Phys. G. Ulbricht Professor an der Fachhochschule München Mit 109 Bildern, 10 Tafeln und zahlreichen Beispielen und Übungsaufgaben B. G.
A1/Ü5: Die Aufgabe 1 von Übungsblatt 5 wird von jedem Studenten im Selbststudium erarbeitet.
 Wirtschaftsingenieurwesen Grundlagen der Elektronik und Schaltungstechnik Prof. Dr. Ing. Hoffmann Übung 5 Operationsverstärker Übungstermin 21.06.2018 A1/Ü5: Die Aufgabe 1 von Übungsblatt 5 wird von jedem
Wirtschaftsingenieurwesen Grundlagen der Elektronik und Schaltungstechnik Prof. Dr. Ing. Hoffmann Übung 5 Operationsverstärker Übungstermin 21.06.2018 A1/Ü5: Die Aufgabe 1 von Übungsblatt 5 wird von jedem
Aktive Filter in RC- und SC-Technik
 Lutz v. Wangenheim Aktive Filter in RC- und SC-Technik Grundlagen Berechnungsverfahren Schaltungstechnik Hüthig Buch Verlag Heidelberg INHALT VORWORT VERWENDETE SYMBOLE UND ABKÜRZUNGEN EINFÜHRUNG 1 KAP.
Lutz v. Wangenheim Aktive Filter in RC- und SC-Technik Grundlagen Berechnungsverfahren Schaltungstechnik Hüthig Buch Verlag Heidelberg INHALT VORWORT VERWENDETE SYMBOLE UND ABKÜRZUNGEN EINFÜHRUNG 1 KAP.
Gedächtnisprotokoll zur ADELE-Klausur vom (Prof. Orglmeister)
 1. Aufgabe: Bandsperre Gegeben war das Toleranzschema einer Bandsperre über der normierten Frequenz (vgl. Abb. 1, links). Abbildung 1: Toleranzschema Die Verstärkung im Durchlassbereich sollte 1/ 2 betragen,
1. Aufgabe: Bandsperre Gegeben war das Toleranzschema einer Bandsperre über der normierten Frequenz (vgl. Abb. 1, links). Abbildung 1: Toleranzschema Die Verstärkung im Durchlassbereich sollte 1/ 2 betragen,
Operationsverstärker. 6.1 Idealer Operationsverstärker Invertierende Schaltung
 Operationsverstärker 6 6.1 Idealer Operationsverstärker 6.1.1 Invertierende Schaltung Berechnung der äquivalenten Eingangsrauschspannung u Ni (Abb. 6.1). Die Rauschspannung u NRi liegt schon an der Stelle
Operationsverstärker 6 6.1 Idealer Operationsverstärker 6.1.1 Invertierende Schaltung Berechnung der äquivalenten Eingangsrauschspannung u Ni (Abb. 6.1). Die Rauschspannung u NRi liegt schon an der Stelle
Aktive NF-Filter. 2.3 Aktive NF-Filter. Bild 2.3.1: Dreistufiger aktiver NF-Tiefpass (Quelle: Hans-Jürgen Kowalski)
 Bild 2.3.1: Dreistufiger aktiver NF-Tiefpass (Quelle: Hans-Jürgen Kowalski) 2.3 Aktive NF-Filter Bei den aktiven Filtern im Amateurbereich kann man zwischen Tiefpässen mit etwa 3 khz Eckfrequenz (für SSB)
Bild 2.3.1: Dreistufiger aktiver NF-Tiefpass (Quelle: Hans-Jürgen Kowalski) 2.3 Aktive NF-Filter Bei den aktiven Filtern im Amateurbereich kann man zwischen Tiefpässen mit etwa 3 khz Eckfrequenz (für SSB)
Einführung in die digitale Signalverarbeitung WS11/12
 Einführung in die digitale Signalverarbeitung WS11/12 Prof. Dr. Stefan Weinzierl Musterlösung 11. Aufgabenblatt 1. IIR-Filter 1.1 Laden Sie in Matlab eine Audiodatei mit Sampling-Frequenz von fs = 44100
Einführung in die digitale Signalverarbeitung WS11/12 Prof. Dr. Stefan Weinzierl Musterlösung 11. Aufgabenblatt 1. IIR-Filter 1.1 Laden Sie in Matlab eine Audiodatei mit Sampling-Frequenz von fs = 44100
Simulation einer Mikrostreifenleitung mit Tiefpasscharakteristik. Khaoula Guennoun Torsten Finger Jan-Frederic Overbeck
 Fachhochschule Aachen Master Telekommunikationstechnik Elektrotechnik und Informationstechnik Lehrgebiet: Hoch- und Höchstfrequenztechnik Prof. Dr. Ing. H. Heuermann Simulation einer Mikrostreifenleitung
Fachhochschule Aachen Master Telekommunikationstechnik Elektrotechnik und Informationstechnik Lehrgebiet: Hoch- und Höchstfrequenztechnik Prof. Dr. Ing. H. Heuermann Simulation einer Mikrostreifenleitung
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 7.03.007 Uhrzeit: 3:30 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 7.03.007 Uhrzeit: 3:30 Uhr Zeitdauer: Stunden Hilfsmittel:
Tontechnik 2. Digitale Filter. Digitale Filter. Zuordnung diskrete digitale Signale neue diskrete digitale Signale
 Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes System (LTD-System)
Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes System (LTD-System)
Messverstärker und Gleichrichter
 Mathias Arbeiter 11. Mai 2006 Betreuer: Herr Bojarski Messverstärker und Gleichrichter Differenz- und Instrumentationsverstärker Zweiwege-Gleichrichter Inhaltsverzeichnis 1 Differenzenverstärker 3 1.1
Mathias Arbeiter 11. Mai 2006 Betreuer: Herr Bojarski Messverstärker und Gleichrichter Differenz- und Instrumentationsverstärker Zweiwege-Gleichrichter Inhaltsverzeichnis 1 Differenzenverstärker 3 1.1
Zeitdiskrete Signalverarbeitung
 Zeitdiskrete Signalverarbeitung Ideale digitale Filter Dr.-Ing. Jörg Schmalenströer Fachgebiet Nachrichtentechnik - Universität Paderborn Prof. Dr.-Ing. Reinhold Haeb-Umbach 7. September 217 Übersicht
Zeitdiskrete Signalverarbeitung Ideale digitale Filter Dr.-Ing. Jörg Schmalenströer Fachgebiet Nachrichtentechnik - Universität Paderborn Prof. Dr.-Ing. Reinhold Haeb-Umbach 7. September 217 Übersicht
Systemtheorie. Vorlesung 16: Interpretation der Übertragungsfunktion. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 16: Interpretation der Übertragungsfunktion Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übertragungsfunktion Bedeutung der Nullstellen Bei der Interpretation
Systemtheorie Vorlesung 16: Interpretation der Übertragungsfunktion Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Übertragungsfunktion Bedeutung der Nullstellen Bei der Interpretation
Partialbruchzerlegung
 Partialbruchzerlegung Lucas Kunz 27. Januar 207 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Nullstellen höheren Grades........................... 2.3 Residuen-Formel................................
Partialbruchzerlegung Lucas Kunz 27. Januar 207 Inhaltsverzeichnis Theorie 2. Definition.................................... 2.2 Nullstellen höheren Grades........................... 2.3 Residuen-Formel................................
