Symmetrieoperation = Deckoperation Kristallsymmetrie bedeutet, daß die Kristallstruktur einer Deckoperation unterworfen wird.
|
|
|
- Lena Pfeiffer
- vor 7 Jahren
- Abrufe
Transkript
1 Teil II Kristallsymmetrie 9 Kristallographische Symmetrie Der Begriff Symmetrie kommt aus dem Griechischen und bedeutet Ebenmaß. Im kristallographischen Sinn bedeutet Symmetrie, daß eine starre Bewegung (sog. Isometrie) ein Muster mit sich selbst zur Deckung bringt, oder mit anderen Worten, auf sich abbildet. Symmetrieoperation = Deckoperation Kristallsymmetrie bedeutet, daß die Kristallstruktur einer Deckoperation unterworfen wird. 9.1 Affine Abbildungen und Isometrien Mathematisch wird die lineare Abbildung eines Punktes X X bei festgehaltenem Koordinatensystem durch X = R X + T = (R, T)X (45) beschrieben, wobei wir abkürzend den Seitzoperator (R, T) benutzt haben. R ist eine quadratische n n-matrix (linearer Anteil) und T eine n 1-Spaltenmatrix (translativer Anteil). Der Seitzoperator erfüllt die Gruppenaxiome: 1. Abgeschlossenheit: (Q, S)(R, T)X = (Q, S)(R X + T) = Q R X + Q T + S = (Q R, QT + S)X 2. Es gibt das Einselement: 3. Es gibt das inverse Element: (I,0)(R, T) = (R, T)(I,0) = (R, T) (R, T)(R, T) 1 = (R, T) 1 (R, T) = (I,0) 4. Das Assoziativgesetz gilt, weil es schon für die Matrixmultiplikation und Vektoraddition erfüllt ist. Die so definierte Verknüpfung ist im allgemeinen nicht kommutativ. Den zu (R, T) inversen Operator findet man wie folgt: (Q, S)(R, T) = (I,0) (Q R, QT + S) = (I,0) = Q = R 1 ; S = R 1 T = (R, T) 1 = (R 1, R 1 T) (46) Die inverse Abbildung existiert nur, wenn R eine reguläre Matrix ist. Das bedeutet, daß det R 0, d.h. die Spaltenvektoren von R sind linear unabhängig. 25
2 Die Länge eines Vektors (s. Gll. (9) und (14)) ändert sich nicht unter einer Symmetrieoperation X = RX. Weil es sich um eine starre Bewegung handelt, gilt x 2 = X t G X = X t R t GRX, folglich ist R t GR = G. Wenn wir davon die Determinante bilden, finden wir, daß (R, T) nur dann eine Isometrie sein kann, wenn det(r) = 1. Für det(r) = +1 ist das eine Drehung, für det(r) = 1 eine Drehinversion (oder Drehspiegelung). 9.2 Symmetrieoperationen in Translationsgittern Ein Kristall zeichnet sich durch die Anordnung seiner Materie (Atome, Ionen, Moleküle) auf einem Gitter aus, was Translationssymmetrie impliziert Translationssymmetrie Grundsätzlich lassen sich immer drei linear unabhängige Translationsvektoren t j finden, für die alle Linearkombinationen mit ganzzahligen Komponenten die Kristallbausteine wieder zur Deckung bringen. Jede Linearkombination von Translationsvektoren der Form ist wieder eine Gittertranslation. m t n = n j t j ; j = 1, 2,...,m; n j, ǫ Z (47) j=1 Die Endpunkte aller Translationsvektoren T n = {t n } bilden ein (Translations-)Gitter. Für einen unendlich ausgedehnt gedachten Kristall bilden alle Gittertranslationen die Kristallstruktur wieder auf sich ab. Gittertranslationen sind Deckoperationen und daher auch Symmetrieoperationen. Die Menge aller Translationsvektoren einer Kristallsruktur beschreibt die Translationssymmetrie dieser Struktur Translationengruppe Der Vektor T der Operation (R, T) lässt sich immer als Summe T = T n + T aus einer Gittertranslation T n und einer Verschiebung T schreiben, die keine Gittertranslation ist. Die Menge aller Gittertranslationen {t n } bildet (bezüglich der Vektoraddition) eine Gruppe: Die Gruppe T n = {(I, T n )} heißt die Translationengruppe einer Kristallstruktur. die Ordnung der Translationengruppe ist unendlich: T n =. In Gittern muß T = 0 sein, weil im Translationsgitter nur reine Gittertranslationen T n möglich sind. In Kristallstrukturen hingegen kann T durchaus von Null verschieden sein (s.u., Abschnitt 9.5). 26
3 9.2.3 Symmetrieoperationen in Gittern Die Operation (R, T) lässt sich in die Nacheinanderausführung einer Drehung oder Drehinversion und einer Translation zerlegen: (I, T n )(R, T) = (R, T n + T) (48) (R, T)(I, T n ) = (R, RT n + T) (49) Damit die Symmetrieoperationen einer Kristallstruktur eine Gruppe nämlich die Raumgruppe der Struktur bilden, muß RT n = T n wieder ein Gittervektor sein. Daraus folgen Beschränkungen für die in Gittern möglichen Drehmatrizen R: Es sind nur solche Matrizen R erlaubt, die ein Gitter auf sich selbst abbilden. Jede dieser im Gitter erlaubten Operationen kann mehrfach nacheinander ausgeführt werden. Gelangt man durch k-fache Ausführung einer Drehoperation zum Ausgangspunkt zurück, dann ist R k = I. Das kleinstmögliche k nennt man Zähligkeit des betreffenden Symmetrielements; sie ist zugleich die Ordnung der zugehörigen Symmetrieoperation. Abbildung 13: Herleitung der im Gitter erlaubten Drehwinkel α. Der Abstand g zwischen P 3 und P 6 muß ein ganzzahliges Vielfaches einer Gittertranslation a sein: g = 2acos α = na α = 0, 60, 90, 120 und 180. In Gittern gibt es nur 1, 2, 3, 4 und 6-zählige Drehachsen. Drehoperationen mit Drehwinkeln ϕ = m 360 /k, m k und teilerfremd zu k, werden mit k m bezeichnet, wobei k die Zähligkeit der Drehung angibt. In den IT/A (International Tables for Crystallography, Vol.A,) werden ür diese Operationen folgende Symbole verwendet: 6 + = 6 1 ; 6 = 6 5 = 6 1 ; 4 + = 4 1 ; 4 = 4 3 = 4 1 ; (50) 3 + = 3 1 ; 3 = 3 2 = 3 1 ; 2 ; 1 Jedes Gitter ist zentrosymmetrisch. Zu jedem Gittervektor t n gibt es nämlich den Gegenvektor t n. Die entsprechende Abbildung wird durch die Abbildungsmatrix Ī = ( 1)I dargestellt. Diese Symmetrieoperation heißt Inversion und bedeutet eine Spiegelung an einem 27
4 Punkt (dem sog. Inversionszentrum). Die Inversionsoperation und das zugehörige Inversionszentrum werden mit dem Symbol 1 ( eins quer ) bezeichnet. Inversion impliziert die Bildung eines Spiegelbildes: ein ursprünglich rechtshändiges Objekt wird dadurch linkshändig und umgekehrt. Folglich sind auch Drehinversionen, das ist eine Kombination von Drehung und anschließender Inversion in eine einzige Operation Ī R = ( R), ebenfalls Symmetrieoperationen, die im Gitter erlaubt sind. Man bezeichnet sie mit 6, 4, 3, 2 = m (Spiegelebene) und 1 (Inversionszentrum). Die Determinante einer Drehinversions-Operation ist detr = 1. Mit einem Gitter kompatibel sind die Drehinversionsachsen 1, 2 m, 3, 4 und 6. Insbesondere ist eine zweizählige Drehinversionsachse 2 m identisch mit einer Spiegelebene m senkrecht zu dieser Achse. Während die Zähligkeit (Ordnung) von einfachen Drehachsen durch das Symbol 1, 2, 3, 4, 6 gegeben ist, ist die Zähligkeit von 1 und 2 = m zwei, die von 4 vier und die von 3 und 6 sechs. Anmerkung: In einem zweidimensionalen ebenen Gitter existieren dieselben Drehoperationen 1, 2, 3, 4, 6 wie in dreidimensionalen Gittern. Diese Drehachsen stehen immer senkrecht zur Gitterebene. Von den Drehinversionen bleiben in zwei Dimensionen nur die Operationen 1 = 2 und 2 = m (Spiegellinie in der Projektionsebene). Die übrigen werden in der Projektion zu einfachen Drehachsen ( 3 6, 4 4, 6 3) Kristallographische Punktgruppen Drehachsen können in Gittern nicht beliebige Orientierungen haben, weil sie Gittertranslationen wieder auf Gittertranslationen abbilden müssen. Parallel zu einer Drehachse liegt immer eine Gittergerade [uvw]; durch geeignete Wahl des Ursprungs läßt sich die Gittergerade [uvw] in die Drehachse legen. Senkrecht zu einer Drehachse gibt es immer eine Netzebene (hkl); der Ursprung läßt sich grundsätzlich in einen Gitterpunkt der Netzebene legen. Die relative Orientierung mehrerer Drehachsen ist nicht beliebig, sondern nur unter bestimmten mit dem Gitter verträglichen Winkeln möglich. Durch geeignete Wahl der kristallographischen Basis läßt sich erreichen, daß Symmetrieachsen entlang den Kanten, Flächen- und Raumdiagonalen der Elementarzelle (oder senkrecht dazu) liegen. Die durch diese Wahl resultierende Elementarzelle muß allerdings nicht mehr primitiv sein (s.u. Bravaisgitter, Abschnitt 9.4). Die Raumdiagonale geht durch eine Ecke der Einheitszelle, an der drei ihrer Begrenzungsflächen zusammenstoßen. Daher sind in der Raumdiagonalen nur die Achsen 3 und 3 möglich. In der Flächendiagonalen kann es nur die Achsen 2 und 2 m geben. In den Kanten sind alle im Gitter erlaubten Dreh- ind Drehinversionsachsen möglich. Die systematische Kombination kristallographischer Symmetrieelemente in diesen ausgezeichneten Richtungen (s.u. Blickrichtungen) gibt insgesamt 32 verschiedene Kombinationen oder kristallographische Punktgruppen, wobei die jeweilige Anordnung der Symmetrieelemente zum Teil eine spezielle Metrik der Elementarzelle erfordert (s.u. Kristallsysteme). 28
5 Die Menge P = {(R, 0)} = {R} bildet eine Gruppe: die Punktgruppe P. Kristallographische Punktgruppen werden auch als Kristallklassen bezeichnet, weil die Punktgruppen der Klassifizierung nach makroskopischen Kristallformen zugrunde liegen. Symmetrieelemente der kristallographischen Punktgruppen sind die in Gittern erlaubten kristallographischen Symmetrieoperationen, nämlich Drehungen 1, 2, 3, 4, 6 und Drehinversionen 1, 2 m, 3, 4, 6. Eine kristallographische Punktgruppe enthält nur kristallographische Punktsymmetrieelemente, die sich in einem gemeinsamen Punkt schneiden. Mindestens dieser Schnittpunkt ist unter allen Operationen der Punktgruppe invariant. Die gegenseitige Lage der Symmetrieelemente einer Punktgruppe ist nicht beliebig. Sie wird dadurch eingeschränkt, daß jede Kombination von zwei Symmetrieoperationen wieder eine Symmetrieoperation sein muß, die mit dem Gitter kompatibel ist. Die Menge aller Symmetrieoperationen muß immer eine Gruppe bilden. Es gibt 32 dreidimensionale kristallographische Punktgruppen. Eine n-zählige Drehachse senkrecht zu einer Spiegelebene m schreibt man in der Hermann- Mauguin Nomenklatur als n/m (gelesen als n über m ); z.b. 2/m für eine zweizählige Drehachse senkrecht zu einer Spiegelebene. Liegt die n-zählige Drehachse in der Spiegelebene, so schreibt man nm, z.b. 2m ( 2mm, eine weitere Spiegelebene wird erzeugt) Holoedrien und Kristallsysteme Kombiniert man die 10 kristallographischen Symmetrielelemente mit einem passenden Gitter, dann werden durch die Gittertranslationen zusätzliche Symmetrieelemente erzeugt und es resultiert eine relativ geringe Anzahl verschiedener Gittersymmetrien oder Holoedrien. Die Punktgruppen der Gittersymmetrien nennt man Holoederien. Zunächst einmal sind alle Gitter zentrosymmetrisch, denn zu jedem Gittervektor t gibt es den Vektor -t. Auf jedem Gitterpunkt (und auch in Mitte zwischen zwei Gitterpunkten) gibt es deshalb Inversionszentren. Hinzufügen eines Inversionszentrums zu den 10 Dreh- und Drehinversionsachsen gibt 1 aus 1 und 1, 2/m aus 2 und m, 3 aus 3 und 3, 4/m aus 4 und 4, sowie 6/m aus 6 und 6. Wiederholt man nun diese 5 Gruppen auf einem Gitter, so findet man die Gittersymmetrien 1 (triklin), 2/m (monoklin), 3m (rhomboedrisch), 4/mmm (tetragonal) und 6/mmm (hexagonal). Zwei weitere Holoedrien findet man als Sonderfälle des rhomboedrischen bzw. tetragonalen sowie des monoklinen Gitters: macht man in einem rhomboedrischen Gitter α = β = γ = 90 oder in einem tetragonalen Gitter a = b = c, dann erhält man ein kubisches Gitter der Symmetrie m 3m; α = β = γ = 90 erzeugt aus einem monoklinen Gitter ein orthorhombisches der Symmetrie mmm. Es gibt 7 Holoedrien, jede mit ihrem eigenen Achsensystem, mit HM-Symbolen: 6/mmm, m 3m, 3m, 4/mmm, mmm, 2/m und 1. 29
6 Diese 7 Holoedrien definieren 7 Kristallsysteme: hexagonal (h), kubisch (c), trigonal (h,r), tetragonal (t), orthorhombisch (o), monoklin (m) und triklin oder anorthisch (a) mit folgender Metrik: Kristallsystem Holoedrie Metrik hexagonal (h) 6/mmm a = b, α = β = 90, γ = 120 kubisch (c) m 3m a = b = c, α = β = γ = 90 trigonal (h) 3m a = b, α = β = 90, γ = 120 hexagonale Achsen trigonal (r) 3m a = b = c, α = β = γ rhomboedr. Achsen tetragonal (t) 4/mmm a = b, α = β = γ = 90 orthorhombisch (o) mmm α = β = γ = 90 monoklin (m) 2/m α = γ = 90 2nd setting monoklin (m) 2/m α = β = 90 1st setting triklin (a) 1 keine Beschränkung Die Symbole a, b, c bezeichnen die Längen der drei Basisvektoren a, b und c (oben b 1, b 2, b 3 genannt). Mit α ist der Winkel zwischen b und c gemeint, mit β der Winkel zwischen c und a und mit γ schließlich der Winkel zwischen a und b. Kristallsystem Punktgruppe Bravaisgitter triklin (a) 1, 1 P monoklin (m) 2, m, 2/m P, C bzw. B orthorhombisch (o) 222, mm2, mmm P, A(B,C), I, F tetragonal (t) 4, 4, 4/m, 422, 4mm, 42m, 4/mmm P, I trigonal (h,r) 3, 3, 32, 3m, 3m P, R hexagonal (h) 6, 6, 6/m, 622, 6mm, 62m, 6/mmm P kubisch (c) 23, m 3, 432, 43m, m 3m P, I, F Die kubische und die hexagonale Holoedrie bilden die beiden sog. Symmetriegipfel. Alle anderen Holoedrien sind Untergruppen von wenigstens einem dieser beiden Symmetriegipfel. Alle echten Untergruppen der Holoedrien nennt man Meroedrien. Typischerweise werden die 32 kristallographischen Punktgruppen nach ihrem Achsensystem in die 7 Kristallsysteme eingeordnet (wie in der obigen Tabelle). 9.3 Blickrichtungen Punkt- und Raumgruppen werden bezüglich eines kristallographischen Koordinatensystems beschrieben, das aus einer kristallographischen Basis und einem kristallographisch sinvoll gewählten Ursprung besteht. Der Ursprung wird in der Regel in ein Symmetriezentrum oder einen anderen Punkt hoher Symmetrie gelegt. Vereinbarungsgemäß wird eine rechtshändige Basis verwendet. Die Wahl des Koordinatensystems ist allerdings nicht zwingend vorgeschrieben. Sie erfolgt so, daß es der Symmetrie der Gitter und der Raumgruppen möglichst gut angepaßt ist. Die Basisvektoren sollen daher nicht nur Gittervektoren sein, sondern auch in symmetriebegabten Richtungen liegen. Eine kristallographische Basis mit Basisvektoren in symmetriebegabten Richtungen bezeichnet man als konventionelle kristallographische Basis. 30
7 Mit dieser Wahl der Basis wird die Darstellung der Symmetrieoperationen besonders einfach, weil Basisvektoren auf andere oder negative oder Summen von Basisvektoren abgebidet werden. Außerdem hängt die Darstellung der Symmetrieoperation nicht vom Gittertyp ab. Mit der konventionellen Basis werden außerdem die Metriktensoren besonders einfach, d.h. sie enthalten möglichst wenige unabhängige und von Null verschiedene Koeffizienten. Kristallsystem erste zweite dritte Blickrichtung kubisch [100] [010] < 111 > < 110 > [001] hexagonal [100] [1 10] [001] [010] [120] [ 1 10] [ 2 10] trigonal [100] [001] [010] hexag. Achsen [ 1 10] trigonal [1 10] [111] [01 1] rhomb. Achsen [ 101] tetragonal [001] [100] [1 10] [010] [110] orthorhombisch [100] [010] [001] monoklin [010] 2nd setting monoklin [001] 1st setting triklin keine In den beiden Symmetriegipfeln (kubisches und hexagonales System) werden die konventionellen Elementarzellen so gewählt, daß Symmetrieelemente parallel zu den Kanten, den Flächen- und den Raumdiagonalen (letztere nur im kubischen System) oder senkrecht zu diesen Richtungen zu liegen kommen. Da alle anderen Punktgruppen Untergruppen davon sind, bleibt beim Symmetrieabbau die relative Orientierung der verbleibenden Symmetrielemente erhalten. Es gibt damit maximal drei symmetrich unabhängige Richtungen (sog. Blickrichtgen, englisch: lattice symmetry directions ); s. folgende Tabelle. Die Hermann-Mauguin Nomenklatur beruht auf diesen Blickrichtungen: Punkt- und Raumgruppen werden mit bis zu drei aufeinanderfolgenden Symbolen beschrieben, wobei jede der drei Stellen eine von maximal drei Blickrichtungen bedeutet. Diese Beschreibung ist eindeutig und erlaubt die Erzeugung von Punkt- und Raumgruppen nur aus diesen Symbolen. 9.4 Bravaisgitter Die verschiedenen erlaubten dreidimensionalen Gittertypen erhält man am schnellsten durch Stapelung zweidimensionaler Netze. Um die in den Netzen vorkommenden Symmetrieelemente zu beizubehalten, muß die Stapelung so erfolgen, daß entsprechende Symmetrielemente aufeinanderfallen. Andernfalls, wenn schief gestapelt wird, gehen in den resultierenden Gittern Symmetrielemente verloren. Es gibt 14 topologisch verschiedene Gittertypen. 31
8 Man findet dabei Gitter, die sich zwar in ihrer Topologie unterscheiden, aber doch das gleiche Symmetriegerüst aufweisen und deshalb zur gleichen Holoedrie gehören. Abbildung 14: Die 14 konventionellen Bravaisgitter (nach Kristallsystemen sortiert). In einer konventionellen Basis sind die erhaltenen Gitter nicht immer primitiv, sondern es entstehen durch diese spezielle Basiswahl auch zentrierte Gitter, die Gittervektoren mit rationalen Koeffizienten haben. Für jedes der zentrierten Gitter läßt sich eine primitive Basis finden, deren Basisvektoren jedoch nicht mehr alle in symmetriebegabten Richtungen liegen. Die unendliche Menge aller möglichen Gitter teilt man in 14 Klassen ein, die Bravais Gitter oder Bravais Typen genannt werden. Die konventionell zentrierten Gitter haben folgende zentrierende Gittervektoren und Bezeichnungen: A: 0, 1 2, 1 2 ; B: 1 2, 0, 1 2 ; C: 1 2, 1 2, 0 ; I: 1 2, 1 2, 1 2 F: 0, 1 2, 1 2 ; 1 2, 0, 1 2 ; 1 2, 1 2, 0 ; R: 2 3, 1 3, 1 3 ; 1 3, 2 3,
9 Die hier gewählte Aufstellung des R-Gitters wird als obverse Aufstellung bezeichnet; die alternative reverse Aufstellung des R-Gitters hat Zentrierungen in 1/3, 2/3, 1/3 und 2/3, 1/3, 2/3. Primitive Gitter erhalten das Symbol P. Es gibt die folgenden Bravaisgitter: ap, mp, mc, op, oa(b,c), oi, of, tp, ti, hp, (hr, rr), cp, ci, cf. hr und rr beziehen sich auf das R-Gitter in hexagonaler (h) bzw. rhomboedrischer (r) Aufstellung. 9.5 Symmetrieoperationen in Kristallstrukturen Die gefundenen zehn Dreh- und Drehinversionsachsen sind Symmetrieelemente, die in Gittern vorkommen können. Das sind jedoch noch nicht alle Symmetrieoperationen, die in Kristallstrukturen auftreten können, wo zum Gitter noch die Atome der Struktur hinzukommen. Durch das Hinzufügen von Materie zum Gitter kann (a) die Punktgruppe des Kristalls eine Untergruppe der Holoedrie werden und (b) können in Kristallstrukturen Schraubenachsen und Gleitspiegelebenen auftreten, die in Gittern allein nicht möglich sind. Als weitere Deckoperationen (starre Bewegungen) können nämlich Kombinationen von Drehungen oder Drehinversionen mit Translationen auftreten, die nicht Gittertranslationen t n sind, aber nicht in Widerspruch zur Translationsymmetrie stehen dürfen. Wendet man eine Operation (R, T) k mal an (k ist die Ordnung oder Zähligkeit von R), so hat man bezüglich des rotativen Anteils R eine identische Abbildung ausgeführt (d.h. R k = I). Insgesamt kann sich dabei die Kristallstruktur (bzw. ihre Atome) nur um einen Gittervektor verschoben haben. Der Anteil T von T = T n + T muss mit dem Gitter verträglich sein. Wenn k die Ordnung der Drehmatrix R ist, muß gelten: (R, T) k = (R k, (R k R + I)T) = (I, T n ) k 1 j=0 R j T = T n Diese Bedingung führt zu Einschränkungen für mögliche Translationen T, die sich aus der Bedingung: k 1 T n = R j T ; mit R 0 = I (51) j=0 ergeben. Die rechte Seite von (51) ist für die Drehinversionen 1, 3, 4, 6 gleich Null. Für diese Operationen treten folglich keine neuen Kombinationen auf. Es bleiben Drehachsen und Spiegelebenen in der Diskussion. Für diese zerlegen wir den Vektor T in einen senkrechten und einen parallelen Anteil bezüglich der Drehachse bzw. Spiegelebene: T = T + T (52) Die Summe in (51) wird mit T allein ebenfalls Null. Folglich bleiben nur Translationsanteile T übrig, die in Drehachsen bzw. Spiegelebenen liegen. Derartige Translationsanteile T sind 33
10 jedoch invariant unter R j, d.h. durch Mehrfachausführung werden sie einfach nur vervielfacht. Daraus folgt: k 1 R j T = T = T n = R j T = k T ; (53) d.h T = T n k j=0 = T = m k T n0 mit 0 < m < k (54) T n ist ein Vielfaches m der kürzesten Translationsperiode T n0 in Richtung der Drehachse bzw. Spiegelebene. Folglich können Translationen, die ganzahlige Bruchteile von Gittervektoren sind, mit Drehachsen und Spiegelebenen so kombiniert werden, daß dabei die Translationssymmetrie des Gitters nicht verletzt wird. Man bezeichnet diese Symmetrieoperationen als Schraubung bzw. Gleitspiegelung und die dazugehörigen Symmetrieelemente als Schraubenachsen bzw. Gleitspiegelebenen. Durch Zerlegung von T in je eine Komponente parallel und senkrecht zur Drehachse folgt: T lässt sich nach T = T + T in einen Kennanteil T (parallel zur Drehachse) und in einen Lageanteil T (senkrecht zur Drehachse) zerlegen. T = T n /k beschreibt eine Gleitkomponente entlang einer Drehachse oder parallel zu einer Spiegelebene. T 0 bedeutet, daß das Symmetrieelement nicht im Ursprung liegt. Schraubenachsen und Gleitspiegelebenen sind nur in Kristallstrukturen, nicht aber in Punktgittern möglich. (a) Schraubenachsen In Kristallstrukturen können folgende Schraubenachsen k m mit den Gleitanteilen T = m/k auftreten: 2 1, 3 1, 3 2, 4 1, 4 2, 4 3, 6 1, 6 2, 6 3, 6 4, 6 5. Die dazu gehörigen Symmetrieoperationen (Schraubungen) sind k m + und km. Die in den IT/A angegebenen Schraubkomponenten T betragen m/k bzw. 1 m/k. (Anmerkung: ; ; ; ; ; ) (b) Gleitspiegelebenen Gleitspiegelebenen werden mit kleinen Buchstaben nach Richtung und Länge ihrer Gleitkomponenten bezeichnet: a, b, c sind Gleitspiegelebenen mit Gleitkomponenten 1 2 in Richtung der Basisvektoren. n bzw. d haben flächen- oder raumdiagonale Gleitkomponenten 1 2 bzw. 1 4 oder ; d-gleitspiegelebenen existiert nur in zentrierten Einheitszellen Gleitspiegellinien der Ebenengruppen werden mit dem Symbol g bezeichnet. 3 Die Bezeichnung d kommt von den Gleitspiegelebenen der Diamantstruktur. 34
11 Gleitspiegelung T c[100], c[010], c[1 10] a[010], a[001] b[100], b[001] n[100] n[010] n[001] n[1 10] d[100] d[010] d[001] d[110] d[1 10] 1 4 Die obigen Symbole definieren nur die Gleitrichtung T. Die Orientierung der Gleitspiegelebene ergibt sich eindeutig aus der Position im HM-Symbol Fixpunkte von Symmetrielementen Punkte X F, die bei einer Abbildung invariant bleiben, also auf sich selbst abgebildet werden, nennt man Fixpunkte dieser Abbildung. Fixpunktgebilde oder Fixpunktmenge sind die Drehachsen, Spiegelebenen und Inversionszentren selbst. Die Fixpunkte der affinen Abbildung erhält aus der Bedingung X F = X F als X F = R X F + T (55) X F = R X F + T ; = (I R)X F = T (56) (a) Kennanteil Für Schraubungen und Gleitspiegelungen hat diese Gleichung keine Lösung, weil der Translationsanteil T immer eine Verschiebung bewirkt und deshalb kein Punkt fest liegen bleibt. Der Schraub bzw. Gleitanteil T kennzeichnet die Schraubenachsen bzw. Gleitspiegelebenen. T wird deswegen auch Gleit- oder Kennanteil genannt. (b) Lageanteil Der senkrechte Anteil T bestimmt die Lage der Fixpunktmenge X F im gewählten Bezugssystem. Aus (56) folgt X F = R X F + T ; T = (I R)X F. (57) Die Verschiebung einer Dreh- oder Schraubenachse, Spiegel- oder Gleitspiegelebene aus dem Ursprung um X F erzeugt in der Spaltenmatrix T einen sog. Lageanteil T. 35
12 9.7 Raumgruppen Eine vollständige Herleitung der 230 Raumgruppentypen erfolgte etwa zeitgleich und unabhängig voneinander durch FEDOROV 1890, SCHOENFLIES 1891 und BARLOW Der translationsperiodische Aufbau der Kristalle wurde jedoch erst 20 Jahre später durch Röntgenbeugungsaufnahmen von LAUE, FRIEDRICH und KNIPPING nachgewiesen. Aufgrund von Symmetriebetrachtungen an makroskopischen Kristallen hatte man deren gitterhaften Aufbau schon lange vorher vermutet. Die Menge aller Symmetrieoperationen G = {(R, T)} einer ebenen Kristallstruktur bildet eine Ebenengruppe. Die Menge aller Symmetrieoperationen G = {(R, T)} einer 3 dimensionalen Kristallstruktur bildet eine Raumgruppe. Mögliche Symmetrieelemente in Raumgruppen sind neben den Gittertranslationen die kristallographischen Dreh- und Drehinversionsachsen sowie Schraubenachsen und Gleitspiegelebenen. Wegen der Translationssymmetrie ist die Ordnung G der Raumgruppe immer unendlich. Die Translationengruppe T ist eine Untergruppe der Raumgruppe G. Für die trikline Raumgruppe P1 gibt es außer den Gittertranslationen T keine weiteren Symmetrieoperationen. Für alle anderen Raumgruppen ist die Translationengruppe T eine echte Untergruppe T < G. Die Translationengruppe T ist ein Normalteiler der Raumgruppe G. Die Faktorgruppe G /T ist isomorph zur Punktgruppe P. Die Ordnung dieser Faktorgruppe ist endlich; sie ist gleich der Ordnung P der Punktgruppe P der Raumgruppe G (s. Anhang). Es gibt zwei Typen von Raumgruppen: symmorphe und nicht-symmorphe Raumgruppen. Die ersteren erhält man aus Punktgruppe und Gitter, die letzteren erfordern zu ihrer Erzeugung translationshaltige Symmetrielemente (Schraubenachsen und/oder Gleitspiegelebenen). a) Symmorphe Raumgruppen: Wiederholung des Symmetriegerüsts einer kristallographischen Punktgruppe P = {(R, 0)} auf den Punkten eines (zur Symmetrie passenden) Translationsgitters führt zur Klasse der symmorphen Raumgruppen. Das Produkt zwischen Translationengruppe T und Punktgruppe P erzeugt eine symmorphe Raumgruppe. Es gibt 13 symmorphe Ebenengruppen und 73 symmorphe Raumgruppen. Wählt man den Nullpunkt im Fixpunkt des Symmetriegerüstes der Punktgruppe, dann bilden die Operationen {(R, 0)} eine Untergruppe der erhaltenen Raumgruppe. Wenn der Ursprung 36
13 nicht im Fixpunkt der Punktgruppe liegt, dann tritt ein Lageanteil T bezüglich des Fixpunktes auf und die Untergruppe ist dann {(R, T )}. Dieser einfache Zusammenhang zwischen Punktgruppe und Raumgruppe findet sich auch im Hermann-Mauguin Symbol symmorpher Raumgruppen: das Hermann-Mauguin Symbol symmorpher Raumgruppen besteht immer aus dem Symbol des Bravaisgitters und einem Punktgruppensymbol. In symmorphen Raumgruppen gibt es Punkte mit der vollen Symmetrie der Punktgruppe der Raumgruppe. Im Symbol symmorpher Raumgruppen erscheinen keine Schraubenachsen oder Gleitspiegelebenen. Trotzdem können auch in symmorphen Raumgruppen solche Elemente vorhanden sein. Sie sind jedoch nie als erzeugende Operationen erforderlich. Schraubenachsen und Gleitspiegelebenen können in symmorphen Raumgruppen dann auftreten, wenn das Gitter zentriert ist oder wenn Drehachsen oder Spiegelebenen nicht parallel oder senkrecht zu den Elementarzellkanten liegen. In beiden Fällen lassen sich nämlich Gittertranslationen in einen Kennanteil T und einen Lageanteil T zerlegen, was neben einem Lageanteil auch eine Gleitkomponente erzeugt. b) Nicht-Symmorphe Raumgruppen: Die symmorphen Raumgruppen sind dadurch ausgezeichnet, daß durch Wahl des Nullpunktes im Fixpunkt des Punktgruppen Symmetriegerüstes als Repräsentanten für die Nebenklassen des Translationen Normalteilers reine Punktgruppen Operationen (R, 0) gewählt werden können. Die Erweiterung auf nichtsymmorphe Raumgruppen kann so geschehen, daß man die Drehungen und Spiegelungen der Punktgruppen (in der Ebene nur die Spiegelgeraden) (R, 0) systematisch durch Schraubungen und Gleitspiegelungen (R, T +T ) ersetzt, wobei sich nun nicht mehr alle Symetrieelemente in einem Punkt schneiden müssen (T 0). In nicht-symmorphen Raumgruppen gibt es keine Punkte mit der vollen Symmetrie der Punktgruppe der Raumgruppe. Das Hermann-Mauguin Symbol nicht-symmorpher Raumgruppen enthält immer wenigstens das Symbol einer Schraubenachse oder Geitspiegelebene. Auf das Symbol des Bravaisgitters folgt deshalb kein Punktgruppensymbol. 37
14 10 Beschreibung der Raumgruppen in IT Vol.A Die Symmetrieoperationen einer Raumgruppe werden in den International Tables A auf drei verschiedene Weisen dargestellt: 1. durch ein oder mehrere Diagramme des Symmetriegerüsts; 2. durch ein Diagramm der Punkte der allgemeinen Punktlage; 3. durch Angabe der Koordinatentripel der allgemeinen Punktlage Diagramme Im allgemeinen findet man zwei Diagramme, die jeweils orthogonale Projektionen einer Elementarzelle und ihrer unmittelbaren Umgebung auf die ab-ebene darstellen: links ein Diagramm des Symmetriegerüsts, rechts ein Diagramm der Punkte eines Orbits allgemeiner Lage. Der Ursprung liegt normalerweise in der linken oberen Ecke; die a-achse weist nach unten, die b-achse horizontal nach rechts. Die Symmetriegerüste trikliner, monokliner und orthorhombischer Raungruppen sind durch drei Projektionen entlang den Achsen a, b und c beschrieben. Monokline Raungruppen sind außerdem noch in erster und zweiter Aufstellung ( 1st bzw. 2nd setting ) angegeben. Wenn es in der Ebene senkrecht zur Hauptachse einen Zentrierungvektor oder eine Gleitkomponente gibt, werden drei verschiedene Zellwahlen (cell choices) unterschieden. Trigonale Raumgruppen mit R-Gittern werden sowohl in hexagonalen als auch in rhomboedrischen Achsen behandelt. Für kubische Raumgruppen mit F-Gitter ist nur 1/4 der Elementarzelle graphisch dargestellt. a) Diagramm des Symmetriegerüsts Die Symmetriegerüste sind mit Hilfe von Symbolen beschrieben, die in IT A, Section 1.4 näher beschrieben sind. Art und Orientierung von Drehachsen und Ebenen geht aus dem graphischen Symbol hervor. Die Höhe von Inversionszentren oder horizontal liegenden Achsen und Ebenen ist als Bruch an das betreffende Element geschrieben, sofern sie von Null verschieden ist. b) Diagramm der allgemeinen Punktlage Für die allgemeine Punktlage gibt es jeweils nur ein Diagramm in der oben beschriebenen Standardorientierung (mit dem Ursprung in der linken oberen Ecke). Die Zellumrisse sind mit dünnen Linien eingezeichnet; zusätzlich noch die Linien durch x,1/2 und 1/2,y. Der Ausgangspunkt x, y, z der allgemeinen Lage liegt im Innern der Zelle etwas oberhalb der Papierebene, was durch das Symbol + (für +z) angedeutet ist. Eingetragen sind die äquivalenten Punkte innerhalb und in der unmittelbaren Ungebung der Zelle; ggf. sind Höhenangaben wie 1/2+ (für 1/2 + z) an die Punkte geschrieben. Die Punkte des Orbits sind als kleine Kreise dargestellt; Punkte, die durch Inversionsoperationen aus dem Ausgangspunkt entstehen also ein Spiegelbild darstellen erhalten zusätzlich ein Komma im Zentrum des Keises. Falls zwei Punkte aufeinander projizieren, ist der Kreis durch einen Vertikalstrich halbiert; beide Hälften erhalten ggf. noch Höhenangaben. Die Diagramme der kubischen Raumgruppen enthalten Stereogramme, in denen Punktkonfigurationen um den Ursprung (und symmetrisch äquivalente Punkte) durch Verbindungslinien hervorgehoben sind. 38
15 10.2 Symmetrieoperationen Unterhalb der Diagramme gibt es den Block Symmetry Operations, der die zur allgemeinen Punktlage gehörenden Symmetrieoperationen beschreibt. Dieser Eintrag enthält folgende Daten: 1. Die Nummer (n) der Symmetrieoperation und des zugehörigen Koordinatentripels. 2. Das Hermann-Mauguin Symbol der Symmetrieoperation. Der Drehsinn wird mit + oder gekennzeichnet, z.b. 3 +, 3. Eine etwaige Gleitkomponente T wird in Klammern angehängt, z.b. n (1/2, 0, 1/2). 3. Die Position des Symmetrieelements, sofern es nicht im Ursprung liegt, z.b. 0,1/4,1/4 oder 0,y,0 oder x,y,1/4. Raumgruppen mit zentrierten Gittern haben mehr als einen Block, je einen für 0,0,0 und für jeden Zentrierungsvektor, der jeweils über dem Block steht Punktlagen Unter Positions sind auf der rechten Tabellenseite die Koordinatentripel der allgemeinen und (soweit vorhanden) speziellen Lagen aufgeführt. Die Tripel der allgemeinen Punktlage sind eine Art Kurzschrift für ein Repräsentantensystem der Nebenklassenzerlegung der Raumgruppe nach ihren Translationen. Die Reihenfolge der Koordinatentripel allgemeiner Lage entspricht der Reihenfolge der Symmetrieoperationen unter dem Eintrag Symmetry Operations. Angegeben sind: 1. Zähligkeit (Multiplizität) der Punktlage. 2. Wyckoff-Symbol (beginnend mit a für die höchstsymmetrische Lage). 3. Orientiertes Hermann-Mauguin Symbol der Lagesymmetrie. 4. Koordinatentripel symmetrisch äquivalenter Pumkte der betreffenden Lage. Die Multiplizität der allgemeinen Punktlage ist das Produkt aus der Ordnung der Kristallklasse und der Anzahl der Zentrierungvektoren, für spezielle Lagen noch dividiert durch die Ordnung der Lagesymmetriegruppe Untergruppen Nach HERMANN sind maximale Untergruppen der Raumgruppen entweder translationenoder klassengleich. Die Klassifizierung der maximalen Untergruppen von Raumgruppen erfolgt daher nach folgendem Schema: Typ I: Translationengleiche maximale Untergruppen. Alle Translationen bleiben erhalten, aber es fallen ganze Nebenklassen weg; die Punktgruppe wird verkleinert. Typ II: Klassengleiche maximale Untergruppen. Die Punktgruppe bleibt erhalten, aber es fallen Translationen weg. a) Die konventionelle Zelle bleibt gleich; es entfallen nur zentrierende Operationen. b) Die konventionelle Zelle wird vergrößert. c) Die Untergruppe gehört zum gleichen (affinen) Raumgruppentyp. 39
16 Abbildung 15: Raumgruppe P2 1 /c (2nd Setting) aus den IT Vol. A (oben: erste Seite, unten: obere Hälfte der zweiten Seite). 40
17 Abbildung 16: Raumgruppe P2 1 /c (2nd Setting) aus den IT Vol. A (Fortsetzung: untere Hälfte der zweiten Seite). 41
18 11 Symmetrie makroskopischer Kristallpolyeder 11.1 Makroskopische Kristallsymmetrie Unter der Punktsymmetrieoperation X = R X transformieren die Komponenten des Produkts H X nach H X = H(RX) = ( HR)X = HX d.h. HR = H = H = HR 1. Millersche Indizes (hkl) transformieren also mit der inversen Operation R 1. Wenn R alle Symmetrieoperationen der Punktgruppe P = {R} durchläuft, dann durchläuft {R 1 } ebenfalls alle Elemente von P, nur in einer anderen Reihenfolge. Die Symmetrie sowohl des reziproken Raums als auch die aller Flächennormalen (hkl) folgt daher der Symmetrie der Punktgruppe P. 4 Die Menge aller Isometrien, die einen idealen Kristallpolyeder auf sich abbilden, nennt man die Symmetrie dieses Polyeders. Unter dieser Symmetrie werden äquivalente Flächen bzw. die dazugehörigen Flächennormalen aufeinander transformiert. Alle Symmetrieoperationen lassen wenigstens den Schwerpunkt fest; wählt man diesen als Ursprung, dann werden alle Symmetrieoperationen durch Seitzoperatoren der Form (R, 0) dargestellt. Die Symmetrie des Kristalls bildet eine endliche Gruppe, nämlich die Punktgruppe (oder Kristallklasse) des Kristalls. Zwei Kristalle gehören zur gleichen Punktgruppe, wenn nach Wahl geeigneter Basissysteme ihre Matrixgruppen {(R, 0)} übereinstimmen Kristallformen (äquivalente Flächen) Die Menge symmetrisch äquivalenter Kristallflächen, die durch die Symmetrieoperationen der Punktgruppe aus einer Fläche (hkl) erzeugt werden, nennt man eine Form und schreibt dafür abkürzend {hkl}. Die Anzahl symmetrisch äquivalenter Flächen einer Form heißt ihre Multiplizität oder Flächenhäufigkeit. Eine Form, die ein geschlossenes Polyeder darstellt nennt man eine geschlossene Form. Andernfalls spricht man von einer offenen Form. Geschlossene Formen im kubischen System sind z.b. die Formen {100} (Würfel), {111} (Oktaeder oder Tetraeder) oder {110} (Rhombendodekaeder). Eine offene Form wäre {100} im triklinen System (paralleles Flächenpaar in 1, sog. Pinakoid). 4 Die Symmetrie des ideal gewachsenen Kristalls zeigt sich besser als an seinen Flächen an dem Bündel seiner Flächennormalen, weil dieses gegen Wachstumsstörungen unempfindlich ist. 42
19 11.3 Äquivalente Zonen Die Menge symmetrisch äquivalenter Richtungen (Kristallkanten oder Zonenachsen), die durch Symmetrieoperationen der Punktgruppe aus einer Gitterrichtung [ uvw ] erzeugt werden, schreibt man abkürzend <uvw> Flächenlagen und Flächensymmetrie Die Menge der Symmetrieoperationen der Punktgruppe P, die eine Fläche fest lassen, nennt man die Flächensymmetrie oder auch Lagesymmetrie dieser Fläche. Die Flächensymmetrie ist immer eine Untergruppe S P der Punktgruppe P. Die Ordnung der Untergruppe S ist ein Teiler der Ordnung von P. Die Flächenhäufigkeit (Anzahl äquivalenter Flächen der Form {hkl}) ist gleich dem Index i = P / S. Enthält die Untergruppe S nur das Einselement, S = {e}, dann spricht man von einer Fläche allgemeiner Lage, andernfalls von einer Fläche spezieller Lage. Eine Menge äquivalenter Kristallflächen der Flächensymmetrie 1 nennt man eine allgemeine Form. Eine Menge äquivalenter Kristallflächen mit Flächensymmetrie größer als 1 nennt man eine spezielle Form. Die Flächennormalen solcher Flächen liegen auf wenigstens einem Symmetrieelement (Dreh- oder Drehinversionsachse; m 2!). Die Gesamtheit der an einem Kristall auftretenden Formen nennt man seine Tracht. Die allgemeine Form enthält die maximal mögliche Flächenzahl P mit der Flächensymmetrie 1. Spezielle Formen haben weniger als P Flächen mit einer Symmetrie größer als 1. In der kubischen Punktgruppe m 3m ist beispielsweise die allgemeine Form {hkl} ein Hexakisoktaeder mit 48 Flächen; spezielle Formen sind der Würfel {100} mit 6 quadratischen Flächen, der Oktaeder {111} mit 8 Dreiecksflächen und der Rhombendodekaeder {110} mit 12 Rautenflächen IT Vol.A, Section 10 In den International Tables A findet man in Section 10 hierzu folgende Angaben: 1. Zähligkeit (Multiplizität, Flächenhäufigkeit). 2. Wyckoff-Symbol (a für die höchstsymmetrische Lage). 3. Orientiertes Hermann-Mauguin Symbol der Lagesymmetrie. 4. Name des Polyeders zur Form {hkl}. 5. Millersche Indizes symmetrisch äquivalenter Flächen. Die Millerschen Indizes (hkl) dieser Tabellen sind auf eine konventionelle Basis bezogen. Sie können außer für trigonale und hexagonale Symmetrien durch Koordinatentripel x, y, z ersetzt werden. 43
20 44
g g 1 = g 1 g = e. (79)
 B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
B Anhang B B.1 Kristallographische Symmetriegruppen B.1.1 Definition Eine Menge G = {g 1, g 2,...,g k,... } von Elementen g k nennt man eine Gruppe, wenn die Verknüpfung (Operator: ) der Elemente g k die
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
Kristallstruktur und Mikrostruktur Teil I Vorlesung 3 1 Wiederholung Punktsymmetrie - Erkennung 1/ Eine Punktsymmetrie-Gruppe {G} mit Ordnung N hat N Punktsymmetrieoperationen G i, i = 1,2, N. aber nur
k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker
 k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker Institut für Geowissenschaften FE Mineralogie JWG-Universität Frankfurt Netzebene Translation: Verschiebung,
k.com Vorlesung Geomaterialien 2. Doppelstunde Kristallographische Grundlagen Prof. Dr. F.E. Brenker Institut für Geowissenschaften FE Mineralogie JWG-Universität Frankfurt Netzebene Translation: Verschiebung,
Röntgenstrukturanalyse von Einkristallen
 Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2017 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah Symmetrie,
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2017 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah Symmetrie,
Festk0203_ /11/2002. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
 Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
Festk234 37 11/11/22 2.9. Drehungen und Drehinversionen Bereits kennen gelernt: Translationssymmetrie. Neben Translationen gibt es noch weitere Deckoperationen die eine Struktur in sich überführen können:
Allgemeine Mineralogie - Kristallographie. Diamant
 Allgemeine Mineralogie - Kristallographie Diamant Bravaisgitter Aus den fünf 2-D Gittern können durch Translation in die dritte Dimension insgesamt 14 Bravaisgitter erzeugt werden Einteilung der Bravais
Allgemeine Mineralogie - Kristallographie Diamant Bravaisgitter Aus den fünf 2-D Gittern können durch Translation in die dritte Dimension insgesamt 14 Bravaisgitter erzeugt werden Einteilung der Bravais
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand
 Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
Kurs Röntgenstrukturanalyse, Teil 1: Der kristalline Zustand Beispiel 1: Difluoramin M. F. Klapdor, H. Willner, W. Poll, D. Mootz, Angew. Chem. 1996, 108, 336. Gitterpunkt, Gitter, Elementarzelle, Gitterkonstanten,
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen. Sommersemester Christoph Wölper
 Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2012 Christoph Wölper Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Script unter: http://www.uni-due.de/~adb297b/ss2012/strukturmethoden_vorlesung.pdf
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2012 Christoph Wölper Christoph Wölper christoph.woelper@uni-due.de http://www.uni-due.de/~adb297b Vorlesungs-Script unter: http://www.uni-due.de/~adb297b/ss2012/strukturmethoden_vorlesung.pdf
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Hexagonal dichtest gepackte Struktur
 Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
Hexagonal dichtest gepackte Struktur Auch diese Struktur ist sehr wichtig, da sie von sehr vielen Systemen angenommen wird (kein Bravaisgitter). Das einfach hexagonale Bravais-Gitter (in 3-dim): zwei-dim:
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallstruktur und Mikrostruktur Teil I Vorlesung 2 1 Kristallstruktur und Teil I Scripte Mikrostruktur http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/lehrangebot.html 2 Wiederholung Koordinatensysteme
Kristallographie. Walter Borchardt-Ott. Eine Einführung für Naturwissenschaftler. Springer. Sechste, überarbeitete und erweiterte Auflage
 Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Walter Borchardt-Ott Kristallographie Eine Einführung für Naturwissenschaftler Sechste, überarbeitete und erweiterte Auflage Mit 290 Abbildungen und 44 Tabellen Springer Inhaltsverzeichnis 1 Einleitung
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 3 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Das Gitter Kristalle bestehen
Wiederholung der letzten Vorlesungsstunde
 Wiederholung der letzten Vorlesungsstunde Festkörper, ausgewählte Beispiele spezieller Eigenschaften von Feststoffen, Kohlenstoffmodifikationen, Nichtstöchiometrie, Unterscheidung kristalliner und amorpher
Wiederholung der letzten Vorlesungsstunde Festkörper, ausgewählte Beispiele spezieller Eigenschaften von Feststoffen, Kohlenstoffmodifikationen, Nichtstöchiometrie, Unterscheidung kristalliner und amorpher
2.1 Translationssymmetrie
 2.1 Translationssymmetrie Die periodische Anordnung eines Kristalls entspricht mathematisch einer Translationssymmetrie. Diese wird mit Hilfe von drei fundamentalen Translationsvektoren beschrieben: T
2.1 Translationssymmetrie Die periodische Anordnung eines Kristalls entspricht mathematisch einer Translationssymmetrie. Diese wird mit Hilfe von drei fundamentalen Translationsvektoren beschrieben: T
Symmetriebeziehungen zwischen verwandten Kristallstrukturen
 Ulrich Müller Symmetriebeziehungen zwischen verwandten Kristallstrukturen Anwendungen der kristallographischen Gruppentheorie in der Kristallchemie unter Verwendung von Textvorlagen von Hans Wondratschek
Ulrich Müller Symmetriebeziehungen zwischen verwandten Kristallstrukturen Anwendungen der kristallographischen Gruppentheorie in der Kristallchemie unter Verwendung von Textvorlagen von Hans Wondratschek
Kristallographie I. Inhalt von Kapitel 3
 62 Kristallographie I Inhalt von Kapitel 3 3 Der Kristall als Diskontinuum... 63 3.1 Zweidimensionale Raumgruppen... 63 3.1.1 Elementarmaschen... 63 3.1.2 Die zweidimensionalen Punkt- und Raumgruppen...
62 Kristallographie I Inhalt von Kapitel 3 3 Der Kristall als Diskontinuum... 63 3.1 Zweidimensionale Raumgruppen... 63 3.1.1 Elementarmaschen... 63 3.1.2 Die zweidimensionalen Punkt- und Raumgruppen...
1.1 Symmetrie im naturwissenschaftlichen Weltbild Platons ( ) und bei Kepler ( )
 C:\DOCUME~1\AG\LOCALS~1\TEMP\VK1_Symmetrie_004.DOC 1 1 Symmetrie Die Invarianz des Kristallsgitters gegenüber bestimmten Symmetrieoperationen, speziell gegenüber Verschiebungen (Translationen) des Gitters
C:\DOCUME~1\AG\LOCALS~1\TEMP\VK1_Symmetrie_004.DOC 1 1 Symmetrie Die Invarianz des Kristallsgitters gegenüber bestimmten Symmetrieoperationen, speziell gegenüber Verschiebungen (Translationen) des Gitters
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen Drehinversionsachsen Schraubenachsen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen Drehinversionsachsen Schraubenachsen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Wiederholung - Gleitspiegelebene A B 2 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 4 Wiederholung - Gleitspiegelebene A B 2 Symmetrieoperationen - Zusammenfassung Fixed Point No fixed Point Drehachsen Translationen keine Translationen
Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt)
 Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0a) Es sollen aus folgenden kubischen Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte
Übungen Festkörper (WS 2017/2018) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0a) Es sollen aus folgenden kubischen Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte
3. Struktur idealer Kristalle
 3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle
 3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
3. Struktur idealer Kristalle 3.1 Raumgitter - 3-D-periodische Anordnungen - Raumgitter und Basis - primitive Translationen - Elementarzelle - Dreh- und Spiegelsymmetrien - Einheitszelle - 7 Kristallsysteme,
2. Punktgruppen/Kristallklassen
 2. Punktgruppen/Kristallklassen Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2016/2017, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen
2. Punktgruppen/Kristallklassen Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2016/2017, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen
= {e} U (1) U (2) U (3) = {e,a,b,c} 4 : e a b e e a b a a c e b b e c
 KONZEPT DER GRUPPE 6.7 Untergruppen U ist eine Gruppe mit derselben Gruppenoperation wie G und der Ordnung h U h G U ist dann eine Untergruppe von G, wenn alle u i G sind. Beispiel 9: Untergruppen von
KONZEPT DER GRUPPE 6.7 Untergruppen U ist eine Gruppe mit derselben Gruppenoperation wie G und der Ordnung h U h G U ist dann eine Untergruppe von G, wenn alle u i G sind. Beispiel 9: Untergruppen von
Struktur von Einkristallen
 Struktur von Einkristallen Beschreibung des einkristallinen Festkörpers Am einfachsten zu beschreiben sind atomare Kristalle bei denen an jedem Punkt des Raumgitters sich genau ein Atom befindet. Man wählt
Struktur von Einkristallen Beschreibung des einkristallinen Festkörpers Am einfachsten zu beschreiben sind atomare Kristalle bei denen an jedem Punkt des Raumgitters sich genau ein Atom befindet. Man wählt
Grundlagen-Vertiefung PW3. Kristalle und Kristallstrukturen Version von 15. Oktober 2013
 Grundlagen-Vertiefung PW3 Kristalle und Kristallstrukturen Version von 15. Oktober 2013 Kristalle besitzen einen geordneten und periodischen Gitteraufbau. Die überwiegende Mehrzahl der anorganischen Festkörper
Grundlagen-Vertiefung PW3 Kristalle und Kristallstrukturen Version von 15. Oktober 2013 Kristalle besitzen einen geordneten und periodischen Gitteraufbau. Die überwiegende Mehrzahl der anorganischen Festkörper
Invarianten eines symmetrischen Tensors unter kristallographischen Symmetriegruppen
 Mathematisches Institut der Ludwig-Maximilians Universität München Invarianten eines symmetrischen Tensors unter kristallographischen Symmetriegruppen Richard Cattien 2011 Diplomarbeit Betreuer: Prof.
Mathematisches Institut der Ludwig-Maximilians Universität München Invarianten eines symmetrischen Tensors unter kristallographischen Symmetriegruppen Richard Cattien 2011 Diplomarbeit Betreuer: Prof.
2. Punktgruppen/Kristallklassen
 Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2018/2019, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen (SO) /Drehachsen (SE) II: Spiegelung
Symmetrie mit konstantem Punkt M+K-Basiskurs Kristallographie und Beugung, WS 2018/2019, C. Röhr 2.1. Einleitung Definitionen, Nomenklatur, Klassifizierung I: Rotationen (SO) /Drehachsen (SE) II: Spiegelung
2. Struktur von Festkörpern
 . Struktur von Festkörpern Energie-Minimum wird erreicht, wenn jedes Atom möglichst dieselbe Umgebung hat Periodische Anordnung von Atomen. Periodische Anordnung erleichtert theoretische Beschreibung erheblich.
. Struktur von Festkörpern Energie-Minimum wird erreicht, wenn jedes Atom möglichst dieselbe Umgebung hat Periodische Anordnung von Atomen. Periodische Anordnung erleichtert theoretische Beschreibung erheblich.
II.3. Primitive Elementarzellen und Basisvektoren
 II.3. Primitive Elementarzellen und Basisvektoren Elementarzelle (EZ): lückenlose Überdeckung des Raumes, Beispiel: Würfel für kubische Gitter, Primitive EZ: enthält 1 Gitterpunkt Beispiel: kubische bcc-struktur
II.3. Primitive Elementarzellen und Basisvektoren Elementarzelle (EZ): lückenlose Überdeckung des Raumes, Beispiel: Würfel für kubische Gitter, Primitive EZ: enthält 1 Gitterpunkt Beispiel: kubische bcc-struktur
Werkstoffe und Sensorik
 1 1. Kristall-Strukturen Kristalline Materialien bestehen aus regelmäßigen Anordnungen von Atomen in 3 Dimensionen. Einheitszelle: Kleinste, sich wiederholende Einheit, die die volle Symmetrie der Kristallstruktur
1 1. Kristall-Strukturen Kristalline Materialien bestehen aus regelmäßigen Anordnungen von Atomen in 3 Dimensionen. Einheitszelle: Kleinste, sich wiederholende Einheit, die die volle Symmetrie der Kristallstruktur
Nachbesprechung. Übung 3
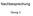 Nachbesprechung Übung 3 Form (a) Pinakoid, (b) allgemeine Fläche (Pfeil) wird durch eine Spiegelebene in ein Doma überführt, (c) Sphenoid (Pfeil), generiert durch die Wirkung einer 2-zähligen Achse, (d)
Nachbesprechung Übung 3 Form (a) Pinakoid, (b) allgemeine Fläche (Pfeil) wird durch eine Spiegelebene in ein Doma überführt, (c) Sphenoid (Pfeil), generiert durch die Wirkung einer 2-zähligen Achse, (d)
Transformation Allgemeines Die Lage eines Punktes kann durch einen Ortsvektor (ausgehend vom Ursprung des Koordinatensystems
 Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Anorganische Chemie III - Festkörperchemie
 Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
Mathematisch-Naturwissenschaftliche Fakultät Institut für Chemie Abteilung Anorganische Chemie/Festkörperchemie Prof. Dr. Martin Köckerling Vorlesung Anorganische Chemie III - Festkörperchemie 1 Wiederholung
A. N. Danilewsky 1. Inhalt des 1. Kapitels
 A. N. Danilewsky 1 Inhalt des 1. Kapitels 1 Vom Raumgitter zur Kristallstruktur... 2 1.1 Definition und Nomenklatur... 2 1.2 Gittergerade...4 1.3 Gitterebene...4 1.4 Raumgitter...5 1.5 Kristallsysteme...
A. N. Danilewsky 1 Inhalt des 1. Kapitels 1 Vom Raumgitter zur Kristallstruktur... 2 1.1 Definition und Nomenklatur... 2 1.2 Gittergerade...4 1.3 Gitterebene...4 1.4 Raumgitter...5 1.5 Kristallsysteme...
Bereits bekannt: Translationssymmetrie zum Aufbau des Raumgitters aus Elementarzellen
 42 Kristallographie I 2.4 Symmetrieprinzip... 43 2.4.1 Symmetrieelemente... 43 2.4.1.1 Drehachsen (Abb. 2.4.1)... 43 2.4.1.2 Spiegelebenen... 46 2.4.1.3 Inversionszentrum... 46 2.4.2 Verknüpfung zweier
42 Kristallographie I 2.4 Symmetrieprinzip... 43 2.4.1 Symmetrieelemente... 43 2.4.1.1 Drehachsen (Abb. 2.4.1)... 43 2.4.1.2 Spiegelebenen... 46 2.4.1.3 Inversionszentrum... 46 2.4.2 Verknüpfung zweier
P 2 - Piezoelektrizität
 56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
56 P2 Piezoelektrizität P 2 - Piezoelektrizität Ein Kristall, dessen Punktgruppe (Kristallklasse) kein Symmetriezentrum (Z) aufweist, kann prinzipiell piezoelektrisch sein Das heißt, der auf den Kristall
Röntgenstrukturanalyse (AC-3) P. G. Jones. Inst. Anorg. Analyt. Chemie, TU Braunschweig. Version: SS Vorwort
 Röntgenstrukturanalyse (AC-3) P. G. Jones Inst. Anorg. Analyt. Chemie, TU Braunschweig Version: SS 2017 Letzte Änderung: 19.08.16 Vorwort Dieses Skript kann uneingeschränkt kopiert und weitergegeben werden.
Röntgenstrukturanalyse (AC-3) P. G. Jones Inst. Anorg. Analyt. Chemie, TU Braunschweig Version: SS 2017 Letzte Änderung: 19.08.16 Vorwort Dieses Skript kann uneingeschränkt kopiert und weitergegeben werden.
Anorganische Chemie III
 Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Gittertypen # Bravaisgitter
Seminar zur Vorlesung Anorganische Chemie III Wintersemester 2015/16 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen Wiederholung Was bisher geschah # Gittertypen # Bravaisgitter
Wiederholung der letzten Vorlesungsstunde
 Wiederholung der letzten Vorlesungsstunde Gitterpunkte, Gittergeraden, Gitterebenen, Weiß'sche Koeffizienten, Miller Indizes Symmetrie in Festkörpern, Symmetrieelemente, Symmetrieoperationen, Punktgruppenymmetrie,
Wiederholung der letzten Vorlesungsstunde Gitterpunkte, Gittergeraden, Gitterebenen, Weiß'sche Koeffizienten, Miller Indizes Symmetrie in Festkörpern, Symmetrieelemente, Symmetrieoperationen, Punktgruppenymmetrie,
2 Symmetrieoperationen und -elemente. 1.8 Klassen 2 SYMMETRIEOPERATIONEN UND -ELEMENTE 7
 SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
SYMMETRIEOPERATIONEN UND -ELEMENTE 7.8 Klassen Zweck: Zusammenfassen zueinander ähnlicher (konjugierter) Elemente einer Gruppe. Durch Bestimmung aller Klassen ergibt sich eine eindeutige Zerlegung on G:
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung # 2D Muster haben keine Spiegelebene in der Projektionebene # Der Verschiebungsvektor v einer Gleitspiegelebene, parallel zur Achse t
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung # 2D Muster haben keine Spiegelebene in der Projektionebene # Der Verschiebungsvektor v einer Gleitspiegelebene, parallel zur Achse t
Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
 5 Zur Geometrie euklidischer Bewegungen 5.1 Bewegungen Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
5 Zur Geometrie euklidischer Bewegungen 5.1 Bewegungen Eine Affinität α eines euklidischen Raumes heißt eine Bewegung, wenn sie Abstände (und damit auch Winkel) erhält, wenn also für alle Punkte X, Y gilt:
4 Lineare Abbildungen
 17. November 2008 34 4 Lineare Abbildungen 4.1 Lineare Abbildung: Eine Funktion f : R n R m heißt lineare Abbildung von R n nach R m, wenn für alle x 1, x 2 und alle α R gilt f(αx 1 ) = αf(x 1 ) f(x 1
17. November 2008 34 4 Lineare Abbildungen 4.1 Lineare Abbildung: Eine Funktion f : R n R m heißt lineare Abbildung von R n nach R m, wenn für alle x 1, x 2 und alle α R gilt f(αx 1 ) = αf(x 1 ) f(x 1
Symmetrie und Struktur in der Chemie
 Dirk Steinborn Symmetrie und Struktur in der Chemie Weinheim New York Basel Cambridge Tokyo V Inhaltsverzeichnis Schreibweise wichtiger im Text verwendeter Symbole VII 1 Einleitung 1 2 Moleküle und ihre
Dirk Steinborn Symmetrie und Struktur in der Chemie Weinheim New York Basel Cambridge Tokyo V Inhaltsverzeichnis Schreibweise wichtiger im Text verwendeter Symbole VII 1 Einleitung 1 2 Moleküle und ihre
Absorptionsspektrum von PTCDA und DiMe-PTCDI
 3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
3. Gruppentheorie Absorption coefficient *10 5 6 4 2 0 Absorptionsspektrum von PTCDA und DiMe-PTCDI PTCDA Wavelength / nm 800 700 600 500 400 HOMO-LUMO Übergang S 0 -S 1 transition S 0 -S 2 transition
Basisvokabular zur Strukturchemie (F. Kubel)
 Basisvokabular zur Strukturchemie (F. Kubel) Ångström Längenmaßeinheit in der Kristallographie 1Å=10-8 cm=100pm Anisotropie Richtungsabhängigkeit einer (vektoriellen) Eigenschaft Apolar Kristallstruktur
Basisvokabular zur Strukturchemie (F. Kubel) Ångström Längenmaßeinheit in der Kristallographie 1Å=10-8 cm=100pm Anisotropie Richtungsabhängigkeit einer (vektoriellen) Eigenschaft Apolar Kristallstruktur
Department Chemie. Röntgenbeugung. ISP-Methodenkurs. Dr. Frank Hoffmann
 Department Chemie Röntgenbeugung ISP-Methodenkurs Dr. Frank Hoffmann 22.01.2008 Ergebnis einer RSA Ä Atomsorten und deren Koordinaten in der asymmetrischen Einheit Ä Bindungslängen und -winkel Ä Elementarzelle
Department Chemie Röntgenbeugung ISP-Methodenkurs Dr. Frank Hoffmann 22.01.2008 Ergebnis einer RSA Ä Atomsorten und deren Koordinaten in der asymmetrischen Einheit Ä Bindungslängen und -winkel Ä Elementarzelle
Einführung in die Kristallographie
 WILL KLEBER Einführung in die Kristallographie 18., stark bearbeitete Auflage von Hans-Joachim Bautsch und Joachim Böhm Verlag Technik Berlin Inhaltsverzeichnis Einleitung 11 1. Kristallstrukturlehre und
WILL KLEBER Einführung in die Kristallographie 18., stark bearbeitete Auflage von Hans-Joachim Bautsch und Joachim Böhm Verlag Technik Berlin Inhaltsverzeichnis Einleitung 11 1. Kristallstrukturlehre und
HÖHERE PHYSIK SKRIPTUM VORLESUNGBLATT XII
 Prof. Dr. F. Koch Dr. H. E. Porteanu fkoch@ph.tum.de porteanu@ph.tum.de SS 2005 HÖHERE PHYSIK SKRIPTUM VORLESUNGBLATT XII 19.05.05 Festkörperphysik - Kristalle Nach unserem kurzen Ausflug in die Molekülphysik
Prof. Dr. F. Koch Dr. H. E. Porteanu fkoch@ph.tum.de porteanu@ph.tum.de SS 2005 HÖHERE PHYSIK SKRIPTUM VORLESUNGBLATT XII 19.05.05 Festkörperphysik - Kristalle Nach unserem kurzen Ausflug in die Molekülphysik
44 Orthogonale Matrizen
 44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
Festkörperphysik I. Wintersemester 2006/07
 Festk060701.doc 1 10/20/2006 Festkörperphysik I Wintersemester 2006/07 Peter Böni Physik-Department E21 Technische Universität München D-85747 Garching Vorlesungsnotizen, Übungsblätter und Lösungen: http://www.ph.tum.de/lehrstuehle/e21
Festk060701.doc 1 10/20/2006 Festkörperphysik I Wintersemester 2006/07 Peter Böni Physik-Department E21 Technische Universität München D-85747 Garching Vorlesungsnotizen, Übungsblätter und Lösungen: http://www.ph.tum.de/lehrstuehle/e21
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 g Wiederholung g 2 Verschiedene Ellementarzellen möglich 2 2 2 m g 2 P4g (p4gm) m 2 m Wiederholung 2 2 2 Verschiedene Ellementarzellen möglich m 2
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 g Wiederholung g 2 Verschiedene Ellementarzellen möglich 2 2 2 m g 2 P4g (p4gm) m 2 m Wiederholung 2 2 2 Verschiedene Ellementarzellen möglich m 2
Symmetrien. Transformationen. Affine und euklidische Räume
 Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
2. Kristallstrukturen 2.1 Bindungsarten
 2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
2. Kristallstrukturen 2.1 Bindungsarten Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome Entstehung von Kristallstrukturen Metall-Ion (+) Metallische Bindung
Vorlesung Festkörperphysik. WS 2014/2015 Vorlesungen Universität Rostock Heinrich Stolz
 Vorlesung Festkörperphysik WS 2014/2015 Vorlesungen 28.10.14 Universität Rostock Heinrich Stolz 1 2. Das Reziproke Gitter Wichtige mathematische Objekt in der Physik mit periodischer Struktur? ebene Welle
Vorlesung Festkörperphysik WS 2014/2015 Vorlesungen 28.10.14 Universität Rostock Heinrich Stolz 1 2. Das Reziproke Gitter Wichtige mathematische Objekt in der Physik mit periodischer Struktur? ebene Welle
Grundlagen der Kristallographie
 Grundlagen der Kristallographie Motivation Reflektionsbedingungen g Begriffsdefinitionen und internationale Konvention Kristall Einheitszelle Quasikristalle Penrose Tiling Die 7 Kristallsysteme Kristallographische
Grundlagen der Kristallographie Motivation Reflektionsbedingungen g Begriffsdefinitionen und internationale Konvention Kristall Einheitszelle Quasikristalle Penrose Tiling Die 7 Kristallsysteme Kristallographische
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie. Was ist Symmetrie?
 Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Anorganische Chemie 3 (3.1) Teil 1 - Symmetrie Was ist Symmetrie? AC3 WS 2011/12 1 Symmetrie (griechisch = Ebenmaß, Gleichmaß) bedeutet die gesetzmäßige Wiederholung eines Motivs und damit die Übereinstimmung
Allgemeine Chemie Symmetrie von Molekülen
 Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Allgemeine Chemie Symmetrie von Molekülen AC_Molekuelsymmetrie.doc Seite 1 von 23 Fck / 12.10.05 Inhaltsverzeichnis 1 Einleitung...3 1.1 Anwendungsbereiche der Molekülsymmetrie...3 1.2 Sinn und Zweck der
Transformation - 3. Für "übliche" Anwendungen in der Geometrie ist es sinnvoll, bei Transformationen eine gleiche
 Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
7 Kristallmorphologie
 7 Kristallmorphologie Das Skalarprodukt eines Translationsvektors t mit einem reziproken Gittervektor h h t = u j b j h k b k = h k b j b ku j = h k δ jk u j = h j u j (25) j k k j k j j ist immer ganzzahlig:
7 Kristallmorphologie Das Skalarprodukt eines Translationsvektors t mit einem reziproken Gittervektor h h t = u j b j h k b k = h k b j b ku j = h k δ jk u j = h j u j (25) j k k j k j j ist immer ganzzahlig:
Physik IV Einführung in die Atomistik und die Struktur der Materie
 Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 2011 Vorlesung 21 30.06.2011 Physik IV - Einführung in die Atomistik Vorlesung 21 Prof. Thorsten Kröll 30.06.2011 1 H 2
Inhaltsverzeichnis. 1 Hardwaregrundlagen
 Inhaltsverzeichnis 1 Hardwaregrundlagen 2.1 Koordinatentransformationen 2.2 Transformationen in der Ebene 2.3 Transformationen im Raum 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität
Inhaltsverzeichnis 1 Hardwaregrundlagen 2.1 Koordinatentransformationen 2.2 Transformationen in der Ebene 2.3 Transformationen im Raum 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Typisch metallische Eigenschaften:
 Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
Typisch metallische Eigenschaften: hohe elektrische Leitfähigkeit hohe thermische Leitfähigkeit bei Energiezufuhr (Wärme, elektromagnetische Strahlung) können Elektronen emittiert werden metallischer Glanz
2.3.4 Drehungen in drei Dimensionen
 2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
Struktur von Festkörpern
 Struktur von Festkörpern Wir wollen uns zunächst mit der Struktur von Festkörpern, daß heißt mit der Geometrie in der sie vorliegen beschäftigen Kovalent gebundene Festkörper haben wir bereits in Form
Struktur von Festkörpern Wir wollen uns zunächst mit der Struktur von Festkörpern, daß heißt mit der Geometrie in der sie vorliegen beschäftigen Kovalent gebundene Festkörper haben wir bereits in Form
++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen dx+ey+f = 0 1.1
 Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
von Robert Krickl Institut für Mineralogie und Kristallographie Universität Wien, Geozentrum, Althanstrasse 14, A-1090 Wien
 MITT.ÖSTERR.MINER.GES. 149 (2004) GEOMETRISCHE STUDIEN ZU DEN PENTAGONALEN UND DEKAGONALEN DREIDIMENSIONALEN PUNKTGRUPPEN von Robert Krickl Institut für Mineralogie und Kristallographie Universität Wien,
MITT.ÖSTERR.MINER.GES. 149 (2004) GEOMETRISCHE STUDIEN ZU DEN PENTAGONALEN UND DEKAGONALEN DREIDIMENSIONALEN PUNKTGRUPPEN von Robert Krickl Institut für Mineralogie und Kristallographie Universität Wien,
Symmetrieelemente C 3 C 2 C 3 O H H N H H H
 Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
Symmetrieelemente Ein Symmetrielement liegt vor, wenn ein Objekt (hier: Molekül) durch eine Symmetrieoperation mit sich selbst zur Deckung gebracht werden kann. neue und alter Orientierung nicht unterscheidbar
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick
 Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Röntgenbeugung und das reziproke
Methoden der Chemie III Teil 1 Modul M.Che.1101 WS 2010/11 6 Moderne Methoden der Anorganischen Chemie Mi 10:15-12:00, Hörsaal II George Sheldrick gsheldr@shelx.uni-ac.gwdg.de Röntgenbeugung und das reziproke
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Lineare Algebra. 1 Lineare Abbildungen
 Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
O ist gegenüber C 2. invariant. Allgemein bezeichnet man mit C n. ist symmetrisch gegenüber, das JCl Ion gegenüber C 4
 107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
107 KAPITEL J Symmetrien 1. Einleitung a) Warum Symmetriebetrachtungen? Je komplizierter die Probleme, desto mehr spielen Symmetriebetrachtungen eine Rolle. Die Symmetriebetrachtungen in der Molekülphysik
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung 2/m 2/m 2/m {1 i 2 x 2 y 2 z m x m y m z } Ordnung 8! m 2 i 2 Wiederholung Spezielle Lagen # spezielle Lagen in zentrierten Raumgruppen
Kristallstruktur und Mikrostruktur Teil I Vorlesung 5 Wiederholung 2/m 2/m 2/m {1 i 2 x 2 y 2 z m x m y m z } Ordnung 8! m 2 i 2 Wiederholung Spezielle Lagen # spezielle Lagen in zentrierten Raumgruppen
Gefüge und Eigenschaften metallischer Werkstoffe WS 17/18
 Gefüge und Eigenschaften metallischer Werkstoffe WS 7/8 Übung 5 Musterlösung 0..07 Aufgabe Welche Bravais-Gittertypen gibt es? Welche Modifikationen besitzen Sie? Nennen Sie Materialbeispiele zu jedem
Gefüge und Eigenschaften metallischer Werkstoffe WS 7/8 Übung 5 Musterlösung 0..07 Aufgabe Welche Bravais-Gittertypen gibt es? Welche Modifikationen besitzen Sie? Nennen Sie Materialbeispiele zu jedem
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6
 Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 Teil I: Zotov 1 Koordinatensysteme, Das Raumgitter, Das reziproke Gitter, Der Metrik-Tensor 2 Abstrakte Gruppen, Symmetrieoperationen, Punktsymmetrie
Kristallstruktur und Mikrostruktur Teil I Vorlesung 6 Teil I: Zotov 1 Koordinatensysteme, Das Raumgitter, Das reziproke Gitter, Der Metrik-Tensor 2 Abstrakte Gruppen, Symmetrieoperationen, Punktsymmetrie
Seminar zum Praktikum Anorganische Chemie III III
 Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
Seminar zum Praktikum Anorganische Chemie III III Metallorganische Chemie Dr. J. Wachter IR-Teil3 www.chemie.uni-regensburg.de/anorganische_chemie/scheer/lehre.html www.chemie.uniregensburg.de/anorganische_chemie/wachter/lehre.html
gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren
 Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
Stefan K. 4.Übungsblatt Algebra I Aufgabe 1 gegeben: G sei endliche Gruppe, jede Untergruppe von G sei ein Normalteiler von G zu zeigen: je zwei Elemente teilerfremder Ordnung kommutieren Beweis: Seien
KRISTALLOGRAPHIE I SS Walter Steurer Thomas Weber
 KRISTALLOGRAPHIE I Walter Steurer Thomas Weber SS 2001 Let us examine a crystal... the equality of the sides pleases us; that of the angles doubles the pleasure. On bringing to view a second face in all
KRISTALLOGRAPHIE I Walter Steurer Thomas Weber SS 2001 Let us examine a crystal... the equality of the sides pleases us; that of the angles doubles the pleasure. On bringing to view a second face in all
Vektoren - Die Basis
 Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie
 Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie Zulässige Hilfsmittel: Charakterentafeln, Schema Hierarchie der Punktgruppen SS 6 Prof. Dr. B. Dick Aufgabe 1 (15P): Finden Sie die Punktgruppe
Klausur zur Vorlesung Symmetrie in Chemie und Spektroskopie Zulässige Hilfsmittel: Charakterentafeln, Schema Hierarchie der Punktgruppen SS 6 Prof. Dr. B. Dick Aufgabe 1 (15P): Finden Sie die Punktgruppe
Anorganische Chemie III
 Seminar zu Vorlesung Anorganische Chemie III Wintersemester 2012/13 Christoph Wölper Universität Duisburg-Essen Symmetrie Kombination von Symmetrie-Elementen Symmetrie Kombination von Symmetrie-Elementen
Seminar zu Vorlesung Anorganische Chemie III Wintersemester 2012/13 Christoph Wölper Universität Duisburg-Essen Symmetrie Kombination von Symmetrie-Elementen Symmetrie Kombination von Symmetrie-Elementen
3.3. Drehungen und Spiegelungen
 3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt)
 Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
Übungen Festkörper (WS 2018/2019) (wird im Laufe des Semesters vervollständigt) Aufgabe 0) (a0) Es sollen aus folgenden Einheitszellen in allen Raumrichtungen unendlich periodisch fortgesetzte Festkörper
1.5 Kongruenz und Ähnlichkeit
 19 1.5 Kongruenz und Ähnlichkeit Definition Sei A n der affine Standardraum zum Vektorraum R n. Eine Abbildung F : A n A n heißt Isometrie, falls d(f (X), F (Y )) = d(x, Y ) für alle X, Y A n gilt. Es
19 1.5 Kongruenz und Ähnlichkeit Definition Sei A n der affine Standardraum zum Vektorraum R n. Eine Abbildung F : A n A n heißt Isometrie, falls d(f (X), F (Y )) = d(x, Y ) für alle X, Y A n gilt. Es
Übersicht Kapitel 9. Vektorräume
 Vektorräume Definition und Geometrie von Vektoren Übersicht Kapitel 9 Vektorräume 9.1 Definition und Geometrie von Vektoren 9.2 Teilräume 9.3 Linearkombinationen und Erzeugendensysteme 9.4 Lineare Abhängigkeiten
Vektorräume Definition und Geometrie von Vektoren Übersicht Kapitel 9 Vektorräume 9.1 Definition und Geometrie von Vektoren 9.2 Teilräume 9.3 Linearkombinationen und Erzeugendensysteme 9.4 Lineare Abhängigkeiten
Strukturmethoden: Röntgenstrukturanalyse von Einkristallen
 Skript zur Vorlesung Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2014 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen letzte Änderung: 8.
Skript zur Vorlesung Strukturmethoden: Röntgenstrukturanalyse von Einkristallen Sommersemester 2014 Christoph Wölper Institut für Anorganische Chemie der Universität Duisburg-Essen letzte Änderung: 8.
09. Lineare Abbildungen und Koordinatentransformationen
 09. Lineare Abbildungen und Koordinatentransformationen Definition. Seien V und W Vektorräume. Unter einer linearen Abbildung versteht man eine Abbildung F : V W, v F v w mit folgender Eigenschaft: F λ
09. Lineare Abbildungen und Koordinatentransformationen Definition. Seien V und W Vektorräume. Unter einer linearen Abbildung versteht man eine Abbildung F : V W, v F v w mit folgender Eigenschaft: F λ
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3
 3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
3 Geometrische Klassifikation der Bewegungen im R 2 und R 3 Sei f : R n R n eine Bewegung Sie kann beschrieben werden in der Form Dabei ist T (f)(x) = A x f(x) = Ax + b mit A O(n) und b R n Definition:
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
Lineare Abbildungen (Teschl/Teschl 10.3, 11.2)
 Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
