Schriftliche Abiturprüfung Mathematik 2013
|
|
|
- Cornelius Fürst
- vor 7 Jahren
- Abrufe
Transkript
1 Schriftliche Abiturprüfung Mathematik 03 Allgemeines Struktur eines Aufgabensatzes Pflichtteil 30 VP keine Auswahlmöglichkeit Pflichtteil P (30 VP) Wahlteil Analysis 5 VP Die Lehrkraft wählt zwischen A und A. Analysis A (5 VP) Analysis A (5 VP) Wahlteil Geometrie/Stochastik 5 VP Die Lehrkraft wählt zwischen B und B. Geometrie B. ( VP) Geometrie B. (8 VP) In jeder kombinierten Wahlteilaufgabe Geometrie/Stochastik entfallen auf die Geometrie mindestens 8 und höchstens VP, die Stochastik mindestens 4 und höchstens 7 VP. Stochastik B. Stochastik B. (7 VP) Seite von 4
2 Schriftliche Abiturprüfung Mathematik 03 Allgemeines Pflichtteil 9 Kategorien (je eine Aufgabe) Gruppe Inhalte Vergleich mit Aufgaben seit 004 () Ableitung Reduktion: ohne Quotientenregel () Stammfunktion, Integral [unverändert] (3) Gleichungslehre Reduktion: ohne Polynomdivision, Wurzelgleichungen (4) Elemente der Kurvendiskussion [unverändert] (5) Funktionenkompetenz (6) Lineare Gleichungssysteme, Inzidenzgeometrie Öffnung: s. Musteraufgaben Reduktion: ohne Nachweis linearer Unabhängigkeit (7) Metrische Geometrie [unverändert] (8) Stochastik neu (9) Beschreiben, Verstehen, Begründen Öffnung: nicht nur innerhalb der Geometrie Wahlteil Analysis neue Inhalte entfallene Inhalte Vertiefung gebrochenrationaler und trigonometrischer Funktionen Folgen, vollständige Induktion Tendenzen keine strenge Unterteilung nach Funktionenklassen verstärkt auch innermathematische Teilaufgaben angemessener GTR-Einsatz zweigeteilt oder durchgehend (vgl. Musteraufgaben A und A) Wahlteil Geometrie neue Inhalte entfallene Inhalte geometrische Beweise Tendenzen ggf. Vernetzung mit Analysis verstärkt auch innermathematische Teilaufgaben Wahlteil Stochastik Inhalte Baumdiagramme, Pfadregeln Binomialverteilung, Erwartungswert Testen von Hypothesen Seite von 4
3 Schriftliche Abiturprüfung Mathematik 03 Inhalte Gleichungen lineare, quadratische Gleichungen einfache Bruchgleichungen Potenzgleichungen Exponentialgleichungen einfache trigonometrische Gleichungen Gleichungen, die auf Nullprodukte führen auch: Lösung durch Substitution nicht: Polynomdivision, Wurzelgleichungen, Näherungsverfahren Funktionen Kenntnis grundlegender Funktionstypen: Potenzfunktionen ganzrationale Funktionen trigonometrische Funktionen natürliche Exponentialfunktion Verschiebungen Streckungen in x- und y-richtung Wirkung von Parametern Zusammengesetzte Funktionen: Summen, Differenzen einfache Produkte und Quotienten einfache Verkettungen senkrechte und waagerechte Asymptoten nicht: schiefe Asymptote, Näherungskurve Nullstellen Bestimmung von Funktionen mit vorgegebenen Eigenschaften in einfachen Fällen nicht: Folgen, Iterationen nicht: vollständige Induktion Differentialrechnung Ableitung (auch höhere Ableitungen) Änderungsrate Ableitungsfunktion Tangente und Normale Ableitungsregeln: Summen- und Faktorregel Potenzregel Produktregel Kettenregel nicht: Quotientenregel Monotonie Extrempunkte, Wendepunkte Seite 3 von 4
4 Schriftliche Abiturprüfung Mathematik 03 Inhalte Integralrechnung Stammfunktionen: Summenregel Faktorregel lineare Substitution Integral Integralfunktion Hauptsatz der Differential- und Integralrechnung Anwendungen des Integrals: Inhalt krummlinig begrenzter Flächen und Volumina Rekonstruierter Bestand Mittelwert nicht: Näherungsverfahren zur Bestimmung von Integralen Wachstum lineares, natürliches, beschränktes Wachstum auch diskrete Vorgänge in kontinuierlicher Modellierung nicht: logistisches Wachstum Differentialgleichung für natürliches und beschränktes Wachstum Analytische Geometrie Lineare Gleichungssysteme (ohne Parameter): Gaußverfahren Bestimmung der Lösungsmenge Vektor, Ortsvektor: Linearkombination lineare Abhängigkeit/Unabhängigkeit nur anschaulich, nicht formal Geraden Ebenen (Parameter-, Koordinaten-, Normalenform) Lagebeziehungen Skalarprodukt Betrag eines Vektors Abstands- und Winkelberechnungen zeichnerische Darstellung von Objekten im Raum: Schrägbilder, Spurpunkte, Spurgeraden nicht: Beweise mit Hilfe von Vektoren Stochastik Baumdiagramme, Pfadregeln Binomialverteilung Erwartungswert Testen von Hypothesen (nur einseitig) nicht: Fehler. Art nicht: stetige Verteilung Seite 4 von 4
5 Schriftliche Abiturprüfung Mathematik 03 Aufgabe (NT 008, Nr.) Musteraufgabensatz Pflichtteil Bilden Sie die Ableitung der Funktion f mit f(x) = 3x e x+ und vereinfachen Sie so weit wie möglich. ( VP) Aufgabe (HT 008, Nr. ) G ist eine Stammfunktion der Funktion g mit g( x) = 3 sin( 4x). Der Punkt P(0 ) liegt auf dem Graphen von G. Bestimmen Sie einen Funktionsterm von G. ( VP) Aufgabe 3 (HT 008, Nr. 3) Lösen Sie die Gleichung ( x 0) 6 + =. (3 VP) 4 x x Aufgabe 4 (HT 008, Nr. 4) Für eine ganzrationale Funktion h zweiten Grades gilt: T( 4) ist der Tiefpunkt und Q( 5) ist ein weiterer Punkt ihres Graphen. Ermitteln Sie eine Funktionsgleichung von h. Aufgabe 5 (HT 007, Nr. 5, leicht gekürzt) Gegeben ist der Graph der Ableitung f der Funktion f. a) Welche Aussagen über die Funktion f ergeben sich daraus im Hinblick auf Monotonie, Wendestellen? Begründen Sie Ihre Aussagen. b) Es gilt f(0) =. Skizzieren Sie den Graphen von f. Seite von 3
6 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 6 (NT 008, Nr. 7) Musteraufgabensatz Pflichtteil Gegeben sind die Ebenen E : x + 3x + 4x3 = und E : 5x 0 = 0. Stellen Sie die beiden Ebenen E und E in einem gemeinsamen Koordinatensystem dar. Zeichnen Sie die Schnittgerade der beiden Ebenen ein. Geben Sie eine Gleichung dieser Schnittgeraden an. Aufgabe 7 (HT 008, Nr. 6) Gegeben sind die beiden parallelen Geraden g und h durch 3 6 g : x = 9 + s 4, h : x = + t Bestimmen Sie den Abstand der beiden Geraden. Aufgabe 8 Eine Urne enthält 5 rote, 3 weiße und gelbe Kugeln. a) Es werden 3 Kugeln mit Zurücklegen gezogen. Mit welcher Wahrscheinlichkeit erhält man keine gelbe Kugel? b) Nun werden Kugeln ohne Zurücklegen gezogen. Mit welcher Wahrscheinlichkeit haben die beiden Kugeln die gleiche Farbe? Aufgabe 9 Mit 3 V = π (x 4) dx wird der Rauminhalt eines Rotationskörpers berechnet. Skizzieren Sie den Sachverhalt. Um welchen Körper handelt es sich? (3 VP) Seite von 3
7 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A. Musteraufgabensatz Wahlteil Analysis Das Schaubild stellt die Geschwindigkeit v eines Testfahrzeugs dar [ t in s, v(t) in m s ]. a) Ergänzen Sie die fehlenden Funktionsterme der Funktion v : ( ) v t 4 + < 50 5 = t t für 0 t 00 für 00 t < 400 für 400 t 600 (3 VP) b) Welche Strecke hat das Fahrzeug nach vier Minuten zurückgelegt? Bestimmen Sie die mittlere Geschwindigkeit für die gesamte Fahrtdauer. c) Beschreiben Sie die zu v gehörende Zeit-Weg-Funktion durch Terme. Aufgabe A. f x = t x + e einen Für jedes t IR besitzt der Graph der Funktion f t mit ( ) x t t Tiefpunkt. Bestimmen Sie t so, dass dieser Tiefpunkt möglichst tief liegt. Seite 3 von 3
8 Schriftliche Abiturprüfung Mathematik 03 Musteraufgabensatz Wahlteil Analysis Aufgabe A (HT 006, I 3, gekürzt) f t = 0t e wird die Konzentration eines Medikaments im Blut eines Durch ( ) 0,5t Patienten beschrieben. Dabei wird t in Stunden seit der Einnahme und f ( t ) in gemessen. Die folgenden Betrachtungen sind nur für die Zeitspanne der ersten Stunden nach der Einnahme des Medikaments durchzuführen. mg l a) Skizzieren Sie den zeitlichen Verlauf der Konzentration. Nach welcher Zeit erreicht die Konzentration ihren höchsten Wert? Wie groß ist dieser höchste Wert? Das Medikament ist nur wirksam, wenn seine Konzentration im Blut mindestens 4 mg l beträgt. Berechnen Sie die Zeitspanne, in der das Medikament wirksam ist. Wie hoch ist die mittlere Konzentration des Medikaments innerhalb der ersten Stunden? (5 VP) b) Zu welchem Zeitpunkt wird das Medikament am stärksten abgebaut? Wie groß ist zum Zeitpunkt t = 4 die momentane Änderungsrate der Konzentration? Ab diesem Zeitpunkt wird die Konzentration des Medikaments nun näherungsweise durch die Tangente an den Graphen von f an der Stelle t = 4 beschrieben. Bestimmen Sie damit den Zeitpunkt, zu dem das Medikament vollständig abgebaut wäre. Wie groß ist zu diesem Zeitpunkt die tatsächliche Konzentration des Medikaments im Blut? (5 VP) c) Anstelle der Näherung aus Teilaufgabe b) wird nun wieder die Beschreibung der Konzentration durch f verwendet. Vier Stunden nach der ersten Einnahme wird das Medikament in der gleichen Dosierung erneut eingenommen. Es wird angenommen, dass sich dabei die Konzentrationen im Blut des Patienten addieren. Skizzieren Sie den zeitlichen Verlauf der Gesamtkonzentration für 0 t. Die Konzentration des Medikaments im Blut darf 0 mg l nicht übersteigen. Wird diese Vorgabe in diesem Fall eingehalten? (5 VP) Seite 4 von 3
9 Schriftliche Abiturprüfung Mathematik 03 Aufgabe B. Musteraufgabensatz Wahlteil Geometrie/Stochastik Ein Flugzeug fliegt bezogen auf ein räumliches Koordinatensystem in Richtung der positiven x -Achse. Seine Geschwindigkeit beträgt zunächst vf = 00. Gleichzeitig steigt ein Ballon mit der Geschwindigkeit vb = 5 vertikal nach oben. Zu Beobachtungsbeginn befinden sich der Ballon im Punkt B( ) und das Flugzeug im Punkt F( ); alle Koordinaten sind in Meter gegeben. m s m s a) Bestimmen Sie den Abstand der beiden Flugbahnen. (3 VP) b) Wie nah kommen sich Flugzeug und Ballon tatsächlich? (3 VP) c) Das Flugzeug fliegt nun mit der Geschwindigkeit v F*. Für einen Beobachter, der sich im Punkt S( ) befindet, stoßen dann der Ballon und das Flugzeug 0 s nach Beobachtungsbeginn scheinbar zusammen. Bestimmen Sie v F*. (5 VP) Aufgabe B. Ein Labor entwickelt einen neuen Impfstoff und testet ihn in einem Tierversuch mit 900 Mäusen. Mit dem Impfstoff dürfen keine klinischen Studien an Menschen durchgeführt werden, wenn sich im Tierversuch in mindestens % der Fälle unerwünschte Nebenwirkungen zeigen. Bestimmen Sie für die Nullhypothese H 0 : p % die Entscheidungsregel für den Test mit 900 Mäusen mit einer Irrtumswahrscheinlichkeit von höchstens %. Seite 5 von 3
10 Schriftliche Abiturprüfung Mathematik 03 Musteraufgabensatz Wahlteil Geometrie/Stochastik Aufgabe B. (HT 006, II., gekürzt) Die Punkte A(3 5 4), B(4 4) und D( 4 9 0) legen eine Ebene E fest. a) Bestimmen Sie eine Koordinatengleichung der Ebene E. Zeigen Sie, dass das Dreieck ABD gleichschenklig, aber nicht gleichseitig ist. Bestimmen Sie die Koordinaten des Punktes C so, dass das Viereck ABCD eine Raute ist. Berechnen Sie die Koordinaten des Diagonalenschnittpunkts M dieser Raute. (Teilergebnisse: E : 4x + 5x + x3 = 9 ; M(0 5 ) ) (5 VP) b) Gegeben ist ein weiterer Punkt S(8 5 6). Die Raute ABCD bildet zusammen mit dem Punkt S eine Pyramide. Bestimmen Sie das Volumen dieser Pyramide. (3 VP) Aufgabe B. Für einen Flug stehen zwei Flugzeuge zur Verfügung, der zweimotorige Adler und die viermotorige Juhu. Der Adler fliegt auch noch, wenn nur ein Motor intakt ist. Die Juhu braucht mindestens zwei intakte Motoren. p ist die Wahrscheinlichkeit, dass ein Motor während des gesamten Fluges einwandfrei arbeitet. a) Welches Flugzeug ist sicherer, wenn p = 0,95 gilt? (3 VP) b) Stellen Sie die Wahrscheinlichkeiten, dass der Adler bzw. die Juhu das Ziel erreicht, jeweils als Funktion von p dar. Für welche Werte von p ist der Adler sicherer als die Juhu? Seite 6 von 3
11 Schriftliche Abiturprüfung Mathematik 03 Aufgabe ( ) ( ) f x = 3e + 3x (-) e = 3 - x e -x+ -x+ -x+ Musteraufgabensatz Lösungen Pflichtteil Aufgabe Es gilt: G ( x) = x + cos( 4x) + c. Aus ( ) c 3 4 Gc 0 = folgt c =. 4 3 G x = x + cos 4x Die gesuchte Stammfunktion ist G mit ( ) ( ) Aufgabe = x x 6 = 0. Die Substitution u = x ergibt u u 6 = 0 mit den 4 x x Lösungen u = und u = 3. Aus der Resubstitution ergeben sich die Lösungen x = - 3 und x = 3. Aufgabe 4 Ganzrationale Funktion zweiten Grades: h(x) = ax + bx + c T( 4) bzw. h( ) = 4: (I) a b + c = 4 und h ( ) = 0: (II) a + b = 0 a = ; b = ; c = 3 Q( 5) bzw. h() = 5: (III) 4a + b + c = 5 Damit ergibt sich h(x) = x + x - 3. Aufgabe 5 a) Für den dargestellten Bereich gilt: b) f ist monoton steigend für x 3 <, da dort ( ) f x 0 gilt. f ist monoton fallend für x > 3, da dort f ( x) < 0 gilt. Graph von f y 5 Graph von f f hat die Wendestellen x = 0 und x =, da f an diesen Stellen lokale Extrema besitzt. O x S. 7/3
12 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 6 Gleichung der Schnittgeraden: 0 3 g : x = + t 0,5,5 E x 3 Musteraufgabensatz Lösungen Pflichtteil A(0,5) E x B(3 0) x g Aufgabe 7 d(g,h) = d(g,p) mit P( 5) h 3 Bestimme Hilfsebene H, die zu g orthogonal ist und P enthält. H: x i 4 = 0. 5 Der Schnittpunkt der Hilfsebene H mit der Geraden g ist der Punkt F(5 5 5). 4 Der gesuchte Abstand d ist d(g,h) = PF = 3 = 5. 0 Aufgabe P "keine gelbe" = = = 0, a) ( ) b) P ("zwei gleiche" ) P( rr ) P( ww) P( gg) = + + = + + = Aufgabe 9 Es handelt sich um einen Kegel. y x S. 8/3
13 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A. 4 t + t für 0 t < a) v(t) = 8 für 00 t < 400 t + 4 für 400 t Musteraufgabensatz Lösungen Wahlteil b) Nach 4 Minuten zurückgelegte Strecke v(t)dt = t + t dt 8 dt = (GTR) Nach 4 Minuten sind ca. 653 Meter zurückgelegt. Mittlere Geschwindigkeit Gesamtstrecke: t + t + t = 3733 (GTR) Mittlere Geschwindigkeit: 3733 m 6, m 600 s s c) Zeit-Weg-Funktion s Für 0 t < 00 : Für 00 t 400 t 0 dt 8dt dt 4 s(t) = x + x dx = t + t < : [ ] Für 400 t 600: t 600 t 800 s(t) = s(00) + 8 dx = + 8x = 8t t 8800 s(t) = s(400) + x + 4 dx = + x + 4x = t + 4t 50 3 t Aufgabe A. Ableitungen: f x t x t t (x) = + e ; f t (x) = e. Tiefpunkt: f t (x) = 0 für x = t ; t f (t) = t t +. Somit: T(t t t + ). Das Minimum von t t + ergibt sich für t = 0,5 (GTR). S. 9/3
14 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A a) Maximum der Konzentration Mit dem GTR erhält man das Maximum von f für t,00. Nach ca. Stunden wird die maximale mg Konzentration von etwa 4,7 l erreicht f(t) in Musteraufgabensatz Lösungen Wahlteil Wirksame Zeitspanne Die Gerade mit der Gleichung y = 4 schneidet das Schaubild von f an den Stellen t 0, und t 7,5 (GTR). Damit ergibt sich eine wirksame Zeitspanne von etwa 6,9 Stunden. Mittlere Konzentration f = f(t) dt 6,55 (GTR). 0 Die mittlere Konzentration des Medikaments während der ersten Stunden mg beträgt etwa 6,6. l t in h b) Stärkster Abbau des Medikaments Zu bestimmen ist die Wendestelle des Schaubilds von f. Mit dem GTR erhält man t w 4,00. Etwa 4 Stunden nach der Einnahme ist der Abbau des Medikaments am stärksten. Änderungsrate zum Zeitpunkt t = 4 Der GTR liefert f (4),7. Die momentane Änderungsrate der Konzentration beträgt nach 4 Stunden mg etwa,7 pro Stunde. l Näherung mithilfe der Wendetangente Mit f (4),7 und f(4) 0,83 erhält man eine Gleichung für die Wendetangente: y =,7(t 4) + 0,83. Schnitt der Wendetangente mit der t-achse: t 8,00. Nach dieser Näherung wäre das Medikament nach 8 Stunden völlig abgebaut. Tatsächliche Konzentration nach 8 Stunden f(8),93 ; Die tatsächliche Konzentration nach 8 Stunden beträgt ca. mg,9 l. S. 0/3
15 Schriftliche Abiturprüfung Mathematik 03 c) Einhalten der Vorgabe Für t 4 wird die Konzentration durch die Funktion k mit k(t) = f(t) + f(t 4) beschrieben. Mit dem GTR erhält man das Maximum von k für t 5,5. Die Konzentration beträgt zu diesem mg Zeitpunkt etwa,0. l Die Vorgabe wird also nicht eingehalten k(t) in mg/l Musteraufgabensatz Lösungen Wahlteil 4 8 t in h Aufgabe B a) Flugzeug: g : x = t 00 ; Ballon: h : x = 30 + t Da die beiden windschiefen Geraden g und h parallel zur x x 3 -Ebene sind, lässt sich ihr Abstand d als Differenz der x -Werte der Stützpunkte berechnen: d = 300 ( 40) = 340. Der Abstand der beiden Flugbahnen beträgt 340 m. b) Zum Zeitpunkt t befindet sich der Ballon im Punkt B t( t), das Flugzeug im Punkt F t( t 800). Der Abstand von Ballon und Flugzeug zum Zeitpunkt t ist: d(t) = B F = ( t) + (780 5t) t t Der GTR liefert das Minimum von d(t) für t,7 mit dmin 799. Ballon und Flugzeug nähern sich bis auf etwa 800 m. c) Zum Zeitpunkt t* = 0 befindet sich der Ballon im Punkt B*( ). Die Sichtlinie durch die Punkte S und B* ist die Gerade 00 k : x = 00 + s. 0 4 Schnitt der Sichtlinie k mit der Flugzeugbahn g liefert s = 00 und t = 30. Das Flugzeug befindet sich zum Zeitpunkt t* also im Punkt F*( ). Der vom Flugzeug in dieser Zeit zurückgelegte Weg in Meter beträgt FF * = m m Die Geschwindigkeit beträgt somit: v F* = = s s S. /3
16 Schriftliche Abiturprüfung Mathematik 03 Aufgabe B. Musteraufgabensatz Lösungen Wahlteil Die Zufallsvariable X gibt die Anzahl der Mäuse, an denen sich Nebenwirkungen zeigen, an. Gilt H 0, dann ist X im Extremfall B900;0,0 -verteilt. Gesucht ist die Zahl k 0 mit P(X k 0 ) 0,0 und P(X k 0 +) > 0,0. Mit dem GTR erhält man P(X 8) 0,00665 und P(X 9) 0,0464. Ergebnis: Falls bei einem Versuch mit 900 Mäusen höchstens 8 Tiere Nebenwirkungen zeigen, dürfen klinische Studien an Menschen durchgeführt werden. Aufgabe B. a) Koordinatengleichung der Ebene E Aus einer Parametergleichung für E: 3 7 x = OA + s AB + t AD = 5 + s 4 + t ergibt sich als Koordinatenform: 4x + 5x + x3 = 9. Form des Dreiecks ABD AB = = 9 ; AD = = 9 ; BD = = Das Dreieck ABD ist gleichschenklig, aber nicht gleichseitig. Koordinaten von C Es gilt OC = OB + AD = + 4 = Somit C( 3 5 8). Skizze: D A M C Koordinaten von M M ist der Mittelpunkt der Strecke BD. Damit: M(0 5 ). B S. /3
17 Schriftliche Abiturprüfung Mathematik 03 Musteraufgabensatz Lösungen Wahlteil b) Die Raute ABCD bildet die Grundfläche der Pyramide. Ihr Flächeninhalt ist 6 8 A R = AC BD = = = = 4. Die Pyramidenhöhe h ist gleich dem Abstand des Punktes S von der Ebene E. 4x + 5x + x3 9 HNF von E: = h = d(s;e) = = = Pyramidenvolumen: V = AR h = = Das Volumen der Pyramide ist V = 360. Aufgabe B. a) Der Adler kommt mit der Wahrscheinlichkeit ( p) = 0,9975 an. Die Juhu kommt mit der Wahrscheinlichkeit an. Also ist die Juhu sicherer als der Adler. 4 3 p + 4p ( p) + 6p ( p) 0,9995 b) Wahrscheinlichkeit, dass der Adler ankommt: f(p) = ( p) Wahrscheinlichkeit, dass die Juhu ankommt: 4 3 g(p) = p + 4p ( p) + 6p ( p) Schnittstelle der Graphen von f und g im Intervall ]0;[ ist p0 0,67 (GTR). Dem Verlauf der beiden Graphen entnimmt man, dass für p < 0,67 der Adler sicherer ist als die Juhu. S. 3/3
18 Schriftliche Abiturprüfung Mathematik 03 () Ableitung Anforderungen wie bisher, allerdings ohne Quotientenregel Pflichtteil Durch den Wegfall der Quotientenregel müssen echte gebrochenrationale Funktionen wie zum Beispiel f(x) x = nicht mehr abgeleitet werden. 3x 4 Sehr wohl denkbar ist beispielsweise aber die Ableitung von f(x) =. 3x 4 () Stammfunktion, Integral Anforderungen wie bisher (3) Gleichungslehre Anforderungen wie bisher, allerdings ohne Polynomdivision und Wurzelgleichungen (4) Elemente der Kurvendiskussion Anforderungen wie bisher (5) Funktionenkompetenz Anforderungen wie bisher, denkbar sind auch Aufgaben der folgenden Art: Aufgabe 5. Gegeben sind die Funktionen f und g mit f (x) = x und g (x) = x + 5. a) Berechnen Sie f(49) f(g(49)) g(f(49)) b) Für welchen Wert x ist f(g(x)) = 4? Seite von 30
19 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 5. 3 Die Funktion f mit f ( x) = 0,5x + 4,5x x + 7,5 Pflichtteil hat den nebenstehenden Graphen. a) Begründen Sie ohne Rechnung, dass die Gleichung 3 0,5x + 4,5x x + 7,5 = 0 nur eine Lösung hat. b) Geben Sie einen Wert von a an, so dass die Gleichung f ( x) = a drei Lösungen hat. Aufgabe 5.3 Welche der folgenden Aussagen sind wahr, welche nicht? Geben Sie jeweils eine Begründung für Ihre Entscheidung an. a) Der Graph der Funktion f mit f ( x) = x a hat zwei Asymptoten. b) Es gibt ganzrationale Funktionen dritten Grades, die genau zwei Nullstellen besitzen. c) Der Graph einer ganzrationalen Funktion vierten Grades hat immer einen tiefsten Punkt. Aufgabe 5.4 (5 VP) Für welche Werte von x ist der Term x ( x + ) positiv? (3 VP) Aufgabe 5.5 Vom Graphen einer ganzrationalen Funktion dritten Grades kennt man den Hochpunkt H(3 5) und den Tiefpunkt T( ). Was kann man ohne Bestimmung des Funktionsterms über die Anzahl der Nullstellen und über die Anzahl der Wendestellen sagen? Begründen Sie Ihre Aussage. (3 VP) Seite von 30
20 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 5.6 Für eine ganzrationale Funktion f gilt f(0) = 5, f (0) = 0, f (0) < 0 f() = 0, f () = 0, f () 0. Skizzieren Sie einen möglichen Verlauf des Graphen von f. Pflichtteil (3 VP) Aufgabe 5.7 Für die Funktion f gilt für alle x [ ; 4 ] f ( x) < 0 f ( x) > 0 f ( x) < 0 Welche Eigenschaften hat demnach der Graph von f? Skizzieren Sie einen möglichen Verlauf des Graphen von f. Aufgabe 5.8 g(x) = sin x Gegeben sind die Funktionen f mit f(x) = sin( x) und g mit ( ) Wie entsteht der Graph von g aus dem Graphen von f? (3 VP) (6) Lineare Gleichungssysteme, Inzidenzgeometrie Anforderungen wie bisher, ohne Nachweis der linearen Unabhängigkeit. (7) Metrische Geometrie Anforderungen wie bisher Seite 3 von 30
21 Schriftliche Abiturprüfung Mathematik 03 (8) Stochastik Pflichtteil Aufgabe 8. In einem Behälter befinden sich rote und 4 blaue Kugeln. Es werden Kugeln mit Zurücklegen gezogen. a) Berechnen Sie die Wahrscheinlichkeit, dass mindestens eine der beiden Kugeln rot ist. b) Wie viele rote Kugeln hätten sich in dem Behälter befinden müssen, damit die Wahrscheinlichkeit, mindestens eine rote Kugel zu ziehen, 0,84 betragen hätte? (5 VP) Aufgabe 8. In einem Behälter befinden sich 6 Kugeln mit den Nummern bis 6. Es wird solange ohne Zurücklegen gezogen, bis eine gerade Nummer gezogen wird. a) Bestimmen Sie die Wahrscheinlichkeit dafür, dass erst im dritten Zug eine gerade Nummer gezogen wird. b) Wie groß ist die Wahrscheinlichkeit, dass man höchstens dreimal zieht? (3 VP) Aufgabe 8.3 Bei einem Glücksspiel wird das abgebildete Glücksrad benutzt. Als Einsatz bezahlt man 3. Das Glücksrad wird einmal gedreht. Man erhält den Betrag ausbezahlt, dessen Sektor über dem Pfeil zu stehen kommt. Bestimmen Sie den Erwartungswert für den Gewinn. 3 4 (3 VP) Seite 4 von 30
22 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 8.4 Ein Glücksrad hat die Sektoren mit den Zahlen, und 3 mit folgender Wahrscheinlichkeitsverteilung: Sektor 3 Wahrscheinlichkeit 0, 0,3 0,5 Pflichtteil Das Glücksrad wird zu folgendem Glücksspiel verwendet: Der Spieler zahlt zunächst Einsatz. Dann wird das Glücksrad dreimal gedreht. Sind die drei ermittelten Zahlen verschieden, bekommt der Spieler seinen Einsatz zurück. Kommt dreimal die, erhält der Spieler 00. Sonst erhält er nichts. Ist dieses Spiel fair? (3 VP) Aufgabe 8.5 Die Zufallsvariable X ist binomialverteilt mit n = 0 und p = 0,6. a) Welche der Abbildungen zeigt die Verteilung von X? Begründen Sie Ihre Entscheidung. b) Bestimmen Sie mithilfe der Abbildung näherungsweise P(4 < X < 7) und P(X 5). 0,30 0,0 0,5 0,0 0,5 0,5 0,0 0,0 0,05 0,05 0,00 0, Abb. k Abb. k P(X=k) P(X=k) P(X=k) 0,30 0,5 0,0 0,5 0,0 0,05 0, Abb. 3 k Abb. 4 k P(X=k) 0,70 0,60 0,50 0,40 0,30 0,0 0,0 0,00 Seite 5 von 30
23 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 8.6 Pflichtteil Ein Basketballspieler übt Freiwürfe. Erfahrungsgemäß trifft er bei 80% seiner Würfe. a) Mit welcher Wahrscheinlichkeit trifft er mit den ersten beiden Würfen zweimal? b) Geben Sie ein Ereignis A und ein Ereignis B an, so dass gilt: P(A)= 0 0,, P(B)= 50 0,8 0, (3 VP) (9) Beschreiben, Begründen Anforderungen wie bisher, denkbar sind auch Aufgaben der folgenden Art: Aufgabe 9. Die täglichen Heizkosten eines Hauses werden durch k(t) dargestellt. Dabei ist t die Zeit in Tagen seit dem. Januar Was bedeutet k ( t) dt bzw. ( ) 0 k t dt? 90 0 ( VP) Aufgabe 9. Es soll eine Gleichung einer ganzrationalen Funktion g dritten Grades ermittelt werden, welche die Extremstellen x = und x = besitzt. Folgende Lösungsschritte werden vorgeschlagen: () Ableitungsfunktion von g : g (x) = (x + ) (x ) () Gleichung einer Stammfunktion von g : a) Begründen Sie die Richtigkeit dieses Vorgehens. g (x) x 4 = 3 g(x) = x 4 x 3 b) Geben Sie die Funktionsgleichung einer weiteren ganzrationalen Funktion dritten Grades an, welche die Extremstellen x = und x = besitzt. Seite 6 von 30
24 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 9.3 Die folgenden Zeilen zeigen einen Teil der Lösung einer Geometrieaufgabe. g: x = + t = + t 3 g E : 5t + ( t) 3 ( + 3t) = 0 Pflichtteil a) Was war gegeben? Wie lautete die Aufgabe? b) Lösen Sie die Aufgabe vollständig. Aufgabe 9.4 Bei einem Fest möchte ein Besucher an einem Glücksrad spielen. Bevor er spielt, stellt er folgende Rechnung auf: x P( x) + x P( x ) + x3 P ( x3 ) = = 3 6 a) Welche Information erhält er durch diese Rechnung? b) Wie könnte das verwendete Glücksrad aussehen und die Gewinnregel lauten? Beschreiben Sie möglichst genau. (3 VP) Seite 7 von 30
25 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A. (HT 008, I 3, gekürzt und modifiziert) Ein Fass mit Zu- und Ablauf besitzt ein Fassungsvermögen von 00 Liter. Wahlteil Analysis a) Die enthaltene Wassermenge zum Zeitpunkt t wird beschrieben durch die Funktion 0,0t f mit f ( t) = e ; t 0 ( t in Minuten, f(t) in Liter). Zu welchem Zeitpunkt ist das Fass zur Hälfte gefüllt? Zeigen Sie, dass die Wassermenge im Fass stets zunimmt. Weisen Sie nach, dass das Fass nicht überläuft. Bestimmen Sie die mittlere Wassermenge während der ersten Stunde. (6 VP) b) Bei einem anderen Füllvorgang befinden sich zunächst 800 Liter Wasser im Fass. Die momentane Abflussrate beträgt 0,5% des jeweiligen Inhalts pro Minute. Die Zuflussrate ist konstant. Wie viele Liter pro Minute müssen zufließen, damit sich die Wassermenge im Fass nicht ändert? Die Zuflussrate wird jetzt so gewählt, dass auf lange Sicht das Fass nicht überläuft, aber immer mindestens zur Hälfte gefüllt ist. Welche Werte für die Zuflussrate sind dafür möglich? Aufgabe A. Gegeben ist für jedes k IR eine Funktion f k mit (x) f k = x + k. x Bestimmen Sie die Anzahl der Extremstellen von f k in Abhängigkeit von k. (5 VP) alternativ: Aufgabe A.* (HT 006, I. a) Für jedes a>0 ist eine Funktion f a gegeben durch f a(x) = sin ax a ( ) Wie wirkt sich eine Veränderung des Parameters a auf den Graphen von f a aus? Berechnen Sie den Inhalt der Fläche, die der Graph von f a mit der x-achse zwischen zwei benachbarten Nullstellen einschließt. (5 VP) Seite 8 von 30
26 Schriftliche Abiturprüfung Mathematik 03 Wahlteil Analysis Aufgabe A. (NT 006, I 3., leicht gekürzt) In einem Land mit ca. 6,0 Millionen Haushalten gab es zu Beginn des Jahres 004 etwa 3,0 Millionen Haushalte mit einem DVD-Player. Die Entwicklung der Anzahlen (in Millionen) seit dem Jahr 000 kann modellhaft durch eine Funktion g dargestellt werden, die für x 0 der Differenzialgleichung ( ) ( ) ( ) g x = 0, 5, g x genügt. Dabei ist x die Anzahl der seit Beginn des Jahres 000 vergangenen Jahre. a) Bestimmen Sie einen Funktionsterm der Funktion g. Mit welcher Anzahl von Haushalten mit DVD-Playern ist langfristig zu rechnen? Zu welchem Zeitpunkt steht in 70% der Haushalte des Landes ein DVD-Player? Bestimmen Sie die mittlere Anzahl von Haushalten mit DVD-Player von Mitte 004 bis zu diesem Zeitpunkt. Wann lag die Änderungsrate der Anzahlen erstmals unter 0,6 Millionen pro Jahr? (7 VP) b) Welche Größe wird durch g (4) beschrieben? Erläutern Sie, wie man nur mit Hilfe von g (4) und g(4) einen Näherungswert für g(4,5) berechnen kann. Bestimmen Sie diesen Näherungswert. Aufgabe A. In der Skizze sind zwei geradlinige Gleise abgebildet, die in den Punkten A bzw. B enden. Diese Gleise sollen durch ein Gleisstück knickfrei verbunden werden. Bestimmen Sie eine ganzrationale Funktion, die dieses y A B x Gleisstück beschreibt. alternativ: Aufgabe A.* Gegeben ist die Funktion f mit f ( x) = 4x x. Wie muss t > 0 gewählt werden, damit der Mittelwert der Funktionswerte von f auf dem Intervall [0;t] möglichst groß ist? Seite 9 von 30
27 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A 3. Die Skizze zeigt den parabelförmigen Querschnitt eines,5 km langen, geradlinig und horizontal verlaufenden Straßentunnels. a) Bestimmen Sie einen Funktionsterm der im Bild dargestellten Funktion f. Die Querschnittsfläche des Tunnels entspricht der Fläche, die der Graph von f und die x-achse begrenzen (Längeneinheit in m). Wahlteil Analysis Wie viel Kubikmeter Gestein mussten beim Bau des Tunnels bewegt werden? (Teilergebnis: ( ) f x = x + x + 4 ) (5 VP) 4 b) Der Formelsammlung ist zu entnehmen, wie die Länge eines Kurvenstücks berechnet werden kann: Das Kurvenstück k: y = f(x) für a x b hat die (Bogen-)Länge b (f '(x)) dx. s = + a Bestimmen Sie mit dieser Formel die Länge des abgebildeten Parabelstücks. Die gesamte innere Wandfläche des Tunnels wird gestrichen. Die Farbe wird in 50-Liter-Behältern geliefert. Wie viele Behälter werden benötigt, wenn ein Liter Farbe für sechs Quadratmeter Wandfläche ausreicht? Seite 0 von 30
28 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A 3. Gegeben ist die Funktion f mit =, x 0. x ( ) f x a) Das gezeichnete Rechteck rotiert um die y-achse, wodurch ein Zylinder entsteht. Zeigen Sie, dass sein Volumen nicht von u abhängt. Wahlteil Analysis b) Der Graph von f, die Gerade x = und die x-achse bestimmen eine nach rechts offene Fläche. Berechnen Sie ihren Inhalt. Welche Parallele zur y-achse halbiert diese Fläche? ( VP) alternativ: Aufgabe A 3.* Gegeben sind die Hyperbel h: Punkt B auf h im. Feld. y = und ein x Die Tangente t in B an h schneidet die x-achse in C und die y-achse in D. Bestimmen Sie einen Punkt B so, dass das Dreieck OCD den Umfang 0 LE besitzt. t y D h B C x (6 VP) Seite von 30
29 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Geo (HT 005, II, gekürzt und verändert) Wahlteil Geometrie Gegeben sind eine Pyramide ABCDS mit den Punkten A(0 0 0), B(8 0 0), C(8 8 0), D(0 8 0) und S(4 4 8) sowie für jedes r IR eine Ebene E : r x + 3 x3 = 8r. a) Stellen Sie die Pyramide in einem Koordinatensystem dar. Zeigen Sie, dass die Gerade durch B und C in jeder Ebene r E r liegt. b) Zeigen Sie, dass für den Winkel α zwischen der Ebene E r und der 3 Grundfläche ABCD der Pyramide cos α = gilt. r + 9 Bestimmen Sie einen Wert für r, für den α = 40 ist. c) Beim Schnitt einer Ebene E r mit der Pyramide entsteht eine Schnittfigur. Welche Schnittfiguren sind möglich? Geben Sie jeweils die zugehörigen Werte von r an. (3 VP) Aufgabe Geo (HT 008, II, Teile a und c) In einem Würfel mit den Eckpunkten O(0 0 0), P(0 0 0) und S(0 0 0) befindet sich eine Pyramide mit einem Dreieck als Grundfläche und der Spitze S (vgl. Skizze). Die Eckpunkte der Pyramidengrundfläche sind A(0 6 0), B(6 0 0) und C(0 0 5). a) Bestimmen Sie eine Koordinatengleichung der Ebene E, in der die Grundfläche der Pyramide liegt. Welchen Winkel schließen die Grundflächen von Würfel und Pyramide ein? Untersuchen Sie, ob die Höhe der Pyramide auf der Diagonalen PS des Würfels liegt. (Teilergebnis: E : 5x + 5x 4x3 = 80 ) (6 VP) b) Zusätzlich zur Pyramide soll nun noch ein Quader der Breite b in den Würfel gelegt werden. Die Abmessungen des Quaders werden so gewählt, dass er die Pyramide nur in einem Punkt Q der Pyramidenkante AS berührt (vgl. Skizze). Welches Volumen hat ein solcher Quader mit der Breite b = 4? Welche Werte kann das Volumen eines solchen Quaders annehmen, wenn die Breite b variabel ist? x x 3 S Q A C P B (5 VP) x Seite von 30
30 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Sto Wahlteil Stochastik In einem Gefäß U sind zwei blaue Kugeln, in einem weiteren Gefäß U sind acht rote Kugeln. Lisa darf mit verbundenen Augen eines der beiden Gefäße wählen und daraus eine Kugel ziehen. Ist die Kugel rot, dann gewinnt Lisa einen Preis. Wie groß ist die Wahrscheinlichkeit, dass Lisa einen Preis gewinnt? Lisa hat 50 weitere rote Kugeln zur Verfügung und darf nun bestimmen, wie viele zusätzliche rote Kugeln in U gelegt werden. Allerdings werden dann genauso viele blaue Kugeln in U gelegt. Lisa wählt fünf zusätzliche rote Kugeln. Hat sich dadurch ihre Gewinnwahrscheinlichkeit vergrößert? Wie viele von den 50 zusätzlichen roten Kugeln hätte Lisa wählen müssen, um ihre Gewinnchancen zu maximieren? (7 VP) Aufgabe Sto Eine Klasse will für einen guten Zweck beim Schulfest ein Glücksrad betreiben. Dieses besteht aus drei Sektoren mit den folgenden Mittelpunktswinkeln: rot: 80, gelb: 90 und blau: 90. Bei einem Spiel dreht der Kunde das Glücksrad dreimal und bezahlt dafür einen Euro. Er erhält zwei Euro, wenn er dreimal dieselbe Farbe erreicht, er bekommt seinen Einsatz zurück, wenn genau zweimal dieselbe Farbe angezeigt wird, in allen anderen Fällen wird sein Einsatz einbehalten. Welchen Gewinn erzielt die Klasse mit diesem Glücksrad pro Spiel durchschnittlich? Die Klasse will im nächsten Jahr durch eine Veränderung der Sektorengrößen die Wahrscheinlichkeit der Fälle, in denen der Einsatz einbehalten wird, erhöhen. Dabei sollen die Spielregeln erhalten bleiben und der rote Sektor soll weiterhin doppelt so groß sein wie der gelbe. Für welche Mittelpunktswinkel der drei Sektoren ist die Wahrscheinlichkeit für den Einbehalt des Einsatzes am größten? (6 VP) Seite 3 von 30
31 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Sto 3 Wahlteil Stochastik a) Eine Urne enthält drei weiße und zwei schwarze Kugeln. Franz und Hilde ziehen abwechselnd ohne Zurücklegen eine Kugel, wobei Franz beginnt. Gewonnen hat, wer zuerst eine schwarze Kugel zieht. Bestimmen Sie die Wahrscheinlichkeiten der Ereignisse A: Franz gewinnt, B: Hilde gewinnt. ( VP) b) In einer anderen Urne sind drei weiße und n schwarze Kugeln. Es werden nacheinander zwei Kugeln mit Zurücklegen gezogen. Für welche Werte von n ist die Wahrscheinlichkeit, genau eine schwarze Kugel zu ziehen, gleich 8 3? Aufgabe Sto 4 Ein Glücksrad hat die Sektoren mit den Zahlen, und 3 mit folgender Wahrscheinlichkeitsverteilung: Sektor 3 Wahrscheinlichkeit 0, 0,3 0,5 a) Wie oft muss man das Glücksrad mindestens drehen, um mit einer Wahrscheinlichkeit von mindestens 95% wenigstens einmal die Zahl zu bekommen? b) Es besteht der Verdacht, dass die Wahrscheinlichkeit für die Zahl größer als 0, ist. Daher wird die Hypothese H 0 : p 0, durch 00 Versuche getestet. ( VP) Wenn mehr als 8 Mal die erscheint, wird die Hypothese abgelehnt. Wie groß ist die Irrtumswahrscheinlichkeit? Aufgabe Sto 5 Eine Firma stellt Solartaschenrechner her. Die Herstellungskosten eines Rechners betragen 5. Die Firma verkauft ihn für 5 an den Händler. 4,5% aller produzierten Rechner sind defekt. Jeder defekte Rechner wird vom Händler entdeckt. Die Firma erstattet den Kaufpreis und nimmt den defekten Rechner zurück. Bei der Rücknahme entstehen der Firma zusätzlich Kosten in Höhe von 5. a) Wie hoch ist der durchschnittliche Gewinn der Firma pro Rechner? ( VP) Seite 4 von 30
32 Schriftliche Abiturprüfung Mathematik 03 Wahlteil Stochastik b) Durch eine Kontrolle kann die Firma 95% der defekten Rechner herausfinden, hält aber auch % der intakten Rechner für defekt. Die beanstandeten Rechner werden dann nicht an den Händler verkauft, sondern ohne weitere Kosten entsorgt. Wie viel darf die Kontrolle eines Rechners höchstens kosten, damit sie sich für die Firma rentiert? Aufgabe Sto 6 Eine Firma, die Handys herstellt, behauptet, dass höchstens 4% der Geräte defekt seien. Die Behauptung soll mit einer Stichprobe von 50 Stück getestet werden. Man erhält 0 defekte Handys. Kann man daraus mit einer Irrtumswahrscheinlichkeit von höchstens 5% schließen, dass die Firmenangabe nicht zutrifft? Aufgabe Sto 7 Ein Computerhersteller bezieht von einem Lieferanten Speicherchips. Erfahrungsgemäß sind 95% der Chips einwandfrei. a) Mit welcher Wahrscheinlichkeit sind von 30 Chips mehr als 6 einwandfrei, mindestens zwei defekt? b) Der Computerhersteller überprüft die Hypothese, dass mindestens 95% der Chips einwandfrei sind, mit einer Stichprobe vom Umfang 00. Die Irrtumswahrscheinlichkeit soll höchstens 0% betragen. Ermitteln Sie den Ablehnungsbereich. ( VP) (3 VP) Aufgabe Sto 8 Ein Computerhersteller bezieht von einem Lieferanten Speicherchips. a) Erfahrungsgemäß sind 80% der Chips einwandfrei. Mit welcher Wahrscheinlichkeit sind von 30 Chips mehr als 0 einwandfrei? ( VP) b) Wie groß dürfte die Defektwahrscheinlichkeit eines Chips höchstens sein, damit von 0 Chips mit mindestens 90% Wahrscheinlichkeit alle einwandfrei sind? (3 VP) Alternative: b*) Die Chips, die zu 80% einwandfrei sind, werden in Viererpackungen geliefert. Ab welcher Anzahl Viererpackungen muss mit mehr als 50% Wahrscheinlichkeit damit gerechnet werden, dass in mindestens einer Packung alle Chips defekt sind? Seite 5 von 30
33 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Sto 9 Wahlteil Stochastik Bei einem Test gibt es 0 Fragen mit jeweils 4 Antworten, von denen nur eine richtig ist. a) Ein Kandidat kreuzt bei jeder Frage rein zufällig eine Antwort an. Mit welcher Wahrscheinlichkeit hat er A: genau 3 richtige Antworten, B: mindestens 3 richtige Antworten, C: mehr als 3, aber weniger als 8 richtige Antworten? (3 VP) b) Es soll nun festgelegt werden, wie viele richtige Antworten zum Bestehen des Tests ausreichen sollen. Bei zufälligem Ankreuzen der Antworten soll die Wahrscheinlichkeit für ein Bestehen des Testes höchstens 5% betragen. Wie viele richtige Antworten müssen dazu mindestens verlangt werden? (3 VP) Seite 6 von 30
34 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 5. ( ) a) f ( 49) = 49 = 7, ( ) f g b) f ( g( x) ) = 4 : x + 5 = 4 liefert x =. ( ) = + =, ( ) g f 49 = = Lösungen Pflichtteil Aufgabe 5. a) Die Lösungen der Gleichung sind die Nullstellen von f. Im Graphen von f sind zwei Extrempunkte unterhalb der x-achse erkennbar. Weitere Extrempunkte kann eine Parabel dritter Ordnung nicht besitzen. Also ist die erkennbare Nullstelle ( x 0,9) die einzige Nullstelle von f. b) Z. B. a = Aufgabe 5.3 a) Aus Für x lim = 0 x a x folgt: y = 0 ist waagrechte Asymptote. = a ist der Nenner des Funktionsterms 0, der Zähler ungleich 0. Daraus folgt: x Die Aussage ist also wahr. b) Die Aussage ist wahr. = a ist senkrechte Asymptote. Beispiel: f mit f ( x) x ( x ) = hat die Nullstellen x = 0 und x =. f x = x. c) Die Aussage ist falsch. Gegenbeispiel: ( ) 4 Aufgabe 5.4 Die Funktion f mit f(x) = x ( x + ) hat die Nullstellen x = und x = 0. Ihr Graph ist eine nach oben geöffnete Parabel. Daher ist der Term x ( x + ) positiv im Bereich x < sowie im Bereich x > 0. Aufgabe 5.5 Jede ganzrationale Funktion dritten Grades besitzt genau eine Wendestelle. Jede ganzrationale Funktion dritten Grades besitzt mindestens eine Nullstelle. Da der Tiefpunkt T eine positive y-koordinate besitzt, kann es keine weiteren Nullstellen geben. Somit besitzt die Funktion genau eine Wendestelle und eine Nullstelle. Seite 7 von 30
35 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 5.6 Aus f ( 0) = 5, f ( 0) = 0 und ( ) f 0 < 0 folgt: Lösungen Pflichtteil H(0 5) ist Hochpunkt. Aus f() = 0, f ( ) = 0 und ( ) W( 0) ist Wendepunkt. f 0 folgt: Aufgabe 5.7 Da f ( x) < 0 ist, verläuft der Graph unterhalb der x-achse. Wegen f ( x) > 0 ist f streng monoton steigend. Wegen f ( x) < 0 nimmt die Steigung des Graphen ab. Aufgabe 5.8 Der Graph von f wird mit dem Faktor in x-richtung und mit dem Faktor 4 in y-richtung gestreckt. Anschließend wird der Graph um 3 Einheiten in y-richtung verschoben. Aufgabe 8. a) P ("mindestens eine rote Kugel" ) ( ) = P bb = = b) Es sind 4 blaue und n rote Kugeln. P ("mindestens eine rote Kugel" ) ( ) 6 6 (n + 4) (n + 4) P bb 4 4 = = n + 4 n + 4 = 0,84 = 0,6 (n + 4) = 00 n = 6 (n= 4 entfällt) Es hätten 6 rote Kugeln im Behälter sein müssen. Seite 8 von 30
36 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 8. u: ungerade Nummer, g: gerade Nummer a) P ( uug) b) = = P("höchstens drei Züge") = P(uuu) = = = Aufgabe 8.3 E(Auszahlung) = = E(Gewinn) = E(Auszahlung) 3 = 8 Der Erwartungswert für den Gewinn beträgt 0,5. Aufgabe 8.4 Das Spiel ist fair, wenn der Erwartungswert für den Gewinn 0 beträgt. 3 E( Auszahlung) = 6 0, 0,3 0,5 + 0, 00 = 0,8 + 0,8 = 0,98 E( Gewinn) = E( Auszahlung) ist negativ, also ist das Spiel nicht fair. Lösungen Pflichtteil Aufgabe 8.5 a) Für den Erwartungswert gilt: E = n p = 6, also muss P(X=6) maximal sein. Daher zeigt Abbildung 3 die Verteilung von X. b) P ( 4 < X < 7) = P ( 5) + P ( 6) 0, + 0,5 = 0,45 P ( X 5) = P ( 5) 0, = 0,8 Aufgabe 8.6 a) P( Treffer ) = 0,8 = 0,64 b) A: Er wirft 0 Mal und trifft nie. B: Er wirft 50 Mal und erzielt dabei genau 40 Treffer. Aufgabe k(t) dt beschreibt die gesamten Heizkosten für die ersten 90 Tage des Jahres k(t) dt 0 des Jahres 03. beschreibt die durchschnittlichen täglichen Heizkosten der ersten 90 Tage Seite 9 von 30
37 Schriftliche Abiturprüfung Mathematik 03 Aufgabe 9. Lösungen Pflichtteil a) g besitzt Extremstellen bei x = und x =, wenn g an diesen Stellen Nullstellen mit Vorzeichenwechsel besitzt. Dies führt auf den Ansatz g mit Lösung. b) Z. B. Aufgabe 9.3 g (x) = (x + ) (x ) = x 4. 3 g(x) = x 4 x ist eine Stammfunktion von g und damit eine mögliche 3 3 h(x) = x 4 x a) Gegeben waren zwei Punkte A ( 0 ) und B ( 5 ) sowie eine Ebene E : x + x 3x3 = 0. Aufgabe: Untersuchen Sie, ob die Ebene E und die Gerade g durch A und B gemeinsame Punkte besitzen. b) 0t + t + 3 9t = 0 5 = 0. Die Gerade g hat keine gemeinsamen Punkte mit der Ebene E. Aufgabe 9.4 a) Durch die Rechnung erhält er den Erwartungswert seines Gewinns. Pro Spiel wird er durchschnittlich 50 Cent verlieren. b) Ein mögliches Glücksrad enthält 3 Sektoren. Die Mittelpunktswinkel der Sektoren sind 0, 80 und 60, der jeweilige Gewinn beträgt, 3 bzw. 4. Seite 0 von 30
38 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A. a) Halbe Füllmenge: f(t) = 600 liefert t = 00 ln(0,5) 69,3. Nach knapp 70 Minuten ist der Behälter bis zur Hälfte gefüllt. Zunahme der Wassermenge: f (t) = 8 e -0,0t > 0 für alle t 0. Die Wassermenge im Behälter nimmt also stets zu. Kein Überlauf: f(t) 000 < 00 für t. Mittlere Wassermenge während der ersten Stunde: Lösungen Wahlteil 60 f dt 60 0 ( t) 398,4 (GTR) Die mittlere Wassermenge beträgt also etwa 398 l während der ersten Stunde. b) Zuflussrate: Weil sich die Wassermenge nicht ändert, fließen konstant 0,5% von 800 (also 4) Liter pro Minute ab, also muss die konstante Zuflussrate ebenfalls 4 Liter pro Minute betragen. Mögliche Werte für die konstante Zuflussrate a : a 0,005. Es gilt f (t) = a 0,005 f(t) und somit f (t) = 0, 005 f ( t) Der Grenzwert der Funktion f ist demnach a 0,005. Aus a 600 0,005 = bzw. a 0,005 = 00 folgt a = 3 bzw. a = 6. Mögliche Werte für die Zuflussrate sind: 3 a 6 (in l/min) Aufgabe A. k k f k '(x) =, f x k ''(x) = 3 x Der Ansatz f k '(x) = 0 führt für x 0 auf x = k. Diese Gleichung besitzt nur für k > 0 Lösungen; diese sind x, = ± k. Da f an diesen beiden Stellen ungleich Null ist, handelt es sich um Extremstellen. Deshalb hat f k für k > 0 genau zwei Extremstellen, für k 0 keine Extremstellen. Seite von 30
39 Schriftliche Abiturprüfung Mathematik 03 Aufgabe A.* Auswirkung einer Veränderung des Parameters a Lösungen Wahlteil Mit wachsendem a wird das Schaubild von f a sowohl in x-richtung als auch in y-richtung gestaucht. Flächenberechnung f a(x) = 0 führt zu sin(a x) = 0. Benachbarte Nullstellen sind z.b. x 0 = und x π =. a Für den Flächeninhalt gilt: π a 0 π a a a 0 a A(a) = sin(ax) dx = cos(ax) =. Aufgabe A. a) Funktionsterm Es liegt beschränktes Wachstum vor. Ansatz: g(x) S c e k x =. Der Differentialgleichung entnimmt man S = 5, und k = 0,. Mit g(4) = 3 ergibt sich c 4,9 (GTR) und damit g(x) 5, 4,9e 0,x =. Langfristige Entwicklung Der Grenzwert der Funktion g ist S = 5,. Langfristig ist mit 5, Millionen Haushalten mit DVD-Playern zu rechnen. DVD-Player in 70% der Haushalte Der Ansatz g(x) = 4, liefert x 7,95 (GTR). Am Ende des Jahres 007 steht in 70% der Haushalte ein DVD-Player. Mittelwert 7,95 3,45 (GTR). 4,5 m = g(x)dx 3,8 Die mittlere Anzahl von DVD-Playern beträgt etwa 3,8 Millionen. Änderungsrate unter 0,6 Millionen pro Jahr Aus g (x) = 0,6 ergibt sich x,45, wobei g an dieser Stelle fällt (GTR). Etwa Mitte 00 lag die Änderungsrate erstmals unter 0,6 Millionen pro Jahr. b) g (4) beschreibt die momentane Änderungsrate der verkauften Stückzahlen nach 4 Jahren, also zu Beginn des Jahres 004. Seite von 30
40 Schriftliche Abiturprüfung Mathematik 03 Lösungen Wahlteil Man erhält einen Näherungswert für g(4,5), indem man ab x=4 die konstante Änderungsrate g (4) ansetzt: g(4,5) g(4) + 0,5 g'(4) 3, Aufgabe A. Ansatz: f(x) = ax 3 + bx + cx + d; f'(x) = 3ax + bx + c Bedingungen: f( ) = : f '( ) = 0 : f() = 3 : f '() = : a + b c + d = 3a b + c = 0 a + b + c + d = 3 3a + b + c = 5 7 Lösung: a = ; b = ; c = ; d = (GTR) f(x) = x + x + x Aufgabe A.* Mittelwert: t t 3 x x t = t m(t) = (4x x )dx = t t m(t) wird maximal für t = 3 (GTR). Der Mittelwert der Funktionswerte ist auf dem Intervall [0;3] am größten. Aufgabe A 3. a) Bestimmung des Funktionsterms Es handelt sich um eine Parabel mit dem Scheitelpunkt S(4 8). Ansatz: f(x) = a (x 4) + 8 Aus f(0) = 4 ergibt sich x Also: f(x) = ( ) Gesteinsvolumen a =. 4 f besitzt die Nullstellen x,657 und x 9,657 (GTR) x Querschnittsfläche: A = ( x 4 ) + 8 dx 4 60,34 (GTR) x Volumen: V = A Es müssen etwa 9050 m 3 Gestein bewegt werden. Seite 3 von 30
41 Schriftliche Abiturprüfung Mathematik 03 b) Länge des Parabelstücks x s = + ( f '( x) ) dx 0,50 (GTR) x Anzahl der Behälter Wandfläche: W = s [m ] Lösungen Wahlteil Farbmenge: M = W / 6 54 [Liter] Man benötigt also Behälter. Aufgabe A 3. a) V(u) = π u f(u) = π u = π u Das Volumen ist also unabhängig von u. b) Flächeninhalt z A(z) = dx = x = x z z Inhalt der nach rechts offenen Fläche: A = lim A(z) = z Halbierung der Fläche A(z) = A = z z = Die Parallele hat die Gleichung x =. Aufgabe A 3.* Berührpunkt sei B k k Tangentengleichung an h in B : Schnittpunkt mit der x-achse: C( k 0 ) Schnittpunkt mit der y-achse: D( 0 k ) Umfang des Dreiecks OCD: y(x) = x + (mit k > 0) k k 4 u(k) = k + 4k k + + k. u(k) = 0 führt z. B. auf k 0,44 und damit auf B(0,44,6) Seite 4 von 30
42 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Geo a) Punktprobe zeigt, dass B und C in allen Ebenen E r liegen. Damit liegt auch die Gerade durch B und C in allen Ebenen E r. Lösungen Wahlteil x 3 S b) r nr = n = 0 ist ein Normalenvektor von E r und ist ein Normalenvektor der Grundflächenebene der Pyramide. n n 3 Dann gilt für den Winkel α : cosα = =. Die Gleichung 3 = cos(40 ) r + 9 r nr n r + 9 besitzt z. B. die Lösung r,5. c) Beim Schnitt der Ebene E r mit der Pyramide entstehen folgende Schnittfiguren: Quadrat für r = 0 (dabei liegt A in E 0 ) gleichschenkliges Trapez für 0 < r < 6 gleichschenkliges Dreieck für r = 6 (dabei liegt S in E 6 ) Für r<0 oder r>6 hat die Ebene E r mit der Pyramide nur die Strecke BC gemeinsam. x B A C D x Aufgabe Geo a) Koordinatengleichung von E Aus einer Parametergleichung von E : x = 6 r 4 s ergibt sich nach Elimination von r und s eine Koordinatenform: E: 5x + 5x 4x 3 = 80. Winkelberechnung Für den Winkel α zwischen der Grundfläche der Pyramide und der Schachtelgrundfläche gilt: cosα = = ; α 60, Seite 5 von 30
43 Schriftliche Abiturprüfung Mathematik 03 Höhe der Pyramide und Diagonale PS Lösungen Wahlteil Ein Richtungsvektor der Geraden, auf der die Höhe der Pyramide liegt, ist 5 ne = 5. Ein Richtungsvektor der Geraden, auf der die Diagonale des Würfels 4 0 liegt, ist SP = 0. 0 Da diese beiden Richtungsvektoren linear unabhängig sind, liegt die Höhe der Pyramide nicht auf der Diagonalen PS. b) Quadervolumen für b = Gerade k durch A und S: k: x = 6 t Für den Berührpunkt Q gilt: x = 4.. Einsetzen in k liefert t =. 3 Die Quaderhöhe ist damit die x3 -Koordinate von Q: Für das Quadervolumen ergibt sich Werte für das Quadervolumen Für den Berührpunkt Q gilt nun: x = b VQ = 4 0 = c = 0 =. 3 3 Einsetzen in die Gleichung von k liefert: b = 6 6t ; t = b. 6 5 Die Quaderhöhe ist dann: c(b) = 0 b Damit ergibt sich für das Quadervolumen: V(b) = b (0 b) 0 = 00 b b Extremwertuntersuchung: V'(b) = 00 b ; V''(b) = < V'(b) = 0 ergibt b = 3. Also: Relatives Maximum an der Stelle 3 mit V(3) = 50. Wegen V(0) = V(6) = 0 ergeben sich für das Quadervolumen V(b) die Werte 0 < V(b) 50. Seite 6 von 30
44 Schriftliche Abiturprüfung Mathematik 03 Aufgabe Sto Lösungen Wahlteil Da die Wahl des Gefäßes über den Gewinn entscheidet, ist die Wahrscheinlichkeit. 5 zusätzliche rote Kugeln 5 Wahrscheinlichkeit aus U eine rote Kugel zu ziehen: 7 8 Wahrscheinlichkeit aus U eine rote Kugel zu ziehen: 3 Wahrscheinlichkeit eine rote Kugel zu ziehen: = 0,665, also hat sich die Gewinnwahrscheinlichkeit von Lisa verbessert. Maximierung der Gewinnchance Lisa legt x ( x 50) rote Kugeln in U und x blaue Kugeln in U,damit ist die Wahrscheinlichkeit aus U eine rote Kugel zu ziehen die Wahrscheinlichkeit aus U eine rote Kugel zu ziehen x + x, x. Die Wahrscheinlichkeit eine rote Kugel zu ziehen beträgt damit: x 8 P(x) = + + x 8 + x Das Maximum liegt bei x 4, mit P(4) 0,667 (GTR). Lisa maximiert mit 4 zusätzlichen Kugeln ihre Gewinnchancen. Aufgabe Sto Erwartungswert für den Gewinn der Klasse P ( r) = ; P( g) = P( b) = 4 ( ) + P( ggg) + P( bbb) P rrr P( alle verschieden ) = ( ) 3 = + + = P rgb = 6 = 4 4 Erwartungswert für den Gewinn der Klasse: E = ( ) + = Pro Spiel werden also durchschnittlich ca. 3 Cent Gewinn erreicht. Seite 7 von 30
45 Schriftliche Abiturprüfung Mathematik 03 Maximaler Gewinn der Klasse Lösungen Wahlteil Setzt man die Wahrscheinlichkeit für den roten Sektor gleich x, dann ergibt sich: P x ( r) = x ; P( g) = ; P( b) = P( r) P( g) = x Ereignis A: Einsatz wird einbehalten. P ( A) = 6 x x x = 3x x Maximale Wahrscheinlichkeit für A ergibt sich für x 0,44 (GTR). Der Mittelpunktswinkel für den roten Sektor muss also x betragen; der gelbe Sektor wird demzufolge 80 und der blaue Sektor 0 erhalten. Aufgabe Sto 3 a) 3 3 P (A) = P(s) + P(wws) = + = P (B) = P(A) = 5 3 n b) P( genau eine schwarze Kugel ) = 3 + n n + 3 Gleichsetzen mit führt auf n 0n + 9 = 0 mit den Lösungen n = und n = 9. Für eine bzw. neun schwarze Kugeln ist die Wahrscheinlichkeit, genau eine schwarze Kugel zu ziehen, gleich 8 3. Aufgabe Sto 4 a) X: Anzahl der Zahl. P(X ) = P(X = 0) = 0,8 n 0,95 ergibt n 4 (GTR). Das Glücksrad muss mindestens 4 Mal gedreht werden. b) Gilt H 0, dann ist X im Extremfall B 00;0, -verteilt. P(X > 8) = P(X 8) = 0, ,0 (GTR) Damit ist die Irrtumswahrscheinlichkeit etwa %. Aufgabe Sto 5 a) Erwartungswert für den Gewinn: 0, ,45 ( 0 ) = 5,65 Der durchschnittliche Gewinn der Firma pro Rechner ist 5,65. Seite 8 von 30
Schriftliche Abiturprüfung Mathematik 2013
 Aufgabe A. (HT 008, I 3, gekürzt und modifiziert) Ein Fass mit Zu- und Ablauf besitzt ein Fassungsvermögen von 00 Liter. Wahlteil Analysis a) Die enthaltene Wassermenge zum Zeitpunkt t wird beschrieben
Aufgabe A. (HT 008, I 3, gekürzt und modifiziert) Ein Fass mit Zu- und Ablauf besitzt ein Fassungsvermögen von 00 Liter. Wahlteil Analysis a) Die enthaltene Wassermenge zum Zeitpunkt t wird beschrieben
Schriftliche Abiturprüfung Mathematik 2013
 (8) Stochasti Pflichtteil Aufgabe 8.1 In einem Behälter befinden sich 2 rote und 4 blaue Kugeln. Es werden 2 Kugeln mit Zurüclegen gezogen. a) Berechnen Sie die Wahrscheinlicheit, dass mindestens eine
(8) Stochasti Pflichtteil Aufgabe 8.1 In einem Behälter befinden sich 2 rote und 4 blaue Kugeln. Es werden 2 Kugeln mit Zurüclegen gezogen. a) Berechnen Sie die Wahrscheinlicheit, dass mindestens eine
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Schriftliche Abiturprüfung Mathematik 2013
 Schriftliche Abiturprüfung Mathematik 0 () Ableitung Anforderungen wie bisher, allerdings ohne Quotientenregel Pflichtteil Durch den Wegfall der Quotientenregel müssen echte gebrochenrationale Funktionen
Schriftliche Abiturprüfung Mathematik 0 () Ableitung Anforderungen wie bisher, allerdings ohne Quotientenregel Pflichtteil Durch den Wegfall der Quotientenregel müssen echte gebrochenrationale Funktionen
 Pflichtteil Aufgaben Aufgabe : ( VP) x Gegeben ist die Funktion f mit f(x) =. x 3 Bilden Sie die Ableitung von f und fassen Sie diese so weit wie möglich zusammen. Aufgabe : ( VP) G ist eine Stammfunktion
Pflichtteil Aufgaben Aufgabe : ( VP) x Gegeben ist die Funktion f mit f(x) =. x 3 Bilden Sie die Ableitung von f und fassen Sie diese so weit wie möglich zusammen. Aufgabe : ( VP) G ist eine Stammfunktion
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
K2 MATHEMATIK KLAUSUR. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 26. 02. 2015 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 5 4 3 3 4 2 WT Ana A.1a) b) c) d) Summe P. (max) 6 4 3
K2 MATHEMATIK KLAUSUR 26. 02. 2015 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 5 4 3 3 4 2 WT Ana A.1a) b) c) d) Summe P. (max) 6 4 3
K2 MATHEMATIK KLAUSUR. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
K2 MATHEMATIK KLAUSUR 4.02.204 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 28 5 5 2 60 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 2 4 5 3 3 4 3 Punkte WT Ana A.a b A2.a b Summe P. (max
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Abiturprüfung an den allgemein bildenden Gymnasien. Musteraufgaben 2017 Hilfsmittelfreier Teil Seite 1-2. = 0. (2 VP) e
 MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Abiturprüfung an den allgemein bildenden Gymnasien Prüfungsfach: M a t h e m a t i k Musteraufgaben 2017 Hilfsmittelfreier Teil Seite 1-2 1. Bilden Sie die erste
MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Abiturprüfung an den allgemein bildenden Gymnasien Prüfungsfach: M a t h e m a t i k Musteraufgaben 2017 Hilfsmittelfreier Teil Seite 1-2 1. Bilden Sie die erste
Baden-Württemberg: Abitur 2014 Pflichtteil Lösungen. Für die Ableitungsfunktion werden die Produkt- und Kettenregel benötigt:
 Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Lösungen Aufgabe : Zunächst wird die Funktionsgleichung von f umgeschrieben in 0,5 x f(x) = x e Für die Ableitungsfunktion werden die Produkt-
Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Lösungen Aufgabe : Zunächst wird die Funktionsgleichung von f umgeschrieben in 0,5 x f(x) = x e Für die Ableitungsfunktion werden die Produkt-
P 0 f (0) schneidet die Gerade mit der Gleichung x Ermitteln Sie die Koordinaten von S.
 Zentralabitur 015 im Fach Mathematik Analysis 1 Im nebenstehenden Bild sind die Graphen dreier Funktionen f, g und h dargestellt Geben Sie an, bei welcher der drei Funktionen es sich um eine Stammfunktion
Zentralabitur 015 im Fach Mathematik Analysis 1 Im nebenstehenden Bild sind die Graphen dreier Funktionen f, g und h dargestellt Geben Sie an, bei welcher der drei Funktionen es sich um eine Stammfunktion
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
Schulcurriculum Mathematik Kursstufe November 2011
 Schulcurriculum Mathematik Kursstufe November 2011 Inhalte Leitidee / Kompetenzen Bemerkungen Die Schülerinnen und Schüler können Analysis Bestimmung von Extrem- und Wendepunkten: Höhere Ableitungen Bedeutung
Schulcurriculum Mathematik Kursstufe November 2011 Inhalte Leitidee / Kompetenzen Bemerkungen Die Schülerinnen und Schüler können Analysis Bestimmung von Extrem- und Wendepunkten: Höhere Ableitungen Bedeutung
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 27.11.2014 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 5 3 2 1 WT Ana A.1a) b) c) Summe P. (max) 6 4 5 15
K2 MATHEMATIK KLAUSUR 2 27.11.2014 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl (max) 28 15 15 2 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 5 3 2 1 WT Ana A.1a) b) c) Summe P. (max) 6 4 5 15
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
 Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Mathematik Übungsklausur 2013 Ausführliche Lösungen
 Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
K2 MATHEMATIK KLAUSUR 3
 K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
MATHEMATIK K1 EINSTIEGSARBEIT (OHNE GTR)
 MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Mathematik. Abiturprüfung Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten
 Mathematik Abiturprüfung 017 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 017 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
Mathematik Curriculum Kursstufe
 Mathematik Curriculum Kursstufe Kompetenzen und Inhalte des Bildungsplans Leitidee Funktionaler können besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen. Unterrichtsinhalte
Mathematik Curriculum Kursstufe Kompetenzen und Inhalte des Bildungsplans Leitidee Funktionaler können besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen. Unterrichtsinhalte
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Summe Pflichtteil: 30
 Aufgaben Pflichtteil 214 VP P1 f(x) = Ü Ú Ü 1. Ableitung f (x) 2 P 2 Ü dx Bestimmtes Integral berechnen 2 P 3 x 4 = 4 + 3x 2 Löse Gleichung 3 P 4 f(x) = cos x u. g(x) = 2 cos á Ü - 2. Wie entsteht g aus
Aufgaben Pflichtteil 214 VP P1 f(x) = Ü Ú Ü 1. Ableitung f (x) 2 P 2 Ü dx Bestimmtes Integral berechnen 2 P 3 x 4 = 4 + 3x 2 Löse Gleichung 3 P 4 f(x) = cos x u. g(x) = 2 cos á Ü - 2. Wie entsteht g aus
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
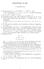 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Kern- und Schulcurriculum Mathematik Klasse 11/12. Stand Schuljahr 2012/13
 Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
Der folgende Katalog soll Beispiele dafür aufzeigen, was konkret verlangt werden kann, ohne dabei den Anspruch auf Vollständigkeit zu erheben.
 Fundus für den Pflichtbereich / Mathematik-Abitur ab 4 Themenbereiche Der Pflichtteil soll aus kleineren Aufgaben bestehen, die ohne Hilfsmittel zu bearbeiten sind. Er soll die Grundkompetenzen abprüfen.
Fundus für den Pflichtbereich / Mathematik-Abitur ab 4 Themenbereiche Der Pflichtteil soll aus kleineren Aufgaben bestehen, die ohne Hilfsmittel zu bearbeiten sind. Er soll die Grundkompetenzen abprüfen.
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Abitur 2015 Mathematik Infinitesimalrechnung I
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
 Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( 3x + ) Aufgabe : ( VP) 9 Berechnen Sie das Integral 4 x dx Aufgabe 3: (3 VP) x. Lösen Sie die Gleichung
Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( 3x + ) Aufgabe : ( VP) 9 Berechnen Sie das Integral 4 x dx Aufgabe 3: (3 VP) x. Lösen Sie die Gleichung
Probleme lösen mit Hilfe von Ableitungen, Extrem- und Wendepunkten
 Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Die Schülerinnen und Schüler können - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen; Bestimmung von Extrem-
Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Die Schülerinnen und Schüler können - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen; Bestimmung von Extrem-
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Abitur-Prüfung 2014 mit Lösungen (Baden-Württemberg)
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 201 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 201 mit
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 201 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 201 mit
Abiturprüfung an den allgemein bildenden Gymnasien
 MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Hinweise für die Abiturientinnen und Abiturienten Abiturprüfung an den allgemein bildenden Gymnasien Haupttermin 017 Prüfungsfach: Bearbeitungszeit: Hilfsmittel:
MINISTERIUM FÜR KULTUS, JUGEND UND SPORT Hinweise für die Abiturientinnen und Abiturienten Abiturprüfung an den allgemein bildenden Gymnasien Haupttermin 017 Prüfungsfach: Bearbeitungszeit: Hilfsmittel:
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Aufgaben sind zum größten Teil ohne CAS zu lösen. Kontrolle mit CAS ist eine gute Übung
 Aufgaben sind zum größten Teil ohne CAS zu lösen. Kontrolle mit CAS ist eine gute Übung Analysis Aufgabe 2 Bestimmen Sie jeweils die Gleichung einer Funktion f mit folgenden Eigenschaften: a) Die Funktion
Aufgaben sind zum größten Teil ohne CAS zu lösen. Kontrolle mit CAS ist eine gute Übung Analysis Aufgabe 2 Bestimmen Sie jeweils die Gleichung einer Funktion f mit folgenden Eigenschaften: a) Die Funktion
Musteraufgaben für das Fach Mathematik
 Musteraufgaben für das Fach Mathematik 1 Musteraufgaben für Aufgabenpool 1... 4 1.1 Analysis... 4 1. Analytische Geometrie/Lineare Algebra... 6 1..1 Analytische Geometrie... 6 1.. Lineare Algebra... 8
Musteraufgaben für das Fach Mathematik 1 Musteraufgaben für Aufgabenpool 1... 4 1.1 Analysis... 4 1. Analytische Geometrie/Lineare Algebra... 6 1..1 Analytische Geometrie... 6 1.. Lineare Algebra... 8
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Jugend forscht - Themenideen
 Jugend forscht - Themenideen Papierflugzeugschleuder Physik des Papierflugzeuges Bundesjugendspiele - Distanznahme usw. intelligenter Drucker - teuer? Programmierung? Lawinen? (was untersuchen und wie
Jugend forscht - Themenideen Papierflugzeugschleuder Physik des Papierflugzeuges Bundesjugendspiele - Distanznahme usw. intelligenter Drucker - teuer? Programmierung? Lawinen? (was untersuchen und wie
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Mit e 0 für alle x IR ergeben sich aus 2 x+ x = 0 die Nullstellen 0 und 2. 2 b) Ableitung mit der Produktregel und Ausklammern der e-funktion 3
 Aufgaben aus dem Aufgabenpool. Analysis A_ Gegeben ist die Funktion f mit x f(x) = e ( x + x ) (x IR). a) Bestimmen Sie die Nullstellen der Funktion f. ( ) x b) Zeigen Sie, dass die Funktion F mit F(x)
Aufgaben aus dem Aufgabenpool. Analysis A_ Gegeben ist die Funktion f mit x f(x) = e ( x + x ) (x IR). a) Bestimmen Sie die Nullstellen der Funktion f. ( ) x b) Zeigen Sie, dass die Funktion F mit F(x)
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
Skizzieren Sie das Schaubild von f einschließlich der Asymptote.
 G13-2 KLAUSUR 24. 02. 2011 1. Pflichtteil (1) (2 VP) Bilden Sie die Ableitung der Funktion f(x) = e2x 1 e x und vereinfachen Sie gegebenenfalls. (2) (2 VP) Geben Sie für die Funktion f(x) = (5 + 3 ) 4
G13-2 KLAUSUR 24. 02. 2011 1. Pflichtteil (1) (2 VP) Bilden Sie die Ableitung der Funktion f(x) = e2x 1 e x und vereinfachen Sie gegebenenfalls. (2) (2 VP) Geben Sie für die Funktion f(x) = (5 + 3 ) 4
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
EdM Kursstufe Baden-Württemberg
 EdM Kursstufe Baden-Württemberg Gegenüberstellung des Bildungsplans für die Kursstufe und der Inhalte des Schülerbandes EdM Kursstufe Die neben den mathematischen Kompetenzen eingeforderte Entwicklung
EdM Kursstufe Baden-Württemberg Gegenüberstellung des Bildungsplans für die Kursstufe und der Inhalte des Schülerbandes EdM Kursstufe Die neben den mathematischen Kompetenzen eingeforderte Entwicklung
Mathematik. Abiturprüfung Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten
 Mathematik Abiturprüfung 2015 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 2015 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik. Abiturprüfung Prüfungsteil A. Arbeitszeit: 90 Minuten. Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden.
 Mathematik Abiturprüfung 017 Prüfungsteil A Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 017 Prüfungsteil A Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Ermitteln Sie das Verhältnis der Inhalte der beiden Teilflächen. 5 BE. A_gA1 (zur Musteraufgabe A1_2) Beispielaufgaben S. 4
 A1_ Musteraufgaben S. 5 Das Rechteck ABCD mit A 1 0, B 4 0, C 4 und 1 Funktion f mit IR 0 f x x x, x in zwei Teilflächen zerlegt. D wird durch den Graphen der Ermitteln Sie das Verhältnis der Inhalte der
A1_ Musteraufgaben S. 5 Das Rechteck ABCD mit A 1 0, B 4 0, C 4 und 1 Funktion f mit IR 0 f x x x, x in zwei Teilflächen zerlegt. D wird durch den Graphen der Ermitteln Sie das Verhältnis der Inhalte der
ABITURPRÜFUNG 2001 GRUNDFACH MATHEMATIK
 ABITURPRÜFUNG 2001 GRUNDFACH MATHEMATIK (HAUPTTERMIN) Arbeitszeit: Hilfsmittel: 210 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig) Tafelwerk Der Prüfungsteilnehmer wählt von den Aufgaben
ABITURPRÜFUNG 2001 GRUNDFACH MATHEMATIK (HAUPTTERMIN) Arbeitszeit: Hilfsmittel: 210 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig) Tafelwerk Der Prüfungsteilnehmer wählt von den Aufgaben
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT. Abitur Januar/Februar Mathematik (Grundkurs) Arbeitszeit: 210 Minuten
 SCHRIFTLICHE ABITURPRÜFUNG 200 KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur Januar/Februar 200 Mathematik (Grundkurs) Arbeitszeit: 210 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten
SCHRIFTLICHE ABITURPRÜFUNG 200 KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur Januar/Februar 200 Mathematik (Grundkurs) Arbeitszeit: 210 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten
K2 MATHEMATIK KLAUSUR 1. Gesamtpunktzahl /30 Notenpunkte. (1) Bilden Sie die erste Ableitung der Funktion f mit f(x) = 1 + x ln(2x + 1).
 K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
K MATHEMATIK KLAUSUR NACHTERMIN..6 Aufgabe 3 4 6 7 8 9 Punkte (max 3 3 4 4 Punkte Gesamtpunktzahl /3 Notenpunkte ( Bilden Sie die erste Ableitung der Funktion f mit f(x = + x ln(x +. ( Bestimmen Sie das
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Fassung Herzog-Christoph-Gymnasium Beilstein. Funktionaler Zusammenhang. Modellieren. Algorithmus -zusammengesetzte Funktionen ableiten.
 Inhalte Leitideen Kompetenzen Analysis Die Schülerinnen und Schüler können Bestimmung von Extrem- und Wendepunkten Höhere Ableitungen Die Bedeutung der zweiten Ableitung Kriterien für Extremstellen Kriterien
Inhalte Leitideen Kompetenzen Analysis Die Schülerinnen und Schüler können Bestimmung von Extrem- und Wendepunkten Höhere Ableitungen Die Bedeutung der zweiten Ableitung Kriterien für Extremstellen Kriterien
Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.
 1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
Aufgabe 2 Die Abbildung zeigt den Graphen einer ganzrationalen Funktion f.
 Aufgabe 1 Die Abbildung zeigt den Graphen G f einer für 1 x 3 mit x R definierten Funktion f, die bei x= 1; x=1und x=3 Nullstellen besitzt. Die Funktion F mit F( x)= 1 6 ( x2 +2 x+3 ) 3 ist eine Stammfunktion
Aufgabe 1 Die Abbildung zeigt den Graphen G f einer für 1 x 3 mit x R definierten Funktion f, die bei x= 1; x=1und x=3 Nullstellen besitzt. Die Funktion F mit F( x)= 1 6 ( x2 +2 x+3 ) 3 ist eine Stammfunktion
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Abitur-Prüfung 2015 mit Lösungen (Baden-Württemberg)
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 015 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 015 mit
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 015 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 015 mit
Aufgaben für das Fach Mathematik
 Niedersächsisches Kultusministerium Referat 33 / Logistikstelle für zentrale Arbeiten August 017 Aufgaben für das Fach Mathematik Eingesetzte Abituraufgaben aus dem länderübergreifenden Abituraufgabenpool
Niedersächsisches Kultusministerium Referat 33 / Logistikstelle für zentrale Arbeiten August 017 Aufgaben für das Fach Mathematik Eingesetzte Abituraufgaben aus dem länderübergreifenden Abituraufgabenpool
Unterrichtsinhalte. Der Aufbau zusammengesetzter Funktionen aus elementaren Funktionen (ca. 3 5 Std.) Produkt, Quotient und Verkettung von Funktionen
 Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Hinweise/Vorschläge zur Erweiterung und Vertiefung des Kompetenzerwerbs - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des
Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Hinweise/Vorschläge zur Erweiterung und Vertiefung des Kompetenzerwerbs - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Analysis: Klausur Analysis
 Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Übungsklausur zu allen Themen Schlittenproduktion oder Flugzeuge Pflichtteil (ohne Hilfsmittel)
 Pflichtteil (ohne Hilfsmittel) 1) Bilde die erste Ableitung der Funktion f mit f(x) 3x sin(x) e. (VP) ) Bestimme eine Stammfunktion von 1 f(x) x cos x. (VP) 3) Löse die Gleichung 5 3 x 4x 5x 0. (3VP) 4)
Pflichtteil (ohne Hilfsmittel) 1) Bilde die erste Ableitung der Funktion f mit f(x) 3x sin(x) e. (VP) ) Bestimme eine Stammfunktion von 1 f(x) x cos x. (VP) 3) Löse die Gleichung 5 3 x 4x 5x 0. (3VP) 4)
1.2 Berechne den Inhalt der Fläche, die das Schaubild von mit 5P der -Achse einschließt.
 Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
3 Differenzialrechnung
 Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
. Ihr Schaubild sei &. a) Geben Sie die Asymptoten von & an. b) Bestimmen Sie den Schnittpunkt der Tangente an & im Punkt 1 1 mit der Achse.
 Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
K2 - Klausur Nr. 3. Generalprobe mit allen Themen. keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt.
 K2 - Klausur Nr. 3 Generalprobe mit allen Themen Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
K2 - Klausur Nr. 3 Generalprobe mit allen Themen Pflichtteil keine Hilfsmittel gestattet, bitte alle Lösungen auf dieses Blatt. Name: 0. Für Pflicht- und Wahlteil gilt: saubere und übersichtliche Darstellung,
SCHRIFTLICHE ABITURPRÜFUNG 2005 Mathematik (Grundkurs)
 Mathematik (Grundkurs) Arbeitszeit: 210 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten G 1, G 2 und G 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Mathematik (Grundkurs) Arbeitszeit: 210 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten G 1, G 2 und G 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Abiturprüfung Baden-Württemberg
 Abiturprüfung Baden-Württemberg Pflichtaufgaben Analysis / Geometrie / Stochastik Hauptprüfungen der Jahrgänge ab 004 Hier nur als Aufgabensammlung ohne Lösungen. Die Analysisaufgaben stehen mit ihren
Abiturprüfung Baden-Württemberg Pflichtaufgaben Analysis / Geometrie / Stochastik Hauptprüfungen der Jahrgänge ab 004 Hier nur als Aufgabensammlung ohne Lösungen. Die Analysisaufgaben stehen mit ihren
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Fachcurriculum Mathematik Kursstufe Kepler-Gymnasium Pforzheim
 Kompetenzen und Inhalte des Bildungsplans - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des CAS bestimmen; Unterrichtsinhalte Analysis Bestimmung von Extrem- und Wendepunkten (ca. 8-11
Kompetenzen und Inhalte des Bildungsplans - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des CAS bestimmen; Unterrichtsinhalte Analysis Bestimmung von Extrem- und Wendepunkten (ca. 8-11
 Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() ( 3) e weit wie möglich. = und vereinfachen Sie so Aufgabe : ( VP) Berechnen Sie das Integral + 4 d e Aufgabe
Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() ( 3) e weit wie möglich. = und vereinfachen Sie so Aufgabe : ( VP) Berechnen Sie das Integral + 4 d e Aufgabe
Lösung Abiturprüfung 1997 Grundkurs (Baden-Württemberg)
 Lösung Abiturprüfung 997 Grundkurs (Baden-Württemberg) Analysis I.. a) f x= x5 x = x5 x = x5 x = f x Somit ist f punktsymmetrisch zum Ursprung. f x= x x ; x = ; x = 5 ; x =5 f geht durch den Urpsrung:
Lösung Abiturprüfung 997 Grundkurs (Baden-Württemberg) Analysis I.. a) f x= x5 x = x5 x = x5 x = f x Somit ist f punktsymmetrisch zum Ursprung. f x= x x ; x = ; x = 5 ; x =5 f geht durch den Urpsrung:
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
K2 MATHEMATIK KLAUSUR 1. Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 1 14.03.2016 Aufgabe PT WTA WTGS Gesamtpunktzahl (max) 30 15 15 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 3 4 4 3 WT Ana A.1a) b) c) Summe P. (max) 7 5 3 15 WT Geo G.a)
K2 MATHEMATIK KLAUSUR 1 14.03.2016 Aufgabe PT WTA WTGS Gesamtpunktzahl (max) 30 15 15 60 Notenpunkte PT 1 2 3 4 5 6 7 8 9 P. (max) 2 2 3 4 5 3 4 4 3 WT Ana A.1a) b) c) Summe P. (max) 7 5 3 15 WT Geo G.a)
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Die Funktion ist gegeben durch ; 0. a) Die Tangente an den Graphen von im Punkt verläuft durch 0 0,5. Bestimmen Sie die Koordinaten von.
 Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Aufgabe A1. Aufgabe A2. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
Extremstellenbestimmung: A'(a) = 50 2a = 0 a = 25 und damit b = 25.
 6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
Grundwissen Jahrgangsstufe 9. Lösungen. Berechne ohne Taschenrechner: a) 2, a) = -1, b) = = = 4000
 Grundwissen Jahrgangsstufe 9 Berechne ohne Taschenrechner: a),5 + 7 1 9 b) 16 000 000 4 c) 81a 8 Gib die Lösungsmenge der folgenden Gleichungen an: a) ( x)² = 9 b) -x² = -5 c) x² + 50 = 0 Sind folgende
Grundwissen Jahrgangsstufe 9 Berechne ohne Taschenrechner: a),5 + 7 1 9 b) 16 000 000 4 c) 81a 8 Gib die Lösungsmenge der folgenden Gleichungen an: a) ( x)² = 9 b) -x² = -5 c) x² + 50 = 0 Sind folgende
