Baden-Württemberg: Abitur 2014 Pflichtteil Lösungen. Für die Ableitungsfunktion werden die Produkt- und Kettenregel benötigt:
|
|
|
- Kristina Rosenberg
- vor 5 Jahren
- Abrufe
Transkript
1 Baden-Württemberg: Abitur 04 Pflichtteil Lösungen Aufgabe : Zunächst wird die Funktionsgleichung von f umgeschrieben in 0,5 x f(x) = x e Für die Ableitungsfunktion werden die Produkt- und Kettenregel benötigt: f (x) = 0,5x e + x e = e + x e x 0,5 x 0,5 x x x Aufgabe : ( ) (x+ ) (x+ ) dx= 4 x+ dx = (x+ ) = = ( ) = 9 9 Aufgabe : Zunächst wird die Gleichung gleich Null gesetzt: 4 x x 4= 0 Mit der Substitution x = u folgt: u u 4= 0 ± 9 4 ( 4) ± 5 Anwendung der Lösungsformel: u, = = u = 4 und u = Rücksubstitution: x = 4 x=± x = ergibt keine Lösung. Lösungsmenge L = {-; } Aufgabe 4: a) Der Graph von f wird mit dem Faktor in y-richtung gestreckt. Anschließend wird er mit dem Faktor π in x-richtung gestaucht. Danach wird er um Längeneinheiten nach unten verschoben. b) Nullstellen von g: g(x) = 0 π π π cos x = 0 cos x = cos x = Die Funktion y= cos(x) nimmt an den Stellen x = 0, π, 4 π,... den Wert an. π x = 0 x = 0 π x = π x = 4 Im gegebenen Intervall gibt es daher zwei Nullstellen x = 0 und x = 4. 4
2 Baden-Württemberg: Abitur 04 Pflichtteil Aufgabe 5: a) Aus dem Schaubild kann man ablesen, dass g() = - ist. Somit ist f(g()) = f(-) = 5. Gesucht ist x, so dass f(g(x)) = 0 ist..lösungsmöglichkeit: Es ist f(4) = 0. Gesucht ist daher ein x-wert, so dass g(x) = 4 ist. Dies wäre für x = - der Fall..Lösungsmöglichkeit: Es ist f(0) = 0. Gesucht ist daher ein x-wert, so dass g(x) = 0 ist. Dies wäre für x = der Fall. b) Mit der Produktregel folgt: h() = f () g() + f() g() Es ist f () = 0, da an der Stelle x = die Parabel einen Tiefpunkt besitzt. Es ist g() =, da die Gerade die Steigung m = - besitzt. Außerdem gilt f() = -4 und g() = 0. h() = ( 4) ( ) = 4 Hinweis: Man könnte auch die Aufgabe dadurch lösen, dass man für die beiden Schaubilder die zugehörigen Funktionsgleichungen aufstellt und das ganze dann rechnerisch löst. Dies wäre jedoch deutlich aufwändiger und würde vom zeitlichen Aufwand her nicht zu der Punktzahl passen, die man bei der Aufgabe erzielen kann. Aufgabe 6: a) Schnittpunkte der Ebene E: x+ x = 4 mit den Koordinatenachsen: S (x /0/0) = S (4/0/0) x x S (0/ x /0) = S (0/ 4/0) x x S (0/0/ x ) existiert nicht, da dies auf einen Widerspruch 0 = 4 führt. x Die Ebene ist folglich parallel zur x-achse. Schnittpunkte der Ebene F: x+ x + x = 4 mit den Koordinatenachsen: S (x /0/0) = S (4/0/0) x x S (0/ x /0) = S (0/ 4/0) x x S (0/0/ x ) = S (0/0/) x x 5
3 Baden-Württemberg: Abitur 04 Pflichtteil Die Schnittgerade der Ebenen E und F ist die Gerade durch die Punkte S (4/0/0) und S (0/ 4/0). x x g: 4 4 x= 0 + s b) Da die Ebene G parallel zur x-achse verläuft, taucht die Variable x nicht in der Koordinatengleichung auf. Ansatz für die Koordinatengleichung von G: bx + cx = d Damit G dieselbe Spurgerade mit der xx-ebene wie F besitzt, muss G die Punkte S x (0/ 4/0) und Einsetzen von Einsetzen von S x (0/0/) besitzen. S x in die Koordinatengleichung: 4b= d S x in die Koordinatengleichung: c = d Wenn man z.b. d = 4 wählt, ergibt sich b = und c =. Eine mögliche Koordinatengleichung von G lautet damit: x + x = 4 Aufgabe 7: Zunächst benötigt man die Gleichung der Geraden g. 4 Es ist g: x= 0 + s 0 Zur Berechnung des Abstandes von g zu Punkt C(//) benötigt man eine Hilfsebene H. Diese Hilfsebene steht orthogonal zur Geraden g und enthält den Punkt C. Der Normalenvektor von H ist der Richtungsvektor von g. 4 Normalenform von H: x = 0 0 Koordinatengleichung von H: 4x+ x = Der Schnittpunkt von g mit H ergibt den Lotfußpunkt F: 4( 4s) + (0+ s) = 4+ 6s+ 0+ 9s= s= Einsetzen von s = - in die Gerade ergibt den Lotfußpunkt F(5/7/). Abstand von g zu C = CF= CF = 4 = = 5 LE 0 6
4 Baden-Württemberg: Abitur 04 Pflichtteil Aufgabe 8: a) Die dargestellte Formel ergibt sich aus der Formel der Binomialverteilung: n k n k P(X= k) = p ( p) k Die Formel P(A) setzt sich aus drei Summanden zusammen: 8 0.Summand = 8 entspricht der obigen Formel mit n = 0, k = 8, p= Dieser stellt die Wahrscheinlichkeit dar, mit der man bei 0 Spielen am Automaten bei einer Verlustwahrscheinlichkeit von genau 8 Spiele verliert..summand = 0 9 entspricht der obigen Formel mit n = 0, k = 9, p= 0 0 Hinweis: Der.Summand lautet ausführlich 9, da = 0 ist 9 Dieser stellt die Wahrscheinlichkeit dar, mit der man bei 0 Spielen am Automaten bei einer Verlustwahrscheinlichkeit von genau 9 Spiele verliert. 9.Summand = 0 entspricht der obigen Formel mit n = 0, k = 0, p= Hinweis: Der.Summand lautet ausführlich 0 0, da = und = 0 Dieser stellt die Wahrscheinlichkeit dar, mit der man bei 0 Spielen am Automaten bei einer Verlustwahrscheinlichkeit von genau 0 Spiele verliert. 0 Fazit: Ereignis A heißt, dass man bei 0 Spielen am Automaten bei einer Verlustwahrscheinlichkeit von mindestens 8 verliert. b) Die Zufallsvariable X gibt die Anzahl der verlorenen Spiele am Automaten an. X ist binomialverteilt mit n = 4 und p= Es ist P(X= ) = 6 = = = Mit der Wahrscheinlichkeit 8 verliert der Spieler genau zwei von vier Spielen. 7 7
5 Baden-Württemberg: Abitur 04 Pflichtteil Aufgabe 9:.Schritt: Man stellt die Gleichung einer Hilfsgeraden g auf. Diese Gerade g steht senkrecht auf der gegebenen Ebene (Richtungsvektor von g ist der Normalenvektor von E) und geht durch den Mittelpunkt M der Kugel (Ortsvektor der Gerade ist OM ).Schritt: Der Schnittpunkt der Geraden g mit der Ebene E ist der gesuchte Berührpunkt B..Schritt: Den Abstand der Punkte M und B erhält man durch Berechnung von MB und entspricht dem Radius der Kugel. 8
6 Baden-Württemberg: Abitur 04 Wahlteil A Lösungen Aufgabe A. a) Koordinaten des Extrempunktes: Notwendige und hinreichende Bedingung: f(x) = 0 und f (x) 0 GTR: Das Schaubild besitzt den Hochpunkt H(/7,6) Koordinaten des Wendepunktes: Notwendige und hinreichende Bedingung: f (x) = 0 und f (x) 0 GTR: Die Ableitungsfunktion hat ihr relatives Minimum bei x = 4. Somit besitzt K die Wendestelle x = 4. Außerdem gilt f(4) = 5,4. Das Schaubild besitzt den Wendepunkt W(4/5,4). Das Schaubild K besitzt für x die waagrechte Asymptote y = 0. Skizze von K:
7 Baden-Württemberg: Abitur 04 Wahlteil A b) Skizze des Dreiecks: Die Fläche des Dreiecks OPQ berechnet sich mit A= OP PQ Mit OP= u und PQ= f(u) ergibt sich als Fläche der Term A(u) = u f(u). Nun soll gelten: u f(u) = 8 für u > 0. Die Gleichung wird mit dem GTR gelöst: Es gibt zwei Werte für u, für die die Dreiecksfläche den Inhalt 8 besitzt: u =,8 oder u = 6,6. Das Dreieck OPQ ist gleichschenklig, wenn die Seiten OP und PQ gleich lang sind. Da das Dreieck rechtwinklig ist bei P und OQ die längste Dreiecksseite darstellt,. gibt es keine andere Möglichkeit. Bedingung für Gleichschenkligkeit: OP PQ u f(u) = = für u > 0 Die Gleichung wird mit dem GTR gelöst: Für u = 4,6 ist das Dreieck OPQ gleichschenklig. 4
8 Baden-Württemberg: Abitur 04 Wahlteil A c) Das gesuchte Intervall mit der Länge hat die Gestalt [x ; x+]. Ansatz für den Mittelwert: Berechnung mit dem GTR: x+ f(x)dx =, x Es existieren zwei Lösungen: x = -0,86 und x = 5,5. Die möglichen Intervalle lauten [-0,86 ;,8] und [5,5 ; 8,5]. Aufgabe A. Berechnung der Ableitungsfunktionen: f(x) t = x t x = t t f(x) x t f (x) = x Notwendige und hinreichende Bedingung für Extrempunkte: f(x) t = 0 und f(x) t 0 t = = =± f(x) 0 x t 0 x t f(t) = t> 0 relatives Minimum ; t Da f(t) = t t = t ergibt sich als Tiefpunkt T(t/ t ) f( t t) = t< 0 relatives Maximum ; Da f( t) = ( t) ( t) = t ergibt sich als Hochpunkt Abstand der Extrempunkte: 4 d(t) = ( t) + ( t ) Bedingung: d(t) = für t > 0 Lösung mit GTR: H( t/ t ) d = (x x ) + (y y ) = ( t t) + ( t ( t )) H T H T Für t =, haben die beiden Extrempunkte den Abstand voneinander. 5
9 Baden-Württemberg: Abitur 04 Wahlteil A Lösungen Aufgabe A. a) Skizze des Graphen von f: Zeitpunkt maximaler Ankunftsrate: Notwendige und hinreichende Bedingung: f(t) = 0 und f (t) 0 Berechnung mit dem GTR: Die Ankunftsrate ist maximal für t = 0. 0 Stunden nach Beobachtungsbeginn ist die momentane Ankunftsrate maximal. Anzahl der Fahrzeuge, die in den ersten 6 Stunden ankommen: Da es sich bei f(t) um die momentane Ankunftsratenfunktion handelt, ergibt sich die Anzahl der Fahrzeuge durch die Berechnung eines Integrals: 6 f(t)dt 769,05 (GTR). 0 In den ersten 6 Stunden kommen etwa 770 Fahrzeuge an.
10 Baden-Württemberg: Abitur 04 Wahlteil A b) Die Gerade y = 0 stellt die Abfertigungsrate dar. Die Fahrzeuge beginnen sich zu stauen, wenn die Ankunftsrate f(t) oberhalb der Abfertigungsrate liegt. Berechnung des linken Schnittpunktes der Schaubilder: f(t) = 0 Mit dem GTR ergibt sich als Schnittstelle t =,54. Die Fahrzeuge beginnen sich etwa,5 Stunden nach Beobachtungsbeginn zu stauen. Die Anzahl der Fahrzeuge, die sich stauen entsprechen der Fläche, die das Schaubild von f(t) und die waagrechte Gerade einschließt. Die rechte Schnittstelle der Schaubilder ist bei t =,86 Stunden. Bis zu diesem Zeitpunkt liegt die Ankunftsrate oberhalb der Abfertigungsrate, das heißt der Stau nimmt zu. Erst für t >,86 Stunden baut sich der Stau wieder ab. Die maximale Anzahl der Fahrzeuge, die sich stauen, berechnen sich folglich mit dem Integral,86 (f(t) 0)dt= 4,97 (GTR),54 Es befinden sich maximal etwa 5 Fahrzeuge vor der Grenze. Wenn die Abfertigungsrate nach Stunden auf 0 Fahrzeuge pro Stunde erhöht wird, ergibt sich folgendes Bild: 4
11 Baden-Württemberg: Abitur 04 Wahlteil A Die Fahrzeuge beginnen sich auch hier nach t =,54 Stunden (linke Schnittstelle) zu stauen. Die rechte Schnittstelle ändert sich nun: Ansatz: f(t) = 0 Die Lösung mit dem GTR lautet t = 5,9 Stunden. Bis zu diesem Zeitpunkt liegt die Ankunftsrate oberhalb der Abfertigungsrate, das heißt der Stau nimmt zu. Erst für t > 5,9 Stunden baut sich der Stau wieder ab. Die maximale Anzahl der Fahrzeuge, die sich stauen, berechnen sich folglich mit dem Integral 5,9 (f(t) 0)dt + (f(t) 0)dt = 4,6+ 79,8 = 60,4 (GTR),54 Es befinden sich maximal etwa 600 Fahrzeuge vor der Grenze. Aufgabe. a) Koordinaten des Extrempunktes: Gegenüber der üblichen Vorgehensweise bei der Extrempunktberechnung ( f a (x) = 0 und f a (x) 0) ist es hier einfacher, auf Basis der bekannten Extrempunkte der Funktion y = cos(x) die Extrempunkte von f a (x) herzuleiten. Im Intervall π< x<π besitzt das Schaubild y = cos(x) nur den Hochpunkt H(0/). Im ersten Schritt wird y = cos(x) mit dem Faktor a in y-richtung gestreckt, dies ergibt y= a cos(x). Dadurch ändert sich nur der y-wert des Hochpunktes zu H(0/ a). Im zweiten Schritt wird y= a cos(x) um Dies ergibt f (x) = acos(x) a. a a nach unten verschoben. Dadurch ändert sich nur der y-wert des Hochpunktes zu gesuchte Extrempunkt. H(0/a a ) und dies ist der 5
12 Baden-Württemberg: Abitur 04 Wahlteil A b) Das Schaubild G a schneidet die y-achse im in a) berechneten Hochpunkt H(0/a a ) für a > 0. Nun ist gefragt, welche Werte von dem Term können. Einzeichnen der Funktion h(a) = a a für a > 0 in den GTR: a a für a > 0 angenommen werden Die Funktion h(a) hat ihr Maximum für a = 0,5 mit h(0,5) = 0,5. Der Term a a kann für a > 0 alle Werte annehmen, die kleiner oder gleich 0,5 sind. Das heißt, dass der y-wert von H keine Werte oberhalb von 0,5 annehmen kann. Daher verläuft durch keinen Punkt P(0/y) mit y > 0,5 ein Graph G a. 6
13 Baden-Württemberg: Abitur 04 Wahlteil B Aufgabe B.: a) Koordinatengleichung von E: Lösungen Die Parametergleichung der Ebene, in der die Punkte B, C und S liegen, ist E: x= 5 + r 0 + s Nun wird der Normalenvektor von E berechnet. Mit dem Kreuzprodukt der Richtungsvektoren ergibt sich 0 Als Normalenvektor kann n* = gewählt werden n= 0 5 = Ansatz für die Koordinatengleichung von E: x + 5x = d Einsetzen des Ebenenpunktes B(5/5/0) ergibt = 60= d Koordinatengleichung von E: x + 5x = 60 Gesucht ist der Schnittwinkel der Ebene E und der xx -Ebene (Normalenvektor cosα= = ; Es ist α= 67, ) Flächeninhalt des Dreiecks BCS: Die Fläche des Dreiecks kann mit der Formel ADreieck = BC BS berechnet werden. 0 Es ist BC BS= 0 (siehe Rechnung oben) und 50 0 BC BS = 0 = = Die Fläche des Dreiecks beträgt ADreieck = 0= 65 Flächeneinheiten. Hinweis: Man hätte die Dreiecksfläche auch mit Hilfe der Eigenschaft der Gleichschenkligkeit des Dreiecks berechnen können.
14 Baden-Württemberg: Abitur 04 Wahlteil B b) Aufgrund der Skizze ergeben sich neben Q(,5/,5/0) als weitere Quadereckpunkte T(,5/-,5/0) und U(-,5/,5/0). Die Länge und die Breite des Quaders sind jeweils 5 LE. Für die Höhe des Quaders benötigt man die Koordinaten des Punktes R(,5/,5/?), der auf der Geraden durch B und S liegt. 5 5 Gleichung der Gerade durch B und S: x= 5 + s 5 0,5 5 5 Punktprobe mit R:,5 = 5 + s 5 daraus folgt s = 0,5 und x = 6 x 0 Mit R(,5/,5/6) ist die Höhe des Quaders h = 6. V = 5 5 6= 50VE Quader Der Quader ist dann ein Würfel, wenn der Eckpunkt R die Koordinaten R(x/x/x) besitzt. Einsetzen von R in die Gerade durch B und S:.Zeile: x= s x= 6s 5.Zeile: 6s= 5 5s s= und damit 0 x= x 5 5 x = 5 + s 5 x 0 Der gesuchte Eckpunkt R des Würfels hat die Koordinaten R( / / ). 4
15 Baden-Württemberg: Abitur 04 Wahlteil B Aufgabe B.: a) Wahrscheinlichkeit für das Ziehen aus G: Die Zufallsvariable X beschreibt die Anzahl der gezogenen schwarzen Kugeln. X ist binomialverteilt mit n = 0 und p = 0,6. Es gilt: P(X ) = P(X ) = 0,596 (GTR) Wahrscheinlichkeit für das Ziehen aus G: Diese Wahrscheinlichkeit kann nicht mit der Binomialverteilung berechnet werden, da vorgegeben ist, an welchen möglichen Stellen die schwarzen Kugeln zu ziehen sind (nämlich hintereinander): Angenommen, die beiden schwarzen Kugeln werden gleich am Anfang gezogen: 6 Dann beträgt die Wahrscheinlichkeit 0, 0,7 Da die beiden schwarzen Kugeln aber auch während der Ziehung oder am Ende der Ziehung gezogen werden können, muss man berechnen, wie viele Möglichkeiten es gibt, die beiden schwarzen Kugeln auf der 8 Stellen zu verteilen. Es gibt hierfür 7 Möglichkeiten. Daher gilt: P(genau schwarze Kugeln direkt hintereinander) = 6 7 0, 0,7 = 0,074 b) Folgende Fälle müssen betrachtet werden: A) Aus G werden schwarze Kugeln gezogen mit Wk 6 5 = 0 9 B) Aus G wird schwarze und weiße Kugel gezogen mit Wk = C) Aus G werden weiße Kugeln gezogen mit Wk 4 = Im Fall A) sind 5 schwarze Kugeln in G: P(schwarze Kugel) = 5 Im Fall B) sind 4 schwarze Kugeln in G: P(schwarze Kugel) = 4 Im Fall C) sind schwarze Kugeln in G: P(schwarze Kugel) = Für die gesuchte Wahrscheinlichkeit gilt: P(schwarze Kugel aus G) = = 0,
16 Baden-Württemberg: Abitur 04 Wahlteil B Aufgabe B.: a) Koordinatengleichung von E: Lösungen Die Parametergleichung der Ebene, in der die Punkte A, B und C liegen, ist E: x= 6 + r 0 + s Nun wird der Normalenvektor von E berechnet Mit dem Kreuzprodukt der Richtungsvektoren ergibt sich n= 0 6 = Als Normalenvektor kann n* = gewählt werden. Ansatz für die Koordinatengleichung: x + x = d Einsetzen von A(0/6/0) in die Koordinatengleichung: 6+ 0= 6= d Koordinatengleichung von E: x + x = 6 Anschauliche Darstellung von Platte, Stab und Lichtquelle: Der Stab FT besitzt den Richtungsvektor 0 0.
17 Baden-Württemberg: Abitur 04 Wahlteil B Winkel zwischen Stab und Platte: sinα= = 5 5 α= 6,4 b) Das obere Ende des Stabes ist der Punkt T(5/6/). Zur Berechnung des Schattenpunktes von T wird eine Gerade durch L(8/0/) und T aufgestellt. 8 g: x= 0 + s 4 0 Schnittpunkt der Ebene E mit g liefert den Schattenpunkt T*: 0 4s+ = 6 s= Einsetzen von s = in g: T*(//) Der Punkt T* liegt als Schnittpunkt von g und E in der Ebene E. Zu begründen ist, dass T* innerhalb des Rechtecks ABCD liegt. Die x-koordinate von T* liegt zwischen den x-koordinaten von A und B. Die x-koordinate von T* liegt zwischen den x-koordinaten von B und C. Damit liegt T* innerhalb des Rechtecks ABCD (also auf der Platte). Der Schattenpunkt von F ist F*. Da F auf der Platte liegt, stimmen F und F* überein. Da sich die Schattenpunkte T* und F* auf der Platte befinden, befindet sich folglich die Schattenstrecke T*F* auch auf der Platte. c) Die zur xx-ebene parallele Kreisbahn liegt in der Ebene H: x =, da die Lichtquelle L die x-koordinate besitzt. Die Kollisionspunkte liegen auf der Schnittgeraden k der Ebenen H und E: Berechnung der Schnittgeraden k: x + x = 6 x = Aus dem Gleichungssystem folgt x =, x =, x= t, t Gleichung der Schnittgeraden: k: 0 x= + s 0 0 Da die Kollisionspunkte auf der Gerade k liegen, haben diese die allgemeinen Koordinaten P(s//). s Der Radius der Kreisbahn beträgt LT = 4 = = 5m. 0 4
18 Baden-Württemberg: Abitur 04 Wahlteil B Nun muss der Parameter s so gewählt werden, dass der Geradenpunkt P s vom Mittelpunkt T der Kreisbahn den Abstand 5 besitzt: TPs = 5 s 5 TPs = 4 = (s 5) Bedingung: (s 5) + 6 = 5 (s 5) + 6= 5 s 5=± (s 5) = 9 Daraus folgt s = 8 oder s =. (Hinweis: Alternativ kann die Quadratklammer auch aufgelöst und die Lösungsformel für quadratische Gleichungen angewandt werden) Die beiden Kollisionspunkte haben die Koordinaten P(//) und P(8//) 8 Aufgabe B.: a) Die Zufallsvariable X ist binomialverteilt mit n = 800 und p = 0,05. P(X 0) = 0,057 (GTR) Der Erwartungswert von X ist E(X) = n p= 800 0,05 = 40. Gesucht ist die Wahrscheinlichkeit P( X 49) : P( X 49) = P(X 49) P(X 0) = 0,947 0,057 = 0,878 (GTR) b) Die Zufallsvariable Y beschreibt die Anzahl der fehlerhaften Stifte. Y ist im Extremfall binomialverteilt mit n = 800 und p = 0,0. Nullhypothese: p 0,0 Gegenhypothese: p> 0,0 Es handelt sich um einen rechtsseitigen Test. Der Ablehnungsbereich ist A = {k+,...,800} Gesucht ist der kleinste Wert von k, so dass gilt: P(Y k+ ) 0,05 umgeformt: P(Y k) 0,05 GTR: P(Y ) = 0,0564 und P(Y ) 0,05 Damit ist k =. Der Ablehnungsbereich ist A = {4,...,800} Bei mindestens 4 fehlerhaften Stiften entscheidet man sich gegen die Nullhypothese. 5
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 14 Wahlteil B www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 14 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung
Baden-Württemberg: Abitur 14 Wahlteil B www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 14 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Summe Pflichtteil: 30
 Aufgaben Pflichtteil 214 VP P1 f(x) = Ü Ú Ü 1. Ableitung f (x) 2 P 2 Ü dx Bestimmtes Integral berechnen 2 P 3 x 4 = 4 + 3x 2 Löse Gleichung 3 P 4 f(x) = cos x u. g(x) = 2 cos á Ü - 2. Wie entsteht g aus
Aufgaben Pflichtteil 214 VP P1 f(x) = Ü Ú Ü 1. Ableitung f (x) 2 P 2 Ü dx Bestimmtes Integral berechnen 2 P 3 x 4 = 4 + 3x 2 Löse Gleichung 3 P 4 f(x) = cos x u. g(x) = 2 cos á Ü - 2. Wie entsteht g aus
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Wahlteil Geometrie/Stochastik B 2
 Abitur Mathematik Baden-Württemberg 24 Abitur Mathematik: Wahlteil Geometrie/Stochastik B 2 Baden-Württemberg 24 Aufgabe B 2. a). SCHRITT: KOORDINATENGLEICHUNG ANGEBEN Als Stützvektor einer Parametergleichung
Abitur Mathematik Baden-Württemberg 24 Abitur Mathematik: Wahlteil Geometrie/Stochastik B 2 Baden-Württemberg 24 Aufgabe B 2. a). SCHRITT: KOORDINATENGLEICHUNG ANGEBEN Als Stützvektor einer Parametergleichung
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 06 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg
 Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Abituraufgaben bis 2018 Baden-Württemberg. Geraden, Ebenen, Abstand
 Abituraufgaben bis 8 Baden-Württemberg Geraden, Ebenen, Abstand allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com August 8 Aufgabe : (Abiturprüfung 8) Gegeben sind die Ebenen E: xx x
Abituraufgaben bis 8 Baden-Württemberg Geraden, Ebenen, Abstand allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com August 8 Aufgabe : (Abiturprüfung 8) Gegeben sind die Ebenen E: xx x
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Analysis: Exponentialfunktionen Analysis
 www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Abitur-Prüfung 2014 mit Lösungen (Baden-Württemberg)
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 201 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 201 mit
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Abitur-Prüfung 201 mit Lösungen (Baden-Württemberg) Das komplette Material finden Sie hier: School-Scout.de Abitur-Prüfung 201 mit
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
 Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 004 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f() = + 3 Aufgabe : ( VP) Geben Sie eine Stammfunktion
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 07 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com Mai 07 Aufgabe : (,5 VP) Bilden Sie die Ableitung
Hauptprüfung Abiturprüfung 07 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com Mai 07 Aufgabe : (,5 VP) Bilden Sie die Ableitung
Lösungen zur Prüfung 2014: Pflichtteil
 Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 26 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 26 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 2 - Lösungen
 Abiturprüfung Mathematik 24 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 2 - Lösungen klaus_messner@web.de www.elearning-freiburg.de Wahlteil 24 Aufgabe
Abiturprüfung Mathematik 24 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 2 - Lösungen klaus_messner@web.de www.elearning-freiburg.de Wahlteil 24 Aufgabe
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
K2 KLAUSUR Pflichtteil
 K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
Pflichtteilaufgaben zu Beschreiben und Begründen. Baden-Württemberg
 Pflichtteilaufgaben zu Beschreiben und Begründen Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 06 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Beschreiben und Begründen Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 06 Abituraufgaben (Haupttermin) Aufgabe
Inhalt der Lösungen zur Prüfung 2012:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analsis... 8 Wahlteil Analsis... Wahlteil Analsis... 4 Wahlteil Analtische Geometrie... 8 Wahlteil Analtische Geometrie... Pflichtteil Lösungen
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 06 Wahlteil B www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung
Baden-Württemberg: Abitur 06 Wahlteil B www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 06 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Hauptprüfung 2006 Aufgabe 1
 Hauptprüfung 6 Aufgabe. Geben Sie eine Funktion h an, deren Schaubild mit der folgenden Kurve übereinstimmt. (6 Punkte). Gegeben ist die Funktion f mit f(x) = x + x, x Ihr Schaubild ist K. Berechnen Sie
Hauptprüfung 6 Aufgabe. Geben Sie eine Funktion h an, deren Schaubild mit der folgenden Kurve übereinstimmt. (6 Punkte). Gegeben ist die Funktion f mit f(x) = x + x, x Ihr Schaubild ist K. Berechnen Sie
Wahlteil Geometrie/Stochastik B 1
 Abitur Mathematik: Wahlteil Geometrie/Stochastik B 1 Baden-Württemberg 214 Aufgabe B 1.1 a) 1. SCHRITT: SKIZZE ANFERTIGEN Die Lage der Pyramide im Koordinatensystem ist wie folgt: 2. KOORDINATENGLEICHUNG
Abitur Mathematik: Wahlteil Geometrie/Stochastik B 1 Baden-Württemberg 214 Aufgabe B 1.1 a) 1. SCHRITT: SKIZZE ANFERTIGEN Die Lage der Pyramide im Koordinatensystem ist wie folgt: 2. KOORDINATENGLEICHUNG
Hauptprüfung Abiturprüfung 2016 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 1 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 016 1 Aufgabe
Hauptprüfung Abiturprüfung 016 (ohne CAS) Baden-Württemberg Wahlteil Analysis 1 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com April 016 1 Aufgabe
3.4 Monotonie. Differenzialrechnung
 Differenzialrechnung 3.4 Monotonie Definition Gilt an der Stelle x 0 Beispiel Wir sehen von der Seite aus auf das Männchen, welches ein hügeliges Gelände durchläuft. Das Gelände ist im Profil dargestellt.
Differenzialrechnung 3.4 Monotonie Definition Gilt an der Stelle x 0 Beispiel Wir sehen von der Seite aus auf das Männchen, welches ein hügeliges Gelände durchläuft. Das Gelände ist im Profil dargestellt.
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Lösung Abiturprüfung 1997 Grundkurs (Baden-Württemberg)
 Lösung Abiturprüfung 997 Grundkurs (Baden-Württemberg) Analysis I.. a) f x= x5 x = x5 x = x5 x = f x Somit ist f punktsymmetrisch zum Ursprung. f x= x x ; x = ; x = 5 ; x =5 f geht durch den Urpsrung:
Lösung Abiturprüfung 997 Grundkurs (Baden-Württemberg) Analysis I.. a) f x= x5 x = x5 x = x5 x = f x Somit ist f punktsymmetrisch zum Ursprung. f x= x x ; x = ; x = 5 ; x =5 f geht durch den Urpsrung:
) (1 BE) 1 2 ln 2. und somit
 1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1 Aufgaben aus dem Aufgabenpool 1 1.1 Analysis A1_1 Eine Funktion f ist durch 1 x f(x) e 1, x IR, gegeben. Ermitteln Sie die Nullstelle der Funktion f. ( ) b) Die Tangente an den Graphen von f im Punkt
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
Begleitbuch für Mathematik Oberstufe für die Abiturprüfungen 2019 und 2020 Baden-Württemberg - allgemeine Gymnasien
 Begleitbuch für Mathematik Oberstufe für die Abiturprüfungen 019 und 00 Baden-Württemberg - allgemeine Gymnasien Aufgabensammlung Pflicht-/Wahlteil Analysis, Stochastik, Analytische Geometrie Dipl.-Math.
Begleitbuch für Mathematik Oberstufe für die Abiturprüfungen 019 und 00 Baden-Württemberg - allgemeine Gymnasien Aufgabensammlung Pflicht-/Wahlteil Analysis, Stochastik, Analytische Geometrie Dipl.-Math.
m und schneidet die y-achse im Punkt P(0/3).
 Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.
 1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.)
 KANTONSSCHULE ROMANSHORN MATHEMATIK - Std. MATURITÄTSPRÜFUNGEN Klasse 4 MC - hcs TYPUS MAR Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.) ) Gegeben sind die Punkte A( 4 ), B( 4 )
KANTONSSCHULE ROMANSHORN MATHEMATIK - Std. MATURITÄTSPRÜFUNGEN Klasse 4 MC - hcs TYPUS MAR Lösungen: (Die Aufgaben sind fett, die Lösungen normal geschrieben.) ) Gegeben sind die Punkte A( 4 ), B( 4 )
Abituraufgaben Analytische Geometrie Wahlteil 2014 BW
 Abituraufgaben Analytische Geometrie Wahlteil 24 BW Aufgabe B Gegeben sind die Punkte 5 5, 5 5, 5 5 und 5 5. Das Quadrat ist die Grundfläche einer Pyramide mit der Spitze 2. a) Die Seitenfläche liegt in
Abituraufgaben Analytische Geometrie Wahlteil 24 BW Aufgabe B Gegeben sind die Punkte 5 5, 5 5, 5 5 und 5 5. Das Quadrat ist die Grundfläche einer Pyramide mit der Spitze 2. a) Die Seitenfläche liegt in
Mathematik Name: Nr.4 K1 Punkte: /30 Note: Schnitt:
 K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
1 aus allen 3 Zeilen folgt t = 1, also liegt A auf g. Orsvektor und Richtungsvektor der Geraden werden übernommen, den zweiten Spannvektor bekommt
 Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
Lösungsskizzen Klassische Aufgaben Lösung zu Abi - PTV Punktprobe: = + t aus allen Zeilen folgt t =, also liegt A auf g. Richtungsvektor von g: u = ; Normalenvektor von E: n = Da die n und u Vielfache
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 205 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Hauptprüfung Abiturprüfung 205 (ohne CAS) Baden-Württemberg Wahlteil Analytische Geometrie / Stochastik Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Mit e 0 für alle x IR ergeben sich aus 2 x+ x = 0 die Nullstellen 0 und 2. 2 b) Ableitung mit der Produktregel und Ausklammern der e-funktion 3
 Aufgaben aus dem Aufgabenpool. Analysis A_ Gegeben ist die Funktion f mit x f(x) = e ( x + x ) (x IR). a) Bestimmen Sie die Nullstellen der Funktion f. ( ) x b) Zeigen Sie, dass die Funktion F mit F(x)
Aufgaben aus dem Aufgabenpool. Analysis A_ Gegeben ist die Funktion f mit x f(x) = e ( x + x ) (x IR). a) Bestimmen Sie die Nullstellen der Funktion f. ( ) x b) Zeigen Sie, dass die Funktion F mit F(x)
Mathematik Name: Nr.5 K2 Punkte: /30 Note: Schnitt:
 Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P] Bestimmen
Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P] Bestimmen
Analysis II. Abitur Mathematik Bayern 2012 Musterlösung. Bayern Teil 1. Aufgabe 1. Aufgabe 2. Abitur Mathematik: Musterlösung.
 Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
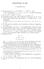 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE]
![Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE] Bayern Aufgabe 1. Abitur Mathematik: Musterlösung. V = 1 G h, wobei G die Fläche des quadratischen Bodens und h die Höhe V = = 384 [VE]](/thumbs/80/80887276.jpg) Abitur Mathematik: Bayern 2 Aufgabe a). SCHRITT: KOORDINATEN DES PUNKTS B ANGEBEN 2 2 OB = OA + AB = OA + DC = ( ) + ( 2) = ( 2) B(2 2 ) 2. SCHRITT: VOLUMEN BERECHNEN V = G h, wobei G die Fläche des quadratischen
Abitur Mathematik: Bayern 2 Aufgabe a). SCHRITT: KOORDINATEN DES PUNKTS B ANGEBEN 2 2 OB = OA + AB = OA + DC = ( ) + ( 2) = ( 2) B(2 2 ) 2. SCHRITT: VOLUMEN BERECHNEN V = G h, wobei G die Fläche des quadratischen
 Abiturprüfung Mathematik 03 Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analytische Geometrie / Stochastik B Aufgabe B. In einem würfelförmigen Ausstellungsraum mit der Kantenlänge 8 Meter ist ein
Abiturprüfung Mathematik 03 Baden-Württemberg (ohne CAS) Wahlteil - Aufgaben Analytische Geometrie / Stochastik B Aufgabe B. In einem würfelförmigen Ausstellungsraum mit der Kantenlänge 8 Meter ist ein
Hauptprüfung Abiturprüfung 2018 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
K2 MATHEMATIK KLAUSUR 3
 K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
6x 2. x 1. Eine Stammfunktion ist damit F( x) x 4sin x
 K 4..15 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P]
K 4..15 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgabe 1: [P]
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans
 Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg Wahlteil Analysis 2 Hilfsmittel: GTR und Formelsammlung allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com März 2015 1 Aufgabe
Abituraufgaben allg. bildendes Gymnasium Pflichtteil 2007 BW Aufgabe A1
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
MATHEMATIK K1. Gesamtpunktzahl /30 Notenpunkte. (1) Bestimmen Sie die erste Ableitung folgender Funktionen: a) f(x) = 2x 3 cos(x) + x
 MATHEMATIK K 06.0.206 Aufgabe 2 3 4 5 6 7 8 Punkte (max 8 2 3 5 4 3 3 2 Punkte Gesamtpunktzahl /30 Notenpunkte ( Bestimmen Sie die erste Ableitung folgender Funktionen: a f(x 2x 3 cos(x + x b g(x 2 3x
MATHEMATIK K 06.0.206 Aufgabe 2 3 4 5 6 7 8 Punkte (max 8 2 3 5 4 3 3 2 Punkte Gesamtpunktzahl /30 Notenpunkte ( Bestimmen Sie die erste Ableitung folgender Funktionen: a f(x 2x 3 cos(x + x b g(x 2 3x
MATHEMATIK K1 EINSTIEGSARBEIT (OHNE GTR)
 MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
Aufgabe A6/13. Aufgabe A7/13. Aufgabe A6/14
 Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
Lösungen der Musteraufgaben 2017. Baden-Württemberg
 Baden-Württemberg: Musteraufgaben 07 Lösungen www.mathe-aufgaben.com Lösungen der Musteraufgaben 07 Baden-Württemberg allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Oktober 05 Baden-Württemberg:
Baden-Württemberg: Musteraufgaben 07 Lösungen www.mathe-aufgaben.com Lösungen der Musteraufgaben 07 Baden-Württemberg allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Oktober 05 Baden-Württemberg:
Aufgabe A1. Aufgabe A2. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 4. Aufgabe A2 Geben Sie eine Stammfunktion der Funktion mit an. Aufgabe A3 Die Funktion mit 3 3 hat die Nullstelle 1. Bestimmen Sie die weiteren Nullstellen.
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Pflichtteil Pflichtteil Pflichtteil Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
G13 KLAUSUR 1. (1) (2 VP) Bilden Sie die erste Ableitung der Funktion f mit. f(x) = e 2x+1 x
 G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x
![b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x b) [2P] 7x Lösungsvorschlag 1: f '(x) = cos 3x 6x = 6x cos 3x](/thumbs/58/42387852.jpg) K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K1 Punkte: / Note: Schnitt:.10.1 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
Aus folgt: 1; 3 Eingesetzt in : $$$$$ #! * 1 + ; # $$$$$$$ # $$$$$ 2 $$$$$! * 3 Der Bildpunkt hat die Koordinaten
 Abituraufgaben Analytische Geometrie (Pflichtteil) ab Lösung A6/ Wir stellen die gegebene Normalengleichung von in die Koordinatengleichung um und bilden. Im Gleichungssystem mit drei Unbekannten und zwei
Abituraufgaben Analytische Geometrie (Pflichtteil) ab Lösung A6/ Wir stellen die gegebene Normalengleichung von in die Koordinatengleichung um und bilden. Im Gleichungssystem mit drei Unbekannten und zwei
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktionen Gymnasium ab Klasse 10 Alexander Schwarz
 Analysis Trigonometrische Funktionen Gymnasium ab Klasse 0 Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Hinweis: Außer bei Aufgabe darf der GTR benutzt werden. Aufgabe : Bestimme ohne GTR: a) sin(405
Analysis Trigonometrische Funktionen Gymnasium ab Klasse 0 Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Hinweis: Außer bei Aufgabe darf der GTR benutzt werden. Aufgabe : Bestimme ohne GTR: a) sin(405
Passerellen Prüfungen 2009 Mathematik
 Passerellen Prüfungen 2009 Mathematik 1. Analysis: Polynom und Potenzfunktionen Gegeben sind die beiden Funktionen 21 und 32. a) Bestimmen Sie die Null, Extremal und Wendepunkte der beiden Funktionen.
Passerellen Prüfungen 2009 Mathematik 1. Analysis: Polynom und Potenzfunktionen Gegeben sind die beiden Funktionen 21 und 32. a) Bestimmen Sie die Null, Extremal und Wendepunkte der beiden Funktionen.
Vektorgeometrie. 1. Vektoren eingeben, Norm, Skalarprodukt. 2 In einem kartesischen Koordinatensystem sind die Vektoren. , v. und. gegeben.
 Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
