8.2 Integralrechnung für mehrere Variable
|
|
|
- Gottlob Winkler
- vor 6 Jahren
- Abrufe
Transkript
1 8.2 Integralrechnung für mehrere Variable Der bisher behandelte Begriff des Integrals einer Funktion mit einer einzigen Variablen lässt sich auf mehrere Arten verallgemeinern. Zunächst führt die Erweiterung der Integranden auf Funktionen mit zwei bzw. drei oder allgemein n Variablen auf den Begriff des Doppelintegrals, Dreifachintegrals und des Mehrfachintegrals. Auch werden Mehrfachintegrale in speziellen Koordinatensystemen wie Polarkoordinaten, Zylinderkoordinaten und Kugelkoordinaten eingeführt Das Doppelintegral Doppelintegral im kartesischen Koordinatensystem Gegeben sei eine Funktion f(x, y) mit dem Definitionsbereich D der Ebene R 2. Sei auch D ein Unterbereich von D, der zunächst einfachheitshalber ein Rechteckbereich sei: = [, x ] [y min, y ] < x, y min < y. In der Fortsetzung wird vorausgesetzt, dass die Funktion f im Bereich überall stetig und beschränkt ist. Der Graph der Funktion f ist bekanntlich eine Fläche Σ im Raum über dem Bereich (Figur 8.10). x z y Abbildung 8.10: Eine Funktion über einem rechteckigen Bereich. Gesucht ist das Volumen des räumlichen Körpers, der vom Rechteck (Grundfläche), von der Fläche Σ (oben), von den vertikalen Ebenen x =, x = x, y = y min, y = y (die Seiten) eingeschlossen wird. 190
2 Zur Berechnung des Volumen wird die Strecke [, x ] in n Teile = x 0 < x 1 < x 2 <... < x n = x zerlegt. Analog wird die Strecke [y min, y ] in m Teile y min = y 0 < y 1 < y 2 <... < y m = y zerlegt. Die respektiven Länge der durch die Zerlegungen produzierten Unterintervalle seien bzw. x 1 = x 1 x 0, x 2 = x 2 x 1,..., x n = x n x n 1, y 1 = y 1 y 0, y 2 = y 2 y 1,..., y m = y m y m 1. Durch diese Zerlegung wird der Bereich mit N = n m kleinen Rechtecken ij überdeckt, deren Flächeninhalte respektiv betragen ij = x i y j. Die Seiten dieser kleinen Rechtecke sind zu den Koordinatenachsen Ox und Oy parallel. Gegeben sei ein beliebiger Punkt P(x i, y j ) in einem der kleinen Rechtecke ij. Das Produkt V ij = f(x i, y j ) x i y j nähert das Volumen einer vertikalen Säule über ij an, deren Deckfläche in der durch f gegebenen Fläche liegt. Die Höhe der Säule beträgt f(x i, y j ). Wenn das Rechteck ij klein genug ist, stellt das Volumen V ij eine gute Annäherung des Raumstückes zwischen ij und der durch f gegebenen Fläche dar. Wenn wir alle elementaren Volumen V ij der Säulen summieren, erhalten wir eine Approximation des Volumen des gesamten Körpers. n m V f(x i, y j ) y j x i i=1 j=1 Streben bei der Zerlegungen der Strecken [, x ] und [y min, y ] die Anzahl Zwischenpunkte n und m gegen Unendlich, so nähert die gesamte Doppelsumme den exakten Wert des Körpersvolumen an. Auf diese Art erhält man die folgende Definition des Doppelintegrales: V = x y y min f(x, y) dy dx. = lim n m n m f(x i, y j ) y j x i (8.19) i=1 j=1 Das in (8.19) definiert Doppelintegral existiert (im mathematischen Sinne), wenn die Funktion f im Integrationsbereich B beschränkt und stetig ist. f heisst dann über integrierbar. Bei der Definition des Doppelintegrales haben wir zuerst die innere Summe für den Index j durchgeführt, dann die aussere Summe für den Index i. Somit haben wir ein Doppelintegral definiert, welches auch mit zwei nacheinanderfolgenden einfachen Integralen mit einer Variablen berechnet werden kann, das erste nach y und das zweite nach x: x y f(x, y) dy dx. y min Wird die Reihenfolge der zwei Zähler i und j vertauscht, so kann auch das Doppelintegral in der folgenden Form berechnet werden: 191
3 y x y min f(x, y) dx dy, Das Doppelintegral erfolgt also mit den zwei nacheinanderfolgenden einfachen Integralen, das innere für y, das äussere für x: y x f(x, y) dx dy. y min Die Resultate beider Doppelintegrale sind die gleichen, unabhängig von der Reihenfolge den Teilintegrale. Es gilt die Regel: Bei dem Doppelintegral einer Funktion über einem Bereich mit konstanten Grenzen spielt die Reihenfolge der nacheinanderfolgenden Teilintegrale keine Rolle, d.h.: x y f(x, y) dy dx = y min y y min x f(x, y) dx dy. (8.20) Beispiel Zu berechnen ist das Doppelintegral x=3 y=2 x=1 y= 1 (2xy y 2 + 3) dy dx, und das Doppelintegral der gleichen Funktion mit der vertauschten Reihenfolge der Integrationsvariablen. Das Symbol dydx bzw. dxdy am Ende des Ausdrucks heisst der Integrationselement des Integrals. Für einen Integrationsbereich kann der Integrationselement auch in der kurzen Form d notiert werden: f(x, y) d. Im allgemeinen Fall ist der Integrationsbereich einer Funktion nicht immer ein Rechteck. In der Fortsetzung ist der Integrationsbereich ein Stück der Ebene, welches von einer geschlossenen (aber sich selbst nicht schneidenden) Kurve Γ in der Ebene begrenzt ist (Siehe Figur 8.12). Der Körper, dessen Volumen zu bestimmen ist, wird jetzt von einer Zylinderfläche mit der Leitkurve Γ, von der Fläche Σ mit der Gleichung z = f(x, y) (oben) und von dem Integrationsbereich (unten) begrenzt. Die Tangenten and die Randkurve Γ parallel zur Oy- bzw. Ox-Achse (in der Ebene) haben die Berührungspunkte A 1, A 2, bzw. B 1 B 2 (Siehe Figur 8.12). Durch A 1 und A 2 wird die Randkurve in zwei Kurvenstücke mit den Gleichungen y = y 1 (x) für den unteren und y = y 2 (x) für den oberen Kurvenstück zerlegt. Der Bereich ist dann die Menge aller Punkte (x, y) in der Ebene R 2, für welche die Ungleichungen x x y 1 (x) y y 2 (x) (8.21) gelten. Analog könnte man für die Randkurve Γ eine Zerlegung in zwei Kurvenstücke betrachten, die durch B 1 und B 2 gehen mit den Gleichungen x = x 1 (y) für den linken und x = x 2 (y) für den rechten Kurvenstück. Der Bereich ist dann die Menge aller Punkte (x, y) in der Ebene R 2, für welche gilt 192
4 Abbildung 8.11: Volumen eines Körpers zwischen der Oxy-Ebene und dem Graphen einer Funktion. y min y y x 1 (y) x x 2 (y) (8.22) Bei der Berechnung des Doppelintegrales der Funktion f(x, y) über den Integrationsbereich kann man dann in zwei möglichen Wege vorgehen: Bei konstant gehaltenem x wird zuerst nach y über das Intervall [y 1 (x), y 2 (x)] integriert: y 2(x) y 1(x) f(x, y) dy Dann wird das Resultat nach x über das Intervall [, x ] integriert: V = f(x, y) d = x y 2(x) y 1(x) f(x, y) dy dx (8.23) Bei konstant gehaltenem y wird zuerst nach x über das Intervall [x 1 (y), x 2 (y)] integriert: x 2(y) x 1(y) f(x, y) dx Dann wird das Resultat nach y über das Intervall [y min, y ] integriert: V = f(x, y) d = y y min x 2(y) x 1(y) f(x, y) dx dy (8.24) 193
5 y x Abbildung 8.12: Integrationsbereich (in der Ebene). Bei der Berechnung des Doppelintegrales wird das Integral mit den variablen Grenzen stets zuerst bestimmt. Nach den Formeln 8.23 oder 8.24 wird also zuerst das innere, dann dass äussere Integral berechnet. Welche Reihenfolge man verwendet, hängt von der konkreten Aufgabenstellung ab. Die Klammern in 8.23 und in 8.24 können weggelassen werden. Beispiel Ein Bereich ist durch die Ungleichungen 0 y x2, 0 x 3. gegeben. Gesucht wird das Volumen des zylindrischen Körpers mit der Grundfläche, dessen Deckfläche der Graphen der Funktion f(x, y) = xy ist. Machen Sie zuerst eine Zeichnung. Beispiel Zu berechnen ist das Doppelintegral der Funktion z = x + 2y über dem Bereich, der durch die Ungleichungen 1 x 5 (x 3) 2 y 4 bestimmt ist. Machen zuerst eine Zeichnung. Ist ein Rechteckbereich und ist die Funktion f(x, y) das Produkt zweier Funktionen, die nur von x bzw. y abhängen, d.h.: f(x, y) = g(x)h(y), dann wird die Berechnung des Doppelintegrales von f über vereinfacht durch folgende mögliche Zerlegung: V = f(x, y) d = x g(x) dx y y min h(y) dy. (8.25) 194
6 Ist die Funktion f über dem gesamten Bereich konstant mit dem Wert 1, dann lässt sich das Doppelintegral V = d (8.26) interpretieren als Volumen eines vertikalen Zylinders mit der Grundfläche und der Höhe 1 oder als Flächeninhalt des Bereiches : Inhalt() = x y 2(y) y 1(x) dx dy = x (y 2 (x) y 1 (x)) dx Variablenänderung in einem Doppelintegral Bei verschiedenen Aufgaben, die zu einem Doppelintegral führen, ist die Verwendung kartesischer Koordinaten wegen Rechnenschwierigkeiten ungeeignet. Durch Übergang zu anderen, dem jeweiligen Problem angepassten Koordinaten, z.b. Polakoordinaten, können diese Aufgaben meist einfacher gelöst werden. Durch die Funktionsgleichungen x = x(u, v) y = y(u, v) (8.27) soll eine umkehrbar eindeutige Transformation zwischen den kartesischen Koordinaten x, y und den neuen Koordinaten u, v beschrieben werden. Für (8.27) sollen stetige partielle Ableitungen 1. Ordnung existieren. Gegeben sei ein Bereich in der Oxy-Ebene. Durch die umkehrbar eindeutige Transformation (8.27) wird der Bereich auf einen Bereich in der u, v-ebene abgebildet: v y u x Abbildung 8.13: Variablenänderung. Der Übergang zu den neuen Variablen u, v entspricht der Substitutionsmethode bei dem einfachen Integral. Anstelle der Berechnung des Doppelintegrals von f(x, y) über dem Bereich führen wir also durch die Variablenänderung die Berechnung des Doppelintegrales über dem neuen Integrationsbereich durch. Analog wie für eine Variablenänderung beim einfachen Integral muss bei dem Doppelintegral die Änderung des alten Flächenelements d in den neuen d berücksichtigt werden. In diesem Kontext sprechen wir von der Jacobischen Determinante der Transformation: Definition 8.7 Die Jacobische Determinante der Transformation (x, y) (u, v) ist die Funktionsdeterminante x x J(u, v) = u v (x, y) y y = (8.28) (u, v) u v 195
7 Dann wird das Flächenelement des alten Integrals durch einen Multiplikationsfaktor in das neue Flächenelement transformiert: d = J(u, v) d. Damit die Transformation (x, y) (u, v) umkehrbar eindeutig ist, muss die Jacobische Determinante J(u, v) im Bereich überall ungleich null sein. Dann erhält man die Formel der Variablenänderung beim Doppelintegral: f(x, y) d = f(x(u, v), y(u, v)) J(u, v) du dv (8.29) Bemerkung: das Integralelement d kann auch in die Form dxdy notiert werden. Analog kann auch das Flächenelement dudv in die Form d notiert werden Doppelintegral in Polarkoordinaten Die Variablenänderung in Polarkoordinaten ist zweifellos eine der nützlichsten: in der Regel wählen wir dazu die zwei Variablen (r, ϕ) an Stelle der Variablen (u, v) und es gilt: x(r, ϕ) = r cosϕ y(r, ϕ) = r sinϕ x x J(r, ϕ) = r ϕ cosϕ r sinϕ y y = sinϕ r cosϕ = r 0 r ϕ Das Doppelintegral in Polarkoordinaten folgt also mit der folgenden Formel: f(x, y) d = f(x(r, ϕ), y(r, ϕ)) r dr dϕ (8.30) phi y r x Abbildung 8.14: Variablenänderung in Polarkoordinaten. Beispiel Zu berechnen ist das Integral 1 e x2 +y 2 dxdy wo der Integrationsbereich die Kreisfläche mit der Gleichung x 2 + y 2 a 2 ist. 196
8 Beispiel Gegeben seien die Halbkugel S mit der Gleichung z = R 2 x 2 y 2 und das Zylinder C mit der Gleichung x 2 +y 2 Rx = 0. Zu bestimmen ist das Volumen des Körpers, der vom Zylinder aus der Halbkugel ausgebohrt wird Aufgaben Aufgabe Zu berechnen sind die folgenden Doppelintegrale: a) a b 0 0 xy dx dy b) 2 π/2 0 0 e x siny dx dy Aufgabe Berechnen Sie mit einem Doppelintegral das Volumen des Tetraeders mit den Eckpunkten (0, 0, 0), (1, 0, 0), (0, 1, 0) und (0, 0, 1). Aufgabe Berechnen Sie das Doppelintegral der Funktion z = x 2 y über dem Bereich, der von der Parabel y 2 = 4x, dem Kreis mit dem Radius 1 und dem Mittelpunkt in (1, 0) und der Geraden x = 2 begrenzt ist. Aufgabe Wie gross ist das Volumen des Körpers, der von den Ebenen z = 0, x = 0, y = 0, 3x + 4y 12 und der Fläche z = x 2 + y 2 begrenzt ist? Aufgabe Unter Verwendung von Polarkoordinaten ist das Doppelintegral der Funktion z = x 2 + y 2 über dem Bereich zu berechnen, der von der Kurve mit der Gleichung x 2 + y 2 = a 2 begrenzt ist, a > 0. Aufgabe Gesucht ist das Doppelintegral der Funktion z = 4(x 2 + y 2 ) 1 über dem Kreisring mit dem Mittelpunkt im Urspring und mit den Radien r 1 = 1 und r 2 = Dreifachintegrale Der Begriff des Doppelintegrales lässt sich zu Integralen in höheren Dimensionen oder Mehrfachintegralen veralgemeinern, speziell zu den Dreifachintegralen. 197
9 Dreifachintegrale in kartesischen Koordinaten Gegeben ist ein räumlicher Bereich. Ein solcher Bereich kann als Teil des euklidischen Raumes R 3 betrachtet werden, der von einer geschlossenen Fläche Σ im Raum begrenzt ist: z.b. ein Würfel, eine volle Kugel, ein volles Ellipsoid, ein Kieselstein, usw. sind mögliche Bereiche. Zu Beginn nehmen wir an, dass der Bereich ein Quader ist und durch die Ungleichungen festgelegt. x x, y min y y, z min z z. Durch ebene Schnitte parallel zu den Koordinatenebenen kann in eine Vereinigung von kleinen Würfeln ijk zerlegt werden, für i = 1, 2,...,n 1, für j = 1, 2,...,n 2 und für k = 1, 2,..., n 3. Hier sind die verwendeten Notationen analog wie beim Doppelintegral. Die Volumen der kleinen Würfel sind gegeben durch ijk = x i y j z k. Gegeben ist auch eine Funktion f(x, y, z) der drei Variablen x, y und z, die im Bereich überall stetig und beschränkt ist. Zum Bespiel kann diese Funktion die Massendichte des dreidimensionalen Körpers an der Stelle (x, y, z) darstellen. Im Würfelchen ijk wählen wir einen beliebigen Punkt (x i, y j, x k ). Ist das Würfelchen klein genug, so stellt der Wert der Funktion f an der Stelle (x i, y j, z k ) eine gute Approximation der Funktionswerte in allen anderen Punkte der Würfelchens dar. Wenn also f eine Massendichte ist, so stellt die Grösse f(x i, y j, z k ) x i y j z k eine Approximation der Masse des Würfelchens ijk dar. Um die gesamte Masse des ganzen Körpers (oder Bereich) zu erhalten, müssen wir dann die Masse aller elementaren Würfelchen ijk summieren, die bilden. Diese Summe kann auf mehrere Weise berechnet werden, je nach der Reihenfolge der Summenindizen i, j und k. Zum Beispiel: ( n 1 n 2 n3 ) M f(x i, y j, z k ) z k y j x i i=1 j=1 k=1 Schliesslich ist der exakte Wert des Dreifachintegrales durch die Grenzübergänge n 1, n 2 und n 3 erhalten, d.h. wenn die Volumen der elementaren Würfelchen ijk gegen null streben. Daraus folgt die Definition des Dreifachintegrals über einem Quader, dessen Seiten parallen zu den Koordinatenachsen sind: f(x, y, z) d. = lim ijk 0 = x y y min n 1 i=1 z n 2 j=1 f(x i, y j, z k ) z k ) y j x i = (8.31) ( n3 k=1 z min f(x, y, z) dz dy dx Das Produkt dzdydx in dieser Formel heisst Volumenelement. Manchmal schreibt man für einen Integrationsbereich das Integrationselement in der kürzeren symbolischen Form d. Nach der Formel (8.31) besteht das Dreifachintegral aus drei nacheinanderfolgenden einfachen Integralen. Das Resultat des Dreifachintegrals ist von der Reihenfolge der drei Integrale unabhängig. 198
10 Beispiel Zu bestimmen ist das Dreifachintegral I = (x 2 2yz) dz dy dx Nun betrachten wir das Dreifachintegral über einem Körper, der kein Quader mehr ist, sondern irgendwelcher Körper im Raum. Das Integral kann aber nur definiert werden, wenn dieser Körper regelmässig genug ist (Siehe Figur 8.15). Abbildung 8.15: Ein dreidimensionaler Bereich. Gegeben sei ein räumlicher Körper, der durch die Ungleichungen x x y 1 (x) y y 2 (x) z 1 (x, y) z z 2 (x, y) definiert ist. Die Grenzen des gegebenen Bereichs sind nicht konstant. Gewisse davon sind von den anderen abhängig. Dann ist das Dreifachintegral einer Funktion f(x, y, z) über dem Integrationsbereich definiert durch 199
11 f(x, y, z) d. = x y 2(x) z 2(x,y) y 1(x) z 1(x,y) f(x, y, z) dz dy dx (8.32) Das Dreifachintegral besteht aus drei nacheinanderfolgen einfachen Integralen, die wegen der Grenzenabhängigkeit vom Innen nach Aussen durchgeführt werden müssen. Die Reihenfolge der Integrale ist durch die inversen Reihenfolge der Faktoren im Volumenelement (z. B. dzdydx) gegeben. Diese Reihenfolge kann frei gewählt werden. Die Grenzen müssen aber entsprechend bestimmt werden. Beispiel Gegeben sei das Tetraeder mit den Eckpunkten (0, 0, 0), (1, 0, 0), (0, 1, 0) und (0, 0, 1). Zu bestimmen ist das Dreifachintegral über der Funktion f(x, y, z) = 1 (1 + x + y + z) 2. Ein spezieller Fall kommt mit der konstanten Funktion 1 vor. Diese Funktion kann als Massendichte des Körpers interpretiert werden, die überall 1 beträgt. Das Dreifachintegral der Massendichte über dem gesamten Körper gibt die gesamte Masse der Körpers, die numerisch auch gleich dem Volumen des Körpers ist. Dann gilt es: Volume() = dz dy dx (8.33) Variablenänderung bei einem Dreifachintegral Analog wir bei den Doppelintegralen, ist es manchmal vorteilhaft, ein anderes Koordinatensystem für ein Dreifachintegral zu wählen. Die Schwierigkeiten bei den Berechnungen können in einem geeigneten Koordinatensystem erheblich vereinfacht werden. Hierunten entwickeln wir eine Formel, die uns erlaubt, ein Dreifachintegral in einem anderen System zu berechnen. Gegeben ist eine invertierbare Transformation x = x(u, v, w), y = y(u, v, w), y = z(u, v, w), (8.34) die erlaubt, die kartesischen Koordinaten(x, y, z) in einem anderen Koordinatensystem(u, v, w) auszudrücken. In der Transformation (8.34) wird vorausgesetzt, dass alle partielle Ableitungen existieren und stetig sind. Sei auch ein Bereich in R 3, der regelmässig genug ist. Durch die Koordinatenänderung (8.34) wird der Bereich in einen neuen räumlichen Bereich im (u, v, w)-koordinatensystem transformiert. An Stelle der Berechnung des Dreifachintegrales einer Funktion f(x, y, z) über dem Bereich, können wir eine Variablenänderung durchführen, um das Integral über dem neuen Bereich zu berechnen. Dazu ist es notwendig, bei der Transformation die entsprechende Änderung des alten Volumenelements dv = dz dy dx in das neue dv = dw dv du zu berücksichtigen. 200
12 Definition 8.8 Als Jacobische Determinante der Transformation (x, y, z) (u, v, w) bezeichnen wir die Funktionsdeterminante x x x u v w J(u, v, w) = y y y (x, y, z) = (8.35) u v w (u, v, w) z z z u v w Dann erhalten wir das Volumenelement im neuen Koordinatensystem mit der folgenden Multiplikation: dv = J(u, v, w) dv. Damit die Koordinatentransformation(x, y, z) (u, v, w) invertierbar ist, muss die Jacobische Determinante J(u, v, w) über dem ganzen Bereich ungleich Null sein, und es gilt die Formel der Variablenänderung beim Dreifachintegral: f(x, y, z) dv = f(x(u, v, w), y(u, v, w), z(u, v, w)) J(u, v, w) du dv dw (8.36) Bemerkung: das alte Volumenelement dv kann auch dxdy dz notiert werden, und das neue dv auch du dv dw, wo die Reihenfolge der Faktoren jeweils frei ist und der Reihenfolge der drei einfachen Integralen entspricht. Zwei räumliche Koordinatensysteme sind speziell zu erwähnen, die am häufigsten benutzt werden: das Kugelkoordinatensystem und das Zylinderkoordinatensystem Dreifachintegral in Kugelkoordinaten Im Kugelkoordinatensystem ist ein Punkt P im Raum (ausser dem Ursprung) durch die drei folgenden Grösse bestimmt (Siehe Figur 8.16): Die euklidische Distanz r zwischen P und dem Ursprung: r = OP ; Der Winkel ϕ in der Oxy-Ebene zwischen der Projektion der Strecke OP und der Achse Ox ; Der Winkel θ zwischen der Strecke OP und der vertikalen Achse Oz. Die kartesischen Koordinaten (x, y, z) des Punkts P können im Kugelkoordinatensystem mit den folgenden Gleichungen ausgedrückt werden: x = r cosϕsinθ y = r sinϕsinθ z = r cosθ (8.37) 201
13 z y x Abbildung 8.16: Kugelkoordinaten. Die Transformation (r, ϕ, θ) (x, y, z) ist invertierbar und es gilt: r = x 2 + y 2 + z 2 tanϕ = tanθ = x y x2 + y 2 z (8.38) Die Funktionaldeterminante ist nach der Formel 8.35 gegeben durch cosϕsinθ r sinϕsinθ r cosϕcosθ (x, y, z) J(r, ϕ, θ) = (r, ϕ, θ) = sinϕsinθ r cosϕsinθ r sinϕcosθ cosθ 0 sinθ = r 2 sinθ (8.39) Dann kann das Dreifachintegral im Kugelkoordinatensystem mit der folgenden Formel berechnet werden: f(x, y, z) dv = θ 2 θ 1 ϕ 2 ϕ 1 r 2 r 1 f(x(r, ϕ, θ), y(r, ϕ, θ), z(r, ϕ, θ)) r 2 sinθ dr dϕdθ (8.40) 202
14 Beispiel Bestimmen Sie das Integral über der zentrierten Kugel mit dem Radius R. 1 x2 + y 2 + z dv Dreifachintegral in Zylinderkoordinaten Im Zylinderkoordinatensystem ist ein Punkt P des Raums (ausser dem Ursprung) durch die drei folgenden Grösse bestimmt (Siehe Figur 8.17): Die Distanz r zwischen dem Punkt P und der vertikalen Achse Oz ; Der Winkel ϕ in der Oxy-Ebene zwischen der Projektion der Strecke OP und der Achse Ox ; Die Höhe z des Punkts P, d.h. seine z-koordinate. z y x Abbildung 8.17: Zylinderkoordinaten. In diesem Koordinatensystem werden die kartesischen Koordinaten (x, y, z) von P durch die folgenden Gleichungen ausgedrückt: x y z = r cosϕ = r sinϕ = z (8.41) 203
15 Die Koordinatentransformation (r, ϕ, z) (x, y, z) ist invertierbar und es gilt: r = x 2 + y 2 tanϕ = y x (8.42) z = z Die Funktionaldeterminante der Transformation (nach der Formel 8.35) ist gegeben durch cosϕ r sinϕ 0 (x, y, z) J(r, ϕ, z) = (r, ϕ, z) = sinϕ r cosϕ 0 = r (8.43) Dann berechnet sich ein Dreifachintegral in Zylinderkoordinaten mit der Formel f(x, y, z) dv = z 2 z 1 ϕ 2 ϕ 1 r 2 r 1 f(x(r, ϕ, z), y(r, ϕ, z), z(r, ϕ, z)) r dr dϕ dz (8.44) Bemerkung: die Variable r hat in Zylinderkoordinaten eine ganz andere Bedeutung als in Kugelkoordinaten! Beispiel Bestimmen das Volumen des räumlichen Körpers über der Oxy-Ebene, der durch das Paraboloid mit der Gleichung z = x 2 + y 2 und das Zylinder mit der Gleichung x 2 + y 2 = a 2 begrenzt ist. Beginnen Sie mit einer Zeichnung der Körpers. ( π 2 a4 ) Einige Anwendungen Es gibt zahlreiche Anwendungen der Mehrfachintegrale in den Wissenschaften und der Technologie (Berechnungen von Massen, elektrischen Ladungen, Energien, usw.). Hier wird nur das Beispiel der Masse und des Schwerpunkts eines räumlichen Körpers zitiert. Gegeben ist ein physikalischer Körper im Raum R 3 mit dem Volumen V und der Masse m. Sei P ein beliebiger Punkt des Körpers, der einem kleinen elementaren Teilbereich gehört (z.b. kann der elementare Teilbereich ein Würfelchen sein). Das Volumen des Teilbereichs bezeichnen wir mit V und seine Masse mit m. Die örtliche Massendichte des Körpers in Punkt P kann durch die folgende Formel definiert werden: m ρ = lim 0 V 204
16 Wenn der Körper homogen ist, ist die Massendichte von dem gewählten Punkt P unabhängig. Sie ist also konstant und es gilt die einfache Formel m = ρ V. Wenn der Körper inhomogen ist, ist die Massendichte ρ = ρ(x, y, z) nicht konstant. Dann muss die gesamte Masse durch Integration der Massendichte über dem ganzen Körper berechnet werden: m = ρ(x, y, z) dv (8.45) Beispiel Ein Hohlzylinder aus Kunststoff, dessen Achse in der z-achse zwischen den Höhen z = 1 und z = 4 liegt, hat den inneren Radius R 1 = 2, den äusseren Radius R 2 = 3. Der Kunststoff ih inhomogen und die Dichte ist ρ = 1 z(x 2 + y 2. Zu bestimmen ist die Masse des Hohlzylinders. ) Die Koordinaten des Schwerpunkts S eines räumlichen Körpers können auch mit Hilfe eines Dreifachintegrales bestimmt werden. Durch physikalische Argumente (u.a. der Momentensatz) kann gezeigt werden, dass die Koordinaten (x S, y S, z S ) des Schwerpunkts sind x S = 1 x dv ; y S = 1 y dv ; z S = 1 z dv. (8.46) V V V Beispiel Ein räumlicher Körper ist von der Fläche mit der Gleichung z = x 2 +y 2 (Rotationsparaboloid) und den Ebenen x = 0, y = 0 und z = 1 begrenzt. Zu bestimmen sind die Koordinaten seines Schwerpunkts. 205
17 Aufgaben Aufgabe Zu bestimmen sind die Dreifachintegrale a) xe y+z dz dy dx b) (xy + yz + xz) dz dy dx Aufgabe Zu berechnen ist das Dreifachintegral x2 + y 2 dv, über dem Bereich in R 3, der durch die Flächen mit den Gleichungen x = 1, y = 0, y = x, z = 0 und z = x 2 + y 2 begrenzt ist. Machen Sie auch von diesem Körper eine Zeichnung. Aufgabe Ein Körper ist von der zylindrischen Fläche mit der Gleichung x 2 + y 2 = 4 und den Ebenen x + y + z 6 = 0 und z = 0 begrenzt. Machen von diesem Körper eine Zeichnung und berechnen Sie sein Volumen. Aufgabe Wie gross ist das Volumen des räumlichen Körpers, der von den Ebenen x = 0, x = 1, y = 0, z = 0 und x + y + z = 2 begrenzt ist? MAchen Sie auch davon eine Zeichnung. Aufgabe Ein Körper ist von der Kugel mit der Gleichung z = 1 x 2 y 2 und vom Kegel mit der Gleichung x 2 + y 2 = 3z 2 begrenzt. Bestimmen Sie sein Volumen mit Hilfe eines Dreifachintegrales in einem geeigneten Koordinatensystem. Aufgabe Eine inhomogene Halbkugel ist von den Flächen mit den Gleichungen x 2 + y 2 + z 2 = 4 und z = 0 begrenzt. Die Dichte des Stoffes an einer Stelle (x, y, z) ist ρ = 1 4 z. Wie gross ist die Masse des Körpers? Aufgabe Zu bestimmen sind die Koordinaten des Schwerpunkts der homogenen Halbkugel, die von den Flächen mit den Gleichungen x 2 + y 2 + z 2 = 1 und z = 0 begrenzt ist. Aufgabe An einer Höhe z weniger als [m] kann die Luftdichte δ in [kg/m 3 der Erdenatmosphäre mit der Formel δ = 1.2 ( )z + ( )z 2 angenähert werden. Zu bestimmen ist eine Schätzung der Masse einer vertikalen zylindrischen Luftsäule 10 km hoch mit dem Radius 3 [m]. 206
18 Aufgabe In dieser Aufgabe ist die Erde als eine perfekte Kugel mit dem Radius 6370 [km] approximiert (was nicht exakt ist). Die Luftdichte δ der Atmosphäre an einer Distanz ρ vom Erdenzentrum kann mit der folgenden Formel angenähert werden (in [kg/m 3 ]): für 6370 ρ 6373 [km]. δ = ( )ρ, 1. Zu bestimmen ist die Atmosphärenmasse zwischen dem Boden und der Höhe 3000 m. 2. Die gesamte Masse zwischen dem Boden und der Höhe 100 km beträgt ca [kg]. Wie gross ist der prozentuale Anteil der Luftmasse, die in den niedrigen Schichten (d.h.: m) der Atmosphäre konzentriert ist? 207
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
Zylinderkoordinaten 1 E1. Ma 2 Lubov Vassilevskaya
 Zylinderkoordinaten E E E3 Berechnung in beliebigen krummlinigen Koordinaten Die Koordinaten sind durch die Beziehungen definiert: x x u, v, w, y y u, v, w, z z u, v, w Für sie sollen stetige partielle
Zylinderkoordinaten E E E3 Berechnung in beliebigen krummlinigen Koordinaten Die Koordinaten sind durch die Beziehungen definiert: x x u, v, w, y y u, v, w, z z u, v, w Für sie sollen stetige partielle
Mehrfachintegrale 1-E1. Ma 2 Lubov Vassilevskaya
 Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Räumliche Bereichsintegrale mit Koordinatentransformation
 Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
Integralrechnung für Funktionen mehrerer Variabler
 Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Serie 6. x 2 + y 2, 0 z 4.
 Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form. ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können.
 142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form
 155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
Mehrdimensionale Integralrechnung 1
 Mehrdimensionale Integralrechnung Im - dimensionalen Fall wurde die Integralrechnung eingeführt, um Flächen unter Kurven zu berechnen. Eine ähnliche Fragestellung führt uns auf die mehrdimensionale Integralrechnung.
Mehrdimensionale Integralrechnung Im - dimensionalen Fall wurde die Integralrechnung eingeführt, um Flächen unter Kurven zu berechnen. Eine ähnliche Fragestellung führt uns auf die mehrdimensionale Integralrechnung.
1 Definition und Konstruktion vektorwertiger Funktionen und Funktionen mehrerer Variabler
 Zusammenfassung Kapitel IV: Funktionen mehrerer Veränderlicher und vektorwertige Funktionen 1 Definition und Konstruktion vektorwertiger Funktionen und Funktionen mehrerer Variabler Definition vektorwertige
Zusammenfassung Kapitel IV: Funktionen mehrerer Veränderlicher und vektorwertige Funktionen 1 Definition und Konstruktion vektorwertiger Funktionen und Funktionen mehrerer Variabler Definition vektorwertige
Höhere Mathematik Vorlesung 5
 Höhere Mathematik Vorlesung 5 März 2017 ii Gibt es etwa eine bessere Motivation als den rfolg?. Ion Tiriac 5 Das Dreifachintegral Ähnlich wie im zweindimensionalen Fall definieren wir das Dreifachintegral
Höhere Mathematik Vorlesung 5 März 2017 ii Gibt es etwa eine bessere Motivation als den rfolg?. Ion Tiriac 5 Das Dreifachintegral Ähnlich wie im zweindimensionalen Fall definieren wir das Dreifachintegral
Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen. D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Bemerkungen:
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen emerkungen: Die Aufgaben der Serie 6 bilden den Fokus der Übungsgruppen vom 3. März/2. April..
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen emerkungen: Die Aufgaben der Serie 6 bilden den Fokus der Übungsgruppen vom 3. März/2. April..
Höhere Mathematik Vorlesung 4
 Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Vorlesung: Analysis II für Ingenieure. Wintersemester 07/08. Michael Karow. Thema: Transformationsformel für Gebietsintegrale
 Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 15
 5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
Mathematischer Vorkurs für Physiker WS 2012/13 Vorlesung 8
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 212/1 Vorlesung 8 Integration über ebene Bereiche Wir betrachten einen regulären Bereich in der x-y Ebene, der einfach zusammenhängend ist.
Mathematik II Frühlingssemester 2019 Kapitel 10: Mehrdimensionale Integrale
 Mathematik II Frühlingssemester 2019 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 40 10. Mehrdimensionale Integrale Doppelintegrale Definition und geometrische Deutung von Doppelintegralen
Mathematik II Frühlingssemester 2019 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 40 10. Mehrdimensionale Integrale Doppelintegrale Definition und geometrische Deutung von Doppelintegralen
Mehrdimensionale Integration
 Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
Kapitel C Mehrdimensionale Integration h s r h h r h r Inhalt dieses Kapitels C000 1 Der Satz von Fubini 3 Aufgaben und Anwendungen 1 Vertauschen von Integral und Reihe Mehrdimensionale Integration #Der
Schwerpunkte des Kapitels Differentialrechnung für skalare Felder Integralrechnung für skalare Felder Kurvenintegrale. Aufgabe 9.2 Aufgabe 9.
 9. Mehrdimensionale Analysis 1/42 9. Mehrdimensionale Analysis Differentialrechnung für skalare Felder 2/42 Schwerpunkte des Kapitels Differentialrechnung für skalare Felder Integralrechnung für skalare
9. Mehrdimensionale Analysis 1/42 9. Mehrdimensionale Analysis Differentialrechnung für skalare Felder 2/42 Schwerpunkte des Kapitels Differentialrechnung für skalare Felder Integralrechnung für skalare
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
D-MAVT/D-MATL FS 2018 Dr. Andreas Steiger Analysis IILösung - Serie1
 D-MAVT/D-MATL FS 8 Dr. Andreas Steiger Analysis IILösung - Serie. Das Volumenelement der Koordinaten, welche in der untenstehenden Abbildung definiert sind, ist gegeben durch z Q Ρ Α Β y (a) ϱ cos β dϱ
D-MAVT/D-MATL FS 8 Dr. Andreas Steiger Analysis IILösung - Serie. Das Volumenelement der Koordinaten, welche in der untenstehenden Abbildung definiert sind, ist gegeben durch z Q Ρ Α Β y (a) ϱ cos β dϱ
Kapitel 4. Mehrfachintegrale. 4.1 Erinnerung an Integrationsrechnung. Geg.: Funktion f : I R, I R ein Intervall, zunächst: f(x) > 0 x I.
 Kapitel 4 Mehrfachintegrale 4.1 Erinnerung an Integrationsrechnung 4.1.1 estimmtes Integral als Fläche Geg.: Funktion f : I R, I R ein Intervall, zunächst: f(x) > 0 x I. Ges.: Fläche F zwischen dem Graphen
Kapitel 4 Mehrfachintegrale 4.1 Erinnerung an Integrationsrechnung 4.1.1 estimmtes Integral als Fläche Geg.: Funktion f : I R, I R ein Intervall, zunächst: f(x) > 0 x I. Ges.: Fläche F zwischen dem Graphen
7 Differential- und Integralrechung für Funktionen
 Differential- und Integralrechung für Funktionen mehrer Veränderlicher 7 7 Differential- und Integralrechung für Funktionen mehrer Veränderlicher Die Differential- und Integralrechung für Funktionen mehrer
Differential- und Integralrechung für Funktionen mehrer Veränderlicher 7 7 Differential- und Integralrechung für Funktionen mehrer Veränderlicher Die Differential- und Integralrechung für Funktionen mehrer
Übungsaufgaben zu Höherer Analysis, WS 2002/03. Aufgaben zu Doppelintegralen.
 Übungsaufgaben zu Höherer Analysis, WS 2002/03 Aufgaben zu Doppelintegralen. (A) Bestimmen Sie den Schwerpunkt des Gebietes 0 x π 2, 0 y cos x. (Antwort: s = ( π 2, π 8 )) (A2) Berechnen Sie die folgenden
Übungsaufgaben zu Höherer Analysis, WS 2002/03 Aufgaben zu Doppelintegralen. (A) Bestimmen Sie den Schwerpunkt des Gebietes 0 x π 2, 0 y cos x. (Antwort: s = ( π 2, π 8 )) (A2) Berechnen Sie die folgenden
1 = z = y + e. Nabla ist ein Vektor, der als Komponenten keine Zahlen sondern Differentiationsbefehle
 Anmerkung zur Notation Im folgenden werden folgende Ausdrücke äquivalent benutzt: r = x y = x 1 x 2 z x 3 1 Der Vektoroperator Definition: := e x x + e y y + e z z = x y z. Nabla ist ein Vektor, der als
Anmerkung zur Notation Im folgenden werden folgende Ausdrücke äquivalent benutzt: r = x y = x 1 x 2 z x 3 1 Der Vektoroperator Definition: := e x x + e y y + e z z = x y z. Nabla ist ein Vektor, der als
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 11. Juli 2016 Ableitungen im Höherdimensionalen Im Eindimensionalen war die Ableitung f (x 0 ) einer Funktion f : R R die
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 11. Juli 2016 Ableitungen im Höherdimensionalen Im Eindimensionalen war die Ableitung f (x 0 ) einer Funktion f : R R die
Musterlösungen Serie 3
 -MAVT -MATL Analysis II FS 1 Prof. r. P. Biran Musterlösungen Serie 1. Frage 1 Berechnen Sie wobei [, 1] [, 1]. xe x+y df, e 1 1 e + 1 xe x+y df Mit einer partiellen Integration erhalten wir xe x+y dydx
-MAVT -MATL Analysis II FS 1 Prof. r. P. Biran Musterlösungen Serie 1. Frage 1 Berechnen Sie wobei [, 1] [, 1]. xe x+y df, e 1 1 e + 1 xe x+y df Mit einer partiellen Integration erhalten wir xe x+y dydx
12 Integralrechnung, Schwerpunkt
 Dr. Dirk Windelberg Leibniz Universität Hannover Mathematik für Ingenieure Mathematik http://www.windelberg.de/agq Integralrechnung, Schwerpunkt Schwerpunkt Es sei ϱ die Dichte innerhalb der zu untersuchenden
Dr. Dirk Windelberg Leibniz Universität Hannover Mathematik für Ingenieure Mathematik http://www.windelberg.de/agq Integralrechnung, Schwerpunkt Schwerpunkt Es sei ϱ die Dichte innerhalb der zu untersuchenden
9 Integralrechnung für Funktionen mehrerer Variabler Integration über ebene Bereiche in kartesischen Koordinaten
 Inhaltsverzeichnis 6 Integralrechnung 6. Einführung.............................................. 6. Unbestimmte Integrale........................................ 6.. Unbestimmte Integrale der rundfunktionen.......................
Inhaltsverzeichnis 6 Integralrechnung 6. Einführung.............................................. 6. Unbestimmte Integrale........................................ 6.. Unbestimmte Integrale der rundfunktionen.......................
12. Mehrfachintegrale
 - 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
- 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
Prüfungsklausur Höhere Mathematik II (22. Juli 2006) - Lösungen zum Theorieteil - für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM
 Prüfungsklausur Höhere Mathematik II (. Juli 6) für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM - Lösungen zum Theorieteil - Aufgabe 1: In der x-y-ebene seien die Mengen A {(x, y) : x } und
Prüfungsklausur Höhere Mathematik II (. Juli 6) für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM - Lösungen zum Theorieteil - Aufgabe 1: In der x-y-ebene seien die Mengen A {(x, y) : x } und
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 9: Mehrdimensionale Integrale Prof. Dr. Erich Walter Farkas Mathematik I+II, 9. Mehrdim. Int. 1 / 39 1 Doppelintegrale 2 Prof.
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 9: Mehrdimensionale Integrale Prof. Dr. Erich Walter Farkas Mathematik I+II, 9. Mehrdim. Int. 1 / 39 1 Doppelintegrale 2 Prof.
1 Lösungsskizzen zu den Übungsaufgaben
 Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
D-MAVT/D-MATL FS 2018 Dr. Andreas Steiger Analysis IILösung - Serie16. y(u, v) = 2u
 -MAVT/-MATL FS 28 r. Andreas Steiger Analysis IILösung - Serie6. ie Koordinatentransformation xu, v = 2v, yu, v = 2u bildet Kreise auf Kreise ab. a Wahr. b Falsch. ie Transformation entspricht einer Stauchung
-MAVT/-MATL FS 28 r. Andreas Steiger Analysis IILösung - Serie6. ie Koordinatentransformation xu, v = 2v, yu, v = 2u bildet Kreise auf Kreise ab. a Wahr. b Falsch. ie Transformation entspricht einer Stauchung
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Lösungen zu Serie 8. F n ds = (0 + 0) dx dy = 0. (1 ( 1)) dx dy = 2
 D-EDW, D-HET, D-UY Mathematik II F Dr. Ana annas Lösungen zu erie 8. a) Wir berechnen den Fluss von F mittels Green F n ds + ) dx dy und die Zirkulation F T ds )) dx dy wobei Vol ) den Flächeninhalt des
D-EDW, D-HET, D-UY Mathematik II F Dr. Ana annas Lösungen zu erie 8. a) Wir berechnen den Fluss von F mittels Green F n ds + ) dx dy und die Zirkulation F T ds )) dx dy wobei Vol ) den Flächeninhalt des
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Serie 8: Satz von Green und Oberflächenintegrale
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 8: Satz von Green und Oberflächenintegrale Bemerkungen: Die Aufgaben der Serie 8 bilden den Fokus der Übungsgruppen vom./3. April.. Den Satz
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 8: Satz von Green und Oberflächenintegrale Bemerkungen: Die Aufgaben der Serie 8 bilden den Fokus der Übungsgruppen vom./3. April.. Den Satz
Serie 5. Figure 1: 1.a)
 Analsis D-BAUG Dr. Cornelia Busch FS 16 Serie 5 1. Bei den folgenden Integralen ist die Reihenfolge der Integrationen umzukehren: Die innere Variable soll zur äusseren werden und umgekehrt. Wie lautet
Analsis D-BAUG Dr. Cornelia Busch FS 16 Serie 5 1. Bei den folgenden Integralen ist die Reihenfolge der Integrationen umzukehren: Die innere Variable soll zur äusseren werden und umgekehrt. Wie lautet
Serie 9: Der Satz von Green und Parametrisierungen von Flächen im Raum
 : Der Satz von Green und Parametrisierungen von Flächen im Raum Bemerkung: Die Aufgaben der sind der Fokus der Übungsstunden vom 6./8. April.. Überprüfung des Satzes von Green Der Satz von Green besagt
: Der Satz von Green und Parametrisierungen von Flächen im Raum Bemerkung: Die Aufgaben der sind der Fokus der Übungsstunden vom 6./8. April.. Überprüfung des Satzes von Green Der Satz von Green besagt
2.3 Gekrümmte Oberflächen
 2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
Integration über allgemeine Integrationsbereiche.
 Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Analysis II für Ingenieure Übersicht: Integration. 1 Kurvenintegral über ein Skalarfeld
 Analysis II für Ingenieure Übersicht: Integration 1 Kurvenintegral über ein Skalarfeld 1.1 erechnung c f ds = b a f ( c(t) ) c(t) dt 1. Kurve c parametrisieren: c : [a, b] R n, t c(t). 2. c(t) und dann
Analysis II für Ingenieure Übersicht: Integration 1 Kurvenintegral über ein Skalarfeld 1.1 erechnung c f ds = b a f ( c(t) ) c(t) dt 1. Kurve c parametrisieren: c : [a, b] R n, t c(t). 2. c(t) und dann
Probeklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
BERGISCHE UNIVERSITÄT WUPPERTAL 21717 Fakultät 4 - Mathematik und Naturwissenschaften Prof N V Shcherbina Dr T P Pawlaschyk wwwkanauni-wuppertalde Probeklausur zur Analysis 2, SoSe 217 Hinweis Die Lösungen
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt
 Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
f(x, y) = x 2 4x + y 2 + 2y
 7. Februar Lösungshinweise Theorieteil Aufgabe : Bestimmen Sie die Niveaumengen (Höhenlinien) der Funktion f(x, y) = x 4x + y + y und skizzieren Sie das zugehörige Höhenlinienbild im kartesischen Koordinatensystem
7. Februar Lösungshinweise Theorieteil Aufgabe : Bestimmen Sie die Niveaumengen (Höhenlinien) der Funktion f(x, y) = x 4x + y + y und skizzieren Sie das zugehörige Höhenlinienbild im kartesischen Koordinatensystem
Analysis II für M, LaG/M, Ph 12. Übungsblatt
 Analysis II für M, La/M, Ph. Übungsblatt Fachbereich Mathematik WS / Prof. Dr. Christian Herrmann 8.. Vassilis regoriades Horst Heck ruppenübung Aufgabe. erechnen Sie das ebietsintegral sin (x y) d, wobei
Analysis II für M, La/M, Ph. Übungsblatt Fachbereich Mathematik WS / Prof. Dr. Christian Herrmann 8.. Vassilis regoriades Horst Heck ruppenübung Aufgabe. erechnen Sie das ebietsintegral sin (x y) d, wobei
Anleitungsaufgaben zu. Analysis III für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2011/12 Dr. K. Rothe Anleitungsaufgaben zu Analysis III für Studierende der Ingenieurwissenschaften Aufgabe 1: Für die folgenden Funktionen f : IR 2
Fachbereich Mathematik der Universität Hamburg WiSe 2011/12 Dr. K. Rothe Anleitungsaufgaben zu Analysis III für Studierende der Ingenieurwissenschaften Aufgabe 1: Für die folgenden Funktionen f : IR 2
R 1. 3 x 1+9. y 1 (x) = x 2, y 2(x) = x 3, y 3(x) = p x
 Studiengang: ME/MB Semester: SS 9 Analysis II Serie: Thema: bestimmtes Integral. Aufgabe: Berechnen Sie den Wert der folgenden bestimmten Integrale: d) g) j) R (x e x )dx, b) R sinx cos7xdx, e) R e R p
Studiengang: ME/MB Semester: SS 9 Analysis II Serie: Thema: bestimmtes Integral. Aufgabe: Berechnen Sie den Wert der folgenden bestimmten Integrale: d) g) j) R (x e x )dx, b) R sinx cos7xdx, e) R e R p
KAPITEL 9. Doppelintegrale
 KAPITEL 9 Doppelintegrale 9.1 Doppelintegrale............................. 305 9.2 erechnung des Doppelintegrals................... 309 9.3 Transformation von Doppelintegralen................ 321 9.4 Zusammenfassung
KAPITEL 9 Doppelintegrale 9.1 Doppelintegrale............................. 305 9.2 erechnung des Doppelintegrals................... 309 9.3 Transformation von Doppelintegralen................ 321 9.4 Zusammenfassung
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
(Analysis und lineare Algebra) im Sommersemester 2018 2. Juli 2018 1/1 Wir geben einige wesentliche Sätze über bestimmte Integrale an, deren Beweise man in den Standardlehrbüchern der Analysis findet.
Mathematik II Lösung 9. Lösung zu Serie 9
 D-EDW, D-HEST, D-USYS Dr. Ana annas 5. April 6 Lösung zu Serie 9. Überprüfung des Satzes von Green Für die Kreisscheibe mit adius a um Null gilt, dass die äußere Einheitsnormalen in einem Punkt (x, y auf
D-EDW, D-HEST, D-USYS Dr. Ana annas 5. April 6 Lösung zu Serie 9. Überprüfung des Satzes von Green Für die Kreisscheibe mit adius a um Null gilt, dass die äußere Einheitsnormalen in einem Punkt (x, y auf
Ferienkurs Elektrodynamik WS 11/12 Übungsblatt 1
 Ferienkurs Elektrodynamik WS / Übungsblatt Tutoren: Isabell Groß, Markus Krottenmüller, Martin Ibrügger 9.3. Aufgabe - Geladene Hohlkugel In einer Hohlkugel befindet sich zwischen den Radien r und r eine
Ferienkurs Elektrodynamik WS / Übungsblatt Tutoren: Isabell Groß, Markus Krottenmüller, Martin Ibrügger 9.3. Aufgabe - Geladene Hohlkugel In einer Hohlkugel befindet sich zwischen den Radien r und r eine
Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang. Sommersemester
 Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 8.6.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 8.6.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
x + y + z = 6, x = 0, z = 0, x + 2y = 4, indem Sie das Volumen als Dreifachintegral schreiben.
 Übungen (Aufg. u. Lösungen) zur Ingenieur-Mathematik II SS 8 Blatt 1 3.7.8 Aufgabe 47: Berechnen Sie das Volumen des von den folgenden Flächen begrenzten Körpers x + y + z 6, x, z, x + y 4, indem Sie das
Übungen (Aufg. u. Lösungen) zur Ingenieur-Mathematik II SS 8 Blatt 1 3.7.8 Aufgabe 47: Berechnen Sie das Volumen des von den folgenden Flächen begrenzten Körpers x + y + z 6, x, z, x + y 4, indem Sie das
Technische Universität Berlin
 Technische Universität Berlin Fakultät II Institut für Mathematik WS 7/8 W. Stannat, A. Gündel-vom ofe..8 Februar Klausur Analysis II für Ingenieurwissenschaften Lösungsskizze Analysis II für Ingenieurwissenschaften
Technische Universität Berlin Fakultät II Institut für Mathematik WS 7/8 W. Stannat, A. Gündel-vom ofe..8 Februar Klausur Analysis II für Ingenieurwissenschaften Lösungsskizze Analysis II für Ingenieurwissenschaften
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
Rückblick auf die letzte Vorlesung
 Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
Höhere Mathematik 3 Herbst 2014
 IMNG, Fachbereich Mathematik Universität Stuttgart Prof. Dr. K. Höllig Höhere Mathematik 3 Herbst 214 Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind. (i) rot(2
IMNG, Fachbereich Mathematik Universität Stuttgart Prof. Dr. K. Höllig Höhere Mathematik 3 Herbst 214 Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind. (i) rot(2
Lösungen zu Koordinatentrafo und Integration im R n
 Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Nachklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
Mathematik II für MB und ME
 Übungsaufgaben Serie : Integralrechnung. Berechnen Sie folgende Integrale 3 + 2 2 d, b) d) sin(3) cos(3) d, e) Mathematik II für MB und ME e a d, c) 6 d, f) + 2 2. Berechnen Sie durch geeignete Substitution
Übungsaufgaben Serie : Integralrechnung. Berechnen Sie folgende Integrale 3 + 2 2 d, b) d) sin(3) cos(3) d, e) Mathematik II für MB und ME e a d, c) 6 d, f) + 2 2. Berechnen Sie durch geeignete Substitution
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 11: e Prof. Dr. Erich Walter Farkas Mathematik I+II, 11. Linienintegrale 1 / 39 1 Ein einführendes Beispiel 2 3 Prof. Dr. Erich
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 11: e Prof. Dr. Erich Walter Farkas Mathematik I+II, 11. Linienintegrale 1 / 39 1 Ein einführendes Beispiel 2 3 Prof. Dr. Erich
24 Mehrdimensionale Integrale
 24 Mehrdimensionale Integrale Jörn Loviscach Versionsstand: 20. März 2012, 16:00 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html
24 Mehrdimensionale Integrale Jörn Loviscach Versionsstand: 20. März 2012, 16:00 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen in der Vorlesung. Videos dazu: http://www.j3l7h.de/videos.html
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Ferienkurs Analysis 3 für Physiker. Integration im R n
 Ferienkurs Analysis 3 für Physiker Integration im R n Autor: Benjamin Rüth Stand: 16. ärz 214 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Definition des Riemann-Integrals über Quadern 3
Ferienkurs Analysis 3 für Physiker Integration im R n Autor: Benjamin Rüth Stand: 16. ärz 214 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Definition des Riemann-Integrals über Quadern 3
8 Beispiele von Koordinatentransformationen
 8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
Mehrdimensionale Analysis
 KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
1.3. DAS COULOMBSCHE GESETZ, ELEKTROSTATISCHES FELD 9
 8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
Klausur HM II/III F 2003 HM II/III : 1
 Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
Trägheitsmomente spielen damit bei Drehbewegungen eine ähnliche Rolle wie die Masse bei Translationsbewegungen.
 Anwendungen der Integralrechnung 1 1 Trägheitsmomente 1. 1 Einleitung, Definition Körper fallen im Vakuum gleich schnell und sie gleiten auf einer reibungsfreien schiefen Ebene gleich schnell. Sie rollen
Anwendungen der Integralrechnung 1 1 Trägheitsmomente 1. 1 Einleitung, Definition Körper fallen im Vakuum gleich schnell und sie gleiten auf einer reibungsfreien schiefen Ebene gleich schnell. Sie rollen
1 Integrale von Funktionen in mehreren Variablen
 $Id: integral.tex,v.0 009//0 :4:35 hk Exp $ Integrale von Funktionen in mehreren Variablen.3 Integration über Jordan-meßbare Mengen Als ein zweites Beispiel der Integration über Jordan-meßbare Mengen wollen
$Id: integral.tex,v.0 009//0 :4:35 hk Exp $ Integrale von Funktionen in mehreren Variablen.3 Integration über Jordan-meßbare Mengen Als ein zweites Beispiel der Integration über Jordan-meßbare Mengen wollen
Ordnen Sie die Bilder den zugehörigen Funktionen z = f(x, y) zu:
 6. Februar 2012 Lösungshinweise Theorieteil Aufgabe 1: Die folgenden Bilder zeigen drei Niveaumengen N 0 {(x, y) R 2 : f(x, y) 0}: Ordnen Sie die Bilder den zugehörigen Funktionen z f(x, y) zu: (a) z (x
6. Februar 2012 Lösungshinweise Theorieteil Aufgabe 1: Die folgenden Bilder zeigen drei Niveaumengen N 0 {(x, y) R 2 : f(x, y) 0}: Ordnen Sie die Bilder den zugehörigen Funktionen z f(x, y) zu: (a) z (x
Mehrdimensionale Integralrechnung 2
 Mehrdimensionale Integralrechnung Quiz Wir wollen die Dynamik zweier Teilchen beschreiben, die über ein hoch elastisches Seil verbunden sind und sich wild im Raum bewegen! Ein Kollege schlägt dazu vor
Mehrdimensionale Integralrechnung Quiz Wir wollen die Dynamik zweier Teilchen beschreiben, die über ein hoch elastisches Seil verbunden sind und sich wild im Raum bewegen! Ein Kollege schlägt dazu vor
Integralrechnung für GLET
 Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
Die nummerierten Felder bitte mithilfe der Videos ausfüllen:
 5 Koordinatensysteme Zoltán Zomotor Versionsstand: 6. August 2015, 21:43 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
5 Koordinatensysteme Zoltán Zomotor Versionsstand: 6. August 2015, 21:43 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
Integrieren Das bestimmte Integral einer Funktion f f(x) in einer Variable über das Intervall [a,b] schreiben wir
![Integrieren Das bestimmte Integral einer Funktion f f(x) in einer Variable über das Intervall [a,b] schreiben wir Integrieren Das bestimmte Integral einer Funktion f f(x) in einer Variable über das Intervall [a,b] schreiben wir](/thumbs/63/49989753.jpg) Klassische Theoretische Physik TP-L - WS 2013/14 Mathematische Methoden 8.1.2014 Frank Bertoldi (Version 2) Abbildungen und Beispiele aus F. Embacher "Mathematische Grundlagen..." und "Elemente der theoretischen
Klassische Theoretische Physik TP-L - WS 2013/14 Mathematische Methoden 8.1.2014 Frank Bertoldi (Version 2) Abbildungen und Beispiele aus F. Embacher "Mathematische Grundlagen..." und "Elemente der theoretischen
Mathematik II für Inf und WInf
 Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Das mehrdimensionale Riemann-Integral. 1. Volumenintegrale
 Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Übungen zur Klassischen Theoretischen Physik III (Theorie C Elektrodynamik) WS 12-13
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt 4: Lösungen
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt 4: Lösungen
Flächeninhalt, Volumen und Integral
 Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS Bauingenieurwesen. Dr. M. Voigt
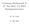 Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS auingenieurwesen Dr. M. Voigt 27. Mai 2013 II Inhaltsverzeichnis 7 Integralrechnung im R n 37 7.1 ereichsintegrale.................... 37 7.1.1 ebene ereichsintegrale.............
Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS auingenieurwesen Dr. M. Voigt 27. Mai 2013 II Inhaltsverzeichnis 7 Integralrechnung im R n 37 7.1 ereichsintegrale.................... 37 7.1.1 ebene ereichsintegrale.............
1 Das Prinzip von Cavalieri
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
Teil 8. Vektoranalysis
 Teil 8 Vektoranalysis 5 6 8. kalar- und Vektorfelder kalarfeld alternative chreibweisen: U = U(x, y, z) = U( r) R 3 P U(P ) R Visualisierung durch Niveaumengen oder Einschränkungen auf achsenparallele
Teil 8 Vektoranalysis 5 6 8. kalar- und Vektorfelder kalarfeld alternative chreibweisen: U = U(x, y, z) = U( r) R 3 P U(P ) R Visualisierung durch Niveaumengen oder Einschränkungen auf achsenparallele
Definition. Eine 2-Form ω auf einem affinen Raum (X, V, +) ist eine differenzierbare Abbildung
 2.6 Flächenintegrale Die passenden Integranden für Flächenintegrale sind weder Vektorfelder noch 1-Formen, sondern sogenannte 2-Formen. 2.6.1 2-Formen In Abschnitt 2.3 haben wir gelernt, dass 1-Formen
2.6 Flächenintegrale Die passenden Integranden für Flächenintegrale sind weder Vektorfelder noch 1-Formen, sondern sogenannte 2-Formen. 2.6.1 2-Formen In Abschnitt 2.3 haben wir gelernt, dass 1-Formen
Implizite Funktionen. Ist für eine stetig differenzierbare Funktion f : R n R m R n. so lässt sich das Gleichungssystem
 Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
19.3 Oberflächenintegrale
 19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
Ein Integral einer stetigen Funktion über einem Elementarbereich. lässt sich durch Hintereinanderausführung eindimensionaler Integrationen berechnen:
 Satz von Fubini Ein Integral einer stetigen Funktion über einem Elementarbereich V : a j (x 1,..., x j 1 ) x j b j (x 1,..., x j 1 ) lässt sich durch Hintereinanderausführung eindimensionaler Integrationen
Satz von Fubini Ein Integral einer stetigen Funktion über einem Elementarbereich V : a j (x 1,..., x j 1 ) x j b j (x 1,..., x j 1 ) lässt sich durch Hintereinanderausführung eindimensionaler Integrationen
Grundzüge der Vektoranalysis
 KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
(u, v) z(u, v) u Φ(u, v) (v = const.) Parameterlinie v = const. v Φ(u, v) (u = const.) Parameterlinie u = const.
 13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
Doppelintegrale. rd dr. Folie 1
 Doppelintegrale G fda f, dd R R G 1 f ( rcos, rsin) rd dr Folie 1 Doppelintegrale einführendes Beispiel Als Vorwissen sollten Sie die Grundlagen ur Integration mitbringen (s..b. L. Papula, Mathematik für
Doppelintegrale G fda f, dd R R G 1 f ( rcos, rsin) rd dr Folie 1 Doppelintegrale einführendes Beispiel Als Vorwissen sollten Sie die Grundlagen ur Integration mitbringen (s..b. L. Papula, Mathematik für
Umkehrfunktion. g (y) = f (x) 1, x = g(y), Umkehrfunktion 1-1
 Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Analysis 5.
 Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle MC Total MC Total 3 4 5 6 -
Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle MC Total MC Total 3 4 5 6 -
Basisprüfung, Gruppe A Analysis I/II
 Offene Aufgaben. Jeder der folgenden sieben offenen Aufgaben ist eine einzelne thematisch verwandte Single Choice-Aufgabe vorangestellt. Beantworten Sie die Single Choice Aufgabe auf dem Antwortzettel.
Offene Aufgaben. Jeder der folgenden sieben offenen Aufgaben ist eine einzelne thematisch verwandte Single Choice-Aufgabe vorangestellt. Beantworten Sie die Single Choice Aufgabe auf dem Antwortzettel.
Serie 6: MC-Zwischentest - Kapitel I und II
 D-ERDW, D-HEST, D-USYS Mathematik II FS 14 Dr. Ana Cannas Serie 6: MC-Zwischentest - Kapitel I und II Einsendeschluss: 11. April 14, 17 Uhr Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des
D-ERDW, D-HEST, D-USYS Mathematik II FS 14 Dr. Ana Cannas Serie 6: MC-Zwischentest - Kapitel I und II Einsendeschluss: 11. April 14, 17 Uhr Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des
46 Der Satz von Fubini
 46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
D-BAUG Analysis I/II Winter 2015 Dr. Meike Akveld
 D-BAUG Analysis I/II Winter 5 Dr. Meike Akveld Lösung. [ Punkte] Es sei das Gebiet B {z C } z + Im(z) gegeben. a) Skizzieren Sie das Gebiet B in der komplexen Ebene. Für z x + iy gilt z + Im(z) x + y +
D-BAUG Analysis I/II Winter 5 Dr. Meike Akveld Lösung. [ Punkte] Es sei das Gebiet B {z C } z + Im(z) gegeben. a) Skizzieren Sie das Gebiet B in der komplexen Ebene. Für z x + iy gilt z + Im(z) x + y +
