Methoden für Individualentscheidungen
|
|
|
- Dagmar Heintze
- vor 6 Jahren
- Abrufe
Transkript
1 Methoden für Individualentscheidungen Mike Hüftle 28. Juli 2006 Inhaltsverzeichnis 1 Einleitung Entscheidungsproblem Entscheidungsmodell Entscheidung bei Sicherheit und mehreren Zielen Allgemeines Zielerreichungsmatrix Nebenpfad: Vektor-Normierung Dominanz-, Maximin- und Maximax-Strategie MADM bei ordinaler Präferenzinformation MADM bei kardinaler Präferenzinformation Nebenpfad: Paarvergleichsmatrix Nebenpfad: Einfache additive Gewichtung Nebenpfad: Analytic Hierarchy Process Outranking-Verfahren Entscheidung bei Unsicherheit Problemstellung Maximin- und Maximax-Strategie Hurwicz-Prinzip und Laplace-Regel Entscheidungen bei Risiko Entscheidungsregeln bei Risiko Bernoulli-Prinzip Nebenpfad: Bernoulli-Nutzenfunktion Mehrperiodige Entscheidungen Problemstellung Entscheidungsbaum Roll-Back-Verfahren Mathematische Optimierung
2 6 Literatur und Methoden Einführende Literatur Weiterführende Literatur Methoden
3 1 Einleitung 1.1 Entscheidungsproblem Individual- vs. Gruppenentscheidungen Eine wesentliches Differenzierungskriterium von Entscheidungsproblemen ist die Frage, wieviele Personen an einer Entscheidung beteiligt sind. Bei Individualentscheidungen trifft ein Entscheider mit Hilfe einer Methode zur Entscheidungsunterstützung die Entscheidung über die Auswahl einer von mehreren Handlungsalternativen. Demgegenüber sind bei Gruppenentscheidungen mehrere Entscheider beteiligt, was ein zusätzliches Entscheidungsproblem bedeutet, da in der Regel die Entscheider unterschiedliche Präferenzen haben. Methoden für Individualentscheidungen Methoden, die den einzelnen Entscheider bei der Alternativenauswahl unterstützen, haben das Ziel, die für den Entscheider gemäß seinen individuellen Präferenzen beste Alternative zu finden. Welche Methode für ein bestimmtes Entscheidungsproblem angewendet wird, hängt davon ab, wieviele und welche Informationen über die Entscheidungssituation vorliegen: Sicherheit: Die zukünftigen Konsequenzen einer Entscheidung können mit Sicherheit vorhergesagt werden. Unsicherheit: Die Konsequenzen einer Entscheidung können nicht definitiv vorhergesagt werden. Wahrscheinlichkeiten über mögliche zukünftige Folgen können nicht beziffert werden. Risiko: Die Folgen einer Entscheidung können zwar nicht definitiv vorhergesagt werden; der Entscheider kann jedoch angeben, mit welcher Wahrscheinlichkeit diese Folgen eintreten. Weiterhin wird unterschieden, ob und wie die einzelnen Methoden die Präferenzen des Entscheiders (risikoscheu, risikoneutral oder risikofreudig) wiedergeben können und ob bei der Entscheidung mehrere Ziele berücksichtigt werden sollen (Multi-Criteria-Analyse). 3
4 1.2 Entscheidungsmodell Komponenten eines Entscheidungsmodells Ein Entscheidungsproblem kann mit folgenden Größen modelliert werden: (Handlungs-) Alternativen: Dies ist eine Menge von Handlungsmöglichkeiten, die vor der Entscheidungsfindung feststehen, und aus denen der Entscheider eine oder mehrere auswählen soll. (Umwelt-) Zustände: Dies sind Ereignisse oder Zustände, die vom Entscheider nicht direkt beeinflusst werden können. Der Entscheider kann aber angeben, welchen Einfluss ein Zustand auf das Ergebnis seiner Entscheidung hat. Bei Entscheidungen unter Risiko kann der Entscheider angeben, mit welcher Wahrscheinlichkeit ein bestimmter Zustand eintritt. Ergebnisse: Dies sind die Folgen aus einer Entscheidung, welche der Entscheider (z.b. monetär oder als Nutzen) bewerten kann. Der Entscheider kann angeben, welches Ereignis unter welchem Zustand bei welcher Entscheidung eintritt. Ziele bzw. Präferenzen: Der Entscheider kann festlegen, welches Ziel oder welche Ziele er mit seiner Entscheidung verfolgt. Mit dem Begriff der Präferenz werden die Einstellungen des Entscheiders zu Ergebnissen bezeichnet, d.h. wann er ein Ergebnis einem anderen Ergebnis bevorzugt. Entscheidungsmatrix Der Zusammenhang zwischen diesen Komponenten lässt sich in Form einer Entscheidungsmatrix mit den Zuständen Z j, den Eintrittswahrscheinlichkeiten der Zustände p(z j ) (nur bei Entscheidungen unter Risiko), den Alternativen A i und den Ergebnissen e ij darstellen: 4
5 Z 1 Z 2... Z n p(z 1 ) p(z 2 ) p(z n ) A 1 e 11 e e 1n A 2 e 21 e e 2n A m e m1 e m2... e mn 5
6 2.1 Allgemeines 2 Entscheidung bei Sicherheit und mehreren Zielen Multi- Attribut- Entscheidungen Multi-Attribut-Entscheidungen ( Multi Attribute Decision Making, MADM) sind mehrkriterielle Entscheidungsprobleme, die durch Auswahl einer von mehreren Handlungsalternativen gelöst werden (im Gegensatz zu Mehrziel-Optimierungsproblemen, bei denen eine Handlungsalternative berechnet wird). Die Ziele des Entscheiders werden als Attribute bezeichnet. Lösungsansätze für MADM- Probleme Die verschiedenen Ansätze zur Lösung von MADM-Problemen werden nach den von ihnen benötigten Informationen klassifiziert. MADM-Verfahren, die einen relativ geringen Informationsbedarf haben, sind die Dominanz-, die Maximin- und die Maximax-Strategie. Die mit diesen Verfahren generierten Entscheidungsvorschläge sind jedoch in vielen Fällen unbrauchbar (vgl. [] S. 26). Verfahren, die mehr Informationen vom Entscheider erfordern, wie die lexikographische Methode oder Gewichtungsmethoden, liefern meist bessere Entscheidungen. Sie erfordern jedoch auch, dass sich der Entscheider in größerem Umfang mit dem Entscheidungsproblem auseinandersetzt. 6
7 2.2 Zielerreichungsmatrix Bei allen MADM-Problemen werden m Alternativen A 1, A 2,... A m im Hinblick auf n Attribute (Ziele) C 1, C 2,... C n bewertet. Mit x ij wird das Ausmaß der Zielerreichung von Alternative A i im Hinblick auf Attribut C j beschrieben. Durch die Koeffizienten x ij wird die Zielerreichungsmatrix X festgelegt C 1 C 2... C n A 1 x 11 x x 1n A 2 x 21 x x 2n A m x m1 x m2... x mn Skalenniveau Die Koeffizienten x ij müssen mindestens ordinales Skalenniveau besitzen, damit sich sinnvolle Aussagen aus der Koeffizientenmatrix treffen lassen. Normierung Für einige MADM-Verfahren ist eine Normierung der Zielerreichungsmatrix notwendig (z.b. Maximin-Strategie, additive Gewichtung, ELECTRE). Hierfür gibt es eine Reihe von Verfahren, wie z.b. die Vektor-Normierung oder die lineare Skalentransformation. Anwendungshinweise finden sich in ([] S. 38 ) beschrieben Nebenpfad: Vektor-Normierung Bei der Vektor-Normierung werden die Spaltenvektoren der Zielerreichungsmatrix X durch ihre euklidische Norm dividiert, so dass die Spaltenvektoren nach der Normierung alle dieselbe euklidische Länge besitzen. 7
8 Die normierten Koeffizienten r ij werden berechnet zu: r ij = x ij m k=1 (x kj) 2 (1) 8
9 2.3 Dominanz-, Maximin- und Maximax-Strategie Dominanz-, Maximin- und Maximax-Strategie benötigen relativ wenig Informationen von Seiten des Entscheiders. Dieser muss keine Präferenzen bezüglich der Alternativen angeben, da diese Präferenzen implizit in den drei Verfahren unterstellt werden. Diese drei Strategien spiegeln jedoch nur in Ausnahmefällen die tatsächlichen Präferenzen des Entscheiders wieder. Dominanz- Strategie Die Dominanz-Strategie vergleicht die Alternativen und eliminiert dominierte Alternativen. Eine dominierte Alternative ist eine Alternative, die bezüglich der Zielerreichung in einem oder mehreren Attributen von einer anderen Alternative übertroffen wird, wobei die Zielerreichung in den anderen Attributen gleichwertig ist. Begonnen wird mit den ersten beiden Alternativen, hiervon wird die dominierte Alternative eliminiert und die nicht-dominierte wird mit der nächsten Alternative verglichen usw. Meist bleiben in diesem Verfahren so viele nicht-dominierte Alternativen übrig, dass zusätzlich ein weiteres Verfahren zur Entscheidungsfindung herangezogen werden muss. Maximin- Strategie Die Maximin-Strategie besteht darin, diejenige Alternative auszuwählen, deren schlechtestes Attribut den besten Wert aller Alternativen aufweist, d.h. eine Alternative wird im Prinzip nur durch ihr Attribut mit dem schlechtesten Ausmaß der Zielerreichung repräsentiert. Für die Maximin-Strategie muss die Zielerreichungsmatrix X normiert werden. Die Strategie wird bei Problemen angewendet, bei der die Wertschätzung für eine Alternative nur durch die schlechteste Attributausprägung bestimmt wird. Dies ist also eine sehr pessimistische Sichtweise auf das Problem. Maximax- Strategie Die Maximax-Strategie hingegen ist eine sehr optimistische Strategie. Sie berücksichtigt bei der Entscheidungsfindung für jede Alternative nur den besten Attributwert. Diejenige Alternative wird ausgewählt, für die der beste Attributwert maximal ist. Die Zielerreichungsmatrix muss normiert werden. 9
10 2.4 MADM bei ordinaler Präferenzinformation Kann der Entscheider die relative Wichtigkeit der verschiedenen Attribute auf einer ordinalen Skala angeben, so kann die lexikographische Methode angewendet werden. LexikographischeDie lexikographische Methode geht davon aus, dass die relative Wichtigkeit Methode der einzelnen Attribute für den Entscheider festgelegt werden kann. Nach demjenigen Attribut, welches am wichtigsten ist, wird der erste Vergleich der Alternativen vorgenommen. Diejenige Alternative, welche die höchste Ausprägung bezüglich dieses Attributes hat, wird als beste Entscheidung ausgewählt. Existieren mehrere Alternativen mit gleichen Ausprägungen des wichtigsten Attributes, so wird das zweitwichtigste Attribut zum Vergleich dieser Alternativen herangezogen. Dies wird so lange fortgesetzt, bis entweder eine Alternative als beste Entscheidung ausgewählt werden konnte oder bis nach allen Attributen verglichen wurde (und somit noch keine beste Alternative gefunden werden konnte). Nachteile der Methode Diese Methode ermöglicht jedoch keine Kompensation, d.h. wenn eine Alternative im wichtigsten Attribut geringfügig schlechter, in anderen Attributen jedoch viel besser abschneidet als eine zweite Alternative, so wird trotzdem die zweite Alternative gewählt. LexikographischeEine Variante der lexikographischen Methode ist die lexikographische Halbordnung, bei der auch Alternativen ausgewählt werden, bei denen die Ausprägung Halbordnung in einem Attribut nicht signifikant von der maximalen Ausprägung über alle Alternativen in diesem Attribut abweicht. Diese Methode ermöglicht also eine teilweise Kompensation zwischen den Attributen. 10
11 2.5 MADM bei kardinaler Präferenzinformation IntervallskalierungKann die Wichtigkeit von Atrributen für den Entscheider durch eine Intervallskala ausgedrückt werden, so kann die relative Wichtigkeit durch Gewichte wiedergegeben werden. Methoden, die mit der Gewichtung der Attribute arbeiten, ermöglichen eine Kompensation zwischen Attributen. D.h. wenn eine Alternative im relativ wichtigsten Attribut geringfügig schlechter, in anderen Attributen jedoch viel besser abschneidet als eine zweite Alternative, so kann auch die erste Alternative gewählt werden. Gewichte Für jedes der n Attribute C 1, C 2,... C n wird ein Gewicht w j definiert, welches die relative Wichtigkeit des j-ten Attributes im Vergleich zu allen anderen Attributen ausdrückt. Die Gewichte werden in der Regel normiert, so dass n j=1 w j = 1 Gewichtevektor Nachdem der Entscheider die relative Wichtigkeit aller Attribute durch 1/2 n (n 1) Paarvergleiche festgelegt hat, kann eine Paarvergleichsmatrix aufgestellt werden. Wiedersprüchliche Paarvergleiche Da jedoch der Entscheider nur selten wiederspruchsfreie Schätzungen für die Paarvergleichsmatrix geben kann, wurden Methoden entwickelt, um den Gewichtevektor auch aus einer inkonsistenten Paarvergleichsmatrix bestimmen zu können. Dies sind z.b. die Methode der kleinsten gewichteten Quadrate oder Saatys Eigenvektor-Methode (beschrieben in [], S. 56 ff). MADM- Methoden auf der Grundlage von Gewichten Es gibt eine Vielzahl von MADM-Methoden, welche Gewichte zur Bestimmung der besten Alternative verwenden. Dies sind beispielsweise: Die lineare Zuordnungsmethode Die einfache additive Gewichtung Der Analytic Hierarchy Process (AHP) [] [] 11
12 2.5.1 Nebenpfad: Paarvergleichsmatrix Die Paarvergleichsmatrix hat folgende Gestalt: C 1... C j... C n C 1 a a 1j... a 1n C i a i1... a ij... a in C n a n1... a nj... a nn Gilt die Gleichung a ik a kj = a ij i, j, k, so ist die Paarvergleichsmatrix wiederspruchsfrei. Ist die Paarvergleichsmatrix wiederspruchsfrei, so können die Gewichte der n Attribute C n durch Normierung der j-ten Spalte der Matrixberechnet werden: w i = a ij n k=1 a kj (2) Nebenpfad: Einfache additive Gewichtung Bestimmen der besten Alternative Bei der einfachen additiven Gewichtung wird für jede Alternative der Wert n v(a i ) = w j x ij (3) j=1 bestimmen, mit x ij als (reelwertigem) Ausmaß der Zielerreichung von Alternative A i im Hinblick auf Attribut C j. 12
13 Anwendungsvoraussetzungen Um die Methode der additiven Gwichtung anwenden zu können, müssen die Attribute präferenzunabhängig sein. Dies bedeutet, dass eine sehr hohe Ausprägung in einem Attribut den Nutzen eines anderen Attributes für den Entscheider nicht beeinflussen darf Nebenpfad: Analytic Hierarchy Process Strukturierung des Entscheidungsproblems Der Analytic Hierarchy Process wurde in den 70er Jahren von T. L. Saaty konzipiert. Er basiert auf der Strukturierung des Entscheidungsproblems in Hierarchien. Hierdurch kann das Gesamtproblem in kleinere, für den Entscheider überschaubare Teilprobleme zerlegt werden. Die Abbildung zeigt eine mögliche hierarchische Gliederung eines Entscheidungsproblems in Oberziel, Ziele, Kriterien und Unterkriterien. Methodenbeschreibung Der AHP umfasst ein mehrstufiges Vorgehen: 1. Im ersten Schritt wird eine Hierarchie der Attribute (Ziele) und der Zielkriterien des Entscheiders aufgestellt. 2. Anschließend werden Paarvergleiche durchgeführt. Dazu wird für die Alternativen im Hinblick auf jedes Ziel und jedes Kriterium der Zielhierarchie eine Paarvergleichsmatrixaufgestellt. Bei einer Hierarchie mit einem Oberziel, drei Zielen und sechs Kriterien werden somit 10 Paarvergleichsmatrizen erstellt. 3. Zu jeder Paarvergleichsmatrix wird ein Gewichtungsvektor nach Saatys Eigenvektormethode berechnet. 4. Die Konsistenz der Paarvergleiche wird mit Hilfe des Konsistenzwertes von Saaty bestimmt. Sind die Vergleiche nicht konsistent, so müssen diese erneut dem Entscheider vorgelegt werden. 5. Bei konsistenten Paarvergleichen werden die Alternativen durch eine einfache lineare Funktion kombiniert, so dass aus den Bewertungen der untersten Hierarchieebene die Bewertung der Alternativen bezüglich des Oberziels berechnet werden kann. 13
14 Bewertung der Alternativen Die Bewertung der Alternativen in Schritt 5 soll an einem Beispiel erläutert werden. Das Gewicht der Alternative Ausbau des Streckennetzes in Hinblick auf das Oberziel wird wie folgt berechnet: w V RZ (ASN) = w V UH (ASN) w V RZ (V UH) + w RV S (ASN) w V RZ (RV S) + w ERG (ASN) w V RZ (ERG) = Ebenso können w V RZ (MSN) = und w V RZ (F P O) = berechnet werden. Demzufolge ist also die Alternative die beste Entscheidung für das Oberziel Veringerung der Reisezeit im ÖPNV. Anwendungsvoraussetzungen Der AHP basiert auf vier wichtigen Voraussetzungen: 1. Die Paarvergleichsmatrix zur Bestimmung der Gewichte muss reziprok sein, d.h. wird Alternative 1 als doppelt so wichtig wie Alternative 2 angesehen, so muss auch umgekehrt Alternative 2 als nur halb so wichtig wie Alternative 1 festgelegt werden. 2. Eine Alternative darf niemals unendlich viel besser als eine andere Alternative sein. 3. Die Entscheidungssituation muss in einer Hierarchie abbildbar sein. Insbesondere muss der Paarvergleich in einer Hierarchieebene unabhängig von den Präferenzen in anderen Hierarchieebenen sein. 4. Sämtliche relevanten Alternativen und Attribute müssen in der Hierarchie enthalten sein. 14
15 2.6 Outranking-Verfahren Schlecht strukturierte Entscheidungsprobleme Outranking-Verfahren unterstützen den Entscheider bei schlecht strukturierten Entscheidungsproblemen oder in Situationen mit unvollständigen Informationen. Z.B. kann der Entscheider oft keine strikte Präferenzordnung über die Handlungsalternativen angeben, wenn er die Ergebnisse verschiedener Handlungsalternativen gar nicht unmittelbar miteinander vergleichen kann oder ihm hierzu die notwendigen Informationen fehlen. Bekannte Beispiele für Outranking-Verfahren sind ELECTRE und PROME- THEE []. ELECTRE ELECTRE [] (Elimination et Choice Translation Reality) wurde in den 60er Jahren entwickelt und später durch zahlreiche Variationen erweitert. Über eine gewichtete, normierte Zielerreichungsmatrix werden so genannte Konkordanzund Diskordanzmatrizen berechnet. Diese enthalten Informationen über die relative Dominanz der Alternativen bezüglich der einzelnen Attribute. Hieraus kann eine Präferenzordnung über alle Alternativen gebildet werden. ELECTRE arbeitet also nicht mit absoluten Dominanzen (eine Alternative dominiert eine andere oder nicht), sondern mit relativen Dominanzen (wie stark dominiert eine Alternative eine andere). 15
16 3 Entscheidung bei Unsicherheit 3.1 Problemstellung Unsicherheit In der Relität kann oft nicht mit Sicherheit vorhergesagt werden, zu welchem Ergebnis die Wahl einer Alternative führen wird. Das tatsächliche Ergebnis einer Alternativenwahl hängt vom zukünftigen, unbekannten Umweltzustand ab. Entscheidung bei Unsicherheit Wird unter solchen Umständen eine Entscheidung getroffen, so wird dies eine Entscheidung unter Unsicherheit genannt. Im Gegensatz zur Entscheidung bei Risiko liegen bei Unsicherheit keine Wahrscheinlichkeiten über die zukünftigen Ergebnisse bzw. Folgen einer Alternativenwahl vor. Entscheidungen unter Unsicherheit haben nur eine geringe praktische Bedeutung, da sich reale Probleme in der Regel besser durch die Angabe von Wahrscheinlichkeiten, also durch eine Entscheidung bei Risiko beschreiben lassen. 16
17 3.2 Maximin- und Maximax-Strategie Maximin- Strategie Bei der Maximin-Strategie wird diejenige Alternative gewählt, welche im ungünstigsten Fall das beste Ergebnis hat. Die Maximin-Strategie geht gewissermaßen davon aus, dass das worst case -Szenario eintritt und dann das beste Ergebnis realisiert wird. Diese extrem pessimistische Sichtweise ist der größte Nachteil der Maximin- Strategie, da dies nur in seltenen Fällen den Präferenzen des Entscheiders entspricht. Maximax- Strategie Bei der Maximin-Strategie wird diejenige Alternative ausgewählt, welche im günstigsten Fall das beste Ergebnis liefert. Die Maximax-Strategie geht also von einem best case -Szenario aus. Diese optimistische Sichtweise wird jedoch in den meisten Fällen nicht den tatsächichen Präferenzen des Entscheiders gerecht. 17
18 3.3 Hurwicz-Prinzip und Laplace-Regel Hurwicz- Prinzip Das Hurwicz-Prinzip ist ein Kompromiss zwischen Maximin- und Maximax- Strategie. Um eine Alternative zu bewerten sind sowohl der worst case als auch der best case von Bedeutung. Aus diesen beiden Ergebnissen wird ein, mit einem Parameter α gewichteter, Durchschnitt gebildet. Somit kann der Entscheider zum Ausdruck geben, in wieweit er eher eine pessimistische oder eine optimistische Sichtweise des Problems hat. Zur Bestimmung des Parameters α muss der Entscheider angeben, bei welchem Ergebnis er indifferent zwischen zwei Alternativen ist. Hieraus kann der Parameter bestimmt werden. Laplace-Regel Bei der Laplace-Regel wird die Unsicherheit in eine Risikosituation transformiert, indem alle Zustände als gleichwahrscheinlich betrachtet werden. Es wird angenommen, dass unter Unsicherheit für keinen Zustand eine höhere Wahrscheinlichkeit als für die anderen Zustände vorausgesetzt werden kann. Die eigentliche Entscheidung wird dann mit einer Methode zur Entscheidungsfindung bei Risiko bestimmt. Ein wichtiger Kritikpunkt an der Laplace-Regel ist, dass die Wahrscheinlichkeit eines Zustandes stark davon abhängt, wieviele Zustände definiert werden, d.h. bei drei Zuständen ist die Eintrittswahrscheinlichkeit eines Zustandes 1/3, wird ein zusätzlicher Zustand definiert nur noch 1/4. 18
19 4 Entscheidungen bei Risiko 4.1 Entscheidungsregeln bei Risiko Praktische Entscheidungssituationen sind meist Situationen unter Risiko, d.h. der Entscheider hat eine Vorstellung darüber, mit welcher Wahrscheinlichkeit ein bestimmter Umweltzustand eintrifft (im Gegensatz zu Entscheidungen unter Unsicherheit, bei denen der Entscheider keine Wahrscheinlichkeiten angeben kann). µ-regel Bei der µ-regel wird der Erwartungswertder Zielgröße als Entscheidungskriterium verwendet. Diejenige Alternative wird ausgewählt, welche diesen Erwartungswert maximiert: max v(a i ) = s p(s j ) v(x ij ) (4) j=1 mit dem Ergebnis der Alternative v(a i ), der Wahrscheinlichkeit des Zustands p(s j ) und dem Ergebnis v(x ij ) der Alternative i im Zustand j. Gibt es mehrere Alternativen mit demselben Erwartungswert, so werden diese als gleichwertig betrachtet. Anwendung der µ-regel Da die µ-regel relativ einfach mit stochastischen Entscheidungsmodellen verknüpft werden kann, ist sie eine der beliebtesten Entscheidungsregeln bei Unsicherheit. Die µ-regel vernachlässigt jedoch die subjektiven Präferenzen und die Risikoeinstellung des Entscheiders (wenn beispielsweise Verluste für den Entscheider sehr viel schwerwiegender sind als Gewinne in der gleichen Höhe). µ, σ-prinzip Das µ, σ-prinzip berücksichtigt neben dem Erwartungswert der Ergebnisse auch das Risiko, indem die Standardabweichungder (zufälligen) Ergebnisse mit einbezogen wird. σ gibt also an, in welchem Umfang die möglicherweise eintretenden Ergebnisse um den Erwartungswert streuen. Ein risikoscheuer Entscheider wird also Situationen mit geringerer Standardabweichung der Ergebnisse bevorzugen, wohingegen ein risikofreudiger Entscheider eine größere Standardabweichung in Kauf nimmt, d.h. akzeptiert 19
20 eine größere positive oder negative Abweichung vom Erwartungswert als der risikoscheue Entscheider. 20
21 4.2 Bernoulli-Prinzip Bernoulli- Prinzip Sowohl die µ-regel als auch das µ, σ-prinzip repräsentieren die Verteilungen der möglichen Ergebnisse durch die Parameter µ, σ. Dies bedeutet einen Informationsverlust gegenüber der expliziten Betrachtung aller möglicher Ergebnisse und deren Eintrittswahrscheinlichkeiten. Nach dem Bernoulli-Prinzip hingegen wird jedem möglichen Ergebnis ein Nutzen gemäß einer vorher festzulegenden individuellen Nutzenfunktion zugewiesen. Nähere Erläuterungen zur Ermittlung der Nutzenfunktion finden Sie hier. Ergebnis der Berechnungen ist eine Entscheidungsmatrix, welche den Nutzen U(e ij ) der Ergebnisse e ij die Nutzenerwartungswerte für die Alternativen enthält. S 1 S 2... S n Nutzenerwartungswerte A 1 U(e 11) U(e 12)... U(e 1n ) n j=1 p(s j) U(e 1j ) A 2 U(e 21) U(e 22)... U(e 2n ) n j=1 p(s j) U(e 2j ) A m U(e m1) U(e m2)... U(e mn ) n j=1 p(s j) U(e mj ) Diejenige Alternative wird ausgewählt, welche den höchsten Nutzenerwartungswert hat. Anwendung des Bernoulli- Prinzips Wenn folgende Voraussetzungen erfüllt sind, kann das Bernoulli-Prinzip zur Entscheidungsfindung eingesetzt werden: Der Entscheider kann für zwei beliebige Ergebnisse angeben, welches er präferiert bzw. ob er indifferent zwischen den Ergebnissen ist. Die Präferenzordnung über alle Ergebnisse ist transitiv, d.h. aus e i e j und e j e k folgt e i e k 21
22 Der Entscheider kann ein α angeben, bei dem er indifferent zwischen dem sicheren Ergebnis und der Lotterie ist Nebenpfad: Bernoulli-Nutzenfunktion Die Bestimmung der individuellen Nutzenfunktion des Entscheiders ist das eigentliche Problem bei der Entscheidung nach dem Bernoulli-Prinzip. Bernoulli- Befragung Die Nutzenfunktion kann beispielsweise mit einer so genannten Bernoulli-Befragung ermittelt werden. Hierzu wird das für den Entscheider ungünstigste Ergebnis e und das günstigste Ergebnis e* erfragt. Das ungünstigste Ergebnis erhält den Nutzen 0 und das günstigste Ergebnis den Nutzen 1. Alle anderen möglichen Ergebnisse e ij werden vom Entscheider günstiger als e und ungünstiger als e* empfunden. Sicheres Ergebnis vs. Lotterie Um den Nutzen eines Ergebnisses e ij zu bestimmen, wird der Entscheider vor die Wahl gestellt, entweder das sichere Ergebnis e ij zu wählen oder an einer Lotterie teilzunehmen, bei welcher e* mit der Wahrscheinlichkeit α und e mit der Wahrscheinlichkeit 1 α eintritt. Diejenige Wahrscheinlichkeit α, bei welcher der Entscheider indifferent zwischen dem sicheren Ergebnis und der Lotterie ist, wird gleich dem Nutzen U(e ij ) dieses Ergebnisses gesetzt. Bestimmung der Nutzenfunktion Führt man dies für jedes mögliche Ergebnis durch, so erhält man die Nutzenfunktion U.Gibt es sehr viele mögliche Ergebnisse, so wird die Nutzenfunktion bestimmt, indem einige Stützstellen durch eine Bernoulli-Befraagung bestimmt werden und die Nutzenfunktion über diese Stützstelle interpoliert wird. 22
23 5 Mehrperiodige Entscheidungen 5.1 Problemstellung Dynamische Entscheidungen Bei vielen Entscheidungsproblemen müssen im Laufe der Zeit mehrere Entscheidungen getroffen werden. Dabei hängen häufig zeitlich aufeinander folgende Entscheidungen voneinander ab, so dass bei der Modellierung des Problems Interdependenzen zwischen den Entscheidungen berücksichtigt werden müssen. Solche Probleme werden auch mehrstufige Entscheidungsprobleme genannt und die Lösung eines solchen Problems wird auch als Strategie bezeichnet. InterdependenzenDie zu berücksichtigenden Interdependenzen bei einem mehrstufigen Entscheidungsproblem können vielfältig sein: Die Wahl einer Alternative zu einem bestimmten Zeitpunkt kann die in einem späteren Zeitpunkt zur Verfügung stehenden Alternativen und die zukünftigen Zustände beeeinflussen. Das Ergebnis in einem Zeitpunkt hängt in der Regel von der Alternativenwahl aller vorhergehender Zeitpunkte ab. Die Wahrscheinlichkeit des Eintritts eines Zustandes kann von der Eintrittswahrscheinlichkeit vorheriger Zustände abhängen. 23
24 5.2 Entscheidungsbaum Folgen von Zuständen und Handlungsalternativen Eine weit verbreitete Methode zur Analyse mehrstufiger Entscheidungen sind Entscheidungsbäume. In einem solchen Entscheidungsbaum werden Folgen von Zuständen und Handlungsalternativen dargestellt. Der Entscheider hat mehrere Alternativen zur Wahl. Die Auswahl einer Alternative beeinflusst das Eintreten des nächsten Zustandes. Das Eintreten der auf eine Alternativenwahl folgenden Zustände wird vom Entscheider mit einer Wahrscheinlichkeit beziffert. Die Wahrscheinlichkeit eines bestimmten Ergebnisses als Resultat einer Folge von Handlungsalternativen kann als Produkt der Wahrscheinlichkeiten bestimmt werden, mit der die Zustände in dieser Folge eintreten. EntscheidungsbaumDie Abbildung zeigt ein Beispiel für solch einen Entscheidungsbaum mit zwei Zustandsebenen (d.h. zwei betrachteten Perioden). 24
25 5.3 Roll-Back-Verfahren Optimale Strategie=Maximaler Erwartungswert Das Roll-Back-Verfahren wird eingesetzt, um die optimale Strategie in einem Entscheidungsbaum zu finden. Die optimale Strategie ist in diesem Sinne diejenige Folge von Handlungsalternativen, welche zum maximalen Erwartungswert des Ergebnisses führt. Hierzu wird der Entscheidungsbaum von rechts nach links aufgerollt. Beginnend mit dem Zustand, der im Entscheidungsbaum am weitesten links steht, d.h. in der zeitlichen Abfolge am spätesten eintreten kann, wird für jeden Zustand der Erwartungswert der Ergebnisse in diesem Zustand berechnet. Die Diashow erläutert das Roll-Back-Verfahren anhand eines Beispiels für einen risikoneutralen Entscheider: Ausgangssituation Beste Entscheidung im Zustand Z1 Erwartungswerte in Z2 und Z3 Beste Entscheidung in Z4 Beste Entscheidung in Z0 Optimale Strategie Die optimale Stragie im obigen Beispiel ist also die folgende: 1. Führe Handlungsalternative A2 mit einem Erwartungswert von 298 Euro durch. 2. Wenn Zustand Z3 eintritt ist das Ergebnis 500 Euro. 3. Wenn Zustand Z4 eintritt, führe Alternative A4 mit dem Erwartungswert 275 Euro durch. 25
26 Risikoscheue und risikofreudige Entscheider Für risikoscheue oder risikofreudige Entscheider kann das Entscheidungsbaumverfahren gleichermaßen angewendet werden. Es müssen dann lediglich statt der Erwartungswerte Nutzenerwartungswerte berechnet werden, indem die Ergebnisse gemäß der Nutzenfunktion des Entscheiders in Nutzenwerte umgewandelt werden. 26
27 5.4 Mathematische Optimierung Hohe Komplexität In vielen Fällen umfasst eine mehrperiodige Entscheidung eine Vielzahl von Handlungsalternativen, Zuständen und Ergebnissen. Dann kann nicht mehr sinnvoll mit einem Entscheidungsbaum gearbeitet werden. Mathematisches Optimierungsmodell Unter diesen Umständen kann die mathematische Optimierung zur Entscheidungsfindung eingesetzt werden ([] S. 297). Hierfür wird das Entscheidungsproblem durch mehrere Zustandsfolgen (in einem Zustandsbaum) betrachtet. Jedem Zustand wird eine Entscheidungsvariable zugeordnet, die ausdrückt, welche Entscheidung in einem Zustand gefällt wird. Weiterhin können den Zuständen Nebenbedingungen zugeordnet werden, welche die möglichen Handlungsalternativen einschränken. In der ZielfunktiondesOptimierungsmodells wird für jede mögliche Zustandsfolge das Ergebnis in Abhängigkeit von der Eintrittswahrscheinlichkeit der Zustandsfolge ausgedrückt. Ein solches Optimierungsmodell lässt sich, je nach den mathematischen Eigenschaften der Zielfunktion und der Nebenbedingungen, mit einer Optimierungsmethode lösen. 27
28 6 Literatur und Methoden 6.1 Einführende Literatur Literaturverzeichnis [] Eisenführ, F./Weber, M.: Rationales Entscheiden. 4. Aufl., Springer, Berlin Heidelberg New York [] Laux, H.: Entscheidungstheorie. %. Aufl., Springer, Berlin Heidelberg New York Saliger, E.: Betriebswirtschaftliche Entscheidungstheorie. 4. Aufl., Oldenbourg [] Nitzsch, R. von: Entscheidungslehre. Schäffer-Poeschel, Stuttgart [] Zimmermann, H.-J./Gutsche, L.: Multi-Criteria Analyse. Springer, Berlin Heidelberg New York Weiterführende Literatur Literaturverzeichnis [] Brans, J.P.Vincke, Ph./Mareschal, B.: How to select and how to rank projects: The PROMETHEE method, in: European Journal of Operations Research, Vol. 24, 1986, pp [] Haedrich, G./Kuß, A./Kreilkamp, E.: Der Analytic Hierarchy Process, in: Wirtschaftswissenschaftliches Studium (WiSt), Heft 3, 1986, pp [] Roy, B.: The Outranking Approach and the Foundations of ELECTRE Methods, in: Bana c Costa, C.A. (ed.): Readings in Multiple Criteria Decision Aid, Springer, Berlin Heidelberg New York 1990, pp [] Saaty, Th. L.: The Analytic Hierarchy Process. McGraw-Hill, New York London Methoden Verzeichnis der erläuterten Methoden µ-regel µ, σ-prinzip Analytic Hierarchy Process Einfache Additive Gewichtung Bernoulli-Lotterie Bernoulli-Prinzip 28
29 Dominanz-Strategie ELECTRE Entscheidungsbaum Maximax-Strategie Maximin-Strategie Hurwicz-Prinzip Laplace-Regel Lexikographische Halbordnung Lexikographische Ordnung Roll-Back-Verfahren Saatys Eigenvektor-Methode Zielgewichtung 29
2.2 Entscheidung bei Sicherheit
 2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
2. Entscheidungsregeln. Handhabung von Unsicherheit
 II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
3. Entscheidungen bei mehreren Szenarien. Entscheidungen. bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
 3. Entscheidungen bei mehreren Szenarien Entscheidungen bei Sicherheit A i und x i sowie die Zielfunktion determinieren das Entscheidungsproblem bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
3. Entscheidungen bei mehreren Szenarien Entscheidungen bei Sicherheit A i und x i sowie die Zielfunktion determinieren das Entscheidungsproblem bei Unsicherheit A i, S j und x ij sowie die Zielfunktion
2.4 Entscheidung bei Risiko
 2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische
Ganzheitliche Analyse und Bewertung. von Strategie-Optionen. Controlling-gestützter Einsatz des Analytic Network Process im Strategischen Management
 Ganzheitliche Analyse und Bewertung von Strategie-Optionen Controlling-gestützter Einsatz des Analytic Network Process im Strategischen Management Inauguraldissertation zur Erlangung des akademischen Grades
Ganzheitliche Analyse und Bewertung von Strategie-Optionen Controlling-gestützter Einsatz des Analytic Network Process im Strategischen Management Inauguraldissertation zur Erlangung des akademischen Grades
Annahme: - Päferenzunabhängigkeit der Ziele - kardinal skalierte Größen!!!!
 Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4 4.4 Nutzwertanalyse Verfahren zur Lösung von Mehrzielentscheidungen Hierarchisch aufgebaute systeme å i.d.r. sind nur zwei oder drei Teilziele
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 4 4.4 Nutzwertanalyse Verfahren zur Lösung von Mehrzielentscheidungen Hierarchisch aufgebaute systeme å i.d.r. sind nur zwei oder drei Teilziele
1. Aufgabe: Entscheidungen bei Ungewissheit
 ( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
https://cuvillier.de/de/shop/publications/6839
 Ralf H. Kaspar (Autor) Ganzheitliche Analyse und Bewertung von Strategie-Optionen Controlling-gestützter Einsatz des Analytic Network Process im Strategischen Management https://cuvillier.de/de/shop/publications/6839
Ralf H. Kaspar (Autor) Ganzheitliche Analyse und Bewertung von Strategie-Optionen Controlling-gestützter Einsatz des Analytic Network Process im Strategischen Management https://cuvillier.de/de/shop/publications/6839
Einführung in die Betriebswirtschaftslehre
 Einführung in die Betriebswirtschaftslehre Entscheidungstheorie Wintersemester 2006/2007 Prof. Dr. M. Ponader Literatur Bartscher, Susanne, Bomke, Paul, Unternehmensführung, Stuttgart 1995; Kapitel 3:
Einführung in die Betriebswirtschaftslehre Entscheidungstheorie Wintersemester 2006/2007 Prof. Dr. M. Ponader Literatur Bartscher, Susanne, Bomke, Paul, Unternehmensführung, Stuttgart 1995; Kapitel 3:
3. Betriebswirtschaftliche Entscheidungslehre 3.6 Entscheidung unter Risiko
 Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Analytischer Hierarchieprozess (AHP)
 Analytischer Hierarchieprozess (AHP) Methodik der multikriteriellen Bewertung Nach den Skripten der BoKu Wien und der Abteilung für Forstökonomie Göttingen (Prof. Möhring) www.boku.ac.at www.uni-goettingen.de
Analytischer Hierarchieprozess (AHP) Methodik der multikriteriellen Bewertung Nach den Skripten der BoKu Wien und der Abteilung für Forstökonomie Göttingen (Prof. Möhring) www.boku.ac.at www.uni-goettingen.de
Vorlesung 1: Einleitung
 Vorlesung 1: Einleitung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 1, FS 12 Einleitung 1/17 1.1 Motivation In der Vorlesung Intermediate Microecoomics haben
Vorlesung 1: Einleitung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 1, FS 12 Einleitung 1/17 1.1 Motivation In der Vorlesung Intermediate Microecoomics haben
Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }.
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
3. Betriebswirtschaftliche Entscheidungslehre 3.1 Einleitung
 3.1 Einleitung Auf Basis von Zielvorstellungen sollen die Konsequenzen von Handlungsalternativen ermittelt werden deskriptive Entscheidungstheorie: beschreibt, wie in der Realität Entscheidungen in konkreten
3.1 Einleitung Auf Basis von Zielvorstellungen sollen die Konsequenzen von Handlungsalternativen ermittelt werden deskriptive Entscheidungstheorie: beschreibt, wie in der Realität Entscheidungen in konkreten
Entscheidungstheorie Teil 4
 Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
TOPSIS. Eine Technik der Effizienzanalyse
 TOPSIS Eine Technik der Effizienzanalyse 1 Literatur Peters, Malte L. und Zelewski, Stephan: TOPSIS als Technik zur Effizienzanalyse. Wirtschaftsstudium, Heft 1, 2007, S. 9-15 http://www.pim.uni-due.de/fileadmin/publikationen/topsis_zur_effizienzanalyse.pdf
TOPSIS Eine Technik der Effizienzanalyse 1 Literatur Peters, Malte L. und Zelewski, Stephan: TOPSIS als Technik zur Effizienzanalyse. Wirtschaftsstudium, Heft 1, 2007, S. 9-15 http://www.pim.uni-due.de/fileadmin/publikationen/topsis_zur_effizienzanalyse.pdf
Analytischer Hierarchieprozess (AHP)
 Analytischer Hierarchieprozess (AHP) Methodik der multikriteriellen Bewertung Nach den Skripten der BoKu Wien und der Abteilung für Forstökonomie Göttingen (Prof. Möhring) www.boku.ac.at/iao/ahp www.uni-goettingen.de/de/101204.html
Analytischer Hierarchieprozess (AHP) Methodik der multikriteriellen Bewertung Nach den Skripten der BoKu Wien und der Abteilung für Forstökonomie Göttingen (Prof. Möhring) www.boku.ac.at/iao/ahp www.uni-goettingen.de/de/101204.html
Präferenzen zu Zahlwerten I
 II-1 Präferenzen zu Zahlwerten I Erster Versuch: Durchzählen a > b > c > d > e Zuordnung von Zahlenwerten durch eine Funktion V e 1, d 2, c 3, b 4, a 5 Es gilt: Wenn x > y, dann V(x) > V(y) Aber: Differenzen
II-1 Präferenzen zu Zahlwerten I Erster Versuch: Durchzählen a > b > c > d > e Zuordnung von Zahlenwerten durch eine Funktion V e 1, d 2, c 3, b 4, a 5 Es gilt: Wenn x > y, dann V(x) > V(y) Aber: Differenzen
Operations Research kompakt
 Operations Research kompakt von Michael Sauer Oldenbourg Verlag München Inhalt s Verzeichnis 1 Einführung 1 1.1 Vorwort 1 1.2 Anwendungsbeispiel 2 1.3 Inhaltsüberblick 3 1.4 Einige Grundlagen 4 1.4.1 Grundbegriffe
Operations Research kompakt von Michael Sauer Oldenbourg Verlag München Inhalt s Verzeichnis 1 Einführung 1 1.1 Vorwort 1 1.2 Anwendungsbeispiel 2 1.3 Inhaltsüberblick 3 1.4 Einige Grundlagen 4 1.4.1 Grundbegriffe
Kapitel 2: Entscheidungstheorie
 Kapitel 2: Entscheidungstheorie 2.1 Einleitung Wie schon im Modulararbeitsbuch angegeben, wollen wir im zweiten Kapitel die Problemgebiete behandeln, die sich auf folgende Situationen beziehen: 2.2 Entscheidungen
Kapitel 2: Entscheidungstheorie 2.1 Einleitung Wie schon im Modulararbeitsbuch angegeben, wollen wir im zweiten Kapitel die Problemgebiete behandeln, die sich auf folgende Situationen beziehen: 2.2 Entscheidungen
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Betriebswirtschaftliche Entscheidungstheorie und Anwendung
 Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 4: Entscheidungen unter Unsicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 4: Entscheidungen unter Unsicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Investitionsrechnung
 Investitionsrechnung 14., neu bearbeitete und erweiterte Auflage Franz Eisenführ Unter Mitarbeit von Kristian Foit und Marc Kastner Kapitel 1 Einführung 1.1 Worum es geht 1 1.1.1 Der Begriff Investition"
Investitionsrechnung 14., neu bearbeitete und erweiterte Auflage Franz Eisenführ Unter Mitarbeit von Kristian Foit und Marc Kastner Kapitel 1 Einführung 1.1 Worum es geht 1 1.1.1 Der Begriff Investition"
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Mikroökonomik. Unsicherheit. Harald Wiese. Universität Leipzig. Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46
 Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
- Entscheidungsmöglichkeit / Alternativen. + (idealerweise) Methode der Entscheidung / Verfahren
 be/ji/3(2) 4-1 4 "Entscheidung" setzt voraus - Entscheidungsmöglichkeit / Alternativen - Prinzip der Entscheidung / Ziel + (idealerweise) Methode der Entscheidung / Verfahren Bisher trivial OR-Optimierungsmodelle
be/ji/3(2) 4-1 4 "Entscheidung" setzt voraus - Entscheidungsmöglichkeit / Alternativen - Prinzip der Entscheidung / Ziel + (idealerweise) Methode der Entscheidung / Verfahren Bisher trivial OR-Optimierungsmodelle
Vorlesung 3: Risikoaversion
 Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
W-Seminar Operations Management
 W-Seminar V3 Bestimmung der Produkteigenschaften (Conjoint Analyse) Gymnasium Bad Königshofen Wirtschaft/Recht Schuljahr 2014-2016 Grundlegende Problemstellung Welche Produkteigenschaften soll unser Produkt
W-Seminar V3 Bestimmung der Produkteigenschaften (Conjoint Analyse) Gymnasium Bad Königshofen Wirtschaft/Recht Schuljahr 2014-2016 Grundlegende Problemstellung Welche Produkteigenschaften soll unser Produkt
Vorlesung 4: Risikoallokation
 Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Vorlesung 4: Risikoallokation Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie, FS 12 Risikoallokation 1/23 2 / 23 4.1 Einleitung Bisher haben wir uns ausschliesslich
Übung zur Vorlesung Multiagentensysteme
 Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Vorlesung: Nicht-kooperative Spieltheorie. Teil 1: Organisatorisches, Inhalte der Vorlesung und Nutzentheorie
 Vorlesung: Nicht-kooperative Spieltheorie Teil 1: Organisatorisches, Inhalte der Vorlesung Dr. Thomas Krieger Wintertrimester 2009 Dr. Thomas Krieger Vorlesung: Nicht-kooperative Spieltheorie 1 / 15 Organisatorisches
Vorlesung: Nicht-kooperative Spieltheorie Teil 1: Organisatorisches, Inhalte der Vorlesung Dr. Thomas Krieger Wintertrimester 2009 Dr. Thomas Krieger Vorlesung: Nicht-kooperative Spieltheorie 1 / 15 Organisatorisches
Wichtige Informationen vorab
 Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
MCDM MULTI CRITERIA DECISION MAKING
 MCDM MULTI CRITERIA DECISION MAKING Einführung Projekt Wall-ie Studiengang Geoinformation und Umwelttechnologien c.erlacher@fh-kaernten.at Folie 1 von 17 Inhalt MCDM-Erläuterung MCDM-Elemente MCDM-Framework
MCDM MULTI CRITERIA DECISION MAKING Einführung Projekt Wall-ie Studiengang Geoinformation und Umwelttechnologien c.erlacher@fh-kaernten.at Folie 1 von 17 Inhalt MCDM-Erläuterung MCDM-Elemente MCDM-Framework
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, Annahmen:
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
Die Nutzwertanalyse - NWA Prof. Dr. Georg Rainer Hofmann Andreas Ziegler
 Die Nutzwertanalyse - NWA Prof. Dr. Georg Rainer Hofmann Andreas Ziegler 15.10.2015 Agenda Aufbau der Nutzwertanalyse Ablauf der Nutzwertanalyse Zieldefinition Ausschluss- und Auswahlkriterien definieren
Die Nutzwertanalyse - NWA Prof. Dr. Georg Rainer Hofmann Andreas Ziegler 15.10.2015 Agenda Aufbau der Nutzwertanalyse Ablauf der Nutzwertanalyse Zieldefinition Ausschluss- und Auswahlkriterien definieren
Einführung in die Wahrscheinlichkeitsrechnung
 Einführung in die Wahrscheinlichkeitsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Wahrscheinlichkeitsrechnung
Einführung in die Wahrscheinlichkeitsrechnung Sven Garbade Fakultät für Angewandte Psychologie SRH Hochschule Heidelberg sven.garbade@hochschule-heidelberg.de Statistik 1 S. Garbade (SRH Heidelberg) Wahrscheinlichkeitsrechnung
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38
 Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus
 Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Mathematik 2 Probeprüfung 1
 WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
WWZ Wirtschaftswissenschaftliche Fakultät der Universität Basel Dr. Thomas Zehrt Bitte in Druckbuchstaben ausfüllen: Name Vorname Mathematik 2 Probeprüfung 1 Zeit: 90 Minuten, Maximale Punktzahl: 72 Zur
Tutorium in Investition und Finanzierung Entscheidungstheorie
 Tutorium in Investition und Finanzierung Entscheidungstheorie Kathrin Holtze, Simon Funken, Sascha Schworm finance-tutorien@wiwi.uni-wuppertal.de Lehrstuhl für Finanzwirtschaft und Corporate Governance
Tutorium in Investition und Finanzierung Entscheidungstheorie Kathrin Holtze, Simon Funken, Sascha Schworm finance-tutorien@wiwi.uni-wuppertal.de Lehrstuhl für Finanzwirtschaft und Corporate Governance
Seminararbeit zur Spieltheorie. Thema: Rationalisierbarkeit und Wissen
 Seminararbeit zur Spieltheorie Thema: Rationalisierbarkeit und Wissen Westfälische-Wilhelms-Universität Münster Mathematisches Institut Dozent: Prof. Dr. Löwe Verfasst von: Maximilian Mümken Sommersemester
Seminararbeit zur Spieltheorie Thema: Rationalisierbarkeit und Wissen Westfälische-Wilhelms-Universität Münster Mathematisches Institut Dozent: Prof. Dr. Löwe Verfasst von: Maximilian Mümken Sommersemester
Carlheinrich Heiland WS 00/01 ABWL- Übungsaufgaben zum Abschnitt I Grundlagen und zum Abschnitt II Entscheidungstheorie Seite 1 von 14
 Seite 1 von 14 I./2. [1] Rationalprinzip a) Welche Handlungsweisen gibt das allgemeine Rationalprinzip vor übertragen auf wirtschaftliche Entscheidungen für die Fälle (1) der output ist fest vorgegeben;
Seite 1 von 14 I./2. [1] Rationalprinzip a) Welche Handlungsweisen gibt das allgemeine Rationalprinzip vor übertragen auf wirtschaftliche Entscheidungen für die Fälle (1) der output ist fest vorgegeben;
Entscheidungs theorie
 Helmut Laux Entscheidungs theorie Sechste, durchgesehene Auflage Mit 95 Abbildungen 4y Springer Inhalts verzeichni s Vorwort Überblick V IX XXI TEILA: EINFÜHRUNG 1 I. Probleme und Lösungskonzepte der Entscheidungstheorie
Helmut Laux Entscheidungs theorie Sechste, durchgesehene Auflage Mit 95 Abbildungen 4y Springer Inhalts verzeichni s Vorwort Überblick V IX XXI TEILA: EINFÜHRUNG 1 I. Probleme und Lösungskonzepte der Entscheidungstheorie
Grundlegende Eigenschaften von Punktschätzern
 Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Grundlegende Eigenschaften von Punktschätzern Worum geht es in diesem Modul? Schätzer als Zufallsvariablen Vorbereitung einer Simulation Verteilung von P-Dach Empirische Lage- und Streuungsparameter zur
Vorlesung 6: Alternativen zur Erwartungsnutzentheorie
 Vorlesung 6: Alternativen zur Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 6 (FS 11) Alternativen zur Erwartungsnutzentheorie 1 / 21 1.
Vorlesung 6: Alternativen zur Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 6 (FS 11) Alternativen zur Erwartungsnutzentheorie 1 / 21 1.
Betriebswirtschaftliche Entscheidungstheorie und Anwendung
 Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 3: Entscheidungen unter Sicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 3: Entscheidungen unter Sicherheit Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft
Formalstruktur: Zur Abbildung der Struktur eines mehrstufigen Entscheidungsproblems ist der Entscheidungsbaum geeignet (ungerichteter Graph)
 Investitionsrechnung 1 Entscheidungsbaumverfahren Entscheidungsbaumverfahren Verfahren zur Berücksichtigung der Unsicherheit bei Investitionseinzelentscheidungen Grundidee: für Beginn eines Planungszeitraums
Investitionsrechnung 1 Entscheidungsbaumverfahren Entscheidungsbaumverfahren Verfahren zur Berücksichtigung der Unsicherheit bei Investitionseinzelentscheidungen Grundidee: für Beginn eines Planungszeitraums
ETWR TEIL B ÜBUNGSBLATT 3 WS14/15
 ETWR TEIL B ÜBUNGSBLATT 3 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
ETWR TEIL B ÜBUNGSBLATT 3 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
3 Wahrscheinlichkeitstheorie
 Einige mathematische Konzepte 3 Wahrscheinlichkeitstheorie 3.1 Wahrscheinlichkeit Die Wahrscheinlichkeitstheorie modelliert Situationen, in denen Unsicherheit über bestimmte Aspekte der Umwelt vorherrscht.
Einige mathematische Konzepte 3 Wahrscheinlichkeitstheorie 3.1 Wahrscheinlichkeit Die Wahrscheinlichkeitstheorie modelliert Situationen, in denen Unsicherheit über bestimmte Aspekte der Umwelt vorherrscht.
37 Gauß-Algorithmus und lineare Gleichungssysteme
 37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
Statische Spiele mit unvollständiger Information: Bayesianische-Spiele
 Statische Spiele mit unvollständiger Information: Bayesianische-Spiele In einigen Situationen verfügen Spieler (nur) über unvollständige Information. Möglicherweise kennen sie die relevanten Charakteristika
Statische Spiele mit unvollständiger Information: Bayesianische-Spiele In einigen Situationen verfügen Spieler (nur) über unvollständige Information. Möglicherweise kennen sie die relevanten Charakteristika
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Prof. Dr. Michael Havbro Faber 28.05.2009 1 Korrektur zur letzten Vorlesung Bsp. Fehlerfortpflanzung in einer Messung c B a 2 2 E c Var c a b A b 2 2 2 n h( x)
Statistik und Wahrscheinlichkeitsrechnung Prof. Dr. Michael Havbro Faber 28.05.2009 1 Korrektur zur letzten Vorlesung Bsp. Fehlerfortpflanzung in einer Messung c B a 2 2 E c Var c a b A b 2 2 2 n h( x)
6. Schätzverfahren für Parameter
 6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung
 Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung Zusammenfassung der Diplomarbeit an der Hochschule Zittau/Görlitz Maria Kiseleva Motivation
Analyse eines zweistufigen, regionalen Clusteralgorithmus am Beispiel der Verbundenen Wohngebäudeversicherung Zusammenfassung der Diplomarbeit an der Hochschule Zittau/Görlitz Maria Kiseleva Motivation
Neue Institutionenökonomik, Aufgabe 18 Seite 1
 Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
 Basiswissen Daten und Zufall Seite 1 von 8 1 Zufallsexperiment Ein Zufallsexperiment ist ein Versuchsaufbau mit zufälligem Ausgang, d. h. das Ergebnis kann nicht vorhergesagt werden. 2 Ergebnis (auch Ausgang)
Basiswissen Daten und Zufall Seite 1 von 8 1 Zufallsexperiment Ein Zufallsexperiment ist ein Versuchsaufbau mit zufälligem Ausgang, d. h. das Ergebnis kann nicht vorhergesagt werden. 2 Ergebnis (auch Ausgang)
Statistik Testverfahren. Heinz Holling Günther Gediga. Bachelorstudium Psychologie. hogrefe.de
 rbu leh ch s plu psych Heinz Holling Günther Gediga hogrefe.de Bachelorstudium Psychologie Statistik Testverfahren 18 Kapitel 2 i.i.d.-annahme dem unabhängig. Es gilt also die i.i.d.-annahme (i.i.d = independent
rbu leh ch s plu psych Heinz Holling Günther Gediga hogrefe.de Bachelorstudium Psychologie Statistik Testverfahren 18 Kapitel 2 i.i.d.-annahme dem unabhängig. Es gilt also die i.i.d.-annahme (i.i.d = independent
Risiko und Versicherung - Übung
 Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
ENTSCHEIDUNGSTHEORIE Klausur vom Die Mindestpunktzahl zum Bestehen der Klausur beträgt 45 Punkte!
 Fachbereich Wirtschaftswissenschaften Professur für Wirtschaftsmathematik Prof. Dr. Heinrich Rommelfanger ENTSCHEIDUNGSTHEORIE Klausur vom 24.02.2006 Als Hilfsmittel sind neben Schreibmaterial zugelassen:
Fachbereich Wirtschaftswissenschaften Professur für Wirtschaftsmathematik Prof. Dr. Heinrich Rommelfanger ENTSCHEIDUNGSTHEORIE Klausur vom 24.02.2006 Als Hilfsmittel sind neben Schreibmaterial zugelassen:
I. Grundlagen. I. Grundlagen 1. Entscheidungen unter Unsicherheit. 1. Entscheidungen unter Unsicherheit
 . Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
. Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
5.2DasKriteriumdeserwartetenNutzens
 5.2DasKriteriumdeserwartetenNutzens BisherhabenwirunsichereSituationen beschrieben, jedoch noch nicht gesagt, wie die HaltunggegenüberRisikodasVerhaltenbeeinflußt.DieswerdenwirindiesemAbschnitt untersuchen.
5.2DasKriteriumdeserwartetenNutzens BisherhabenwirunsichereSituationen beschrieben, jedoch noch nicht gesagt, wie die HaltunggegenüberRisikodasVerhaltenbeeinflußt.DieswerdenwirindiesemAbschnitt untersuchen.
6.6 Poisson-Verteilung
 6.6 Poisson-Verteilung Die Poisson-Verteilung ist eine Wahrscheinlichkeitsverteilung, die zur Modellierung der Anzahl von zufälligen Vorkommnissen in einem bestimmten räumlichen oder zeitlichen Abschnitt
6.6 Poisson-Verteilung Die Poisson-Verteilung ist eine Wahrscheinlichkeitsverteilung, die zur Modellierung der Anzahl von zufälligen Vorkommnissen in einem bestimmten räumlichen oder zeitlichen Abschnitt
9 Lineare Gleichungssysteme
 9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
9 Lineare Gleichungssysteme Eine der häufigsten mathematischen Aufgaben ist die Lösung linearer Gleichungssysteme In diesem Abschnitt beschäftigen wir uns zunächst mit Lösbarkeitsbedingungen und mit der
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz
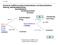 Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Probleme bei reinen Strategien. Nash Gleichgewichte in gemischten Strategien Kopf 1, 1 1, 1 Zahl 1, 1 1, 1. Gemischte Strategien
 Probleme bei reinen Strategien Bisher hatten wir angenommen, daß sich jeder Spieler b auf genau eine Strategie S b S b festlegt. Das ist nicht immer plausibel. Nash Gleichgewichte in gemischten Strategien
Probleme bei reinen Strategien Bisher hatten wir angenommen, daß sich jeder Spieler b auf genau eine Strategie S b S b festlegt. Das ist nicht immer plausibel. Nash Gleichgewichte in gemischten Strategien
Ein multikriterielles, fuzzy- und risikobasiertes Decision Analysis Modell am Beispiel der Planung unterirdischer Infrastruktur
 Ein multikriterielles, fuzzy- und risikobasiertes Decision Analysis Modell am Beispiel der Planung unterirdischer Infrastruktur Bochum 30.09.03 Dipl.-Ing. Dipl.-Wirt.-Ing. Sissis Kamarianakis - Welches
Ein multikriterielles, fuzzy- und risikobasiertes Decision Analysis Modell am Beispiel der Planung unterirdischer Infrastruktur Bochum 30.09.03 Dipl.-Ing. Dipl.-Wirt.-Ing. Sissis Kamarianakis - Welches
Risikomessung mit dem Conditional Value-at-Risk
 Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Vorlesung 2: Erwartungsnutzen
 Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
0607 Investition. Inhalt
 0607 Investition 1 Inhalt 1 Einführung... 13 2 Der Investitionsentscheidungsprozess... 16 2.1 Preview... 16 2.2 Das Wesen einer Investition... 17 2.2.1 Der Investitionsbegriff... 17 2.2.2 Investitionsarten...
0607 Investition 1 Inhalt 1 Einführung... 13 2 Der Investitionsentscheidungsprozess... 16 2.1 Preview... 16 2.2 Das Wesen einer Investition... 17 2.2.1 Der Investitionsbegriff... 17 2.2.2 Investitionsarten...
Einführung in die Maximum Likelihood Methodik
 in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre. Lösungshinweise zur Einsendearbeit 2 (WS 2010/2011)
 Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Übungsaufgaben Lösungen
 Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Erwartungswert, Varianz und Standardabweichung einer Zufallsgröße. Was ist eine Zufallsgröße und was genau deren Verteilung?
 Erwartungswert, Varianz und Standardabweichung einer Zufallsgröße Von Florian Modler In diesem Artikel möchte ich einen kleinen weiteren Exkurs zu meiner Serie Vier Wahrscheinlichkeitsverteilungen geben
Erwartungswert, Varianz und Standardabweichung einer Zufallsgröße Von Florian Modler In diesem Artikel möchte ich einen kleinen weiteren Exkurs zu meiner Serie Vier Wahrscheinlichkeitsverteilungen geben
Reinforcement Learning
 Reinforcement Learning 1. Allgemein Reinforcement Learning 2. Neuronales Netz als Bewertungsfunktion 3. Neuronales Netz als Reinforcement Learning Nils-Olaf Bösch 1 Allgemein Reinforcement Learning Unterschied
Reinforcement Learning 1. Allgemein Reinforcement Learning 2. Neuronales Netz als Bewertungsfunktion 3. Neuronales Netz als Reinforcement Learning Nils-Olaf Bösch 1 Allgemein Reinforcement Learning Unterschied
3.2 Lineare Optimierung (Entscheidungen unter Sicherheit)
 3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
Betriebswirtschaftliche Entscheidungstheorie und Anwendung
 Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 5: Entscheidungen unter Risiko Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft Universität
Betriebswirtschaftliche Entscheidungstheorie und Anwendung Kapitel 5: Entscheidungen unter Risiko Prof. Dr. Thorsten Poddig Lehrstuhl für Allgemeine Betriebswirtschaftslehre, insbes. Finanzwirtschaft Universität
Forschungsstatistik I
 Psychologie Prof. Dr. G. Meinhardt 6. Stock, TB II R. 06-206 (Persike) R. 06-321 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de http://psymet03.sowi.uni-mainz.de/
Psychologie Prof. Dr. G. Meinhardt 6. Stock, TB II R. 06-206 (Persike) R. 06-321 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de http://psymet03.sowi.uni-mainz.de/
8. Reinforcement Learning
 8. Reinforcement Learning Einführung 8. Reinforcement Learning Wie können Agenten ohne Trainingsbeispiele lernen? Auch kennt der Agent zu Beginn nicht die Auswirkungen seiner Handlungen. Stattdessen erhält
8. Reinforcement Learning Einführung 8. Reinforcement Learning Wie können Agenten ohne Trainingsbeispiele lernen? Auch kennt der Agent zu Beginn nicht die Auswirkungen seiner Handlungen. Stattdessen erhält
Vorlesung 2: Präferenzen über Lotterien
 Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 13 Präferenzen über Lotterien 1/26 2.1 Modellrahmen Wir betrachten im
Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 13 Präferenzen über Lotterien 1/26 2.1 Modellrahmen Wir betrachten im
Klassifikation von Daten Einleitung
 Klassifikation von Daten Einleitung Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Klassifikation von Daten Einleitung
Klassifikation von Daten Einleitung Lehrstuhl für Künstliche Intelligenz Institut für Informatik Friedrich-Alexander-Universität Erlangen-Nürnberg (Lehrstuhl Informatik 8) Klassifikation von Daten Einleitung
Vorlesung 2: Präferenzen über Lotterien
 Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 12 Präferenzen über Lotterien 1/24 2.1 Modellrahmen Wir betrachten im
Vorlesung 2: Präferenzen über Lotterien Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2, FS 12 Präferenzen über Lotterien 1/24 2.1 Modellrahmen Wir betrachten im
Die Psychologie der Entscheidung
 Helmut Jungermann, Hans-Rüdiger Pfister, Katrin Fischer Die Psychologie der Entscheidung Eine Einführung Spektrum Akademischer Verlag Heidelberg Berlin Inhalt Vorwort xi 1 Gegenstandsbereich l 1.1 Der
Helmut Jungermann, Hans-Rüdiger Pfister, Katrin Fischer Die Psychologie der Entscheidung Eine Einführung Spektrum Akademischer Verlag Heidelberg Berlin Inhalt Vorwort xi 1 Gegenstandsbereich l 1.1 Der
Euklidische und unitäre Vektorräume
 Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Grundzüge der. Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit
 Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof. Dr. Ulrich Reif
 14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
Lineares Gleichungssystem - Vertiefung
 Lineares Gleichungssystem - Vertiefung Die Lösung Linearer Gleichungssysteme ist das "Gauß'sche Eliminationsverfahren" gut geeignet - schon erklärt unter Z02. Alternativ kann mit einem Matrixformalismus
Lineares Gleichungssystem - Vertiefung Die Lösung Linearer Gleichungssysteme ist das "Gauß'sche Eliminationsverfahren" gut geeignet - schon erklärt unter Z02. Alternativ kann mit einem Matrixformalismus
Anlage 025. zum Abschlussbericht ExpG-R. Kostennutzwertanalyse
 Anlage 025 zum Abschlussbericht ExpG-R Kostennutzwertanalyse Nutzwertanalyse der 1. Generation relativ einfach trotzdem effektiv komplexe Entscheidungsprozesse mit o quantitativen und/oder o qualitativen
Anlage 025 zum Abschlussbericht ExpG-R Kostennutzwertanalyse Nutzwertanalyse der 1. Generation relativ einfach trotzdem effektiv komplexe Entscheidungsprozesse mit o quantitativen und/oder o qualitativen
Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza)
 SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
SS 2013 Zentralübung Diskrete Wahrscheinlichkeitstheorie (zur Vorlesung Prof. Esparza) Dr. Werner Meixner Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2013ss/dwt/uebung/ 10. Mai 2013
Statistische Tests (Signifikanztests)
 Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
Statistische Tests (Signifikanztests) [testing statistical hypothesis] Prüfen und Bewerten von Hypothesen (Annahmen, Vermutungen) über die Verteilungen von Merkmalen in einer Grundgesamtheit (Population)
2.3 Kriterien der Entscheidungsfindung: Präferenzen
 .3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
.3 Kriterien der Entscheidungsfindung: Präferenzen Der Einfachheit halber beschränken wir uns auf n = ( zwei Güter). Annahme: Konsumenten können für sich herausfinden, ob sie x = ( x, ) dem Güterbündel
2. Lösung weitere Übungsaufgaben Statistik II WiSe 2016/2017
 . Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
. Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
Grundlagen der Versicherungs- und Sozialversicherungsökonomik. Risiko: objektive oder subjektive Wahrscheinlichkeiten
 Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Beispiele 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix (A
 133 e 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 2. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 Schritte des
133 e 1. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 2. Gegeben sei das lineare Gleichungssystem mit erweiterter Matrix 1 3 2 1 1 2 3 0. 1 3 2 1 Schritte des
Beispiele 1. Gegeben ist das lineare System. x+4y +3z = 1 2x+5y +9z = 14 x 3y 2z = 5. Die erweiterte Matrix ist
 127 Die Schritte des Gauß-Algorithmus sind nun die Folgenden: 1. Wir bestimmen die am weitesten links stehende Spalte, die Einträge 0 enthält. 2. Ist die oberste Zahl der in Schritt 1 gefundenen Spalte
127 Die Schritte des Gauß-Algorithmus sind nun die Folgenden: 1. Wir bestimmen die am weitesten links stehende Spalte, die Einträge 0 enthält. 2. Ist die oberste Zahl der in Schritt 1 gefundenen Spalte
Eigenwerte und Eigenvektoren
 Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
Eigenwerte und Eigenvektoren Siehe Analysis (von der Hude, Folie 20: Definition 2.3. Ein Vektor x R n heißt Eigenvektor der quadratischen n n-matrix A zum Eigenwert λ R, wenn gilt Ax = λx Die Eigenwerte
Die Nutzwertanalyse - NWA Prof. Dr. Wolfgang Alm Prof. Dr. Georg Rainer Hofmann
 Die Nutzwertanalyse - NWA Prof. Dr. Wolfgang Alm Prof. Dr. Georg Rainer Hofmann 03.03.2016 Copyright Der nachfolgende Foliensatz basiert auf einem Foliensatz von Herrn Andreas Ziegler vom 15.10.2015 Er
Die Nutzwertanalyse - NWA Prof. Dr. Wolfgang Alm Prof. Dr. Georg Rainer Hofmann 03.03.2016 Copyright Der nachfolgende Foliensatz basiert auf einem Foliensatz von Herrn Andreas Ziegler vom 15.10.2015 Er
