2.4 Entscheidung bei Risiko
|
|
|
- Liese Kramer
- vor 6 Jahren
- Abrufe
Transkript
1 2.4 Entscheidung bei Risiko Entscheidung bei Risiko nimmt an, dass für jeden Zustand S j seine Eintrittswahrscheinlichkeit P(S j ) bekannt ist Eintrittswahrscheinlichkeiten bestimmbar als statistische Wahrscheinlichkeiten basierend auf Erfahrungen aus der Vergangenheit (z.b. wie oft hat es an diesem Tag in den letzten 100 Jahren geregnet) subjektive Wahrscheinlichkeiten basierend auf den Erwartungen des Entscheiders 54
2 Diskrete Zufallsvariable Sei X eine diskrete Zufallsvariable mit möglichen Werten {a 1,,a n } und Wahrscheinlichkeiten P(X = a i ), Erwartungswert einer diskreten Zufallsvariable X ist µ = E(X) = nÿ a i P (X = a i ) i=1 Beispiel: Fairer Würfel mit sechs Seiten E(X) = =3.5 55
3 Diskrete Zufallsvariable Varianz einer diskreten Zufallsvariable X ist nÿ 2 = V (X) = (a i µ) 2 P (X = a i ) und es gilt i=1 V (X) =E(X E(X)) 2 = E(X 2 ) (E(X)) 2 Größe σ heißt Standardabweichung (auch: Streuung) Beispiel: Fairer Würfel mit sechs Seiten V (X) =(1 3.5) (2 3.5) (6 3.5)2 1 6 =
4 Dominanz bei Unsicherheit Konzept der Dominanz lässt sich auf den Fall mehrerer Zustände erweitern absolute Dominanz betrachtet nur das schlechtmöglichste und bestmöglichste Ergebnis je Alternative Zustandsdominanz vergleich die Ergebnisse der Alternativen zustandsweise stochastische Dominanz (erster Ordnung) betrachtet auch die Wahrscheinlichkeiten der Zustände 57
5 Absolute Dominanz Alternative A i dominiert Alternative A j im Sinne absoluter Dominanz, wenn gilt min k (x ik ) Ø max d.h. das schlechteste Ergebnis von A i ist mindestens so gut wie das beste Ergebnis von A j k (x jk) Beispiel: S 1 S 2 S 3 S A A A 1 dominiert A 2 58
6 Zustandsdominanz Alternative A i dominiert Alternative A j im Sinne der Zustandsdominanz, wenn gilt k : x ik Ø x jk : k : x ik >x jk d.h. A i ist in allen Zuständen mindestens so gut wie A j und in mindestens einem besser Beispiel: S 1 S 2 S 3 S A A A 2 dominiert A 1 59
7 Stochastische Dominanz Stochastische Dominanz beruht auf Vergleich der Wahrscheinlichkeitsverteilungen der Alternativen Betrachte Alternative A i als Zufallsvariable, dann sei P (A i Æ x i ) die Wahrscheinlichkeit, dass A i zu einen Ergebnis kleiner gleich x i führt 60
8 Stochastische Dominanz Beispiel: S 1 S 2 S 3 S A A P (A i Æ 10) P (A i Æ 20) P (A i Æ 50) P (A i Æ 100) A A A 1 A
9 Stochastische Dominanz Stochastische Dominanz (erster Ordnung) der Alternative A i über die Alternative A j liegt vor, wenn x : P (A i Æ x) Æ P (A j Æ x) x : P (A i Æ x) <P(A j Æ x) x : P (A i >x) Ø P (A j >x) x : P (A i >x) >P(A j >x) Beispiel: Alternative A 2 dominiert Alternative A 1 A 1 A
10 Risikoeinstellung des Entscheiders Risikoneutralität Entscheider ist indifferent zwischen Alternativen mit gleichem Erwartungswert Risikoaversion Entscheider zieht bei zwei Alternativen mit gleichem Erwartungswert diejenige mit geringerer Streuung vor Risikofreude Entscheider zieht bei zwei Alternativen mit gleichem Erwartungswert diejenige mit höherer Streuung vor 63
11 Risikoeinstellung des Entscheiders Beispiel: Entscheidung über Teilnahme an einfachem Glücksspiel (z.b. Münzwurf) mit Einsatz 10 A 1 : Teilnahme, A 2 : Nicht-Teilnahme S 1 : Gewinn, S 2 : Kein Gewinn S 1 S 2 µ A A A 1 oder A 2 bei Risikoneutralität A 1 bei Risikofreude A 2 bei Risikoaversion 64
12 Indifferenzkurven nach Risikoeinstellung µ µ µ Risikoneutralität Risikoaversion Risikofreude 65
13 µ-regel μ-regel beurteilt Alternativen nach ihrem Erwartungswert (ursprünglich formuliert für den Fall einer Zielgröße) (A i )=E(x ij )= nÿ x ij P (S j ) j=1 Risikoeinstellung des Entscheiders nicht berücksichtigt 66
14 µ-regel Beispiel: Lotterie mit 5 Millionen im Jackpot und Einsatz 3 A 1 : Teilnahme, A 2 : Nicht-Teilnahme S 1 : Gewinn, S 2 : Kein Gewinn S 1 S 2 µ A 1 4, 999, A Entscheider wird niemals an der Lotterie teilnehmen, sofern er die µ-regel anwendet 67
15 (µ,σ)-prinzip (µ,σ)-prinzip berücksichtigt neben dem Erwartungswert die Standardabweichung der Ergebnisse zur Beurteilung der Alternativen Präferenzfunktion Φ(A i ) = Φ(µ i, σ i ) z.b. als Linearkombination von Erwartungswert µ i und Standardabweichung σ i definiert (A i )=µ i i mit α als Gewichtungsparameter, welcher die Risikoeinstellung des Entscheiders erfasst (α > 0 : Risikoaversion; α < 0 : Risikofreude) 68
16 (µ,σ)-prinzip Beispiel: S 1 S 2 S 3 µ =+1 =0 = A A A
17 (μ,σ)-prinzip und stochastische Dominanz Stochastische Dominanz erster Ordnung und (µ,σ)-prinzip sind inkompatibel, d.h. wir eliminieren u.u. optimale Alternativen Beispiel: S 1 S 2 µ A A A 2 würde eliminiert, ist aber für risikofreudige Entscheider (z.b. α = -1.0) u.u. optimal A 1 A
18 Petersburger Spiel Petersburger Spiel (auch: Petersburger Paradoxon) wiederholter Wurf einer fairen Münze (Kopf oder Zahl) fällt im n-ten Münzwurf erstmals Zahl, so erhält Spieler 2 n Erwartungswert des Petersburger Spiels µ = = Œ Ein nach der µ-regel handelnder Entscheider wäre also immer bereit, einen beliebig großen Betrag einzusetzen und am Spiel teilnehmen 71
19 Bernoulli-Prinzip Bisherige Ansätze zur Entscheidung bei Risiko betrachten nur eine Zielgröße und verdichten Zielgrößenwerte in den Parametern µ und σ Bernoulli-Prinzip besteht aus zwei Schritten bestimme für den Entscheider eine Nutzenfunktion U(x i ) (z.b. mittels Durchführung einer Bernoulli-Befragung) wähle eine Alternative mit höchstem erwarteten Nutzen (auch: Bernoulli-Nutzen, Erwartungsnutzen) (A i )= nÿ U(x ij ) P (S j ) j=1 72
20 Bernoulli-Prinzip Wo liegt der Unterschied zur µ-regel und (µ,σ)-prinzip? es können mehrere Zielgrößen betrachtet werden explizite Betrachtung von Nutzen anstelle von Zielgröße Nutzenfunktion erfasst Risikoeinstellung des Entscheiders 73
21 Nutzenfunktionen und Risikoeinstellung Krümmung der Nutzenfunktion lässt auf die tionale Entscheidung bei Risiko: Das Bernoulli-Prinzip 118 Rationale Entscheidung bei Risiko: Das Bernoulli-Pr x 0 Risikoeinstellung des Entscheiders5 schließen Risikoneutralität U(x) x 0 U(x) U(x) U(x) U(x) Risikoaversion konkav x 0 U(x) Risikoneutralität x 00 U Risikoaversion Risikofreude xx konvex Abb. 5.1U(x) Der Verlauf unterschiedlicher Nutzenfun veranschaulicht bereits Abschn. Quelle: Laux,werden Gillenkirch(vgl. und Schenk-Mathes [1] die Entscheidung gestellt, an einem Glückssp Wahrscheinlichkeit 0,5 (z. B. durch den Wurf e verlieren kann. Beträgt sein gegenwärtiges Verm am Glücksspiel entweder W +! oder W!. x x x 0 0 sind,xbeträgt0der Erwartungswert W. Ist der Ent Risikofreude ferent bezüglich der Teilnahme am Glücksspiel. zenfunktionen Abb. 5.1 Der Verlauf unterschiedlicher Nutzenfunktionen strikt ab. Ein risikofreudiger Entscheider dageg Um dieses Entscheidungsverhalten über da Entscheidungsunterstützende Systeme / Kapitel 2: Entscheidungstheorie 74 bschn. 4.4 des Kap. 4): Ein Entscheider veranschaulicht wird vor werden (vgl. bereits Abschn. 4.4der despräferenzfunktion Kap. 4): Ein Entscheider wird tierung an (5.1) nachzu
22 Bernoulli-Befragung Nutzenfunktion des Entscheiders lässt sich mittels Bernoulli-Befragung approximieren bestimme schlechtestes und bestes Ergebnis x w und x b für jedes Ergebnis bestimmt man die Wahrscheinlichkeit w i, so dass der Entscheider indifferent ist zwischen dem sicheren Ergebnis x i einer Lotterie, die mit Wahrscheinlichkeit w i das Ergebnis x b und mit Wahrscheinlichkeit (1-w i ) das Ergebnis x w auszahlt die ermittelten Wahrscheinlichkeiten w i können als Werte der Nutzenfunktion U(x i ) interpretiert werden 75
23 Bernoulli-Befragung Beispiel: Ergebnisse x w = 0, 20, 40, 60, 80, 100 = x b möglich für x 0 = 0 gibt Entscheider Wahrscheinlichkeit w 0 = 0.0 an für x 1 = 20 gibt Entscheider Wahrscheinlichkeit w 1 = 0.4 an für x 2 = 40 gibt Entscheider Wahrscheinlichkeit w 2 = 0.6 an für x 3 = 60 gibt Entscheider Wahrscheinlichkeit w 3 = 0.8 an für x 4 = 80 gibt Entscheider Wahrscheinlichkeit w 4 = 0.9 an für x 5 = 100 gibt Entscheider Wahrscheinlichkeit w 5 = 1.0 an 76
24 Bernoulli-Befragung Beispiel: Ermittelte Nutzenfunktion w Risikoaverser Entscheider x 77
25 Zusammenfassung Risikoeinstellung des Entscheiders spielt eine Rolle risikoavers, risikoneutral oder risikofreudig Entscheidung bei Risiko und einer Zielgröße μ-regel betrachtet nur Erwartungswert (µ,σ)-prinzip betrachtet Erwartungswert und Streuung Bernoulli-Prinzip bei Risiko und beliebig vielen Zielgrößen Bernoulli-Befragung zum Bestimmen einer Nutzenfunktion Auswahl der Alternative mit höchstem erwarteten Nutzen 78
26 Literatur [1] H. Laux, R. M. Gillenkirch und H. Y. Schenk-Mathes: Entscheidungstheorie, Springer 2014 (Kapitel 4 und 5) [2] Hagenloch T.: Grundzüge der Entscheidungslehre, Books on Demand GmbH 2009 (Kapitel 4) 79
2.2 Entscheidung bei Sicherheit
 2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
2.2 Entscheidung bei Sicherheit Umweltzustand ist bekannt oder irrelevant, so dass die Ergebnisse der Handlungsalternativen sicher sind Bei mehreren Zielgrößen besteht die Herausforderung darin, den Entscheider
3. Betriebswirtschaftliche Entscheidungslehre 3.6 Entscheidung unter Risiko
 Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Dominanzprinzipien : Absolute Dominanz: Eine Alternative A i dominiert eine Alternative A j absolut, wenn das geringstmögliche Ergebnis von A i nicht kleiner ist als das grösstmögliche Ergebnis von A j,
Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }.
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
I. Grundlagen. I. Grundlagen 1. Entscheidungen unter Unsicherheit. 1. Entscheidungen unter Unsicherheit
 . Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
. Entscheidungen unter Unsicherheit I. Grundlagen. Entscheidungen unter Unsicherheit Elemente des Entscheidungsproblems eines Wirtschaftssubekts: Der Entscheidungsträger kann zwischen verschiedenen Aktionen
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Stefan Neuß Sebastian Soika http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_203/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko und Versicherung Entscheidungstheoretische Grundlagen
 Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Übung zu Risiko Entscheidungstheoretische Grundlagen Christoph Lex Dominik Lohmaier http://www.inriver.bwl.lmu.de Newsletter Auf der Homepage unter http://www.inriver.bwl.uni-muenchen.de/studium/sommer_04/bachelorveranstaltungen/risiko_und_versicherungen/index.html
Grundzüge der. Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit
 Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Grundzüge der Kapitel 5 Mikroökonomie (Mikro I) Entscheidungen unter Unsicherheit 1 BESCHREIBUNG VON RISIKO 2 Entscheidung unter Risiko Annahme: Wir kennen alle möglichen (sich gegenseitig ausschliessenden)
Kapitel 8. Erwarteter Nutzen. Intertemporaler Nutzen für Mehrperioden-Entscheidungen
 Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Kapitel 8 Erwarteter Nutzen Josef Leydold c 2006 Mathematische Methoden VIII Erwarteter Nutzen / 27 Lernziele Nutzenfunktion zur Risikobewertung Erwarteter Nutzen Maße für Risikoaversion Indifferenzkurven
Wichtige Informationen vorab
 Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
Wichtige Informationen vorab Wir haben eine Mailing Liste "Vorles- UebSS09Kapitalmarkt" eingerichtet. Über diese Mailingliste erhalten Sie in Zukunft die Vorlesungsunterlagen und die Übungsunterlagen.
Vorlesung 3: Risikoaversion
 Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Vorlesung 3: Risikoaversion Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 3 (FS 11) Risikoaversion 1 / 21 1. Modellrahmen In diesem Kapitel betrachten wir nur monetäre
Mikroökonomik. Unsicherheit. Harald Wiese. Universität Leipzig. Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46
 Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
Mikroökonomik Unsicherheit Harald Wiese Universität Leipzig Harald Wiese (Universität Leipzig) Unsicherheit 1 / 46 Gliederung Einführung Haushaltstheorie Das Budget Präferenzen, Indi erenzkurven und Nutzenfunktionen
2. Entscheidungsregeln. Handhabung von Unsicherheit
 II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
II Agenda 1. Sensitivitätsanalyse 2. Entscheidungsregeln 3. Dialektische Planung 2 1. Sensitivitätsanalyse 3 Definition: Sensitivitätsanalyse = Sensibilitätsanalyse Empfindlichkeitsanalyse Verfahren zur
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38
 Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Prof. Dr. H. Rommelfanger: Entscheidungstheorie, Kapitel 3 38 Offene Fragen Warum ist ein ET bereit, für eine Feuerversicherung mit einer Versicherungshöhe von 1 Million und einer Jahreseintrittswahrscheinlichkeit
Grundlagen der Versicherungs- und Sozialversicherungsökonomik. Risiko: objektive oder subjektive Wahrscheinlichkeiten
 Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Grundlagen der Versicherungs- und Sozialversicherungsökonomik Entscheidungstheorie bei Sicherheit (z. B. trad. Mikroökonomik, lineare Programmierung etc. bei Risiko (Unsicherheit und Ungewissheit Risiko:
Übung zur Vorlesung Multiagentensysteme
 Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Ludwig-Maximilians-Universität München SS 2007 Institut für Informatik Aufgabenblatt 1 Dr. Brandt / Fischer & Harrenstein 23. April 2007 Übung zur Vorlesung Multiagentensysteme Tutorübung: 25. April 2007
Vorlesung 2: Risikopräferenzen im Zustandsraum
 Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
Vorlesung 2: Risikopräferenzen im Zustandsraum Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie VL 2, FS 12 Risikopräferenzen im Zustandsraum 1/29 2.1 Motivation
1.5 Erwartungswert und Varianz
 Ziel: Charakterisiere Verteilungen von Zufallsvariablen (Bildbereich also reelle Zahlen, metrische Skala) durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere:
Ziel: Charakterisiere Verteilungen von Zufallsvariablen (Bildbereich also reelle Zahlen, metrische Skala) durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere:
Entscheidungstheorie Teil 4
 Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
Entscheidungstheorie Teil 4 Sommersemester 2011 Prof. Dr. Antje Mahayni Mercator School of Management Department of Accounting & Finance Prof. Dr. Antje Mahayni Entscheidungstheorie Teil 4 1/74 Gliederung
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz
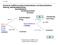 Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
Nochmal: Indifferenzwahrscheinlichkeiten und Nutzenfunktion Reihung: Selbständigkeit Erfolg Geschäftsführer Vorstandsassistent Insolvenz Ref.-L.1: Selbst. Erfolg Sicher (300000) π = 1 1-π = 0 Selbständigkeit
1.5 Erwartungswert und Varianz
 Ziel: Charakterisiere Verteilungen von Zufallsvariablen durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere: a) durchschnittlicher Wert Erwartungswert, z.b.
Ziel: Charakterisiere Verteilungen von Zufallsvariablen durch Kenngrößen (in Analogie zu Lage- und Streuungsmaßen der deskriptiven Statistik). Insbesondere: a) durchschnittlicher Wert Erwartungswert, z.b.
73 Hypothesentests Motivation Parametertest am Beispiel eines Münzexperiments
 73 Hypothesentests 73.1 Motivation Bei Hypothesentests will man eine gewisse Annahme über eine Zufallsvariable darauf hin überprüfen, ob sie korrekt ist. Beispiele: ( Ist eine Münze fair p = 1 )? 2 Sind
73 Hypothesentests 73.1 Motivation Bei Hypothesentests will man eine gewisse Annahme über eine Zufallsvariable darauf hin überprüfen, ob sie korrekt ist. Beispiele: ( Ist eine Münze fair p = 1 )? 2 Sind
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
70 Wichtige kontinuierliche Verteilungen
 70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
70 Wichtige kontinuierliche Verteilungen 70. Motivation Zufallsvariablen sind nicht immer diskret, sie können oft auch jede beliebige reelle Zahl in einem Intervall [c, d] einnehmen. Beispiele für solche
STATISTIK Teil 2 Wahrscheinlichkeitsrechnung und schließende Statistik
 Kapitel 11 Diskrete Zufallsvariablen 11.1. Wahrscheinlichkeits- und diskret Wahrscheinlichkeitsverteilungen Wahrscheinlichkeitsfunktion von X Nimmt abzählbare Anzahl von Ausprägungen an (z.b. Zählvariablen)
Kapitel 11 Diskrete Zufallsvariablen 11.1. Wahrscheinlichkeits- und diskret Wahrscheinlichkeitsverteilungen Wahrscheinlichkeitsfunktion von X Nimmt abzählbare Anzahl von Ausprägungen an (z.b. Zählvariablen)
Finanzierung und Investition
 Kruschwitz/Husmann (2012) Finanzierung und Investition 1/40 Finanzierung und Investition Kruschwitz/Husmann (2012) Oldenbourg Verlag München 7. Auflage, Kapitel 2 Kruschwitz/Husmann (2012) Finanzierung
Kruschwitz/Husmann (2012) Finanzierung und Investition 1/40 Finanzierung und Investition Kruschwitz/Husmann (2012) Oldenbourg Verlag München 7. Auflage, Kapitel 2 Kruschwitz/Husmann (2012) Finanzierung
Vergleich von Entscheidungsträgern bzgl. ihrer Risikoaversion:
 Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Wann ist diese Vorgehensweise berechtigt? Hierzu:
 IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
IV. Risiko und Unsicherheit Risiko: Eine Entscheidung treffen, ohne den wahren Zustand der Welt zu kennen. Aber man kennt die Wahrscheinlichkeitsverteilung für die relevanten Zustände der Welt. z. B. {
Vorlesung 1: Einleitung
 Vorlesung 1: Einleitung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 1, FS 12 Einleitung 1/17 1.1 Motivation In der Vorlesung Intermediate Microecoomics haben
Vorlesung 1: Einleitung Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 1, FS 12 Einleitung 1/17 1.1 Motivation In der Vorlesung Intermediate Microecoomics haben
Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz 1 betragen (2) Weniger als 3 mal Wappen ( ) 32 (3) Mindestens 1 mal Wappen ( )
 R. Brinkmann http://brinkmann-du.de Seite 7.09.0 Lösungen Stochastik vermischt II Ergebnisse: E E E E4 E E6 Ergebnis Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz betragen. Ergebnisse
R. Brinkmann http://brinkmann-du.de Seite 7.09.0 Lösungen Stochastik vermischt II Ergebnisse: E E E E4 E E6 Ergebnis Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz betragen. Ergebnisse
Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt, dann erwarten wir im Mittel 8 Treffer.
 R. Brinkmann http://brinkmann-du.de Seite 1 06.1008 Erwartungswert binomialverteilter Zufallsgrößen. Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt,
R. Brinkmann http://brinkmann-du.de Seite 1 06.1008 Erwartungswert binomialverteilter Zufallsgrößen. Wird ein Bernoulli- Versuch, bei dem die Trefferwahrscheinlichkeit p = 0,2 ist, n = 40 mal durchgeführt,
Kapitel VII - Funktion und Transformation von Zufallsvariablen
 Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel VII - Funktion und Transformation von Zufallsvariablen Markus Höchstötter Lehrstuhl
Universität Karlsruhe (TH) Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel VII - Funktion und Transformation von Zufallsvariablen Markus Höchstötter Lehrstuhl
Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre. Lösungshinweise zur Einsendearbeit 2 (WS 2010/2011)
 Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Wahrscheinlichkeitstheorie 2
 Wahrscheinlichkeitstheorie 2 Caroline Sporleder Computational Linguistics Universität des Saarlandes Sommersemester 2011 19.05.2011 Caroline Sporleder Wahrscheinlichkeitstheorie 2 (1) Wiederholung (1):
Wahrscheinlichkeitstheorie 2 Caroline Sporleder Computational Linguistics Universität des Saarlandes Sommersemester 2011 19.05.2011 Caroline Sporleder Wahrscheinlichkeitstheorie 2 (1) Wiederholung (1):
Risikomessung mit dem Conditional Value-at-Risk
 Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Vorlesung 6: Alternativen zur Erwartungsnutzentheorie
 Vorlesung 6: Alternativen zur Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 6 (FS 11) Alternativen zur Erwartungsnutzentheorie 1 / 21 1.
Vorlesung 6: Alternativen zur Erwartungsnutzentheorie Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 6 (FS 11) Alternativen zur Erwartungsnutzentheorie 1 / 21 1.
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik. PD Dr. U. Ludwig. Vorlesung 7 1 / 19
 Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, Annahmen:
 1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
1 Grundlagen Entscheidungstheorie: Der Entscheidungsträger wählt aus einer Menge von Alternativen, dem Aktionenraum A = {a 1, a 2, a m }. Annahmen: Der Entscheidungsträger ist gezwungen, eine der betrachteten
Neue Institutionenökonomik, Aufgabe 18 Seite 1
 Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Neue Institutionenökonomik, Aufgabe 18 Seite 1 Allgemeine Informationen zum Principal-Agent-Modell Es geht hier nun um die Vertragsausgestaltung zwischen dem Eigentümer (Prinzipal) einer Firma und dem
Finanzwirtschaft. Foliensatz Vertiefungskurs aus ABWL: im Sommersemester Teil / 2 und 7 Univ. Ass. Dr. Matthias G.
 Universität Wien Institut für Betriebswirtschaftslehre ABWL IV: Finanzwirtschaft 400 026/2+7 Univ. Ass. Dr. M.G. Schuster Foliensatz Vertiefungskurs aus ABWL: Finanzwirtschaft im Sommersemester 2004 2.
Universität Wien Institut für Betriebswirtschaftslehre ABWL IV: Finanzwirtschaft 400 026/2+7 Univ. Ass. Dr. M.G. Schuster Foliensatz Vertiefungskurs aus ABWL: Finanzwirtschaft im Sommersemester 2004 2.
Musterklausur zur MSc-Vorlesung Entscheidungsverhalten
 Dr. Moritz Lukas und Prof. Dr. Markus Nöth Institut für Versicherungsbetriebslehre und Lehrstuhl für Bankbetriebslehre und Behavioral Finance Musterklausur zur MSc-Vorlesung Entscheidungsverhalten Name,
Dr. Moritz Lukas und Prof. Dr. Markus Nöth Institut für Versicherungsbetriebslehre und Lehrstuhl für Bankbetriebslehre und Behavioral Finance Musterklausur zur MSc-Vorlesung Entscheidungsverhalten Name,
K3 (Diskrete) Zufallsvariablen 3.1 Basis
 K3 (Diskrete) Zufallsvariablen 3.1 Basis Ω = {ω}, X(ω) ist eine Größe die durch ω bestimmt ist. Bei der zufälligen Auswahl von ω bekommen wir den Wert, X(ω). Definition: Ist (Ω, F, P) ein Wahrscheinlichkeitsraum
K3 (Diskrete) Zufallsvariablen 3.1 Basis Ω = {ω}, X(ω) ist eine Größe die durch ω bestimmt ist. Bei der zufälligen Auswahl von ω bekommen wir den Wert, X(ω). Definition: Ist (Ω, F, P) ein Wahrscheinlichkeitsraum
Stimmt das immer und in welchem Sinne?
 1 KAP 6. Dominanz und Nash-GG Nash-GG (teilweise) dadurch motiviert: schränkt Menge möglicher Spielausgänge stärker ein als Dominanz Stimmt das immer und in welchem Sinne? Gibt s stets weniger Nash-GGe
1 KAP 6. Dominanz und Nash-GG Nash-GG (teilweise) dadurch motiviert: schränkt Menge möglicher Spielausgänge stärker ein als Dominanz Stimmt das immer und in welchem Sinne? Gibt s stets weniger Nash-GGe
Beispiel 37. Wir werfen eine Münze so lange, bis zum ersten Mal
 Beispiel 37 Wir werfen eine Münze so lange, bis zum ersten Mal Kopf erscheint. Dies geschehe in jedem Wurf unabhängig mit Wahrscheinlichkeit p. Wir definieren dazu die Zufallsvariable X := Anzahl der Würfe.
Beispiel 37 Wir werfen eine Münze so lange, bis zum ersten Mal Kopf erscheint. Dies geschehe in jedem Wurf unabhängig mit Wahrscheinlichkeit p. Wir definieren dazu die Zufallsvariable X := Anzahl der Würfe.
Statistik III. Walter Zucchini Fred Böker Andreas Stadie
 Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
4.4 Punktschätzung. E(X 1 )+ +E(X n ) Var(ˆµ) = 1 n 2 ( Var(X1 )+ +Var(X n ) ) = 1 n 2nσ2 = σ2
 4 4.4 Punktschätzung Wir betrachten eine endliche oder unendliche Grundgesamtheit, zum Beispiel alle Studierenden der Vorlesung Mathe II für Naturwissenschaften. Im endlichen Fall soll die Anzahl N ihrer
4 4.4 Punktschätzung Wir betrachten eine endliche oder unendliche Grundgesamtheit, zum Beispiel alle Studierenden der Vorlesung Mathe II für Naturwissenschaften. Im endlichen Fall soll die Anzahl N ihrer
Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
 Die Riskoprämie ergibt sich also als ein Vielfaches der Varianz der zugrundeliegenden Unsicherheit Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
Die Riskoprämie ergibt sich also als ein Vielfaches der Varianz der zugrundeliegenden Unsicherheit Dieses Vielfach hängt ab von der Form der Nutzenfunktion. Man bezeichnet dies auch als Arrow-Pratt Koeffizient.
Investitionsmanagement
 Investitionsmanagement - Vorlesung 12 am 31012017 - Laura Gerke-Teufel, MA, LLM Ausgewählte Verfahren der unterjährigen Verzinsung - 2 - Unterjährige Effektivzinsberechnung Investitionsmanagement Vorlesung
Investitionsmanagement - Vorlesung 12 am 31012017 - Laura Gerke-Teufel, MA, LLM Ausgewählte Verfahren der unterjährigen Verzinsung - 2 - Unterjährige Effektivzinsberechnung Investitionsmanagement Vorlesung
9 Erwartungswert, Varianz und Standardabweichung einer Zufallsgröÿe
 Übungsmaterial 9 Erwartungswert, Varianz und Standardabweichung einer Zufallsgröÿe 9. Erwartungswert Fragt man nach dem mittleren Wert einer Zufallsgröÿe X pro Versuch, so berechnet man den Erwartungswert
Übungsmaterial 9 Erwartungswert, Varianz und Standardabweichung einer Zufallsgröÿe 9. Erwartungswert Fragt man nach dem mittleren Wert einer Zufallsgröÿe X pro Versuch, so berechnet man den Erwartungswert
Grundbegriffe der Wahrscheinlichkeitsrechnung
 Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Propädeutikum Wahrscheinlichkeitsrechnung
 Winter 010/011 Propädeutikum Wahrscheinlichkeitsrechnung Ferdinand Zahn Johannes Jaspersen Vijay Aseervatham Arthur Seibold Maximilian Engel Ansprechpartner Andreas Richter Sprechstunde: siehe Homepage
Winter 010/011 Propädeutikum Wahrscheinlichkeitsrechnung Ferdinand Zahn Johannes Jaspersen Vijay Aseervatham Arthur Seibold Maximilian Engel Ansprechpartner Andreas Richter Sprechstunde: siehe Homepage
2. Rechnen Sie auf mindestens fünf genaue Ziffern (das sind nicht notwendigerweise fünf Nachkommastellen) im Endergebnis. 1
 Fach: Prüfer: Finanzierung und Investition Prof. Dr. Dr. A. Löffler Veranstaltung: W2261 Entscheidungstheorie WS 8/9 Name Vorname Matrikelnummer Punkte Note Beachten Sie bitte folgende Hinweise: 1. Schreiben
Fach: Prüfer: Finanzierung und Investition Prof. Dr. Dr. A. Löffler Veranstaltung: W2261 Entscheidungstheorie WS 8/9 Name Vorname Matrikelnummer Punkte Note Beachten Sie bitte folgende Hinweise: 1. Schreiben
Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel
 Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel Aufgaben Lösen Sie A1 und A sowohl mit der Bernoulli-Formel als auch mit dem TR(BV), die anderen Aufgaben lösen sie mit dem TR(BV). A1 Eine Familie
Wahrscheinlichkeit3 Binomialverteilung/Bernoulli-Formel Aufgaben Lösen Sie A1 und A sowohl mit der Bernoulli-Formel als auch mit dem TR(BV), die anderen Aufgaben lösen sie mit dem TR(BV). A1 Eine Familie
ETWR TEIL B ÜBUNGSBLATT 3 WS14/15
 ETWR TEIL B ÜBUNGSBLATT 3 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
ETWR TEIL B ÜBUNGSBLATT 3 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
5 Binomial- und Poissonverteilung
 45 5 Binomial- und Poissonverteilung In diesem Kapitel untersuchen wir zwei wichtige diskrete Verteilungen d.h. Verteilungen von diskreten Zufallsvariablen): die Binomial- und die Poissonverteilung. 5.1
45 5 Binomial- und Poissonverteilung In diesem Kapitel untersuchen wir zwei wichtige diskrete Verteilungen d.h. Verteilungen von diskreten Zufallsvariablen): die Binomial- und die Poissonverteilung. 5.1
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
Motivation. Benötigtes Schulwissen. Übungsaufgaben. Wirtschaftswissenschaftliches Zentrum 10 Universität Basel. Statistik
 Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Statistik Dr. Thomas Zehrt Ausblick Motivation Wir werfen einen Würfel 000-mal und wir möchten die Wahrscheinlichkeit P bestimmen, dass zwischen
Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Statistik Dr. Thomas Zehrt Ausblick Motivation Wir werfen einen Würfel 000-mal und wir möchten die Wahrscheinlichkeit P bestimmen, dass zwischen
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilung diskreter Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilung diskreter Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
1. Aufgabe: Entscheidungen bei Ungewissheit
 ( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
( WS 2012/13) 1. Aufgabe: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a 1, a 2,..., a 5 ) die beste Alternative auszuwählen. Zu welchem
Risiko und Versicherung - Übung
 Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
67 Zufallsvariable, Erwartungswert, Varianz
 67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
Aufgabe 1.3. Teil a) Teil b)
 Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
Informationsökonomik: Anreize, Verträge, Institutionen L ösung Blatt 1 FT 2012 Aufgabe 1.3 Faire Prämie Versicherungen können nicht beobachten, welchen Typen sie vor sich haben, daher werden sie den Erwartungswert
Modellanpassung und Parameterschätzung. A: Übungsaufgaben
 7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
Zufallsgröße: X : Ω R mit X : ω Anzahl der geworfenen K`s
 4. Zufallsgrößen =============================================================== 4.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
4. Zufallsgrößen =============================================================== 4.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
Vorlesung 2: Erwartungsnutzen
 Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
Vorlesung 2: Erwartungsnutzen Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Entscheidung VL 2 (FS 11) Erwartungsnutzen 1 / 28 1. Modellrahmen 1.1 Die Alternativen Wir betrachten
Historische Renditen, Experteninterviews, Analyse von Marktpreisen
 1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
1 Portfoliotheorie 1.1 Grundlagen der Portfoliotheorie 1.1.1 Welche vier grundsätzlichen Anlageziele werden von Investoren verfolgt? Minimales Risiko Liquidation wenn nötig Hohe Rendite Gewinnmaximierung
Programm. Wiederholung. Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung. Binomialverteilung. Hypergeometrische Verteilung
 Programm Wiederholung Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung Binomialverteilung Hypergeometrische Verteilung Wiederholung verschiedene Mittelwerte für verschiedene Skalenniveaus
Programm Wiederholung Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung Binomialverteilung Hypergeometrische Verteilung Wiederholung verschiedene Mittelwerte für verschiedene Skalenniveaus
1 Stochastische Konvergenz 2. 2 Das Gesetz der grossen Zahlen 4. 3 Der Satz von Bernoulli 6
 Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilung diskreter Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilung diskreter Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Wir erinnern uns: Um eine Zufallsvariable mit N verschiedenen, gleichwahrscheinlichen Zuständen binär zu codieren, benötigen wir
 Kapitel 3: Entropie Motivation Wir erinnern uns: Um eine Zufallsvariable mit N verschiedenen, gleichwahrscheinlichen Zuständen binär zu codieren, benötigen wir log N Bits log p N Bits Die Information steht
Kapitel 3: Entropie Motivation Wir erinnern uns: Um eine Zufallsvariable mit N verschiedenen, gleichwahrscheinlichen Zuständen binär zu codieren, benötigen wir log N Bits log p N Bits Die Information steht
Kapitel 9. Lösung Schritt: Normierung der Nutzenfunktionen. Aufgabe 9.1
 Kapitel 9: Entscheidung bei Risiko und einem Ziel 37 Kapitel 9 Lösung 9. Aufgabe 9. Welche Beziehung besteht zwischen Wert - und Nutzenfunktionen? Beschreiben Sie zwei Verfahren zur Ermittlung von Nutzenfunktionen
Kapitel 9: Entscheidung bei Risiko und einem Ziel 37 Kapitel 9 Lösung 9. Aufgabe 9. Welche Beziehung besteht zwischen Wert - und Nutzenfunktionen? Beschreiben Sie zwei Verfahren zur Ermittlung von Nutzenfunktionen
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Wahrscheinlichkeit und Statistik BSc D-INFK
 Prof. Dr. P. Bühlmann ETH Zürich Winter 2010 Wahrscheinlichkeit und Statistik BSc D-INFK 1. (10 Punkte) Bei den folgenden 10 Fragen ist jeweils genau eine Antwort richtig. Es gibt pro richtig beantwortete
Prof. Dr. P. Bühlmann ETH Zürich Winter 2010 Wahrscheinlichkeit und Statistik BSc D-INFK 1. (10 Punkte) Bei den folgenden 10 Fragen ist jeweils genau eine Antwort richtig. Es gibt pro richtig beantwortete
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus
 Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Überblick: Entscheidungstheoretische Konzepte Seminar Online-Optimierung Diana Balbus Einleitung Ein Online-Algorithmus muss Ausgaben berechnen, ohne zukünftige Eingaben zu kennen. Für die Bewertung von
Entscheidungstheoretische Grundlagen
 Entscheidungstheoretische Grundlagen Yves Breitmoser, HU Berlin Entscheidung unter Risiko Ein Entscheider, seine Entscheidung betrifft nur ihn selbst, aber es gibt Risiko: Themen: Risikopräferenzen: Ein
Entscheidungstheoretische Grundlagen Yves Breitmoser, HU Berlin Entscheidung unter Risiko Ein Entscheider, seine Entscheidung betrifft nur ihn selbst, aber es gibt Risiko: Themen: Risikopräferenzen: Ein
ETWR Teil B. Entscheidungen unter Risiko
 ETWR Teil B 2 Ziele Bisher Beschreibung sicherer Entscheidungen Ableitung von Wahrscheinlichkeiten Ziel dieses Kapitels Kombination beider vorangegangener Kapitel Motivation Theorie Bei wird praktische
ETWR Teil B 2 Ziele Bisher Beschreibung sicherer Entscheidungen Ableitung von Wahrscheinlichkeiten Ziel dieses Kapitels Kombination beider vorangegangener Kapitel Motivation Theorie Bei wird praktische
Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion
 Kapitel 2 Erwartungswert 2.1 Erwartungswert einer Zufallsvariablen Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion È ist definiert als Ü ÜÈ Üµ Für spätere
Kapitel 2 Erwartungswert 2.1 Erwartungswert einer Zufallsvariablen Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion È ist definiert als Ü ÜÈ Üµ Für spätere
Grundlagen der Wahrscheinlichkeitstheorie
 Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Vorlesung 3a. Der Erwartungswert. von diskreten reellwertigen Zufallsvariablen
 Vorlesung 3a Der Erwartungswert von diskreten reellwertigen Zufallsvariablen X sei eine Zufallsvariable, deren Zielbereich R (die Menge der reellen Zahlen) (oder eine Teilmenge davon) ist. Es existiere
Vorlesung 3a Der Erwartungswert von diskreten reellwertigen Zufallsvariablen X sei eine Zufallsvariable, deren Zielbereich R (die Menge der reellen Zahlen) (oder eine Teilmenge davon) ist. Es existiere
Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung
 R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
Grundwissen zur Stochastik
 Grundwissen zur Stochastik Inhalt: ABHÄNGIGE EREIGNISSE...2 ABHÄNGIGKEIT UND UNABHÄNGIGKEIT VON ERGEBNISSEN...2 ABHÄNGIGKEIT UND UNABHÄNGIGKEIT VON MERKMALEN IN VIERFELDERTAFELN...2 ABSOLUTE HÄUFIGKEIT...2
Grundwissen zur Stochastik Inhalt: ABHÄNGIGE EREIGNISSE...2 ABHÄNGIGKEIT UND UNABHÄNGIGKEIT VON ERGEBNISSEN...2 ABHÄNGIGKEIT UND UNABHÄNGIGKEIT VON MERKMALEN IN VIERFELDERTAFELN...2 ABSOLUTE HÄUFIGKEIT...2
Übung zur Vorlesung Statistik I WS Übungsblatt 12
 Übung zur Vorlesung Statistik I WS 2013-2014 Übungsblatt 12 20. Januar 2014 Die folgenden ufgaben sind aus ehemaligen Klausuren! ufgabe 38.1 (1 Punkt: In einer Studie werden 10 Patienten therapiert. Die
Übung zur Vorlesung Statistik I WS 2013-2014 Übungsblatt 12 20. Januar 2014 Die folgenden ufgaben sind aus ehemaligen Klausuren! ufgabe 38.1 (1 Punkt: In einer Studie werden 10 Patienten therapiert. Die
Übungsklausur zur Vorlesung Wahrscheinlichkeit und Regression Thema: Wahrscheinlichkeit. Übungsklausur Wahrscheinlichkeit und Regression
 Übungsklausur Wahrscheinlichkeit und Regression 1. Welche der folgenden Aussagen treffen auf ein Zufallsexperiment zu? a) Ein Zufallsexperiment ist ein empirisches Phänomen, das in stochastischen Modellen
Übungsklausur Wahrscheinlichkeit und Regression 1. Welche der folgenden Aussagen treffen auf ein Zufallsexperiment zu? a) Ein Zufallsexperiment ist ein empirisches Phänomen, das in stochastischen Modellen
2 Zufallsvariable und Verteilungsfunktionen
 8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
i Pr(X = i). Bsp: Sei X die Summe zweier Würfe eines Würfels. Dann gilt E[X] =
![i Pr(X = i). Bsp: Sei X die Summe zweier Würfe eines Würfels. Dann gilt E[X] = i Pr(X = i). Bsp: Sei X die Summe zweier Würfe eines Würfels. Dann gilt E[X] =](/thumbs/70/63647743.jpg) Erwartungswert Definition Erwartungswert Der Erwartungswert einer diskreten ZV ist definiert als E[X] = i i Pr(X = i). E[X] ist endlich, falls i i Pr(X = i) konvergiert, sonst unendlich. Bsp: Sei X die
Erwartungswert Definition Erwartungswert Der Erwartungswert einer diskreten ZV ist definiert als E[X] = i i Pr(X = i). E[X] ist endlich, falls i i Pr(X = i) konvergiert, sonst unendlich. Bsp: Sei X die
STOCHASTISCHE UNABHÄNGIGKEIT. Annika Pohlmann Philipp Oel Wilhelm Dück
 STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
TU DORTMUND Sommersemester 2018
 Fakultät Statistik. April 08 Blatt Aufgabe.: Wir betrachten das Zufallsexperiment gleichzeitiges Werfen zweier nicht unterscheidbarer Würfel. Sei A das Ereignis, dass die Augensumme beider Würfel ungerade
Fakultät Statistik. April 08 Blatt Aufgabe.: Wir betrachten das Zufallsexperiment gleichzeitiges Werfen zweier nicht unterscheidbarer Würfel. Sei A das Ereignis, dass die Augensumme beider Würfel ungerade
Mathematik für Naturwissenschaften, Teil 2
 Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Zusammenfassung Mathe II. Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen
 Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 23. Dezember 2011 1 Stetige Zufallsvariable, Normalverteilungen Der zentrale Grenzwertsatz und die 3-Sigma Regel
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 23. Dezember 2011 1 Stetige Zufallsvariable, Normalverteilungen Der zentrale Grenzwertsatz und die 3-Sigma Regel
Unabhängige Zufallsvariablen
 Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
- Entscheidungsmöglichkeit / Alternativen. + (idealerweise) Methode der Entscheidung / Verfahren
 be/ji/3(2) 4-1 4 "Entscheidung" setzt voraus - Entscheidungsmöglichkeit / Alternativen - Prinzip der Entscheidung / Ziel + (idealerweise) Methode der Entscheidung / Verfahren Bisher trivial OR-Optimierungsmodelle
be/ji/3(2) 4-1 4 "Entscheidung" setzt voraus - Entscheidungsmöglichkeit / Alternativen - Prinzip der Entscheidung / Ziel + (idealerweise) Methode der Entscheidung / Verfahren Bisher trivial OR-Optimierungsmodelle
Verteilung von Summen
 Verteilung von Summen Beispiel: Würfelwurf Frage: Wie verhält sich die Verteilung der Augensumme von -Würfeln bei wachsendem? Zur Beantwortung führen wir ein Simulationseperiment durch. 6 Würfe mit 1 Würfel
Verteilung von Summen Beispiel: Würfelwurf Frage: Wie verhält sich die Verteilung der Augensumme von -Würfeln bei wachsendem? Zur Beantwortung führen wir ein Simulationseperiment durch. 6 Würfe mit 1 Würfel
Zufallsvariablen. Diskret. Stetig. Verteilung der Stichprobenkennzahlen. Binomial Hypergeometrisch Poisson. Normal Lognormal Exponential
 Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Zufallsvariable Erinnerung: Merkmal, Merkmalsausprägung Deskriptive Statistik:
Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Zufallsvariable Erinnerung: Merkmal, Merkmalsausprägung Deskriptive Statistik:
Sigma-Umgebung. Vergleichen wir die beiden Binomialverteilungen: n = 30 p = 0,5. n = 20 p = 0,75
 Sigma-Umgebung Vergleichen wir die beiden Binomialverteilungen: n = 30 p = 0,5 0,2 (z.b. 30-maliges Werfen einer Münze, X Anzahl von Zahl ) 5 10 15 20 n = 20 p = 0,75 0,2 5 10 15 20 Der Erwartungswert
Sigma-Umgebung Vergleichen wir die beiden Binomialverteilungen: n = 30 p = 0,5 0,2 (z.b. 30-maliges Werfen einer Münze, X Anzahl von Zahl ) 5 10 15 20 n = 20 p = 0,75 0,2 5 10 15 20 Der Erwartungswert
2. Lösung weitere Übungsaufgaben Statistik II WiSe 2016/2017
 . Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
. Lösung weitere Übungsaufgaben Statistik II WiSe 016/017 1. Aufgabe: Bei der Produktion eines Werkstückes wurde die Bearbeitungszeit untersucht. Für die als normalverteilt angesehene zufällige Bearbeitungszeit
Einführung in die Statistik Kapitel 6: Crash-Course in Statistik: Testtheorie
 Einführung in die Statistik Kapitel 6: Crash-Course in Statistik: Testtheorie Jung Kyu Canci Universität Basel HS2015 1 / 15 Literatur Kapitel 6 Statistik in Cartoons : Kapitel 8 Krengel : 6 und 14 Storrer
Einführung in die Statistik Kapitel 6: Crash-Course in Statistik: Testtheorie Jung Kyu Canci Universität Basel HS2015 1 / 15 Literatur Kapitel 6 Statistik in Cartoons : Kapitel 8 Krengel : 6 und 14 Storrer
Mathematische und statistische Methoden II
 Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung Wallstr. 3, 6. Stock, Raum 06-206 Mathematische und statistische Methoden II Dr. Malte Persike persike@uni-mainz.de lordsofthebortz.de lordsofthebortz.de/g+
Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung Wallstr. 3, 6. Stock, Raum 06-206 Mathematische und statistische Methoden II Dr. Malte Persike persike@uni-mainz.de lordsofthebortz.de lordsofthebortz.de/g+
