Theoretische Physik: Elektrodynamik
|
|
|
- Ferdinand Geisler
- vor 8 Jahren
- Abrufe
Transkript
1 Ferienkurs Theoretische Physik: Elektrodynamik Übungsblatt Technische Universität München Fakultät für Physik
2 Verifikation des Stokesschen Satzes Verifizieren Sie den Stokeschen Satz für das Vektorfeld: und die Fläche: V = (4x/3 2y) e x + (3y x) e y () Lösung: A = { r : (x/3) 2 + (y/2) 2, z = } (2) Zunächst berechnet man rot V = ( V y / x V x / y) e z = e z. Die Fläche ist eine Ellipse mit den Halbachsen a = 3 und b = 2. Damit wird die linke Seite des Stokesschen Satzes zu: A d A rot V = A da = πab = 6π (3) Um das Wegintegral auf der rechten Seite zu berechnen, parametrisieren wir den Weg: r = 3cosα e x + 2sinα e y, d r = ( 3sinα e x + 2cosα e y )dα (4) Der Weg (Ellipse) wird durchlaufen, wenn α die Werte von bis 2π annimmt. Längs des Weges ist das Vektorfeld V = (4cosα 4sinα) e x + (6sinα 3cosα) e y. Damit wird das Wegintegral zu: C d r V = 2π dα(2sin 2 α 6cos 2 α) = 6π (5) Beide Integrale sind gleich. Damit haben wir den Stokesschen Satz in diesem speziellen Fall verifiziert. 2 Verifikation des Gaußschen Satzes Verifizieren Sie den Gaußschen Satz für das Vektorfeld: und die Kugel x 2 + y 2 + z 2 R 2. Lösung: V = ax e x + by e y + cz e z (6) Zunächst berechnet man div V = V x / x + V y / y + V z / z = a + b + c. Damit wird die linke Seite des Gaußschen Satzes zu: V dv V = (a + b + c) d 3 r = 4π r R 3 R3 (a + b + c) (7) Technische Universität München 2 Fakultät für Physik
3 Für das Flächenintegral au der rechten Seite verwenden wir Kugelkoordinaten: d A = R 2 dcosϑdϕ e r, e r VR(asin 2 ϑcos 2 ϕ + bsin 2 ϑsin 2 ϕ + ccos 2 ϑ) (8) Die ϕ - Integration über cos 2 ϕ und sin 2 ϕ liefert π. Damit wird das Flächenintegral zu: A d A V = 2πR 3 [ ] a + b dcosϑ 2 ( cos2 ϑ) + cos 2 ϑ = 4π 3 R3 (a + b + c) (9) Beide Integrale sind gleich. Damit haben wir den Gaußschen Satz in diesem speziellen Fall verifiziert. 3 Rechnen mit Gradient, Divergenz und Rotation Zeigen Sie div( V W) = W rot V V rot W durch Auswertung in kartesischen Komponenten. Werten Sie analog dazu die Ausdrücke rot(φ V), rot( V W) und grad( V W) aus, Lösung: In kartesischen Koordinaten erhalten wir: div( V W) = i (ε i jk V j W k ) = ε i jk (W k i V j V j i W k ) = i, j,k i, j,k = W ( V) V ( W) = W rot V V rot W () Dabei ist i = x i. Analog dazu berechnen wir: (rot(φ V)) i = ε i jk j (ΦV k ) = ε i jk (Φ j V k + V k j Φ) = j,k j,k () = Φ(rot V) i ( V gradφ) i In der folgenden Umformung wird die Kontraktion zweier total antisymmetrischer Tensoren verwendet: (rot( V W)) i = ε i j ε klm j (V l W m ) = (δ il δ jm δ im δ jl )(W m j V l + V l j W m ) = j,k,l,m j,k,l,m = (W j j V i + V i j W j W i j V j V j j W i ) = j (2) = [( W ) V W( V) + V( W) ( V W) W] i Die Auswertung von grad( V W) erfolgt nach der Produktregel: (grad( V W)) i = j (V j W j ) = [V j ( i W j ) + W j ( i V j )] (3) i j Technische Universität München 3 Fakultät für Physik
4 4 Ladungsdichte für Kugelschale und Kreisscheibe Eine Kugelschale und eine Kreisscheibe (beide infinitesimal dünn, und mit dem Radius R) sind homogen geladen (Gesamtladung q). Geben Sie für beide Fälle die Ladungsdichte an (mit Hilfe von δ - und Θ - Funktionen). Lösung: Für die Kugelschale verwenden wir Kugelkoordinaten, ρ( r) = ρ(r, ϑ, ϕ). Eine homogene Ladungsverteilung impliziert sphärische Symmetrie, also ρ(r). Die Vorgabe infinitesimal dünn bedeutet dann ρ( r) = c δ(r R). Die Konstante c folgt aus: q = d 3 rρ( r) = 4πc drr 2 δ(r R) = 4πc R 2 (4) Damit ist die Ladungsdichte der Kugelschale: ρ( r) = q δ(r R) (5) 4πR2 Für die Kreisscheibe verwenden wir Zylinderkoordinaten, ρ( r)ρ(p, ϕ, z). Eine homogene Ladungsverteilung impliziert, dass ρ nicht von ϕ und im Inneren der Scheibe nicht von p abhängt. Die Begrenzung auf p R wird durch den Faktor Θ(R p), die Vorgabe infinitesimal dünn durch den Faktor δ(z) berücksichtigt, also ρ = c 2 Θ(R p)δ(z). Die Konstante c 2 folgt aus: q = d 3 rρ( r) = 2πc 2 dpp dzθ(r p)δ(z) = πc 2 R 2 (6) Damit ist Ladungsdichte der Kreisscheibe: 5 Homogen geladene Kugel Bestimmen Sie das elektrostatische Potential: ρ( r) = 4 Θ(R p)δ(z) (7) πr2 Φ( r) = d 3 r ρ( r ) r r (8) für eine homogen geladene Kugel (Ladung q, Radius R). Legen Sie dazu r in z Richtung und führen Sie die Integration in Kugelkoordinaten aus. Berechnen Sie das elektrische Feld E( r). Lösung: Mit r = r e z und der homogenen Ladungsdichte ρ = q V mit V = 4π 3 R3 erhalten wir: Technische Universität München 4 Fakultät für Physik
5 R Φ( r) = 2πρ dr r 2 dcosϑ = 2πρ r R dr r ( r + r r r ) r2 + r 2 2rr cosϑ = (9) Die Fälle r > R und r R werden getrennt ausgewertet: Für r R: Φ( r) = 4πρ r [ r dr r 2 + r R r ] ( ) R dr r 2 = 4πρ 6 r2 6 (2) Für r > R: Φ( r) = 4πρ r R dr r 2 = 4πρ r R 3 3 (2) Damit lautet das Potential der homogen geladenen Kugel: Für r R: Φ( r) = q R ( ) 3 2 r2 2R 2 (22) Für r > R: Φ( r) = q r (23) Das dazugehörige Feld ist: Für r R: E( r) = Φ( r) = qr R 3 e r (24) Für r > R: E( r) = Φ( r) = q r 2 e r (25) 6 Homogen geladener Kreiszylinder Bestimmen Sie das elektrische Feld eines homogen geladenen unendlich langen Kreiszylinders (Radius R, Länge L, Ladung/Länge = q/l, L ). Lösen sie das Problem:. mit Hilfe des Gaußschen Gesetzes. Technische Universität München 5 Fakultät für Physik
6 2. über die Poisson-Gleichun. Beachten Sie, dass das Potential im Unendlichen nicht verschwindet. Lösung: Wir verwenden Zylinderkoordinaten ρ, ϕ und z. Die homogene Ladungsdichte im Bereich des Zylinders ist ρ = q. Wegen der Symmetrie des Problems kann das Potential nur vom Abstand πr 2 L ρ von der Zylinderachse abhängen, also Φ = Φ(ρ). Dann ist das elektrische Feld von der Form E = E(ρ) e ρ. Das Gaußsche Gesetz wenden wir auf einen Zylinder mit dem Radius ρ und der Länge L an. Die Zylinderoberfläche besteht zum einen aus der Boden- und Deckfläche, und zum anderen aus der Mantelfläche. Im Bereich der Boden- und Deckfläche ist das Flächenelement d A ± e z, sodass E d A =. Auf der Mantelfläche ist d A = ρdϕdz e ρ. Damit erhalten wir: Für ρ R: Für ρ > R: Daraus ergibt sich das gesuchte elektrische Feld: Für ρ R: Für ρ > R: A A d A E = 2πρLE(ρ) = 4πQ V = 4πρ πρ 2 L (26) d A E = 2πρLE(ρ) = 4πQ V = 4πρ πr 2 L (27) E(ρ) = 2q L ρ R 2 (28) E(ρ) = 2q L ρ (29) Als Alternative gehen wir von der Poissongleichung aus. Für Φ(ρ) wird die Poissongleichung zu der gewöhnlichen Differentialgleichung: Für ρ R: Für ρ > R: Die zweimalige Integration ergibt: ρ (ρφ (ρ )) = 4πρ (3) ρ (ρφ (ρ )) = (3) Technische Universität München 6 Fakultät für Physik
7 Für ρ R: Φ(ρ) = πρ ρ 2 + c ln ρ R + d (32) Für ρ > R: Φ(ρ) = c 2 ln ρ R + d 2 (33) Für ρ > R liefert die Integration zunächst ln(ρ) + const. Dies kann durch ln(ρ/r) + const. + ln(r) ersetzt werden, also durch ln(ρ/r) und eine andere Integrationskonstante. Für eine homogene Ladungsdichte darf das Potential bei ρ = nicht singulär werden. Daher gilt c =. Da das Potential nur bis auf eine Konstante festliegt, kann d 2 = gewählt werden. Die Ladungsdichte hat bei ρ = R einen Sprung. Damit hat auch die zweite Ableitung Φ (ρ) einen Sprung, nur so kann die Poissongleichung erfüllt werden. Damit sind aber Φ (ρ) und Φ(ρ) an dieser Stelle stetig. Diese Bedingungen ergeben d = πρ R 2 = q L und c 2 = 2πρ R 2 = 2q L. Damit erhalten wir für das Potential des unendlich langen homogen geladenen Zylinders: Für ρ R: Φ(ρ) = q L ) ( ρ2 R 2 (34) Für ρ > R: Φ(ρ) = 2q L ln ρ R (35) Das elektrische Feld: E = Φ(ρ) = Φ (ρ) e ρ = E(ρ) e ρ (36) stimmt mit dem zuvor errechneten elektrischen Feld überein. 7 Punktladung vor geerdeten Metallplatten Das Volumen: V = { r : x, y, z } (37) ist bei x = und y = durch geerdete Metallplatten begrenzt. Innerhalb von V befindet sich eine Punktladung q. Bestimmen Sie das Potential Φ( r) in V (mit Hilfe von Bildladungen). Berechnen Sie die Flächenladungsdichte und die Gesamtladung auf den Platten. Welche Kraft wirkt auf die Punktladung? Lösung: Technische Universität München 7 Fakultät für Physik
8 Es handelt sich um ein zweidimensionales Problem, Φ( r) = Φ(x, y). Die Punktladung q = q kann ohne Einschränkung der Allgemeinheit an die Position r = (a, b, ) gesetzt werden. Mit einer ersten Bildladung q = q bei ( a, b, ) könnte man die Bedingung Φ(, y) = erfüllen, mit einer zweiten Bildladung q 2 = q bei (a, b, ) die Bedingung Φ(x, ) =. Diese Bildladungen verletzen jedoch die jeweils andere Randbedingung. Dies kann durch eine dritte Bildladung q 3 ersetzt werden. Zu der gegebenen Punktladung wählen wir drei Bildladungen: q = q, r = (a, b, ) (38) q = q, r = ( a, b, ) (39) q 2 = q, r 2 = (a, b, ) (4) q 3 = q, r 3 = ( a, b, ) (4) Die vier Punktladungen ergeben das Potential null auf den Ebenen x = und y =. Das Potential aller Ladungen ist: Φ( r) = 3 k= q k r r k (42) Dieses Potential löst das Randwertproblem: Φ( r) = 4πqδ( r r )inv, Φ( r) R = (43) Die Flächenladungsdichte σ auf den Platten berechnet sich aus der Normalkomponente des elektrischen Feldes: 4πσ( r) R = n E( r) R, E( r) = E(x, y, z) = sum 3 k= q r r k k (44) r r k 3 Für die Flächenladungsdichten σ y (x, z) = E y (x,, z) und σ x (y, z) = E x (, y, z) erhalten wir: Für x > : σ y (x, z) = qb [ ] 2π ((x a) 2 + b 2 + z 2 ) 3/2 ((x + a) 2 + b 2 + z 2 ) 3/2 (45) Für y > : σ x (y, z) = qb [ ] 2π (a 2 + (y b) 2 + z 2 ) 3/2 (a 2 + (y + b) 2 + z 2 ) 3/2 (46) Technische Universität München 8 Fakultät für Physik
9 Die Ladungsdichten gelten auf den Metallplatten, also in der x z Ebene für x >, und in der y z Ebene für y >. Wir berechnen die Influenzladung auf der Platte in der x z Ebene: y= = dx q in f l = qb π a a dzσ y (x, z) = qb π dx x 2 + b = 2q 2 π arctana b [ dx (x a) 2 + b 2 (x + a) 2 + b 2 ] = (47) Mit dem entsprechenden Resultat für die y z Ebene erhalten wir für die Gesamtladung auf beiden Metallplatten: q in f l = q in f l y= + qin f l x= = 2q π [ arctan a ] b + arctanb = q (48) a Die Kraft auf die Punktladung q bei r ist durch das elektrische Feld gegeben, das nicht von dieser Ladung selbst stammt, also durch das Feld der drei Bildladungen: F = 3 K= [( r r k q k r r k = 3 q2 4 a 2 ) ( a e (a 2 + b 2 ) 3/2 c + b 2 ] b ) e (a 2 + b 2 ) 3/2 y (49) 8 Punktladung vor Metallkugel Außerhalb einer geerdeten, leitenden Hohlkugel (Radius R, Zentrum r = ) befindet sich eine Punktladung q bei r. Berechnen Sie das Potential im Innen- und Außenraum der Kugel. Verwenden Sie hierzu eine geeignete Bildladung q 2 bei r 2. Berechnen Sie die Ladungsdichte und die Gesamtladung auf der Kugeloberfläche. Welche Kraft wirkt zwischen Punktladung und Kugel? Was ändert sich, wenn die Ladung innerhalb der Kugel ist? Welche Lösung ergibt sich, wenn das Potential auf der Kugeloberfläche einen endlichen Wert Φ = Φ(R) Φ( ) hat? Lösung: Das Randwertproblem lautet: Φ( r) = 4πq δ( r r ) für r > R, undφ(r) = (5) Wir setzen eine Bildladung q 2 bei r 2 (mit r 2 < R) an: Φ( r) = q r r + q 2 r r 2 (5) Die Bildladung ist so zu wählen, dass die Randbedingung: Φ(R) = q R e r r + q 2 R e r r 2 = (52) Technische Universität München 9 Fakultät für Physik
10 erfüllt ist, dabei ist R = R e r eine Vektor zu einem Punkt der Kugeloberfläche. Hieraus folgt: (q 2 q2 2 )R2 2R(q 2 r 2 q 2 2 r ) e r = q 2 2 r2 q2 r2 2 (53) Da dies für alle Richtungen e r gilt, muss der Koeffizient von e r verschwinden, also: Damit ist die Bildladung wie folgt zu wählen: q 2 r 2 = q 2 2 r und (q 2 q2 2 )R2 = q 2 2 r2 q2 r2 2 (54) q 2 = R q bei r 2 = R2 r r r 2 (55) Das Vorzeichen von q 2 folgt aus der Randbedingung. Wie vorrausgesetzt, gilt r 2 < R. Damit wird das Potential für r > R zu: Φ( r) = q r r R r r (R 2 /r 2) r (56) Gelegentlich formuliert man zunächst das Randwertproblem für eine Green sche Funktion g( r, r ). Die Bedingungen für die Greensche Funktion sind: G( r, r ) = 4πδ( r r ) inv und G r, r r R = (57) Die Greensche Funktion ist also das Potential an der Stelle r, das sich für eine Punktladung der Stärke bei r ergibt. Im vorliegenden Problem ist G( r, r ) = Φ( r) q. Die Greensche Funktion ist symmetrisch, G( r, r ) = G( r, r). Aus obigem Potential folgt diese Symmetrie, wenn man r ( 2 R/r 2) r = (R/r )(R 2 2 r r + r 2 r 2/R2 ) /2 berücksichtigt. An der Kugeloberfläche bei R = R e r ist das elektrische Feld: R r E( R) = q R r + q R R (R 2 /r 2) r 3 r R (R 2 /r 2) r = q r 2 R2 3 R r R 3 e r (58) Dabei wurde R (R 2 /r 2 ) r = (R/r ) R r verwendet. Die Normalkomponente des Felds bestimmt die induzierte Oberflächenladung: σ( R) = 4π e r E( R) = q 4πR r 2 R2 r R 3 (59) Die gesamte Influenzladung auf der Kugeloberfläche ist gleich der negativen Bildladung: q in f l = R 2 dcosϑ = q (r 2 R2 ) 2r [ 2π dϕσ( R) = q R r 2 dcosϑ R2 2 (r 2 + R2 2r Rcosϑ) = 3/2 ] (6) = Rr q = q 2 r R r + R Technische Universität München Fakultät für Physik
11 Die Kraft auf die Punktladung q ist durch das elektrische Feld gegeben, das nicht von dieser Ladung selbst stammt, also durch das Feld der Bildladung: r r 2 F = q q 2 r r 2 = R r q 2 3 q2 = R r ( R 2 /r 2)2 r 3 (R 2 r 2)2 r (6) Es wurde q 2 = (R/r )q und r r 2 = ( R 2 /r 2 ) r eingesetzt. Die Kraft zwischen Punktladung und Metalkugel ist attraktiv. Das zuvor errechnete Potential errechnet auch das andere Randwertproblem: Φ( r) = 4πq 2 δ( r r 2 ) für r < R, und Φ(R) = (62) In diesem Fall ist eine Ladung q 2 innerhalb der Kugel gegeben, und gesucht ist das Feld innerhalb der Kugel, die Lösung des Problems erfolgt durch eine Bildladung q bei r 2 (mit r > R). Die Oberflächenladung σ = n E R /4π ändert das Vorzeichen, weil der Normalenvektror n = e r jetzt nach innen zeigt. Um einen endlichen Potentialwert Φ = Φ(R) Φ( ) auf der Kugel zu erreichen, wird zusätzlich die Punktladung q 3 bei r 3 = eingeführt. Diese erzeugt das Potential q 3 /R = Φ auf der Kugel, es muss also q 3 = RΦ gewählt werden. 9 Green sche Funktion Lösung Technische Universität München Fakultät für Physik
12 Technische Universität München 2 Fakultät für Physik
13 Technische Universität München 3 Fakultät für Physik
14 Technische Universität München 4 Fakultät für Physik
15 Technische Universität München 5 Fakultät für Physik
16 Technische Universität München 6 Fakultät für Physik
17 Technische Universität München 7 Fakultät für Physik
18 Technische Universität München 8 Fakultät für Physik
Formelsammlung Elektrodynamik
 Formelsammlung Elektrodynamik SS 2006 RWTH Aachen Prof. Kull Skript Simon Sawallich Inhaltsverzeichnis 1 Allgemeines 3 1.1 Funktionen............................................ 3 Trigonometrische Funktionen..................................
Formelsammlung Elektrodynamik SS 2006 RWTH Aachen Prof. Kull Skript Simon Sawallich Inhaltsverzeichnis 1 Allgemeines 3 1.1 Funktionen............................................ 3 Trigonometrische Funktionen..................................
Übungen zur Klassischen Theoretischen Physik III (Theorie C Elektrodynamik) WS Aufgabe 1: Ampère-Gesetz (2+2+2=6 Punkte)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III (Theorie Elektrodynamik) WS 1-13 Prof. Dr. Alexander Mirlin Musterlösung:
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III (Theorie Elektrodynamik) WS 1-13 Prof. Dr. Alexander Mirlin Musterlösung:
10.1 Ampère sches Gesetz und einfache Stromverteilungen
 1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
12. Mehrfachintegrale
 - 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
- 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Aufgabe Summe max. P Punkte
 Klausur Theoretische Elektrotechnik TET Probeklausur xx.xx.206 Name Matr.-Nr. Vorname Note Aufgabe 2 3 4 5 6 7 Summe max. P. 5 0 5 5 5 5 5 00 Punkte Allgemeine Hinweise: Erlaubte Hilfsmittel: Taschenrechner,
Klausur Theoretische Elektrotechnik TET Probeklausur xx.xx.206 Name Matr.-Nr. Vorname Note Aufgabe 2 3 4 5 6 7 Summe max. P. 5 0 5 5 5 5 5 00 Punkte Allgemeine Hinweise: Erlaubte Hilfsmittel: Taschenrechner,
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n
![2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n](/thumbs/49/25862272.jpg) 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
5 Elektrizität und Magnetismus
 5.1 Elektrische Ladung q Ursprung: Existenz von subatomaren Teilchen Proton: positive Ladung Elektron: negative Ladung besitzen jeweils eine Elementarladung e = 1.602 10 19 C (Coulomb) Ladung ist gequantelt
5.1 Elektrische Ladung q Ursprung: Existenz von subatomaren Teilchen Proton: positive Ladung Elektron: negative Ladung besitzen jeweils eine Elementarladung e = 1.602 10 19 C (Coulomb) Ladung ist gequantelt
Vorlesungsfolien Mathematik 3 WS 2010/11 UMIT. Einleitung
 Vorlesungsfolien Mathematik 3 WS 2010/11 Dr. Leonhard Wieser UMIT Einleitung Begriff Vektoranalysis: Kombination aus Linearer Algebra/Vektorrechnung mit Differential- und Integralrechnung Inhaltsangabe:
Vorlesungsfolien Mathematik 3 WS 2010/11 Dr. Leonhard Wieser UMIT Einleitung Begriff Vektoranalysis: Kombination aus Linearer Algebra/Vektorrechnung mit Differential- und Integralrechnung Inhaltsangabe:
1 Felder bewegter Ladungen
 Universität Leipzig, Fakultät für Physik und Geowissenschaften Vorlesung zur Experimentalphysik III Wintersemester 2008/2009 Prof. Dr. Josef A. Käs Vorlesungsmitschrift zur Vorlesung vom 16.10.2008 1 Felder
Universität Leipzig, Fakultät für Physik und Geowissenschaften Vorlesung zur Experimentalphysik III Wintersemester 2008/2009 Prof. Dr. Josef A. Käs Vorlesungsmitschrift zur Vorlesung vom 16.10.2008 1 Felder
Experimentalphysik II: Elektrostatik I
 Experimentalphysik II: Elektrostatik I Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 07/09/09 Inhaltsverzeichnis Elektrische Ladung, Coulomb-Kraft 2 2 Das elektrische Feld 2 3 Der Satz von Gauß
Experimentalphysik II: Elektrostatik I Zweitversuch-Ferienkurs Sommersemester 09 William Hefter 07/09/09 Inhaltsverzeichnis Elektrische Ladung, Coulomb-Kraft 2 2 Das elektrische Feld 2 3 Der Satz von Gauß
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
14.3 Berechnung gekrümmter Flächen
 4.3 Berechnung gekrümmter Flächen Gekrümmte Flächen werden berechnet, indem sie als Graph einer Funktion zweier Veränderlicher aufgefasst werden. Fläche des Graphen einer Funktion zweier Veränderlicher
4.3 Berechnung gekrümmter Flächen Gekrümmte Flächen werden berechnet, indem sie als Graph einer Funktion zweier Veränderlicher aufgefasst werden. Fläche des Graphen einer Funktion zweier Veränderlicher
Elektromagnetische Felder und Wellen
 Elektromagnetische Felder und Wellen Name : Matrikelnummer : Aufgabe 1: Aufgabe 2: Aufgabe 3: Aufgabe 4: Aufgabe 5: Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: Aufgabe 10: Aufgabe 11: Gesamtpunktzahl:
Elektromagnetische Felder und Wellen Name : Matrikelnummer : Aufgabe 1: Aufgabe 2: Aufgabe 3: Aufgabe 4: Aufgabe 5: Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: Aufgabe 10: Aufgabe 11: Gesamtpunktzahl:
Felder ausgewählter Konfigurationen
 Felde ausgewählte Konfiguationen Anwendung von Supepositionspinzip Gauß sche Satz Feldbeechung aus Potenzial. Feld und Potenzial innehalb und außehalb eine Vollkugel. Feld und Potenzial innehalb und außehalb
Felde ausgewählte Konfiguationen Anwendung von Supepositionspinzip Gauß sche Satz Feldbeechung aus Potenzial. Feld und Potenzial innehalb und außehalb eine Vollkugel. Feld und Potenzial innehalb und außehalb
12. Übungsblatt zur Mathematik II für MB
 Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 1 5.7.21 12. Übungsblatt zur Mathematik II für MB Aufgabe 39 Divergenz Berechnen Sie die Divergenz folgender Vektorfelder: xyz + 2xy F 1
Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 1 5.7.21 12. Übungsblatt zur Mathematik II für MB Aufgabe 39 Divergenz Berechnen Sie die Divergenz folgender Vektorfelder: xyz + 2xy F 1
19.3 Oberflächenintegrale
 19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
3. Erhaltungsgrößen und die Newton schen Axiome
 Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray [email protected] 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray [email protected] 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Ferienkurs Experimentalphysik II Elektrodynamik. Magnetostatik. 12. September 2011 Michael Mittermair
 Ferienkurs Experimentalphysik II Elektrodynamik Magnetostatik 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Permanentmagnete und Polstärke 2 2 Magnetfelder stationärer Ströme 3 2.1 Magnetfeldstärke
Ferienkurs Experimentalphysik II Elektrodynamik Magnetostatik 12. September 2011 Michael Mittermair Inhaltsverzeichnis 1 Permanentmagnete und Polstärke 2 2 Magnetfelder stationärer Ströme 3 2.1 Magnetfeldstärke
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Aufgabenblatt zum Seminar 12 PHYS70357 Elektrizitätslehre und Magnetismus (Physik, Wirtschaftsphysik, Physik Lehramt, Nebenfach Physik)
 Aufgabenblatt zum Seminar 2 PHYS7357 Elektrizitätslehre und Magnetismus (Physik, Wirtschaftsphysik, Physik Lehramt, Nebenfach Physik) Othmar Marti, ([email protected]) 8. 7. 29 Aufgaben. In der Vorlesung
Aufgabenblatt zum Seminar 2 PHYS7357 Elektrizitätslehre und Magnetismus (Physik, Wirtschaftsphysik, Physik Lehramt, Nebenfach Physik) Othmar Marti, ([email protected]) 8. 7. 29 Aufgaben. In der Vorlesung
1.4 Gradient, Divergenz und Rotation
 .4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
.4 Gradient, Divergenz und Rotation 5.4 Gradient, Divergenz und Rotation Die Begriffe Gradient, Divergenz und Rotation erfordern die partiellen Ableitung aus Abschnitt.. sowie das Konzept des Differentialoperators.
Mitschrieb zu Theoretische Physik C: Elektrodynamik und Optik
 Mitschrieb zu Theoretische Physik C: Elektrodynamik und Optik Prof. Dr. Kühn und Dr. Roth Vorlesung Wintersemester /3 Letzte Aktualisierung und Verbesserung:. Februar 4 Mitschrieb der Vorlesung Theoretische
Mitschrieb zu Theoretische Physik C: Elektrodynamik und Optik Prof. Dr. Kühn und Dr. Roth Vorlesung Wintersemester /3 Letzte Aktualisierung und Verbesserung:. Februar 4 Mitschrieb der Vorlesung Theoretische
Übungsaufgaben z. Th. Plattenkondensator
 Übungsaufgaben z. Th. Plattenkondensator Aufgabe 1 Die Platten eines Kondensators haben den Radius r 18 cm. Der Abstand zwischen den Platten beträgt d 1,5 cm. An den Kondensator wird die Spannung U 8,
Übungsaufgaben z. Th. Plattenkondensator Aufgabe 1 Die Platten eines Kondensators haben den Radius r 18 cm. Der Abstand zwischen den Platten beträgt d 1,5 cm. An den Kondensator wird die Spannung U 8,
Differentialgleichungen. Aufgaben mit Lösungen. Jörg Gayler, Lubov Vassilevskaya
 Differentialgleichungen Aufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya ii Inhaltsverzeichnis. Tabelle unbestimmter Integrale............................... iii.. Integrale mit Eponentialfunktionen........................
Differentialgleichungen Aufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya ii Inhaltsverzeichnis. Tabelle unbestimmter Integrale............................... iii.. Integrale mit Eponentialfunktionen........................
elektrischespotential =
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #6 am 02.05.2007 Vladimir Dyakonov Elektrisches Potential Wieviel Arbeit muss ich aufwenden
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 2007 VL #6 am 02.05.2007 Vladimir Dyakonov Elektrisches Potential Wieviel Arbeit muss ich aufwenden
Kapitel 3. Koordinatensysteme
 Kapitel 3 Koordinatensysteme Bisher haben wir uns bei der Beschreibung von Vektoren auf das kartesische Koordinatensystem konzentriert. Für viele physikalische Anwendungen sind aber kartesische Koordinaten
Kapitel 3 Koordinatensysteme Bisher haben wir uns bei der Beschreibung von Vektoren auf das kartesische Koordinatensystem konzentriert. Für viele physikalische Anwendungen sind aber kartesische Koordinaten
Mathematische Methoden für Informatiker
 Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
Prof. Dr. www.math.tu-dresden.de/ baumann 8.12.2016 20. Vorlesung Differentialgleichungen n-ter Ordnung Lösung einer Differentialgleichung Veranschaulichung der Lösungsmenge Anfangswertprobleme Differentialgleichungen
WELLEN im VAKUUM. Kapitel 10. B t E = 0 E = B = 0 B. E = 1 c 2 2 E. B = 1 c 2 2 B
 Kapitel 0 WELLE im VAKUUM In den Maxwell-Gleichungen erscheint eine Asymmetrie durch Ladungen, die Quellen des E-Feldes sind und durch freie Ströme, die Ursache für das B-Feld sind. Im Vakuum ist ρ und
Kapitel 0 WELLE im VAKUUM In den Maxwell-Gleichungen erscheint eine Asymmetrie durch Ladungen, die Quellen des E-Feldes sind und durch freie Ströme, die Ursache für das B-Feld sind. Im Vakuum ist ρ und
3.4 Magnetfelder. µ im Magnetfeld Æ B ein Drehmoment. M = Æ µ Æ B.
 - 151-3.4 Magnetfelder 3.4.1 Grundlagen Während die Wechselwirkungen zwischen statischen elektrischen Ladungen sich durch das Coulomb'sche Gesetz, resp. ein elektrisches Feld beschreiben lassen, treten
- 151-3.4 Magnetfelder 3.4.1 Grundlagen Während die Wechselwirkungen zwischen statischen elektrischen Ladungen sich durch das Coulomb'sche Gesetz, resp. ein elektrisches Feld beschreiben lassen, treten
Aufgabensammlung. Elektromagnetische Felder und Wellen. J. Mähnß. zur Vorlesung. Stand: 8. April 2009 c J. Mähnß
 Aufgabensammlung zur Vorlesung Elektromagnetische Felder und Wellen J. Mähnß Stand: 8. April 2009 c J. Mähnß 2 Inhaltsverzeichnis 1 Grundlegende Gesetze der Elektrostatik 5 1.1 Das Coulombsche Gesetz und
Aufgabensammlung zur Vorlesung Elektromagnetische Felder und Wellen J. Mähnß Stand: 8. April 2009 c J. Mähnß 2 Inhaltsverzeichnis 1 Grundlegende Gesetze der Elektrostatik 5 1.1 Das Coulombsche Gesetz und
Klassische Theoretische Physik II. V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch. Klausur 2 Lösung. 22. September 2015, 12-14 Uhr
 KIT SS 15 Klassische Theoretische Physik II V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch Klausur Lösung. September 15, 1-14 Uhr Aufgabe 1: Kurzfragen (3+4+1+1 Punkte (a Die erhaltenen Größen und evtl.
KIT SS 15 Klassische Theoretische Physik II V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch Klausur Lösung. September 15, 1-14 Uhr Aufgabe 1: Kurzfragen (3+4+1+1 Punkte (a Die erhaltenen Größen und evtl.
Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.
![Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t. Formelsammlung. Physik. [F] = kg m s 2 = N (Newton) v = ṡ = ds dt. [v] = m/s. a = v = s = d2 s dt 2 [s] = m/s 2. v = a t.](/thumbs/48/24282507.jpg) Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Formelsammlung Physik Mechanik. Kinematik und Kräfte Kinematik Erstes Newtonsches Axiom (Axio/Reaxio) F axio = F reaxio Zweites Newtonsches Axiom Translationsbewegungen Konstante Beschleunigung F = m a
Lösung zu den Testaufgaben zur Mathematik für Chemiker II (Analysis)
 Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS
 ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Gegeben sei die Gleichung 2x 2 4xy +y 2 3x+4y = 0. Verifizieren Sie, dass diese Gleichung
ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Gegeben sei die Gleichung 2x 2 4xy +y 2 3x+4y = 0. Verifizieren Sie, dass diese Gleichung
Rotationskörper. Ronny Harbich. 1. August 2003 (geändert 24. Oktober 2007)
 Rotationskörper Ronny Harbich 1. August 2003 geändert 24. Oktober 2007) Inhaltsverzeichnis 1 Einführung 3 2 Anschauliche Herleitung 4 2.1 Darstellungen................................. 4 2.2 Gleichungen
Rotationskörper Ronny Harbich 1. August 2003 geändert 24. Oktober 2007) Inhaltsverzeichnis 1 Einführung 3 2 Anschauliche Herleitung 4 2.1 Darstellungen................................. 4 2.2 Gleichungen
Elektromagnetische Felder und Wellen: Lösung zur Klausur E x = E 0 cos 2 { ωz c ωt }
 Elektromagnetische Felder und Wellen: zur Klausur 202- Aufgabe ( 6 Punkte) Gegeben ist das H-Feld einer elektromagnetischen Welle als H = H 0 exp{i(ωt kz)} e y + ih exp{i(ωt kz)} e x Geben Sie die Polarisation
Elektromagnetische Felder und Wellen: zur Klausur 202- Aufgabe ( 6 Punkte) Gegeben ist das H-Feld einer elektromagnetischen Welle als H = H 0 exp{i(ωt kz)} e y + ih exp{i(ωt kz)} e x Geben Sie die Polarisation
Mathematik Übungsblatt - Lösung. b) x=2
 Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 9: Mehrdimensionale Integrale Prof. Dr. Erich Walter Farkas Mathematik I+II, 9. Mehrdim. Int. 1 / 39 1 Doppelintegrale 2 Prof.
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 9: Mehrdimensionale Integrale Prof. Dr. Erich Walter Farkas Mathematik I+II, 9. Mehrdim. Int. 1 / 39 1 Doppelintegrale 2 Prof.
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
Weitere Aufgaben zu Mathematik C
 Bergische Universität Wuppertal Fachbereich C PD Dr. Schuster Weitere Aufgaben zu Mathematik C A. Kurvenintegrale und Stammfunktionen. Das Vektorfeld F: R 3 R 3 sei gegeben durch F(x, y, z) = 2z(x + y)
Bergische Universität Wuppertal Fachbereich C PD Dr. Schuster Weitere Aufgaben zu Mathematik C A. Kurvenintegrale und Stammfunktionen. Das Vektorfeld F: R 3 R 3 sei gegeben durch F(x, y, z) = 2z(x + y)
Vektoranalysis. Kapitel Felder Gradient und Kurvenintegral. Skalare Felder. Vektorfelder. Gradient
 Kapitel 11 ektoranalysis 111 Felder kalare Felder Eine skalare Größe φ, die jedem Raumpunkt r = rx, y, z zugeordnet ist, heißt skalares Feld: φ = φ r =φx, y, z Wenn die Werte der Funktion φ nur von dem
Kapitel 11 ektoranalysis 111 Felder kalare Felder Eine skalare Größe φ, die jedem Raumpunkt r = rx, y, z zugeordnet ist, heißt skalares Feld: φ = φ r =φx, y, z Wenn die Werte der Funktion φ nur von dem
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Übungsblatt 09. Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik
 Übungsblatt 9 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik 9.6.8 Aufgaben. Durch eine Spule mit n Windungen, die einen Querschnitt A 7, 5cm hat, fliesst
Übungsblatt 9 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik 9.6.8 Aufgaben. Durch eine Spule mit n Windungen, die einen Querschnitt A 7, 5cm hat, fliesst
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009
 Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009 Aufgabe 35: Thema: Singulärwertzerlegung und assoziierte Unterräume Sei A eine m n Matrix mit Rang r und A = UDV T ihre Singulärwertzerlegung.
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt 10 21.12.2009 Aufgabe 35: Thema: Singulärwertzerlegung und assoziierte Unterräume Sei A eine m n Matrix mit Rang r und A = UDV T ihre Singulärwertzerlegung.
Korrelationsmatrix. Statistische Bindungen zwischen den N Zufallsgrößen werden durch die Korrelationsmatrix vollständig beschrieben:
 Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
Korrelationsmatrix Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit N Dimensionen bietet sich zweckmäßiger Weise
Vorkurs Mathematik für Wirtschaftsingenieure und Wirtschaftsinformatiker
 Vorkurs Mathematik für Wirtschaftsingenieure und Wirtschaftsinformatiker Übungsblatt Musterlösung Fachbereich Rechts- und Wirtschaftswissenschaften Wintersemester 06/7 Aufgabe (Definitionsbereiche) Bestimme
Vorkurs Mathematik für Wirtschaftsingenieure und Wirtschaftsinformatiker Übungsblatt Musterlösung Fachbereich Rechts- und Wirtschaftswissenschaften Wintersemester 06/7 Aufgabe (Definitionsbereiche) Bestimme
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
Vorlesungsskript PHYS Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik
 Vorlesungsskript PHYS 70357 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik Othmar Marti Institut für Experimentelle Physik Universität Ulm 14. Oktober 2011
Vorlesungsskript PHYS 70357 Elektrizitätslehre und Magnetismus Bachelor Physik Bachelor Wirtschaftsphysik Lehramt Physik Othmar Marti Institut für Experimentelle Physik Universität Ulm 14. Oktober 2011
Mathematik II für Inf und WInf
 Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
5.5 Elektrisches Zentralfeld, Coulombsches Gesetz
 5 Elektrizität und Magnetismus 5.5 Elektrisches Zentralfeld, Coulombsches Gesetz Elektrisches Zentralfeld Kugel mit Radius r um eine Punktladung = ǫ 0 Ed A = ǫ 0 E E d A Kugel da = ǫ 0 E(4πr 2 ) (5.26)
5 Elektrizität und Magnetismus 5.5 Elektrisches Zentralfeld, Coulombsches Gesetz Elektrisches Zentralfeld Kugel mit Radius r um eine Punktladung = ǫ 0 Ed A = ǫ 0 E E d A Kugel da = ǫ 0 E(4πr 2 ) (5.26)
"wahre Anomalie": (= Winkel bzgl. Fokus) "exzentrische Anomalie": const =
 Beipiel 4: Iteratives Lösen von Gleichungen Kepler-Gleichung: Finde Lösung für bis inklusive! Physikalische Anwendung im Kepler-Problem: Gl. (1) bestimmt den Zusammenhang zwischen Laufzeit t und der "exzentrischen
Beipiel 4: Iteratives Lösen von Gleichungen Kepler-Gleichung: Finde Lösung für bis inklusive! Physikalische Anwendung im Kepler-Problem: Gl. (1) bestimmt den Zusammenhang zwischen Laufzeit t und der "exzentrischen
Elektromagnetische Felder und Wellen: Lösung zur Klausur Gegeben sind die folgenden elektrischen und magnetischen Feldkomponenten: Z =
 Elektromagnetische Felder und Wellen: zur Klausur 2011-1 1 Aufgabe 1 Gegeben sind die folgenden elektrischen und magnetischen Feldkomponenten: 1. E1 ( r) = E 0 cos{kz ωt} e x 2. E2 ( r) = ie 0 exp{ i(kz
Elektromagnetische Felder und Wellen: zur Klausur 2011-1 1 Aufgabe 1 Gegeben sind die folgenden elektrischen und magnetischen Feldkomponenten: 1. E1 ( r) = E 0 cos{kz ωt} e x 2. E2 ( r) = ie 0 exp{ i(kz
2. Klausur in K1 am
 Name: Punkte: Note: Ø: Physik Kursstufe Abzüge für Darstellung: Rundung:. Klausur in K am 7.. 00 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: e =,60
Name: Punkte: Note: Ø: Physik Kursstufe Abzüge für Darstellung: Rundung:. Klausur in K am 7.. 00 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: e =,60
1 Vorlesungen: und Vektor Rechnung: 1.Teil
 1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
2.4 Eine positive Ladung Q ist gleichmäßig auf einer ringförmigen Linie mit dem Radius R verteilt.
 Das statische Feld 2 2 Statische Felder 2.1 Superpositionsprinzip 2.1 a) Beschreiben Sie das Feld einer Punktladung im Vakuum durch den Vektor der Feldstärke E(r)! b) Überprüfen Sie, ob es sich dabei um
Das statische Feld 2 2 Statische Felder 2.1 Superpositionsprinzip 2.1 a) Beschreiben Sie das Feld einer Punktladung im Vakuum durch den Vektor der Feldstärke E(r)! b) Überprüfen Sie, ob es sich dabei um
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof Dr D Castrigiano Dr M Prähofer Zentralübung 85 Oberfläche des Torus im R 4 TECHNICHE UNIVERITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis http://wwwmatumde/hm/ma924 2W/ Gegeben
Prof Dr D Castrigiano Dr M Prähofer Zentralübung 85 Oberfläche des Torus im R 4 TECHNICHE UNIVERITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis http://wwwmatumde/hm/ma924 2W/ Gegeben
300 Arbeit, Energie und Potential 310 Arbeit und Leistung 320 Felder und Potentiale
 300 Arbeit, Energie und Potential 30 Arbeit und Leistung 30 Felder und Potentiale um was geht es? Arten on (mechanischer) Energie Potentialbegriff Beschreibung on Systemen mittels Energie 3 potentielle
300 Arbeit, Energie und Potential 30 Arbeit und Leistung 30 Felder und Potentiale um was geht es? Arten on (mechanischer) Energie Potentialbegriff Beschreibung on Systemen mittels Energie 3 potentielle
Physik III Übung 1 - Lösungshinweise
 Physik III Übung 1 - Lösungshinweise Stefan Reutter WiSe 212 Moritz Kütt Stand: 16.11.212 Franz Fujara Aufgabe 1 [P] ermanentmagnete (Diskussion) Benötigt man, um ein Magnetfeld zu erhalten, immer einen
Physik III Übung 1 - Lösungshinweise Stefan Reutter WiSe 212 Moritz Kütt Stand: 16.11.212 Franz Fujara Aufgabe 1 [P] ermanentmagnete (Diskussion) Benötigt man, um ein Magnetfeld zu erhalten, immer einen
Elektrodynamik. Theoretische Physik B WS 2010/2011. Prof. Dr. Wolf Gero Schmidt Universität Paderborn, Lehrstuhl für Theoretische Physik
 Elektrodynamik Theoretische Physik B WS 2010/2011 Prof. Dr. Wolf Gero Schmidt Inhaltsverzeichnis 1 Die Maxwellgleichungen 4 1.1 Ladungen und Ströme............................ 4 1.2 Differentielle Maxwellgleichungen......................
Elektrodynamik Theoretische Physik B WS 2010/2011 Prof. Dr. Wolf Gero Schmidt Inhaltsverzeichnis 1 Die Maxwellgleichungen 4 1.1 Ladungen und Ströme............................ 4 1.2 Differentielle Maxwellgleichungen......................
Klausur zur Vorlesung Physikalische Chemie V Elektrochemie 6. bzw. 8. Fachsemester am , 10:00 bis 12:00 Uhr
 Universität Regensburg Institut für Physikalische und Theoretische Chemie Prof. Dr. G. Schmeer 18. Juli 27 Bitte füllen Sie zuerst dieses Deckblatt aus, das mit Ihren Lösungen abgegeben werden muss....
Universität Regensburg Institut für Physikalische und Theoretische Chemie Prof. Dr. G. Schmeer 18. Juli 27 Bitte füllen Sie zuerst dieses Deckblatt aus, das mit Ihren Lösungen abgegeben werden muss....
Übungsblatt 02. PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti,
 Übungsblatt 2 PHYS4 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, ([email protected]) 2. 4. 25 22. 4. 25 Aufgaben. Das Plancksche Strahlungsgesetz als Funktion der
Übungsblatt 2 PHYS4 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, ([email protected]) 2. 4. 25 22. 4. 25 Aufgaben. Das Plancksche Strahlungsgesetz als Funktion der
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
6.2 Extremwertaufgaben mit Nebenbedingung
 6.. Extremwertaufgaben mit Nebenbedingung 87 6. Extremwertaufgaben mit Nebenbedingung Betrachten wir jetzt eine differenzierbare Funktion f:u R n R U offen in R n. Ist n = 3 und U eine glatte Fläche, dann
6.. Extremwertaufgaben mit Nebenbedingung 87 6. Extremwertaufgaben mit Nebenbedingung Betrachten wir jetzt eine differenzierbare Funktion f:u R n R U offen in R n. Ist n = 3 und U eine glatte Fläche, dann
Grundlagen der Elektrotechnik 1
 Grundlagen der Elektrotechnik 1 Kapitel 5: Elektrisches Strömungsfeld 5 Elektrisches Strömungsfeld 5.1 Definition des Feldbegriffs 5. Das elektrische Strömungsfeld 3 5..1 Strömungsfeld in einer zylindrischen
Grundlagen der Elektrotechnik 1 Kapitel 5: Elektrisches Strömungsfeld 5 Elektrisches Strömungsfeld 5.1 Definition des Feldbegriffs 5. Das elektrische Strömungsfeld 3 5..1 Strömungsfeld in einer zylindrischen
4 Das Riemann-Integral im R n
 $Id: nintegral.tex,v 1.11 2012/11/27 14:07:09 hk Exp hk $ 4 Das Riemann-Integral im R n 4.3 Jordan-meßbare engen In der letzten Sitzung hatten wir schließlich das n-dimensionale Riemann-Integral auch auf
$Id: nintegral.tex,v 1.11 2012/11/27 14:07:09 hk Exp hk $ 4 Das Riemann-Integral im R n 4.3 Jordan-meßbare engen In der letzten Sitzung hatten wir schließlich das n-dimensionale Riemann-Integral auch auf
Nichtlineare Gleichungssysteme
 Kapitel 2 Nichtlineare Gleichungssysteme Problem: Für vorgegebene Abbildung f : D R n R n finde R n mit oder ausführlicher f() = 0 (21) f 1 ( 1,, n ) = 0, f n ( 1,, n ) = 0 Einerseits führt die mathematische
Kapitel 2 Nichtlineare Gleichungssysteme Problem: Für vorgegebene Abbildung f : D R n R n finde R n mit oder ausführlicher f() = 0 (21) f 1 ( 1,, n ) = 0, f n ( 1,, n ) = 0 Einerseits führt die mathematische
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Füllstand eines Behälters
 Füllstand eines Behälters Der Behälter ist eines der häufigsten Apparate in der chemischen Industrie zur Aufbewahrung von Flüssigkeiten. Dabei ist die Kenntnis das Gesamtvolumens als auch des Füllvolumens
Füllstand eines Behälters Der Behälter ist eines der häufigsten Apparate in der chemischen Industrie zur Aufbewahrung von Flüssigkeiten. Dabei ist die Kenntnis das Gesamtvolumens als auch des Füllvolumens
Ferienkurs Experimentalphysik II Elektrodynamik. Übung zur Magnetostatik Musterlösung. 12. September 2011 Michael Mittermair
 Ferienkurs Experimentalphysik II Elektrodynamik Übung zur Magnetostatik Musterlösung 12. September 211 Michael Mittermair Aufgabe 1 Bestimmen sie das B-Feld eines dünnen,(unendlich)langen, geraden Leiters,
Ferienkurs Experimentalphysik II Elektrodynamik Übung zur Magnetostatik Musterlösung 12. September 211 Michael Mittermair Aufgabe 1 Bestimmen sie das B-Feld eines dünnen,(unendlich)langen, geraden Leiters,
Zwei Paradoxa zur Existenz magnetischer Felder
 Zwei Paradoa zur Eistenz magnetischer Felder Claus W. Turtur, Fachhochschule Braunschweig-Wolfenbüttel Wolfenbüttel, 14. Dez. 7 Zusammenfassung Ein Gedankeneperiment wird betrachtet, in welchem ein Beobachter
Zwei Paradoa zur Eistenz magnetischer Felder Claus W. Turtur, Fachhochschule Braunschweig-Wolfenbüttel Wolfenbüttel, 14. Dez. 7 Zusammenfassung Ein Gedankeneperiment wird betrachtet, in welchem ein Beobachter
Zusammenfassung Grundgebiete der Elektrotechnik 3
 Zusammenfassung Grundgebiete der Elektrotechnik 3 RWTH Aachen, WS 2005, Univ.-Prof. Dr. Tobias Noll c 2005 by Ralf Wilke, DH3WR Korrekturen bitte an [email protected] 7. Januar 2006 Inhaltsverzeichnis
Zusammenfassung Grundgebiete der Elektrotechnik 3 RWTH Aachen, WS 2005, Univ.-Prof. Dr. Tobias Noll c 2005 by Ralf Wilke, DH3WR Korrekturen bitte an [email protected] 7. Januar 2006 Inhaltsverzeichnis
Theoretische Physik II Elektrodynamik Blatt 9. k (
 PDDr. S.Mertens M. Hummel Theoretische Physik II Elektrodynamik Blatt 9 SS 29.6.29. Energie und Impuls elektromagnetischer Wellen. Eine transversale elektromagnetische 4Pkt.) Welle in einem nicht leitenden,
PDDr. S.Mertens M. Hummel Theoretische Physik II Elektrodynamik Blatt 9 SS 29.6.29. Energie und Impuls elektromagnetischer Wellen. Eine transversale elektromagnetische 4Pkt.) Welle in einem nicht leitenden,
Raum- und Flächenmessung bei Körpern
 Raum- und Flächenmessung bei Körpern Prismen Ein Prisma ist ein Körper, dessen Grund- und Deckfläche kongruente Vielecke sind und dessen Seitenflächen Parallelogramme sind. Ist der Winkel zwischen Grund-
Raum- und Flächenmessung bei Körpern Prismen Ein Prisma ist ein Körper, dessen Grund- und Deckfläche kongruente Vielecke sind und dessen Seitenflächen Parallelogramme sind. Ist der Winkel zwischen Grund-
i j Verwenden Sie die Komponentenschreibweise und, soweit möglich, den ɛ-tensor. g i ( r ) d s, C
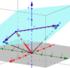 SS 2008 Blatt 1 Aufgabe 1: ɛ-tensor Für den ɛ-tensor gilt ɛ 123 = 1 = ɛ 321 und zyklisch, sowie ɛ i j k = 0 falls zwei Indizes gleich sind. Beweisen Sie folgende Relationen: a) i ɛ i j k ɛ ilm = δ j l
SS 2008 Blatt 1 Aufgabe 1: ɛ-tensor Für den ɛ-tensor gilt ɛ 123 = 1 = ɛ 321 und zyklisch, sowie ɛ i j k = 0 falls zwei Indizes gleich sind. Beweisen Sie folgende Relationen: a) i ɛ i j k ɛ ilm = δ j l
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
12 Gewöhnliche Differentialgleichungen 121 Einführende Beispiele und Grundbegriffe Beispiel 1 ( senkrechter Wurf ) v 0 Ein Flugkörper werde zum Zeitpunkt t = 0 in der Höhe s = 0 t = 0 s = 0 mit der Startgeschwindigkeit
Elektrodynamik. Theoretische Physik 3
 Elektrodynamik Theoretische Physik 3 WS 2008/9 Gerhard Ecker Fakultät für Physik Universität Wien Inhaltsverzeichnis Inhaltsverzeichnis..................................... 2 Danksagung........................................
Elektrodynamik Theoretische Physik 3 WS 2008/9 Gerhard Ecker Fakultät für Physik Universität Wien Inhaltsverzeichnis Inhaltsverzeichnis..................................... 2 Danksagung........................................
2 Euklidische Vektorräume
 Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Vakuum und Gastheorie
 Vakuum und Gastheorie Jan Krieger 9. März 2005 1 INHALTSVERZEICHNIS 0.1 Formelsammlung.................................... 2 0.1.1 mittlere freie Weglänge in idealen Gasen................... 3 0.1.2 Strömungsleitwerte
Vakuum und Gastheorie Jan Krieger 9. März 2005 1 INHALTSVERZEICHNIS 0.1 Formelsammlung.................................... 2 0.1.1 mittlere freie Weglänge in idealen Gasen................... 3 0.1.2 Strömungsleitwerte
Klassifikation von partiellen Differentialgleichungen
 Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
Studiengänge) Beispiele
 Grundkurs Höhere Mathematik I (für naturwissenschaftliche Studiengänge) Beispiele Prof. Dr. Udo Hebisch Diese Beispielsammlung ergänzt das Vorlesungsskript und wird ständig erweitert. DETERMINANTEN Determinanten
Grundkurs Höhere Mathematik I (für naturwissenschaftliche Studiengänge) Beispiele Prof. Dr. Udo Hebisch Diese Beispielsammlung ergänzt das Vorlesungsskript und wird ständig erweitert. DETERMINANTEN Determinanten
Thema 10 Gewöhnliche Differentialgleichungen
 Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
Thema 10 Gewöhnliche Differentialgleichungen Viele Naturgesetze stellen eine Beziehung zwischen einer physikalischen Größe und ihren Ableitungen (etwa als Funktion der Zeit dar: 1. ẍ = g (freier Fall;
Universität Regensburg Fakultät Physik. Experimentalphysik 2. Elektrodynamik. Prof. Christian Schüller. Sommersemester L A TEX: Frank Reinhold
 Universität Regensburg Fakultät Physik Experimentalphysik 2 Elektrodynamik Prof. Christian Schüller Sommersemester 2008 L A TEX: Frank Reinhold Inhaltsverzeichnis Einführung/Motivation 5 1 Elektrostatik
Universität Regensburg Fakultät Physik Experimentalphysik 2 Elektrodynamik Prof. Christian Schüller Sommersemester 2008 L A TEX: Frank Reinhold Inhaltsverzeichnis Einführung/Motivation 5 1 Elektrostatik
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
(3) Grundlagen II. Vorlesung CV-Integration S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 (3) Grundlagen II Vorlesung CV-Integration S. Müller KOBLENZ LANDAU Wiederholung I Strahlungsphysik (Radiometrie) Lichttechnik (Photometrie) V(λ)-Kurve.0 0.8 0.6 0.4 0. 0 400 500 600 700 800λ[nm] violett
(3) Grundlagen II Vorlesung CV-Integration S. Müller KOBLENZ LANDAU Wiederholung I Strahlungsphysik (Radiometrie) Lichttechnik (Photometrie) V(λ)-Kurve.0 0.8 0.6 0.4 0. 0 400 500 600 700 800λ[nm] violett
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Serie 9: Satz von Stokes und Divergenzsatz
 D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas Serie 9: Satz von Stokes und Divergenzsatz Bemerkungen: Die Aufgaben der Serie 9 bilden den Fokus der Übungsgruppen vom 28./30. April. 1. Berechnen
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas Serie 9: Satz von Stokes und Divergenzsatz Bemerkungen: Die Aufgaben der Serie 9 bilden den Fokus der Übungsgruppen vom 28./30. April. 1. Berechnen
Magnetismus. Prinzip: Kein Monopol nur Dipole. Kräfte:
 Elektromagnetismus Magnetismus Prinzip: Kein Monopol nur Dipole Kräfte: S N Richtung des Magnetischen Feldes I B Kraft auf Ladungen im B-Feld + Proportionalitätskonstante B FM = q v B Durch Messung: LORENTZ
Elektromagnetismus Magnetismus Prinzip: Kein Monopol nur Dipole Kräfte: S N Richtung des Magnetischen Feldes I B Kraft auf Ladungen im B-Feld + Proportionalitätskonstante B FM = q v B Durch Messung: LORENTZ
Physik 1 für Ingenieure
 Physik 1 für Ingenieure Othmar Marti Experimentelle Physik Universität Ulm [email protected] Skript: http://wwwex.physik.uni-ulm.de/lehre/physing1 Übungsblätter und Lösungen: http://wwwex.physik.uni-ulm.de/lehre/physing1/ueb/ue#
Physik 1 für Ingenieure Othmar Marti Experimentelle Physik Universität Ulm [email protected] Skript: http://wwwex.physik.uni-ulm.de/lehre/physing1 Übungsblätter und Lösungen: http://wwwex.physik.uni-ulm.de/lehre/physing1/ueb/ue#
= 0a. r κ = 0. = 0 κ =
 Aufgabe 1 16 Punkte) Eine nichtleitende Kugel des Radius a mit der Raumladungsdichte = a r ist im Ursprung zentriert und wird von einer Kugelschale aus unendlich gut leitendem Metall mit Radius b und der
Aufgabe 1 16 Punkte) Eine nichtleitende Kugel des Radius a mit der Raumladungsdichte = a r ist im Ursprung zentriert und wird von einer Kugelschale aus unendlich gut leitendem Metall mit Radius b und der
PS II - Verständnistest
 Grundlagen der Elektrotechnik PS II - Verständnistest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 4 2 2 5 3 4 4 erreicht Aufgabe 8 9 10 11 Summe Punkte 3 3 3 2 35 erreicht Hinweise:
Grundlagen der Elektrotechnik PS II - Verständnistest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 4 2 2 5 3 4 4 erreicht Aufgabe 8 9 10 11 Summe Punkte 3 3 3 2 35 erreicht Hinweise:
7.2.1 Zweite partielle Ableitungen
 72 72 Höhere Ableitungen 72 Höhere Ableitungen Vektorwertige Funktionen sind genau dann differenzierbar, wenn ihre Koordinatenfunktionen differenzierbar sind Es ist also keine wesentliche Einschränkung,
72 72 Höhere Ableitungen 72 Höhere Ableitungen Vektorwertige Funktionen sind genau dann differenzierbar, wenn ihre Koordinatenfunktionen differenzierbar sind Es ist also keine wesentliche Einschränkung,
= 1 und der Ladung Q aufgefasst. Die elektrische Feldstärke beträgt 1, N/C, so dass die Entladung durch einen Blitz unmittelbar bevorsteht.
 Aufgaben Konensator 57. Zwei kreisförmige Metallplatten mit em Raius 0 cm, ie parallel im Abstan von 0 cm angeornet sin, bilen einen Plattenkonensator. In er Mitte zwischen en Platten hängt an einem ünnen
Aufgaben Konensator 57. Zwei kreisförmige Metallplatten mit em Raius 0 cm, ie parallel im Abstan von 0 cm angeornet sin, bilen einen Plattenkonensator. In er Mitte zwischen en Platten hängt an einem ünnen
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
