Funktionale Programmierung. Funktionale Programmierung: Vorlesungsüberblick. Eigenschaften rein funktionaler Programmierung
|
|
|
- Ruth Dresdner
- vor 8 Jahren
- Abrufe
Transkript
1 Funktionale Programmierung 1 Funktionale Programmierung: Vorlesungsüberblick 1. Funktionale Programmierung Prinzipien funktionaler Programmierung Funktionale Programmierung in prozeduralen Sprachen Rekursive Programmierung Aufwandsbetrachtungen rekursiver Programme 2. Semantik funktionaler Programme Induktiver Beweis Induktive Deutung Fixpunktdeutung 3. Einführung in die rein funktionale Programmiersprache Scheme 4. Verfahren zur automatischen Speicherverwaltung 2 Eigenschaften rein funktionaler Programmierung Alle Programme und Prozeduren sind Funktionen und unterscheiden deutlich zwischen hereinkommenden Werten (Parameter) und herausgehenden Werten (Ergebnisse) Programmausführung in funktionalen Programmen ist die Auswertung eines Ausdrucks Es gibt keine Variablen Variablen werden durch Parameter ersetzt Es gibt keine Zuweisungen und keine Schleifen Schleifen werden durch rekursive Aufrufe ersetzt Der Wert einer Funktion hängt nur vom Wert der Parameter ab und nicht von der Reihenfolge der Berechnungen 3
2 Funktionale und imperative Programmierung Vorteile funktionaler Programmierung gegenüber imperativer Programmierung einheitliche Betrachtung von Programmen als Funktionen Behandlung von Funktionen als Daten (=Werte) Einschränkung von Seiteneffekten Automatische Speicherfreigabe Flexibilität, Prägnanz in der Notation, einfache Semantik Hauptnachteil funktionaler Programmierung ist die Ineffizienz der Programmausführung Anwendungsgebiete: künstliche Intelligenz, mathematische Beweissysteme, Logikanwendungen 4 Funktionales Programmieren in imperativen Sprachen Imperative Programmiersprachen (wie Modula-3) besitzen im allgemeinen ebenfalls mehr oder weniger ausgereifte Formen der funktionalen Programmierung rein funktionale Programmierung in imperativen Sprachen kann durch folgende Einschränkungen bei der Auswahl der gewählten Programmierelemente erreicht werden ausschließliche Verwendung von Funktionen zur Beschreibung des Kontrollflusses eines Programms wird alleinig auf Selektion und Funktionsaufruf zurückgegriffen keine Verwendung von Variablen, Zuweisungen und Schleifen in den Programmen Mächtigkeit des so eingeschränkten Programmiermodells entspricht dem der uneingeschränkten imperativen Sprache 5 Voraussetzungen (Euklidischer Algorithmus) Euklidischer Algorithmus kann zur Berechnung des größten gemeinsamen Teilers (ggt) benutzt werden Eine Zahl ggt heißt größter gemeinsamer Teiler zweier Zahlen a und b falls gilt: ggt teilt a und b für jeden gemeinsamen Teiler d von a und b gilt: d teilt die Zahl ggt wichtige Eigenschaften des ggt: ggt(x,0) = x ggt(x, y) = ggt(y, x mod y) für x,y > 0 6
3 Modula-3 Programm (Euklidischer Algorithmus) PROCEDURE ggt(a,b : INTEGER) : INTEGER= VAR tmp : INTEGER; LOOP IF b = 0 THEN RETURN a; tmp := a; a := b; b := tmp MOD b; 7 Modula-3-Programm (Rekursive Funktion) PROCEDURE ggt(a,b : INTEGER) : INTEGER= IF b = 0 THEN RETURN a; RETURN ggt(b, a MOD b) 8 Allgemeiner Entwurf rekursiver Funktionen analog zum Beweisen mit vollständiger Induktion stellt man sich die Frage: wie wird der Basisfall gelöst? der absolute Trivialfall der einfachste nicht-triviale Fall wie kann der allgemeine Fall der Größe n auf die Lösung für eine Größe n < n reduziert werden? aus der so erzeugten Spezifikation können bedingte Gleichungen abgeleitet werden, die dann in Programmcode umgesetzt werden derartig konstruierte rekursive Funktionen können dann mittels Induktion als korrekt bewiesen werden 9
4 Rekursive Funktionen: Mathematische Operationen PROCEDURE mod (n,m:integer):integer = (* n 0, m > 0*) IF n < m THEN RETURN n; RETURN mod(n-m,m); END mod; 10 Rekursive Funktionen: Mathematische Operationen PROCEDURE binom (n,k:integer):integer =(*n,k 0, n k*) IF n = k OR k = 0 THEN RETURN 1; RETURN binom(n-1,k-1) + binom(n-1,k); END binom; 11 Rekursive Funktion: Erkennen eines Palindroms PROCEDURE h (n : INTEGER) : INTEGER = (* n 0 *) IF n < 10 THEN RETURN 1 RETURN 10 * h(n / 10) END h; PROCEDURE spiegel (n : INTEGER) : INTEGER = (* n 0 *) IF n < 10 THEN RETURN n RETURN mod(n,10) * h(n) + spiegel(n/10) END spiegel; PROCEDURE palindrom (n: INTEGER) : BOOLEAN = (*n 0*) RETURN spiegel(n) = n END palindrom; 12
5 Rekursionsformen: Lineare Rekursion in einer rekursiven Funktionsdeklaration für f tritt ein Aufruf von f in jedem Zweig einer Fallunterscheidung höchstens einmal auf PROCEDURE sum(i, j : INTEGER) : INTEGER = IF i > j THEN RETURN 0; RETURN i + sum(i + 1, j); END sum; 13 Rekursionsformen: Repetitive Rekursion eine linear rekursive Funktion f heißt repetitiv rekursiv, falls alle rekursiven Aufrufe in den Zweigen einer Fallunterscheidung als äußerste (letzte) Aktion vorkommen PROCEDURE ggt(u,v : INTEGER) : INTEGER = IF v = 0 THEN RETURN u; RETURN ggt(v, u MOD v); 14 Rekursionsformen: Kaskardenartige Rekursion treten in mindestens einem Zweig einer Fallunterscheidung zwei oder mehr rekursive Aufrufe auf, so spricht man von einer kaskaden- oder baumartigen, nichtlinearen Rekursion PROCEDURE binom (n,k:integer):integer = IF n = k OR k = 0 THEN RETURN 1; RETURN binom(n-1,k-1) + binom(n-1,k); END binom; 15
6 Rekursionsformen: Vernestete Rekursion treten im Rumpf einer rekursiven Funktion f in den aktuellen Parameterausdrücken eines rekursiven Aufrufs von f weitere rekursive Aufrufe von f auf, so heißt f vernestet. PROCEDURE ackermann (m,n:integer):integer = (*m,n 0*) IF m = 0 THEN RETURN n + 1; IF n = 0 THEN RETURN ackermann(m-1,1) RETURN ackermann(m-1, ackermann(m,n-1)); END ackermann; 16 Effizienz funktionaler Programme Bewertungskriterien für den Auswertungsaufwand eines funktionalen Programms Anzahl der auf algorithmischer Basis bei der Berechnung auszuführenden Grundoperationen Anzahl der durchgeführten rekursiven Funktionsaufrufe Aufruftiefe der rekursiven Funktionen Effizienz funktionaler Programme leidet oft besonders unter dem sehr kostspieligen Aufbau der Funktionsrahmen während der rekursiven Berechnung der Funktionsergebnisse zur Effizienzverbesserung werden funktionale Programme vom Übersetzer oft vor der Ausführung wieder in eine nicht rekursive Form gebracht 17 Laufzeitstapel beim rekursiven Aufruf Basis Stapel Wachstum Rahmen der aufrufenden Funktion Rahmen der aufgerufenen Funktion top of stack 18
7 Bestandteile von Funktionsrahmen Parameter Temporär genutzter Platz Rücksprungadresse Statischer Verweis Dynamischer Verweis 19 Automatische Transformation rekursiver Aufrufe Anlegen der Funktionsrahmen zur Ausführung einer rekursiven Funktion ist sowohl sehr speicher- als auch sehr zeitintensiv Übersetzer für funktionale Sprachen versuchen daher bei der Programmerzeugung intern rekursive Funktionen wieder in Schleifen zu transformieren repetitiv rekursive Funktionen eignen sich besonders zur einfachen und schnellen Rücktransformation in Schleifen nicht repetitiv rekursive Funktionen können mittels akkumulierender Parameter in repetitive Funktionen transformiert werden 20 Transformation von rekursiven Aufrufen in Schleifen Eigenschaften repetitiv rekursiver Funktionen: vor Auswertung eines neuen rekursiven Aufrufs ist die Auswertung des vorhergehenden rekursiven Aufrufs völlig abgeschlossen aktuelle Parameterwerte müssen nicht aufbewahrt werden Umwandlung repetitiv rekursiver Funktionen in Schleifen: für jeden Funktionsparameter p i wird eine Variable t i angelegt Funktionsrumpf wird in eine Endlosschleife umgewandelt nicht rekursive Fallunterscheidungen bleiben unverändert rekursive Fallunterscheidungen werden in 2 Schritten modelliert: Zuweisungen der aktuellen Parameterwerte a i des rekursiven Aufrufs zu den temporären Variablen t i Zuweisung der den t i zugewiesenen Werte an die formalen Parametern der Funktion p i 21
8 Beispiel: Repetitiv rekursive Funktion PROCEDURE ggt(u,v : INTEGER) : INTEGER = IF v = 0 THEN RETURN u; RETURN ggt(v, u MOD v); 22 Beispiel: Transformation in eine Schleife PROCEDURE ggt(u,v : INTEGER) : INTEGER = (* Vom Übersetzer eingefügte Hilfsvariablen *) VAR t1, t2 : INTEGER; LOOP IF v = 0 THEN RETURN u; (* Auswertung der aktuellen Parameter *) t1 := v; t2 := u MOD v; (* Neuzuweisung der Parameter *) u := t1; v := t2; (* IF *) (* Schleife *) 23 Transformation nicht repetitiv rekursiver Funktionen prinzipiell kann jede rekursive Funktion in die repetitive Form gebracht und anschließend in eine Schleife transformiert werden einfach gestaltet sich die Transformation von nur linearen Rekursionen in das repetitiv rekursive Gegenstück in nur linearen Rekursionsformen ist in jeder Fallunterscheidung höchsten ein rekursiver Aufruf erlaubt rekursiver Aufruf in nur linearen Funktionen muss jedoch nicht die letzte Operation einer Fallunterscheidung sein Transformation von nur linearer in repetitiv lineare Rekursion rekursive Funktionsdeklaration wird um einen zusätzlichen Ergebnisparameter erweitert Operationen, die sonst erst nach Beendigung des rekursiven Aufrufes durchgeführt würden, werden vorab berechnet und dem Ergebnisparameter beim rekursiven Aufruf übergeben 24
9 Beispiel: Nicht repetitiv rekursive Funktion PROCEDURE sum(i, j : INTEGER) : INTEGER = IF i > j THEN RETURN 0; RETURN i + sum(i + 1, j); END sum; 25 Beispiel: Transformation in repetitiv rekursive Form PROCEDURE sum1(i, j, sumsofar : INTEGER) : INTEGER = IF i > j THEN RETURN sumsofar; RETURN sum1(i + 1, j, sumsofar + i) END sum1; PROCEDURE sum(i, j : INTEGER) : INTEGER = RETURN sum1(i, j, 0); END sum; 26
Einführung in die Programmierung
 : Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
: Inhalt Einführung in die Programmierung Wintersemester 2008/09 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering Fakultät für Informatik TU Dortmund - mit / ohne Parameter - mit / ohne Rückgabewerte
Grundlagen der Programmierung (Vorlesung 14)
 Grundlagen der Programmierung (Vorlesung 14) Ralf Möller, FH-Wedel Vorige Vorlesung Verifikation von Anweisungen und Anweisungsfolgen Schleifen Inhalt dieser Vorlesung Funktionen und Prozeduren Lernziele
Grundlagen der Programmierung (Vorlesung 14) Ralf Möller, FH-Wedel Vorige Vorlesung Verifikation von Anweisungen und Anweisungsfolgen Schleifen Inhalt dieser Vorlesung Funktionen und Prozeduren Lernziele
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Was ist Logische Programmierung?
 Was ist Logische Programmierung? Die Bedeutung eines Computer-Programms kann durch Logik erklärt werden. Die Idee der logischen Programmierung besteht darin, die Logik eines Programms selber als Programm
Was ist Logische Programmierung? Die Bedeutung eines Computer-Programms kann durch Logik erklärt werden. Die Idee der logischen Programmierung besteht darin, die Logik eines Programms selber als Programm
Erwin Grüner 09.02.2006
 FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
FB Psychologie Uni Marburg 09.02.2006 Themenübersicht Folgende Befehle stehen in R zur Verfügung: {}: Anweisungsblock if: Bedingte Anweisung switch: Fallunterscheidung repeat-schleife while-schleife for-schleife
Kontrollstrukturen, Strukturierte Programmierung
 , Strukturierte Programmierung Steuer- und Kontrollfluss Strukturierte Programmierung Arten von Strukturblöcken Sequenz Alternative Iteration C-Spezifisches Seite 1 Elementare Algorithmen SelectionSort
, Strukturierte Programmierung Steuer- und Kontrollfluss Strukturierte Programmierung Arten von Strukturblöcken Sequenz Alternative Iteration C-Spezifisches Seite 1 Elementare Algorithmen SelectionSort
Inhalt. 1. Einführung in die Informatik. 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele.
 1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Darstellung von Algorithmen Aus den Einführungsbeispielen und
1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Darstellung von Algorithmen Aus den Einführungsbeispielen und
Entwurf von Algorithmen - Kontrollstrukturen
 Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
Entwurf von Algorithmen - Kontrollstrukturen Eine wichtige Phase in der Entwicklung von Computerprogrammen ist der Entwurf von Algorithmen. Dieser Arbeitsschritt vor dem Schreiben des Programmes in einer
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Arge Betriebsinformatik GmbH & Co.KG, CAP News 40, Februar 2013. CAP-News 40
 CAP-News 40 CAP-News ist in unrägelmäßigen Abständen erscheinende Information zum Produktkonfigurator CAP/VARIANTS. Hier werden die neuen Befehle, Funktionen und Möglichkeiten beschrieben. In CAP-News
CAP-News 40 CAP-News ist in unrägelmäßigen Abständen erscheinende Information zum Produktkonfigurator CAP/VARIANTS. Hier werden die neuen Befehle, Funktionen und Möglichkeiten beschrieben. In CAP-News
Java Kurs für Anfänger Einheit 5 Methoden
 Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
Einführung in die Informatik für Naturwissenschaftler und Ingenieure (alias Einführung in die Programmierung)
 Wintersemester 2007/08 Einführung in die Informatik für Naturwissenschaftler und Ingenieure (alias Einführung in die Programmierung) (Vorlesung) Prof. Dr. Günter Rudolph Fakultät für Informatik Lehrstuhl
Wintersemester 2007/08 Einführung in die Informatik für Naturwissenschaftler und Ingenieure (alias Einführung in die Programmierung) (Vorlesung) Prof. Dr. Günter Rudolph Fakultät für Informatik Lehrstuhl
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
SOI 2013. Die Schweizer Informatikolympiade
 SOI Die Schweizer Informatikolympiade Lösung SOI Wie schreibe ich eine gute Lösung? Bevor wir die Aufgaben präsentieren, möchten wir dir einige Tipps geben, wie eine gute Lösung für die theoretischen
SOI Die Schweizer Informatikolympiade Lösung SOI Wie schreibe ich eine gute Lösung? Bevor wir die Aufgaben präsentieren, möchten wir dir einige Tipps geben, wie eine gute Lösung für die theoretischen
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Kontrollstrukturen - Universität Köln
 Kontrollstrukturen - Universität Köln Mario Manno Kontrollstrukturen - Universität Köln p. 1 Was sind Sprachen Auszeichnungssprachen HTML, XML Programmiersprachen ASM, Basic, C, C++, Haskell, Java, Pascal,
Kontrollstrukturen - Universität Köln Mario Manno Kontrollstrukturen - Universität Köln p. 1 Was sind Sprachen Auszeichnungssprachen HTML, XML Programmiersprachen ASM, Basic, C, C++, Haskell, Java, Pascal,
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Lehrstuhl Informatik VI Grundzüge der Informatik * WS 2008/2009 Prof. Dr. Joachim Biskup
 Universität Dortmund Lehrstuhl Informatik VI Grundzüge der Informatik * WS 28/29 Prof. Dr. Joachim Biskup Leitung der Übungen: Arno Pasternak Lösungs-Ideen Übungsblatt 6 A: Grammatiken, Syntaxdiagramme
Universität Dortmund Lehrstuhl Informatik VI Grundzüge der Informatik * WS 28/29 Prof. Dr. Joachim Biskup Leitung der Übungen: Arno Pasternak Lösungs-Ideen Übungsblatt 6 A: Grammatiken, Syntaxdiagramme
Gesicherte Prozeduren
 Gesicherte Prozeduren Wenn eine Anwendung auf einer Client-Maschine läuft, wird normalerweise jede SQL-Anweisung einzeln vom Client an den Server gesandt, und jedes Ergebnistupel wird einzeln zurückgeliefert.
Gesicherte Prozeduren Wenn eine Anwendung auf einer Client-Maschine läuft, wird normalerweise jede SQL-Anweisung einzeln vom Client an den Server gesandt, und jedes Ergebnistupel wird einzeln zurückgeliefert.
Programmierparadigmen. Programmierparadigmen. Imperatives vs. objektorientiertes Programmieren. Programmierparadigmen. Agenda für heute, 4.
 Agenda für heute, 4. Mai, 2006 Programmierparadigmen Imperative Programmiersprachen In Prozeduren zusammengefasste, sequentiell ausgeführte Anweisungen Die Prozeduren werden ausgeführt, wenn sie als Teil
Agenda für heute, 4. Mai, 2006 Programmierparadigmen Imperative Programmiersprachen In Prozeduren zusammengefasste, sequentiell ausgeführte Anweisungen Die Prozeduren werden ausgeführt, wenn sie als Teil
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Lehrer: Einschreibemethoden
 Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Einführung in die Informatik I
 Einführung in die Informatik I Algorithmen und deren Programmierung Prof. Dr. Nikolaus Wulff Definition Algorithmus Ein Algorithmus ist eine präzise formulierte Handlungsanweisung zur Lösung einer gleichartigen
Einführung in die Informatik I Algorithmen und deren Programmierung Prof. Dr. Nikolaus Wulff Definition Algorithmus Ein Algorithmus ist eine präzise formulierte Handlungsanweisung zur Lösung einer gleichartigen
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Programmieren in C. Rekursive Funktionen. Prof. Dr. Nikolaus Wulff
 Programmieren in C Rekursive Funktionen Prof. Dr. Nikolaus Wulff Rekursive Funktionen Jede C Funktion besitzt ihren eigenen lokalen Satz an Variablen. Dies bietet ganze neue Möglichkeiten Funktionen zu
Programmieren in C Rekursive Funktionen Prof. Dr. Nikolaus Wulff Rekursive Funktionen Jede C Funktion besitzt ihren eigenen lokalen Satz an Variablen. Dies bietet ganze neue Möglichkeiten Funktionen zu
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Klausurteilnehmer. Wichtige Hinweise. Note: Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 HS OWL, FB 7, Malte Wattenberg.
 Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Quadratische Gleichungen
 Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Programmierung 2. Übersetzer: Code-Erzeugung. Sebastian Hack. Klaas Boesche. Sommersemester 2012. hack@cs.uni-saarland.de. boesche@cs.uni-saarland.
 1 Programmierung 2 Übersetzer: Code-Erzeugung Sebastian Hack hack@cs.uni-saarland.de Klaas Boesche boesche@cs.uni-saarland.de Sommersemester 2012 Bytecodes Der Java Übersetzer erzeugt keine Maschinensprache
1 Programmierung 2 Übersetzer: Code-Erzeugung Sebastian Hack hack@cs.uni-saarland.de Klaas Boesche boesche@cs.uni-saarland.de Sommersemester 2012 Bytecodes Der Java Übersetzer erzeugt keine Maschinensprache
Anlegen eines Speicherbereichs mit DB, DW eleganter in Kombination mit EQU, Timer-Interrupt
 Anlegen eines Speicherbereichs mit DB, DW eleganter in Kombination mit EQU, Timer-Interrupt AMPEL-Steuerung(en) Die Beschreibung und Programmierung der Ampel (vor allem Ampel_5) können sehr kompliziert
Anlegen eines Speicherbereichs mit DB, DW eleganter in Kombination mit EQU, Timer-Interrupt AMPEL-Steuerung(en) Die Beschreibung und Programmierung der Ampel (vor allem Ampel_5) können sehr kompliziert
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 9 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Grundlagen der Künstlichen Intelligenz 27. Aussagenlogik: Logisches Schliessen und Resolution Malte Helmert Universität Basel 28. April 2014 Aussagenlogik: Überblick Kapitelüberblick Aussagenlogik: 26.
Wir arbeiten mit Zufallszahlen
 Abb. 1: Bei Kartenspielen müssen zu Beginn die Karten zufällig ausgeteilt werden. Wir arbeiten mit Zufallszahlen Jedesmal wenn ein neues Patience-Spiel gestartet wird, muss das Computerprogramm die Karten
Abb. 1: Bei Kartenspielen müssen zu Beginn die Karten zufällig ausgeteilt werden. Wir arbeiten mit Zufallszahlen Jedesmal wenn ein neues Patience-Spiel gestartet wird, muss das Computerprogramm die Karten
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Grundlagen der Künstlichen Intelligenz
 Grundlagen der Künstlichen Intelligenz 22. Constraint-Satisfaction-Probleme: Kantenkonsistenz Malte Helmert Universität Basel 14. April 2014 Constraint-Satisfaction-Probleme: Überblick Kapitelüberblick
Grundlagen der Künstlichen Intelligenz 22. Constraint-Satisfaction-Probleme: Kantenkonsistenz Malte Helmert Universität Basel 14. April 2014 Constraint-Satisfaction-Probleme: Überblick Kapitelüberblick
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Programmierung in C. Grundlagen. Stefan Kallerhoff
 Programmierung in C Grundlagen Stefan Kallerhoff Vorstellungsrunde Name Hobby/Beruf Schon mal was programmiert? Erwartungen an den Kurs Lieblingstier Für zu Hause C-Buch online: http://openbook.rheinwerk-verlag.de/c_von_a_bis_z/
Programmierung in C Grundlagen Stefan Kallerhoff Vorstellungsrunde Name Hobby/Beruf Schon mal was programmiert? Erwartungen an den Kurs Lieblingstier Für zu Hause C-Buch online: http://openbook.rheinwerk-verlag.de/c_von_a_bis_z/
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens 1 Organisatorisches Freitag, 05. Mai 2006: keine Vorlesung! aber Praktikum von 08.00 11.30 Uhr (Gruppen E, F, G, H; Vortestat für Prototyp)
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens 1 Organisatorisches Freitag, 05. Mai 2006: keine Vorlesung! aber Praktikum von 08.00 11.30 Uhr (Gruppen E, F, G, H; Vortestat für Prototyp)
Automatisches Parallelisieren
 Automatisches Parallelisieren Vorlesung im Wintersemester 2010/11 Eberhard Zehendner FSU Jena Thema: Datenabhängigkeitsanalyse Eberhard Zehendner (FSU Jena) Automatisches Parallelisieren Datenabhängigkeitsanalyse
Automatisches Parallelisieren Vorlesung im Wintersemester 2010/11 Eberhard Zehendner FSU Jena Thema: Datenabhängigkeitsanalyse Eberhard Zehendner (FSU Jena) Automatisches Parallelisieren Datenabhängigkeitsanalyse
Bevor lineare Gleichungen gelöst werden, ein paar wichtige Begriffe, die im Zusammenhang von linearen Gleichungen oft auftauchen.
 R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Mächtigkeit von WHILE-Programmen
 Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Mächtigkeit von WHILE-Programmen Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 26. November 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T:
 Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Binäre Bäume Binärbäume als weiteres Beispiel für abstrakte Datentypen in PVS mit in Knoten gespeicherten Werten vom Typ T: BinTree [T: TYPE]: DATATYPE empty: empty? node (key: T, left:bibtree, right:bibtree):
Bereich METIS (Texte im Internet) Zählmarkenrecherche
 Bereich METIS (Texte im Internet) Zählmarkenrecherche Über die Zählmarkenrecherche kann man nach der Eingabe des Privaten Identifikationscodes einer bestimmten Zählmarke, 1. Informationen zu dieser Zählmarke
Bereich METIS (Texte im Internet) Zählmarkenrecherche Über die Zählmarkenrecherche kann man nach der Eingabe des Privaten Identifikationscodes einer bestimmten Zählmarke, 1. Informationen zu dieser Zählmarke
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),
![Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x), Institut für Programmierung und Reaktive Systeme 25. August 2014. Programmier-Labor. 04. + 05. Übungsblatt. int binarysearch(int[] a, int x),](/thumbs/29/13862323.jpg) Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Technische Universität Braunschweig Dr. Werner Struckmann Institut für Programmierung und Reaktive Systeme 25. August 2014 Programmier-Labor 04. + 05. Übungsblatt Aufgabe 21: a) Schreiben Sie eine Methode
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Java Kurs für Anfänger Einheit 4 Klassen und Objekte
 Java Kurs für Anfänger Einheit 4 Klassen und Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 13. Juni 2009 Inhaltsverzeichnis klasse
Java Kurs für Anfänger Einheit 4 Klassen und Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 13. Juni 2009 Inhaltsverzeichnis klasse
Softwarelösungen: Versuch 4
 Softwarelösungen: Versuch 4 Nichtstun in Schleife wird ersetzt durch zeitweilige Zurücknahme der Anforderung, um es anderen Prozessen zu erlauben, die Ressource zu belegen: /* Prozess 0 */ wiederhole flag[0]
Softwarelösungen: Versuch 4 Nichtstun in Schleife wird ersetzt durch zeitweilige Zurücknahme der Anforderung, um es anderen Prozessen zu erlauben, die Ressource zu belegen: /* Prozess 0 */ wiederhole flag[0]
Programmieren Formulierung eines Algorithmus in einer Programmiersprache
 Zum Titel der Vorlesung: Programmieren Formulierung eines in einer Programmiersprache Beschreibung einer Vorgehensweise, wie man zu jedem aus einer Klasse gleichartiger Probleme eine Lösung findet Beispiel:
Zum Titel der Vorlesung: Programmieren Formulierung eines in einer Programmiersprache Beschreibung einer Vorgehensweise, wie man zu jedem aus einer Klasse gleichartiger Probleme eine Lösung findet Beispiel:
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
1. EINLEITUNG 2. GLOBALE GRUPPEN. 2.1. Globale Gruppen anlegen
 GLOBALE GRUPPEN 1. EINLEITUNG Globale Gruppen sind system- oder kategorieweite Gruppen von Nutzern in einem Moodlesystem. Wenn jede Klasse einer Schule in eine globale Gruppe aufgenommen wird, dann kann
GLOBALE GRUPPEN 1. EINLEITUNG Globale Gruppen sind system- oder kategorieweite Gruppen von Nutzern in einem Moodlesystem. Wenn jede Klasse einer Schule in eine globale Gruppe aufgenommen wird, dann kann
R ist freie Software und kann von der Website. www.r-project.org
 R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
R R ist freie Software und kann von der Website heruntergeladen werden. www.r-project.org Nach dem Herunterladen und der Installation von R kann man R durch Doppelklicken auf das R-Symbol starten. R wird
Rundung und Casting von Zahlen
 W E R K S T A T T Rundung und Casting von Zahlen Intrexx 7.0 1. Einleitung In diesem Werkstattbeitrag erfahren Sie, wie Zahlenwerte speziell in Velocity, aber auch in Groovy, gerundet werden können. Für
W E R K S T A T T Rundung und Casting von Zahlen Intrexx 7.0 1. Einleitung In diesem Werkstattbeitrag erfahren Sie, wie Zahlenwerte speziell in Velocity, aber auch in Groovy, gerundet werden können. Für
Vereinsverwaltung DFBnet Verein. Anleitung Familienbeiträge und Gemeinschaften
 Vereinsverwaltung DFBnet Verein Anleitung Familienbeiträge und Gemeinschaften 26.02.2014 Inhaltsverzeichnis 1 WICHTIGE ERLÄUTERUNGEN... 3 1.1 Familienbeitrag... 3 1.2 Familienzugehörigkeiten... 3 2 FAMILIENBEITRAG...
Vereinsverwaltung DFBnet Verein Anleitung Familienbeiträge und Gemeinschaften 26.02.2014 Inhaltsverzeichnis 1 WICHTIGE ERLÄUTERUNGEN... 3 1.1 Familienbeitrag... 3 1.2 Familienzugehörigkeiten... 3 2 FAMILIENBEITRAG...
The B Method. B ist eine Methode zur Spezifikation zum Entwurf zur Implementierung von Software Systemen. Bücher zur B-Methode
 The B Method B ist eine Methode zur Spezifikation zum Entwurf zur Implementierung von Software Systemen. Bücher zur B-Methode P. Schmitt: Formal Specification and Verification of Software p.1 The B Method
The B Method B ist eine Methode zur Spezifikation zum Entwurf zur Implementierung von Software Systemen. Bücher zur B-Methode P. Schmitt: Formal Specification and Verification of Software p.1 The B Method
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Übung Theoretische Grundlagen Berechenbarkeit/Entscheidbarkeit Nico Döttling November 26, 2009 INSTITUT FÜR KRYPTOGRAPHIE UND SICHERHEIT KIT University of the State of Baden-Wuerttemberg and National Laboratory
Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen:
 Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Pädagogische Hochschule Thurgau. Lehre Weiterbildung Forschung
 Variante 1 Swisscom-Router direkt ans Netzwerk angeschlossen fixe IP-Adressen (kein DHCP) 1. Aufrufen des «Netz- und Freigabecenters». 2. Doppelklick auf «LAN-Verbindung» 3. Klick auf «Eigenschaften» 4.
Variante 1 Swisscom-Router direkt ans Netzwerk angeschlossen fixe IP-Adressen (kein DHCP) 1. Aufrufen des «Netz- und Freigabecenters». 2. Doppelklick auf «LAN-Verbindung» 3. Klick auf «Eigenschaften» 4.
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16. Vorbereitende Aufgaben
 Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16 Fakultät für Informatik Lehrstuhl 14 Lars Hildebrand, Marcel Preuß, Iman Kamehkhosh, Marc Bury, Diana Howey Übungsblatt
Praktikum zu Einführung in die Informatik für LogWiIngs und WiMas Wintersemester 2015/16 Fakultät für Informatik Lehrstuhl 14 Lars Hildebrand, Marcel Preuß, Iman Kamehkhosh, Marc Bury, Diana Howey Übungsblatt
Ihr Ideen- & Projektmanagement-Tool
 Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Planungsbox 2.9 Ihr Ideen- & Projektmanagement-Tool Planungsbox verknüpft Notizen, Termine, Dateien, email- & Internetadressen, ToDo-Listen und Auswertungen Planungsbox verwaltet ToDo-Listen, Termine und
Grundlagen der Programmierung Prof. H. Mössenböck. 3. Verzweigungen
 Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Grundlagen der Programmierung Prof. H. Mössenböck 3. Verzweigungen If-Anweisung n > 0? j n if (n > 0) x = x / n; ohne else-zweig x x / n j max x x > y? n max y if (x > y) max = x; else max = y; mit else-zweig
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Wintersemester Maschinenbau und Kunststofftechnik. Informatik. Tobias Wolf http://informatik.swoke.de. Seite 1 von 22
 Kapitel 19 Vererbung, UML Seite 1 von 22 Vererbung - Neben der Datenabstraktion und der Datenkapselung ist die Vererbung ein weiteres Merkmal der OOP. - Durch Vererbung werden die Methoden und die Eigenschaften
Kapitel 19 Vererbung, UML Seite 1 von 22 Vererbung - Neben der Datenabstraktion und der Datenkapselung ist die Vererbung ein weiteres Merkmal der OOP. - Durch Vererbung werden die Methoden und die Eigenschaften
Access 2010. Grundlagen für Anwender. Andrea Weikert 1. Ausgabe, 1. Aktualisierung, Juli 2012. inkl. zusätzlichem Übungsanhang ACC2010-UA
 Andrea Weikert 1. Ausgabe, 1. Aktualisierung, Juli 2012 Access 2010 Grundlagen für Anwender inkl. zusätzlichem Übungsanhang ACC2010-UA 3 Access 2010 - Grundlagen für Anwender 3 Daten in Formularen bearbeiten
Andrea Weikert 1. Ausgabe, 1. Aktualisierung, Juli 2012 Access 2010 Grundlagen für Anwender inkl. zusätzlichem Übungsanhang ACC2010-UA 3 Access 2010 - Grundlagen für Anwender 3 Daten in Formularen bearbeiten
Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter.
 Stundenverwaltung Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter. Dieses Programm zeichnet sich aus durch einfachste
Stundenverwaltung Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter. Dieses Programm zeichnet sich aus durch einfachste
Druckerscriptsprache
 Druckerscriptsprache Die Druckerscriptsprache stellt Ihnen ein mächtiges Werkzeug zur Erstellung und Automatisierung von komplexen Druckvorgängen zur Verfügung. Vom Folgedruck bis zum Archivfunktion ist
Druckerscriptsprache Die Druckerscriptsprache stellt Ihnen ein mächtiges Werkzeug zur Erstellung und Automatisierung von komplexen Druckvorgängen zur Verfügung. Vom Folgedruck bis zum Archivfunktion ist
Software Engineering Interaktionsdiagramme
 Software Engineering Interaktionsdiagramme Prof. Adrian A. Müller, PMP, PSM 1, CSM Fachbereich Informatik und Mikrosystemtechnik 1 Nachrichtenaustausch Welche Nachrichten werden ausgetauscht? (Methodenaufrufe)
Software Engineering Interaktionsdiagramme Prof. Adrian A. Müller, PMP, PSM 1, CSM Fachbereich Informatik und Mikrosystemtechnik 1 Nachrichtenaustausch Welche Nachrichten werden ausgetauscht? (Methodenaufrufe)
Bitte wenden. Name: KURSARBEIT NR. 4 (10 DIFF GA) 18.06.2002. Seite 1
 Aufgabe 1: Gegeben ist das folgende Programm: PR figur :n :Länge WH 3 [ VW :Länge WENN :n>1 DANN ( RE 90 figur :n-1 :Länge/2 RW :Länge Seite 1 Zeichne das Bild, welches beim Aufruf der Prozedur mit figur
Aufgabe 1: Gegeben ist das folgende Programm: PR figur :n :Länge WH 3 [ VW :Länge WENN :n>1 DANN ( RE 90 figur :n-1 :Länge/2 RW :Länge Seite 1 Zeichne das Bild, welches beim Aufruf der Prozedur mit figur
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
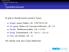 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
7DVWH.HOOQHU. Kassensystem SANYO (X&D6RIWKapitel 42
 7DVWH.HOOQHU Sie befinden sich im Dialog 5DXP%LOG Sie Tippen auf die Taste.HOOQHU Sie gelangen danach in den Dialog.HOOQHU/RJLQ. Alle Handlungen, die YRQ,KQHQ durchgeführt werden können sind schwarz dargestellt.
7DVWH.HOOQHU Sie befinden sich im Dialog 5DXP%LOG Sie Tippen auf die Taste.HOOQHU Sie gelangen danach in den Dialog.HOOQHU/RJLQ. Alle Handlungen, die YRQ,KQHQ durchgeführt werden können sind schwarz dargestellt.
Prozeß P1 Prozeß P2. Zur Synchronisation stehen den beiden Prozessen binäre Semaphore und die beiden Funktionen
 Seite 8 A UFGABE 11 INTERP ROZEßKOMMUNIKATION Das folgende Petrinetz zeigt zwei verkoppelte Prozesse P1 und P2. Die Transitionen a und b beschreiben Aktionen von P1, die Transitionen c und d Aktionen von
Seite 8 A UFGABE 11 INTERP ROZEßKOMMUNIKATION Das folgende Petrinetz zeigt zwei verkoppelte Prozesse P1 und P2. Die Transitionen a und b beschreiben Aktionen von P1, die Transitionen c und d Aktionen von
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
SCHRITT 1: Öffnen des Bildes und Auswahl der Option»Drucken«im Menü»Datei«...2. SCHRITT 2: Angeben des Papierformat im Dialog»Drucklayout«...
 Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Kapitel MK:IV. IV. Modellieren mit Constraints
 Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
Kapitel MK:IV IV. Modellieren mit Constraints Einführung und frühe Systeme Konsistenz I Binarization Generate-and-Test Backtracking-basierte Verfahren Konsistenz II Konsistenzanalyse Weitere Analyseverfahren
Kapitel 6: Graphalgorithmen Gliederung
 Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Übersicht Programmablaufsteuerung
 Übersicht Programmablaufsteuerung Konditionale Verzweigung: if - else switch-anweisung Schleifenkonstrukte: while, do - while for Schleife Sprung-Anweisungen: break, continue, goto, return Anweisungen
Übersicht Programmablaufsteuerung Konditionale Verzweigung: if - else switch-anweisung Schleifenkonstrukte: while, do - while for Schleife Sprung-Anweisungen: break, continue, goto, return Anweisungen
Kapitel 7 - Wägungen
 Kapitel 7 - Wägungen 7.1 Übersicht der Wägefunktionen Im WinScale Programm können folgende Wägefunktionen durchgeführt werden: - Erstwägungen - Zweitwägungen - Kontrollwägungen Diese Funktionen können
Kapitel 7 - Wägungen 7.1 Übersicht der Wägefunktionen Im WinScale Programm können folgende Wägefunktionen durchgeführt werden: - Erstwägungen - Zweitwägungen - Kontrollwägungen Diese Funktionen können
Java-Programmierung mit NetBeans
 Java-Programmierung mit NetBeans Steuerstrukturen Dr. Henry Herper Otto-von-Guericke-Universität Magdeburg - WS 2012/13 Steuerstrukturen Steuerstrukturen Verzweigungen Alternativen abweisende nichtabweisende
Java-Programmierung mit NetBeans Steuerstrukturen Dr. Henry Herper Otto-von-Guericke-Universität Magdeburg - WS 2012/13 Steuerstrukturen Steuerstrukturen Verzweigungen Alternativen abweisende nichtabweisende
Kundenspezifische Preise im Shop WyRu Online-Shop
 Kundenspezifische Preise im Shop WyRu Online-Shop Team WyRu Christian Wyk / Günter Rubik SCS Bürocenter B1, A-2334 Vösendorf Internet http://www.wyru.at Kundenspezifische Preise sind ein Feature des WyRu
Kundenspezifische Preise im Shop WyRu Online-Shop Team WyRu Christian Wyk / Günter Rubik SCS Bürocenter B1, A-2334 Vösendorf Internet http://www.wyru.at Kundenspezifische Preise sind ein Feature des WyRu
Diana Lange. Generative Gestaltung Operatoren
 Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Diana Lange Generative Gestaltung Operatoren Begriffserklärung Verknüpfungsvorschrift im Rahmen logischer Kalküle. Quelle: google Operatoren sind Zeichen, die mit einer bestimmten Bedeutung versehen sind.
Übung Grundlagen der Programmierung. Übung 05: Arrays. Abgabetermin: xx.xx.xxxx. Java-Programm Testplan Testergebnisse
 Übung 05: Arrays Abgabetermin: xx.xx.xxxx Name: Name, Vorname Matrikelnummer: 0XXXXXX Gruppe: G1 (Prähofer) G2 (Wolfinger) G3 (Wolfinger) Aufgabe Punkte gelöst abzugeben schriftlich abzugeben elektronisch
Übung 05: Arrays Abgabetermin: xx.xx.xxxx Name: Name, Vorname Matrikelnummer: 0XXXXXX Gruppe: G1 (Prähofer) G2 (Wolfinger) G3 (Wolfinger) Aufgabe Punkte gelöst abzugeben schriftlich abzugeben elektronisch
Plotten von Linien ( nach Jack Bresenham, 1962 )
 Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
