Das Sightseeing Problem

Transkript

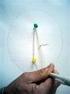
1 as Sightseeing Problem Wie plane ich meinen Urlaub optimal? Melanie erzog Wolfgang erdinand Riedl Lehrstuhl M9 für ngewandte eometrie und iskrete Mathematik Technische Universität München Voraussetzungen: rundlagen: raphen und rundlagen: Kombinatorische xplosion 1 Motivation as Sightseeing Problem beschäftigt sich mit einem bekannten touristischen Problem: Ich besuche München, stehe gerade auf dem Marienplatz, habe sechs Stunden Zeit und 20 uro. Welche Sehenswürdigkeiten sollte ich in welcher Reihenfolge besuchen, damit mein esuch möglichst interessant ist und ich am nde wieder am Marienplatz bin? bbildung 1: Wie ndet man eine optimale Tour, die interessante Sehenswürdigkeiten besucht und nicht zu viel eld und Zeit kostet? 1 Was muss ich dabei alles beachten? herzog@ma.tum.de riedl@ma.tum.de 1 Quelle: Melanie erzog, Lehrstuhl M9, Technische Universität München 1

2 ˆ Ich will für mich interessante Sehenswürdigkeiten besuchen. eshalb ordne ich jeder Sehenswürdigkeit eine Punktzahl zu (bspw. 10 Punkte = super interessant, 1 Punkt = total langweilig). Mein Ziel ist es, so viele Punkte wie möglich zu sammeln. ˆ Ich habe nur sechs Stunden Zeit, das heiÿt ich muss ungefähr wissen, wie lange ich für jede Sehenswürdigkeit brauche und ich darf nicht zu viel Zeit damit verbringen, von einer ttraktion zur Nächsten zu fahren. ˆ Ich habe nur 20 uro zur Verfügung. Ich muss also wissen, wie teuer der esuch der Sehenswürdigkeiten ist und sie so auswählen, dass mein eld ausreicht. ˆ Ich möchte am nde wieder am Marienplatz sein und für die ahrten zwischen den Sehenswürdigkeiten auch einen Plan haben, der mir immer sagt, wohin ich als nächstes fahren soll. Unter dem folgenden Link ndet sich ein pplet, in welchem eine Sightseeing-Tour für München geplant werden kann. Zur erechnung der Tour werden unter anderem auch hier vorgestellte orschungsergebnisse verwendet. 2 enition ormal wird das Sightseeing Problem wie auch viele andere Routing Probleme auf einem gerichteten raphen = (V, ) deniert. Weiterhin benötigen wir natürlich noch die unktionen P unkte : V R, c : V R und t : R. ie erste bzw. zweite unktion gibt für jeden Knoten des raphen an, wie viele Punkte wir bekommen bzw. was wir bezahlen müssen, wenn wir ihn besuchen. ie dritte unktion gibt für jede Kante die ahrzeit an. as Sightseeing Problem ist dann wie folgt deniert. enition 2.1 (Sightseeing Problem): ingabe: in gerichteter und gewichteter raph = (V,, t), ein Start- und ndknoten v V, die unktionen P unkte : V R und c : V R, sowie eine Kostenschranke und eine Zeitschranke T. usgabe: ine Rundtour, startend und endend in v, welche Zeit- und Kostenschranke einhält und möglichst viele Punkte einsammelt. 3 Unterschied zum TSP uf den ersten lick hat das Sightseeing Problem einige Ähnlichkeit mit dem Problem des andlungsreisenden (siehe auch die ufbereitung Traveling Salesman Problem). In beiden ällen hat man eine Menge von Orten, welche man besuchen will und für die man eine Rundtour sucht. s existieren allerdings einige Unterschiede, welche das Sightseeing Problem interessant machen: eim TSP müssen alle Orte besucht werden, während das beim Sightseeing Problem oft gar nicht möglich ist, da die Zeit dafür nicht ausreicht. eim Sightseeing Problem ist es vielmehr ein wichtiger Schritt, eine Menge an Orten zu nden, die möglichst interessant sind (d.h. viele Punkt bringen) und gleichzeitig in der gegebenen Zeit und mit dem gegebenen eld besucht werden können. ieses Problem wird auch oft als uswahlproblem oder Rucksackproblem bezeichnet (engl. Knapsack Problem). 2

3 4 as uswahlproblem 4.1 Problembeschreibung eim uswahlproblem sind eine Menge von egenständen mit bestimmtem Wert und ewicht gegeben. iese egenstände sollen nun so in einen Rucksack gepackt werden, dass dieser nicht zu schwer wird und dass gleichzeitig die egenstände im Rucksack möglichst viel wert sind. eispiel 4.1 (uswahlproblem): In bbildung 2 ist ein eispiel für ein uswahlproblem mit fünf verschiedenen egenständen und einem Rucksack mit einer röÿe von sechs inheiten gezeichnet. ewicht: 2, Wert: 3 ewicht: 4, Wert: 5 ewicht: 1, Wert: 2 max. ewicht: 6 ewicht: 3, Wert: 6 ewicht: 2, Wert: 2 bbildung 2: eispiel für ein uswahlproblem mit fünf verschiedenen egenständen und einem Rucksack mit einem maximalen ewicht von 6 Neben der Möglichkeit nichts einzupacken gibt es noch 15 weitere Packmöglichkeiten, welche das Maximalgewicht nicht überschreiten. ie optimale uswahl an egenständen sind hierbei egenstände 1, 3 und 4 mit einem esamtwert von 11. as Seightseeing Problem übersetzt sich in das uswahlproblem wie folgt: (ie Zeitbeschränkung wird hier für eine einfachere arstellung vernachlässigt.) Sightseeing Problem Sehenswürdigkeit Punkte Kosten Kostenschranke uswahlproblem egenstand Wert ewicht ewichtsschranke Man versucht nun, ttraktionen so auszuwählen (= in den Rucksack zu packen), dass man noch alles bezahlen kann (= den Rucksack noch tragen kann) und gleichzeitig die besuchten ttraktionen möglichst interessant sind (= der Inhalt des Rucksacks möglichst wertvoll ist). ieses Problem ist mathematisch schwer. ormal kann es wie folgt deniert werden: enition 4.2 (uswahlproblem): ingabe: n egenstände mit Wert w i und ewicht g i sowie eine Rucksackgröÿe. usgabe: ine uswahl I {1,..., n} der egenstände, so dass der Wert i I w i maximal ist und für das ewicht der egenstände gilt: i I g i. 3

4 4.2 in Lösungsverfahren elöst werden kann das Problem beispielsweise mit der nachfolgend beschriebenen Methode. ierzu denieren wir W j (g) als den maximalen Wert einer uswahl der ersten j egenstände, welche genau ewicht g hat. a aus keinen egenständen (d. h. wenn j = 0) kein Wert erlangt werden kann, gilt W 0 (g) = 0 für alle 1 g. Zudem nehmen wir an, dass es keine egenstände mit ewicht 0 gibt (diese könnten wir sonst erst mal beiseite lassen und später immer noch hinzufügen). eshalb gilt weiterhin W j (0) = 0 für alle 1 j n. er lgorithmus benutzt nun die folgende Rekursionsformel: W j+1 (g) = max { W j (g), W j (g g j+1 ) + w j+1 } iese kann man sich wie folgt erklären: Will man den maximalen Wert einer uswahl aus den ersten j + 1 egenständen, welche ewicht g hat, so ist in dieser entweder egenstand j + 1 enthalten oder nicht. Ist er nicht enthalten, so ist der maximale Wert der leiche wie der von W j (g). ndernfalls ist er gleich der Summe des maximalen Wertes einer uswahl aus den ersten j egenständen, welche ewicht g g j+1 hat und des Wertes des j+1-ersten egenstandes. Stellt man nun eine Tabelle für 0 j n und 0 g auf und trägt alle bekannten Werte für W j (g) ein, so kann man diese Tabelle mit ilfe der oberen ormel Zeile für Zeile ausfüllen. er intrag mit dem maximalen Wert stellt die optimale Lösung dar. eispiel 4.3 (Lösung des uswahlproblems): Im oben eingeführten uswahlproblem hatten wir folgende aten gegeben: ˆ w 1 = 3, w 2 = 5, w 3 = 2, w 4 = 6, w 5 = 2 ˆ g 1 = 2, g 2 = 4, g 3 = 1, g 4 = 3, g 5 = 2 ˆ = 6 ie ntwicklung der Tabelle während des lgorithmus ist in Tabelle 1 zu nden. Zu eginn sind alle W 0 (g) = 0, auÿerdem ist W j (0) = 0. In der ersten Zeile ist es mit egenstand 1 nur möglich, ein ewicht von 2 zu kombinieren. ieses hat dann einen Wert von 3. Mit egenständen 1 und 2 können die ewichte 2, 4 und 6 mit den Werten 3, 5 und 8 kombiniert werden. üllt man die Tabelle entsprechend weiter aus, so ergibt sich die nale Tabelle wie gezeigt. er maximale Wert eine Kombination von egenständen ist 11, wie oben bereits gesehen. ür das uswahlproblem gibt es also einen lgorithmus, der es gut löst. So müssen wir insgesamt n Zahlen berechnen, für jede erechnung brauchen wir vier Schritte (Nachschauen der beiden Zahlen, ddition und Vergleich). Zuletzt müssen wir noch einmal alle Zahlen durchsuchen, um die röÿte zu nden. Insgesamt benötigen wir 5n Schritte. Leider ist das keine polynomielle Laufzeit, da die ingabedaten des Problems (und somit auch ) auf einem omputer binär kodiert werden. eshalb wächst exponentiell in seiner ingabegröÿe (um einen polynomiellen lgorithmus zu erhalten, müssten wir irgendwie die bhängigkeit von loswerden). 4

5 0 j n 0 j n 0 j n 0 j n 1 g g g g Tabelle 1: ntwicklung der Tabelle während der usführung des lgorithmus. 5

6 Item g i w i Tabelle 2: Wie lautet die optimale Lösung dieses uswahlproblems? iese eststellung überrascht nicht besonders, da bekannt ist, dass das Problem mathematisch schwierig ist. a beim Sightseeing Problem nicht nur die zu besuchenden Sehenswürdigkeiten gewählt werden müssen, sondern auch noch eine Rundtour dazu gesucht werden muss, ist es ebenfalls mathematisch schwierig. 4.3 ufgaben ufgabe 4.4: etrachte das in Tabelle 2 gegebene uswahlproblem und nde mit ilfe des oben vorgestellten lgorithmus eine Lösung dafür. Ist die gefundene Lösung eindeutig? ufgabe 4.5: nalog zum vorgestellten Lösungsverfahren kann man noch eine alternative Lösungsmethode nden. ierbei deniert man j (w) als das minimale ewicht einer uswahl aus den ersten j egenständen, die genau Wert w hat. Wie können diese Werte initialisiert werden und welche Rekursionsformel kann verwendet werden? Wie viele Rechenoperationen benötigt er? Wendet den lgorithmus auf das uswahlproblem aus Tabelle 2 an. 5 in Lösungsverfahren für das Sightseeing Problem Im folgenden bschnitt wird ein Verfahren vorgestellt, das Lösungen für das Sightseeing Problem berechnet. as Verfahren ndet nicht zwangsläug immer die beste Lösung und kann manchmal auch sehr schlechte Lösungen produzieren, in den meisten ällen sind die produzierten Lösungen aber sehr gut. s wird deshalb auch euristik genannt. Um eine möglichst gute Lösung zu nden, sucht sich die euristik am nfang zuerst eine Menge von möglichen Lösungen (das heiÿt möglichen esuchstouren). iese Touren werden so lang wie möglich gemacht, das heiÿt wir nutzen unsere sechs Stunden komplett aus. anach versuchen wir durch verschiedene ktionen, diese Touren immer weiter zu verbessern. twas detaillierter funktioniert die euristik wie folgt (siehe [3] für die Originalarbeit): Initialisierung In diesem Schritt wird eine Menge von Touren konstruiert. Man beginn mit einer Route zu einer weit vom Startknoten entfernten Sehenswürdigkeit und zurück und fügt weitere ttraktionen ein, solange Zeit- und Kostenschranke eingehalten werden. Kann keine weitere Sehenswürdigkeit mehr eingefügt werden, beginnt man eine neue Route mit einer noch unbesuchten ttraktion und fügt wie zuvor weitere Sehensüwrdigkeiten ein. ies wird solange wiederholt bis alle Sehenswürdikeiten in einer Tour enthalten sind. ie Route mit den meisten Punkten wird beste Route genannt. 6

7 Verbesserung Nun wird versucht, die beste Route nach und nach zu verbessern. ierfür werden die folgenden Schritte immer wieder wiederholt: 1. Zuerst wird versucht, eine ttraktion aus einer anderen Route mit einer ttraktion der besten Route zu vertauschen. Wenn dieser Tausch die beste Route nicht zu sehr verschlechtert, wird er durchgeführt, ansonsten wird ein anderes Paar ausprobiert. 2. nschlieÿend wird versucht, eine Sehenswürdigkeit in eine andere Tour zu schieben. Wie auch im vorherigen Schritt wird dies nur ausgeführt, wenn sich die Route dadurch nicht zu sehr verschlechtert (das heiÿt optimalerweise bessere Sehenswürdigkeiten zusammenkommen, kleine Verschlechterungen sind jedoch auch erlaubt). 3. Nun wird versucht, jede einzelne Tour zu verbessern, indem man zwei Kanten aus der Tour entfernt und durch zwei andere ersetzt. ierdurch können zum eispiel sich überkreuzende Kanten entfernt werden und die Länge der Tour verkürzt werden. ies wird für verschiedene Paare von Kanten ausprobiert. 4. Zuletzt werden einige Sehenswürdigkeiten aus der besten Tour entfernt. ierdurch wird Platz für neue ttraktionen geschaen, die in der nächsten Runde eingefügt werden können. Natürlich werden nur ttraktionen entfernt, welche im Vergleich zu den anderen relativ unattraktiv sind. eispiel 5.1 (euristik): in eispiel (nach [3]) für die verschiedenen Schritte der euristik ist in bbildung 3 gegeben. In Teilabbildung (a) sind die verschiedenen Sehenswürdigkeiten mit ihren Punktzahlen gegeben. nschlieÿend werden die verschiedenen Schritte der euristik durchlaufen. In Teilabbildung (b) sind die Touren, welche in der Initialisierung erstellt wurden, angegeben. ie beste Route besucht Sehenswürdigkeiten, und und hat 8 Punkte. nschlieÿend wird versucht, diese Touren zu verbessern. azu wird in (c) der erste Schritt ausgeführt, bei dem die ttraktionen und vertauscht werden. ieser Tausch macht die beste Route etwas schlechter (nur noch 7 Punkte statt 8), was aber im nächsten Schritt Vorteile hat. eshalb werden auch leichte Verschlechterungen erlaubt. Im nächsten Schritt wird in (d) Sehenswürdigkeit von der Tour in die Tour verschoben. iese neue Tour ( ) wird dadurch mit 9 Punkten beste Route. nschlieÿend wird im dritten Schritt versucht, diese Tour kürzer zu machen, durch Umstellen der Reihenfolge zu ist das möglich. ierdurch erhält die Tour zwar nicht mehr Punkte, sie wird aber kürzer, so dass im nächsten urchlauf mehr Sehenswürdigkeiten hinzugefügt werden können. ies sieht man in (f), wo durch inzufügen von ttraktion im nächsten urchgang der euristik eine Tour mit 11 Punkten erstellt wird. n diesem eispiel ist gut zu sehen, dass es sich langfristig lohnt, manchmal auch schlechter zu werden (das heiÿt gute Sehenswürdigkeiten aus der besten Route zu entfernen oder zu tauschen). Nur so kann man in manchen ällen zu noch besseren Routen gelangen. Zugleich darf man jedoch auch nicht zu schlecht werden, da man sonst viel mehr Routen erzeugt und auch efahr läuft, keine bessere Tour zu nden. Um das Problem optimal zu lösen, sind tiefer gehende mathematische Kenntnisse nötig. s gibt jedoch noch zahlreiche weitere euristiken, welche mehr oder weniger gute Lösungen in schneller Zeit berechnen. ie rundlagen und verschiedene etails für ein optimales 7

8 : 4 Pkte : 2 Pkte : 2 Pkte : 3 Pkte : 4 Pkte : 2 Pkte : 2 Pkte : Start & Ziel este Route: 8 Pkte (a) Sehenswürdigkeiten und Punkte (b) Touren nach Initialisierung este Route: 7 Pkte este Route: 9 Pkte (c) Schritt 1 der Verbesserung (d) Schritt 2 der Verbesserung este Route: 9 Pkte este Route: 11 Pkte (e) Schritt 3 der Verbesserung (f) Schritt 2 der Verbesserung bbildung 3: Verschiedene Schritte der euristik, die beste Route ist hierbei immer fett hervorgehoben. 8

9 Lösungsverfahren werden in [2] präsentiert, weitere euristiken und ein Vergleich mit einem optimalen Lösungsverfahren werden in [1] vorgestellt. 6 usblick as Sightseeing Problem lässt sich natürlich noch beliebig erweitern. Naheliegend ist dabei die rweiterung der Planung auf mehrere Tage oder die erücksichtigung der Önungszeiten der Sehenswürdigkeiten. in Thema, an welchem zur Zeit geforscht wird, ist die erücksichtigung von verschiedenen Verkehrsmitteln. isher wurde angenommen, dass immer dasselbe Verkehrsmittel benutzt wird, wodurch es nur eine kürzeste Möglichkeit gibt, von einer Sehenswürdigkeit zur Nächsten zu gelangen. esonders in Städten kann man jedoch ein Taxi, die S-ahn, die U-ahn oder den us nehmen oder auch zu uÿ laufen. Jedes dieser Verkehrsmittel hat andere ahrtkosten und -zeiten. So kann es beispielsweise wenn die Zeit knapp ist, sinnvoll sein, eine längere Strecke mit dem Taxi anstelle des langsameren usses zurückzulegen, auch wenn das etwas teurer ist. Umgekehrt lassen sich die meisten Sehenswürdigkeiten in der Innenstadt sehr billig zu uÿ erreichen. urch die Wahl zwischen verschiedenen Verkehrsmitteln wird das Sightseeing Problem noch etwas schwieriger. es Weiteren beschäftigt sich die orschung mit zeitabhängigen ahrtzeiten, denn insbesondere wenn man den öentlichen Nahverkehr verwendet, gelten zu verschiedenen Zeiten verschiedene ahrpläne, woraus sich andere ahrtzeiten ergeben. ber auch wenn man mit dem uto unterwegs ist, kann es vorkommen, dass man im abendlichen eierabendverkehr für dieselbe Strecke wesentlich mehr Zeit benötigt als nachmittags. Literatur [1] Melanie estle. Sightseeing: Routenplanung unter eachtung von inanz- und Zeitbudgets. iplomarbeit. Technische Universität München, [2] hristian öhm. Routenplanung unter udgetrestriktionen Polytopale Untersuchungen zur Verwendung in ranch&ut-verfahren. iplomarbeit. Technische Universität München, [3] I-Ming hao, ruce L. olden und dward. Wasil. fast and eective heuristic for the orienteering problem. In: uropean Journal of Operational Research 88.3 (1996), S issn: doi: / (95 ) url: http : // [4] M9 Lehrstuhl für ngewandte eometrie und iskrete Mathematik, TU München. Sightseeing Spiel. Juli url: http : / / www - m9. ma. tum. de / llgemeines / Stadtbesichtigung. 9