Geometrie und Pflanzenwachstum
|
|
|
- Irmela Beutel
- vor 7 Jahren
- Abrufe
Transkript
1 Hans Studerus Geometrie und Pflanzenwachstum Suchen wir uns einmal einen Föhren- oder Tannenzapfen und betrachten ihn genau: bald stellen wir fest, dass die Samenlappen sich spiralförmig um ihn winden. Wir finden zwei Arten von solchen Kurven; die eine windet sich lang gezogen links herum, die andere eng geführt rechtsherum. Von der ersteren sind es jeweils 5, von den letzteren 8 Spiralkurven. Untersuchen wir auf die gleiche Weise die Zapfen der Weymouthskiefer oder der Douglastanne, können wir die Zahlen 3 und 5 finden. Bei den prächtigen Pinienzapfen sind die beiden Spiralkurven besonders ausgeprägt. Hier sind aber die Zahlen 8 und 13 feststellbar. Nehmen wir uns die Kakteengewächse vor, z. B. eine Mammillaria, so zeigt uns das Bild der beiden Spiralen die Zahlen 13 und 21. Auch auf dem Blütenboden einer Silberdistel finden wir eine solche Anordnung; linksherum erkennen wir 21, rechtsherum 34 Kurven. Wenn wir noch den Samenstand unserer grössten Einjahrespflanze, der Sonnenblume hinzunehmen stossen wir auf 34 und 55 Spiralkurven. Kurvenbild Pinienzapfen In der Regel finden sich bei diesen Pflanzen immer dieselben Zahlenverhältnisse. Nun hat ein Mathematiker, Leonardo Fibonacci ( ) die so genannte Fibonacci - Reihe aufgestellt. Diese Zahlenfolge ist so aufgebaut, dass die neue Zahl sich aus den zwei vorhergegangenen ergibt: 1+1= 2, 1+2= 3, 2+3= 5, 3+5= 8, 5+8= 13, 8+13= 21 usw. Fibonacci-Reihe : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, usw.
2 Es sind dies die gleichen Zahlen welche wir in den Spiralanordnungen der Pflanzen gefunden haben. Das Verhältnis je zwei dieser Zahlen entspricht dem Verhältnis des so genannten Goldenen Schnittes. Durch die Division je zwei sich folgende Zahlen erhält man folgende Resultate: 1 : 2 = 0,5 2 : 3 = 0, : 5 = 0,6 5 : 8 = 0,625 8 : 13 = 0, : 21 = 0, : 34 = 0, : 55 = 0, usw. Der Durchschnitt dieser Verhältnisse liegt bei 0, der Zahl des Goldenen Schnittes. Augenfälliger als in Zahlen ist der Goldene Schnitt in einem Bild zu betrachten, z. B. im Fünfstern. Die kleine Strecke (b) ist zur grösseren (a) im gleichen Verhältnis wie die kleine (b) und grössere (a) zusammen zur ganzen Strecke (aba). Formel: a : b = (a+b) : a Man kann davon ausgehen, dass diese Zahlengesetzmässigkeiten sich durch das gesamte Pflanzenreich durchziehen. Die Pflanzen richten sich in der Anordnung ihrer Samenstände, Knospen, Blätter usw. nach dieser Zahlengeometrie. Dort, wo sich die Spiralen kreuzen, entstehen neue Organe, neues Leben. Allerdings ist es nicht überall so leicht die Spiralen zu erkennen. Auf eher ebenen Flächen (Blütenständen, Früchten) sind die Spiralformen leicht zu zählen. Will man aber Knospen oder Blattansätze am Stengel einer Pflanze unter diesem Gesichtspunkte verstehen, muss man die Spiralen sich als Schraubbewegung vorstellen. Stellen wir uns also vor, dass zwei dieser Spiralen, eine links windende und eine rechts windende, sich als Kurvenpaar dem Pflanzenstengel nach unten ( oder nach oben ) schrauben; immer dort wo sie sich kreuzen, würde eine Knospe oder ein Blatt wachsen. Wir würden so die so genannte 1/2 - Stellung oder einfache Wechselstellung erhalten, wie sie zum Beispiel der Hasel zeigt.
3 Probieren wir noch uns vorzustellen wie die Knospen- oder Blattanordnung aussehen würde, wenn sich zwei Kurvenpaare am Stengel hinauf- oder hinunterschrauben würden. Zwei Spiralen linksherum und zwei rechtsherum. Dadurch, dass sich das erste Kurvenpaar nicht nur mit sich selbst, sondern auch mit dem zweiten Kurvenpaar kreuzt, erhalten wir die so genannte Kreuzgegenständigkeit. Ein Beispiel dafür ist die Brennnessel.
4 Wir können nun alle in der Natur vorkommenden Möglichkeiten an Knospen - oder Blattstellungen untersuchen und ihre Gesetzmässigkeiten durch gedachte Spiralanordnungen beobachten. Lässt man gedanklich 3 Kurvenpaare, also 6 Schraubenlinien am Stengel emporlaufen, entsteht der 3 er - Wirtel, übereinander versetzt über die jeweilige Lücke des vorhergehenden Wirtels, wie zum Beispiel beim Oleander. Bei entsprechenden Kurvenpaaren sind auch die 4er-, 5er- und 6er-Wirtel von Blutund Gilbweiderich oder der 8er- Wirtel des Waldmeisters zu sehen. Lassen wir eine Spirale rechts - und zwei linksherum wandern, ergibt dies die 1/3- Wechselstellung, wobei die 3 Blätter immer senkrecht übereinander stehen, zum Beispiel beim Weissen Germer. Wenn wir jetzt noch 2 Kurven links- und 3 rechtsherum laufen lassen bekommen wir die 2/5 Blattstellung, was uns ja die Rosengewächse vor allem vormachen. Nach 5 mal 2/5 Umdrehung steht das 6. Blatt wieder über dem 1. Was in der Natur nicht vorkommt ist die zweireihige paarige Blattstellung. Diese ist auch durch entsprechende Spiralanordnungen nicht konstruierbar. Daraus ersieht man, wie die Natur sich an geometrische Gesetzmässigkeiten halten muss. Ueberall in der Natur finden wir Spiralformen. Die uns noch sehr unbekannten Kräfte des Wachstums, des Lebens, haben diese Form gewählt um zu erschaffen. Diese unsichtbaren, aus dem Unendlichen kommenden Lebenskräfte ergreifen die Materie (innerer Anfang der Spirale) formen sie zu einem Körper bestimmter Grösse und verlassen diesen wieder (äusseres Ende der Spirale), ins Unendliche entschwindend. Zurück bleibt das Naturobjekt. Spiralformen finden wir in der Natur in manigfaltigsten Ausgestaltungen; runde, weite, enge, langgezogene usw.. Die Natur variiert in allen möglichen Formen. Wenn man den Durchschnitt all dieser Formen herausarbeiten könnte, könnte es wohl sein, dass die Fibonacci - Spirale erscheinen würde.
5 Wenn wir einen Tannzapfen sprechen" lassen, kann er uns zeigen, dass hinter der Natur keine Willkür herrscht, sondern Ordnung, basierend auf mathematischen, geometrischen Gesetzmässigkeiten. Wir finden in der Natur Weisheit und Intelligenz. Intelligenz setzt aber auch ein Bewusstsein voraus. Bewusstsein schliesst wiederum Leben in sich ein. Wenn wir hinter der Natur ein lebendiges Bewusstsein akzeptieren können, gibt uns dies auch ein Vertrauen in das ganze Naturgeschehen. Werden die Kräfte in der Natur und ihre Auswirkungen als unberechenbar und zufällig betrachtet, bewirkt eine solche Anschauungsweise Angst im Menschen. Aus dieser Angst heraus entsteht eine Haltung des Bekämpfens der wilden Natur", mit allen ihren negativen Folgeerscheinungen. Wenn wir aber die Weisheit hinter der Natur erkennen können, entsteht anstelle der Angst Vertrauen in sie, so dass wir sie auch nicht beherrschen" müssen. Ein achtungs- und rücksichtsvoller Umgang mit der Natur kann die Folge sein. Als Gartenbaulehrer haben wir die Möglichkeit die Schülerinnen da und dort auf Naturgesetzmässigkeiten hinzuweisen. An einem regnerischen Tag kann im Unterricht die Fibonacci-Reihe erarbeitet werden. Anschliessend bekommt jeder z. B. einen Nadelbaumzapfen, welcher untersucht werden muss. An der Wand hängt ein grösseres Blatt Papier, wo die Zahlen der Fibonacci-Reihe (immer als Zahlenpaar) auf der linken Seite untereinander stehen. Wenn nun im Schulgarten oder irgendwo, gelegentlich ein entsprechendes Naturobjekt (Blütenboden, Samenstand, Frucht usw.) gefunden wird, kann dessen Name rechts neben den Zahlen eingetragen werden. Solche Tätigkeiten verstärken eine ehrfurchtsvolle Beziehung zur Natur und wecken Interesse und Freude der Schülerinnen.
6 Verwendete Literatur: Gottfried Bergmann; Pflanzenstudien; Freier Pädagogischer Arbeitskreis, Zug 1998 Callum Coats; Naturenergien verstehen und nutzen; Omega-Verlag, Düsseldorf Drunvalo Melchizedek; Die Blume des Lebens; Koha-Verlag, Burgrain
Fibonacci Folge ASSIGNMENT A. Muster der Logik, mit denen Zusammenhänge und Verbindungen im Gehirn erreicht werden könnten
 ASSIGNMENT A Stavric, Milena, Dipl.-Ing. Dr.techn. Gruppe 7 / Dezember 3, 2013 Fibonacci Folge Entwurf einer Sequence des Universums Muster der Logik, mit denen Zusammenhänge und Verbindungen im Gehirn
ASSIGNMENT A Stavric, Milena, Dipl.-Ing. Dr.techn. Gruppe 7 / Dezember 3, 2013 Fibonacci Folge Entwurf einer Sequence des Universums Muster der Logik, mit denen Zusammenhänge und Verbindungen im Gehirn
Anlage des Spiels. Forschungsgruppe. Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern
 Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels. Forschungsgruppe. Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern
 Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Anlage des Spiels Forschungsgruppe Ein Spiel entwickelt durch Patrik Böhler Fachstelle Religionspädagogik, Mittelstrasse 6a Bern Ziel Die SuS erkennen, dass auf drei verschiedenen Wegen drei ähnliche Erkenntnisse
Was uns die Natur über Heilige Geometrie lehren kann
 transinformation.net http://transinformation.net/was-uns-die-natur-ueber-heilige-geometrie-lehren-kann/ Was uns die Natur über Heilige Geometrie lehren kann Taygeta Eines der grossartigsten Geschenke,
transinformation.net http://transinformation.net/was-uns-die-natur-ueber-heilige-geometrie-lehren-kann/ Was uns die Natur über Heilige Geometrie lehren kann Taygeta Eines der grossartigsten Geschenke,
Phyllotaxis Seminararbeit
 Christina Imp Phyllotaxis Seminararbeit Karl-Franzens-Universität Graz Institut für Mathematik und Wissenschaftliches Rechnen LV-Leiterin: Univ.-Prof. Dr.phil. Karin Baur Graz, Oktober 2014 Inhaltsverzeichnis
Christina Imp Phyllotaxis Seminararbeit Karl-Franzens-Universität Graz Institut für Mathematik und Wissenschaftliches Rechnen LV-Leiterin: Univ.-Prof. Dr.phil. Karin Baur Graz, Oktober 2014 Inhaltsverzeichnis
4 Die Fibonacci-Zahlen
 4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
Mathematische Überraschungen in der Natur
 Mathematische Überraschungen in der Natur Die Goldene Zahl ist wahrscheinlich die außergewöhnlichste aller Zahlen. Sie hat hunderterlei einzigartige Eigenschaften wie sonst keine andere Zahl und so verwundert
Mathematische Überraschungen in der Natur Die Goldene Zahl ist wahrscheinlich die außergewöhnlichste aller Zahlen. Sie hat hunderterlei einzigartige Eigenschaften wie sonst keine andere Zahl und so verwundert
Zeitschrift für Eltern und Freunde der Rudolf Steiner Schule Aargau
 Zeitschrift für Eltern und Freunde der Rudolf Steiner Schule Aargau Mitteilungen Michaeli 2004 Irlandwoche Freitag, 17. September bis Freitag 24. September Titelbild: Nautilusspirale, aufgeschnittene Schale
Zeitschrift für Eltern und Freunde der Rudolf Steiner Schule Aargau Mitteilungen Michaeli 2004 Irlandwoche Freitag, 17. September bis Freitag 24. September Titelbild: Nautilusspirale, aufgeschnittene Schale
Fibonacci-Folge Mathematik»Facharbeit«
 Mathematik»Facharbeit«Mathias Dirksmeier Sven Wilkens Jahrgangsstufe 12 Thomas-Morus-Gymnasium, 2009 Gliederung 1 Allgemeines 2 Allgemein Formel von Moivre-Binet Beziehung zum Goldenen Schnitt 3 Modell
Mathematik»Facharbeit«Mathias Dirksmeier Sven Wilkens Jahrgangsstufe 12 Thomas-Morus-Gymnasium, 2009 Gliederung 1 Allgemeines 2 Allgemein Formel von Moivre-Binet Beziehung zum Goldenen Schnitt 3 Modell
WOZU DIENT PROJEKTIVE GEOMETRÍE? WELCHE DENKKRÄFTE WERDEN DURCH SIE ENTWICKELT? Ana Ayllón Cesteros Escuela Libre Micael Las Rozas, España
 WOZU DIENT PROJEKTIVE GEOMETRÍE? WELCHE DENKKRÄFTE WERDEN DURCH SIE ENTWICKELT? Ana Ayllón Cesteros Escuela Libre Micael Las Rozas, España Es ist sonderbar, dass ich, obwohl ich mich nicht genau an den
WOZU DIENT PROJEKTIVE GEOMETRÍE? WELCHE DENKKRÄFTE WERDEN DURCH SIE ENTWICKELT? Ana Ayllón Cesteros Escuela Libre Micael Las Rozas, España Es ist sonderbar, dass ich, obwohl ich mich nicht genau an den
Walter Orlov. Goldener Schnitt und Euleresche Zahl
 Walter Orlov Goldener Schnitt und Euleresche Zahl August 2004 Euklid (325-270 vor Christus) wird die Entdeckung des Streckenverhältnis Goldenen Schnittes zugeschrieben. Unter Goldenem Schnitt versteht
Walter Orlov Goldener Schnitt und Euleresche Zahl August 2004 Euklid (325-270 vor Christus) wird die Entdeckung des Streckenverhältnis Goldenen Schnittes zugeschrieben. Unter Goldenem Schnitt versteht
DER GOLDENE SCHNITT. Ein Verhältnis, das es in sich hat A B C D E F G
 DER GOLDENE SCHNITT Ein Verhältnis, das es in sich hat A B C D E F G Welches der sieben Rechtecke gefällt die am besten? Miss bei jedem Rechteck die Seitenlänge ab und trage ihr Längen in die nachfolgende
DER GOLDENE SCHNITT Ein Verhältnis, das es in sich hat A B C D E F G Welches der sieben Rechtecke gefällt die am besten? Miss bei jedem Rechteck die Seitenlänge ab und trage ihr Längen in die nachfolgende
Fibonaccizahlen in der Natur
 Fibonaccizahlen in der Natur Doris Abraham 0506087 0. Januar 010 1.1 Worum geht es? So unglaublich auch manches in der Welt erscheint so unglaublich ist es doch diese Erscheinungen mit anderen naturwissenschaftlichen
Fibonaccizahlen in der Natur Doris Abraham 0506087 0. Januar 010 1.1 Worum geht es? So unglaublich auch manches in der Welt erscheint so unglaublich ist es doch diese Erscheinungen mit anderen naturwissenschaftlichen
Abb. 1: Aus Rechtecken zusammengesetzte Spirale. Bauteile
 Hans Walser Folgen sehen Publiziert in: Mathematik Lehren. Heft 96, Oktober 1999. S. 47-50 Kurzfassung Figurenfolgen entstehen entweder aufbauend durch schrittweises Ansetzen einer einfachen Grundfigur
Hans Walser Folgen sehen Publiziert in: Mathematik Lehren. Heft 96, Oktober 1999. S. 47-50 Kurzfassung Figurenfolgen entstehen entweder aufbauend durch schrittweises Ansetzen einer einfachen Grundfigur
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Pythagoreische Rechtecke Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Startdreieck
 Hans Walser, [20040416a] Pythagoreische Rechtecke 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Wir starten mit einem beliebigen rechtwinkligen Dreieck in der üblichen Beschriftung. Startdreieck
Hans Walser, [20040416a] Pythagoreische Rechtecke 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Wir starten mit einem beliebigen rechtwinkligen Dreieck in der üblichen Beschriftung. Startdreieck
Lichtgitter-Mandala. Berechnet nach dem ältesten Weisheitsbuch Chinas I Ging Das Buch der Wandlung
 Lichtgitter-Mandala Berechnet nach dem ältesten Weisheitsbuch Chinas I Ging Das Buch der Wandlung Aktiviere deine Schöpferkraft - Jetzt! Dieses Lichtgitter-Mandala wurde ganz speziell für mich erstellt
Lichtgitter-Mandala Berechnet nach dem ältesten Weisheitsbuch Chinas I Ging Das Buch der Wandlung Aktiviere deine Schöpferkraft - Jetzt! Dieses Lichtgitter-Mandala wurde ganz speziell für mich erstellt
Mathematische Gesetzmäßigkeiten in der Blattstellungslehre
 Mathematische Gesetzmäßigkeiten in der Blattstellungslehre Hauptseminar Mathematische Modellierung - Prof. Dr. Mária Lukácová Dominik Hartmann, 30.10.2018 Gliederung Motivation Phyllotaxis botanische Grundlagen
Mathematische Gesetzmäßigkeiten in der Blattstellungslehre Hauptseminar Mathematische Modellierung - Prof. Dr. Mária Lukácová Dominik Hartmann, 30.10.2018 Gliederung Motivation Phyllotaxis botanische Grundlagen
Fibonacci-Zahlen und der goldene Schnitt
 Fibonacci-Zahlen und der goldene Schnitt Behandlung von rekursiven Zahlenfolgen zum Umgang mit Excel, Mathematica, Maple und Octave (Matlab), sowie Einüben von Diagonalisierung und Stellenwertsystemen
Fibonacci-Zahlen und der goldene Schnitt Behandlung von rekursiven Zahlenfolgen zum Umgang mit Excel, Mathematica, Maple und Octave (Matlab), sowie Einüben von Diagonalisierung und Stellenwertsystemen
Schreibe die jeweilige Dreieckszahl unter die Zeichnung. Wie heißen die nächsten vier Dreieckszahlen?
 Hier siehst du Figuren, die aus Kreisen bestehen. Schon ab der zweiten Figur ergibt sich ein Dreieck. Die Anzahl der Kreise, die ein Dreieck bilden, nennt man Dreieckszahlen. Man tut so, als ob auch der
Hier siehst du Figuren, die aus Kreisen bestehen. Schon ab der zweiten Figur ergibt sich ein Dreieck. Die Anzahl der Kreise, die ein Dreieck bilden, nennt man Dreieckszahlen. Man tut so, als ob auch der
Die Blume des Lebens
 Die Blume des Lebens Erste Übungen aus der heiligen Geometrie zum persönlichen Nachvollzug und zur Vertiefung. Von Franz Delaquis Aus den Quellen des eindrücklichen Buches Vom ewig beginnenden Ende von
Die Blume des Lebens Erste Übungen aus der heiligen Geometrie zum persönlichen Nachvollzug und zur Vertiefung. Von Franz Delaquis Aus den Quellen des eindrücklichen Buches Vom ewig beginnenden Ende von
Webinar zum Thema. Technische Analyse mit Fibonacci - am Beispiel von DAX & Co Sven Weisenhaus. Webinar
 zum Thema Technische Analyse mit Fibonacci - am Beispiel von DAX & Co. Sven Weisenhaus 22.05.2012 1 Zu meiner Person Einführung in die Thematik Grundlagen der Fibonacci-Zahlen Praktische Anwendung Handlungsempfehlungen
zum Thema Technische Analyse mit Fibonacci - am Beispiel von DAX & Co. Sven Weisenhaus 22.05.2012 1 Zu meiner Person Einführung in die Thematik Grundlagen der Fibonacci-Zahlen Praktische Anwendung Handlungsempfehlungen
2. Aufgabe zu Unterrichtsplanung für eine Klasse der Unterstufe
 2. Aufgabe zu 31.05.2017 1. Unterrichtsplanung für eine Klasse der Unterstufe Thema: Pythagoräischer Baum und Wurzelschnecke Unterrichtsablauf Zu Beginn der Einheit wird der kürzlich gelernte Pythagoräische
2. Aufgabe zu 31.05.2017 1. Unterrichtsplanung für eine Klasse der Unterstufe Thema: Pythagoräischer Baum und Wurzelschnecke Unterrichtsablauf Zu Beginn der Einheit wird der kürzlich gelernte Pythagoräische
Geschichte Grundlagen Fibonacci-Zahlen Geometrischer Trugschluß Anwendung Fazit und Ausblick. Der Goldene Schnitt. Dario Jotanovic
 Der Goldene Schnitt Dario Jotanovic Mathematisches Proseminar Implementierung mathematischer Algorithmen Hochschule Darmstadt 19. Dezember 2013 Inhaltsangabe 1 Geschichte 2 Grundlagen Teilung im goldenen
Der Goldene Schnitt Dario Jotanovic Mathematisches Proseminar Implementierung mathematischer Algorithmen Hochschule Darmstadt 19. Dezember 2013 Inhaltsangabe 1 Geschichte 2 Grundlagen Teilung im goldenen
Fibonacci-Zahlen. Geschichte. Definition. Quotienten
 Mathematik/Informatik Die Fibonacci-Zahlen Gierhardt Fibonacci-Zahlen Geschichte Im Jahre 0 wurde in Pisa ein Buch über das indischarabische Dezimalsystem von dem italienischen Mathematiker Leonardo Fibonacci
Mathematik/Informatik Die Fibonacci-Zahlen Gierhardt Fibonacci-Zahlen Geschichte Im Jahre 0 wurde in Pisa ein Buch über das indischarabische Dezimalsystem von dem italienischen Mathematiker Leonardo Fibonacci
1 Goldener Schnitt. und a = m + M. 1, und wird im Allgemeinen mit τ (griechisch: tau) bezeichnet. Das Verhältnis M m hat den Wert 1+ 5
 1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
1 Goldener Schnitt Definition und Satz 1.1 (Goldener Schnitt) Sei AB die Strecke zwischen den Punkten A und B. Ein Punkt S von AB teilt AB im Goldenen Schnitt, falls sich die größere Teilstrecke M (Major)
Andreas Beutel. Die Blume des Lebens in dir
 Andreas Beutel Die Blume des Lebens in dir Andreas Beutel Die Blume des Lebens in dir Inhalt 1. Die Blume des Lebens 7 Um die ganze Welt 10 Geheimnisse der Blume des Lebens 12 Geschichte 14 Thot 16 2.
Andreas Beutel Die Blume des Lebens in dir Andreas Beutel Die Blume des Lebens in dir Inhalt 1. Die Blume des Lebens 7 Um die ganze Welt 10 Geheimnisse der Blume des Lebens 12 Geschichte 14 Thot 16 2.
Fibonaccizahlen. elementar, schön und real. Bodo Werner. Department Mathematik Universität Hamburg. Tag der Mathematik 5.
 Fibonaccizahlen elementar, schön und real Bodo Werner Department Mathematik Universität Hamburg Tag der Mathematik 5. Juli 2008 Jahr der Mathematik Kalenderblatt der DMV Geschichte Fibonacci I Leonardo
Fibonaccizahlen elementar, schön und real Bodo Werner Department Mathematik Universität Hamburg Tag der Mathematik 5. Juli 2008 Jahr der Mathematik Kalenderblatt der DMV Geschichte Fibonacci I Leonardo
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /18 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /18 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
Der Goldene Schnitt - Geheimnisvolle Ordnung der Natur
 Manuskript radiowissen Der Goldene Schnitt - Geheimnisvolle Ordnung der Natur AUTORIN: Maike Brzoska REDAKTION: Gerda Kuhn Was ist der Goldene Schnitt? Eine Zahl mit besonderen Eigenschaften? Ein Muster,
Manuskript radiowissen Der Goldene Schnitt - Geheimnisvolle Ordnung der Natur AUTORIN: Maike Brzoska REDAKTION: Gerda Kuhn Was ist der Goldene Schnitt? Eine Zahl mit besonderen Eigenschaften? Ein Muster,
Hans Walser. Die allgemeine Fibonacci-Folge
 Hans Walser Die allgemeine Fibonacci-Folge Hans Walser: Die allgemeine Fibonacci-Folge ii Inhalt Die Rekursion... Heuristischer Hintergrund... 3 Formel von Binet... 4 Übersicht... 5 Sonderfälle...3 6 Beispiele...3
Hans Walser Die allgemeine Fibonacci-Folge Hans Walser: Die allgemeine Fibonacci-Folge ii Inhalt Die Rekursion... Heuristischer Hintergrund... 3 Formel von Binet... 4 Übersicht... 5 Sonderfälle...3 6 Beispiele...3
Leonardo da Pisa alias Fibonacci
 Leonardo da Pisa alias Fibonacci 1. Juli 003 Weber Tony, Ramagnano Nicola Mathematik Fibonacci Seite / 9 Inhaltsverzeichnis Biographie...3 Fibonacci Zahlen...5 Definition...5 Fibonacci Spirale...5 Goldener
Leonardo da Pisa alias Fibonacci 1. Juli 003 Weber Tony, Ramagnano Nicola Mathematik Fibonacci Seite / 9 Inhaltsverzeichnis Biographie...3 Fibonacci Zahlen...5 Definition...5 Fibonacci Spirale...5 Goldener
Die Barth-Sextik ein ewiger Weltrekord. 3D-Skulptur von Oliver Labs
 Die Barth-Sextik ein ewiger Weltrekord 3D-Skulptur von Oliver Labs Auch in der Mathematik gibt es Weltrekorde und die Barth-Sextik, entdeckt um 1996 vom Erlanger Professor Wolf Barth, stellt einen solchen
Die Barth-Sextik ein ewiger Weltrekord 3D-Skulptur von Oliver Labs Auch in der Mathematik gibt es Weltrekorde und die Barth-Sextik, entdeckt um 1996 vom Erlanger Professor Wolf Barth, stellt einen solchen
Einführung in die Drei Prinzipien
 Einführung in die Drei Prinzipien Teil 1: Ist Stress nur eine Illusion? Teil 2: Inspiration für eigene Einsichten copyright DreiPrinzipien.org Illustrationen Alessandra Sacchi & Katja Symons mail@dreiprinzipien.org
Einführung in die Drei Prinzipien Teil 1: Ist Stress nur eine Illusion? Teil 2: Inspiration für eigene Einsichten copyright DreiPrinzipien.org Illustrationen Alessandra Sacchi & Katja Symons mail@dreiprinzipien.org
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 407 Der Goldene Schnitt Lernumgebung Hans Walser: Modul 407, Der Goldene Schnitt. Lernumgebung ii Inhalt 1 Streifen-Pentagramm... 1 2 Näherungskonstruktionen
Hans Walser Mathematik für die Sekundarstufe 1 Modul 407 Der Goldene Schnitt Lernumgebung Hans Walser: Modul 407, Der Goldene Schnitt. Lernumgebung ii Inhalt 1 Streifen-Pentagramm... 1 2 Näherungskonstruktionen
Eine transfinite Zahl als Grenzwert
 Eine transfinite Zahl als Grenzwert von Thomas Limberg, am 03.04.2010 Ist im Folgenden von reellen Zahlen, Zahlenfolgen, o.ä. die Rede, so sollen damit stets die nichtnegativen reellen Zahlen, Zahlenfolgen,
Eine transfinite Zahl als Grenzwert von Thomas Limberg, am 03.04.2010 Ist im Folgenden von reellen Zahlen, Zahlenfolgen, o.ä. die Rede, so sollen damit stets die nichtnegativen reellen Zahlen, Zahlenfolgen,
Über mich Organisatorisches Mathematik Wiederholung Mengenlehre Zahlen. Mathematik W1. Mag. Rainer Sickinger LMM, BRP
 Mathematik W1 Mag. Rainer Sickinger LMM, BRP v 3 Mag. Rainer Sickinger Mathematik W1 1 / 47 Mag. rer. nat. Rainer Peter Josef Sickinger 2010-2015: Informatik und Mathematikstudium an der Johannes Kepler
Mathematik W1 Mag. Rainer Sickinger LMM, BRP v 3 Mag. Rainer Sickinger Mathematik W1 1 / 47 Mag. rer. nat. Rainer Peter Josef Sickinger 2010-2015: Informatik und Mathematikstudium an der Johannes Kepler
Zahlenzauber Kinderuni. Robert Strich Ysette Weiss-Pidstrygach
 Zahlenzauber Kinderuni Robert Strich Ysette Weiss-Pidstrygach Muggelschule! Zählen und Zahlen Braucht man überhaupt Zahlen? Zählen und Zahlen Seit 30000 Jahren ohne Zahlen? Ohne Zahlen Eins Wie antworten
Zahlenzauber Kinderuni Robert Strich Ysette Weiss-Pidstrygach Muggelschule! Zählen und Zahlen Braucht man überhaupt Zahlen? Zählen und Zahlen Seit 30000 Jahren ohne Zahlen? Ohne Zahlen Eins Wie antworten
In Form mit Formeln Formeln spielen in der Mathematik und in der Physik eine wichtige Rolle. Bring dich in Form mit Formeln.
 In Form mit Formeln Formeln spielen in der Mathematik und in der Physik eine wichtige Rolle. Bring dich in Form mit Formeln. Die Schülerinnen und Schüler können Zahl- und Operationsbeziehungen sowie arithmetische
In Form mit Formeln Formeln spielen in der Mathematik und in der Physik eine wichtige Rolle. Bring dich in Form mit Formeln. Die Schülerinnen und Schüler können Zahl- und Operationsbeziehungen sowie arithmetische
Was sind Zahlen? von. Karl Gruber. TU Wien Institut für Chemische Technologie und Analytik/EC164 Getreidemarkt 9 A-1060 Wien.
 Was sind Zahlen? von Karl Gruber TU Wien Institut für Chemische Technologie und Analytik/EC164 Getreidemarkt 9 A-1060 Wien Zusammenfassung: Natürliche Zahlen sind ein Maß für Relationen und Grenzen, die
Was sind Zahlen? von Karl Gruber TU Wien Institut für Chemische Technologie und Analytik/EC164 Getreidemarkt 9 A-1060 Wien Zusammenfassung: Natürliche Zahlen sind ein Maß für Relationen und Grenzen, die
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /16 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 3 Folie 1 /16 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 3. Zahlenfolgen und Grenzwerte
WER BIN ICH? ENDLICH SEIN!
 WER BIN ICH? ENDLICH SEIN! GRUNDLAGEN DER ENTWICKLUNG UND DES LERNENS WESHALB EINE EINFÜHRUNG IN GRUNDLAGEN DER ENTWICKLUNG UND DES LERNENS? WIE ENTWICKELN SICH MENSCHEN? WAS BEDEUTET ENTWICKLUNG? WIE
WER BIN ICH? ENDLICH SEIN! GRUNDLAGEN DER ENTWICKLUNG UND DES LERNENS WESHALB EINE EINFÜHRUNG IN GRUNDLAGEN DER ENTWICKLUNG UND DES LERNENS? WIE ENTWICKELN SICH MENSCHEN? WAS BEDEUTET ENTWICKLUNG? WIE
Ein Mind Map erstellen - Schritt für Schritt
 Ein Mind Map erstellen - Schritt für Schritt Beim Mind Mapping notieren Sie Ihre Gedanken nicht wie üblich hinter- oder untereinander. Anstelle dessen schreiben Sie das Hauptthema Ihrer Notizen auf die
Ein Mind Map erstellen - Schritt für Schritt Beim Mind Mapping notieren Sie Ihre Gedanken nicht wie üblich hinter- oder untereinander. Anstelle dessen schreiben Sie das Hauptthema Ihrer Notizen auf die
Reelle Zahlenfolgen, Einleitung Fibonacci Folge
 Reelle Zahlenfolgen, Einleitung Fibonacci Folge 1-E Einleitung Folgen und Reihen bilden eine wichtige Grundlage der Analysis. Sie führen zum Begriff des Grenzwertes, der für die Differential- und die Integralrechnung
Reelle Zahlenfolgen, Einleitung Fibonacci Folge 1-E Einleitung Folgen und Reihen bilden eine wichtige Grundlage der Analysis. Sie führen zum Begriff des Grenzwertes, der für die Differential- und die Integralrechnung
FIBONACCI- UND LUCASFOLGEN IN DER PHYLLOTAXIS
 1 alfredhoehn 06.12.2011 FIBONACCI- UND LUCASFOLGEN IN DER PHYLLOTAXIS Unter Phyllotaxis wird allgemein in der Botanik die Blattanordnung, die Position der Scheinblüten z.b. der Sonnenblume und die Schuppen
1 alfredhoehn 06.12.2011 FIBONACCI- UND LUCASFOLGEN IN DER PHYLLOTAXIS Unter Phyllotaxis wird allgemein in der Botanik die Blattanordnung, die Position der Scheinblüten z.b. der Sonnenblume und die Schuppen
Portfolio Selection. Die Grundlagen der optimalen Portfolio-Auswahl. Harry M. Markowitz
 Portfolio Selection Die Grundlagen der optimalen Portfolio-Auswahl Harry M. Markowitz Teil II Die Beziehung zwischen einzelnen Wertpapieren und Portfolios Kapitel 3 Durchschnitte und Erwartungswerte Zum
Portfolio Selection Die Grundlagen der optimalen Portfolio-Auswahl Harry M. Markowitz Teil II Die Beziehung zwischen einzelnen Wertpapieren und Portfolios Kapitel 3 Durchschnitte und Erwartungswerte Zum
( Mathematik verstehen 6, Kapitel 7,S.116 ff) Eine Folge ( ) kann man auch als eine f: auffassen, die jeder von 0
 Factsheet 1 Folgen und Reihen Folgen ( Mathematik verstehen 6, Kapitel 7,S.116 ff) Wichtige Begriffe und Defintionen: (Zahlen)Folge.. (a n *) mit (a 1, a 2,.), oder ( a o, a 1, a 2, ), a n n-tes Folgenglied
Factsheet 1 Folgen und Reihen Folgen ( Mathematik verstehen 6, Kapitel 7,S.116 ff) Wichtige Begriffe und Defintionen: (Zahlen)Folge.. (a n *) mit (a 1, a 2,.), oder ( a o, a 1, a 2, ), a n n-tes Folgenglied
Aufgaben Fibonacci-Folgen 7. April 2006 B. Werner SoSe 06
 19. April 2006 Aufgaben Fibonacci-Folgen 7. April 2006 B. Werner SoSe 06 Präsenzaufgaben: Aufgabe P1: Eine spezielle Lucasfolge (L n ) ist durch L n = L n 1 + L n 2, L 0 = 2, L 1 = 1 definiert. Berechnen
19. April 2006 Aufgaben Fibonacci-Folgen 7. April 2006 B. Werner SoSe 06 Präsenzaufgaben: Aufgabe P1: Eine spezielle Lucasfolge (L n ) ist durch L n = L n 1 + L n 2, L 0 = 2, L 1 = 1 definiert. Berechnen
Fibonaccizahlen. Auftreten in der Biologie. Bodo Werner. Department Mathematik Universität Hamburg
 Fibonaccizahlen Auftreten in der Biologie Department Mathematik Universität Hamburg Fibonacci I Geschichte Leonardo da Pisa, genannt FIBONACCI (etwa 1170-1250) Liber Abbici (1202): Indisch-arabische Ziffern
Fibonaccizahlen Auftreten in der Biologie Department Mathematik Universität Hamburg Fibonacci I Geschichte Leonardo da Pisa, genannt FIBONACCI (etwa 1170-1250) Liber Abbici (1202): Indisch-arabische Ziffern
Aufgabensammlung für die Primar- und Vorschulstufe
 . Lehre Weiterbildung Forschung Aufgabensammlung für die Primar- und Vorschulstufe Mögliche ergänzende Aufgabenstellungen für Vorschul- und Primarschülerinnen und - schüler zur Ausstellung Matheliebe von
. Lehre Weiterbildung Forschung Aufgabensammlung für die Primar- und Vorschulstufe Mögliche ergänzende Aufgabenstellungen für Vorschul- und Primarschülerinnen und - schüler zur Ausstellung Matheliebe von
Verbindet uns mit der Energie:
 Verbindet uns mit der Energie: vom Regenbogen reine Farbenschwingung Lebendig sein Wohlfühlen der Spirale Verbundenheit Ganzheit vom Herz Liebe Harmonie Gesundheit Lebensfreude Leichtigkeit www.farbheilkreis.at
Verbindet uns mit der Energie: vom Regenbogen reine Farbenschwingung Lebendig sein Wohlfühlen der Spirale Verbundenheit Ganzheit vom Herz Liebe Harmonie Gesundheit Lebensfreude Leichtigkeit www.farbheilkreis.at
Department Mathematik. MatheNatur. Dr. Eva Hoffart Kinderuni Siegen 18. September 2018
 MatheNatur Dr. Eva Hoffart Kinderuni Siegen 18. September 2018 Mathematik? Mathematik? Mathematik als Wissenschaft von Mustern und Strukturen Muster im Mathematikunterricht Mathematik? Mathematik als Wissenschaft
MatheNatur Dr. Eva Hoffart Kinderuni Siegen 18. September 2018 Mathematik? Mathematik? Mathematik als Wissenschaft von Mustern und Strukturen Muster im Mathematikunterricht Mathematik? Mathematik als Wissenschaft
Begegnungen mit Mathematik
 Markus Stroppel Begegnungen mit Mathematik Regeln im Unregelmäßigen Rational im Angesicht des Irrationalen Häufiges Umsteigen: Der Weg ist das Ziel In alle Richtungen gleich dicktlst das ein Kreis? Logik,
Markus Stroppel Begegnungen mit Mathematik Regeln im Unregelmäßigen Rational im Angesicht des Irrationalen Häufiges Umsteigen: Der Weg ist das Ziel In alle Richtungen gleich dicktlst das ein Kreis? Logik,
Grabgestaltung. Anwendung von Gestaltungsgrundsätzen Formatvorlage des Untertitelmasters durch Klicken bearbeiten
 Grabgestaltung Anwendung von Gestaltungsgrundsätzen Formatvorlage des Untertitelmasters durch Klicken bearbeiten Gliederung: 2 Gestaltungsrichtlinien des Bundes deutscher Friedhofsgärtner Aufteilung der
Grabgestaltung Anwendung von Gestaltungsgrundsätzen Formatvorlage des Untertitelmasters durch Klicken bearbeiten Gliederung: 2 Gestaltungsrichtlinien des Bundes deutscher Friedhofsgärtner Aufteilung der
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 1
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie. Frage Welche der Aussagen sind richtig? Eine divergente Folge ist nicht beschränkt. Falsch. Z.B. ist {( ) n } n N beschränkt und divergent.
Materialien zur Mathematik II
 Joachim Stiller Materialien zur Mathematik II Die Quadratur des Kreises Alle Rechte vorbehalten Euklidische Geometrie Die Griechen kannten innerhalb der Euklidischen Geometrie drei Probleme, die auf direktem
Joachim Stiller Materialien zur Mathematik II Die Quadratur des Kreises Alle Rechte vorbehalten Euklidische Geometrie Die Griechen kannten innerhalb der Euklidischen Geometrie drei Probleme, die auf direktem
MEDITATION 3DER WEG ZUM INNEREN HEILIGTUM IM HERZEN
 Der Weg zum inneren Heiligtum ist bei Männern und Frauen unterschiedlich. Das heißt die Frauen vertrauen ihrer Intuition und die Männer hören mir genau zu. Atme entspannt und rhythmisch,..das Einatmen
Der Weg zum inneren Heiligtum ist bei Männern und Frauen unterschiedlich. Das heißt die Frauen vertrauen ihrer Intuition und die Männer hören mir genau zu. Atme entspannt und rhythmisch,..das Einatmen
Geometrische Optik Die Linsen
 1/1 29.09.00,19:40Erstellt von Oliver Stamm Geometrische Optik Die Linsen 1. Einleitung 1.1. Die Ausgangslage zum Experiment 2. Theorie 2.1. Begriffe und Variablen 3. Experiment 3.1.
1/1 29.09.00,19:40Erstellt von Oliver Stamm Geometrische Optik Die Linsen 1. Einleitung 1.1. Die Ausgangslage zum Experiment 2. Theorie 2.1. Begriffe und Variablen 3. Experiment 3.1.
Verteilung der Lernabschnitte des Lehrplans Mathematik GemS Erläuterungen
 Verteilung der Lernabschnitte des Lehrplans Mathematik GemS Erläuterungen Vorschlag zur Verteilung der Lernabschnitte für die Doppeljahrgänge 5/6, 7/8 sowie 9/10 zum Lehrplan Mathematik für die Gemeinschaftsschule
Verteilung der Lernabschnitte des Lehrplans Mathematik GemS Erläuterungen Vorschlag zur Verteilung der Lernabschnitte für die Doppeljahrgänge 5/6, 7/8 sowie 9/10 zum Lehrplan Mathematik für die Gemeinschaftsschule
Beispiellösungen zu Blatt 99
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 99 99 Luftballons fliegen am Horizont ganz friedlich in rechteckiger
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 99 99 Luftballons fliegen am Horizont ganz friedlich in rechteckiger
Die Goldene Spirale... 1. Der Goldene Schnitt... 3. Das Goldene Rechteck... 7. Gruppenarbeit... 8
 Die Goldene Spirale Fach: Mathematik Hauptseminar: Spiralen, WS 2005/2006 Dozent: Prof. Dr. R. Deißler Referenten: Judith Stoiber 1389024 Peter Rath 1389345 Handout zum Referat vom 24.01.2006 Inhaltsverzeichnis:
Die Goldene Spirale Fach: Mathematik Hauptseminar: Spiralen, WS 2005/2006 Dozent: Prof. Dr. R. Deißler Referenten: Judith Stoiber 1389024 Peter Rath 1389345 Handout zum Referat vom 24.01.2006 Inhaltsverzeichnis:
AG 2.1 Einfache Terme und Formeln aufstellen, umformen und im Kontext deuten können
 AG 2.1 Einfache Terme und Formeln aufstellen, umformen und im Kontext deuten können Beispiel 2.1.a: Kreuze die richtige Aussage an! Welcher Term modelliert folgenden Satz: Die Hälfte der Quadratwurzel
AG 2.1 Einfache Terme und Formeln aufstellen, umformen und im Kontext deuten können Beispiel 2.1.a: Kreuze die richtige Aussage an! Welcher Term modelliert folgenden Satz: Die Hälfte der Quadratwurzel
MT3 jahresplanung Stoffverteilung zum Mathetiger
 MATHE IGER 3 B R DA N A ST ve! S G si UN nklu D i IL DS MT3 jahresplanung Stoffverteilung zum Mathetiger 2 1 Üben und wiederholen 1 Im Einmaleins-Dschungel Zurück aus den Ferien Das ganze Einmaleins üben
MATHE IGER 3 B R DA N A ST ve! S G si UN nklu D i IL DS MT3 jahresplanung Stoffverteilung zum Mathetiger 2 1 Üben und wiederholen 1 Im Einmaleins-Dschungel Zurück aus den Ferien Das ganze Einmaleins üben
Was haben die folgenden Dinge gemeinsam?
 Was haben die folgenden Dinge gemeinsam? Parthenon zu Athen Mona Lisa von Leonardo da Vinci Nautilus Berliner Fernsehturm CN Tower Obelix Brüder Grimm Ananas Rose Biene Apple Das goldene Zeitalter Der
Was haben die folgenden Dinge gemeinsam? Parthenon zu Athen Mona Lisa von Leonardo da Vinci Nautilus Berliner Fernsehturm CN Tower Obelix Brüder Grimm Ananas Rose Biene Apple Das goldene Zeitalter Der
IKM M7. Einführung zu den Antwortformaten. Format 1: Kästchen
 Einführung zu den Antwortformaten Format 1: Kästchen Eine Ergebniszahl ist zu ermitteln oder zu berechnen. Diese Zahl ist in ein leeres Kästchen (kleines freies Textfeld) einzutragen. Für die Ermittlung/Berechnung
Einführung zu den Antwortformaten Format 1: Kästchen Eine Ergebniszahl ist zu ermitteln oder zu berechnen. Diese Zahl ist in ein leeres Kästchen (kleines freies Textfeld) einzutragen. Für die Ermittlung/Berechnung
Die Fibonacci-Zahlen 1
 Die Fibonacci-Zahlen 1 Leonardo Pisano Leonardo von Pisa ca. 1170 bis 1250 Sohn eines Kaufmanns aus Pisa Sein Vater war Handelsattaché der Republik Pisa in Bugia (im heutigen Algerien). Er zeigte früh
Die Fibonacci-Zahlen 1 Leonardo Pisano Leonardo von Pisa ca. 1170 bis 1250 Sohn eines Kaufmanns aus Pisa Sein Vater war Handelsattaché der Republik Pisa in Bugia (im heutigen Algerien). Er zeigte früh
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII. Bruce Rawles
 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII Bruce Rawles Alle Rechte vorbehalten. Außer zum Zwecke kurzer Zitate für Buchrezensionen darf kein Teil dieses Buches
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII Bruce Rawles Alle Rechte vorbehalten. Außer zum Zwecke kurzer Zitate für Buchrezensionen darf kein Teil dieses Buches
DIE KOMMUNIONEN => Ihre praktische Ausübung
 DIE KOMMUNIONEN => Ihre praktische Ausübung zu den Kommunionen: Bevor sie die eigentlichen Worte einer Kommunion sprachen, wiederholten die Essener feierlich und ehrfurchtsvoll die folgende Einleitung:
DIE KOMMUNIONEN => Ihre praktische Ausübung zu den Kommunionen: Bevor sie die eigentlichen Worte einer Kommunion sprachen, wiederholten die Essener feierlich und ehrfurchtsvoll die folgende Einleitung:
n x n y n Tab.1: Zwei Beispiele
 Hans Walser, [0404] Konvergente Fibonacci-Folgen Worum geht es? Die klassische Fibonacci-Folge,,,, 5, 8,,,... ist divergent. Wir untersuchen Beispiele von konvergenten Folgen mit der Rekursion: a n = pa
Hans Walser, [0404] Konvergente Fibonacci-Folgen Worum geht es? Die klassische Fibonacci-Folge,,,, 5, 8,,,... ist divergent. Wir untersuchen Beispiele von konvergenten Folgen mit der Rekursion: a n = pa
Mathematik 1 (Studiengang Betriebsökonomie) Themenblock 2: Folgen und Reihen
 Mathematik 1 (Studiengang Betriebsökonomie) Building Competence. Crossing Borders. Lernziele Sie können erklären, was man unter einer Folge versteht. die explizite und rekursive Definition von Zahlenfolgen
Mathematik 1 (Studiengang Betriebsökonomie) Building Competence. Crossing Borders. Lernziele Sie können erklären, was man unter einer Folge versteht. die explizite und rekursive Definition von Zahlenfolgen
DIE KOMMUNIONEN => Ihre praktische Ausübung
 DIE KOMMUNIONEN => Ihre praktische Ausübung zu den Kommunionen: Bevor sie die eigentlichen Worte einer Kommunion sprachen, wiederholten die Essener feierlich und ehrfurchtsvoll die folgende Einleitung:
DIE KOMMUNIONEN => Ihre praktische Ausübung zu den Kommunionen: Bevor sie die eigentlichen Worte einer Kommunion sprachen, wiederholten die Essener feierlich und ehrfurchtsvoll die folgende Einleitung:
Prof. Dr. Dörte Haftendorn, Leuphana Universität Lüneburg, 2013
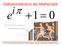 Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Vorlesung. Vollständige Induktion 1
 WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
Eckhart tolle. leben im Jetzt
 Eckhart tolle leben im Jetzt Eckhart tolle J Leben im Etzt lehren, Übungen und Meditationen aus»the Power of Now«aus dem amerikanischen von Erika Ifang Die originalausgabe erschien 2001 unter dem titel»practicing
Eckhart tolle leben im Jetzt Eckhart tolle J Leben im Etzt lehren, Übungen und Meditationen aus»the Power of Now«aus dem amerikanischen von Erika Ifang Die originalausgabe erschien 2001 unter dem titel»practicing
Der Goldene Schnitt und das Taiji
 Der Goldene Schnitt und das Taiji 30. 01. 2006 Taiji und Taijiquan Oft spricht man vom Taiji und meint damit das Taijiquan. Dies ist aber nicht ganz richtig. Das Wort Taijiquan setzt sich nämlich aus zwei
Der Goldene Schnitt und das Taiji 30. 01. 2006 Taiji und Taijiquan Oft spricht man vom Taiji und meint damit das Taijiquan. Dies ist aber nicht ganz richtig. Das Wort Taijiquan setzt sich nämlich aus zwei
5. Anwendungsaufgaben
 5. Anwendungsaufgaben 5.1 Dose Titel V2 5-1 Dose 2 Version Mai 2011 Themenbereich Themen Rolle des CAS Methoden Hinweise Quelle Zeitlicher Rahmen Anwendungsaufgaben zur Differenzialrechnung Optimierung
5. Anwendungsaufgaben 5.1 Dose Titel V2 5-1 Dose 2 Version Mai 2011 Themenbereich Themen Rolle des CAS Methoden Hinweise Quelle Zeitlicher Rahmen Anwendungsaufgaben zur Differenzialrechnung Optimierung
3. Untergruppen. 3. Untergruppen 23
 3. Untergruppen 23 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 23 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Mathematik und Naturwissenschaften- 2011
 Mathematik und Naturwissenschaften in der Grundschule Thema Klassenstufe Naturwissenschaftlicher Bezug Was gibt es dazu im Schulbiologiezentrum? Größen und Messen: Zeitmessung Ende der 2. Klasse Bei Versuchen
Mathematik und Naturwissenschaften in der Grundschule Thema Klassenstufe Naturwissenschaftlicher Bezug Was gibt es dazu im Schulbiologiezentrum? Größen und Messen: Zeitmessung Ende der 2. Klasse Bei Versuchen
Fibonacci-Zahlen. Teilnehmer: Herder-Oberschule, Berlin. Käthe-Kollwitz-Oberschule, Berlin. Gruppenleiter:
 Fibonacci-Zahlen Teilnehmer: Jiafan He Viet Duc Hoang Maximilian Kube Sarah Lengfeld Mona Mattner Duc Anh Vu Andreas-Oberschule, Berlin Immanuel-Kant-Oberschule, Berlin Andreas-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
Fibonacci-Zahlen Teilnehmer: Jiafan He Viet Duc Hoang Maximilian Kube Sarah Lengfeld Mona Mattner Duc Anh Vu Andreas-Oberschule, Berlin Immanuel-Kant-Oberschule, Berlin Andreas-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
MATHEMATIK IN KUNST UND NATUR. Fibonacci Zahlen und der goldene Schnitt
 MATHEMATIK IN KUNST UND NATUR Fibonacci Zahlen und der goldene Schnitt BEGLEITVORTRAG ZUR AUSSTELLUNG MATHEMATIK ZUM ANFASSEN DES MATHEMATIKUMS GIEßEN AN DER HOCHSCHULE PFORZHEIM Prof. Dr. Kirsten Wüst
MATHEMATIK IN KUNST UND NATUR Fibonacci Zahlen und der goldene Schnitt BEGLEITVORTRAG ZUR AUSSTELLUNG MATHEMATIK ZUM ANFASSEN DES MATHEMATIKUMS GIEßEN AN DER HOCHSCHULE PFORZHEIM Prof. Dr. Kirsten Wüst
MB 10. Seiten im Materialblock: Wissensspeicher ab Seite MB 11 Methodenspeicher Seite MB 14 Arbeitsmaterial ab Seite MB 15 Checkliste Seite MB 23
 MB 10 Seiten im Materialblock: Wissensspeicher ab Seite MB 11 Methodenspeicher Seite MB 14 ab Seite MB 15 Checkliste Seite MB 23 Wissensspeicher Körper und Flächen MB 11 Wissensspeicher Fachwörter zu Körpern
MB 10 Seiten im Materialblock: Wissensspeicher ab Seite MB 11 Methodenspeicher Seite MB 14 ab Seite MB 15 Checkliste Seite MB 23 Wissensspeicher Körper und Flächen MB 11 Wissensspeicher Fachwörter zu Körpern
Mathematik in der Natur
 Mathematik in der Natur Fibonacci und die Ananas Jan Schneider Hommage an das Oberfeld Atelierhaus Vahle February 25, 207 / 28 Fibonacci-Folge (F n ) n N =,, 2, 3, 5, 8, 3, 2, 34, 55,... Divina Proportione
Mathematik in der Natur Fibonacci und die Ananas Jan Schneider Hommage an das Oberfeld Atelierhaus Vahle February 25, 207 / 28 Fibonacci-Folge (F n ) n N =,, 2, 3, 5, 8, 3, 2, 34, 55,... Divina Proportione
Das Geheimnis der Dankbarkeit
 Das Geheimnis der Dankbarkeit Das Geheimnis der Dankbarkeit In unserer heutigen Welt, bekommt Dankbarkeit wieder eine bedeutendere Stellung. Wenn wir einige Jahre zurückblicken, waren viele Menschen sehr
Das Geheimnis der Dankbarkeit Das Geheimnis der Dankbarkeit In unserer heutigen Welt, bekommt Dankbarkeit wieder eine bedeutendere Stellung. Wenn wir einige Jahre zurückblicken, waren viele Menschen sehr
Arnold-von-Wied-Schule. Gemeinschaftsgrundschule der Stadt Bonn. Vilicher Straße 2 in Bonn. Schuleingangsstufe. Kriteriengestütztes Zeugnis
 Arnold-von-Wied-Schule Gemeinschaftsgrundschule der Stadt Bonn Vilicher Straße 2 in 53225 Bonn Schuleingangsstufe Kriteriengestütztes Zeugnis für geb. am Klasse: 2 Schuljahr: 2014/15 Versäumte Stunden:
Arnold-von-Wied-Schule Gemeinschaftsgrundschule der Stadt Bonn Vilicher Straße 2 in 53225 Bonn Schuleingangsstufe Kriteriengestütztes Zeugnis für geb. am Klasse: 2 Schuljahr: 2014/15 Versäumte Stunden:
Liebe Lehrerin, lieber Lehrer
 Liebe Lehrerin, lieber Lehrer Stellen Sie sich folgende Situation vor: Eben noch sind einige Schülerinnen und Schüler durchs Klassenzimmer gerannt, haben sich über die gerade absolvierte Französischprüfung
Liebe Lehrerin, lieber Lehrer Stellen Sie sich folgende Situation vor: Eben noch sind einige Schülerinnen und Schüler durchs Klassenzimmer gerannt, haben sich über die gerade absolvierte Französischprüfung
Binomialverteilung Vertrauensbereich für den Anteil
 Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
Übungen mit dem Applet Binomialverteilung Vertrauensbereich für den Anteil Binomialverteilung Vertrauensbereich für den Anteil 1. Statistischer Hintergrund und Darstellung.... Wie entsteht der Vertrauensbereich?...
Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten
 http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
Didaktik der Geometrie Kopfgeometrie
 Didaktik der Geometrie Kopfgeometrie Steffen Hintze Mathematisches Institut der Universität Leipzig - Abteilung Didaktik 26.04.2016 Hintze (Universität Leipzig) Kopfgeometrie 26.04.2016 1 / 7 zum Begriff
Didaktik der Geometrie Kopfgeometrie Steffen Hintze Mathematisches Institut der Universität Leipzig - Abteilung Didaktik 26.04.2016 Hintze (Universität Leipzig) Kopfgeometrie 26.04.2016 1 / 7 zum Begriff
2. Am Meer und auf dem Land
 2. Am Meer und auf dem Land Am Meer und auf dem Land 2 Fotos schöner Landschaften sollen die Menschen, die sie betrachten, fesseln und ihren Sinn für Ästhetik ansprechen. Sie sollen sich im Idealfall gedanklich
2. Am Meer und auf dem Land Am Meer und auf dem Land 2 Fotos schöner Landschaften sollen die Menschen, die sie betrachten, fesseln und ihren Sinn für Ästhetik ansprechen. Sie sollen sich im Idealfall gedanklich
Eine Frucht für die Götter
 Eine Frucht für die Götter Ratet Kinder, wer ich bin, hänge hoch im Baume drin, hab rote Bäckchen, nen Stiel hab ich auch und einen dicken, runden Bauch. Es war einmal vor langer Zeit. Da schuf Gott Himmel
Eine Frucht für die Götter Ratet Kinder, wer ich bin, hänge hoch im Baume drin, hab rote Bäckchen, nen Stiel hab ich auch und einen dicken, runden Bauch. Es war einmal vor langer Zeit. Da schuf Gott Himmel
Theater St. Gallen. Codex. Material zur Vor. Nachbereitung des Theaterbesuchs. mit der Schulklasse. Tanzstück von Marco Santi.
 Theater St. Gallen Codex Tanzstück von Marco Santi Material zur Vor or-/nach Nachbereitung des Theaterbesuchs mit der Schulklasse Spielzeit 2011/12 Theater St.Gallen, 13. Januar 2012 Liebe Lehrerinnen
Theater St. Gallen Codex Tanzstück von Marco Santi Material zur Vor or-/nach Nachbereitung des Theaterbesuchs mit der Schulklasse Spielzeit 2011/12 Theater St.Gallen, 13. Januar 2012 Liebe Lehrerinnen
Wenn du dir deine Klasse als Apfelkiste gut vorstellen kannst, kannst du die Augen öffnen und anfangen zu malen.
 Die Apfelkiste Diese Übung fördert die Selbstwahrnehmung und die Wahrnehmung anderer. Über die Metapher des Apfels drücken die Kinder ihre momentane Befindlichkeit aus. Sie geben an, wie sie sich selbst
Die Apfelkiste Diese Übung fördert die Selbstwahrnehmung und die Wahrnehmung anderer. Über die Metapher des Apfels drücken die Kinder ihre momentane Befindlichkeit aus. Sie geben an, wie sie sich selbst
Illustrierende Aufgaben zum LehrplanPLUS
 Jahrgangsstufen 1/2 Der Herbst ist da - Wir gestalten mit Heckenfrüchten Stand: 02.02.2016 Fach/Fächer Zeitrahmen Benötigtes Material Heimat- und Sachunterricht 4-5 Unterrichtseinheiten Zweige von Heckensträuchern
Jahrgangsstufen 1/2 Der Herbst ist da - Wir gestalten mit Heckenfrüchten Stand: 02.02.2016 Fach/Fächer Zeitrahmen Benötigtes Material Heimat- und Sachunterricht 4-5 Unterrichtseinheiten Zweige von Heckensträuchern
Mein Geschenk an Dich O. Drei verschiedene Mandala Mal-Meditationen mit Anleitung. Erschaffe Deinen perfekten kreativen Moment und verbinde
 Mandala Meditation Mein Geschenk an Dich O Drei verschiedene Mandala Mal-Meditationen mit Anleitung. Erschaffe Deinen perfekten kreativen Moment und verbinde Dich mit Deiner positiven Schöpferkraft. Mandala
Mandala Meditation Mein Geschenk an Dich O Drei verschiedene Mandala Mal-Meditationen mit Anleitung. Erschaffe Deinen perfekten kreativen Moment und verbinde Dich mit Deiner positiven Schöpferkraft. Mandala
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Differentialgeometrie I (Kurventheorie) SS 2013
 Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 1 18. April 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 1 18. April 2013 1 / 23 Organisatorisches Allgemeines Dozentin: Dr. Darya Apushkinskaya
Differentialgeometrie I (Kurventheorie) SS 2013 Lektion 1 18. April 2013 c Daria Apushkinskaya 2013 () Kurventheorie: Lektion 1 18. April 2013 1 / 23 Organisatorisches Allgemeines Dozentin: Dr. Darya Apushkinskaya
