Höhere Mathematik II. (Vorlesungskript)
|
|
|
- Stephanie Straub
- vor 9 Jahren
- Abrufe
Transkript
1 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L A TEX-Satz des Manuskripts: Christian Pappert und Dennis Thielsen
2 2
3 Inhaltsverzeichnis I. Folgen und Reihen 7 1. Zahlenfolgen Einfachste Eigenschaften von Zahlenfolgen Konvergente Zahlenfolgen Konvergenzkriterien Einige spezielle Zahlenfolgen Häufungspunkte Limes superior, Limes inferior Unendliche Reihen Summe einer Reihe Bestimmte Divergenz Elementare Eigenschaften von Reihen Konvergenzkriterien Reihen mit nichtnegativen Gliedern Quotienten- und Wurzelkriterium Das Integralkriterium Kriterium für alternierende Reihen Absolute Konvergenz Eigenschaften absolut konvergenter Reihen Multiplikation von Reihen Funktionenreihen Gleichmäßige Konvergenz Ein Kriterium für gleichmäßige Konvergenz Eigenschaften gleichmäßig konvergenter Reihen
4 Inhaltsverzeichnis 4. Potenzreihen Konvergenzverhalten von Potenzreihen Berechnung des Konvergenzradius r Eigenschaften von Potenzreihen Identitätssatz für Potenzreihen Rechnen mit Potenzreihen Addition, Subtraktion, λ-faches Multiplikation Division Taylorreihen Praktische Bedeutung der Taylorentwicklung Taylorentwicklung einiger Funktionen II. Differentialrechnung im R n Definition, Beispiele Graphische Darstellung von Funktionen 2er Variabler Grenzwerte von Funktionen mehrerer Variabler Stetigkeit Partielle Ableitungen Partielle Ableitungen 1.Ordnung Partielle Ableitungen im R Partielle Ableitungen im R n Partielle Ableitungen höherer Ordnung Die verallgemeinerte Kettenregel 85 1.Mittelwertsatz Folgerungen aus dem MWS Anwendungen des totalen Differentials in der Fehlerrechnung Implizite Funktionen, implizite Differentiation Implizite Funktionen zweier Variabler Implizite Funktionen mehrerer Variabler Auflösbarkeit Berechnung der ersten partiellen Ableitungen
5 Inhaltsverzeichnis 12.Die Richtungsableitung Eine weitere Eigenschaft des Gradienten f Satz von Taylor Eigenschaften von F (t) Anwendung der Taylorformel für Funktionen einer Variablen auf die Funktion F Extremwertaufgaben Kriterien für lokale Extremalstellen Notwendige Bedingung 1. Art Notwendige Bedingungen 2. Art Hinreichende Bedingung Extremwertaufgaben mit Nebenbedingungen Notwendige Optimalitätsbedingungen Verfahren von Lagrange Hinreichende Optimalitätsbedingungen für (P ) Parameterintegrale Fourier-Reihen Periodische Funktionen Harmonische Analyse Fourierreihen Periodische Funktionen mit speziellen Eigenschaften (Symmetrien) Einige konkrete Fourierentwicklungen Transformation von f mittels eines Tiefpasses: Filterung von f Die Laplace-Transformation von DGLn Die Laplace-Transformation von Funktionen Anwendung der L-Transformation Anfangswertprobleme bei Systemen linearer DGLn Systeme 1. Ordnung mit konstanten Koeffizienten Systeme von DGLn m-ter Ordnung Index 193 5
6 Inhaltsverzeichnis 6
7 Teil I. Folgen und Reihen 7
8
9 1. Zahlenfolgen Definition 1.1 (Zahlenfolge) Eine Zahlenfolge (a n ) oder a n, a n +1, a n +2,..., a n,... liegt dann vor, wenn jeder natürlichen Zahl n n (häufig ist n = oder n = 1) in 1 deutiger Weise eine Zahl a n R (auch b n, x n usw.) zugeordnet ist: n a n = f(n), a n R für n n ; a n heißt n-tes Glied der Folge (a n ). Eine Zahlenfolge ist also eine Funktion f mit Definitionsbereich D f = {n N : n n } für ein n =, 1,.... Praktische Bedeutung: reelle Zahlen lassen sich als konvergente Folgen rationaler Zahlen darstellen: 2 : 1, 1.4, 1.41, 1.414,... mathematische Behandlung unendlicher Summen (Reihen) Diskretisierung technischer Prozesse zur numerischen Verarbeitung in Computern Numerik: Iterationsverfahren zur Lösung von Gleichungen Beispiel: (a) arithmetische Zahlenfolge: a, d seien beliebige Zahlen, d a n = a + nd, n =, 1,... (b) geometrische Zahlenfolge: a, q beliebige Zahlen a n = aq n, n =, 1,... 9
10 1. Zahlenfolgen (c) a n = 1 n, b n = n = 4 ( n) n, n = 1, 2,..., c n = 1 (n 1)(n 2)(n 3), n Die Folgen in (a-c) sind durch Rechenvorschriften definiert, die nächsten Folgen sind definiert durch sogenannte Rekursionsvorschriften. (d) Sei c R fest. (e) a = 1, a n+1 = 1 2 a = 1 a n = 1 + ca n 1, n = 1, 2,... (a n + 2an ), n =, 1,... (a n ) lässt sich zur Berechnung von 2 verwenden. } = a n = 1 + c + c c n Definition 1.2 (Teilfolge) Sei ν < ν 1 < ν 2 <... < ν k < ν k+1 <... eine Folge natürlicher Zahlen. Dann heißt die Folge (b k ) eine Teilfolge von (a n ). b k := a νk, k =, 1,..., Beispiel: b k = (q 5 ) k ist eine Teilfolge von a n = q n (setze ν k = 5k) Einfachste Eigenschaften von Zahlenfolgen Definition 1.3 (Monotonie) (a) Eine Zahlenfolge (a n ) heißt monoton wachsend bzw. monoton fallend, wenn a n a n+1 bzw. a n a n+1 für alle n n. (b) Eine Zahlenfolge (a n ) heißt streng monoton wachsend bzw. fallend, wenn a n < a n+1 bzw. a n > a n+1 für alle n n. Definition 1.4 (Alternierende Folge) Eine Zahlenfolge (a n ) heißt alternierend, wenn sgn a n+1 = sgn a n für alle n n. 1
11 1.1. Einfachste Eigenschaften von Zahlenfolgen Satz 1.1 Sei q R. Die Folge a n = q n, n =, 1,..., also 1, q, q 2, q 3,..., ist (a) streng monoton wachsend für alle q > 1 (b) streng monoton fallend für alle < q < 1 (c) konstant für q = (n 1) und q = 1 (d) alternierend für alle q < Definition 1.5 (Beschränkte Folgen) Eine Zahlenfolge (a n ) heißt (a) beschränkt nach unten, wenn a n s für alle n n, (b) beschränkt nach oben, wenn a n S für alle n n, (c) beschränkt, wenn s a n S oder a n C für alle n n, wobei s, S, C, von n unabhängige Zahlen sind. Beispiel: a n = q n (a) q 1 = a n ist beschränkt (b) q > 1 = a n ist beschränkt nach unten Bemerkung: Für < q < 1 ist a n = q n streng monoton fallend und beschränkt. Definition 1.6 (Grenzwert, Konvergenz, Divergenz) Sei (a n ) eine Zahlenfolge. a R heißt Grenzwert von (a n ), wenn zu jedem, auch beliebig kleinem ε > eine Zahl N = N(ε) existiert, so dass a n a < ε für alle n > N(ε). Falls (a n ) einen Grenzwert a besitzt, dann heißt (a n ) auch konvergent (gegen a), und man schreibt lim n a n = a oder a n a, n. Eine nicht konvergente Zahlenfolge heißt divergent. 11
12 1. Zahlenfolgen Bemerkung: (a) Geometrische Bedeutung: Für hinreichend großes n liegen sämtliche Glieder der Folge in einer beliebig kleinen Umgebung von a. U ε (a) = {x : a ε < x < a + ε} (b) Der Grenzwert ist, falls er existiert, 1 deutig bestimmt. Beispiel: (a) Geometrische Folge a n = q n mit q < 1 Sei h := 1 q 1 = h > 1 q = 1 + h = 1 = (1 + h)n q n 1 q n = (1 + h)n 1 + nh (Bernoulli-Ungleichung) nh = q n 1 nh = qn 1 nh Sei ε >. Dann gilt: q n < ε = 1 nh < ε 1 εh < n. Definitionsmöglichkeit für N(ε) : N(ε) = 1 εh = q n, n. Satz 1.2 Für jedes q < 1 gilt lim n q n =. (b) a n a = lim n a n = a (c) a n = 1 für ein festes q N, q 1 nq lim n 1 = für alle q = 1, 2,.... nq 1 (aber auch εh + ϕ(ε) ) }{{} 12
13 1.2. Konvergente Zahlenfolgen Definition 1.7 (Nullfolge) Eine Zahlenfolge mit Grenzwert heißt Nullfolge (N.F.). (d) a n = 1 + 3n + 5n2 = n 2 }{{} 4n 2 }{{} 4n 4 N.F. N.F. = lim n a n = 5 4 (e) a n = ( 1) n, b n = sin n, c n = n 2, d n = log 1 n Folgen. sind Beispiele divergenter (f) lim n q n = ± für alle q > 1, lim n log 1 n =. Definition 1.8 (Bestimmte Divergenz) lim a n = + (oder ) bedeutet: Zu jedem beliebig großen A gibt es ein N = N(A), so dass a n > A n bzw. a n < A für alle n > N(A) Konvergente Zahlenfolgen Satz 1.3 Eine Folge hat höchstens einen Grenzwert. Satz 1.4 Jede konvergente Zahlenfolge ist beschränkt. Bemerkung: (a) Aus Satz 1.4 folgt: (a n ) unbeschränkt (a n ) divergent (evtl. bestimmt divergent). (b) (a n ) beschränkt (a n ) konvergent. Beispiel: a n = ( 1) n Satz 1.5 Jede Teilfolge einer konvergenten Folge a n gegen a. a, n konvergiert 13
14 1. Zahlenfolgen Satz 1.6 (Grenzwertsätze) ( Sei ) a n a, b n b für n. Dann sind auch an die Folgen (a n ± b n ), (a n b n ),, wenn b, und a n konvergent, und es gilt b n lim (a n ± b n ) = lim a n ± lim b n, n n n lim (a n b n ) = lim a n lim b n, n n n a n lim = n b n lim a n = n lim a n n lim b, wenn b, n n lim a n n Beispiel: a n = 7 + 3n + 4n2 5n 3 2n + 1n 3 = 7 n n n 5 2 n = 1 2, n Satz 1.7 Die Abänderung von (nur) endlich vielen Gliedern einer Folge ändert deren Konvergenzverhalten nicht. Satz 1.8 Ist a n, n und (b n ) eine beschränkte Folge, dann gilt lim a nb n =. n Satz 1.9 Ist a n a, b n b für n und a n b n für alle n, so folgt a b Konvergenzkriterien Satz 1.1 Ist eine Folge monoton wachsend und nach oben beschränkt bzw. monoton fallend und nach unten beschränkt, dann ist sie konvergent. 14
15 Beispiel: a n = ! + 1 2! n! = n 1 k! a n ist sicher streng monoton wachsend. Ferner gilt: n 1 n k! = k! k=2 = < = < = (a n ) ist beschränkt. Satz 1.1 n 1 = a = lim n k! existiert! 1.4. Einige spezielle Zahlenfolgen ( ) n ( ) n ( 1 3 = ) k = ( 1 3 )n Satz 1.11 Sei a n a, b n a, n. Ist a n c n b n für alle n n, dann gilt c n a, n. Satz 1.12 (Cauchysches Konvergenzkriterium) Die Zahlenfolge (a n ) ist genau dann konvergent, wenn zu jedem, auch beliebig kleinen ε > ein N = N(ε) existiert, so dass a n a m < ε, wenn m, n > N(ε). Bemerkung: In diesem Konvergenzkriterium kommt der Grenzwert a nicht explizit vor! 1.4. Einige spezielle Zahlenfolgen (a) a n = an für festes a > 1, α > nα lim a n = + bestimmte Divergenz n 15
16 1. Zahlenfolgen (b) lim n n = 1 Sei a n = n n = 1 + d n, d n >. n n ( ) ( ) n n = n = a n n = (1+d n ) n = d i n > d 2 n = i 2 i= 2 = n > n2 4 ( n n 1) }{{} 2 d n 4 n > ( n n 1) 2 2 > n n 1 n > n Satz 1.11 n > 1 = lim n n = 1. n n (c) log a n, n n f(x) = log a x ist stetig in x = 1. Daraus folgt mit (b): (d) Sei a n a, n. Dann gilt: f( n n) f(1), n. }{{}}{{} 1 n log a n n(n 1) d 2 n > n2 2 4 d2 n für n Satz 1.13 (Arithmetisches Mittel der Teilsummen) Sei a n a, n. Dann gilt b n = a 1 + a a n a, n. n (e) lim n ( n) n = e = 2, Häufungspunkte Divergente Folgen besitzen manchmal noch Häufungspunkte. Definition 1.9 (Häufungspunkt) Eine Zahl a heißt Häufungspunkt (H.P.) einer Folge (a n ), wenn zu jedem beliebig kleinen ε > eine Indexfolge n 1 < n 2 <... existiert, so dass a nk a < ε für alle k = 1, 2,..., d.h., in jeder Umgebung eines H.P. von (a n ) liegen viele Glieder der Folge. Beispiel: 16
17 1.6. Limes superior, Limes inferior (a) a n = ( 1) n hat die beiden H.P. a = ±1 (Jede beliebig kleine Umgebung von 1 bzw. +1 enthält alle Glieder a 2k+1 bzw. a 2k für alle k =, 1,...) (b) Sei a n a, n. Dann ist der Grenzwert a der einzige H.P. von (a n ). (c) a n = n! = (a n ) hat keinen H.P. Satz 1.14 Ist a ein H.P. von (a n ), dann gibt es eine Teilfolge (a nk ), so dass a = lim k a n k. Bemerkung: Aus Satz 1.14 folgt: H.P. sind die Grenzwerte konvergenter Teilfolgen! Satz 1.15 Jede beschränkte Folge hat mindestens einen H.P. und damit mindestens eine konvergente Teilfolge Limes superior, Limes inferior Gegeben sei eine beschränkte Zahlenfolge (a n ), also a n C für alle n. Sei a H.P. von (a n ). = a = lim k a nk = a C (Satz 1.14 und Satz 1.9). = Die Menge aller H.P. von (a n ) ist beschränkt. Satz 1.16 Ist (a n ) eine beschränkte Zahlenfolge, dann hat (a n ) einen größten H.P. a und einen kleinsten H.P. a. Definition 1.1 (Limes inferior, Limes superior) Sei (a n ) eine beschränkte Zahlenfolge, dann heißen a =: lim a n =: lim sup a n limes superior (oberer Grenzwert) und n n a =: lim a n =: lim inf n n a n limes inferior (unterer Grenzwert). Bemerkung: 17
18 1. Zahlenfolgen (a) lim n a n ist der größte Grenzwert einer konvergenten Teilfolge. (b) lim n a n ist der kleinste Grenzwert einer konvergenten Teilfolge. Satz 1.17 Eine beschränkte Zahlenfolge ist genau dann konvergent, wenn a = a. ( Beispiel: a n = ( 1) n ) n a = 1, a = +1 = (a n ) ist divergent 18
19 2. Unendliche Reihen Praktische Bedeutung: Unendliche Reihen dienen der Definition von Summen mit unendlich vielen Summanden: Entwicklung komplizierter Funktionen, z. B. sin, cos, log usw., in Potenzreihen Darstellung periodischer Vorgänge durch Fourierreihen Lösung von Differentialgleichungen, die nicht durch elementare Integrationsmethoden lösbar sind, mittels Funktionsreihen-Ansatz Definition 2.1 (Reihe) Ist a, a 1,..., a k,... eine Zahlenfolge, dann heißt der rein formale Ausdruck a + a 1 + a a k + oder eine unendliche Reihe (kurz Reihe). Die Zahlen a k heißen Glieder oder Summanden der Reihe. a k 2.1. Summe einer Reihe Definition der Summe s der Reihe: Wir betrachten die sog. n-ten Partialsummen s n, n =, 1, 2,...: s = a s 1 = a + a 1 s 2 = a + a 1 + a 2. s n = a + a 1 + a a n =. n a k 19
20 2. Unendliche Reihen Definition 2.2 (Summe, Konvergenz, Divergenz) Eine Reihe a k heißt konvergent bzw. divergent, wenn die Folge (s n ) ihrer n-ten Partialsummen konvergent bzw. divergent ist. Der Grenzwert s = lim s n heißt Summe der Reihe, und n man schreibt auch s = a k oder s = a + a 1 + a Bemerkung: Das Zeichen a k ihren Grenzwert s, falls dieser existiert. Beispiele: bezeichnet sowohl die formale Reihe, als auch (a) Geometrische Reihe: 1 + q + q 2 + q q k +..., also a k = q k 1 q n+1 s n = 1 + q + + q n, q 1 = 1 q n + 1, q = 1 Es sind dann 4 Fälle zu unterscheiden: i) 1 < q < +1 = q n, n = s n 1 1 q, n = s = 1 1 q ii) q = 1 = s n = n + 1 = (s n ) ist bestimmt divergent nach + iii) q = 1 = s n = 1 2 (1 ( 1)n+1 ) = = (s n ) ist divergent iv) q > 1 = q n ist nicht beschränkt = (s n ) ist unbeschränkt = (s n ) ist divergent (Satz 1.4) Insgesamt erhalten wir also Satz 2.1 (Geometrische Reihe) wenn 1 < q < +1, wobei dann q 1. { 1, n gerade, n ungerade 1+q+q 2 + +q n + ist konvergent, q k 1 = und divergent, wenn 1 q 2
21 2.2. Bestimmte Divergenz (b) Harmonische Reihe: k +..., also a k = 1 k 1 Behauptung: ist divergent. k k=1 Man betrachte die Glieder s 2 i, i = 1, 2,... s 2 1 = s 2 = > 2 2 s 2 2 = s 4 = s > = 3 2 s 2 3 = s 8 = s > = 4 2 s 2 4 = s 16 = s 8 = > = 5 2. = s 2 i > 1 (i + 1) 2 = s n > 1 2 (i + 1) n > 2i und jedes i = 1, 2,... = (s n ) ist nicht beschränkt = (s n ) ist divergent 1 = ist divergent. k k= Bestimmte Divergenz Definition 2.3 (Bestimmte Divergenz) wenn (s n ) bestimmt divergent ist. Man schreibt dann Beispiele: a k a k = ±, wenn lim n s n = ±. heißt bestimmt divergent, (a) k=1 1 k = + 21
22 2. Unendliche Reihen (b) q k = +, q Elementare Eigenschaften von Reihen Satz 2.2 Verändert man in einer Reihe sich deren Konvergenzverhalten nicht. a k endlich viele Glieder a k, so ändert Satz 2.3 (Grenzwertsätze) (a) Ist a k = s R, dann ist auch c a k konvergent für jedes c R, und es gilt c a k = c a k. (b) Sind a k = s, b k = t konvergente Reihen, dann konvergiert auch (a k + b k ), und es gilt (a k + b k ) = a k + b k. Bemerkung: a k = s, b k = t i.a. a k b k = s t (vgl. Satz 2.18) Konvergenzkriterien Satz 2.4 (Notwendiges Konvergenzkriterium) Ist gilt lim a k =, die Folge (a k ) ihrer Glieder ist also eine Nullfolge. k a k konvergent, dann Bemerkung: (a k ) Nullfolge a k konvergent 22
23 2.4. Konvergenzkriterien Beispiel: ist aber divergent. ( ) 1 ist eine Nullfolge. Die (harmonische) Reihe k k=1 1 k Satz 2.5 (Cauchysches Konvergenzkriterium) Die Reihe a k ist genau dann konvergent, wenn zu jedem ε >, auch beliebig klein, eine Zahl N(ε) existiert, so dass a n+1 + a n a n+p < ε für alle n > N(ε) und jedes p =, 1,... Beweis: Mit Hilfe des Cauchy-Kriteriums für die Folge (s n ). 1 Beispiel: k(k + 1) k=1 1 k(k + 1) = 1 k 1 k + 1 a n+1 + a n a n+p = 1 n n n n n + p 1 n + p + 1 Gegeben: ε >, man wähle = Die Reihe ist konvergent nach Satz 2.5. Berechnung des Grenzwertes: n 1 n ( 1 s n = k(k + 1) = k 1 ) k + 1 = k=1 k=1 k=1 1 k(k + 1) = 1 = i=2 = 1 n n + p + 1 < 1 n + 1 p 1 1 n + 1 < ε 1 ε 1 < n, also N(ε) = 1 ε 1 1 (i 1)i = 1 1 n + 1 1, n Reihen mit nichtnegativen Gliedern Man betrachte Reihen a k mit a k k =, 1, 2,... 23
24 2. Unendliche Reihen = s n = n a k Daraus folgt mit Satz 1.1: ist monoton wachsend. Satz 2.6 Eine Reihe mit nichtnegativen Gliedern ist genau dann konvergent, wenn (s n ) beschränkt ist. Satz 2.7 (Vergleichskriterium I) Eine Reihe a k mit nichtnegativen Glie- dern ist konvergent, wenn eine Reihe b k existiert, so dass (a) b k ist als konvergent bekannt, (b) a k b k für alle k k, mit einem gewissen (festen) k. Bemerkung: b k heißt konvergente Majorante von a k. Das Vergleichskriterium I heißt daher auch Majorantenkriterium. 1 Beispiel: k, also a 2 k = 1 k 2 k=1 Es ist 1 k = 1 2 k 1 k < 1 k 1 1 k für alle k k = 2 1 = (k 1)k ist eine konvergente Majorante von k=2 Das Majorantenkriterium liefert dann: Später zeigt sich: k=1 1 k = π2 2 6 k=1 k=1 1 k 2 1 ist konvergent. k2 Satz 2.8 (Vergleichskriterium II) Eine Reihe a k ist divergent, wenn eine Reihe b k existiert, so dass 24
25 (a) b k ist als divergent bekannt, (b) a k b k für alle k k mit einem gewissen (festen) k. Bemerkung: 2.4. Konvergenzkriterien b k heißt divergente Minorante von a k. Das Vergleichskriterium II heißt daher auch Minorantenkriterium. 1 Beispiel:, a k = 1 k k Sei k 1. k=1 = k k = 1 k = a k b k = 1 k = = k=1 k=1 1 k ist divergente Minorante von 1 k ist divergent. k=1 1 k Quotienten- und Wurzelkriterium Gegeben: Reihe a k mit nichtnegativen Gliedern a k. Satz 2.9 (Quotientenkriterium) (a) Quotientenkriterium: i) Existiert ein festes q < 1 und eine Zahl N, so dass a k > für k N und a k+1 a k q für alle k N, dann ist a k konvergent. ii) Gilt hingegen a k >, k N, und dann ist a k divergent. a k+1 a k 1 für alle k N, 25
26 2. Unendliche Reihen (b) Limesform des Quotientenkriteriums: Für die Reihe a k existiere der Grenzwert Q = lim Bemerkung: (a) Gilt a k+1 a k a k konvergent, wenn Q < 1 divergent, wenn Q > 1 < 1 für alle k N i.a. Konvergenz. a k+1 k a k. Dann ist (b) Ist Q = 1, dann ist sowohl Konvergenz als auch Divergenz möglich! Beispiele: (a) (b) a k, a k = k! 2 k (2k)! > = a k+1 1 = a k 4(2k + 1) 1 4 = a k ist konvergent k=1 (c) a k = 1 k 1 k : a k+1 a k = k k + 1 < 1 k = a k+1 a k =, α feste positive Zahl α ( k α k (k + 1) = α k + 1 = Q = 1 für alle α > α = 1 = Divergenz, α 2 = Konvergenz ) α 1, k für alle α > Satz 2.1 (Wurzelkriterium) (a) Wurzelkriterium: i) Existiert ein < q < 1 und eine Zahl N, so dass k ak q für alle k N, dann ist a k konvergent. 26
27 2.4. Konvergenzkriterien ii) Gilt hingegen dann ist a k divergent. k ak 1 für alle k N, (b) Limesform des Wurzelkriteriums: Für a k existiere der Grenzwert W = lim k a k. k Dann ist a k konvergent, wenn W < 1 divergent, wenn W > 1 Beispiel: a k = ( ) k 2k + 1 3k + 1 = k a k = 2k + 1 3k + 1 < 7 8 für k N = 3 = W = 2 3 ( ) k 2k + 1 = ist konvergent. 3k + 1 Bemerkung: W = 1 bringt keine Entscheidung über Konvergenz oder Divergenz. Beispiel: a k = 1 = k a k = = W = 1 k α ( ) 1 1 k 1 = k α k α k = ( 1 k k ) α 1, k = α = 1: Divergenz und α 2: Konvergenz Das Integralkriterium Satz 2.11 (Integralkriterium) Die Reihe a k mit nichtnegativen Gliedern a k sei definiert durch k=1 a k = f(k), k = 1, 2,..., 27
28 2. Unendliche Reihen wobei f : [1, + ) R eine monoton fallende, stetige Funktion ist. Dann ist a k genau dann konvergent, wenn der Grenzwert existiert. + 1 f(x) dx := A lim A + 1 k=1 f(x) dx Beispiel: k=1 1 k α = f(x) = 1 mit α > stetig und monoton fallend auf [1, + ) xα { 1 1 = f(x) dx = x dx = α α + 1 x α+1, α 1 ln x, α = 1 = A 1 = lim A + = k=1 = Es ist f(x) dx = A 1 { 1 1 α (A1 α 1), α 1 ln A, α = 1 f(x) dx = { 1 α 1, α > 1 existiert nicht für < α 1 { 1 konvergiert für α > 1 k α divergiert für < α 1 k=1 1 k α = +, < α Kriterium für alternierende Reihen Satz 2.12 (Leibnizsches Konvergenzkriterium) Eine alternierende Reihe ist konvergent, wenn die Folge ( a k ) monoton fallend und eine Nullfolge ist. a k 28
29 2.5. Absolute Konvergenz Beispiel: a k = ( 1) k 1 1 k, k = 1, 2,..., = = a k = 1 k ist monoton fallend, ( a k ) ist Nullfolge = ( 1) k 1 1 ist konvergent. k k=1 Bemerkung: a k ist divergent k= Absolute Konvergenz Definition 2.4 (Absolute Konvergenz) Eine Reihe a k heißt absolut kon- vergent, wenn die Reihe a k konvergiert. Satz 2.13 Jede absolut konvergente Reihe ist konvergent. Bemerkung: (a) Konvergenz i.a. Absolute Konvergenz. (b) Eine konvergente Reihe mit nichtnegativen Gliedern a k auch absolut konvergent. ist natürlich Beispiel: ist konvergent, nicht aber absolut konvergent. 4 Satz 2.14 (Majoranten- und Minorantenkriterium) (a) Majorantenkriterium: a k ist absolut konvergent (und damit auch konvergent), wenn eine Reihe b k mit nichtnegativen Gliedern b k existiert, so dass i) b k konvergent ist und ii) a k b k für alle k N (für eine Zahl N ). 29
30 2. Unendliche Reihen (b) Minorantenkriterium: Gilt a k b k für alle k N, wobei nicht absolut konvergent. b k divergent ist, dann ist a k Satz 2.15 (Quotientenkriterium) (a) Quotientenkriterium: i) Existiert ein < q < 1 und eine Zahl N, so dass dann ist a k absolut konvergent. ii) Gilt hingegen so ist a k divergent. a k+1 a k q für alle k N, a k+1 a k 1 für alle k N, (b) Limesform des Quotientenkriteriums: Es existiere Q = lim k a k+1 a k. Wenn Q < 1 bzw. Q > 1, so ist a k absolut konvergent bzw. divergent. Bemerkung: Für Q = 1 ist kein Entscheid zwischen Konvergenz und Divergenz möglich. Beispiele: (a) , a k = ( 1) k 1 1 k Q = lim a k+1 k a k = 1, Reihe konvergiert Aber = Q = 1, Reihe divergiert 3
31 2.5. Absolute Konvergenz (b) x k für eine feste Zahl x. k! Q = lim a k+1 k a k = lim x k k + 1 = = absolute Konvergenz für alle x R. Satz 2.16 (Wurzelkriterium) (a) Wurzelkriterium: i) Existiert ein < q < 1 und eine Zahl N, so daß k ak q für alle k N, dann ist a k absolut konvergent. ii) Gilt hingegen dann ist a k divergent. (b) Limesform des Wurzelkriteriums: Es existiere k ak 1 für alle k N, W = lim k k a k. Wenn W < 1 bzw. W > 1, dann ist a k absolut konvergent bzw. divergent. Bemerkung: Für W=1 ist kein Entscheid zwischen Konvergenz und Divergenz möglich! Beispiel: = W = 1, Konvergenz = W = 1, Divergenz 4 31
32 2. Unendliche Reihen Eigenschaften absolut konvergenter Reihen Satz 2.17 Ist a k eine absolut konvergente Reihe, so ist ihre Summe unabhängig von der Reihenfolge ihrer Glieder a k. Ist also k, k 1, k 2,... eine beliebige Umordnung der Folge, 1, 2,..., so gilt a k = a kj. (2.1) Definition 2.5 (Bedingte Konvergenz) Reihen mit der Eigenschaft (2.1) heißen auch unbedingt konvergent. Andernfalls heißt die Reihe bedingt konvergent. Beispiel: j= (a) k=1 ( 1) k 1 1 ist absolut und damit unbedingt konvergent. k2 (b) = ln 2 (siehe Taylor-Reihen) ist nur bedingt konvergent. 5 Bemerkung: Ist eine Reihe bedingt konvergent, so lässt sich durch Umordnung der Glieder jede Zahl s als Summe der Reihe darstellen Multiplikation von Reihen Geg.: Reihen a k, b k. b b 1 b 2 b 3... a a b a b 1 a b 2 a b 3... c = a b a 1 a 1 b a 1 b 1 a 1 b 2 a 1 b 3... c 1 = a b 1 + a 1 b a 2 a 2 b a 2 b 1 a 2 b 2 a 2 b 3... c 2 = a b 2 + a 1 b 1 + a 2 b a 3 a 3 b a 3 b 1 a 3 b 2 a 3 b 3... c 3 = a b 3 + a 1 b 2 + a 2 b 1 + a 3 b... 32
33 2.6. Multiplikation von Reihen Definition 2.6 (Cauchysche Produktreihe) Die Produktreihe c k ist definiert durch k c k = a j b k j, k =, 1,.... j= Satz 2.18 Sind a k, b k absolut konvergente Reihen mit Summen s bzw. t, dann ist auch c k absolut konvergent und hat die Summe s t. 33
34 2. Unendliche Reihen 34
35 3. Funktionenreihen Definition 3.1 (Funktionenfolge, Funktionenreihe) Eine Folge (f k ) bzw. eine Reihe f k, deren Glieder Funktionen f k = f k (x) einer reellen Variablen x aus dem Intervall I sind, heißt Funktionenfolge bzw. Funktionenreihe auf I. Beispiele: (a) f k (x) = x k, x X = R, = x k (b) f k (x) = xk k!, x X = R, = x k k! (c) f k (x) = a k sin kωx + b k sin kωx = (a k sin kωx + b k sin kωx) (trigonometrische Reihe) Definition 3.2 (Konvergenz, Konvergenzbereich, Summenfunktion) (a) Die Funktionenreihe f k heißt konvergent bzw. divergent in x I, wenn die Zahlenreihe f k (x ) konvergent bzw. divergent ist. (b) Die Menge M = {x I : f k (x) ist konvergent} heißt Konvergenzbereich (oder Konvergenzmenge) der Funktionenreihe f k. 35
36 3. Funktionenreihen (c) Die Funktion Beispiel: s(x) = f k (x), x M heißt Summenfunktion (oder Grenzfunktion) der Reihe f k. (a) f k (x) = x k = f k (x) = x k geometrische Reihe mit q = x Satz 2.1 = M = ( 1, +1), s(x) = 1 1 x, x < 1 (b) f k (x) = xk k! = x k k! Q.K. = Die Reihe konvergiert für alle x R = M = R x k s(x) = k!, x R Bemerkung: Später zeigt sich, dass s(x) = e x. (c) f k (x) = 1 k + cos kx, k 2 = 1 k + cos kx k=2 1 Es ist cos kx 1 = k + cos kx 1 k + 1 = M =, d.h. die Reihe ist überall divergent = s(x) existiert nicht! Problem: Welche Eigenschaften (Stetigkeit, Differenzierbarkeit, Integrierbarkeit) hat die Summenfunktion? Zur Behandlung dieses Problems benötigen wir noch den Begriff der gleichmäßigen Konvergenz einer Funktionenreihe. Sei s n (x) = f k (x). Konvergenz von f k in x I: Zu jedem ε > und jedem x I existiert eine Zahl N = N(ε, x), so dass s n (x) s(x) < ε für alle n N(ε, x). Bemerkung: Im allgemeinen ist N eine Funktion von ε > und vom Punkt x. 36
37 3.1. Gleichmäßige Konvergenz 3.1. Gleichmäßige Konvergenz Definition 3.3 (Gleichmäßige Konvergenz) Die Reihe f k heißt gleichmäßig konvergent in einem Intervall I mit der Summenfunktion s = s(x), wenn zu jedem ε > eine von x unabhängige Zahl N = N(ε) existiert, so dass s n (x) s(x) < ε für alle n N(ε) und jedes x I. Bemerkung: (a) f k gleichmäßig konvergent in I f k konvergent in I, (b) f k konvergent in I i.a. (c) I kann auch ein Intervall sein. f k gleichmäßig konvergent in I, Beispiel: f k (x) = x 2 (1 x 2 ) k mit x X = [ 1, +1] (a) x = = s(x) = (b) < x 1 = 1 x 2 < 1 = x 2 (1 x 2 ) k = x 2 = s(x) = {, x = 1, < x 1 Problem: Für welche n gilt (1 x 2 ) k = x (1 x 2 ) = 1 s n (x) s(x) < ε(< 1). (3.1) i) x = = s n (x) = s(x) = = (3.1) ist stets erfüllt ii) < x 1: n s n (x) = x 2 (1 x 2 ) k = x 2 1 (1 x2 ) n+1 1 (1 x 2 ) = 1 (1 x 2 ) n+1 (3.1) s(x) s n (x) = (1 x 2 ) m+1 < ε stets erfüllt, wenn x = ±1 37
38 3. Funktionenreihen Sei jetzt < x < 1: (3.1) (n + 1) ln (1 x 2 ) < ln ε, < ε < 1 n + 1 > ln ε ln (1 x 2 ) n ln ε > ln (1 x 2 ) 1 }{{} N(ε, x) = N ist abhängig von ε und x = auf [ 1, +1] ist x 2 (1 x 2 ) k nicht gleichm. konvergent! Bemerkung: Man betrachte nur das Teilintervall I = [a, 1], a >, von X = [ 1, +1] ((3.1) gilt für alle n, falls x = 1 oder x = 1). a x < 1 = < 1 x 2 1 a 2 < 1 = ln (1 x 2 ) ln (1 a 2 ) 1 = ln (1 a 2 ) 1 ln (1 x 2 ) = ln ε ln (1 a 2 ) ln ε ln (1 x 2 ) ln ε Man wähle N(ε) := unabhängig von x I = [a, 1] ln (1 a 2 ) ln ε n N(ε) = n ln (1 x 2 ) = s n(x) s(x) < ε x I = gleichmäßige Konvergenz auf I = [a, 1] < a Ein Kriterium für gleichmäßige Konvergenz Satz 3.1 (Kriterium für gleichmäßige Konvergenz) Eine Funktionenreihe ist gleichmäßig konvergent in einem Intervall I, wenn eine konvergente Zahlenreihe a k, a k, existiert, so dass f k (x) a k für alle k =, 1, 2,... und jedes x I. f k Beispiel: k=1 1 sin (kx) k2 38
39 3.1. Gleichmäßige Konvergenz f k (x) = 1 sin (kx) k2 1 k = a 2 k = gleichmäßige Konvergenz auf I = R Eigenschaften gleichmäßig konvergenter Reihen Satz 3.2 (Stetigkeit der Summenfunktion) Ist f k gleichmäßig konvergent in einem Intervall I und sind die Glieder f k stetig auf I, dann ist auch die Summenfunktion s(x) stetig auf I. Beispiel: Siehe Reihe x 2 (1 x 2 ) k Satz 3.3 (Gliedweise Integration) Ist f k im Intervall I gleichmäßig konvergent gegen die Summenfunktion s(x), dann gilt für beliebige a, b I b b ( ) b s(x) dx = f k (x) dx = f k (x) dx. a a a Satz 3.4 (Gliedweise Differentiation) Die Reihe f k sei in I konvergent gegen die Summenfunktion s(x), die Glieder f k seien differenzierbar auf I, und die Reihe f k sei gleichmäßig konvergent auf I. Dann ist die Reihe f k gleichmäßig konvergent in I, ihre Summenfunktion s(x) ist differenzierbar in I, und es gilt ( s (x) = f k (x)) = f k(x) für alle x I. 39
40 3. Funktionenreihen 4
41 4. Potenzreihen Zur Entwicklung von Funktionen in Reihen braucht man den Begriff der Potenzreihe. Definition 4.1 (Potenzreihe) Eine Funktionenreihe der Form c k (x x ) k heißt Potenzreihe mit Mittelpunkt x. Die Zahlen c k heißen Koeffizienten der Potenzreihe. Bemerkung: Beispiele: Mittelpunkt x Substitution x x = x x = (a) c k = f (k) (x ) k! Taylorreihe (b) x =, c k = 1 geometrische Reihe 4.1. Konvergenzverhalten von Potenzreihen Sei P x := c k (x x ) k. (a) P x konvergiert sicher für x = x. (b) Satz 4.1 Ist c k (x x ) k konvergent für ein x 1 x, so konvergiert die Reihe absolut für alle x {x : x x < x 1 x }. Ist hingegen c k (x x ) k divergent für ein x = x 2, so divergiert sie auch für alle x {x : x x > x 2 x }. 41
42 4. Potenzreihen Beweis: Folgerung: i) P x sei konvergent für ein x 1 x und x x < x 1 x = c k (x x ) k = c k (x 1 x ) k k x x x 1 x = c k (x 1 x ) k q k }{{} q c k (x 1 x ) k konvergent = ( c k (x 1 x ) k) ist N.F. = ck (x 1 x ) k C k =, 1,..., mit einem festen C. x x < x 1 x = q < 1 = Cq k ist konvergente Majorante von c k (x x ) k Satz 2.13 = x 1 x ii) x x > x 2 x, c k (x x ) k ist absolut konvergent für x x < c k (x 2 x ) k divergent Annahme: P x konvergiert für ein x mit x x > x 2 x a) = P x2 ist konvergent = Widerspruch = P x divergent für alle x mit x x > x 2 x Satz 4.2 Zu jeder Potenzreihe oder aber das Zeichen +, so dass i) P x ist konvergent für x = x ist divergent, wenn x x }, falls r = P x ist absolut konvergent für alle x mit x x < r ii),falls r > ist divergent für alle x mit x x > r c k (x x ) k gibt es genau eine Zahl r 42
43 4.2. Berechnung des Konvergenzradius r iii) P x ist absolut konvergent für alle x R, wenn r = + Die Zahl r oder das Zeichen r = + heißt Konvergenzradius der Potenzreihe Berechnung des Konvergenzradius r Satz 4.3. (a) Existiert der Grenzwert µ = lim k c k, so ist r = 1, wenn µ >, r = k µ +, wenn µ =, r =, wenn µ = (bestimmte Divergenz), also r = lim k 1 k ck (b) Existiert der Grenzwert ν = lim c k+1 k c k, so ist Beweis: also r = +, wenn ν = r = 1 lim c k+1 c k k (a) W.K. für c k (x x ) k = P x = a k Man betrachte: k ck (x x ) k = k c k x x = W = x x lim k k c k = µ x x µ = = W = x x = für alle x R = P x konvergiert überall absolut = r = + = 1 µ µ > = P x konvergiert absolut, wenn µ x x = W < 1 43
44 4. Potenzreihen x x < 1 µ P x divergiert, wenn µ x x > 1 r = 1 µ x x > 1 µ µ = + = W = +, wenn x x, W =, x = x = r = (b) Q.K. für P x = c k (x x ) k Man betrachte: c k+1 (x x ) k+1 c k (x x ) k = c k+1 c k x x = Q = x x lim c k+1 k c k Rest wie oben! Bemerkung: Die allgemeinste Formel für den Konvergenzradius r lautet r = 1 lim sup k c k k Beispiele: x k k! = c k = 1 k! c k+1 c k = 1 k + 1 k=1 c k+1 c k = x k k = c k = 1 k, k = ν = = r = + k k + 1 1, k = ν = 1 = r = 1 ν = 1 44
45 4.3. Eigenschaften von Potenzreihen = absolute Konvergenz im offenen Intervall I = ( 1, +1) x = 1= k=1 x = +1= k=1 ( 1) k 1 k k konvergiert divergiert = Am Rande des Konvergenzintervalls x r < x < x + r kann P x sowohl konvergent als auch divergent sein. Achtung: Satz 4.3 liefert über das Konvergenzverhalten in keine Aussage! x = x ± r 3. x k k p für ein festes p > = c k = 1 k p ck = (k p ) 1 k = (k 1 k k ) p 1 p = 1, k = µ = 1 = r = 1 µ = 1 für alle p > x = ±1 = (±1) k k p konvergiert für p > Eigenschaften von Potenzreihen Satz 4.4 ( Gleichmäßige Konvergenz) Eine Potenzreihe konvergiert in jedem abgeschlossenen Teilintervall ihres Konvergenzintervalls (x r, x + r) absolut und gleichmäßig. Beweis: Man betrachte ein Intervall I ϱ = [x ϱ, x + ϱ] für ein < ϱ < r. x = x + ϱ = c k ((x + ϱ) x }{{} ) k konvergiert absolut. ϱ Sei nun x x ϱ 45
46 4. Potenzreihen = ck (x x ) k = ck x x k c k ϱ k }{{} k-tes Glied einer konvergenten Reihe Satz 3.1 = c k (x x ) k konvergiert gleichmäßig in I ϱ. = c k (x x ) k konvergiert in jedem abgeschlossenen Teilintervall von (x r, x + r) gleichmäßig. Folgerungen aus 3: Satz 3.2 = Satz 4.5 Die Summenfunktion s(x) einer Potenzreihe c k (x x ) k ist im ganzen Konvergenzintervall (x r, x + r) stetig. Beweis: f k (x) = c k (x x ) k ist stetig für jedes k. Satz 4.4 Satz 3.3 = Satz 4.6 Eine Potenzreihe c k (x x ) k darf über jedes abgeschlossenes Intervall [a, b] mit x r < a, b < x + r gliedweise integriert werden. Es gilt also b a s(x)dx = = b a ( c k (x x ) k ) dx = c k b a (x x ) k dx c k ( (b x ) k+1 (a x ) k+1) für alle x r < a, b < x + r k
47 4.3. Eigenschaften von Potenzreihen Bemerkung: Auch mit Hilfe der obigen Sätze beweist man, dass die Reihe auf der rechten Seite von = absolut konvergiert. c k k + 1 (x x ) k+1 = x x } k {{ + 1 } beschränkt c k (x x ) k }{{} konvergiert für x r < x < x + r = mindestens gleicher Konvergenzradius! Beispiel: x k = 1 1 x für 1 < x < +1, x =, r = 1 a =, b = x, x < 1 x x 1 dx = ln (1 x) 1 x x ( ) = x k dx = Satz 3.4 = = = ln (1 x) = ln x x k dx 1 1 x x k+1 k + 1 = x + x2 2 + x = ln 1 1 x für alle x < 1 Satz 4.7 Sei c k (x x ) k eine Potenzreihe mit Konvergenzradius r. Die durch gliedweise Differentiation entstehende Reihe absolut konvergent im Intervall (x r, x + r), und es gilt kc k (x x ) k 1 ist ebenfalls k=1 ( c k (x x ) k ) = kc k (x x ) k 1 für alle x x < r k=1 Beweis: Man betrachte ein x mit x x < r 47
48 4. Potenzreihen = Es existiert ein x 1 mit x x < x 1 x < r = c k (x 1 x ) ist absolut konvergent. Man betrachte die Reihe k=1 kc k (x x ) k 1 i) x = x = Konvergenz (absolute) ii) x x = kc k (x x ) k 1 = 1 x x kc k (x x ) k c k (x 1 x ) k = 1 c k (x 1 x ) k kc k(x x ) k x x c k (x 1 x ) k = kck (x x ) k 1 1 = ck (x 1 x ) k x x k x x x 1 x konvergent = ck (x 1 x ) k C für alle k = kck (x x ) k 1 C x x }{{} kqk mit q = x x x 1 x, < q < 1 α k k α k+1 α k = (k + 1)qk+1 = k + 1 q q, k kq k k kq k ist konvergent! Satz 2.13 = kc k (x x ) k 1 ist absolut konvergent für alle x x < r Satz 3.4, Satz 4.4 = ( c k (x x ) k ) = kc k (x x ) k 1, x x < r }{{} Potenzreihe, die im Intervall x x < r konvergiert 48
49 4.3. Eigenschaften von Potenzreihen Satz 4.7 = Satz 4.8 In ihrem Konvergenzintervall (x r, x + r) ist eine Potenzreihe c k (x x ) k beliebig oft differenzierbar. Die Ableitungen s (k) (x) der Summenfunktion s(x) erhält man durch gliedweise Differentiation. Also gilt in x r < x < x + r s(x) = c + c 1 (x x )+ c 2 (x x ) 2 + c 3 (x x ) c k (x x ) k +... s (x) = c 1 + 2c 2 (x x )+ 3c 3 (x x ) kc k (x x ) k s (x) = 2c c 3 (x x )+...+k(k 1)c k (x x ) k s (x) = 3 2c c 4 (x x ) +... = s (j) (x) = k=j c k k(k 1)... (k j + 1)(x x ) k j = s (j) (x ) = c j j(j 1)(j 2) = c j j! = j!c j Beispiel: 1 1 x =1+ x+ x2 + x x k +..., x < 1 (1 x) 2 = ( ) 1 = 1+ 2x+3x kx k , x < 1 1 x 2(1 x) 3 = = ( ) 1 = 2+ 6x+... +k(k 1)x k , x < 1 1 x 1 (1 x) = 1 ( ) (n) 1 = n+1 n! 1 x ( ) n + j x j, x < 1 n j= 49
50 4. Potenzreihen 4.4. Identitätssatz für Potenzreihen Satz 4.9 Gegeben seien zwei Potenzreihen c k (x x ) k und d k (x x ) k, die im Intervall x ϱ < x < x + ϱ konvergieren und dort die gleiche Summenfunktion haben. Dann gilt c k = d k für alle k =, 1, 2,..., d.h. die beiden Reihen sind identisch. Beweis: Voraussetzung: c k (x x ) k = d k (x x ) k für alle x x < ϱ x = x = c = d = k=1 Differentiation= k=1 c k (x x ) k = d k (x x ) k, x x < ρ k=1 c k k(x x ) k 1 = d k k(x x ) k 1 für x x < ϱ k=1 x = x = c 1 = d 1 Vollständige Induktion = c k = d k für alle k =, 1, 2, Rechnen mit Potenzreihen Addition, Subtraktion, λ-faches Gegeben: c k (x x ) k Konvergenzradius r 1 d k (x x ) k Konvergenzradius r 2 5
51 4.5. Rechnen mit Potenzreihen Satz 4.1 Für alle x mit x x < r = min {r1, r2} gilt (a) (b) λ Beispiel: c k (x x ) k ± c k (x x ) k = d k (x x ) k = λc k (x x ) k (c k ± d k )(x x ) k für alle λ R sin x = x x3 3! + x5 5! x (siehe Kapitel 5), r = + 7! λ = x = sin x x = 1 x2 3! + x4 5! x6 7! +... (gerade) Multiplikation c k (x x ) k Konvergenzradius r 1 d k (x x ) k Konvergenzradius r 2 r = min {r 1, r 2 } Satz 2.17 (Cauchysche Produktreihe) = Satz 4.11 Für alle x mit x x < r gilt ( ) ( ) c k (x x ) k d k (x x ) k = Beispiel: ( k j= c j d k j ) (x x ) k x = e x = 1 + x + x2 2! + x3 3! +..., r 1 = x = 1 + x + x2 + x , r 2 = 1 r = 1 51
52 4. Potenzreihen e x 1 x = = ( k ) c j d k j x k mit c j = 1 j!, d k j = 1 j= ( ! + 1 2! ) x k k! = 1 + 2x x x Division Ohne Beweis geben wir den folgenden Satz 4.12 Eine Potenzreihe c k (x x ) k mit Konvergenzradius r habe die Summe s(x), und es sei c. Dann gibt es ein ρ > und eine Potenzreihe d k (x x ) k, so dass 1 s(x) = d k (x x ) k für alle x x < ρ. Bestimmung der Koeffizienten d k : Sei x x < min {r, ϱ} = r 52
53 4.5. Rechnen mit Potenzreihen 1 s(x) = d k (x x ) k, x x < r 1 = s(x) Satz 4.11 }{{} = d k (x x ) k = ( c k (x x ) k ) ( ( k ) c j d k j (x x ) k für alle x x < r j= d k (x x ) k ) = 1 = α k (x x ) k mit α = 1, α k =, k 1 Satz 4.9 (Identitätssatz) = k c j d k j = α k, k =, 1, 2,..., α = 1, α 1 = α 2 =... = j= = k = : c d = α = 1 = d = 1 c k = 1 : c d 1 + c 1 d = α 1 = = d 1 = c 1 c 2 k = 2 : c d 2 + c 1 d 1 + c 2 d = = d 2 = c 1 2 c c 2 c 3 usw. Analog stellt man den Quotienten zweier Potenzreihen b k (x x ) k c k (x x ) k 53
54 4. Potenzreihen wieder als Potenzreihe dar! Beispiel: 1 + x + x , x < 1, x =, r = 1, s(x) = 1 1 x = c k = 1, k =, 1,... 1 x = 1 s(x) = d + d 1 x + d 2 x 2 + d 3 x d = 1 c = 1 d 1 = c 1 c 2 = 1 d 2 = c 1 2 c c 2 c 3 = usw. 54
55 5. Taylorreihen Aus Satz 4.8 folgt: Die Summenfunktion s(x) einer Potenzreihe ist im Konvergenzintervall beliebig oft differenzierbar, und es ist s (k) (x ) k! = c k, k =, 1,.... Problem: Lässt sich umgekehrt eine oft differenzierbare Funktion durch eine Potenzreihe darstellen? Geg.: Offenes Intervall I; Funktion f, die unendlich oft differenzierbar ist; x (fest) I. Definition 5.1 (Taylorreihe) Unter der Taylorreihe von f mit Entwicklungspunkt x I versteht man die Potenzreihe f (k) (x ) T (x) := (x x ) k k! = f(x ) + f (x ) 1! (x x ) + f (x ) (x x ) ! Aus Satz 4.2 folgt: Als Potenzreihe konvergiert T (x) in einem Intervall (x r, x + r). Problem: Zusammenhang zwischen T (x) und f(x), d.h. wo gilt T (x) = f(x)? Bemerkung: Sicher ist T (x) = f(x) für x = x. Betrachte das n-te Taylorpolynom: also T n (x) = T (x) = f(x ) n T 1 (x) = f(x ) + f (x )(x x ) f (k) (x ) (x x ) k, k! T 2 (x) = f(x ) + f (x )(x x ) + f (x ) (x x ) 2 2!. 55
56 5. Taylorreihen Satz 5.1 (Satz von Taylor) Ist f auf dem offenen Intervall I mindestens n + 1 mal differenzierbar und x I eine feste Zahl, dann gilt f(x) = T n (x) + R n (x) für alle x I (Taylorformel) mit und T n (x) = n f (k) (x ) (x x ) k (n-tes Taylorpolynom) k! R n (x) = (x x ) n+1 f (n+1) (x + ϑ(x x )) (Restglied nach Lagrange), (n + 1)! wobei ϑ = ϑ(x, x ) zwischen und 1 liegt. Beweis: M.W.S. Bemerkung: Andere Restgliedformen: (a) R n (x) = (x x ) n+1 (1 n! ϑ) n f (n+1) (x + ϑ(x x )), < ϑ < 1 (Cauchy-Form) x (b) R n (x) = 1 f (n+1) (t)(x t) n dt (Integralform) n! x Anwendung der Taylorformel: Voraussetzung: f sei oft differenzierbar auf dem offenen Intervall I. In diesem Fall gilt die Taylorformel für alle n =, 1, 2,..., d.h., es ist f(x) = T n (x) + R n (x), x I, für alle n =, 1, 2,.... Satz 5.2 Sei x I. Genau dann ist T (x) konvergent und T (x) = f(x), wenn lim n R n(x) =. = Die Entwicklung einer Funktion f(x) in eine Taylorreihe T (x) erfordert somit die Untersuchung, ob das Restglied R n (x) für n gegen Null konvergiert. 56
57 5.1. Praktische Bedeutung der Taylorentwicklung 5.1. Praktische Bedeutung der Taylorentwicklung Voraussetzung: Für alle x I sei (R n (x)) eine Nullfolge. Aus Satz 5.2 folgt: Für alle x I ist f(x) = T (x) = f(x ) + f (x )(x x ) + f (x ) (x x ) = lim T n (x). 2! n Daraus folgt: (a) f(x) T n (x) = n f (k) (x ) (x x ) k, x I, für hinreichend großes n k! = Approximation von f durch ein Näherungspolynom, das Taylorpolynom T n (b) Approximationsfehler: e = e f (x, n) (Absolutfehler) e = f(x) T n (x) = R n (x) }{{} Restglied Kriterium für die Konvergenz des Lagrangeschen Restgliedes gegen Null: R n (x) = f (n+1) (ξ) (n + 1)! (x x ) (n+1), ξ zwischen x und x, ξ = x + ϑ(x x ), < ϑ < 1 = x x n+1 f (n+1) (ξ) (n + 1)! Falls f (n+1) (ξ) C(x, x ) < + für alle ξ zwischen x und x, n =, 1, 2,... so folgt: R n (x) C x x n+1, n. (n + 1)! Satz 5.3 Falls f (n+1) (ξ) C für alle ξ zwischen x und x und n = 1, 2,..., dann gilt R n (x), n und damit f(x) = lim n T n (x), also T (x) = f(x). 57
58 5. Taylorreihen 5.2. Taylorentwicklung einiger Funktionen (a) f(x) = e x, x = f (k) (x) = e x, k =, 1,... f (k) (x ) = 1, k =, 1,... Daraus folgt: T (x) = = f (k) (x ) (x x ) k k! x k k! Taylorreihe ist überall konvergent (Q.K.)! Restglied: R n (x) = f (n+1) (x + ϑ(x x )) (x x ) (n+1) (Lagrange) (n + 1)! e ϑx = (n + 1)! xn+1 Wegen ϑx ϑ x x folgt: R n (x) e x x n+1 (n + 1)! }{{} Nullfolge Daraus folgt: ( ) x k x k konvergiert nach dem Q.K. absolut = k! k! muss eine Nullfolge sein! Aus Satz 5.2 folgt für alle x I = R: e x = T (x) = 1 + x + x2 2! + x3 3! + + xk k! + 58
59 5.2. Taylorentwicklung einiger Funktionen Aus Kapitel 5.1 folgt: e x 1 + x + x2 2! + + xn mit dem absoluten Fehler n! e f (x, n) e x x n+1 (n + 1)!. (b) f(x) = sin x, x = f (2ν) () =, ν =, 1, 2,... f (2ν+1) () = ( 1) ν, ν =, 1, 2,... Daraus folgt: T (x) = x x3 3! + x5 5! x7 7! ± + ( 1)k x 2k+1 (2k + 1)! +. Taylorreihe ist überall konvergent (Q.K.)! Restglied: R n (x) = f (n+1) (ξ) (n + 1)! (x x ) n+1 (Lagrange) = sin(n+1) (ξ) x n+1. (n + 1)! Daraus folgt: da sin (n+1) (ξ) 1. Aus Satz 5.2 folgt: R n (x) x n+1, (n + 1)! }{{} N.F. sin x = T (x) = x x3 3! + x5 5! x7 7! ±... für alle x I = R. Aus Kapitel 5.1 folgt: sin x x x3 3! + x5 5! x7 7! ± + x 2k+1 ( 1)k (2k + 1)! mit dem absoluten Fehler e f (x, n) x 2k+2 (2k + 2)!. 59
60 5. Taylorreihen (c) f(x) = cos x, x = Analog zu f(x) = sin x ergibt sich für alle x I = R: cos x = 1 x2 2! + x4 4! x6 x2k ± + ( 1)k 6! (2k)! +... mit dem absoluten Fehler cos x 1 x2 2! + x4 4! x6 x2k ± + ( 1)k 6! (2k)! e f (x, n) x 2k+1 (2k + 1)! (d) f(x) = ln(1 + x), x > 1, x = f (k) k 1 (k 1)! (x) = ( 1), k = 1, 2,... (1 + x) k f (k) (x ) = ( 1) k 1 (k 1)!, k = 1, 2,... f () (x ) = Daraus folgt: T (x) = = k=1 ( 1) k 1 (k 1)! x k k! ( 1) k 1 k=1 k x k = x x2 2 + x3 3 x ( 1)k 1 x k + k 6
61 5.2. Taylorentwicklung einiger Funktionen Restglied: R n (x) = f (n+1) (ϑx) x n+1 mit < ϑ < 1 (Lagrange) (n + 1)! = = ( 1) n n! (1 + ϑx) n+1 x n+1 (n + 1)! ( 1) n (1 + ϑx) n+1 x n+1 n + 1 Konvergenzradius r der Taylorreihe (Satz 4.3): ( r = lim c k+1 1 ( ) 1 k k c k ) = lim = 1 k k + 1 Daraus folgt: Taylorreihe für ln(1 + x) konvergiert für x < 1, divergiert für x > 1. Gilt T (x) = ln(1 + x) für x < 1? i) Intervall x < 1: Lagrange-Form des Restgliedes: R n (x) = ( 1) n xn+1 (1 + ϑx) n+1 n + 1, < ϑ < 1. Für x 1 ist 1 + ϑx 1 und daher R n (x) 1 n + 1 Aus Satz 5.2 folgt für alle x < 1:, n. ln(1 + x) = x x2 2 + x3 3 x4 4 + x Da aber (R n (1)) ebenfalls eine Nullfolge ist, erhält man aus Satz 5.2 die Konvergenz von T (x) und T (x) = f(x) auch noch im rechten Randpunkt x = +1 des Konvergenzintervalls ] 1, +1[ von T (x). Es gilt also ln 2 =
62 5. Taylorreihen ii) Intervall 1 < x < : Hier ist die Lagrange-Form des Restgliedes ungeeignet. Cauchysche Form des Restgliedes: R n (x) = xn+1 (1 n! ϑ) n f (n+1) ( ϑx) mit < ϑ < 1 R n (x) = Ferner gilt: Also 1 < x < < ϑ < 1 (1 n! ϑ) n ( 1) n n! (1 + ϑx) = ( 1)n (1 ϑ) n n+1 (1 + ϑx) n+1 xn+1, ( 1 ϑ ) n ϑx xn ϑx. = xn+1 = < 1 ϑ < 1 + ϑx 1 + ϑx > 1 + x > = R n (x) x x n+1, für n. < 1 ϑ 1 + ϑx < ϑx < x Aus Satz 5.2 folgt: ln(1 + x) = x x2 2 + x3 3 x4 ±... für 1 < x < 4 und somit ( 1) k 1 ln(1 + x) = x k 1 < x +1. k k=1 k=1 Bemerkung: T (x) divergiert für x = 1 ( 1) k 1 ( 1) k 1 T ( 1) = = k k k=1 (e) f(x) = (1 + x) α, x > 1, α R beliebig, x = harmonische Reihe. f (k) (x) = α(α 1)... (α k + 1) (1 + x) α k, k = 1, 2,... f (k) () = α(α 1)... (α k + 1), k = 1, 2,... f() = 1 62
63 5.2. Taylorentwicklung einiger Funktionen Daraus folgt: T (x) = f (k) (x ) (x x ) k = k! ( ) ( ) α α x + x = 1 + Lagrange-Restglied: ( α k ) x ( α 3 ) x k Binomische Reihe ( ) α x k +... k R n (x) = f (n+1) (ξ) (n + 1)! (x x ) n+1 α(α 1)... (α n) = (1 + ϑx) α n 1 x n+1 (n + 1)! ( ) α = (1 + ϑx) α n 1 x n+1, < ϑ < 1 n + 1 Cauchy-Restglied: R n (x) = xn+1 (1 n! ϑ) n f (n+1) ( ϑx) ( ) α = (n + 1) (1 n + 1 ϑ) n (1 + ϑx) α n 1 x n+1, < ϑ < 1 Konvergenz der Taylorreihe: ( ) α c k = k c k+1 c k = α(α 1)(α 2)... (α k) k (k + 1) α(α 1)... (α k + 1) = α k k + 1 1, für k Aus Satz 4.3 folgt: Konvergenzradius r = 1, d.h. T (x) = ( ) α x k k konvergiert für x < 1 divergiert für x > 1 Gilt T (x) = (1 + x) α für alle x < 1? 63
64 5. Taylorreihen i) Intervall x < 1: Es gilt 1 + ϑx 1, da < ϑ < 1. Falls nun n > α 1 ( > α n 1 (α ist fest!)) gilt (1 + ϑx) α n 1 = 1 1. (1 + ϑx) n+1 α Lagrange-Restgliedform: ( ) ( ) R n (x) = α x (1+ϑx) n+1 α n 1 α n + 1 x n+1 für n > α 1. n + 1 ( ) α Dabei ist x n+1 das (n + 1)-te Glied der Taylorreihe T (x) von n + 1 (1 + x) α. ( ) α Also konvergiert T (x) für x < 1 = x n+1, für n. n + 1 ii) Intervall 1 < x < : Cauchy-Restglied: ( ) α R n (x) = (n + 1) (1 n + 1 ϑ) n (1 + ϑx) α n 1 x n+1, < ϑ < 1 ( ) α = (n + 1) ( 1 ϑ n ϑx )n (1 + ϑx) α 1 x n+1 Ferner gilt 1 < x < = < 1 ϑ < 1, 1 + ϑx < ϑ < 1 (1 + ϑx) 1 < (1 + x) 1. Daraus folgt: ( ) R n (x) α (n + 1) (1 + n + 1 ϑx) α 1 x n+1. Sei α 1( 1 α ). Dann gilt: ϑx < x = 1 (1 + ϑx) < 1 1 α (1 + x) = (1+ ϑx) α 1 < (1+x) α 1 1 α 64
65 5.2. Taylorentwicklung einiger Funktionen Für α 1( α 1 ) hingegen gilt: α 1 (1 + ϑx) 1. }{{} <1 = (1 + ϑx) α 1 max {1, (1 + x) α 1 } =: γ(x) ( ) = R n (x) γ(x) α (n + 1) x n+1 n + 1 ( ) α Behauptung: a n+1 = (n + 1) x n+1 ist eine Nullfolge. n + 1 Beweis: a n+1 α(α 1)(α 2)... (α n) = (n + 1) a n (n + 1) = α n x n = a n+1 a n x < 1 für n. Aus dem Quotientenkriterium folgt: x n+1 a k ist konvergent n n α(α 1)... (α n + 1) x n = a k für k = R n (x) für n und für 1 < x <. Aus i), ii) folgt schließlich: (1 + x) α = ( ) α x k für alle x < 1 und jedes α R. k Beispiel: x = (1+x) 1 2 = ( ) 1 2 x k = 1 1 k 2 x x x3 + Bemerkung: Taylorentwicklung von f(x) außerhalb x x < r: (a) Entwicklung von ln z, z = 1 + x, im Intervall (, 2]: ln(1 + x) = ( 1) k 1 x k, 1 < x 1, x =. (5.1) k k=1 65
66 5. Taylorreihen Betrachte nun a > beliebig und f(x) = ln(a + x), a + x > ( ( ln(a + x) = ln a 1 + x )) ( = ln a + ln 1 + x ). a a Aus (5.1) folgt somit: ln(a + x) = ( 1) k 1 ( x ) k x ln a +, 1 < k a a 1 k=1 = ( 1) k 1 ln a + x k, a < x +a. k a k }{{} f() k=1 }{{} f (k) () k! = Taylorentwicklung von f(x) = ln(a+x) in x = konvergiert im Intervall a < x +a. = Entwicklung von ln z im Intervall (, 2a] für beliebiges a >. (b) Entwicklung von z α, z = 1 + x, im Intervall (, 2): (1 + x) α = Betrachte nun a > beliebig und (a + x) α = a α ( 1 + x a) α = aα = a α a k ( ) α x k, x < 1, α R, x =. k ( ) α x k = k ( α k ( α a α k k ) (x ) k a ) x k, x a < 1. = Taylorentwicklung von f(x) = (a+x) α in x = konvergiert im Intervall a < x < +a. = Entwicklung von z α im Intervall (, 2a) für beliebiges a >. 66
67 Teil II. Differentialrechnung im R n 67
68
69 6. Definition, Beispiele Definition 6.1 (Funktion) Sei D R n eine Teilmenge des R n. Eine Funktion von n (unabhängigen) Variablen x 1,..., x n ist eine Abbildung f : D R, die jedem Vektor x D 1-deutig eine Zahl z = f(x) = f(x 1, x 2,..., x n ) zuordnet; D ist dann der (Mindest-) Definitionsbereich von f., BN O O N N 4 Bemerkung: (a) Statt f(x 1, x 2 ) schreibt man oft z = f(x, y) für n = 2. (b) Statt f(x 1, x 2, x 3 ) schreibt man oft w = f(x, y, z) für n = 3. Beispiele: (a) Gleichung eines idealen Gases p = p(t, V ) = R T V, V > } mit D = {(T, V ) : T (b) Volumen eines Quaders V = V (x, y, z) = xyz, D = {x R 3 : x, y, z } (c) Ohmsches Gesetz I = I(U, R) = U R mit U = Spannung, R = Widerstand 69
70 6. Definition, Beispiele 6.1. Graphische Darstellung von Funktionen 2er Variabler Entsprechende Graphik-Software (2D, 3D) ist heute für alle Arten von Rechnern verfügbar. (a) (Perspektivische) Darstellung der Fläche Φ einer Funktion f = f(x, y): Φ = {(x, y, z) : z = f(x, y)} Beispiel: D = {(x, y) : x, y 1}, f(x, y) = x + 2y + 1 Stück einer Ebene (b) Karte einer Funktion f = f(x, y): Definition 6.2 (Karte) Unter der Karte von f versteht man die Menge aller Niveaulinien von f, d.h. die Menge aller Kurven y = y(x; C), so dass f(x, y) C mit beliebigem C R. Beispiel: 6 y 4 xy = 1 xy = 4 xy = 8 i) f(x, y) = x y, x, y R Sei x y = C. C = f = f(x; y = C x ) C = = x = oder y = ii) f(x, y) = x α y 1 α, x, y iii) f(x, y) = x + y x y 2 x Praktische Anwendung: } Höhenlinien {{}, Isobaren, Isothermen }{{} Landkarten Wetterkarten 7
71 7. Grenzwerte von Funktionen mehrerer Variabler Definition 7.1 (Grenzwert) Die Zahl G heißt Grenzwert von f in a R n, wenn zu jedem, auch beliebig kleinen ε >, eine Zahl δ = δ(ε) > existiert, so dass f(x 1,..., x n ) G < ε, falls x D \ {a} und Man schreibt dann x k a k < δ(ɛ) für alle 1 k n. (7.1) G = lim x a oder f(x) G für x a. 4 = N = = N N 7 / A BN / / A Abbildung 7.1.: Grenzwertbegriff im R 2 71
72 7. Grenzwerte von Funktionen mehrerer Variabler Bemerkung: (a) Geometrische Interpretation für n = 2: (7.1) x a liegt im offenen Rechteck U δ (a) = {(x 1, x 2 ) : x i a i < δ, i = 1, 2} (U δ (a): offene δ-umgebung von a). Daraus folgt: Zu jedem ε > existiert eine Umgebung U δ (a) mit δ = δ(ε) >, so dass für x U δ (a) \ {a} folgt f(x) U ε (G) =]G ε, G + ε[ (vgl. Abb. 7.1). (b) Äquivalente Grenzwertdefinition: Definition 7.2 (Konvergenz einer Punktfolge) Sei x j = (x 1j, x 2j,..., x nj ), j = 1, 2,.... Die Folge (x j ) heißt konvergent gegen den Punkt a R n, in Zeichen lim x j = a, wenn lim x j a =, d.h. wenn lim x kj = a k für j j j alle k = 1,..., n. Beispiel: x j = ( (3 + 5j2, 1, ) ) j lim x j j = a = (3, 1, e) j Satz 7.1 Es gilt lim f(x) = G genau dann, wenn lim f(x j ) = G für jede Punktfolge (x j ) in D \ {a}, so dass lim x j = a. x a j j Beispiele: (a) f(x, y) = x 2 + y 2, a = (a, b) R 2 beliebig x j = (x j, y j ) (a, b), j x j a y j b, j = x j 2 a 2, y j 2 b, j = lim f(x, y) = a 2 + b 2 = f(a, b) (x,y) (a,b) (b) f(x, y) = (x 1)2 (y 3) 2 (x 1) 2 + (y 3), lim f(x, y) =? 2 (x,y) (1,3) f(x, y) ((x 1)2 + (y 3) 2 ) 2 (x 1) 2 + (y 3) 2 = (x 1) 2 + (y 3) 2 für (x, y) (1, 3) = lim f(x, y) = (x,y) (1,3) 72
73 (c) f(x, y) = xy x 2 + y, lim f(x, y) existiert nicht! 2 (x,y) Man betrachte den Strahl: (x, y) = r(cos ϕ, sin ϕ), r, ϕ fest = f(x, y) = r2 cos ϕ sin ϕ = cos ϕ sin ϕ für alle r r 2 = lim (x,y) f(x, y) = cos ϕ sin ϕ hängt vom Strahl S ϕ ab Stetigkeit = lim f(x, y) existiert nicht, denn sonst wäre lim f(x) = cos ϕ sin ϕ für (x,y) x alle ϕ, was bestimmt falsch ist! Satz 7.2 (Grenzwertsätze) Existieren die Grenzwerte lim f(x) und lim g(x) zweier Funktionen f, g in a, dann gilt x a x a auch lim(f(x) ± g(x)) = lim f(x) ± lim g(x), x a x a x a lim c f(x) = c lim f(x) für alle c R, x a x a lim f(x)g(x) = lim f(x) lim g(x), x a x a x a f(x) lim x a g(x) = lim f(x) x a lim x a g(x), falls lim x a g(x) Stetigkeit Definition 7.3 (Stetigkeit) Die Funktion f : D R, D R n, heißt stetig in x D, wenn lim x x f(x) = f(x ). Beispiel: f(x, y) = xy, (x, y) x 2 + y2, (x, y) = f ist stetig in jedem x f ist unstetig in x (lim x a f(x) existiert nicht!) 73
74 7. Grenzwerte von Funktionen mehrerer Variabler Satz 7.3 Ist f stetig in x und gilt f(x ) > bzw. f(x ) <, dann gibt es eine δ Umgebung U δ (x ) von x, δ >, so daß f(x) > bzw. f(x) < für alle x U δ (x ). Satz 7.4 Seien f, g stetig in x. Dann sind auch f ± g, f g stetig in x, sowie f g, falls g(x ). Satz 7.5 Die Funktion f sei auf einer Menge M R n definiert. M sei kompakt, d.h. M sei abgeschlossen (jeder Randpunkt von M gehört zu M) und beschränkt (es gibt eine Konstante C >, so daß x C für alle x M). Ist f stetig auf M, dann besitzt f auf M ein absolutes Maximum und ein absolutes Minimum, d.h. es gibt Punkte a, b M, so daß f(a) f(x) f(b) für alle x M. Definition 7.4 (Gebiet) Eine Menge G R n heißt Gebiet, wenn (a) x G = U δ (x) G für ein δ = δ(x) > und (b) je zwei Punkte von G lassen sich durch einen Streckenzug mit nur endlich vielen Ecken verbinden. Satz 7.6 (Zwischenwertsatz) Die Funktion f(x) sei auf einem Gebiet G definiert. Ferner sei f stetig auf G, und es gelte f(a) < für ein a G und f(b) > für ein b G. Dann gibt es ein x G, so daß f(x ) =. Beispiele: (a) n = 1: f(x) = x 2 sin 1 x, x, x = f (x) = 2x sin 1 cos x, x x, x = überall differenzierbar. Aber: lim x f (x) existiert nicht = f nicht stetig in x =. 74
75 7.1. Stetigkeit (b) n = 2: f(x, y) = y x 2 sin 1 x, x x = = f x existiert, ist aber nicht stetig in (, y). (c) n = 2: f(x, y) = xy x 2 + y 2, x, x = f x, f y existieren überall, f ist aber nicht stetig in x =. 75
76 7. Grenzwerte von Funktionen mehrerer Variabler 76
77 8. Partielle Ableitungen 8.1. Partielle Ableitungen 1.Ordnung Partielle Ableitungen im R 2 Definition 8.1 (partielle Ableitung) (a) Die partielle Ableitung f x (x, y ) von f = f(x, y) nach x im Punkt (x, y ) ist definiert durch f x (x f(x + h, y ) f(x, y ), y ) = lim h h f(x, y ) f(x, y ) = lim x x x x Statt f x (x, y ) schreibt man auch f x (x, y ). (b) Die partielle Ableitung f y (x, y ) von f = f(x, y) nach y im Punkt (x, y ) ist definiert durch f y (x f(x, y + k) f(x, y ), y ) = lim k k f(x, y) f(x, y ) = lim. y y y y Statt f y (x, y ) schreibt man auch f y (x, y ). Bemerkung: (a) f x = f x (x, y), f y = f (x, y) sind wieder Funktionen 2er Variabler x und y y. 77
78 8. Partielle Ableitungen (b) Praktische Berechnung von f x, f y : Betrachte die Schnittfunktionen f 1 (x) = f(x, y ) Schnitt von z = f(x, y) mit der Ebene y = y, f 2 (y) = f(x, y) Schnitt von z = f(x, y) mit der Ebene x = x. Nach Definition 8.1a gilt dann f x (x, y ) = f 1(x ) = f erhält man durch Differentiation von f nach x bei festem y. x Mit Definition 8.1b folgt f y (x, y ) = f 2(y ) = f erhält man durch Differentiation von f nach y bei festem x. y (c) Geometrische Deutung der partiellen Ableitungen (siehe Abb. 8.1): i) f x (x, y ) = f 1(x ): Steigung der Tangente an die Schnittkurve z = f 1 (x) := f(x, y ) der Fläche Φ(z = f(x, y)) mit der Ebene y = y im Punkt (x, y, z ), z = f(x, y ). ii) f y (x, y ) = f 2(y ): Steigung der Tangente an die Schnittkurve z = f 2 (y) := f(x, y) der Fläche Φ mit der Ebene x = x im Punkt (x, y, z ). Gleichung der Tangentialebene: z = z + f x (x, y )(x x ) + f y (x, y )(y y ) mit z = f(x, y ). 78
79 8.1. Partielle Ableitungen 1.Ordnung. BN O J B O N 6 O B N BN O - > A A O O N O t 1 =Tangente an f 1 in (x, y, z ) mit Steigung f x (x, y ) t 2 =Tangente an f 2 in (x, y, z ) mit Steigung f y (x, y ) Die beiden Tangenten t 1, t 2 an die Schnittkurven z = f 1 (x) bzw. z = f 2 (y) spannen die Tangentialebene T an die Fläche Φ(z = f(x, y)) im Punkt (x, y, z ) auf. Abbildung 8.1.: Partielle Ableitungen im R 2 J 79
80 8. Partielle Ableitungen Beispiele: (a) p = RT V, R = const. V = RT p p T = R V, p V = RT V 2 V = T = R p, V p = RT p 2 T = 1 T pv = R p = V R, T V = p R (b) f(x, y) = arctan y ( x, (arctan t) = 1 ) 1 + t 2 f x = 1 ( y 1 + x f y = ( y x ) 2 y x 2 = y x 2 + y 2 ) 2 1 x = x x 2 + y 2 p V V T T p Partielle Ableitungen im R n Definition 8.2 (Partielle Ableitung II) Die partielle Ableitung f x k (a) von f = f(x 1, x 2,..., x n ) nach x k im Punkt a ist definiert durch f f(a 1,..., a k 1, a k + h, a k+1,..., a n ) f(a 1,..., a k 1, a k, a k+1,..., a n ) (a) = lim x k h h f(a 1,..., a k 1, x k, a k+1,..., a n ) f(a 1,..., a k 1, a k,..., a n ) = lim x k a k x k a k für k = 1, 2,..., n. Statt f x k schreibt man auch f xk. Bemerkung: Praktische Berechnung von f x k = f xk : (a) f = f (x) sind wieder Funktionen von x = (x 1,..., x n ) x k x k 8
81 8.2. Partielle Ableitungen höherer Ordnung (b) f = f (x) erhält man durch Differentiation von f nach x k bei x k x k festen x 1,..., x k 1, x k+1,..., x n. Beispiele: (a) f(x) = x = n x k2 = f = x k, k = 1, 2,..., n x k x k=1 (b) f(x) = x 2 = n k=1 x k 2 = f x k = 2x k, k = 1, 2,..., n Satz 8.1 (Ableitungsregeln) Seien f = f(x), g = g(x) Funktionen von n Variablen. Dann gilt für alle k = 1, 2,..., n: (f(x) ± g(x)) = f (x) ± g (x), x k x k x k (f(x) g(x)) = g(x) f (x) + f(x) g (x), x k x k x k (cf(x)) = c f (x) für alle c R, x k x k x k ( ) f(x) g(x) = g(x) f x k (x) f(x) g x k (x) [g(x)] 2. Bemerkung: (a) f ist partiell differenzierbar nach x k i.a. f xk stetig. (b) f ist nach allen Variablen partiell differenzierbar i.a. f stetig Partielle Ableitungen höherer Ordnung Für f = f(x, y) sind 81
82 8. Partielle Ableitungen f x = f (x, y) x wieder Funktionen 2er Variablen x, y. f y = f (x, y) y = Für f x, f y lassen sich wieder partielle Ableitungen nach x und y definieren. Definition 8.3 (Partielle Ableitungen 2.Ordnung) 2 f = f x 2 xx := x 2 f y x = f xy := y 2 f x y = f yx := x 2 f y 2 = f yy := y ( ) f x ( ) f x ( ) f y ( ) f y = x f x = y f x = x f y = y f y Bemerkung: Analog werden die partiellen Ableitungen 3., 4.,... Ordnung f xxx, f xxy,..., f xxxx, f xxxy,... definiert. Beispiel: f(x, y) = arctan y x = f x = y x 2 + y, f 2 y = f xx = Hier: f xy = f yx. Dies ist kein Zufall! 2xy (x 2 + y 2 ) 2, f yy = 2xy (x 2 + y 2 ) 2 f xy = y2 x 2 (x 2 + y 2 ) 2, f yx = y2 x 2 (x 2 + y 2 ) 2 x x 2 + y 2 Satz 8.2 (Schwarz) Wenn die partiellen Ableitungen f x, f y, 2 f x y ( vorhanden sind in einer Umgebung U δ (x, y ) von (x, y ) und 2 f x y ( bzw. bzw. ) 2 f y x ) 2 f y x 82
83 stetig ist in (x, y ), dann existiert auch gilt 8.2. Partielle Ableitungen höherer Ordnung 2 f y x ( bzw. 2 f x y (x, y ) = 2 f y x (x, y ). ) 2 f x y in (x, y ), und es 83
84 8. Partielle Ableitungen 84
85 9. Die verallgemeinerte Kettenregel Problem: (a) n = 1: f = f(x), x = x(t), F (t) := f(x(t)) zusammengesetzte Funktion. = F (t) = f (x(t)) x (t) (Kettenregel) (b) n = 2: f = f(x, y) x = x(t) = F (t) = f(x(t), y(t)) zusammengesetzte Funktion. y = y(t) = df dt =? Satz 9.1 (Verallgemeinerte Kettenregel) Die Funktion f = f(x, y) sei definiert auf einem offenen Rechteck a < x < b, c < y < d und besitze dort stetige partielle Ableitungen f x, f y. Für ein Intervall t 1 < t < t 2 gelte ferner a < x(t) < b und c < y(t) < d, wobei x(t), y(t) stetige Funktionen seien. Dann ist F auf t 1 < t < t 2 differenzierbar, und es gilt F (t) = f x (x(t), y(t)) x (t) + f y (x(t), y(t)) y (t), t 1 < t < t 2 oder F (t) = f dx x dt + f dy y dt = f x x + f y y. 85
86 9. Die verallgemeinerte Kettenregel Bemerkung: Verallgemeinerung auf n 2: Mit den gegebenen Funktionen f = f(x 1, x 2,..., x n ), x k = x k (t), t 1 t t 2, k = 1, 2,..., n erhält man die zusammengesetzte Funktion F (t) = f(x 1 (t), x 2 (t),..., x n (t)). In diesem Fall gilt dann: df dt = n k=1 f dx k x k dt = f dx 1 x 1 dt + f dx 2 x 2 dt + + f dx n x n dt Beispiel: Berechnung der Ableitung F (t) von F (t) = (ln t) sin t, t > 1 F (t) = f(x(t), y(t)) mit f(x, y) = x y, x(t) = ln t, y(t) = sin t Verallgemeinerte Kettenregel: F (t) = f x dx dt + f y dy dt = y x y 1 1 t + (ln x)xy cos t = 1 t sin t(ln t)sin t 1 + (ln ln t) (ln t) sin t cos t Satz 9.2 (Erweiterte verallgemeinerte Kettenregel) f = f(x, y), x = x(u, v), y = y(u, v) = F (u, v) = f(x(u, v), y(u, v)). Unter analogen Voraussetzungen wie in Satz 9.1 gilt: Beispiel: F u = f x x u + f y y u, F v = f x x v + f y y v. Gegeben: Punktladungen Q 1 in P 1 (1,, ), Q 2 in P 2 (, 1, ) Gesucht: Feldstärke E in einem beliebigen Raumpunkt x = (x, y, z) 86
87 (a) Potential ϕ der beiden Punktladungen φ = 1 ( Q1 + Q ) 2 4πε r 1 r 2 r 1 = Abstand zwischen P (x) und P = ϕ = ϕ(r 1, r 2 ) 1 r 2 = Abstand zwischen P (x) und P 2 (b) Feldstärke E in x = (x, y, z) ( ) ϕ E = x, ϕ y, ϕ z Aus Satz 9.1 folgt dann: ϕ r 1 = Q 1 4πε r 1 2, ϕ x = ϕ r 1 r 1 x + ϕ r 2 r 2 x ϕ = ϕ r 1 y r 1 y + ϕ r 2 r 2 y ϕ z = ϕ r 1 r 1 z + ϕ r 2 r 2 z ϕ r 2 = Q 2 4πε r 2 2 r 1 = (x 1) 2 + y 2 + z 2, r 2 = x 2 + (y 1) 2 + z 2 r 1 x = x 1 r 2 r 1 x = x r 2 r 1 y = y r 1 r 2 y = y 1 r 2 Daraus folgt usw. r 1 z = z r 1 r 2 z = z r 2 ϕ x = Q 1 4πε r x = 1 4πε Q 2 r 1 4πε r x 2 2 r ) 2 ( x 1 x Q 1 + Q r r
88 9. Die verallgemeinerte Kettenregel 88
89 1. Der Mittelwertsatz für Funktionen mehrerer Variabler Bemerkung: Der Mittelwertsatz (MWS) in R: (a) f(x + h) f(x ) }{{} = f = hf (x + ϑh), < ϑ < 1 hf (x ) = df, wenn h klein = f df, wenn h klein. (b) Statt h schreibt man auch h = x oder h = dx. Problem: Analoge Darstellung von f im R n, n > 1, wie im Fall n = 1. Gegeben sei eine Funktion f = f(x 1, x 2,..., x n ), beliebiger, aber fester Punkt x = (x 1, x 2,..., x n ) und h = (h 1, h 2,..., h n ) R n. Bemerkung: Statt h schreibt man auch h = x = ( x 1, x 2,..., x n ) oder h = dx = (dx 1, dx 2,..., dx n ). Zu untersuchen ist f = f(x 1 + h 1, x 2 + h 2,..., x n + h n ) f(x 1, x 2,..., x n ). Zurückführung des Problems von n > 1 auf n = 1: Sei F (t) := f(x + th) = f(x 1 + th 1, x 2 + th 2,..., x n + th n ). Dann gilt: F () = f(x ) F (1) = f(x + h) f = F (1) F (). 89
90 1. Mittelwertsatz Mit x = x(t) = x + th oder x k = x k (t) = x k + th k, k = 1,..., n, gilt dann nach der verallgemeinerten Kettenregel, Satz 9.1: F (t) = f dx 1 x 1 dt + f dx 2 x 2 dt + + f dx n x n dt = n k=1 f x k (x + th)h k. Die Anwendung des MWS für Funktionen einer Variablen liefert schließlich f = F (1) F () = F ( + ϑ(1 ))(1 ) = F (ϑ) mit < ϑ < 1. Daraus folgt der Satz 1.1 (Verallgemeinerter MWS) Es gibt ein < ϑ < 1, so dass f(x + h) f(x ) = n k=1 f x k (x + ϑh) h k. Definition 1.1 (Gradient) f(x) := grad f (x) := f x 1 (x) f x 2 (x). f x n (x) Bemerkung: Damit lautet der MWS: f = f(x + h) (f(x ) = f(x + ϑh) h =< f(x + ϑh), h >, < ϑ < 1. 9
91 1.1. Folgerungen aus dem MWS 1.1. Folgerungen aus dem MWS Voraussetzung: Die partiellen Ableitungen f x k (x), k = 1, 2,..., n, sind stetig. = f x k (x + ϑh) f x k (x ), wenn h klein. ( alle h k, k = 1,..., n, klein) = f = f(x + h) f(x ) = f(x + ϑh) h f(x ) h Satz 1.2 Ist h klein ( alle h k sind klein), dann gilt f = f(x + h) f(x) f(x) h = n k=1 f x k (x) h k. Definition 1.2 (Totales Differential) Bemerkung: df = df x,h := f(x) h = f(x) dx = f(x) x = n f n f (x)h k = (x)dx k = x k x k k=1 k=1 (a) Nach Satz 1.2 gilt für den totalen Zuwachs f von f: wenn h ( dx, x ) klein ist. (b) Es gilt auch f(x + h) f(x) + df. f = f(x + h) f(x) df n k=1 f x k (x) x k (c) Ist z = f(x), w = f(x) usw., dann schreibt man auch df = dz, df = dw usw Anwendungen des totalen Differentials in der Fehlerrechnung Problem: Abschätzung des Fehlers bei der Berechnung einer Größe z = f(x, y) aus Näherungswerten x, ỹ von x bzw. y: z.b. Widerstandsmessung aus Spannung und Stromstärke. 91
92 1. Mittelwertsatz } x Näherungswerte von ỹ f(x, y), d.h. { x y = z = f( x, ỹ) ist eine Approximation von z = x = x + dx y }{{} exakte Werte = ỹ }{{} Messwerte + dy }{{} Messfehler Somit gilt für den Fehler z bei der Approximation: z = z z = f(x, y) f( x, ỹ) = f( x + dx, ỹ + dy) f( x, ỹ) dz, wenn die Messfehler dx, dy betragsmäßig klein sind. Daraus folgt Bemerkung: (a) Abschätzung des Absolutfehlers: z dz = f f ( x, ỹ)dx + ( x, ỹ)dy. x y z dz f ( x, ỹ) dx + f ( x, ỹ) dy. x y (b) Abschätzung des relativen Fehlers: z z = dz z 1 z ( f x ) f ( x, ỹ)dx + ( x, ỹ)dy. y Beispiel: z = f(x, y) = x y, z := f( x, ỹ) = x ỹ (z.b. R = U I ) dz = f f dx + x y dy = dx y x y dy 2 z dz ( x,ỹ),(dx,dy) = dx ỹ x ỹ dy 2 z dz z z = ỹ ( dx x ỹ x ) ỹ dy dỹ = dx x 2 y 92
93 = 1.1. Folgerungen aus dem MWS z z dx z dx x + dy ỹ }{{} Summe der relativen Fehler von Zähler und Nenner 93
94 1. Mittelwertsatz 94
95 11. Implizite Funktionen, implizite Differentiation Implizite Funktionen zweier Variabler Die Lösung eines technischen Problems sei beschreibbar durch eine Funktion y = y(x) = ϕ(x). In einigen Fällen erhält man die Lösungsfunktion y = y(x) = ϕ(x) nicht in expliziter Form, sondern in impliziter Form f(x, y(x)) = f(x, ϕ(x)) (11.1) wobei f = f(x, y) eine (komplizierte) Funktion der Variablen x, y ist. Beispiel: Berechnung von Planetenbahnen y = y(x)(= ϕ(x)). y = ϕ(x) implizit definiert durch = f(x, y) := x + y E sin y Gleichung) (Keplersche E: Exzentrizität der Bahnellipse Definition 11.1 (Implizite Funktion) Gilt (11.1), so heißt die Funktion y = y(x)(= ϕ(x)) implizit durch die Beziehung f(x, y) = definiert. Problem: (a) Auflösbarkeit von f(x, y) = nach y = y = y(x) = ϕ(x) (b) Formel für die Ableitung dy dx = ϕ (x) (implizite Differentiation) Beispiele: 95
96 11. Implizite Funktionen, implizite Differentiation (a) f(x, y) = ax + by c, a, b, c Konstanten = f(x, y) by = ax + c y = 1 ( ax + c), falls b b Bemerkung: b = f y Hier also: f(x, y) = auflösbar nach y, wenn f y (b) f(x, y) = ax 2 + by 2 c = f(x, y) by 2 = c ax 2 c ax 2 = y 1,2 = ±, wenn c ax2 b b Also: f(x, y) = auflösbar nach y, wenn b = f y y = 2by, wenn Satz 11.1 (Existenz von y = y(x)) Für einen Punkt (x, y ) gelte: (a) f(x, y ) =, (b) f y (x, y) existiere in einer Umgebung V (x, y ) von (x, y ) und sei dort auch stetig, (c) f y (x, y ). Dann gibt es in einer Umgebung U(x ) genau eine Funktion y = y(x), so dass (a) y = y(x ), (b) = f(x, y(x)) für alle x U(x ). Satz 11.2 (Implizite Differentiation) Zu den Voraussetzungen (a)-(c) von Satz(11.1) gelte noch (d) f x existiere in der Umgebung V (x, y ) von (x, y ) und sei dort stetig. 96
97 11.1. Implizite Funktionen zweier Variabler Dann existiert dy dx = y (x) in einer Umgebung U 1 (x ) von x, und es gilt Beweis: dy dx = y (x) = f x(x, y(x)) (implizite Differentiation) f y (x, y(x)) = f (x, y) x f (x, y) y y=y(x) oder f(x,y)= Man betrachte: F (x) := f(x(y)) = f x f y, y = y(x) Definition von y(x) : F (x) = für alle x U(x ) x U(x ) = = d dx = df dx = f x (x, y(x)) dx + f (x, y(x)) y (x) }{{} dx y }{{} =1 in einer Umgebung U 1 (x ) = ϕ (x) = f x(x, y(x)) f y (x, y(x)) Bemerkung: (a) Mit der Formel dy dx = f x, y = y(x), lässt sich die Ableitung dy f y dx = y (x) in jedem Kurvenpunkt (x, y), y = y(x) berechnen. (b) Analog lassen sich die höheren Ableitungen y (x), y (x),... implizit berechnen! Beispiel: Problem: f(x, y) = xe y ye x + x = (11.2) (a) Lässt sich f(x, y) = in einer Umgebung von x = eindeutig nach y = y(x) auflösen? 97
98 11. Implizite Funktionen, implizite Differentiation (b) y () =? Sei x = x =. Dann folgt mit (11.2) y =, also y = und somit y() =. Insgesamt (a) (x, y ) = (, ) erfüllt (11.2), also f(x, y ) = (b) f y = xe y e x existiert und ist stetig in (x, y) (c) f y (x, y ) = f y (, ) = 1 Satz 11.1: = f(x, y) lässt sich in einer Umgebung von x = nach y = y(x) auflösen, wobei y() = Ableitung dy dx (auch f x existiert und ist stetig!) Satz 11.2: y (x) = f x = ey ye x + 1, y = ϕ(x) f y xe y e x y () = +2 {}}{ x = = y = y(x ) = Implizite Funktionen mehrerer Variabler An der Stelle der einen Bedingung f(x, y) = hat man oft das Gleichungssystem f 1 (x 1,..., x n, y 1,..., y m ) = f 2 (x 1,..., x n, y 1,..., y m ) =. f(x, y) = f m (x 1,..., x n, }{{} unabh. Variablen y 1,..., y m ) }{{} abh. Variablen = 98
99 11.2. Implizite Funktionen mehrerer Variabler zur impliziten Definition von Funktionen y 1 = y 1 (x 1, x 2,..., x n ) y 2 = y 2 (x 1, x 2,..., x n ).. y = y(x) Vektorfunktion. y m = y m (x 1, x 2,..., x n ) Problem: (a) Auflösbarkeit von f(x, y) nach y (b) Berechnung der partiellen Ableitungen y i x k, i = 1,..., m, k = 1,..., n Auflösbarkeit Satz 11.3 Für ein System von Werten (x ; y ) = (x 1,..., x n ; y 1,..., y m ) gelte (a) f(x, y ) =. (b) Die Funktionen f k = f k (x, y) seien in einer Umgebung des Punktes (x, y ) nach allen Variablen x 1,..., x n, y 1,..., y m partiell differenzierbar und die partiellen Ableitungen seien stetig. (c) Die (m, m)-funktionalmatrix f 1 (x, y) y 1 f y = f 2 y 1 (x, y). f m y 1 (x, y) f 1 y 2 (x, y)... f 2 y 2 (x, y).... f m y 2 (x, y).... f 1 y m (x, y) f 2 y m (x, y) f m y m (x, y) = f (x, y) y ist im Punkt (x, y ) nicht singulär. 99
100 11. Implizite Funktionen, implizite Differentiation Dann gibt es in einer Umgebung U(x ) genau ein System von Funktionen y 1 = y 1 (x), y 2 = y 2 (x),..., y m = y m (x), kurz y = y(x), so dass (a) y = y(x ) (b) = f(x, y(x)) für alle x U(x ). Bemerkung: Die Funktionalmatrix f y ist in (x, y ) genau dann nicht singulär, wenn dort det f y ist. Definition 11.2 (Jacobideterminante) Die Determinante det f (x, y) der Funktionalmatrix heißt Funktionaldeterminante oder Jacobische Determinante y von f in (x, y). Sie wird auch mit bezeichnet. (f 1,..., f m ) (y 1,..., y m ) = det f y Berechnung der ersten partiellen Ableitungen Es seien dieselben Voraussetzungen wie in Satz 11.3 erfüllt. Die Ableitungen y i x k existieren also in einer Umgebung von x. Die Funktionen erfüllen die Gleichungen: = f i (x 1, x 2,..., x n, y 1 (x 1,..., x n ), y 2 (x 1,..., x n ),..., y m (x 1,..., x n )) für i = 1, 2,..., m und alle x in einer Umgebung von x. Sei 1 k n. Dann gilt nach der verallgemeinerte Kettenregel = x k = f i x k (x, y(x)) + m j=1 f i y j (x, y(x)) y j x k für alle i = 1, 2,..., m. 1
101 11.2. Implizite Funktionen mehrerer Variabler Vektorielle Darstellung dieser m Gleichungen: f 1 (x, y(x)) f 1 (x, y(x))... y 1 (x) y m.. f m (x, y(x)) f m (x, y(x))... y 1 y }{{ m } f = (x, y(x)) y y 1 (x) x k. y m (x) x k = f 1 (x, y(x)) x k. f m (x, y(x)) x k. Da f y in (x, y ), y = y(x ) nicht singulär ist, ist die Funktionalmatrix in einer ganzen Umgebung von (x, y ) nicht singulär. Somit gilt der folgende Satz 11.4 (Implizite Differentiation, allgemeiner Fall) Die Voraussetzungen von Satz 11.3 seien erfüllt. Dann existieren in einer Umgebung U(x ) partiell differenzierbare Funktionen y(x) = (y 1 (x),..., y m (x)), so dass f(x, y(x)) = für alle x U(x ), und ihre ersten partiellen Ableitungen sind gegeben durch y 1 (x) x k. y m (x) x k ( f = (x, y(x)) y ) 1 f 1 (x, y(x)) x k., k = 1,..., n für alle x U(x ). f m (x, y(x)) x k Bemerkung: Dieses Resultat ist analog zu Satz 11.2 für y = y(x). Beispiel: m = 2, n = 3: ax bx cx 3 2 = d αx βx γx 3 2 = δ f(x 1, x 2, x 3 ) = (System quadratischer Gleichungen) (a) x 1 = x 1 (x 3 ), x 2 = x 2 (x 3 ), d.h. y = (x 1, x 2 ) 11
102 11. Implizite Funktionen, implizite Differentiation f y = f 1x1 f 2x1 f 1x2 f 2x2 = 2ax 1 2bx 2 2αx 1 2βx 2 (f 1, f 2 ) (x 1, x 2 ) = 4x 1x 2 (aβ αb) (b) x 1 = x 1 (x 2 ), x 3 = x 3 (x 2 ), d.h. y = (x 1, x 3 ) f y = f 1x1 f 2x1 f 1x3 f 2x3 (f 1, f 2 ) (x 1, x 3 ) = 4x 1x 3 (aγ αc) = 2ax 1 2cx 3 2αx 1 2γx 3 (c) x 2 = x 2 (x 1 ), x 3 = x 3 (x 1 ), d.h. y = (x 2, x 3 ) f y = f 1x2 f 2x2 f 1x3 f 2x3 (f 1, f 2 ) (x 2, x 3 ) = 4x 2x 3 (bγ βc) = 2bx 2 2cx 3 2βx 2 2γx 3 12
103 12. Die Richtungsableitung Gegeben seien: (a) Funktion f = f(x) = f(x 1, x 2,..., x n ), (b) fester Punkt x = (x 1, x 2,..., x n ), (c) Richtungsvektor h = (h 1, h 2,..., h n ), h = 1, (d) Gerade g durch x in Richtung h. N N C N D I )? D I A N N Dann gilt: x g(= s-achse ) x = x(s) = x + sh, s R, (d.h. das Argument x wird jetzt auf die s-achse eingeschränkt). 13
104 12. Die Richtungsableitung Problem: Gesucht (a) lokales Verhalten von f in x längs der s-achse (b) Richtung der größten Zuwachs- oder Anstiegsrate (Zuwachs pro s-maßeinheit) von f in x Betrachte hierzu die Funktion F = F (s): F (s) = f(x(s)) = f(x + sh) = f(x 1 + sh 1, x 2 + sh 2,..., x n + sh n ) F () = f(x ). (a) Lokales Verhalten von f in x längs der s-achse Dieses wird beschrieben durch den Grenzwert F lim s s = lim F (s) F () s } s {{ } relativer Zuwachs von f = F F (s) F () () = lim s s Richtung h. = F () ist die Zuwachsrate von f im Punkt x in Definition 12.1 (Richtungsableitung) Der Grenzwert F () heißt Richtungsableitung von f im Punkt x in Richtung h; diese wird mit f h (x f ), s (x ) oder f (x ; h) bezeichnet, es gilt also Beispiel: f s (x ) = f h (x f(x ) := lim + sh) f(x ). s s h = e k = (,...,, 1,,..., ) T k-te Komponente 14
105 f e k (x ) (Richtungsableitung in Richtung des k-ten Einheitsvektors) = f x k (x ) k-te partielle Ableitung in x. Berechnung der Richtungsableitung: Satz 12.1 Es gilt f s (x ) = F () F (s) = f(x + sh) T h. f s (x ) = f h (x ) = f(x ) h =< f(x ), h > (b) Bestimmung der Richtung h mit der maximalen Zuwachsrate (des maximalen relativen Zuwachses) von f in x Aus (a) folgt für die Zuwachsrate (den relativer Zuwachs) von f in x in Richtung h: f s (x ) =< f(x ), h >= f(x ) h cos ( f(x }{{}}{{} ), h) = f(x }{{} ) cos ϕ. feste Zahl = 1 nur abhängig von h Offensichtlich ist cos ϕ und damit auch f s (x ) maximal, wenn ϕ =, d.h., wenn h in Richtung von f(x ) zeigt! BN D Satz 12.2 Der Gradient f(x ) zeigt in Richtung des stärksten Anstiegs von f, also h max. Zuwachsrate in x = f(x ) f(x ). 15
106 12. Die Richtungsableitung Eine weitere Eigenschaft des Gradienten f Wir betrachten die Niveau-Flächen Φ im R n von f Φ = Φ C = {x R n : f(x) = f(x 1, x 2,..., x n )}. mit einer Konstanten C. In Kurzform setzt man auch Φ : f(x 1, x 2,..., x n ) = C. (12.1) Beispiele: (a) n = 2 Φ : f(x 1, x 2 ) = C = x 2 = ϕ(x 1 ; C) Kurve im R 2 (b) n = 3 Φ : f(x 1, x 2, x 3 ) = C = x 3 = ϕ(x 1, x 2 ; C) Fläche im R 3 Voraussetzung: (12.1) lässt sich nach mindestens einer der Variablen x 1, x 2,..., x n auflösen, also x n = ϕ(x 1, x 2,..., x n 1 ) mit einer Funktion ϕ der Variablen x 1,..., x n. Betrachte dann die Tangentialebene T an Φ in einem Punkt x Φ, d.h. x n = ϕ(x 1, x 2,..., x n 1, ). Bemerkung: Für n = 3 hat T nach Kapitel 8 die Darstellung x 3 = x 3 + ϕ x1 (x 1, x 2 )(x 1 x 1 ) + ϕ x2 (x 1, x 2 )(x 2 x 2 ). Für beliebiges n 2 gilt der folgende Satz 12.3 (Gleichung der Tangentialebene) Problem: ϕ x k =? x n = x n + Nach Definition von ϕ gilt n 1 k=1 ϕ x k (x 1, x 2,..., x n 1, )(x k x k ). C f(x 1, x 2,..., x n 1, ϕ(x 1, x 2,..., x n 1 )). }{{} C g(x 1, x 2,..., x n 1 ) 16
107 12.1. Eine weitere Eigenschaft des Gradienten f Daraus folgt mit der verallgemeinerten Kettenregel: Für x = x folgt dann = C x k = g x k = f x k + f x n ϕ x k für alle 1 k n 1. = f x k (x ) + f x n ϕ x k (x 1,..., x n 1, ), k = 1, 2,..., n 1, Mit der hinreichenden Voraussetzung f x n für die Auflösbarkeit von f(x 1,..., x n ) = C nach x n in einer Umgebung von x, folgt dann: ϕ x k (x 1,..., x n 1, ) = Damit gilt für T auch die Darstellung: x n = x n n 1 k=1 f (x x ) k f (x x ) n f (x x ) k (x f k x k ). (x x ) n Dies ist genau dann der Fall, wenn n f (x x )(x k x k ) =, k also k=1 < grad f(x ), x x >= = f(x ) (x x ). Satz 12.4 (Gleichung der Tangentialebene) Die Tangentialebene T an Φ: f(x 1, x 2,..., x n ) = C im Punkt x hat die Darstellung < grad f(x ), x x >= oder f(x ) x = f(x ) x. Bemerkung: Die Gleichung der Tangentialebene T bedeutet auch, dass d.h. der Gradient steht senkrecht auf T. Damit gilt: x T = x x f(x ),. 17
108 12. Die Richtungsableitung Korollar 12.1 Der Gradient f(x ) steht senkrecht auf der Tangentialebene T an die Fläche Φ : f(x 1,..., x n ) = C im Punkt x und weist in Richtung des stärksten Anstiegs von f (bzw. C). Beispiel: f(x) = x x x 3 2 = Φ : x x x 2 3 = C ist die Oberfläche einer Kugel im R 3 ( ) T f f f f(x) =,, = 2(x 1, x 2, x 3 ) T = 2x x 1 x 2 x 3 Hier weist der Gradient f(x) in x in dieselbe Richtung wie der Vektor x. 18
109 13. Der Satz von Taylor für Funktionen von mehreren Variablen Gegeben seien: (a) Funktion f = f(x) = f(x 1, x 2,..., x n ), (b) fester Punkt x = (x 1, x 2,..., x n ), (c) Vektor x = dx = h = (h 1, h 2,..., h n ). Problem: Analog zum Fall n = 1 (eine Variable x 1 = x) finde man eine Entwicklung des Zuwachses nach Potenzen von h 1, h 2,..., h n. f = f(x + h) f(x ) Wie beim MWS für Funktionen von mehreren Variablen erfolgt die Zurückführen des Problems von n > 1 auf n = 1 durch Einführung einer geeigneten Funktion F = F (t) einer einzigen Variablen t. Definiere (wie beim verallgemeinerten MWS): F (t) := f(x + th) = f(x 1 + th 1, x 2 + th 2,..., x n + th n ) Ferner sei vorausgesetzt: f ist hinreichend oft differenzierbar nach allen Variablen x 1, x 2,..., x n. 19
110 13. Satz von Taylor Eigenschaften von F (t) (a) F (t) = f(x + th), t 1, d.h. F () = f(x ) F (1) = f(x + h) = f = F (1) F () = F = F (t + t) F (t ) mit t =, t = 1 (b) Alle Ableitungen F (t), F (t),..., F (M) (t) bis zu einer gewissen Ordnung M existieren und alle Ableitungen lassen sich mit der verallgemeinerten Kettenregel berechnen. Aus Kapitel 1 folgt: F (t) = d dt f(x + th) = < f(x + th), h >= n k=1 f x k (x + th)h k, F (t) = d dt F (t) = n d f h k (x dt x + th). k k=1 Zur Vereinfachung sei n = 2: x(t) := (x 1 (t), x 2 (t)) = (x 1 + th 1, x 2 + th 2 ) = x + th. 11
111 13.1. Eigenschaften von F (t) Dann gilt nach der Kettenregel: Bemerkung: F (t) = d h 1 dt f d x 1 (x + th) + h 2 dt f x 2 (x + th) = h 1 (f x1 x 1 (x + th)h 1 + f x1 x 2 (x + th)h 2 ) +h 2 (f x2 x 1 (x + th)h 1 + f x2 x 2 (x + th)h 2 ) = h 1 f x1 x 1 (x + th)h 1 + h 1 f x1 x 2 (x + th)h 2 +h 2 f x2 x 1 (x + th)h 1 + h 2 f x2 x 2 (x + th)h 2 = f x1 x 1 h f x1 x 2 h 1 h 2 + h 2 2f x2 x 2 (Satz von Schwarz) = f x1 x 1 f x1 x 2 (h 1, h 2 ) f x2 x 1 f x2 x 2 } {{ } 2 F (x +th) h 1 h 2 = h 2 fh (a) 2 f(x + th) ist die Matrix der 2. partiellen Ableitung und heißt auch Hessematrix. (b) Dieselbe Formel für F (t) gilt auch für ein beliebiges n 2. Satz 13.1 Für F (t) = f(x + th) gilt wobei 2 f definiert ist durch F (t) = h 2 f(x + th)h, 2 f = 2 xf = f x1 x 1 f x1 x 2... f x1 x n f x2 x 1 f x2 x 2... f x2 x n... f xnx1 f xnx2... f xnxn (Matrix der 2. partiellen Ableitungen). 111
112 13. Satz von Taylor Bemerkung: (a) Nach dem Satz von Schwarz (Satz 8.2) ist 2 f eine symmetrische Matrix. (b) Analog lassen sich die höheren Ableitungen F (t), F (4) (t),... mit Hilfe der verallgemeinerten Kettenregel berechnen Anwendung der Taylorformel für Funktionen einer Variablen auf die Funktion F Seien T m das m-te Taylorpolynom von F und R m das Restglied von F in Lagrange- Form. Dann gilt: allgemeines t, t Entwicklungspunkt t =, t = 1 F (t) = T m (t) + R m (t) F (1) = T m (1) + R m (1) T m (t) = m F (k) (t ) (t t ) k T m (1) = k! m F (k) () k! R m (t) = F (m+1) (t + ϑ(t t )) (t t ) m+1 R m (1) = F (m+1) (ϑ) (m + 1)! (m + 1)! wobei < ϑ < 1. Also ist: F (1) = m F (k) () k! + F (m+1) (ϑ) (m + 1)! = F () + F () + 1 2! F () m! F (m) () + F (m+1) (ϑ) (m + 1)! }{{} Restglied mit < ϑ < 1. Wegen F (1) = f(x + h) F () = f(x ) F () = < f(x ), h >= df x,h 112
113 13.2. Anwendung der Taylorformel für Funktionen einer Variablen auf die Funktion F gilt der folgende Satz 13.2 (Taylorformel für Funktionen mehrerer Variabler) f(x +h) f(x ) = df x,h + 1 2! F ()+ + 1 m! F (m) ()+ F (m+1) (ϑ) (m + 1)! mit < ϑ < 1. Definition 13.1 (Differentiale höherer Ordnung) d (k) f = d (k) f x,h := F (k) () heißt Differential k-ter Ordnung. Damit gilt auch f(x + h) = f(x ) + m k=1 1 1 k! d(k) f + (m + 1)! F (m+1) (ϑ) }{{} Restglied mit < ϑ < 1. Spezialfälle: (a) m = = f(x + h) = f(x ) + F (ϑ) = f(x ) + f(x + ϑh) h, < ϑ < 1. Das ist der MWS für Funktionen mehrerer Variabler. (b) m = 1 f(x + h) = f(x ) + df x,h + 1 2! F (ϑ) mit < ϑ < 1 = f(x ) + df x,h h 2 f(x + ϑh) x 2 h. Für Vektoren h mit kleiner Norm erhält man f(x + h) f(x ) + f(x ) h h 2 f x 2 (x )h, (c) m = 2 f(x + h) = f(x ) + df x,h d2 f x,h + 1 3! F (ϑ), < ϑ <
114 13. Satz von Taylor Zur Vereinfachung sei n = 2. Dann gilt für F (t) = f(x + th): F (t) = f x1 x 1 h f x1 x 2 h 1 h 2 + f x2 x 2 h 2 2 F (t) = f x1 x 1 x 1 h f x1 x 1 x 2 h 2 1h 2 + 2f x1 x 2 x 1 h 2 1h 2 + 2f x1 x 2 x 2 h 1 h f x2 x 2 x 1 h 2 2h 1 + f x2 x 2 x 2 h 3 2 = f x1 x 1 x 1 h f x1 x 1 x 2 h 2 1h 2 + 3f x1 x 2 x 2 h 1 h f x2 x 2 x 2 h 3 2 (Satz von Schwarz) 114
115 14. Extremwertaufgaben: Maxima und Minima bei Funktionen mehrerer Variabler Sei f = f(x) = f(x 1, x 2,..., x n ) definiert auf einem Gebiet G R n und x = (x 1, x 2,..., x n ) T ein fester Punkt aus G. Definition 14.1 (Minima und Maxima) x heißt lokale (oder relative) Minimalbzw. Maximalstelle von f, wenn eine Umgebung U δ (x ) G existiert mit δ >, so dass f(x) f(x ) bzw. f(x) f(x ) für alle x U δ (x ) (14.1) f(x ) heißt dann lokales Minimum bzw. Maximum. Gilt die Ungleichung (14.1) für alle x G, so heißt x eine globale Minimal- bzw. Maximalstelle von f bez. G und f(x ) heißt dann globales Minimum bzw. Maximum von f bez. G. Ein Minimal- oder Maximalpunkt heißt auch Extremalpunkt. N! BN N 6 BN N N N Bemerkung: Ein globaler Extremalpunkt, der im Inneren von G liegt, ist auch ein lokaler Extremalpunkt. 115
116 14. Extremwertaufgaben Kriterien für lokale Extremalstellen Notwendige Bedingung 1. Art Satz 14.1 (Notwendige Optimalitätsbedingung) Sei x eine lokale Extremalstelle (lok. Minimal- oder lok. Maximalstelle). Existieren die partiellen Ableitungen f x k (x ), k = 1, 2,..., n, so ist f(x ) =, d.h. f x k (x ) = für alle k = 1, 2,..., n. Beweis: Wir betrachten die Richtungsableitung f (x ; h) für beliebige h R m. Da x lokale Extremalstelle von f ist, folgt f (x ; h) =. Wegen = f (x ; h) = f(x ) T h für beliebiges h R n, gilt dann f(x ) =. Beispiel: a) f(x, y) = x 2 + y 2 hat in x = ein absolutes Minimum f(x, y) = 2x f(x ) = 2x = b) f(x, y) = x 2 y 2 f(x, y) = 2(x, y) T f() = Aber x = ist keine Extremalstelle, sondern ein sog. Sattelpunkt: in x = x = f(x) steigt in x- Richtung f(x) fällt in y- Richtung = x = kann weder Maximal- noch Minimalstelle sein. Bemerkung: a) f(x ) = i.a. x = Extremalstelle b) Punkte x mit f(x ) = sind wegen Satz 14.1 Kandidaten für lokale Extremalstellen, sie heißen deswegen auch kritische oder stationäre Punkte. 116
117 Notwendige Bedingungen 2. Art Kriterien für lokale Extremalstellen Zur Vorbereitung der hinreichenden Bedingungen für ein Extremum betrachten wir nun eine weitere notwendige Optimalitätsbedingung, die Ableitungen 2. Ordnung voraussetzt: Satz 14.2 (Notwendige Bedingung 2. Art) Die Funktion f = f(x) sei mindestens zweimal stetig partiell differenzierbar nach allen Variablen x 1,..., x n. Ist x G eine lokale Minimal- bzw. lokale Maximalstelle von f, so gilt f(x ) =, und die Hessematrix 2 f(x ) von f in x ist positiv bzw. negativ semidefinit. Beweis: Die Gleichung f(x ) = ergibt sich sofort aus Satz Wir betrachten dann wieder die Funktion F (t) := f(x + th), t R, mit einem beliebigen, aber festen Vektor h R n. Die Taylorformel 1. Ordnung von F in t = lautet dann f(x + th) = F (t) = F () + F ()(t ) F (ϑ)(t ) 2 = f(x ) + t f(x ) T h + t2 2 ht 2 f(x + ϑth) h = f(x ) + t2 2 ht 2 f(x + ϑth) h mit einem ϑ, < ϑ < 1. Nach Voraussetzung ist x eine lokale Minimal- bzw. Maximalstelle. Aus der obigen Gleichung folgt daher t 2 2 ht 2 f(x + ϑth) h = f(x + th) f(x ) ( ) für alle t mit t < δ(h) und einem festen δ = δ(h) >. Damit ist aber auch Durch t folgt dann h T 2 f(x + ϑth) h ( ) für alle t < δ(h). h T 2 f(x )h ( ). Da h R n ein beliebiger, fester n Vektor ist, bedeutet dies, dass die Hessematrix 2 f(x ) von f in x positiv bzw. negativ semidefinit sein muß. Aus dem obigen Satz 14.2 erhalten wir sofort das nachfolgende Ergebnis: 117
118 14. Extremwertaufgaben Korollar 14.1 Die Funktion f = f(x) sei zweimal stetig differenzierbar auf dem Gebiet G. Ist x G ein innerer Punkt von G, so dass f(x ) = und die Hessematrix 2 f(x ) indefinit ist, so ist x kein lokaler Extremalpunkt. Beispiel: Für die Funktion f(x) = f(x, y) = x 2 y 2, (x, y) T R 2, gelten im Punkt x = die Gleichungen f(x ) = (2x, 2y ) T = 2 f(x ) = 2. 2 Der Gradient verschwindet zwar in x =, die Hessematrix ist aber indefinit. Tatsächlich ist x = keine Extremalstelle von f, sondern ein sog. Sattelpunkt, siehe folgende Abbildung: f(x,y) = x² y²
119 Hinreichende Bedingung Kriterien für lokale Extremalstellen Satz 14.3 (Hinreichende Optimalitätsbedingung) Die Funktion f besitze in x stetige partielle Ableitungen 2.Ordnung. (a) Ist f(x ) = und 2 f(x ) positiv definit, so ist x eine lokale Minimalstelle. (b) Ist f(x ) = und 2 f(x ) negativ definit, so ist x eine lokale Maximalstelle. Beweis: Taylorformel mit m = 1: Damit ist f(x + h) f(x ) = f(x + h) = f(x ) + f (x ; h) + 1 }{{} 2 ht 2 f(x + ϑh)h, < ϑ < 1. = f(x ) T h = ht 2 f(α + ϑh) }{{} bzw. >= >; für alle h mit h δ und ein festes δ > Beispiel: Quadratische Funktionen f(x) = p + q T x + x T Qx = f(x) = q + 2Qx Gradient 2 f(x) = 2Q Hessematrix f(x ) = Qx = 1 2 q x = 1 2 Q 1 q, wenn Q regulär ist. 119
120 14. Extremwertaufgaben = x ist lokale Minimalstelle, wenn Q positiv definit ist, lokale Maximalstelle, wenn Q negativ definit ist, Bemerkung: x ist unter diesen Voraussetzungen sogar globale Extremstelle! Diskussion der Definitheitsvoraussetzung in Satz 14.3: 2 f positiv (negativ) definit Alle Eigenwerte von 2 f sind positiv (negativ). Wir untersuchen jetzt den Spezialfall: n = 2, f = f(x, y). Es gilt: 2 f = f xx f xy f yx f yy, f xy = f yx. Da die Determinante D(x) von 2 f(x) das Produkt der (reellen) Eigenwerte λ 1, λ 2 ist, gilt in jedem Fall: D(x) = λ 1 λ 2 >, falls 2 f(x) positiv oder negativ definit, D(x) = λ 1 λ 2 <, falls 2 f(x) indefinit ist. Ferner gilt immer: 2 f(x) positiv (negativ) definit f xx (x) >, f yy (x) > ( f xx (x) <, f yy (x) < ). Die Eigenwerte λ 1, λ 2 von 2 f sind dann gegeben durch die Gleichungen λ 1/2 = f xx + f yy 2 ± 1 2 (f xx f yy ) 2 + 4f 2 xy = f xx + f yy ± ((f xx + f yy ) 2 4(f xx f yy fxy)) 2 1/2 ( ) ( (fxx ) ) 2 1/2 fxx + f yy + f yy = ± D, D = det 2 f(x) = D(x), 2 2 Daraus folgt: Satz 14.4 Sei n = 2 und f habe stetige partielle Ableitungen in x = x. 12
121 14.1. Kriterien für lokale Extremalstellen (a) Gilt f(x ) = f xx (x ) > ( f yy (x ) > ) D(x ) >, dann ist x eine lokale Minimalstelle. (b) Gilt f(x ) = f xx (x ) < ( f yy (x ) < ), D(x ) >, dann ist x eine lokale Maximalstelle. Beispiel: Gegeben sei die quadratische Funktion f(x, y) = 1 2 x2 4xy + 9y 2 + 3x 14y f (x) = x 4y + 3 x f (x) = 4x + 18y 14 y f(x ) = = x = (1, 1) T f(x) = = D(x) = det 2 f = = 2 > Weiter ist f xx = 1 >, f yy = 18 >. Nach Satz 14.4 ist x = (1, 1) T (sogar globale) Minimalstelle. also eine 121
122 14. Extremwertaufgaben Bemerkung: (a) f(x ) =, 2 f(x) ist positiv semidefinit in einer Umgebung von x = x ist eine schwache lokale Minimalstelle (b) f(x ) =, D(x ) < 2 f(x ) ist indefinit (die Eigenwerte von 2 f(x ) haben verschiedene Vorzeichen) = x ist ein Sattelpunkt. 122
123 15. Extremwertaufgaben mit Nebenbedingungen Bei vielen Problemen der Naturwissenschaften, Technik und Ökonomie treten Extremwertaufgaben auf, bei denen nicht einfach ein lokales Extremum einer Funktion f = f(x) = f(x 1, x 2,..., x n ) gesucht ist, sondern es müssen bei der Minimierung oder Maximierung von f noch gewisse gegebene Bedingungen (Restriktionen) der Art g 1 (x) = g 1 (x 1, x 2..., x n ) = g 2 (x) = g 2 (x 1, x 2..., x n ) =... m(< n) Restriktionen g m (x) = g m (x 1, x 2..., x n ) = beachtet werden. Dabei sind g i = g i (x), i = 1,..., m, gegebene Funktionen von x. Man spricht hierbei auch von einem restringierten Problem. Problem (P) Man finde eine lokale Extremalstelle x von f unter den Nebenbedingungen g i (x) =, i = 1, 2..., m, d.h. man finde ein x R n, so dass für ein δ > gilt: f(x ) ( )f(x) für alle x U δ (x ) mit g i (x) =, i = 1, 2..., m (U δ (x ) = δ Umgebung von x ). Bemerkung: Ist f(x ) ( )f(x) für alle x R n mit g i (x) =, i = 1,..., m, so heißt x eine globale Extremalstelle unter den Nebenbedingungen g i (x) =, i = 1,..., m. Beispiel: Gegeben sei ein fester Punkt a R n und eine Hyperebene H : c T x = d des R n. Gesucht ist die Projektion x von a auf H, d.h. der Punkt x = x H mit dem kürzesten Abstand zu a. 123
124 15. Extremwertaufgaben mit Nebenbedingungen Diese Aufgabe führt auf das Optimierungsproblem: Minimiere die Funktion: f(x) := x a 2 E,. E = Euklidische Norm unter der Gleichungsbedingung g(x) = c T x d =. Mit Hilfe der Theorie der impliziten Funktionen kann das restringierte Problem (P ) unter bestimmten Bedingungen wieder auf ein unrestringiertes Problem zurückgeführt werden. Dazu zerlegen wir die Variablen x 1,..., x n in zwei Gruppen, die nach einem evtl. Variablentausch immer wie folgt gewährt werden können: x = ) ( x mit x := y x 1 x 2. x n m, y = y 1 y 2. y m := Die Restriktionen lassen sich dann wie folgt schreiben: x n m+1 x n m+2. x n, m < n. g 1 (x 1, x 2,..., x n m, x n m+1,..., x n ) = g 2 (x 1, x 2,..., x n m, x n m+1,..., x n ) =.. g m (x 1, x 2,..., x }{{ n m, x } n m+1,..., x n ) =, }{{} = x =y oder in der vektoriellen Form (vgl. Kapitel 11) g(x) = g( x, y) =. Wir setzen nun voraus, dass x = ( x, y ) eine lokale Extremalstelle von f ist unter den Restriktionen g(x) = g( x, y) =. Ferner machen wir die folgenden Annahmen: 124
125 15.1. Notwendige Optimalitätsbedingungen a) Die partiellen Ableitungen 1.Ordnung von f und g i, i = 1,..., m, existieren und sind stetig. b) Regularitätsbedingung: Die Funktionalmatrix g y (x ), x = ( x, y ), ist regulär im Punkt x. Mit Hilfe des impliziten Funktionentheorems, d.h. mit Satz 11.3 und Satz 11.4, folgt dann: Die Gleichung g(x) = g( x, y) = lässt sich in einer Umgebung von x nach dem Teilvektor y auflösen, und die partiellen Ableitungen von y = y( x) lassen sich mittels impliziter Differentiation berechnen. Dabei ist y( x ) = y. Die Restriktionen g(x) = g( x, y) = sind somit äquivalent mit der Beziehung y = y( x) in einer Umgebung von x. In dieser Umgebung von x läßt sich damit das restringierte Problem (P ) in das unten angegebene unrestringierte Problem ( P ) verwandeln: (P ) Problem mit Restr. ( P ) Problem ohne Restr. mit Lösung x Theorie impl. Funkt. mit Lösung x min(max)f(x) min(max)f( x, y) min(max)f( x, y( x)) bez. bez. bez. g(x) = g( x, y) = }{{} y = y( x) x R n m Das Ausgangsproblem (P ) mit Restriktionen ist also in einer gewissen Umgebung von x äquivalent zum unrestringierten Problem ( P ). Da x eine lokale Extremalstelle von (P ) ist, folgt, dass x eine lokale Extremalstelle von ( P ) ist und umgekehrt. Die notwendigen und hinreichenden Optimalitätsbedingungen für x und damit auch für x erhält man dann aus Satz 14.1 und Satz Notwendige Optimalitätsbedingungen Nach dem Obigen setzen wir f( x) := f( x, y( x)). Aus Satz 14.1 folgt dann f( x ) = als notwendige Bedingung für ein lokales Extremum. Zu berechnen ist somit der 125
126 15. Extremwertaufgaben mit Nebenbedingungen Gradient ( f( x) = f,..., x 1 f x n m ) T. Für 1 k n m ist nach der verallgemeinerten Kettenregel und Satz 11.4 über implizite Funktionen f = f + x k x k = f x k + n i=n m+1 m i=1 f y i y i x k f x i x i x k = f x k ( x, y( x)) + y f( x, y( x)) T = f x k ( x, y( x)) + y f( x, y( x)) T y( x) x ( k g ( x, ) y( x)) 1 g(x, y( x)). y x k Somit gilt für x die notwendige Optimalitätsbedingung (x = ( x, y( x ))) : = f (x x ) y f(x ) g T k y (x ) 1 g(x x ) für alle k = 1,..., n m, (15.1) k wobei g(x ) = und ( y f) T = ( f,..., f ) T ( f =,..., x n m+1 x n y 1 ) T f. y m Verfahren von Lagrange Da die Variablen y 1 = x n m+1,..., y m = x n, nach denen die Gleichung g(x) = g( x, y) = aufgelöst werden kann, in der Praxis nur schwer bestimmt werden können, benötigt man zur Herleitung der notwendigen Bedingungen (15.1) ein anderes, praktikableres Verfahren. Dieses basiert auf der sog. Lagrange-Funktion: Definition 15.1 (Lagrangefunktion, Lagrange-Multiplikatoren) Die Funktion m L = L(x, λ) = L(x 1, x 2,..., x n, λ 1,..., λ m ) := f(x) + λ i g i (x) = f(x) + λ T g(x) in den Variablen x 1,..., x n, λ 1,... λ m heißt Lagrangefunktion. Die Parameter λ 1, λ 2,..., λ m heißen Lagrange-Multiplikatoren i=1 126
127 15.1. Notwendige Optimalitätsbedingungen Anstelle von (P ) betrachten wir dann das freie Minimierungs- bzw. Maximierungsproblem min x R (max n, m)l(x, λ). (15.2) λ R Nach Abschnitt 14 hat man für einen Optimalpunkt (x, λ ) von (15.2) die folgenden notwendigen Bedingungen: = L, k = 1, 2..., n x k (15.3) = L, i = 1, 2,..., m λ i oder explizit = f x k + m i=1 λ i g i x k, k = 1,..., n = g i (x), i = 1, 2,..., m. Diskussion von (15.3) bzw. (15.4) (15.4) a) Wir untersuchen nun die Gleichungen k = n m + 1,..., n von (15.4) mit x = x. Vektoriell geschrieben lauten sie: T = y f(x ) T + λ T g y (x ), wobei y = (x n m+1,..., x n ) T. Unter der Regularitätsbedingung zu Beginn des Abschnitts 15, also Rg g y (x ) = m, (15.5) lassen sich die Lagrange-Multiplikatoren somit darstellen durch ( ) g 1 λ T = y f(x ) T y (x ). b) Einsetzen von λ in die restlichen Gleichungen k = 1,..., n m von (15.4) ergibt mit x = x die Gleichung wobei g(x ) =. = f x k (x ) + λ T g(x x ) k = f x k (x ) y f(x ) T ( g y (x ) ) 1 g(x x ), k 127
128 15. Extremwertaufgaben mit Nebenbedingungen Da dieses System genau mit dem System (15.1) übereinstimmt, ist folgender Satz bewiesen: Satz 15.1 (Verfahren von Lagrange) L(x, λ) = f(x) + b) Man betrachte das Gleichungssystem a) Man definiere die Lagrange-Funktion m λ i g i (x). i=1 = L x k, k = 1, 2,..., n = L λ i, i = 1, 2,..., m in den n + m Unbekannten x 1, x 2,..., x n, λ 1, λ 2,..., λ m. c) Man eliminiere die Lagrangemultiplikatoren λ 1,..., λ m. Das resultierende Gleichungssystem in x = (x 1,..., x n ) T stellt dann die notwendigen Optimalitätsbedingungen für eine lokale Extremalstelle x = x des Ausgangsproblems (P ) dar. Bemerkung: Die Elimination von λ erfordert, dass ein Teilvektor y von x mit m Komponenten existiert, so dass die Funktionalmatrix g y in dem Punkt x regulär ist! Dies wird garantiert durch die Rangbedingung (15.5). Dies ist aber äquivalent mit der leichter nachprüfbaren Bedingung Rg g x (x ) = m. (15.6) Beispiel: Wir betrachten die Projektion des Nullpunkts R 2 auf eine Gerade im R 2. Dazu setzen wir n = 2, m = 1, f(x, y) = x 2 + y 2, g(x, y) = ax + by c. Diese Aufgabe läßt sich beschreiben durch das Minimierungsproblem (P ) min x 2 + y 2 bez. ax + by = c mit Konstanten a, b, c. Für dieses Problem haben wir die Lagrange-Funktion L(x, y, λ) = f(x, y) + λg(x, y) = x 2 + y 2 + λ(ax + by c). 128
129 15.2. Hinreichende Optimalitätsbedingungen für (P ) Die notwendigen Optimalitätsbedingungen gemäss Satz 15.1 lauten dann: = L x = L y = L λ = 2x + λa = 2y + λb = ax + by c Gleichungssystem in x, y, λ Zur Elimination von λ benötigt man offensichtlich die Bedingung a oder b. Dies ist gleichbedeutend mit der Rangbedingung (15.6), also Unter dieser Annahme gilt dann Rg g x (x ) = Rg(a, b) = m = 1. λ = 2x a, falls a bzw. λ = 2y b ), falls b. Als Lösung des Projektionsproblems erhält man schließlich x = c a 2 + b 2 a b. Dieser Vektor steht senkrecht auf der Geraden ax + by = c Hinreichende Optimalitätsbedingungen für (P ) Hinreichende Optimalitätsbedingungen für (P ) erhält man wieder mit Hilfe des äquivalenten unrestringierten Problems ( P ). Nach Abschnitt 14 müssen wir somit die Hessematrix 2 f( x ) untersuchen. Wie zu Beginn von Kapitel 15 setzen wir 129
130 15. Extremwertaufgaben mit Nebenbedingungen x = x 1 x 2. x s... y 1 y 2. y m mit s + m = n. Nach Abschnitt 15.1 gilt dann: f = f + x k x k m i=1 f y i y i x k, k = 1, 2,..., s, wobei die Ableitungen y i x k bestimmt sind durch die Gleichungen = x k g j ( x, y( x)) = g j x k + m i=1 g j y i y i x k, k = 1,..., s, j = 1,..., m. Berechnung der 2.Ableitungen von f( x): 2 f x k x l = = 2 f x k x l + 2 f x k x l + + m i=1 m t=1 m i=1 m i=1 2 f x k y i y i x l + 2 f x k y i y i x l + 2 f y i y t y i x k y t x l + m i=1 m i=1 i=1 x l ( ) f y i + y i x k 2 f y i x l y i x k m f 2 y i y i x k x l i=1 m f 2 y i für k, l = 1,..., s. y i x k x l 13
131 15.2. Hinreichende Optimalitätsbedingungen für (P ) Gestalt von 2 f(x): Es ist 2 f(x) = f x1 x 1... f x1 x s f x1 y 1... f x1 y m.... f xsx1... f xsxs f xsy1... f xsym f y1 x 1... f y1 x s f y1 y 1... f y1 y m.... = 2 f x x 2 f y x 2 f x y 2 f y y f ymx 1... f ymx s f ymy 1... f ymy m und y x = y 1 x y m x 1... y 1 x s. y m x s. Nach dieser Zerlegung von 2 f(x) gilt: Zu berechnen bleibt: ( y 2 f( x) 2 f = x x + 2 f x y y x + ( ) y T 2 f y m + x y y x + i=1 = ( I 2 y i x x. x ( ) y T ) I 2 f(x) x y ) T 2 f y x f 2 y i y i x x x + m f 2 y i y i x x i=1 131
132 15. Extremwertaufgaben mit Nebenbedingungen Es gilt: = g j x k + m i=1 g j y i y i x k, j = 1, 2,..., m, k = 1,..., s. Durch Differentiation nach x l, l = 1,..., s, folgt = 2 g j x k x l + + m i=1 m i=1 2 g j x k y i y i x l + m i=1 2 g j y i x l y i x k + g j 2 y i, k, l = 1,..., s, j = 1,..., m. y i x k x l m i=1 m t=1 2 g j y i y t y i x k y t x l Mit der obigen Zerlegung folgt dann: = 2 g j x x + 2 g j x y m + i=1 g j y i y x + ( y x 2 y i, j = 1,..., m. x x ) T 2 g j y x + ( y x ) T 2 g j y y ( ) y x Voraussetzung: Die Lagrange-Multiplikatoren λ = (λ 1,..., λ m ) seien nun nach dem Lagrange-Verfahren bestimmt, d.h. = L x k (x, λ) = f x k + m i=1 λ i g i x k, k = 1,..., n. = λ T = f ( ) g 1 y (x ) T y (x ) für ein bestimmtes x. Multiplikation der Matrixgleichung mit λ j und Summation über j = 1,..., m 132
133 liefert mit x = x und h := Hinreichende Optimalitätsbedingungen für (P ) m λ j g j : j=1 = 2 h x x + 2 h x y ( m m g j = λ j = i=1 ( I } y j=1 i {{ } = f y i ( ) y T ) x ( y y x + x ) 2 y i x x 2 h(x, λ) x x ) T 2 h y x + I y x ( y i=1 x ) T 2 h y y m f 2 y i y i x x. ( ) y x Damit gilt schließlich 2 f( x ) = = ( ( ) y T ) I x ( x I ) 2 f(x ) y x ( x ) m ( ( ) y T ) 2 λ i g i ( x ) + I x ( x I i=1 ) x x y x ( x ) ( I ( ) y T ) x ( x ) 2 xl(x, λ) I y x ( x ). 133
134 15. Extremwertaufgaben mit Nebenbedingungen Satz 15.2 (Hinreichende Bedingungen) Für einen Punkt x mit Rg g y (x ) = m gelte = L x k (x, λ), k = 1,..., n = L λ i (x, λ), i = 1,..., m. (= notwendige Bedingungen für eine lokale Extremalstelle x von (P ) sind erfüllt!) Dann gilt Ist die Matrix 2 f( x ) = ( I ( ) y T ) x ( x ) 2 xl(x, λ) 2 xl(x, λ) = 2 f(x ) + I y x ( x ) m λ i 2 g i (x ) dann positiv bzw. negativ definit, so ist x eine lokale Minimal- bzw. Maximalstelle. i=1. Beweis: Beispiel: ( ( ) y T ) w T 2 f( x )w = w T, x ( x )w 2 xl(x, λ) (a) min f(x) bez. Ax = b, (A, b) m (n + 1) Matrix w y x ( x )w ( ) L(x, λ) = f(x) + λ T (Ax b) x L(x, λ) = f(x) + A T λ, λ L(x, λ) = Ax b 2 xl(x, λ) = 2 f(x) = Definitheit von 2 xl(x, λ) ist durch die Definitheit von 2 f(x) bestimmt. 134
135 15.2. Hinreichende Optimalitätsbedingungen für (P ) (b) min f(x 1, x 2, x 3 ) bez. ax bx cx 2 3 = d αx βx γx 2 3 = δ L = f(x 1, x 2, x 3 ) + λ 1 (ax bx cx 2 3 d) + λ 2 (αx βx γx 2 3 δ) L = f + 2aλ 1 x 1 + 2αλ 2 x 1 x 1 x 1 L = f + 2bλ 1 x 2 + 2βλ 2 x 2 x 2 x 2 L = f + 2cλ 1 x 3 + 2γλ 2 x 3 x 3 x 3 L x1 x 1 = f x1 x 1 + 2aλ 1 + 2αλ 2, L x1 x 2 = f x1 x 2, L x2 x 1 = f x2 x 1, L x2 x 2 = f x2 x 2 + 2bλ 1 + 2βλ 2, L x3 x 1 = f x3 x 1, L x3 x 2 = f x3 x 2 + 2cλ 1 + 2γλ 2, L x1 x 3 = f x1 x 3, L x2 x 3 = f x2 x 3, L x3 x 3 = f x3 x 3. = 2 xl = 2 f + 2λ 1 a b c + 2λ 2 α β γ Bemerkung: Die Bedingung, dass 2 xl(x, λ) positiv bzw. negativ definit ist, lässt sich wie folgt abschwächen: 2 xl(x, λ) ist positiv bzw. negativ definit bezüglich 135
136 15. Extremwertaufgaben mit Nebenbedingungen dem Teilraum Beweis: Man betrachte: u = Dann gilt: U = {u R n : g x (x )u = }. w y x ( x )w. g x (x )u = g x (x )w + g y (x ) y x (x )w ( g = x (x ) + g y (x ) y ) x (x ) w = w =. 136
137 16. Parameterintegrale: Integrale, die von einem Parameter abhängen Gegeben: (a) Eine Funktion f = f(x, y), wobei f und f x stetig seien. (b) Differenzierbare Funktionen y = α(x) y = β(x) in [a, b]. Man betrachte den damit definierten Bereich B: O > N * = N = N > N Spezialfall: α(x) α = konstant = B ist ein Rechteck β(x) β = konstant 137
138 16. Parameterintegrale (c) f sei mindestens auf B definiert. Durch Integration über y bei festgehaltenem x wird folgende Funktion F = F (x) definiert: β(x) F (x) = f(x, y) dy, a x b. α(x) Zu beachten: Der Parameter x tritt sowohl im Integranden als auch in den Integrationsgrenzen auf. Problem: Differentiation von F. Satz 16.1 (Leibniz-Regel) Unter den obigen Voraussetzungen gilt die Differentiationsformel F (x) = d dx β(x) α(x) f(x, y) dy = β(x) α(x) f (x, y) } x {{} dy + f(x, β(x))β (x) f(x, α(x))α (x) }{{} Beitrag der Grenzen Differentiation unter dem Integral Spezialfälle: (a) α(x) α, β(x) β F (x) = β α f (x, y) dy, x 138
139 (b) α(x) α, β(x) = x F (x) = (c) f(x, y) = f(y) unabh. von x = f x = x α f (x, y) dy + f(x, y), x F (x) = f(x, β(x))β (x) f(x, α(x))α (x). 139
140 16. Parameterintegrale 14
141 17. Fourier-Reihen (Harmonische Analyse) Periodische Funktionen Harmonische Analyse In vielen technischen Prozessen stößt man auf Schwingungsvorgänge oder allgemeine periodische Vorgänge (Signale), die man mittels periodischer Funktionen beschreibt: Definition 17.1 Eine (reelle) Funktion f : R R heißt periodisch mit der Periode T >, wenn f(x + T ) = f(x) für alle x R. Einfache Eigenschaften periodischer Funktionen: (a) f(x + nt ) = f(x) für alle x R, n = 1, 2, 3,... (b) f(x T ) = f(x) mit T hat f auch die Periode nt, n = 2, 3,... für alle x R f hat auch die Periode T ( ) (c) f x + ( mt ) = f(x) für alle x R, m = 1, 2,... f hat auch die Periode nt, n = 1, 2,... f hat auch die Perioden nt, n = ±1, ±2, ±3,... Konvention: T > sei die kleinste Periode 141
142 17. Fourier-Reihen Die mathematisch einfachsten periodischen Funktionen mit der Periode T > sind nun: cos ωx, sin ωx cos 2ωx, sin 2ωx.. mit ω := 2π T cos kωx, cos kωx Beweis: Sei f(x) := cos kωx.. ( ) f(x + T ) = cos kω(x + T ) ( = cos kωx + k 2π ) T T = f(x) = cos(kωx + kωt ) = cos(kωx + k2π ) = cos kωx }{{} cos hat Periode 2π Lemma 17.1 Für jede beliebige Wahl der Koeffizienten a, a 1, a 2,..., a n, b 1, b 2,..., b n 142
143 17.1. Periodische Funktionen Harmonische Analyse ist das sog. trigonometrische Polynom s n (x) = a n 2 + (a k cos kωx + b k sin kωx) k=1 = a n 2 + a k cos kωx + k=1 eine periodische Funktion mit der Periode T. n b k sin kωx k=1 Bemerkung: Der Faktor 1 2 bei a steht nur aus Konventionsgründen. Spezialfälle: (a) b 1 = b 2 =... = b n = s n (x) ist gerade, d.h. s n ( x) = s n (x) für alle x R (b) a = a 1 = a 2 =... = a n = s n (x) ist ungerade, d.h. s n ( x) = s n (x) für alle x R Problem: Läßt sich die periodische Funktion f bei geeigneter Wahl der Koeffizienten a, a 1,..., a n, b 1, b 2,..., b n beliebig genau durch die trignonometrischen Polynome s n = s n (x) approximieren, wenn n, d.h. gilt f(x) = lim s n (x) = a n 2 + (a k cos kωx + b k sin kωx) k=1 = a 2 + a k cos kωx + k=1 mit gewissen Koeffizienten a, a 1,..., b 1, b 2,...? b k sin kωx 143
144 17. Fourier-Reihen Definition 17.2 a 2 + (a k cos ωx + b k sin kωx) heißt eine trigonometrische Reihe. Bemerkung: Es gilt: mit A k = a 2 k + b2 k, tan ϕ k = a k b k a k cos kωx + b k sin kωx = A k sin(kωx + ϕ k ) Problem:[Harmonische Analyse] Kann eine gegebene Welle in Sinuswellen zerlegt (aufgelöst) werden? Fourierreihen Gegeben sei die periodische Funktion f mit der Periode T >. Definition 17.3 (Die Fourierkoeffizienten von f) a k = 2 T = 2 T T +T/2 f(x) cos kωx dx f(x) cos kωx dx = 2 T = 2 T x +T f(x) cos kωx dx (für alle Konstanten x ) x T/2 ( ) f(x) + f( x) cos kωx dx T/2 k =, 1, 2,... b k = 2 T = 2 T T +T/2 f(x) sin kωx dx f(x) sin kωx dx = 2 T = 2 T x +T f(x) sin kωx dx (für alle x R) x T/2 ( ) f(x) f( x) sin kωx dx T 2 k = 1, 2,... Eulersche Formeln 144
145 17.2. Fourierreihen Definition 17.4 Die mit den Fourierkoeffizienten gebildete trigonometrische Reihe heißt die Fourierreihe von f. a = 2 T T f(x)dx a 2 = 1 T T f(x)dx Eigenschaften der Fourierkoeffizienten und der Fourierreihen 1) f gerade, d.h. f( x) = f(x) für alle x R a k = 4 T T/2 f(x) cos kωx dx, b k =, k =, 1, 2,... 2) f ungerade, d.h. f( x) = f(x) für alle x R f() = a k =, b k = 4 T T/2 f(x) sin kωx dx, k =, 1, 2,... Satz 17.1 (Konvergenz im quadratischen Mittel) Sei f beschränkt und stückweise stetig im Intervall < x < T. Dann gilt f(x) s n (x)) T ( 2dx, n. Satz 17.2 (Parsevalsche Gleichung) f sei beschränkt und stückweise stetig im Intervall < x < T. Dann gilt 2 T T f(x) 2 dx = a2 2 + (a 2 k + b 2 k), und die Fourierkoeffizienten (a k ), (b k ) bilden je eine Nullfolge. Bemerkung: Konvergenz der Kourierreihe im quadratischen Mittel (Satz 17.1) i.a. Konvergenz in jedem Punkt x R }{{} technische bedeutsame Konvergenzart! k=1 Die Dirichlet-Bedingungen (D.B.) Definition 17.5 Die D.B. für die periodische Funktion f = f(x) mit der Periode T > lauten 145
146 17. Fourier-Reihen s n x f x T D.B.1 T f(x) dx < + D.B.2 Innerhalb der Periode t T (und damit in jedem anderen Intervall x x x + T ) hat f nur eine endliche Anzahl von Maxima und Minima. D.B.3 Innerhalb der Periode t T hat f nur endlich viele Unstetigkeitsstellen Bemerkung: Da f periodisch mit der Periode T ist, kann statt dem in D.B. verwendeten Intervall t T jedes andere Intervall x t x + T verwendet werden. 146
147 17.2. Fourierreihen Satz 17.3 (Punktweise Konvergenz der Fourierreihe) Die D.B. seien erfüllt. Dann gilt: a) f stetig in x lim M s n(x) = f(x), d.h. die Fourierreihe konvergiert an jeder Stetigkeitsstelle x von f gegen den Funktionswert f(x) von f in x. b) f unstetig in x lim s n(x) = 1 ( ) f(x ) + f(x + ) n 2 = 1 ( ) lim 2 y x f(y) + lim y x f(x) y<x y> Damit ist 2 + (a k cos kωx + b k sin kωx) = a k=1 f(x), f stetig in x f(x ) + f(x + ), f unstetig in x 2 wobei a, a 1,..., b 1, b 2,... durch die Eulerschen Formeln (Def. 17.3) definiert sind. Beweise: a) Verschiedene Varianten der Eulerschen Formeln Zu zeigen ist das folgende Lemma 17.2 Ist g(x) eine periodische Funktion mit der Periode T >, dann gilt für jedes feste x R x +T x g(x)dx = T g(x)dx. Beispiel: Beweis:von Lemma
148 17. Fourier-Reihen g x T T x T g x dx = x x x T g x dx x i) Zu x existiert ganze Zahl m, so dass x + mt T. Wegen 148
149 17.2. Fourierreihen g(x) = g(x + mt ) ist x +T x g(x)dx = x +T x g(x + mt )dx = x +mt +T x +mt g(x)dx = y +T y g(x)dx mit y = x + mt ii) Es ist nun x +T x g(x)dx = = = y +T y g(x)dx = T y g(x)dx + T y T y g(x)dx + g(x)dx q. e. d. y +T T T g(x)dx g(x + T ) dx = }{{} g(x)dx + =g(x) y y g(x)dx T g(x)dx = x +T x g(x)dx für alle x R. b) Satz 17.4 Berechnung der Fourierkoeffizienten a k, b k Annahme: f(x) = a 2 + (a k cos kωx + b k sin kωx) für alle x k=1 149
150 17. Fourier-Reihen i) T f(x) cos mωx dx = Nun gilt T T a 2 cos mωx dx + + cos m }{{} ωx cos kωx dx = =y= 2π T x k=1 a k b k T T k=1 2π T 2π cos mωx cos kωx dx cos mωx sin kωx dx cos my cos ky dy = T 2π π, m = k, m k 2π, m = k = T 2π cos mωx sin kωx dx = T cos my sin ky dy 2π = T 2π = für alle m, k. Daraus folgt T f(x) cos mωx dx = T a 2 1dx = a T, wenn m = 2 T a k cos mωx cos kωx dx = a k T π, wenn k = m 2π 15
151 17.2. Fourierreihen Somit ist dann a = 2 T T f(x)dx = 2 T T f(x) cos mωx dx für m = a k = 2 T T f(x) cos kωx dx ii) T f(x) sin mωx = T a 2 sin mωx dx + + a k T k=1 T b k k=1 sin mωx cos kωx dx sin mωx sin kωx dx. T Nun gilt sin m ωx }{{} = y = 2π T x dx = T 2π 2π sin my dy = T m2π cos my 2π = T 2π sin mωx cos kωx dx = T sin my cos ky dy = für alle m, k 2π T 2π sin mωx sin kωx dx = T sin my sin ky dy 2π = T 2π, m k π, m = k. 151
152 17. Fourier-Reihen Daraus folgt jetzt, m = Somit ist T f(x) sin mωx dx = b k = 2 T T b k T sin mωx sin kωx dx = b k T π, m = k. 2π f(x) sin kωx dx, k =, 1,... Unter den Annahmen von Satz 17.3 hat f dann für jedes x R die Darstellung (Punktweise Konvergenz der Fourier-Reihe gegen f) f(x ) + f(x + ) = 1 T f(x)dx + 2 T f(x) cos kωx dx cos kωx 2 T T k=1 + 2 T T f(x) sin kωx dx sin kωx Fourierreihen-Darstellung von f Periodische Funktionen mit speziellen Eigenschaften (Symmetrien) a) Symmetrie 1. Art f gerade b) Symmetrie 2. Art f ungerade Diese beiden Symmetrien wurden bereits zu Beginn des Abschnitts 17.2 behandelt. c) Symmetrie 3. Art einer periodischen Funktion f mit der Periode T ( f x + T ) = f(x) 2 In diesem Fall gilt: 152
153 17.2. Fourierreihen i) Fourierkoeffizienten mit geradem Index a 2k = b 2k =, k =, 1, 2,... ii) Fourierkoeffizienten mit ungeradem Index a 2k+1 = 4 T b 2k+1 = 4 T T/2 T/2 f(x) cos(2k + 1)ωx dx mit ω = 2π T f(x) sin(2k + 1)ωx dx d) Symmetrie der Art 4.a Diese Symmetrie liegt vor, wenn f ungerade ist und die Symmetrie 3. Art hat. Daraus folgt: f ( x + T ) (( = f x T ) 4 4 Symmetrie 3. Art {}}{ + T ) ( = f x T ) 2 4 f ( x + T ) ( = f x T 4 4 f ungerade }{{} ) = f ( ( x T )) ( ) T = f 4 4 x Lemma 17.3 Im Falle einer Symmetrie der Art 4a gilt: Damit ergibt sich dann f ( ) ( ) T T 4 + x = f 4 x für alle x R a k = b 2k =, k =, 1, 2,... b 2k+1 = 8 T/4 f(x) sin(2k + 1)ωx dx, k =, 1, 2,... T e) Symmetrie der Art 4.b In diesem Fall ist f gerade (Symmetrie 1. Art) und hat die Symmetrie
154 17. Fourier-Reihen Art. Dies ergibt Somit folgt: f ( x + T ) 4 (( = f x T ) + T ) 4 2 ( ( = f x T )) 4 = f = f ( x T ) 4 ( ) T 4 x Lemma 17.4 Hat die periodische Funktion f eine Symmetrie der Art 4b, so gilt: ( ) ( ) T T f 4 + x = f 4 x für alle x R Daraus folgt: b k = a 2k =, k =, 1, 2,... a 2k+1 = 8 T/4 f(x) cos(2k + 1)ωx dx, k =, 1, 2,... T Einige konkrete Fourierentwicklungen Die Dirichletschen Bedingungen (D.B.) seien erfüllt. Nach Satz 17.3 gilt dann: ( ) f(x ) + f(x + ) f(x) = a (a k cos kωx + b k sin kωx) x Stetigkeits- x Unstetigkeitsstelle von f stelle von f 154
155 17.3. Einige konkrete Fourierentwicklungen Beispiel: A) Definition 17.3 ergibt: a = a k = {}} = { k 1 b k = = 2 T 2 T 2 T 2 T 2 T i i 1 T dx = 2 T f(x) cos kωx dx = 2 T 1 sin kωx kω T 1 kω Es gilt also für alle k 1 und damit i i 1 f(x) sin kωx dx = 2 T ( cos kωx) a k = 2 T kω b k = 2 T kω i i 1 i i 1 1 cos kωx dx = 2 1 ( ) sin kωi sin kω(i 1) T kω = 2 T i i 1 1 sin kωx dx ( ) sin kωi sin kω(i 1) ( cos kω(i 1) cos kωi a k 4 T kω lim k a k = b k 4 T kω lim k b k = 1 ( ) cos kω(i 1) cos kωi kω ) 155
156 17. Fourier-Reihen Wegen ω = 2π T ist insgesamt: a = 2 T a k = 1 ( ) sin kωi sin kω(i 1), b k = 1 ( ) cos kω(i 1) cos kωi, k 1 kπ kπ mit festem i, 1 < i T. Ein Spezialfall: Gerade Pulsfunktion f wird eine gerade periodische Funktion, wenn die Stelle i, so gewählt wird, dass (i 1) + i 2 = T 2 2i 1 = T i = 1 + T 2 Für eine gerade periodische Funktion gilt aber b k =, k = 1, 2,
157 17.3. Einige konkrete Fourierentwicklungen Überprüfung: Es gilt k πb k = cos kω(i 1) cos kωi = cos k 2π ( 1 + T T 2 = cos k 2π ( ) T 1 cos k 2π 1 + T T 2 T 2 ( = cos k 2π T T 2 k 2π T 1 ) ( cos k 2π 2 T ( = cos kπ kπ ) ( cos kπ + kπ ) T T ) 1 cos k 2π 1 + T T k 2π ) T T 2 = cos kπ cos kπ kπ + sin kπ sin T T =, da sin kπ = für alle k. Damit ist also bestätigt, dass b k = für alle k = 1, 2,.... Weiter gilt: kπa k = sin kωi sin kω(i 1) = sin k 2π 1 + T ( T 2 = sin kπ + kπ ) ( sin kπ kπ ) T T ( = } sin{{ kπ} cos kπ kπ + cos kπ sin T T sin }{{ kπ} = = = cos kπ 2 sin kπ T ( cos kπ cos kπ ) kπ sin kπ sin T T sin k 2π T cos kπ T T 1 2 ) kπ cos kπ sin T Somit gilt a k = 2 k π sin kπ T, ( sin kπ T wenn k gerade ), wenn k ungerade Beispiel: B) f ungerade Pulsfunktion Da f ungerade ist, gilt a k =, k =, 1, 2,... (Symmetrie 2. Art). 157
158 17. Fourier-Reihen Nach Def hat man b k = 4 T T/2 f(x) sin kωx dx = 4 2L L f(x) sin kωx dx = 2 L = 2 1 ( cos kωx) L kω i i 1 i i 1 = 2 L 1 sin kωx dx 1 ( ) cos kω(i 1) cos kωi. kω Nun gilt 2 L 1 kω = 2 L 1 k T 2π = 1 2L kl π = 2 kπ 2π und ω = T = 2π 2L = π L. Dies ergibt dann für ein fest gegebenes i, 1 < i L, a k =, k =, 1, 2,... b k = 2 ( ) cos kω(i 1) cos kωi, k = 1, 2,.... kπ }{{} =γ ik Gestalt der Terme γ ik = cos kω(i 1) cos kωi, i = 1, 2,..., T 2 = L für bel., 158
159 17.3. Einige konkrete Fourierentwicklungen aber festes k i = 1 : γ ik = cos cos kω = cos cos kπ L i = 2 : γ 2k = cos kω cos 2kω = cos kπ L cos 2kπ L i = 3 : γ 3k = cos 2kω cos 3kω = cos 2kπ L 2kπ cos L cos 3kπ L [, kπ] wird.. in L Intervalle i : γ ik = cos kω(i 1) cos kωi = cos(i 1) kπ L cos ikπ L der Länge kπ L. zerlegt i = L 1 : γ L 1k = cos kω(l 2) cos kω(l 1) = cos(l 2) kπ L cos(l 1)kπ L i = L : γ Lk = cos kω(l 1) cos kωl = cos(l 1) kπ L cos L L kπ Vergleich von γ ik und γ (L i+1)k : L gerade : i = 1, 2,..., L (= M) 2 L ungerade : sei M = 1 (L 1) i = 1, 2,..., M 2 i = M + 1 bleibt dann als Zentrum übrig 159
160 17. Fourier-Reihen γ (L } {{ i + 1 = cos(j 1) kπ )k } L cos j kπ L j ( ) kπ = cos (L i + 1) 1 L cos(l i + 1)kπ L = cos(l i) kπ ) kπ (L L cos (i 1) ( L = cos L kπ ) L cos ikπ + sin Lkπ L L sin ikπ L ( cos L kπ ) L cos(i 1)kπ + sin Lkπ L L sin(i 1)kπ L = cos kπ cos i kπ L cos kπ cos(i 1)kπ ( L = cos kπ cos i kπ ) L cos(i 1)kπ }{{ L} wegen sin kπ = k γ (L i+1)k = (cos kπ)γ ik = γ ik, γ ik = cos(i 1) kπ L cos ikπ L Satz 17.5 γ (L i+1)k = γ ik, γ ik, k gerade k ungerade und alle i = 1, 2,..., L, wenn L gerade 2 i = 1, 2,..., M = L 1, wenn L ungerade 2 16
161 17.3. Einige konkrete Fourierentwicklungen Beispiel: C) Allgemeine ungerade Pulsfunktion mit Werten +1 und -1 f ungerade es genügt, die Werte f(x) auf x L = T 2 vorzugeben. Definition 17.6 Die Funktionen 1 1 (x), 1 2 (x),..., 1 L 1 (x) seien wie folgt definiert: 1 1 (x) := 1 2 (x) := 1 i (x) := Schliesslich setzen wir 1, < x 1, 1 < x L = T 2 und x = 1, 1 < x 2, x [, L]\(1, 2] 1, i 1 < x i, x [, L]\(i 1, i] für i < i < L 1 L = 1, L 1 < x L, x L
162 17. Fourier-Reihen Beispiel: L = 4 162
163 17.3. Einige konkrete Fourierentwicklungen Modifikation: Auch die folgende Wahl ist zulässig: 1 1 (x) = 1, < x < 1, sonst auf [, L].. 1 i (x) = 1, i 1 < x < i, sonst auf [, L] für 1 i L.. 1 L (x) = 1, L 1 < x < L, sonst auf [, L] mit beliebigen Werten f(1), f(2),..., f(l) (z.b. alle =). Auf dem Intervall x T = L gilt dann 2 L f(x) = α i 1 i (x), x L i=1 mit α i = +1 oder α i = 1 damit ist die periodische, ungerade f ungerade Auf dem Intervall T 2 x gilt f( x) := L α i 1 i (x), x T 2 = L i=1 Untersuchung der Unstetigkeitsstellen: Funktion vollständig erklärt! Mögliche Unstetigkeits- oder Sprungstellen sind: i =, 1, 2,..., L (L + 1, L + 2,..., 1, 2,...). 163
164 17. Fourier-Reihen Für jede Stelle i gilt: f(i ) = f(i + ) = +1, α i 1 = +1 1, α i 1 = 1 +1, α i = +1 1, α i = 1. Daraus folgt 1, α i 1 = α i = +1 a 2 + (a k cos kωx + b k sin kωx) }{{} = x=i }{{} Summe der F-Reihe f(i ) + f(i + ) 2 =, α i 1 = 1, α i = 1, α i 1 = 1, α i = 1 1, α i 1 = α i = 1 Für i = gilt in jedem Fall: Summe der F-Reihe = = = f(). Die Fourier-Entwicklung von f Für eine ungerade Funktion gilt nach Abschnitt 17.2 a k =, k =, 1, 2,... b k = 4 T T 2 f(x) sin kωx dx. 164
165 17.3. Einige konkrete Fourierentwicklungen Wegen T = 2L gilt dann b k = 4 2L = 2 L = 2 L L L i=1 L i=1 = 2 1 L kω ( L ) α i 1 i (x) sin kωx dx α i i=1 L 1 i (x) sin kωx dx = 2 L L i=1 1 α i (cos kω(i 1) cos kωi kω }{{} L α i γ ik = 2 1 L L k π i=1 =γ ik ) L α i γ ik, i=1 α i i i 1 1 sin kωx dx da ω = 2π T = 2π 2L. Somit hat man für die Koeffizienten folgende Darstellung: Satz 17.6 b k = 2 k π L α i γ ik, k = 1, 2,..., i=1 a k =, k =, 1, 2,.... Der obige Satz liefert dann die folgende Abschätzung: b k 2 k π also L α i }{{} i=1 =1 γ ik }{{} 2 2 k π 2 L, b k 4L π 1 k. Zusätzliche spezielle Annahmen über das Eingangssignal f(x) Folgende Annahmen wurden bisher gemacht: * f periodisch mit Periode T, L = T 2 165
166 17. Fourier-Reihen * f ungerade * f bestimmt durch f(x) = T α i 1 i (x), x < L i=1 Wir machen jetzt noch die folgende zusätzliche Annahme: ( * f (4a)-symmetrisch, d.h. f sei ungerade und f x + T ) = f(x). 2 Daraus folgt f ( ) ( ) T T 4 + x = f 4 x Lemma 17.5 Ist f ungerade und gilt f folgt Beweis: von Lemma 17.5 ( f x + T ) = f 2 Es folgt: f ( ) T 4 + x für alle x. = f ( x + T ) = f(x) (Symmetrie 3. Art). 2 ( T T 4 + = f( x) = f(x). ) ( ) 4 + x T = f 4 x = f }{{} x ( ) T 4 x für alle x, dann ( T ( T )) x Korollar 17.1 Sei f ungerade. f ist genau dann (4a)-symmetrisch, d.h. f ( ) ( ) T T f(x), wenn f 4 + x = f 4 x für alle x. ( x + T ) = 2 Beweis: Lemma 17.3 und Lemma Analog: (4b)-Symmetrie Lemma 17.6 Sei f gerade und f ( f x + T ) = f(x). 2 ( ) ( ) T T 4 + x = f 4 x für alle x. Dann ist 166
167 17.3. Einige konkrete Fourierentwicklungen Beweis: f ( x + T ) 2 = f T 4 + T 4 + x = f }{{} x = f( x) = f(x). ( ) ( ( )) T T T 4 x = f x Korollar 17.2 Sei f gerade. f ist genau dann (4b)-symmetrisch, d.h. f ( ) ( ) T T f(x), wenn f 4 + x = f 4 x für alle x. ( x + T ) = 2 Beweis: Lemma 17.4 und Lemma Folgerungen im Falle der (4a)-Symmetrie Da f ungerade ist, gilt f (3)-symmetrisch } L = T 2 ( ) T f 4 + x ( ) L f 2 + x ( ) T = f 4 x ( ) L = f 2 x für alle x für alle x. Somit genügt die Bedingung: ( ) L f 2 + x = f ( ) L 2 x, x L 2 Konsequenzen für die Variablen α i, i = 1, 2,..., L: α i = α L i+1, i = 1, 2,..., M L M = 2, L gerade L 1, L ungerade 2 167
168 17. Fourier-Reihen Achtung: In diesem Fall ist 1 i = 1 (i 1,i) zu verwenden und f() = f(l) =, f(1) = f(l 1), f(2) = f(l 2),... f(m 1), M gerade bzw. f(m) = f(m + 1), M ungerade, zu setzen. Konsequenzen für die Fourierkoeffizienten L Sei also α i = α L i+1, i = 1, 2,..., M = 2, L gerade L 1, L ungerade (α M+1 = α L+1 beliebig) 2 2 und f(1), f(2),..., f(l) sei gemäß obiger Bemerkung, d.h. (4a)-Symmetrie, gewählt. Damit gilt f ist (4a)-symmetrisch a k =, k =, 1, 2,... (da f ungerade) b 2m =, m = 1, 2,... Bemerkung: b 2m = folgt auch direkt bei beliebigen Werten f(i). Beweis: Zu untersuchen ist b 2m = 2 L α i γ i2m. 2mπ i=1 }{{} gemäß Satz 17.6 i) L gerade: L α i γ i2m = i=1 = = L/2 (α i γ i2m + α L i+1 γ (L i+1)2m ) }{{} i=1 = γ i2m (Satz 17.5) LL/2 i=1 γ i2m (α i α }{{ L i+1 ) } = Beweis: 168
169 17.3. Einige konkrete Fourierentwicklungen ii) L ungerade: L α i γ i2m = i=1 = M (α i γ i2m + α L i+1 γ (L i+1)2m }{{} ) + α (M+1) γ (M+1)2m = γ i2m (Satz 17.5) M γ i2m (α i α }{{ L i+1 ) + α } (M+1) γ (M+1)2m i=1 i=1 = = α (M+1) γ (M+1)2m Für i = M + 1 ist γ (M+1)2m = cos 2mπ L = cos 2mπ L ( = ( L ( L 2 1 cos mπ cos 2mπ L = cos mπ cos 2mπ l ) 1 ) cos 2mπ ( ) L + 1 L 2 cos 2mπ ( ) L L ) ( sin 2mπ L + } sin{{ mπ} = ( = cos mπ 2mπ L cos mπ cos 2mπ L ) ( cos mπ + 2mπ ) L ) sin 2mπ L sin }{{ mπ} = cos mπ cos 2mπ L = Satz 17.7 Falls α i = α L i+1, i = 1, 2,..., M (α M+1 beliebig, wenn L ungerade), dann ist b 2 = b 4 = b 6 =... = b 2m =... = für alle m. Gestalt der Fourierkoeffizienten b 1, b 3, b 5,..., für ungerade k i) L gerade: M = L 2 Für l = 1, 3, 5,... gilt b k = 2 kπ = 2 kπ L i=1 α i γ ik = 2 kπ M (α i + α L i+1 )γ ik i=1 M ( ) α i γ ik + α L i+1 γ (L i+1)k }{{} i=1 =γ ik 169
170 17. Fourier-Reihen ii) L ungerade: M = L 1 2 Für k = 1, 3, 5,... ist b k = 2 kπ L α i γ ik = 2 M ( kπ i=1 i=1 α i γ ik + α L i+1 γ (L i+1)k }{{} =γ ik ( = 2 M ) (α i + α L i+1 )γ ik + α M+1 γ (M+1)k kπ i=1 Ist min α L i+1 = α i, i = 1, 2,..., M, dann gilt L gerade: b k = 2 kπ M 2α i γ ik i=1 L ungerade: b k = 2 ( m ) 2α i γ ik + α M+1 γ (M+1)k kπ i=1 ) + α M+1 γ (M+1)k Satz 17.8 Falls α i = α L i+1, i = 1, 2,..., M (α M+1 beliebig bei ungeradem L), dann gilt für ungerade k = 1, 3, 5,... 4 M α i γ ik, L gerade kπ i=1 b k = ( M ) 4 γ (M+1)k α i γ ik + α M+1, L ungerade kπ 2 i= Transformation von f mittels eines Tiefpasses: Filterung von f Tiefpass: Lineares Input Output System, das nur tiefe Frequenzen durchläßt. Mathematisch wird ein Tiefpass oder allgemeiner ein lineares Input Output Sy- 17
171 17.4. Transformation von f mittels eines Tiefpasses: Filterung von f stem wie folgt beschrieben: y(t) = + h(t s)f(s)ds = + h(s)f(t s)ds, wobei h = h(s) die Gewichtsfunktion des linearen System ist. Beschreibung im Frequenzbereich: Dazu betrachtet man die Fouriertransformierte F = F (ω), Y = Y (ω), H = H(ω), ω R, der Zeitfunktion f = f(t), y = y(t), h = h(t), wobei ω nicht mit ω := 2π T verwechselt werden darf: F (ω) := Y (ω) := H(ω) := f(t)e iωt dt f(t) = 1 2π + y(t)e iωt dt y(t) = 1 2π + h(t)e iωt dt h(t) = 1 2π + f(ω)e iωt dω Y (ω)e iωt dω H(ω)e iωt dω Aus der Definition von y = y(t) folgt dann + + y(t) = f(s)h(t s)dx = 1 2π = 1 2π + = 1 2π + F (ω) ( + + ) h(t s)e iωs ds dω f(ω)e iωs dω h(t s)ds + dωf (ω)e iωt h(t s)e iω(t s) ds = 1 2π } {{ } =H(ω) + F (ω)h(ω)e iωt dω, also Y (ω) = F (ω) H(ω). 171
172 17. Fourier-Reihen H(ω) heißt Übertragungsfunktion oder Frequenzgang des linearen Systems Definition des Tiefpasses: (Idealfall) Definition 17.7 Nur tiefe Frequenzen ν mit ν = passieren. ω 2π ω c 2π können das Filter 172
173 17.4. Transformation von f mittels eines Tiefpasses: Filterung von f Zu beachten: Der ideale Tiefpass ist physikalisch nicht realisierbar Übertragungsfunktion eines realisierbaren Tiefpasses: Andere Filter zum Vergleich: Mit ω = 2π T = π L, L = T, betrachten wir das Eingangssignal 2 f(t) = b 2k+1 sin(2k + 1)ω t = b 1 sin w t + b 3 sin 3w t Die Fouriertransformierte von f = f(t) lautet: F (ω) = = + f(t)e iωt dt = b 2k+1 =iπ ( ) b 2k+1 iπ δ (ω + (2k + 1)ω + sin(2k + 1)ω te iωt dt ( }{{} ) ( ) ) δ (ω+(2k+1)ω δ ω (2k+1)ω ( ) ) δ ω (2k + 1)ω. 173
174 17. Fourier-Reihen Am Ausgang des Filters erhält man: y(t) = 1 2π + = 1 2π +ω c ω c F (ω) H(ω)e iωt dω = 1 +ω c F (ω) 2π ω c Tiefpass ) ( ) iπe iωt b 2k+1 (δ (ω ) + (2k + 1)ω δ ω((2k + 1)ω dω = +ω c ( 1 ) ( ) b 2k+1 iπ δ (ω ) + (2k + 1)ω δ ω (2k + 1)ω dω 2π ω } c {{} 8 >< = sin(2k + 1)ω t, wenn (2k + 1)ω ω c >:, sonst Satz 17.9 y(t) = (2k+1)ω ω c b 2k+1 sin(2k + 1)ω t Ausgang des Tiefpass-Filters [ ] [ ] ωc ωc T Sei = := kleinste in ω c enthaltene natürliche Zahl 2π ω ω Wegen 2k + 1 ωc T 2π folgt: y(t) = h 1 ωc i 1 2 ω b 2k+1 sin(2k + 1)ω t Korollar 17.3 Nur die Koeffizienten b 2k+1 mit 2k + 1 ω c T 2π sind zu betrachten. Sei nun N die größte ungerade Zahl, so dass die Frequenz Nω gerade noch passieren kann, die höheren Frequenzen sollen herausfiltriert werden Nω ω c 174
175 17.4. Transformation von f mittels eines Tiefpasses: Filterung von f Daraus folgt y(t) = b 1 sin ω t }{{} +b 3 sin 3 ω t + b 5 sin 5ω t b N sin N ω }{{} t Grund- Schwingung Oberwellen 175
176 17. Fourier-Reihen 176
177 18. Die Laplace-Transformation von DGLn Die Laplace-Transformation von Funktionen Gegeben: Für eine Funktion y = y(x), definiert (mind.) für alle x, bezeichnet { } L(y) = L y(x) die Laplace-Transformation der Funktion y(x). Diese ist wie folgt definiert: Definition 18.1 { } L y(x) = Y (s) := + e sx y(x)dx, s R (18.1) { } + C 2 L y 2 (x) für belie- Eigenschaften der Laplace-Transformation L: { } } 1. Linearität: L C 1 y 1 (x) + C 2 y 2 (x) = C 1 L{y 1 (x) bige Konstanten C 1, C 2 R Deutigkeit: { } { } Sei Y 1 (s) = L y 1 (x), Y 2 = L y 2 (x). Es gilt Y 1 (s) Y 2 (s) = = y 1(x) y 2 (x). Die Urbildfunktion y(x) ist also durch ihre Bildfunktion Y (s) 1- deutig bestimmt: y(x) Y (s), also: { } Y (x) = L y(x) Laplace-Transformation { } y(x) = Λ Y (s) Rücktransformation (existiert!) ist auch linear! (18.2) 177
178 18. Die Laplace-Transformation von DGLn 3. a) y(x) 1 L{1} = + e sx dx = 1 s für s > b) y(x) = x r Durch partielle Integration ergibt sich die Rekursionsvorschrift: L{x r } = + e sx x r dx = 1 s e sx x r + + r s = r s L{xr 1 } für r > und s >. x r 1 e sx dx Mit 3a) gilt dann r = 1 : L{x} = 1 s L{1} = 1 s 2, s > r = 2 : L{x 2 } = 2 s L{x} = 2 s 3 = 2! s 3, x > r = 3 : L{x 3 } = 3 s L{x2 } = 6 s 4 = 3! s 4, s >. r = n : L{x n } = n! s n+1 für s > 4. a) y(x) = e x L{e x } = = + e sx e x dx = 1 s 1 für s > 1 + e x(1 s) dx = + e x(s 1) dx = e x(s 1) s a) b) y(x) = e x L{e x } = 1 s + 1 für s > 1 L{cos x} = sl{sin x} L{sin x} = 1 sl{cos x} 178
179 18.1. Die Laplace-Transformation von Funktionen Dies ergibt b) 6. Dämpfungssatz L{cos x} = s s L{sin x} = 1 s L{cosh x} = s s 2 1 L{sinh x} = 1 s 2 1 für alle s > für alle s > für alle s > 1 für alle s > 1 } L {y(x)e αx mit } L {y(x)e αx = Y (s + α), α R { } Y (s) = L y(x) = Y (s α) Beispiele: L{e αx } = L{1 e αx } = 1 s α, s > α, da Y (s) = L{1} = 1 s, s > L{xe αx } = 1 (s α), s > α, da Y (s) = L{x} = 1 2 s, s > 2 7. Ähnlichkeitssatz Sei a > { } L y(ax) = + + e sx y(ax)dx = e s u du a y(u) a {}}{ u = ax du = adx = 1 a + e s a u y(u)du = 1 a Y ( s a ), 179
180 18. Die Laplace-Transformation von DGLn { } mit Y (s) = L y(x). Beispiele: { } L cos(ωx) Weiter ist L{sin ωx} = = 1 ( s ) ω Y = 1 ω ω ω s 2 + ω, ω >, s > 2 s/w (s/w) = s s 2 + w 2, w >, s > L{e δx sin ωx} = Dämpfungssatz ω (s + δ) 2 + ω 2 für ω >, s > 8. Verschiebungssatz { } L y(x b) = + e sx y(x b)dx = + e s(u+b) y(u)du = e sb + b {}}{ u = x b e su y(u)du = e bs + e su y(u)du b { } = e bs L y(x), wenn b > und y(x) =, x < 9. Differentiationssatz Mittels partieller Integration ergibt sich { } L y(x) } s > = + = y() s e sx }{{} v y(x) }{{} u + dx = 1 s e sx y(x) e sx y (x)dx. s } { {{ } } =L y (x) + e sx s y (x)dx 18
181 18.1. Die Laplace-Transformation von Funktionen Damit ist { } L y(x) { } L y (x) = 1 } {y s y() +1 s L (x) { } = y() +sl y(x) für s >. (18.3) (18.4) Folgerung aus 18.4: { } { } L y (x) = L (y ) (x) { { } L y (x)} = L (y ) (x) { } = y () + sl y (x) { } ( = s 2 L y(x) { = y () + sl y (x) ( { } +s s 2 L y(x) { } = s 3 L y(x) ( = y () + s ) sy() + y () } = y () ) sy() y () ( s 2 y() + sy () + y () { }) y() + sl y(x) ). { } L y (n) (x) { } = s n L y(x) ( s n 1 y() + s n 2 y () sy (n 2) () ) +y (n 1) () (18.5) Aus (18.5) ergibt sich dann { } L y(x) = 1 s y() + 1 s 2 y () s n 1 y(n 2) () + 1 s n y(n 1) () + 1 } {y }{{} s L (n) (x) } n {{} Polynom in 1 Restglied R s n(s) }{{ { } } Entwicklung von L y(x) (18.6) 181
182 18. Die Laplace-Transformation von DGLn Rücktransformation { { }} { y(x) = Λ L y(x) (18.6) 1 Λ = s y() + 1 s 2 y () } s n y(n 1) () + R n (s) { } { } { } (Linearität von Λ ) = y() Λ +y () Λ y (n 1) () Λ s s }{{}}{{ 2 s }}{{ n } 1 x 1 (n 1)! } xn 1 { + Λ R(s) } {{ } r(x) = y() + y ()x + y () 2! x y(n 1) () (n 1)! } {{ } Taylorpolynom von y=y(x) x n 1 in x = } {{ } Satz von Taylor Somit ist (18.6) die Laplace-Transformation des Satzes von Taylor von y(x) mit Entwicklungspunkt x =. Anwendung: Wir setzen voraus, dass R n (s) und r n (x), n für alle x, s. Aus (18.6) und (18.7) folgt dann +r n (x) }{{} Restglied (18.7) y(x) = y() + y () 1! x + y () 2! x y(k) () k! x k +... Taylorentwicklung von y(x) in x = Y (s) = 1 s ( y() + 1 s y () + 1 s 2 y () s k y (k) () +... ) Entwicklung von Y (s) nach Potenzen von 1 s Beispiel: Y (s) = 1 s 1, s > 1 { } Die Rücktransformation in den Zeitbereich liefert y(x) = Λ Y (s) siehe Punkt 4. = e x, 182
183 18.1. Die Laplace-Transformation von Funktionen a) Entwicklung von Y (s) nach Potenzen von 1 s 1 s 1 = 1 s s = geom. Reihe ( ( 2 1 s s s) ( ) k ) = s k=1 1 s k, falls s > 1 ( s > 1). b) Rücktransformation y(x) = { } { } 1 1 Λ = Λ = s 1 s k k=1 = x n n! = ex. n= k=1 { } 1 Λ = s k k=1 x k 1 (k 1)! 1. Integrationssatz { x L } y(x)dx = partielle Integration 1 { } s L y(x) (18.8) Beispiel: Aus folgt sinh x = x cosh x dx L{sinh x} = 1 L{cosh x} }{{} s }{{} 1 s s 2 1 s
184 18. Die Laplace-Transformation von DGLn 11. Multiplikationssatz { } Y (s) = L y(x) = e sx y(x) dx Y (s) = Y (s) = { } ( x)e sx y(x) dx = L xy(x) { } ( x) 2 e sx y(x) dx = +L x 2 y(x). { } Y (n) (s) = ( 1) n L x n y(x). (18.9) Aus (18.9) folgt sowie { } Λ Y (n) (s) { } L x n y(x) = ( 1) n Y (n) (s) (18.1) { { }} = Λ ( 1) n L x n y(x) { { = ( 1) n Λ L x n y(x) }} = x n y(x)( 1) n, also Für n = 1 gilt 12. Faltungssatz { } y(x) = ( 1)n Λ Y (n) (s). (18.11) x n y(x) = 1 { } x Λ Y (s). y 1 = y 1 (x), y 2 = y 2 (x) seien zwei gegebene Funktionen. Definition 18.2 Unter der Faltung (y 1 y 2 )(x) = y 1 (x) y 2 (x) von y 1 und y 2 versteht man die Funktion y 1 (x) y 2 (x) := x y 1 (t)y 2 (x t)dt x y 1 (x t)y 2 (t)dt. (18.12) Offensichtlich ist y 1 (x) y 2 (x) = y 2 (x) y 1 (x) Kommutativität. 184
185 18.2. Anwendung der L-Transformation Es gilt nun { L y 1 (x) y 2 (x) } { } = L y 1 (x) { } L y 2 (x) = Y 1 (s) Y 2 (s) (18.13) Faltung von Multiplikation der y 1 (x) und y 2 (x) { } Λ Y 1 (s)y 2 (s) }{{} einfache Operation im Bereich der L-Transf. Laplacetransformierten = y 1 (x) y 2 (x) }{{} komplizierte Oper. im Bereich der Originalfunktionen (18.14) Beispiel: Es folgt Y (s) = 1 s 3 + s = 1 1 s s = Y 1(s) Y 2 (s) = L{1} L{sin x} { } { } y(x) = Λ Y (s) = Λ Y 1 (s) Y 2 (s) (18.13) 1 sin x = = x 1 sin(x t)dt = cos(x t) x = 1 cos x Anwendung der L-Transformation auf Anfangswertprobleme bei linearen DGLn mit konstanten Koeffizienten Wir betrachten zunächst eine DGL 2. Ordnung: a 2 y + a 1 y + a y = f(x), y() = y, y () = y (18.15) { } L{a 2 y + a 1 y + a y} = L f(x) =: F (s) (18.16) a 2 L{y } + a 1 L{y } + a L{y} = F (s) (18.17) 185
186 18. Die Laplace-Transformation von DGLn Wir setzen Aus (18.5) folgt dann { } L y (x) { } L y (x) { } Y (s) = L y(x). { } = y() + sl y(x) = y() + sy (s) = sy() y () + s 2 Y (s). Einsetzen in (18.17) ergibt ) ( ) a 2 (s 2 Y (s) sy() y () + a 1 sy (s) y() + a Y (s) = F (s), also ( ) (a 2 s 2 + a 1 s + a ) Y (s) sa }{{} 2 y() P (s)=char. Polynom von (18.15) a 2 y () + a 1 y() = F (s). Damit ist P (s)y (s) = sa 2 y + a 2 y + a 1 y }{{} +F (s) =:Q(s) Für dies F -Transformierte Y (s) von y(t) erhält man damit die explizite Darstellung: Y (s) = Q(s) P (s) + 1 F (s). (18.18) P (s) Die Rücktransformation ergibt nun { } { } { } Q(s) 1 y(x) = Λ Y (s) = Λ + Λ P (s) P (s) F (s). Wir setzen Λ { } { } Q(s) 1 := y 2 (x), Λ := y 1 (x) (18.19) P (s) P (s) und erhalten aus (18.19) die Darstellung { { } y(x) = y 2 (x) + Λ L y 1 (x) Mit dem Faltungssatz (18.13), (18.14) gilt dann y(x) = y 2 (x) + y 1 (x) f(x) = y 2 (x) + x { }} L f(x). f(x t)y 1 (t)dt (18.2) 186
187 18.2. Anwendung der L-Transformation { } Man beachte, dass F (s) = L f(x) nicht berechnet werden muss! Allgemeiner Fall: Anfangswertproblem für lineare DGLn n-ter Ordnung mit konstanten Koeffizienten Analog zum Fall n = 2 erhalten wir n a k y (k) = f(x), y (k) () = y (k), k =, 1,..., n 1 (18.21) { n } L a k y (k) n } a k L {y (k) Wir setzen wieder und erhalten aus (18.5) Setzt man dies in (18.23) ein, so folgt also { } = L f(x) = F (s) (18.22) = F (s) (18.23) { } Y (s) := L y(x) } k 1 L {y (k) = s k Y (s) s j y (k 1 j). j= j= n k 1 ) a k (s k Y (s) s j y (k 1 j) = F (s), P (s)y (s) n mit dem charakteristischen Polynom a k k 1 j= s j y (k 1 j) } {{ } =Q(s) P (s) = n a k s k und dem Polynom höchstens (n 1)-ten Grades = F (s), Q(s) = s n 1 a n y + s n 2 (a n 1 y + a n y ) (a 1 y + a 2 a a n y (n 1) ). 187
188 18. Die Laplace-Transformation von DGLn Damit gilt wieder Wir setzen und erhalten schließlich y 2 (x) := Λ y(x) = Y (s) = Q(s) P (s) + 1 F (s). (18.24) P (s) { } { } Q(s) 1, y 1 (x) := Λ P (s) P (s) Bemerkung zur Berechnung von y 1 (x), y 2 (x) x (18.25) f(x t)y 1 (t)dt + y 2 (x). (18.26) Q(s), P (s) sind Polynome (n 1)-ten bzw. n-ten Grades. Damit sind Y 1 := 1 P (s), Y 2 = Q(s) P (s) rationale Funktionen, wobei die Zählerfunktion einen niedrigeren Grad als die Nennerfunktion hat. 1. Fall: P (s) hat nur einfache reelle Nullstellen s = λ 1,..., λ n Partialbruchzerlegung liefert 1 P (s) Q(s) P (s) = = n k=1 n k=1 a k mit a k = 1 s λ k P (λ k ) C k s λ k mit C K = Q(λ k) P (λ k ). In praktischen Fällen werden die Koeffizienten a k bzw. C k, k = 1,..., n, durch Koeffizientenvergleich ermittelt. Durch Rücktransformation ergibt sich { } 1 y 1 (x) = Λ = P (s) y 2 (x) = Λ { } Q(s) = P (s) n { } 1 a k Λ = s λ }{{ k } =e λ k x n C k e λ kx k=1 k=1 n a k e λ kx k=1 188
189 18.2. Anwendung der L-Transformation Aus (18.26) folgt dann die Lösungsdarstellung x y(s) = y 2 (x) + f(x t)y 1 (t)dt = n C k e λ kx k=1 } {{ } =y h (x) x + ( n f(x t) k=1 ) a k e λ kt dt } {{ } =y p(x) wobei die Konstanten C k jetzt durch die Anfangsbedingungen bestimmt sind! 2. Fall: P (s) hat nur reelle, aber mehrfache Nullstellen 3. Fall: P (s) hat einfache reelle und komplexe Nullstellen 4. Fall: P (s) hat mehrfache reelle und komplexe Nullstellen Analoges Vorgehen, aber in der Partialbruchzerlegung treten Terme der Art 1 (x λ k ) j, j = 1,..., m k,... auf. Beispiel: 1. y + y = f(x), y() = y, y () = y Nach (18.18) hat man wobei Y (s) = Q(s) P (s) + 1 P (s) F (s), Q(s) = sa 2 y + a 2 y + a 1 y = sy + y P (s) = a 2 s 2 + a 1 s + a = s Dies ergibt Y (s) = sy + y s s F (s) = y s s y s s F (s), 189
190 18. Die Laplace-Transformation von DGLn also y(s) = { } { } { } s 1 Λ Y (s) = y Λ + y s 2 Λ + 1 s = y cos x + y sin x + f(x) sin x = y cos x + y sin x + x f(t) sin(x t)dt. { } 1 + Λ f(x) s Beispiele für Störungsfunktion f: a) f(x) = x f(x) sin x = x sin x y = y cos x + (y 1) sin x + x b) f(x) = e x f(x) sin x = 1 2 (ex cos x sin x) y = ( y 1 ) ( cos x + y 1 ) sin x ex c) f(x) = cos x f(x) sin x = x 2 sin x y = y cos x + y sin x + x 2 sin x 2. y + 2y + 2y =, y() = 1, y () = Q(s) = sa 2 y + a 2 y + a 1 y = s + 2, P (s) = s 2 + 2s + 2 Da f = und damit auch F =, ergibt sich aus (18.18) die Gleichung Y (s) = Q(s) P (x) + 1 P (s) F (s) = s + 2 = s + 1 (s + 1) (s + 1) s 2 + 2s + 2 Mit dem Dämpfungssatz folgt jetzt y(x) = e x (cos x + sin x). 19
191 18.3. Anfangswertprobleme bei Systemen linearer DGLn Anfangswertprobleme bei Systemen linearer DGLn Systeme 1. Ordnung mit konstanten Koeffizienten y 1(x) +a 11 y 1 (x) a 1n y n (x) = f 1 (x), y 1 () = y 1 y 2(x) +a 21 y 1 (x) a 2n y n (x) = f 2 (x), y 2 () = y (18.27) y n(x) +a n1 y 1 (x) a nn y n (x) = f n (x), y n () = y n Gesucht: y 1 (x),..., y n (x) Gegeben: Konstante Koeff. a ik, i, k = 1,..., n Funktionen f 1 (x),..., f n (x) Laplace-Transformation von (18.27) Definition 18.3 Analog zu Abschnitt 18.2 setzen wir { } Y j (s) := L y j (x), j = 1,..., n { } F j (s) := L f j (x), j = 1,..., n. Das DGL-System (18.27) ist dann äquivalent mit { L y i(x) + n j=1 } { } a ij y j (x) = L f i (x), i = 1, 2,..., n, also { } L y i(x) + n j=1 { } a ij L y j (x) = F i (s), i = 1, 2,..., n. 191
192 18. Die Laplace-Transformation von DGLn Mit (18.4) folgt und damit { } y i () + sl y i (x) + sy i (x) + n a ij Y j (s) = F j (s), i = 1, 2,..., n, j=1 n a ij Y j (s) = F j (s) + y i, i = 1,..., n. (18.28) j=1 Offensichtlich ist (18.28) ein LGS für Y (s) = ( Y 1 (s),..., Y n (s)) T : (s + a 11 ) a 12 a a 1n Y 1 (s) a 21 (s + a 22 ) a a 2n..... Y n (s) a n1 a n2 a n3... (s + a nn ) F 1 (s) + y 1 F 2 (s) + y 2 =. (18.29). F n (s) + y n Nach der Auflösung von (18.29) nach Y 1 (s),..., Y n (s) ergeben sich die Lösungen y 1 (x),..., y n (x) von (18.27) durch Rücktransformation Systeme von DGLn m-ter Ordnung Systeme dieses Typs lassen sich ganz analog wie Systeme 1. Ordnung behandeln. Beispiele: 192
193 18.3. Anfangswertprobleme bei Systemen linearer DGLn 1. y 1 = y 2, y 1 () = 1 y 2 = y 1, y 2 () = (18.3) Nach der Laplacetransformation von (18.3) ergibt sich y 1 + sy 1 = Y 2 sy 1 Y 2 = y 1 = 1 y 2 + sy 2 = Y 1 Y 1 + sy 2 = y 2 =, also Y 1 = Durch Rücktransformation findet man s s 2 1, Y 2 = 1 s 2 1. y 1 (x) = cosh x, y 2 (x) = sinh x. 2. y 1 = y 2, y 1 () =, y 1() = 1 (18.31) y 2 = y 1, y 2 /) =, y 2() = Die Laplacetransformation dieses Systems liefert { } { } ( ) L y 1(x) = L y 2(x) = y 2 () + sy 2 (s) = sy 2 (s) { } L y 2(x) { } = L y 1(x) = y 1 () + sy 1 (s) = sy 1 (s), also { } L y 1(x) = sy 1 () y 1() + s 2 Y 1 (s) = 1 + s 2 Y 1 (s) { } L y 2(x) = sy 2 () y 2() + s 2 Y 2 (s) = s 2 Y 2 (s). 193
194 18. Die Laplace-Transformation von DGLn Somit ist (18.31) mit folgendem LGS: 1 + s 2 Y 1 (s) = sy 2 (s) s 2 Y 2 (s) = sy 1 (s) Offensichtlich ist dies ein LGS für Y (s) = System 1. Ordnung. Auflösung des LGS für ( Y 1 (s), Y 2 (s)) T wie bei DGL- ( Y 1 (s), Y 2 (s)) T und Rücktransformation ergibt: Y 1 (s) = 1 s 2 +1 y 1 (x) = sin t y 2 (s) = 1 = 1 s y s(s 2 +1) s s (x) = 1 cos t. 194
195 Index Ähnlichkeitssatz, Deutigkeit, 175 abgeschlossen, 74 Ableitungsregeln, 81 Absolutfehler, 57, 92 allemgeine ungerade Pulsfunktion, 16 alternierende Folge, 1 Approximationsfehler, 57 arithmetische Zahlenfolge, 9 Arithmetisches Mittel, 16 Bandpass-Filter, 171 Bernoulli-Ungleichung, 12 beschränkt, 74 beschränkte Folgen, 11 Cauchy-Form, 56 Cauchysche Produktreihe, 33 Cauchysches Konvergenzkriterium, 15 Dämpfungssatz, 177 Definitionsbereich, 69 Differentiale höherer Ordnung, 113 Differentiationssatz, 178 Dirichlet-Bedingungen, 146 divergent, 11, 2, 35 bestimmt, 13, 21 Eigenwerte, 12 Entwicklungspunkt, 55, 112 Euklidische Norm, 124 Eulersche Formel, 147 Eulersche Formeln, 144 Extremalpunkt, 115 Faltung, 182 Faltungssatz, 182, 184 Fehlerrechnung, 91 Fourier-Entwicklung, 163 Fourier-Reihen, 141 Fourierentwicklungen, 153 Fouriertransformierte, 169 Funktion, 69 implizite, 95 Funktionalmatrix, 99 Funktionenfolge, 35 Funktionenreihe, 35 Gebiet, 74 geometrische Zahlenfolge, 9, 12 gerader Index, 152 Gewichtsfunktion, 169 Glieder, 19 Gliedweise Differentiation, 39 Integration, 39 Gradient, 9 Grenzfunktion, 36 Grenzwert, 11, 71 größte, 18 kleinste, 18 Grenzwertsätze, 14, 22,
196 Index Häufungspunkt, 16 Hessematrix, 111 Hochpass-Filter, 171 Hyperebene, 123 implizite Differentiation, 95, 96 Differentiation, allgemeiner Fall, 11 Form, 95 Integralform, 56 Integralkriterium, 27 Integrationssatz, 181 Karte, 7 Keplersche Gleichung, 95 Kettenregel, 85 erweiterte allgemeine, 86 verallgemeinerte, 85 Koeffizienten, 41 kompakt, 74 konvergent, 11, 2, 35 absolut, 29 bedingt, 32 gegen einen Punkt, 72 gleichmäßig, 37 unbedingt, 32 Konvergenz im quadratischen Mittel, 145 Konvergenzbereich, 35 Konvergenzkriterium Cauchysches, 23 Notwendiges, 22 Konvergenzmenge, 35 Konvergenzradius, 43, 44 kritischer Punkt, 116 Lagrange (Restglied), 56 Lagrange (Verfahren), 128 Lagrange-Multiplikatoren, 126 Lagrangefunktion, 126 Laplace-Transformation, 175 Leibniz-Regel, 138 Leibnizsches Konvergenzkriterium, 28 limes inferior, 17 superior, 17 Linearität, 175 Majorante, 24 Majorantenkriterium, 24, 29 Maximum globales, 115 lokales, 115 Minimum globales, 115 lokales, 115 Minorante, 25 Minorantenkriterium, 25, 3 Mittelwertsatz in R, 89 verallgemeinerter, 9 Monotonie, 1 Multiplikationssatz, 182 Näherungspolynom, 57 N.F., 13 Niveau-Flächen, 16 notwendige Bedingungen, 117 Nullfolge, 13 Optimalitätsbedingung hinreichende, 134 Optimalitatsbedingung hinreichende, 119 notwendige, 116 Parsevalsche Gleichung, 145 Partialsummen, 19 partielle Ableitung, 77 2.Ordnung, 82 periodische Funktionen, 141 periodische Vorgange, 141 Potenzreihe, 41 punktweise Konvergenz,
197 Index Quotientenkriterium, 25, 3 Rücktransformation, 18 Reihe, 19 geometrische, 2 harmonische, 21 Identitätssatz, 5 Summe, 2 unendliche, 19 Rekursionsvorschriften, 1 relative Maximalstelle, 115 Minimalstelle, 115 relativer Fehler, 92 relativer Zuwachs, 14 Restglied, 56, 112 Restriktionen, 123 restringiert, 123 Richtungsableitung, 14 Richtungsvektor, 13 trigonometrisches Polynom, 143 Ubertragungsfunktion, 17 ungerade Pulsfunktion, 156 ungerader Index, 152 Variable, 69 Vergleichskriterium, 24 Verschiebungssatz, 178 Wurzelkriterium, 31 Wurzelkritrium, 26 Zahlenfolge, 9 arithmetische, 9 geometrische, 9, 12 Zuwachsrate, 14 Zwischenwertsatz, 74 Sattelpunkt, 116, 118, 122 Schwarz, 82 Schwingungsvorgange, 141 singulär, 99, 1 stationarer Punkt, 116 stetig, 73 Summenfunktion, 36 Stetigkeit, 39 Symmetrien, 151 Tangente, 78 Tangentialebene, 78, 16 Gleichung, 16, 17 Taylorformel, 56, 113 Taylorpolynom, 56 Taylorreihe, 55 Teilfolge, 1 Tiefpass, 169, 171 Totales Differential, 91 Transformation, 169 trigonometrische Reihe,
Höhere Mathematik II
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Beilagen) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L A TEX-Satz
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Beilagen) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L A TEX-Satz
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
Kap. 10: Folgen und Reihen. Eine Funktion a : N Ñ R
 Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe. a 0 + a 1 + a 2 +
 8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
8 Reihen 38 8 Reihen Wenn man eine Folge gegeben hat, so kann man auch versuchen, eine Summe a 0 + a + a 2 + zu bilden. Wir wollen nun erklären, was wir darunter verstehen wollen. Zunächst kann man die
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler [email protected] mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler [email protected] mathe.stevenkoehler.de 2 Die Regeln von de l
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
k=1 {S n } n N konvergiert, so schreibt man: a n n=1 und spricht dann von Konvergenz oder Divergenz der unendlichen Reihe
 7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
7 Reihen sind spezielle Folgen, die durch Summation entstehen. Definition 7. : {a n } n N sei Folge in C; S n := n Folge {S n } n N unendliche Reihe. Falls a k statt lim S n. a k heißt {S n } n N konvergiert,
Folgen und Reihen. 1 Konvergenz
 Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler [email protected] mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler [email protected] mathe.stevenkoehler.de 2 Die Regeln von de l
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
GRUNDLAGEN MATHEMATIK
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 2. Folgen Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies Grundlagen Mathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 2. Folgen Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies Grundlagen Mathematik
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
KAPITEL 2. Folgen und Reihen
 KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
LS Informatik 4 & Folgen und Reihen. Buchholz / Rudolph: MafI 2 38
 3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
3. Folgen und Reihen Buchholz / Rudolph: MafI 2 38 Kapitelgliederung 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
ANALYSIS I FÜR TPH WS 2018/19 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
Folgen und Reihen. Mathematik-Repetitorium
 Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu. MC-Fragen Serie 1. Einsendeschluss: Freitag, der :00 Uhr
 D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
D-INFK Analysis I FS 2017 Prof. Dr. Özlem Imamoglu MC-Fragen Serie 1 Einsendeschluss: Freitag, der 26.09.2014 12:00 Uhr 1. Welche der folgenden Aussagen sind richtig? (a) Eine divergente Folge ist nicht
Kapitel 3: Folgen und Reihen
 Kapitel 3: und Reihen Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 3: und Reihen 1 / 29 Gliederung 1 Grundbegriffe 2 Abbildungen und elementare
Kapitel 3: und Reihen Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 3: und Reihen 1 / 29 Gliederung 1 Grundbegriffe 2 Abbildungen und elementare
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
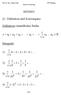 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
(alternierendes Vorzeichen) a n := ( 1)n n + 1 a n := 3n 2 7n a n := n(n 1)(n 2), n 3
 ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 43 2. Folgen und Reihen Folgen und Reihen werden in jedem Analysislehrbuch besprochen, siehe etwa [H, Kapitel III], [K, Kapitel 5], [J2, Kapitel 23] oder [M,
ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 43 2. Folgen und Reihen Folgen und Reihen werden in jedem Analysislehrbuch besprochen, siehe etwa [H, Kapitel III], [K, Kapitel 5], [J2, Kapitel 23] oder [M,
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
n=1 a n mit reellen Zahlen a n einen
 4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
Karteikarten, Analysis 2, Sätze und Definitionen nach der Vorlesung von PD Hanke
 Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, [email protected] Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, [email protected] Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Analysis I Lösung von Serie 14. Um die Inhomogene DGl zu lösen, müssen wir partikuläre Lösungen finden. (a) Wir machen den Ansatz:
 d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
d-infk Lösung von Serie 4 FS 07 4.. Inhomogene Lineare Differentialgleichungen Das charakteristische Polynom der homogenen DGl y (4) + y + y = 0 ist λ 4 + λ + = (λ + ). Seine Wurzeln sind ±i und jede hat
Kapitel IV. Analysis 2. 1 Reihen von Zahlen und Funktionen
 Kapitel IV Analysis 2 1 Reihen von Zahlen und Funktionen Sei a 0, a 1, a 2,... eine Folge von (reellen oder komplexen) Zahlen. Mit N S N := a n bezeichnet man die N-te Partialsumme der a n. Die Folge (S
Kapitel IV Analysis 2 1 Reihen von Zahlen und Funktionen Sei a 0, a 1, a 2,... eine Folge von (reellen oder komplexen) Zahlen. Mit N S N := a n bezeichnet man die N-te Partialsumme der a n. Die Folge (S
Beispiel. Gegeben sei die Folge (a n ) n N mit. a n := n 2 + 5n + 1 n. Es gilt. (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n n, woraus folgt
 Beispiel. Gegeben sei die Folge (a n ) n N mit a n := n 2 + 5n + 1 n Es gilt ( ( ) (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n + 1 + n, woraus folgt a n = (n2 + 5n + 1) n 2 n2 + 5n + 1 + n = 5n + 1 n2
Beispiel. Gegeben sei die Folge (a n ) n N mit a n := n 2 + 5n + 1 n Es gilt ( ( ) (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n + 1 + n, woraus folgt a n = (n2 + 5n + 1) n 2 n2 + 5n + 1 + n = 5n + 1 n2
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Kapitel 4 Folgen, Reihen & Funktionen
 Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Analysis I - Ferienkurs
 TU-München, Dienstag, der 6.03.200 Analysis I - Ferienkurs Andreas Schindewolf 5. März 200 Inhaltsverzeichnis. Folgen 3.. Konvergenz und Cauchy-Folgen..................... 3.2. Konvergenz-Kriterien für
TU-München, Dienstag, der 6.03.200 Analysis I - Ferienkurs Andreas Schindewolf 5. März 200 Inhaltsverzeichnis. Folgen 3.. Konvergenz und Cauchy-Folgen..................... 3.2. Konvergenz-Kriterien für
1 Folgen und Stetigkeit
 1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
Folgen und Reihen von Funktionen
 Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
HM I Tutorium 5. Lucas Kunz. 24. November 2016
 HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
HM I Tutorium 5 Lucas Kunz 24. November 206 Inhaltsverzeichnis Theorie 2. Definition einer Reihe.............................. 2.2 Wichtige Reihen................................. 2.3 Limites inferior
a 0, a 1, a 2, a 3,... Dabei stehen die drei Pünktchen für unendlich oft so weiter.
 7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
2 k k 1 k(k + 1) = 2n+1. n = 0 = k(k + 1) = 2n+1 n n. = 2 n+1 n + 2 (n + 1)(n + 2) + n. (n + 1)(n + 2)
 Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
Prof. Hesse Höhere Mathematik I und II Musterlösung 7. 0. 0, 80min Aufgabe (3 Punkte) Zeigen Sie mit vollständiger Induktion: Für alle n N gilt n k= k k k(k + ) = n+ n +. Induktionsanfang: k= Induktionsschluss
x k = s k=1 y k = y konvergent. Dann folgt (cx k ) = cx für c K. Partialsummenfolge konvergiert
 4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
,...) ist eine Folge, deren Glieder der Null beliebig nahe kommen. (iii) Die Folge a n = ( 1) n + 1 n oder (a n) = (0, 3 2, 2 3, 5 4, 4 5
 10 Folgen und Reihen 10.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n)schreibenwirkürzera n undbezeichnendieganzefolgemit(a n ) n Æ odereinfach(a n ),wasaber nicht
10 Folgen und Reihen 10.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n)schreibenwirkürzera n undbezeichnendieganzefolgemit(a n ) n Æ odereinfach(a n ),wasaber nicht
Folgen und Reihen. Mathematik I für Chemiker. Daniel Gerth
 Folgen und Reihen Mathematik I für Chemiker Daniel Gerth Überblick Folgen und Reihen Dieses Kapitel erklärt: Was man unter Folgen und Reihen versteht; Was man unter Grenzwert von Folgen und Reihen versteht;
Folgen und Reihen Mathematik I für Chemiker Daniel Gerth Überblick Folgen und Reihen Dieses Kapitel erklärt: Was man unter Folgen und Reihen versteht; Was man unter Grenzwert von Folgen und Reihen versteht;
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG [email protected] http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG [email protected] http://www2.mathematik.uni-wuerzburg.de
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
9 Konvergenz und absolute Konvergenz von Reihen
 9 Konvergenz und absolute Konvergenz von Reihen 9.2 Konvergenz von Reihen 9.5 Monotoniekriterium für Reihen 9.6 Konvergenzkriterium von Cauchy für Reihen 9.9 Rechenregeln für konvergente Reihen 9.10 Absolute
9 Konvergenz und absolute Konvergenz von Reihen 9.2 Konvergenz von Reihen 9.5 Monotoniekriterium für Reihen 9.6 Konvergenzkriterium von Cauchy für Reihen 9.9 Rechenregeln für konvergente Reihen 9.10 Absolute
Funktionsgrenzwerte, Stetigkeit
 Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I
 Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I Komplexe Zahlen Definition komplexer Zahlen in der Gaußschen Zahlenebene, algebraische Form, trigonometrische Form, exponentielle
Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I Komplexe Zahlen Definition komplexer Zahlen in der Gaußschen Zahlenebene, algebraische Form, trigonometrische Form, exponentielle
Mathematische Anwendersysteme Einführung in MuPAD
 Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Folgen und Reihen. Beschränkte Folge: Es gibt eine Zahl c = const.
 Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
Folgen und Reihen Folgen: Def.: Eine Abbildung a N K, n a(n) := a n (K = R C) wird Zahlenfolge genannt. Sie heißt reelle (komplexe) Zahlenfolge, falls K = R(C) ist. Symbole: a n K: Elemente der Folge,
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
V.1 Konvergenz, Grenzwert und Häufungspunkte
 V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
= (n 2 ) 1 (Kurzschreibweise: a n = n 2 ) ergibt die Zahlenfolge 1, 4, 9, 16, 25, 36,.
 2 Folgen, Reihen, Grenzwerte 2.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind (n N; auch
2 Folgen, Reihen, Grenzwerte 2.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind (n N; auch
