7. Der biegesteife Träger
|
|
|
- Samuel Kalb
- vor 7 Jahren
- Abrufe
Transkript
1 7. Der iegesteife Träger 7. Schnittgrößen - Begriffsidung In diesem schnitt so es um die inneren Kräfte in Bakentragwerken gehen. Gefühsmäßig wird man sagen, dass diese ein aß für die Beanspruchung des Bakenmaterias sind, und es ist eineuchtend festzusteen, dass ihre Kenntnis wichtig ist, wenn es darum geht, die Tragfähigkeit eines Rahmens zu untersuchen oder eine Tragwerk für vorgegeene Lasten richtig zu dimensionieren. Der Einfachheit haer eschränken wir uns im fogenden auf eene Tragwerke, die durch Kräftegruppen in der Zeicheneene eastet sind, so wie in der idung 7.. gezeigt. Die im Baken herrschenden inneren Kräfte werden an einer interessierenden Stee durch einen Schnitt senkrecht zur Schwerachse des Bakens sichtar gemacht. n der Schnittstee wirken dann üer die uerschnittsfäche verteite innere Kräfte, genannt p : idung 7... Dieses System kontinuierich verteiter ächenkräfte können wir nach den vorangegangenen usführungen durch eine Resutierende R sowie ein resutierendes oment ( S ) ersetzen. s Bezugspunkt für diese Reduktion wähen wir den Schwerpunkt S der etreffenden uerschnittsfäche. Im fogenden woen wir diese Wah stischweigend voraussetzen und assen den Inde S am omentensymo daher weg. Die Resutierende R zeregen wir in zwei Komponenten. Die erste wirkt in Richtung der Schwerachse (norma zur Schnitteene). Wir nennen sie N. Die andere,, wirkt in der Schnitteene, senkrecht zur Schwerachse. Wir sprechen auch von der Normakraft N, der uerkraft und dem Biegemoment, und ae drei Schnittgrößen sind in der idung 7.. dargestet. n Schnitt Schnitt p S ( S ) N. 7..: Zur Definition der Schnittgrößen. Offenar esteht der Baken nach dem Schnitt aus zwei Teien, an deren Schnittfächen jeweis N, und anzuringen sind und zwar so, dass eim Zusammenschuss eider Teie sich ae Schnittgrößen gegeneinander aufheen. Dieses zeigt die idung 7... Zur Charakteri- R 9
2 sierung der Vorzeichen der Schnittgrößen am inken wie am rechten Schnittufer führen wir, wie gezeigt, ein rechtwinkig kartesisches Koordinatensystem, y, z ein (mathematisch positiv orientiert), dessen -Richtung in Richtung der Schwerachse zeigt. m inken Schnittufer, das wie gezeigt durch eine ächennormae n charakterisiert ist, zeigt aso die -chse in Richtung dieser ächennormae, am rechten entgegengesetzt dazu. Die Vorzeichenfestegung autet nun: Positive Schnittgrößen zeigen am positiven / negativen Schnittufer in mathematisch positive Koordinatenrichtungen, und diese sind in der idung 7.. zu sehen. Diese Vorzeichenregeung git für die Kraftgrößen N und aer auch für die Schnittmomente, woei man im Hinick auf idung 7.. nur daran denken muss, dass eine Linksdrehung positiv und eine Rechtsdrehung negativ (Drehung hier in ezug auf die y -chse) gezäht wird. y z n N N inkes Schnittufer N n rechtes Schnittufer. 7..: Zur Bedeutung der Schnittufer. 7. Zur Berechnung von Schnittgrößen am geraden Baken 7.. Gerader Baken unter Einzeasten Wir etrachten den in idung 7.. dargesteten unter der Wirkung verschiedener Einzeasten iegenden Baken. Wir schneiden den Baken zunächst an seinen ufagern und B frei und estimmen die ufagerkräfte mit den ethoden, die in den vorangegangenen schnitten eräutert wurden. an erhät die ufagerkräfte, z und Bz. z y 9
3 z z nz n B N( ) n z z z z a a z nz n Bz ( ) ( ) z nz z z ( ) ( ) nz n a z Bz ( ) a 3 y N ( ) N( ) ( ) ( ) Bz. 7..: Gerader Baken mit Einzeasten. Nun schneiden wir den Baken an einer interessierenden uerschnittsstee senkrecht zur Schwerachse durch. Es entstehen die in der idung unten gezeigten Teiaken. n der Schnittstee werden die Schnittgrößen mit positivem Richtungssinn eingezeichnet. Nach dem Schnittprinzip iden ae auf einen Teiaken wirkenden Kräfte ein Geichgewichtssystem, und sie werden aus den für jeden Teiaken gütigen Geichgewichtsedingungen ermittet. Die Ergenisse einer sochen Rechnung werden oft in Diagrammen, den sogenannten Normakraft-, uerkraft- und omentenfächen zusammengefasst. ür das etreffende Bakeneispie sind diese in der idung 7.. zu sehen. Um die Bider zu verstehen, werten wir die Geichgewichtseziehungen aus. Zunächst fragen wir nach den Lagerreaktionen, und dazu werten wir die Geichgewichtseziehungen für den gesamten Baken aus: n n :, Bz aiiz Bz aiiz (7..) i i n n : ( ) ( ), B z ai iz z ai iz (7..) i i 9
4 n :. (7..3) i i Daei ezeichnet die Länge des Bakens und die Größen a i kennzeichnen von inks gemessen die ufpunkte der verschiedenen am Baken angreifenden Kräfte. Nachdem wir nun die ufagerkräfte as unktion ekannter Größen, nämich der am Baken vorgegeenen angreifenden Kräfte und omente, dargestet haen, untersuchen wir nun die Geichgewichtsedingungen am inken Teiaken. it anderen Worten, wir steen uns die ufgae, die isang unekannten Schnittgrößen N,, und zu erechnen. Eemparisch geschieht das für den inken Teiaken, und es findet sich: : i + N, (7..4) z : z iz, (7..5) n i S : z + ( ai ) iz +. (7..6) Daraus ermitten wir, dass git: + N i, (7..7), (7..8) z iz z ( ai ) iz. (7..9) In den etzten drei ormen sind die Summationen daei nur üer die für den inken Teiaken reevanten Kräfte und omente zu erstrecken. Zeichnerisch ist dieses Ergenis wie ereits gesagt in idung 7.. zu sehen. ithin ergeen sich im a der Norma- und uerkraftfächen aschnittsweise Geraden, nämich Paraeen zur Bakenachse und die omentenfächen esteht aus aschnittsweise unterschiedich geneigten Geraden (aktor in Geichung (7..9)). uf jedem a verschwinden die omentenfächen in den Bakenenden, und dies ist verständich, denn der Baken wird auf zwei Lagern gehaten, die keinerei omente aufnehmen können. an eachte, dass sich diese Zeichnungen stets durch konseuente uswertung (Kurvendiskussion) der Geichungen (7..7) is (7..9) ersteen assen. Dies kann sich as etwas mühseig erweisen. Praktischer ist der fogende Weg. an erechne zunächst ae ufagerkräfte. Ist dies geschehen, so fängt man entweder am inken oder am rechten Ende des nicht durchgeschnittenen Bakens an, Normakräfte, uerkräfte zw. omente zu erechnen. Beginnen wir eispiehaft am inken Ende und definieren die positive -Richtung as mit der Schwerachse nach rechts fortschreitend. Dann aut die Kraftkomponente z mit anwachsendem eine inear ansteigende omentenfäche auf, is zu dem Punkt, an dem die erste äußere uerkraftkomponente z eingeeitet wird. Die omentenfäche steigt von nun a weniger stei an. ehr noch: Sie wird sukzessive ageaut, ihre anfängich positive Steigung geht in eine negative Steigung üer, und das oment verschwindet schießich am Ende des Bakens. Das Vorzeichen der omentenfäche ermittet man ei dieser Vorgehensweise am einfachsten anhand des Verhatens der unter dem Baken eingezeichneten, strichierten Hifsinie. Wird diese i 93
5 durch die Wirkung der jeweis sichtaren Kräfte und omente gedehnt, so ist die omentenfäche positiv, wird sie gestaucht, hingegen negativ. Eine weitere Bemerkung ist angeracht. Differenziert man die Geichung (7..9) für das Schnittmoment nach dem Ort, so entsteht die Geichung (7..8) für die uerkraft, offenar esteht zwischen eiden Größen ein Zusammenhang. Wir schreien: d z + iz. (7..) d 7.. Baken auf zwei Stützen unter Einzeast (Dreipunktiegeproe) Gesucht sind die Normakraft-, uerkraft- und die omentenfäche für den in idung 7.. dargesteten Baken auf zwei Stützen unter Einzeast, aso eine Dreipunktiegeproe. Wir fogen zunächst dem formaen Weg, indem wir die ormen des etzten schnitts anwenden. Offenar git für die ufagerkräfte gemäß den Geichungen (7..-3): a Bz, z,. (7..) ithin fogt aus den Geichungen (7..7-9): a N,, für a,, für a, (7..), für a, a, für a. (7..3) Die zeichnerische Darsteung dieser Ergenisse ist in idung 7.. im rechten Tei zu sehen. an muss jedoch die Geichungen des etzten schnittes üerhaupt nicht parat haen, um schne die uerkraft- zw. die omentenfäche für dieses Proem zu zeichnen. Wenn man die ufagerkräfte kennt, so startet man einfach am inken zw. am rechten Bakenende und aut nach rechts zw. nach inks gehend die jeweiigen ächen auf. Beispiehaft sei dies für das rechte Ende eräutert. Die uerkraft ist hier geich dem negativen Wert von Bz, da die Normae auf der rechten Seitenfäche nach rechts zeigt, und die Kraft Bz offenar in negative Richtung von z weist. Der Wert der uerkraft ändert sich soange nicht, is die Stee der Krafteineitung erreicht ist. Die eingeeitete Kraft zeigt in positive z -Richtung und die uerkraftfäche erfährt einen Schu nach oen. it dem oment ist es ähnich: Die Kraft Bz aut die omentenfäche eim Wegschreiten vom rechten Ende inear auf und zwar is zu der Stee, wo die Kraft eingeeitet wird. Das oment ist nach unserer Vereinarung positiv (eachte die eingezeichnete strichierte Hifsinie) und erreicht an der Stee der Krafteineitung den Wert a /. Danach wird das oment wieder ageaut, denn die Kraft resutiert in einem negativen Beitrag zur omentenfäche (gesehen vom rechten Ende), der inear animmt und schießich eim inken Ende den Wert a erreicht. Dort jedoch hat die Kraft Bz das oment a geschaffen, so dass sich insgesamt der Wert Nu ergit. 94
6 a B z Bz ( ) z ( ) z. 7..: Baken auf zwei Stützen unter Einzeast Kragträger unter Einzeast und omentenwirkung Betrachte den unter Wirkung einer ußenast sowie eines omentes stehenden Kragträger der idung Der reischnitt ergit für die ufagereaktionen im Punkt :,,. (7..4) z Baut man die uerkraftfäche von der inken Seite auf (zum Beispie), so erkennt man, dass sich ein positiver Wert, nämich, ergit. Die uerkraft eit konstant, is ganz zum Schuss, wo die eingeeitete Kraft zu einem (vom inken Schnittufer aus as negativ eurteiten) Beitrag führt. z 3 z 95
7 . 7..3: Kragträger Bei der Konstruktion der omentenfäche geht man sinnvoerweise vom rechten Bakenende aus. Die Kraft staucht die strichierte Hifsinie unter dem Baken und die entsprechend negative omentenfäche aut sich von Nu kommend inear is auf den inimawert auf. Bei Üerschreiten der Bakenmitte wird pötzich das in ezug auf die Hifsinie positiv zu wertende oment sichtar. ithin erfogt ein Sprung auf den positiven Wert 3. Geht man weiter nach inks, so sammet die am rechten Bakenende immer noch sichtare Kraft weiterhin Heearm an und aut damit immer weiter oment a, een nochmas um. Damit vereit am inken Bakenende der omentenwert, was nicht weiter verwundert, denn schießich ist der Kragträger dort ja eingespannt. it ähnichen rgumenten geingt es, die omentenfäche auch von inks kommend aufzuziehen Zusammenhang zwischen Beastung und Schnittgrößen Zwischen der uerkraft und dem Schnittmoment esteht ein Zusammenhang, der im vorigen schnitt ereits für Einzekräfte hergeeitet wurde: Geichung (7..). Diesen Zusammenhang woen wir nun auf den a eieig verteiter Lasten (und etztich auch eieig geformter Baken) veragemeinern. Wir etrachten zu diesem Zweck einen unter einer Lastverteiung ( ) stehenden, statisch estimmt geagerten Baken (siehe idung 7..4) und denken uns in diesem ein Eement der Länge d herausgeschnitten. d ( ) d d ( ) d ( ) + d + d d d. 7..4: Ein eieig easteter Baken. Um diesen Schnitt durchführen zu können, muss man an eiden Seiten Schnittgrößen anringen und zwar auf der inken Seite die Größen N,, und auf der rechten Seite die Größen N + dn, + d und + d. Das Eement so sich im statischen Geichgewicht efinden, und infogedessen müssen die Geichgewichtsedingungen der Statik eachtet werden, die da auten: z d : d ( + d) ( ), (7..5) d d d S : d + d + + d. (7..6) d Dieses sind zwei gewöhniche Differentiageichungen erster Ordnung für die uerkraftfäche und für die omentenfäche. Wir können die Differentiageichung für die omentenfäche nochmas nach differenzieren und finden so unter Verwendung der Differentiageichung für die uerkraft den fogenden Zusammenhang: 96
8 d d ( ). (7..7) Integrieren wir die Beziehungen (7..5) und (7..6) nach, so entsteht: ( ) d + C, ( ) d C +. (7..8) Üer- Die eiden Integrationskonstanten C und C müssen aus sogenannten Rand- und gangsedingungen ermittet werden. Wie dies geht, wird im fogenden Beispie eräutert Integration der Differentiageichungen für uerkraft- und omentenfäche 7..6 Randedingungen für die uerkraft- und für die omentenfäche Wir eräutern den Begriff der Randedingungen an dem in idung 7..5 gezeigten Beispie. Dort sind drei unter der geichen konstanten Streckenast stehende Baken zu sehen, die jeweis verschieden geagert sind. Damit fogt aus der Geichung (7..8) zunächst: + C, + C + C. (7..9) Wir wissen, dass für den ersten Baken die omentenfäche jeweis an den Endpunkten verschwinden muss, denn eim reischnitt würden wir an eiden Endpunkten geeignete Kräfte in z -Richtung anringen, und diese haen in unmittearer Umgeung der Enden jeweis den Heearm Nu zur Verfügung. athematisch edeutet dieser a, dass: ( ), ( ). (7..) Im zweiten a muss mit dem geichen rgument wie een die omentenfäche zwar an der rechten Seite verschwinden, keineswegs jedoch an der inken Seite. Der Baken ist dort fest eingespannt. Dies entspricht, wie wir wissen, einer festen Einspannung, aso dreiwertigen Lagerung, und eine soche kann auch ein oment aufnehmen. m rechten Ende muss jedoch auch die uerkraftfäche verschwinden, denn schießich git es keine ufagerkraft, und die konstante Streckenast hat auch noch nicht angefangen zu wirken. so wird: ( ), ( ). (7..) Der dritte a schießich führt mit ähnichen rgumenten auf fogende Randedingungen: ( ), ( ). (7..) an estimmt nun die Konstanten aus Geichung (7..9) für jeden a getrennt, indem man die Beziehungen (7..-) einsetzt. Dies ergit jeweis zwei Geichungen für die eiden unekannten Integrationskonstanten, und die Endösung autet im a a):, ; (7..3) im a ): 97
9 , ; (7..4) und im a c):,. (7..5) Skizzen der uerkraft- und omentenfächen sind in idung 7..5 zu finden. an eachte die Struktur der uadratischen Parae, die sich in aen drei Lagerungsfäen as oge der Beastung mit einer konstanten Streckenast ergeen hat. B B : Unterschiedich geagerte Baken ei geicher Krafteegung Üergangsedingungen für die uerkraft- und für die omentenfäche Das Proem der Üergangsedingungen stet sich, soad die Beastung ( ) üer dem Baken nicht durch eine einzige unktion gegeen ist, sondern in Teiereichen durch mehrere unktionen dargestet wird. Wir woen uns das an dem in idung 7..6 gezeigten geenkigen Baken kar machen, für den wieder die uerkraft- und die omentenfäche gesucht sind. Wegen der unstetigen Beastung teien wir den Baken in zwei Bereiche, genannt I vor der Kraft, und II nach der Kraft. Wir verwenden dazugehörige Koordinaten und wie gezeichnet und setzen die Geichungen (7..8) für jeden Bereich getrennt an. 98
10 99 Parae uadratische Parae kuische a B B. 7..6: Baken mit zwei Beastungsfunktionen. Die Integration ergit: ( ) I I I : I C C C +, (7..6) ( ). 6 II : II 3 II II C C C (7..7) Die vier Integrationskonstanten ergeen sich aus den vier nachstehenden Rand- und Üergangsedingungen: ( ) ( ) ( ) ( ) ( ) ( ),,,, I II I II II I a a (7..8) denn es git ja keine freien omente und daher sote die omentenfäche üera stetig sein. Insgesamt erhaten wir aso vier Geichungen zur Bestimmung von vier Unekannten und wir finden die Lösung as: a + + II I 6, 6 (7..9) sowie:
11 I II +, a a (7..3) 7..8 omentenfäche ei kompizierteren Beastungen Betrachte die in idung 7..7 dargestete Situation: Ein in a und geagerter Baken der Länge steht unter einer Sinusast mit maimaer mpitude. Gesucht ist die uerkraftsowie die omentenfäche. ür diese Beastung setzen wir an: ( ) sin( B). (7..3) Darin sind und B zwei Konstanten, die wir geeignet anpassen müssen, nämich wieder üer Randedingungen. So wissen wir, dass die Last (gemäß der Skizze) an den Punkten a zw. verschwinden muss. so git: ( ) sin( B), ( ) sin( B). (7..3) ( ) π ( ) B ( ) ( π). 7..7: Schnittfächen eines Baken unter hügeformiger Beastung. Beide Bedingungen könnten wir dadurch erfüen, dass wir die Konstante geich setzen. Damit würde jedoch die Beastung identisch verschwinden, und das widerspricht unserer orderung, dass die Last nicht voständig verschwindet. Eine andere ögichkeit an den Randpunkten (und nur da) verschwindende Kräfteampituden zu ekommen, esteht darin, zu fordern, dass:
12 π B, B π B. (7..33) Damit erhaten wir aus den eiden für die Ränder formuierten orderungen nur ein Ergenis, nämich die Konstante B. Um die Konstante zu ermitten, denken wir daran, dass auf der itte des Bakens die Lastampitude gerade etragen so, aso geten muss: ( / ) sin( π/ ). (7..34) Wir erhaten somit: π. (7..35) ( ) sin Damit gehen wir in die Geichung zur Berechnung der uerkraft- und der omentenfäche, d.h. (7..5) und (7..6). Wir erhaten: und: ( ) ( ) d + C cos π + C (7..36) π ( ) ( ) d + C sin π + C + C. (7..37) π Die eiden Integrationskonstanten werden wieder aus geeigneten Randedingungen für die uerkraft- zw. für die omentenfäche ermittet. Es git offenar: ( ), ( ) (7..38) und somit fogt: C C. (7..39) Wir erhaten as Endergenis:, (7..4) π π ( ) cos π, ( ) sin π was in idung 7..7 graphisch dargestet ist. Beachte, dass dort, wo ( ) sein aimum hat, die uerkraft ( ) Nu wird, wie es nach dem differentieen Zusammenhang in (7..5) und (7..6) auch zu erwarten ist (Etremumsedingung).
13 7..9 Ein vergeichendes Beispie kn 5 knm m m m kn B kn z 5 kn "+" Bz 5 kn + kn N ( ) +d.h.zug +5kN ( ) ( ) 5 kn. 7..8: Schnittgrößen ei Beastung durch Punktkraft und oment. Wir etrachten die in idung 7..8 dargestete Situation: Ein Baken iegt auf zwei ufagern und wird mit Kräften kn sowie kn und einem oment 5 knm, wie gezeichnet, eastet. Wir woen die Norma-, uerkraft- sowie die Schnittmomentenfäche für diese Situation ermitten und zwar sowoh mit dem im Kapite 7.. vorgesteten an Einzeasten orientierten Verfahren, wie auch üer das im schnitt 7..4 eschrieene Differentiageichungsverfahren. Beginnen wir mit dem Einzeastverfahren. Wir ermitten zunächst die zum Geichgewicht nötigen ufagerasten. Eine einfache Rechnung iefert, dass git: kn, 5 kn, 5 kn. (7..3) z Bz Wir eginnen mit der Konstruktion der Normakraftfäche. Dazu starten wir (zum Beispie) am inken Bakenende. Es handet sich daei offenar um ein negatives Schnittufer. nhand der im schnitt 7. eräuterten Vorzeichendefinition schießen wir, dass es sich ei der nach inks weisenden Kraftkomponente um einen positiven Beitrag zur Normakraftfäche handen muss. Schreiten wir nach rechts in Richtung höherer Werte von ( Bakenachsenkoor-
14 dinate) voran, so ergit sich keine Änderung für N ( ). it anderen Worten: Die Normakraftfäche ist einfach geich einem positiven Wert, een 5 kn. Beachte, dass wir auch am rechten Bakenende hätten eginnen können. In diesem a iegt nämich ein positives Schnittufer vor. Gemäß der im schnitt 7. vorgesteten Vorzeichenregeung ergit sich der Normakrafteitrag von as positiv, denn der Pfei weist ja nach rechts. Schreiten wir in Richtung keinerer Werte von voran (mit anderen Worten, gehen wir nach inks), so ergit sich für die Normakraft keine Änderung. Wir erhaten aso das geiche Endresutat für die Normakraftfäche, unahängig davon, an wechem Ende wir eginnen, die äche aufzuzäumen. Und so muss es sein, denn ein Ergenis, das vom Beginn ahinge, wäre zweifesohne sinnos, wenn es darum geht, den Baken hinsichtich seiner Tragfähigkeit zu emessen. Und diese Bemerkung ringt uns noch darauf, auch das Vorzeichen der Normakraft zu eachten. Es ist positiv, aso wird der Baken in chsrichtung auf Zug eansprucht und wir müssen sichersteen, dass das gewähte Bakenmateria auch die (auf der chse üera konstante) Zugkraft aushät. Darauf werden wir später noch zu sprechen kommen. Nun zur uerkraftfäche: Wieder eginnen wir am inken Bakenende. Die dort eingeeitete uerkraft ist offenar durch den Wert z 5 kn gegeen. Wieder emerken wir, dass es sich eim inken Bakenende um ein negatives Schnittufer handet. so iefert genannte Kraft, da sie nach oen weist, einen positiven Beitrag zur uerkraftfäche. Dieser ändert sich nicht, wenn wir nach rechts in Richtung höherer Werte von voranschreiten, jedenfas soange nicht, is wir die Stee kreuzen, an der die uerkraft kn eingeeitet wird. Hier kommt offenar ein negativer Beitrag zur uerkraftfäche hinzu ( z 5 kn zeigt nach unten und wir fogen einem negativen Schnittufer). Die uerkraftfäche fät entsprechend vom Wert + 5 kn auf den Wert 5 kn. Danach eit sie wieder konstant und ändert sich nicht, is wir am rechten Bakenende anschagen. Wir hätten aternativ auch mit dem rechten Bakenende eginnen können. Hier handet es sich ja um ein positives Schnittufer. Der uerkraftfächeneitrag aufgrund der senkrecht zur Bakenachse eingeeiteten Kraft Bz 5 kn ist daher negativ, denn die genannte Kraft zeigt ja nach oen, was nach unserer Definition aus dem schnitt 7. einem negativen Beitrag entspricht. Schreiten wir nach inks, so passiert soange nichts, is wir wieder die Stee der Krafteineitung kn kreuzen. ür ein positives Schnittufer ergit sich somit ein positiver Beitrag, der die uerkraftfäche aus dem negativen auf den positiven Wert + 5 kn anhet. Dieser eit danach konstant und ändert sich nicht, is wir am inken Bakenende anschagen. so ergit sich wieder diesee äche, geichgütig von wechem Bakenende aus wir eginnen. Schießich zur omentenfäche: Wir eginnen am negativen Schnittufer, d.h. am inken Bakenende. Die Kraft z 5 kn eginnt dort ein oment aufzuauen. Dieses ist eingangs, d.h. ei, geich Nu, da dort noch kein Heearm zur Verfügung steht, und es wächst inear an, je weiter man nach rechts geht. Kommt man zum Punkt der Krafteineitung kn, so erwächst der Kraft z auf einma Konkurrenz. Von nun an geht es inear awärts, denn die Kraft ist doppet so groß wie die Kraft z und schon ei m ist der eingangs durch den ängeren Heearm gegeene Vorsprung kompensiert, und man erhät as resutierendes oment den Wert Nu. n der Stee m passiert jedoch noch etwas anderes: Ein freies oment greift in das Geschehen ein. ür ein negatives Schnittufer iefert es nach den usführungen aus dem schnitt 7. offenar einen positiven Beitrag. it anderen Worten: n der 3
15 Stee m springt die omentenfäche vom Wert Nu auf der Wert 5 knm. Danach geht es wieder inear awärts und zwar as oge der nach wie vor aktiven Kräfte z und. m Ende des Bakens erreichen wir gerade wieder den Wert Nu. Wir hätten aer auch am rechten Bakenende, aso ei einem positiven Schnittufer eginnen können. Hier eginnt die Kraft Bz ein oment aufzuauen. Dieses ist nach der Vorzeichenkonvention aus schnitt 7. positiv. Beim ortschreiten nach inks wächst das oment inear an, is wir an die Stee der freien oments kommen. ür ein positives Schnittufer stet dieses offenar einen negativen Beitrag zur omentenfäche da. Diesee fät schagartig nach unten und zwar in diesem Beispie auf den Wert Nu zurück. Danach geht es wieder inear aufwärts, denn die Kraft Bz ist nach wie vor aktiv und es geingt, den soeen erfogten Einruch in der omentenfäche durch einen ansteigenden Heearm wettzumachen. Schießich kommt der Punkt, an dem die Kraft eingeeitet wird. ür ein positives Schnittufer führt diese auf einen negativen Beitrag zur omentenfäche. Der aus der Kraft Bz resutierende nstieg wird sukzessive ageaut, is am inken Bakenende schießich der Wert Nu erreicht ist. Damit hat sich wieder diesee omentenfäche ergeen. Wir woen nun üeregen, was es vom Standpunkt der Differentiageichungen aus dem schnitt 7..5 zu dem hier vorgesteten Baken zu sagen git. Da keine uereastung voriegt, ist kar, dass die uerkraftfäche konstant sein muss (siehe Geichung (7..9)). Sie darf aerdings Sprünge aufweisen, da der Baken zwischen den Enden eastet wird, was auf Üergangsedingungen führt. an spricht von einer aschnittsweise konstanten unktion. Im geichen Sinne ist die omentenfäche stückweise inear (siehe Geichung (7..9)). uch sie kann springen (ei ), da das freie oment auf eine Üergangsedingung führt. an eachte, dass die eitung der omentenfäche auf die uerkraftfäche führen muss (Geichung (7..6)). Hat man aso die omentenfäche gefunden, so kann man die uerkraftfäche inkusive der richtigen Vorzeichen durch Differentiation ermitten. an spart sich so die etwas schwerfäige rgumentation üer die richtigen Vorzeichen am jeweiigen Schnittufer. Natürich muss man daei die richtige omentenfäche kennen, inkusive der richtigen Vorzeichen. Bisher haen wir diese auch aus Üeregungen am Schnittufer gefunden. Es git jedoch eine einfache ingenieurmäßige ternative: die strichierte Linie. Das Rezept autet wie fogt: an zeichne sich unter die Schwerachse des Bakens eine strichierte Linie. Wird diese von einer am Baken angreifenden uerkraft gestaucht, so ist das auf diese Kraft zurückgehende oment negativ zu rechnen. Bei Zug ist es entsprechend positiv. Diese aser ist nachträgich in unserem Bakenproem eingezeichnet. Offenar führen die Kräfte z und Bz zu einer Streckung der aser, ihr Beitrag (fas reevant, je nachdem an wechem Bakenende man eginnt) ist positiv zu rechnen. Dagegen führt die Kraft offenar zu einer Stauchung, aso auf einen negativen Beitrag. ür das freie oment ässt sich üer die strichierte aser eenfas schne ein Entscheidung üer das jeweis reevante Vorzeichen fäen. Kommt man von inks, so streckt das freie oment die strichierte aser. Das entspricht einem positiven Beitrag. Kommt man von rechts, so staucht es die strichierte aser, was einem negativen Beitrag entspricht. 4
16 7.3 Zur Berechnung von Schnittgrößen am Rahmentragwerk Bisher haen wir die Schnittgrößen N, und ausschießich für gerade Baken ermittet. Diese Schnittgrößen eistieren jedoch auch im a mehrerer aneinandergeschweißter gerader Trägerstücke, aso für den a eines Rahmentragwerks, sowie schießich für einen eieig gekrümmten Träger, d.h. einen Bogen. Der erste a so in diesem schnitt untersucht werden Der rechtwinkige Rahmen,6m i z m k 3 B 9,6 kn Bz kn m 9,6 kn N ( ) 9,kNmk kn 9,6kN kn ( ) kn ( ) knm. 7.3.: Rechtwinkiger Rahmen. Wir etrachten die idung 7.3., wo ein rechtwinkiger Rahmen zu sehen ist, der, gestützt auf zwei Lager genannt und B, einer Kraft von kn unteriegt, die im Punkt k angreift. Gesucht sind ( ) N, ( ) und ( ). Daei woen wir die Koordinate vom ufagerpunkt üer die Punkte i und k is hin zum ufagerpunkt B as positiv ansteigend zähen (wiküriche Konvention). ußerdem zeichnen wir wieder eine strichierte aser (unter oder neen der Bakenschwerachse, woei ei Üerschreiten der Ecke nicht üer die Schwerachse gesprungen wird) ein. Wie zuvor eim geraden Baken ermitten wir as erstes die ufagerkräfte und erhaten: kn, 9,6 kn, 9,6 kn. (7.3.) z Bz Wir eginnen nun mit der Konstruktion der Normakraftfäche und zwar im Punkt. Hier iefert die Kraftkomponente einen Beitrag zur Normakraft, denn es ist nicht immer die - z 5
17 Komponente einer Kraft, die daei reevant ist, sondern stets diejenige Komponente, die senkrecht zum Bakenuerschnitt steht. Die Normakraft eit offenar konstant ( 9,6 kn ) is in den Punkt i hinein, und es handet sich um eine Druckkraft. Üerschreiten wir den Punkt i, so üernimmt nun die Druckkraft kn die Roe der Normakraft. Und nach Passieren des Punktes k stoßen wir schießich auf die Zugkraft Bz 9,6 kn. Beim Zeichnen der Normakraftfächen (wie auch der uerkraft- und der omentenfäche) woen wir nach außen atragen, um Üerschneidungen eim Passieren der Eckpunkte zu vermeiden. Die Vorzeichen tragen wir in die ächen ein. Charakteristische Punkte versehen wir mit vorzeichenehafteten Zahenwerten. Um die omentenfäche zu zeichnen, eginnen wir wieder am inken Bakenende, d.h. am ufagerpunkt. Die reevante Kraftkomponente ist hier, weche die strichierte aser staucht, aso einen negativen Beitrag zur omentenfäche iefert, der inear afät. Nach Passieren des Knickpunktes i üertragen wir zunächst das is dahin aufgeaute oment von 9, knm auf die andere Seite. Bei weiterem ortschreiten nach rechts wird nun die Komponente z 9,6 kn aktiv zum ufau der omentenfäche eitragen und zwar im positiven Sinne, denn sie versucht die strichierte aser üer der Heeänge von m zu dehnen. Das oment wird somit sukzessive ageaut und zwar is auf den Wert Nu (wie man nachrechnet). Wir üertragen den Wert Nu nach Passieren des Punktes k auf die andere Seite. In der Tat eit die omentenfäche danach auf dem Wert Nu stehen, denn die Kraftkomponente Bz versucht, auf dem verieenen Stück die strichierte aser weder zu stauchen noch zu strecken und die drei anderen Kräfte, z sowie die kn haten sich ezügich ihrer omentenwirkung gemeinsam die Waage ( z ezeichnet die Lage irgendeines eieigen Punkt auf dem etreffenden Bakenaschnitt): ( ) z + z m kn,6 m z. (7.3.) Sestverständich hätten wir die omentenfäche auch von rechts aufauen können und wären auf den geichen Verauf gekommen. Die uerkraftfäche erhaten wir schießich durch Differentiation nach aus der omentenfäche. Bis zum Knickpunkt i erhät man einen konstanten negativen Wert von kn (aso ) danach einen weiteren konstanten Wert von 9,6 kn (aso Bz ). Das etzte Teistück (hinter dem Punkt k ) ist frei von uerkräften. Die rgumentation üer positive und negative Schnittufer wäre sestverständich auch mögich gewesen Beieiger gerader Träger Betrachte die in idung 7.3. dargestete Situation: Ein geknickter Träger wird am einen Ende einer Last von 3 N ausgesetzt. Gesucht sind die Normakraft-, uerkraft- und die omentenfäche. Zur Lösung schneiden wir die Stee frei und finden, dass dort git:, 3 N, 9 Nm. (7.3.3) z Von nun an erfogt die Ermittung der ächen uasi zwangsäufig, und es ergit sich das in idung 7.3. gezeigte Ergenis, worin der Üergang an der ersten Ecke von inks zur Verdeutichung nochmas esonders hervorgehoen wurde. 6
18 α 3 3N -5 N 5 N N,5m m m -5 N N( ) 3 N z -3 N 6 N 3 N 6 N 3 N N -9 Nm -3 Nm 6 N ( ) ( ) N -3 Nm -9 Nm. 7.3.: Schnittgrößen am geknickten Träger Der stetig gekrümmte Träger - Theorie Zur Einführung etrachten wir den in idung dargesteten gekrümmten Träger, der an der inken Seite eingespannt ist und an der rechten Seite unter der Last steht. Wir fragen uns, wie an einer eieigen Schnittstee k die Normakraft, uerkraft, sowie das Schnittmoment aussehen. Dazu schneiden wir die Stee k frei. Diesee ist charakterisiert durch eine Normaen- sowie eine Tangentiarichtung. Wir zeregen die am rechten Trägerstück angreifende Kraft in eine Norma- sowie eine Tangentiakomponente. Indem wir die Geichgewichtsedingungen am rechten Träger anaysieren, finden wir, dass git: N k + N, + k, k h, (7.3.4) und somit fogt, dass: N,, h. (7.3.5) k N k k 7
19 h k N s ρ n () s s N ds s L : Schnittgrößen am stetig gekrümmten Träger. Der Heearm h ist karerweise eine von der Position k ahängige Größe, und somit wird die omentenfäche am gekrümmten Träger sich i.a. von Position zu Position auf dem Träger ändern. Dassee git für die uerkraft- und die Normakraftverteiung. Das sote uns aer nicht weiter verwundern, denn auch eim geraden Träger variierten ja i.a. die Normakraft-, uerkraft-, und die omentenfäche. z ϕ s dϕ / dϕ N () s ( s + ds) N( s + ds) () s () s N ρ ()s s d dϕ s + ds ( ) : Geichgewicht am gekrümmten Bogeneement. Diskutieren wir nun den a, dass zusätzich zu Punktasten auch noch normae Beastungen am Träger angreifen, so wie in idung dargestet. Diese nennen wir N () s, und durch den Bogenängenparameter s können wir eindeutig jede Position auf dem gekrümmten Träger erfassen, genauso wie wir das zuvor mit der Koordinate eim geraden Träger getan haen. Wir etrachten nun ein keines Bogenstück aus dem Träger, wie gezeichnet. ür dieses Bogenstück steen wir die Geichgewichtsedingungen um den Schwerpunkt S auf (wikürich), woei zu eachten ist, dass ae Kräfte nach einer festen (, z) -Richtung hin agetragen werden. Es ergit sich: () s + ( s + d s) sin( dϕ) + N ( s + ds) cos( dϕ) + () s ds sin( dϕ ) ( s) ( s + d s) cos( dϕ) + N ( s + ds) sin( dϕ) ( s) ds cos( dϕ ) N N, (7.3.6) N. (7.3.7) 8
20 () s () s ρ d ϕ + ( s + ds) ( s + ds) ρ dϕ. (7.3.8) Indem man diese usdrückung in Tayorreihen entwicket, nach inearem Giedern aricht und außerdem eachtet, dass für den Schmiegekreisradius ρ (siehe idung 7.3.4) git: ds ρ dϕ, (7.3.9) fogt: dn ds () s () s d() s ρ, ds () s N + ρ () s d () s N, ds () s. (7.3.) Darin ezeichnet ϕ den zur Bogenänge s gehörigen Bogenwinke Der stetig gekrümmte Träger - Ein Hakreisogen ϕ h k ϕ R ψ sin( ϕ) cos( ϕ) cos( ψ) ψ sin( ψ) ( ϕ) N( ϕ) ( ϕ) R : Schnittgrößen am hakreisförmigen Baken unter Punktasten. Wir etrachten die in idung dargestete Situation: Ein Haogen steht unter den gezeigten zwei Lasten der Stärke. nwendung der theoretischen Üeregungen aus dem vorherigen schnitt ergit die in idung gezeigten uerkraft-, Normakraft- sowie omentenfächen. ternativ ässt sich aer auch wie in schnitt für den geraden Träger vorgeführt verfahren. R 9
q = 3 kn/m Abb. 1: Eingespannter, abgeknickter Träger unter Gleichstrecken-und Punktlast.
 ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
1. Klausur Mechanik I SS 05, Prof. Dr. V. Popov
 . Kausur Mechanik I SS 05, Prof. Dr. V. Popov itte deutich schreiben! Name, Vorname: Matr.-Nr.: Studiengang: itte inks und rechts ankreuen! Studienbegeitende Prüfung Ergebnis ins WWW Übungsscheinkausur
. Kausur Mechanik I SS 05, Prof. Dr. V. Popov itte deutich schreiben! Name, Vorname: Matr.-Nr.: Studiengang: itte inks und rechts ankreuen! Studienbegeitende Prüfung Ergebnis ins WWW Übungsscheinkausur
Aufgabe 1 (Seite 1 von 2) Das dargestellte Fachwerk ist in den Punkten A und B gelagert und wird durch die Einzelkräfte F 1,F 2 und F 3 belastet.
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 2) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird durch die Einzekräfte F 1,F 2 und F 3
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 2) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird durch die Einzekräfte F 1,F 2 und F 3
Anschluss von Kragplatten an Stahlbetondeckenplatten. Prof. Dr.-Ing. Erhard Gunkler Dipl.-Ing. Alice Becke
 Anschuss von patten an Stahetondeckenpatten Prof. Dr.-Ing. Erhard Gunker Dip.-Ing. Aice Becke Detmod, Jui 2003 (üerareitet August 2004) Anschuss von patten an St.-Deckenpatten Seite 2 1 Agemeines Die Bemessung
Anschuss von patten an Stahetondeckenpatten Prof. Dr.-Ing. Erhard Gunker Dip.-Ing. Aice Becke Detmod, Jui 2003 (üerareitet August 2004) Anschuss von patten an St.-Deckenpatten Seite 2 1 Agemeines Die Bemessung
Baustatik 2. Berechnung statisch unbestimmter Tragwerke. von Raimond Dallmann. 1. Auflage
 Baustatik Berechnung statisch unbestimmter Tragwerke von Raimond Damann 1. Aufage Baustatik Damann schne und portofrei erhätich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 006 Verag C.H. Beck
Baustatik Berechnung statisch unbestimmter Tragwerke von Raimond Damann 1. Aufage Baustatik Damann schne und portofrei erhätich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 006 Verag C.H. Beck
Intensivkurs Statik Teil 1
 Intensivkurs Statik Tei 1 Themen: Aufagekräfte und Zwischenreaktionen berechnen Kräftezeregung Geichgewichtsbedingungen Statische Bestimmtheit Notwendige Bedingungen: Abzähkriterium Hinreichende Bedingung:
Intensivkurs Statik Tei 1 Themen: Aufagekräfte und Zwischenreaktionen berechnen Kräftezeregung Geichgewichtsbedingungen Statische Bestimmtheit Notwendige Bedingungen: Abzähkriterium Hinreichende Bedingung:
Lösungen zum Crashkurs: Statik Teil 1 Thema: Gleichgewichtsbedingungen, Schnittgrö ßen und Fla chenschwerpunkte
 1 Lösungen zum Crashkurs: Statik Tei 1 Thema: Geichgewichtsbedingungen, Schnittgrö ßen und Fa chenschwerpunkte Aufgabe zum Fächenschwerpunkt y 6 2 8 Gebe die Schwerpunktkoordinaten für das oben dargestete
1 Lösungen zum Crashkurs: Statik Tei 1 Thema: Geichgewichtsbedingungen, Schnittgrö ßen und Fa chenschwerpunkte Aufgabe zum Fächenschwerpunkt y 6 2 8 Gebe die Schwerpunktkoordinaten für das oben dargestete
3.7 Sonderprobleme Ausnutzung der Symmetrie und Antimetrie. Größe. Belastung
 VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
VORLESUGSAUSKRIPT BAUSTATIK I II (UVERTIEFT).7 Sonderrobeme.7. Ausnutzung der Symmetrie und Antimetrie Durch die Ausnutzung der Symmetrie und Antimetrie kann der Grad der statischen Unbestimmtheit (u.
Institut für Allgemeine Mechanik der RWTH Aachen
 Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
DÜNNE LINSEN UND LINSEN-SYSTEM
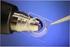 Versuch 10/1 DÜNNE LINSEN UND LINSEN-SYSTEM (9-05-008) Batt 1 DÜNNE LINSEN UND LINSEN-SYSTEM Es werden die optischen Eigenschaften dünner Linsen sowie die eines Linsen-Systems vorgestet. Es so die Brennweite
Versuch 10/1 DÜNNE LINSEN UND LINSEN-SYSTEM (9-05-008) Batt 1 DÜNNE LINSEN UND LINSEN-SYSTEM Es werden die optischen Eigenschaften dünner Linsen sowie die eines Linsen-Systems vorgestet. Es so die Brennweite
Kapitel 7. Balken, Rahmen, Bogen
 Kpite 7 ken, Rhmen, ogen 7 7 ken, Rhmen, ogen 7. Schnittgrößen... 7 7.2 Schnittgrößen m gerden ken... 76 7.2. ken unter Einzesten... 76 7.2.2 Zusmmenhng zwischen estung und Schnittgrößen... 83 7.2.3 Integrtion
Kpite 7 ken, Rhmen, ogen 7 7 ken, Rhmen, ogen 7. Schnittgrößen... 7 7.2 Schnittgrößen m gerden ken... 76 7.2. ken unter Einzesten... 76 7.2.2 Zusmmenhng zwischen estung und Schnittgrößen... 83 7.2.3 Integrtion
1. Aufgabe: (ca. 11% der Gesamtpunktzahl) Bitte beantworten Sie folgende Fragen: 1. Wie ist der Schubmittelpunkt definiert?
 . Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
. Aufgabe: (ca. % der Gesamtunktzah) Bitte beantworten Sie fogende Fragen:. Wie ist der Schubmitteunkt definiert?. Durch weche Einschränkungen des agemeinen dreidimensionaen Sannungszustandes ergibt sich
Sessionsprüfung Baustatik I+II. Winter 2008/09. Montag, 26. Januar 2009, Uhr, HIL E7
 Sessionsprüfung austatik I+II Winter 2008/09 Montag, 26. Januar 2009, 09.00 12.00 Uhr, HIL E7 Name, Vorname : Studenten-Nr. : emerkungen 1. e ufgaben haben das geiche Gewicht. 2. Die ufgaben dürfen in
Sessionsprüfung austatik I+II Winter 2008/09 Montag, 26. Januar 2009, 09.00 12.00 Uhr, HIL E7 Name, Vorname : Studenten-Nr. : emerkungen 1. e ufgaben haben das geiche Gewicht. 2. Die ufgaben dürfen in
NUMERISCHE METHODEN DER MECHANIK
 ÜBUNG 1 n(), n() = n (2 sin(π )) 2 ÊA() = EA Gesucht: a) Randbedingungen für = und = b) Näherungsösung für die Verschiebung u() mit Hife der Methode der finiten Differenzen (MFD) und N = 4 (4 Abschnitte,
ÜBUNG 1 n(), n() = n (2 sin(π )) 2 ÊA() = EA Gesucht: a) Randbedingungen für = und = b) Näherungsösung für die Verschiebung u() mit Hife der Methode der finiten Differenzen (MFD) und N = 4 (4 Abschnitte,
Mathematische Probleme, SS 2017 Donnerstag 1.6. $Id: dreieck.tex,v /06/01 11:41:57 hk Exp $ 2.1 Dreiecksberechnung mit Seiten und Winkeln
 Mathematische Proleme SS 2017 Donnerstag 1.6 $Id: dreieck.texv 1.31 2017/06/01 11:41:57 hk Exp $ 2 Dreiecke 2.1 Dreieckserechnung mit Seiten und Winkeln Am Ende der letzten Sitzung hatten wir eine weitere
Mathematische Proleme SS 2017 Donnerstag 1.6 $Id: dreieck.texv 1.31 2017/06/01 11:41:57 hk Exp $ 2 Dreiecke 2.1 Dreieckserechnung mit Seiten und Winkeln Am Ende der letzten Sitzung hatten wir eine weitere
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 akutät Maschinenbau Prof. Dr.-Ing.. Menze Prof. Dr.-Ing. J. Moser ufgabe 1 (Seite 1 von 3) Das dargestete achwerk ist in den Punkten und geagert und wird durch vier unterschiediche Einzekräfte, 1, 2, 3
akutät Maschinenbau Prof. Dr.-Ing.. Menze Prof. Dr.-Ing. J. Moser ufgabe 1 (Seite 1 von 3) Das dargestete achwerk ist in den Punkten und geagert und wird durch vier unterschiediche Einzekräfte, 1, 2, 3
Festigkeitslehre. Aufgaben
 Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
Modurüfung in Technischer Mechanik am 8. März 06 Festigkeitsehre Aufgaben Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnungen müssen sauber und übersichtich
Leseprobe. Wolfgang H. Müller, Ferdinand Ferber. Übungsaufgaben zur Technischen Mechanik ISBN:
 Leseprobe Wofgng H. üer, Ferdinnd Ferber Übungsufgben zur Technischen echnik ISBN: 978--44-488-7 Weitere Infortionen oder Besteungen unter http://www.hnser.de/978--44-488-7 sowie i Buchhnde. Cr Hnser Verg,
Leseprobe Wofgng H. üer, Ferdinnd Ferber Übungsufgben zur Technischen echnik ISBN: 978--44-488-7 Weitere Infortionen oder Besteungen unter http://www.hnser.de/978--44-488-7 sowie i Buchhnde. Cr Hnser Verg,
Aus Kapitel 6. Technische Mechanik. Aufgaben. 6.1 Berechnen Sie mithilfe des Arbeitssatzes die Lagerreaktionen des abgebildeten Trägers.
 6 ufgaben Kap 6 us Kapite 6 ufgaben 6 erechnen Sie mithife des rbeitssatzes die Lagerreaktionen des abgebideten Trägers 6 erechnen Sie mithife des rbeitssatzes die Veräufe von Querkraft und iegemoment
6 ufgaben Kap 6 us Kapite 6 ufgaben 6 erechnen Sie mithife des rbeitssatzes die Lagerreaktionen des abgebideten Trägers 6 erechnen Sie mithife des rbeitssatzes die Veräufe von Querkraft und iegemoment
E > 0. V eff (r) r. V eff,min < E < 0. r min. V (r)
 II.2 Zwei-Körper-Systeme 43 2 2µr 2 r min E > 0 r V eff (r) r max r min V eff,min < E < 0 V (r) E < V eff,min Abbidung II.4 Effektives Potentia V eff (r) für das Keper-Probem. Mit dem newtonschen Gravitationspotentia
II.2 Zwei-Körper-Systeme 43 2 2µr 2 r min E > 0 r V eff (r) r max r min V eff,min < E < 0 V (r) E < V eff,min Abbidung II.4 Effektives Potentia V eff (r) für das Keper-Probem. Mit dem newtonschen Gravitationspotentia
Mathematische Probleme, SS 2013 Donnerstag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
$Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
Projektion. Kapitel Bildebene P 2. Sehstrahlen P 1. Projektionszentrum (Augenpunkt) Objekt. Bildebene
 Kapite 14 Projektion 14.1 Bidebene Für die Aneige am weidimensionaen Ausgabegerät muß eine Abbidung (Projektion) der räumichen, dreidimensionaen Sene auf eine weidimensionae Projektionsebene erfogen. Gegeben
Kapite 14 Projektion 14.1 Bidebene Für die Aneige am weidimensionaen Ausgabegerät muß eine Abbidung (Projektion) der räumichen, dreidimensionaen Sene auf eine weidimensionae Projektionsebene erfogen. Gegeben
Statik, insbesondere Schnittprinzip
 Statik, insbesondere Schnittprinzip von erhard Knappstein überarbeitet Statik, insbesondere Schnittprinzip Knappstein schne und portofrei erhätich bei beck-shop.de DIE CUCNDLUN arri Deutsch 005 Verag C..
Statik, insbesondere Schnittprinzip von erhard Knappstein überarbeitet Statik, insbesondere Schnittprinzip Knappstein schne und portofrei erhätich bei beck-shop.de DIE CUCNDLUN arri Deutsch 005 Verag C..
Geometrisch nichtlineares Verhalten
 Geometrisch nichtineares Verhaten.1 Grundbegriffe der geometrischen Nichtinearitäten Bei einer geometrisch inearen Berechnung geht man von fogenden Voraussetzungen aus: 1. Geichgewicht am unverformten
Geometrisch nichtineares Verhaten.1 Grundbegriffe der geometrischen Nichtinearitäten Bei einer geometrisch inearen Berechnung geht man von fogenden Voraussetzungen aus: 1. Geichgewicht am unverformten
405. Ein Strommesser hat einen Messwiderstand von 200 Ohm und einen Endausschlag. Aufgaben zur E-Lehre (Widerstand)
 ufgaben zur E-Lehre (Widerstand) 6. In eine aten Haus wurden die uiniueitungen durch Kupfereitungen ersetzt; insgesat wurden 50 Kabe veregt. Jedes Kabe besteht aus einer Hin- und einer ückeitung und hat
ufgaben zur E-Lehre (Widerstand) 6. In eine aten Haus wurden die uiniueitungen durch Kupfereitungen ersetzt; insgesat wurden 50 Kabe veregt. Jedes Kabe besteht aus einer Hin- und einer ückeitung und hat
Prüfung in Methode der finiten Elemente. Matrikelnummer: Studiengang: Wiederholer
 Universität Stuttgart INSTITUT MECH NIK FUR Prüfung in Methode der finiten Eemente Name, Vorname: Matrikenummer: Studiengang: Wiederhoer Emai: Unterschrift: Hauptfach: Bitte beachten Sie Fogendes: 1. Es
Universität Stuttgart INSTITUT MECH NIK FUR Prüfung in Methode der finiten Eemente Name, Vorname: Matrikenummer: Studiengang: Wiederhoer Emai: Unterschrift: Hauptfach: Bitte beachten Sie Fogendes: 1. Es
a) Zeigen Sie, dass sich für eine lange Spule die magn. Flussdichte in der Mitte mit der Näherungsformel berechnen lässt.
 Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Interferenz an einer CD
 Interferenz an einer CD Oaf Merkert (Manue Sitter) 18. Dezember 2005 1 Versuchsaufbau Abbidung 1: Versuchsanordnung mit Laser und CD [1] Ein auf einem Tisch aufgesteter Laser mit der Weenänge λ wird im
Interferenz an einer CD Oaf Merkert (Manue Sitter) 18. Dezember 2005 1 Versuchsaufbau Abbidung 1: Versuchsanordnung mit Laser und CD [1] Ein auf einem Tisch aufgesteter Laser mit der Weenänge λ wird im
3.4 Kondition eines Problems
 38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
38 KAPITEL 3. FEHLERANALYSE Beispiel 3.18 Betrachte M(10, 5, 1). Dann sind x 4.2832, y 4.2821, z 5.7632 darstellare Zahlen und (x y)z 0.00633952. Das korrekte Ergenis in M ist daher 0.0063395. Der Ausdruck
= p u. Ul x 0 U r x > 0
 Das Riemann-Probem Das zu ösende Geichungssystem besteht aus den eindimensionaen hydrodynamischen Geichungen ohne Viskosität und externe Kräfte, den Euer-Geichungen. Beschränkung auf eine Dimension (x)
Das Riemann-Probem Das zu ösende Geichungssystem besteht aus den eindimensionaen hydrodynamischen Geichungen ohne Viskosität und externe Kräfte, den Euer-Geichungen. Beschränkung auf eine Dimension (x)
Tragwerksentwurf III+IV HS 2018
 S. 1 / 6 Lernzie Entwicken des Verständnisses für Kräfteveräufe im bau unter variierenden Last- und Aufagersituationen sowie verschiedenen Fachwerkgeometrien. Aufgabe 1 Kräfteverauf in Fachwerkträgern
S. 1 / 6 Lernzie Entwicken des Verständnisses für Kräfteveräufe im bau unter variierenden Last- und Aufagersituationen sowie verschiedenen Fachwerkgeometrien. Aufgabe 1 Kräfteverauf in Fachwerkträgern
5.1.5 Pendel = Sinusbewegung ******
 V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
1 (bekannt) (4 Punkte)
 . Proekusur Mechnik I WS 003/04, Prof. r. rer. nt. Ventin Popov itte deutich schreien! Nme, Vornme: Mtr.-Nr.: Studiengng: itte inks und rechts nkreuzen! Studienegeitende Prüfung Üungsscheinkusur rgenis
. Proekusur Mechnik I WS 003/04, Prof. r. rer. nt. Ventin Popov itte deutich schreien! Nme, Vornme: Mtr.-Nr.: Studiengng: itte inks und rechts nkreuzen! Studienegeitende Prüfung Üungsscheinkusur rgenis
Berechnung von Wurzeln
 Sieginde Fürst Berechnung von Wurzen Rekursive Fogen Zinseszinsforme; Heronverfahren Inhate Berechnung eines mit Zinsesezins verzinsten Kapitas auf zwei Arten Heronforme Einschranken von Wurzen Ziee Erernen
Sieginde Fürst Berechnung von Wurzen Rekursive Fogen Zinseszinsforme; Heronverfahren Inhate Berechnung eines mit Zinsesezins verzinsten Kapitas auf zwei Arten Heronforme Einschranken von Wurzen Ziee Erernen
TU Dortmund. Vorname: Nachname: Matr.-Nr.:
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 3) a) Die nebenstehend skizzierte, inks eingespannte Konsoe wird wie dargestet durch Traktionen (eingeprägte
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Aufgabe 1 (Seite 1 von 3) a) Die nebenstehend skizzierte, inks eingespannte Konsoe wird wie dargestet durch Traktionen (eingeprägte
2. Stabilitätsprobleme und Theorie II. Ordnung
 Baustatik WS 212/213 2. Stabiitätsprobeme und Theorie II. Ordnung 2.6 Berücksichtigung der geometrischen Imperfektionen Imperfektionen Bisher: Annahme der perfekten Tragwerke und des perfekten Bauprozesses!
Baustatik WS 212/213 2. Stabiitätsprobeme und Theorie II. Ordnung 2.6 Berücksichtigung der geometrischen Imperfektionen Imperfektionen Bisher: Annahme der perfekten Tragwerke und des perfekten Bauprozesses!
6 Lineare Abbildungen der euklidischen Ebene
 6 Lineare Aildungen der euklidischen Eene In diesem Kapitel etrachten wir nur noch lineare Aildungen der euklidischen Eene auf sich seler: f : E E oder f : R 2 R 2 Zudem verwenden wir das Skalarprodukt
6 Lineare Aildungen der euklidischen Eene In diesem Kapitel etrachten wir nur noch lineare Aildungen der euklidischen Eene auf sich seler: f : E E oder f : R 2 R 2 Zudem verwenden wir das Skalarprodukt
Komplexe Zahlen - Rechenregeln
 Technische Universität Dresden Fakutät Maschinenwesen / IFKM Professur für Getriebeehre Prof. Dr. rer. nat. habi. Moder Kompexe Zahen - Rechenregen Rechenregen Kompexe Zahen = x + iy = r e e i = cos +
Technische Universität Dresden Fakutät Maschinenwesen / IFKM Professur für Getriebeehre Prof. Dr. rer. nat. habi. Moder Kompexe Zahen - Rechenregen Rechenregen Kompexe Zahen = x + iy = r e e i = cos +
Spezielle Funktionen. Kapitel Legendre-Polynome
 Kapite 3 Speziee Funtionen Funtionen wie die Legendre-Poynome 3.), die Bessefuntion 3.), die Hermite-Poynome 3.3) oder die Laguerre-Poynome 3.4) hängen mit den Lösungen diverser Randwertprobeme zusammen,
Kapite 3 Speziee Funtionen Funtionen wie die Legendre-Poynome 3.), die Bessefuntion 3.), die Hermite-Poynome 3.3) oder die Laguerre-Poynome 3.4) hängen mit den Lösungen diverser Randwertprobeme zusammen,
Elliptische Integrale und das allgemeine geometrische Mittel (agm):
 Elliptische Integrale und das allgemeine geometrische Mittel (agm): Typische Aufgaen der Analysis waren im 8. Jahrhundert nach der Erfindung der Differential- und Integralrechnung durch Leiniz und Newton,
Elliptische Integrale und das allgemeine geometrische Mittel (agm): Typische Aufgaen der Analysis waren im 8. Jahrhundert nach der Erfindung der Differential- und Integralrechnung durch Leiniz und Newton,
1 PdvV für ein System aus starren Körpern
 Materiatheorie - LKM, Sekr. MS PdvV und PdvK Energiemethoden 06. Übungsbatt, WS 01/13, S. 1 1 PdvV für ein System aus starren Körpern Zur Bestimmung der fünf gesuchten Lagerreaktionen muss das System auf
Materiatheorie - LKM, Sekr. MS PdvV und PdvK Energiemethoden 06. Übungsbatt, WS 01/13, S. 1 1 PdvV für ein System aus starren Körpern Zur Bestimmung der fünf gesuchten Lagerreaktionen muss das System auf
Technische Universität Berlin. Abt. I Studierenden Service Studienkolleg / Preparatory Course
 Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Fourierreihenentwicklung Prof. K. Weinberg Universität Siegen Lehrstuhl für Festkörpermechanik
 Fourierreihenentwickung Prof. K. Weinberg Universität Siegen Lehrstuh für Festkörpermechanik Mathematische Grundagen für Einfachreihenentwickungen Für viee mathematische, physikaische und technische Probeme
Fourierreihenentwickung Prof. K. Weinberg Universität Siegen Lehrstuh für Festkörpermechanik Mathematische Grundagen für Einfachreihenentwickungen Für viee mathematische, physikaische und technische Probeme
Aufgabe 1: Gegeben ist das dargestellte statische System, das aus einer starren Stange und zwei Fachwerkstäben (Dehnsteifigkeit EA ) besteht.
 ufgabe : Gegeben ist das dargestete statische System, das aus einer starren Stange und zwei achwerkstäben (Dehnsteifigkeit E ) besteht. starr B Bestimmen Sie die kritische Knickast krit für das dargestete
ufgabe : Gegeben ist das dargestete statische System, das aus einer starren Stange und zwei achwerkstäben (Dehnsteifigkeit E ) besteht. starr B Bestimmen Sie die kritische Knickast krit für das dargestete
PP - Physikalisches Pendel Blockpraktikum Frühjahr 2005
 PP - Physikaisches Pende Bockpraktikum Frühjahr 2005 Regina Schweizer, Aexander Seizinger, Tobias Müer Assistent Heiko Eite Tübingen, den 14. Apri 2005 1 Theoretische Grundagen 1.1 Mathematisches Pende
PP - Physikaisches Pende Bockpraktikum Frühjahr 2005 Regina Schweizer, Aexander Seizinger, Tobias Müer Assistent Heiko Eite Tübingen, den 14. Apri 2005 1 Theoretische Grundagen 1.1 Mathematisches Pende
Musterlösung zu Aufgabe 10)
 Musterösung zu Aufgabe ) Seien n, K Körper, A K n n, b K n, und f: K n K n mit f x Ax für x K n. a) Zeigen Sie: f bidet Affinkombinationen von Vektoren in Affinkombinationen von deren Bidern unter f ab.
Musterösung zu Aufgabe ) Seien n, K Körper, A K n n, b K n, und f: K n K n mit f x Ax für x K n. a) Zeigen Sie: f bidet Affinkombinationen von Vektoren in Affinkombinationen von deren Bidern unter f ab.
27. Vorlesung Wintersemester
 27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
Musterlösung zur Übung am Donnerstag
 Musterösung zur Übung am Donnerstag Aufgabe 1: Strategie: 1. Man nimmt einen beiebigen Massepunkt m (z.b. Stein), hängt ihn an die Feder und enkt die Feder aus. Man misst die Schwingungsfrequenz (bzw.
Musterösung zur Übung am Donnerstag Aufgabe 1: Strategie: 1. Man nimmt einen beiebigen Massepunkt m (z.b. Stein), hängt ihn an die Feder und enkt die Feder aus. Man misst die Schwingungsfrequenz (bzw.
2. Statisch bestimmte Systeme
 1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
Kapitel 8. Haftung und Reibung
 Kapite 8 Haftung und Reibung 8 19 Haftung Haftung (Haftreibung) ufgrund der Oberfächenrauhigkeit beibt ein Körper im eichgewicht, soange die Haftkraft H keiner ist as der renzwert H 0.Der Wert H 0 ist
Kapite 8 Haftung und Reibung 8 19 Haftung Haftung (Haftreibung) ufgrund der Oberfächenrauhigkeit beibt ein Körper im eichgewicht, soange die Haftkraft H keiner ist as der renzwert H 0.Der Wert H 0 ist
1. Ebene gerade Balken
 1. Ebene gerade Balken Betrachtet werden gerade Balken, die nur in der -Ebene belastet werden. Prof. Dr. Wandinger 4. Schnittlasten bei Balken TM 1 4.1-1 1. Ebene gerade Balken 1.1 Schnittlasten 1.2 Balken
1. Ebene gerade Balken Betrachtet werden gerade Balken, die nur in der -Ebene belastet werden. Prof. Dr. Wandinger 4. Schnittlasten bei Balken TM 1 4.1-1 1. Ebene gerade Balken 1.1 Schnittlasten 1.2 Balken
Darstellende Geometrie Übungen. Tutorial zu Übungsblatt: Schatten in Axonometrie
 Tutoria zu Übungsbatt: Schatten in Axonometrie BEISIEL Schatten des otrechten Stabes durch auf der waagrechten Grundebene:. Um diesen Schatten zu finden wird der Lichtstrah L durch den unkt und der Grundrissichtstrah
Tutoria zu Übungsbatt: Schatten in Axonometrie BEISIEL Schatten des otrechten Stabes durch auf der waagrechten Grundebene:. Um diesen Schatten zu finden wird der Lichtstrah L durch den unkt und der Grundrissichtstrah
Projekt Experimentelle Mathematik mit GeoGebra
 Projekt Experimentee Mathematik mit GeoGebra (Projekt für Q1, G. vom Stein) Gefäße mit unterschiedichen Formen werden mit einer variaben, aber konstanten Wasserzufuhr befüt. Es so jeweis die Funktion Zeit
Projekt Experimentee Mathematik mit GeoGebra (Projekt für Q1, G. vom Stein) Gefäße mit unterschiedichen Formen werden mit einer variaben, aber konstanten Wasserzufuhr befüt. Es so jeweis die Funktion Zeit
C Mathematische Grundlagen
 C Mathematische Grundagen C.1 Summen Mit dem Summenzeichen werden Rechenanweisungen zum Addieren kompakt geschrieben. Sie assen sich oft mit Hife der Summenregen vereinfachen. C.1 Gibt es insgesamt n Werte
C Mathematische Grundagen C.1 Summen Mit dem Summenzeichen werden Rechenanweisungen zum Addieren kompakt geschrieben. Sie assen sich oft mit Hife der Summenregen vereinfachen. C.1 Gibt es insgesamt n Werte
Einführung in die lineare FEM
 Kapite 2 Einführung in die ineare FEM In diesem Kapite werden die einzenen Schritte einer Finite-Eemente-Berechnung detaiiert am einfachst mögichen Beispie eines mechanischen Fachwerks aus Stäben erkärt.
Kapite 2 Einführung in die ineare FEM In diesem Kapite werden die einzenen Schritte einer Finite-Eemente-Berechnung detaiiert am einfachst mögichen Beispie eines mechanischen Fachwerks aus Stäben erkärt.
Das Trägheitsmoment und der Satz von Steiner
 Übungen zu Theoretische Physik I - echanik im Sommersemester 3 Batt 9 vom 4.6.3 Abgabe:.7. Aufgabe 38 Punkte Das Trägheitsmoment und der Satz von Steiner Berechnen Sie das Trägheitsmoment eines Zyinders
Übungen zu Theoretische Physik I - echanik im Sommersemester 3 Batt 9 vom 4.6.3 Abgabe:.7. Aufgabe 38 Punkte Das Trägheitsmoment und der Satz von Steiner Berechnen Sie das Trägheitsmoment eines Zyinders
Modellierung eines Bioreaktors Hagen Sparka
 Gruppenaufgabe für das GdP-Praktikum Modeierung eines Bioreaktors Hagen Sparka 1 Eineitung In diesr Gruppenaufgabe für das GdP Praktikum im WS 2012/2013 so es um die Modeierung eines Bioreaktors gehen.
Gruppenaufgabe für das GdP-Praktikum Modeierung eines Bioreaktors Hagen Sparka 1 Eineitung In diesr Gruppenaufgabe für das GdP Praktikum im WS 2012/2013 so es um die Modeierung eines Bioreaktors gehen.
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3) a) Ein as masseos anzusehender Baken, bestehend aus einem dünnwandigen U-Profi (t a), ist an der inken Seite eingespannt und wird an seinem rechten
Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3) a) Ein as masseos anzusehender Baken, bestehend aus einem dünnwandigen U-Profi (t a), ist an der inken Seite eingespannt und wird an seinem rechten
Endliche Automaten. aus. Abbildung 1: Modell eines einfachen Lichtschalters
 Endliche Automaten In der ersten Vorlesungswoche wollen wir uns mit endlichen Automaten eschäftigen. Um uns diesen zu nähern, etrachten wir zunächst einen einfachen Lichtschalter. Dieser kann an oder aus
Endliche Automaten In der ersten Vorlesungswoche wollen wir uns mit endlichen Automaten eschäftigen. Um uns diesen zu nähern, etrachten wir zunächst einen einfachen Lichtschalter. Dieser kann an oder aus
Integralrechnung - Einführung Seite 1 von 6. Vergleicht man die Ergebnisse miteinander, so kann man folgende Entdeckung machen:
 Integralrechnung - Einführung Seite von 6 Berechnung von Flächeninhalten zwischen dem Graphen einer Funktion und der x-achse: Beispiel : f(x)= Fläche zwischen Graph und x-achse üer dem Intervall [;]: Bei
Integralrechnung - Einführung Seite von 6 Berechnung von Flächeninhalten zwischen dem Graphen einer Funktion und der x-achse: Beispiel : f(x)= Fläche zwischen Graph und x-achse üer dem Intervall [;]: Bei
a) Das dargestellte Fachwerk ist in den Punkten A und B gelagert und wird, wie dargestellt, durch drei Einzelkräfte belastet. L 1
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 2) a) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird, wie
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 2) a) Das dargestete Fachwerk ist in den Punkten A und B geagert und wird, wie
Innere Beanspruchungen - Schnittgrößen
 Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
Schnittgrößen und Vorzeichenkonvention
 Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Mathematische Probleme, SS 2017 Donnerstag 22.6
 $Id: dreieck.tex,v 1.38 017/06/19 16:13:49 hk Exp $ $Id: trig.tex,v 1.17 017/06/ 1:46:01 hk Exp $ Dreiecke.4 Einige Sätze üer Kreise m Ende der letzten Sitzung hatten wir den Umkreisradius R eines Dreiecks
$Id: dreieck.tex,v 1.38 017/06/19 16:13:49 hk Exp $ $Id: trig.tex,v 1.17 017/06/ 1:46:01 hk Exp $ Dreiecke.4 Einige Sätze üer Kreise m Ende der letzten Sitzung hatten wir den Umkreisradius R eines Dreiecks
Interferenzen gleicher Dicke
 Fakutät für Physik und Geowissenschaften Physikaisches Grundpraktikum O9 Interferenzen geicher Dicke Aufgaen 1. Bestimmen Sie den Krümmungsradius einer konvexen Linsenfäche durch Ausmessen Newtonscher
Fakutät für Physik und Geowissenschaften Physikaisches Grundpraktikum O9 Interferenzen geicher Dicke Aufgaen 1. Bestimmen Sie den Krümmungsradius einer konvexen Linsenfäche durch Ausmessen Newtonscher
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Frühjahr 2016
 Frühjahr 2016 Frühjahr 2016 Aufgabe 1 (Seite 1 von 3) a) Das rechts dargestete System wird durch eine inear veraufende Streckenast (Maximawert q 0 ) beastet. Der Baken weist die Biegesteifigkeit EI und
Frühjahr 2016 Frühjahr 2016 Aufgabe 1 (Seite 1 von 3) a) Das rechts dargestete System wird durch eine inear veraufende Streckenast (Maximawert q 0 ) beastet. Der Baken weist die Biegesteifigkeit EI und
KIT SS Klassische Theoretische Physik II. V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch. Klausur 2 Lösung. 11. Oktober 2012, Uhr
 KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
Musterlösung. für die Klausur MA1_07.1 vom 07. Februar Labor für Mathematik und Statistik. Prof. Norbert Heldermann.
 Fachereich Produktion und Wirtschaft Musterlösung für die Klausur MA_07. vom 07. Feruar 007 Laor für Mathematik und Statistik Prof. Norert Heldermann Richard Münder Bei dem vorliegenden Dokument handelt
Fachereich Produktion und Wirtschaft Musterlösung für die Klausur MA_07. vom 07. Feruar 007 Laor für Mathematik und Statistik Prof. Norert Heldermann Richard Münder Bei dem vorliegenden Dokument handelt
10.5 Schub infolge Querkraft beim Biegeträger
 0.5 chu infolge uerkraft eim Biegeträger 0.5. Zur Berechnung der chuspannungen F F ( x) ( x). 0.5.: Balken unter uerlast. Betrachte die in ildung 0.5. dargestellte ituation. Ein Biegeträger mit rechteckigem
0.5 chu infolge uerkraft eim Biegeträger 0.5. Zur Berechnung der chuspannungen F F ( x) ( x). 0.5.: Balken unter uerlast. Betrachte die in ildung 0.5. dargestellte ituation. Ein Biegeträger mit rechteckigem
Vom Fallkreis zur Bahnellipse und zum Hodographen
 Vom Fakreis zur Bahneipse und zum Hodographen Q R v P r X S F Y Gegeben: S P v Ort der Sonne Ort des Paneten zu irgendeinem Zeitpunkt t 0 Geschwindigkeit des Paneten zum Zeitpunkt t 0 Version 1.1 Frauenfed,
Vom Fakreis zur Bahneipse und zum Hodographen Q R v P r X S F Y Gegeben: S P v Ort der Sonne Ort des Paneten zu irgendeinem Zeitpunkt t 0 Geschwindigkeit des Paneten zum Zeitpunkt t 0 Version 1.1 Frauenfed,
Lösungen zu den. Übungsaufgaben. Höhere Festigkeitslehre
 akutät 3 zu den Übungsaufgaben Wintersemester 4/5 Dr. C. Katzenschwanz festigkeit.userweb.mwn.de Die mit( ) gekennzeichneten Aufgaben sind ehemaige Prüfungsaufgaben. Version.5 Wintersemester 4/5 8. Oktober
akutät 3 zu den Übungsaufgaben Wintersemester 4/5 Dr. C. Katzenschwanz festigkeit.userweb.mwn.de Die mit( ) gekennzeichneten Aufgaben sind ehemaige Prüfungsaufgaben. Version.5 Wintersemester 4/5 8. Oktober
Technische Universität Berlin. Abt. I Studierenden Service Studienkolleg / Preparatory Course
 Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Technische Universität Berin Abt. I Studierenden Service Studienkoeg / Preparatory Course Schriftiche Prüfung zur Feststeung der Eignung ausändischer Studienbewerber zum Hochschustudium im Lande Berin
Geschichte und Theorie
 Eektrotechnikprotoko 1 rspannung (EMK) und innerer Widerstand Moser Guido eines Gavanischem Eements Fuda, den 9.03.00 Geschichte und Theorie Die ersten Spannungsqueen, die gebaut wurden, waren gavanische
Eektrotechnikprotoko 1 rspannung (EMK) und innerer Widerstand Moser Guido eines Gavanischem Eements Fuda, den 9.03.00 Geschichte und Theorie Die ersten Spannungsqueen, die gebaut wurden, waren gavanische
80 Schwingende Saiten
 80 Schwingende Saiten 331 80 Schwingende Saiten 80.1 Probem. Es werden die Schwingungen einer (Geigen-) Saite der Länge > 0 und Massendichte ρ(x) > 0, 0 x, untersucht. Ist diese in den Punkten x = 0 und
80 Schwingende Saiten 331 80 Schwingende Saiten 80.1 Probem. Es werden die Schwingungen einer (Geigen-) Saite der Länge > 0 und Massendichte ρ(x) > 0, 0 x, untersucht. Ist diese in den Punkten x = 0 und
1.1 Zug und Druck. Aufgaben
 Technische Mechanik 2 1.1-1 Prof. Dr. Wandinger Aufgae 1 1.1 Zug und Druck Aufgaen Der ageildete Sta ist am linken Ende Ende durch die Kraft elastet. Ermitteln Sie die Normalspannung in den Schnitten A
Technische Mechanik 2 1.1-1 Prof. Dr. Wandinger Aufgae 1 1.1 Zug und Druck Aufgaen Der ageildete Sta ist am linken Ende Ende durch die Kraft elastet. Ermitteln Sie die Normalspannung in den Schnitten A
4. Balken. Brücken Tragflügel KFZ-Karosserie: A-Säule, B-Säule Rahmen: Fahrrad, Motorrad. Prof. Dr. Wandinger 2. Festigkeitslehre TM 2.
 4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
Illustrierende Aufgaben zum LehrplanPLUS. Schaukeln
 Jahrgangsstufen FOS 12, BOS 12 Schauken Stand: 08.12.2017 Fach/Fächer Übergreifende Bidungs- und Erziehungsziee Physik Medienbidung/digitae Bidung, sprachiche Bidung Benötigtes Materia - Kompetenzerwartungen
Jahrgangsstufen FOS 12, BOS 12 Schauken Stand: 08.12.2017 Fach/Fächer Übergreifende Bidungs- und Erziehungsziee Physik Medienbidung/digitae Bidung, sprachiche Bidung Benötigtes Materia - Kompetenzerwartungen
(Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.)
 K, 8.6.8 Seite Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen agegeen sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgae :
K, 8.6.8 Seite Pflichtteil (etwa min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen agegeen sein, ehe der GTR und die Formalsammlung verwendet werden dürfen.) Aufgae :
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
1 Technische Mechanik. 3. Klausur. Die Aufgaben wurden mit Genehmigung der Verlage aus folgenden Büchern entnommen:
 achschue für. Kausur Schujahr 8/9 emerkung: Die ufgaen wuren mit Genehmigung er Verage aus fogenen üchern entnommen: Nr., un : ayer u.a.: un estigkeitsehre, Verag Hanwerk un Technik, 5. üerareitete ufage,
achschue für. Kausur Schujahr 8/9 emerkung: Die ufgaen wuren mit Genehmigung er Verage aus fogenen üchern entnommen: Nr., un : ayer u.a.: un estigkeitsehre, Verag Hanwerk un Technik, 5. üerareitete ufage,
Vorwort 6 1 Der TI-Nspire CX CAS 7
 Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der TI-Nspire CX CAS 7 1.1 Der Hauptbidschirm............................... 8 1.2 Die Bidschirmeemente des TI-Nspire CX CAS................ 9 1.3 Das
Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der TI-Nspire CX CAS 7 1.1 Der Hauptbidschirm............................... 8 1.2 Die Bidschirmeemente des TI-Nspire CX CAS................ 9 1.3 Das
Kapitel 1. Zug und Druck in Stäben
 Kapite 1 Zug und Druck in Stäben 1 1 Zug und Druck in Stäben 1.1 Spannung... 7 1.2 Dehnung... 13 1.3 Stoffgesetz... 14 1.4 Einzestab... 18 1.5 Statisch bestimmte Stabsysteme... 28 1.6 Statisch unbestimmte
Kapite 1 Zug und Druck in Stäben 1 1 Zug und Druck in Stäben 1.1 Spannung... 7 1.2 Dehnung... 13 1.3 Stoffgesetz... 14 1.4 Einzestab... 18 1.5 Statisch bestimmte Stabsysteme... 28 1.6 Statisch unbestimmte
Technische Mechanik 2
 Springer-Lehrbuch Technische Mechanik 2 Eastostatik von Dietmar Gross, Werner Hauger, Jörg Schröder, Wofgang A. Wa 11., bearb. Auf. 2012 Technische Mechanik 2 Gross / Hauger / Schröder / et a. schne und
Springer-Lehrbuch Technische Mechanik 2 Eastostatik von Dietmar Gross, Werner Hauger, Jörg Schröder, Wofgang A. Wa 11., bearb. Auf. 2012 Technische Mechanik 2 Gross / Hauger / Schröder / et a. schne und
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Frühjahr 2016
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Aufgabe 1 (Seite 1 von 2) Das dargestete
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Aufgabe 1 (Seite 1 von 2) Das dargestete
Physik 4, Übung 7, Prof. Förster
 Physik 4, Übung 7, Prof. Förster Christoph Hansen Emaikontakt Dieser Text ist unter dieser Creative Commons Lizenz veröffenticht. Ich erhebe keinen Anspruch auf Voständigkeit oder Richtigkeit. Fas ihr
Physik 4, Übung 7, Prof. Förster Christoph Hansen Emaikontakt Dieser Text ist unter dieser Creative Commons Lizenz veröffenticht. Ich erhebe keinen Anspruch auf Voständigkeit oder Richtigkeit. Fas ihr
Pharmakokinetik-Grundlagen, Teil 1
 Pharmakokinetik-Grundagen, Tei 1 Thomas Schnider 29. ärz 2016 1 Grundbegriffe Die kassische Pharmakokinetik beschreibt u.a Begriffe wie Verteiungsvoumen, Cearance und Habwertszeit. Es ist wichtig diese
Pharmakokinetik-Grundagen, Tei 1 Thomas Schnider 29. ärz 2016 1 Grundbegriffe Die kassische Pharmakokinetik beschreibt u.a Begriffe wie Verteiungsvoumen, Cearance und Habwertszeit. Es ist wichtig diese
Übungen zu Theoretischer Mechanik (T1)
 Arnod Sommerfed Center Ludwig Maximiians Universität München Prof. Dr. Viatchesav Muhanov Sommersemester 0 Übungen zu Theoretischer Mechani T) Übungsbatt 7, Besprechung ab.05.0 Aufgabe 7. Gedämpfter harmonischer
Arnod Sommerfed Center Ludwig Maximiians Universität München Prof. Dr. Viatchesav Muhanov Sommersemester 0 Übungen zu Theoretischer Mechani T) Übungsbatt 7, Besprechung ab.05.0 Aufgabe 7. Gedämpfter harmonischer
Biegelinie: PSfrag replacements. I : w I (x) = q 1l 4 [( x. II : w II (x) = (q 2 q 1 )l 4 [ ( x. ges (x) = w I (x) + w II (x) (19) l 24 + q x 3 )
 Mechanik I Prof. Popov SS 05, 9. Woche Lösungshinweise Seite Biegeinienberechnung statisch bestimmter und unbestimmter Systeme Version. Juni 005 aus schanken Baken Aufgabe 9 a PSfrag repacements qx = q
Mechanik I Prof. Popov SS 05, 9. Woche Lösungshinweise Seite Biegeinienberechnung statisch bestimmter und unbestimmter Systeme Version. Juni 005 aus schanken Baken Aufgabe 9 a PSfrag repacements qx = q
= 1kN F 1 F 2. = 2,5 kn. 2m 4m 2m. = 0,75 kn/m. Webinar: Statik Thema: Schnittgrößen
 Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Webinar Statik Thema Schnittgrößen Bestimme für die nachfolgenden beiden Aufgaben die Schnittgrößen und Schnittgrößenverläufe! F 1 = 1k = 2,5 k a) 30 = 0,75 k/m b) Lösung Teil a) Wir beginnen damit den
Statik und Tragwerkslehre B
 Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 27.02.2012 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
Bacheor - Studiengang Bauingenieurwesen Prüfungsfach Statik und Tragwerksehre B Kausur am 27.02.2012 Name: Vorname: Matr.-Nr.: (bitte deutich schreiben) (9-steig) Aufgabe 1 2 3 4 Summe mögiche Punkte 15
Theoretische Physik: Mechanik
 Ferienkurs Merin Mitschek, Phiipp Landgraf 30.09.06 Ferienkurs Theoretische Physik: Mechanik Probekausur - Lösung Technische Universität München Fakutät für Physik Ferienkurs Merin Mitschek, Phiipp Landgraf
Ferienkurs Merin Mitschek, Phiipp Landgraf 30.09.06 Ferienkurs Theoretische Physik: Mechanik Probekausur - Lösung Technische Universität München Fakutät für Physik Ferienkurs Merin Mitschek, Phiipp Landgraf
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Herbst 2014
 Herbst 2014 Herbst 2014 Aufgabe 1 (Seite 1 von 3) a) Der dargestete, in A und C geagerte Baken wird durch eine Streckenast q 0 sowie eine Einzekraft F beastet. Im Punkt B befindet sich ein Vogeenk. q 0
Herbst 2014 Herbst 2014 Aufgabe 1 (Seite 1 von 3) a) Der dargestete, in A und C geagerte Baken wird durch eine Streckenast q 0 sowie eine Einzekraft F beastet. Im Punkt B befindet sich ein Vogeenk. q 0
Partialbruchzerlegung
 Partialruchzerlegung Unknown: www.gute-mathe-fragen.de/user/unknown Letzte Änderung: 11.09.2013 1 Contents 1 Nutzen/Ziel [Integration] 3 2 Partialruchzerlegung 4 2.1 Rellee Nullstellen (einfach).....................
Partialruchzerlegung Unknown: www.gute-mathe-fragen.de/user/unknown Letzte Änderung: 11.09.2013 1 Contents 1 Nutzen/Ziel [Integration] 3 2 Partialruchzerlegung 4 2.1 Rellee Nullstellen (einfach).....................
Praktikumsprotokoll Physikalisch-Chemisches Anfängerpraktikum
 Tobias Schabe Datum des Praktikumstags: 25.10.2005 Matthias Ernst Protoko-Datum: 26.10.2005 Gruppe A-11 1. Versuch: KH - Ketonhaogenierung Assistent: D. Santi Aufgabensteung In diesem Versuch wird die
Tobias Schabe Datum des Praktikumstags: 25.10.2005 Matthias Ernst Protoko-Datum: 26.10.2005 Gruppe A-11 1. Versuch: KH - Ketonhaogenierung Assistent: D. Santi Aufgabensteung In diesem Versuch wird die
Finite-Elemente-Methode
 11. Übung Prof. Dr.-Ing. W. Fischer Fachhochschue Dortmund Knicken und Beuen 1. Bestimmen Sie sowoh anaytisch wie auch mit Hife des FEM-Systems HyperWorks 14 für einen Stah-Kragträger der Länge = 1 m (quadratischer
11. Übung Prof. Dr.-Ing. W. Fischer Fachhochschue Dortmund Knicken und Beuen 1. Bestimmen Sie sowoh anaytisch wie auch mit Hife des FEM-Systems HyperWorks 14 für einen Stah-Kragträger der Länge = 1 m (quadratischer
Lösung zu Übungsblatt 1
 Technische Universität München Fakutät für Physik Ferienkurs Theoretische Physik 1 Lösung zu Übungsbatt 1 Grundagen der Newton schen Mechanik, Zweiteichensysteme 1. Vektoranaysis (*) (a) Der Gradient eines
Technische Universität München Fakutät für Physik Ferienkurs Theoretische Physik 1 Lösung zu Übungsbatt 1 Grundagen der Newton schen Mechanik, Zweiteichensysteme 1. Vektoranaysis (*) (a) Der Gradient eines
