Verfahren des Operations Research
|
|
|
- Nicolas Arnold
- vor 5 Jahren
- Abrufe
Transkript
1 Verfahren des Operations Research Blatt 1 (WS 2017/18) wird bearbeitet am Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80 kg/stk und für G kg/stk von dem Rohstoff. An Arbeitszeit sind bei G 1 6 h/stk, bei G 2 10 h/stk und bei G 3 3 h/stk aufzuwenden. Im betrachteten Planungzeitraum stehen Arbeitsstunden und kg Rohstoff zur Verfügung. Aus technischen Gründen (die meistens sehr undurchschaubar sind) muss von G 1 mindestens die doppelte Stückzahl wie von G 2 produziert werden. Es wird erwartet, dass pro hergestelltem Stück bei G 1 C 30., bei G 2 C 50. und bei G 3 C 60. Gewinn erzielt wird. Stellen Sie zur Bestimmung der gewinnmaximierenden Stückzahlen ein lineares Programm auf und lösen Sie es mit Excel. 2. Modellieren Sie das folgende Problem eines Barkeepers: In der Bar werden drei verschiedene Cocktails angeboten: a) Daiquiri (45 ml weißer Rum, 30 ml Cointreau, 25 ml Zitronensaft, 15 ml Zuckersirup, Eis), Preis: C 5.80 b) Kamikaze (30 ml Wodka, 30 ml Cointreau, 25 ml Zitronensaft, 1 Schuß Limonensirup, Eis), Preis: C 4.70 c) Long Island Ice Tea (20 ml Wodka, 20 ml weißer Rum, 20 ml Gin, 20 ml Cointreau, 4 TL Zitronensaft, 4 TL Orangensaft, 1/8 l Cola, 1 Orangenscheibe, Eis), Preis: C 7.00 Der Vorrat des Barkeepers besteht aus 5 l weißem Rum, 6 l Cointreau, 4 l Wodka und 3 l Gin. Die übrigen Zutaten sind ausreichend vorhanden. Welche Cocktails muss der Barkeeper mixen und verkaufen, um möglichst viel Geld einzunehmen? (Hinweis: 1 l = 1000 ml) Formulieren Sie für dieses Problem ein lineares Programm und bestimmen Sie die Optimallösung mit Excel. 3. Zeigen Sie graphisch, dass die lineare Optimierungsaufgabe max 3x 1 + 4x 2 x 1 + x 2 4 x 1 + 2x 2 10 x 1 + 4x 2 4
2 mit x 1, x 2 0 eine optimale Lösung besitzt, obwohl die Menge der zulässigen Lösungen nicht beschränkt ist. 4. Giffen Paradoxon: Herr K. will 40km zurücklegen. Dafür stehen Boot und Zug zur Verfügung, die beliebig kombiniert werden können. Das Boot benötigt 2 Zeiteinheiten pro km und kostet C 5. pro km. Der Zug benötigt nur 1 Zeiteinheit pro km, kostet aber C 10. pro km. Wie schnell kann Herr K. die Strecke absolvieren, wenn er C 300. zur Verfügung hat? Stellen Sie ein lineares Programm auf und lösen Sie es mit Excel. Paradoxon: Der Preis des Bootes wird nun auf C 6. pro km erhöht. Weisen Sie nach, dass die mit dem Boot zurückgelegte Strecke dennoch steigt! 5. Lösen Sie das folgende lineare Programm händisch mit dem Simplexalgorithmus: max 3 4 x 1 + x 2 bzgl. x 1 + 2x 2 10 x 1 + x 2 7 x 2 4 x 1, x Lösen Sie das folgende lineare Programm händisch mit dem Simplexalgorithmus: max 6x 1 + 3x 2 9x x 4 bzgl. x 1 + 2x 2 + 4x 3 x x 1 + 3x 2 x 3 + x 4 72 x 1 + x 3 + x 4 24 x 1, x 2, x 3, x Gegeben sei folgendes (LP1): (LP1) maximiere 3x 1 + x 2 + x 3 bzgl. 3x 1 + 2x 2 + 2x 3 10 x 1 + 3x 2 x 3 13 x 2 x 3 7 2x 1 + x 3 = 2 ( ) x 1 0, x 2 0
3 a) Schreiben Sie obiges Programm (LP1) als ein lineares Programm (LP2) mit 2 Variablen und 3 Restriktionen an. Hinweis: Verwenden Sie die Gleichung ( ) um eine Variable zu eliminieren. b) Bestimmen Sie graphisch den zulässigen Bereich und die Optimallösung von (LP2). c) Welche Probleme ergeben sich, wenn Sie versuchen die Programme (LP1) bzw. (LP2) mit dem Simplexalgorithmus zu lösen? (keine Rechnung notwendig) 8. Eine Legierung besteht aus Material A und Material B. Die variablen Kosten für die Ausgangsprodukte betragen 3000 bzw C /t (Euro pro Tonne). Von der Legierung müssen mindestens 5 t und können aus Kapazitätsgründen höchstens 10 t hergestellt werden. Von Material A sind zur Zeit nur 5 t verfügbar, von Material B hingegen 7 t. Das Verhältnis von Material A zu Material B darf 7/8 nicht übersteigen. Es stehen 20 Stunden Vorbereitungszeit zur Verfügung, wobei Material A 2.5 Std./t und Material B 1.5 Std./t benötigen. a) Formulieren Sie eine lineares Programm zur Minimierung der Kosten! b) Lösen Sie das LP graphisch und interpretieren Sie die Lösung. c) Welche Restriktionen werden aktiv und was bedeutet das? 9. Die Green Bully AG will einen neuen Softdrink auf den Markt bringen. Das neue Getränk soll aus drei flüssigen Zutaten zusammengemischt werden, wobei die erste Zutat 5 C pro Liter, die zweite Zutat 2 C pro Liter und die dritte Zutat 25 Cent pro Liter kostet. Zutat 1 enthält 3g/l Zucker und 4 Einheiten/l eines streng geheimen Aromastoffes, während die zweite Zutat 7g/l Zucker und 8 Einheiten/l des Aromastoffes und die dritte Zutat 20g/l Zucker und keinen Aromastoff enthält. Aus produktionstechnischen Gründen müssen pro Produktionsvorgang mindestens 100 Liter des Getränks hergestellt werden. Die Marktforschung hat ergeben, dass das Getränk von der Zielgruppe angenommen wird, falls sich die Parameter in folgenden Intervallen bewegen: Das fertige Getränk soll mindestens 3g/l und höchtens 6g/l Zucker enthalten. In einem Liter des Getränks sollen sich mindestens 3 Einheiten des Aromastoffes befinden. Außerdem soll das Getränk zu mindestens 40% aus Zutat 1 bestehen, während Zutat 2 höchstens 50% und Zutat 3 höchstens 30% des neuen Getränks ausmachen darf. Wie soll der neue Softdrink bei minimalen Produktionskosten zusammengemixt werden? Achten Sie auf die exakte Bedeutung der von ihnen verwendeten Variablen.
4 10. Konstruieren Sie ein lineares Programm mit zwei Variablen, bei dem die übliche Spaltenauswahlregel für das Simplexverfahren nicht die kleinstmögliche Anzahl von Iterationen liefert. (Es ist hilfreich mit einer Skizze zu beginnen.) 11. Versuchen Sie eine Methode zu finden, um die zweitbeste zulässige Basislösung eines linearen Programms zu bestimmen. 12. Stellen Sie das folgende lineare Programm in Standardform dar: min 5x 1 3x 2 4x 3 + 7x unter x 1 2x 2 2x 4 8 x 2 + 2x 3 + x 4 6 5x 1 + x 3 = 5 x 2 + 2x 4 4 3x 2 2x 4 = 6 x 1 0 x 2 0 x 3, x 4 R 13. Betrachten Sie das folgende Endtableau eines LP in Normalform mit den Modellvariablen x 1,..., x 4. x 1 x 2 x 3 x 4 x 5 x 6 x 7 ZF a) Welche Variablen sind Basisvariablen und wie lauten die Optimalwerte der Modellvariablen? b) Wie ändert sich der Zielfunktionswert, wenn x 3 um eine Einheit erhöht wird? c) Welche Restriktion(en) können gestrichen werden, ohne dass sich die Optimallösung ändert? d) Die Angabe des LP beginnt mit max 3x 1 2x Aus welchem Bereich können die Koeffizienten von x 1 und x 2 gewählt werden, sodass die optimale Basislösung unverändert bleibt?
5 e) In welchem Bereich kann die Kapazitätsschranke der ersten Restriktion des LP gewählt werden, sodass die optimale Basislösung unverändert bleibt, wenn sie zu Beginn mit 15 festgesetzt war? 14. Wie lautet die Optimallösung der Dual-Variablen für das LP aus Beispiel 13? (Das duale LP muss nicht angegeben werden.) 15. Stellen Sie das duale LP zum linearen Programm aus Beispiel 5. auf. 16. Gegeben ist das folgende LP: (PP) maximiere 4x 1 3x 2 2x 3 + 7x 4 bzgl. x 1 2x 2 + 2x 4 8 x 2 + 2x 3 + x 4 3 5x 1 + x 3 = 3 x 2 + 2x 4 4 x 1 3x 2 + 2x 4 = 6 x 1 0, x 2 0, x 3, x 4 R Stellen Sie das dazugehörige duale LP (DP) auf!
Verfahren des Operations Research
 Verfahren des Operations Research Blatt 1 (WS 2018/19) wird bearbeitet am 31.10.2018 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Verfahren des Operations Research Blatt 1 (WS 2018/19) wird bearbeitet am 31.10.2018 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Übung 3, Simplex-Algorithmus
 Übung 3, 21.6.2011 Simplex-Algorithmus Aufgabe 3.1 Lösen Sie das folgende Optimierungsproblem (von Aufgabe 2.3) graphisch. Substituieren Sie dazu z = 5 y um ein 2-dimensionales Problem zu erhalten. Rechnung
Übung 3, 21.6.2011 Simplex-Algorithmus Aufgabe 3.1 Lösen Sie das folgende Optimierungsproblem (von Aufgabe 2.3) graphisch. Substituieren Sie dazu z = 5 y um ein 2-dimensionales Problem zu erhalten. Rechnung
Eigenschaften von LPs
 2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
Simplex-Verfahren. Kapitel 4. Simplex-Verfahren. Peter Becker (H-BRS) Operations Research I Sommersemester / 298
 Kapitel 4 Simplex-Verfahren Peter Becker (H-BRS) Operations Research I Sommersemester 24 86 / 298 Inhalt Inhalt 4 Simplex-Verfahren Dualer Simplexalgorithmus Vermeidung von Zyklen Peter Becker (H-BRS)
Kapitel 4 Simplex-Verfahren Peter Becker (H-BRS) Operations Research I Sommersemester 24 86 / 298 Inhalt Inhalt 4 Simplex-Verfahren Dualer Simplexalgorithmus Vermeidung von Zyklen Peter Becker (H-BRS)
Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung
 Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung Sascha Kurz Jörg Rambau 24. November 2009 2 Aufgabe 3.1. Ein in m Depots gelagertes homogenes
Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung Sascha Kurz Jörg Rambau 24. November 2009 2 Aufgabe 3.1. Ein in m Depots gelagertes homogenes
Abbildung 1: Graphische Lösung der ersten Übungsaufgabe
 Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Schnittebenenverfahren von Gomory. Stefan Allescher 30. Juni 2005
 Schnittebenenverfahren von Gomory Stefan Allescher 30. Juni 2005 Inhaltsverzeichnis 1. Grundprinzip 2. Das Verfahren von Gomory 2.1. Vorgehen 2.2. Beweis der Endlichkeit 2.3. Algorithmische Durchführung
Schnittebenenverfahren von Gomory Stefan Allescher 30. Juni 2005 Inhaltsverzeichnis 1. Grundprinzip 2. Das Verfahren von Gomory 2.1. Vorgehen 2.2. Beweis der Endlichkeit 2.3. Algorithmische Durchführung
Probeklausur Optimierung
 Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
1. Transport- und Zuordnungsprobleme
 1. Transport- und Zuordnungsprobleme Themen 1. Transport- und Zuordnungsprobleme Themen: Analyse der Problemstruktur Spezielle Varianten des Simplexalgorithmus für Transport- und Zuordnungsprobleme Bezug
1. Transport- und Zuordnungsprobleme Themen 1. Transport- und Zuordnungsprobleme Themen: Analyse der Problemstruktur Spezielle Varianten des Simplexalgorithmus für Transport- und Zuordnungsprobleme Bezug
1. Hausaufgabenblatt (16.04./ )
 Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
AUFGABENTEIL. Klausur: Modul Optimierungsmethoden des Operations Research. Termin:
 Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Univ.-Prof. Dr. Andreas Kleine AUFGABENTEIL Klausur: Modul 32621 Termin: 14.09.2015 Prüfer: Prof. Dr. Andreas
Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Univ.-Prof. Dr. Andreas Kleine AUFGABENTEIL Klausur: Modul 32621 Termin: 14.09.2015 Prüfer: Prof. Dr. Andreas
Optimierung für Wirtschaftsinformatiker: Lineare Programme
 Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Caipirinha. Zutaten: 1 unbehandelte Limette. 6 cl Cachaça. 2 TL brauner Zucker
 Caipirinha 1 unbehandelte Limette 6 cl Cachaça 2 TL brauner Zucker 1. Die Limette in acht Teile schneiden, diese in ein Glas geben und den braunen Zucker darüber streuen. Anschließend mit einem Stößel
Caipirinha 1 unbehandelte Limette 6 cl Cachaça 2 TL brauner Zucker 1. Die Limette in acht Teile schneiden, diese in ein Glas geben und den braunen Zucker darüber streuen. Anschließend mit einem Stößel
Tequila Sunrise. Zutaten: 5 cl heller Tequila. 12 cl Orangensaft. 1 cl Zitronensaft. 1-2 cl Grenadine
 Tequila Sunrise 5 cl heller Tequila 12 cl Orangensaft 1 cl Zitronensaft 1-2 cl Grenadine 1. Den Tequila, Orangen- und Zitronensaft zusammen mit ein paar Eiswürfeln shaken. (~10 Sekunden). 3. Die Grenadine
Tequila Sunrise 5 cl heller Tequila 12 cl Orangensaft 1 cl Zitronensaft 1-2 cl Grenadine 1. Den Tequila, Orangen- und Zitronensaft zusammen mit ein paar Eiswürfeln shaken. (~10 Sekunden). 3. Die Grenadine
Kurseinheit 2»Dualität und weiterführende Methoden«
 Inhaltsübersicht 1 Gliederung Kurseinheit 1»Simpleverfahren«1. Einleitung 1.1. Einordnung und Übersicht des Stoffes 1.2. Einführendes Beispiel und Grundlagen 2. Lineare Gleichungssysteme 2.1. Die allgemeine
Inhaltsübersicht 1 Gliederung Kurseinheit 1»Simpleverfahren«1. Einleitung 1.1. Einordnung und Übersicht des Stoffes 1.2. Einführendes Beispiel und Grundlagen 2. Lineare Gleichungssysteme 2.1. Die allgemeine
Aufgabenkomplex 5: Hauptachsentransformation, Lineare Optimierung, Differentialrechnung in mehreren Veränderlichen
 Aufgabenkomplex 5: Hauptachsentransformation, Lineare Optimierung, Differentialrechnung in mehreren Veränderlichen 1. Bestimmen Sie für die folgenden Funktionen zunächst die kritischen Stellen und entscheiden
Aufgabenkomplex 5: Hauptachsentransformation, Lineare Optimierung, Differentialrechnung in mehreren Veränderlichen 1. Bestimmen Sie für die folgenden Funktionen zunächst die kritischen Stellen und entscheiden
Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge)
 Beispiel: Produktionsplanung Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge) Produktionskapazität Ressourcenmenge bei als fest angenommenem
Beispiel: Produktionsplanung Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge) Produktionskapazität Ressourcenmenge bei als fest angenommenem
Lineare Programmierung (2)
 Inhalt Rückblick Motivation - linearen Programmierung Flussprobleme Multiple Warenflüsse Fortsetzung Simplex Algorithmus Initialisierung Fundamentalsatz der linearen Programmierung schwache Dualität Dualität
Inhalt Rückblick Motivation - linearen Programmierung Flussprobleme Multiple Warenflüsse Fortsetzung Simplex Algorithmus Initialisierung Fundamentalsatz der linearen Programmierung schwache Dualität Dualität
Übungsaufgaben. Teil Bergstadt-Gymnasium Ma/Inf (WPII-8) (ht) aufgabe_2017_05_12. Teil 2
 1 Gegeben ist das System linearer Ungleichungen: 2x + y 4 (1) x 2y 7 (2) 1.1 Bestimme rechnerisch den Schnittpunkt der zugehörigen Geraden! 1.2 Bestimme graphisch das Lösungsgebiet! 1 Lösungen 1 1.1 1.1.1
1 Gegeben ist das System linearer Ungleichungen: 2x + y 4 (1) x 2y 7 (2) 1.1 Bestimme rechnerisch den Schnittpunkt der zugehörigen Geraden! 1.2 Bestimme graphisch das Lösungsgebiet! 1 Lösungen 1 1.1 1.1.1
Übungsaufgaben. Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler. Teil 1: Lineare Algebra und Optimierung.
 Übungsaufgaben Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler Teil : Lineare Algebra und Optimierung Wintersemester Matrizenrechnung Aufgabe ( 3 0 Gegeben sind die Matrizen A = 2 5 2 4 D =
Übungsaufgaben Grundkurs Höhere Mathematik für Wirtschaftswissenschaftler Teil : Lineare Algebra und Optimierung Wintersemester Matrizenrechnung Aufgabe ( 3 0 Gegeben sind die Matrizen A = 2 5 2 4 D =
Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler
 Wintersemester 2007/08 27.2.2008 Dr. Sascha Kurz Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler Bitte lesbar ausfüllen, Zutreffendes ankreuzen Herr Frau Name, Vorname: Anschrift:
Wintersemester 2007/08 27.2.2008 Dr. Sascha Kurz Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler Bitte lesbar ausfüllen, Zutreffendes ankreuzen Herr Frau Name, Vorname: Anschrift:
Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel:
 Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel: Eine Firma produziert die Produkte P 1, P 2,..., P q aus den Rohstoffen R 1, R 2,..., R m. Dabei stehen b j Einheiten
Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel: Eine Firma produziert die Produkte P 1, P 2,..., P q aus den Rohstoffen R 1, R 2,..., R m. Dabei stehen b j Einheiten
4.3.3 Simplexiteration
 7. Januar 2013 53 4.3.3 Simplexiteration Eine Simplexiteration entspricht dem Übergang von einer Ecke des zulässigen Bereiches in eine benachbarte Ecke Dabei wird genau eine Nichtbasisvariable (die zugehörige
7. Januar 2013 53 4.3.3 Simplexiteration Eine Simplexiteration entspricht dem Übergang von einer Ecke des zulässigen Bereiches in eine benachbarte Ecke Dabei wird genau eine Nichtbasisvariable (die zugehörige
1 Der Simplex Algorithmus I
 1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
Computer Science Department - High Performance and Web Computing Group. Optimierungsprobleme
 Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
AUFGABEN. Klausur: Modul Optimierungsmethoden des Operations Research. Termin:
 Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Prof. Dr. Andreas Kleine AUFGABEN Klausur: Modul 32621 Optimierungsmethoden des Operations Research Termin:
Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Prof. Dr. Andreas Kleine AUFGABEN Klausur: Modul 32621 Optimierungsmethoden des Operations Research Termin:
1.4 Aufgaben. 2002/2003
 .4 Aufgaben. 00/003 Aufgabe. Eine Firma stellt zwei Sorten A und B einer Meterware her. Pro Meter entstehen folgende Kosten und Erlöse in Euro: Rohstoffkosten Bearbeitungskosten Verkaufserlös A 6 3 5 B
.4 Aufgaben. 00/003 Aufgabe. Eine Firma stellt zwei Sorten A und B einer Meterware her. Pro Meter entstehen folgende Kosten und Erlöse in Euro: Rohstoffkosten Bearbeitungskosten Verkaufserlös A 6 3 5 B
Fachakademie für Wirtschaft der FHM A2: Lineare Optimierung und das Simplexverfahren
 A2.1 Lineare Optimierung mit dem Simplexverfahren Wenn ein Unternehmen ermitteln möchte, wie viele Mengeneinheiten von verschiedenen Produkten zu produzieren sind, damit bei gegebenen Verkaufspreisen der
A2.1 Lineare Optimierung mit dem Simplexverfahren Wenn ein Unternehmen ermitteln möchte, wie viele Mengeneinheiten von verschiedenen Produkten zu produzieren sind, damit bei gegebenen Verkaufspreisen der
Lineare Optimierung Ergänzungskurs
 Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA Mögliche Fälle für Z Etschberger - WS2016 1 Z =, d.h., es existiert keine zulässige (x 1, x 2 )-Kombination. 2
Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA Mögliche Fälle für Z Etschberger - WS2016 1 Z =, d.h., es existiert keine zulässige (x 1, x 2 )-Kombination. 2
Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel 3 - Lineare Optimierung
 Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel - Lineare Optimierung Sascha Kurz Jörg Rambau 8. August Lösung Aufgabe.. Da es sich um ein homogenes
Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel - Lineare Optimierung Sascha Kurz Jörg Rambau 8. August Lösung Aufgabe.. Da es sich um ein homogenes
Minimumproblem. Definition 4.7. Ein LP der Form. unter den Nebenbedingungen. d ij x j b i (i =1,...,m)
 Minimumproblem Definition 4.7 Ein LP der Form nx Minimiere Z = c j x j j=1 unter den Nebenbedingungen nx d ij x j b i (i =1,...,m) j=1 und den Vorzeichenbedingungen x j 0(j =1,...,n) heißt Minimumproblem.
Minimumproblem Definition 4.7 Ein LP der Form nx Minimiere Z = c j x j j=1 unter den Nebenbedingungen nx d ij x j b i (i =1,...,m) j=1 und den Vorzeichenbedingungen x j 0(j =1,...,n) heißt Minimumproblem.
Dualitätssätze der linearen Optimierung
 Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
F u n k t i o n e n Lineare Optimierung
 F u n k t i o n e n Lineare Optimierung Das Simplex-Verfahren läuft die Ecken des Polyeders ab, bis es an einer Optimallösung angekommen ist. 1. Einführung Während des 2. Weltkrieges und in den darauf
F u n k t i o n e n Lineare Optimierung Das Simplex-Verfahren läuft die Ecken des Polyeders ab, bis es an einer Optimallösung angekommen ist. 1. Einführung Während des 2. Weltkrieges und in den darauf
Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester 2007/2008
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Klausur zur Vorlesung Operations Research im Sommersemester 2009
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Operations Research im Sommersemester 2009 Hinweise:
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Operations Research im Sommersemester 2009 Hinweise:
Produktionsplanung und Lineare Optimierung im Rahmen des Projekts Mathematik und Ökonomie 12./13. November 2003 in Düsseldorf.
 Übungsaufgaben Aufgabe 1a Medikamentenmischung Ein Pharmaziehersteller möchte ein neues Medikament auf den Markt bringen. Das Medikament kann aus vier verschiedenen Komponenten (K1 K4) zusammengestellt
Übungsaufgaben Aufgabe 1a Medikamentenmischung Ein Pharmaziehersteller möchte ein neues Medikament auf den Markt bringen. Das Medikament kann aus vier verschiedenen Komponenten (K1 K4) zusammengestellt
Zugeordneter bipartiter Graph
 Zugeordneter bipartiter Graph Für ein Transportproblem sei A = {A 1,...,A m } die Menge der Fabriken und B = {B 1,...,B n } sei die Menge der Warenhäuser. Wir ordnen nun einem Transportproblem einen bipartiten
Zugeordneter bipartiter Graph Für ein Transportproblem sei A = {A 1,...,A m } die Menge der Fabriken und B = {B 1,...,B n } sei die Menge der Warenhäuser. Wir ordnen nun einem Transportproblem einen bipartiten
Kosten und Umsatzfunktionen
 In den folgenden Abschnitten wenden wir gelegentlich Anwendungen aus der Wirtschaft behandeln. Wir stellen deshalb einige volks- und betriebswirtschaftliche Funktionen vor. Dabei handelt es sich stets
In den folgenden Abschnitten wenden wir gelegentlich Anwendungen aus der Wirtschaft behandeln. Wir stellen deshalb einige volks- und betriebswirtschaftliche Funktionen vor. Dabei handelt es sich stets
Operations Research. Die Simplexmethode. LP-Dualität. Die Simplexmethode. Rainer Schrader. 18. Juni Zur Erinnerung: Gliederung
 Operations Research Rainer Schrader Die Simplexmethode Zentrum für Angewandte Informatik Köln 18 Juni 00 1 / 1 / 1 Gliederung LP-Dualität ein lineares Produktionsmodell der Simplexalgorithmus Phase I Endlichkeit
Operations Research Rainer Schrader Die Simplexmethode Zentrum für Angewandte Informatik Köln 18 Juni 00 1 / 1 / 1 Gliederung LP-Dualität ein lineares Produktionsmodell der Simplexalgorithmus Phase I Endlichkeit
1.6 lineare Optimierung
 1.6 lineare Optimierung Inhaltsverzeichnis 1 Lineare Gleichung mit 2 Unbekannten 2 1.1 Was ist eine lineare Gleichung mit 2 Unbekannten?..................... 2 1.2 Was ist eine Lösung einer linearen Gleichung
1.6 lineare Optimierung Inhaltsverzeichnis 1 Lineare Gleichung mit 2 Unbekannten 2 1.1 Was ist eine lineare Gleichung mit 2 Unbekannten?..................... 2 1.2 Was ist eine Lösung einer linearen Gleichung
Lineare Optimierung: Simplexverfahren Phase Ⅰ
 Lineare Optimierung: Simplexverfahren Phase Ⅰ Zur Erinnerung: Die Lineare Optimierungsaufgabe in Standardform lautet z = c T x + c 0 min (.) bei Ax = b, x 0. Revidiertes Simplexverfahren Mit dem Simplexverfahren
Lineare Optimierung: Simplexverfahren Phase Ⅰ Zur Erinnerung: Die Lineare Optimierungsaufgabe in Standardform lautet z = c T x + c 0 min (.) bei Ax = b, x 0. Revidiertes Simplexverfahren Mit dem Simplexverfahren
VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt)
 VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 96 H. Meyerhenke: Kombinatorische Optimierung Dualität bei linearen Programmen Def.: Es sei (L): c T x max
VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 96 H. Meyerhenke: Kombinatorische Optimierung Dualität bei linearen Programmen Def.: Es sei (L): c T x max
Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
Der Simplex-Algorithmus
 5 Lineare Programmierung Simplex-Algorithmus Der Simplex-Algorithmus Standardverfahren zur Lösung von LPs, von G B Dantzig entwickelt Grundidee: Versuche ausgehend von einer Startecke mit einer Ausgangsbasis
5 Lineare Programmierung Simplex-Algorithmus Der Simplex-Algorithmus Standardverfahren zur Lösung von LPs, von G B Dantzig entwickelt Grundidee: Versuche ausgehend von einer Startecke mit einer Ausgangsbasis
Studientag zur Algorithmischen Mathematik
 Studientag zur Algorithmischen Mathematik Lineare Optimierung Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 1. Juli 2012 Outline Lineares Programm (LP) in Standardform
Studientag zur Algorithmischen Mathematik Lineare Optimierung Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 1. Juli 2012 Outline Lineares Programm (LP) in Standardform
3.2.5 Dualität der linearen Optimierung I
 3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung
 Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Vorlesung Wirtschaftsmathematik I WS 2007/2008, Wirtschaftingenieurwesen. Kapitel IV: Grundlagen der Linearen Optimierung
 Vorlesung Wirtschaftsmathematik I WS 2007/2008, Wirtschaftingenieurwesen Kapitel IV: Grundlagen der Linearen Optimierung Inhaltsverzeichnis Abschnitt 3-5 3 Der Simplexalgorithmus 58 3.1 Grundlagen..............................
Vorlesung Wirtschaftsmathematik I WS 2007/2008, Wirtschaftingenieurwesen Kapitel IV: Grundlagen der Linearen Optimierung Inhaltsverzeichnis Abschnitt 3-5 3 Der Simplexalgorithmus 58 3.1 Grundlagen..............................
Zutaten gut im Shaker schütteln und im Longdrinkglas auf Eis servieren.
 Alkoholfrei Virgin Colada - 8 cl EL PUENTE Orangensaft - 8 cl Ananassaft - 2 cl Kokosmilch Zutaten gut im Shaker schütteln und im Longdrinkglas auf Eis servieren. Alice - 8 cl EL PUENTE Orangensaft - 8
Alkoholfrei Virgin Colada - 8 cl EL PUENTE Orangensaft - 8 cl Ananassaft - 2 cl Kokosmilch Zutaten gut im Shaker schütteln und im Longdrinkglas auf Eis servieren. Alice - 8 cl EL PUENTE Orangensaft - 8
Aufgabe 3.1: LP-Informationen im Optimum
 Johann Wolfgang Goethe-Universität Frankfurt am Main Lehrst.f.BWL, insb. Quant. Methoden Prof. Dr. Dietrich Ohse LPUE:SQM6 LP und Erweiterungen lpueb03_ 2003s.doc Aufgabe 3.1: LP-Informationen im Optimum
Johann Wolfgang Goethe-Universität Frankfurt am Main Lehrst.f.BWL, insb. Quant. Methoden Prof. Dr. Dietrich Ohse LPUE:SQM6 LP und Erweiterungen lpueb03_ 2003s.doc Aufgabe 3.1: LP-Informationen im Optimum
Lösung allgemeiner linearer Programme
 Lösung allgemeiner linearer Programme Bisher: Für Anwendung des Simplexalgorithmus muss eine primal oder eine dual zulässige Basislösung vorliegen. Für allgemeine lineare Programme können wir dies direkt
Lösung allgemeiner linearer Programme Bisher: Für Anwendung des Simplexalgorithmus muss eine primal oder eine dual zulässige Basislösung vorliegen. Für allgemeine lineare Programme können wir dies direkt
würde eine Reduktion der Kapazität um = 100 h ebenfalls eine Änderung des
 Aufgabe 4.: Sensitivitätsanalyse (a) 60 c 30 Deckungsbeitrag: (30 db 60) (b) 20 3 c C 0 3 Das heißt, die Restkapazität kann bis zu 20 3 Erträge bringen, bzw. bis zu 0 3 Kosten verursachen, ohne die Lösung
Aufgabe 4.: Sensitivitätsanalyse (a) 60 c 30 Deckungsbeitrag: (30 db 60) (b) 20 3 c C 0 3 Das heißt, die Restkapazität kann bis zu 20 3 Erträge bringen, bzw. bis zu 0 3 Kosten verursachen, ohne die Lösung
Math. II, Numerik, Uebung 2, Termin Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen
 Math. II, Numerik, Uebung 2, Termin 25.10.2012 1-Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen ALLGEMEINES Detaillierter Bewertungsbogen auf der Rückseite des Deckblatts 1. Nur Verfahren der angewandten
Math. II, Numerik, Uebung 2, Termin 25.10.2012 1-Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen ALLGEMEINES Detaillierter Bewertungsbogen auf der Rückseite des Deckblatts 1. Nur Verfahren der angewandten
Lineare (Un-)Gleichungen und lineare Optimierung
 Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung In der linearen
Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung In der linearen
AUFGABENTEIL. Klausur: Modul Optimierungsmethoden des Operations Research. Termin:
 Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Univ.-Prof. Dr. Andreas Kleine AUFGABENTEIL Klausur: Modul 32621 Termin: 23.03.2017 Prüfer: Prof. Dr. Andreas
Lehrstuhl für Betriebswirtschaftslehre, insb. Quantitative Methoden und Wirtschaftsmathematik Univ.-Prof. Dr. Andreas Kleine AUFGABENTEIL Klausur: Modul 32621 Termin: 23.03.2017 Prüfer: Prof. Dr. Andreas
Lösung von Optimierungsproblemen anhand von Simplex- Verfahren
 Lineare Optimierung Lösung von Optimierungsproblemen anhand von Simplex- Verfahren Informatik-Seminar Studiengang: Informatik Autor: Zemp Michael Betreuer: Schwab Peter Auftraggeber: Schwab Peter Experten:
Lineare Optimierung Lösung von Optimierungsproblemen anhand von Simplex- Verfahren Informatik-Seminar Studiengang: Informatik Autor: Zemp Michael Betreuer: Schwab Peter Auftraggeber: Schwab Peter Experten:
Optimierung. Optimierung. Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus Fabian Kuhn
 Optimierung Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus 1 Resource Allocation Beispiel aus Vorlesung 6 Primales LP: Duales LP: max 3 4 2 2 4 2 8 3 6 0, 0, 0 min 4 8 6 2 3 3 4 2 2 0, 0,
Optimierung Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus 1 Resource Allocation Beispiel aus Vorlesung 6 Primales LP: Duales LP: max 3 4 2 2 4 2 8 3 6 0, 0, 0 min 4 8 6 2 3 3 4 2 2 0, 0,
(Technisch: Setze alle Skalarprodukte der allgemeinen Lösung mit den Basisvektoren des Kerns gleich Null eindeutige leastsqares Lösung)
 Lineare Optimierung Unterbestimmte LGS und Optimierung Bei lösbaren unterbestimmten linearen Gleichungssystemen haben wir die Qual der Wahl in Abhängigkeit von den freien Parametern (Anzahl = Anzahl Unbekannte
Lineare Optimierung Unterbestimmte LGS und Optimierung Bei lösbaren unterbestimmten linearen Gleichungssystemen haben wir die Qual der Wahl in Abhängigkeit von den freien Parametern (Anzahl = Anzahl Unbekannte
Fachhochschule Bochum Fachhochschule Münster Fachhochschule Südwestfalen
 Fachhochschule Bochum Fachhochschule Münster Fachhochschule Südwestfalen Verbundstudiengang Wirtschaftsingenieurwesen Prof. Dr. rer. nat. habil. J. Resch Prüfung: Mathematik Termin: 1. September 2012 Bearbeitungszeit:
Fachhochschule Bochum Fachhochschule Münster Fachhochschule Südwestfalen Verbundstudiengang Wirtschaftsingenieurwesen Prof. Dr. rer. nat. habil. J. Resch Prüfung: Mathematik Termin: 1. September 2012 Bearbeitungszeit:
Lineare Optimierung. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet.
 Lineare Optimierung Dr. Bommhardt. Das ervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Gleichungen und Ungleichungen n der Wirtschaft sind häufig
Lineare Optimierung Dr. Bommhardt. Das ervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Gleichungen und Ungleichungen n der Wirtschaft sind häufig
Lineare Optimierung Teil 2
 Lineare Optimierung Teil 2 Primale Degeneration Duale Degeneration = Mehrdeutigkeit Normalform kanonische Form Duale Simplexmethode HTW-Berlin FB3 Prof. Dr.F. Hartl 1 Primale Degeneration/1 Besitzt eine
Lineare Optimierung Teil 2 Primale Degeneration Duale Degeneration = Mehrdeutigkeit Normalform kanonische Form Duale Simplexmethode HTW-Berlin FB3 Prof. Dr.F. Hartl 1 Primale Degeneration/1 Besitzt eine
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse
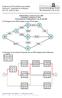 Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Schranken für zulässige Lösungen
 Schranken für zulässige Lösungen Satz 5.9 Gegeben seien primales und duales LP gemäß der asymmetrischen Form der Dualität. Wenn x eine zulässige Lösung des primalen Programms und u eine zulässige Lösung
Schranken für zulässige Lösungen Satz 5.9 Gegeben seien primales und duales LP gemäß der asymmetrischen Form der Dualität. Wenn x eine zulässige Lösung des primalen Programms und u eine zulässige Lösung
Lineare Optimierungsmodelle
 Lineare Optimierungsmodelle Simplex-Methode Vortragender: Michael Schneider Agenda Motivation Operations Research Aufbau linearer Optimierungsmodelle Simplex-Methode Ausblick 2 Problemstellung Futtermischung
Lineare Optimierungsmodelle Simplex-Methode Vortragender: Michael Schneider Agenda Motivation Operations Research Aufbau linearer Optimierungsmodelle Simplex-Methode Ausblick 2 Problemstellung Futtermischung
10. Die Berücksichtigung nicht vorzeichenbeschränkter Variablen
 10. Die Berücksichtigung nicht vorzeichenbeschränkter Variablen Bisher haben wir immer vorausgesetzt, dass alle Variablen eines LOP der Bedingung x i 0 liegen. Im Folgenden wollen wir auch sogenannte freie
10. Die Berücksichtigung nicht vorzeichenbeschränkter Variablen Bisher haben wir immer vorausgesetzt, dass alle Variablen eines LOP der Bedingung x i 0 liegen. Im Folgenden wollen wir auch sogenannte freie
Wiederholung. Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b
 Wiederholung Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b x 0. x R n heißt Basislösung, wenn Ax = b und rang(a J ) = J, wobei J = {j x (j) 0}; Basislösung
Wiederholung Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b x 0. x R n heißt Basislösung, wenn Ax = b und rang(a J ) = J, wobei J = {j x (j) 0}; Basislösung
Aussage: richtig falsch Entscheidungen über Investitionen werden stets in der kurzfristigen (operativen) Planung getroffen.
 Aufgabe 1 Richtig oder Falsch? (20 Punkte) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an. Stimmt Ihre Bewertung einer Aussage
Aufgabe 1 Richtig oder Falsch? (20 Punkte) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an. Stimmt Ihre Bewertung einer Aussage
1 Lineare Optimierung, Simplex-Verfahren
 1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
z = c T x : Ax = b, x 0 }, - die Darstellung der Nichtbasisvektoren durch die Basis ist
 Kapitel 5 Die Simplexmethode Es werden folgende Bezeichnungen verwendet: - das untersuchte Problem ist min x R n { z = c T x : Ax = b, x 0 }, - die erste zulässige Basislösung sei x = x 1, x 2,, x m, 0,,
Kapitel 5 Die Simplexmethode Es werden folgende Bezeichnungen verwendet: - das untersuchte Problem ist min x R n { z = c T x : Ax = b, x 0 }, - die erste zulässige Basislösung sei x = x 1, x 2,, x m, 0,,
Optimale Steuerung 1 Prozessoptimierung 1
 Optimale Steuerung 1 Prozessoptimierung 1 Kapitel 2: Lineare Optimierung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Lineare Algebra (Mathematische Grundlagen) 2 Beispiel: Produktionsplanung
Optimale Steuerung 1 Prozessoptimierung 1 Kapitel 2: Lineare Optimierung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Lineare Algebra (Mathematische Grundlagen) 2 Beispiel: Produktionsplanung
Inhaltsverzeichnis Grundlagen der Linearen Optimierung
 Inhaltsverzeichnis 4 Grundlagen der Linearen Optimierung 1 4.1 Grundbegriffe............................. 1 4.1.1 Lineare Optimierung..................... 1 4.1.2 Das Grundmodell eines linearen Optimierungsproblems
Inhaltsverzeichnis 4 Grundlagen der Linearen Optimierung 1 4.1 Grundbegriffe............................. 1 4.1.1 Lineare Optimierung..................... 1 4.1.2 Das Grundmodell eines linearen Optimierungsproblems
Optimierung I, SS 2008
 Aufgabe. ca. 4 Punkte Technische Universität München Zentrum Mathematik Prof. Dr. P. Gritzmann, Dipl.-Math. M. Ritter, Dipl.-Inf. Dipl.-Math. S. Borgwardt Optimierung I, SS 2008 Übungsblatt Um gegen die
Aufgabe. ca. 4 Punkte Technische Universität München Zentrum Mathematik Prof. Dr. P. Gritzmann, Dipl.-Math. M. Ritter, Dipl.-Inf. Dipl.-Math. S. Borgwardt Optimierung I, SS 2008 Übungsblatt Um gegen die
10.2 Dualitätstheorie Operations Research. In der Standardform eines Maximierungsproblem: b e ) mit ( w) + a ej ) x j + x g = ( b g + g G
 48 0 Operations Research In der Standardform eines Maximierungsproblem: Max ( w) mit ( w) + u. d. N. z + x l + n ( a gj + j= g G e E n d j x j = z 0 j= n a l j x j = b l für alle l L j= x g n + a gj x
48 0 Operations Research In der Standardform eines Maximierungsproblem: Max ( w) mit ( w) + u. d. N. z + x l + n ( a gj + j= g G e E n d j x j = z 0 j= n a l j x j = b l für alle l L j= x g n + a gj x
Kap. 4.3: Das Dualitätstheorem der linearen Optimierung
 Kap. 4.3: Das Dualitätstheorem der linearen Optimierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 18. VO A&D WS 08/09 18.12.2008 1 Literatur
Kap. 4.3: Das Dualitätstheorem der linearen Optimierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 18. VO A&D WS 08/09 18.12.2008 1 Literatur
2. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner
 . Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner Arbeitszeit: 50 Minuten Lernstoff: Mathematische Grundkompetenzen: AG1.1 Wissen über die Zahlenmengen,,, verständig einsetzen können
. Mathematik-Schularbeit für die 5. Klasse Autor: Gottfried Gurtner Arbeitszeit: 50 Minuten Lernstoff: Mathematische Grundkompetenzen: AG1.1 Wissen über die Zahlenmengen,,, verständig einsetzen können
"Produktion und Logistik"
 Prof. Dr. Jutta Geldermann, Dipl.-Kfm. Harald Uhlemair Klausur im Fach "Produktion und Logistik" zur Veranstaltung "Produktion und Logistik" Wintersemester 2007/08 Name:... Vorname:... Matrikelnummer:...
Prof. Dr. Jutta Geldermann, Dipl.-Kfm. Harald Uhlemair Klausur im Fach "Produktion und Logistik" zur Veranstaltung "Produktion und Logistik" Wintersemester 2007/08 Name:... Vorname:... Matrikelnummer:...
Verfahren des Operations Research
 Verfahren des Operations Research Blatt 3 (WS 2017/18) wird bearbeitet am 8.1.2018 26. Erweitern Sie das Xpress Modell für das Zuordnungsproblem aus der LV: Es gibt n Mitarbeiter und m Jobs, wobei n m
Verfahren des Operations Research Blatt 3 (WS 2017/18) wird bearbeitet am 8.1.2018 26. Erweitern Sie das Xpress Modell für das Zuordnungsproblem aus der LV: Es gibt n Mitarbeiter und m Jobs, wobei n m
KLAUSUR zu Einführung in die Optimierung. Studiengang: Bachelor Master Diplom (bitte ankreuzen)
 Mathematisches Institut WS 2012/13 der Heinrich-Heine-Universität 7.02.2013 Düsseldorf Prof. Dr. Achim Schädle KLAUSUR zu Einführung in die Optimierung Bitte folgende Angaben ergänzen und DEUTLICH LESBAR
Mathematisches Institut WS 2012/13 der Heinrich-Heine-Universität 7.02.2013 Düsseldorf Prof. Dr. Achim Schädle KLAUSUR zu Einführung in die Optimierung Bitte folgende Angaben ergänzen und DEUTLICH LESBAR
1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme. Duales Problem. a i u i + i=1. j=1
 1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme Duales Problem Lemma 1.4. Das zum Transportproblem duale Problem lautet: max unter den Nebenbedingungen m a i u i + i=1
1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme Duales Problem Lemma 1.4. Das zum Transportproblem duale Problem lautet: max unter den Nebenbedingungen m a i u i + i=1
1. Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme. f(x) min, x G (1.1) (Legende)
 . Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme X Banachraum, wobei X = R n G zulässige Menge des Optimierungsproblems f: G R Zielfunktion f(x) min, x G (.) (Legende)
. Lineare Optimierungsaufgaben (LOA) als Teilklasse konvexer Optimierungsprobleme X Banachraum, wobei X = R n G zulässige Menge des Optimierungsproblems f: G R Zielfunktion f(x) min, x G (.) (Legende)
Über- und unterbestimmte
 Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Über- und unterbestimmte Systeme (verallgemeinerte Lösungen) Über- und unterbestimmte Systeme Ax = b ist genau dann für alle b R m eindeutig lösbar, wenn m = n und rk A = n. Falls m n oder rk A < min{m,
Kapitel 5. Peter Becker (H-BRS) Operations Research I Sommersemester / 298
 Kapitel 5 Dualität Peter Becker (H-BRS) Operations Research I Sommersemester 2014 241 / 298 Inhalt 5 Dualität Dualitätssätze Zweiphasen-Simplexalgorithmus Peter Becker (H-BRS) Operations Research I Sommersemester
Kapitel 5 Dualität Peter Becker (H-BRS) Operations Research I Sommersemester 2014 241 / 298 Inhalt 5 Dualität Dualitätssätze Zweiphasen-Simplexalgorithmus Peter Becker (H-BRS) Operations Research I Sommersemester
Optimierung. Vorlesung 08
 Optimierung Vorlesung 08 Heute Dualität Ganzzahligkeit Optimierung der Vorlesung durch Evaluierung 2 Das duale LP Das primale LP Maximiere c T x unter Ax b, x R d 0. wird zu dem dualen LP Minimiere b T
Optimierung Vorlesung 08 Heute Dualität Ganzzahligkeit Optimierung der Vorlesung durch Evaluierung 2 Das duale LP Das primale LP Maximiere c T x unter Ax b, x R d 0. wird zu dem dualen LP Minimiere b T
Die Lagrange-duale Funktion
 Die Lagrange-duale Funktion Gregor Leimcke 21. April 2010 1 Die Lagrangefunktion Wir betrachten das allgemeine Optimierungsproblem wobei minimiere f 0 über D sodass f i 0, i = 1,..., m 1.1 D = h i = 0,
Die Lagrange-duale Funktion Gregor Leimcke 21. April 2010 1 Die Lagrangefunktion Wir betrachten das allgemeine Optimierungsproblem wobei minimiere f 0 über D sodass f i 0, i = 1,..., m 1.1 D = h i = 0,
Die duale Simplexmethode zur Lösung rein ganzzahliger linearer Programme
 Kapitel 11 Die duale Simplexmethode zur Lösung rein ganzzahliger linearer Programme Wir betrachten folgendes Optimierungsproblem z = c T x min! Ax = b (11.1) (11.2) x j ganz für j = 1,..., n 1 n, (11.3)
Kapitel 11 Die duale Simplexmethode zur Lösung rein ganzzahliger linearer Programme Wir betrachten folgendes Optimierungsproblem z = c T x min! Ax = b (11.1) (11.2) x j ganz für j = 1,..., n 1 n, (11.3)
Klausur Mathematik. Note:
 Fachhochschule Südwestfalen Fachhochschule Münster Hochschule Bochum Verbundstudiengang Wirtschaftsingenieurwesen Hochschule Bochum Hochschule für Technik und Wirtschaft Klausur Mathematik Datum: 18.09.2010
Fachhochschule Südwestfalen Fachhochschule Münster Hochschule Bochum Verbundstudiengang Wirtschaftsingenieurwesen Hochschule Bochum Hochschule für Technik und Wirtschaft Klausur Mathematik Datum: 18.09.2010
Aufgabenkomplex 5: Inhomogene Differenzialgleichungssysteme; Lineare Optimierung
 Technische Universität Chemnitz. Juni 9 Fakultät für Mathematik Höhere Mathematik I. Aufgabenkomplex : Inhomogene Differenzialgleichungssysteme; Lineare Optimierung Letzter Abgabetermin: 9. Juli 9 in Übung
Technische Universität Chemnitz. Juni 9 Fakultät für Mathematik Höhere Mathematik I. Aufgabenkomplex : Inhomogene Differenzialgleichungssysteme; Lineare Optimierung Letzter Abgabetermin: 9. Juli 9 in Übung
COCKTAIL SELECTION. Fruchtiger Cocktail. Zutaten. Zubereitung. Dekoration
 Fruchtiger Cocktail 6 cl Gin TL Grenadine 2 cl Orangensaft 2 cl Zitronensaft Eis Sodawasser 3 Tropfen Angostura Die ersten 4 mit Eis in einem Shaker mischen. Abseihen in großes Glas und mit Sodawasser
Fruchtiger Cocktail 6 cl Gin TL Grenadine 2 cl Orangensaft 2 cl Zitronensaft Eis Sodawasser 3 Tropfen Angostura Die ersten 4 mit Eis in einem Shaker mischen. Abseihen in großes Glas und mit Sodawasser
Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler
 Wintersemester 2006/07 05.03.2007 Dr. Priska Jahnke Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler Bitte lesbar ausfüllen, Zutreffendes ankreuzen Herr Frau Name, Vorname:
Wintersemester 2006/07 05.03.2007 Dr. Priska Jahnke Klausur zur Vorlesung Mathematische Grundlagen für Wirtschaftswissenschaftler Bitte lesbar ausfüllen, Zutreffendes ankreuzen Herr Frau Name, Vorname:
3. Schnittebenenverfahren
 3. Schnittebenenverfahren Themen 3. Schnittebenenverfahren Ganzzahlige lineare Programmierung Schnittebenenverfahren Konstruktion von Schnittebenen Auswahl von Schnittrestriktionen Operations Research
3. Schnittebenenverfahren Themen 3. Schnittebenenverfahren Ganzzahlige lineare Programmierung Schnittebenenverfahren Konstruktion von Schnittebenen Auswahl von Schnittrestriktionen Operations Research
Prüfungsklausur Wirtschaftsmathematik I Studiengang Wirtschaftsinformatik, (180 Minuten)
 HTW Dresden 11. Februar 2014 FB Informatik/Mathematik Prof. Dr. J. Resch Prüfungsklausur Wirtschaftsmathematik I Studiengang Wirtschaftsinformatik, (180 Minuten) Name, Vorname: Matr.-nr.: Anzahl der abge-
HTW Dresden 11. Februar 2014 FB Informatik/Mathematik Prof. Dr. J. Resch Prüfungsklausur Wirtschaftsmathematik I Studiengang Wirtschaftsinformatik, (180 Minuten) Name, Vorname: Matr.-nr.: Anzahl der abge-
Mitschrift der Vorlesung: Kombinatorische Optimierung
 Mitschrift der Vorlesung: Kombinatorische Optimierung bei Prof. Socher-Ambrosius Niels-Peter de Witt 26. April 2002 Inhaltsverzeichnis 1 Einführung 2 1.1 Beispiel: Profil zersägen.......................
Mitschrift der Vorlesung: Kombinatorische Optimierung bei Prof. Socher-Ambrosius Niels-Peter de Witt 26. April 2002 Inhaltsverzeichnis 1 Einführung 2 1.1 Beispiel: Profil zersägen.......................
1.8 lineare Optimierung
 1.8 lineare Optimierung Inhaltsverzeichnis 1 Einführung des Begriffs lineare Optimierung 2 2 Das Planungspolygon 2 3 Die Optimierungsgerade 3 1 lineare Optimierung 02.04.2008 Theorie und Übungen 2 1 Einführung
1.8 lineare Optimierung Inhaltsverzeichnis 1 Einführung des Begriffs lineare Optimierung 2 2 Das Planungspolygon 2 3 Die Optimierungsgerade 3 1 lineare Optimierung 02.04.2008 Theorie und Übungen 2 1 Einführung
Kaufmännische Berufsmatura 2016
 Prüfungsdauer: 150 Minuten Hilfsmittel: Bedingungen: Netzunabhängiger Taschenrechner Beigelegte Formelsammlung Dokumentieren Sie den Lösungsweg auf dem Aufgabenblatt. Unbelegte Resultate werden nicht berücksichtigt
Prüfungsdauer: 150 Minuten Hilfsmittel: Bedingungen: Netzunabhängiger Taschenrechner Beigelegte Formelsammlung Dokumentieren Sie den Lösungsweg auf dem Aufgabenblatt. Unbelegte Resultate werden nicht berücksichtigt
max 16x x 2 (1) 4x 1 + 2x (2) 10x (3) 2x 1 + 4x (4) 2x (5) x 1, x 2 0 (6)
 Aufgabe 1 (33 Punkte, ca. 20 Minuten) Ein Konditor stellt zu Ostern besonders exklusive Osterhasen (x 1 ) und Ostereier (x 2 ) her. Diese bestehen aus einer Schokoladengrundmasse und werden mit weiteren
Aufgabe 1 (33 Punkte, ca. 20 Minuten) Ein Konditor stellt zu Ostern besonders exklusive Osterhasen (x 1 ) und Ostereier (x 2 ) her. Diese bestehen aus einer Schokoladengrundmasse und werden mit weiteren
ist ein Polyeder. c) Sei F eine Seite von P. Wann ist f 1 (F ) eine Seite von f 1 (P )? Begründen Sie Ihre Antwort. x 1. x = max{ x i i N n }.
 alteklausuraufgaben 1 LinOpt Klausur Sommersemester 05 Aufgabe 1 a) Definieren Sie den Begriff der konischen Hülle. b) Sei S R n. Zeigen Sie: Cone S = Lin S x S : x Cone (S \ {x}). Aufgabe 2 a) Definieren
alteklausuraufgaben 1 LinOpt Klausur Sommersemester 05 Aufgabe 1 a) Definieren Sie den Begriff der konischen Hülle. b) Sei S R n. Zeigen Sie: Cone S = Lin S x S : x Cone (S \ {x}). Aufgabe 2 a) Definieren
Unimodularität. Kapitel 1. Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206
 Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
