1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
|
|
|
- Elmar Fischer
- vor 8 Jahren
- Abrufe
Transkript
1 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet dnn, wenn chlter UND gedrückt ist = ( = AND ) UND 3. Ohm = ODER LED leuchtet dnn, wenn entweder chlter ODER gedrückt ist = ( = OR ) ODER 4. Negtor Wert Negtion von Wert mbol Negtor = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von entspr. entspr. 6. = ( ODER ) negiert LED leuchtet dnn, wenn kein chlter gedrückt ist; Wenn weder noch gedrückt wird. = NO ( ) = = NOR (, ) 5. = ( UND ) negiert LED leuchtet dnn, wenn kein chlter oder ein chlter gedrückt ist; LED leuchtet nicht, wenn beide chlter gedrückt werden. = NO ( ) = = NAND (, )
2 Verwendung des Busteins 4 7. ¼ Bustein Die chltung funktioniert nicht, d lle Eingänge ein undefiniertes ignl erhlten. Auch wenn der chlter gedrückt wird, bleibt der obere undefiniert. Die Lösung zeigt die nächste chltung. 8. ¼ Bustein PullDown Widerstnd = NO ( ) = NO ( ) = Ges.: = PullUp ¼ Bustein Widerstnd 9. PullDown Widerstnd = NO ( ) = NO ( ) = Ges.2: = PullDown Widerstnd ¼ Bustein = NO ( ) = NO ( ) =. PullDown Widerstnd LED leuchtet immer Ges.3: =. ¼ Bustein = NO ( ) = = NAND (, )
3 2. ¼ Bustein ¼ Bustein = = AND (, ) Ges.4: = AND us NAND s erzeugen 3. ¾ Bustein = OR (, ) = = > = ODER us NAND s erzeugen Ges.5: = (Erweiterung der chltung zu NOR ist ebenflls möglich) 5. = = 3fch NAND us NAND s mit 2 Eingängen erzeugen = ndere chreibweise = wird in der Folge nun weggelssen ODER chltg = = = = Die beiden Negtionen heben sich uf (s. Ges.4) können entfllen
4 5. ¾ Bustein = = Nur wenn lle 3 chlter gedrückt sind ist ds Ergebnis sonst 3fch AND us NAND s mit 2 Eingängen erzeugen = = = = = = = Negtion = NAND NAND 6. Negtion 4/4 Bustein = = Nur wenn lle 3 chlter gedrückt sind ist ds Ergebnis sonst
5 7. = XOR (, ) bzw. Antivlenz =... = = = Die chltung ist ein eil eines Addierwerkes eines Computers, denn es gilt: ummnd ummnd 2 = Ergebnis Übertrg Die chltung ist noch nicht komplett, d uch der Übertrg von der Vorstelle berücksichtigt werden muss! Der Übertrg selbst knn mit einem UND erzeugt werden, denn nur wenn beide Eingänge sind, ist uch = Rückkopplung 8. rückgekoppelte digitle chltung ndere Drstellung n chltung ht zwei Eingänge (R und ) und zwei Ausgänge ( und n). Beim Drücken von chlter erscheint m Ausgng eine, die uch bestehen bleibt, wenn mn den chlter wieder losläßt (nlog bei R und n), die chltung speichert den eingestellten Wert. Diese Anordnung knn lso genu Bit speichern. But mn (lso: 6 ) solcher chltungen uf, ht mn den gnz bruchbren RAMHuptspeicher eines Computers von 2GBte (sttisches RAM wird mit dnmischen RAM relisiert, stt. RAM im Cche).. Die technische Bezeichnung ist: RLtch R = n
6 Die chltung, ds Ltch, knn folgende Zustände nnehmen: n R Ds ist ein Zustnd speichern ; die chlter sind nicht betätigt Forml ht sich nichts geändert, es ist jedoch der et Zustnd, der Ausgng wird uf gesetzt, ws er schon wr. Ds ist der Reset Zustnd, der Ausgng wird zurück uf gesetzt, n zeigt jetzt den negierten Wert. Läßt mn dnch den chlter wieder los kommt mn wieder in den peicherzustnd von den jetzt eingestellten Werten.?? Drückt mn beide chlter, entsteht uch ein Ausgngssignl, ds ist grntiert flsch, d unerlubt. teuerung mit Pegel Ds oben beschriebene Ltch wird mit gesteuert. Ds funktioniert zwr, entspricht ber nicht den Vorschriften, es soll mit gesteuert werden. Ds knn mn mit den vorhndenen NANDGttern des Busteins uch relisieren: 9. n R?? et Reset unerlubt R n Die in der belle gezeigten Zustände entsprechen nun ekt der heorie. Unerlubt bedeutet, dss ds möglich ist, ber flsche Ergebnisse bringt. Insbesondere wenn dnch der peicher Zustnd folgt, ist der Wert für und n undefiniert. Anwendung: z.b. Ein Ausschlter; teuerung von Lichtsignlen uf Modellbhnen; steuert mn gleichzeitig ein Relis mit n, knn uch eine Fhrstrombschltung erfolgen
7 2. R ktzustnd gesteuertes RLtch n R?? et Reset unerlubt R n Wenn der chlter offen ist, liegt n den ersten beiden Gttern n einem Eingng immer eine n, der Ausgngswert dieser Gtter wird lso immer sein, denn und ist und drüber die Negtion ist, die chltung bleibt immer im peicherzustnd! Nur wenn gedrückt wird, lso gleich ist, knn der Zustnd des Ltch verändert werden. Diese chltung ist wichtig in der Rechentechnik, es wird beim peichern erst ds Einschwingen der Dtenleitungen bgewrtet, dnn durch = die Übernhme in den peicher vollzogen. Auch in nderen chltkreisen, wie beispielsweise chieberegister oder Decoder wird ähnlich verfhren. Ds ignl heißt zumeist dnn trobe. chltungssmbol für ein ktzustndsgesteuertes RLtch Anwendung: Verriegelung von chltern 2. ktzustnd gesteuertes DLtch n Vorteil der Anordnung ist, dss es keine unerlubte Eingngsbelegung gibt. Immer wenn ds ktsignl nliegt, wird ds RLtch entsprechend gesetzt. Ist ds ktsignl, wird die Einstellung gespeichert. D n D Fll Fll2 chltungssmbol für ein ktzustndsgesteuertes DLtch D
8 ktflnken gesteuerte Kippschltung FlipFlop 22. 4,7uF C 5K 75K R n In R Die veränderte chltung m kteingng wird ls Hochpß bezeichnet. Wird ngelegt, fällt die pnnung über R etws b. Der Kondenstor wird über R2 ufgelden, so dss ds proportionle ignl zum trom n R2 zur Verfügung steht. D der trom nur gnz kurz den mimlen Wert nnimmt und dnch rsch uf zurückgeht, entsteht ein Ndelimpuls für den kteingng. C R2 Out chlter ein pnnung n R t trom durch bzw. pnnung n R2 t D für die Gtter nun nur noch einen kleinen Augenblick lng eine bereitgestellt wird, wird nur für diese kleine Zeit der Zustnd des Ltch verändert. Mn sgt, dss die chltung mit positiver Flnke gesteuert wird. Für diese chltung gibt es eine neue Bezeichnung: FlipFlop Der Zeitpunkt der Umschltung knn nun gnz genu festgelegt werden. Zur Kontrolle knn mn m Punkt C eine weitere LED nschließen, diese blitzt bei Betätigung von miniml uf RFlipFlop Flnken gesteuert R Mit nsteigender Flnke gesteuertes RFlipFlop
9 ktflnken gesteuerte rigger Kippschltung 23. 4,7uF C R R2 5K 75K R n FlipFlop D die Erzeugung des Ndelimpulses nur eine Erstzlösung ist, funktioniert ds Gnze zuweilen schlecht. Es gibt einen speziellen chltkreis mit 2 JKFlipFlops (427), der brucht ntürlich viel mehr Gtter und funktioniert sehr gut. Hier soll nur ml gezeigt werden, dss lle Kippglieder nur durch Veränderte äußere Beschltung des RLtsch erzeugt werden können und ds lles mit einem einzigen chltkreis. Die chltung kippt bei Betätigung des sters (positive Flnke) zwischen = und = (entspr. n= und n=) hin und her. Problem ist, welcher Zustnd sich beim Einschlten der Betriebsspnnung einstellt? Hier ist eine ResetMöglichkeit notwendig. Würde mn nstelle des Impulses ds schon beknnte längere ktsignl zur teuerung nutzen, würde die chltung pusenlos hin und herkippen. Ds ist schlecht ber Bsis für schwingende chltungen, wie Blinklicht oder onerzeugung, ber uch für JKFlipFlops. Anwendung: In Kombintion mit Relis ls Lichtschlter 24. Atbiler Multivibrtor Blinkschltung / ongenertor 22uF 22uF n Die chltung unterscheidet sich vom R Ltch nur wenig. Der zweite Eingng wird über einen Kondenstor gesteuert, der seinerseits über einen Widerstnd entlden wird. Umgeschltet wird nur dnn, wenn mindest ein Eingng uf liegen. Ht der Ausgng unten eine, so sind beide eiten des Kondenstors. Lngsm wird der Kondenstor entlden, kommt er zum Pegel, erschein m Ausgng oben eine ( und = negiert ), der ndere Kondenstor wird ufgelden usw. Die chltung blinkt mit etw 2Hz. Werden die Kondenstoren und die Widerstände verkleinert, schwingt die chltung mit höherer Frequenz. Ab einer bestimmten Frequenz knn mn die chwingungen hören wir hben einen ongenertor mit Rechecksignl.
10 24. Atbiler Multivibrtor unterbrechbr 22uF Unterbrechbr ist ds Blinken, indem die Verbindung zu einem Widerstnd zur Msse (nch ) unterbrochen wird. Anstelle eines chlters knn uch der Ausgng eine nderen Gtters geschltet werden, somit ist ds Blinken über eine vorgeschltete Logik steuerbr. 22uF n K 22uF n Monotbiler Multivibrtor Bei Betätigung des chlters kippt die chltung in den nderen Zustnd. Mit Entldung des Kondenstors kippt die chltung nch einer gewissen Zeit, bestimmt durch den Kondenstor und den Widerstnd 75K wieder in den Ausgngszustnd zurück und bleibt in diesem Zustnd. Nch etw 6sec ist wieder der Ausgngszustnd erreicht. Grundzustnd: Ausg. oben, unten Eing. unten und ( und = negiert ) chlter: unten und = negiert Eing. oben beide, Ausg., der oberste wird über den Widerstnd lngsm ( und = negiert ) chltung kippt zurück. Anwendungen: Nchlufschltung, reppenlicht usw.
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Technische Informatik 2
 TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
Keil Telecom Homepage - Hersteller von Isdn Tk Anlagen und Türsprechsystemen für Heim und Bü...
 Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Keil Telecom Homepge - Hersteller von Isdn Tk Anlgen und Türsprechsystemen für Heim und Bü... Seite 1 von 1 Einutürlutsprecher esonders kleine und kompkte Buform Einu üerll dort wo Pltz knpp ist Briefkästen,
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Boole'sche Algebra. Inhaltsübersicht. Binäre Funktionen, Boole'sche Algebren, Schaltalgebra. Verknüpfungen der mathematischen Logik
 Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Technische Informatik Basispraktikum Sommersemester 2001
 Technische Informatik Basispraktikum Sommersemester 2001 Protokoll zum Versuchstag 4 Datum: 21.6.2001 Gruppe: David Eißler/ Autor: Verwendete Messgeräte: - digitales Experimentierboard (EB6) - Netzgerät
Technische Informatik Basispraktikum Sommersemester 2001 Protokoll zum Versuchstag 4 Datum: 21.6.2001 Gruppe: David Eißler/ Autor: Verwendete Messgeräte: - digitales Experimentierboard (EB6) - Netzgerät
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
AGROPLUS Buchhaltung. Daten-Server und Sicherheitskopie. Version vom 21.10.2013b
 AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
AGROPLUS Buchhaltung Daten-Server und Sicherheitskopie Version vom 21.10.2013b 3a) Der Daten-Server Modus und der Tresor Der Daten-Server ist eine Betriebsart welche dem Nutzer eine grosse Flexibilität
RS-Flip Flop, D-Flip Flop, J-K-Flip Flop, Zählschaltungen
 Elektronik Praktikum / Digitaler Teil Name: Jens Wiechula, Philipp Fischer Leitung: Prof. Dr. U. Lynen Protokoll: Philipp Fischer Versuch: 3 Datum: 24.06.01 RS-Flip Flop, D-Flip Flop, J-K-Flip Flop, Zählschaltungen
Elektronik Praktikum / Digitaler Teil Name: Jens Wiechula, Philipp Fischer Leitung: Prof. Dr. U. Lynen Protokoll: Philipp Fischer Versuch: 3 Datum: 24.06.01 RS-Flip Flop, D-Flip Flop, J-K-Flip Flop, Zählschaltungen
Handbuch ECDL 2003 Modul 2: Computermanagement und Dateiverwaltung Der Task-Manager
 Handbuch ECDL 2003 Modul 2: Computermanagement und Dateiverwaltung Der Task-Manager Dateiname: ecdl2_03_05_documentation Speicherdatum: 22.11.2004 ECDL 2003 Modul 2 Computermanagement und Dateiverwaltung
Handbuch ECDL 2003 Modul 2: Computermanagement und Dateiverwaltung Der Task-Manager Dateiname: ecdl2_03_05_documentation Speicherdatum: 22.11.2004 ECDL 2003 Modul 2 Computermanagement und Dateiverwaltung
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Abtastung. Kontinuierliches Signal: Signalspektrum: Abgetastetes Signal: ( t) Abtastfunktion: 1 f a. Spektrum der Abtastfunktion:
 Pro. Dr.-In. W.-P. Buchwld Sinl- und Sysemheorie 8. Absun Koninuierliches Sinl: u() Sinlspekrum: U() Abesees Sinl: ( ) = u( ) ( ) u Absunkion: + n= ( ) = δ ( n ) Spekrum der Absunkion: + n= Spekrum des
Pro. Dr.-In. W.-P. Buchwld Sinl- und Sysemheorie 8. Absun Koninuierliches Sinl: u() Sinlspekrum: U() Abesees Sinl: ( ) = u( ) ( ) u Absunkion: + n= ( ) = δ ( n ) Spekrum der Absunkion: + n= Spekrum des
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
Dein Trainingsplan. sportmannschaft. ... und was sonst noch wichtig ist. Deine Zähne sind wie deine. und du bist der Trainer!
 hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Qualität und Verlässlichkeit Das verstehen die Deutschen unter Geschäftsmoral!
 Beitrag: 1:43 Minuten Anmoderationsvorschlag: Unseriöse Internetanbieter, falsch deklarierte Lebensmittel oder die jüngsten ADAC-Skandale. Solche Fälle mit einer doch eher fragwürdigen Geschäftsmoral gibt
Beitrag: 1:43 Minuten Anmoderationsvorschlag: Unseriöse Internetanbieter, falsch deklarierte Lebensmittel oder die jüngsten ADAC-Skandale. Solche Fälle mit einer doch eher fragwürdigen Geschäftsmoral gibt
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Inhaltsverzeichnis Seite
 Inhaltsverzeichnis Seite 1. Email mit Anhang versenden 2 1.a Email vorbereiten und zweites Fenster (Tab) öffnen. 2 1. b. Bild im Internet suchen und speichern. 3 1.c. Bild als Anlage in Email einbinden
Inhaltsverzeichnis Seite 1. Email mit Anhang versenden 2 1.a Email vorbereiten und zweites Fenster (Tab) öffnen. 2 1. b. Bild im Internet suchen und speichern. 3 1.c. Bild als Anlage in Email einbinden
AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung
 AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung Problem: Um AutoCAD abwechselnd auf mehreren Rechnern einsetzen zu können konnte man bis AutoCAD 2000 einfach den Dongle umstecken. Seit AutoCAD 2000i
AutoCAD 2007 - Dienstprogramm zur Lizenzübertragung Problem: Um AutoCAD abwechselnd auf mehreren Rechnern einsetzen zu können konnte man bis AutoCAD 2000 einfach den Dongle umstecken. Seit AutoCAD 2000i
Grundtypen Flip-Flops
 FLIP-FLOPs, sequentielle Logik Bei den bislang behandelten Logikschaltungen (chaltnetzen) waren die Ausgangsgrößen X, Y... zu jeder Zeit in eindeutiger Weise durch die Kombination der Eingangsvariablen
FLIP-FLOPs, sequentielle Logik Bei den bislang behandelten Logikschaltungen (chaltnetzen) waren die Ausgangsgrößen X, Y... zu jeder Zeit in eindeutiger Weise durch die Kombination der Eingangsvariablen
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Serienbrieferstellung in Word mit Kunden-Datenimport aus Excel
 Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
Sehr vielen Mitarbeitern fällt es schwer, Serienbriefe an Kunden zu verschicken, wenn sie die Serienbrieffunktion von Word nicht beherrschen. Wenn die Kunden mit Excel verwaltet werden, genügen nur ein
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 7. Übung/Lösung Mathematik für Studierende der Biologie 25.11.2015
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anres Herz, Dr. Stefn Häusler emil: heusler@biologie.uni-muenchen.e Deprtment Biologie II Telefon: 089-280-74800 Großhernerstr. 2 Fx:
ACDSee Pro 2. ACDSee Pro 2 Tutorials: Übertragung von Fotos (+ Datenbank) auf einen anderen Computer. Über Metadaten und die Datenbank
 Tutorials: Übertragung von Fotos (+ ) auf einen anderen Computer Export der In dieser Lektion erfahren Sie, wie Sie am effektivsten Fotos von einem Computer auf einen anderen übertragen. Wenn Sie Ihre
Tutorials: Übertragung von Fotos (+ ) auf einen anderen Computer Export der In dieser Lektion erfahren Sie, wie Sie am effektivsten Fotos von einem Computer auf einen anderen übertragen. Wenn Sie Ihre
Installation der Eicon Diva PCI Karte unter Windows XP
 Installation der Eicon Diva PCI Karte unter Windows XP Wenn Sie die ADSL Karte korrekt in Ihren Rechner eingebaut haben, sollte kurz nach dem Start von Windows XP diese Fenster erscheinen. Eine Einbauanleitung
Installation der Eicon Diva PCI Karte unter Windows XP Wenn Sie die ADSL Karte korrekt in Ihren Rechner eingebaut haben, sollte kurz nach dem Start von Windows XP diese Fenster erscheinen. Eine Einbauanleitung
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Grundtypen Flip-Flops
 FLIP-FLOPs, sequentielle Logik Bei den bislang behandelten Logikschaltungen (Schaltnetzen) waren die Ausgangsgrößen X, Y... zu jeder Zeit in eindeutiger Weise durch die Kombination der Eingangsvariablen
FLIP-FLOPs, sequentielle Logik Bei den bislang behandelten Logikschaltungen (Schaltnetzen) waren die Ausgangsgrößen X, Y... zu jeder Zeit in eindeutiger Weise durch die Kombination der Eingangsvariablen
TYPO3 Tipps und Tricks
 TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
TYPO3 Tipps und Tricks Seiten als Shortcut. Hiermit ist gemeint, dass eine Oberseite direkt auf eine tiefere Unterseite verlinkt. Dies kann bei Themen ohne gesonderte Übersichtsseite hilfreich sein. Zum
Dennis S. Weiß & Christian Niederhöfer. Versuchsprotokoll. (Fortgeschrittenen-Praktikum) zu Versuch 15. Digitalelektronik
 Montag, 31.5.1999 Dennis S. Weiß & Christian Niederhöfer Versuchsprotokoll (Fortgeschrittenen-Praktikum) zu Versuch 15 Digitalelektronik 1 Inhaltsverzeichnis 1 Problemstellung 3 2 nwendungen des de Morgan
Montag, 31.5.1999 Dennis S. Weiß & Christian Niederhöfer Versuchsprotokoll (Fortgeschrittenen-Praktikum) zu Versuch 15 Digitalelektronik 1 Inhaltsverzeichnis 1 Problemstellung 3 2 nwendungen des de Morgan
Anleitung zur Daten zur Datensicherung und Datenrücksicherung. Datensicherung
 Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Anleitung zur Daten zur Datensicherung und Datenrücksicherung Datensicherung Es gibt drei Möglichkeiten der Datensicherung. Zwei davon sind in Ges eingebaut, die dritte ist eine manuelle Möglichkeit. In
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Anleitung über den Umgang mit Schildern
 Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Anleitung über den Umgang mit Schildern -Vorwort -Wo bekommt man Schilder? -Wo und wie speichert man die Schilder? -Wie füge ich die Schilder in meinen Track ein? -Welche Bauteile kann man noch für Schilder
Programmierung Weichenmodul S/D Tafel 1
 Programmierung Weichenmodul S/D Tafel 1 Voraussetzungen: Fahrspannung ist abgeschalten (rote Taste an MC 2004 oder Einfrieren im Traincontroller) Programmiertaste am Modul ist gedrückt (rote LED leuchtet),
Programmierung Weichenmodul S/D Tafel 1 Voraussetzungen: Fahrspannung ist abgeschalten (rote Taste an MC 2004 oder Einfrieren im Traincontroller) Programmiertaste am Modul ist gedrückt (rote LED leuchtet),
Dokumentenverwaltung im Internet
 Dokumentenverwaltung im Internet WS 09/10 mit: Thema: Workflow und Rollenverteilung im Backend Gruppe: DVI 10 Patrick Plaum und Kay Hofmann Inhalt 1. Benutzer und Benutzergruppen erstellen...2 1.1. Benutzergruppen...2
Dokumentenverwaltung im Internet WS 09/10 mit: Thema: Workflow und Rollenverteilung im Backend Gruppe: DVI 10 Patrick Plaum und Kay Hofmann Inhalt 1. Benutzer und Benutzergruppen erstellen...2 1.1. Benutzergruppen...2
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Mandant in den einzelnen Anwendungen löschen
 Mandant in den einzelnen Anwendungen löschen Bereich: ALLGEMEIN - Info für Anwender Nr. 6056 Inhaltsverzeichnis 1. Allgemein 2. FIBU/ANLAG/ZAHLUNG/BILANZ/LOHN/BELEGTRANSFER 3. DMS 4. STEUERN 5. FRISTEN
Mandant in den einzelnen Anwendungen löschen Bereich: ALLGEMEIN - Info für Anwender Nr. 6056 Inhaltsverzeichnis 1. Allgemein 2. FIBU/ANLAG/ZAHLUNG/BILANZ/LOHN/BELEGTRANSFER 3. DMS 4. STEUERN 5. FRISTEN
Historical Viewer. zu ETC5000 Benutzerhandbuch 312/15
 Historical Viewer zu ETC5000 Benutzerhandbuch 312/15 Inhaltsverzeichnis 1 Allgemeine Hinweise... 3 1.1 Dokumentation...3 2 Installation... 3 3 Exportieren der Logdatei aus dem ETC 5000... 3 4 Anlegen eines
Historical Viewer zu ETC5000 Benutzerhandbuch 312/15 Inhaltsverzeichnis 1 Allgemeine Hinweise... 3 1.1 Dokumentation...3 2 Installation... 3 3 Exportieren der Logdatei aus dem ETC 5000... 3 4 Anlegen eines
Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.)
 Seite 1/7 Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.) Hier sehen Sie eine Anleitung wie man einen Serienbrief erstellt. Die Anleitung
Seite 1/7 Anleitung zur Erstellung von Serienbriefen (Word 2003) unter Berücksichtigung von Titeln (wie Dr., Dr. med. usw.) Hier sehen Sie eine Anleitung wie man einen Serienbrief erstellt. Die Anleitung
Enigmail Konfiguration
 Enigmail Konfiguration 11.06.2006 Steffen.Teubner@Arcor.de Enigmail ist in der Grundkonfiguration so eingestellt, dass alles funktioniert ohne weitere Einstellungen vornehmen zu müssen. Für alle, die es
Enigmail Konfiguration 11.06.2006 Steffen.Teubner@Arcor.de Enigmail ist in der Grundkonfiguration so eingestellt, dass alles funktioniert ohne weitere Einstellungen vornehmen zu müssen. Für alle, die es
Anton Ochsenkühn. amac BUCH VERLAG. Ecxel 2016. für Mac. amac-buch Verlag
 Anton Ochsenkühn amac BUCH VERLAG Ecxel 2016 für Mac amac-buch Verlag 2 Word-Dokumentenkatalog! Zudem können unterhalb von Neu noch Zuletzt verwendet eingeblendet werden. Damit hat der Anwender einen sehr
Anton Ochsenkühn amac BUCH VERLAG Ecxel 2016 für Mac amac-buch Verlag 2 Word-Dokumentenkatalog! Zudem können unterhalb von Neu noch Zuletzt verwendet eingeblendet werden. Damit hat der Anwender einen sehr
123 Familienausgleichskasse
 1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
1 Fmilienzulgen: Anmeldung für Arbeitnehmende eines nicht beitrgspflichtigen Arbeitgebers (Anobg) Antrgstellerin / Antrgsteller Abrechnungsnummer (xxx.xxx) 123 Fmilienusgleichsksse Sozilversicherungsnstlt
Bevor Sie mit dem Wechsel Ihres Sicherheitsmediums beginnen können, sollten Sie die folgenden Punkte beachten oder überprüfen:
 Die personalisierte VR-NetWorld-Card wird mit einem festen Laufzeitende ausgeliefert. Am Ende der Laufzeit müssen Sie die bestehende VR-NetWorld-Card gegen eine neue Karte austauschen. Mit der begrenzten
Die personalisierte VR-NetWorld-Card wird mit einem festen Laufzeitende ausgeliefert. Am Ende der Laufzeit müssen Sie die bestehende VR-NetWorld-Card gegen eine neue Karte austauschen. Mit der begrenzten
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7
 FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
FuxMedia Programm im Netzwerk einrichten am Beispiel von Windows 7 Die Installation der FuxMedia Software erfolgt erst NACH Einrichtung des Netzlaufwerks! Menüleiste einblenden, falls nicht vorhanden Die
WinVetpro im Betriebsmodus Laptop
 WinVetpro im Betriebsmodus Laptop Um Unterwegs Daten auf einem mobilen Gerät mit WinVetpro zu erfassen, ohne den Betrieb in der Praxis während dieser Zeit zu unterbrechen und ohne eine ständige Online
WinVetpro im Betriebsmodus Laptop Um Unterwegs Daten auf einem mobilen Gerät mit WinVetpro zu erfassen, ohne den Betrieb in der Praxis während dieser Zeit zu unterbrechen und ohne eine ständige Online
Eingangsseite Umwelt-online
 Mit dem Erwerb einer Lizenz haben Sie die Möglichkeit, sich ein auf Ihre Bedürfnisse abgestimmtes Kataster zu erstellen. Die Funktionen dieses Rechtskataster wird nachstehend erläutert. Eingangsseite Umwelt-online
Mit dem Erwerb einer Lizenz haben Sie die Möglichkeit, sich ein auf Ihre Bedürfnisse abgestimmtes Kataster zu erstellen. Die Funktionen dieses Rechtskataster wird nachstehend erläutert. Eingangsseite Umwelt-online
Browsereinstellungen für moneycheck24 in Explorer unter Windows
 Browsereinstellungen für moneycheck24 in Explorer unter Windows Wichtige Einstellungen im + Um zu prüfen, welche Version Sie nutzen Einstellungen: Klicken Sie im Menü INTERNETOPTIONEN Extras [oder Tastenkürzel
Browsereinstellungen für moneycheck24 in Explorer unter Windows Wichtige Einstellungen im + Um zu prüfen, welche Version Sie nutzen Einstellungen: Klicken Sie im Menü INTERNETOPTIONEN Extras [oder Tastenkürzel
Installation OMNIKEY 3121 USB
 Installation OMNIKEY 3121 USB Vorbereitungen Installation PC/SC Treiber CT-API Treiber Einstellungen in Starke Praxis Testen des Kartenlesegeräts Vorbereitungen Bevor Sie Änderungen am System vornehmen,
Installation OMNIKEY 3121 USB Vorbereitungen Installation PC/SC Treiber CT-API Treiber Einstellungen in Starke Praxis Testen des Kartenlesegeräts Vorbereitungen Bevor Sie Änderungen am System vornehmen,
Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden.
 WORD 2010 Etiketten drucken Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden. Diese Anwendung erfolgt über die Registerkarte Sendungen 1
WORD 2010 Etiketten drucken Mit dem sogenannten Seriendruck können Etiketten und Briefe mit einer Adressdatei (z. B. Excel) verknüpft werden. Diese Anwendung erfolgt über die Registerkarte Sendungen 1
Password Depot für ios
 Password Depot für ios Inhaltsverzeichnis Erste Schritte... 1 Kennwörterdatei erstellen... 1 Neue Einträge erstellen... 3 Einträge / Gruppen hinzufügen... 3 Einträge / Gruppen kopieren oder verschieben...
Password Depot für ios Inhaltsverzeichnis Erste Schritte... 1 Kennwörterdatei erstellen... 1 Neue Einträge erstellen... 3 Einträge / Gruppen hinzufügen... 3 Einträge / Gruppen kopieren oder verschieben...
Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage
 Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage Inhaltsverzeichnis 1. Anmeldung... 2 1.1 Startbildschirm... 3 2. Die PDF-Dateien hochladen... 4 2.1 Neue PDF-Datei erstellen... 5 3. Obelix-Datei
Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage Inhaltsverzeichnis 1. Anmeldung... 2 1.1 Startbildschirm... 3 2. Die PDF-Dateien hochladen... 4 2.1 Neue PDF-Datei erstellen... 5 3. Obelix-Datei
D a s P r i n z i p V o r s p r u n g. Anleitung. E-Mail- & SMS-Versand mit SSL (ab CHARLY 8.11 Windows)
 D a s P r i n z i p V o r s p r u n g Anleitung E-Mail- & SMS-Versand mit SSL (ab CHARLY 8.11 Windows) 2 Inhalt Inhalt 1. E-Mail-Einrichtung 3 1.1 E-Mail-Einrichtung in Windows 3 2. SMS-Einrichtung 5 2.1
D a s P r i n z i p V o r s p r u n g Anleitung E-Mail- & SMS-Versand mit SSL (ab CHARLY 8.11 Windows) 2 Inhalt Inhalt 1. E-Mail-Einrichtung 3 1.1 E-Mail-Einrichtung in Windows 3 2. SMS-Einrichtung 5 2.1
Tutorial about how to use USBView.exe and Connection Optimization for VNWA.
 Tutorial about how to use USBView.exe and Connection Optimization for VNWA. Tutorial über den Gebrauch von USBView.exe und die Anschluss-Optimierung für den VNWA. Es wurde beobachtet, dass bestimmte VNWA
Tutorial about how to use USBView.exe and Connection Optimization for VNWA. Tutorial über den Gebrauch von USBView.exe und die Anschluss-Optimierung für den VNWA. Es wurde beobachtet, dass bestimmte VNWA
RailMaster Neues mit Version 7.00.p27.07 zum 01.04.2015
 RailMaster Neues mit Version 7.00.p27.07 zum 01.04.2015 Bahnbuchungen so einfach und effizient wie noch nie! Copyright Copyright 2015 Travelport und/oder Tochtergesellschaften. Alle Rechte vorbehalten.
RailMaster Neues mit Version 7.00.p27.07 zum 01.04.2015 Bahnbuchungen so einfach und effizient wie noch nie! Copyright Copyright 2015 Travelport und/oder Tochtergesellschaften. Alle Rechte vorbehalten.
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server
 Hallo Leute Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server (= echtes - zeug ) liegt! Die neue Form hat insbesondere folgende Vorteile: Du bekommst einen
Hallo Leute Das Festkomitee hat die Abi-Seite neu konzipiert, die nun auf einem (gemieteten) Share Point Server (= echtes - zeug ) liegt! Die neue Form hat insbesondere folgende Vorteile: Du bekommst einen
<ruske.s@web.de> Oliver Liebold. NAND (negierte Undverknüpfung) L L H L H H H L H H H L
 Elektronische Grundlagen Versuch E7, Grundelemente der Digitaltechnik Praktikumsgruppe IngIF, 04. Juni 2003 Stefan Schumacher Sandra Ruske Oliver Liebold
Elektronische Grundlagen Versuch E7, Grundelemente der Digitaltechnik Praktikumsgruppe IngIF, 04. Juni 2003 Stefan Schumacher Sandra Ruske Oliver Liebold
ZeppelinAir AirPlay -Konfiguration wireless
 ZeppelinAir AirPlay -Konfiguration wireless Um das AirPlay-Feature nutzen zu können, muss der Zeppelin Air an Ihr bestehendes Heimnetzwerk (im folgenden Text als Ihr Heimnetzwerk bezeichnet) angeschlossen
ZeppelinAir AirPlay -Konfiguration wireless Um das AirPlay-Feature nutzen zu können, muss der Zeppelin Air an Ihr bestehendes Heimnetzwerk (im folgenden Text als Ihr Heimnetzwerk bezeichnet) angeschlossen
2. Im Admin Bereich drücken Sie bitte auf den roten Button Webseite bearbeiten, sodass Sie in den Bearbeitungsbereich Ihrer Homepage gelangen.
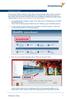 Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Bildergalerie einfügen Wenn Sie eine Vielzahl an Bildern zu einem Thema auf Ihre Homepage stellen möchten, steht Ihnen bei Schmetterling Quadra das Modul Bildergalerie zur Verfügung. Ihre Kunden können
Beispiel des Zusammenführens der APV- Tabellen Stammdaten und Verlaufsdaten mithilfe von Access
 Beispiel des Zusammenführens der APV- Tabellen Stammdaten und Verlaufsdaten mithilfe von Access Diese Übersicht stellt die Zusammenführung der APV Tabellen Stammdaten und Verlaufdaten mithilfe der Datenbank
Beispiel des Zusammenführens der APV- Tabellen Stammdaten und Verlaufsdaten mithilfe von Access Diese Übersicht stellt die Zusammenführung der APV Tabellen Stammdaten und Verlaufdaten mithilfe der Datenbank
Anleitung zum Herunterladen von DIN-Vorschriften außerhalb des internen Hochschulnetzes
 Anleitung zum Herunterladen von DIN-Vorschriften außerhalb des internen Hochschulnetzes Als Professor, Mitarbeiter oder Student der HTWK Leipzig ist es möglich über eine Datenbank auf verschiedene DIN-Normen
Anleitung zum Herunterladen von DIN-Vorschriften außerhalb des internen Hochschulnetzes Als Professor, Mitarbeiter oder Student der HTWK Leipzig ist es möglich über eine Datenbank auf verschiedene DIN-Normen
Strom in unserem Alltag
 Strom in unserem Alltag Kannst du dir ein Leben ohne Strom vorstellen? Wir verbrauchen jeden Tag eine Menge Energie: Noch vor dem Aufstehen klingelt der Radiowecker, dann schalten wir das Licht ein, wir
Strom in unserem Alltag Kannst du dir ein Leben ohne Strom vorstellen? Wir verbrauchen jeden Tag eine Menge Energie: Noch vor dem Aufstehen klingelt der Radiowecker, dann schalten wir das Licht ein, wir
2. Im Admin Bereich drücken Sie bitte auf den roten Button Webseite bearbeiten, sodass Sie in den Bearbeitungsbereich Ihrer Homepage gelangen.
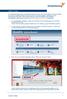 Deeplink einfügen Zur Angebotserstellung über Ihre Buchungsmaschine können Sie mit Schmetterling Quadra Deeplinks durch einen speziellen Deeplink Generator auf Ihre Homepage einfügen. Abhängig von Ihrer
Deeplink einfügen Zur Angebotserstellung über Ihre Buchungsmaschine können Sie mit Schmetterling Quadra Deeplinks durch einen speziellen Deeplink Generator auf Ihre Homepage einfügen. Abhängig von Ihrer
CADEMIA: Einrichtung Ihres Computers unter Mac OS X
 CADEMIA: Einrichtung Ihres Computers unter Mac OS X Stand: 28.01.2016 Java-Plattform: Auf Ihrem Computer muss die Java-Plattform, Standard-Edition der Version 7 (Java SE 7) oder höher installiert sein.
CADEMIA: Einrichtung Ihres Computers unter Mac OS X Stand: 28.01.2016 Java-Plattform: Auf Ihrem Computer muss die Java-Plattform, Standard-Edition der Version 7 (Java SE 7) oder höher installiert sein.
1) Farbsteuergerät in der Nikobus-Software unter Modul zufügen hinzufügen.
 Programmierung des Farbsteuergeräts 340-00112 für Nikobus Diese Bedienungsanleitung gilt auch für die Nikobus-Produkte 340-00111 und 340-00113. Achtung: einige der aufgeführten Betriebsarten sind nur auf
Programmierung des Farbsteuergeräts 340-00112 für Nikobus Diese Bedienungsanleitung gilt auch für die Nikobus-Produkte 340-00111 und 340-00113. Achtung: einige der aufgeführten Betriebsarten sind nur auf
Simulation LIF5000. Abbildung 1
 Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Reinigung 146. Reinigen des Hindernissensors. Reinigung der Projektoroberfläche. Reinigen des Projektionsfensters. Warnung. Warnung.
 Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Reinigung 146 Bei Verschmutzung oder Bildverschlechterung muss der Projektor gereinigt werden. Schlten Sie den Projektor vor der Reinigung us. Reinigung der Projektoroberfläche Reinigen Sie die Projektoroberfläche
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7
 Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Einrichtung des Cisco VPN Clients (IPSEC) in Windows7 Diese Verbindung muss einmalig eingerichtet werden und wird benötigt, um den Zugriff vom privaten Rechner oder der Workstation im Home Office über
Lehrer: Einschreibemethoden
 Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Nutzung von GiS BasePac 8 im Netzwerk
 Allgemeines Grundsätzlich kann das GiS BasePac Programm in allen Netzwerken eingesetzt werden, die Verbindungen als Laufwerk zu lassen (alle WINDOWS Versionen). Die GiS Software unterstützt nur den Zugriff
Allgemeines Grundsätzlich kann das GiS BasePac Programm in allen Netzwerken eingesetzt werden, die Verbindungen als Laufwerk zu lassen (alle WINDOWS Versionen). Die GiS Software unterstützt nur den Zugriff
Dialyse Benchmark - Online so funktioniert s
 Datenanalyse Dialyse Dialyse Benchmark - Online so funktioniert s Der Online-Dienst Dialyse Benchmark ist im Mitglieder -Bereich auf der Internetseite (www.kvhessen.de, https://mitglieder.kvh.kv-safenet.de/
Datenanalyse Dialyse Dialyse Benchmark - Online so funktioniert s Der Online-Dienst Dialyse Benchmark ist im Mitglieder -Bereich auf der Internetseite (www.kvhessen.de, https://mitglieder.kvh.kv-safenet.de/
Vorgestellt vom mexikanischen Rat für Fremdenverkehr
 Vorgestellt vom mexikanischen Rat für Fremdenverkehr Willkommen bei Explore México, die Kartenfunktion von Visitmexico.com. Unser Ziel ist es, Ihnen die Möglichkeit zu geben, sowohl den kulturellen Reichtum
Vorgestellt vom mexikanischen Rat für Fremdenverkehr Willkommen bei Explore México, die Kartenfunktion von Visitmexico.com. Unser Ziel ist es, Ihnen die Möglichkeit zu geben, sowohl den kulturellen Reichtum
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Windows 7 Ordner und Dateien in die Taskleiste einfügen
 WI.005, Version 1.1 07.04.2015 Kurzanleitung Windows 7 Ordner und Dateien in die Taskleiste einfügen Möchten Sie Ordner oder Dateien direkt in die Taskleiste ablegen, so ist das nur mit einem Umweg möglich,
WI.005, Version 1.1 07.04.2015 Kurzanleitung Windows 7 Ordner und Dateien in die Taskleiste einfügen Möchten Sie Ordner oder Dateien direkt in die Taskleiste ablegen, so ist das nur mit einem Umweg möglich,
Einführungskurs MOODLE Themen:
 Einführungskurs MOODLE Themen: Grundlegende Einstellungen Teilnehmer in einen Kurs einschreiben Konfiguration der Arbeitsunterlagen Konfiguration der Lernaktivitäten Die Einstellungen für einen Kurs erreichst
Einführungskurs MOODLE Themen: Grundlegende Einstellungen Teilnehmer in einen Kurs einschreiben Konfiguration der Arbeitsunterlagen Konfiguration der Lernaktivitäten Die Einstellungen für einen Kurs erreichst
1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden.
 Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
Der Serienversand Was kann man mit der Maske Serienversand machen? 1. Adressen für den Serienversand (Briefe Katalogdruck Werbung/Anfrage ) auswählen. Die Auswahl kann gespeichert werden. 2. Adressen auswählen,
Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter.
 Stundenverwaltung Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter. Dieses Programm zeichnet sich aus durch einfachste
Stundenverwaltung Mit dem Tool Stundenverwaltung von Hanno Kniebel erhalten Sie die Möglichkeit zur effizienten Verwaltung von Montagezeiten Ihrer Mitarbeiter. Dieses Programm zeichnet sich aus durch einfachste
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Transaktionsempfehlungen im ebase Online nutzen
 Transaktionsempfehlungen im ebase Online nutzen Anleitung ebase Inhalt 1. Einführung und Voraussetzungen 2. Transaktionsempfehlung für einen Kunden erstellen 3. Möglichkeiten des Kunden 4. Verwaltung von
Transaktionsempfehlungen im ebase Online nutzen Anleitung ebase Inhalt 1. Einführung und Voraussetzungen 2. Transaktionsempfehlung für einen Kunden erstellen 3. Möglichkeiten des Kunden 4. Verwaltung von
PIXMA MG3500. series. Einrichtungshandbuch
 PIXMA MG3500 series Einrichtungshandbuch CANON INC. 2013 Einrichtungshandbuch Dieses Handbuch enthält Informationen zum Einrichten einer Netzwerkverbindung für den Drucker. Netzwerkverbindung Drahtlose
PIXMA MG3500 series Einrichtungshandbuch CANON INC. 2013 Einrichtungshandbuch Dieses Handbuch enthält Informationen zum Einrichten einer Netzwerkverbindung für den Drucker. Netzwerkverbindung Drahtlose
SPSS Clementine. Auswertung von offenen Fragen mit TextMining für Clementine. Beispiel: Haustiere
 V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
V1.1 Auswertung von offenen Frgen mit TextMining für Clementine Beispiel: Hustiere Im Dezember 2005 ht SPSS (Schweiz) AG im Auftrg von NZZ Folio eine Online-Umfrge unter den Lesern und Leserinnen durchgeführt.
S7-Hantierungsbausteine für R355, R6000 und R2700
 S7-Hantierungsbausteine für R355, R6000 und R2700 1. FB90, Zyklus_R/W Dieser Baustein dient zur zentralen Kommunikation zwischen Anwenderprogramm und dem Modul R355 sowie den Geräten R6000 und R2700 über
S7-Hantierungsbausteine für R355, R6000 und R2700 1. FB90, Zyklus_R/W Dieser Baustein dient zur zentralen Kommunikation zwischen Anwenderprogramm und dem Modul R355 sowie den Geräten R6000 und R2700 über
User Manual Data 24. Login und Layout
 User Manual Data 24 Login und Layout Auf der Loginseite www.kern.data24.ch geben Sie Ihren Benutzernamen sowie Ihr Kennwort in die beiden Felder ein. Mit Klick auf den Button «Anmeldung» werden Ihre Daten
User Manual Data 24 Login und Layout Auf der Loginseite www.kern.data24.ch geben Sie Ihren Benutzernamen sowie Ihr Kennwort in die beiden Felder ein. Mit Klick auf den Button «Anmeldung» werden Ihre Daten
Installation des Add-Ins für Lineare Algebra in Microsoft Excel
 Installation des Add-Ins für Lineare Algebra in Microsoft Excel Matrix 2.2 by The Foxes Team http://digilander.libero.it/foxes/ Download der Matrix 2.2 Im Browser die Seite http://digilander.libero.it/foxes/download.htm
Installation des Add-Ins für Lineare Algebra in Microsoft Excel Matrix 2.2 by The Foxes Team http://digilander.libero.it/foxes/ Download der Matrix 2.2 Im Browser die Seite http://digilander.libero.it/foxes/download.htm
Teaser-Bilder erstellen mit GIMP. Bildbearbeitung mit GIMP 1
 Teaser-Bilder erstellen mit GIMP 08.08.2014 Bildbearbeitung mit GIMP 1 Auf den folgenden Seiten werden die wichtigsten Funktionen von GIMP gezeigt, welche zur Erstellung von Bildern für die Verwendung
Teaser-Bilder erstellen mit GIMP 08.08.2014 Bildbearbeitung mit GIMP 1 Auf den folgenden Seiten werden die wichtigsten Funktionen von GIMP gezeigt, welche zur Erstellung von Bildern für die Verwendung
Erweiterungen Webportal
 Erweiterungen Webportal Adress-Suche Inaktive Merkmale und gelöschte Adresse Die Suche im Webportal wurde so erweitert, dass inaktive Adresse (gelöscht) und inaktive Merkmale bei der Suche standardmässig
Erweiterungen Webportal Adress-Suche Inaktive Merkmale und gelöschte Adresse Die Suche im Webportal wurde so erweitert, dass inaktive Adresse (gelöscht) und inaktive Merkmale bei der Suche standardmässig
nach der FIT-Methode HANDBALL LEKTÜRE Mannhard Bech Malte Gertenbach Mehr Stabilität Mehr Kraft Mehr Leistung
 Mnnhrd Bech Mlte Gertenbch Athletiktrining nch der FIT-Methode Mehr Stbilität Speziell für den Hndbllsport entwickelt Für bessere Körperbeherrschung, Leistungssteigerung und Verletzungsprävention Ab der
Mnnhrd Bech Mlte Gertenbch Athletiktrining nch der FIT-Methode Mehr Stbilität Speziell für den Hndbllsport entwickelt Für bessere Körperbeherrschung, Leistungssteigerung und Verletzungsprävention Ab der
easyident Türöffner easyident Türöffner Art. Nr. FS-0007 FS Fertigungsservice
 easyident Türöffner Art. Nr. FS-0007 Wir freuen uns, das sie sich für unser Produkt easyident Türöffner, mit Transponder Technologie entschieden haben. Easyident Türöffner ist für Unterputzmontage in 55mm
easyident Türöffner Art. Nr. FS-0007 Wir freuen uns, das sie sich für unser Produkt easyident Türöffner, mit Transponder Technologie entschieden haben. Easyident Türöffner ist für Unterputzmontage in 55mm
Elektrische Logigsystem mit Rückführung
 Mathias Arbeiter 23. Juni 2006 Betreuer: Herr Bojarski Elektrische Logigsystem mit Rückführung Von Triggern, Registern und Zählern Inhaltsverzeichnis 1 Trigger 3 1.1 RS-Trigger ohne Takt......................................
Mathias Arbeiter 23. Juni 2006 Betreuer: Herr Bojarski Elektrische Logigsystem mit Rückführung Von Triggern, Registern und Zählern Inhaltsverzeichnis 1 Trigger 3 1.1 RS-Trigger ohne Takt......................................
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Im Prinzip wie ein Fotokopierer
 Im Prinzip wie ein Fotokopierer Mit diesem Experiment kannst Du das Grundprinzip verstehen, wie ein Fotokopierer funktioniert. Du brauchst : Styropor-Kügelchen Im Bild sind welche abgebildet, die es in
Im Prinzip wie ein Fotokopierer Mit diesem Experiment kannst Du das Grundprinzip verstehen, wie ein Fotokopierer funktioniert. Du brauchst : Styropor-Kügelchen Im Bild sind welche abgebildet, die es in
Erste Hilfe. «/IE Cache & Cookies» Logout, alte Seiten erscheinen, Erfasstes verschwindet?
 Erste Hilfe «/IE Cache & Cookies» Logout, alte Seiten erscheinen, Erfasstes verschwindet? Cache Einstellungen Im Internet Explorer von Microsoft wie auch in anderen Browsern (zum Beispiel Firefox) gibt
Erste Hilfe «/IE Cache & Cookies» Logout, alte Seiten erscheinen, Erfasstes verschwindet? Cache Einstellungen Im Internet Explorer von Microsoft wie auch in anderen Browsern (zum Beispiel Firefox) gibt
AVIRA ANTIVIRUS Pro - LIZENZERNEUERUNG
 AVIRA ANTIVIRUS Pro - LIZENZERNEUERUNG Autor: Dipl.-Inform.(FH) Markus Weis - www.markus.weis.de Inhaltsverzeichnis 1: Allgemeines zur Vorgehensweise...1 2: So erneuern Sie Ihre Avira Antivir-Lizenz...2
AVIRA ANTIVIRUS Pro - LIZENZERNEUERUNG Autor: Dipl.-Inform.(FH) Markus Weis - www.markus.weis.de Inhaltsverzeichnis 1: Allgemeines zur Vorgehensweise...1 2: So erneuern Sie Ihre Avira Antivir-Lizenz...2
Versuch 3. Frequenzgang eines Verstärkers
 Versuch 3 Frequenzgang eines Verstärkers 1. Grundlagen Ein Verstärker ist eine aktive Schaltung, mit der die Amplitude eines Signals vergößert werden kann. Man spricht hier von Verstärkung v und definiert
Versuch 3 Frequenzgang eines Verstärkers 1. Grundlagen Ein Verstärker ist eine aktive Schaltung, mit der die Amplitude eines Signals vergößert werden kann. Man spricht hier von Verstärkung v und definiert
Handbuch Programmierung teknaevo APG
 Handbuch Programmierung teknaevo APG Handbuch Programmierung teknaevo APG Seite 2 Inhalt 1 Vorwort... 4 2 Erklärung der Steuertafel... 5 3 Erste Schritte... 6 3.1 Anbringen des Standfußes... 6 3.2 Erster
Handbuch Programmierung teknaevo APG Handbuch Programmierung teknaevo APG Seite 2 Inhalt 1 Vorwort... 4 2 Erklärung der Steuertafel... 5 3 Erste Schritte... 6 3.1 Anbringen des Standfußes... 6 3.2 Erster
Windows. Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1
 Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Workshop Internet-Explorer: Arbeiten mit Favoriten, Teil 1 Wenn der Name nicht gerade www.buch.de oder www.bmw.de heißt, sind Internetadressen oft schwer zu merken Deshalb ist es sinnvoll, die Adressen
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
