Digitale Bildverarbeitung

Transkript

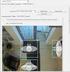
1 Digitale Bildverarbeitung Prof. Dr. Sibylle Schwarz HTWK Leipzig, Fakultät IMN Gustav-Freytag-Str. 42a, Leipzig Zimmer Z 411 (Zuse-Bau) [email protected] Sommersemester

2 Bildverarbeitung Motivation Menschen entnehmen visuellen Eindrücken sehr viel Information (ca. 90%) oft Bilder dreidimensionaler Szenen maschinelle Bildverarbeitungsverfahren dienen der Informationsgewinnung aus Bildern (Bilderkennung, Bildanalyse) Unterstützung der Informationsgewinnung aus Bildern (Bildbearbeitung) Darstellung der Information aus Bildern (Szenenrepräsentation) 2

3 Bildwahrnehmung Szene: Objekte: Regionen: Texturen: Ecken, Kanten: Pixel: Rohdaten: Foto vom Laborgebäude Wolken, Gebäude, Kunst Himmel, Fassadenteile Wirbel-, Linienstrukturen (Farb-)Kontrast Farbwert Fotoaufnahme 3

4 Digitale Bildbearbeitung Ziele Informationsgewinn Extraktion / Hervorhebung der relevanten Bildinhalte zur menschlichen oder maschinellen Weiterverarbeitung Informationsverlust beabsichtigt Abstraktion von unwichtigen Details (entfernen, abschwächen) 4

5 Bildverarbeitung Einsatzgebiete Medizin, Biologie, Astronomie: Aufnahme und Auswertung z.b. von Mikroskop-, Teleskop-, Röntgen-, Ultraschall-, CT-Bildern Zeichenerkennung (OCR): Text, Handschrift, Symbole, Noten Überwachung, z.b. industrieller Prozesse, Verkehr, Qualitätskontrolle, Materialprüfung Luftbilder und Satellitenaufnahmen z.b. bei Kartierung, Erkundung, Meteorologie Biometrie (Identifikation zur Authentifizierung, Kriminalistik): Finger-, Handabdruck, Iris-Scan zur Robotik Bewegungsplanung und -korrektur, Orientierung 5

6 Bildverarbeitung Aufgaben Aufnahme durch technische Systeme Erzeugung künstlicher Bilder (z.b. Texturen) Wiedergabe Bildschirm, Druck Analyse statistischer Merkmale Transformation, z.b. Entrauschen, Kontrastverstärkung Restaurierung gestörter Bilder Erkennung im Bild enthaltener Kanten, Ecken, Objekte Interpretation der dargestellten Szene (Art, Anordnung der Objekte) z.b. in medizinischer BV, Lokalisierung Kompression zur effizienten Speicherung mit möglichst wenig visuellen Verlusten digitaler Bilder 6

7 Bildverarbeitung Verwandte Gebiete Signalverarbeitung, (z.b. Audiosignale) ähnliche Techniken (z.b. statistische Merkmale, Fourier-Transformation, Filter) Bildbearbeitung häufig mit spezialisierter Software Computergraphik Erzeugung von Bildern aus geometrischen Objektmodellen Virtual Reality kombinierte Darstellung realer und künstlicher Szenen, z.b. für Spiele, Filme, Anleitungen Computer Vision (Bildverstehen, Bilderkennung) Transformation von Bildern in abstrakte Beschreibungen der im Bild dargestellten Szene, z.b. für Anwendungen in der Robotik Algorithmische Geometrie Datenstrukturen und effiziente Algorithmen für typische geometrische Aufgaben (z.b. für Gestenerkennung, Geoinformationssysteme) 7

8 Einordnung in die Informatik Informatik Lehre von der Darstellung und Verarbeitung von Information durch Algorithmen Teilgebiete der Informatik: theoretisch technisch Sprachen zur Formulierung von Information und Algorithmen, Möglichkeiten und Grenzen der Berechenbarkeit durch Algorithmen, Grundlagen für technische und praktische (und angewandte) Informatik maschinelle Darstellung von Information Mittel zur Ausführung von Algorithmen (Rechnerarchitektur, Hardware-Entwurf, Netzwerk,... ) praktisch Entwurf und Implementierung von Datenstrukturen und Algorithmen (Betriebssysteme, Compilerbau, SE,... ) angewandt Anwendung von Algorithmen: Text- und Bildverarbeitung, Datenbanken, KI, Wirtschafts-, Medizin-, Bio-, Medieninformatik,... 8

9 Inhalte der Lehrveranstaltung digitale Bilder statistische Merkmale Punktoperationen (Farb-, Helligkeits-, Kontraständerungen) geometrische Operationen (Projektionen, Verschiebungen, Verzerrungen, Koordinatentransformation) Spektrum, Fourier-Transformation Lokale Operationen, Filter (Hochpass-, Tiefpass-) Merkmalserkennung: Ecken, Kanten, Kurven morphologische Operationen, Skelettierung Segmentierung, Objekterkennung, Klassifikation 9

10 Organisation Vorlesung: 3 Wochen je 2 V 6 Wochen je 1 V + 1 P 3 Wochen je 2 P Anwendungsprojekte) 2 Wochen je 2 V (Projektpräsentationen) Übungsaufgaben zur Prüfungsvorbereitung: gelegentlich Übungsserien als Hausaufgaben, Besprechung in den letzten Vorlesungen Praktikum: ab Ende April zunächst: Praktikum-Aufgaben (ImageJ) nach Pfingsten: Arbeit an Anwendungsprojekten Prüfungsvorleistung: zwei Projekte : 1. Praktikum-Aufgabenserien 2. Anwendungsprojekt mit Selbstudium-Anteil (Recherche, Entwicklung, Dokumentation, Präsentation in letzten LV-Wochen) Prüfung: Klausur (120 min) Aufgabentypen wie Übungsaufgaben (Notenverbesserung durch Projekt-Bonus möglich) 10

11 Anwendungs-Projekte Themenbereich: autonomes Fahren, Fahrassistenzsysteme, Robotik Projektaufgaben: Detektion in Bildern (Fotos), z.b. von Fahrspuren, Fahrspurbegrenzungen Fahrbahnrichtungsmarkierungen (Pfeile) Brücken, Tunneleinfahrten Fahrzeugen und anderen Objekten verschiedene Fahrzeugtypen Frontscheinwerfern, Rück- und Bremslichtern KFZ-Kennzeichen Höchstgeschwindigkeitsschildern 11

12 Bilder Bild ist Funktion B : pos col mit pos : Menge der Positionen im Bild col : Menge der Werte (Farben) im Bild mit verschiedenen Bedeutungen, z.b. Intensitäten (Grauwerte), Tupel von Farbintensitäten, Adressen (Hashwerte) in Lookup-Tabellen, Tiefen-Information (Abstand) reale Bilder: pos R n und col R R unendliche stetige Bereiche digitale Bilder: pos und col endliche diskrete Bereiche N n pos meist Rechteckgitter {0,..., m 1 } {0,..., m n }, z.b. pos = {0, 1, 2} {0,..., 3} (0, 0) (0, 1) (0, 2) (0, 3) (1, 0) (1, 1) (1, 2) (1, 3) (2, 0) (2, 1) (2, 2) (2, 3) 12

13 Digitale 2D-Bilder digitales Bild (2D) mit rechteckigem Positionen-Raster pos = {0,..., m 1} {0,..., n 1} (Höhe m, Breite n), kann betrachtet werden als 1. Funktion B : pos col (ordnet jeder Position einen Farbwert zu) 2. 2D-Matrix B col m n (mit Farbwerten als Einträgen) Pixel (picture element): Eintrag in dieser Matrix mit seiner Position, Adresse: (Zeile, Spalte) z.b. Pixel an Adresse (1, 2) hat Wert 1 im Bild B B = B(1, 2) = 1 13

14 Farbwertbereiche Schwarz-Weiß-Bilder mit Werten aus col = {0, 1} meist 0 für schwarz und 1 für weiß Grauwertbilder mit Intensitäten (Helligkeiten) aus col = {0,..., k} N meist 0 für schwarz und k für maximale Intensität, oft k = 2 n 1 für ein n N, meist n = 8, also Intensitäten {0,..., 255} (eindimensional) Farbbilder mit k Farbkomponenten (Spektrum) meist col N k oder col [0, 1] k R k (k-dimensional, Koordinaten bedeuten Farbintensitäten) Beispiel RGB: col {0,..., 255} 3 14

15 Was bisher geschah Ziele maschineller Bildverarbeitung automatische Informationsextraktion aus Bildern Bildaufbereitung zur Unterstützung der visuellen Informationsextraktion Anwendungsbereiche Aufgaben maschineller Bildverarbeitung: Erzeugung, Wiedergabe, Transformation, Analyse, Interpretation digitaler Bilder digitale Bilder: Funktion B : pos col Matrix B col pos mit den Mengen pos von Positionen (Adressen), meist {0,..., m} {0,..., n} col von Farben, Intensitäten, Tupeln von Intensitäten 15

16 Auflösungen Ortsauflösung pos (Rasterung): Anzahl der Positionen (Zeilen und Spalten) oft hohe Auflösung notwendig zum Erkennen der dargestellten Szene Farb-, Kontrastauflösung col (Quantisierung): Anzahl der Farbwerte, oft geringe Auflösung ausreichend zum Erkennen der dargestellten Szene 16

17 Menschliches Sehen Auge: Linse bildet Original auf Netzhaut (Retina) ab Netzhaut enthält Fotorezeptoren: Stäbchen registrieren Intensität ( < 100 Grauwerte, 2 8 = 256 Grauwerte genügen für realistischen visuellen Eindruck) Zapfen registrieren Farben ( Farbtöne) je ein Zapfentyp für Grün, Rot, Blau (in absteigender Empfindlichkeit) Durch Mischung der drei RGB-Farbkanäle (Spektralbereichen) lässt sich redundanzarm ein visueller Eindruck erzeugen, der dem natürlich wahrgenommenen Bild recht ähnlich ist. Für Bilder zur automatischen Auswertung sind oft auch andere Spektralbereiche und Auflösungen sinnvoll. Das im Auge empfangene diskrete Signal wird im Gehirn zu einem stetigen Gesamteindruck interpoliert 17

18 Farben in Kamerasystemen Jeder Sensor registriert einen festen Spektralbereich (nur Intensität in diesem Bereich). Multispektralkamera enthält mehrere Sensoren für verschiedene Spektralbereiche Ausgabe der Intensitäten meist diskret, also N Farbbereich mit k Farbkomponenten: col N k Zuordnung von (Sensor-)Werten zu Farben oft in Lookup-Tabellen (LUT) 18

19 Farbmodelle Farbmischung: additiv Kombination von Lichtquellen verschiedener Farben z.b. RGB (Rot, Grün, Blau) col = {0,..., 255} 3 = {0,..., 2 8 1} 3 zur Erzeugung realitätsnaher visueller Eindrücke im Display subtraktiv Kombination von Filtern für verschiedene Farben z.b. CMYK (Cyan, Magenta, Yellow, Key) col = {0,..., 255} 4 = {0,..., 2 8 1} 4 zur Erzeugung realitätsnaher visueller Eindrücke beim Druck für wissenschaftliche Bildverarbeitung auch andere (größere, feinere) Spektralbereiche Falschfarben Kontrasterhöhung Überlagerung verschiedener Informationen 19

20 Statistische Bildmerkmale (von Grauwertbildern) Merkmale der Menge aller im Bild(-ausschnitt) vorkommenden Intensitäten (Grauwerte) Extremwerte Mittelwerte Kontrast Helligkeit Histogramme kumulative Histogramme Entropie Merkmale der Anordnung aller im Bild(-ausschnitt) vorkommenden Intensitäten Linien- und Bereichsprofile Co occurrence Matrix (Grauwerteübergangs Matrix) Was lässt sich daraus über ein Bild schließen? 20

21 Extrem- und Mittelwerte gegeben: B col pos (und evtl. Auswahl pos pos) geringste / größte Intensität min, max : col pos col min(b) = min{b(p) p pos} max(b) = max{b(p) p pos} größter Intensitätsunterschied maxdiff : col pos col (Kontrastumfang des Bildes) maxdiff(b) = max(b) min(b) 21

22 Mittelwerte gegeben: B col pos (und evtl. pos pos) durchschnittliche Intensität avg : col pos col p pos avg(b) = B(p) pos Gesamthelligkeit des Bildes Median (Zentralwert) med : col pos col: Wert am mittleren Index der sortierten Folge aller Bildwerte B(p) 22

23 Abweichungen gegeben: B col pos (und evtl. Auswahl pos pos) mittlere quadratische Abweichung σ 2 : col pos R σ 2 (B) = 1 pos und Standardabweichung σ (B(p) avg(b)) 2 p pos Aussagen über den Kontrastumfang des Bildes 23

24 Histogramme gegeben: B col pos (und evtl. Auswahl pos pos) Histogram H : col pos col N mit B col pos c col : H(B, c) = {p pos B(p) = c} (Häufigkeiten der Intensitäten im Bild) Histogramm ist unabhängig vom Ort der Intensitäten kumulatives Histogram H : col pos col N mit B col pos c col : H(B, c) = {p pos B(p) c} 24

25 Informationen aus dem Histogramm alle im Bild vorkommenden Intensitäten Intensitäts-Extrema häufig, selten vorkommende Intensitäten mittlere Intensität (Durchschnitt, Median) Kontrastumfang Standard-Abweichung Aussagen über Belichtung, Ausleuchtung, Dynamik 25

26 Histogramm-Formen häufige Formen der Funktion H: ausgeglichen etwa Gleichverteilung aller Intensitäten wirkt oft recht hell bimodal zwei deutlich voneinander getrennte lokale Maxima günstig für Segmentierung ( Objekt-Hintergrund-Trennung) 26

27 Intensitätsprofile Profil: Darstellung der Intensität als Höhe über der Profillinie bzw. Profilfläche Linienprofil: Intensitätsverlauf entlang einer Linie (Zeile, Spalte, Gerade, Kurve) scharfe Intensitätsunterschiede im Bild entsprechen steilen Kanten im Linienprofil Integriertes Linienprofil: Summe der Intensitätsverläufe entlang mehrerer benachbarter Linien (Zeilen, Spalten) zum schnellen Vergleich von Bildern Lokalisierung von Abweichungen durch Kombination von Zeilen- und Spaltenprofilen Profil über Bildbereich: 3D-Darstellung der Intensitäten als über einem zweidimensionalen Bildbereich 27

28 Co occurrence Matrix gegeben: B col pos (und evtl. Auswahl pos pos) Co occurrence Matrix C N col col mit c, d col : C(c, d) = {p = (p x, p y ) pos : B(p) = c B(p x, p y+1 ) = d} Anzahl der Vorkommen von Intensitäts-Paaren zwischen Nachbar-Pixeln (verschiedene Nachbarschafts-Beziehungen) Beispiel (horizontale Nachbarschaft): B = C(B) =

29 Co occurrence Matrix Informationen große gleichfarbige Flächen in B hohe Werte auf der Hauptdiagonale in C(B) scharfe Kontraste in B hohe Werte links unten und rechts oben C(B) Länge von Grenzen zwischen Bereichen gleicher Intensitäten Texturmerkmal (zur texturbasierten Segmentierung) 29

30 Entropie gegeben: B col pos (und evtl. Auswahl pos pos) Entropie H : col pos R H(B) = (h(b, c) log 2 (h(b, c))) c col mit relativer Häufigkeit des Intensitätswertes c in B: h(b, c) = {p pos B(p) = c} pos Aussage über Informationsgehalt des Bildes (auch für Co-occurrence-Matrix und andere Bildmerkmale) Beispiele: einfarbiges ( )-Bild B mit Grauwert 10 hat Entropie H(B) =... ( )-Schwarz-Weiß-Bild mit gleicher Anzahl schwarzer und weißer Pixel hat Entropie H(B) =... ( )-Bild mit jeweils gleicher Anzahl an Pixeln in 8 Intensitätswerten hat Entropie H(B) =... untere Schranke für Bitzahl zur Codierung des Bildes 30

31 Was bisher geschah Aufgaben maschineller Bildverarbeitung: Transformation, Analyse, Interpretation (, Erzeugung, Wiedergabe) digitaler Bilder digitale Bilder: Funktion B : pos col Matrix B col pos mit den Mengen pos von Positionen (Adressen) col von Farben, Intensitäten Orts- und Kontrastauflösung Farbmodelle statistische Merkmale (Bildanalyse) Bild Wert: Extrema, Mittelwerte, Abweichung, Entropie Bild Funktion col N: Histogramme, kumulierte Histogramme, Linien- und Bereichsprofile, Co occurrence Matrix und ihre Aussagen über das Bild 31

32 Bildbearbeitung durch Punktoperationen Punktoperation zwischen verschiedenen Farbbereichen Funktion f : col 1 col 2 (neuer) Wert eines Pixels nur abhängig vom (alten) Wert dieses Pixels Fortsetzung f : col pos 1 col pos 2 der Funktion f auf Bilder durch punktweise Anwendung p pos : f (B)(p) = f (B(p)) Beispiel: f : {3,..., 6} {0,..., 7} mit f (x) = 7(x 3) 3 f ( ) = ( f (4) f (5) f (3) f (4) ) ( 7 = ) ( ) 32

33 Punktoperationen Beispiele Transformation von RGB (col 1 = {0,..., 255} 3 ) in Graustufenintensität (col 2 = {0,..., 255}) f : {0,..., 255} 3 {0,..., 255} mit (r, g, b) col 1 : f (r, g, b) = (r + g + b)/3 bzw. (r, g, b) col 1 : f (r, g, b) = 0.299r g b Umrechnung 8-Bit-Intensität (col 1 = {0,..., 255}) in relative Intensität (col 2 = [0, 1]) in f : {0,..., 255} [0, 1] mit c col 1 : f (c) = c/255 Falschfarbendarstellung von Intensitäten (z.b. für Infrarot-, Tiefeninformation) f : [0, 1] [0, 1] 3 mit f (x) = x, }{{}}{{} x 3, sin (2πx) }{{} r g b (nachträgliche Colorierung von Grauwertbildern) Transformationen für col 1 = col 2 (gleicher Farbbereich) meist zur Kontrasterhöhung oder Invertierung 33

34 Prominente Punktoperationen z.b. zur Bildverbesserung durch Kontrasterhöhung lineare Funktionen (Kontrast- und Helligkeitsänderung) f (c) = ac + b f (c) = max(col) ac + b Stufenfunktionen (Abbildung auf weniger Werte) Spezialfall Binarisierung mit Schwellwert θ col { 1 falls c θ f (c) = 0 sonst weitere nichtlineare Funktionen, z.b. f (c) = c 2 max(col) f (c) = c max(col) 34

35 Histogrammspreizung (-normalisierung) gegeben: B col pos ( und evtl. Auswahl pos pos) punktweise Anwendung der (linearen) Punktoperation f : col col mit max(col) min(col) f (c) = (c min(b)) + min(col) max(b) min(b) sorgt für volles Ausschöpfen der gesamten Intensitätsskala Clipping: Ignorieren (häufig informationsarmer) Bereiche sehr geringer (< θ 1 ) und sehr hoher (> θ 2 ) Intensitäten durch Histogrammspreizung des Farbbereiches [θ 1, θ 2 ] 35

36 Histogrammausgleich (-äqualisierung) gegeben: B col pos, Auswahl pos pos von Positionen im Bild B Punktoperation f : col col mit {p pos B(p) c} f (c) = (max(col) min(col)) pos sorgt für annähernd lineares kumulatives Histogramm annähernd konstantes Histogramm ähnlich häufige Auftreten aller Intensitäten 36

37 Posterizing Abbildung auf vorgegebene Anzahl k von Intensitätsstufen (häufig geringer als Anzahl der Intensitätsstufen des Originalbildes) gegeben: gesucht: B {0,..., k} pos B {0,..., k } pos durch Stufenfunktion mit k Schwellwerten θ i {1,..., k } 0 falls x < θ 1 1 falls θ 1 x < θ 2 f (x) =. k falls θ k 1 x θ k 37

38 Binarisierung Abbildung von Bildern mit Wertebereich col = {0,..., k} (Intensitäten) auf Schwarz-weiß-Bilder (mit Wertebereich col = {0, 1}) gegeben: gesucht: B {0,..., k} pos B {0, 1} pos abhängig von einem Schwellwert θ col { 1 falls x θ f (x) = 0 sonst oder abhängig von zwei Schwellwerten θ 1, θ 2 col { 1 falls θ1 < x θ f (x) = 2 0 sonst 38

39 Schwellwertbestimmung mittlerer Grauwert θ = avg(b) bei bekanntem prozentualem Anteil p% der (angenommen helleren) Objektpunkte: Auswahl des maximalen θ mit c<θ h(b, c) 1 p/100 bei bimodalen Histogrammen: θ = lokales Minimum zwischen beiden Maxima Schwellwertberechnung nach Otsu adaptive Schwellwertberechnung verschiedene Schwellwerte für verschiedene Bildbereiche anhand lokaler Merkmale (z.b. avg, med) des Bildbereiche 39

40 Schwellwertbestimmung nach Otsu Jeder Schwellwert θ col zerlegt col in zwei Farbbereiche. col<θ = {c col c < θ} (Hintergrund) col θ = {c col c θ} (Vordergrund) statistische Größen dieser beiden Farbereiche innerhalb B: Auftrittswahrscheinlichkeit p <θ (B) = c col <θ h(b, c) = {p pos B(p)<θ} pos Mittelwert avg<θ (B) = 1 p <θ (B) c<θ c h(b, c) Varianz σ 2 <θ (B) = 1 p <θ (B) c<θ (h(b, c)(c avg <θ (B))2 gesucht: θ mit beiden folgenden Eigenschaften minimale Varianz innerhalb der Klassen σ 2 θ,w (B) = p <θ (B)σ 2 <θ(b) + p θ (B)σ 2 θ(b) maximale between-class-varianz σ 2 θ,b(b) = p <θ (B) ( σ 2 <θ(b) avg(b) ) 2 +p θ (B) ( σ 2 θ(b) avg(b) ) 2 Für jeden Schwellwert θ ist σ 2 θ,w (B) + σ2 θ,b (B) = σ2 (B) konstant. Es existiert ein θ, so dass σ 2 θ,w (B) minimal und σ2 θ,b (B) maximal. 40

41 Kombinationen mehrerer Bilder Eingabe: Ausgabe: Bilder B, C col pos Bild D col pos Beispiele für punktweise Operationen f : col col col auf Binärbildern (col = {0, 1}): logische Operationen (Mengenoperationen) Grauwertbilder (col = {0,..., k}): arithmetische Operationen z.b. min, max, Differenz, Mittelwert Farbbildern Grauwertbild-Operationen auf jeder Farbkomponente einzeln Transformation in andere Farbbereiche (z.b. Grauwerte) durch Operationen zur Kombination mehreren Farbkomponenten 41

42 Binärbilder als Mengen von Positionen Bild B : pos {0, 1} ist charakteristische Funktion der Menge aller weißen Pixel (meist als Vordergrund interpretiert) Bild B repräsentiert die Menge B 1 (1) (Urbild von 1) B B 1 (1) Transformation von B durch Anwendung von Mengenoperationen auf B B = (0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 2), (2, 3), (3, 1), (4, 1) 42

43 Mengenoperationen auf Binärbildern Komplement eines Bildes B : pos {0, 1}: B : pos {0, 1} mit B B 1 (1) = B 1 (0) punktweise: (Farb-Invertierung) p pos : B(p) = B(p) = 1 B(p) Vereinigung zweier Bilder B, C : pos {0, 1} (B C) : pos {0, 1} mit (B C) B 1 (1) C 1 (1) = {p pos B(p) = 1 C(p) = 1} punktweise: p pos : (B C)(p) = B(p) C(p) = max(b(p), C(p)) Schnitt zweier Bilder B, C : pos {0, 1} (B C) : pos {0, 1} mit (B C) B 1 (1) C 1 (1) = {p pos B(p) = 1 C(p) = 1} punktweise: p pos : (B C)(p) = B(p) C(p) = min(b(p), C(p)) 43

44 Mengenoperationen auf Binärbildern Differenz zweier Bilder B, C : pos {0, 1} (B \ C) : pos {0, 1} mit (B \ C) B 1 (1) \ C 1 (1) punktweise: = {p pos B(p) = 1 C(p) = 0} p pos : (B\C)(p) = B(p) C(p) = min(b(p), 1 C(p)) Symmetrische Differenz zweier Bilder B, C : pos {0, 1} (B C) : pos {0, 1} mit (B C) (B C) \ (B C) = (B \ C) (C \ B) punktweise: = {p pos B(p) = 1 XOR C(p) = 0} p pos : (B C)(p) = B(p) XOR C(p) = (B(p) + C(p)) mod 2 44

45 Logische Masken zur Darstellung und Verwaltung relevanter Bildbereiche Logische Maske (Binärmaske): Binärbild {0, 1} pos mit Werten 0 für irrelevante Positionen 1 für relevante (transparente) Positionen Multiplikation einer Maske mit Originalbild ergibt 0 (schwarz) an irrelevanten Positionen Originalwerte an relevanten Positionen Anwendungen bei Arbeit mit Bildausschnitten Segmentierung Hintergrund-Entfernung Montage mehrerer Bilder Definition von Nachbarschaften von Positionen 45

46 Arithmetische Operationen auf Grauwertbildern gegeben: B, C col pos mit col = {0,..., k} N typische Punktoperationen: B, C col pos p pos Differenz (B C)(p) = B(p) C(p) zum Vergleich von Bildern, Hintergrund-Entfernung, Bewegungsdetektion häufig auch max(b(p) C(p), 0) zur Vermeidung negativer Farbwerte n i=1 B i (p) Mittelwert avg(b 1,..., B n )(p) = n zur Entfernung zufälliger Störungen, Entrauschen Addition (B + C)(p) = B(p) + C(p) häufig auch min(b(p) + C(p), max(col)) zur Vermeidung von Werten außerhalb des Farbbereiches Multiplikation (BC)(p) = B(p)C(p) Verhältnis (B/C)(p) = B(p)/C(p) 46

47 Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale (Bildanalyse) Bild Wert: Extrema, Mittelwerte, Abweichung, Entropie Bild Funktion col N: (kumulierte) Histogramme Bild Funktion von Teilmenge von pos N: Linienprofile, integriertes Linienprofil Bild Funktion col 2 N: Co-occurrence-Matrix und ihre Aussagen über das Bild Punktoperationen f : col 1 col 2 (Farbtransformation) und ihre Fortsetzung f : col pos 1 col pos 2 p pos : f (B)(p) = f (B(p)) Intensitäts-, Kontrasterhöhung Histogrammstreckung Farbtransformationen Binarisierung 47

48 Nachbarschaftsbeziehungen zwischen Positionen Zur Identifikation zusammenhängender Bilddteile (Linien, Flächen) veschiedene Nachbarschaftsbeziehungen üblich, z.b. Zwei Positionen p, q pos = {0,..., m 1} {0,..., n 1} heißen genau dann benachbart, wenn sie 1. ungleich sind und 2. wenigstens einen gemeinsame Kante besitzen, 4-Nachbarschaft von p = (z, s): N 4 (p) = {(z 1, s), (z + 1, s), (z, s 1), (z, s + 1)} pos p Ecke besitzen, 8-Nachbarschaft von p = (z, s): (z 1, s 1), (z, s 1), (z + 1, s 1), N 8 (p) = (z 1, s), (z + 1, s), (z 1, s + 1), (z, s + 1), (z + 1, s + 1) p pos 48

49 Geometrische Operationen in der DBV Anwendungen z.b. in Geoinformatik: Satellitenbilder geographische Daten Bereinigung um Verzerrungen durch Höhenunterschiede Objekterkennung Robotik: Kamerabild Umgebungskarte Schrifterkennung: Zeilenausrichtung Normierung der Zeichengröße Schrägschrift-Korrektur QR-Codes: Entzerrung Bildvergrößerung und -verkleinerung 49

50 Geometrische Operationen Operationen auf der Menge pos, wobei Intensitäten Nachbarschaftsbeziehungen zwischen Positionen weitgehend unverändert bleiben gegeben: B col pos 1 gesucht: C col pos 2 Transformationen: linear Kombinationen von Spiegelung Verschiebung Skalierung (Zoom) Drehung nichtlinear z.b. perspektivische Abbildungen, Warping, Swirl 50

51 Transformationen im R 2 Transformation f : R 2 R 2 für digitale Bildverarbeitung (Beschränkung auf Stützstellen im Raster): f : pos pos hier mit rechteckigen Rastern (Adressen in Matrizen) pos = {0,..., m 1} {0,..., n 1} und pos = {0,..., m 1} {0,..., n 1} Probleme bei Transformationen R 2 R 2 : Zielpositionen evtl. nicht in pos nicht jede Position in pos ist Bild einer Position im Original berechnete Zielposition liegt i.a. nicht auf Rasterpunkt Festlegung des Farbwertes im transformierten Bild nötig (Interpolation) 51

52 Translation (Verschiebung) im R 2 Verschiebung (2D) um einen Vektor (v 1, v 2 ) R 2 : V (v1,v 2 ) : R 2 R 2 mit ( ) ( ) ( ) ( x1 x1 v1 x1 + v V (v1,v 2 ) = + = 1 v 2 x 2 + v 2 x 2 x 2 ) Verschiebung (2D) als Multiplikation mit Matrix V (v1,v 2 ) R 3 3 in homogenen Koordinaten: V (v1,v 2 ) = 1 0 v v V (v1,v 2 ) x 1 x 2 1 = x 1 + v 1 x 2 + v 2 1 zu V (v1,v 2 ) inverse Transformation: V 1 (v 1,v 2 ) = V ( v 1, v 2 ) 52

53 Spiegelung (Reflexion) im R 2 Spiegelung (2D) an x 2 -Achse S h : R 2 R 2 mit ( ) x1 S h = x 2 ( ) ( x1 x 2 ) ( x1 = x 2 ) Spiegelung an x 2 -Achse als Multiplikation mit Matrix S h R 3 3 in homogenen Koordinaten: x 1 x 1 S h = S h x 2 = x x 1 -Achse S v : R 2 R 2 analog: S v = S v x 1 x 2 1 = x 1 x 2 1 Spiegelungen sind involutiv (selbstinvers): S 1 h = S h, Sv 1 = S v 53

54 Skalierung im R 2 Skalierung (Stauchung, Streckung) aus dem Ursprung (0, 0) R 2 mit Skalierungsfaktoren s 1 R und s 2 R S (s1,s 2 ) : R 2 R 2 mit x R 2 : S (s1,s 2 )(x) = (s 1 x 1, s 2 x 2 ) Skalierung (2D) als Matrixmultiplikation in homogenen Koordinaten: s x 1 s 1 x 1 S (s1,s 2 ) = 0 s 2 0 S (s1,s 2 ) x 2 = s 2 x zu S (s1,s 2 ) inverse Transformation: S 1 (s 1,s 2 ) = S (1/s 1,1/s 2 ) Spiegelungen sind Skalierungen: S h = S ( 1,1) und S v = S (1, 1) 54

55 Rotation (Drehung) im R 2 Drehung um einen Winkel ϕ [0, 2π] im mathematischen Drehsinn (entgegen Uhrzeigersinn) um Ursprung (0, 0) R 2 D ϕ : R 2 R 2 mit x R 2 : D ϕ (x) = (x 1 cos ϕ x 2 sin ϕ, x 1 sin ϕ + x 2 cos ϕ) Drehung (2D) als Matrix in homogenen Koordinaten: cos ϕ sin ϕ 0 x 1 x 1 cos ϕ x 2 sin ϕ D ϕ = sin ϕ cos ϕ 0 D ϕ x 2 = x 1 sin ϕ + x 2 cos ϕ zu D ϕ inverse Transformation: D 1 ϕ = D ϕ 55

56 Affine Transformationen Matrixdarstellung der linearen Transformationen ermöglicht die Zusammenfassung der Nacheinanderausführung mehrerer Transformationen (Matrixmultiplikation) allgemeine Form affiner Transformationen im R 2 (in homogenen Koordinaten): a 1 a 2 v 1 M = b 1 b 2 v Jede Transformation (Matrix) dieser Form lässt sich durch eine endliche Verkettung der elementaren Transformationen (Matrix-Multiplikationen) Verschiebung Skalierung Drehung um Ursprung (0, 0) R 2 erzeugen. für M = T 1 T n gilt M 1 = Tn 1 T

57 Beispiel p q Koordinaten p = (1, 1) und q = (2, 1) Verschiebung um ( 1, 1) und danach Drehung um π/ Schrittweise Anwendung auf p = (1, 1) und q = (2, 1) Gesamttransformation: Matrixmultiplikation in umgekehrter Reihenfolge =

58 Bestimmung affiner Transformationen gegeben: Zuordnung {(p 1, q 1 ),..., (p n, q n )} zwischen Positionen {p 1,..., p n } pos(b) im Bild B und {q 1,..., q n } pos(a) im Original A gesucht: Beschreibung der Transformation A B durch Matrix M mit i {1,..., n} : M(q i ) = p i a 1 a 2 v 1 M = b 1 b 2 v d.h. gesucht sind die sechs Koeffizienten a 1, a 2, b 1, b 2, v 1, v 2 mit q i1 p i1 i {1,..., n} : M q i2 1 = p i2 1 als lineares Gleichungssystem mit Unbekannten a 1, a 2, b 1, b 2, v 1, v 2 : q i1 a 1 + q i2 a 2 + v 1 = p i1 q i1 b 1 + q i2 b 2 + v 2 = p i2 eindeutig lösbar für sechs Gleichungen = drei (nicht kollineare) Referenzpunkte 58

59 Beispiel Gesucht ist die affine Transformation M = a 1 a 2 v 1 b 1 b 2 v , welche die folgenden Punkte aufeinander abbildet: ( ) ( ) ( ) ( ) ( ) ( ) Gleichungssystem 2a 1 + 2a 2 + v 1 = 0 (1) 2b 1 + 2b 2 + v 2 = 2 (2) 3a 1 + 2a 2 + v 1 = 1 (3) 3b 1 + 2b 2 + v 2 = 3 (4) 3a 1 + a 2 + v 1 = 2 (5) 3b 1 + b 2 + v 2 = 2 (6) (3) (1): a 1 = 1, (4) (2): b 1 = 1,... M =

60 Projektive Abbildungen (perspektivische Abbildungen) Projektive Abbildung mit affiner Transformation M = Projektionskoeffizienten p 1, p 2 a 1 a 2 v 1 b 1 b 2 v und Projektive Abbildung (2D) als Matrix in homogenen Koordinaten: a 1 a 2 v 1 P M,p1,p 2 = b 1 b 2 v 2 p 1 p 2 1 x 1 a 1 x 1 + a 2 x 2 + v 1 y 1 P M,p1,p 2 x 2 = b 1 x 1 + b 2 x 2 + v 2 = y 2 1 p 1 x 1 + p 2 x y 3 Umrechnung nach R 2 : y 1 = y 1 /y 3, y 2 = y 2 /y 3 (nichtlinear) 60

61 Bestimmung projektiver Transformationen typischer Ausgangspunkt: (projektiv) verzerrtes Bild Menge von Referenzpunkten, für die Position im Ursprungs- und im Zielbild bekannt sind gesucht: Transformationsmatrix zur Entzerrung des Bildes (8 Koeffizienten a 1, a 2, b 1, b 2, v 1, v 2, p 1, p 2 ) Gleichungssystem mit 8 Unbekannten also wenigstens 4 Referenzpunkte nötig Auflösen der Gleichungen y 1 = a 1x 1 + a 2 x 2 + v 1 p 1 x 1 + p 2 x y 2 = b 1x 1 + b 2 x 2 + v 2 p 1 x 1 + p 2 x für jeden Referenzpunkt y = (y 1, y 2 ) nach den Koeffizienten 61

62 Rasterung Abbildung eines Bildes B col (R2) mit stetiger Positionsmenge (Ebene R 2 ) auf ein digitales Bild C col pos mit diskreter Menge von Positionen pos = {0,..., m 1} {0,..., n 1} (Rasterpunkte) besteht aus zwei Teilaufgaben: 1. Abbildung R 2 pos 2. Bestimmung der Farbwerte C(p) für Rasterpunkte p pos, verschiedene Möglichkeiten C(p) := B(p) (Farbwert an Stützstelle p) nur möglich, wenn Farbwert B(p) für p pos gegeben ist C(p) := f (U(p)) als Funktion aller Farben in einer geeignet definierten Umgebung U(p) R 2 von p (z.b. Mittelwert C(p) := q U(p) B(q) U(p) ) 62

63 Interpolation der Intensitäten Das geometrische Transformationen nicht immer Pixel auf Pixel abbilden, wird der Farbwert eines Pixels q pos im transformierten Bild häufig aus den Farbwerten einer Umgebung (Menge von Pixeln) von T 1 (q) pos im Original berechnet (interpoliert). gegeben: digitales (Original-)Bild B col pos, geometrische Transformation T : R 2 R 2 gesucht: Annahmen: transformiertes digitales Bild C col pos Ursprungs- und Zielbild sind Approximationen desselben stetigen (beliebig fein aufgelösten) Bildes (dessen Werte aber i.a. nur an den Stützstellen pos bekannt ist) Positionen werden als Rasterpunkte im R 2 betrachtet Farbwert eines Rasterpunktes q pos im Zielbild lässt sich aus den Farbwerten der Rasterpunkte in einer Umgebung U(T 1 (q)) 2 pos des rücktransformierten Rasterpunktes T 1 (q) R 2 berechnen durch Interpolationsfunktion g : col pos R 2 2 pos col Transformation digitaler Bilder: T : col pos (R 2 R 2 ) col pos mit q pos : T (B, T, q) = g(b, T 1 (q), U(T 1 (q))) 63

64 Interpolationsfunktionen prominente Interpolationsfunktionen g : col pos R 2 2 pos col: Mittelwerte der Umgebungswerte g(b, p, U) = avg{b(r) r U} (med{b(r) r U}) Farbe des (eines) nächsten Nachbarn (Rasterpunkt in der Umgebung U pos mit geringstem Abstand zu p) p R 2 : g(b, p, U) = B(r) wobei d(r, p) = min{d(s, p) s U} lineare Interpolation (der 1 bis 4 nächsten Punkte im Original) für p = (z, s ) R 2 mit z z z + 1, s s s + 1 Umgebung U(z, s ) = {(z, s), (z, s + 1), (z + 1, s), (z + 1, s + 1)} g(b, (z, s ), {(z, s), (z, s + 1), (z + 1, s), (z + 1, s + 1)}) = a 1 B(z, s) + a 2 B(z, s + 1) + a 3 B(z + 1, s) + a 4 B(z + 1, s + 1) (gewichtete Summe der Farbwerte) mit a 1 = (1 + z z )(1 + s s ), a 2 = (1 + z z )(s s), a 3 = (z z)(1 + s s ), a 4 = (z z)(s s) kubische Interpolation 64

65 Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale und ihre Aussagen über das Bild (Bildanalyse) Punktoperationen f : col 1 col 2 (Farbtransformation) und ihre Fortsetzung f : col pos 1 col pos 2 p pos : f (B)(p) = f (B(p)) Intensitäts-, Kontrasterhöhung Histogrammstreckung Binarisierung Geometrische Operationen f : pos 1 pos 2 (Koordinatentransformation) Verschiebung, Skalierung, Drehung Projektion Interpolation der Intensitäten (Farben) 65

66 Eindimensionale Signale analog : Funktion R R digital : Funktion pos col mit pos, col N, oft pos = {0,..., m 1} N, col = {0,..., n 1} N (Array / Liste / 1D-Matrix natürlicher Zahlen) Beispiele: Temperaturverläufe Börsenkurse Töne (Schallwellen) 66

67 Abtastung eindimensionaler Signale (Transformation eines Signals mit stetigem Definitionsbereich in ein Signal mit diskretem Definitionsbereich) gegeben: Funktion B : R R (eindimensionales Bild), Menge pos = {0,..., m 1} gesucht: Funktion B : R R mit { p R : B B(p) falls p pos (p) = 0 sonst Ziel: Transformation f : (R R) (pos R) mit B (R R ) p pos : f (B)(p) = B(p) Realisierung von f durch Multiplikation von B mit Dirac-Impulsen δ : R R mit δ(x)dx = 1 und x R : x 0 δ(x) = 0 67

68 Dirac-Impuls Dirac-Impuls δ : R R mit δ(x)dx = 1 und x R : x 0 δ(x) = 0 Approximation von δ durch Rechteck-Impulse: x R : { 1 falls 1/2 x 1/2 f 1 (x) = 0 sonst { 2 falls 1/4 x 1/4 f 2 (x) = 0 sonst. f i (x) = { 2 i 1 falls 2 i x 2 i 0 sonst. i > 0 : f i (x)dx = 2 i 2 i 2 i 1 dx = 2 i i = 1 68

69 Multiplikation mit Dirac-Impuls { 2 i 1 falls 2 i N : f i (x) = i t 2 i 0 sonst Wirkung der Multiplikation eines Bildes B : R R mit f i : 2 i B(x)f i (x)dx = 2 i 1 B(x)dx 2 i { = avg B(x) x [ 2 i, 2 i]} für i : δ : B(x)δ(x)dx = B(0) 69

70 Dirac-Kamm Dirac-Impuls δ : R R mit δ(x)dx = 1 und x R : x 0 δ(x) = 0 Verschiebung von B um p entlang der t-achse: B(x + p)δ(x)dx = B(x)δ(x p)dx = B(p) (wegen δ(x p) 0 gdw. x = p) Dirac-Kamm: Summe mehrerer Dirac-Impulse, eins an jedem p pos x R : δ pos (x) = δ(x p) p pos Transformation f : (R R) (R R) mit B (R R ) p pos : f (B)(p) = = B(x)δ pos (x)dx { B(p) falls p pos 0 sonst Ziel erreicht: Abtastung der Funktion B : R R an den Stellen pos 70

71 Beispiele B : R {0, 1} mit x R : B(x) = x mod 2 Abtastung an allen Positionen pos = {n/2 n {0,..., 10}} B = {(0, 0), (1/2, 0), (1, 1), (3/2, 1), (2, 0), (5/2, 0),...} pos = {3n/2 n {0,..., 10}} B = {(0, 0), (3/2, 1), (3, 1), (9/2, 0), (6, 0), (15/2, 1),...} Unterabtastung pos = {4n n {0,..., 10}} B = {(0, 0), (4, 0), (8, 0),...} Unterabtastung B : R [ 1, 1] mit t R : B(x) = c sin(x) Aliasing: Rekonstruktion nicht im Original vorhandener Frequenzen (Alias-Frequenzen, Schwebungen) 71

72 Probleme bei der Abtastung Durch Digitalisierung (Transformation stetiger Signale in diskrete) entstehen möglicherweise Informationsverlust bei Unterabtastung verfälschte Strukturen : Alias-Effekte Nyquist-Shannon-Abtasttheorem: Zur verlustfreien Rekonstruktion darf das Abtastraster (Abstand zwischen den Abtast-Positionen) nicht gröber sein als die halbe Größe des kleinsten abzubildenden Details. alternative Formulierung: Abtastrate (1/ ) muss wenigstens doppelt so groß wie die höchste im Signal vorkommende Frequenz sein 72

73 Zusammenfassung Abtastung 1D Transformation einer stetigen Funktion B : R R (analoges Signal) in eine Funktion B : pos R (diskretes Signal) mathematische Beschreibung dieser Transformation durch Funktion(al) f pos : (R R) (pos R) Dirac-Impuls δ : R R mit δ(x)dx = 1 und x R : x 0 δ(x) = 0 Dirac-Kamm δ pos an Abtaststellen pos R: x R : δ pos (x) = p pos δ(x p) abgetastetes Signal f pos (B) an Abtaststellen pos R: x R : (f pos (B))(x) = B(x)δ pos (x)dx = B(x)δ(x p)dx p pos Abtasttheorem (Nyquist-Shannon): Zur verlustfreien Rekonstruktion darf das Abtastraster (Abstand zwischen benachbarten Abtast-Positionen) nicht gröber sein als die halbe Größe des kleinsten abzubildenden Details. 73

74 Faltung Verschiebung eines Dirac-Impulses um p entlang der x-achse: B(x + p)δ(x)dx = = B(x)δ(x p)dx B(x)δ(p x)dx = B δ ist Spezialfall einer Operation mit zwei Funktionen: Für f, g : R R ist die Faltung (Convolution) von f und g definiert durch p R : (f g)(p) = f (x)g(p x)dx 74

75 Faltung Beispiel { 1 falls 1 x 1 f (x) = χ [ 1,1] = 0 sonst { 2 falls 0 x 2 g(x) = 2χ [0,2] = 0 sonst an Stellen p { 2, 1, 0, 1, 2, 3, 4} ausrechnen: p R : (f g)(p) = f (x)g(p x)dx = max(0, 4 2 p 1 ) anschaulich: 1. Spiegelung von g an y-achse 2. gespiegeltes g wird entlang der x-achse geschoben 3. (f g)(p) ist der Flächeninhalt der vom Produkt beider Funktionen überdeckten Fläche 75

76 Faltung Eigenschaften kommutativ, d.h. f, g : f g = g f assoziativ, d.h. f, g, h : (f g) h = f (g h) Dirac-Impuls δ ist neutrales Element bzgl. : Für jede Funktion B : R R gilt x R : (B δ)(p) = also B δ = B für verschobenen Dirac-Impuls δ p mit x R : δ p (x) = δ(x p) und jede Funktion B : R R gilt B(x)δ(p x)dx = B(p) x R : (B δ p )(x) = B(x p) bilinear, d.h. linear in jeder Komponente (af + bf ) g = a(f g) + b(f g) (analog für ag + bg ) 76

77 Diskrete Faltung stetig: Für f, g : R R ist die Faltung von f und g definiert durch p R : (f g)(p) = f (x)g(p x)dx diskret: Für f, g : Z Z ist die Faltung (Convolution) von f und g definiert durch p Z : (f g)(p) = f (x)g(p x) x= diskret mit endlichem Definitionsbereich pos: Für f, g : pos R ist die Faltung (Convolution) von f und g definiert durch p pos : (f g)(p) = f (x)g(p x) x pos 77

78 Diskrete Faltung Beispiel f, g : Z N mit 3 falls x = 1 f (x) = 1 falls x = 2 0 sonst 2 falls x = 1 g(x) = 1 falls x = 2} 0 sonst als Vektoren mit endlichem Definitionsbereich pos = {0,..., 3}: f = (0, 3, 1, 0), g = (0, 2, 1, 0) 6 falls p = 2 5 falls p = 3 (f g)(p) = 1 falls p = 4 0 sonst als Vektor: f g = (0, 6, 5, 1) (relevanter Teil) 78

79 Zweidimensionale Signale analog : Funktion R 2 R digital : Funktion pos col mit col N und pos N 2, meist pos = {0,..., m 1} pos = {0,..., n 1} N 2 und col = {0,..., k 1} N (Matrix natürlicher Zahlen, Bilder) 79

80 Abtastung (2D) Transformation eines Signals mit stetigem Definitionsbereich in ein Signal mit diskretem Definitionsbereich (Raster) gegeben: Funktion B : R 2 R gesucht: Funktion B : pos R mit pos = {0,..., m 1} {0,..., n 1} Transformation f : (R 2 R) (pos R) mit B : R 2 R p = (p x, p y ) pos : { B(px, p f (B)(p x, p y ) = y ) falls (p x, p y ) pos 0 sonst Realisierung durch Multiplikation von B mit Dirac-Impulsen δ : R 2 R mit δ(x, y)dxdy = 1 und (x, y) R 2 : (x, y) (0, 0) δ(x) = 0 80

81 Dirac-Kamm (2D) Dirac-Impuls δ : R 2 R mit δ(x, y)dxdy = 1 und (x, y) R 2 : (x, y) (0, 0) δ(x, y) = 0 Verschiebung in der Ebene um (p x, p y ) R 2 : = = B(p x, p y ) B(x + p x, y + p y )δ(x, y)dxdy B(x, y)δ(x p x, y p y )dxdy 2D-Dirac-Kamm: Summe mehrerer Dirac-Impulse (x, y) R 2 : δ pos (x, y) = δ(x p x, y p y ) p pos Abtastung der Funktion B : R 2 R an den Stellen pos R 2 : (x, y) pos : B (x, y) = B(x, y)δ pos (x, y)dxdy = B(x, y) 81

82 Faltung (2D) Für f, g : R 2 R ist die Faltung (Convolution) von f und g definiert durch (p x, p y ) R 2 : (f g)(p x, p y ) = f (x, y)g(p x x, p y y)dxdy diskreter Fall (Bilder): Für f, g : {0,..., m 1} {0,..., m 1} col ist die Faltung (Convolution) von f und g definiert durch (x, y) {0,..., m 1} {0,..., m 1} : (f g)(p x, p y ) = m 1 n 1 f (x, y)g(p x x, p y y) x=0 y=0 82

83 Was bisher geschah digitale Bilder Funktion B : pos col Matrix B col pos statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Operationen f : pos 1 pos 2 (Koordinatentransformation) Interpolation der Intensitäten 1D- und 2D-Signale (analog, digital) Digitalisierung (Abtastung) von 1D- und 2D-Signalen Alias-Effekte Faltung von Signalen (Funktionen) 83

84 Signale stetige Signale auf Bereichen pos R m und col R m Darstellung als Funktion B : pos col bisher: Transformationen durch (Punkt-)Operationen auf Funktionswerte p : col col also Nacheinanderausführung B p : pos col Koordinatentransformationen (geometrisch) t : pos pos also Nacheinanderausführung t B : pos col diskrete Signale auf Bereichen pos Z m und col Z m (meist) erzeugt durch Abtastung stetiger Signale Darstellung durch Angabe der Werte an den Stützstellen (endliche) Menge von Position-Wert-Paaren Darstellung von Bildern (2D-Funktionen) durch Farbwerte an Pixelpositionen Transformationen durch (Punkt-)Operationen auf Funktionswerte p : col col punktweise Anwendung von p an jeder Position Koordinatentransformationen (geometrisch) t : pos pos (meist) Interpolation der Farbwerte nötig 84

85 Transformation stetiger Signale bisher: Diskretisierte Funktion f : pos col als Linearkombinationen (gewichtete Summe) von verschobenen Dirac-Impulsen δ : R R (Basis) Transformationen durch Operationen auf col : (punktweise) Farbtransformationen pos : geometrisch (Verschiebung, Skalierung,... ) alternativ: Beschreibung von Funktionen f : R R als Linearkombinationen (gewichtete Summe) festgelegter (stetiger) Basisfunktionen g i : R R (geeignet skaliert und verschoben) x R : f (x) = i I a i g i (x) Darstellung von Bildern als Linearkombinationen (stetiger) Standardbilder (evtl. skaliert, verschoben und rotiert) Transformationen durch Operationen auf den Koeffizienten a i der Standardfunktionen 85

86 Periodische Funktionen (1D, Wiederholung) Funktion f : R R heißt periodisch gdw. p R x R i Z : f (x) = f (x + ip) p R heißt Periode von f Funktion f : R R heißt gerade gdw. x R : f (x) = f ( x) (Symmetrie an y-achse) z.b. x x 2, x cos(x) ungerade gdw. x R : f (x) = f ( x) z.b. x x 3, x sin(x) 86

87 Fouriertransformation (1D) Wiederholung Darstellung von (periodischen) Funktionen f : R R als Linearkombination (gewichtete Summe) periodischer zueinander orthogonaler Standard -Funktionen mit Perioden p k = 2πk p für Periode p von f und alle k Z. Für Fouriertransformation trigonometrische Funktionen mit Periode 2π cos gerader Anteil sin ungerader Anteil x R : f (x) = a (a k cos (kx) + b k sin (kx)) mit Koeffizienten a k, b k R a k = 1 π b k = 1 π 2π 0 2π 0 k=1 f (x) cos(kx)dx f (x) sin(kx)dx ( insbesondere a 0 = 1 π 2π 0 f (x)dx ) 87

88 Beispiel: cos Funktion f : R R mit x R : f (x) = 3 cos(2x) x R : 3 cos(2x) = a (a k cos (kx) + b k sin (kx)) mit Koeffizienten: a 2 = 3, k N \ {2} : a k = 0, k N : b k = 0 k=1 88

89 Beispiel: Rechteckschwingung Funktion f : R R mit { 1 falls k Z : x [2kπ, (2k + 1)π) x R : f (x) = 1 falls k Z : x [(2k 1)π, 2kπ) (stückweise konstante Funktion mit Periode 2π) x R : f (x) = a (a k cos (kx) + b k sin (kx)) k=1 mit Koeffizienten k N : a k = 0, k N : b k = 1 π 2π 0 f (x) sin(kx)dx = { 4 kπ falls k 1 (mod 2) 0 sonst also x R : f (x) = 4 π k N k 1 (mod 2) sin (kx) k 89

90 Komplexe Darstellung Transformation von Linearkombinationen reellwertiger trigonometrischer Funktionen in C-wertige Funktionen mit Hilfe der Euler-Identität: x R : e ix = cos(x) + i sin(x) e ikx = cos(kx) + i sin(kx) e ikx = cos(kx) i sin(kx) Darstellung von f : R R als Fourier-Reihe: x R : f (x) = c k e ikx mit den Fourier-Koeffizienten c k = 1 2π f (x)e ikx dx = 2π 0 a 0 /2 falls k = 0 (a k ib k )/2 falls k > 0 (a k ib k )/2 falls k < 0 90

91 Fourier-Reihen periodischer Funktionen (1D) f : R R stückweise stetig und periodisch, d.h. p R x R n Z : f (x) = f (x + np) Darstellung von f : R R als Fourier-Reihe: x R : f (x) = ( ( ) ( )) 2πkx 2πkx a k cos + b k i sin = ) (c k e i 2πkx p p p k Z k Z mit den Fourier-Koeffizienten k Z : c k C mit c k = 1 p p 0 f (x)e 2πkx i p dx = 1 p p/2 p/2 f (x)e 2πkx i p dx Grundfrequenz von f : f p = 1/p c k 0 gdw. Frequenz k/p kommt in f mit Amplitude c k vor (diskretes) Fourier-Spektrum von f : c : Z C mit k Z : c(k) = c k (Folge (c k ) k Z ) anschaulich: f hat einen Frequenzanteil k/p gdw. c k 0 c k ist die Amplitude des Frequenzanteils k/p 91

92 Fourier-Transformation nicht-periodischer Funktionen Idee: Grenzübergang von diskreten Frequenzen 2πk/p R zu kontinuierlichen Frequenzen u R Falls zu einer (nicht notwendig periodischen) Funktion f : R R für jedes u R das Integral R f (x)e iux dx existiert, Fourier-Transformation F : R R C R mit u R : F(f )(u) = f (x)e iux dx F (f ) heißt die Fourier-Transformierte von f (kontinuierliches Fourier-Spektrum) inverse Fourier-Transformation F 1 : C R R R x R : F 1 (d)(x) = d(u)e iux du R R 92

93 Diskrete Fourier-Transformation (1D) gegeben: f : pos R mit pos = {0,..., m 1} Idee: periodische Fortgesetzung von f auf Z (mit Periode m, Frequenz 1/m) diskrete Fourier-Transformation von f : pos R (1-DFT): F : R pos C pos mit u {0,..., m 1} : F(f )(u) = m 1 k=0 f (k)e 2πiku/m inverse Fourier-Transformation von g : pos C: F 1 : C pos R pos mit x {0,..., m 1} : F 1 (g)(x) = m 1 k=0 g(k)e 2πikx/m 93

94 Eigenschaften der 1D-DFT 1D-DFT F : R pos C pos F(f )(x) = m 1 k=0 f (k)e 2πikx/m für alle f : pos R gilt: F(f )(x) = F(f )( x) (symmetrisch) F(f )(x) = F(f )( x) F(f )(x + m) = F(f )(x) (unendlich periodisch) 94

95 Diskrete Fourier-Transformation (2D) gegeben: f : pos R mit pos = {0,..., m 1} {0,..., n 1} periodische Fortgesetzung von f auf Z 2 diskrete Fourier-Transformation von f : pos R (2-DFT): F : R pos C pos mit (u x, u y ) pos : F(f )(u x, u y ) = m 1 n 1 x=0 y=0 2πi(xux /m+yuy /n) f (x, y)e inverse Fourier-Transformation von g : pos C: F 1 : C pos R pos mit (u x, u y ) pos : F 1 (g)(u x, u y ) = m 1 n 1 x=0 y=0 2πi(xux /m+yuy /n) g(x, y)e 95

96 Fourier-Spektren (2D) Fourier-Transformation F : R pos C pos mit (u x, u y ) pos : F(f )(u x, u y ) = m 1 m 1 x=0 y=0 Fourier-Spektrum: Matrix S(f ) R pos mit (x, y) pos : S(f )(x, y) = F(f )(x, y) Leistungs-Spektrum: Matrix L(f ) R pos mit (x, y) pos : P(f )(x, y) = F(f )(x, y) 2 2πi(xux /m+yuy /n) f (x, y)e Phasen-Spektrum: Matrix φ(f ) R pos mit ( ) I(F(f )(x, y)) (x, y) pos : φ(f )(x, y) = tan 1 R(F(f )(x, y)) 96

97 Eigenschaften der 2D-DFT Fourier-Transformation F : R pos C pos mit (u x, u y ) pos : F(f )(u x, u y ) = m 1 m 1 x=0 y=0 2πi(xux /m+yuy /n) f (x, y)e Für alle Funktionen f : pos R gilt: F(f )(0, 0) = max(f ) (mitunter auch avg(f ), je nach Faktor) F(f )(x, y) = F (f )( x, y) (symmetrisch) F(f )(x, y) = F(f )( x, y) f, g : pos R a, b R: F(af + bg)(x, y) = af(f )(x, y) + bf(g)(x, y) (linear) F(f )(x + m, y + n) = F(f )(x + m, y) = F(f )(x, y + n) = F(f )(x, y) (unendlich periodisch in beide Richtungen) 97

98 DFT von Bildern Bild B col pos Fourier-Transformierte F (B) C pos (x, y) pos : F(B)(x, y) = m 1 m 1 x=0 y=0 2πi(xux /m+yuy /n) B(x, y)e mit Ortsfrequenz F(B)(x, y) C Spektrum F(B)(x, y) R ( ) Phase φ(x, y) = tan 1 I(F (B)(x,y)) R(F (B)(x,y)) R 98

99 Anwendung in der Bildverarbeitung Erkennung typischer Bildeigenschaften, z.b. Größe, dominante Richtungen der Strukturen Transformation eines (Gesamt-)Bildes B in drei Schritten: 1. Fourier-Transformation C = F(B) C pos 2. Änderung der Fourier-Transformierten zu C (z.b. Löschen von Teilbildern) 3. inverse Fourier-Transformation B = F 1 (C ) Kanten-Betonung durch Entfernen (Wert 0) niedriger Frequenzen (um Ursprung) Glättung durch Entfernen (Wert 0) hoher Frequenzen (entfernt vom Ursprung) 99

100 Transformationen im Frequenzraum punktweise Transformation f : pos C der Werte der Fourier-Transformierten C C pos durch Multiplikation mit einer Funktion f : pos R Beispiel ( mit Abstand d, z.b. d(u, v) = u 2 + v 2 ): Tiefpass mit Schwellwert (Cut-Off-Frequenz) θ R { 1, falls d(u, v) θ f T (θ) (u, v) = 0 sonst Glättung, aber Ringing-Artefakte möglich 100

101 Mehr Beispiele Hochpass mit Schwellwert (Cut-Off-Frequenz) θ R { 0, falls d(u, v) θ f H(θ) (u, v) = 1 sonst Hervorhebung von Kanten Bandpass mit Schwellwerten θ 1, θ 2 R { 1, falls θ1 d(u, v) θ f B(θ1,θ 2 )(u, v) = 2 0 sonst Bandstop (analog) mit Schwellwerten θ 1, θ 2 R 101

102 Vermeidung von Ringing-Artefakten Idee: Wert (Amplitude) bei steigenden / fallenden Frequenzen stetig (statt stufenförmig) ändern Beispiel: Butterworth-Filter f T (θ) (u, v) = ( d(u,v) θ ) 2n (Tiefpass) analog: f H(θ) (u, v) = 1 ( ) 2n (Hochpass) 1 + θ d(u,v) 102

103 Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Operationen f : pos 1 pos 2 (Koordinatentransformation) Interpolation der Intensitäten 1D- und 2D-Signale (analog, digital) Digitalisierung (Abtastung) von 1D- und 2D-Signalen Aliasing-Effekte Faltung von Signalen (Funktionen) Fourier-Transformierte / inverse Fourier-Transformierte und darin enthaltene Informationen über das Bild Bildtransformationen durch Transformationen im Frequenzraum 103

104 Wiederholung Fourier-Transformation Bild B col pos (im Ortsraum) Diskrete Fourier-Transformation F : col pos C pos (u, v) pos : F (B)(u, v) = m 1 m 1 x=0 y=0 B(x, y)e 2πi(ux/m+vy/n) inverse Fourier-Transformation F 1 : C pos R pos mit (x, y) pos : F 1 (C)(x, y) = 1 mn m 1 n 1 C(u, v)e 2πi(ux/m+vy/n) u=0 v=0 Abbildungen zwischen Ortsraum col pos und Frequenzraum C pos 104

105 Wiederholung Fourier-Transformation Anwendungen der Fourier-Transformation in der Bildverarbeitung: Erkennung typischer Bildeigenschaften, z.b. Größe, dominante Richtungen der Strukturen Transformation eines (Gesamt-)Bildes B col pos in drei Schritten: 1. Fourier-Transformation F (B) = C C pos 2. Änderung der Fourier-Transformierten C C pos durch Multiplikation mit einer Funktion h : (u, v) pos : C (u, v) = F (B)(u, v) h (u, v) (oft Löschen / Abschwächen von Teilbildern durch Multiplikation mit Werten nahe 0 an ausgewählten Stellen) 3. inverse Fourier-Transformation für h = F (h) also B (x, y) = F 1 (F (B) F(h))(x, y) 104

106 Wiederholung Fourier-Transformation Wirkung verschiedener Operationen im Frequenzraum: Entfernen / Abschwächen hoher Frequenzen (kleiner Wellenlängen) Tiefpass-Filter bewirkt Glättung, Entrauschen Entfernen / Abschwächen niedriger Frequenzen (großer Wellenlängen) Hochpass-Filter bewirkt Betonung von Kanten Vermeidung von Ringing-Artefakten 104

107 Ziel: Bildtransformationen im Ortsraum Transformation des Bildes B col pos in drei Schritten 1. Fourier-Transformation F(B) = C C pos 2. Änderung der Fourier-Transformierten C C pos durch Multiplikation mit einer Funktion h: (u, v) pos : C (u, v) = F(B)(u, v) h (u, v) 3. inverse Fourier-Transformation B (x, y) = F 1 (F(B) F(h))(x, y) ersetzen durch eine Operation im Ortsraum h : col pos col pos mit B col pos (x, y) pos : h(b)(x, y) = F 1 (F(B) F(h))(x, y)) 105

108 Faltungssatz Wiederholung: Faltung f g der Funktionen f, g : {0,..., m 1} {0,..., m 1} R ist definiert durch (p x, p y ) {0,..., m 1} {0,..., m 1} : (f g)(p x, p y ) = f (p x x, p y y)g(x, y) (assoziativ, kommutativ, linear) Es gilt der Faltungssatz: f, g : pos col: x= y= (p x, p y ) pos : F (f g)(p x, p y ) = F(f )(p x, p y ) F (g)(p x, p y ) Faltung im Ortsraum entspricht Multiplikation im Frequenzraum also B : pos col h : pos R (p x, p y ) pos : F (B h)(p x, p y ) = F(B)(p x, p y ) F (h)(p x, p y ) = (F(B) F (h))(p x, p y ) und damit B : pos col h : pos R (B h) = F 1 (F(B h)) = F 1 (F(B) F(h)) also Ziel erreicht: Faltung B h ersetzt die Operation (drei Schritte) F 1 (F (B) F (h)) : col pos col pos 106

109 Lineare Filter (B h)(p x, p y ) = mit Koeffizienten h(i, j) häufiger Spezialfall: x= y= B(p x x, p y y)h(x, y) Koeffizienten h(x, y) verschwinden mit größerem Abstand von (0, 0), und außerhalb eines Bereiches (x, y) { k,..., k} 2 gilt h(x, y) = 0 Angabe von h auf dem (quadratischen) Ausschnitt (i, j) { k,..., k} 2 als (2k + 1) (2k + 1)-Matrix genügt Filterkern, Filtermaske, Filtermatrix, Faltungskern (zentriert um Ursprung, oft symmetrisch) dargestellt als Funktion h : pos R mit pos = { k,..., k} 2 R 107

110 Lineare Filter Faltung von Bild B : pos col mit Filtermatrix h( k, k)... h( k, 0)... h( k, k)... h = h(0, k)... h(, 0)... h(0, k)... h(k, k)... h(k, 0)... h(k, k) transformiert jeden Wert B(x, y) zu (B h)(x, y) = B(x i, y j)h(i, j) i= j= k k = B(x i, y j)h( i, j) ( ) i i j j (gespiegelte Filtermatrix) = i= k j= k k k B(x + i, y + j)h( i, j) i= k j= k 108

111 Lineare Filter Beispiele Glättungsfilter (3 3) mit normalisierter Filtermatrix, z.b. h Box = h 9 Circ = h Bin = h Gauss = 1 40 Differenzenfilter (5 5) mit normalisierter Filtermatrix, z.b h Laplace =

112 Lineare Filter Faltung von Bild B : pos col mit (3 3)-Filtermatrix h( 1, 1) h( 1, 0) h( 1, 1) h = h(0, 1) h(0, 0) h(0, 1) h(1, 1) h(1, 0) h(1, 1) transformiert jeden Wert B(x, y) zu B (x, y) = 1 i= 1 j= 1 1 B(x + i, y + j)h( i, j) gewichtete Summe aller Bildpunkte im Bereich (x 1, x, x + 1) (y 1, y, y + 1) (lineare Operation) meist normalisierte Filtermatrizen h mit k k i= k j= k h(i, j) = 1 Normierung (für Beispiel k = 1): h( 1, 1) h( 1, 0) h( 1, 1) 1 k k h(0, 1) h(0, 0) h(0, 1) i= k j= k h(i, j) h(1, 1) h(1, 0) h(1, 1) 110

113 Faltung am Bildrand Problem: B (x, y) = k i= k j= k k B(x + i, y + j)h( i, j) an Randpunkten (x, y) hängt B (x, y) von Werten B(x, y ) an Positionen (x, y ) pos ab. B(x, y ) ist dort nicht definiert. mögliche Lösungen: Randbereiche nicht filtern (Werte B(x, y) bleiben) spezielle Rand-Filtermasken konstante Fortsetzung auf Positionen außerhalb pos schwarzer Rand (Zero-Padding): (x, y) pos : B(x, y) := 0 gespiegelter Rand: (x, y) pos : B(x, y) := B( x, y) (bzw. einem der Werte B( x, y), B( x, y), B(x, y)) periodisch fortgesetzte Werte Interpolation 111

114 Filter zur Kantenverstärkung Ziel: Unterschiede zwischen benachbarten Pixeln verstärken (positive und negative Koeffizienten, Summe aller Koeffizienten = 0) Beispiele: ( ) ( ) Roberts-Operator: und (Summe) Prewitt-Operator: h: v: Sobel-Operator: h: v: Differenz-Filter:

115 Nichtlineare Filter Funktion f : col pos col pos mit (x, y) pos : f (B)(x, y) = f (B(x k, y k),..., B(x + k, y + k)) nicht durch Faltung mit einer Matrix (lineare Funktion) gegeben, sondern nichtlinear Beispiele: Rangordnungsfilter Minimum: f (B)(x, y) = min{b(x k, y k),..., B(x + k, y + k)} Maximum: f (B)(x, y) = max{b(x k, y k),..., B(x + k, y + k)} Median: f (B)(x, y) = med{b(x k, y k),..., B(x + k, y + k)} gewichteter Medianfilter, abhängig von Matrix h : { k,..., k} 2 N, Gewicht (i, j) bestimmt Anzahl der Vorkommen des Wertes B(x + i, y + j) in der Medianliste 113

116 Was bisher geschah digitale Bilder: Funktion B : pos col Matrix B col pos statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Operationen f : pos 1 pos 2 (Koordinatentransformation) Interpolation der Intensitäten Digitalisierung (Abtastung) von 1D- und 2D-Signalen Aliasing-Effekte Faltung von Signalen (Funktionen) Fourier-Transformierte / inverse Fourier-Transformierte und darin enthaltene Informationen über das Bild Operationen im Frequenzbereich Filter zur Glättung, Kanten-Hervorhebung 114

117 Wiederholung Filter Glättungsfilter: Tiefpassfilter (mit Normierung) Mittelwert Gauß 1 10 Median (nichtlinear)

118 oft Linearkombinationen (Matrix-Addition der Filterkerne) 116 Gradienten-Filter (Approximation der 1. oder 2. Ableitung, Hochpass) zur Kanten-Hervorhebung, z.b. horizontale / vertikale Differenzen, z.b. ( 1 1 ) ( 1 1 ) ( Roberts: diagonale Differenzen, z.b. ( ) ( ) ) ( ) Prewitt: Differenzen und Mittelung senkrecht dazu Sobel: Differenzen und Gauß senkrecht dazu

119 Template-Matching Filterung mit mehreren rotierten Filterkernen (für Kanten verschiedener Richtungen) nacheinander Ergebnisbild: punktweise Maximum der Beträge geeignete Filterkerne (besser als Prewitt, Sobel) Kompass-Gradient Kirsch-Operator

120 Laplace-Operator Differenzenfilter, Approximation der 2. Richtungsableitungen Linearkombinationen, z.b = =

121 Transformation von Binärbildern Bild = Matrix B col pos hier Binärbilder mit Farben col = {0, 1} (0 für schwarz, 1 für weiß) Annahmen: Vordergrund und Hintergrund getrennt (z.b. durch Binarisierung mit Schwellwert) Vordergrund weiß (1), Hintergrund schwarz (0) Ziel: Merkmale (z.b. Form) der (weißen) Regionen hervorheben, um Störungen bereinigen, (einzelne Punkte, Löcher, zerklüftete Ränder) erkennen Mustern zuordnen (klassifizieren) 119

122 Morphologische Operationen Idee: Transformation von Binärbildern B {0, 1} pos durch Verknüpfung von B mit bestimmten (geeignet transformierten) Strukturelementen (Masken) durch Mengenoperationen Strukturelement M : pos {0, 1} definiert Bezugspunkt (0, 0) pos (hot spot) relevante Positionen p pos mit M(p) = 1 (an der Mengenoperation mit B beteiligt) irrelevante Positionen p pos mit M(p) = 0 Beispiele:

123 Strukturelemente Form und Bezugspunkt abhängig von gewünschter Wirkung prominente Formen (häufig symmetrisch mit Bezugspunkt in der Mitte): Kreuz (z.b. 4-Nachbarschaft) Quadrat (z.b. 8-Nachbarschaft) Rechtecke mit verschiedenen Positionen des Bezugspunktes Kreise, Ellipsen (diskrete Approximationen) Wiederholung (geometrische Transformationen): Verschiebung V p (B) : {0, 1} pos {0, 1} pos um p = (p x, p y ) pos (x, y) pos : V p (B)(x, y) = (x + p x, y + p y ) 121

124 Erosion gegeben: B : pos {0, 1} Strukturelement M : pos {0, 1} Erosion: Bildpunkt p weiß (Vordergrund) gdw. alle relevanten Positionen des mit dem Bezugspunkt in p verschobenen Strukturelementes weiß B M = {p pos V p (M) B} = {p pos V p (M) B = } p pos : (B M) = min{b(q) q V p (M)} = min{b(q) (V p (M))(q) = 1} { 1, falls q Vp (M) : B(q) = 1 = 0 sonst 122

125 Erosion Beispiel B = M = 1 1 B M =

126 Erosion Eigenschaften nicht kommutativ: B, M : B M M B nicht assoziativ: B, M, M : (B M) M B (M M ) Wirkung: Abtragen der Vordergrundregionen an Randpunkten kleinen isolierten Punktgruppen konvexen Randbereichen Erosion mit quadratischem Strukturelement: Minimum-Filter 124

127 Dilatation gegeben: B : pos {0, 1} Strukturelement M : pos {0, 1} Dilatation: Bildpunkt p weiß gdw. wenigstens eine relevante Position des mit dem Bezugspunkt in p verschobenen Strukturelementes weiß B M = {p pos V p (M) B } p pos : (B M)(p) = max{b(q) q V p (M)} = max{b(q) (V p (M))(q) = 1} { 1, falls q Vp (M) : B(q) = 1 = 0 sonst 125

128 Dilatation Beispiel B = M = 1 1 B M =

129 Dilatation Eigenschaften kommutativ: B, M : B M = M B assoziativ: B, M, M : (B M) M = B (M M ) Wirkung: Auffüllen von Vordergrundregionen an konkaven Randbereichen Löchern Dilatation mit quadratischem Strukturelement: Maximum-Filter 127

130 Beziehungen zwischen Erosion und Dilatation Für alle Bilder B {0, 1} pos und alle Strukturelemente M, M {0, 1} pos mit 1 im Referenzpunkt gilt: B M B B M (B M) M = B (M M ) B M = B M B M = B M Kombinationen von Erosions- und Dilatationschritten: Opening, Closing 128

131 Morphologisches Öffnen (Opening) gegeben: B : pos {0, 1} Strukturelement (Maske) M : pos {0, 1} Opening B M = (B M) M M : Strukturelement M am Referenzpunkt gespiegelt (um 180 gedreht) Wirkung: Dilatation macht die Verkleinerung der die Erosion überlebenden (hellen) Regionen rückgängig Beseitigung von kleinen oder schmalen hellen Bereichen (falsch als Vordergrund interpretierte Stellen) Trennung von gerinfügig verbundenen (hellen) Regionen 129

132 Opening Beispiel B = M = 1 1 B M = B M = (B M) M mit M = 1 1 B M =

133 Morphologisches Schließen (Closing) gegeben: B : pos {0, 1} Strukturelement (Maske) M : pos {0, 1} Closing B M = (B M) M M : Strukturelement M am Referenzpunkt gespiegelt (um 180 gedreht) Wirkung: Erosion macht die Ausdehnung der (hellen) Regionen bei Dilation rückgängig Beseitigung von kleinen oder schmalen dunklen Bereichen (Störungen in Vordergrund-Regionen) Verbindung nahe benachbarter Vordergrundregionen 131

134 Closing Beispiel B = M = 1 1 B M = B M = (B M) M mit M = 1 1 B M =

135 Beziehungen zwischen morphologischem Öffnen und Schließen Für alle Bilder B, C {0, 1} pos und alle Strukturelemente M {0, 1} pos gilt B M B B M (B M) M = (B M) (B M) M = (B M) A M = A M A M = A M A M = A M A M = A M B C gdw. (B M C M) (B M C M) Beseitigung größerer Störungen durch geeignete Folgen von Öffnen- und Schließen-Schritten 133

136 Was bisher geschah digitale Bilder B : pos col statistische Merkmale Punktoperationen f : col 1 col 2 (Bildanalyse) (Farbtransformation) Geometrische Transformationen f : pos 1 pos 2 Interpolation der Intensitäten Digitalisierung (Abtastung) von 1D- und 2D-Signalen Faltung von Signalen (Funktionen) Fourier-Transformierte / inverse Fourier-Transformierte Operationen im Frequenzbereich, Filter Morphologische Operationen auf Binärbildern: Erosion, Dilatation, Opening, Closing 134

137 Morphologische Operationen auf Grauwertbildern Bild col pos mit Farbbereich col = {0,..., k} statt {0, 1} Übergang von charakteristischer Funktion B : pos {0, 1} zu Funktion B : pos {0,..., k} geeignete Erweiterungen der Mengenoperationen (punktweise Boolesche Operationen) vom Farbbereich {0, 1} auf {0,..., k}, z.b.: min max λx.k x (für Spezialfall k = 1 genau die Booleschen Operationen) 135

138 Beispiel: Erosion von Grauwertbildern gegeben: B : pos {0,..., k} Strukturelement (Maske) M : pos {0, 1} Erosion: p pos : (B M)(p) = min{b(p + v) M(v) = 1} Wirkung: Verdunklung der hellen Regionen (Vordergrund) (ähnlich Minimum-Filter mit Strukturelement) Dilatation: p pos : (B M)(p) = max{b(p + v) M(v) = 1} Opening, Closing damit analog zu Binärbildern 136

139 Hit-or-Miss-Transformation auf Binärbildern Ziel: Identifizierung von im Bild vorkommenden Pixelmustern mit Toleranz, z.b. Linien der Länge von... bis... Idee: Schnitt von 1. Erosion des Bildes mit Positiv-Maske M 1 zur Beseitigung aller zu kleinen Vordergrund-Regionen (Hit-Transformation) 2. Erosion des invertierten Bildes mit Negativ-Maske (Umriss) M 2 zur Beseitigung aller zu großen Vordergrund-Regionen (Miss-Transformation) gegeben: B : pos {0, 1} Strukturelemente M 1 : pos 1 {0, 1}, M 2 : pos 2 {0, 1} mit M 1 M 2 = Hit-or-Miss-Transformation: B (M 1, M 2 ) = (B M 1 ) (B M 2 ) 137

140 Beispiel B = B = M 1 = M 2 = B M 1 = B M 2 = (hier mit Randfortsetzung in B durch 0 und B durch 1) B (M 1, M 2 ) = (B M 1 ) (B M 2 ) = {(6, 2)} 138

141 Hit-or-Miss-Transformation Hit-or-Miss-Transformation: B (M 1, M 2 ) = (B M 1 ) (B M 2 ) = (B M 1 ) B M 2 Zusammenfassung von Hit-Maske M 1 : pos {0, 1} und Miss-Maske M 2 : pos {0, 1} mit pos = { m,..., m} { n,..., n} (gleiche Größe, ggf. um 0 erweitern) zu spezieller Hit-or-Miss-Maske M : pos {0, 1, } möglich: { p pos M1 (p), falls M : M(p) = 2 (p) = 1 M 1 (p), sonst 139

142 Hit-or-Miss-Transformation Beispiel M 1 = M 2 = M = B = B M = (hier mit Randfortsetzung in B durch 0)

143 Hit-or-Miss-Transformation ermöglicht Erkennung spezieller Strukturen im Bild, z.b. M 1 = M 2 = M 3 = M 4 = M 5 = isolierte Punkte untere rechte Ecken linker Rand, Zusammenhangs-erhaltend Thickening: B (B M) (konvexe Hülle) untere Endpunkte 141

144 Wirkung morphologischer Operationen gegeben: Bild B : pos {0, 1} Strukturelement M : pos {0, 1}, (markiert relevante Pixel) Erosion: Abtragung (Verkleinerung der Vordergrund-Regionen) Minimum über alle relevanten Pixel Dilatation: Anlagerung (Vergrößerung der Vordergrund-Regionen) Maximum über alle relevanten Pixel Opening: morphologisches Öffnen, 1. Entfernen kleiner Vordergrundeobjekte 2. Wiederherstellung der größeren Objekte auch zum Finden von Regionen bestimmter Form Closing: morphologisches Schließen 1. Entfernen kleiner Vordergrund-Störungen 2. Wiederherstellung des Vordergrund ohne Störung Hit-or-Miss: Finden von Regionen bestimmter Form mit Toleranzbereich 142

145 Regionen im Bild Region R pos im Bild B : pos {0, 1} (bzgl. einer Nachbarschaft zusammenhängend) Annahmen: jede Region hat eine Bedeutung, Positionen in einer Region gehören zur selben Bedeutung Erkennung von Regionen (semantische Einheiten) durch Gemeinsamkeiten aller Positionen(-gruppen) innerhalb der Region, z.b. Intensität, Farbe, Textur Unterschieden zwischen benachbarten Positionen(-gruppen), Erkennung der Grenzen der Region Merkmale von Regionen R: Kontur K (R): Menge der Randpixel (verschiedene Codierungen, z.b. Freeman-Kettencode, Differential-Code) Skelett S(R): topologieerhaltendes Bild aus Linien von 1 Pixel Dicke 143

146 Beschreibung von Regionen Darstellung als Menge aller zur Region gehörenden Positionen Kontur (Positionen am Rand der Region) Skelett (zentrale Positionen der Region) Verfahren zur Erkennung zusammenhängender Regionen Menge von Positionen: 1. Schwellwert-Verfahren, 2. Identifikation zusammenhängender Positionsmengen Kontur: Konturbestimmung Skelett: Skelettierung morphologische Operationen hilfreich 144

147 Konturen von Regionen Region R pos Rand (Kontur) von R: K (R) Menge aller Positionen p pos mit 1. p R und 2. in der (geeignet definierten) Nachbarschaft von p existiert (wenigstens) ein q mit p R Rand in 4-Nachbarschaft: geschlossener Pfad in 8-Nachbarschaft 8-Nachbarschaft: geschlossener Pfad in 4-Nachbarschaft 145

148 Konturbestimmung K = B \ (B M) = B B M Beispiel: Bestimmung des Randes in 4- bzw. 8-Nachbarschaft durch 1. Erosion mit Strukturelement M 4 = M 8 = (entfernt alle Pixel, deren 4- bzw. 8-Nachbarschaft wenigstens einen Punkt außerhalb der Region enthält) 2. Differenz zwischen Original- und erodiertem Bild enthält genau alle Randpunkte (innerhalb der Region) analog lässt sich definieren: Randpunkte außerhalb der Region K = (B M) \ B = (B M) B 146

149 Konturbestimmung Beispiel B = B M 4 = B \ (B M 4 ) =

150 Abstände zwischen Positionen Abstandsfunktion d : pos R mit den Eigenschaften: p, q pos : d(p, q) = 0 gdw. p = q p, q pos : d(p, q) = d(q, p) (kommutativ) p, q, r pos : d(p, q) + d(q, r) d(p, r) (Dreiecksungleichung) Beispiele: für pos = {0,..., m} {0,..., n} und k N: p = (p z, p s ), q = (q z, q s ) pos : d k (p, q) = k (p z q z ) k + (p s q s ) k für k = 2: d 2 (p, q) = 2 (p z q z ) 2 + (p s q s ) 2 Euklidischer Abstand für k = 1: d 1 (p, q) = p z q z + p s q s Manhattan-Metrik (minimale Anzahl der zu einem p und q verbindenden Pfad in 4-Nachbarschaft notwendigen Positionen) für k : d (p, q) = max ( p z q z, p s q s ) Maximum-Metrik (minimale Anzahl der zu einem p und q verbindenden Pfad in 8-Nachbarschaft notwendigen Positionen) 148

151 Distanztransformation von Binärbildern ordnet jeder Position innerhalb einer Region den kürzesten Abstand zum Rand der Region zu (Abstand bzgl. gegebener Nachbarschaftsrelation) Idee: wiederholte Erosion des Binärbildes B pos Distanzmaß ordnet jeder Position p in einer Region R B 1 (1) die Anzahl der Erosionen bis zur Entfernung von p aus B zu (geeignet definierter Mindestabstand zum Rand K (R)) d B : pos N mit p pos : d B (p) = 0, falls p B 1, falls p B \ B M. k + 1, falls p B( M) k \ B( M) k+1 übliche Visualisierung: Distanzbild Intensität von p B umgekehrt proportional zu d B (p) 149

152 Distanztransformation Beispiel

153 Skelette von Regionen Ziel: Reduktion der Vordergrundregionen zu Linien unter Beibehaltung wichtiger topologischer Merkmale (z.b. Zusammenhang, Löcher) Anwendungen zur Beschreibung von Regionen, für die das Vorhandensein von Linien relevant ist, deren Breite jedoch nicht z.b. Straßen-, Gesten-, Zeichenerkennung (OCR) 151

154 Skelett von Regionen Anforderungen Skelett ist Teilmenge der Region Erhaltung der Zusammenhangseigenschaften der Region Skelett ist minimal, d.h. keine weiteren Punkte können entfernt werden, ohne Zusammenhang zu zerstören bevorzugt Mittelachsen M der Vordergrundregionen (gleicher Abstand zu den nächsten Randpunkten) 152

155 Skelettierung Idee mehrfach wiederholtes Entfernen von (weißen Vordergrund-) Positionen, bis nur noch Skelett weiß nur Entfernung der Punkte, die nicht zum Skelett gehören Identifikation typischer Pixelmuster für Skelettlinien (Enden, Verzweigungen von Linien von 1 Pixel Breite) Identifikation typischer Pixelmuster (Enden, Verzweigungen) für Linien größerer Breite Hit-or-Miss-Transformation mit geeigneten Strukturelementen (Pixelmustern) zur Identifikation zu breiter Bereiche Entfernen der gefundenen Positionen aus dem Bild 153

156 Thinning (Verdünnung) Strukturelmente zur Identifikation zu breiter Bereiche M o = M r = M u = M l = M or = M ur = M ul = M ol = Thinning: Wiederholte Folge dieser 8 Hit-or-Miss-Transformationen nacheinander (4 achsenparallel und 4 diagonal) zur Entfernung von Randpositionen ohne Verletzung des Zusammenhanges 154

157 Thinning Schritte gegeben: Region R pos Verfahren: in jedem Schritt: für jede der 8 Hit-or-Miss-Masken M i (nacheinander): 1. Hit-or-Miss-Transformation: (B M i ) 2. passende Bereiche aus B entfernen: B \ (B M i ) Verfahren endet, wenn in einem Schritt (Anwendung aller 8 Hit-or-Miss-Transformationen) kein Pixel geändert wurde mögliche Vor- und Nachbereitung: vor Beginn: Distanztransformation (Speichern der Distanzwerte für jedes p R) vor Ende: Distanzwert jedes Skelettpunktes p ist Radius des größten Kreises um p, der vollständig in B enthalten ist häufige Nachbearbeitung bei Skelettierung: Entfernung von Verzweigungen an den Linienenden 155

158 Thinning Anwendungen Skelettierung nach Detektion von Randbereichen (z.b. mit Sobel-Filter): Verdünnung der Kanten Schrifterkennung Probleme: empfindlich gegenüber kleinen Störungen, z.b. Rauschen, Binarisierungsungenauigkeiten erzeugtes Skelett enthält kurze Ausläufer an den Enden 156

159 Thickening (Verdickung) analog zum Thinning Auffüllen konkaver Randbereiche durch wiederholte Anwendung einer Folge von 8 Hit-or-Miss-Transformationen, z.b. M 1 = M 2 = M 3 = M 4 = M 5 = M 6 = M 7 = M 8 = Ergebnis: Approximation der konvexen Hüllen von Regionen 157

160 Was bisher geschah Definition digitaler Bilder B : pos col Bildanalyse, statistische Merkmale Signale im Orts- und Frequenzraum Bildbearbeitung durch Punktoperationen (Farbtransformation) f : col 1 col 2 (punktweise Fortsetzung auf Gesamtbild) geometrische Transformationen (Koordinatentransformation) f : pos 1 pos 2 lokale Operationen (abhängig von Nachbarschaft): Filter, morphologische Operationen Merkmale von Regionen im Bild: Kontur Distanzbild Skelett 158

161 Regionen Region: zusammenhängende Gruppe von Positionen Segmentierung: Extraktion und Trennung von Regionen im Bild Annahmen: jede Region hat eine Bedeutung, Positionen in einer Region haben dieselbe Bedeutung, verschiedene Regionen haben verschiedene Bedeutung z.b. enthalten verschiedene Objekte, Teile Erkennung von Regionen (semantische Einheiten) durch gemeinsame Eigenschaften aller Pixel oder Pixelgruppen der Region, z.b. Intensität, Farbe, Textur signifikanten Unterschieden zwischen benachbarten Positionen (Erkennung der Konturen) 159

162 Segmentierung Anforderungen gegeben: gesucht: Bild B : pos col endliche Menge R = {r 1,..., r n } von Regionen mit i {1,..., n} : r i pos und den folgenden Eigenschaften: Menge R = {r 1,..., r n } aller Regionen bildet eine Zerlegung von pos, d.h. 1. i {1,...,n} r i = pos 2. i, j {1,..., n} : i j r i r j = Jede Region r R ist zusammenhängend (bildet eine Zusammenhangskomponente im Nachbarschaftsgraphen) Darstellung der Segmentierung (Zerlegung): Region r pos: endliche Menge von Bild-Positionen, Segmentierung R = {r 1,..., r n }: endliche Menge von Regionen (endlichen Mengen von Bild-Positionen), Zuordnung r : pos R von Bild-Postionen p pos zu Regionen 160

163 Segmentierung Verfahren Punkt-basiert: Zuordnung pos R anhand des Wertes B(p) col und evtl. Merkmale des Bildes / der Region (Schwellwertverfahren, evtl. adaptiv, verschiedene Schwellwerte für verschiedene Bildbereiche) Zusammenhangs-basiert: Zuordnung pos R anhand von Merkmalen in Nachbarschaft von p pos Regionen-orientiert: Erkennung zusammenhängender Regionen (Homogenität) meist aus dem Inneren heraus Form-orientiert: Finden von Regionen bekannter Form und Ausdehnung (z.b. durch morphologische Operationen mit geeigneten Strukturelementen: Opening, Hit-or-Miss) Kanten-orientiert: Erkennung der Regionengrenzen (Diskontinuität) Erkennung von Randpositionen z.b. durch Fourier-Transformation, Filter, morphologische Operationen 161

164 Homogenitätskriterien Ähnlichkeiten einzelner Positionen, z.b. Intensität Farbe (Kombination von Intensitäten) z.b. Mittelwerte, Intensitäts-Verhältnisse Texturen (charakteristische Intensitätsverteilungen) von Gruppen von Positionen häufig verwendete Texturmerkmale: statistische Merkmale Co-Occurrenz-Matrix Fourier-Spektrum 162

165 Gebietswachstum (Region Growing, flood fill) zur Erkennung zusammenhängender Regionen Idee: Wiederholung der folgenden Schritte, solange noch Positionen ohne Regionenzuordnung existieren: 1. Beginn mit beliebiger (noch nicht einer Region zugeordneter) Startposition p pos, für die auch noch kein Nachbar einer Region zugeordnet ist, 2. neue Region r initialisieren, p zu r hinzufügen 3. rekursiv: alle zu p ähnlichen Nachbarn von p zu r hinzufügen abhängig von: Nachbarschaftsrelation N pos pos Ähnlichkeitsrelation S col col (bzw. col m n col m n ) z.b. Intensität, Farbe, Textur Startpositionen z.b. Position mit minimalem Abstand von (0, 0) pos, interaktiv, zufällig, Erfahrungswerte, Cluster-Schwerpunkte je nach Anwendung, Bildqualität,... verschieden 163

166 Markierung zusammenhängender Regionen (Region Labeling, Connected component labeling) Bestimmen und gleichzeitiges Zählen der Regionen ordnet jeder Region (Vordergrund) eines Binärbildes eine eindeutige Markierung zu Idee: einfache Modifikation des Region-Growing-Verfahrens vor Beginn Initialisierung aller Positionen mit Markierung 0 (noch nicht zugeordnet) für jede neu angelegte Region Markierung (Zähler) um 1 erhöhen Markierung an hinzugefügte Nachbarn übergeben praktisch häufig (zeilenweise) Markierung in zwei Phasen: 1. provisorische Markierung 2. Verschmelzen verbundener Regionen (Ummarkierung) 164

167 Multiskalen-Strategien Ziel: Bildanalyse in verschieden Größen (Auflösungsstufen) wenig aufwendige Untersuchung grober Strukturen feinere Untersuchung feiner Strukturen im Bild Idee: Multiskalenraum (ähnlich menschlicher Wahrnehmung) enthält Originalbild B 0 und weniger detaillierte Versionen B k Erzeugung der Multiskalen-Bilder (Pyramiden) (B 0, B 1, B 2,...) durch wiederholte Ausführung der Schrittfolge 1. Glättung (durch Tiefpass-Filter, z.b. Gauß-Filter) 2. reduce: Komprimierung durch geringere Abtastrate, z.b. Gauß-Pyramide: Löschen jeder zweiten Zeile und Spalte 3. expand: Umkehrung durch Interpolation (nicht verlustfrei) zur Vergleichbarkeit der Bilder verschiedener Auflösungen Laplace-Pyramide (redundanzarme Darstellung): Schichten enthalten Differenz zwischen Bild B k und expand(reduce B k ) 165

168 Region-Merging zur Erkennung zusammenhängender Regionen Idee: Regionen-Adjazenz-Graph (RAG) Beginn: jede Bildposition ist eine Region (Knoten) und hat Kanten zu jedem Nachbarn wiederholte Vereinigung benachbarter Regionen mit gleichen / ähnlichen Eigenschaften (Homogenitätsbed.), (Verschmelzen der Knoten benachbarter ähnlicher Regionen) Ende, sobald keine Änderung mehr eintritt (nur noch Kanten zwischen unähnlichen Regionen) nebenbei möglich: Zuordnung eindeutiger Markierungen zu den Regionen (Region Labeling) und damit auch das Zählen der Regionen (Anzahl der verbliebenen Markierungen) 166

169 Split-and-Merge-Verfahren zur Erkennung zusammenhängender Regionen Idee: Region-Merging mit Multiskalen-Strategie Region-Merging mit Regionen verschiedener Größen Beginn: gesamtes Bild bildet eine Region wiederholte Auführung folgender Schitte: split: rekursive Zerlegung inhomogener Regionen in Teilbilder (Quadranten) (Quad-Tree mit Regionen als Blättern) merge : Vereinigung benachbarter Regionen mit gemeinsamer Eigenschaft, solange möglich Ende, sobald keine Änderung mehr eintritt 167

170 Merkmale von Regionen im Bild Region R pos im Bild B : pos {0, 1} (bzgl. einer Nachbarschaft zusammenhängend) Merkmale (Features): topologische Merkmale quantitative Merkmale Formmerkmale geometrische Merkmale ideal: Merkmale invariant gegenüber Verschiebung, Drehung, Skalierung, Verzerrung 168

171 Topologische Merkmale Kontur: Menge der Randpixel (verschiedene Codierungen) Skelett: topologieerhaltendes Bild aus Linien von 1 Pixel Dicke Zusammenhangseigenschaften Anzahl von Löchern (Euler-Zahl = Regionen - Löcher ) Kontur der konvexen Hülle 169

172 Quantitative Merkmale Länge, Breite Flächeninhalt A(R): Anzahl der Positionen in der Region Umfang der Kontur: U(R): Länge, Anzahl der Randpositionen (evtl. verschieden gewichtet) Durchmesser: größter (minimaler Umkreis), kleinster (maximaler Inkreis) Masse: Summe der Intensitäten aller Pixel der Region 170

173 Geometrische Merkmale Verhältnisse Seitenverhältnis: des kleinsten umschließenden (achsenparallelen) Rechtecks (bounding box) Kompaktheit: Verhältnis A(R) : U(R) Kreisförmigkeit: 4πA(R)/U(R) 2 fill factor: Verhältnis A(R) : Fläche der Bounding-Box Dichte: Verhältnis A(R) : Fläche der konvexen Hülle der Region Konvexität: Verhältnis U(R) : Umfang der konvexen Hülle der Region Symmetrien Projektionen (z.b. Linescans) 171

174 Statistische Merkmale Schwerpunkt s x (R) = 1 A(R) s y (R) = 1 A(R) r R r R r x r y Intensitäts-Schwerpunkt von Regionen in Bildern B : pos col s x(r) 1 = r R B(r) r x B(r) r R s y(r) 1 = r R B(r) r y B(r) r R 172

175 Momente (Region als 2d-Verteilung) Momente der Region R im Bild B : pos col m pq (R) = r R B(r)r p x r q y Momente der Region R B im Binärbild B : pos {0, 1} m pq (R) = r R r p x r q y Beispiele (für Binärbilder): m 00 (R) = r R r x 0 ry 0 = r R 1 = A(R) s x (R) = 1 A(R) r R r x 1 ry 0 = m 10 (R), s y (R) = 1 A(R) r R r x 0 ry 1 = m 01 (R) 173

176 Zentrale Momente Idee: Verschiebungs-Invarianz um Schwerpunkt zentrale Momente der Region R B: µ pq (R) = r R B(r)r p x s x (R) r q y s y (R) Verschiebungs-, aber nicht Größen-invariant Größen-invariante zentrale Momente der Region R B: µ pq(r) = µ pq (R) µ 00 (R) (p+q+2)/2 Daraus lassen sich weitere häufig verwendete Merkmale berechnen, z.b. Orientierung, Exzentrizität, Hu-Momente. 174

177 Was bisher geschah Definition digitaler Bilder B : pos col Bildanalyse, statistische Merkmale Signale im Orts- und Frequenzraum Bildbearbeitung durch Punktoperationen (Farbtransformation) f : col1 col 2 (punktweise Fortsetzung auf Gesamtbild) geometrische Transformationen (Koordinatentransformation) f : pos 1 pos 2 lokale Operationen (abhängig von Nachbarschaft): Filter, morphologische Operationen Segmentierung: Erkennung von Regionen im Bild punktbasiert, z.b. Schwellwertverfahren regionenbasiert, z.b. region growing (kantenbasiert) Merkmale von Regionen: quantitativ, z.b. Ausdehmungen, Fläche, Konturlänge topologisch, z.b. Kontur, Skelett, Zusammenhang geometrisch, z.b. Seitenverhältnisse, Symmetrien statistisch, z.b. Schwerpunkt, Momente 175

178 Extraktion von Konturen Darstellung von Konturen: gegeben: Menge von Positionen P pos (mit großen Unterschieden zu Nachbarpositionen) gesucht: geschlossene Kontur zusammenhängende Menge (bzgl. einer Nachbarschaft) Repräsentation von Konturen: Menge aller Kontur-Positionen K pos Freeman-Kettencode Polygonzug (Folge von Streckenabschnitten) Folge von Kurvenabschnitten 176

179 Repräsentation von Konturen durch Kettencodes Folge von Richtungen beim Umrunden der Kontur (entgegen Uhr) N 4 (p) = N 8 (p) = Beispiel: C 4 (R) = , C 8 (R) = D 8 (R) = 00111( 2)210201( 2)1 ermöglicht Kompression und einfache Nachbearbeitung, z.b. Konturglättung, Bestimmung von Randpunkten hoher Krümmung 177

180 Modellbasierte Segmentierung gezielte Suche nach Regionen mit bekannten Merkmalen im Bild übliche Verfahren verwenden Merkmale der gesuchten Regionen (z.b. durch Hit-and-Miss-Transformation, Ähnlichkeit der topologischen, geometrischen und statistischen Merkmale) Merkmale der Kontur der gesuchten Regionen, (z.b. durch Ähnlichkeit der Kettencodes) Merkmale von Standard-Konturteilen, z.b. (Ausschnitte von) Geraden, Kreise, Ellipsen (Hough-Transformation) 178

181 Finden von Geraden Idee Annahme (Modell): gesuchte Konturteile = Geraden(abschnitte) im Bild Idee (Voting-Verfahren): Gerade in R 2 : g = {(x, y) R 2 y = mx + n} Voting: für jede potentielle Gerade g im Bild B: Zählen der Kontur-Positionen (p x, p y ) pos mit p y mp x + n Geraden, auf denen sehr viele Konturpunkte liegen, enthalten wahrscheinlich Streckenabschnitte im Bild Zählen in Akkumulator-Zellen: Punkt (m, n) R 2 repräsentiert Gerade g = {(x, y) R 2 y = mx + n} Problem: senkrechte Geraden nicht darstellbar, kommen aber häufig in Bildern vor 179

182 Hough-Raum (für Geraden) Idee (Hough, 1962): alternative Geraden-Darstellung (Hesse-Normalform) g = {cos(α)x + sin(α)y d = 0} mit α [0, 2π] Winkel von g zur x-achse (Normale) d R 0 Abstand von g zu (0, 0) R 2 (maximaler Abstand durch Bildgröße bestimmt) Hough-Raum: H = [0, 2π] R 0 Geraden im R 2 repräsentiert durch Punkte (α, d) H Jeder Punkt p = (p x, p y ) R 2 liegt auf unendlich viele Geraden im R 2. Jeder Punkt p = (p x, p y ) R 2 entspricht der Kurve d(α) = p x cos(α) + p y sin(α) im Hough-Raum H. Die Gerade durch p und q in R 2 entspricht dem Schnittpunkt der H-Kurven der Punkte p und q. Schnittpunkte vieler Kurven im Hough-Raum deuten auf Geraden(abschnitte) im Bild hin 180

183 Hough-Transformation (für Geraden) modifiziertes Voting-Verfahren: Akkumulator-Zellen (Repräsentation der Geraden): Hough-Raum H = [0, 2π] R 0 für jede (potentielle) Kantenposition p pos: Wert jeder Akkumulatorzelle auf H-Kurve von p erhöhen hohe akkumulierte Werte in (α, d) H) entsprechen Geraden im Bild Hough-Transformation ist robust gegenüber Unterbrechungen, verdeckte Bereiche, Rauschen und damit geeignet z.b. zur Erkennung Ergänzung (Fortsetzung) teilweise sichtbarer gerader Konturbereiche (z.b. Fahrbahnmarkierungen) 181

184 Weitere Hough-Transformationen analoge Verfahren für andere geometrische Formen Kreise c = {(x, y) R 2 (x m x ) 2 + (y m y ) 2 r = 0} Parameterraum (m x, m y, r) pos R 0 (3dimensional) (Dimensionsreduktion bei bekanntem Radius) Ellipsen (5dimensional) c = {(x, y) R 2 ax 2 + by 2 + cxy + dx + ey 1 = 0} (Reduktion auf kleinere Dimensionen möglich) andere parametrisch darstellbare Kurven 182

185 Kantenbasierte Segmentierung Kanten / Konturen: meist starke Unterschiede in Intensität, Farbe oder Textur innerhalb kleiner Nachbarschaften Vorsicht: Unterschiede haben mitunter andere Ursachen, z.b. Schatten Schritte der kantenbasierten Segmentierung: 1. Kantenextraktion (Finden potentieller Kantenpunkte) z.b. durch Filter, morphologische Operationen Ergebnis: Menge von Positionen (evtl. gewichtet) 2. Kantenverfolgung: Zusammenfügen von Kanten zu geschlossenen Konturen (dabei evtl. Lücken schließen) z.b. Edge linking, Canny-Edge-Detector 3. Bestimmung / Markierung der Regionen innerhalb der Konturen 183

186 Edge-Linking gegeben: gesucht: Idee: Bild B : pos col, Menge P pos von potentiellen Kantenpositionen (z.b. durch Filter, morphologische Operationen) zusammenhängende Menge K pos von Positionen (Konturen) systematische Untersuchung aller potentiellen Kantenpositionen in P jeweils Suche nach Kantenpositionen in einer Nachbarschaft in bisheriger Kantenrichtung (parametrisiert durch Richtungsabweichung und Abstand) dabei Konstruktion einer zusammenhängenden Menge K der tatächlichen Kantenpositionen evtl. auch durch Einfügen kurzer Verbindungen zwischen Kantenpositionen 184

187 Edge-Linking-Algorithmus Beginn an beliebiger potentieller Kantenposition p P Wiederholung, solange P 1. Auswahl eines beliebigen p P, 2. p zu (neuem) Konturabschnitt K hinzufügen, 3. zu p (in bisheriger Kantenrichtung) benachbarte Positionen q pos mit ähnlichen Kanteneigeschaften (Richtung, Intensität) zu P und K hinzufügen, 4. p aus P entfernen, Ende, wenn alle Kantenpositionen in P verarbeitet Ergebnis abhängig von (richtungsabhängiger) Nachbarschaftrelation Ähnlichkeitbedingung Nachbearbeitung möglich, z.b. isolierte Kantenpositionen entfernen Kantenverdünnung / Skelettierung 185

188 Canny-Edge-Detector 1. Glättung mit Gauß-Filter (Tiefpass, Entrauschen) z.b oder Kantendetektion (Sobel-Filter) , Bestimmung der Richtung (aus den in 2. berechneten partiellen Ableitungen) und der Stärke der Kante 4. Reduktion der Kanten auf Breite 1 (Pixel) Entfernen der Nachbarpixel senkrecht zur Kantenrichtung mit geringerer Intensität (non-maximal suppression) 5. Kantenverfolgung mit zwei Schwellwerten (Hysterese) zur Trennung: sicherer / unsicherer / kein Kantenpixel 6. Zuordnung der unsicheren Kantenpunkte durch (Versuch der) Verbindung mit benachbarten sicheren Kantenpunkten Ausgangspunkt: sicherer Kantenpunkt unsichere 8-Nachbarn in Kante aufnehmen, wenn Verbindung nur durch sichere Nachbarn nicht möglich ist 186