Lösungsblatt 2 Signalverarbeitung und Klassifikation
|
|
|
- Guido Friedrich
- vor 7 Jahren
- Abrufe
Transkript
1 Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 06 M. Sperber S. Nguyen Lösungsblatt Signalverarbeitung und Klassifikation Aufgabe : Faltung Abbildung : Faltung a) Bestimmen Sie die Faltung der Funktion f(x) mit sich selbst (f(x) f(x)) rechnerisch. Rechnung: f(x) f(x) = f(t)f(x t)dt () Gemäß der Definition der Faltung erhält man die Faltung von f(x) mit sich selbst durch die Integration von f(t) mit der gespiegelten Funktion f( t). Bildlich gesprochen wird für die Integration f( t) von links über f(t) geschoben. Lösungsblatt zu Kognitive Systeme Seite
2 Fallunterscheidung: Fall : x < 0 f(t) f(x t)dt = 0 Fall : Wenn die gespiegelte Funktion f( x) (rotes Quadrat) über f(x) (blaues Quadrat) geschoben wird, entsteht ein Bereich der Überlappung (lila Quadrat). 0 x < f(t) f(x t)dt x = dt = x 0 Fall 3: x = x f(t) f(x t)dt dt = x + Lösungsblatt zu Kognitive Systeme Seite
3 Fall 4: x > f(t) f(x t)dt = 0 Das Faltungsergebnis ist demnach: b) Bestimmen Sie f(x) g(x) grafisch. Rechnung: f(x) g(x) = g(t) f(x t)dt () Lösungsblatt zu Kognitive Systeme Seite 3
4 Fallunterscheidung: Fall : x < 0 g(t) f(x t)dt = 0 Fall : 0 x < = x 0 g(t) f(x t)dt t dt = x Fall 3: x < = = x ] [ t g(t) f(x t)dt t dt + x x dt + x = x + x Fall 4: x g(t) f(x t)dt = x dt = t x = x + 3 Ausgehend von den vorangegangenen Berechnungen kann das Faltungsergebnis wie folgt visualisiert werden: Lösungsblatt zu Kognitive Systeme Seite 4
5 = i δ(f + 400) i δ(f 400) + δ(f + 00) + δ(f 00) (3) Onlinefrage Nr. : Was ist der größte Wert des Ergebnisses der Faltung f(x) g(x)? i) 0,5 ii) 0,75 iii),0 iv),5 v),5 Der größte Wert des Ergebnisses der Faltung f(x) g(x) ist, siehe Lösung der Aufgabe b). Aufgabe : Digitalisierung von Signalen Gegeben sei die Funktion f(t) = sin(π400t) + cos(π00t) Hinweise: Zur Vereinfachung sei in der Zeichnung die Höhe von δ =. Zur Fouriertransformation existieren diverse Konventionen! Lassen Sie sich davon nicht verwirren und verwenden Sie zur Lösung dieser Aufgabe die folgenden Informationen: Funktion Fouriertransformierte i sin(πf 0 t) (δ(f + f 0) δ(f f 0 )) cos(πf 0 t) (δ(f + f 0) + δ(f f 0 )) + k= δ(t kt ) + T k= δ(f k/t ) a) Zeichnen Sie das komplexe Spektrum der mit 500Hz abgetasteten Funktion f(t), t in Sekunden. Die Fouriertransformation der Funktion f(t) ist: F (f) = i (δ(f + 400) δ(f 400)) + (δ(f + 00) + δ(f 00)) Lösungsblatt zu Kognitive Systeme Seite 5
6 Re Abtastung: Faltung des Spektrums mit pulszug Re /T Verschiebung des pulszugs mit f o = 0: Re F (0) δ(0) = 0 Verschiebung des pulszugs mit f o = 00: (F δ)(f o = 00) = T + i T = T + i (F δ)(f o = 400) = (F δ)(f o = 00) = (F δ)(f o = 600) Lösungsblatt zu Kognitive Systeme Seite 6
7 Re Verschiebung des pulszugs mit f o = 400: Re (F δ)(f o = 400) = T i T = T i (F δ)(f o = 00) = (F δ)(f o = 400) = (F δ)(f o = 900) Komplexes Spektrum mit einer Samplefrequenz von 500Hz: (F δ)(f o = 00) = T + i (F δ)(f o = 00) = T i (F δ)(f o = 400) = T i (F δ)(f o = 400) = T + i Re /T Berechnung des Betragsspektrums nach Abtastung mit 500Hz: Lösungsblatt zu Kognitive Systeme Seite 7
8 (F δ)(f o = 00) = (F δ)(f o = 400) = ) = 5 5 ( T ) + ( ( T ) + ( ) = Re Lösungsblatt zu Kognitive Systeme Seite 8
9 b) Welches Phänomen tritt auf, wie kommt es dazu und wie kann verhindert werden, dass es auftritt? Die gegebene Abtastfrequenz von 500Hz wurde gemäß des Abtasttheorems zu klein gewählt. Daher tritt Aliasing auf, d.h. wiederholte Spektren überlagern sich. gegebenen Fall überlagern sich Frequenzen des Realteils und aginärteils. Weitere denkbare Effekte: Auftreten von im Originalsignal nicht vorhandener Frequenzen, und Verschwinden von im Originalsignal vorhandener Frequenzen. Bei einer D/AWandlung kann das Originalsignal nicht mehr aus den abgetasteten Werten rekonstruiert werden. Um Aliasing zu verhindern, muss als Abtastfrequenz eine Frequenz gewählt werden, die echt größer ist als das fache der höchsten Frequenz im Signal, also > 400 Hz. c) Zeichnen Sie das Betragsspektrum der mit 900Hz abgetasteten Funktion. Faltung des Spektrums vor der Abtastung mit dem pulszug mit Frequenz 900Hz: Verschiebung des pulszugs mit f o = 0: Re (F δ)(f o = 0) = 0 Verschiebung des pulszugs mit f o = 00: (F δ)(f o = 00) = T = T (F δ)(f o = 00) = (F δ)(f o = 800) = T = T Verschiebung des pulszugs mit f o = 400: Lösungsblatt zu Kognitive Systeme Seite 9
10 Re Re (F δ)(f o = 400) = i T = i (F δ)(f o = 400) = (F δ)(f o = 500) = i Das komplexe Spektrum nimmt nach der Abtastung folgende Werte an: (F δ)(f o = 400) = i (F δ)(f o = 00) = T (F δ)(f o = 400) = i (F δ)(f o = 00) = T Re /T Berechnung des Betragsspektrums nach Abtastung mit 900Hz: (F δ)(f o = 400) = 0 + ( i (F δ)(f o = 00) = ( T ) + 0 = T ) = Lösungsblatt zu Kognitive Systeme Seite 0
11 (F δ)(f o = 400) = 0 + ( i ) = Re + /T / Bei einer Abtastfrequenz von 900Hz wird das Abtasttheorem befolgt und es kommt nicht zu Aliasing. Lösungsblatt zu Kognitive Systeme Seite
12 Onlinefrage Nr. : Was ist der größte reale Anteil aller Funktionswerte im komplexen Spektrum von f(t) vor der Abtastung? i) ii) T iii) iv) v) Der größte reale Anteil aller Funktionswerte im komplexen Spektrum von f(t) vor der Abtastung beträgt. Aufgabe 3: Filtern a) Gegeben sei die Funktion v(t) = π δ(t) sin(3ω 0t) sin(ω 0 t) t mit der Zeitvariablen t und ω 0 > 0. Die Multiplikation ihrer Fouriertransformierten V (ω) mit der Fouriertransformierten eines Signals stellt einen Filter dar. Um welchen Filter handelt es sich dabei? Hinweis: Die Funktion f(t) = sin(πt) πt entspricht der Funktion f(t) = sinc(t). Benutzen Sie als Fouriertransformierte von g(t) = sinc(at) folgende Funktion: G(ω) = a rect( ω 0, t > { πa ) mit rect(t) =, t Umformung: v(t) = πδ(t) sin(3ω ot) sin(ω o t) t (4) = πδ(t) ( 3ω o sin(3ω o t) ω o sin(ω o t) ) 3ω o t ω o t (5) sin(3π ωo π = πδ(t) (3ω ω sin(π o o 3π ωo π t ω π t) o π ωo π t ) (6) = πδ(t) (3ω o sinc( 3ω o π t) ω osinc( ω o π t)) Fouriertransformation: Laut Formelsammlung ist die Fouriertransformierte von f(x) = δ(x) die Funktion F (ω) =. V (ω) = F (v(t)) = F (πδ(t) (3ω o sinc( 3ωo π t) ω osinc( ωo π t))) Gegeben sei: Die Fouriertransformation von g(t) = sinc(at) sei G(ω) = a rect( ω πa ), wobei rect(t) definiert { } 0, t > ist als, t Lösungsblatt zu Kognitive Systeme Seite
13 V (ω) = π (3ω o 3ωo rect(t) ist definiert als ω ) ω o ωo ω π ωo π π rect( π 3ωo π π rect( π = π (3ω o rect( ω π ) ω o rect( ω )) (7) 3ω o 6ω o ω o ω o = π (πrect( ω 6ω o ) πrect( ω ω o )) (8) = π πrect( ω 6ω o ) + πrect( ω ω o ) (9) { 0, t >, t rect( ω 6ω o ) ist nur dann wenn ω 3ω o rect( ω ω o ) ist nur dann wenn ω ω o } )) (0) Onlinefrage Nr. 3: Um welches Filter handelt es sich in Aufgabe 3a)? i) Tiefpass ii) Hochpass iii) Bandpass iv) Bandsperre Es handelt sich um eine Bandsperre (siehe Lösung 3a). Aufgabe 4: Diskrete Fouriertransformation, Sampling Die Frequenzauflösung der DFT hängt von der zeitlichen Auflösung ab. Je feiner die zeitliche Auflösung ist, desto gröber ist die Frequenzauflösung und umgekehrt. Berechnet man beispielsweise die DFT über einem gesamten Musikstück, so erhält man detaillierte Informationen über die auftretenden Frequenzen, dies jedoch nur kumuliert über das gesamte Musikstück hinweg. Berechnet man die DFT auf Basis von beispielsweise 00 Werten, so erhält man als Ergebnis ebenfalls 00 Werte. Da das Resultat der DFT symmetrisch ist, trägt nur die Hälfte der Werte Informationen. Somit verteilt sich die Frequenzinformation auf 50 Werte. Betrachten wir zur Verdeutlichung ein Beispiel mit unterschiedlichen Samplingraten, berechnen dabei die DFT aber stets auf Basis von 00 Samples: Lösungsblatt zu Kognitive Systeme Seite 3
14 Samplingrate Grenzfrequenz Frequenzauflösung Zeitauflösung 000 Hz 500 Hz 0 Hz 0. s 00 Hz 50 Hz Hz s 0 Hz 5 Hz 0. Hz 0 s Es wird deutlich, dass die Frequenzauflösung in einem reziproken Verhältnis zur zeitlichen Auflösung steht. a) Berechnen Sie die Anzahl N der Samples, die benötigt werden, damit eine DFT eine Frequenzauflösung von 0Hz erreichen kann, wenn ein Signal mit 33kHz abgetastet wurde. Bei einer Abtastung mit 33kHz beträgt die Grenzfrequenz 6.5kHz. Bei einer gewünschten Frequenzauflösung von 0Hz benötigen wir somit 650 Werte. Dies entspricht einer DFT mit 3300 Werten. Folglich benötigen wir N = 3300 Samples zur Berechnung der DFT. Onlinefrage Nr. 4: Welche zeitliche Auflösung wird benötigt, damit eine DFT eine Frequenzauflösung von 0Hz erreichen kann, wenn ein Signal mit 33kHz abgetastet wurde? i) 0.ms ii) 3.3ms iii) 0.33ms iv) 00ms Aus Teilaufgabe a) wissen wir, dass wir 3300 Samples benötigen. Bei einer Abtastrate von 33kHz entspricht dies einer zeitlichen Auflösung von 0.s bzw. 00ms. Lösungsblatt zu Kognitive Systeme Seite 4
Lösungsblatt 2 Signalverarbeitung
 Fakultät für nformatik Übung zu Kognitive Systeme Sommersemester 208 S. Constantin (stefan.constantin@kit.edu) T. Nguyen (thai.nguyen@kit.edu) Lösungsblatt 2 Signalverarbeitung Aufgabe : Faltung Abbildung
Fakultät für nformatik Übung zu Kognitive Systeme Sommersemester 208 S. Constantin (stefan.constantin@kit.edu) T. Nguyen (thai.nguyen@kit.edu) Lösungsblatt 2 Signalverarbeitung Aufgabe : Faltung Abbildung
Grundlagen der Signalverarbeitung
 Grundlagen der Signalverarbeitung Zeitdiskrete Signale Wintersemester 6/7 Kontinuierliche und diskrete Signale wertkontinuierlich wertdiskret Signal Signal Signal Signal zeitdiskret zeitkontinuierlich
Grundlagen der Signalverarbeitung Zeitdiskrete Signale Wintersemester 6/7 Kontinuierliche und diskrete Signale wertkontinuierlich wertdiskret Signal Signal Signal Signal zeitdiskret zeitkontinuierlich
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
Spektrum zeitdiskreter Signale
 Spektrum zeitdiskreter Signale 1 Aufgabenstellung Mithilfe der Fouriertransformation können zeitkontinuierliche Signale in den Frequenzbereich transformiert werden, um die im Signal enthaltenen Frequenzanteile
Spektrum zeitdiskreter Signale 1 Aufgabenstellung Mithilfe der Fouriertransformation können zeitkontinuierliche Signale in den Frequenzbereich transformiert werden, um die im Signal enthaltenen Frequenzanteile
Übung 3: Fouriertransformation
 ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
Signale, Transformationen
 Signale, Transformationen Signal: Funktion s(t), t reell (meist t die Zeit, s eine Messgröße) bzw Zahlenfolge s k = s[k], k ganzzahlig s reell oder komplex s[k] aus s(t): Abtastung mit t = kt s, s[k] =
Signale, Transformationen Signal: Funktion s(t), t reell (meist t die Zeit, s eine Messgröße) bzw Zahlenfolge s k = s[k], k ganzzahlig s reell oder komplex s[k] aus s(t): Abtastung mit t = kt s, s[k] =
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
Beispiel-Klausuraufgaben Digitale Signalverarbeitung. Herbst 2008
 Beispiel-Klausuraufgaben Digitale Signalverarbeitung Herbst 8 Zeitdauer: Hilfsmittel: Stunden Formelsammlung Taschenrechner (nicht programmiert) eine DIN A4-Seite mit beliebigem Text oder Formeln (beidseitig)
Beispiel-Klausuraufgaben Digitale Signalverarbeitung Herbst 8 Zeitdauer: Hilfsmittel: Stunden Formelsammlung Taschenrechner (nicht programmiert) eine DIN A4-Seite mit beliebigem Text oder Formeln (beidseitig)
Zusammenfassung der 1. Vorlesung
 Zusammenfassung der. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Quantisiertes Signal Zeitdiskretes Signal Digitales Signal Auflösung der A/D- Umsetzer der MicroAutoBox
Zusammenfassung der. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Quantisiertes Signal Zeitdiskretes Signal Digitales Signal Auflösung der A/D- Umsetzer der MicroAutoBox
Computergraphik I. Das Abtasttheorem. Problem bei räumlicher Abtastung: Oliver Deussen Abtasttheorem 1
 Das Abtasttheorem Problem bei räumlicher Abtastung: Oliver Deussen Abtasttheorem 1 Problem bei zeitlicher Abtastung: Oliver Deussen Abtasttheorem 2 Darstellung auf Monitor Was geschieht eigentlich, wenn
Das Abtasttheorem Problem bei räumlicher Abtastung: Oliver Deussen Abtasttheorem 1 Problem bei zeitlicher Abtastung: Oliver Deussen Abtasttheorem 2 Darstellung auf Monitor Was geschieht eigentlich, wenn
- Sei r(x,y) Eingangsbild, dass nur Rauschen (Quantenrauschen) enthält.
 Eingang System Ausgang - Sei r(x,y) Eingangsbild, dass nur (Quantenrauschen) enthält. - Das Bild enthalte keinerlei Information, d.h. das Spektrum ist weiß und es gibt keine Korrelationen zwischen den
Eingang System Ausgang - Sei r(x,y) Eingangsbild, dass nur (Quantenrauschen) enthält. - Das Bild enthalte keinerlei Information, d.h. das Spektrum ist weiß und es gibt keine Korrelationen zwischen den
Klausur zur Vorlesung Signale u. Systeme I
 Name: 8. Februar 2001, 11.30-13.00 Uhr Allgemeine Hinweise: Dauer der Klausur: Zugelassene Hilfsmittel: 90 min, 1.5 Zeitstunden Skript, Vorlesungsmitschrift, Formelsammlung Schreiben Sie bitte auf dieses
Name: 8. Februar 2001, 11.30-13.00 Uhr Allgemeine Hinweise: Dauer der Klausur: Zugelassene Hilfsmittel: 90 min, 1.5 Zeitstunden Skript, Vorlesungsmitschrift, Formelsammlung Schreiben Sie bitte auf dieses
Zusammenfassung der 1. Vorlesung
 Zusammenfassung der 1. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Zeitdiskretes Signal Quantisiertes Signal Digitales Signal Kontinuierliches System Abtastsystem
Zusammenfassung der 1. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Zeitdiskretes Signal Quantisiertes Signal Digitales Signal Kontinuierliches System Abtastsystem
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien 4-1
 4. Signalverarbeitung 4.1 Grundbegrie 4.2 Frequenzspektren, Fourier-Transormation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterührende Literatur (z.b.): Beate Meert, Ola Hochmuth: Werkzeuge der
4. Signalverarbeitung 4.1 Grundbegrie 4.2 Frequenzspektren, Fourier-Transormation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterührende Literatur (z.b.): Beate Meert, Ola Hochmuth: Werkzeuge der
Schnelle Fouriertransformation (FFT)
 Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
Diskrete Fourier-Transformation und FFT. 1. Die diskrete Fourier-Transformation (DFT) 2. Die Fast Fourier Transform (FFT)
 Diskrete Fourier-Transformation und FFT 2. Die Fast Fourier Transform (FFT) 3. Anwendungsbeispiele der DFT 1 Wiederholung: Fourier-Transformation und Fourier-Reihe Fourier-Transformation kontinuierlicher
Diskrete Fourier-Transformation und FFT 2. Die Fast Fourier Transform (FFT) 3. Anwendungsbeispiele der DFT 1 Wiederholung: Fourier-Transformation und Fourier-Reihe Fourier-Transformation kontinuierlicher
Digitale Signalverarbeitung Bernd Edler
 Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Prüfungsklausur Digitale Signalverarbeitung Ergebnis der Klausur
 Fakultät für Mathematik und Informatik Elektronische Schaltungen 58084 Hagen 02331 987 1166 Prüfungsklausur Digitale Signalverarbeitung 21411 Datum: 19. März 2011 (Bearbeitungszeit 120 Minuten, 6 Blätter)
Fakultät für Mathematik und Informatik Elektronische Schaltungen 58084 Hagen 02331 987 1166 Prüfungsklausur Digitale Signalverarbeitung 21411 Datum: 19. März 2011 (Bearbeitungszeit 120 Minuten, 6 Blätter)
Digitale Signalverarbeitung Bernd Edler
 Digitale Signalverarbeitung Bernd Edler Wintersemester 2007/2008 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Digitale Signalverarbeitung Bernd Edler Wintersemester 2007/2008 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
2. Anordnung zur digitalen Signalverarbeitung
 2. Anordnung zur digitalen Signalverarbeitung Prof. Dr.-Ing. Dr. h.c. Norbert Höptner Prof. Dr.-Ing. Stefan Hillenbrand Ergänzende Informationen zur Vorlesung Signalverarbeitungssysteme Abschnitte 2.1-2.5.
2. Anordnung zur digitalen Signalverarbeitung Prof. Dr.-Ing. Dr. h.c. Norbert Höptner Prof. Dr.-Ing. Stefan Hillenbrand Ergänzende Informationen zur Vorlesung Signalverarbeitungssysteme Abschnitte 2.1-2.5.
Digitale Signalverarbeitung Bernd Edler
 Digitale Signalverarbeitung Bernd Edler Wintersemester 2010/2011 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Filterentwurf
Digitale Signalverarbeitung Bernd Edler Wintersemester 2010/2011 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Filterentwurf
Grundlagen der Signalverarbeitung
 Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
FH Jena Prüfungsaufgaben - Master Prof. Giesecke FB ET/IT Digitale Signalverarbeitung SS 2012
 FB ET/IT Digitale Signalverarbeitung SS 0 Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner ein mathematisches Formelwerk eine selbsterstellte Formelsammlung Wichtige Hinweise:
FB ET/IT Digitale Signalverarbeitung SS 0 Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner ein mathematisches Formelwerk eine selbsterstellte Formelsammlung Wichtige Hinweise:
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe 4.2! Frequenzspektren, Fourier-Transformation 4.3! Abtasttheorem: Eine zweite Sicht 4.4! Filter! Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe 4.2! Frequenzspektren, Fourier-Transformation 4.3! Abtasttheorem: Eine zweite Sicht 4.4! Filter! Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
Bildpunkt auf dem Gitter: Pixel (picture element) (manchmal auch Pel)
 4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.006 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.006 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter
 4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
Puls-Code-Modulation. Thema: PCM. Ziele
 Puls-Code-Modulation Ziele Mit diesen rechnerischen und experimentellen Übungen wird die Vorgehensweise zur Abtastung und linearen Quantisierung eines analogen Signals erarbeitet. Bei der Abtastung werden
Puls-Code-Modulation Ziele Mit diesen rechnerischen und experimentellen Übungen wird die Vorgehensweise zur Abtastung und linearen Quantisierung eines analogen Signals erarbeitet. Bei der Abtastung werden
und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei t=0 mit dem Zeitindex n=0.
 Aufgabe 1 Das periodische Signal x t) 0,5 sin(2 f t) 0,5 cos(2 f t) mit f 1000Hz und mit f 2000Hz ( 1 2 1 2 und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei
Aufgabe 1 Das periodische Signal x t) 0,5 sin(2 f t) 0,5 cos(2 f t) mit f 1000Hz und mit f 2000Hz ( 1 2 1 2 und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei
4. Beschreibung von LTI-Systemen mit der Fourier-Transformation
 Die Fourier-Transformation 1. Anwendungsbeispiele der Fourier-Transformation 2. Die kontinuierliche Fourier-Transformation 3. Die Fourier-Reihe 4. Beschreibung von LTI-Systemen mit der Fourier-Transformation
Die Fourier-Transformation 1. Anwendungsbeispiele der Fourier-Transformation 2. Die kontinuierliche Fourier-Transformation 3. Die Fourier-Reihe 4. Beschreibung von LTI-Systemen mit der Fourier-Transformation
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/48/24765147.jpg) Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
Abschlussprüfung Nachrichtentechnik 03. August 2015
 Abschlussprüfung Nachrichtentechnik 03. August 2015 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Abschlussprüfung Nachrichtentechnik 03. August 2015 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
3.7 Anti-Alias-Verfahren
 3.7 Anti-Alias-Verfahren Wir hatten Treppeneffekte bereits beim Rastern von Bildern kennengelernt. Aber auch beim Wiederholen verkleinerter Texturen können sich durch Rasterungseffekte unschöne Interferenzerscheinungen
3.7 Anti-Alias-Verfahren Wir hatten Treppeneffekte bereits beim Rastern von Bildern kennengelernt. Aber auch beim Wiederholen verkleinerter Texturen können sich durch Rasterungseffekte unschöne Interferenzerscheinungen
Test = 28 Punkte. 1: 2: 3: 4: 5: Punkte: Note:
 ZHAW, DSV1, FS2010, Rumc, 1 Test 1 5 + 5 + 5 + 8 + 5 = 28 Punkte Name: Vorname: 1: 2: : 4: 5: Punkte: Note: Aufgabe 1: AD-DA-System. + 1 + 1 = 5 Punkte Das analoge Signal x a (t) = cos(2πf 0 t), f 0 =750
ZHAW, DSV1, FS2010, Rumc, 1 Test 1 5 + 5 + 5 + 8 + 5 = 28 Punkte Name: Vorname: 1: 2: : 4: 5: Punkte: Note: Aufgabe 1: AD-DA-System. + 1 + 1 = 5 Punkte Das analoge Signal x a (t) = cos(2πf 0 t), f 0 =750
1 Fourier-Reihen und Fourier-Transformation
 Fourier-Reihen und Fourier-ransformation Fourier-Reihen und Fourier-ransformation J.B.J. de Fourier beobachtete um 8, dass sich jede periodische Funktion durch Überlagerung von sin(t) und cos(t) darstellen
Fourier-Reihen und Fourier-ransformation Fourier-Reihen und Fourier-ransformation J.B.J. de Fourier beobachtete um 8, dass sich jede periodische Funktion durch Überlagerung von sin(t) und cos(t) darstellen
Einführung in die Signalverarbeitung
 Einführung in die Signalverarbeitung Phonetik und Sprachverarbeitung, 2. Fachsemester, Block Sprachtechnologie I Florian Schiel Institut für Phonetik und Sprachverarbeitung, LMU München Signalverarbeitung
Einführung in die Signalverarbeitung Phonetik und Sprachverarbeitung, 2. Fachsemester, Block Sprachtechnologie I Florian Schiel Institut für Phonetik und Sprachverarbeitung, LMU München Signalverarbeitung
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
3. Basisbandtransformation durch Integerband-Abtastung
 Bearbeiten von Frequenzbändern 1. Analyse-Filterbank, Basisbandtransformation 2. Basisbandtransformation durch Modulation 3. Basisbandtransformation durch Integerband-Abtastung 1 1. Analyse-Filterbank
Bearbeiten von Frequenzbändern 1. Analyse-Filterbank, Basisbandtransformation 2. Basisbandtransformation durch Modulation 3. Basisbandtransformation durch Integerband-Abtastung 1 1. Analyse-Filterbank
(Fast) Fourier Transformation und ihre Anwendungen
 (Fast) Fourier Transformation und ihre Anwendungen Johannes Lülff Universität Münster 14.01.2009 Definition Fouriertransformation F (ω) = F [f(t)] (ω) := 1 2π dt f(t)e iωt Fouriersynthese f(t) = F 1 [F
(Fast) Fourier Transformation und ihre Anwendungen Johannes Lülff Universität Münster 14.01.2009 Definition Fouriertransformation F (ω) = F [f(t)] (ω) := 1 2π dt f(t)e iωt Fouriersynthese f(t) = F 1 [F
Musterlösung zur Klausur Digitale Signalverarbeitung
 Musterlösung zur Klausur Digitale Signalverarbeitung Arbeitsgruppe Digitale Signalverarbeitung Ruhr-Universität Bochum 1. Oktober 2007 Aufgabe 1: Transformationen 25 Pkt. Gegeben war das reellwertige kontinuierliche
Musterlösung zur Klausur Digitale Signalverarbeitung Arbeitsgruppe Digitale Signalverarbeitung Ruhr-Universität Bochum 1. Oktober 2007 Aufgabe 1: Transformationen 25 Pkt. Gegeben war das reellwertige kontinuierliche
ZHAW, DSV1, FS2010, Rumc, 1. H(z) a) Zeichnen Sie direkt auf das Aufgabenblatt das Betragsspektrum an der Stelle 1.
 ZHAW, DSV, FS200, Rumc, DSV Modulprüfung 7 + 4 + 5 + 8 + 6 = 30 Punkte Name: Vorname: : 2: 3: 4: 5: Punkte: Note: Aufgabe : AD-DA-Umsetzung. + + +.5 +.5 + = 7 Punkte Betrachten Sie das folgende digitale
ZHAW, DSV, FS200, Rumc, DSV Modulprüfung 7 + 4 + 5 + 8 + 6 = 30 Punkte Name: Vorname: : 2: 3: 4: 5: Punkte: Note: Aufgabe : AD-DA-Umsetzung. + + +.5 +.5 + = 7 Punkte Betrachten Sie das folgende digitale
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 2016
 Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 1 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Übungsblatt 3 Maschinelles Lernen und Klassifikation Abgabe online
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 1 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Übungsblatt 3 Maschinelles Lernen und Klassifikation Abgabe online
SiSy1, Praktische Übung 3. Fourier-Analyse (periodischer Signale) kann als Fourier-Reihe 1 beschrieben werden:
 /5 Fourier-Analyse (periodischer Signale) Grundlagen Ein periodisches, kontinuierliches Signal x(t) der Periodendauer kann als Fourier-Reihe beschrieben werden: wie folgt ( ) = c k x t + e j k 2πf t k=
/5 Fourier-Analyse (periodischer Signale) Grundlagen Ein periodisches, kontinuierliches Signal x(t) der Periodendauer kann als Fourier-Reihe beschrieben werden: wie folgt ( ) = c k x t + e j k 2πf t k=
Abschlussprüfung Digitale Signalverarbeitung. Aufgaben, die mit einem * gekennzeichnet sind, lassen sich unabhängig von anderen Teilaufgaben lösen.
 Name: Abschlussprüfung Digitale Signalverarbeitung Studiengang: Elektrotechnik IK, E/ME Wahlfach SS2015 Prüfungstermin: Prüfer: Hilfsmittel: 3.7.2015 (90 Minuten) Prof. Dr.-Ing. Großmann, Prof. Dr.-Ing.
Name: Abschlussprüfung Digitale Signalverarbeitung Studiengang: Elektrotechnik IK, E/ME Wahlfach SS2015 Prüfungstermin: Prüfer: Hilfsmittel: 3.7.2015 (90 Minuten) Prof. Dr.-Ing. Großmann, Prof. Dr.-Ing.
3.3 Das Abtasttheorem
 17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
Systemtheorie Teil B
 d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie eil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt Musterlösungen - Signalabtastung und Rekonstruktion...
d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie eil B - Zeitdiskrete Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt Musterlösungen - Signalabtastung und Rekonstruktion...
Systemtheorie Teil B
 d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme Übungsaufgaben Manfred Strohrmann Urban Brunner Inhalt Übungsaufgaben - Signalabtastung und Rekonstruktion...
d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme Übungsaufgaben Manfred Strohrmann Urban Brunner Inhalt Übungsaufgaben - Signalabtastung und Rekonstruktion...
Übung Grundlagen der Elektrotechnik B
 Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
Technik der Fourier-Transformation
 Was ist Fourier-Transformation? Fourier- Transformation Zeitabhängiges Signal in s Frequenzabhängiges Signal in 1/s Wozu braucht man das? Wie macht man das? k = 0 Fourier- Reihe f ( t) = Ak cos( ωkt) +
Was ist Fourier-Transformation? Fourier- Transformation Zeitabhängiges Signal in s Frequenzabhängiges Signal in 1/s Wozu braucht man das? Wie macht man das? k = 0 Fourier- Reihe f ( t) = Ak cos( ωkt) +
Filterentwurf. Aufgabe
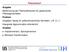 Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Übungsaufgaben Digitale Signalverarbeitung
 Übungsaufgaben Digitale Signalverarbeitung Aufgabe 1: Gegeben sind folgende Zahlenfolgen: x(n) u(n) u(n N) mit x(n) 1 n 0 0 sonst. h(n) a n u(n) mit 0 a 1 a) Skizzieren Sie die Zahlenfolgen b) Berechnen
Übungsaufgaben Digitale Signalverarbeitung Aufgabe 1: Gegeben sind folgende Zahlenfolgen: x(n) u(n) u(n N) mit x(n) 1 n 0 0 sonst. h(n) a n u(n) mit 0 a 1 a) Skizzieren Sie die Zahlenfolgen b) Berechnen
FH Jena FB Elektrotechnik/Informationstechnik Prof. Giesecke Prüfungsaufgaben Signalverarbeitung SS 2012
 Name, Vorname: Matr.-Nr.: Wichtige Hinweise: Ausführungen, Notizen und Lösungen auf den Aufgabenblättern werden nicht gewertet. Vor der entsprechenden Lösung ist deutlich die dazugehörige Nummer der Aufgabe
Name, Vorname: Matr.-Nr.: Wichtige Hinweise: Ausführungen, Notizen und Lösungen auf den Aufgabenblättern werden nicht gewertet. Vor der entsprechenden Lösung ist deutlich die dazugehörige Nummer der Aufgabe
Diskretisierung und Quantisierung (Teil 1) Prof. U. Rüde - Algorithmik kontinuierlicher Systeme
 Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
Bildverarbeitung Herbstsemester 2012. Fourier-Transformation
 Bildverarbeitung Herbstsemester 2012 Fourier-Transformation 1 Inhalt Fourierreihe Fouriertransformation (FT) Diskrete Fouriertransformation (DFT) DFT in 2D Fourierspektrum interpretieren 2 Lernziele Sie
Bildverarbeitung Herbstsemester 2012 Fourier-Transformation 1 Inhalt Fourierreihe Fouriertransformation (FT) Diskrete Fouriertransformation (DFT) DFT in 2D Fourierspektrum interpretieren 2 Lernziele Sie
Diskretisierung und Quantisierung (Teil 1) Prof. U. Rüde - Algorithmik kontinuierlicher Systeme
 Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
Erarbeiten der Diskreten Fourier Transformation (GFT) unter Verwendung von Scilab zur Veranschaulichung
 Erarbeiten der Diskreten Fourier Transormation (GFT) unter Verwendung von Scilab zur Veranschaulichung 1. Das Prinzip verstehen 2. DFT beschreiben 3. DFT mit Scilab testen 4. Umsetzung der DFT ür einen
Erarbeiten der Diskreten Fourier Transormation (GFT) unter Verwendung von Scilab zur Veranschaulichung 1. Das Prinzip verstehen 2. DFT beschreiben 3. DFT mit Scilab testen 4. Umsetzung der DFT ür einen
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Systemtheorie Teil A - Zeitkontinuierliche Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 6 Musterlösungen Spektrum von Signalen 6. Approximation eines periodischen Signals
Systemtheorie Teil A - Zeitkontinuierliche Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 6 Musterlösungen Spektrum von Signalen 6. Approximation eines periodischen Signals
Digitale Signalverarbeitung, Vorlesung 11 - Kurzzeitfouriertransformation
 Digitale Signalverarbeitung, Vorlesung 11 - Kurzzeitfouriertransformation 30. Januar 2017 Siehe Skript Digitale Signalverarbeitung, Abschnitte 11 und 12, Kammeyer & Kroschel (Absatz 8.4.1) Anwendungen
Digitale Signalverarbeitung, Vorlesung 11 - Kurzzeitfouriertransformation 30. Januar 2017 Siehe Skript Digitale Signalverarbeitung, Abschnitte 11 und 12, Kammeyer & Kroschel (Absatz 8.4.1) Anwendungen
5. Fourier-Transformation
 5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter
 4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/55/37142352.jpg) Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 2 Zeitkontinuierliche
Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 2 Zeitkontinuierliche
Spektralanalyse physiologischer Signale
 Spektralanalyse physiologischer Signale Dr. rer. nat. Axel Hutt Vorlesung 1 - WS 2016/17 über mich Studium der Physik an U Stuttgart Promotion: Nichtlineare Dynamik in Gehirnsignalen Forschung in Neurowissenschaften
Spektralanalyse physiologischer Signale Dr. rer. nat. Axel Hutt Vorlesung 1 - WS 2016/17 über mich Studium der Physik an U Stuttgart Promotion: Nichtlineare Dynamik in Gehirnsignalen Forschung in Neurowissenschaften
Abtastung. Normalisierte Kreisfrequenz = DSP_9-Abtasttheorem 2
 Abtasttheorem Abtastung xn [ ] = xnt ( ) = Acos( ωnt+ ϕ) = Acos( ωˆ n+ ϕ) s s Normalisierte Kreisfrequenz ωˆ = ωt s DSP_9-Abtasttheorem 2 Normalisierte Kreisfrequenz ω hat die Einheit rad/sec, ω ˆ = ωt
Abtasttheorem Abtastung xn [ ] = xnt ( ) = Acos( ωnt+ ϕ) = Acos( ωˆ n+ ϕ) s s Normalisierte Kreisfrequenz ωˆ = ωt s DSP_9-Abtasttheorem 2 Normalisierte Kreisfrequenz ω hat die Einheit rad/sec, ω ˆ = ωt
Aufgabe 1: Kontinuierliche und diskrete Signale
 ufgabe (5 Punkte) ufgabe : Kontinuierliche und diskrete Signale. Zeichnen Sie jeweils den geraden und den ungeraden nteil des Signals in bb..!. Sind Sie folgenden Signale periodisch? Falls ja, bestimmen
ufgabe (5 Punkte) ufgabe : Kontinuierliche und diskrete Signale. Zeichnen Sie jeweils den geraden und den ungeraden nteil des Signals in bb..!. Sind Sie folgenden Signale periodisch? Falls ja, bestimmen
3.6 Analog-Digital-Umsetzung
 3.6 AnalogDigitalUmsetzung 1 Abtastung von Signalen FlashUmsetzer (ParallelUmsetzer) Stufenumsetzer (Successive Approximation) Integrierende Umsetzer DeltaSigma Umsetzer Anhang Abtastung 2 Abtastung (Sampling):
3.6 AnalogDigitalUmsetzung 1 Abtastung von Signalen FlashUmsetzer (ParallelUmsetzer) Stufenumsetzer (Successive Approximation) Integrierende Umsetzer DeltaSigma Umsetzer Anhang Abtastung 2 Abtastung (Sampling):
d 1 P N G A L S2 d 2
 Abschlussprüfung Nachrichtentechnik 28. Juli 2014 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Abschlussprüfung Nachrichtentechnik 28. Juli 2014 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Digitale Medien. Vorlesung: Heinrich Hußmann Übung: Renate Häuslschmid. Übung zur Vorlesung
 Übung zur Vorlesung Digitale Medien Vorlesung: Heinrich Hußmann Übung: Renate Häuslschmid Wintersemester 2016/17 LZW-Komprimierung Idee: Nicht einzelne Zeichen werden günstig kodiert, sondern ganze Zeichenketten
Übung zur Vorlesung Digitale Medien Vorlesung: Heinrich Hußmann Übung: Renate Häuslschmid Wintersemester 2016/17 LZW-Komprimierung Idee: Nicht einzelne Zeichen werden günstig kodiert, sondern ganze Zeichenketten
Einführung in die Signalverarbeitung Übung I
 Einführung in die Signalverarbeitung Phonetik und Sprachverarbeitung, 2. Fachsemester, Block Sprachtechnologie I Florian Schiel Institut für Phonetik und Sprachverarbeitung, LMU München Signalverarbeitung
Einführung in die Signalverarbeitung Phonetik und Sprachverarbeitung, 2. Fachsemester, Block Sprachtechnologie I Florian Schiel Institut für Phonetik und Sprachverarbeitung, LMU München Signalverarbeitung
Labor SMV Versuch 1. Erläuterungen zum Aliasing. Prof. Dr.-Ing. Gernot Freitag. FB: EuI, FH Darmstadt. Darmstadt, den
 Labor SMV Versuch Erläuterungen zum Aliasing FB: EuI, Darmstadt, den 26.5 Elektrotechnik und Informationstechnik Rev., 9.5 Auf den folgenden Seiten sind einige typische Abtastsituationen zusammengestellt,
Labor SMV Versuch Erläuterungen zum Aliasing FB: EuI, Darmstadt, den 26.5 Elektrotechnik und Informationstechnik Rev., 9.5 Auf den folgenden Seiten sind einige typische Abtastsituationen zusammengestellt,
1.3 Digitale Audiosignale
 Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.00 Uhrzeit: 09:00
INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum:.08.00 Uhrzeit: 09:00
4. Übung für Übungsgruppen Musterlösung
 Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, FB Informatik der Universität Hamburg). Übung für Übungsgruppen Musterlösung (N. Stein, Institut für Angewandte Physik,
Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, FB Informatik der Universität Hamburg). Übung für Übungsgruppen Musterlösung (N. Stein, Institut für Angewandte Physik,
Übung 2: Spektrum periodischer Signale
 ZHAW, SiSy, Rumc, Übung : Spektrum periodischer Signale Augabe Verschiedene Darstellungen der Fourierreihe. Betrachten Sie das periodische Signal s(t) = + sin(π t). a) Bestimmen Sie die A k - und B k -Koeizienten
ZHAW, SiSy, Rumc, Übung : Spektrum periodischer Signale Augabe Verschiedene Darstellungen der Fourierreihe. Betrachten Sie das periodische Signal s(t) = + sin(π t). a) Bestimmen Sie die A k - und B k -Koeizienten
Die Wärmeleitungsgleichung
 Die Wärmeleitungsgleichung In einem Stab der Länge 1 wird die Temperaturverteilung gegeben durch die Funktion u : ([0,1] [0, )) R, u(x,t) ist die Temperatur am Punkt x zum Zeitpunkt t. Die Funktion erfüllt
Die Wärmeleitungsgleichung In einem Stab der Länge 1 wird die Temperaturverteilung gegeben durch die Funktion u : ([0,1] [0, )) R, u(x,t) ist die Temperatur am Punkt x zum Zeitpunkt t. Die Funktion erfüllt
,Faltung. Heavisidefunktion σ (t), Diracimpuls δ (t) Anwendungen. 1) Rechteckimpuls. 2) Sprungfunktionen. 3) Schaltvorgänge
 Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Kontrollfragen zum Skript Teil 1 beantwortet
 Kontrollfragen zum Skript Teil 1 beantwortet Von J.S. Hussmann Fragen zu SW 1.1 Welche Vorteile hat die DSVB? Programmierbar Parametrierbar Reproduzierbar Wie heisst die Umwandlung eines Zeit-diskreten
Kontrollfragen zum Skript Teil 1 beantwortet Von J.S. Hussmann Fragen zu SW 1.1 Welche Vorteile hat die DSVB? Programmierbar Parametrierbar Reproduzierbar Wie heisst die Umwandlung eines Zeit-diskreten
TET - Formelsammlung
 TET - Formelsammlung Matthias Jung 30. August 2008 1 Dierentialgleichungen Characterisierung von DGLn: Linear: y(t) sowie ẏ(t), ÿ(t)... kommen nur in der 1. Potenz vor Gewöhnlich: y(t) hängt nur von einer
TET - Formelsammlung Matthias Jung 30. August 2008 1 Dierentialgleichungen Characterisierung von DGLn: Linear: y(t) sowie ẏ(t), ÿ(t)... kommen nur in der 1. Potenz vor Gewöhnlich: y(t) hängt nur von einer
Bildsignaltechnik. Name:... Matrikelnummer:...
 Fachbereich lektrotechnik Fachgebiet Kounikationstechnik Schriftliche Prüfung Bildsignaltechnik.9. Nae:... Matrikelnuer:... zugelassene Hilfsittel : Vorlesungshilfsblätter ohne zusätzliche Blätter, keine
Fachbereich lektrotechnik Fachgebiet Kounikationstechnik Schriftliche Prüfung Bildsignaltechnik.9. Nae:... Matrikelnuer:... zugelassene Hilfsittel : Vorlesungshilfsblätter ohne zusätzliche Blätter, keine
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Signale und Systeme II
 TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme II Lösung zur Modulklausur SS 201 Prüfer: Prof. Dr.-Ing. Gerhard Schmidt
TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme II Lösung zur Modulklausur SS 201 Prüfer: Prof. Dr.-Ing. Gerhard Schmidt
Laborprotokoll SSY Abtastung
 Laborprotokoll SSY Abtastung Daniel Schrenk, Andreas Unterweger SSYLB WS 05/06 Abtastung Seite 1 von 12 Einleitung Ziel der Übung In dieser Laborübung sollte ein Signal abgetastet werden und anschließend
Laborprotokoll SSY Abtastung Daniel Schrenk, Andreas Unterweger SSYLB WS 05/06 Abtastung Seite 1 von 12 Einleitung Ziel der Übung In dieser Laborübung sollte ein Signal abgetastet werden und anschließend
Diskretisierung und Quantisierung (Teil 1) Prof. U. Rüde - Algorithmik kontinuierlicher Systeme
 Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
Algorithmik kontinuierlicher Systeme Diskretisierung und Quantisierung (Teil ) Digitalisierung und Quantisierung Motivation Analoge Aufnahme von Sprache, Bildern, Digitale Speicherung durch Diskretisierung
5. Übung für Übungsgruppen Musterlösung
 Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, Department Informatik der Universität Hamburg) 5. Übung für Übungsgruppen Musterlösung (U. Köthe, Department Informatik,
Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, Department Informatik der Universität Hamburg) 5. Übung für Übungsgruppen Musterlösung (U. Köthe, Department Informatik,
Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches
 Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches Signal Periodisch harmonische Schwingung Summe harmonischer
Zufallssignal Stationär (z.b. gleichverteiltes Rauschen) Nicht-stationär (z.b. normalverteiltes Rauschen mit wechselnder Streuung) Deterministisches Signal Periodisch harmonische Schwingung Summe harmonischer
Grundlagen der Schwingungslehre
 Grundlagen der Schwingungslehre Einührung. Vorgänge, bei denen eine physikalische Größe in estem zeitlichen Abstand ein und denselben Werteverlau auweist, werden als periodisch bezeichnet. Den zeitlichen
Grundlagen der Schwingungslehre Einührung. Vorgänge, bei denen eine physikalische Größe in estem zeitlichen Abstand ein und denselben Werteverlau auweist, werden als periodisch bezeichnet. Den zeitlichen
Fachprüfung. Signal- und Systemtheorie
 Fachprüfung Signal- und Systemtheorie 15. September 2010 Prüfer: Prof. Dr. P. Pogatzki Bearbeitungszeit: 2 Stunden Hilfsmittel: Taschenrechner, Formelblatt (2 DIN A4-Seiten) Name: Vorname: Matr.-Nr.: Unterschrift:
Fachprüfung Signal- und Systemtheorie 15. September 2010 Prüfer: Prof. Dr. P. Pogatzki Bearbeitungszeit: 2 Stunden Hilfsmittel: Taschenrechner, Formelblatt (2 DIN A4-Seiten) Name: Vorname: Matr.-Nr.: Unterschrift:
Lineare zeitinvariante Systeme
 Lineare zeitinvariante Systeme Signalflussgraphen Filter-Strukturen Fouriertransformation für zeitdiskrete Signale Diskrete Fouriertransformation (DFT) 1 Signalflussgraphen Nach z-transformation ist Verzögerung
Lineare zeitinvariante Systeme Signalflussgraphen Filter-Strukturen Fouriertransformation für zeitdiskrete Signale Diskrete Fouriertransformation (DFT) 1 Signalflussgraphen Nach z-transformation ist Verzögerung
Medien- Technik. Digital Audio
 Digital Audio Medientyp digital audio representation Abtastfrequenz /sampling frequency Quantisierung (Bittiefe) Anzahl der Kanäle/Spuren Interleaving bei Mehrkanal Positiv/negativ Codierung operations
Digital Audio Medientyp digital audio representation Abtastfrequenz /sampling frequency Quantisierung (Bittiefe) Anzahl der Kanäle/Spuren Interleaving bei Mehrkanal Positiv/negativ Codierung operations
einige Zusatzfolien für s Seminar
 Signale und Systeme einige Zusatzfolien für s Seminar Dr. Mike Wolf, Fachgebiet Nachrichtentechnik Signale und Systeme Fourierreihe reelle Fourierreihe betrachtet wird ein periodisches Zeitsignal u p mit
Signale und Systeme einige Zusatzfolien für s Seminar Dr. Mike Wolf, Fachgebiet Nachrichtentechnik Signale und Systeme Fourierreihe reelle Fourierreihe betrachtet wird ein periodisches Zeitsignal u p mit
Datenaquisition. Verstärker Filter. Sensor ADC. Objekt. Rechner
 Datenaquisition Sensor Verstärker Filter ADC Objekt Rechner Datenaquisition Verstärker: - linearer Arbeitsbereich - linearer Frequenzgang - Vorkehrungen gegen Übersteuerung (trends, shot noise) - Verstärkerrauschen
Datenaquisition Sensor Verstärker Filter ADC Objekt Rechner Datenaquisition Verstärker: - linearer Arbeitsbereich - linearer Frequenzgang - Vorkehrungen gegen Übersteuerung (trends, shot noise) - Verstärkerrauschen
Signalprozessoren. Digital Signal Processors VO [2h] , LU 2 [2h]
![Signalprozessoren. Digital Signal Processors VO [2h] , LU 2 [2h] Signalprozessoren. Digital Signal Processors VO [2h] , LU 2 [2h]](/thumbs/92/108836937.jpg) Signalprozessoren Digital Signal Processors VO [2h] 182.082, LU 2 [2h] 182.084 http://ti.tuwien.ac.at/rts/teaching/courses/sigproz Herbert Grünbacher Institut für Technische Informatik (E182) Herbert.Gruenbacher@tuwien.ac.at
Signalprozessoren Digital Signal Processors VO [2h] 182.082, LU 2 [2h] 182.084 http://ti.tuwien.ac.at/rts/teaching/courses/sigproz Herbert Grünbacher Institut für Technische Informatik (E182) Herbert.Gruenbacher@tuwien.ac.at
Übungen zu Transformationen. im Bachelor ET oder EW. Version 2.0 für das Wintersemester 2014/2015 Stand:
 Fachhochschule Dortmund University of Applied Sciences and Arts Institut für Informationstechnik Software-Engineering Signalverarbeitung Regelungstechnik IfIT Übungen zu Transformationen im Bachelor ET
Fachhochschule Dortmund University of Applied Sciences and Arts Institut für Informationstechnik Software-Engineering Signalverarbeitung Regelungstechnik IfIT Übungen zu Transformationen im Bachelor ET
