Mathematisches Modellieren zu schwer für Schüler und Lehrer?
|
|
|
- Maja Bader
- vor 7 Jahren
- Abrufe
Transkript
1 Werner BLUM, Kassel Mathematisches Modellieren zu schwer für Schüler und Lehrer? 1. Einführung Ein Beispiel zur Einstimmung: Gegeben ist das Foto eines Paars von Riesenschuhen (2,37 m breit und 5,29 m lang). Aufgabe: Wie groß wäre der Riesenmensch, dem diese Schuhe passen würden? Zwei Hauptschüler (9. Klasse) haben die Aufgabe so gelöst: Diese Lösung folgt der bekannten Schülerstrategie: Entnimm dem Aufgabentext die gegebenen Größen und rechne mit ihnen nach einem vertrauten Schema (und denk dabei nicht über den Kontext nach). Riesenschuhe ist ein Beispiel für eine realitätsbezogene Aufgabe mit einer Modellierungsanforderung (Welche Annahmen über den Zusammenhang Fußgröße Körpergröße kann ich sinnvoll treffen?). Das Beispiel zeigt exemplarisch, dass Modellieren schwer sein kann. Realitätsbezüge waren stets ein wichtiges Thema der didaktischen Diskussion zum Mathematikunterricht (siehe Blum/Niss 1991 sowie insbesondere Kap. 1 in Blum et al. 2007). Realität ist dabei (nach Pollak 1979) der Rest der Welt außerhalb der Mathematik. Das Wort Modellieren selbst (das inzwischen geradezu ein Modewort geworden ist) kam dabei erst relativ spät auf. Mathematisches Modellieren soll das Übersetzen zwischen Realität und Mathematik bezeichnen (genauer in 3). Träger von Modellierungsaktivitäten sind Aufgaben (in einem weiten Sinne). Unter einer Modellierungsaufgabe verstehe ich eine realitätsbezogene Aufgabe, die substantielle Anforderungen in Bezug auf die Übersetzungsprozesse Realität Mathematik stellt. Beispiele hierfür sind etwa: - Lohnt es sich, zum Tanken von Trier nach Luxemburg (20 km entfernt) zu fahren? (Aufgabe Tanken, siehe Blum/Leiß 2005) - Wie sollte man die für ein bestimmtes Einkommen zu zahlenden Einkommensteuern festsetzen? - Wie viel Papier erhält ein Haushalt innerhalb eines Jahres alleine durch Werbung? (Maaß 2007)
2 Bei solchen Aufgaben ist das primäre Ziel, das jeweilige Realproblem in den Griff zu bekommen. Dagegen dienen die schulklassischen eingekleideten Textaufgaben in erster Linie dazu, Anlässe zur Beschäftigung mit Mathematik zu schaffen. Bei solchen Aufgaben ist a priori klar, dass es genau eine Lösung gibt, dass genau die zur Lösung benötigten Daten gegeben sind und dass der grade vorher gelernte Stoff zur Lösung ausreicht. Nach Kirsch (1991) sind solche Aufgaben so konstruiert, dass die Rechnung funktioniert, auch wenn der Sachverhalt gedanklich nicht voll erfasst ist. Im Folgenden beschäftige ich mich mit dem Thema Modellieren unter verschiedenen Blickwinkeln (beschränkt auf 10 Seiten). Viele Beispiele (wie schon das einleitende) stammen dabei aus dem DFG-Projekt DISUM (Genaueres hierzu ist in den Beiträgen von Leiß/Blum, Müller u.a. und Schukajlow/Messner in diesem Band zu finden). In DISUM wird das Lehrerund Schülerhandeln in Lernumgebungen mit Modellierungsaufgaben untersucht, mit einem Schwerpunkt auf den Klassen Entsprechend konzentriert sich auch die vorliegende Arbeit auf diese Klassenstufen. 2. Wunsch und Wirklichkeit Realitätsbezüge, Anwendungen und Modellieren sind fast immer als wichtig für den Mathematikunterricht angesehen worden. Die wesentlichen Gründe hierfür sind (vgl. Blum/Niss 1991, Kaiser 2006 und Winter 1995): - Mathematik als Hilfe zum Weltverstehen - Realitätsbezüge als ein Vehikel zur Entwicklung von Kompetenzen und von adäquaten Einstellungen und Haltungen - Realitätsbezüge als Beitrag zu einem angemessenen Mathematikbild - Realitätsbezüge als Hilfe beim Mathematiklernen (Motivation, Begriffsbildung, Verstehen, Behalten, Begründen) Allgemeiner: Realitätsbezüge als ein Beitrag (natürlich nicht der einzige!), dem Unterricht mehr Sinn zu geben. Mit Recht ist Modellieren auch eine der zentralen Kompetenzen in den Bildungsstandards Mathematik. Je nach den verfolgten Zielen sind unterschiedliche Typen von Aufgaben optimal. Dabei haben, wenn es um Kompetenzentwicklung und Lernunterstützung geht, auch eingekleidete Aufgaben ihren Platz. Wichtig ist nur, dass ihr Charakter offengelegt wird und nicht Fiktionen für die Wirklichkeit ausgegeben werden. Und wichtig ist natürlich eine ausgewogene Mischung verschiedener Typen, von authentischen Modellierungsaufgaben bis zu künstlichen Einkleidungen. So weit die normativen Wunschvorstellungen. Hierzu gibt es einen breiten Konsens in der nationalen und internationalen didaktischen Diskussion,
3 und es gibt ermutigende Trends in den letzten 25 Jahren (vgl. Blum 1996). Wie sieht die Unterrichtsrealität aus? Die PISA-Ergebnisse zeigen: Schüler haben weltweit große Probleme mit Modellierungsaufgaben, Modellieren ist offensichtlich schwer! Das liegt auch (natürlich nicht nur) am Mathematikunterricht. Alle Untersuchungen zeigen, dass im Alltagsunterricht in Deutschland (und auch anderswo) Modellieren eher wenig vorkommt. Wenn Realitätsbezüge behandelt werden, dann sind es vorwiegend Textaufgaben zum jeweiligen Stoffgebiet, die für die nächste Klassenarbeit eingeübt werden. Wie gering der Anteil des Modellierens ist, zeigen unsere Erhebungen im Rahmen des COACTIV-Projekts (siehe Brunner u.a. 2006). U. a. haben wir sämtliche Klassenarbeiten der deutschen PISA-Klassen 2003 und 2004 erhoben und nach vielen Facetten (siehe Jordan u.a. 2005) klassifiziert. Die durchschnittliche Modellierungsintensität betrug hier auf einer von 0 bis 3 reichenden Skala 0.21 bzw Zum Vergleich: Die Modellierungsintensität der PISA-Aufgaben 2003 liegt auf dieser Skala immerhin bei In diesem Lichte sind die enttäuschenden Modellierungsfähigkeiten der Schüler eigentlich wenig überraschend. Weshalb ist die Situation im Unterricht so? Das liegt wesentlich daran, dass Modellieren auch für Lehrer schwer ist, der Unterricht wird hierdurch komplexer und weniger vorhersagbar, und es ist außermathematisches Sachwissen nötig (Freudenthal 1973, Pollak 1979, Blum 1996, Burkhardt 2004). Oft wird als Grund für die mangelnde Berücksichtigung von Realitätsbezügen auch fehlendes Beispielmaterial für den Unterricht genannt. Das mag vor 25 Jahren noch richtig gewesen sein, aber inzwischen gibt es eine große Fülle erprobter und bewährter Materialien. Von den deutschsprachiger Quellen seien hier nur erwähnt die MUED-Materialien, die ISTRON-Schriftenreihe bei Franzbecker oder Bücher wie Herget/Jahnke/Kroll 2001, Blum u.a oder Maaß Überhaupt hat sich die Situation in den letzten 10 Jahren schon verbessert, insbesondere dank Projekten wie SINUS. Dennoch gibt es bei uns und anderswo noch immer eine große Lücke zwischen der didaktischen Diskussion und der Wirklichkeit des Unterrichts. 3. Ein kognitiver Blick auf das Modellieren Weshalb ist Modellieren so schwer? Das liegt wesentlich auch an den kognitiven Ansprüchen von Modellierungsaufgaben per se. Um dies besser zu verstehen, ist ein Modell des Modellierungsprozesses nützlich. In der Literatur gibt es Dutzende solcher Modelle. Wir haben im DISUM-Projekt ein siebenschrittiges Modell entwickelt, das vor allem diagnostisch hilfreich ist. Idealtypisch steht dabei am Anfang (Schritt 1) das Konstruieren eines
4 mentalen Modells der gegebenen Problemsituation. Dies wird dann (Schritt 2) durch Vereinfachungs-, Idealisierungs- und Strukturierungsaktivitäten in ein Realmodell überführt, das einer mathematischen Behandlung zugänglich ist. Mathematisierung (Schritt 3) führt zu einem mathematischen Modell, das (Schritt 4) mit mathematischen Methoden bearbeitet wird. Die entstehenden mathematischen Ergebnisse werden (Schritt 5) in die Realität zurückübersetzt und dann (Schritt 6) validiert. Eventuell wird dieser Zyklus mehrfach durchlaufen. Am Ende (Schritt 7) steht die Darlegung einer Antwort auf das Ausgangsproblem. Der Vorzug dieses Modells ist die idealtypische Isolierung der wesentlichen Schritte beim Modellieren. Jeder dieser Schritte ist eine potentielle kognitive Hürde beim Lösen von Modellierungsaufgaben (siehe 4). Reale Bearbeitungsprozesse laufen natürlich i. a. nicht so linear ab, vielmehr gibt es spezifische Modellierungsverläufe (Borromeo Ferri 2007; vgl. auch Leiß 2007), die sich dann günstig in diesem Modell verorten lassen. Unter mathematischem Modellieren möchte ich die vier Schritte 2, 3, 5 und 6 verstehen. Vom kognitiven Standpunkt ist es sinnvoll, entsprechend diesen Schritten verschiedene Teilkompetenzen des Modellierens zu definieren. Mit Modellierungskompetenz möchte ich die Fähigkeit bezeichnen, diese Prozessschritte problemadäquat ausführen zu können sowie gegebene Modelle analysieren und vergleichen zu können (Blum et al. 2007, Kap. 1). Beim Lösen von eingekleideten Textaufgaben sind nur vier Schritte nötig: 1) Durchlesen, 2) Entkleiden, 3) Rechnen, 4) Rechnung kontrollieren und Antwortsatz schreiben. Die notwendigen Modellierungsaktivitäten sind hierbei also sehr bescheiden. Auf diesem Hintergrund wird noch klarer, was Modellieren so schwer macht: Man muss, bevor es zum eigentlichen Mathematisieren kommt, die Schritte des Konstruierens eines Situationsmodells und hieraus eines mathematisierbaren Realmodells selbst vollziehen. Griesel (2005) spricht von der nötigen idealisierenden Abstraktion, die Lernenden naturgemäß schwerfällt und die eine völlig neue Qualität des Mathematikunterrichts erfordert. Die Kompetenz des mathematischen Modellierens ist, wie gesehen, untrennbar mit anderen Kompetenzen verwoben, nämlich mit Text-Lesen und Ergebnis-Darlegen ( Kommunizieren ), Entwerfen und Anwenden von Bearbeitungsstrategien ( Problemlösen ) sowie vielfältigem innermathematischen Arbeiten. Alleine deshalb ist Modellieren kognitiv anspruchsvoll. Hinzu kommt, dass in allen Modellierungsschritten inhaltliche Vorstellungen von den involvierten mathematischen Inhalten benötigt werden, z. B. zu proportionalen Funktionen bei der einführenden Aufgabe Riesenschuhe. Realsituationen sind auch deshalb schwer zu durchschauen, weil
5 oft spezifisches Weltwissen notwendig ist. Fazit (nicht überraschend): Modellieren ist eine äußerst vielschichtige und kognitiv anspruchsvolle Tätigkeit. Dies in den Unterricht zu integrieren und bei Schülern entsprechende Kompetenzen aufzubauen, ist für Lehrer bestimmt sehr anspruchsvoll. Ist das vielleicht doch zu schwer für Schüler und Lehrer? 4. Einige empirische Erkenntnisse Dass die Schwierigkeit von Modellierungsaufgaben tatsächlich nicht an Äußerlichkeiten liegt, sondern wesentlich an der kognitiven Komplexität der nötigen Übersetzungsprozesse, zeigen mehrere regressionsanalytisch angelegte Studien, so von Blum u.a. und von Cohors-Fresenborg u.a. zu den PISA-2000-Aufgaben (in Neubrand 2004) und jüngst von der internationalen PISA Mathematics Expert Group (noch unveröffentlicht) zu den PISA-2003-Aufgaben; die aufgeklärte Varianz liegt hier bei über 60 %. Mehrere qualitative Studien zeigen: Alle potentiellen kognitiven Hürden bei Modellierungsaufgaben (siehe 3) lassen sich auch beobachten, spezifisch je nach Aufgabe und Individuum. Es gibt also empirische Hinweise darauf, dass man tatsächlich unterschiedliche Teilkompetenzen des Modellierens unterscheiden kann (siehe schon Treilibs 1979). Z.B. liegen die im einführenden Beispiel erkennbaren Schülerschwierigkeiten schon im ersten Bearbeitungsschritt. Statt ein adäquates Situationsmodell zu konstruieren, weichen die Schüler in eine Ersatzstrategie aus. Dies ist eine häufig zu beobachtende und im Alltagsunterricht durchaus erfolgreiche Strategie (Verschaffel/Greer/deCorte 2005). Ebenso lassen sich Schwierigkeiten bei allen anderen Schritten identifizieren. Eigenständige Validierungsaktivitäten von Schülern sind dabei kaum zu beobachten, vielmehr scheint für die Korrektheit von Lösungen ausschließlich die Lehrkraft zuständig zu sein. Auffallend ist, dass bei Schülern kaum Lösungsstrategien erkennbar sind. Auch das Bewusstsein für sinnvolle Ergebnis-Genauigkeiten ist nur schwach ausgeprägt. Das gilt mitunter sogar für Lehrer. Weitere Beobachtungen zum Lehrerverhalten: Spontane Lehrerhilfen bei Schülerschwierigkeiten sind meist nicht adaptiv und minimal, i. a. geben Lehrer inhaltliche statt bloß strategische Hilfen. Oft sind die Pole Schüler arbeiten alleine und Schüler arbeiten unselbständig anzutreffen, d.h. es fehlt eine adäquate Balance zwischen Lehreranleitung und Schülerselbständigkeit. Besonders wichtig und keinesfalls selbstverständlich ist die Feststellung, dass es einen fundamentalen Unterschied macht, ob Schüler alleine oder selbständig mit Lehrerunterstützung arbeiten, kurz: dass Lehrer unentbehrlich sind (Pauli/Reusser 2000). Überhaupt zeigen ja neueste Ergebnisse aus dem COACTIV-Projekt, wie entscheidend wichtig für die Lernfortschritte der
6 Schüler die professionelle Kompetenz der Lehrkraft ist, insbesondere ihr fachdidaktisches Wissen. Im Folgenden einige weitere empirische Erkenntnisse zum Modellieren aus verschiedenen Studien (wobei die Forschungslage insgesamt noch nicht befriedigend ist, siehe Niss 2001 und Blum et al. 2007). Ich beschränke mich hier auf die Wiedergabe von Resultaten, weitgehend ohne Belege: Gemäß Situated Cognition lernt man Modellieren nicht durch einen mystischen Transfer aus irgendwelchen andersartigen Aktivitäten, vielmehr muss Modellieren explizit gelernt werden, durch zielgerichtete Aktivitäten in geeigneten Lernumgebungen. Modellieren kann gelernt werden (u. a.: Kaiser-Meßmer 1986, Maaß 2004), es braucht Zeit und es kommt auf den Unterricht an. Dabei sind die bekannten und empirisch gut gesicherten Qualitätskriterien auch für einen Mathematikunterricht wichtig, der auf Modellierungskompetenzen abzielt, nämlich: - eine fachlich gehaltvolle Unterrichtsgestaltung, - die kognitive Aktivierung der Lernenden, - eine effektive und schülerorientierte Unterrichtsführung. Speziell ist strategisches Verhalten auch beim Modellieren hilfreich (vgl. Kap. 3.3 in Blum et al. 2007). Solche metakognitiven Aktivitäten sind für alle Schüler sinnvoll und profitabel, nicht nur für die guten. Schüler- und Lehrer-Beliefs sind ein bedeutsamer Einflussfaktor auch beim Modellieren. Sie sind kurzfristig stabil, aber mittelfristig veränderbar (u. a. Maaß 2004). Schüler- und Lehrer-Denkstile sind ein bedeutsamer Einflussfaktor auch beim Modellieren (Borromeo Ferri 2007). 5. Folgerungen Die Titelfrage Ist Modellieren zu schwer? lässt sich sowohl aus theoretisch-kognitiver als auch aus empirischer Sicht kurz so beantworten: Modellieren ist schwer, aber nicht zu schwer, vielmehr gibt es dichte Hinweise auf Gelingensbedingungen, deren Berücksichtigung bei Konstanthalten anderer Bedingungen bessere Lernerfolge mit sich bringt. Insofern liegen entsprechende Folgerungen für das Lehren und Lernen nahe. Die erste Folgerung ist selbstverständlich, aber höchst konsequenzenreich: Folgerung 1: Die bekannten Qualitätskriterien für guten Mathematikunterricht (siehe 4) müssen speziell auch in einem modellierungsorientierten Un-
7 terricht berücksichtigt werden. Der Ansatz der Neuen Aufgabenkultur (wie beim SINUS-Projekt) ist dabei ein Schlüssel zum Erfolg. Speziell scheint entscheidend zu sein: Folgerung 2: Auch im modellierungsorientierten Mathematikunterricht muss stets die Balance zwischen größtmöglicher Schülerselbständigkeit und geringstmöglicher Lehreranleitung gewahrt werden (im Sinne des bekannten Montessori-Prinzips Hilf mir, es selbst zu tun ). Auch dies klingt fast selbstverständlich, ist aber in der Unterrichtspraxis höchst selten zu finden. Entsprechende Schulungen kommen in der bisherigen Lehrerbildung kaum vor. Über ein gelungenes Beispiel (konstruktives Umgehen mit einem Schülerfehler im Zusammenhang mit der Modellierungsaufgabe Leuchtturm ) habe ich in Blum (2007) im Detail berichtet. Zum strategischen Verhalten: Zum Glück gibt es für das Modellieren ein spezifisches strategisches Werkzeug, nämlich den Modellierungskreislauf. Nun ist das in 3 vorgestellte siebenschrittige Modell für Forschungszwecke höchst adäquat, für Schüler und mitunter auch für Lehrer aber zu subtil. Wir haben in DISUM eine vierschrittige Variante für Schüler entwickelt, den sogenannten Lösungsplan (für Details siehe Blum 2006): 1) Aufgabe verstehen, 2) Modell erstellen, 3) Mathematik benutzen, 4) Ergebnis erklären. Wir konnten mehrfach dessen erfolgreichen Einsatz bei Schülerschwierigkeiten beobachten, teilweise vom Lehrer induziert, teilweise von den Schülern selbständig herangezogen. Insofern liegt nahe: Folgerung 3: Hilfreich für Schüler und Lehrer ist ein Werkzeug analog zum Lösungsplan (für Schüler als Hilfe bei allfälligen Schwierigkeiten im Lösungsprozess, für Lehrer als Basis für Diagnosen und Interventionen). Nötig ist eine systematische Einübung in dessen Gebrauch. Schließlich ist eine entscheidende globale Folgerung diese: Folgerung 4: Modellierungskompetenz muss langfristig und gestuft aufgebaut werden, u. a. durch - eine allmähliche Steigerung der Komplexität von Aufgaben, - ein breites Spektrum von Aufgabentypen und eine systematische Variation der Kontexte, - den parallelen Aufbau heuristischer Fähigkeiten, - häufige Übungs- und Festigungsphasen. Hiermit sollte möglichst schon in der Grundschule begonnen werden. Dies sollte nicht losgelöst vom lehrplangemäßen Aufbau der Stoffinhalte geschehen, sondern in diesen integriert.
8 6. Ermutigende Ergebnisse Zahlreiche empirische Untersuchungen ebenso wie inzidentielle Unterrichtsbeobachtungen legen den Schluss nahe, dass es ein enormes Potential für Verbesserungen des Mathematikunterrichts gibt, in Deutschland wie auch anderswo. Dies gilt speziell auch für den Aufbau von Modellierungskompetenz. Wir haben im Rahmen von DISUM eine zehnstündige Unterrichtseinheit zum Modellieren konstruiert, um kontrolliert zu untersuchen, unter welchen Bedingungen was für Lernzuwächse möglich sind. Die Unterrichtseinheit war curricular in das Thema Satzgruppe des Pythagoras eingebunden. Sie wurde in mehreren Haupt- und Realschulklassen durchgeführt. Insbesondere haben wir im Herbst 2006 in vier Realschulklassen untersucht, wie sich zwei Unterrichtsformen, operativ-strategischer und direktiver Unterricht, auswirken. Das Design war klassisch angelegt: Auswahltest (PISA) zur Homogenisierung/ Vortest (Pythagoras und Modellieren)/ Treatment mit Begleitbefragungen/ Nachtest/ Follow-Up-Test. Die bei der Homogenisierung ausgesonderten Schüler bildeten eine eigene Untersuchungsgruppe; sie bekamen keinerlei Lehrerunterstützung, sondern mussten alleine arbeiten. Alle Schüler, ob im Unterricht oder in den alleinarbeitenden Gruppen, bekamen dieselben Aufgaben in derselben Abfolge. Was operativ-strategischer bzw. direktiver Unterricht bedeutet, ist in den Beiträgen von Leiß/Blum und von Müller u.a. in diesem Band nachzulesen. Kurz gesagt soll im operativ-strategischen Design jene Balance zwischen Lehreranleitung und Schülerselbständigkeit (wie sie oben in Folgerung 2 formuliert ist) realisiert werden, wobei die Lehrerinterventionen auf Basis der Lösungspläne (siehe Folgerung 3) erfolgen sollen. Das direktive Design soll den deutschen Alltagsunterricht modellieren. Beide Designvarianten wurden als Optimalunterricht konzipiert und von erfahrenen und gezielt geschulten SINUS-Lehrkräften realisiert. Hier sind einige wesentliche Ergebnisse unserer Untersuchung: - Die Realisierung eines designadäquaten operativ-strategischen Unterrichts ist höchst anspruchsvoll. Lehrer tendieren trotz Schulung öfter zu inhaltlichen, mitunter fehlerpräventiven, jedenfalls selbständigkeitseinschränkenden Interventionen. Es gelingt auch bei Kleingruppenarbeit nicht immer, die geistige Aktivität aller Schüler aufrechtzuerhalten. - Die mittleren Lernzuwächse zwischen Vortest und Nachtest sind bei beiden Designvarianten signifikant. Normativ gesehen bleiben die Modellierungsleistungen aber auch nach dem Treatment eher enttäuschend. - Die Lernzuwächse der operativ-strategisch unterrichteten Schüler sind im Mittel höher und vor allem (Follow-Up-Test) deutlich nachhaltiger
9 als die der direktiv unterrichteten Schüler, und deren Zuwächse sind wiederum deutlich höher als die der alleine arbeitenden Schüler. - Beim operativ-strategischen Design profitieren leistungsstärkere Schüler mehr als beim direktiven Design. Bei Alleinarbeit erreichen i. W. nur leistungsstärkere Schüler Lernzuwächse. Wegen der geringen Fallzahlen sind dies i. W. nur Tendenzaussagen. Wir planen für Herbst 2007 eine größere Studie, um belastbarere Resultate zu bekommen. Und natürlich kann eine zehnstündige Unterrichtsreihe nur begrenzte Wirkung haben. Doch bereits die jetzigen Resultate sind durchaus ermutigend: Modellieren scheint lehr- und lernbar zu sein! Mit diesen Ergebnissen im Hintergrund ist es eigentlich nicht weiter gerechtfertigt, tagtäglich allüberall gegen lernwirksame Lehr-/Lernprinzipien zu verstoßen. Vielmehr sind alle Anstrengungen darauf zu richten, diese Prinzipien im Alltagsunterricht zu implementieren. Notwendig hierfür ist eine Implementation der vorliegenden Erkenntnisse in die Lehreraus- und - fortbildung. Beide Forderungen werden sicher nicht zum ersten Mal erhoben. Mein Optimismus, dass beides realisierbar ist, gründet vor allem auf den neuen Möglichkeiten, die sich durch die Bildungsstandards eröffnen. Natürlich gibt es weiterhin eine Fülle offener Fragen, die einer systematischen wissenschaftlichen Untersuchung bedürfen, u. a.: - Was ist bei einem langfristig angelegten Aufbau von Modellierungskompetenz tatsächlich erreichbar? Speziell dabei: Wie kann man den Aufbau von Teilkompetenzen optimieren? - Wie kann das Zusammenspiel verschiedener Kompetenzen systematisch gefördert werden? Die letzte Frage liegt im Zentrum aller Anstrengungen, geht es doch nicht nur um die Förderung von Modellierungskompetenz, sondern um eine umfassende mathematische Bildung unserer Kinder und Jugendlichen. Literatur Blum, W. (1996): Anwendungsbezüge im Mathematikunterricht Trends und Perspektiven. In: Trends und Perspektiven (Hrsg.: Kadunz, G. u.a.), Schriftenreihe Didaktik der Mathematik, Bd. 23. Hölder- Pichler-Tempsky, Wien, Blum, W. (2006): Modellierungsaufgaben im Mathematikunterricht Herausforderung für Schüler und Lehrer. In: Realitätsnaher Mathematikunterricht vom Fach aus und für die Praxis (Hrsg.: Büchter, A. u.a.). Franzbecker, Hildesheim, 8-23 Blum, W./ Drüke-Noe, C./ Hartung, R./ Köller, O. (Hrsg., 2006): Bildungsstandards Mathematik: konkret. Cornelsen-Scriptor, Berlin Blum, W./ Galbraith, P./ Henn, H.-W./ Niss, M. (Eds, 2007): Modelling and Applications in Mathematics Education. Springer, New York
10 Blum, W./ Leiß, D. (2005): Modellieren im Unterricht mit der Tanken -Aufgabe. In: mathematik lehren, H. 128, Blum, W./ Niss, M. (1991): Applied Mathematical Problem Solving, Modelling, Applications, and Links to Other Subjects State, Trends and Issues in Mathematics Instruction. In: Educational Studies in Mathematics 22(1), Borromeo Ferri, R. (2007): Modelling Problems from a Cognitive Perspective. In: Mathematical Modelling (ICTMA 12): Education, Engineering and Economics (Eds: Haines, C. et al.). Horwood, Chichester, Brunner, M. u.a. (2006): Die professionelle Kompetenz von Mathematiklehrkräften: Konzeptualisierung, Erfassung und Bedeutung für den Unterricht. Eine Zwischenbilanz des COACTIV-Projekts. In: Untersuchungen zur Bildungsqualität von Schule (Hrsg.: Prenzel, M./ Allolio-Näcke, L.). Waxmann, Münster, Burkhardt, H. (2004): Establishing Modelling in the Curriculum: Barriers and Levers. In: ICMI Study 14: Applications and Modelling in Mathematics Education Pre-Conference Volume (Eds: Henn, H.-W./ Blum, W.). Universität Dortmund Freudenthal, H. (1973): Mathematik als pädagogische Aufgabe, Band 1. Stuttgart, Klett Griesel, H. (2005): Modelle und Modellieren. In: Mathematikunterricht im Spannungsfeld von Evolution und Evaluation (Hrsg.: Henn, H.-W./ Kaiser, G.). Franzbecker, Hildesheim, Herget, W./ Jahnke, T./ Kroll, W. (2001): Produktive Aufgaben für den Mathematikunterricht in der Sekundarstufe I. Cornelsen, Berlin Jordan, A. u.a. (2005): Klassifikationsschema für Mathematikaufgaben. Dokumentation der Aufgabenkategorisierung im COACTIV-Projekt. Materialien aus der Bildungsforschung Nr. 81, Max-Planck-Institut für Bildungsforschung, Berlin Kaiser-Meßmer, G. (1986): Anwendungen im Mathematikunterricht, Band 2. Franzbecker, Salzdetfurth Kaiser, G. (2006): A Global Survey of International Perspectives on Modelling in Mathematics Education. In: Zentralblatt für Didaktik der Mathematik 38(3), Kirsch, A. (1991): Formalismen oder Inhalte? Schwierigkeiten mit linearen Gleichungssystemen im 9. Schuljahr. In: Didaktik der Mathematik 19(4), Leiß, D. (2007): Lehrerinterventionen im selbständigkeitsorientierten Prozess der Lösung einer mathematischen Modellierungsaufgabe Maaß, K. (2004): Mathematisches Modellieren im Unterricht. Franzbecker, Hildesheim Maaß, K. (2007): Mathematisches Modellieren. Aufgaben für die Sekundarstufe I. Cornelsen-Scriptor, Berlin Neubrand, M. (Hrsg., 2004): Mathematische Kompetenzen von Schülerinnen und Schülern in Deutschland Vertiefende Analysen im Rahmen von PISA Verlag für Sozialwissenschaften, Wiesbaden Niss, M. (1991): ). Issues and Problems of Research on the Teaching and Learning of Applications and Modelling. In: Modelling and Mathematics Education: ICTMA-9 (Eds: Matos, J. F. et al.). Horwood, Chichester, Pauli, C./ Reusser, K. (2000): Zur Rolle der Lehrperson beim kooperativen Lernen. In: Schweizerische Zeitschrift für Bildungswissenschaften 3, Pollak, H. (1979): The Interaction between Mathematics and Other School Subjects. In: New Trends in Mathematics Teaching IV (Ed.: UNESCO). UNESCO, Paris, Treilibs, V. (1979): Formulation Processes in Mathematical Modelling. Shell Centre for Mathematical Education, University of Nottingham Verschaffel, L./ Greer, B./ decorte, E. (2000): Making Sense of Word Problems. Lisse: Swets&Zeitlinger Winter, H. (1995): Mathematikunterricht und Allgemeinbildung. In: Mitteilungen der Gesellschaft für Didaktik der Mathematik Nr. 61, 37 46
Kann mathematisches Modellieren selbständig gelernt werden? Ergebnisse aus der Lehr-/Lernforschung
 Kann mathematisches Modellieren selbständig gelernt werden? Ergebnisse aus der Lehr-/Lernforschung Universität Paderborn, 29.4.2010 Werner Blum, Universität Kassel 3 1 2 4 7 6 5 Programm: 1 Die Neue Aufgabenkultur
Kann mathematisches Modellieren selbständig gelernt werden? Ergebnisse aus der Lehr-/Lernforschung Universität Paderborn, 29.4.2010 Werner Blum, Universität Kassel 3 1 2 4 7 6 5 Programm: 1 Die Neue Aufgabenkultur
Modellierungsaufgaben in Klassenarbeiten
 Modellierungsaufgaben in Klassenarbeiten Gerechte Bewertung (un)möglich? Ziele Modellierungen und Realitätsbezüge Mathematik im Leben anwenden Bedeutung von Mathematik für das Leben und unsere Gesellschaft
Modellierungsaufgaben in Klassenarbeiten Gerechte Bewertung (un)möglich? Ziele Modellierungen und Realitätsbezüge Mathematik im Leben anwenden Bedeutung von Mathematik für das Leben und unsere Gesellschaft
Das Backsteinhaus ist ungefähr 3,875 m hoch Zum Einfluss der Größenvorstellungen auf die Modellierungskompetenz
 Maike HAGENA, Kassel Das Backsteinhaus ist ungefähr 3,875 m hoch Zum Einfluss der Größenvorstellungen auf die Modellierungskompetenz von Studierenden Im vorliegenden Beitrag werden der Aufbau einer Interventionsstudie
Maike HAGENA, Kassel Das Backsteinhaus ist ungefähr 3,875 m hoch Zum Einfluss der Größenvorstellungen auf die Modellierungskompetenz von Studierenden Im vorliegenden Beitrag werden der Aufbau einer Interventionsstudie
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Mathematisch Modellieren am Beispiel von Eisverkäufern und Dönerimbissen
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Mathematisch Modellieren am Beispiel von Eisverkäufern und Dönerimbissen Das komplette Material finden Sie hier: School-Scout.de S
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Mathematisch Modellieren am Beispiel von Eisverkäufern und Dönerimbissen Das komplette Material finden Sie hier: School-Scout.de S
Selbständigkeitsorientierter Unterricht mit Modellierungsaufgaben Stanislaw Schukajlow
 ISTRON-Gruppe Selbständigkeitsorientierter Unterricht mit Modellierungsaufgaben Stanislaw Schukajlow ISTRON-Tagung, Wien, 6.11.2009 Gliederung 1. Einleitung: Selbständiges Lernen 2. Einstimmung auf die
ISTRON-Gruppe Selbständigkeitsorientierter Unterricht mit Modellierungsaufgaben Stanislaw Schukajlow ISTRON-Tagung, Wien, 6.11.2009 Gliederung 1. Einleitung: Selbständiges Lernen 2. Einstimmung auf die
Kompetenzentwicklung im Mathematik-Unterricht: Modellieren *
 Kompetenzentwicklung im Mathematik-Unterricht: Modellieren * 1. Zur Kompetenz Modellieren 1.1. Modelle und Modellieren Sowohl in der nationalen als auch in der internationalen mathematikdidaktischen Diskussion
Kompetenzentwicklung im Mathematik-Unterricht: Modellieren * 1. Zur Kompetenz Modellieren 1.1. Modelle und Modellieren Sowohl in der nationalen als auch in der internationalen mathematikdidaktischen Diskussion
1.5 Modellieren Maximilian Geier Institut für Mathematik, Landau Universität Koblenz-Landau
 Maximilian Geier Institut für Mathematik, Landau Universität Koblenz-Landau Modellieren & Sachrechnen - werden mal als Gegensätze - mal als mehr oder weniger identisch - und mal wird Modellieren als Teil
Maximilian Geier Institut für Mathematik, Landau Universität Koblenz-Landau Modellieren & Sachrechnen - werden mal als Gegensätze - mal als mehr oder weniger identisch - und mal wird Modellieren als Teil
Von der kompetenzorientierten Aufgabe zu kompetenzorientiertem Unterricht
 Von der kompetenzorientierten Aufgabe zu kompetenzorientiertem Unterricht Mathematik-Tagung 2010 Mit Vielfalt rechnen Hamburg, 07./ 08. Mai 2010 Christina Drüke-Noe 1 Gliederung 1. Zwei Aufgaben zur Einstimmung
Von der kompetenzorientierten Aufgabe zu kompetenzorientiertem Unterricht Mathematik-Tagung 2010 Mit Vielfalt rechnen Hamburg, 07./ 08. Mai 2010 Christina Drüke-Noe 1 Gliederung 1. Zwei Aufgaben zur Einstimmung
Realitätsbezüge im Mathematikunterricht
 Realitätsbezüge im Mathematikunterricht Mathematisches Modellieren ist ein zentrales Thema des Mathematikunterrichts und ein Forschungsfeld, das in der nationalen und internationalen mathematikdidaktischen
Realitätsbezüge im Mathematikunterricht Mathematisches Modellieren ist ein zentrales Thema des Mathematikunterrichts und ein Forschungsfeld, das in der nationalen und internationalen mathematikdidaktischen
Entwicklung einer rechnergestützten mathematischen Lernumgebung für interaktiven Kompetenzerwerb
 Entwicklung einer rechnergestützten mathematischen Lernumgebung für interaktiven Kompetenzerwerb Svetlana Polushkina Graduiertenkolleg Qualitätsverbesserung im E-Learning durch rückgekoppelte Prozesse
Entwicklung einer rechnergestützten mathematischen Lernumgebung für interaktiven Kompetenzerwerb Svetlana Polushkina Graduiertenkolleg Qualitätsverbesserung im E-Learning durch rückgekoppelte Prozesse
Didaktik des Sachrechnens 4. Probleme von SuS beim Lösen von Sachaufgaben
 Didaktik des Sachrechnens 4. Probleme von SuS beim Lösen von Sachaufgaben 1 Probleme beim Lösen von Sachaufgaben Veröffentlicht in: MDMV 20, 2012, S. 235 2 4. Probleme von SuS beim Lösen von Sachaufgaben
Didaktik des Sachrechnens 4. Probleme von SuS beim Lösen von Sachaufgaben 1 Probleme beim Lösen von Sachaufgaben Veröffentlicht in: MDMV 20, 2012, S. 235 2 4. Probleme von SuS beim Lösen von Sachaufgaben
BLK-Programm SINUS-Transfer Workshop II: Kompetenzorientierte Aufgaben
 BLK-Programm SINUS-Transfer Workshop II: Kompetenzorientierte Aufgaben Alexander Jordan, Kassel/Bielefeld Soltau, 30. März 2006 Gliederung: Was erwartet Sie? Die Konstruktion und Klassifikation standardbezogener
BLK-Programm SINUS-Transfer Workshop II: Kompetenzorientierte Aufgaben Alexander Jordan, Kassel/Bielefeld Soltau, 30. März 2006 Gliederung: Was erwartet Sie? Die Konstruktion und Klassifikation standardbezogener
"MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN
 1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Inhalte: Modellierungskompetenzen Gestufte Hilfen
1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Inhalte: Modellierungskompetenzen Gestufte Hilfen
EV 4.4 Aufgabenkultur
 Fakultät MN, Fachrichtung Psychologie, Professur für die Psychologie des Lehrens und Lernens EV 4.4 Aufgabenkultur Dresden, 08.06.2006 Lernen Bild: http://www.finanzkueche.de/aufgaben-der-schule/ TU Dresden,
Fakultät MN, Fachrichtung Psychologie, Professur für die Psychologie des Lehrens und Lernens EV 4.4 Aufgabenkultur Dresden, 08.06.2006 Lernen Bild: http://www.finanzkueche.de/aufgaben-der-schule/ TU Dresden,
Biomathematik als Unterrichtseinheit I. Jasmin Sima
 Biomathematik als Unterrichtseinheit I Jasmin Sima 0802181 Was ist guter Unterricht? Fachlich gehaltvolle Unterrichtsgestaltung Kognitive Aktivierung der Schülerinnen und Schüler Effektive und schülerorientierte
Biomathematik als Unterrichtseinheit I Jasmin Sima 0802181 Was ist guter Unterricht? Fachlich gehaltvolle Unterrichtsgestaltung Kognitive Aktivierung der Schülerinnen und Schüler Effektive und schülerorientierte
Unterricht mit Guten Aufgaben vorbereiten
 Unterricht mit Guten Aufgaben vorbereiten Aufgabenauswahl, Aufgabenanalyse, Aufgabenvariation Brigitte Döring (IPN) und Gerd Walther (Mathematisches Seminar der CAU zu Kiel) Gliederung 1. Das tägliche
Unterricht mit Guten Aufgaben vorbereiten Aufgabenauswahl, Aufgabenanalyse, Aufgabenvariation Brigitte Döring (IPN) und Gerd Walther (Mathematisches Seminar der CAU zu Kiel) Gliederung 1. Das tägliche
"MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN
 1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Fragen von Lehrenden in der Praxis: Mathematisches
1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Fragen von Lehrenden in der Praxis: Mathematisches
3 Etappen im IQB. Perspektiven und Visionen
 3 Etappen im IQB Grundsätzliches zum Institut und zum Testen Eigene Testphase (Ma oder En) und allgemeine Reflexion zu den Aufgaben Implementationsprojekt IQB und LISUM Perspektiven und Visionen Arbeitsbereiche
3 Etappen im IQB Grundsätzliches zum Institut und zum Testen Eigene Testphase (Ma oder En) und allgemeine Reflexion zu den Aufgaben Implementationsprojekt IQB und LISUM Perspektiven und Visionen Arbeitsbereiche
Schweizer MINT Studie: Vorbereitung auf zukünftiges Lernen. Naturwissenschaftliches Denken ab der Primarschule fördern
 DAS -LERNZENTRUM DER ETH ZÜRICH Schweizer MINT Studie: Vorbereitung auf zukünftiges Lernen Naturwissenschaftliches Denken ab der Primarschule fördern Ralph Schumacher & Elsbeth Stern, ETH Zürich Mai 2018
DAS -LERNZENTRUM DER ETH ZÜRICH Schweizer MINT Studie: Vorbereitung auf zukünftiges Lernen Naturwissenschaftliches Denken ab der Primarschule fördern Ralph Schumacher & Elsbeth Stern, ETH Zürich Mai 2018
Realitätsbezüge im Mathematikunterricht
 Realitätsbezüge im Mathematikunterricht Mathematisches Modellieren ist ein zentrales Thema des Mathematikunterrichts und ein Forschungsfeld, das in der nationalen und internationalen mathematikdidaktischen
Realitätsbezüge im Mathematikunterricht Mathematisches Modellieren ist ein zentrales Thema des Mathematikunterrichts und ein Forschungsfeld, das in der nationalen und internationalen mathematikdidaktischen
Auf dem Weg zu einer kompetenzorientierten Unterrichts- und Aufgabenkultur
 Auf dem Weg zu einer kompetenzorientierten Unterrichts- und Aufgabenkultur Jahrestagung des ZLB Kassel, 18. Juni 2010 Werner Blum, Universität Kassel Argumentationsstrang: Vergleichsstudien Bildungsstandards
Auf dem Weg zu einer kompetenzorientierten Unterrichts- und Aufgabenkultur Jahrestagung des ZLB Kassel, 18. Juni 2010 Werner Blum, Universität Kassel Argumentationsstrang: Vergleichsstudien Bildungsstandards
Prozessorientierte Kompetenzen
 Prozessorientierte Kompetenzen diagnostizieren und fördern im Mathematikunterricht Mathematische Kompetenzen Mathematisch argumentieren Kommunizieren Math. Darstellungen verwenden Problemlösen Modellieren
Prozessorientierte Kompetenzen diagnostizieren und fördern im Mathematikunterricht Mathematische Kompetenzen Mathematisch argumentieren Kommunizieren Math. Darstellungen verwenden Problemlösen Modellieren
LEMA - Learning in and through modelling and applications
 LEMA - Learning in and through modelling and applications Worum geht es bei LEMA? In ganz Europa steigt das Bewusstsein, dass Schüler das kritische und reflektierte Anwenden von Mathematik lernen müssen,
LEMA - Learning in and through modelling and applications Worum geht es bei LEMA? In ganz Europa steigt das Bewusstsein, dass Schüler das kritische und reflektierte Anwenden von Mathematik lernen müssen,
Reichhaltige Aufgaben auch in den Klassenarbeiten! Was machen wir heute?
 Reichhaltige Aufgaben auch in den Klassenarbeiten! Mathematikunterricht neu entdecken Dortmund, 5. März 2008 Motto des Workshops Die Förderung prozessbezogener Kompetenzen von Schülerinnen und Schülern
Reichhaltige Aufgaben auch in den Klassenarbeiten! Mathematikunterricht neu entdecken Dortmund, 5. März 2008 Motto des Workshops Die Förderung prozessbezogener Kompetenzen von Schülerinnen und Schülern
Situiertes Lernen. Seminar zum semesterbegleitenden fachdidaktischen Praktikum Mathematik. Referentin: Stephanie Jennewein
 Situiertes Lernen Seminar zum semesterbegleitenden fachdidaktischen Praktikum Mathematik Referentin: Stephanie Jennewein Verlauf 1. Situiertes Lernen 2. Situiertes Lernen im Unterricht 3. Gruppenarbeit
Situiertes Lernen Seminar zum semesterbegleitenden fachdidaktischen Praktikum Mathematik Referentin: Stephanie Jennewein Verlauf 1. Situiertes Lernen 2. Situiertes Lernen im Unterricht 3. Gruppenarbeit
Gliederung 1. Was lernen unsere Schülerinnen und Schüler im Mathematikunterricht? 2. Was lernen unsere Schülerinnen und Schüler im naturwissenschaftli
 Manfred Prenzel Leibniz-Institut für die Pädagogik der Naturwissenschaften (IPN) an der Universität Kiel Zur Situation des mathematischen und naturwissenschaftlichen Unterrichts 8. Münchner Wissenschaftstage
Manfred Prenzel Leibniz-Institut für die Pädagogik der Naturwissenschaften (IPN) an der Universität Kiel Zur Situation des mathematischen und naturwissenschaftlichen Unterrichts 8. Münchner Wissenschaftstage
8 Planarbeit zur Vertiefung der Inhalte
 8 Planarbeit zur Vertiefung der Inhalte 8.1 Tabellarische Übersicht Zunächst sei eine Übersicht gegeben, aus der hervorgeht, mit welchen Aufgaben über welche Grundideen nachgedacht werden soll. Die Aufgaben
8 Planarbeit zur Vertiefung der Inhalte 8.1 Tabellarische Übersicht Zunächst sei eine Übersicht gegeben, aus der hervorgeht, mit welchen Aufgaben über welche Grundideen nachgedacht werden soll. Die Aufgaben
Material U.2.1 Ein Ford Transit Kleintransporter ist innen 2458 mm lang. Ein DIN A4 Blatt Papier gibt es in unterschiedlichen Ausführungen. Es gibt es
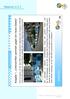 Material U.2.1 Methoden Kompetenzen Inhalt Technologie Aufgabe 1: Unterschriften sammeln gegen ein neues Gesetz Erst vor kurzem, am 25. April 2006, hat die spanische Opposition dem Kongress 4.000.000 Unterschriften
Material U.2.1 Methoden Kompetenzen Inhalt Technologie Aufgabe 1: Unterschriften sammeln gegen ein neues Gesetz Erst vor kurzem, am 25. April 2006, hat die spanische Opposition dem Kongress 4.000.000 Unterschriften
Bildungserfolgreiche Migranten und alltagsweltliche Öffnung der Schule
 Bildungserfolgreiche Migranten und alltagsweltliche Öffnung der Schule Untersuchungen an Mathematikaufgaben Nikola Leufer IEEM, TU Dortmund Michael Sertl PH Wien Gliederung Ausgangspunkt: Alltagsbezogene
Bildungserfolgreiche Migranten und alltagsweltliche Öffnung der Schule Untersuchungen an Mathematikaufgaben Nikola Leufer IEEM, TU Dortmund Michael Sertl PH Wien Gliederung Ausgangspunkt: Alltagsbezogene
Rückmeldung als zentrales Element formativen Assessments
 Rückmeldung als zentrales Element formativen Assessments wissenschaftliche Erkenntnisse und praktische Umsetzung im Mathematikunterricht (Projekt Co 2 CA) Katrin Rakoczy & Birgit Harks Formatives Assessment:
Rückmeldung als zentrales Element formativen Assessments wissenschaftliche Erkenntnisse und praktische Umsetzung im Mathematikunterricht (Projekt Co 2 CA) Katrin Rakoczy & Birgit Harks Formatives Assessment:
Stell dir doch die Situation mal konkret vor! Lehrerinterventionen im Kontext mathematischer Modellierungsaufgaben Tropper, Natalie
 Stell dir doch die Situation mal konkret vor! Lehrerinterventionen im Kontext mathematischer Modellierungsaufgaben Tropper, Natalie Published in: Beiträge zum Mathematikunterricht 2011 Publication date:
Stell dir doch die Situation mal konkret vor! Lehrerinterventionen im Kontext mathematischer Modellierungsaufgaben Tropper, Natalie Published in: Beiträge zum Mathematikunterricht 2011 Publication date:
Spezielle Fragen der Mathematikdidaktik: Realitätsnaher Mathematikunterricht in der Grundschule
 Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Realitätsnaher Mathematikunterricht in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen I. Theoretische
Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Realitätsnaher Mathematikunterricht in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen I. Theoretische
Bei den Aufgabenbeispielen lassen sich folgende Anforderungsbereiche unterscheiden:
 aus den Bildungsstandards Allgemeines zu den n Bei den n lassen sich folgende Anforderungsbereiche unterscheiden: Anforderungsbereich Reproduzieren (AB I) Das Lösen der Aufgabe erfordert Grundwissen und
aus den Bildungsstandards Allgemeines zu den n Bei den n lassen sich folgende Anforderungsbereiche unterscheiden: Anforderungsbereich Reproduzieren (AB I) Das Lösen der Aufgabe erfordert Grundwissen und
6 Forschungsfragen und Untersuchungsdesign
 6.1 Liste der Forschungsfragen 143 Das Ziel der vorliegenden Arbeit ist die Verfolgung von Vernetzungen bei ihrer Übertragung durch Lehr- und Lernprozesse aus dem Unterrichtsstoff Mathematik auf die kognitive
6.1 Liste der Forschungsfragen 143 Das Ziel der vorliegenden Arbeit ist die Verfolgung von Vernetzungen bei ihrer Übertragung durch Lehr- und Lernprozesse aus dem Unterrichtsstoff Mathematik auf die kognitive
Vorträge und Workshops von S. Schukajlow Stand: Mai 2017
 Vorträge und Workshops von S. Schukajlow Stand: Mai 2017 Vortrag im mathematischen Kolloquium der TU Darmstadt am 17.05.2017. Titel Emotionen und Motivation von Lehramtsstudierenden Vortrag mit J. Rellensmann
Vorträge und Workshops von S. Schukajlow Stand: Mai 2017 Vortrag im mathematischen Kolloquium der TU Darmstadt am 17.05.2017. Titel Emotionen und Motivation von Lehramtsstudierenden Vortrag mit J. Rellensmann
Bei den Aufgabenbeispielen lassen sich folgende Anforderungsbereiche unterscheiden:
 Bei den Aufgabenbeispielen lassen sich folgende Anforderungsbereiche unterscheiden: Anforderungsbereich Reproduzieren (AB I) Das Lösen der Aufgabe erfordert Grundwissen und das Ausführen von Routinetätigkeiten.
Bei den Aufgabenbeispielen lassen sich folgende Anforderungsbereiche unterscheiden: Anforderungsbereich Reproduzieren (AB I) Das Lösen der Aufgabe erfordert Grundwissen und das Ausführen von Routinetätigkeiten.
Studie gezeigt werden, wie Schüler und Lehrer mit Modellierungsaufgaben umgehen,
 VOM FACH AUS UND FÜR DIE PRAXIS Lieber Wolfgang, die herzlichsten Glückwünsche zu Deinem Sechziger! Nicht zuletzt in unserem eigenen Interesse wünschen wir Dir für die nächsten 5 Berufsjahre und auch weit
VOM FACH AUS UND FÜR DIE PRAXIS Lieber Wolfgang, die herzlichsten Glückwünsche zu Deinem Sechziger! Nicht zuletzt in unserem eigenen Interesse wünschen wir Dir für die nächsten 5 Berufsjahre und auch weit
Realitätsbezüge im Mathematikunterricht
 Realitätsbezüge im Mathematikunterricht Herausgegeben von Prof. Dr. Werner Blum, Universität Kassel Prof. Dr. Rita Borromeo Ferri, Universität Kassel Prof. Dr. Gilbert Greefrath, Universität Münster Prof.
Realitätsbezüge im Mathematikunterricht Herausgegeben von Prof. Dr. Werner Blum, Universität Kassel Prof. Dr. Rita Borromeo Ferri, Universität Kassel Prof. Dr. Gilbert Greefrath, Universität Münster Prof.
Realitätsnaher Mathematikunterricht vom Fach aus und für die Praxis
 Andreas Büchter, Hans Humenberger, Stephan Hußmann, Susanne Prediger (Hrsg.) Realitätsnaher Mathematikunterricht vom Fach aus und für die Praxis Festschrift für Hans-Wolfgang Henn zum 60. Geburtstag Verlag
Andreas Büchter, Hans Humenberger, Stephan Hußmann, Susanne Prediger (Hrsg.) Realitätsnaher Mathematikunterricht vom Fach aus und für die Praxis Festschrift für Hans-Wolfgang Henn zum 60. Geburtstag Verlag
4.3 Anforderungsbereich und Schwierigkeitsgrad
 4.3 Anforderungsbereich und Schwierigkeitsgrad Begriffe wie Anforderungsbereich, Anforderungsniveau, Schwierigkeitsgrad, Kompetenzstufen werden häufig im Zusammenhang mit dem Entwickeln, Stellen bzw. Analysieren
4.3 Anforderungsbereich und Schwierigkeitsgrad Begriffe wie Anforderungsbereich, Anforderungsniveau, Schwierigkeitsgrad, Kompetenzstufen werden häufig im Zusammenhang mit dem Entwickeln, Stellen bzw. Analysieren
Methode zur Beurteilung von S- Leistung & Methodenkritik
 Methode zur Beurteilung von S- Leistung & Methodenkritik Kranz/Schorn (Hrsg.) (2012): Chemie Methodik. Handbuch für die Sekundarstufe I und II. Berlin: Cornelsen, S. 189-205 1 Seminar: Fachdidaktik Chemie
Methode zur Beurteilung von S- Leistung & Methodenkritik Kranz/Schorn (Hrsg.) (2012): Chemie Methodik. Handbuch für die Sekundarstufe I und II. Berlin: Cornelsen, S. 189-205 1 Seminar: Fachdidaktik Chemie
Sachrechnen (Grundschule)
 Sachrechnen (Grundschule) 6. Schwierigkeiten beim Lösen von Sachaufgaben, 1 Probleme beim Lösen von Sachaufgaben Veröffentlicht in: MDMV 20, 2012, S. 235 2 6.1 Hauptursachen für Schwierigkeiten von SuS
Sachrechnen (Grundschule) 6. Schwierigkeiten beim Lösen von Sachaufgaben, 1 Probleme beim Lösen von Sachaufgaben Veröffentlicht in: MDMV 20, 2012, S. 235 2 6.1 Hauptursachen für Schwierigkeiten von SuS
Vereinbarung über Bildungsstandards (KMK, ):
 Bildungsstandards: Ein Überblick Vereinbarung über Bildungsstandards (KMK, 15.10.2004): Die Länder haben sich zur Implementierung in Prüfungen, Lehrplan, Unterricht und Lehrerausbildung und Lehrerfort-
Bildungsstandards: Ein Überblick Vereinbarung über Bildungsstandards (KMK, 15.10.2004): Die Länder haben sich zur Implementierung in Prüfungen, Lehrplan, Unterricht und Lehrerausbildung und Lehrerfort-
MaMut. Materialien für den Mathematikunterricht
 MaMut Materialien für den Mathematikunterricht 4 MaMut - Materialien für den Mathematikunterricht 4 Eva-Maria Plackner, Nicolai von Schroeders (Hrsg.) Kompetenzorientierter Mathematikunterricht 1. Auflage
MaMut Materialien für den Mathematikunterricht 4 MaMut - Materialien für den Mathematikunterricht 4 Eva-Maria Plackner, Nicolai von Schroeders (Hrsg.) Kompetenzorientierter Mathematikunterricht 1. Auflage
Leistungsbewertung Mathematik
 Leistungsbewertung Mathematik Sekundarstufe 1 Grundsätze zur Leistungsbewertung im Fach Mathematik 1 von 5 Stand 05.01.2017 (gemäß Abschnitt 5 des Kernlehrplans Mathematik für SI-G8, verkürzt) Bei der
Leistungsbewertung Mathematik Sekundarstufe 1 Grundsätze zur Leistungsbewertung im Fach Mathematik 1 von 5 Stand 05.01.2017 (gemäß Abschnitt 5 des Kernlehrplans Mathematik für SI-G8, verkürzt) Bei der
Impulse zur Weiterentwicklung des Sachunterrichts
 Impulse zur Weiterentwicklung des Sachunterrichts SINUS-Transfer Grundschule Dr. Karen Rieck Leibniz-Institut für die Pädagogik der Naturwissenschaften Übersicht Stand des Sachunterrichts - Bildungsauftrag
Impulse zur Weiterentwicklung des Sachunterrichts SINUS-Transfer Grundschule Dr. Karen Rieck Leibniz-Institut für die Pädagogik der Naturwissenschaften Übersicht Stand des Sachunterrichts - Bildungsauftrag
Universität Bereinigte Sammlung der Satzungen Ziffer Duisburg-Essen und Ordnungen Seite 3
 Duisburg-Essen und Ordnungen Seite 3 Anlage 1: Studienplan für das Fach Mathematik im Bachelor-Studiengang mit der Lehramtsoption Grundschulen 1 Credits pro Zahl und Raum 12 Grundlagen der Schulmathematik
Duisburg-Essen und Ordnungen Seite 3 Anlage 1: Studienplan für das Fach Mathematik im Bachelor-Studiengang mit der Lehramtsoption Grundschulen 1 Credits pro Zahl und Raum 12 Grundlagen der Schulmathematik
MaMut primar. Materialien für den Mathematikunterricht 2
 MaMut primar Materialien für den Mathematikunterricht 2 MaMut primar 2 Materialien für den Mathematikunterricht Eva-Maria Plackner, Jennifer Postupa (Hrsg.) Kompetenzorientierter Mathematikunterricht in
MaMut primar Materialien für den Mathematikunterricht 2 MaMut primar 2 Materialien für den Mathematikunterricht Eva-Maria Plackner, Jennifer Postupa (Hrsg.) Kompetenzorientierter Mathematikunterricht in
Jun. Prof. Dr. Christina Drüke-Noe Publikationen
 Jun. Prof. Dr. Christina Drüke-Noe Publikationen Monografien Drüke-Noe, C. (2014). Aufgabenkultur in Klassenarbeiten im Fach Mathematik. Empirische Untersuchungen in neunten und zehnten Klassen. Wiesbaden:
Jun. Prof. Dr. Christina Drüke-Noe Publikationen Monografien Drüke-Noe, C. (2014). Aufgabenkultur in Klassenarbeiten im Fach Mathematik. Empirische Untersuchungen in neunten und zehnten Klassen. Wiesbaden:
Dortmund Spring School Diskurswerkstatt 3a: Coaching 3. März 2010
 Dortmund Spring School 2010 Diskurswerkstatt 3a: Coaching 3. März 2010 Hospitationen an Universitäten und Hochschulen mit Hilfe des Fachspezifisch-Pädagogischen Coachings?, lic. phil. Ausgangslage Hospitationen
Dortmund Spring School 2010 Diskurswerkstatt 3a: Coaching 3. März 2010 Hospitationen an Universitäten und Hochschulen mit Hilfe des Fachspezifisch-Pädagogischen Coachings?, lic. phil. Ausgangslage Hospitationen
Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule. Themen- und Literaturliste
 Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen
Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen
Dr. Axel Schulz (Universität Bielefeld)
 Am Montag, dem 10. Oktober 2016, 13:00 Uhr, Raum SRZ 5 (Orléans-Ring 12) Dr. Axel Schulz (Universität Bielefeld) Inverses Schreiben, Zahlendreher und Stellenwertverständnis Eine empirische Studie zur inversen
Am Montag, dem 10. Oktober 2016, 13:00 Uhr, Raum SRZ 5 (Orléans-Ring 12) Dr. Axel Schulz (Universität Bielefeld) Inverses Schreiben, Zahlendreher und Stellenwertverständnis Eine empirische Studie zur inversen
Entdeckendes Lernen mit
 Entdeckendes Lernen mit Hubert Pöchtrager www.jku.at/lzmd Zum Nachdenken Dieser unserer Didaktik Hauptplan sei folgender: Eine Anweisung zu suchen und zu finden, wie die Lehrenden weniger lehren, die Lernenden
Entdeckendes Lernen mit Hubert Pöchtrager www.jku.at/lzmd Zum Nachdenken Dieser unserer Didaktik Hauptplan sei folgender: Eine Anweisung zu suchen und zu finden, wie die Lehrenden weniger lehren, die Lernenden
Teilbarkeitsbetrachtungen in den unteren Klassenstufen - Umsetzung mit dem Abakus
 Naturwissenschaft Melanie Teege Teilbarkeitsbetrachtungen in den unteren Klassenstufen - Umsetzung mit dem Abakus Examensarbeit Inhaltsverzeichnis Abkürzungsverzeichnis... 2 1 Einleitung... 3 2 Anliegen
Naturwissenschaft Melanie Teege Teilbarkeitsbetrachtungen in den unteren Klassenstufen - Umsetzung mit dem Abakus Examensarbeit Inhaltsverzeichnis Abkürzungsverzeichnis... 2 1 Einleitung... 3 2 Anliegen
Schulbücher im Fokus
 Jörg Doll Keno Frank Detlef Fickermann Knut Schwippert (Hrsg.) Schulbücher im Fokus Nutzungen, Wirkungen und Evaluation Waxmann 2012 Münster / New York / München / Berlin Inhalt Jörg Doll, Detle! Fickermann,
Jörg Doll Keno Frank Detlef Fickermann Knut Schwippert (Hrsg.) Schulbücher im Fokus Nutzungen, Wirkungen und Evaluation Waxmann 2012 Münster / New York / München / Berlin Inhalt Jörg Doll, Detle! Fickermann,
Zaubern im Mathematikunterricht
 Zaubern im Mathematikunterricht 0011 0010 1010 1101 0001 0100 1011 Die Mathematik als Fachgebiet ist so ernst, dass man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.
Zaubern im Mathematikunterricht 0011 0010 1010 1101 0001 0100 1011 Die Mathematik als Fachgebiet ist so ernst, dass man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.
Von Dagstuhl in die Zukunft - Bildung in der digitalen vernetzten Welt
 1 Von Dagstuhl in die Zukunft - Bildung in der digitalen vernetzten Welt Prof. Dr. Ira Diethelm Didaktik der Informatik - Carl von Ossietzky Universität Oldenburg und bildungspolitische Außenministerin
1 Von Dagstuhl in die Zukunft - Bildung in der digitalen vernetzten Welt Prof. Dr. Ira Diethelm Didaktik der Informatik - Carl von Ossietzky Universität Oldenburg und bildungspolitische Außenministerin
Zauberquadrate entdecken
 Haus 7: Gute Aufgaben Zauberquadrate entdecken Von Mathematik kann man natürlich erst auf den höheren Stufen sprechen. In der Grundschule wird ja nur gerechnet (Moderator der Sendung Kulturzeit im 3sat,
Haus 7: Gute Aufgaben Zauberquadrate entdecken Von Mathematik kann man natürlich erst auf den höheren Stufen sprechen. In der Grundschule wird ja nur gerechnet (Moderator der Sendung Kulturzeit im 3sat,
Literale und Mathematische Kompetenzen. der Universität Bielefeld
 Geistes-, Natur-, Sozial- und Technikwissenschaften Transcending Boundaries Förderung der Studierfähigkeit in der Studieneingangsphase durch Gestaltung von effizienten Unterstützungsmaßnahmen Literale
Geistes-, Natur-, Sozial- und Technikwissenschaften Transcending Boundaries Förderung der Studierfähigkeit in der Studieneingangsphase durch Gestaltung von effizienten Unterstützungsmaßnahmen Literale
Förderung (meta-)kognitiver Strategien im Mathematikunterricht
 Förderung (meta-)kognitiver Strategien im Mathematikunterricht Atelier-Tagung Lerncoaching im Unterricht Baden, 31.8.2013 1. Ein Problemaufriss Rechne aus: 701 698 Lösung einer Schülerin: 701-698 003 Das
Förderung (meta-)kognitiver Strategien im Mathematikunterricht Atelier-Tagung Lerncoaching im Unterricht Baden, 31.8.2013 1. Ein Problemaufriss Rechne aus: 701 698 Lösung einer Schülerin: 701-698 003 Das
Grundlagen des Mathematikunterrichts in der Sekundarstufe
 Hans-Joachim Vollrath Grundlagen des Mathematikunterrichts in der Sekundarstufe Spektrum Akademischer Verlag Heidelberg Berlin Inhalt Einleitung XI I Mathematik als Unterrichtsfach 1 1 Mathematik in der
Hans-Joachim Vollrath Grundlagen des Mathematikunterrichts in der Sekundarstufe Spektrum Akademischer Verlag Heidelberg Berlin Inhalt Einleitung XI I Mathematik als Unterrichtsfach 1 1 Mathematik in der
Literaturverzeichnis
 Literaturverzeichnis Adams, R. J., Wilson, M. & Wang, W.-C. (1997). The Multidimensional Random Coefficients Multinomial Logit Model. Applied Psychological Measurement 21(1), 1-23. Adams, R. J. & Wu, M.
Literaturverzeichnis Adams, R. J., Wilson, M. & Wang, W.-C. (1997). The Multidimensional Random Coefficients Multinomial Logit Model. Applied Psychological Measurement 21(1), 1-23. Adams, R. J. & Wu, M.
"MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN
 1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Aufgabenanalyse: 3 Inhalte: Welche Aufgaben sind
1 "MATHEMATISCHES MODELLIEREN THEORETISCHE HINTERGRÜNDE, AUFGABENENTWICKLUNG, ANALYSEN UND ANSÄTZE ZUM EINFÜHREN UND UNTERRICHTEN" Dr. des. Katja Eilerts 2 Aufgabenanalyse: 3 Inhalte: Welche Aufgaben sind
VELM-8 ein Projekt zur Nutzung der Lernstandserhebungen für Unterrichtsentwicklung und Förderung
 ein Projekt zur Nutzung der Lernstandserhebungen für Unterrichtsentwicklung und Förderung Sebastian Vogel, Kay Achmetli, Werner Blum, Janina Krawitz Universität Kassel Gliederung 1. Wozu Lernstandserhebungen/VerA-8?
ein Projekt zur Nutzung der Lernstandserhebungen für Unterrichtsentwicklung und Förderung Sebastian Vogel, Kay Achmetli, Werner Blum, Janina Krawitz Universität Kassel Gliederung 1. Wozu Lernstandserhebungen/VerA-8?
Inhaltsverzeichnis... V Einleitung... IX 1 Mathematik als Unterrichtsfach Mathematik in der Schule... 1
 Inhaltsverzeichnis Inhaltsverzeichnis... V Einleitung... IX 1 Mathematik als Unterrichtsfach... 1 1.1 Mathematik in der Schule... 1 1.1.1 Einschätzungen des Fachs... 1 1.1.2 Schule für alle... 3 1.1.3
Inhaltsverzeichnis Inhaltsverzeichnis... V Einleitung... IX 1 Mathematik als Unterrichtsfach... 1 1.1 Mathematik in der Schule... 1 1.1.1 Einschätzungen des Fachs... 1 1.1.2 Schule für alle... 3 1.1.3
Strukturgenetische didaktische Analysen die empirische Forschung erster Art
 Strukturgenetische didaktische Analysen die empirische Forschung erster Art mathe 2000 http://www.tu-dortmund.de/mathe2000 Intention des Vortrags: Rehabilitierung und Weiterentwicklung der sogenannten
Strukturgenetische didaktische Analysen die empirische Forschung erster Art mathe 2000 http://www.tu-dortmund.de/mathe2000 Intention des Vortrags: Rehabilitierung und Weiterentwicklung der sogenannten
Idee und Aufgabenentwurf Nicole Mai und Birgit Amann, Mellinschule, Sulzbach, Klassenstufe 3 (November 2012)
 Aufgabe 1.3 Idee und Aufgabenentwurf Nicole Mai und Birgit Amann, Mellinschule, Sulzbach, Klassenstufe 3 (November 2012) Schreibe Sachaufgaben zum Bild. - Du darfst addieren. Du darfst subtrahieren. -
Aufgabe 1.3 Idee und Aufgabenentwurf Nicole Mai und Birgit Amann, Mellinschule, Sulzbach, Klassenstufe 3 (November 2012) Schreibe Sachaufgaben zum Bild. - Du darfst addieren. Du darfst subtrahieren. -
Entdeckendes Lernen im Mathematikunterricht
 Entdeckendes Lernen im Mathematikunterricht Zum Nachdenken Dieser unserer Didaktik Hauptplan sei folgender: Eine Anweisung zu suchen und zu finden, wie die Lehrenden weniger lehren, die Lernenden aber
Entdeckendes Lernen im Mathematikunterricht Zum Nachdenken Dieser unserer Didaktik Hauptplan sei folgender: Eine Anweisung zu suchen und zu finden, wie die Lehrenden weniger lehren, die Lernenden aber
Praktische Implikationen der Kompetenzorientierung
 Praktische Implikationen der Kompetenzorientierung Dr. Maike Abshagen 12.10.2017 Schleswig-Holstein. Der echte Norden. Übersicht 1) Kompetenzorientierung im Mathematikunterricht ein Beispiel 2) Woran kann
Praktische Implikationen der Kompetenzorientierung Dr. Maike Abshagen 12.10.2017 Schleswig-Holstein. Der echte Norden. Übersicht 1) Kompetenzorientierung im Mathematikunterricht ein Beispiel 2) Woran kann
Zum Konzept des Lehrplanes für die Grundschule Präsentation zu Fortbildungszwecken
 Zum Konzept des Lehrplanes für die Grundschule Präsentation zu Fortbildungszwecken die Struktur des Lehrplanes Kompetenzerwartungen statt Lehrziele Schwerpunktsetzung innerhalb der Fächer fächerübergreifende
Zum Konzept des Lehrplanes für die Grundschule Präsentation zu Fortbildungszwecken die Struktur des Lehrplanes Kompetenzerwartungen statt Lehrziele Schwerpunktsetzung innerhalb der Fächer fächerübergreifende
Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule. Themen- und Literaturliste
 Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen
Dr. Astrid Brinkmann Spezielle Fragen der Mathematikdidaktik: Mathematisches Modellieren und Problemlösen in der Grundschule Themen- und Literaturliste Einführung 1. Vorstellung und Verteilung der Themen
Mathematik ist mehr als Rechnen
 Mathematik ist mehr als Rechnen mit produktiven Lernumgebungen zu einem kompetenzorientierten Unterricht Anforderungen an einen modernen Mathematikunterricht Lernumgebung zur Multiplikation Kriterien einer
Mathematik ist mehr als Rechnen mit produktiven Lernumgebungen zu einem kompetenzorientierten Unterricht Anforderungen an einen modernen Mathematikunterricht Lernumgebung zur Multiplikation Kriterien einer
INTELLIGENTES ÜBEN TERME
 INTELLIGENTES ÜBEN TERME Gliederung Lernvoraussetzungen Einordnung in den Lehrgang Stundenreihe Intelligentes Üben Arbeitsauftrag Quellen Lernvoraussetzungen Die Schülerinnen und Schüler...... kennen Variablen...
INTELLIGENTES ÜBEN TERME Gliederung Lernvoraussetzungen Einordnung in den Lehrgang Stundenreihe Intelligentes Üben Arbeitsauftrag Quellen Lernvoraussetzungen Die Schülerinnen und Schüler...... kennen Variablen...
RCAE Research Center for Applied Education. Lernfortschrittsblatt SCHREIBEN. Begleitdokument
 RCAE Research Center for Applied Education Lernfortschrittsblatt SCHREIBEN Begleitdokument Lernfortschrittsblatt Schreiben RCAE Research Center for Applied Education GmbH Khevenhüllerstraße 9 Klagenfurt
RCAE Research Center for Applied Education Lernfortschrittsblatt SCHREIBEN Begleitdokument Lernfortschrittsblatt Schreiben RCAE Research Center for Applied Education GmbH Khevenhüllerstraße 9 Klagenfurt
Pressemitteilung Berlin, 11. Dezember 2012
 Pressemitteilung Berlin, 11. Dezember 2012 Deutschlands Grundschülerinnen und Grundschüler im Lesen, in Mathematik und in den Naturwissenschaften im internationalen Vergleich weiterhin im oberen Drittel
Pressemitteilung Berlin, 11. Dezember 2012 Deutschlands Grundschülerinnen und Grundschüler im Lesen, in Mathematik und in den Naturwissenschaften im internationalen Vergleich weiterhin im oberen Drittel
Kurzbeschreibungen der Workshops
 Kurzbeschreibungen der Workshops auf der Auftaktveranstaltung von SINUS an Grundschulen in Soltau (29.-31.10.2009) Freitag, 30.10.2009 Petra Scherer (Universität Bielefeld) Umgang mit Heterogenität Möglichkeiten
Kurzbeschreibungen der Workshops auf der Auftaktveranstaltung von SINUS an Grundschulen in Soltau (29.-31.10.2009) Freitag, 30.10.2009 Petra Scherer (Universität Bielefeld) Umgang mit Heterogenität Möglichkeiten
Konzept zur Leistungsmessung und Leistungsbewertung im Mathematikunterricht des 3. und 4. Schuljahres
 Konzept zur Leistungsmessung und Leistungsbewertung im Mathematikunterricht des 3. und 4. Schuljahres 1. Leistungsmessung und Leistungsbewertung im Mathematikunterricht (Auszüge LP Mathematik, Schulentwicklung
Konzept zur Leistungsmessung und Leistungsbewertung im Mathematikunterricht des 3. und 4. Schuljahres 1. Leistungsmessung und Leistungsbewertung im Mathematikunterricht (Auszüge LP Mathematik, Schulentwicklung
Kommentiertes Inhaltsverzeichnis
 2 Kommentiertes Inhaltsverzeichnis Kommentiertes Inhaltsverzeichnis Kapitel I: Unterrichtsmethoden 7 Aufgaben im Mathematikunterricht von Schüler/innen variieren zu lassen, kann Anliegen in jeder Schulstufe
2 Kommentiertes Inhaltsverzeichnis Kommentiertes Inhaltsverzeichnis Kapitel I: Unterrichtsmethoden 7 Aufgaben im Mathematikunterricht von Schüler/innen variieren zu lassen, kann Anliegen in jeder Schulstufe
Institut für Bildungsforschung in der School of Education. Kati Trempler Judith Schellenbach-Zell Cornelia Gräsel
 Prädiktoren der naturwissenschaftlichen Kompetenz und des naturwissenschaftlichen Interesses von Grundschulkindern der Einfluss von individuellen Schülermerkmalen und Lehrermerkmalen Kati Trempler Judith
Prädiktoren der naturwissenschaftlichen Kompetenz und des naturwissenschaftlichen Interesses von Grundschulkindern der Einfluss von individuellen Schülermerkmalen und Lehrermerkmalen Kati Trempler Judith
Inhalt. Vorwort Einleitung Ausgangslage Zielstellung Aufbau der Arbeit I: Theoretischer Teil
 Inhalt Vorwort...15 1 Einleitung...17 1.1 Ausgangslage...17 1.2 Zielstellung...18 1.3 Aufbau der Arbeit...20 I: Theoretischer Teil 2 Individuelle Lernunterstützung als Form der Individualisierung im Unterricht...22
Inhalt Vorwort...15 1 Einleitung...17 1.1 Ausgangslage...17 1.2 Zielstellung...18 1.3 Aufbau der Arbeit...20 I: Theoretischer Teil 2 Individuelle Lernunterstützung als Form der Individualisierung im Unterricht...22
1 Das Grundvorstellungskonzept
 1 Das Grundvorstellungskonzept Die theoretische Analyse von mathematischen Inhalten auf der einen Seite und der Deskription der tatsächlichen Vorgehensweisen, Vorstellungen und Kompetenzen der Schülerinnen
1 Das Grundvorstellungskonzept Die theoretische Analyse von mathematischen Inhalten auf der einen Seite und der Deskription der tatsächlichen Vorgehensweisen, Vorstellungen und Kompetenzen der Schülerinnen
Daten und Zufall Beitrag 14 Erwartungswert kennenlernen 1 von 32. Welchen Gewinn kann man bei Glücksspielen erwarten? Den Erwartungswert kennenlernen
 IV Daten und Zufall Beitrag Erwartungswert kennenlernen von Welchen Gewinn kann man bei Glücksspielen erwarten? Den Erwartungswert kennenlernen Von Alessandro Totaro, Stuttgart Illustriert von Oliver Wetterauer,
IV Daten und Zufall Beitrag Erwartungswert kennenlernen von Welchen Gewinn kann man bei Glücksspielen erwarten? Den Erwartungswert kennenlernen Von Alessandro Totaro, Stuttgart Illustriert von Oliver Wetterauer,
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 1 Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 1. Ziele und Grundpositionen
A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 1 Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 1. Ziele und Grundpositionen
Begabungsförderung forschend lernen Lehramtsstudierende als Projekt-Mentoren
 Begabungsförderung forschend lernen Lehramtsstudierende als Projekt-Mentoren David Rott Fachbereich Erziehungswissenschaft und Sozialwissenschaften Institut für Erziehungswissenschaft IFE Kontakt: david.rott@uni-muenster.de
Begabungsförderung forschend lernen Lehramtsstudierende als Projekt-Mentoren David Rott Fachbereich Erziehungswissenschaft und Sozialwissenschaften Institut für Erziehungswissenschaft IFE Kontakt: david.rott@uni-muenster.de
Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe
 Übersicht Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe Raum und Form Daten und Zufall Zahlen und Operationen Muster und Strukturen Messen und Größen Jgst. 3 und 4 Jgst. 1 und 2 1 Thema 1:
Übersicht Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe Raum und Form Daten und Zufall Zahlen und Operationen Muster und Strukturen Messen und Größen Jgst. 3 und 4 Jgst. 1 und 2 1 Thema 1:
Kompetenzorientierter Mathematikunterricht
 1 Kompetenzorientierter Mathematikunterricht Prozessbezogene Kompetenzen fördern Christoph Selter, Karina Höveler, Maren Laferi & Lilo Verboom, 05.09.13 2 Themen»Kompetenzorientierter Mathematikunterricht«Förderung
1 Kompetenzorientierter Mathematikunterricht Prozessbezogene Kompetenzen fördern Christoph Selter, Karina Höveler, Maren Laferi & Lilo Verboom, 05.09.13 2 Themen»Kompetenzorientierter Mathematikunterricht«Förderung
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungen für VERA 3: Stationenlernen - Zahlen und Operationen
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungen für VERA 3: Stationenlernen - Zahlen und Operationen Das komplette Material finden Sie hier: School-Scout.de Titel: VERA 3
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungen für VERA 3: Stationenlernen - Zahlen und Operationen Das komplette Material finden Sie hier: School-Scout.de Titel: VERA 3
Programmatischer Text
 Stand: 17.08.2012 Sektion 1 Inhaltverzeichnis Grundsätzliches 4 Anspruchsniveaus pädagogischer Diagnostik im Bereich Schule 4 Funktionen und Ziele pädagogischer Diagnostik 5 Bedeutung von Lernprozessdiagnostik
Stand: 17.08.2012 Sektion 1 Inhaltverzeichnis Grundsätzliches 4 Anspruchsniveaus pädagogischer Diagnostik im Bereich Schule 4 Funktionen und Ziele pädagogischer Diagnostik 5 Bedeutung von Lernprozessdiagnostik
1.4 Sachrechnen in den Bildungsstandards
 1.4 Sachrechnen in den Bildungsstandards http://www.kmk.org/fileadmin/veroe ffentlichungen_beschluesse/2004/20 04_10_15-Bildungsstandards-Mathe- Primar.pdf Mathematikunterricht in der Grundschule Allgemeine
1.4 Sachrechnen in den Bildungsstandards http://www.kmk.org/fileadmin/veroe ffentlichungen_beschluesse/2004/20 04_10_15-Bildungsstandards-Mathe- Primar.pdf Mathematikunterricht in der Grundschule Allgemeine
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 1 Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 1. Ziele und Grundpositionen
A. Filler Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 1 Folie 1 /15 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 1. Ziele und Grundpositionen
Zerlegungen von {1, 2,..., n} in gleichmächtige summengleiche Teilmengen
 01-1 07-1 1 Eingliederung im Mathematikunterricht Klasse/Stufe: ab Klasse 5 Stoffliche Einordnung: Das Arbeitsblatt gehört primär zum Thema Problemlösen, die Schüler/innen sollen dabei vor allem selbstständig
01-1 07-1 1 Eingliederung im Mathematikunterricht Klasse/Stufe: ab Klasse 5 Stoffliche Einordnung: Das Arbeitsblatt gehört primär zum Thema Problemlösen, die Schüler/innen sollen dabei vor allem selbstständig
2 Multiple Lösungsmöglichkeiten und ihre Nutzung beim mathematischen Modellieren
 25 2 Multiple Lösungsmöglichkeiten und ihre Nutzung beim mathematischen Modellieren Kay Achmetli, André Krug, Stanislaw Schukajlow Westfälische Wilhelms-Universität Münster Beim Bearbeiten von realitätsbezogenen
25 2 Multiple Lösungsmöglichkeiten und ihre Nutzung beim mathematischen Modellieren Kay Achmetli, André Krug, Stanislaw Schukajlow Westfälische Wilhelms-Universität Münster Beim Bearbeiten von realitätsbezogenen
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Erwachsen werden, erwachsen sein. Texte mit der 5-Schritt- Lesemethode erarbeiten Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Erwachsen werden, erwachsen sein. Texte mit der 5-Schritt- Lesemethode erarbeiten Das komplette Material finden Sie hier: School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Ein Stationenzirkel zum Thema "Quader"
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Ein Stationenzirkel zum Thema "Quader" Das komplette Material finden Sie hier: School-Scout.de S 1 Ein Stationenzirkel zum Thema Quader
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Ein Stationenzirkel zum Thema "Quader" Das komplette Material finden Sie hier: School-Scout.de S 1 Ein Stationenzirkel zum Thema Quader
Einführung in die Pädagogische Psychologie HS Vorlesung 1: Pädagogische Psychologie: Was - Wozu? Prof. Dr. Franz Baeriswyl
 Einführung in die Pädagogische Psychologie HS 2013 Vorlesung 1: Pädagogische Psychologie: Was - Wozu? Prof. Dr. Franz Baeriswyl Pisa 2009. Schülerinnen und Schüler der Schweiz im internationalen Vergleich.
Einführung in die Pädagogische Psychologie HS 2013 Vorlesung 1: Pädagogische Psychologie: Was - Wozu? Prof. Dr. Franz Baeriswyl Pisa 2009. Schülerinnen und Schüler der Schweiz im internationalen Vergleich.
Zum Verhältnis der Wissenschaften Mathematik und Didaktik des Mathematikunterrichts. Hans Dieter Sill, Universität Rostock
 Zum Verhältnis der Wissenschaften Mathematik und Didaktik des Mathematikunterrichts Hans Dieter Sill, Universität Rostock Gliederung 1. Phänomene 2. Ursachen 3. Konsequenzen 2 Phänomene Studenten, Lehrer
Zum Verhältnis der Wissenschaften Mathematik und Didaktik des Mathematikunterrichts Hans Dieter Sill, Universität Rostock Gliederung 1. Phänomene 2. Ursachen 3. Konsequenzen 2 Phänomene Studenten, Lehrer
Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe
 Übersicht Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe Raum und Form Daten und Zufall Zahlen und Operationen Muster und Strukturen Messen und Größen Jgst. 3 und 4 Jgst. 1 und 2 Thema 1: Leitidee
Übersicht Wahl des Fachdidaktischen Schwerpunkts in der Primarstufe Raum und Form Daten und Zufall Zahlen und Operationen Muster und Strukturen Messen und Größen Jgst. 3 und 4 Jgst. 1 und 2 Thema 1: Leitidee
Themenplan: Fachseminar Mathematik ( H. Schmitt, Fr. Thönnes )
 Erwartete Kompetenzen Themenplan: Fachseminar Mathematik ( H. Schmitt, Fr. Thönnes ) ( 22 Ausbildungseinheiten á 90 Minuten) 1 FS 1 Verlauf und Struktur der Ausbildung im FS Mathematik 05.02.2013 Studienseminar
Erwartete Kompetenzen Themenplan: Fachseminar Mathematik ( H. Schmitt, Fr. Thönnes ) ( 22 Ausbildungseinheiten á 90 Minuten) 1 FS 1 Verlauf und Struktur der Ausbildung im FS Mathematik 05.02.2013 Studienseminar
Die Lehrperson als Regisseur einer gelungenen Aufgabenkultur in Volksschule und NMS. Dir. Christina Frotschnig, BEd MA Volksschule Markt Allhau
 Die Lehrperson als Regisseur einer gelungenen Aufgabenkultur in Volksschule und NMS Dir. Christina Frotschnig, BEd MA Volksschule Markt Allhau Abstract Aufgabenkultur ist auch in der Volksschule ein Thema,
Die Lehrperson als Regisseur einer gelungenen Aufgabenkultur in Volksschule und NMS Dir. Christina Frotschnig, BEd MA Volksschule Markt Allhau Abstract Aufgabenkultur ist auch in der Volksschule ein Thema,
