a) Die Donau von Wien nach Budapest, Gefälle 0,018 %, Höhendifferenz 65 m b) Rhein von Mainz nach Köln, Gefälle 0,024 %, Höhendifferenz 45 m
|
|
|
- Elvira Schuler
- vor 7 Jahren
- Abrufe
Transkript
1 I l)ll'l Anlagen - und Apparatebau Steigung MO Schiefe Ebene, Keil Ubungsaufgaben Aufgabe 1 Die Horizontaldistanz der Strasse Gams - Wildhaus misst rund 9 km. Gams liegt 478 m ü. M., Wildhaus 1090 m ü. M. Wie gross ist die durchschnittliche Steigung in Prozent? Aufgabe 2 Die Horizontaldistanz der Strasse Reichenau Flims beträgt rund 11,5 km, die durchschnittliche Steigung 4,14 o/o. Wie hoch liegt Flims ungefähr, wenn Reichenau 604 m ü. M. liegt? Aufgabe 3 Bei der Säntisbahn beträgt die durchschnittliche Steigung 62,1 o/o. Die Horizontaldistanz von der Schwägalp zum Säntisgipfel (2501 m ü. M.) misst 1,85 km. Wie hoch liegt die Talstation auf der Schwägalp? Aufgabe 4 Eine schräg gestellte Kletterstange weist eine Steigung von 210 o/o auf. Zeichne die Situation auf. Wie viele Grad Steigung sind das? Aufgabe 5 Ein Schlittelweg von 3 km Länge weist ein Gefälle von 6 o/o auf. Er beginnt auf 1240 m ü. M. Auf welcher Höhe endet er? Aufgabe 6 Flussschifffahrt: Wie lang sind die befahrenen Flussstrecken? a) Die Donau von Wien nach Budapest, Gefälle 0,018 %, Höhendifferenz 65 m b) Rhein von Mainz nach Köln, Gefälle 0,024 %, Höhendifferenz 45 m a-::\ Aufgabe 7 Oberlauf, Mittellauf und Unterlauf eines Baches: a) Auf 6 km Länge - gemäss Karte - beträgt das Gefälle durchschnittlich 12 o/o. Berechne die Höhendifferenz in m. b) Auf 8 km Länge - gemäss Karte - verliert der Bach 200 m an Höhe. Berechne das Gefälle in %. c) lm untersten Teil beträgt das Gefälle nur noch 0,2 oä, und der Flusslauf senkt sich dabei um 50 m. Berechne die Projektionslänge in km. c
2 I l)il'11 Anlagen - und Apparatebau Mathematik Aufgabe I Drahtseilbahnen: Bestimme die Höhe der Bergstationen über Meer. a) Gurtenbahn: Wabern: 576 m ü. M. b) Niesenbahn: Projektionslänge: Steigung: Mülenen: Projektionslänge: Steigung: 1000 m 27 o/o 687 m ü. M m 56% Auf diesen Verkehrstafeln wird bei... a) vor einem Gefälle von 15 7o gewarnt, b) vor einer Steigung von 23 o/o. Die Neigungswinkel in den Verkehrstafeln sind aber nicht richtig! Zeichne die richtige Steigung - das richtige Gefälle - grafisch mit den richtigen Winkeln auf! Aufgabe 10 Eine Terrasse ist 24 m von der Strasse entfernt und 4,8 m erhöht. Es soll eine Zufahrtsrampe aufgeschüttet werden. Wie gross wird die Steigung in Promille sein? Aufgabe 11 Der Aarelauf zwischen Thun und Bern misst 30 km, der Höhenunterschied beträgt 37 m. Welches durchschnittliche Gefälle in Promille hat die Aare auf dieser Strecke? Aufgabe 12 Garageneinfahrt: Der Garagenboden liegt '1,5 m unter der Strassenhöhe. Die Steigung der Einfahrtsrampe soll nicht mehr als 150 %o betragen. Welche Entfernung muss deshalb zwischen Strassenrand und Garagentor liegen? Aufgabe 13 Berechne die Steigung oder das Gefälle für die folgenden Teilstrecken beider Profile a) und b). ai".. IG
3 I I)l» Anlagen - und Apparatebau Mathemät{ffi Profil a) Teitstrecke l-ll,,,",nung =? Teitstrecke l-t,,r",nung -? Teitstrecke f-ll, o"ra,le =? Teirstrecke l---.i, c"räre =? Profil b) Teitstrecke l-j, s,"'gung -? Teirstrecke ll,,r",gung =? Teitstrecke l- I I, O"räte =? Teitstrecke [], Getatt" = z Aufgabe 14 A-Dorf und B-Dorf liegen 3,5 km (Prolektion) auseinander. Die Verbindungsstrasse hat eine durchschnittliche Steigung von 1,5 o/o. Das tiefer gelegene A-Dorf liegt auf 620 Meter über Meer. Wie hoch liegt B-Dorf? Aufgabe 15 Eine Strasse mit einer durchschnittlichen Steigung von 0,5 % führt von A-Stadt nach B-Stadt. A-Stadt liegt auf einer Höhe von 550 Meter über Meer, B-Stadt auf einer Höhe von 600 Meter. Wie weit (Projektionslänge) liegen die beiden Städte auseinander? Aufgabe 16 Ein Autobahnteilstück misst 3,5 km (Projektion) und steigt im Ganzen 56 Meter. Berechne die Steigung in %! Aufgabe 17 Eine Rampe hat eine Steigung von 50 % und ist in der Projektion 15 Meter lang. Berechne die Höhe vom Boden bis zum obersten Punkt der Rampe! Aufgabe 18 Ein Fluss hat ein Gefälle von Nasshausen nach Tropfstadt von 6 %0. Nasshausen liegt 27 Meter höher als Tropfstadt. Berechne wie weit die beiden Orte auseinander liegen (Projektion)! Aufgabe 19 Gib die Steigung dieser Rampe an (du musst messen!).
4 I l)ll1 Anlagen - und Apparatebau Aufgabe 20 Gib die Steigung dieser Auffahrt an (du musst messen!). Aufgabe 21 Zeichne eine Steigung von 1OO o/o aufl (Masse frei wählbar) Aufgabe 22 Ergänze die Tabelle! Aufgabe 23 Eine steile Zufahrtsstrasse zu einem Chalet hat eine Steigung von 12 o/o. Die Strasse ist nach Karte (Projektion) 350 m lang. Berechne den Höhenunterschied zwischen dem Anfang und dem Ende der Strasse. Aufgabe 24 Zwei Seilbahnmasten liegen laut Karte (Projektion) 240 m auseinander. Der untere Masten steht auf einer Höhe von 1050 m über Meer, der obere auf einer Höhe von 1146 m. Berechne die Steigung arvischen den Masten in %. Aufgabe 25 Ein Fluss fliesst von A-Stadt nach B-Stadt mit einem Gefälle von 8 %o. A-Stadt liegt 172 m höher als B-Stadt. Berechne in km, wie weit (Projektion) die beiden Städte auseinander liegen. Aufgabe 26 Ein Bach führt von A-Dorf nach B-Dorf und hat ein Gefälle von 3,5 %. Das höher gelegene A- Dorf liegt 585 m über Meer. Die beiden Ortschaften liegen 3,8 km (Projektion) auseinander. Auf welcher Höhe liegt B-Dorf? Aufgabe 27 Gib die Steigung dieser Felswand an (du musst messen!). C:/Math, Steigung/ Neigung/ Konizität Kasteler Patrick
5 I l)!11 Antagen - und Rpparatebau Mathem 1) 6,8 o/o 2) 1080,1 m ü. M. 3) 1352,15 m ü. M. 4) a=64,54" (rechnerisch), o = 65'(zeichnerisch) 5) 6) 7) 8) e) 10) 11) 12) 13) 14) 15) 16) 17) 18) 1e) 20) 21) 22) (Tangens q = Gegenkathete: Ankathete =210: 100 = 2,1 larctan2,l = d=64,54") 1060 m ü. M. (Die 3 km Länge in Aufgabe: als Horizontaldistanz gerechnet!) a) 361,111 km b) 187,500 km a) 720 m (Höhendifferenz) b) 2,5 o/o c) 25 km (Projektionslänge) a) 846 m ü. M. b) 2350,2 m ü. M. a) o = 8,53'(zeichnerisch: = 8-9') b) I = 12,95" (zeichnerisch:=12-13') 2OO Voo (oder 20 %) 1,23 o/o" 10m Profil a) Teilstrecke I t l, st"igung - 5o % Teitstrecke l ll, st"igung - 3o % Teitstrecke [-ll, o"tate = 5o % Teilstrecke I - l l, Cetalle = 2oo o/o B-Dorf liegt auf 672,5 m ü. M. Profil b) Teitstrecke l-ll, sr",nung = ooo % Teitstrecke l-t,,,",nung = 2oo % Teitstrecke I-T, o"rrlle = 1o % Teitstrecke l-1, o"ra,, e = 4oo oä 10'000 m oder 10 km 1,6 0/o 7,5 m 4'500 m oder 4,5 km 4O o/o (auf 5 cm waagrecht steigt es 2 cm) 20 % (auf 10 cm waagrecht steigt es 2 cm) Die Waagrechte und die Senkrechte sind beieiner 100 %-Steigung gleich lang; die Masse sind frei wählbar! --\'J *'-l-:-) 23) 42m 24) 4O o/o 25) 21,5 km 26) B-Dorf liegt auf 452 m ü. M. 27) 200 % (auf 2,5 cm waagrecht steigt es 5 cm senkrecht)
a) Wie hoch ist die Leiter? b) Wie weit stehen die beiden Fußpunkte auseinander? Abbildung 1: Eine Stehleiter
 1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
8.6.1 Real Sachrechnen Rabatt/Skonto Ankauf/Verkauf/Zins
 8.6.1 Real Sachrechnen Rabatt/Skonto Ankauf/Verkauf/Zins P8: Mathematik 8 S2: komb.büchlein Zeitraum : 3 Wochen Inhalte Kernstoff Zusatzstoff Erledigt am Währungen; P8: 186,187,188,189 P8: 190,191 Kurs,
8.6.1 Real Sachrechnen Rabatt/Skonto Ankauf/Verkauf/Zins P8: Mathematik 8 S2: komb.büchlein Zeitraum : 3 Wochen Inhalte Kernstoff Zusatzstoff Erledigt am Währungen; P8: 186,187,188,189 P8: 190,191 Kurs,
4. Das (symmetrische) - im Querschnitt dreieckige - Dach eines Hauses ist 3,50 Meter
 1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
St. Gallische Kantonsschulen Aufnahmeprüfung 2011 FMS / WMS / WMI Mathematik / 1. Teil
 St. Gallische Kantonsschulen Aufnahmeprüfung 011 FMS / WMS / WMI Mathematik / 1. Teil ohne Taschenrechner Dauer: 40 Minuten Kandidatennummer: Geburtsdatum: Abteilung: 1. Teil. Teil Summe Punkte Note Die
St. Gallische Kantonsschulen Aufnahmeprüfung 011 FMS / WMS / WMI Mathematik / 1. Teil ohne Taschenrechner Dauer: 40 Minuten Kandidatennummer: Geburtsdatum: Abteilung: 1. Teil. Teil Summe Punkte Note Die
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis
 Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
Aufgaben zu den Themen: Rechtwinkliges Dreieck und Sinus, Cosinus und Tangens im Einheitskreis 1. Eine Rampe hat eine Steigung von 5%. Wie groß ist der Steigungswinkel? 2. Gegeben ist ein rechtwinkliges
14 B Steigung. 1 Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berechne die Steigung.
 Steigung 4 6 Arbeitseft+ Teste dic selbst Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berecne die Steigung. a a a Keil Keil 2 Keil 3 Keil Keil 2 Keil 3 Horizontale
Steigung 4 6 Arbeitseft+ Teste dic selbst Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berecne die Steigung. a a a Keil Keil 2 Keil 3 Keil Keil 2 Keil 3 Horizontale
Mathematik. Name: Aufnahmeprüfung Klasse FMS. Zeit: 2 Stunden. Bewertung: 1. Löse die Gleichungen nach x auf. a) 3x(4x + 1) = (6x 1)(2x + 3)
 Name: Mathematik Aufnahmeprüfung 01 1. Klasse FMS Zeit: Stunden Bewertung: Aufgabe 1 4 5 6 7 8 9 10 11 1 Punktzahl 1. Löse die Gleichungen nach x auf. a) x(4x + 1) = (6x 1)(x + ) 4 b) x 1 x 1 4 c) Löse
Name: Mathematik Aufnahmeprüfung 01 1. Klasse FMS Zeit: Stunden Bewertung: Aufgabe 1 4 5 6 7 8 9 10 11 1 Punktzahl 1. Löse die Gleichungen nach x auf. a) x(4x + 1) = (6x 1)(x + ) 4 b) x 1 x 1 4 c) Löse
Textbeispiele mit trigonometrischen Lösungen
 Textbeispiele mit trigonometrischen Lösungen Anfangsbemerkung: Die folgenden Beispiele stammen aus Übungsblättern von höheren berufsbildenden Schulen. Sie sind sehr vereinfachte Aufgaben von technischen
Textbeispiele mit trigonometrischen Lösungen Anfangsbemerkung: Die folgenden Beispiele stammen aus Übungsblättern von höheren berufsbildenden Schulen. Sie sind sehr vereinfachte Aufgaben von technischen
Mathematik 2: Korrekturanleitung (mit Taschenrechner)
 Kanton St.Gallen Bildungsdepartement BM/FMS/IMS/WMI/WMS Aufnahmeprüfung Frühling 2017 Mathematik 2: Korrekturanleitung (mit Taschenrechner) Die Korrekturanleitung legt die Verteilung der Punkte auf die
Kanton St.Gallen Bildungsdepartement BM/FMS/IMS/WMI/WMS Aufnahmeprüfung Frühling 2017 Mathematik 2: Korrekturanleitung (mit Taschenrechner) Die Korrekturanleitung legt die Verteilung der Punkte auf die
Anwendung 1: Rabatt und Skonto
 Anwendung 1: Rabatt und Skonto Herr Gerber kauft sich ein Mountainbike. Dieses kostet gemäss Katalogpreis 2400. Franken. Weil Herr Gerber Stammkunde ist, gewährt ihm der Velohändler 15% Rabatt. Somit muss
Anwendung 1: Rabatt und Skonto Herr Gerber kauft sich ein Mountainbike. Dieses kostet gemäss Katalogpreis 2400. Franken. Weil Herr Gerber Stammkunde ist, gewährt ihm der Velohändler 15% Rabatt. Somit muss
Lösungen. z6gy96 Lösungen. z6gy96. Name: Klasse: Datum: Von 300 wurden 30 % gespart. 300 entspricht dem. Grundwert 30 % ist der.
 Name: Klasse: Datum: 1) Überlege, welcher der Begriffe passt. Von 300 wurden 30 % gespart. 300 entspricht dem. 30 % ist der. 12 % Rabatt, oder 25 konnten sich die Kunden vom Kaufpreis abziehen. 25 entspricht
Name: Klasse: Datum: 1) Überlege, welcher der Begriffe passt. Von 300 wurden 30 % gespart. 300 entspricht dem. 30 % ist der. 12 % Rabatt, oder 25 konnten sich die Kunden vom Kaufpreis abziehen. 25 entspricht
Übungsbeispiele- Mathematik 2. Schularbeit, am
 011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
Download. Hausaufgaben: Lineare Funktionen und Gleichungen. Üben in drei Differenzierungsstufen. Otto Mayr. Downloadauszug aus dem Originaltitel:
 Download Otto Mar Hausaufgaben: Lineare Funktionen und Gleichungen Üben in drei Differenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Lineare Funktionen und Gleichungen Üben in drei
Download Otto Mar Hausaufgaben: Lineare Funktionen und Gleichungen Üben in drei Differenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Lineare Funktionen und Gleichungen Üben in drei
!Utlt. Kantonsschule Zürcher Oberland Wetzikon. Wohnort:... Punkte: Note: Name:... Vorname:... Aufnahmeprüfung 2006 Mathematik schriftlich
 !Utlt Kantonsschule Zürcher Oberland Wetzikon Aufnahmeprüfung 26 Mathematik schriftlich Unterstufe 6 Minuten Name:... Vorname:... Allgemeine Hinweise Schreibe auf dieses erste Blatt deinen Namen, Vornamen
!Utlt Kantonsschule Zürcher Oberland Wetzikon Aufnahmeprüfung 26 Mathematik schriftlich Unterstufe 6 Minuten Name:... Vorname:... Allgemeine Hinweise Schreibe auf dieses erste Blatt deinen Namen, Vornamen
Trigonometrische Funktionen
 Trigonometrische Funktionen Inhaltlicher Überblick Trigonometrie im Lehrplan Geschichtlicher Hintergrund Wdh.: Bogenmaß/ Winkelmaß Einführungsmöglichkeiten Sinus, Kosinus, Tangens im rechtwinkeligen Dreieck
Trigonometrische Funktionen Inhaltlicher Überblick Trigonometrie im Lehrplan Geschichtlicher Hintergrund Wdh.: Bogenmaß/ Winkelmaß Einführungsmöglichkeiten Sinus, Kosinus, Tangens im rechtwinkeligen Dreieck
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Prozentrechnung Lösungen
 1) Überlege, welcher der Begriffe passt. Von 300 wurden 30 % gespart. 300 entspricht dem. 30 % ist der. 12 % Rabatt, oder 25 konnten sich die Kunden vom Kaufpreis abziehen. 25 entspricht dem. 12 % ist
1) Überlege, welcher der Begriffe passt. Von 300 wurden 30 % gespart. 300 entspricht dem. 30 % ist der. 12 % Rabatt, oder 25 konnten sich die Kunden vom Kaufpreis abziehen. 25 entspricht dem. 12 % ist
Grundfertigkeiten Grundoperationen mit natürlichen Zahlen
 Grundfertigkeiten Grundoperationen mit natürlichen Zahlen Stelleneinmaleins A 70 80 = 700 9 = 0 000 = 00 700 = B 000 : 9 = 000 : 80 = 7000 : 800 = 9000 : 70 = C 70 000 = 00 : 0 = 0000 : 0 = 000 00 = Runde
Grundfertigkeiten Grundoperationen mit natürlichen Zahlen Stelleneinmaleins A 70 80 = 700 9 = 0 000 = 00 700 = B 000 : 9 = 000 : 80 = 7000 : 800 = 9000 : 70 = C 70 000 = 00 : 0 = 0000 : 0 = 000 00 = Runde
Mathematik 16 Koordinatensystem 01 Name: Vorname: Datum:
 Mathematik 16 Koordinatensystem 01 Name: Vorname: Datum: Aufgabe 1: Gib an, wie gross der Temperaturunterschied ist: a) 90 C / 40 C: b) 75 C / 38 C: c) 82 C / 17 C: d) 42 C / 8 C: e) 33 C / 67 C: f) 21
Mathematik 16 Koordinatensystem 01 Name: Vorname: Datum: Aufgabe 1: Gib an, wie gross der Temperaturunterschied ist: a) 90 C / 40 C: b) 75 C / 38 C: c) 82 C / 17 C: d) 42 C / 8 C: e) 33 C / 67 C: f) 21
Zentrale Prüfungen 2015 Mathematik
 Name: Zentrale Prüfungen 2015 Mathematik Realschule / Gesamtschule (Erweiterungskurs) / Hauptschule (Klasse 10 Typ B) Prüfungsteil I Aufgabe 1 Ordne folgende Zahlen der Größe nach: 10 ; 2 ; 10 ; 2 Aufgabe
Name: Zentrale Prüfungen 2015 Mathematik Realschule / Gesamtschule (Erweiterungskurs) / Hauptschule (Klasse 10 Typ B) Prüfungsteil I Aufgabe 1 Ordne folgende Zahlen der Größe nach: 10 ; 2 ; 10 ; 2 Aufgabe
Mathematik W18. Mag. Christina Sickinger. Berufsreifeprüfung. Trigonometrie am rechtwinkligen Dreieck
 Mathematik W18 Mag. Christina Sickinger Berufsreifeprüfung v 0 Mag. Christina Sickinger Mathematik W18 1 / 41 Das Problem v 0 Mag. Christina Sickinger Mathematik W18 2 / 41 Wir wollen das Problem lösen!
Mathematik W18 Mag. Christina Sickinger Berufsreifeprüfung v 0 Mag. Christina Sickinger Mathematik W18 1 / 41 Das Problem v 0 Mag. Christina Sickinger Mathematik W18 2 / 41 Wir wollen das Problem lösen!
1 Zeichne eine Skizze deines Schulweges. ( / 3 P.) stimmt 3 Punkte stimmt überwiegend 2 Punkte stimmt teilweise 1 Punkt stimmt nicht 0 Punkte
 1. a) Ich kann Skizzen eines (Schul-) Weges erstellen. (S. 12/13) 1 Zeichne eine Skizze deines Schulweges. ( / 3 P.) b) Ich kann Orte auf Karten auffinden und angeben. (S. 12 15, S. 24/25) 2 Suche im Atlas
1. a) Ich kann Skizzen eines (Schul-) Weges erstellen. (S. 12/13) 1 Zeichne eine Skizze deines Schulweges. ( / 3 P.) b) Ich kann Orte auf Karten auffinden und angeben. (S. 12 15, S. 24/25) 2 Suche im Atlas
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lineare Funktionen an der Berufsschule: Übungsaufgaben
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare Funktionen an der Berufsschule: Übungsaufgaben Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Übungsaufgaben:
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare Funktionen an der Berufsschule: Übungsaufgaben Das komplette Material finden Sie hier: School-Scout.de SCHOOL-SCOUT Übungsaufgaben:
2016/17 Jahrgangsstufe 7 A. Jahrgangsstufentest im Fach Mathematik am Hanns-Seidel-Gymnasium am
 206/7 Jahrgangsstufe 7 A Jahrgangsstufentest im Fach Mathematik am Hanns-Seidel-Gymnasium am 22.9.206 Name: Note: Klasse: Punkte: Aufgabe Berechne: ( 4 45 5 9 ) 0,2 = / 2 Aufgabe 2 Bestimme den Bruchteil
206/7 Jahrgangsstufe 7 A Jahrgangsstufentest im Fach Mathematik am Hanns-Seidel-Gymnasium am 22.9.206 Name: Note: Klasse: Punkte: Aufgabe Berechne: ( 4 45 5 9 ) 0,2 = / 2 Aufgabe 2 Bestimme den Bruchteil
ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese Aufgabenblätter
 Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 01 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 01 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Probematura Mathematik
 BRP Mathematik VHS Floridsdorf 05/06 2012 Seite 1/5 Probematura Mathematik Volkshochschule Floridsdorf / Frühjahr 2012 Beurteilungsschlüssel: 55-60 P.: 1, 8-5 P.: 2. 39-7 P.: 3, 30-39 P.: 5, 0-29 P.: 5
BRP Mathematik VHS Floridsdorf 05/06 2012 Seite 1/5 Probematura Mathematik Volkshochschule Floridsdorf / Frühjahr 2012 Beurteilungsschlüssel: 55-60 P.: 1, 8-5 P.: 2. 39-7 P.: 3, 30-39 P.: 5, 0-29 P.: 5
Mathematik II Prüfung für den Übertritt aus der 8. Klasse
 Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Bayerischer Mathematiktest an Realschulen 2006
 Jgst. 6 Aufgabe: 1.1 Die vier Grundrechenarten 1.0 Berechne: 1.1 73 3 22 + 30 = 37 Aufgabe 1.1 76,4% 23,6% Jgst. 6 Aufgabe: 1.2 Potenzen 1.0 Berechne: 1.2 2 2 2 5 4 + 3 = 18 Aufgabe 1.2 80,4% 19,6% - 2
Jgst. 6 Aufgabe: 1.1 Die vier Grundrechenarten 1.0 Berechne: 1.1 73 3 22 + 30 = 37 Aufgabe 1.1 76,4% 23,6% Jgst. 6 Aufgabe: 1.2 Potenzen 1.0 Berechne: 1.2 2 2 2 5 4 + 3 = 18 Aufgabe 1.2 80,4% 19,6% - 2
1 Finanzmathematik (21 Punkte)
 - 2 - AP WS 04M 1 Finanzmathematik (21 Punkte) Herr A freut sich über seinen Lottogewinn in Höhe von 141.783,76. Er legt 75 % davon bei seiner Bank zu einem Zinssatz von 3,5 % an. 1.1 Berechnen Sie, über
- 2 - AP WS 04M 1 Finanzmathematik (21 Punkte) Herr A freut sich über seinen Lottogewinn in Höhe von 141.783,76. Er legt 75 % davon bei seiner Bank zu einem Zinssatz von 3,5 % an. 1.1 Berechnen Sie, über
JAHRGANGSSTUFENTEST 2009 IM FACH MATHEMATIK FÜR DIE JAHRGANGSSTUFE 8 DER REALSCHULEN WAHLPFLICHTFÄCHERGRUPPE I NAME: KLASSE: 8 NOTE: PUNKTE: /21
 JAHRGANGSSTUFENTEST 29 IM FACH MATHEMATIK FÜR DIE JAHRGANGSSTUFE 8 DER REALSCHULEN WAHLPFLICHTFÄCHERGRUPPE I (ARBEITSZEIT: MINUTEN) NAME: PUNKTE: /21 KLASSE: 8 NOTE: 1 Aus einer Zeitungsmeldung: Die Zahl
JAHRGANGSSTUFENTEST 29 IM FACH MATHEMATIK FÜR DIE JAHRGANGSSTUFE 8 DER REALSCHULEN WAHLPFLICHTFÄCHERGRUPPE I (ARBEITSZEIT: MINUTEN) NAME: PUNKTE: /21 KLASSE: 8 NOTE: 1 Aus einer Zeitungsmeldung: Die Zahl
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Strahlensätze: Aufgaben
 Strahlensätze: Aufgaben 1. Zwei parallele Geraden schneiden zwei Strahlen mit gemeinsamen Anfangspunkt S. Berechne die in der Tabelle fehlenden Streckenlängen. a b c d (a) 5 cm 4cm 6cm (b) 3.6cm 9.2cm
Strahlensätze: Aufgaben 1. Zwei parallele Geraden schneiden zwei Strahlen mit gemeinsamen Anfangspunkt S. Berechne die in der Tabelle fehlenden Streckenlängen. a b c d (a) 5 cm 4cm 6cm (b) 3.6cm 9.2cm
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
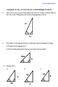 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Fachmittelschul-Ausweis 2016 Mathematik
 Bildungs-, Kultur- und Sportdirektion Kanton Basel-Landschaft Fachmittelschule am Gymnasium Oberwil Fachmittelschul-Ausweis 2016 Anzahl Seiten (mit Deckblatt): 7 Inhalt: FMS Abschlussprüfung 2016 schriftlich
Bildungs-, Kultur- und Sportdirektion Kanton Basel-Landschaft Fachmittelschule am Gymnasium Oberwil Fachmittelschul-Ausweis 2016 Anzahl Seiten (mit Deckblatt): 7 Inhalt: FMS Abschlussprüfung 2016 schriftlich
Ballon. Bestimme, in welcher Höhe der Ballon über dem Punkt G schwebt m über dem Punkt G. Der Ballon schwebt in einer Höhe von
 Ballon Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66 und β = 24 angepeilt. Bestimme, in welcher Höhe der Ballon
Ballon Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66 und β = 24 angepeilt. Bestimme, in welcher Höhe der Ballon
Naturwissenschaften Teil 1
 Naturwissenschaften Teil Auswertung von Messreihen Grafische Darstellung Die nachfolgende Tabelle enthält die Messwerte zur Aufnahme einer Abkühlungskurve für reines Zinn. Stelle die Messwerte in einem
Naturwissenschaften Teil Auswertung von Messreihen Grafische Darstellung Die nachfolgende Tabelle enthält die Messwerte zur Aufnahme einer Abkühlungskurve für reines Zinn. Stelle die Messwerte in einem
Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen.
 Lösung Selbsttest Karte / Kompass Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen. Falls bei der einen oder anderen Prüfungsaufgabe Probleme aufgetaucht sind,
Lösung Selbsttest Karte / Kompass Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen. Falls bei der einen oder anderen Prüfungsaufgabe Probleme aufgetaucht sind,
Geraden Anwendungen. z.b. A(1 4), in die Geradengleichung ein. Löse sie nach b auf, es ergibt sich b = 13
 Geraden Anwendungen 1. Berechne die Nullstelle, d. h. den Schnittpunkt der Geraden mit der x-achse. a) y = 4x+ 1 b) y = 3 5 x+ 1 3 1. Eine Nullstelle ist der Schnittpunkt mit der x-achse. Weil der Punkt
Geraden Anwendungen 1. Berechne die Nullstelle, d. h. den Schnittpunkt der Geraden mit der x-achse. a) y = 4x+ 1 b) y = 3 5 x+ 1 3 1. Eine Nullstelle ist der Schnittpunkt mit der x-achse. Weil der Punkt
Mathematik II Prüfung für den Übertritt aus der 8. Klasse
 Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Bei Windstille bilden die Regentropfen am Fenster eines mit einer Geschwindigkeit v z
 Aufgabe 1 (Verkehrsschild) a) Unter welchem Winkel steigt die Straße an? Schätze zuerst. b) Die Straße überwindet einen Höhenunterschied von 100m. Wie lang ist die Straße? c) Welchen Höhenunterschied überwindet
Aufgabe 1 (Verkehrsschild) a) Unter welchem Winkel steigt die Straße an? Schätze zuerst. b) Die Straße überwindet einen Höhenunterschied von 100m. Wie lang ist die Straße? c) Welchen Höhenunterschied überwindet
Fachrechnen für Bauberufe. 1 Arithmetik Algebra. 2 Proportionalität. 3 Trigonometrie. 4 Planimetrie. 5 Stereometrie. 6 Allgemeines Rechnen
 Fachrechnen für Bauberufe 1 Arithmetik Algebra 2 Proportionalität 3 4 Planimetrie 5 Stereometrie 6 Allgemeines Rechnen Inhaltsverzeichnis 1... 3 1.1 im rechtwinkligen Dreieck... 3 1.2 Winkeleinheiten...
Fachrechnen für Bauberufe 1 Arithmetik Algebra 2 Proportionalität 3 4 Planimetrie 5 Stereometrie 6 Allgemeines Rechnen Inhaltsverzeichnis 1... 3 1.1 im rechtwinkligen Dreieck... 3 1.2 Winkeleinheiten...
Hauptprüfung Abiturprüfung 2018 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
Hauptprüfung Abiturprüfung 08 (ohne CAS) Baden-Württemberg Wahlteil Analysis A Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Juni 08 Aufgabe A. Der
Maßstab Infoblatt. Maßstab wirkliche Länge Verhältniszahl (Naturmaß)
 www.klassenarbeiten.de Seite 1 Maßstab Infoblatt Um Gebäude auf Zeichnungen darstellen zu können, muss man sie verkleinern. Der Maßstab beschreibt diesen Verkleinerungsfaktor. M.: 1 : 100 Maßstab wirkliche
www.klassenarbeiten.de Seite 1 Maßstab Infoblatt Um Gebäude auf Zeichnungen darstellen zu können, muss man sie verkleinern. Der Maßstab beschreibt diesen Verkleinerungsfaktor. M.: 1 : 100 Maßstab wirkliche
Name & Klasse: Naturwissenschaft und Technik Datum: Trigonometrie. Trigonometrie. Wir interessieren uns hier lediglich für rechtwinklige Dreiecke.
 Trigonometrie Trigonometrie Wir interessieren uns hier lediglich für rechtwinklige Dreiecke. Satz des Pythagoras Mit dem Satz des Pythagoras ist es möglich in einem rechtwinkligen Dreieck aus zwei bekannten
Trigonometrie Trigonometrie Wir interessieren uns hier lediglich für rechtwinklige Dreiecke. Satz des Pythagoras Mit dem Satz des Pythagoras ist es möglich in einem rechtwinkligen Dreieck aus zwei bekannten
Sinus, Cosinus und Tangens. Sinus, Cosinus und Tangens. Gruppenmitglieder: Gruppenmitglieder: Station Aufgabenstellung Kontrolle
 Sinus, Cosinus und Tangens Sinus, Cosinus und Tangens Gruppenmitglieder: Gruppenmitglieder: Bearbeitet gemeinsam die Aufgabenstellungen, die bei den einzelnen Stationen bereitliegen (in beliebiger Reihenfolge!
Sinus, Cosinus und Tangens Sinus, Cosinus und Tangens Gruppenmitglieder: Gruppenmitglieder: Bearbeitet gemeinsam die Aufgabenstellungen, die bei den einzelnen Stationen bereitliegen (in beliebiger Reihenfolge!
Mathematik - Arbeitsblatt Lineare Funktionen
 Mathematik - Arbeitsblatt Lineare Funktionen 1.(a) Welche der drei roten Graphen gehört zur Funktion == +5? Wie lautet die Funktionsgleichung des blauen Graphen? Bestimme rechnerisch die Nullstelle des
Mathematik - Arbeitsblatt Lineare Funktionen 1.(a) Welche der drei roten Graphen gehört zur Funktion == +5? Wie lautet die Funktionsgleichung des blauen Graphen? Bestimme rechnerisch die Nullstelle des
Lineare Funktion Eigenschaften von linearen Funktionen Übungen Bearbeite zu jeder der gegebenen Funktionen die Fragen:
 Lineare Funktion Eigenschaften von linearen Funktionen Übungen - 3 2.0 Bearbeite zu jeder der gegebenen Funktionen die Fragen: steigt oder fällt der Graph der Funktion? schneidet der Graph die y-achse
Lineare Funktion Eigenschaften von linearen Funktionen Übungen - 3 2.0 Bearbeite zu jeder der gegebenen Funktionen die Fragen: steigt oder fällt der Graph der Funktion? schneidet der Graph die y-achse
Übungen: Lineare Funktionen
 Übungen: Lineare Funktionen 1. Zeichnen Sie die Graphen der folgenden Funktionen und berechnen Sie die Nullstelle. a) f: y = 2x - 3 b) f: y = -3x + 6 c) f: y = ¼ x + 3 d) f: y = - 3 / 2 x + 9 e) f: y =
Übungen: Lineare Funktionen 1. Zeichnen Sie die Graphen der folgenden Funktionen und berechnen Sie die Nullstelle. a) f: y = 2x - 3 b) f: y = -3x + 6 c) f: y = ¼ x + 3 d) f: y = - 3 / 2 x + 9 e) f: y =
DER PYTHAGORÄISCHE LEHRSATZ
 DER PYTHAGORÄISCHE LEHRSATZ Für ein rechtwinkeliges Dreieck mit den Kathetenlänge a, b und der Hypotenusenlänge c gilt nach dem pythagoräischen Lehrsatz: c 2 = a 2 + b 2 oder c = a 2 + b 2 1) Von einem
DER PYTHAGORÄISCHE LEHRSATZ Für ein rechtwinkeliges Dreieck mit den Kathetenlänge a, b und der Hypotenusenlänge c gilt nach dem pythagoräischen Lehrsatz: c 2 = a 2 + b 2 oder c = a 2 + b 2 1) Von einem
Unser Schulweg O
 Unser Schulweg Inga und Carlo besuchen beide die Gesamtschule Wald. Inga hat einen ca. 6 km langen Schulweg. Carlo wohnt näher an der Schule. Beide starten zur gleichen Uhrzeit von zu Hause aus. Das Diagramm
Unser Schulweg Inga und Carlo besuchen beide die Gesamtschule Wald. Inga hat einen ca. 6 km langen Schulweg. Carlo wohnt näher an der Schule. Beide starten zur gleichen Uhrzeit von zu Hause aus. Das Diagramm
Mathematik II Prüfung für den Übertritt aus der 9. Klasse
 Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 2018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Repetition Mathematik 8. Klasse
 Repetition Mathematik 8. Klasse. Berechne schrittweise mit einem korrekten Lösungsweg: + 3 3 4 : 3. Berechne schrittweise mit einem korrekten Lösungsweg: 0 + 0 b.) 3 4 + 3 5 c.) 9 8 8 9 5 3. Berechne schrittweise
Repetition Mathematik 8. Klasse. Berechne schrittweise mit einem korrekten Lösungsweg: + 3 3 4 : 3. Berechne schrittweise mit einem korrekten Lösungsweg: 0 + 0 b.) 3 4 + 3 5 c.) 9 8 8 9 5 3. Berechne schrittweise
Gruppenrallye zum Thema Rechtwinkliges Dreieck
 Gruppenrallye zum Thema Rechtwinkliges Dreieck Hinweise für Lehrerinnen und Lehrer Voraussetzungen Winkelfunktionen am rechtwinkligen Dreieck Arcusfunktionen im rechtwinkligen Dreieck Einfache Übungsaufgaben
Gruppenrallye zum Thema Rechtwinkliges Dreieck Hinweise für Lehrerinnen und Lehrer Voraussetzungen Winkelfunktionen am rechtwinkligen Dreieck Arcusfunktionen im rechtwinkligen Dreieck Einfache Übungsaufgaben
2. Berechnungen mit Pythagoras
 2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
Berechnungen am Dreieck
 1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
Aufgaben mit Lösungen zum Themengebiet: Geometrie bei rechtwinkligen Dreiecken
 Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Vorbereitungsaufgaben für den Teil 1 der 3. Klausur am
 Vorbereitungsaufgaben für den Teil 1 der 3. Klausur am 24.2.15 1 NT 2013: Quadratische und lineare Funktionen Die abgebildete Parabel gehört zur Funktion f mit f(x) = x 2 5 x + 4. a) Zeige durch eine Rechnung,
Vorbereitungsaufgaben für den Teil 1 der 3. Klausur am 24.2.15 1 NT 2013: Quadratische und lineare Funktionen Die abgebildete Parabel gehört zur Funktion f mit f(x) = x 2 5 x + 4. a) Zeige durch eine Rechnung,
9 Rettungsring Funktionen. Darstellen von funktionalen Abhängigkeiten. ganz klar: Mathematik 4 - Das Ferienheft mit Erfolgsanzeiger.
 ganz klar: Mathematik - Das Ferienheft mit Erfolgsanzeiger Darstellen von funktionalen Abhängigkeiten Merke Bei einer Funktion wird jedem -Wert genau ein -Wert zugeordnet, das heißt, der -Wert ist vom
ganz klar: Mathematik - Das Ferienheft mit Erfolgsanzeiger Darstellen von funktionalen Abhängigkeiten Merke Bei einer Funktion wird jedem -Wert genau ein -Wert zugeordnet, das heißt, der -Wert ist vom
Wiederholungsaufgaben Klasse 10
 Wiederholungsaufgaben Klasse 10 (Lineare und quadratische Funktionen / Sinus, Kosinus, Tangens und Anwendungen) 1. In welchem Punkt schneiden sich zwei Geraden, wenn eine Gerade g durch die Punkte A(1
Wiederholungsaufgaben Klasse 10 (Lineare und quadratische Funktionen / Sinus, Kosinus, Tangens und Anwendungen) 1. In welchem Punkt schneiden sich zwei Geraden, wenn eine Gerade g durch die Punkte A(1
Berufsmatu rität 2 Aufnahmeprüfu ng März 2014
 Berufsschule Aarau Berufsmatu rität 2 Aufnahmeprüfu ng März 2014 Mathematik Kandidaten-Nr. Name Vorname Zeit 60 Minuten Hilfsmittel Netzunabhängiger Taschenrechner ohne Textspeicher und ohne alphanumerische
Berufsschule Aarau Berufsmatu rität 2 Aufnahmeprüfu ng März 2014 Mathematik Kandidaten-Nr. Name Vorname Zeit 60 Minuten Hilfsmittel Netzunabhängiger Taschenrechner ohne Textspeicher und ohne alphanumerische
BMT Bayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien. Name: Note: Klasse: Punkte: / 21
 MT8 2011 ayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Punkte: 1 ufgabe 1 Lukas macht eine Mountainbike-Tour rund um den Hochfelln. Die bbildung zeigt das Streckenprofil
MT8 2011 ayerischer Mathematik-Test für die Jahrgangsstufe 8 der Gymnasien Name: Note: Klasse: Punkte: 1 ufgabe 1 Lukas macht eine Mountainbike-Tour rund um den Hochfelln. Die bbildung zeigt das Streckenprofil
E r g ä n z u n g. zur Trigonometrie
 E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
Kandidatennummer / Name... Gruppennummer... Aufgabe Total Note
 Mathematik Zweiter Teil mit Taschenrechner Kandidatennummer / Name... Gruppennummer... Vorname... Aufgabe 1 2 3 4 5 6 Total Note Punkte total Punkte erreicht 4 5 4 5 6 5 29 Die Prüfung dauert 45 Minuten.
Mathematik Zweiter Teil mit Taschenrechner Kandidatennummer / Name... Gruppennummer... Vorname... Aufgabe 1 2 3 4 5 6 Total Note Punkte total Punkte erreicht 4 5 4 5 6 5 29 Die Prüfung dauert 45 Minuten.
Anwendungen der Mathematik
 Gymnasium Muttenz Maturitätsprüfung 2012 Anwendungen der Mathematik (Profil A ) Kandidatin / Kandidat Name Vorname:... Klasse 4A Hinweise - Die Prüfung dauert 4 Stunden. - Es können maximal 48 Punkte erreicht
Gymnasium Muttenz Maturitätsprüfung 2012 Anwendungen der Mathematik (Profil A ) Kandidatin / Kandidat Name Vorname:... Klasse 4A Hinweise - Die Prüfung dauert 4 Stunden. - Es können maximal 48 Punkte erreicht
Mathematik II Prüfung für den Übertritt aus der 9. Klasse
 Aufnahmeprüfung 018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 018 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Abschlussprüfung Name Klasse MATHEMATIK
 Gym Oberwil FMS Abteilung Abschlussprüfung 2012 Name Klasse MATHEMATIK Zeit Hilfsmittel 3 h Taschenrechner (nicht graphikfähig), Formelsammlung Verwenden Sie bitte für jede Aufgabe ein neues Blatt und
Gym Oberwil FMS Abteilung Abschlussprüfung 2012 Name Klasse MATHEMATIK Zeit Hilfsmittel 3 h Taschenrechner (nicht graphikfähig), Formelsammlung Verwenden Sie bitte für jede Aufgabe ein neues Blatt und
Warm-up Wie groß sind die Winkel α, β, γ? Es gilt: a b und c d. α = 58 (Wechselwinkel zu γ) β = 122 (Scheitelwinkel)
 Winkel Textaufgabe Maßstab Warm-up 24. Wie groß sind die Winkel α, β, γ? Es gilt: a b und c d α = 58 (Wechselwinkel zu γ) β = 2 (Scheitelwinkel) γ = 58 (Nebenwinkel 80 2 ) 2. Für 4 Eiskugeln muss Felix
Winkel Textaufgabe Maßstab Warm-up 24. Wie groß sind die Winkel α, β, γ? Es gilt: a b und c d α = 58 (Wechselwinkel zu γ) β = 2 (Scheitelwinkel) γ = 58 (Nebenwinkel 80 2 ) 2. Für 4 Eiskugeln muss Felix
DOWNLOAD. Lernzirkel Längen. Albrecht Schiekofer. Downloadauszug aus dem Originaltitel:
 DOWNLOAD Albrecht Schiekofer Lernzirkel Längen Downloadauszug aus dem Originaltitel: Albrecht Schiekofer: Lernzirkel Längen Persen Verlag GmbH, Buxtehude 1 Lernzirkel: inhaltlicher Aufbau 1 2 3 4 5 6 7
DOWNLOAD Albrecht Schiekofer Lernzirkel Längen Downloadauszug aus dem Originaltitel: Albrecht Schiekofer: Lernzirkel Längen Persen Verlag GmbH, Buxtehude 1 Lernzirkel: inhaltlicher Aufbau 1 2 3 4 5 6 7
Anwendungen 1. b) Berechnen Sie die Hypothenuse c: c) Berechnen Sie die Winkelfunktionen sinα, cosα, und tanα. d) Berechnen Sie die Winkel α und β :
 Für alle Aufgaben gilt: 1. Winkel und Strecken sind auf eine, Winkelfunktionen auf 4 Nachkommastellen zu runden; nehmen Sie für Zwischenresultate mit denen Sie weiterrechnen eine Stelle mehr 2. Erstellen
Für alle Aufgaben gilt: 1. Winkel und Strecken sind auf eine, Winkelfunktionen auf 4 Nachkommastellen zu runden; nehmen Sie für Zwischenresultate mit denen Sie weiterrechnen eine Stelle mehr 2. Erstellen
Kapitel 3 Mathematik. Kapitel 3.8 Geometrie Trigonometrie REPETITIONEN. Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL
 Kapitel 3 Mathematik Kapitel 3.8 Geometrie Trigonometrie REPETITIONEN Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn Telefon 055 654 12 87 Telefax 055 654 12 88 E-Mail
Kapitel 3 Mathematik Kapitel 3.8 Geometrie Trigonometrie REPETITIONEN Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn Telefon 055 654 12 87 Telefax 055 654 12 88 E-Mail
Koordinatensystem, Strecken, Geraden
 Koordinatensystem, Strecken, Geraden Zeichne eine Rechts- und eine Hochachse und trage folgende Punkte ein: P(2 1), Q(10 1), R(10 9), S(2 9), T(4 3), U(8 3), V(8 7), W(4 7). Zeichne die Strecken PQ QR
Koordinatensystem, Strecken, Geraden Zeichne eine Rechts- und eine Hochachse und trage folgende Punkte ein: P(2 1), Q(10 1), R(10 9), S(2 9), T(4 3), U(8 3), V(8 7), W(4 7). Zeichne die Strecken PQ QR
Schriftliche Abiturprüfung Grundkursfach Mathematik -NACHTERMIN-
 Sächsisches Staatsministerium für Kultus und Sport Schuljahr 2009/10 Geltungsbereich: - allgemeinbildendes Gymnasium - Abendgymnasium und Kolleg - schulfremde Prüfungsteilnehmer Schriftliche Abiturprüfung
Sächsisches Staatsministerium für Kultus und Sport Schuljahr 2009/10 Geltungsbereich: - allgemeinbildendes Gymnasium - Abendgymnasium und Kolleg - schulfremde Prüfungsteilnehmer Schriftliche Abiturprüfung
Aufnahmeprüfung 2008 LÖSUNGEN Mathematik Serie 1
 Aufnahmeprüfung 008 LÖSUNGEN Mathematik Serie 1 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtig!
Aufnahmeprüfung 008 LÖSUNGEN Mathematik Serie 1 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtig!
M3/I Übung für die 5. Schularbeit Name:
 1)Das Dreieck ABC ist vom Eckpunkt A aus im Verhältnis : 4 zu vergrößern. a = 45 mm, b = 40 mm, c = 60 mm 2)Vergrößere das Rechteck (a = 46 mm; b = 25 mm) im Verhältnis 2 :. Wähle als Zentrum den Eckpunkt
1)Das Dreieck ABC ist vom Eckpunkt A aus im Verhältnis : 4 zu vergrößern. a = 45 mm, b = 40 mm, c = 60 mm 2)Vergrößere das Rechteck (a = 46 mm; b = 25 mm) im Verhältnis 2 :. Wähle als Zentrum den Eckpunkt
Aufgaben. zu Inhalten der 5. Klasse
 Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Die lineare Funktion; Steigung einer Strecke
 linft.nb Die lineare Funktion; Steigung einer Strecke. Steigung und Gefälle einer Strasse Einleitung: -Wie würden Sie die Steilheit einer Strasse "messen"? Wie kann man die Steilheit einer Strasse, einer
linft.nb Die lineare Funktion; Steigung einer Strecke. Steigung und Gefälle einer Strasse Einleitung: -Wie würden Sie die Steilheit einer Strasse "messen"? Wie kann man die Steilheit einer Strasse, einer
Übung 11. Fachwerkträger. Aufgabe 01: Aufgabe 02: Aufgabe 03: Aufgabe 04: Aufgabe 05: 170 m. 85 m SEE. E 160 m. x =? 4,4 m.
 Übung 11 Aufgabe 01: C D 170 m 85 m Aufgabe 02: E 160 m B SEE =? A Fachwerkträger 5 m 3 m 3 m 4,4 m Aufgabe 03: 10 40 36 z 15 25 Aufgabe 04: 4 13 18 10 Aufgabe 05: 7 3 Aufgabe 06: 4 m 1 m Aufgabe 07: Ein
Übung 11 Aufgabe 01: C D 170 m 85 m Aufgabe 02: E 160 m B SEE =? A Fachwerkträger 5 m 3 m 3 m 4,4 m Aufgabe 03: 10 40 36 z 15 25 Aufgabe 04: 4 13 18 10 Aufgabe 05: 7 3 Aufgabe 06: 4 m 1 m Aufgabe 07: Ein
Kaufmännische Berufsmatura im Kanton Zürich. Mathematik Serie 1. Name... Vorname... Adresse
 Aufnahmeprüfung 008 Mathematik Serie 1 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtig! - Die
Aufnahmeprüfung 008 Mathematik Serie 1 (60 Min.) Hilfsmittel: Taschenrechner Name... Vorname... Adresse...... ACHTUNG: - Resultate ohne Ausrechnungen bzw. Doppellösungen werden nicht berücksichtig! - Die
Tägliche Nutzungsdauer in Minuten
 Mathematik 6. Schulstufe 1) Von einem Dreieck sind die Winkel α = 20 und β = 70 bekannt. Warum muss in diesem Dreieck der dritte Winkel 90 betragen? 2) Bei der Schuluntersuchung stellte der Schularzt fest,
Mathematik 6. Schulstufe 1) Von einem Dreieck sind die Winkel α = 20 und β = 70 bekannt. Warum muss in diesem Dreieck der dritte Winkel 90 betragen? 2) Bei der Schuluntersuchung stellte der Schularzt fest,
Erreichte Punkte ALLGEMEINE MATHEMATISCHE KOMPETENZEN:
 GRUNDWISSENTEST 05 IM FACH MATHEMATIK FÜR DIE JAHRGANGSSTUFE 7 DER REALSCHULE HINWEISE: Beim Kopieren der Aufgabenblätter ist auf die Maßhaltigkeit zu achten, um Verzerrungen zu vermeiden. Bei formalen
GRUNDWISSENTEST 05 IM FACH MATHEMATIK FÜR DIE JAHRGANGSSTUFE 7 DER REALSCHULE HINWEISE: Beim Kopieren der Aufgabenblätter ist auf die Maßhaltigkeit zu achten, um Verzerrungen zu vermeiden. Bei formalen
Standards Mathematik Klasse 7
 Standards Mathematik Klasse 7 ) Ein Hobby-Imker füllt seinen Jahresertrag an Honig in Gläser mit je 500 g Inhalt ab. Er kann Gläser füllen. Wie viele Gläser zu je 50 g Inhalt könnte er mit diesem Jahresertrag
Standards Mathematik Klasse 7 ) Ein Hobby-Imker füllt seinen Jahresertrag an Honig in Gläser mit je 500 g Inhalt ab. Er kann Gläser füllen. Wie viele Gläser zu je 50 g Inhalt könnte er mit diesem Jahresertrag
Rechtwinklige Dreiecke konstruieren
 1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
1 Vertiefen 1 Rechtwinklige Dreiecke konstruieren zu Aufgabe Schulbuch, Seite 106 Dreiecke konstruieren a) Konstruiere die Dreiecke mit den Angaben aus der Tabelle. Miss dann die übrigen Maße und vervollständige
Arbeitsblatt Mathematik
 Rationale Zahlen Teste dich! Rationale Zahlen (/) Welche Zahlen sind markiert? a) b) c) 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Stelle die Zahlen jeweils auf einer Zahlengerade dar. a) 0,;
Rationale Zahlen Teste dich! Rationale Zahlen (/) Welche Zahlen sind markiert? a) b) c) 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Stelle die Zahlen jeweils auf einer Zahlengerade dar. a) 0,;
Mathematik. Kantonale Fachmittelschulen Aufnahmeprüfung Beachten Sie bitte folgende Rahmenbedingungen:
 Kantonale Fachmittelschulen Aufnahmeprüfung 2016 Mathematik Beachten Sie bitte folgende Rahmenbedingungen: Zum Lösen der Aufgaben stehen Ihnen 120 Minuten zur Verfügung. Schreiben Sie auf jedes Blatt Ihren
Kantonale Fachmittelschulen Aufnahmeprüfung 2016 Mathematik Beachten Sie bitte folgende Rahmenbedingungen: Zum Lösen der Aufgaben stehen Ihnen 120 Minuten zur Verfügung. Schreiben Sie auf jedes Blatt Ihren
Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich
 Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich Mathematik Serie: E1 Basierend auf dem Lehrmittel Mathematik Hohl Dauer: 90 Minuten Name: Vorname: Adresse: Prüfungsnummer: Hilfsmittel:
Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich Mathematik Serie: E1 Basierend auf dem Lehrmittel Mathematik Hohl Dauer: 90 Minuten Name: Vorname: Adresse: Prüfungsnummer: Hilfsmittel:
1. Aufgabe: Grundwissen
 NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
EXPEDITION Mathematik 3 / Übungsaufgaben
 1 Bestimme das Verhältnis folgender Größen. a) 2 mm : 4 m c) 8 m 2 : 0,2 ha e) 12 km : 0,3 m b) 3 kg : 6 t d) 13,2 : 396 Cent f) 2,5 hl : 15 l 2 Stelle das Verhältnis so dar, dass eine der beiden Zahlen
1 Bestimme das Verhältnis folgender Größen. a) 2 mm : 4 m c) 8 m 2 : 0,2 ha e) 12 km : 0,3 m b) 3 kg : 6 t d) 13,2 : 396 Cent f) 2,5 hl : 15 l 2 Stelle das Verhältnis so dar, dass eine der beiden Zahlen
Serie W1 Klasse 8 RS. 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3
 Serie W1 Klasse 8 RS 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3 3 c = 4 2a - b; a + b; b : c 4. 36:0,4 = 5. Vergleiche. 30+2 10+5 30+2 (10+5) 6. Kürze 12 44 7. Berechne a 8a - 28
Serie W1 Klasse 8 RS 1. 7,4 dm³ = cm³ 2. 5 (13-6) = 3. Berechne für a = - 4,5 b = - 3 3 c = 4 2a - b; a + b; b : c 4. 36:0,4 = 5. Vergleiche. 30+2 10+5 30+2 (10+5) 6. Kürze 12 44 7. Berechne a 8a - 28
Montag, 3. September 2018, Uhr (45 Minuten) Name / Vorname: Kandidatennummer:... Bisherige Schule:... Klasse:...
 Lösungen Aufnahmeprüfung BM (BBZ / WMS) und FMS Mathematik 2018 Teil 2 Mit Taschenrechner Prüfungsbedingungen: Erlaubte Hilfsmittel: Taschenrechner (keine CAS-Rechner), keine Handys. Die Aufgaben sind
Lösungen Aufnahmeprüfung BM (BBZ / WMS) und FMS Mathematik 2018 Teil 2 Mit Taschenrechner Prüfungsbedingungen: Erlaubte Hilfsmittel: Taschenrechner (keine CAS-Rechner), keine Handys. Die Aufgaben sind
(Tip zu g): Die Ziffern bestehen aus aufeinanderfolgenden Quadratzahlen).
 Aufgabenblatt Funktionen. Entscheide für die folgenden Zahlen, zu welcher der Mengen N, Z, Q, R sie gehören? a), b).87, c) 8, d) π, e) 0..., f) 8 g) 0.4965649648... (Tip zu g): Die Ziffern bestehen aus
Aufgabenblatt Funktionen. Entscheide für die folgenden Zahlen, zu welcher der Mengen N, Z, Q, R sie gehören? a), b).87, c) 8, d) π, e) 0..., f) 8 g) 0.4965649648... (Tip zu g): Die Ziffern bestehen aus
1.3. Aufgaben zur Statik
 1.3. Aufgaben ur Statik Aufgabe 1: Kräfteerlegung Ein Schlitten kann auf einer Schiene horiontal bewegt werden. Im Winkel von = 40 ur Schiene ieht ein Seil mit der Kraft = 100 N an dem Schlitten. Bestimme
1.3. Aufgaben ur Statik Aufgabe 1: Kräfteerlegung Ein Schlitten kann auf einer Schiene horiontal bewegt werden. Im Winkel von = 40 ur Schiene ieht ein Seil mit der Kraft = 100 N an dem Schlitten. Bestimme
1.6 Direkte, indirekte Proportionalität. Beispiel : x y 20. Funktionsgleichung : Allgemein: (Direkte) Proportionalität.
 1 1.6 Direkte, indirekte Proportionalität Beispiel : 1 2 4 6 8 12 y 20 40 60 80 120 160 240 Funktionsgleichung : f : y = 20 Allgemein: (Direkte) Proportionalität f : y = m m R, m 0 f : Funktionsvorschrift:
1 1.6 Direkte, indirekte Proportionalität Beispiel : 1 2 4 6 8 12 y 20 40 60 80 120 160 240 Funktionsgleichung : f : y = 20 Allgemein: (Direkte) Proportionalität f : y = m m R, m 0 f : Funktionsvorschrift:
Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren
 Schüler/in Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren LERNZIELE: Flächeninhalt mit Rasterzählmethode bestimmen Flächeninhalt und Umfang mit Formeln berechnen Flächeninhalt durch Zerlegen
Schüler/in Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren LERNZIELE: Flächeninhalt mit Rasterzählmethode bestimmen Flächeninhalt und Umfang mit Formeln berechnen Flächeninhalt durch Zerlegen
Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich
 Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich Mathematik Serie: E2 Basierend auf dem Lehrmittel Mathematik Hohl Dauer: 90 Minuten Name: Vorname: Adresse: Prüfungsnummer: Hilfsmittel:
Aufnahmeprüfung 2016 für die Berufsmaturitätsschulen des Kantons Zürich Mathematik Serie: E2 Basierend auf dem Lehrmittel Mathematik Hohl Dauer: 90 Minuten Name: Vorname: Adresse: Prüfungsnummer: Hilfsmittel:
1 Die Geschwindigkeit
 1 Die Geschwindigkeit 1.1 Bestimmung der Geschwindigkeit Fahrtrichtung Maßstab 1 : 1000 Zeit Weg Geschw. 1 s 2 s 3 s 4 s 5 s Ein Auto verliert in jeder Sekunde einen Tropfen Öl. Miss die Entfernungen zwischen
1 Die Geschwindigkeit 1.1 Bestimmung der Geschwindigkeit Fahrtrichtung Maßstab 1 : 1000 Zeit Weg Geschw. 1 s 2 s 3 s 4 s 5 s Ein Auto verliert in jeder Sekunde einen Tropfen Öl. Miss die Entfernungen zwischen
Analytische Geometrie
 Analytische Geometrie 1 Punkte und Vektoren im Raum G 1.1 Gegeben sind die Vektoren in nebenstehender Abbildung. Drücke die Vektoren AC durch a und b AB durch z und w BC durch c und d DB durch b und u
Analytische Geometrie 1 Punkte und Vektoren im Raum G 1.1 Gegeben sind die Vektoren in nebenstehender Abbildung. Drücke die Vektoren AC durch a und b AB durch z und w BC durch c und d DB durch b und u
Ein Lichtstrahl fällt aus der Luft ins Wasser. Man hat den Einfallswinkel α und den Brechungswinkel β gemessen und in folgende Tabelle eingetragen.
 1 Optik 1.1 Brechung des Lichtes Ein Lichtstrahl fällt aus der Luft ins Wasser. Man hat den Einfallswinkel α und den Brechungswinkel β gemessen und in folgende Tabelle eingetragen. α β 0 0 10 8 17 13 20
1 Optik 1.1 Brechung des Lichtes Ein Lichtstrahl fällt aus der Luft ins Wasser. Man hat den Einfallswinkel α und den Brechungswinkel β gemessen und in folgende Tabelle eingetragen. α β 0 0 10 8 17 13 20
AUFNAHMEPRÜFUNG BERUFSMATURA 2013 MATHEMATIK
 Berufsfachschulen Graubünden 3. April 2013 AUFNAHMEPRÜFUNG BERUFSMATURA 2013 MATHEMATIK Name:. Vorname:.. Zeitrahmen 90 Minuten Hinweise: Löse die Aufgaben auf den beigelegten leeren Blättern. Alle Lösungsblätter
Berufsfachschulen Graubünden 3. April 2013 AUFNAHMEPRÜFUNG BERUFSMATURA 2013 MATHEMATIK Name:. Vorname:.. Zeitrahmen 90 Minuten Hinweise: Löse die Aufgaben auf den beigelegten leeren Blättern. Alle Lösungsblätter
