Abschnitt 1. Jordan Normalform
|
|
|
- Gerburg Huber
- vor 6 Jahren
- Abrufe
Transkript
1 Abschnitt Jordan Normalform
2 Beispiel & Eigenschaften λ λ λ λ 2 λ 2 λ 2 λ 3 Voraussetzung: χ zerfällt Dann: ex. Basis, s.d. Darstellungsmatrix Jordan-Form hat Minimalpolynom µ hat Faktor zu jedem EW in Potenz Größe des größten zum EW gehörigen Jordankästchens (z.b. hier µ = (X λ ) 3 (X λ 2) 2 (X λ 3)) bis auf Anordnung der EW: eindeutig, bzw. Matrizen ähnlich gleiche JNF
3 Interpretation Da Haupträume f stabil (und damit (f t id) stabil für alle t K), können wir die Blöcke zu jedem EW stets separat betrachten. λ λ λ λ λ λ λ Mit g := f λ id (d.h. Matrix hat 0en statt λ) und (v,..., v 7) der Jordan Basis in diesem Beispiel sehen wir sofort v 3 g v2 v 5 v 7 g v g v4 g v6 g 0, g 0 g 0,
4 λ λ λ λ λ λ λ d.h. v, v 4, v 6 ker g (die ersten Indizes in jedem Jordan Block), v 2, v 5, v 7 ker g 2 \ ker g (die zweiten Indizes in jedem Jordan Block), v 3 ker g 3 \ ker g 2 (die dritten Indizes in jedem Jordan Block) Wir haben stets dim ker g k dim ker g k Jordan Blöcke der Größe k.
5 Bestimmung der JNF Gemäß dem vorigen berechnen wir für jeden EW λ i jeweils rg(f λ i id), rg(f λ i id) 2,... (in Aufgaben meist direkt ablesbar, notfalls Gauß) und daraus die dim ker g k = n rg g k. Die Anzahl der Jordan Blöcke mit Größe genau k ergibt sich aus obiger Überlegung als rg g k+ 2 rg g k + rg g k.
6 Bestimmung der Jordan Basis Für jeden EW λ i: Beginne mit leerer Menge B :=. Solange B < n i mit n i der Dimension des Hauptraumes H(f, λ i), also der alg. Vielfachheit von λ i: Finde v B mit maximaler Periode, d.h. k maximal, s.d. v ker g k \ ker g k \ B. (Dies entspricht dem letzten Index eines der größten verbliebenen Jordan Blöcke) Füge die Vektoren g k (v),..., v zu B hinzu. (Dies entspricht den Indizes, die durch den gewählten größten Block laufen)
7 Aufgaben Siehe Aufgabenblatt, Aufgaben 5.
8 Aufgabe : Sei f : C 7 C 7 linear mit den Eigenschaften gemäß folgender Tabelle: k dim ker(f 2 id) k dim ker(f 3 id) k 0 dim ker(f 4 id) k Bestimme die JNF der Darstellungsmatrix von f. Lösung: Wir lesen ab, daß wir zum EW 2 fünf Jordan Blöcke haben, alle mit Größe 3, und genau einer davon mit Größe 4, aber keinen mit Größe 5. Zum EW 3 sehen wir einen Block der Größe. 4 ist gar kein EW, und weitere gibt es auch nicht, da wir die Dimension 7 schon erreicht haben. Insgesamt: M = diag (J 4(2), J 3(2), J 3(2), J 3(2), J 3(2), J (3))
9 Aufgabe 2: Falls möglich, bestimme die JNF von A = a) K = R b) K = C c) K = F 2 Lösung: Es ist χ = X 2 +. a) χ zerfällt nicht. ( ) 0 Mat 0 2 2(K) für b) Es ist χ = (X i)(x + i). Aus Dimensionsgründen ( kommen ) nur zwei i 0 Blöcke der Größe in Frage, und es folgt M =. 0 i c) Es ist χ = (X + ( ) 2 = ) (X ) 2, d.h. (= ) ist der einzige Eigenwert. Es ist A id = mit Rang, es gibt also genau einen Jordan Block: ( ) M =. 0
10 Aufgabe 3: Überprüfe mit Hilfe der JNF, welche der folgenden reellen Matrizen zueinander ähnlich sind: A = 0 0, B = 0 2, C = 0 0, D =
11 Lösung: Berechne jeweils JNF: 2 0 Zu A = 0 0 : χ A = (X + ) 2 (X ). Zum EW ist rg(a + ) = rg =, also gibt es 2 Jordan Blöcke. Die JNF ist damit. 0 2 Zu B = 0 2 ist χ B = (X + )(X ) 2. Zum EW ist rg(b ) = rg = 2, also gibt es einen JB, und die JNF ist.
12 2 0 Zu C = 0 0 : χ C = (X + ) 2 (X ). Zum EW ist rg(c + ) = rg =, also gibt es 2 JB. Die JNF ist damit. 0 2 Zu D = 0 2 : χ D = (X + )(X 2 ) = (X + ) 2 (X ). 0 0 Zum EW ist 2 rg(d + ) = rg 2 = 2, also gibt es einen JB. Die JNF ist damit. Wir sehen, daß A und C ähnlich sind, die übrigen zu keiner der anderen.
13 Aufgabe 4: Bestimme JNF, Minimalpolynom und eine Jordan Basis zu 2 0 A =. 0 3 Lösung: χ = X 3 6X 2 + 2X 8 = (X 2) N := A 2 =. 0 rg(n) = 2, d.h. ein JB. Minimalpolynom ist damit µ = χ. Wir brauchen also nur ein v ker(n 3 ) \ ker(n 2 ), dann sind N 2 v, Nv, v die gewünschte Basis. ker(n 2 ) = ker = ker ( ) 0 = 0,, 0 ker(n 3 ) = R 3 schon aus Dimensionsgründen. v := 0 leistet beispielsweise 0 0 das Gewünschte. Die Basis ist dann N 2 v = 0, Nv =, v = 0.
14 Aufgabe 5: K Körper, A, B Mat n n(k). Welche der folgenden Aussagen sind richtig? (Begründung!) a) Zerfällt χ A, so zerfällt auch µ A. b) Ist µ A = µ B, so sind A und B ähnlich. c) Ist A nilpotent, so ist 0 der einzige EW von A. d) Ist A nilpotent und diagonalisierbar, so ist A = 0. Lösung: a) Ja, da µ χ. b) Nein, z.b. 0 und 0. 0 c) Ja, da 0 = A k v = λ k v, also λ = 0 für EV v zu EW λ. d) Ja, da alle EW 0 und damit A ähnlich zu 0.
15 Abschnitt 2 Skalarprodukte
16 Gram Schmidt B = b,..., b n Basis. Konstruiere ONB C = c,..., c n: c := b b induktiv c i := b i i k= bi, c k c k und c i = c i ci Die auftretenden Koeffizienten (Normierung nicht vergessen!) ergeben die Basiswechselmatrix T : obere Dreiecksmatrix mit positiven Diagonaleinträgen. Ist M die Strukturmatrix des Skalarprodukts bzgl. B, so ist M = S T S mit S = T.
17 Hauptminorenkriterium Symmetrische Matrix A positiv definit gdw. alle Hauptminoren positiv (Determinanten der oberen linken Teilmatrizen)
18 Iwasawa Zerlegung A invertierbare Matrix. Dann eindeutige Zerlegung A = DNT mit D Diagonalmatrix mit pos. Einträgen, N obere Dreiecksmatrix mit auf der Diagonale, T orthogonal. Dazu: Spalten von A mit Gram Schmidt zu ONB, Basiswechsel S obere Dreiecksmatrix mit pos. Diagonaleinträgen. T = A S die Matrix mit den Spalten die Vektoren der ONB, also T orthogonal. D die Diagonaleinträge aus S und N := D S. Dann A = ST = DNT T wie gewünscht.
19 Adjungierte Abbildung f : V V Endomorphismus auf eukl./unitärem VR. Adjungierte Abbildung f charakterisiert durch f (v), w = v, f(w). f selbstadjungiert, falls f = f f normal, falls ff = f f Darst. Matrix bzgl. ONB: A = A T
20 Spektralsatz V unitär, endlichdim., f : V V normal. Dann ex. ONB aus Eigenvektoren von f. bzw. A Mat n(c) normal, dann ist U AU diagonal für ein unitäres U. Für reelle Matrizen nur im symmetrischen( Fall; sonst ) 2 dim. invariante α β Unterräume ohne EW, dort Blockmatrix. β α
21 Zerlegungen Wurzeln A selbstadjungiert und pos. definit, dann ex. eindeutiges B selbstadjungiert und pos. def. so daß B 2 = A Aus Spektralsatz A = S DS mit S unitär/orthogonal und D diagonal, mit pos. Einträgen wg. pos. def. Setze D die Diagonalmatrix mit den Wurzeln der Einträge. Dann D 2 = D, und für B := S DS ist B 2 = A. Polarzerlegung A invertierbar, dann A = P T mit eindeutigen T unitär/orthogonal, P selbstadj. pos. def. Setze P als Wurzel von AA. T := P A. Cartanzerlegung A invertierbar, dann A = T DT 2 für gewisse T, T 2 unitär/orthogonal und D diagonal mit pos. Einträgen Zuerst Polar A = P T Spektralsatz: P = SDS mit D wie gewünscht und S unitär/orthogonal Setze T := S, T 2 := S T
22 Quadriken A symmetrisch reell, X = (X,..., X n) T Quadrik Q(X) = X T AX + 2b T X + c Äquivalenz Quadriken Q(X) = X T AX + 2b T X + c und Q (X) = X T A X + 2b T X + c äquivalent, falls durch Koordinatentransformation (S orthogonal, v 0 Translationsvektor) auseinander hervorgegangen wie folgt: A = S T AS b = S T b + A v 0 c = c + v T 0 A v 0 + 2b T Sv 0 Normalform Jede Quadrik äquivalent zu einem der Typen: Q(X) = r i= λix2 i + c mit λ,..., λ r 0 Q(X) = r i= λix2 i + cx n mit r < n, λ i 0, c 0 Transformiere: A orthogonal diagonalisieren: A = S T AS, falls A invertierbar in zweitem Schritt verschieben mit v 0 := A b, dann erste Art.
23 Aufgaben Siehe Aufgabenblatt, Aufgaben 6 2.
24 Aufgabe 6 Betrachte die bilineare Abbildung β : R 3 R 3 R, β(x, y) = x y + x 2y 2 + x 3y 3 x y 3 x 3y. a) Gib die Strukturmatrix von β bzgl. der Standardbasis an. b) Ist β symmetrisch? c) Ist β ein Skalarprodukt? d) Bestimme die Orthogonalräume {e, e 2}, {e + e 2} und {e, e 2}. Lösung: 0 a) B = b) Ja. c) Nein, rg B = 2, also ausgeartet. ( ) ( ) d) {e, e 2} = ker B = ker = ( 0 ) T, {e + e 2} = ker ( 0 ) B = ker ( ) = ( 0 ) T, ( 0 ) T, {e, e 2} = ker ( 0 ) B = ker 0 = R 3.
25 Aufgabe 7 Sei A Mat n n(r) symmetrisch. Zeige: a) Ist A invertierbar, so ist auch A symmetrisch. b) A ist genau dann positiv definit, wenn A invertierbar und A positiv definit ist. Lösung: a) A A = = A T (A ) T = A(A ) T (A ) T = A. b) Sei A pos. def. Damit ist A auch invertierbar, denn sonst hätte sie nichttrivialen Kern, bzw ist nach dem Hauptminorenkriterium insbes. det A > 0, also A invertierbar. Sei nun v R n \ {0}. Dann ist v = Aw für ein w 0, und v T A v = w T A T w = w T Aw > 0.
26 Aufgabe 8 Betrachte auf R 3 die Bilinearform β gegeben durch die Strukturmatrix (bzgl. Standardbasis) 5 0 B = 0 2. a) Zeige, daß β ein Skalarprodukt ist. b) Bestimme aus der Standardbasis mittels Gram-Schmidt eine ONB bzgl. β. c) Gib eine obere Dreiecksmatrix S mit positiven Koeffizienten auf der Diagonalen an, so daß B = S T S. Lösung: a) Offensichtlich symmetrisch. Hauptminoren sind 5, 0 und det B = 5(2 ) + ( 2) = 3 > 0. b) Es ist e = 5, und damit c = 5 e. Da e 2, c = 0 und e 2 = 2, ist c 2 = 2 e 2. Weiter ist e 3, c = 5 und e 3, c 2 = 2, und wir setzen c 3 = e 3 5 c erhalten c 3 = ( 2 c 2 = e 3 5 e e2. Wir berechnen c3 = 3 und 2 0 ) T
27 0 5 c) Aus b) lesen wir die Basiswechselmatrix T = und invertieren zu S = T = ab
28 Aufgabe 9 ( ) 2 7 Bestimme die Iwasawa Zerlegung A = DNT für A =. 3 ( ) 3 7 Lösung: Wir invertieren zu A =, auf die Spalten (b 2, b 2) wenden wir Gram Schmidt an: c = 0 b, c 2 = b b = ( ) 3 T 0 0, c 2 = 0 c 2. Diese ONB schreiben wir in die orthogonale Matrix ( C, für die dann gilt C = A S, wobei wir die Basiswechselmatrix S = 0 23 ) aus der Konstruktion ablesen. ( Mit T := C T gilt dann A = ST, und wir ) ( ) zerlegen noch S in D = und N := D S = ( ) ( ) Insgesamt A = 0 0 ( )
29 Aufgabe 0 Sei (V,, ) ein endlich dimensionaler unitärer Vektorraum und f : V V linear. Zeige: a) Ist f normal, so gilt f(v), f(w) = f (v), f (w) für alle v, w. b) Ist f normal, so gilt V (f, λ) = V (f, λ) für alle λ. c) Ist f normal, so sind Eigenvektoren zu verschiedenen Eigenwerten von f zueinander orthogonal. d) Ist f selbstadjungiert, so sind alle Eigenwerte reell. e) Ist f normal und sind alle Eigenwerte reell, so ist f selbstadjungiert. Lösung: a) f(v), f(w) = f f(v), w = ff (v), w = f (v), f (w). b) Aus a) für g normal insbes ker g = ker g. Mit f ist auch g := f λ id normal, und g = f λ id. c) Sei v EV zu λ, w EV zu µ. 0 = f(v) λv, w = v, f (w) λ v, w = v, µw λ v, w = (µ λ) v, w d) v EV zu λ, dann λ v, v = λv, v = f(v), v = v, f(v) = v, λv = λ v, v, und v, v = 0. e) f selbstadj. gdw Matrix für eine ONB selbstadj.; Spektralsatz: Diagonalmatrix, Einträge reell, also selbstadj.
30 Aufgabe Bestimme ( die Polar ) und eine Cartanzerlegung von 2 A = GL 2 2(R). Lösung: ( ) 5 4 H := AA T = ist symmetrisch pos. def., es existiert also eine 4 5 Wurzel P. Dazu: ( χ H = X ) 2 0X ( ) + 9 = (X 9)(X ( ), ) ( ) V (H, ) = ker =, V (H, 9) = ker = ( ) ( ) Für die orthogonale Matrix Q := 0 2 gilt Q T HQ =, und 0 9 ( ) ( ) 0 2 wir setzen P := Q Q T = ; damit gilt P 2 = H. Die Polarzerlegung ist( dann ) A ( = P T mit) ( ) T := P A = =. Für Cartan: ( ) 0 D := Q T P Q = ist positive Diagonalmatrix; wir haben A = QDQ T T ; 0 3 ( ) setze T := Q und T 2 := Q T T = 2.
31 Aufgabe 2 Bestimme die Normalform der Quadrik Q(X) = 2X 2 2X X 2 + 2X X + 2X 2 +. Lösung: ( ) ( ) 2 Es ist Q(X) = X T AX + 2b T X + c mit A =, b = und c =. 2 ( ) ( ) 0 Wir wissen aus Aufgabe, daß S T AS = für S = Damit ( ist Q ) äquivalent zu Q ( mit ) Q (X) = X T A X + 2b T + c mit 0 A =, b = S T 2 b =, c = c =. Wir verschieben nun noch den ( ) Ursprung mittels v 0 := A b 2 =, und erhalten, daß Q äquivalent 0 ist zu Q (X) = X T A X + 2b T X + c mit A = A, b = b + A v 0 = 0 und c = c + v0 T A v 0 + 2b T v 0 = =. Also ist die Normalform Q (X) = X 2 + 3X2 2.
32
33 Abschnitt 3 Tensorprodukt
34 Tensorprodukt V, W Vektorräume. Gibt V W und η : V W V W bilinear mit der universellen Eigenschaft: U Vektorraum und ξ : V W U bilinear, dann faktorisiert ξ eindeutig über V W, d.h. es gibt eine eindeutige lineare Abb. ξ : V W U mit ξ = ξ η. (V W, η) ist eindeutig bis auf eindeutigen Isomorphismus, d.h. für (V W, η ) mit der selben Eigenschaft gibt es genau einen Isomorphismus ϕ : V W V W mit ϕη = η
35 Aufgaben Siehe Aufgabenblatt, Aufgaben 3 4.
36 Aufgabe 3 Wie folgt die Eindeutigkeit des Tensorproduktes aus der charakterisierenden universellen Eigenschaft? Lösung: Seien η : V W V W und η : V W V W die bilinearen Abbildungen in zwei Tensorprodukte. Dann gibt es nach Def. genau eine lineare Abbildung ϕ : V W V W mit ϕη = η und genau eine lineare Abbildung ψ : V W V W mit ψη = η. ϕ und ψ sind zueinander inverse Isomorphismen: Zur bilinearen Abbildung η gibt es genau eine lineare Abbildung η : V W V W mit η = η η, und sowohl id als auch ψϕ erfüllen dies, also schon ψϕ = id. Analog mit η und ϕψ.
37 Aufgabe 4 Wie werden die kanonischen Isomorphismen V W (V W ) und V W Hom(V, W ) konstruiert? Lösung: Seien ϕ V, ψ W. Dann ist ϕ ψ : V W K, (v, w) ϕ(v)ψ(w) bilinear und induziert (ϕ ψ) : V W K linear, also (ϕ ψ) (V W ). Auch die Zuordnung V W (V W ), (ϕ, ψ) (ϕ ψ) ist bilinear und induziert die gewünschte Abbildung. Die Abbildung V W Hom(V, W ), (ϕ, w) (v ϕ(v)w) ist bilinear und induziert die gewünschte Abbildung auf V W.
38 Abschnitt 4 Darstellungen
39 Definitionen Darstellung auf V ist Gruppenhomomorphismus ρ : G GL(V ) Einschränkung auf invarianten Unterraum ist Unterdarstellung Darstellung ist irreduzibel, falls V 0 ist und sie keine nichttrivialen (d.h. außer 0, V ) Unterdarstellungen hat. Charakter einer komplexen Darstellung ist die Abb. χ : G C, g tr(ρ(g))
40 Eigenschaften Satz von Maschke V Darst, char K = 0 oder char K kein Teiler von G, W V Unterdarstellung. Dann hat W Komplement, das auch Unterdarst. ist. Für das Skalarprodukt (ϕ ψ) = G g G ϕ(g)ψ(g) auf Funktionen G C gilt: Ist V Darstellung von G mit Charakter ϕ und V = W... W k eine Zerlegung in irreduzible Unterdarst, so ist für jede irreduzible Darst. W von G mit Charakter χ die Anzahl der W i isomorph zu W gleich (ϕ χ).
41 Aufgaben Siehe Aufgabenblatt, Aufgabe 5.
42 Aufgabe 5 Betrachte die symmetrische Gruppe S 3 mit der Darstellung durch Koordinatenvertauschung auf C 3, d.h. ρ : S 3 GL(C 3 ), ρ(π)(x, x 2, x 3) = (x π (), x π (2), x π (3)). a) Gib die Werte der Charaktere von ρ, der trivialen und der Signum Darstellung an. b) Berechne (χ ρ χ triv) und (χ ρ χ sgn). c) Zerlege ρ in irreduzible Unterdarstellungen. Lösung a) Mit Repräsentanten der Konjugationsklassen: id (2) (23) χ triv χ sgn χ ρ 3 0 b) Die Konjugationsklassen haben Mächtigkeiten, 3 und 2, und damit (χ ρ χ triv) = 6 ( ) = und (χρ χsgn) = 6 ( ) = 0. c) Wir haben eine Unterdarstellung isomorph zur trivialen, U = (,, ) T. Permutationmatrizen sind orthogonal, also ist U invariant, und U = (,, 0) T, (, 0, ) T ist Unterdarstellung. Sie muß irreduzibel sein, da es nur die bereits untersuchten eindimensionalen Darstellungen der S n gibt.
Lösung zu Serie 18. Lineare Algebra D-MATH, HS Prof. Richard Pink
 Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform
 LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
LinAlg II Version 1 29. Mai 2006 c Rudolf Scharlau 219 3.5 Trigonalisierbarkeit, verallgemeinerte Eigenräume und Jordansche Normalform Das Problem der Normalformen für Endomorphismen handelt kurz gesprochen
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
Musterlösung der Klausur zur linearen Algebra II
 David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
David Blottière SS 7 Patrick Schützdeller Universität Paderborn Julia Sauter Musterlösung der Klausur zur linearen Algebra II Aufgabe 1 Bestimmen Sie Jordan-Normalformen der folgenden Matrizen, und schreiben
Musterlösungen zur Linearen Algebra II Weihnachtszettel
 Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Lineare Algebra II Lösungen zu ausgewählten Aufgaben
 Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra II Lösungen zu ausgewählten Aufgaben Blatt 2, Aufgabe 3 a) Wir zeigen, daß das Ideal (2, X) kein Hauptideal in Z[X] ist. (Dieses Ideal besteht aus allen Elementen in Z[X], die von der Form
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lina II - Aufgaben zur Vorbereitung für die Klausur (Teil 1) - Lösungen
 Lina II - Aufgaben zur Vorbereitung für die Klausur (Teil 1) - en Kommentare an HannesKlarner@FU-Berlinde FU Berlin SS 1 Dia- und Trigonalisierbarkeit Aufgabe (1) Gegeben seien A = i i C 3 3 und B = 1
Lina II - Aufgaben zur Vorbereitung für die Klausur (Teil 1) - en Kommentare an HannesKlarner@FU-Berlinde FU Berlin SS 1 Dia- und Trigonalisierbarkeit Aufgabe (1) Gegeben seien A = i i C 3 3 und B = 1
Ausgewählte Lösungen zu den Übungsblättern 9-10
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Dezember Ausgewählte Lösungen zu den Übungsblättern 9- Übungsblatt
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 2016
 Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
a b Q = b a 0 ) existiert ein Element p Q, so dass gilt: q 1 q 2 = 2 b 1 b 2 a 1 b 2 a 2 b 1 a 1 a 2 b 1 b 2 a 1 b 2 a 2 b 1 a b p = 1 det(q) C 2 2,
 Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
Aufgabe I Es sei Q die folgende Teilmenge von C 2 2 : { ( ) a b Q a, b C b a Hier bezeichnet der Querstrich die komplexe Konjugation Zeigen Sie: (a) Mit den üblichen Verknüpfungen + und für Matrizen ist
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008
 KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
KLAUSUR ZUR LINEAREN ALGEBRA II 19. Juli 2008 MUSTERLÖSUNG Name: Studiengang: Aufgabe 1 2 3 4 5 6 Summe Punktzahl /50 Allgemeine Hinweise: Bitte schreiben Sie Ihre Lösungen jeweils unter die Aufgabenstellung
KAPITEL 8. Normalformen. 1. Blockmatrizen. ,C K m 2 n 1. X = K (m 1+m 2 ) (n 1 +n 2 ) K L. und Y = M N Blockmatrizen mit.
 KAPITEL 8 Normalformen Definition 8.1 (Blockmatrizen). Sind 1. Blockmatrizen A K m 1 n 1,B K m 1 n 2,C K m 2 n 1 und D K m 2 n 2 so nennet man die Matrix X = ( A B C D ) K (m 1+m 2 ) (n 1 +n 2 ) eine Blockmatrix
KAPITEL 8 Normalformen Definition 8.1 (Blockmatrizen). Sind 1. Blockmatrizen A K m 1 n 1,B K m 1 n 2,C K m 2 n 1 und D K m 2 n 2 so nennet man die Matrix X = ( A B C D ) K (m 1+m 2 ) (n 1 +n 2 ) eine Blockmatrix
Lineare Algebra II 11. Übungsblatt
 Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
6 Eigenwerte und Eigenvektoren
 6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
6.1 Eigenwert, Eigenraum, Eigenvektor Definition 6.1. Es sei V ein Vektorraum und f : V V eine lineare Abbildung. Ist λ K und v V mit v 0 und f(v) = λv gegeben, so heißt die Zahl λ Eigenwert (EW) von f,
6 Hauptachsentransformation
 6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
23. Die Jordan sche Normalform
 Chr.Nelius, Lineare Algebra II (SS 2005) 1 23. Die Jordan sche Normalform Wir suchen für einen trigonalisierbaren Endomorphismus unter seinen dreiecksförmigen Darstellungsmatrizen eine Darstellungsmatrix,
Chr.Nelius, Lineare Algebra II (SS 2005) 1 23. Die Jordan sche Normalform Wir suchen für einen trigonalisierbaren Endomorphismus unter seinen dreiecksförmigen Darstellungsmatrizen eine Darstellungsmatrix,
Eigenwerte und Diagonalisierung
 Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
1 Grundlagen zur Darstellungstheorie
 Seminar Gruppen in der Physik SS 06 Vortrag 1 Gruppen und ihr Darstellung Matthias Nagl 1 Grundlagen zur Darstellungstheorie In diesem Vortrag wird es nur um lineare Darstellungen endlicher Gruppen in
Seminar Gruppen in der Physik SS 06 Vortrag 1 Gruppen und ihr Darstellung Matthias Nagl 1 Grundlagen zur Darstellungstheorie In diesem Vortrag wird es nur um lineare Darstellungen endlicher Gruppen in
Zusammenfassung Lineare Algebra II
 Zusammenfassung Lineare Algebra II CC BY: Tim Baumann, http://timbaumanninfo/uni-spicker Notation Sofern nicht anders angegeben, bezeichne K im folgenden einen beliebigen Körper, V einen (möglicherweise
Zusammenfassung Lineare Algebra II CC BY: Tim Baumann, http://timbaumanninfo/uni-spicker Notation Sofern nicht anders angegeben, bezeichne K im folgenden einen beliebigen Körper, V einen (möglicherweise
3 Definition: 1. Übungsblatt zur Vorlesung Lineare Algebra I. im WS 2003/2004 bei Prof. Dr. S. Goette
 1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016
 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016 Bearbeiten Sie bitte zwei
Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4 Lineare Algebra/Analytische Geometrie II SoSe 2016 Bearbeiten Sie bitte zwei
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
6 Die Schursche Normalform und einige Klassen von Matrizen
 ME Lineare Algebra HT 28 111 6 Die Schursche Normalform und einige Klassen von Matrizen 61 Die Schur-Normalform und Hauptvektoren Für nichtdiagonalisierbare Matrizen gibt es andere Normalformen: Jordan-
ME Lineare Algebra HT 28 111 6 Die Schursche Normalform und einige Klassen von Matrizen 61 Die Schur-Normalform und Hauptvektoren Für nichtdiagonalisierbare Matrizen gibt es andere Normalformen: Jordan-
Klausur Lineare Algebra I am Es sind insgesamt 60 Punkte bei der Klausur zu erreichen.
 Klausur Lineare Algebra I am 03.02.10 Es sind insgesamt 60 Punkte bei der Klausur zu erreichen. Aufgabe 1. (6 Punkte insgesamt) a.) (3P) Definieren Sie, was eine abelsche Gruppe ist. b.) (3P) Definieren
Klausur Lineare Algebra I am 03.02.10 Es sind insgesamt 60 Punkte bei der Klausur zu erreichen. Aufgabe 1. (6 Punkte insgesamt) a.) (3P) Definieren Sie, was eine abelsche Gruppe ist. b.) (3P) Definieren
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Musterlösungen zur Linearen Algebra II Übungsklausur
 Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
Musterlösungen zur Linearen Algebra II Übungsklausur Aufgabe. Sei A R 3 3. Welche der folgenden Aussagen sind richtig? a Ist det(a =, dann ist A eine orthogonale Matrix. b Ist A eine orthogonale Matrix,
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall
 44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
Aufgabe I.1 (4 Punkte) Gegeben seien die Matrix H := und die Menge L := {A R 4 4 A HA = H} Zeigen Sie:
 Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
Steilkurs Lineare Algebra 1 einige wichtige Stationen
 Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Lineare Algebra I/II LVA ,
 Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
Lineare Algebra I/II LVA 401-1151-00,401-1152-00 Prof. G. Wüstholz, C. Fuchs Lösungen zur Basisprüfung, HS08/FS09 09.02.2010 1. a) (1 Punkt) Wir beginnen mit dem charakteristischen Polynom der Matrix A:
10. Übung zur Linearen Algebra II -
 0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
0. Übung zur Linearen Algebra II - Lösungen Kommentare an Hannes.Klarner@Fu-Berlin.de FU Berlin. SS 00. Aufgabe 7 Der ( linearen ) Abbildung ϕ : R R sei bzgl. der kanonischen Basis die Matrix zugeordnet.
Übungen zur Linearen Algebra II
 Blatt 1 Aufgabe 1. Sei V = Mat(n, K) und U V der Untervektorraum der Diagonalmatrizen. Welche Dimension hat der Quotientenvektorraum V/U? Aufgabe 2. Sei G eine Gruppe. Wir betrachten die Relation auf G.
Blatt 1 Aufgabe 1. Sei V = Mat(n, K) und U V der Untervektorraum der Diagonalmatrizen. Welche Dimension hat der Quotientenvektorraum V/U? Aufgabe 2. Sei G eine Gruppe. Wir betrachten die Relation auf G.
Lineare Algebra Klausur 1
 Lineare Algebra Klausur 1 (29.7.2015 Dozent: Ingo Runkel) Name Vorname Matrikelnr. Anweisungen: Hilfsmittel: Für die Bearbeitung sind nur Stift und Papier erlaubt. Benutzen Sie einen permanenten Stift
Lineare Algebra Klausur 1 (29.7.2015 Dozent: Ingo Runkel) Name Vorname Matrikelnr. Anweisungen: Hilfsmittel: Für die Bearbeitung sind nur Stift und Papier erlaubt. Benutzen Sie einen permanenten Stift
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
4.2 Die adjungierte Abbildung
 4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
Lineare Algebra II 12. Übungsblatt
 Lineare Algebra II 12. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 13. / 14. Juli 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Probeklausur) Sprechen Sie über die Probeklausur
Lineare Algebra II 12. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 13. / 14. Juli 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Probeklausur) Sprechen Sie über die Probeklausur
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12
 Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lösung 7: Bilinearformen
 D-MATH Lineare Algebra II FS 207 Dr. Meike Akveld Lösung 7: Bilinearformen. a). Seien u, u 2 V, λ K, dann gelten nach Voraussetzung: L v (u + λu 2 ) =β(v, u + λu 2 ) = β(v, u ) + β(v, λu 2 ) =β(v, u )
D-MATH Lineare Algebra II FS 207 Dr. Meike Akveld Lösung 7: Bilinearformen. a). Seien u, u 2 V, λ K, dann gelten nach Voraussetzung: L v (u + λu 2 ) =β(v, u + λu 2 ) = β(v, u ) + β(v, λu 2 ) =β(v, u )
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Mat(2 2, R) Wir bestimmen das charakterische Polynom 1 f A (t) = t 2 t 2 = (t 2)(t + ( 1). ) 2 2. Eigenvektor zu EW 2 ist v 2 = 1 1
 Aufgabe. Bestimmen Sie das Exponential expa) der Matrix ) 5 6 A = Mat, R). 4. Wir bestimmen das charakterische Polynom f A t) = t t = t )t + ). ). Eigenvektor zu EW ist v = ). Eigenvektor zu EW ist v =
Aufgabe. Bestimmen Sie das Exponential expa) der Matrix ) 5 6 A = Mat, R). 4. Wir bestimmen das charakterische Polynom f A t) = t t = t )t + ). ). Eigenvektor zu EW ist v = ). Eigenvektor zu EW ist v =
Übungen zur Vorlesung Lineare Algebra
 Übungen zur Vorlesung Lineare Algebra Institut für Reine Mathematik WS 2009/10 & SS 2010 Kapitel 1. Vektorräume Was ist ein Vektorraum? Sei X und K ein Körper. Wie macht man Abb (X, K) zu einem K -Vektorraum?
Übungen zur Vorlesung Lineare Algebra Institut für Reine Mathematik WS 2009/10 & SS 2010 Kapitel 1. Vektorräume Was ist ein Vektorraum? Sei X und K ein Körper. Wie macht man Abb (X, K) zu einem K -Vektorraum?
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS. Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF
 TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07.03.2016-11.03.2016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Darstellungsmatrizen 2 2 Diagonalisierbarkeit
TECHNISCHE UNIVERSITÄT MÜNCHEN FERIENKURS Lineare Algebra FLORIAN NIEDERREITER & AILEEN WOLF 07.03.2016-11.03.2016 Inhaltsverzeichnis Inhaltsverzeichnis 1 Darstellungsmatrizen 2 2 Diagonalisierbarkeit
Kapitel 11. Bilinearformen über beliebigen Bilinearformen
 Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
1 Die Jordansche Normalform
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 4/5 A Die Jordansche Normalform Vierter Tag (9.03.205) Im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme
a) Ein Gruppenhomomorphismus von G nach H ist eine Abbildung Φ : G H, sodass für alle g 1, g 2 G die Gleichung Φ(g 1 g 2 ) = Φ(g 1 ) Φ(g 2 )
 I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
I. (4 Punkte) Es seien (G, ) eine Gruppe mit neutralem Element e G und (H, ) eine weitere Gruppe. a) Geben Sie die Definition eines Gruppenhomomorphismus Φ : G H an und beweisen Sie, dass für solch einen
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10)
 Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
Vorlesung Mathematik für Ingenieure 3 (Wintersemester 2009/10) Kapitel 15: Eigenwerte und -vektoren Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 5. November 2009) Diagonalisierbarkeit
9. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 9. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS /..-4.. Aufgabe G (Koordinatentransformation)
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 9. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS /..-4.. Aufgabe G (Koordinatentransformation)
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II
 Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Verständnisfragen: Lineare Algebra und Analytische Geometrie I und II Matrizen, lineare Gleichungssysteme Wie kommt man von einem linearen Gleichungssystem zu einer Matrix? Was ist die Zeilenstufenform?
Lineare Algebra 2 SS2012 Übungsblatt
 Lineare Algebra 2 SS2012 Übungsblatt 1 Übung 1. Seien A 1, A 2,..., A k quadratische n n-matrizen über einem Körper K. Zeige, daß das Produkt A 1 A 2... A k invertierbar ist genau dann, wenn alle A i invertierbar
Lineare Algebra 2 SS2012 Übungsblatt 1 Übung 1. Seien A 1, A 2,..., A k quadratische n n-matrizen über einem Körper K. Zeige, daß das Produkt A 1 A 2... A k invertierbar ist genau dann, wenn alle A i invertierbar
VII.2. INNERE PRODUKTE 227
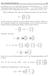 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
(also ) Oft wird Zusammenhang zwischen und mit einem Index angedeutet, z.b. wird der Eigenvektor v. durch gekennzeichnet.
 L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
Analytische Geometrie
 21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
Technische Universität München Zentrum Mathematik. Übungsblatt 12
 Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 12 Hausaufgaben Aufgabe 12.1 Sei f : R 3 R 3 gegeben durch f(x) :=
Technische Universität München Zentrum Mathematik Mathematik 1 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 12 Hausaufgaben Aufgabe 12.1 Sei f : R 3 R 3 gegeben durch f(x) :=
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
LINEARE ALGEBRA II. Inhaltsverzeichnis
 LINEARE ALGEBRA II OLIVER C. SCHNÜRER Zusammenfassung. Bei diesem Manuskript handelt es sich um Notizen zu einer Vorlesung Lineare Algebra II (B2) an der Universität Konstanz im Sommersemester 2011. Vielen
LINEARE ALGEBRA II OLIVER C. SCHNÜRER Zusammenfassung. Bei diesem Manuskript handelt es sich um Notizen zu einer Vorlesung Lineare Algebra II (B2) an der Universität Konstanz im Sommersemester 2011. Vielen
Klausur zu. Lineare Algebra II. Viel Erfolg! Fachbereich Mathematik WS 2012/13 Dr. habil. Matthias Schneider. Bonus Note. Aufgabe
 Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Lineare Algebra Vordiplom Kurs
 Lineare Algebra Vordiplom Kurs Gabriel Puebla-Hellmann 19. Juli 2004 Inhaltsverzeichnis 1 Grundbegriffe 3 1.1 Lineare Gleichungssysteme...................... 3 1.2 Vektorräume.............................
Lineare Algebra Vordiplom Kurs Gabriel Puebla-Hellmann 19. Juli 2004 Inhaltsverzeichnis 1 Grundbegriffe 3 1.1 Lineare Gleichungssysteme...................... 3 1.2 Vektorräume.............................
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld. Clicker Fragen
 D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 2017/18 Blatt 3 - Lösung
 Technische Universität München Physik Department Pablo Cova Fariña, Claudia Nagel Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 207/8 Blatt 3 - Aufgabe : Darstellungsmatrizen Sei
Technische Universität München Physik Department Pablo Cova Fariña, Claudia Nagel Übungen zum Ferienkurs Ferienkurs Lineare Algebra für Physiker WiSe 207/8 Blatt 3 - Aufgabe : Darstellungsmatrizen Sei
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
18 λ 18 + λ 0 A 18I 3 = / Z 2 Z 2 Z Z Z 1
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive
Klausur Lineare Algebra I & II
 Prof. Dr. G. Felder, Dr. Thomas Willwacher ETH Zürich, Sommer 2010 D MATH, D PHYS, D CHAB Klausur Lineare Algebra I & II Bitte ausfüllen! Name: Vorname: Studiengang: Bitte nicht ausfüllen! Aufgabe Punkte
Prof. Dr. G. Felder, Dr. Thomas Willwacher ETH Zürich, Sommer 2010 D MATH, D PHYS, D CHAB Klausur Lineare Algebra I & II Bitte ausfüllen! Name: Vorname: Studiengang: Bitte nicht ausfüllen! Aufgabe Punkte
Hauptachsentransformation: Eigenwerte und Eigenvektoren
 Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Lineare Algebra II. Inhalt und Begriffe. Lineare Algebra II p. 1
 Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Lineare Algebra II Inhalt und Begriffe Lineare Algebra II p. 1 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen Algebra... Lineare Algebra II p. 2 Inhaltsverzeichnis Kapitel II Grundlagen der Linearen
Klausur zur Vorlesung Lineare Algebra II
 Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Universität zu Köln Sommersemester 06 Mathematisches Institut 9. Juli 06 Prof. Dr. P. Littelmann Dr. Teodor Backhaus Klausur zur Vorlesung Lineare Algebra II Bearbeitungszeit 80 Minuten Bitte geben Sie
Lineare Algebra für PhysikerInnen
 Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
Universität Wien, SS 2015 Lineare Algebra für PhysikerInnen Beispiele für Multiple-Choice-Fragen Punkteschlüssel: [Typ 1 aus 4] und [Typ 3 aus 4]... 0.8 Punkte [Typ 2 aus 4]... 1 Punkt Bei der schriftlichen
3.3 Skalarprodukte 3.3. SKALARPRODUKTE 153
 3.3. SKALARPRODUKTE 153 Hierzu müssen wir noch die Eindeutigkeit (Unabhängigkeit von der Wahl der Basis bzw. des Koordinatensystems) zeigen. Sei hierzu β eine Bilinearform und q die entsprechende quadratische
3.3. SKALARPRODUKTE 153 Hierzu müssen wir noch die Eindeutigkeit (Unabhängigkeit von der Wahl der Basis bzw. des Koordinatensystems) zeigen. Sei hierzu β eine Bilinearform und q die entsprechende quadratische
Kapitel 3 Lineare Algebra
 Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren. Gegeben. Gesucht: Diagonalform: Finde und! Definition: Eigenvektor, Eigenwert
 L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
L7 Diagonalisierung einer Matrix: Eigenwerte und Eigenvektoren Viele Anwendungen in der Physik: z.b. Bestimmung der - Haupträgheitsmomente eines starren Körpers durch Diagonalisierung des Trägheitstensors
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Lösungsskizze zur Wiederholungsserie
 Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
Lineare Algebra D-MATH, HS Prof. Richard Pink Lösungsskizze zur Wiederholungsserie. [Aufgabe] Schreibe die lineare Abbildung f : Q Q 5, x +x +x x x +x +6x f x := x +x +8x x x +x +x. x +x +5x als Linksmultiplikation
5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit
 ME Lineare Algebra HT 2008 99 5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit 5.1 Ein Beispiel zur Motivation Als einfachstes Beispiel eines dynamischen Systems untersuchen wir folgendes Differentialgleichungssystem
ME Lineare Algebra HT 2008 99 5 Eigenwerte, Eigenvektoren und Diagonalisierbarkeit 5.1 Ein Beispiel zur Motivation Als einfachstes Beispiel eines dynamischen Systems untersuchen wir folgendes Differentialgleichungssystem
4 Lineare Abbildungen Basisdarstellungen
 4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
Lineare Darstellungen von Symmetrischen Gruppen
 Lineare Darstellungen von Symmetrischen Gruppen 150 232 (Holtkamp) 2st., Mi 12.00-14.00, NA 2/24 1 Beispiel 1. Freies Monoid über Alphabet X Beispiel 2. S 1, S 2, S 3,... Satz 1. (Bijektion zw. Partitionen
Lineare Darstellungen von Symmetrischen Gruppen 150 232 (Holtkamp) 2st., Mi 12.00-14.00, NA 2/24 1 Beispiel 1. Freies Monoid über Alphabet X Beispiel 2. S 1, S 2, S 3,... Satz 1. (Bijektion zw. Partitionen
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
und Unterdeterminante
 Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
Zusammenfassung: Determinanten Definition: Entwicklungssätze: mit und Unterdeterminante (streiche Zeile i & Spalte j v. A, bilde dann die Determinante) Eigenschaften v. Determinanten: Multilinearität,
6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar.
![6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar. 6.3 Eigenwerte. γ ist Eigenwert von T [T] B B γi ist nicht invertierbar.](/thumbs/70/62033901.jpg) Um zu zeigen, dass die irreduziblen Teiler eines reellen Polynoms höchstens den Grad 2 haben, fassen wir nun (x γ) und (x γ) zusammen und stellen fest, dass (x (a + b i))(x ((a b i)) = x 2 2a + (a 2 +
Um zu zeigen, dass die irreduziblen Teiler eines reellen Polynoms höchstens den Grad 2 haben, fassen wir nun (x γ) und (x γ) zusammen und stellen fest, dass (x (a + b i))(x ((a b i)) = x 2 2a + (a 2 +
ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT
 ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT G.FELDER, LINEARE ALGEBRA II, FS 2013 27.03.2013 Inhaltsverzeichnis 1. Selbstadjungierte Abbildungen 1 1.1. Adjungierte Abbildungen 1 1.2. Spektralsatz
ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT G.FELDER, LINEARE ALGEBRA II, FS 2013 27.03.2013 Inhaltsverzeichnis 1. Selbstadjungierte Abbildungen 1 1.1. Adjungierte Abbildungen 1 1.2. Spektralsatz
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG
 KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
Grundbegriffe aus der Vorlesung Lineare Algebra I+II
 Grundbegriffe aus der Vorlesung Lineare Algebra I+II 30. Juli 2009 Eine Gruppe ist ein Paar (G, ) bestehend aus einer Menge G und einer Verknüpfung : G G G, (a, b) a b, mit: 1. (a b) c = a (b c) (Assoziativität)
Grundbegriffe aus der Vorlesung Lineare Algebra I+II 30. Juli 2009 Eine Gruppe ist ein Paar (G, ) bestehend aus einer Menge G und einer Verknüpfung : G G G, (a, b) a b, mit: 1. (a b) c = a (b c) (Assoziativität)
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom
 Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom Eine Fragestellung, die uns im weiteren beschäftigen wird, ist das Finden eines möglichst einfachen Repräsentanten aus jeder Äquivalenzklasse
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom Eine Fragestellung, die uns im weiteren beschäftigen wird, ist das Finden eines möglichst einfachen Repräsentanten aus jeder Äquivalenzklasse
2.11 Eigenwerte und Diagonalisierbarkeit
 2.11. EIGENWERTE UND DIAGONALISIERBARKEIT 127 Die Determinante eines Endomorphismus Wir geben uns jetzt einen endlichen erzeugten K-Vektorraum V und einen Endomorphismus ϕ : V V vor. Wir wollen die Determinante
2.11. EIGENWERTE UND DIAGONALISIERBARKEIT 127 Die Determinante eines Endomorphismus Wir geben uns jetzt einen endlichen erzeugten K-Vektorraum V und einen Endomorphismus ϕ : V V vor. Wir wollen die Determinante
Prüfung Lineare Algebra Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr?
 1. Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr? A. Wenn n = 3 ist, sind mindestens zwei der drei Euler-Winkel einer Drehung kleiner oder gleich π. B. Wenn n = 2
1. Sei V ein n-dimensionaler euklidischer Raum. Welche der folgenden Aussagen ist wahr? A. Wenn n = 3 ist, sind mindestens zwei der drei Euler-Winkel einer Drehung kleiner oder gleich π. B. Wenn n = 2
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
Skalarprodukte. Kapitel Bilinearformen
 Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
Kapitel 11 Skalarprodukte Das bekannte Skalarprodukt auf dem n dimensionalen Euklidischen Raum R n ist ein Spezialfall einer für viele Bereiche der linearen Algebra und der Funktionalanalysis außerordentlich
Tutorium 4. 1 Bilinearformen. Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Bemerkung. Dies ist äquivalent zu:
 1 Bilinearformen Tutorium 4 Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Φ(αv + w, x) = α Φ(v, x) + Φ(w, x) und Φ(v, βx + y) = β Φ(v, x) + Φ(v, y) Bemerkung. Dies ist
1 Bilinearformen Tutorium 4 Definition. Seien U, V, W Vektorräume. Eine Abbildung Φ : V W U heißt bilinear: Φ(αv + w, x) = α Φ(v, x) + Φ(w, x) und Φ(v, βx + y) = β Φ(v, x) + Φ(v, y) Bemerkung. Dies ist
5 Diagonalisierbarkeit
 5 Diagonalisierbarkeit Sei V ein K Vektorraum mit einer Basis B = (v 1,..., v n ) Wiederholung aus 2: Sei f : V V K linear. Stelle f(v j ) für j = 1,..., n dar in der Form a 1j Das n Tupel a j =. a nj
5 Diagonalisierbarkeit Sei V ein K Vektorraum mit einer Basis B = (v 1,..., v n ) Wiederholung aus 2: Sei f : V V K linear. Stelle f(v j ) für j = 1,..., n dar in der Form a 1j Das n Tupel a j =. a nj
Grundlagen der Mathematik 2 Nachklausur
 Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
Andreas Gathmann und Yue Ren Sommersemester 6 Grundlagen der Mathematik Nachklausur Bearbeitungszeit: 8 Minuten Aufgabe (6 Punkte): Es sei f : R R, (x,y) xye (x+y). (a) Bestimme alle lokalen Maxima und
