Computer Vision: Segmentierung I
|
|
|
- Astrid Huber
- vor 8 Jahren
- Abrufe
Transkript
1 Computer Vision: Segmentierung I D. Schlesinger TUD/INF/KI/IS Der Plan: D. Schlesinger () CV: Segmentierung I 1 / 13
2 Segmentierung Man hat das... Man braucht das. D. Schlesinger () CV: Segmentierung I 2 / 13
3 Segmentierung Was braucht man? ein schlecht gestelltes Problem (d.h. es gibt keine einheitliche Definition). Normalerweise soll ein Objekt segmentiert werden. Was wird dabei benötigt? Farbmodelle A-priori Wissen über Form alles mit zugelassenen Transformationen evtl. Beziehungen zu anderen Objekten, Lage, Geometrie, Topologie etc. Man hat nun das... D. Schlesinger () CV: Segmentierung I 3 / 13
4 (Einfache) Clusterung Idee: Für jeden Pixel werden Merkmale berechnet, Die so entstehende Menge wird geclustert Beispiel: Zwei Clusters (Segmente), Grauwertbilder, Merkmal Grauwert Geclustert wird nach dem K-Means Prinzip (mithilfe der Histogramme) Binarisierung mit einem Schwellwert Erweiterungen: Glättung vorher/nachher Kompliziertere lokale Merkmale Andere Clusterung Methoden/Abstände... D. Schlesinger () CV: Segmentierung I 4 / 13
5 Aktive Konturen (Snakes) [Kass, Witkin, Terzopoulos, 1988] Eine Segmentierung ist es nicht ganz Eine Kontur ist parametrisch beschrieben: v(s) = x(s), y(s), s [0, 1] (geschlossen, nicht geschlossen) parametrisch, mit Slpines usw. Seine Energie ist: E(v) = Z 1h i Eint v(s) + Eimage v(s) + Econ v(s) ds 0 Interne Energie: Eint v(s) = α(s) vs (s) 2 + β(s) vss (s) 2 /2 mit vs und vss die erste bzw. die zweite Ableitungen, α(s) und β(s) sind positionspezifische Gewichte repräsentieren die gewünschte Form z.b. β(s ) = 0 bedeutet Ecke an der Stelle s ist möglich Eimage v(s) ist der Datenterm I x(s), y(s) (Intensität), I x(s), y(s) 2 (Kanten)... Econ v(s) sind zusätzliche Kräfte (z.b. vom Nutzer explizit angegeben). D. Schlesinger () CV: Segmentierung I 5 / 13
6 Aktive Konturen (Snakes) Paar Beispiele: Andrew Blake and Michael Isard: Active Contours contours/ D. Schlesinger () CV: Segmentierung I 6 / 13
7 Region Growing Man hat bereits eine Region (diskret eine Teilmenge der Pixel) und lässt sie wachsen: Für die aktuelle Region werden bestimmte Charakteristika berechnet, wie z.b. den mittleren Grauwert, Streuung, andere Farbcharakteristika (Statistik der Kanten Ecken usw.), Größe, Ausdehnung, Umfang (Geometrische Merkmale)... Pixel zu der aktuellen Region benachbarten Pixel werden betrachtet Abhängig von den lokalen Pixelmerkmalen und den Charakteristika der Region wird entschieden, ob der Pixel zu der Region gehört. Ergänzungen: Mehrere Regionen Split, Merge... Ähnlichkeiten zu Aktiven Konturen: eine lokale Vorgehensweise Evaluierung einer Kontur eine Initialisierung ist notwendig Unterschiede: Topologie: RG automatisch, AK problematisch Metrische Fehler (durch Diskretisierung) bei RG Globale Charakteristika sind bei AK schwierig zu berücksichtigen Modell bei RG ist meist nicht explizit definiert D. Schlesinger () CV: Segmentierung I 7 / 13
8 Mumford-Shah Funktional [Mumford, Shah, 1989] Motivation: Das betrachtete 2-dimensionale Bild ist eine Projektion einer 3D-Szene Lichtstrahlen treffen Objekte Bildfunktion innerhalb der Projektion eines Objektes ist glatt Objektgrenzen in 3D verursachen Diskontinuitäten der Bildfunktion Bildfunktion soll stückweise glatt sein R R 2 Bilddomäne, Γ Diskontinuitäten (Segmentgrenzen) g : R R (die zu approximierende) Bildfunktion f : R R stückweise glatte Approximation E(f, Γ) = µ 2 (f g) 2 dxdy + f 2 dxdy + ν Γ min f,γ R R Γ Die Approximation soll mit der Bildfunktion möglichst übereinstimmen glatt sein möglichst wenig Grenzen haben D. Schlesinger () CV: Segmentierung I 8 / 13
9 Mumford-Shah Funktional Beispiele für unterschiedliche µ und ν Problem der Topologie wieder!!! Dies ist keine Segmentierung im Sinne der Partitionierung des Bildes auf disjunkte Gebiete. Die gefundenen Kanten sind nicht unbedingt Segmentgrenzen D. Schlesinger () CV: Segmentierung I 9 / 13
10 Mumford-Shah Funktional Spezialfall: Stückweise konstante Approximation Cartoon-Limit E(f, Γ) = µ 2 (f g) 2 dxdy + f 2 dxdy + ν Γ min f,γ R R Γ geht bei µ, ν 0 gegen E(a, Γ) = (g a i ) 2 dxdy + ν Γ min a,γ i R i Die Lösung bezüglich a i bei der fixierten Partitionierung Γ ist: a i = 1 g dxdy R i R i das Bild wird in die Regionen zerlegt (partitioniert), Farbwert innerhalb einer Region ist konstant Jetzt ist die Topologie in Ordnung: die Kanten dürfen nicht mehr willkürlich enden, denn das ist offensichtlich energetisch ungünstig (wegen Γ ). D. Schlesinger () CV: Segmentierung I 10 / 13
11 Chan-Vese Modell Bei Cartoon-Limit wird die Anzahl der Segmente nicht festgelegt. Diese Anzahl ergibt sich automatisch. Moch spezieller: nur zwei Regionen [Chan, Vese, 2001]: E(c 1, c 2, C) = µ Length(C) + ν Area(C) +λ 1 u 0 (x, y) c 1 2 dxdy inside(c) +λ 2 u 0 (x, y) c 2 2 dxdy outside(c) Kann effizient mit Level Set Methoden gelöst werden. D. Schlesinger () CV: Segmentierung I 11 / 13
12 Level Set Methoden [Osher, Sethian, 1988?] Idee: eine Kontur wird durch Nullstelle einer Levelset Funktion φ : R 2 R beschrieben, d.h. C = {(x, y) Ω : φ(x, y) = 0}, inside(c) = {(x, y) Ω : φ(x, y) > 0}, outside(c) = {(x, y) Ω : φ(x, y) < 0} Heaviside Funktion H(z) = 1I(z > 0) ( Step ), Dirac Funktion δ(z) = H(z) ( Delta ) Mit diesen Hilfsfunktionen lassen sich alle Bestandteile wie folgt schreiben: Length(C) = inside(c) Ω ( ) δ φ(x, y) dxdy, Area(C) = bla(x, y)dxdy = Ω Ω H ( φ(x, y) ) bla(x, y)dxdy H ( φ(x, y) ) dxdy Andere Charakteristika der Kontur (wie z.b. die Krümmung) lässt sich auch relativ einfach ausdrücken. usw. Integrale über bestimmte Gebiete werden durch Integrale über den gesamten Ω ersetzt. D. Schlesinger () CV: Segmentierung I 12 / 13
13 Level Set Methoden Weiter: Nichtdifferenzierbare H und δ werden durch etwas differenzierbares ersetzt entweder - Gateau Ableitungen auf Null setzen Euler-Lagrange Gleuchungen - Diskretisieren Gleichungssystem - Mit iterativen Methoden lösen oder - Gateau Ableitungen Gragienten - Gradientabstieg Die Topologie ist korrekt Die Topologie kann sich während der Evaluation der Kurve ändern Weniger sensitiv zur Initialisierung Vieles lässt sich einheitlich und bequem ausdrücken Nur mühsam für mehr als zwei Segmente übertragbar Statistische Interpretation schwierig Probleme mit dem Lernen (betrifft alle kontinuierliche Ansätze) D. Schlesinger () CV: Segmentierung I 13 / 13
Shape Gradient for Image and Video Segmentation
 Shape Gradient for Image and Video Segmentation [1] S. Jehan-Besson, A. Herbulot, M. Barlaud und G. Aubert 23. Mai 2007 Martin Schröttner und Michael Schneeberger Mat Vis-Gra SS07 1 Überblick Aktive Konturen
Shape Gradient for Image and Video Segmentation [1] S. Jehan-Besson, A. Herbulot, M. Barlaud und G. Aubert 23. Mai 2007 Martin Schröttner und Michael Schneeberger Mat Vis-Gra SS07 1 Überblick Aktive Konturen
Computer Vision: Kalman Filter
 Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung Herbstsemester
 Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Komplexe regionenbasierte Segmentierungsverfahren mit der Level Set Methode in der medizinischen Bildverarbeitung
 Komplexe regionenbasierte Segmentierungsverfahren mit der Level Set Methode in der medizinischen Bildverarbeitung Diplomarbeit im Studiengang Mathematik mit Studienrichtung Informatik vorgelegt von Björn
Komplexe regionenbasierte Segmentierungsverfahren mit der Level Set Methode in der medizinischen Bildverarbeitung Diplomarbeit im Studiengang Mathematik mit Studienrichtung Informatik vorgelegt von Björn
Computer Vision: Optische Flüsse
 Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt
 Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
Bildverarbeitung/Mustererkennung: Zusammenfassung und Ausblick
 Bildverarbeitung/Mustererkennung: Zusammenfassung und Ausblick D. Schlesinger TUD/INF/KI/IS D. Schlesinger () BV/ME: Zusammenfassung 1 / 6 Organisatorisches Es gibt keine Scheine und keine bestanden Abschlüsse
Bildverarbeitung/Mustererkennung: Zusammenfassung und Ausblick D. Schlesinger TUD/INF/KI/IS D. Schlesinger () BV/ME: Zusammenfassung 1 / 6 Organisatorisches Es gibt keine Scheine und keine bestanden Abschlüsse
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Bild-Erkennung & -Interpretation
 Kapitel I Bild-Erkennung & -Interpretation FH Aachen / Jülich, FB 9 Prof. Dr. rer.nat. Walter Hillen (Dig Img I) 1 Einführung Schritte zur Bilderkennung und Interpretation: Bild-Erfassung Vorverarbeitung
Kapitel I Bild-Erkennung & -Interpretation FH Aachen / Jülich, FB 9 Prof. Dr. rer.nat. Walter Hillen (Dig Img I) 1 Einführung Schritte zur Bilderkennung und Interpretation: Bild-Erfassung Vorverarbeitung
EVC Repetitorium Blender
 EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
(x, x + y 2, x y 2 + z 3. = e x sin y. sin y. Nach dem Umkehrsatz besitzt f dann genau auf der Menge
 ÜBUNGSBLATT 0 LÖSUNGEN MAT/MAT3 ANALYSIS II FRÜHJAHRSSEMESTER 0 PROF DR CAMILLO DE LELLIS Aufgabe Finden Sie für folgende Funktionen jene Punkte im Bildraum, in welchen sie sich lokal umkehren lassen,
ÜBUNGSBLATT 0 LÖSUNGEN MAT/MAT3 ANALYSIS II FRÜHJAHRSSEMESTER 0 PROF DR CAMILLO DE LELLIS Aufgabe Finden Sie für folgende Funktionen jene Punkte im Bildraum, in welchen sie sich lokal umkehren lassen,
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Klausur zu Analysis II - Lösungen
 Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
1.6 Implizite Funktionen
 1 1.6 Implizite Funktionen Wir werden uns jetzt mit nichtlinearen Gleichungen beschäftigen, f(x) = 0, wobei f = (f 1,..., f m ) stetig differenzierbar auf einem Gebiet G R n und m < n ist. Dann hat man
1 1.6 Implizite Funktionen Wir werden uns jetzt mit nichtlinearen Gleichungen beschäftigen, f(x) = 0, wobei f = (f 1,..., f m ) stetig differenzierbar auf einem Gebiet G R n und m < n ist. Dann hat man
Faltung und Approximation von Funktionen
 Faltung und Approximation von Funktionen Lisa Bauer und Anja Moldenhauer 9. Juni 2008 1 Die Faltung von Funktionen 1.1 Die Faltung Eine kleine Widerholung mit einem Zusatz: Vergleiche den Vortrag von Benjamin
Faltung und Approximation von Funktionen Lisa Bauer und Anja Moldenhauer 9. Juni 2008 1 Die Faltung von Funktionen 1.1 Die Faltung Eine kleine Widerholung mit einem Zusatz: Vergleiche den Vortrag von Benjamin
1 Eingebettete Untermannigfaltigkeiten des R d
 $Id: unter.tex,v 1.2 2014/04/14 13:19:35 hk Exp hk $ 1 Eingebettete Untermannigfaltigkeiten des R d In diesem einleitenden Paragraphen wollen wir Untermannigfaltigkeiten des R d studieren, diese sind die
$Id: unter.tex,v 1.2 2014/04/14 13:19:35 hk Exp hk $ 1 Eingebettete Untermannigfaltigkeiten des R d In diesem einleitenden Paragraphen wollen wir Untermannigfaltigkeiten des R d studieren, diese sind die
1.3. DAS COULOMBSCHE GESETZ, ELEKTROSTATISCHES FELD 9
 8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
Dynamische Systeme eine Einführung
 Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla
 Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla Sätze über Konvexität von Kapitel 4.7 bis 4.10 Theorem 4.7-1. Sei U ein konvexer Unterraum eines normierten Vektorraums. Dann
Universität des Saarlandes Seminar der Fachrichtung Mathematik Rudolf Umla Sätze über Konvexität von Kapitel 4.7 bis 4.10 Theorem 4.7-1. Sei U ein konvexer Unterraum eines normierten Vektorraums. Dann
κ Κα π Κ α α Κ Α
 κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Taylorreihen. Kapitel 9. Lernziele. Taylorreihe. (x x 0 ) + f (x 0 ) 2! (x x 0 ) f (n) (x 0 ) (x x 0 ) n. Taylorreihe und MacLaurinreihe
 Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
Kapitel 9 Taylorreihen Josef Leydold c 2006 Mathematische Methoden IX Taylorreihen 1 / 25 Lernziele Taylorreihe und MacLaurinreihe Beispiele Alternative Schreibweisen Approimation der Veränderung einer
ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS
 ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Gegeben sei die Gleichung 2x 2 4xy +y 2 3x+4y = 0. Verifizieren Sie, dass diese Gleichung
ÜBUNGSBLATT 11 LÖSUNGEN MAT121/MAT131 ANALYSIS II FRÜHJAHRSSEMESTER 2011 PROF. DR. CAMILLO DE LELLIS Aufgabe 1. a) Gegeben sei die Gleichung 2x 2 4xy +y 2 3x+4y = 0. Verifizieren Sie, dass diese Gleichung
Inhaltsbasierte Bildsuche. Matthias Spiller. 17. Dezember 2004
 Kantenbasierte Merkmale für die Bildsuche Inhaltsbasierte Bildsuche Matthias Spiller 17. Dezember 2004 Übersicht Übersicht Einleitung Was sind Kanten? Kantenrichtungs Histogramm Der Canny-Algorithmus Feature-Erzeugung
Kantenbasierte Merkmale für die Bildsuche Inhaltsbasierte Bildsuche Matthias Spiller 17. Dezember 2004 Übersicht Übersicht Einleitung Was sind Kanten? Kantenrichtungs Histogramm Der Canny-Algorithmus Feature-Erzeugung
f f(x ɛξ) f(x) 0, d.h. f (x)ξ = 0 für alle ξ B 1 (0). Also f (x) = 0. In Koordinaten bedeutet dies gerade, dass in Extremstellen gilt: f(x) = 0.
 Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
12. Übungsblatt zur Analysis II
 Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
5 Der Gaußsche und Stokes sche Integralsatz
 HM III = MATH III FT 2013 50 5 Der Gaußsche und Stokes sche Integralsatz Der Gaußsche Integralsatz umgangssprachlich am eispiel strömender Flüssigkeiten: Die Flüssigkeitsmenge, die durch die Oberfläche
HM III = MATH III FT 2013 50 5 Der Gaußsche und Stokes sche Integralsatz Der Gaußsche Integralsatz umgangssprachlich am eispiel strömender Flüssigkeiten: Die Flüssigkeitsmenge, die durch die Oberfläche
Kapitel XIII - p-wert und Beziehung zwischen Tests und Konfidenzintervallen
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XIII - p-wert und Beziehung zwischen Tests und Konfidenzintervallen Induktive Statistik Prof. Dr. W.-D. Heller
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel XIII - p-wert und Beziehung zwischen Tests und Konfidenzintervallen Induktive Statistik Prof. Dr. W.-D. Heller
Konvexe Hülle. Konvexe Hülle. Mathematik. Konvexe Hülle: Definition. Mathematik. Konvexe Hülle: Eigenschaften. AK der Algorithmik 5, SS 2005 Hu Bin
 Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Konvexe Hülle Konvexe Hülle AK der Algorithmik 5, SS 2005 Hu Bin Anwendung: Computergraphik Boundary Kalkulationen Geometrische Optimierungsaufgaben Konvexe Hülle: Definition Mathematik Konvex: Linie zwischen
Symplektische Geometrie
 Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
Bildverbesserung (Image Enhancement)
 Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Bildverarbeitung: Fourier-Transformation. D. Schlesinger () BV: Fourier-Transformation 1 / 16
 Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y
 Approximationen In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y y = f (x) x Um das Arbeiten mit einer komplizierten Funktion zu vermeiden, können wir versuchen, diese Funktion
Approximationen In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y y = f (x) x Um das Arbeiten mit einer komplizierten Funktion zu vermeiden, können wir versuchen, diese Funktion
Überlagerung I. Überlagerung für z z 2 : komplexe Quadratwurzel. Christoph Schweigert, Garben p.1/19
 Überlagerung I Überlagerung für z z 2 : komplexe Quadratwurzel Christoph Schweigert, Garben p.1/19 Überlagerung II Überlagerung für z z 3 : komplexe dritte Wurzel Christoph Schweigert, Garben p.2/19 Überlagerung
Überlagerung I Überlagerung für z z 2 : komplexe Quadratwurzel Christoph Schweigert, Garben p.1/19 Überlagerung II Überlagerung für z z 3 : komplexe dritte Wurzel Christoph Schweigert, Garben p.2/19 Überlagerung
Lösungen zu den Hausaufgaben zur Analysis II
 Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
8 Spontane Symmetriebrechung
 8 SPONTANE SYMMETRIEBRECHUNG 111 8 Spontane Symmetriebrechung 8.1 Gebrochene diskrete Symmetrie Betrachte die φ 4 -Theorie eines reellen Skalarfeldes mit der Lagrangedichte L = 1 ( µφ)( µ φ) 1 m φ λ 4!
8 SPONTANE SYMMETRIEBRECHUNG 111 8 Spontane Symmetriebrechung 8.1 Gebrochene diskrete Symmetrie Betrachte die φ 4 -Theorie eines reellen Skalarfeldes mit der Lagrangedichte L = 1 ( µφ)( µ φ) 1 m φ λ 4!
Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen)
 Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen) Fachbereich Mathematik Wintersemester 0/0 Prof. Dr. Burkhard Kümmerer./3. November 0 Andreas Gärtner Walter Reußwig
Analysis III Gewöhnliche Differentialgleichungen 3. Übungsblatt (mit Lösungshinweisen) Fachbereich Mathematik Wintersemester 0/0 Prof. Dr. Burkhard Kümmerer./3. November 0 Andreas Gärtner Walter Reußwig
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
Bildverarbeitung: 3D-Geometrie. D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13
 Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Computer Vision: 3D-Geometrie. D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17
 Computer Vision: 3D-Geometrie D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Computer Vision: 3D-Geometrie D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
) auf dem Band auf Osiris zu, während Osiris sich auf dem Weg in die Unterwelt mit der Geschwindigkeit 0.35 Schoinen pro Stunde (v 2 = 1 m s
 1 Das Rätsel vom Käfer auf dem Gummiband Die alten Ägypter glaubten angeblich, Osiris habe am Tempel in Luor ein unsichtbares Gummiband der Länge L = 1m befestigt, auf dessen Anfang er einen Scarabaeus
1 Das Rätsel vom Käfer auf dem Gummiband Die alten Ägypter glaubten angeblich, Osiris habe am Tempel in Luor ein unsichtbares Gummiband der Länge L = 1m befestigt, auf dessen Anfang er einen Scarabaeus
Übersicht der Vorlesung
 Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
3.3 Das Abtasttheorem
 17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
Outline. 1 Funktionen von mehreren Veränderlichen. 2 Grenzwert und Stetigkeit. 3 Partielle Ableitungen. 4 Die verallgemeinerte Kettenregel
 Outline 1 Funktionen von mehreren Veränderlichen 2 Grenzwert und Stetigkeit 3 Partielle Ableitungen 4 Die verallgemeinerte Kettenregel 5 Das totale Differential 6 Extremstellen Roman Wienands (Universität
Outline 1 Funktionen von mehreren Veränderlichen 2 Grenzwert und Stetigkeit 3 Partielle Ableitungen 4 Die verallgemeinerte Kettenregel 5 Das totale Differential 6 Extremstellen Roman Wienands (Universität
1 Einleitung. 1.1 Motivation. 6 Differentialgeometrie: Grundlagen Vorlesung 1
 6 Differentialgeometrie: Grundlagen Vorlesung Einleitung. Motivation.. Name of the game Geometer bezeichnet klassisch einen Landvermesser (heute ist eher Geodät gebräuchlich. Die klassische Differentialgeometrie
6 Differentialgeometrie: Grundlagen Vorlesung Einleitung. Motivation.. Name of the game Geometer bezeichnet klassisch einen Landvermesser (heute ist eher Geodät gebräuchlich. Die klassische Differentialgeometrie
Die Interpolationsaufgabe besteht darin, eine (einfache) Funktion u n U n zu finden,
 Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
4. Vortrag - Garben. Ling Lin, Kristijan Cule Datum: 26. April 2009
 4. Vortrag - Garben Datum: 26. April 2009 1 Graduierte Ringe Definition 4.1.1. Eine k-algebra R heißt graduiert, wenn sie dargestellt werden kann als eine direkte Summe R = R n, wobei die R n als k-unterräume
4. Vortrag - Garben Datum: 26. April 2009 1 Graduierte Ringe Definition 4.1.1. Eine k-algebra R heißt graduiert, wenn sie dargestellt werden kann als eine direkte Summe R = R n, wobei die R n als k-unterräume
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II. x 2
 Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Bayessche Tomographie
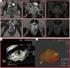 Seminar: Bayessche Ansätze in der Bildanalyse Fakultät für Mathematik und Wirtschaftswissenschaften Universität Ulm 19.Juni 2006 Inhaltsverzeichnis 1 2 3 4 5 Literaturangaben Definition Tomographie Unter
Seminar: Bayessche Ansätze in der Bildanalyse Fakultät für Mathematik und Wirtschaftswissenschaften Universität Ulm 19.Juni 2006 Inhaltsverzeichnis 1 2 3 4 5 Literaturangaben Definition Tomographie Unter
10.6. Implizite ebene Kurven und Tangenten
 0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
Einführung in die medizinische Bildverarbeitung WS 12/13
 Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Prozess einer räumliche Transformation zu finden um ein Bild auf ein anderes Bild abzubilden Eingabe: Fixed und
Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Prozess einer räumliche Transformation zu finden um ein Bild auf ein anderes Bild abzubilden Eingabe: Fixed und
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
2 Die Dimension eines Vektorraums
 2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
KAPITEL 1: ENDLICHE KÖRPER 1 ALLGEMEINES 2 GLEICHUNGEN ÜBER EINEM ENDLICHEN KÖRPER
 RUPRECHT-KARLS-UNIVERSITÄT HEIDELBERG MATHEMATISCHES INSTITUT SEMINAR: QUADRATISCHE FORMEN ÜBER DEN RATIONALEN ZAHLEN SOMMERSEMESTER 2007 DOZENT: PROF. DR. KAY WINGBERG ASSISTENT: JOHANNES BARTELS KAPITEL
RUPRECHT-KARLS-UNIVERSITÄT HEIDELBERG MATHEMATISCHES INSTITUT SEMINAR: QUADRATISCHE FORMEN ÜBER DEN RATIONALEN ZAHLEN SOMMERSEMESTER 2007 DOZENT: PROF. DR. KAY WINGBERG ASSISTENT: JOHANNES BARTELS KAPITEL
Definition 1.1 (Wirkung) Wir wollen die Kurvenverläufe x(t) finden, die das Funktional
 Christina Schindler Karolina Stoiber Ferienkurs Analysis für Physiker SS 13 A 1 Variationsrechnung 1.1 Lagrange. Art Wir führen die Überlegungen von gestern fort und wollen nun die Lagrangegleichungen.
Christina Schindler Karolina Stoiber Ferienkurs Analysis für Physiker SS 13 A 1 Variationsrechnung 1.1 Lagrange. Art Wir führen die Überlegungen von gestern fort und wollen nun die Lagrangegleichungen.
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
- 1 - zum Extremum macht, wenn y(x) eine bestimmte, genau charakterisierte Funktionenklasse ( n
 - 1 - Variationsrechnung Die Variationsrechnung spielt in der Physik eine entscheidende Rolle. So kann man die Grundgleichungen der Newtonschen Mechanik aus einem Lagrangeschen Variationsprinzip herleiten.
- 1 - Variationsrechnung Die Variationsrechnung spielt in der Physik eine entscheidende Rolle. So kann man die Grundgleichungen der Newtonschen Mechanik aus einem Lagrangeschen Variationsprinzip herleiten.
Bootstrap: Punktschätzung
 Resampling Methoden Dortmund, 2005 (Jenő Reiczigel) 1 Bootstrap: Punktschätzung 1. Die Grundidee 2. Plug-in Schätzer 3. Schätzung des Standardfehlers 4. Schätzung und Korrektur der Verzerrung 5. Konsistenz
Resampling Methoden Dortmund, 2005 (Jenő Reiczigel) 1 Bootstrap: Punktschätzung 1. Die Grundidee 2. Plug-in Schätzer 3. Schätzung des Standardfehlers 4. Schätzung und Korrektur der Verzerrung 5. Konsistenz
Differentialformen Äußere Ableitung Abbildungen Konverse Poincaré Lemma. Die Äußere Ableitung. Felix Retter
 25.06.2008 Inhaltsangabe Differentialformen Äußere Ableitung Abbildungen Konverse Poincaré Lemma Die p-form Sei P ein Punkt in E n. Der n-dimensionale lineare Raum L = L p wird dann gebildet von n a i
25.06.2008 Inhaltsangabe Differentialformen Äußere Ableitung Abbildungen Konverse Poincaré Lemma Die p-form Sei P ein Punkt in E n. Der n-dimensionale lineare Raum L = L p wird dann gebildet von n a i
Ljapunov Exponenten. Reiner Lauterbach
 Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
3 Grundlagen statistischer Tests (Kap. 8 IS)
 3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
Musterlösung. TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik. Klausur Mathematik für Physiker 3 (Analysis 2) I... II...
 ................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
................ Note I II Name Vorname 1 Matrikelnummer Studiengang (Hauptfach) Fachrichtung (Nebenfach) 2 3 Unterschrift der Kandidatin/des Kandidaten 4 TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Mathematik
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
4 Die Fibonacci-Zahlen
 4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
4 Die Fibonacci-Zahlen 4.1 Fibonacci-Zahlen und goldener Schnitt Die Fibonacci-Zahlen F n sind definiert durch die Anfangsvorgaben F 0 = 0, F 1 = 1, sowie durch die Rekursion F n+1 = F n + F n 1 für alle
Rekonstruktion 3D-Datensätze
 Rekonstruktion 3D-Datensätze Messung von 2D Projektionsdaten von einer 3D Aktivitätsverteilung Bekannt sind: räumliche Anordnung der Detektoren/Projektionsflächen ->Ziel: Bestimmung der 3D-Aktivitätsverteilung
Rekonstruktion 3D-Datensätze Messung von 2D Projektionsdaten von einer 3D Aktivitätsverteilung Bekannt sind: räumliche Anordnung der Detektoren/Projektionsflächen ->Ziel: Bestimmung der 3D-Aktivitätsverteilung
4.7 Der Taylorsche Satz
 288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
Segmentierung. Seminar: Medizinische Visualisierung. Daniel Lange
 Segmentierung Daniel Lange 06.05.2004 Seminar: Medizinische Visualisierung Segmentierung 2 Überblick Einführung / Begriffsdefinition Punktorientierte Verfahren Kanten-/Konturorientierte Verfahren Regionenorientierte
Segmentierung Daniel Lange 06.05.2004 Seminar: Medizinische Visualisierung Segmentierung 2 Überblick Einführung / Begriffsdefinition Punktorientierte Verfahren Kanten-/Konturorientierte Verfahren Regionenorientierte
Bildverarbeitung Herbstsemester. Mustererkennung
 Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Mustererkennung 1 Inhalt Einführung Mustererkennung in Grauwertbildern Ähnlichkeitsmasse Normalisierte Korrelation Korrelationskoeffizient Mustererkennung
Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Mustererkennung 1 Inhalt Einführung Mustererkennung in Grauwertbildern Ähnlichkeitsmasse Normalisierte Korrelation Korrelationskoeffizient Mustererkennung
Statistik IV für Studenten mit dem Nebenfach Statistik Lösungen zu Blatt 9 Gerhard Tutz, Jan Ulbricht SS 07
 Statistik IV für Studenten mit dem Nebenfach Statistik Lösungen zu Blatt 9 Gerhard Tutz, Jan Ulbricht SS 07 Ziel der Clusteranalyse: Bilde Gruppen (cluster) aus einer Menge multivariater Datenobjekte (stat
Statistik IV für Studenten mit dem Nebenfach Statistik Lösungen zu Blatt 9 Gerhard Tutz, Jan Ulbricht SS 07 Ziel der Clusteranalyse: Bilde Gruppen (cluster) aus einer Menge multivariater Datenobjekte (stat
Ein Buch. Für Anwendungen des Stoffs in den Wirtschaftswissenschaften: Knut Sydsæter, Peter Hemmond: Mathematik für Wirtschaftswissenschaftler
 Ein Buch Für Anwendungen des Stoffs in den Wirtschaftswissenschaften: Knut Sydsæter, Peter Hemmond: Mathematik für Wirtschaftswissenschaftler (Aber bei der Mathematik ein bisschen aufpassen!) 4 Extremstellen
Ein Buch Für Anwendungen des Stoffs in den Wirtschaftswissenschaften: Knut Sydsæter, Peter Hemmond: Mathematik für Wirtschaftswissenschaftler (Aber bei der Mathematik ein bisschen aufpassen!) 4 Extremstellen
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Numerische Methoden I FEM/REM
 Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: [email protected] Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: [email protected] Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Optimierung für Wirtschaftsinformatiker: Lineare Programme
 Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Stochastik für die Naturwissenschaften
 Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 4. Zufallsgrösse X Literatur Kapitel 4 * Storrer: Kapitel (37.2)-(37.8), (38.2)-(38.3), (38.5), (40.2)-(40.5) * Stahel: Kapitel 4, 5 und 6 (ohne
Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 4. Zufallsgrösse X Literatur Kapitel 4 * Storrer: Kapitel (37.2)-(37.8), (38.2)-(38.3), (38.5), (40.2)-(40.5) * Stahel: Kapitel 4, 5 und 6 (ohne
Einführung in Support Vector Machines (SVMs)
 Einführung in (SVM) Januar 31, 2011 Einführung in (SVMs) Table of contents Motivation Einführung in (SVMs) Outline Motivation Vektorrepräsentation Klassifikation Motivation Einführung in (SVMs) Vektorrepräsentation
Einführung in (SVM) Januar 31, 2011 Einführung in (SVMs) Table of contents Motivation Einführung in (SVMs) Outline Motivation Vektorrepräsentation Klassifikation Motivation Einführung in (SVMs) Vektorrepräsentation
Nichtlineare Optimierung ohne Nebenbedingungen
 Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
Kapitel 2 Nichtlineare Optimierung ohne Nebenbedingungen In diesem Abschnitt sollen im wesentlichen Verfahren zur Bestimmung des Minimums von nichtglatten Funktionen in einer Variablen im Detail vorgestellt
55 Lokale Extrema unter Nebenbedingungen
 55 Lokale Extrema unter Nebenbedingungen Sei f : O R mit O R n differenzierbar. Notwendige Bescheinigung für ein lokales Extremum in p 0 ist dann die Bedingung f = 0 (siehe 52.4 und 49.14). Ist nun F :
55 Lokale Extrema unter Nebenbedingungen Sei f : O R mit O R n differenzierbar. Notwendige Bescheinigung für ein lokales Extremum in p 0 ist dann die Bedingung f = 0 (siehe 52.4 und 49.14). Ist nun F :
3.2 Implizite Funktionen
 3.2 Implizite Funktionen Funktionen können explizit als y = f(x 1, x 2,..., x n ) oder implizit als F(x 1, x 2,..., x n ;y) = 0 gegeben sein. Offensichtlich kann man die explizite Form immer in die implizite
3.2 Implizite Funktionen Funktionen können explizit als y = f(x 1, x 2,..., x n ) oder implizit als F(x 1, x 2,..., x n ;y) = 0 gegeben sein. Offensichtlich kann man die explizite Form immer in die implizite
Dreiecke, Geraden, Lineare Gleichungssysteme
 Dreiecke, Geraden, Lineare Gleichungssysteme Jörn Loviscach Versionsstand: 18. April 2009, 19:46 1 Cosinussatz Mit Hilfe des Skalarprodukts kann man den Cosinussatz [law of cosines] zeigen. Seien a und
Dreiecke, Geraden, Lineare Gleichungssysteme Jörn Loviscach Versionsstand: 18. April 2009, 19:46 1 Cosinussatz Mit Hilfe des Skalarprodukts kann man den Cosinussatz [law of cosines] zeigen. Seien a und
Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung
 M.Sc. Brice Hakwa [email protected] Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung - Zusammenfassung zum Thema: Berechnung von Value-at-Risk
M.Sc. Brice Hakwa [email protected] Seminar im Wintersemester 2010/2011: Quantitative und implementierte Methoden der Marktrisikobewertung - Zusammenfassung zum Thema: Berechnung von Value-at-Risk
FEM isoparametrisches Konzept
 FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert
 Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Konfidenzintervalle Grundlegendes Prinzip Erwartungswert Bekannte Varianz Unbekannte Varianz Anteilswert Differenzen von Erwartungswert Anteilswert Beispiel für Konfidenzintervall Im Prinzip haben wir
Interpolation und Approximation
 Interpolation und Approximation Fakultät Grundlagen Mai 2006 Fakultät Grundlagen Interpolation und Approximation Übersicht 1 Problemstellung Polynominterpolation 2 Kubische Fakultät Grundlagen Interpolation
Interpolation und Approximation Fakultät Grundlagen Mai 2006 Fakultät Grundlagen Interpolation und Approximation Übersicht 1 Problemstellung Polynominterpolation 2 Kubische Fakultät Grundlagen Interpolation
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
Fehlerfortpflanzung & Extremwertbestimmung. Folie 1
 Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
Der Laplace-Operator auf einer Riemannschen Mannigfaltigkeit
 Der Laplace-Operator auf einer Riemannschen Mannigfaltigkeit (Eine kurze Einführung im Rahmen des Seminars Spektraltheorie des Laplace-Operators, Sommersemester 2009) Inhalt: 1) Einführung 2) (Unter-)
Der Laplace-Operator auf einer Riemannschen Mannigfaltigkeit (Eine kurze Einführung im Rahmen des Seminars Spektraltheorie des Laplace-Operators, Sommersemester 2009) Inhalt: 1) Einführung 2) (Unter-)
Kapitel VIII - Tests zum Niveau α
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel VIII - Tests zum Niveau α Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh Testsituationen
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel VIII - Tests zum Niveau α Induktive Statistik Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh Testsituationen
Principal Component Analysis (PCA)
 Principal Component Analysis (PCA) Motivation: Klassifikation mit der PCA Berechnung der Hauptkomponenten Theoretische Hintergründe Anwendungsbeispiel: Klassifikation von Gesichtern Weiterführende Bemerkungen
Principal Component Analysis (PCA) Motivation: Klassifikation mit der PCA Berechnung der Hauptkomponenten Theoretische Hintergründe Anwendungsbeispiel: Klassifikation von Gesichtern Weiterführende Bemerkungen
3 Lineare Differentialgleichungen
 3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
Technische Universität Berlin Fakultät II Institut für Mathematik SS 13 G. Bärwolff, C. Mehl, G. Penn-Karras
 Technische Universität Berlin Fakultät II Institut für Mathematik SS 3 G. Bärwolff, C. Mehl, G. Penn-Karras 9..3 Oktober Klausur Analysis II für Ingenieure Rechenteil. Aufgabe Punkte i) Wir berechnen zunächst
Technische Universität Berlin Fakultät II Institut für Mathematik SS 3 G. Bärwolff, C. Mehl, G. Penn-Karras 9..3 Oktober Klausur Analysis II für Ingenieure Rechenteil. Aufgabe Punkte i) Wir berechnen zunächst
Orientierung der Vektoren b 1,..., b n. Volumen des von den Vektoren aufgespannten Parallelotops
 15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
