Schwache Konvergenz. Ivan Lecei. 18. Juni Institut für Stochastik
|
|
|
- Anton Kolbe
- vor 6 Jahren
- Abrufe
Transkript
1 Institut für Stochastik 18. Juni 2013
2 Inhalt
3 Nach ZGWS konvergiert für n F n (x) = P{ X X n np npq x} gegen F(x) = 1 2π x e 1 2 u2 du, wenn die X i unabhängig und bernoulliverteilt sind (Erfolgswahrscheinlichkeit p=1-q) Analog: P n ((, x]) = F n (x) konvergiert gegen P((, x]) = F(x), wobei P({x}) = 0 Vorteil: Verteilungskonvergenz an euklidischen Raum gebunden, schwache für allgemeine metrische Räume (M, δ) mit σ -Algebra M B δ ausdehnbar
4 Dann konvergiert das Wahrscheinlichkeitsmaß P n schwach gegen P, wenn für alle Borelmengen A M B δ mit P( A) = 0 gilt P n (A) P(A) Aus der schwachen von X n gegen X kann die Verteilungskonvergenz bestimmter Funktionale ψ(x n ) D ψ(x) gefolgert werden
5 Zufälliges Element (Ω, A, P) ein Wahrscheinlichkeitsraum und (S, B) ein messbarer Raum mit Ω, S Ø. Zufälliges Element Ein zufälliges Element X : Ω S ist eine A B -messbare Abbildung, das heißt für alle B B gilt X 1 (B) = {ω Ω : X(ω) B} A Die Verteilung von X ist ein Wahrscheinlichkeitsmaß P X auf (S, B), so dass für alle B B gilt P X (B) = P(X 1 (B)) jedes Wahrscheinlichkeitsmaß µ auf (S, B) kann als Verteilung eines Zufallselementes X betrachtet werden.
6 Stochastischer Prozess (S t, B t ) t T eine Famile von messbaren Räumen. Stochastischer Prozess/Zufällige Funktion Eine Familie X = {X(t), t T } von Zufallselementen X(t) : Ω S t, die auf (Ω, A, P) definiert und für alle t T A B t -messbar sind heißt stochastischer Prozess Jede Famile von Wahrscheinlichkeitsmaßen {P t1,...,t n, n N, {t 1,..., t n } T } auf (R m... R m, B(R m )... B(R m )) die symmetrisch und konsistent ist kann als endlich-dimensionale Verteilung für einen stochastischen Prozess, der auf einem Wahrscheinlichkeitsraum (Ω, A, P) definiert ist, betrachtet werden (Kolmogorov)
7 Natürliche Projektion Natürliche Projektion Für beliebige Punkte t 1,..., t k [0, 1] ist die natürliche Projektion von dem Raum D[0,1] der cádlàg-stetigen Funktionen in R k definiert über π t1,...,t k (x) = (x(t 1 ),..., x(t k )), x D[0, 1] Die endlichdimensionalen Verteilungen von X lassen sich dann über Pπ 1 t 1,...,t k angeben, wobei P das von X induzierte Wahrscheinlichkeitsmaß ist. Wenn T 0 1 enthält und dicht in [0, 1] liegt, dann wird P eindeutig über Pπ 1 t 1,...,tk, t 1,..., t k T 0 bestimmt
8 (M, δ) beliebiger metrischer Raum und M B δ diejenige σ -Algebra, die von den offenen Bällen erzeugt wird. Seien X n, n 0 Zufallselemente bezüglich (M, M B δ ) auf (Ω, A, P) und sei P n das von X n induzierte Wahrscheinlichkeitsmaß X n konvergiert schwach gegen X 0, wenn für n M fdp n = Ef (X n ) Ef (X 0 ) = M fdp 0 für alle reellen, beschränkten, bezüglich der Metrik δ stetigen und M B δ -messbaren Funktionen f auf M. Man schreibt X n X 0 (bzw. P n P 0 ) auf (M, M B δ, δ). X n D X0 X n X 0 für Zufallsvariablen X n, X 0.
9 Straffheit/schwache Kompaktheit Straffheit Eine Folge X n, n 1 von (M, δ) -wertigen Zufallselementen ist straff, wenn auch die zugehörigen induzierten Wahrscheinlichkeitsmaße P n straff sind. Für jedes ε > 0 muss dann eine kompakte Menge K M existieren, sodass für alle n 1 P n (K ) = P(X n K ) > 1 ε. Kompaktheit Eine Familie von Verteilungen P auf (M, M B δ ) nennt man schwach kompakt, wenn jede Folge von Verteilungen von P eine Teilfolge enhält, die schwach gegen eine Verteilung auf (M, M B δ ) konvergiert (aber nicht notwendigerweise in P liegt).
10 Portmanteau Theorem Folgende Aussagen sind äquivalent 1. P n P 0 auf (M, M B δ, δ) 2. lim inf n P n (G) P 0 (G) für alle offenen Mengen G 3. lim sup n P n (F) P 0 (F) für alle abgeschlossenen F 4. lim n P n (B) = P 0 (B) für all diejenigen Borel-messbaren Mengen B, für welche gilt P 0 ( B) = 0 Aus P n P folgt für ψ : (M, M B δ, δ) (M, (M B δ ), δ ), dass ψ(x n ) D ψ(x) (bzw. P n ψ 1 Pψ 1 ) für alle M B δ -messbaren ψ, wenn zusätzlich P(X D ψ) = 0 mit D ψ Menge der Unstetigkeitspunkte von ψ (Abschwächung des Continous Mapping Theorems)
11 1. Kriterium Sei mesh(t m ) = max{t i t i 1 : 1 i k m } für ein beliebiges Gitter T m auf [0,1] (t m,0 = 0, t m,km = 1) Für ein x D nennen wir die Funktion A m (x) D, die auf allen Intervallen der Form [t m,i 1, t m,i ) (0 i k m ) konstant x(t m,i ) entspricht die T m -Approximation von x 1. Kriterium Für stochastische Prozesse X n, n 0 auf (D, D) mit X n (0) = 0, für die für mesh(t m ) 0 (m ) die folgenden Bedingungen erfüllt sind 1. X n f.d. X 0 für n und wobei P(X 0 C) = 1 2. lim sup n P( X n A m (X n ) ε) d ε,m für alle ε > 0 und d ε,m 0 für m gilt X n X 0 auf (D, D, ) für n
12 2. Kriterium (Straffheit) 2.Kriterium Für einen separablen metrischen Raum (M, δ) gelte X n X 0 für n und zusätzlich f.d. X n, n 1 ist straff (sowie die induzierten Wahrscheinlichkeitsmaße P n, n 1 ). Dann gilt X n X 0 auf (M, M B δ, δ) Mit f.d. (=finite dimensional distributions) sei hier die schwache der endlichdimensionalen Verteilungen gemeint, d.h. (X n (t 1 ),..., X n (t k )) T (X 0 (t 1 ),...X n (t k )) T k N, t 1,...t k [0, 1]
13 Beweis 2. Kriterium Zum Beweis: 1. Es gilt P n P, genau dann wenn jede Teilfolge {P n } eine weitere Teilfolge {P n } enthält, für die gilt P n P 2. Prohorovs Theorem: Ist eine Familie P von Wahrscheinlichkeitsmaßen straff, so ist sie schwach kompakt. Ist sie umgekehrt schwach kompakt, muss zusätlich gelten, dass M separabel und vollständig ist, damit P straff ist.
14 Partialsummenprozess Partialsummenprozess Seien X 1, X 2,... unabhängige und identisch verteilte Zufallsvariablen, die jeweils Erwartungswert 0 und Varianz 1 haben. Die i-te Partialsumme ist dann für i 1 definiert als S i = X X i, S 0 = 0 und für t 0 ist S(t)=S t eine zufällige Funktion auf [0, ). Der n-te Partialsummen Prozess S n auf (D, D) ist dann für 0 t 1 S n (t) = S(nt) n Für alle t, die i n t < i+1 n erfüllen ist der Wert von S n dann konstant S i n
15 Partialsummenprozess t Abbildung : X i N(0,1)-verteilt,i=1,...,n ; n=10
16 des Partialsummenprozesses Donsker Der Partialsummenprozess S n konvergiert schwach gegen einen Wiener Prozess für n Hinreichende Bedingung für die Straffheit: E{ X n (t) X n (t 1 ) γ X n (t 2 ) X n (t) γ } [F(t 2 ) F(t 1 )] 2α für t 1 t t 2 und n 1, wobei γ 0, α > 1 2 und F ist eine nichtfallende, stetige Funktion auf [0,1]
17 Literatur Skript Stochastik II (2010) Prof. Dr. Evgeny Spodarev Convergence of Probability Measures P. Billingsley Wiley (1968) Weak Convergence and Empirical Processes Aad W. Van der Vaart, Jon A. Wellner Springer (1996) Empirical Processes with Applications to Statistics G.R. Shorack, Jon A. Wellner Wiley (1986)
Brownsche Bewegung. Satz von Donsker. Bernd Barth Universität Ulm
 Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Kapitel II. Brownsche Bewegung. Literatur: Karatzas, Shreve (1999, Chap. 2).
 Kapitel II Brownsche Bewegung Literatur: Karatzas, Shreve (1999, Chap. 2). Gegeben: Wahrscheinlichkeitsraum (Ω, A, P) mit Filtration F = (F t ) t I, wobei I = [0, [. Definition 1. W = (W t ) t I Brownsche
Kapitel II Brownsche Bewegung Literatur: Karatzas, Shreve (1999, Chap. 2). Gegeben: Wahrscheinlichkeitsraum (Ω, A, P) mit Filtration F = (F t ) t I, wobei I = [0, [. Definition 1. W = (W t ) t I Brownsche
Schwache Konvergenz. Kapitel 8
 Im Hinblick auf die funktionalen Grenzwertsätze wird in diesem Kapitel die Theorie der schwachen Konvergenz endlicher Maße auf separablen metrischen, vorallem polnischen Räumen entwickelt. In dieser Situation
Im Hinblick auf die funktionalen Grenzwertsätze wird in diesem Kapitel die Theorie der schwachen Konvergenz endlicher Maße auf separablen metrischen, vorallem polnischen Räumen entwickelt. In dieser Situation
3 Markov-Eigenschaft der Brownschen Bewegung
 Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
Gesetze der großen Zahlen
 Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
2 Zufallsvariable, Verteilungen, Erwartungswert
 2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
Brownsche Bewegung. M. Gruber SS 2016, KW 11. Zusammenfassung
 Brownsche Bewegung M. Gruber SS 2016, KW 11 Zusammenfassung Stochastische Prozesse, Pfade; Definition der Brownschen Bewegung; Eigenschaften der Brownschen Bewegung: Kovarianz, Stationarität, Selbstähnlichkeit;
Brownsche Bewegung M. Gruber SS 2016, KW 11 Zusammenfassung Stochastische Prozesse, Pfade; Definition der Brownschen Bewegung; Eigenschaften der Brownschen Bewegung: Kovarianz, Stationarität, Selbstähnlichkeit;
Seminar stabile Zufallsprozesse
 Definitionen und Eigenschaften stabiler Verteilungen 2. November 2011 Inhalt 1 Definitionen Definitionen Beweis der Äquivalenz Beispiele 2 Eigenschaften 3 Charakteristische Funktion 4 Laplace Transformation
Definitionen und Eigenschaften stabiler Verteilungen 2. November 2011 Inhalt 1 Definitionen Definitionen Beweis der Äquivalenz Beispiele 2 Eigenschaften 3 Charakteristische Funktion 4 Laplace Transformation
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Stochastik. 1. Wahrscheinlichkeitsräume
 Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
HANDOUT #1 KONVERGENZ VON W-MASSEN, VERTEILUNGEN UND ZUFALLSVARIABLEN
 HANDOUT #1 KONVERGENZ VON W-MASSEN, VERTEILUNGEN UND ZUFALLSVARIABLEN FOLKMAR BORNEMANN Die Vielfalt der Konvergenzberiffe für W-Maße, Verteilungen und Zufallsvariablen (wie vage, schwache, stochastische
HANDOUT #1 KONVERGENZ VON W-MASSEN, VERTEILUNGEN UND ZUFALLSVARIABLEN FOLKMAR BORNEMANN Die Vielfalt der Konvergenzberiffe für W-Maße, Verteilungen und Zufallsvariablen (wie vage, schwache, stochastische
Brownsche Bewegung. M. Gruber. 19. März Zusammenfassung
 Brownsche Bewegung M. Gruber 19. März 2014 Zusammenfassung Stochastische Prozesse, Pfade; Brownsche Bewegung; Eigenschaften der Brownschen Bewegung: Kovarianz, Stationarität, Selbstähnlichkeit, quadratische
Brownsche Bewegung M. Gruber 19. März 2014 Zusammenfassung Stochastische Prozesse, Pfade; Brownsche Bewegung; Eigenschaften der Brownschen Bewegung: Kovarianz, Stationarität, Selbstähnlichkeit, quadratische
Vollständiger Raum, Banachraum
 Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Auf dem R n gibt es sehr viele verschiedene Normen, allerdings hängen sehr viele wichtige Begriffe wie die Konvergenz
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Auf dem R n gibt es sehr viele verschiedene Normen, allerdings hängen sehr viele wichtige Begriffe wie die Konvergenz
Mathematische Ökonometrie
 Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Etwas Topologie. Handout zur Vorlesung Semi-Riemannsche Geometrie, SS 2004 Dr. Bernd Ammann
 Etwas Topologie Handout zur Vorlesung Semi-Riemannsche Geometrie, SS 2004 Dr. Bernd Ammann Literatur Abraham, Marsden, Foundations of Mechanics, Addison Wesley 1978, Seiten 3 17 Definition. Ein topologischer
Etwas Topologie Handout zur Vorlesung Semi-Riemannsche Geometrie, SS 2004 Dr. Bernd Ammann Literatur Abraham, Marsden, Foundations of Mechanics, Addison Wesley 1978, Seiten 3 17 Definition. Ein topologischer
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Primzahlen Primzahlsatz Satz von Szemerédi Verallg. von Green/Tao Anwendung. Arithmetische Progressionen von Primzahlen
 Arithmetische Progressionen von Primzahlen Sei N := {1, 2, 3,... } die Menge der natürlichen Zahlen. Definition Eine Primzahl ist eine natürliche Zahl > 1, die nur durch 1 und durch sich selbst teilbar
Arithmetische Progressionen von Primzahlen Sei N := {1, 2, 3,... } die Menge der natürlichen Zahlen. Definition Eine Primzahl ist eine natürliche Zahl > 1, die nur durch 1 und durch sich selbst teilbar
Cauchy-Folgen und Kompaktheit. 1 Cauchy-Folgen und Beschränktheit
 Vortrag zum Seminar zur Analysis, 10.05.2010 Michael Engeländer, Jonathan Fell Dieser Vortrag stellt als erstes einige Sätze zu Cauchy-Folgen auf allgemeinen metrischen Räumen vor. Speziell wird auch das
Vortrag zum Seminar zur Analysis, 10.05.2010 Michael Engeländer, Jonathan Fell Dieser Vortrag stellt als erstes einige Sätze zu Cauchy-Folgen auf allgemeinen metrischen Räumen vor. Speziell wird auch das
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
1 Erwartungswert und Kovarianzmatrix von Zufallsvektoren
 Erwartungswert und Kovarianzmatrix von Zufallsvektoren Erwartungswert und Kovarianzmatrix von Zufallsvektoren. Definition Ist X X,...,X p ein p-dimensionaler Zufallsvektor mit E X j < für alle j, so heißt
Erwartungswert und Kovarianzmatrix von Zufallsvektoren Erwartungswert und Kovarianzmatrix von Zufallsvektoren. Definition Ist X X,...,X p ein p-dimensionaler Zufallsvektor mit E X j < für alle j, so heißt
Diskrete Wahrscheinlichkeitstheorie - Probeklausur
 Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Definition Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) :=
 Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
3. Kombinatorik und Wahrscheinlichkeit
 3. Kombinatorik und Wahrscheinlichkeit Es geht hier um die Bestimmung der Kardinalität endlicher Mengen. Erinnerung: Seien A, B, A 1,..., A n endliche Mengen. Dann gilt A = B ϕ: A B bijektiv Summenregel:
3. Kombinatorik und Wahrscheinlichkeit Es geht hier um die Bestimmung der Kardinalität endlicher Mengen. Erinnerung: Seien A, B, A 1,..., A n endliche Mengen. Dann gilt A = B ϕ: A B bijektiv Summenregel:
Fraktale Geometrie. 9: Metrische äußere Maße II. Universität Regensburg Sommersemester Daniel Heiß:
 Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
Optimale Steuerung, Prof.Dr. L. Blank 1. II Linear-quadratische elliptische Steuerungsprobleme
 Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
30 Metriken und Normen
 31 Metriken und Normen 153 30 Metriken und Normen Lernziele: Konzepte: Metriken, Normen, Skalarprodukte, Konvergenz von Folgen Frage: Versuchen Sie, möglichst viele verschiedene Konvergenzbegriffe für
31 Metriken und Normen 153 30 Metriken und Normen Lernziele: Konzepte: Metriken, Normen, Skalarprodukte, Konvergenz von Folgen Frage: Versuchen Sie, möglichst viele verschiedene Konvergenzbegriffe für
Satz von Borel-Cantelli. Limes inferior von Mengen. Limes superior von Mengen. Stetigkeit. Konvergenz von Zufallsvariablen. Kolmogorow-Ungleichung
 Satz von Borel-Cantelli Limes inferior von Mengen Limes superior von Mengen Stetigkeit Konvergenz von Zufallsvariablen Kolmogorow-Ungleichung Tschebyschow-Ungleichung Konvergenzkriterien Starkes Gesetz
Satz von Borel-Cantelli Limes inferior von Mengen Limes superior von Mengen Stetigkeit Konvergenz von Zufallsvariablen Kolmogorow-Ungleichung Tschebyschow-Ungleichung Konvergenzkriterien Starkes Gesetz
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Asymptotische Stochastik (SS 2010)
 Institut für Stochastik PD. Dr. Dieter Kadelka Daniel Gentner Asymptotische Stochastik (SS 2010) Lösungen zu Übungsblatt 4 Aufgabe 1 (lokaler Grenzwertsatz von de Moivre und Laplace und eine Verallgemeinerung)
Institut für Stochastik PD. Dr. Dieter Kadelka Daniel Gentner Asymptotische Stochastik (SS 2010) Lösungen zu Übungsblatt 4 Aufgabe 1 (lokaler Grenzwertsatz von de Moivre und Laplace und eine Verallgemeinerung)
Kompaktheit und Überdeckungen. 1 Überdeckungskompaktheit
 Vortrag zum Proseminar zur Analysis, 17.05.2010 Min Ge, Niklas Fischer In diesem Vortrag werden die Eigenschaften von kompakten, metrischen Räumen vertieft. Unser Ziel ist es Techniken zu erlernen, um
Vortrag zum Proseminar zur Analysis, 17.05.2010 Min Ge, Niklas Fischer In diesem Vortrag werden die Eigenschaften von kompakten, metrischen Räumen vertieft. Unser Ziel ist es Techniken zu erlernen, um
7.2 Moment und Varianz
 7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
Stochastische Finanzmathematik I
 Notizen zu der Vorlesung Stochastische Finanzmathemati I 1 Zum Ein-perioden-Modell 1.1 Beispiel: Zwei-wertiges Modell: π 0 = 1, S 0 =, { b Wahrs. p S 1 = a Wahrs. 1 p Arbitrage frei: Es gibt p 0, 1) mit
Notizen zu der Vorlesung Stochastische Finanzmathemati I 1 Zum Ein-perioden-Modell 1.1 Beispiel: Zwei-wertiges Modell: π 0 = 1, S 0 =, { b Wahrs. p S 1 = a Wahrs. 1 p Arbitrage frei: Es gibt p 0, 1) mit
Zufallsgröße X : Ω R X : ω Anzahl der geworfenen K`s
 X. Zufallsgrößen ================================================================= 10.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
X. Zufallsgrößen ================================================================= 10.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
Unabhängige Zufallsvariablen
 Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
7. Die Brownsche Bewegung
 7. DIE BROWNSCHE BEWEGUNG 7 5 5 50 00 50 200 250 0 5 20 Abbildung 7.: Pfad einer Brownschen Bewegung 7. Die Brownsche Bewegung Definition 7.. Ein cadlag stochastischer Prozess {W t } mit W 0 = 0, unabhängigen
7. DIE BROWNSCHE BEWEGUNG 7 5 5 50 00 50 200 250 0 5 20 Abbildung 7.: Pfad einer Brownschen Bewegung 7. Die Brownsche Bewegung Definition 7.. Ein cadlag stochastischer Prozess {W t } mit W 0 = 0, unabhängigen
Martingal-Maße. Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Manuel Müller Mathematisches Institut
 Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Exkurs: Polnische Räume
 Ein normaler Hausdorff-Raum mit abzählbarer Basis kann auf viele Weisen metrisiert werden; man kann insbesondere eine einmal gewonnene Metrik in vielerlei Weise abändern, ohne die von ihr erzeugte Topologie
Ein normaler Hausdorff-Raum mit abzählbarer Basis kann auf viele Weisen metrisiert werden; man kann insbesondere eine einmal gewonnene Metrik in vielerlei Weise abändern, ohne die von ihr erzeugte Topologie
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
Beispiel. Gegeben sei die Folge (a n ) n N mit. a n := n 2 + 5n + 1 n. Es gilt. (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n n, woraus folgt
 Beispiel. Gegeben sei die Folge (a n ) n N mit a n := n 2 + 5n + 1 n Es gilt ( ( ) (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n + 1 + n, woraus folgt a n = (n2 + 5n + 1) n 2 n2 + 5n + 1 + n = 5n + 1 n2
Beispiel. Gegeben sei die Folge (a n ) n N mit a n := n 2 + 5n + 1 n Es gilt ( ( ) (n 2 + 5n + 1) n 2 = n2 + 5n + 1 n) n2 + 5n + 1 + n, woraus folgt a n = (n2 + 5n + 1) n 2 n2 + 5n + 1 + n = 5n + 1 n2
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME
 Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
Analysis II (FS 2015): ZUSAMMENHÄNGENDE METRISCHE RÄUME Dietmar A. Salamon ETH-Zürich 23. Februar 2015 1 Topologische Grundbegriffe Sei (X, d) ein metrischer Raum, d.h. X ist eine Menge und d : X X R ist
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung
 2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
1 Stochastische Konvergenz 2. 2 Das Gesetz der grossen Zahlen 4. 3 Der Satz von Bernoulli 6
 Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
Lösungsvorschlag zu den Hausaufgaben der 8. Übung
 FAKULTÄT FÜR MATHEMATIK Prof Dr Patrizio Ne Frank Osterbrink Johannes Lankeit 9503 Lösungsvorschlag zu den Hausaufgaben der 8 Übung Hausaufgabe : Beweise den Satz über die Parallelogrammgleichung Sei H
FAKULTÄT FÜR MATHEMATIK Prof Dr Patrizio Ne Frank Osterbrink Johannes Lankeit 9503 Lösungsvorschlag zu den Hausaufgaben der 8 Übung Hausaufgabe : Beweise den Satz über die Parallelogrammgleichung Sei H
Topologische Aspekte: Eine kurze Zusammenfassung
 Kapitel 1 Topologische Aspekte: Eine kurze Zusammenfassung Wer das erste Knopfloch verfehlt, kommt mit dem Zuknöpfen nicht zu Rande J. W. Goethe In diesem Kapitel bringen wir die Begriffe Umgebung, Konvergenz,
Kapitel 1 Topologische Aspekte: Eine kurze Zusammenfassung Wer das erste Knopfloch verfehlt, kommt mit dem Zuknöpfen nicht zu Rande J. W. Goethe In diesem Kapitel bringen wir die Begriffe Umgebung, Konvergenz,
Kompaktheit und Überdeckungen. 1 Überdeckungskompaktheit
 Vortrag zum Proseminar zur Analysis, 17.05.2010 Min Ge, Niklas Fischer 1 Überdeckungskompaktheit Einleitung P T Q A R S U B (a) (b) Abbildung 1: Beispiele verschiedener Überdeckungen (1.1) Definition (Überdeckung)
Vortrag zum Proseminar zur Analysis, 17.05.2010 Min Ge, Niklas Fischer 1 Überdeckungskompaktheit Einleitung P T Q A R S U B (a) (b) Abbildung 1: Beispiele verschiedener Überdeckungen (1.1) Definition (Überdeckung)
Topologische Begriffe
 Kapitel 3 Topologische Begriffe 3.1 Inneres, Rand und Abschluss von Mengen Definition (innerer Punkt und Inneres). Sei (V, ) ein normierter Raum über K, und sei M V eine Menge. Ein Vektor v M heißt innerer
Kapitel 3 Topologische Begriffe 3.1 Inneres, Rand und Abschluss von Mengen Definition (innerer Punkt und Inneres). Sei (V, ) ein normierter Raum über K, und sei M V eine Menge. Ein Vektor v M heißt innerer
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 2006
 Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Zufallsvariablen [random variable]
![Zufallsvariablen [random variable] Zufallsvariablen [random variable]](/thumbs/52/29710821.jpg) Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Schwache Konvergenz von W-Verteilungen auf der Zahlengeraden
 Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
Kapitel 5 Schwache Konvergenz von W-Verteilungen auf er Zahlengeraen 5.1 Schwache Konvergenz bzw. Verteilungskonvergenz Bezeichne W(, B 1 ie Menge aller W-Verteilungen auf (, B 1. Definition 5.1 (Schwache
Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen
 Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen Georg Bol georg.bol@statistik.uni-karlsruhe.de Markus Höchstötter hoechstoetter@statistik.uni-karlsruhe.de Stetige Verteilungen Definition: Sei
Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen Georg Bol georg.bol@statistik.uni-karlsruhe.de Markus Höchstötter hoechstoetter@statistik.uni-karlsruhe.de Stetige Verteilungen Definition: Sei
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
also ist Sx m eine Cauchyfolge und somit konvergent. Zusammen sagen die Sätze 11.1 und 11.2, dass B (X) ein abgeschlossenes zweiseitiges
 11. Kompakte Operatoren Seien X, Y Banachräume, und sei T : X Y ein linearer Operator. Definition 11.1. T heißt kompakt, enn T (B) eine kompakte Teilmenge von Y ist für alle beschränkten Mengen B X. Wir
11. Kompakte Operatoren Seien X, Y Banachräume, und sei T : X Y ein linearer Operator. Definition 11.1. T heißt kompakt, enn T (B) eine kompakte Teilmenge von Y ist für alle beschränkten Mengen B X. Wir
Stochastik für die Naturwissenschaften
 Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 4. Zufallsgrösse X Literatur Kapitel 4 * Storrer: Kapitel (37.2)-(37.8), (38.2)-(38.3), (38.5), (40.2)-(40.5) * Stahel: Kapitel 4, 5 und 6 (ohne
Stochastik für die Naturwissenschaften Dr. C.J. Luchsinger 4. Zufallsgrösse X Literatur Kapitel 4 * Storrer: Kapitel (37.2)-(37.8), (38.2)-(38.3), (38.5), (40.2)-(40.5) * Stahel: Kapitel 4, 5 und 6 (ohne
8 Verteilungsfunktionen und Dichten
 8 Verteilungsfunktionen und Dichten 8.1 Satz und Definition (Dichten) Eine Funktion f : R R heißt Dichtefunktion, kurz Dichte, wenn sie (Riemann-) integrierbar ist mit f(t) 0 für alle t R und Setzt man
8 Verteilungsfunktionen und Dichten 8.1 Satz und Definition (Dichten) Eine Funktion f : R R heißt Dichtefunktion, kurz Dichte, wenn sie (Riemann-) integrierbar ist mit f(t) 0 für alle t R und Setzt man
6. Übungsblatt zur Einführung in die Stochastik
 Fachbereich Mathematik Prof. Dr. Michael Kohler Dipl.-Math. Andreas Fromkorth Dipl.-Inf. Jens Mehnert SS 9 1.6.29 6. Übungsblatt zur Einführung in die Stochastik Aufgabe 22 Sei P ein auf der Borelschen
Fachbereich Mathematik Prof. Dr. Michael Kohler Dipl.-Math. Andreas Fromkorth Dipl.-Inf. Jens Mehnert SS 9 1.6.29 6. Übungsblatt zur Einführung in die Stochastik Aufgabe 22 Sei P ein auf der Borelschen
2 Brownsche Bewegung. Wahrscheinlichkeitstheorie III Teil Der Wienerraum
 8 Wahrscheinlichkeitstheorie III Teil 3 Brownsche Bewegung Wir haben die Brownsche Bewegung bereits als Grenzwert reskalierter Irrfahrten in der VL WTH II kennengelernt siehe dazu Abschnitt 5.. In diesem
8 Wahrscheinlichkeitstheorie III Teil 3 Brownsche Bewegung Wir haben die Brownsche Bewegung bereits als Grenzwert reskalierter Irrfahrten in der VL WTH II kennengelernt siehe dazu Abschnitt 5.. In diesem
1 Elemente der Wahrscheinlichkeitstheorie
 H.-J. Starkloff Unendlichdimensionale Stochastik Kap. 01 11. Oktober 2010 1 1 Elemente der Wahrscheinlichkeitstheorie 1.1 Messbare Räume Gegeben seien eine nichtleere Menge Ω und eine Menge A von Teilmengen
H.-J. Starkloff Unendlichdimensionale Stochastik Kap. 01 11. Oktober 2010 1 1 Elemente der Wahrscheinlichkeitstheorie 1.1 Messbare Räume Gegeben seien eine nichtleere Menge Ω und eine Menge A von Teilmengen
Funktionsgrenzwerte, Stetigkeit
 Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
α + x x 1 F c y + x 1 F (y) c z + x 1 F (z) für alle y, z M. Dies folgt aus
 4. Dualräume und schwache Topologien Den Begriff des Dualraums hatten wir bereits in Kapitel 2 definiert. Der Dualraum X eines Banachraums X ist X = B(X, C). X ist mit der Abbildungsnorm F = sup x =1 F
4. Dualräume und schwache Topologien Den Begriff des Dualraums hatten wir bereits in Kapitel 2 definiert. Der Dualraum X eines Banachraums X ist X = B(X, C). X ist mit der Abbildungsnorm F = sup x =1 F
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
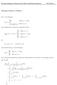 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Übungen zur Wahrscheinlichkeitstheorie und Statistik
 Übungen zur Wahrscheinlichkeitstheorie und Statistik Prof. Dr. C. Löh/M. Blank Blatt 0 vom 16. April 2012 Aufgabe 1 (Wahrscheinlichkeitsräume). Welche der folgenden Aussagen sind wahr? Begründen Sie jeweils
Übungen zur Wahrscheinlichkeitstheorie und Statistik Prof. Dr. C. Löh/M. Blank Blatt 0 vom 16. April 2012 Aufgabe 1 (Wahrscheinlichkeitsräume). Welche der folgenden Aussagen sind wahr? Begründen Sie jeweils
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Kapitel 6 Martingale
 Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
Stochastische FEM mit elementaren Zufallselementen
 Stochastische FEM mit elementaren Zufallselementen Hans-Jörg Starkloff Westsächsische Hochschule Zwickau 13. Südostdeutsches Kolloquium zur Numerischen Mathematik 2007 Freiberg, 27. April 2007 Einführung
Stochastische FEM mit elementaren Zufallselementen Hans-Jörg Starkloff Westsächsische Hochschule Zwickau 13. Südostdeutsches Kolloquium zur Numerischen Mathematik 2007 Freiberg, 27. April 2007 Einführung
MAA = MAB + B AA = B CA + CAA BA A Nun sehen wir mit Proposition 10.7 aus dem Skript, dass A M AB gelten muss.
 1. Konvexität in der absoluten Ebene In einem Dreieck in der Euklidischen Ebene hat die Strecke zwischen zwei Seitenmittelpunkten die halbe Länge der dritten Seite. In der absoluten Ebene hat man eine
1. Konvexität in der absoluten Ebene In einem Dreieck in der Euklidischen Ebene hat die Strecke zwischen zwei Seitenmittelpunkten die halbe Länge der dritten Seite. In der absoluten Ebene hat man eine
ist reelles lineares Funktional. x(t) ϕ(t) dt ist reelles lineares Funktional für alle ϕ L 2 (0, 1).
 Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Kapitel 16 : Differentialrechnung
 Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Ljapunov Exponenten. Reiner Lauterbach
 Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Stetigkeit. Definitionen. Beispiele
 Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
Stetigkeit Definitionen Stetigkeit Sei f : D mit D eine Funktion. f heißt stetig in a D, falls für jede Folge x n in D (d.h. x n D für alle n ) mit lim x n a gilt: lim f x n f a. Die Funktion f : D heißt
Euklidische und unitäre Vektorräume
 Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen
 Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Kapitel 8 Darstellungsformeln für die Lösung von parabolischen Differentialgleichungen Wir hatten im Beispiel 5. gesehen, dass die Wärmeleitungsgleichung t u u = f auf Ω (0, ) (8.1) eine parabolische Differentialgleichung
Das Singularitätentheorem von Hawking Teil 2
 Das Singularitätentheorem von Hawking Teil Jakob Hedicke 0.06.06 In diesem Vortrag werden wir den Beweis des Singularitätentheorems von Stephen Hawking vervollständigen. Im letzten Vortrag wurde bereits
Das Singularitätentheorem von Hawking Teil Jakob Hedicke 0.06.06 In diesem Vortrag werden wir den Beweis des Singularitätentheorems von Stephen Hawking vervollständigen. Im letzten Vortrag wurde bereits
Wahrscheinlichkeitsrechnung und Quantentheorie
 Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Simulation von Zufallsvariablen und Punktprozessen
 Simulation von Zufallsvariablen und Punktprozessen 09.11.2009 Inhaltsverzeichnis 1 Einleitung 2 Pseudozufallszahlen 3 Punktprozesse Zufallszahlen Definition (Duden): Eine Zufallszahl ist eine Zahl, die
Simulation von Zufallsvariablen und Punktprozessen 09.11.2009 Inhaltsverzeichnis 1 Einleitung 2 Pseudozufallszahlen 3 Punktprozesse Zufallszahlen Definition (Duden): Eine Zufallszahl ist eine Zahl, die
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Mengensysteme, Wahrscheinlichkeitsmaße
 Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
Zufallsvariablen. Diskret. Stetig. Verteilung der Stichprobenkennzahlen. Binomial Hypergeometrisch Poisson. Normal Lognormal Exponential
 Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Zufallsvariable Erinnerung: Merkmal, Merkmalsausprägung Deskriptive Statistik:
Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Zufallsvariable Erinnerung: Merkmal, Merkmalsausprägung Deskriptive Statistik:
Konstruktion der reellen Zahlen
 Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Kapitel 5 KONVERGENZ
 Kapitel 5 KONVERGENZ Fassung vom 21. April 2002 Claude Portenier ANALYSIS 75 5.1 Metrische Räume 5.1 Metrische Räume DEFINITION 1 Sei X eine Menge. Eine Abbildung d : X X! R + heißt Metrik oder Distanz
Kapitel 5 KONVERGENZ Fassung vom 21. April 2002 Claude Portenier ANALYSIS 75 5.1 Metrische Räume 5.1 Metrische Räume DEFINITION 1 Sei X eine Menge. Eine Abbildung d : X X! R + heißt Metrik oder Distanz
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Zusammenfassung Mathe II. Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen
 Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
3.4 Asymptotische Evaluierung von Sch atzer Konsistenz Konsistenz Definition 3.4.1: konsistente Folge von Sch atzer
 3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
STOCHASTISCHE UNABHÄNGIGKEIT. Annika Pohlmann Philipp Oel Wilhelm Dück
 STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
