Ganzzahlige OR-Methoden: Operations Research II a. Übungsblatt 12

Transkript

1 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dr. Eva-Maria Sprengel Ganzzahlige OR-Methoden: Operations Research II a Übungsblatt 12 Aufgabe 37 Auf einem Güterumschlagplatz werden täglich m i Paletten angeliefert, die zu verschiedenen, fest vorgegebenen Standorten (x i,y i ),i = 1,...,n, transportiert werden müssen. Für den Transport der Paletten steht ein Kran zur Verfügung, der aufgrund seiner Konstruktion nur rechtwinklige Änderungen seiner Bewegungsrichtung zulässt. Außerdem kann der Kran immer nur eine Palette versetzen. Es soll nun derjenige Anlieferungsort für die Paletten bestimmt werden, von dem aus die gesamte, vom Kran zurückzulegende Wegstrecke minimal ist. a) Stellen Sie ein entsprechendes Optimierungsmodell auf. b) Überführen Sie das Optimierungsmodell in ein lineares Programmierungsmodell. (4 Punkte) Lösungsvorschlag: a) Die Standorte der Paletten seien (x i,y i ) und der gesuchte Anlieferungsort (x,y). Wenn der Kran den kürzesten Weg von (x,y) zu einem Standort (x i,y i ) fahren soll, so muss er x x i Längeneinheiten parallel zur x-achse zurücklegen und y y i Längeneinheiten parallel zur y-achse. Für jede Palette muss ein Hin- und ein Rückweg beachtet werden, so dass insgesamt w(x,y) = 2 n m i ( x x i + y y i ) i=1 Längeneinheiten zurückzulegen sind. Da keine weiteren Beschränkungen gegeben sind, besteht das Optimierungsproblem aus der Minimierung der Funktion w(x, y): min w(x,y) b) Die Beträge in der Zielfunktion machen dieses unbeschränkte Problem zu einem nichtlinearen Optimierungsproblem. Um also ein lineares Modell zu erhalten, müssen die Beträge anders formuliert werden. Beachte dazu, dass folgende Ungleichungen gelten: x x i x x i und x x i x i x für i = 1,...,n y y i y y i und y y i y i y für i = 1,...,n

2 Führt man also Variable u i und v i ein mit u i = max{x x i,x i x} = x x i und v i = max{y y i,y i y} = y y i für i = 1,...,n so erhält man das neue lineare Modell min w = 2 n i=1 m i(u i + v i ) u.d.n. : u i x x i für i = 1,...,n u i x i x für i = 1,...,n v i y y i für i = 1,...,n v i y i y für i = 1,...,n Das Minimum von w wird angenommen, wenn u i,v i so klein wie möglich sind und stimmt mit dem Minimum des unrestringierten Problems überein. Aufgabe 38 Gegeben sei ein vollständiger, gewichteter Graph G = (K n,c) mit K n = (V,E). Es gelte c(e) Ê e E, die Kantengewichte seien also nicht notwendigerweise nichtnegativ. Gesucht ist eine Partitionierung der Knoten, für die V i V j l i=1 P = {V 1,...,V l } V i V i = 1,...,l, V i = i j, i,j = 1,...,l und = V gilt (die also eine vollständige disjunkte Zerlegung der Knotenmenge darstellt) und die maximiert, wobei c(v i ) := l c(v i ) i=1 (v,w) E,v,w V i c(v,w) sei, also die Summe der Kantengewichte aller Kanten innerhalb von V i. a) Fomulieren Sie ein (binäres) lineares Programm, mit dessen Hilfe sich für einen gegebenen Graphen G die Partitionierung P ermitteln lässt.

3 b) Wie lautet eine Optimallösung, wenn c(e) 0 e E gilt? (Beweis!) c) Wie lautet eine Optimallösung, wenn c(e) 0 e E gilt? (Beweis!) (4 Punkte) Lösungsvorschlag: a) Fomulieren Sie ein (binäres) lineares Programm, mit dessen Hilfe sich für einen gegebenen Graphen G die Partitionierung P ermitteln lässt. Modell: Entscheidungsfrage: Soll Knoten i in der selben Knotenteilmenge wie Knoten j sein? Entscheidungsvariable: { 1, Knoten i ist in der selben Knotenteilmenge wie Knoten j x ij := 0, sonst (i,j) E,i < j Entscheidungsschranken: Es gilt, dass wenn sowohl Knoten i und Knoten j in der selben Knotenteilmenge liegen als auch Knoten j und Knoten k, auch Knoten i in der selben Knotenteilmenge wie Knoten k liegen muss (es gilt Transitivität). Dies lässt sich wie folgt modellieren: x ij + x jk 1 x ik 1 i < j < k n. Wenn x ij = 1 und x jk = 1 gilt, wird hiermit auch forciert, dass x ik = 1 gilt. Da dies jetzt nur für i < j < k gilt, muss man weiterhin noch und x ij + x ik 1 x jk 1 i < j < k n x ik + x jk 1 x ij 1 i < j < k n fordern, also wenn zwei der Aussagen x ij = 1, x jk = 1, x ik = 1 gelten, folgt die dritte. Weiterhin gilt für die x ij die Binaritätsbedingung x ij {0,1} (i,j) E,i < j. Entscheidungsziel: Maximierung der gesamten gewählten Kantengewichte: max c(i,j)x ij

4 b) Wie lautet eine Optimallösung, wenn c(e) 0 e E gilt? (Beweis!) Wegen c(e) 0 und x ij {0,1} gilt c(i,j)x ij c(i, j) für alle zulässigen Lösungen x. Wählt man nun P = {V } (nur eine Teilmenge, die aber ganz V ist, es sind also alle Knoten in derselben Knotenteilmenge), so erhält man das zugehörige x = (1,...,1) und somit c(i,j)x ij = c(i,j). Die Lösung x ist also optimal. c) Wie lautet eine Optimallösung, wenn c(e) 0 e E gilt? (Beweis!) Wegen c(e) 0 und x ij {0,1} gilt c(i,j)x ij 0 für alle zulässigen Lösungen x. Wählt man nun P = {{v 1 },..., {v V }} (alle Teilmengen einelementig, es ist also kein Knoten mit einem anderen in einer gemeinsamen Knotenteilmenge), so erhält man das zugehörige x = (0,...,0) und somit c(i,j)x ij = 0. Die Lösung x ist also optimal. Aufgabe 39 Betrachten Sie bitte folgenden Flugplan der Air Billig-OR: Start Ziel Abflug Ankunft Start Ziel Abflug Ankunft Ber Dort Ber HH Ber M Dort Düss Dort Ber Düss Ber Düss M Düss HH HH M HH Ber M Dort M Düss M Düss Sie können davon ausgehen, dass ausreichend Flugzeuge zu Beginn des Tages am jeweiligen Flughafen vorhanden sind. Um den Kunden auch weiterhin den billigstmöglichen Flugpreis anbieten zu können, werden Sie beauftragt, die Anzahl der Flugzeuge zur

5 Durchführung dieses Planes zu minimieren und ferner und viel wichtiger eine Kostenminimale Zuordnung von Flugcrews zu den einzelnen Flügen auszuarbeiten. Dazu gibt Ihnen die Air Billig-OR folgende Daten: Jede Crew hat regulär einen 8-Stunden-Tag und kostet C pro Tag. (Die Arbeitszeit beginnt mit dem ersten Abflug der Crew am Tag und endet mit der letzten Ankunft am gleichen Tag.) Überstunden kosten zusätzlich 200 C pro Stunde und Crew. Aus Sicherheitsgründen sind pro Crew nur täglich 5 Stunden Flugzeit erlaubt jeder Verstoß kostet eine Konventionalstrafe von 5000 C. Ist eine Crew am Ende des Tages nicht am gleichen Ort, wo sie gestartet ist, so muss die Air Billig-OR für die auswärtige Unterbringung der Crew in einem Hotel weitere 150 C zahlen. Zu guter letzt fordert Ihr Auftraggeber, dass in keinem Flug mehrere Crews mitfliegen. a) Zur Lösung des Problems formulieren Sie den Sachverhalt bitte als Set Partitioning Problem, wie Sie es aus der Vorlesung kennen gelernt haben. (Geben Sie dazu bitte die Entscheidungsfragen, -variablen, Nebenbedingungen und die Zielfunktion an.) b) Wie viele Flugzeuge werden mindestens zur Durchführung des Plans benötigt? (5 Punkte) Lösungsvorschlag: Set Partitioning Probleme haben allgemein folgende Gestalt: maxc x u.d.n. Ax=e x {0,1} wobei a ij {0,1} und e = (1,...,1). Um nun das vorliegende Flugplanungs-Problem hierauf zurückzuführen, ist ein großer Teil an Vorarbeiten zu leisten, da die noch zu definierenden Variablen lediglich Ja-Nein-Entscheidungen modellieren können: Die Zeile i von A gehört zum Flug i des Plans, während jede Spalte j für eine mögliche Zuteilung (Pairing) einer Crew zu einem oder mehreren Flügen steht. Die zu einer Zuteilung j gehörenden Kosten c j sind dann entsprechend aus den Angaben der Aufgabe zu ermitteln. Um genauer sehen zu können, welche Flüge überhaupt von ein und derselben Crew begleitet werden können, zeichnen wir uns die Flüge zunächst in folgende Abbildung. Ber Dort Duss Ä HH M

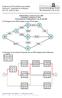
6 Daraus können wir nach Nummerierung der Flüge in Folge ihrer Abflugzeiten den folgenden Graphen entwickeln, dessen Knoten für einzelne Flüge i und j stehen und zwei Knoten genau dann miteinander verbunden werden, wenn sie von einer Crew in der Reihenfolge i vor j durchgeführt werden können Aus diesem Graphen kann man nun alle (34) denkbaren Zuordnungen von Crews zu Flügen ablesen, dabei entspricht jeder Weg in diesem Graphen einem Pairing (es sei hierbei auch ein einzelner Knoten ein Weg). (13: jeden Flug einzeln; 13: zwei aufeinander folgende; 6: drei aufeinander folgende; 2: vier aufeinander folgende Flüge) Zu jeder einzelnen Zuordnung j bestimmen wir die Kosten c j entsprechend der Aufgabenstellung; etwa für die Flugserie 34 Ber Dort Düss M Düss erhalten wir c 34 = = C. Für eine Zuteilung j = {f 1,...,f l } lassen sich die Kosten also durch c j = ½ Dauer(j)> ½ Dauer(j)>8 (Dauer(j) 8) 200+½ Startort(f1 ) Endort(f l ) 150 berechnen Weiter definieren wir a ij = 1, falls Flug i in Zuteilung j vorkommt und a ij = 0 sonst. Mit diesen Koeffizienten können wir das Problem wie folgt definieren: Entscheidungsfrage: Soll Zuteilung j vorgenommen werden? Entscheidungsvariable: { 1 ja, sie soll vorgenommen werden; x j = 0 nein, soll sie nicht Nebenbedingungen: Jeder Flug soll von genau einer Crew (also Zuteilung) bedient werden. 34 j=1 a ij x j = 1 für alle i = 1,...,13 Zielfunktion: Suche einen Kosten-minimalen Flugplan. min c x Um noch die Frage zur minimalen Anzahl an Flugzeugen zu beantworten: Es sind mindestens sechs Maschinen notwendig, um den Betrieb aufrecht zu halten. Zu Beginn des ersten Tages der Gültigkeit des Flugplanes müssen je 1 in Ber und Düss, sowie je 2 in HH und M zur Verfügung stehen. (Am Abend steht die gleiche Anzahl an Fliegern wieder an den einzelnen Flughäfen.)

7 Wie man bereits an diesem kleinen Beispiel sieht, besteht die Schwierigkeit der Lösung eines Set Packing Problems zu großen Teilen in der Aufgabe, sinnvolle Zuordnungen auszuwählen, da in großen Anwendungen nicht alle simultan in die Nebenbedingungsmatrix aufgenommen werden können.