Praktikum Wissenschaftliches Rechnen 3. Aufgabenblatt
|
|
|
- Susanne Kaufer
- vor 8 Jahren
- Abrufe
Transkript
1 Institut für Wissenschaftliches Rechnen Technische Universität Braunschweig Prof. Hermann G. Matthies, Ph. D. Dipl.-inform. Oliver Kayser-Herold Praktikum Wissenschaftliches Rechnen 3. Aufgabenblatt Wir wollen uns jetzt der Implementierung des auf dem letzten Aufgabenblatt beschriebenen Algorithmus zuwenden. Als erstes stellen wir noch einmal die benötigten Problemgrößen und die verwendeten Datenstrukturen zusammen. Weiterhin geben wir noch die Strukturen der Matlab-Funktionen an, die die einzelnen Komponenten des Programms bilden, und behandeln ein erstes Beispiel, das sogenannte Driven-Cavity-Problem. 1 Die Problemgrößen und Datenstrukturen Der auf dem zweiten Aufgabenblatt beschriebene Algorithmus benötigt die folgenden Größen, die zu Beginn in einer Eingabedatei zur Verfügung gestellt werden sollen: Geometriegrößen: imax jmax delx dely Anzahl der inneren Zellen in x-richtung, Anzahl der inneren Zellen in y-richtung, δx, Größe einer Zelle in x-richtung, δy, Größe einer Zelle in y-richtung. Größen für die Zeititeration: T end Endzeit T end, delt δt, Zeitschrittweite. Parameter für die Druckiteration: itermax Maximale Anzahl von Druck-Iterationen pro Zeitschritt, epsi ɛ, Genauigkeitskriterium für die Druckiteration (res < epsi), omg ω, Relaxationsparameter für SOR-Iteration, alpha α, Diskretisationsparameter (vgl. Blatt 2). 1
2 Problemabhängige Größen: U I, V I, P I GX, GY nu Anfangsbelegung der Geschwindigkeiten und des Drucks, g x, g y, äußere Kräfte, z.b. Gravitation, ν, Viskosität (1/Reynoldszahl). Weiter sollen die folgenden Felder (Matrizen) der Dimension (imax + 2) (jmax + 2) als Datenstrukturen verwendet werden: U: Geschwindigkeit in x-richtung, V: Geschwindigkeit in y-richtung, P: Druck, RHS: Rechte Seite f für die Druckiteration, F, G: Hilfsgrößen F und G. In Matlab können Felder wie U, V, P, etc. nur von 1:n+2 und nicht von 0:n+1 indiziert werden. Es muß also eine Indexverschiebung vorgenommen werden. 2 Das Programm und seine Komponenten Das zu erstellende Programm besitzt die folgende Strukturierung: 1. Einlesen der Programmparameter. 2. Initialisierung. 3. T := Solange T T end: (a) Berechne Randwerte von U und V. (b) Berechne F, G und RHS. (c) Löse das LGS für P mit dem SOR-Verfahren. (d) Berechne U und V. (e) T := T + delt. 5. Graphische Ausgabe der Ergebnisse (Visualisierung). Die einzelnen Komponenten des Programms sollen dabei als Matlab-Routinen implementiert werden: 2
3 progpar(): Die Größen imax, jmax, delx, dely, delt, T end, itermax, epsi, omg, nu, GX, GY, U I, V I, P I werden in diesem Skript gesetzt. alpha, [U,V,P] = initgitter(imax,jmax,u I,V I,P I): Die Felder U, V, P werden auf dem ganzen Gebiet mit den konstanten Werten U I, V I und P I als Anfangswerte vorbelegt. [U,V] = randwerte(u,v,imax,jmax): Die Randwerte für die Felder U und V werden gemäß den Formeln von Abschnitt 4.4 auf Blatt 2 gesetzt. [F,G] = berechne FG(U,V,imax,jmax,delt,delx,dely,GX,GY,alpha,nu): Berechnung von F und G, dabei müssen am Rand die Formeln aus Abschnitt 4.4 berücksichtigt werden. RHS = berechne RHS(F,G,imax,jmax,delt,delx,dely): Berechnung der rechten Seite der Druckgleichung. [P,it,res] = SOR(P,RHS,U,V,GX,GY,imax,jmax,delx,dely,epsi,itermax,omg,nu): SOR-Iteration für die Druck-(Poisson-)Gleichung. Die Iteration wird abgebrochen, wenn das Residuum res die Toleranzgrenze epsi unterschreitet oder die maximale Iterationszahl itermax erreicht ist. Nach dem Abbruch wird die Anzahl it der benötigten Iterationen, das Residuum res und die neue Druckmatrix P zurückgegeben. berechne UV(F,G,P,imax,jmax,delt,delx,dely): Die neuen Geschwindigkeiten werden berechnet. visual(u,v,p): Zur Visualisierung der berechneten Werte sollen mit Hilfe des Matlabbefehls mesh die Geschwindigkeitskomponenten U, V und die Druckmatrix P aus dem letzten Zeitschritt dargestellt werden. Dabei ist darauf zu achten, daß die Randwerte künstlich gesetzt wurden und daher das Ergebnis verfälschen. Deshalb sollten diese bei der Visualisierung weggelassen werden. Weiter kann man sich mit dem Befehl quiver das Geschwindigkeitsfeld der Strömung anschauen. Die einzelnen Bilder sollten dabei durch den Befehl pause getrennt werden. Im Hauptprogramm inkompvis soll schließlich der oben angegebene Algorithmus umgesetzt werden. Mit dem Programm weiter soll eine angefangene Simulation bis zu einem neuen Zeitpunkt T end fortgesetzt werden. Für das SOR-Verfahren ergeben sich zwei Möglichkeiten, die Sie auch beide programmieren sollen: 3
4 Als erstes können Sie die SOR-Iteration gitterorientiert durchführen, d.h., Sie gehen punktweise durch das Gitter und berechnen an jedem Gitterpunkt den neuen Druckwert. Dieses können Sie durch mehrere for-schleifen realisieren. Dabei werden in jeder Iteration zunächst die Randwerte für P neu gesetzt, um die Stabilität dieser Variante des Verfahrens zu gewährleisten, d.h. p it+1 0,j = p it 1,j, p it+1 imax+1,j = p it imax,j p it+1 i,0 = p it i,1, p it+1 i,jmax+1 = p it i,jmax für j = 1,..., jmax, für i = 1,..., imax. Die zweite (in Matlab schnellere) Variante besteht darin, ein Gleichungssystem Ax = b aufzustellen, wobei der Vektor x die Komponenten der Druckmatrix P und der Vektor b die rechte Seite der Druck-Poisson-Gleichung und die entsprechenden Druckrandwerte enthalten. Danach können Sie das auf dem ersten Blatt implementierte SOR-Verfahren oder auch das PCG-Verfahren zur Lösung des Gleichungssystems verwenden. 3 Das erste Beispiel: Driven Cavity Als erstes Beispiel soll ein typisches Modellproblem der numerischen Stömungsmechanik, das sogenannte Driven-Cavity-Problem, simuliert werden. Es handelt sich dabei um einen mit einer Flüssigkeit gefüllten Topf, über den ein Band mit konstanter Geschwindigkeit gezogen wird. Dabei werden an allen vier Rändern Haftbedingungen verwendet. Am oberen Rand wird hingegen die Geschwindigkeit in x-richtung u nicht auf 0, sondern auf 1 gesetzt, um das gezogene Band zu simulieren. Im Programm wird das realisiert, indem die oberen Randwerte mittels U(2:imax+1,jmax+2) = 2 - U(2:imax+1,jmax+1) gesetzt werden. Als weitere Parameter, die aus einer Eingabedatei eingelesen werden, sollen verwendet werden: imax = 16 jmax = 16 delx = 0.2 dely = 0.2 delt = 0.02 T end = 0.2 epsi = 0.01 omg = 1.7 alpha = 0.12 itermax = 150 GX = 0 GY = 0 nu = 0.4 U I = 0 V I = 0 P I = 0 4
5 4 Weitere Aufgaben Aufgabe 1 Verwenden Sie zur Lösung des linearen Glecihungssystems Ax = b auch das Verfahren der konjugierten Gradienten. Stellen Sie eine Statistik für die Anzahl der Iterationen und die benötigte Rechenzeit pro Zeitschritt auf und geben Sie diese in geeigneter graphischer Form ab. Aufgabe 2 In Matlab können Sie mit dem Befehl movie kleine Filme erstellen, mit dem Sie die Strömungskomponenten zeitlich darstellen können. Wenn man einen Film erzeugen will, der die zeitliche Entwicklung der Strömung zeigt, so muß man die Visualisierung mit in die Zeitschleife hineinnehmen und in jedem Zeitschritt die Bildersequenzen abspeichern. Außerdem muß man die Achsen geeignet skalieren, um keine Sprünge zwischen den einzelnen Bildern zu haben. Aufgabe 3 Um den Einfluß der Parameter näher kennenzulernen, verändern Sie einige der gegebenen Parameter, und spielen Sie etwas mit dem Beispiel! Abgabe der Aufgaben:
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter
 Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter Aufgabe 3: Konto Um Geldbeträge korrekt zu verwalten, sind zwecks Vermeidung von Rundungsfehlern entweder alle Beträge in Cents umzuwandeln und
Informatik 2 Labor 2 Programmieren in MATLAB Georg Richter Aufgabe 3: Konto Um Geldbeträge korrekt zu verwalten, sind zwecks Vermeidung von Rundungsfehlern entweder alle Beträge in Cents umzuwandeln und
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Beispiel(unten ist der Spielfeldrand):
 Anleitung Side by Side ist ein Puzzle mit einfachen Regeln, das in einem 6x6 (oder größerem) Gitter gespielt wird. Ziel des Spieles ist es, die leeren Kästchen mit den Zahlen 1, 2, 3, 4 oder einem X zu
Anleitung Side by Side ist ein Puzzle mit einfachen Regeln, das in einem 6x6 (oder größerem) Gitter gespielt wird. Ziel des Spieles ist es, die leeren Kästchen mit den Zahlen 1, 2, 3, 4 oder einem X zu
Schritt für Schritt zur Krankenstandsstatistik
 Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Schritt für Schritt zur Krankenstandsstatistik Eine Anleitung zur Nutzung der Excel-Tabellen zur Erhebung des Krankenstands. Entwickelt durch: Kooperationsprojekt Arbeitsschutz in der ambulanten Pflege
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
impact ordering Info Produktkonfigurator
 impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
impact ordering Info Copyright Copyright 2013 veenion GmbH Alle Rechte vorbehalten. Kein Teil der Dokumentation darf in irgendeiner Form ohne schriftliche Genehmigung der veenion GmbH reproduziert, verändert
Kurzanleitung OOVS. Reseller Interface. Allgemein
 Kurzanleitung OOVS Reseller Interface Allgemein Durch die Einführung des neuen Interfaces hat sich für Reseller von Syswebcom etwas geändert. Die Struktur der Kundenverwaltung ist einprägsamer, wenn man
Kurzanleitung OOVS Reseller Interface Allgemein Durch die Einführung des neuen Interfaces hat sich für Reseller von Syswebcom etwas geändert. Die Struktur der Kundenverwaltung ist einprägsamer, wenn man
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
Dossier: Rechnungen und Lieferscheine in Word
 www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
www.sekretaerinnen-service.de Dossier: Rechnungen und Lieferscheine in Word Es muss nicht immer Excel sein Wenn Sie eine Vorlage für eine Rechnung oder einen Lieferschein erstellen möchten, brauchen Sie
UNIGLAS - Handbuch zum Forum
 UNIGLAS - Handbuch zum Forum Stand: November 2014 Das Forum im der UNIGLAS im Intranet der Website soll dem Informationsaustausch dienen und gleichzeitig Plattform sein, um gemeinsam verschiedene Themen
UNIGLAS - Handbuch zum Forum Stand: November 2014 Das Forum im der UNIGLAS im Intranet der Website soll dem Informationsaustausch dienen und gleichzeitig Plattform sein, um gemeinsam verschiedene Themen
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt!
 Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt! Sehr geehrte(r) Geschäftspartner(in), Um Ihre Transaktionen schneller durchzuführen, bieten wir
Wollen Sie einen mühelosen Direkteinstieg zum Online Shop der ÖAG? Sie sind nur einen Klick davon entfernt! Sehr geehrte(r) Geschäftspartner(in), Um Ihre Transaktionen schneller durchzuführen, bieten wir
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik
 Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
Projekt 2HEA 2005/06 Formelzettel Elektrotechnik Teilübung: Kondensator im Wechselspannunskreis Gruppenteilnehmer: Jakic, Topka Abgabedatum: 24.02.2006 Jakic, Topka Inhaltsverzeichnis 2HEA INHALTSVERZEICHNIS
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Computeria Rorschach Mit Excel Diagramme erstellen
 Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
Mit Excel Diagramme erstellen 25.12.2010 Roland Liebing Mit Excel Diagramme erstellen Diagramme können Zahlenwerte veranschaulichen, das heisst, mit Hilfe eines Diagramms können Zahlen besser miteinander
Noten ausrechnen mit Excel/Tabellenkalkulation. 1) Individuellen Notenschlüssel/Punkteschlüssel erstellen
 Noten ausrechnen mit Excel/Tabellenkalkulation online unter: www.lehrerfreund.de/in/schule/1s/notenschluessel-excel Dies ist eine Einführung in die Funktionen von Excel, die Sie brauchen, um Noten und
Noten ausrechnen mit Excel/Tabellenkalkulation online unter: www.lehrerfreund.de/in/schule/1s/notenschluessel-excel Dies ist eine Einführung in die Funktionen von Excel, die Sie brauchen, um Noten und
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen der Barcode-Etiketten:
 Erstellen der Barcode-Etiketten: 1.) Zuerst muss die Schriftart Code-39-Logitogo installiert werden! Das ist eine einmalige Sache und muss nicht zu jeder Börse gemacht werden! Dazu speichert man zunächst
Erstellen der Barcode-Etiketten: 1.) Zuerst muss die Schriftart Code-39-Logitogo installiert werden! Das ist eine einmalige Sache und muss nicht zu jeder Börse gemacht werden! Dazu speichert man zunächst
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Excel Pivot-Tabellen 2010 effektiv
 7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
Ihre Interessentendatensätze bei inobroker. 1. Interessentendatensätze
 Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
Ihre Interessentendatensätze bei inobroker Wenn Sie oder Ihre Kunden die Prozesse von inobroker nutzen, werden Interessentendatensätze erzeugt. Diese können Sie direkt über inobroker bearbeiten oder mit
Jede Zahl muss dabei einzeln umgerechnet werden. Beginnen wir also ganz am Anfang mit der Zahl,192.
 Binäres und dezimales Zahlensystem Ziel In diesem ersten Schritt geht es darum, die grundlegende Umrechnung aus dem Dezimalsystem in das Binärsystem zu verstehen. Zusätzlich wird auch die andere Richtung,
Binäres und dezimales Zahlensystem Ziel In diesem ersten Schritt geht es darum, die grundlegende Umrechnung aus dem Dezimalsystem in das Binärsystem zu verstehen. Zusätzlich wird auch die andere Richtung,
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
BIA-Wissensreihe Teil 4. Mind Mapping Methode. Bildungsakademie Sigmaringen
 BIA-Wissensreihe Teil 4 Mind Mapping Methode Bildungsakademie Sigmaringen Inhalt Warum Mind Mapping? Für wen sind Mind Maps sinnvoll? Wie erstellt man Mind Maps? Mind Mapping Software 3 4 5 7 2 1. Warum
BIA-Wissensreihe Teil 4 Mind Mapping Methode Bildungsakademie Sigmaringen Inhalt Warum Mind Mapping? Für wen sind Mind Maps sinnvoll? Wie erstellt man Mind Maps? Mind Mapping Software 3 4 5 7 2 1. Warum
Gitterherstellung und Polarisation
 Versuch 1: Gitterherstellung und Polarisation Bei diesem Versuch wollen wir untersuchen wie man durch Überlagerung von zwei ebenen Wellen Gttterstrukturen erzeugen kann. Im zweiten Teil wird die Sichtbarkeit
Versuch 1: Gitterherstellung und Polarisation Bei diesem Versuch wollen wir untersuchen wie man durch Überlagerung von zwei ebenen Wellen Gttterstrukturen erzeugen kann. Im zweiten Teil wird die Sichtbarkeit
Dow Jones am 13.06.08 im 1-min Chat
 Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Dow Jones am 13.06.08 im 1-min Chat Dieser Ausschnitt ist eine Formation: Wechselstäbe am unteren Bollinger Band mit Punkt d über dem 20-er GD nach 3 tieferen Hoch s. Wenn ich einen Ausbruch aus Wechselstäben
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung. Autor: Dr. Heinz Peter Reidmacher
 Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
Planen mit mathematischen Modellen 00844: Computergestützte Optimierung Leseprobe Autor: Dr. Heinz Peter Reidmacher 11 - Portefeuilleanalyse 61 11 Portefeuilleanalyse 11.1 Das Markowitz Modell Die Portefeuilleanalyse
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHISCHE UIVERSITÄT MÜCHE Zentrum Mathematik PRF. R.R. JÜRGE RICHTER-GEBERT, VAESSA KRUMMECK, MICHAEL PRÄHFER Höhere Mathematik für Informatiker I (Wintersemester 003/004) Aufgabenblatt 1 (4. ktober 003)
TECHISCHE UIVERSITÄT MÜCHE Zentrum Mathematik PRF. R.R. JÜRGE RICHTER-GEBERT, VAESSA KRUMMECK, MICHAEL PRÄHFER Höhere Mathematik für Informatiker I (Wintersemester 003/004) Aufgabenblatt 1 (4. ktober 003)
Klassenarbeit zu linearen Gleichungssystemen
 Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Klassenarbeit zu linearen Gleichungssystemen Aufgabe : Bestimme die Lösungsmenge der Gleichungssysteme mit Hilfe des Additionsverfahrens: x + 4y = 8 5x y = x y = x y = Aufgabe : Bestimme die Lösungsmenge
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage
 Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage Inhaltsverzeichnis 1. Anmeldung... 2 1.1 Startbildschirm... 3 2. Die PDF-Dateien hochladen... 4 2.1 Neue PDF-Datei erstellen... 5 3. Obelix-Datei
Handbuch zur Anlage von Turnieren auf der NÖEV-Homepage Inhaltsverzeichnis 1. Anmeldung... 2 1.1 Startbildschirm... 3 2. Die PDF-Dateien hochladen... 4 2.1 Neue PDF-Datei erstellen... 5 3. Obelix-Datei
LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME)
 LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME) Aufgabe 1: Tanzkurs ( * ) Zu einem Tanzkurs erscheinen dreimal so viele Mädchen wie Jungen. Nachdem 15 Mädchen gegangen sind, sind noch doppelt so viele
LANGFRISTIGE HAUSAUFGABE (LINEARE GLEICHUNGSSYSTEME) Aufgabe 1: Tanzkurs ( * ) Zu einem Tanzkurs erscheinen dreimal so viele Mädchen wie Jungen. Nachdem 15 Mädchen gegangen sind, sind noch doppelt so viele
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
PVL 3 - Roulette. (5 Punkte) Abgabe bis 20.12.2015
 PVL 3 - Roulette (5 Punkte) Abgabe bis 20.12.2015 Beim Roulette wird in jeder Runde eine von 37 Zahlen (0-36) ausgespielt. Dabei können Geldbeträge direkt auf eine Zahl zwischen 1 und 36 gesetzt werden
PVL 3 - Roulette (5 Punkte) Abgabe bis 20.12.2015 Beim Roulette wird in jeder Runde eine von 37 Zahlen (0-36) ausgespielt. Dabei können Geldbeträge direkt auf eine Zahl zwischen 1 und 36 gesetzt werden
Kurzanleitung. MEYTON Aufbau einer Internetverbindung. 1 Von 11
 Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
Kurzanleitung MEYTON Aufbau einer Internetverbindung 1 Von 11 Inhaltsverzeichnis Installation eines Internetzugangs...3 Ist mein Router bereits im MEYTON Netzwerk?...3 Start des YAST Programms...4 Auswahl
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS. Herbstsemester 2015. gehalten von Harald Baum
 Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
Fachschaft Mathematik und Informatik (FIM) LA I VORKURS Herbstsemester 2015 gehalten von Harald Baum 2. September 2015 Inhaltsverzeichnis 1. Stichpunkte zur Linearen Algebra I 2. Körper 3. Vektorräume
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
mysql - Clients MySQL - Abfragen eine serverbasierenden Datenbank
 mysql - Clients MySQL - Abfragen eine serverbasierenden Datenbank In den ersten beiden Abschnitten (rbanken1.pdf und rbanken2.pdf) haben wir uns mit am Ende mysql beschäftigt und kennengelernt, wie man
mysql - Clients MySQL - Abfragen eine serverbasierenden Datenbank In den ersten beiden Abschnitten (rbanken1.pdf und rbanken2.pdf) haben wir uns mit am Ende mysql beschäftigt und kennengelernt, wie man
Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme
 Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
Übung Lineare Algebra und Lösung linearer zeitinvarianter Differentialgleichungssysteme Diese Übung beschäftigt sich mit Grundbegriffen der linearen Algebra. Im Speziellen werden lineare Abbildungen, sowie
W-Rechnung und Statistik für Ingenieure Übung 11
 W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER
 Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Abamsoft Finos im Zusammenspiel mit shop to date von DATA BECKER Abamsoft Finos in Verbindung mit der Webshopanbindung wurde speziell auf die Shop-Software shop to date von DATA BECKER abgestimmt. Mit
Registrierung als Android Market Developer
 Registrierung als Android Market Developer Bitte befolgen Sie für die Registrierung als Android Market Developer folgende Schritte: Öffnen Sie die Website http://market.android.com/publish/. Zur Registrierung
Registrierung als Android Market Developer Bitte befolgen Sie für die Registrierung als Android Market Developer folgende Schritte: Öffnen Sie die Website http://market.android.com/publish/. Zur Registrierung
Professionelle Seminare im Bereich MS-Office
 Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Gegenüber PowerPoint 2003 hat sich in PowerPoint 2007 gerade im Bereich der Master einiges geändert. Auf Handzettelmaster und Notizenmaster gehe ich in diesen Ausführungen nicht ein, die sind recht einfach
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
1. LINEARE FUNKTIONEN IN DER WIRTSCHAFT (KOSTEN, ERLÖS, GEWINN)
 1. LINEARE FUNKTIONEN IN DER WIRTSCHAFT (KOSTEN, ERLÖS, GEWINN) D A S S O L L T E N N A C H E U R E M R E F E R A T A L L E K Ö N N E N : Kostenfunktion, Erlösfunktion und Gewinnfunktion aufstellen, graphisch
1. LINEARE FUNKTIONEN IN DER WIRTSCHAFT (KOSTEN, ERLÖS, GEWINN) D A S S O L L T E N N A C H E U R E M R E F E R A T A L L E K Ö N N E N : Kostenfunktion, Erlösfunktion und Gewinnfunktion aufstellen, graphisch
ALEMÃO. Text 1. Lernen, lernen, lernen
 ALEMÃO Text 1 Lernen, lernen, lernen Der Mai ist für viele deutsche Jugendliche keine schöne Zeit. Denn dann müssen sie in vielen Bundesländern die Abiturprüfungen schreiben. Das heiβt: lernen, lernen,
ALEMÃO Text 1 Lernen, lernen, lernen Der Mai ist für viele deutsche Jugendliche keine schöne Zeit. Denn dann müssen sie in vielen Bundesländern die Abiturprüfungen schreiben. Das heiβt: lernen, lernen,
Step by Step Remotedesktopfreigabe unter Windows Server 2003. von Christian Bartl
 Step by Step Remotedesktopfreigabe unter Windows Server 2003 von Remotedesktopfreigabe unter Windows Server 2003 Um die Remotedesktopfreigabe zu nutzen muss diese am Server aktiviert werden. Außerdem ist
Step by Step Remotedesktopfreigabe unter Windows Server 2003 von Remotedesktopfreigabe unter Windows Server 2003 Um die Remotedesktopfreigabe zu nutzen muss diese am Server aktiviert werden. Außerdem ist
Die Beschreibung bezieht sich auf die Version Dreamweaver 4.0. In der Version MX ist die Sitedefinition leicht geändert worden.
 In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
In einer Website haben Seiten oft das gleiche Layout. Speziell beim Einsatz von Tabellen, in denen die Navigation auf der linken oder rechten Seite, oben oder unten eingesetzt wird. Diese Anteile der Website
EINFACHES HAUSHALT- KASSABUCH
 EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
EINFACHES HAUSHALT- KASSABUCH Arbeiten mit Excel Wir erstellen ein einfaches Kassabuch zur Führung einer Haushalts- oder Portokasse Roland Liebing, im November 2012 Eine einfache Haushalt-Buchhaltung (Kassabuch)
Wir machen neue Politik für Baden-Württemberg
 Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Wir machen neue Politik für Baden-Württemberg Am 27. März 2011 haben die Menschen in Baden-Württemberg gewählt. Sie wollten eine andere Politik als vorher. Die Menschen haben die GRÜNEN und die SPD in
Kurzanweisung für Google Analytics
 Kurzanweisung für Google Analytics 1. Neues Profil für eine zu trackende Webseite erstellen Nach dem Anmelden klicken Sie rechts oben auf den Button Verwaltung : Daraufhin erscheint die Kontoliste. Klicken
Kurzanweisung für Google Analytics 1. Neues Profil für eine zu trackende Webseite erstellen Nach dem Anmelden klicken Sie rechts oben auf den Button Verwaltung : Daraufhin erscheint die Kontoliste. Klicken
1) Farbsteuergerät in der Nikobus-Software unter Modul zufügen hinzufügen.
 Programmierung des Farbsteuergeräts 340-00112 für Nikobus Diese Bedienungsanleitung gilt auch für die Nikobus-Produkte 340-00111 und 340-00113. Achtung: einige der aufgeführten Betriebsarten sind nur auf
Programmierung des Farbsteuergeräts 340-00112 für Nikobus Diese Bedienungsanleitung gilt auch für die Nikobus-Produkte 340-00111 und 340-00113. Achtung: einige der aufgeführten Betriebsarten sind nur auf
Java-Programmierung mit NetBeans
 Java-Programmierung mit NetBeans Steuerstrukturen Dr. Henry Herper Otto-von-Guericke-Universität Magdeburg - WS 2012/13 Steuerstrukturen Steuerstrukturen Verzweigungen Alternativen abweisende nichtabweisende
Java-Programmierung mit NetBeans Steuerstrukturen Dr. Henry Herper Otto-von-Guericke-Universität Magdeburg - WS 2012/13 Steuerstrukturen Steuerstrukturen Verzweigungen Alternativen abweisende nichtabweisende
Tutorial: Entlohnungsberechnung erstellen mit LibreOffice Calc 3.5
 Tutorial: Entlohnungsberechnung erstellen mit LibreOffice Calc 3.5 In diesem Tutorial will ich Ihnen zeigen, wie man mit LibreOffice Calc 3.5 eine einfache Entlohnungsberechnung erstellt, wobei eine automatische
Tutorial: Entlohnungsberechnung erstellen mit LibreOffice Calc 3.5 In diesem Tutorial will ich Ihnen zeigen, wie man mit LibreOffice Calc 3.5 eine einfache Entlohnungsberechnung erstellt, wobei eine automatische
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT?
 ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT? Wenn Sie das Projekt DIE ANFÄNGERIN unterstützen wollen, können Sie das mit oder ohne Registrierung auf www.startnext.com tun. Sie können also als Gast unterstützen
ANLEITUNG - WIE UNTERSTÜTZE ICH AUF STARTNEXT? Wenn Sie das Projekt DIE ANFÄNGERIN unterstützen wollen, können Sie das mit oder ohne Registrierung auf www.startnext.com tun. Sie können also als Gast unterstützen
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Inhalt. 1 Einleitung AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER
 AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
Ist Excel das richtige Tool für FMEA? Steve Murphy, Marc Schaeffers
 Ist Excel das richtige Tool für FMEA? Steve Murphy, Marc Schaeffers Ist Excel das richtige Tool für FMEA? Einleitung Wenn in einem Unternehmen FMEA eingeführt wird, fangen die meisten sofort damit an,
Ist Excel das richtige Tool für FMEA? Steve Murphy, Marc Schaeffers Ist Excel das richtige Tool für FMEA? Einleitung Wenn in einem Unternehmen FMEA eingeführt wird, fangen die meisten sofort damit an,
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Erfahrungen mit Hartz IV- Empfängern
 Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Erfahrungen mit Hartz IV- Empfängern Ausgewählte Ergebnisse einer Befragung von Unternehmen aus den Branchen Gastronomie, Pflege und Handwerk Pressegespräch der Bundesagentur für Arbeit am 12. November
Einfache Varianzanalyse für abhängige
 Einfache Varianzanalyse für abhängige Stichproben Wie beim t-test gibt es auch bei der VA eine Alternative für abhängige Stichproben. Anmerkung: Was man unter abhängigen Stichproben versteht und wie diese
Einfache Varianzanalyse für abhängige Stichproben Wie beim t-test gibt es auch bei der VA eine Alternative für abhängige Stichproben. Anmerkung: Was man unter abhängigen Stichproben versteht und wie diese
Ebenenmasken Grundlagen
 Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
Ebenenmasken Grundlagen Was sind Ebenmasken? Was machen sie? Wofür braucht man sie? Wie funktionieren sie? Ebenmasken sind eines der sinnvollsten Tools in anspruchvollen EBV Programmen (EBV = elektronische
Anleitung Redmine. Inhalt. Seite 1 von 11. Anleitung Redmine
 Seite 1 von 11 Anleitung Inhalt Inhalt... 1 1. Installation... 2 2. Setup... 2 2.1 Login... 2 2.2 Benutzer erstellen... 2 2.3 Projekt erstellen... 4 2.4 SVN/Git Integration... 6 2.4.1 Konfiguration für
Seite 1 von 11 Anleitung Inhalt Inhalt... 1 1. Installation... 2 2. Setup... 2 2.1 Login... 2 2.2 Benutzer erstellen... 2 2.3 Projekt erstellen... 4 2.4 SVN/Git Integration... 6 2.4.1 Konfiguration für
Mind Mapping am PC. für Präsentationen, Vorträge, Selbstmanagement. von Isolde Kommer, Helmut Reinke. 1. Auflage. Hanser München 1999
 Mind Mapping am PC für Präsentationen, Vorträge, Selbstmanagement von Isolde Kommer, Helmut Reinke 1. Auflage Hanser München 1999 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 21222 0 schnell
Mind Mapping am PC für Präsentationen, Vorträge, Selbstmanagement von Isolde Kommer, Helmut Reinke 1. Auflage Hanser München 1999 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 21222 0 schnell
Empfehlungen zur Nutzung der CD zum Buch: Klee & Wiemann: Beweglichkeit und Dehnfähigkeit. Schorndorf: Hofmann, 2005. 1
 Empfehlungen zur Nutzung der CD zum Buch: Klee & Wiemann: Beweglichkeit und Dehnfähigkeit. Schorndorf: Hofmann, 2005. 1 Starten der CD Nach dem Einlegen der CD in Ihr CD-Laufwerk müsste die CD von selbst
Empfehlungen zur Nutzung der CD zum Buch: Klee & Wiemann: Beweglichkeit und Dehnfähigkeit. Schorndorf: Hofmann, 2005. 1 Starten der CD Nach dem Einlegen der CD in Ihr CD-Laufwerk müsste die CD von selbst
e-books aus der EBL-Datenbank
 e-books aus der EBL-Datenbank In dieser Anleitung wird erklärt, wie Sie ein ebook aus der EBL-Datenbank ausleihen und mit dem Programm Adobe Digital Edition öffnen. Folgende Vorraussetzungen sind eventuell
e-books aus der EBL-Datenbank In dieser Anleitung wird erklärt, wie Sie ein ebook aus der EBL-Datenbank ausleihen und mit dem Programm Adobe Digital Edition öffnen. Folgende Vorraussetzungen sind eventuell
Lösung. Prüfungsteil 1: Aufgabe 1
 Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Zentrale Prüfung 01 Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacher. Sie ist keine offizielle Lösung des Ministeriums für Schule und Weiterbildung des Landes. Prüfungsteil 1: Aufgabe 1 a)
Plotten von Linien ( nach Jack Bresenham, 1962 )
 Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Bedienungsanleitung für den Online-Shop
 Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Hier sind die Produktgruppen zu finden. Zur Produktgruppe gibt es eine Besonderheit: - Seite 1 von 18 - Zuerst wählen Sie einen Drucker-Hersteller aus. Dann wählen Sie das entsprechende Drucker- Modell
Installation eines BM-33k6/ISDN pro USB an einem Windows XP-Rechner
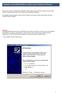 Installation eines BM-33k6/ISDN pro USB an einem Windows XP-Rechner Falls Sie den Treiber für das Modem BM-33k6/ISDN pro USB updaten wollen, sollten Sie zunächst den alten Treiber entfernen. Danach können
Installation eines BM-33k6/ISDN pro USB an einem Windows XP-Rechner Falls Sie den Treiber für das Modem BM-33k6/ISDN pro USB updaten wollen, sollten Sie zunächst den alten Treiber entfernen. Danach können
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Mit Excel Strickvorlagen erstellen (GRUNDKURS)
 Mit Excel Strickvorlagen erstellen (GRUNDKURS) Themen: Einstellen der Spaltenbreite Einfärben von Flächen Umranden oder Unterteilen von Flächen Strickschriften erstellen Zellen formatieren So geht s: Einstellen
Mit Excel Strickvorlagen erstellen (GRUNDKURS) Themen: Einstellen der Spaltenbreite Einfärben von Flächen Umranden oder Unterteilen von Flächen Strickschriften erstellen Zellen formatieren So geht s: Einstellen
Andreas Rühl. Investmentfonds. verstehen und richtig nutzen. Strategien für die optimale Vermögensstruktur. FinanzBuch Verlag
 Andreas Rühl Investmentfonds verstehen und richtig nutzen Strategien für die optimale Vermögensstruktur FinanzBuch Verlag 1. Kapitel Wollen Sie Millionär werden? Kennen Sie die Formel zur ersten Million?
Andreas Rühl Investmentfonds verstehen und richtig nutzen Strategien für die optimale Vermögensstruktur FinanzBuch Verlag 1. Kapitel Wollen Sie Millionär werden? Kennen Sie die Formel zur ersten Million?
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Leitfaden #1a. "zanox Publisher-Statistik" (next generation)
 Leitfaden #1a "zanox Publisher-Statistik" (next generation) Thema: Sortieren von Leads und Sales nach dem Bearbeitungsdatum (inklusive Abschnitt "Filterung nach Transaktionsstatus") 1/8 Leitfaden "Sortieren
Leitfaden #1a "zanox Publisher-Statistik" (next generation) Thema: Sortieren von Leads und Sales nach dem Bearbeitungsdatum (inklusive Abschnitt "Filterung nach Transaktionsstatus") 1/8 Leitfaden "Sortieren
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754. Berechnung von Gleitkommazahlen aus Dezimalzahlen. HSLU T&A Informatik HS10
 Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
