Ausblick. nicht alle bekannten Geometrien thematisiert.
|
|
|
- Manuela Linden
- vor 5 Jahren
- Abrufe
Transkript
1 Ausblick Kennen wir uns nach der Lektüre dieses Buches mit Geometrie aus? Bei der Beantwortung dieser rhetorisch gemeinten Frage sollten wir bescheiden vorgehen, denn wir haben uns im Wesentlichen auf die Beschäftigung mit den Eigenschaften der elementarsten geometrischen Objekte Punkt, Gerade und Ebene beschränkt, auf einen vollständigen synthetischen Aufbau der Geometrien von einem Axiomensystem aus verzichtet, nicht alle bekannten Geometrien thematisiert. Auf der Haben-Seite können wir allerdings feststellen, dass wir für viele weiterführende Betrachtungen sehr gut vorbereitet sind, da wir unsere Vorkenntnisse aus dem Geometrieunterricht der Schule wesentlich ausgebaut haben. Wir sind auf einem Stand, dass wir uns mit den Kegelschnitten sowie allgemeinen Kurven und Flächen weitere geometrische Objekte leicht erarbeiten können (mit den Hyperbeln haben wir den kompliziertesten Vertreter der Kegelschnitte bereits thematisiert, auch die von uns durchgeführte Hauptachsentransformation unterstützt diese Erweiterung), unsere Erfahrungen mit Axiomensystemen in das Verständnis der synthetischen Geometrie einbringen können, insbesondere sind wir sensibilisiert, dass scheinbar kleine Änderungen der Axiome zu großen Auswirkungen führen können (die von uns vorgenommene Typisierung der Sätze von Pappos und Desargues sollte sich als hilfreich erweisen, ebenso die von uns bewusst ausführlich vorgestellten geometrischen Beweise von unterschiedlichem Typ ), weitere Geometrien erschließen können, indem wir von deren grundlegenden Ideen ausgehen (diese Erweiterung haben wir durch die Erkundung unterschiedlicher Modelle für verschiedene Geometrien vorbereitet, auch die Einbeziehung von Determinanten und komplexen Koordinaten bei der Einführung von Maßen in der projektiven Geometrie unterstützt die Einarbeitung in weitere Geometrien). Springer-Verlag GmbH Deutschland 2017 J. Wagner, Einblicke in die euklidische und nichteuklidische Geometrie, DOI /
2 272 Ausblick Als besonders bedeutsam bewerten wir die durch das Kennenlernen nichteuklidischer Geometrien angeregte Weiterentwicklung unserer Raumvorstellung, die unser Denken öffnet für ein besseres Verständnis der uns umgebenden Welt im Großen und im Kleinen. Neben dieser weltanschaulichen Dimension besitzen einige der von uns angesprochenen Themen eine unmittelbare Anwendung, z. B. sind die von uns thematisierten Koordinatentransformationen und Kompositionen von Abbildungen bedeutsam für die Grafikprogrammierung und Robotik. Wir haben aus Platzgründen auf einen streng synthetischen Aufbau und aus inhaltlichen Gründen auf die algebraische Durchdringung der Geometrie verzichtet und diese Betrachtungsweisen in die Ausbildung an der Hochschule verlagert. Die Anwendung algebraischer Methoden in der Geometrie erweist sich insbesondere bei Beweisführungen als sehr effektiv und fruchtbar. Allerdings besteht die Gefahr, dass der falsche Eindruck erweckt werden könnte, die Geometrie wäre ein Anwendungsfeld der Algebra. Die Geometrie hat in ihrer mehrere Jahrtausende umfassenden Geschichte viele Sternstunden erlebt, von denen wir stellvertretend folgende nennen: Axiomatisierung: Euklid von Alexandria axiomatisierte in seinem Werk Elemente ca. 325 v. Chr. die Planimetrie und schuf damit nicht nur die Grundlage der synthetischen Geometrie, sondern eine zentrale Säule der Methodologie der Mathematik. Verknüpfung von Geometrie und Algebra: René Descartes verknüpfte in seinem 1637 erschienenen Werk Discours de la méthode Geometrie und Algebra miteinander und legte damit den Grundstein für die Entwicklung der analytischen Geometrie, in der geometrische Probleme durch Berechnungen gelöst werden. Verknüpfung von Geometrie und Analysis: Die Anwendung von Methoden der Analysis in der Geometrie führte zur Differenzialgeometrie. Als besonders bedeutsam erwies sich die Entdeckung des Theorema egregium durch Carl Friedrich Gauß im Jahr Dieser Satz besagt, dass die Krümmung einer Fläche allein aus Längen- und Winkelmessungen auf dieser Fläche bestimmt werden kann. Theorie der Mannigfaltigkeiten: Ausgehend von der klassischen Differenzialgeometrie mit der Kurven- und Flächentheorie (auf Grundlage der Arbeiten von Gauß) sowie der Topologie stellte Bernhard Riemann in seinem Habilitationsvortrag 1854 eine n-dimensionale Differenzialgeometrie mit den zentralen Begriffen Krümmung und lokale Metrik vor, die aus der differenziellen Weglänge ermittelt werden. Die Riemann sche Geometrie wird in der allgemeinen Relativitätstheorie und Kosmologie genutzt. Beziehung zwischen der euklidischen Geometrie und nichteuklidischen Geometrien: Felix Klein schuf 1871 die Cayley-Klein-Geometrien, indem er die Formel von Laguerre verallgemeinerte. Er wählte einen Kegelschnitt als Fundamentalgebilde, den er unter Verwendung komplexer Koordinaten mit der Verbindungsgeraden zweier Punkte zum Schnitt brachte bzw. an den er die Tangenten vom Schnittpunkt zweier Geraden aus bestimmte. Auf diese Weise
3 Ausblick 273 führte er die Messung des Abstands zweier Punkte und des Winkels zwischen zwei Geraden auf ein Doppelverhältnis von Strecken bzw. Winkeln zurück. In Abhängigkeit vom gewählten Kegelschnitt und der Art der entstehenden Schnittpunkte ergibt sich die euklidische, elliptische, hyperbolische Geometrie, die Minkowski-Geometrie (die in der speziellen Relativitätstheorie eine Anwendung findet) oder eine von drei weiteren Geometrien. Verknüpfung von Geometrie und linearer Algebra: Bei seinem Eintritt in die Universität Erlangen stellte Felix Klein 1872 mit dem Erlanger Programm eine Schrift vor, in der die Klassifikation der Geometrie in die euklidische, hyperbolische und elliptische Geometrie durch invariante Eigenschaften bei Transformationen erfolgte. Mengen von Transformationen mit der Operation der Komposition (Hintereinanderausführung) bilden Gruppen. Beispielsweise kann die euklidische Geometrie als Gruppe der Bewegungen (Translationen, Rotationen, Spiegelungen) aufgefasst werden. Auf die Transformationsgruppen sind Methoden der linearen Algebra anwendbar. Herstellung von Bezügen zwischen geometrischen und natürlichen Formen: Benoît Mandelbrot veröffentlichte 1977 den Essay Fractals: form, chance and dimension, in dem er die fraktale Geometrie vorstellte, welche sich zur Beschreibung von Formen der Natur eignet. Die fraktale Geometrie ist insbesondere dadurch gekennzeichnet, dass die Dimension der betrachteten Objekte in der Regel nicht ganzzahlig ist und dass Selbstähnlichkeit auftritt. Gewiss wird die altehrwürdige Geometrie noch viele weitere Sternstunden erleben. Eine Rückkopplung zur eingangs gestellten Frage offenbart, dass wir nur einige der genannten Sternstunden der Geometrie näher beleuchten konnten. Dabei zeigten bereits unsere kurzen Ausflüge in unterschiedliche Geometrien, wie lebendig, dynamisch, vielgestaltig und interessant die Geometrie ist. Der Autor dieses Buches hofft, dass er bei seinen Lesern nicht nur Einblicke in unterschiedliche Geometrien ermöglichen konnte, sondern auch das Interesse zur weiteren Beschäftigung mit Geometrie angeregt hat. Dabei wünscht er viel Erfolg und ästhetischen Genuss.
4 Glossar Achse s. Fixpunktgerade affine Abbildung Eine affine Abbildung ist eine geraden- und teilverhältnistreue Abbildung zwischen zwei affinen Räumen. Eine bijektive geraden- und teilverhältnistreue Abbildung eines affinen Raumes auf sich selbst wird Affinität oder affine Transformation genannt. Die Geraden- und Teilverhältnistreue der affinen Abbildungen und damit auch der Affinitäten bedingt die Invarianz der Parallelität bei diesen Abbildungen. Eine affine Abbildung f setzt sich aus einer linearen Abbildung ϕ und einer Translation (Parallelverschiebung) t zusammen. Ihre analytische Beschreibung lautet: f ( x ) = ϕ ( x ) + t = A x + t. affine Transformation s. affine Abbildung Affinität s. affine Abbildung Ähnlichkeit s. Ähnlichkeitsabbildung Ähnlichkeitsabbildung Eine bijektive geraden- und streckenverhältnistreue Abbildung zwischen euklidischen Räumen gleicher Dimension heißt Ähnlichkeitsabbildung, äquiforme Abbildung oder Ähnlichkeit, eine derartige Selbstabbildung heißt Ähnlichkeitstransformation. Aus der Geraden- und Streckenverhältnistreue einer Ähnlichkeitsabbildung ergibt sich, dass sie auch winkel-, flächenverhältnis- und parallelentreu ist (damit ist diese Abbildung formtreu). Die Menge der Ähnlichkeitsabbildungen besteht aus der Menge aller Kongruenzabbildungen, zentrischen Streckungen und deren Verkettungen. Ähnlichkeitstransformation s. Ähnlichkeitsabbildung äquiforme Abbildung s. Ähnlichkeitsabbildung Bewegung s. Kongruenzabbildung Springer-Verlag GmbH Deutschland 2017 J. Wagner, Einblicke in die euklidische und nichteuklidische Geometrie, DOI /
5 276 Glossar Ecktransversale im Dreieck s. Transversale im Dreieck Ekliptik Die scheinbare Bahn der Sonne an der scheinbaren Himmelskugel im Laufe eines Jahres (es handelt sich um einen Großkreis) wird als Ekliptik, Finsternislinie oder Tierkreis bezeichnet. Die Ekliptik wird seit babylonischer Zeit in zwölf Sternzeichen von jeweils 30 Länge eingeteilt, die nicht mit den Sternbildern zu verwechseln sind. euklidische Transformation s. Kongruenzabbildung Fernpunkt In der projektiven Geometrie wird jeder Geraden genau ein unendlich ferner (uneigentlicher) Urbildpunkt zugeordnet, der als Fernpunkt bezeichnet wird. Finsternislinie s. Ekliptik Fixgerade Wird jeder Punkt einer Geraden auf den gleichen oder einen anderen Punkt dieser Geraden abgebildet, dann wird diese Gerade als Fixgerade bezeichnet. Fixpunktgerade Ist jeder Punkt einer Geraden ein Fixpunkt einer Abbildung, dann wird diese Gerade Fixpunktgerade oder Achse genannt. Fluchtpunkt In der projektiven Geometrie wird der Bildpunkt des Fernpunktes einer Geraden als Fluchtpunkt bezeichnet. Konstruktiv ergibt sich der Fluchtpunkt Qu c einer Schar nach affiner Auffassung paralleler Geraden, welche die Gerade q enthält, als Schnitt der zu q parallelen Geraden q Z durch das Projektionszentrum Z mit der Bildebene π : Qu c = q Z π. Geodäte Die kürzeste Verbindung zweier Punkte wird Geodäte, geodätische Linie oder Orthodrome genannt. geodätische Linie s. Geodäte kollinear Mehrere Punkte sind kollinear, wenn sie mit derselben Geraden inzidieren, d. h., wenn sie auf genau einer Geraden liegen. Kollineation Eine Kollineation ist eine geradentreue Transformation. Komposition Die Hintereinanderausführung geometrischer Abbildungen wird als Komposition bezeichnet. Kongruenz s. Kongruenzabbildung Kongruenzabbildung Eine bijektive geraden- und längentreue Abbildung zwischen euklidischen Räumen gleicher Dimension heißt Kongruenzabbildung oder Kongruenz, eine derartige Selbstabbildung heißt Kongruenztransformation, Bewegung oder euklidische Transformation.
6 Glossar 277 Aus der Geraden- und Längentreue einer Kongruenzabbildung ergibt sich, dass sie auch winkel-, flächen- und parallelentreu ist (damit ist diese Abbildung formund größentreu). Die Menge der Kongruenzabbildungen besteht aus der Menge aller Verschiebungen, Drehungen, Geradenspiegelungen und deren Verkettungen. Kongruenztransformation s. Kongruenzabbildung konkurrent s. kopunktal kopunktal Mehrere Geraden sind kopunktal, konkurrent, zentral oder perspektivisch, wenn sie alle mit demselben Punkt inzidieren, d. h., wenn sie sich in genau einem Punkt schneiden. Loxodrome Die Loxodrome ist die Kurve, die zwei Orte auf einer Sphäre so miteinander verbindet, dass bei einer Fahrt zwischen diesen Orten der Kurs konstant ist. Orthodrome s. Geodäte perspektivisch s. kopunktal projektive Abbildung Eine projektive Abbildung ist eine geraden- und doppelverhältnistreue Abbildung zwischen zwei projektiven Räumen. Eine bijektive geraden- und doppelverhältnistreue Abbildung eines projektiven Raumes auf sich selbst wird Projektivität oder projektive Transformation genannt. Bei ebenen projektiven Abbildungen erfolgt die Transformation der Koordinaten mithilfe ( ) ) x gebrochen linearer Abbildungsgleichungen: =. 1 x 2 ( a11 x 1 +a 12 x 2 +a 13 a 31 x 1 +a 32 x 2 +a 33 a 21 x 1 +a 22 x 2 +a 23 a 31 x 1 +a 32 x 2 +a 33 Bei Verwendung homogener Koordinaten lässt sich für ebene projektive Abbildungen eine lineare Transformationsgleichung angeben: f h ( xh ) = Aerw x h mit homogenen Koordinaten x ih. projektive Transformation s. projektive Abbildung Projektivität s. projektive Abbildung Tierkreis s. Ekliptik Transformation Eine Transformation ist eine bijektive Abbildung einer Menge auf sich selbst. Jede Transformation lässt sich aus Translationen (Verschiebungen), Skalierungen (Verkleinerungen/Vergrößerungen) und Rotationen (Drehungen) zusammensetzen.
7 278 Glossar Transversale im Dreieck Eine Gerade, die jede Trägergerade der Seiten eines Dreiecks in genau einem Punkt schneidet, wird als Transversale bezeichnet. Verläuft eine Transversale durch einen Eckpunkt des Dreiecks, dann wird sie Ecktransversale genannt. Verschwindungsebene In der projektiven Geometrie wird die zur Bildebene parallele Ebene, die das Projektionszentrum enthält, als Verschwindungsebene bezeichnet. zentral s. kopunktal
8 Sachverzeichnis A Abbildung affine analytische Beschreibung, 58 Definition, 51 äquiforme, 44 projektive analytische Beschreibung, 63 Definition, 61 Abstand, hyperbolischer, 252 Achse, 45 Adjungieren, 113 Affinität axiale, 52 Definition, 51 ebene axiale, 53 ebene zentrale, 57 perspektive, 52 Ähnlichkeitsabbildung, 44 Anschauungsraum, viii Äquinoktien, 203 Areafunktion, 264 Atomzeit, internationale, 232 Axiom, 1 Axiomensystem, Eigenschaften, 6 Axonometrie Frontalaxonometrie, 50 genormte orthogonale Dimetrie, 50 genormte orthogonale Isometrie, 50 Horizontalaxonometrie, 50 B Beltrami, Eugenio, 238 Beziehung hyperbolische, 264 trigonometrische, 260 Bogenmaß, 181 Brennpunkt, 261 Brunelleschi, Filippo, 39 C Ceva, Giovanni, 20 D Definition, 1 Dehomogenisierung, 130, 142, 144 Desargues, 159 Descartes, René, 272 Distanzkreis, 164 Doppelverhältnis, 12, 142 Drehmatrix, 80 Dreieck astronomisches, 223 nautisches, 221 Dualitätsprinzip, 115 Dürer, Albrecht, 39 E Ebene, projektive, 120 Ecktransversale im Dreieck, 16 Eigenwertproblem, 83, 86 Ekliptik, 202 Elation, 62 Erdrotation, 200 Erdumlauf, 202 Euklid von Alexandria, 1, 272 Euler, Leonhard, 71 Eulersches Dreieck, 187 Exzess, sphärischer, 188 F Fernelement, 119 Ferngerade, 119 Springer-Verlag GmbH Deutschland 2017 J. Wagner, Einblicke in die euklidische und nichteuklidische Geometrie, DOI /
9 280 Fernpunkt, 117 Fibonacci-Folge, 70, 72 Finsternislinie, 202 Fixgerade, 45 Fixpunkt, 45 Fixpunktgerade, 45 Fluchtgerade, 119 Fluchtpunkt, 117 Form, quadratische, 78 Formel von Binet, 74 von Laguerre, 151 Frühlingspunkt, 204 G Gauß, Carl Friedrich, 272 Gerade parallele, 3 projektive, 120 Goldene Zahl, 68 Goldener Schnitt, 68 Goldener Winkel, 70 Goldenes Rechteck, 76 Gradmaß, 181 H Hauptachsentransformation, 37 Hauptlinie, 166 Hilbert, David, 6 Himmelskugel, scheinbare, 200 Himmelsmeridian, 201 Homogenisierung, 130, 142, 144 Homologie, 62 Horizont, 213 Hyperbel, 261 Hyperbelfunktion, 264 I Internationale Atomzeit, 232 J Jahr, platonisches, 204 Julianisches Datum, 210 K Kettenbruch, 70 Klein, Felix, 241, 272, 273 Kollineation, 44 Konchoide von Nikomedes, 258 Kongruenzabbildung, 44 Koordinaten, homogene, 59, 130, 141 Kreis, 259 Kulmination, 201 L Lagrange-Identität, 195 Linearform, 78 Loxodrome, 227 M Mandelbrot, Benoît, 273 Menelaos, 18 Mercator-Karte, 231 Metrik, 236 Minkowski, Hermann, 7 Möbiustransformation, 145 N Napier, John, 180 Normierung, 130, 142 Nullmeridian, 206 Nutation, 205 O Obliquität, 203 Ordnung A-Geometrie, 111 P-Geometrie, 114 Orthodrome, 230 Ortssternzeit, 209 Sachverzeichnis P Pappos von Alexandria, 156 Parallelenaxiom, 6 endliche affine Geometrie, 108 endliche projektive Geometrie, 114 hyperbolische Geometrie, 235 projektive Geometrie, 235 Taxi-Geometrie, 100 Parallelenpostulat, 5 Parallelprojektion Eigenschaften, 47 orthogonale, 46 schiefe, 46 Teilverhältnistreue, 9 Perspektive, 46
10 Sachverzeichnis 281 Poincaré, Henri, 241 Pol, 185 Polare, 185 Postulat, 1 Präzession, 204 Projektivität Definition, 61 ebene Perspektivität, 62 Eigenschaften, 64 perspektive Kollineation, 61 zentral-axiale Kollineation, 62 Pseudosphäre, 237, 257 Ptolemäus, Claudius, 179 Pythagoras, sphärischer, 199 Q Quadrik, 78 R Raum, viii affiner, viii euklidischer, viii projektiver, viii Regiomontanus, 180 Riemann, Bernhard, 272 Riemann sche Zahlenkugel, 146 Sehkreis, 164 Solstitien, 204 Sonnentag mittlerer, 206 wahrer, 205 Sternbild, 200 Sterntag, 205 Sternzeichen, 202 Strecke, orientierte, 7 Streckung, zentrische, 58 T Teilung, harmonische, 16 Teilverhältnis, 8, 142 Term, primitiver, 6 Tiefenlinie, 165 Tierkreis, 202 Traktrix, 237, 256 Transformation, 44 affine, 51 Transversale im Dreieck, 16 Trigonometrie, sphärische Kotangenssatz Form 1, 197 Kotangenssatz Form 2, 198 Seitenkosinussatz, 193 Sinussatz, 193 Winkelkosinussatz, 196 S Satz von Ceva, 20 von Desargues großer affiner, 176 großer projektiver, 159 kleiner affiner, 176 kleiner projektiver, 175 von Menelaos, 18 von Pappos großer affiner, 173 großer projektiver, 156 kleiner affiner, 174 kleiner projektiver, 173 Schlitzen, 114 Schrägspiegelung, 56 Seemeile, 232 Sehkegel, 164 V Verschwindungsebene, 118 Verschwindungspunkt, 118 W Weltzeit, koordinierte, 233 Winkel, orientierter, 7 Z Zahl, noble, 70 Zeit, dynamische, 232 Zeitgleichung, 207 Zeitzonen, 206 Zentralprojektion Doppelverhältnistreue, 13 Eigenschaften, 124, 167
11
Kapitel I. Grundlagen der ebenen euklidischen Geometrie... 5 Einleitung Affine Ebenen... 7
 Inhaltsverzeichnis Prolog. Die Elemente des Euklid... 1 1. Euklid 2. Axiome 3. Über die Sprache der Geometrie Kapitel I. Grundlagen der ebenen euklidischen Geometrie... 5 Einleitung... 5 1. Affine Ebenen...
Inhaltsverzeichnis Prolog. Die Elemente des Euklid... 1 1. Euklid 2. Axiome 3. Über die Sprache der Geometrie Kapitel I. Grundlagen der ebenen euklidischen Geometrie... 5 Einleitung... 5 1. Affine Ebenen...
Springer-Lehrbuch. Ebene Geometrie. Bearbeitet von Max Koecher, Aloys Krieg
 Springer-Lehrbuch Ebene Geometrie Bearbeitet von Max Koecher, Aloys Krieg erweitert, überarbeitet 2008. Taschenbuch. xii, 280 S. Paperback ISBN 978 3 540 49327 3 Format (B x L): 15,5 x 23,5 cm Gewicht:
Springer-Lehrbuch Ebene Geometrie Bearbeitet von Max Koecher, Aloys Krieg erweitert, überarbeitet 2008. Taschenbuch. xii, 280 S. Paperback ISBN 978 3 540 49327 3 Format (B x L): 15,5 x 23,5 cm Gewicht:
Stichwortliste zur Vorlesung. Elementargeometrie. Gabriela Weitze-Schmithüsen. Übungsleiterin: Anja Randecker. Karlsruhe, Sommersemester 2012
 Stichwortliste zur Vorlesung Elementargeometrie Gabriela Weitze-Schmithüsen Übungsleiterin: Anja Randecker Karlsruhe, Sommersemester 2012 Kapitel 0: Eine Motivation Eine kleine Einführung mit fünf Thesen
Stichwortliste zur Vorlesung Elementargeometrie Gabriela Weitze-Schmithüsen Übungsleiterin: Anja Randecker Karlsruhe, Sommersemester 2012 Kapitel 0: Eine Motivation Eine kleine Einführung mit fünf Thesen
Hyperbolische Symmetrien
 Hyperbolische Symmetrien Nina Dietsche Robert Papin 01.07.2010 1 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Hyperbolische Symmetrien 2 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Inhaltsverzeichnis
Hyperbolische Symmetrien Nina Dietsche Robert Papin 01.07.2010 1 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Hyperbolische Symmetrien 2 Nina Dietsche, Robert Papin Hyperbolische Symmetrien Inhaltsverzeichnis
Lineare Algebra und analytische Geometrie
 Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
Geometrie (4b) Wintersemester 2015/16. Kapitel 2. Abbildungsgeometrie. Teil 2
 Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
ANALYTISCHE GEOMETRIE EINE EINFÜHRUNG IN GEOMETRIE UND LINEARE ALGEBRA
 * ANALYTISCHE GEOMETRIE EINE EINFÜHRUNG IN GEOMETRIE UND LINEARE ALGEBRA DR. GUNTER PICKERT PROFESSOR AN DER UNIVERSITÄT GIESSEN MIT 77 ABBILDUNGEN 7., DURCHGESEHENE UND ERWEITERTE AUFLAGE LEIPZIG 1976
* ANALYTISCHE GEOMETRIE EINE EINFÜHRUNG IN GEOMETRIE UND LINEARE ALGEBRA DR. GUNTER PICKERT PROFESSOR AN DER UNIVERSITÄT GIESSEN MIT 77 ABBILDUNGEN 7., DURCHGESEHENE UND ERWEITERTE AUFLAGE LEIPZIG 1976
UNVERGÄNGLICHE GEOMETRIE
 H.S.M. COXETER UNVERGÄNGLICHE GEOMETRIE Ins Deutsche übersetzt von J. J. Burckhardt 1963 BIRKHAUSER VERLAG BASEL UND STUTTGART INHALTSVERZEICHNIS Teil I 1. Dreiecke 1.1 Euklid 15 1.2 Grundbegriffe und
H.S.M. COXETER UNVERGÄNGLICHE GEOMETRIE Ins Deutsche übersetzt von J. J. Burckhardt 1963 BIRKHAUSER VERLAG BASEL UND STUTTGART INHALTSVERZEICHNIS Teil I 1. Dreiecke 1.1 Euklid 15 1.2 Grundbegriffe und
Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
 2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus vom euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
GRUNDZUGE DER MATHEMATIK
 40483 GRUNDZUGE DER MATHEMATIK FÜR LEHRER AN GYMNASIEN SOWIE FÜR MATHEMATIKER IN INDUSTRIE UND WIRTSCHAFT BAND II GEOMETRIE Mit zahlreichen Abbildungen GÖTTINGEN VANDENHOECK & RUPRECHT 1960 INHALT Zeichen
40483 GRUNDZUGE DER MATHEMATIK FÜR LEHRER AN GYMNASIEN SOWIE FÜR MATHEMATIKER IN INDUSTRIE UND WIRTSCHAFT BAND II GEOMETRIE Mit zahlreichen Abbildungen GÖTTINGEN VANDENHOECK & RUPRECHT 1960 INHALT Zeichen
Seminar für LAGym/LAB: Analytische Geometrie
 Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
Geometrie. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 5.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 5.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Geometrie 5.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 5.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg,
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Gliederung 4 Invarianten Isometrien (Kongruenzen) Ähnlichkeitsabbildungen Affine Transformationen Projektive Transformationen 2 von
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Gliederung 4 Invarianten Isometrien (Kongruenzen) Ähnlichkeitsabbildungen Affine Transformationen Projektive Transformationen 2 von
VI.0 Vorbemerkungen S A. Bereitstellung von notwendigem Handwerkszeug:
 VI.0 Vorbemerkungen S. 160 161 A. Bereitstellung von notwendigem Handwerkszeug: Punktmenge P = {A, B, P, Q...}, Geradenmenge G = {a, b, g, h,...} P g (bedeutet P liegt auf g) Geraden der Anschauungsebene:
VI.0 Vorbemerkungen S. 160 161 A. Bereitstellung von notwendigem Handwerkszeug: Punktmenge P = {A, B, P, Q...}, Geradenmenge G = {a, b, g, h,...} P g (bedeutet P liegt auf g) Geraden der Anschauungsebene:
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Historisches zur Gruppentheorie
 Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Historisches zur Gruppentheorie Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 20 Gruppen: Abstrakte Definition Eine Gruppe
Gert Bär. Geometrie. Eine Einführung für Ingenieure und Naturwissenschaftler. 2., überarbeitete und erweiterte Auflage
 Gert Bär Geometrie Eine Einführung für Ingenieure und Naturwissenschaftler 2., überarbeitete und erweiterte Auflage Teubner B.G.Teubner Stuttgart Leipzig Wiesbaden Inhalt 1 Aus der analytischen Geometrie
Gert Bär Geometrie Eine Einführung für Ingenieure und Naturwissenschaftler 2., überarbeitete und erweiterte Auflage Teubner B.G.Teubner Stuttgart Leipzig Wiesbaden Inhalt 1 Aus der analytischen Geometrie
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projektive Geometrie SS 2016 www-m10.ma.tum.de/projektivegeometriess16 Lösungen zu Aufgabenblatt 11
Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projektive Geometrie SS 2016 www-m10.ma.tum.de/projektivegeometriess16 Lösungen zu Aufgabenblatt 11
eine O fixierende Bewegung.
 1. Bewegungen der hyperbolischen Ebene Sei nun H eine hyperbolische Ebene. Dann erhält man dieselben Klassen von Bewegungen wie im Euklidischen Fall und eine weitere Klasse. Wir haben oben nur ein einziges
1. Bewegungen der hyperbolischen Ebene Sei nun H eine hyperbolische Ebene. Dann erhält man dieselben Klassen von Bewegungen wie im Euklidischen Fall und eine weitere Klasse. Wir haben oben nur ein einziges
ENZYKLOPÄDIE DER ELEMENTARMATHEMATIK
 HOCHSCHULBÜCHER FÜR MATHEMATIK HERAUSGEGEBEN VON H. GRELL, K.MARUHN UND W.RINOW BAND 10 ENZYKLOPÄDIE DER ELEMENTARMATHEMATIK REDAKTION: P.S. ALEXANDROFF A.I.MARKUSCHEWITSCH A.J.CHINTSCHIN BAND IV GEOMETRIE
HOCHSCHULBÜCHER FÜR MATHEMATIK HERAUSGEGEBEN VON H. GRELL, K.MARUHN UND W.RINOW BAND 10 ENZYKLOPÄDIE DER ELEMENTARMATHEMATIK REDAKTION: P.S. ALEXANDROFF A.I.MARKUSCHEWITSCH A.J.CHINTSCHIN BAND IV GEOMETRIE
Hyperbolische Geometrie
 Hyperbolische Geometrie von Sebastian Kalinka und Alexander Thomaso nach dem Buch Elementare Differentialgeometrie von Christian Bär Wiederholung Für κ R setzt man ˆM κ := {(x, y, z) R 3 x 2 + κ(y 2 +
Hyperbolische Geometrie von Sebastian Kalinka und Alexander Thomaso nach dem Buch Elementare Differentialgeometrie von Christian Bär Wiederholung Für κ R setzt man ˆM κ := {(x, y, z) R 3 x 2 + κ(y 2 +
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 8
 Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Dr. Erwin Schörner Klausurenkurs zum Staatseamen (SS 205): Lineare Algebra und analtische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Geraden-Schnittpunkte
 Geraden-Schnittpunkte Erinnerung: Axiom. Durch zwei verschiedene Punkte geht höchstens eine Gerade. Anders ausgedrückt: Seien P und Q Punkte und g und h Geraden. Wenn g und h durch P und Q gehen... und
Geraden-Schnittpunkte Erinnerung: Axiom. Durch zwei verschiedene Punkte geht höchstens eine Gerade. Anders ausgedrückt: Seien P und Q Punkte und g und h Geraden. Wenn g und h durch P und Q gehen... und
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
GEOMETRIE (4a) Kurzskript
 GEOMETRIE (4a) Kurzskript Dieses Kurzskript ist vor allem eine Sammlung von Sätzen und Definitionen und sollte ausdrücklich nur mit weiteren Erläuterungen in der Veranstaltung genutzt werden. Fehler sind
GEOMETRIE (4a) Kurzskript Dieses Kurzskript ist vor allem eine Sammlung von Sätzen und Definitionen und sollte ausdrücklich nur mit weiteren Erläuterungen in der Veranstaltung genutzt werden. Fehler sind
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Michael Strobel Geometriekalküle WS 217/18 http://www-m1.ma.tum.de/geometriekalkuelews1718 Lösungen zu Aufgabenblatt 7 (29. Februar 217) Aufgabe 1. Abstand
Technische Universität München Zentrum Mathematik Michael Strobel Geometriekalküle WS 217/18 http://www-m1.ma.tum.de/geometriekalkuelews1718 Lösungen zu Aufgabenblatt 7 (29. Februar 217) Aufgabe 1. Abstand
Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 204): Lineare Algebra und analytische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 204): Lineare Algebra und analytische Geometrie 8 8. (Herbst 202, Thema 3, Aufgabe 4) Bestimmen Sie die euklidische Normalform der Quadrik Q, gegeben
Weitere geometrische Abbildungen
 Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Weitere geometrische Abbildungen Anna Wegener, Matthias Wegen, Daniel Kretschmer 15.01.2015 1 / 38 Affinitätsabbildungen - Motivation Kongruenzabbildungen Ähnlichkeitsabbildungen Affinitätsabbildungen
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Übersicht zu den Textinhalten
 Abbildungen Übersicht zu den Textinhalten Zum Thema Abbildungen gibt es mehrere Texte. Hier wird aufgelistet, wo man was findet. Datei Nr. 11050 Stand 3. Oktober 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
Abbildungen Übersicht zu den Textinhalten Zum Thema Abbildungen gibt es mehrere Texte. Hier wird aufgelistet, wo man was findet. Datei Nr. 11050 Stand 3. Oktober 2013 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK
3: Bewegungen und Ähnlichkeiten:
 3: Bewegungen und Ähnlichkeiten: Was sind kongruente (bzw. deckungsgleiche) Figuren? [Box2-94] [Kra2-138] [Rei2-173a] [Rei2-173b] Zwei Teilmengen M,M einer Euklidischen Ebene (E,G) heißen kongruent, wenn
3: Bewegungen und Ähnlichkeiten: Was sind kongruente (bzw. deckungsgleiche) Figuren? [Box2-94] [Kra2-138] [Rei2-173a] [Rei2-173b] Zwei Teilmengen M,M einer Euklidischen Ebene (E,G) heißen kongruent, wenn
Prof. S. Krauter Endliche Geometrie SS_2005 Klausurbeispiele.doc
 Prof. S. Krauter Endliche Geometrie SS_2005 Klausurbeispiele.doc Der Lösungsgang ist jeweils knapp aber vollständig darzustellen. Die Darstellung soll sauber, genau und übersichtlich sein. Konstruktionen
Prof. S. Krauter Endliche Geometrie SS_2005 Klausurbeispiele.doc Der Lösungsgang ist jeweils knapp aber vollständig darzustellen. Die Darstellung soll sauber, genau und übersichtlich sein. Konstruktionen
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Technische Universität München Fakultät für Mathematik. Klausur. Geometriekalküle. Modul MA März 2018, 16:00 17:00 Uhr
 Technische Universität München Fakultät für Mathematik Klausur Geometriekalküle Modul MA2203 1. März 2018, 16:00 17:00 Uhr Prof. Dr. Dr. Jürgen Richter-Gebert Musterlösung Aufgabe 1. Kegelschnitt mit Parameter
Technische Universität München Fakultät für Mathematik Klausur Geometriekalküle Modul MA2203 1. März 2018, 16:00 17:00 Uhr Prof. Dr. Dr. Jürgen Richter-Gebert Musterlösung Aufgabe 1. Kegelschnitt mit Parameter
Vortragsthemen. Proseminar Geometrie. JProf. Dr. Petra Schwer
 Proseminar Geometrie JProf. Dr. Petra Schwer Dieses Proseminar zur Geometrie bietet anhand vielfältiger Themen eine Einführung in die klassische und moderne Geometrie. Als Grundlage dient uns das Buch
Proseminar Geometrie JProf. Dr. Petra Schwer Dieses Proseminar zur Geometrie bietet anhand vielfältiger Themen eine Einführung in die klassische und moderne Geometrie. Als Grundlage dient uns das Buch
Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen?
 Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen? MNU-Landestagung. 02/2012. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Zwei Paradigmen der modernen (theoretischen)
Gruppen, Graphen, Symmetrie Was sind negativ gekrümmte Gruppen? MNU-Landestagung. 02/2012. Regensburg Clara Löh Fakultät für Mathematik. Universität Regensburg Überblick Zwei Paradigmen der modernen (theoretischen)
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
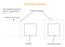 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
6. Die Gruppe der Euklidischen Kongruenztransformationen
 6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
EINFÜHRUNG IN DIE ANALYTISCHE GEOMETRIE UND LINEARE ALGEBRA
 EINFÜHRUNG IN DIE ANALYTISCHE GEOMETRIE UND LINEARE ALGEBRA VON SIEGFRIED BREHMER UND HORST BELKNER MIT 146 A B B I L D U N G E N VEB DEUTSCHER VERLAG DER WISSENSCHAFTEN BERLIN 1966 INHALTSVERZEICHNIS
EINFÜHRUNG IN DIE ANALYTISCHE GEOMETRIE UND LINEARE ALGEBRA VON SIEGFRIED BREHMER UND HORST BELKNER MIT 146 A B B I L D U N G E N VEB DEUTSCHER VERLAG DER WISSENSCHAFTEN BERLIN 1966 INHALTSVERZEICHNIS
3. Ähnlichkeitsabbildungen
 3. Ähnlichkeitsabbildungen 3.1 Definitionen: Ähnlichkeitsabbildungen, Dilatationen Bis jetzt haben wir Isometrien (Kongruenzabbildungen) betrachtet. Diese bbildungen wurden aufgebaut aus den Geradenspiegelungen.
3. Ähnlichkeitsabbildungen 3.1 Definitionen: Ähnlichkeitsabbildungen, Dilatationen Bis jetzt haben wir Isometrien (Kongruenzabbildungen) betrachtet. Diese bbildungen wurden aufgebaut aus den Geradenspiegelungen.
1 Analytische Geometrie
 Analytische Geometrie. Grundlagen, Begriffe, Schreibweisen Achsenkreuz Die Achsen heißen in dieser Darstellung x und -Achse. Punkte Punkte werden weiterhin mit großen, lateinischen Buchstaben bezeichnet
Analytische Geometrie. Grundlagen, Begriffe, Schreibweisen Achsenkreuz Die Achsen heißen in dieser Darstellung x und -Achse. Punkte Punkte werden weiterhin mit großen, lateinischen Buchstaben bezeichnet
Lösungsvorschläge für die Geometrie-Klausur vom 28.7.
 Lösungsvorschläge für die Geometrie-Klausur vom 28.7. Aufgabe 1: (a) Die beiden Punkte liegen offensichtlich auf der hyperbolischen Geraden g = {z H R(z) = 1}. Die beiden idealen Punkte sind a = 1, b =.
Lösungsvorschläge für die Geometrie-Klausur vom 28.7. Aufgabe 1: (a) Die beiden Punkte liegen offensichtlich auf der hyperbolischen Geraden g = {z H R(z) = 1}. Die beiden idealen Punkte sind a = 1, b =.
1 Einführung: Analytische Geometrie/Lineare Algebra und Allgemeinbildung
 1 Einführung: Analytische Geometrie/Lineare Algebra und Allgemeinbildung 1 1.1 Schwerpunkte der Weiterentwicklung des Unterrichts 3 1.2 Grundvorstellungen und fundamentale Ideen 6 2 Lineare Gleichungssysteme
1 Einführung: Analytische Geometrie/Lineare Algebra und Allgemeinbildung 1 1.1 Schwerpunkte der Weiterentwicklung des Unterrichts 3 1.2 Grundvorstellungen und fundamentale Ideen 6 2 Lineare Gleichungssysteme
4 Ein wenig analytische Geometrie. 4.1 Einige Grundgebilde der projektiven Geometrie Geraden in homogenen Koordinaten
 4 Ein wenig analytische Geometrie 4.1 Einige Grundgebilde der projektiven Geometrie 4.1.1 Geraden in homogenen Koordinaten (a) Im Raum/Ebene in Parameterform Siehe Figur-4-1-1-a (ohne X g = P Q) P ( p),
4 Ein wenig analytische Geometrie 4.1 Einige Grundgebilde der projektiven Geometrie 4.1.1 Geraden in homogenen Koordinaten (a) Im Raum/Ebene in Parameterform Siehe Figur-4-1-1-a (ohne X g = P Q) P ( p),
Projektive Geometrie
 Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Symmetrien. Transformationen. Affine und euklidische Räume
 Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Symmetrien Transformationen Der Gruppenbegriff entwickelte sich aus dem Begriff der Transformationsgruppe. In dieser Form tauchen auch die meisten Gruppen in der Mathematik, Physik, Chemie, Kristallographie,
Vorlesungen über höhere Geometrie
 Oswald Giering Vorlesungen über höhere Geometrie unter Mitwirkung von Johann Hartl Mit zahlreichen Aufgaben, Figuren und Tabellen Technische Hochschule Darmstadt F d v Friedr. Vieweg & Sohn BraunschweigA/Viesbaden
Oswald Giering Vorlesungen über höhere Geometrie unter Mitwirkung von Johann Hartl Mit zahlreichen Aufgaben, Figuren und Tabellen Technische Hochschule Darmstadt F d v Friedr. Vieweg & Sohn BraunschweigA/Viesbaden
6. Euklidische und nichteuklidische Geometrien
 6. Euklidische und nichteuklidische Geometrien 6.1 Axiomensystem der ebenen euklidischen Geometrie 62 Euklids Elemente bestehen aus 13 Büchern. Sie haben kein Vorwort, keine Einleitung. Es werden keine
6. Euklidische und nichteuklidische Geometrien 6.1 Axiomensystem der ebenen euklidischen Geometrie 62 Euklids Elemente bestehen aus 13 Büchern. Sie haben kein Vorwort, keine Einleitung. Es werden keine
Triangulierungen und Kartographie
 Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 30. Oktober 2015 Was
Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 30. Oktober 2015 Was
Zwillinge von Archimedes (1)
 Zwillinge von Archimedes (1) Zwillinge von Archimedes (2) Zwillinge von Archimedes (3) DIDAKTIK DER GEOMETRIE Elementargeometrie 2 Prof. Heinz Klemenz Universität Zürich, Kantonsschule Rychenberg Winterthur
Zwillinge von Archimedes (1) Zwillinge von Archimedes (2) Zwillinge von Archimedes (3) DIDAKTIK DER GEOMETRIE Elementargeometrie 2 Prof. Heinz Klemenz Universität Zürich, Kantonsschule Rychenberg Winterthur
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Lineare und affine Abbildungen im zweidimensionalen Anschauungsraum R 2
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare und affine Abbildungen im zweidimensionalen Anschauungsraum R Das komplette Material finden Sie hier: School-Scout.de S 1
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Lineare und affine Abbildungen im zweidimensionalen Anschauungsraum R Das komplette Material finden Sie hier: School-Scout.de S 1
Hyperbolische Geometrie
 Hyperbolische Geometrie Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 18. August 2014 Ein Wort über metrische Räume Ein metrischer Raum X ist ein Raum, in dem eine Distanzfunktion (die Metrik),
Hyperbolische Geometrie Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 18. August 2014 Ein Wort über metrische Räume Ein metrischer Raum X ist ein Raum, in dem eine Distanzfunktion (die Metrik),
Tarnkappen und mathematische Räume
 Tarnkappen und mathematische Räume Stefan Müller-Stach http://hodge.mathematik.uni-mainz.de/ stefan/biblio.html Ein Raum Mathematische Räume Die moderne Mathematik bietet einen universellen Baukasten zur
Tarnkappen und mathematische Räume Stefan Müller-Stach http://hodge.mathematik.uni-mainz.de/ stefan/biblio.html Ein Raum Mathematische Räume Die moderne Mathematik bietet einen universellen Baukasten zur
Triangulierungen und Kartographie
 Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Triangulierungen und Kartographie Ein Einblick in geometrische und topologische Methoden Stefan Krauss, Clara Löh Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg 23. Juli 2014 Was verraten
Nichteuklidische Geometrie
 Nichteuklidische Geometrie Teilnehmer: Phuong Anh Le Viet Son Pham Tillman Ritschl Marian Stengl Max Streese Chi Trung Vo Gruppenleiter: Andreas Filler Käthe-Kollwitz-Oberschule, Berlin Heinrich-Hertz-Oberschule,
Nichteuklidische Geometrie Teilnehmer: Phuong Anh Le Viet Son Pham Tillman Ritschl Marian Stengl Max Streese Chi Trung Vo Gruppenleiter: Andreas Filler Käthe-Kollwitz-Oberschule, Berlin Heinrich-Hertz-Oberschule,
2. Isometrien oder Kongruenzabbildungen
 6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
Perlen der Mathematik
 Claudi Alsina Roger B. Nelsen Perlen der Mathematik 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen Aus dem Englischen übersetzt von Thomas Filk ~ Springer Spektrum Inhaltsverzeichnis
Claudi Alsina Roger B. Nelsen Perlen der Mathematik 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen Aus dem Englischen übersetzt von Thomas Filk ~ Springer Spektrum Inhaltsverzeichnis
Nichteuklidische Geometrien und gekrümmte Räume
 Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Nichteuklidische Geometrien und gekrümmte Räume Es begann mit dem Problem der Landvermessung... Carl Friedrich Gauß (1777-1855): Theorie gekrümmter Flächen Landesvermessung des Königreichs Hannover Entdeckung
Wiederholungsblatt Elementargeometrie LÖSUNGSSKIZZE
 Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
5A. Von der Perspektive zu den projektiven Ebenen.
 5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
5A. Von der Perspektive zu den projektiven Ebenen. Neben der Euklidischen Geometrie, wie sie im Buch von Euklid niedergelegt und wie wir sie im vorigen Abschnitt behandelt haben, gibt es noch weitere Geometrien.
DR. JOACHIM MOHR AFFINE ABBILDUNGEN
 DR. JOACHIM MOHR Delphi, Mathematik, Musik AFFINE ABBILDUNGEN und - kurzgefasst - AFFINER RAUM Der affine Raum Diese knappe Einführung zu dem Begriff des affinen Raumes soll die Schreibweise bei den Beispielen
DR. JOACHIM MOHR Delphi, Mathematik, Musik AFFINE ABBILDUNGEN und - kurzgefasst - AFFINER RAUM Der affine Raum Diese knappe Einführung zu dem Begriff des affinen Raumes soll die Schreibweise bei den Beispielen
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 5. Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 5. Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Elemente der Geometrie
 Elemente der Geometrie Harald Scheid Wolfgang Schwarz Elemente der Geometrie 5. Auflage Harald Scheid Wuppertal, Deutschland Wolfgang Schwarz Wuppertal, Deutschland ISBN 978-3-662-50322-5 DOI 10.1007/978-3-662-50323-2
Elemente der Geometrie Harald Scheid Wolfgang Schwarz Elemente der Geometrie 5. Auflage Harald Scheid Wuppertal, Deutschland Wolfgang Schwarz Wuppertal, Deutschland ISBN 978-3-662-50322-5 DOI 10.1007/978-3-662-50323-2
3.1.1 Anes Koordinatensystem im Raum
 3 Einführung von Koordinaten 3. Ane Koordinaten 3.. Anes Koordinatensystem im Raum Tafelskizze Im dreidimensionalen euklidischen Anschauungsraum E 3 wählen wir einen Punkt O, den Koordinatenursprung und
3 Einführung von Koordinaten 3. Ane Koordinaten 3.. Anes Koordinatensystem im Raum Tafelskizze Im dreidimensionalen euklidischen Anschauungsraum E 3 wählen wir einen Punkt O, den Koordinatenursprung und
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 4 Transformation der Elemente der projektiven Geometrie Transformation von Geraden Transformation des Axiators Transformation
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 4 Transformation der Elemente der projektiven Geometrie Transformation von Geraden Transformation des Axiators Transformation
inb.-htsvfvrzetehnis digitalisiert durch: IDS Basel Bern
 inb.-htsvfvrzetehnis 1 Der Stuhl der Braut 1 1.1 Der Satz des Pythagoras - Euklids und andere Beweise 2 1.2 Die Vecten-Figur 4 1.3 Der Kosinussatz 7 1.4 Der Satz von Grebe und die Erweiterung von van Lamoen...
inb.-htsvfvrzetehnis 1 Der Stuhl der Braut 1 1.1 Der Satz des Pythagoras - Euklids und andere Beweise 2 1.2 Die Vecten-Figur 4 1.3 Der Kosinussatz 7 1.4 Der Satz von Grebe und die Erweiterung von van Lamoen...
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.12.2013 Alexander Lytchak 1 / 15 Motivation Für das Verständis affiner Teilräume eines Vektorraums sind Translationen
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.12.2013 Alexander Lytchak 1 / 15 Motivation Für das Verständis affiner Teilräume eines Vektorraums sind Translationen
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Warum konnten wir Inversionen so erfolgreich beim Lösen von schulgeometrischen Aufgaben anwenden?
 Warum konnten wir Inversionen so erfolgreich beim Lösen von schulgeometrischen Aufgaben anwenden? Weil bei einigen Aufgaben die Problemstellung einfacher wird, wenn wir Inversionen anwenden, die Aufgabenstellung
Warum konnten wir Inversionen so erfolgreich beim Lösen von schulgeometrischen Aufgaben anwenden? Weil bei einigen Aufgaben die Problemstellung einfacher wird, wenn wir Inversionen anwenden, die Aufgabenstellung
Über die Schmiegtangentenkongruenz der Cayley-Fläche
 Über die Schmiegtangentenkongruenz der Cayley-Fläche gemeinsam mit Rolf Riesinger (Wien) HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN INSTITUT FÜR DISKRETE MATHEMATIK
Über die Schmiegtangentenkongruenz der Cayley-Fläche gemeinsam mit Rolf Riesinger (Wien) HANS HAVLICEK FORSCHUNGSGRUPPE DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN INSTITUT FÜR DISKRETE MATHEMATIK
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Universität Bielefeld. Elementare Geometrie. Sommersemester Grundlagen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Meyers Handbuch über die Mathematik
 Meyers Handbuch über die Mathematik Herausgegeben von Herbert Meschkowski in Zusammenarbeit mit Detlef Laugwitz 2. erweiterte Auflage BIBLIOGRAPHISCHES INSTITUT MANNHEIM/WIEN/ZÜRICH LEXIKONVEK.1AG INHALT
Meyers Handbuch über die Mathematik Herausgegeben von Herbert Meschkowski in Zusammenarbeit mit Detlef Laugwitz 2. erweiterte Auflage BIBLIOGRAPHISCHES INSTITUT MANNHEIM/WIEN/ZÜRICH LEXIKONVEK.1AG INHALT
Inversion an Kegelschnitten mit CINDERELLA
 Inversion an Kegelschnitten mit CINDERELLA Hermann Vogel, TU-München In diesem Vortrag wird aufgezeigt, wie man mit Hilfe des Programms CINDERELLA die bekannte Inversion am Kreis auf die Inversion an Kegelschnitten
Inversion an Kegelschnitten mit CINDERELLA Hermann Vogel, TU-München In diesem Vortrag wird aufgezeigt, wie man mit Hilfe des Programms CINDERELLA die bekannte Inversion am Kreis auf die Inversion an Kegelschnitten
4 Geometrische Abbildungen
 Albrecht: Vorkurs Geometrie S. 48 4 Geometrische Abbildungen Funktionen und Abbildungen sind synonyme Begriffe, beide bezeichnen grundlegende Objekte der Mathematik. Den Begriff Funktion verwendet man
Albrecht: Vorkurs Geometrie S. 48 4 Geometrische Abbildungen Funktionen und Abbildungen sind synonyme Begriffe, beide bezeichnen grundlegende Objekte der Mathematik. Den Begriff Funktion verwendet man
Klausurenkurs zum Staatsexamen (WS 2016/17): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Differentialgeometrie. Lehre Differentialgeometrie
 Differentialgeometrie 1.1 Differentialgeometrie http://www.juergen-roth.de Lehre Differentialgeometrie Differentialgeometrie 1.2 Differentialgeometrie?! Elementare Differentialgeometrie Ziel: Untersuchung
Differentialgeometrie 1.1 Differentialgeometrie http://www.juergen-roth.de Lehre Differentialgeometrie Differentialgeometrie 1.2 Differentialgeometrie?! Elementare Differentialgeometrie Ziel: Untersuchung
Inhaltsverzeichnis. I Lineare Gleichungssysteme und Matrizen 1. Vorwort
 Vorwort V I Lineare Gleichungssysteme und Matrizen 1 1 Der Begriff des Körpers 3 1.1 Mengen 3 1.2 Köiperaxiome 3 1.3 Grundlegende Eigenschaften von Körpern 5 1.4 Teilkörper 7 1.5 Aufgaben 8 1.5.1 Grundlegende
Vorwort V I Lineare Gleichungssysteme und Matrizen 1 1 Der Begriff des Körpers 3 1.1 Mengen 3 1.2 Köiperaxiome 3 1.3 Grundlegende Eigenschaften von Körpern 5 1.4 Teilkörper 7 1.5 Aufgaben 8 1.5.1 Grundlegende
Universität Bielefeld. Elementare Geometrie. Sommersemester Grundlagen. Stefan Witzel
 Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Universität Bielefeld Elementare Geometrie Sommersemester 2018 Grundlagen Stefan Witzel Punkte, Abstand Die Euklidische Ebene E 2 besteht aus Punkten. Zwei Punkte P, Q E 2 haben einen Abstand PQ 0. Axiome
Seminar über ebene projektive Geometrie Wintersemester 2011/2012
 Seminar über ebene projektive Geometrie Wintersemester 2011/2012 Prof. Dr. J. Heinloth Ort und Zeit: T03 R04 D10, Montag, 14-16 Uhr, erster Termin zur Vergabe der Vortrge am 10. Oktober Inhalt: Wir werden
Seminar über ebene projektive Geometrie Wintersemester 2011/2012 Prof. Dr. J. Heinloth Ort und Zeit: T03 R04 D10, Montag, 14-16 Uhr, erster Termin zur Vergabe der Vortrge am 10. Oktober Inhalt: Wir werden
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern PROJEKTIVE GEOMETRIE Lösungen zur Semestral-Klausur (5. Februar 22, : 2:3 Uhr) Musterlösung Aufgabe.
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern PROJEKTIVE GEOMETRIE Lösungen zur Semestral-Klausur (5. Februar 22, : 2:3 Uhr) Musterlösung Aufgabe.
Strophoiden. Eckart Schmidt
 Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
Strophoiden Eckart Schmidt Strophoiden sind als anallagmatische Kurven invariant gegenüber einer Kreisspiegelung; sie sind weiterhin das Inverse einer gleichseitigen Hyperbel, die Fußpunktkurve einer Parabel
1 Abbildungen in der Ebene
 1 Inhalt 1 Abbildungen in der Ebene... 2 1.1 Verschiebung... 3 1.2 Spiegelung... 3 1.2.1 Achsenspiegelung... 3 1.3 Drehung... 4 1.3.1 Die Drehung... 4 1.4 Zentrische Streckung... 5 2 Funktionen... 7 2.1
1 Inhalt 1 Abbildungen in der Ebene... 2 1.1 Verschiebung... 3 1.2 Spiegelung... 3 1.2.1 Achsenspiegelung... 3 1.3 Drehung... 4 1.3.1 Die Drehung... 4 1.4 Zentrische Streckung... 5 2 Funktionen... 7 2.1
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Einige Ergebnisse der euklidischen Geometrie
 1 Teil I Einige Ergebnisse der euklidischen Geometrie In Teil I setzen wir den euklidischen Raum als bekannt voraus (aus der Schule oder aus der Vorlesung Lineare lgebra und nalytische Geometrie). Da wir
1 Teil I Einige Ergebnisse der euklidischen Geometrie In Teil I setzen wir den euklidischen Raum als bekannt voraus (aus der Schule oder aus der Vorlesung Lineare lgebra und nalytische Geometrie). Da wir
Materialien zur Mathematik VI
 Joachim Stiller Materialien zur Mathematik VI Intensionale, extensionale und projektive Geometrie Alle Rechte vorbehalten Der Aufbau der Geometrie Riemannsche Geometrie Hyperbolische, Parabolische, Elliptische
Joachim Stiller Materialien zur Mathematik VI Intensionale, extensionale und projektive Geometrie Alle Rechte vorbehalten Der Aufbau der Geometrie Riemannsche Geometrie Hyperbolische, Parabolische, Elliptische
Elementare Mathematik 1 WS 2005/06. Prof. Dr. Klaus Johannson Johann Wolfgang Goethe-Universität Frankfurt
 Elementare Mathematik 1 WS 2005/06 Prof. Dr. Klaus Johannson Johann Wolfgang Goethe-Universität Frankfurt Einleitung. Die vorliegende Skripte stellt das Material dar nach dem ich die Vorlesung Elementare
Elementare Mathematik 1 WS 2005/06 Prof. Dr. Klaus Johannson Johann Wolfgang Goethe-Universität Frankfurt Einleitung. Die vorliegende Skripte stellt das Material dar nach dem ich die Vorlesung Elementare
Das Zebra-Buch zur Geometrie
 Springer-Lehrbuch Das Zebra-Buch zur Geometrie Bearbeitet von Ferdinand Verhulst, Sebastian Walcher 1st Edition. 2010. Taschenbuch. xii, 296 S. Paperback ISBN 978 3 642 05247 7 Format (B x L): 15,5 x 23,5
Springer-Lehrbuch Das Zebra-Buch zur Geometrie Bearbeitet von Ferdinand Verhulst, Sebastian Walcher 1st Edition. 2010. Taschenbuch. xii, 296 S. Paperback ISBN 978 3 642 05247 7 Format (B x L): 15,5 x 23,5
DEUTSCHE SCHULE MONTEVIDEO BIKULTURELLES DEUTSCH-URUGUAYISCHES ABITUR ( AUF SPANISCH )
 Grundlegende Bemerkungen : Der Begriff des Vektors wurde in den vergangenen Jahren im Geometrieunterricht eingeführt und das mathematische Modell des Vektors wurde vor allem auch im Physikunterricht schon
Grundlegende Bemerkungen : Der Begriff des Vektors wurde in den vergangenen Jahren im Geometrieunterricht eingeführt und das mathematische Modell des Vektors wurde vor allem auch im Physikunterricht schon
Der Satz von Gérard Desargues
 2008 Jens Scherdin Andreas Meyburg Universität Bremen Juni 2008 Der Satz von Gérard Desargues Veranstaltung: Geometrie Seminarleiter: Dr. Reimund Albers Bearbeiter: Andreas Meyburg, Matrikel-Nr.: 2172110
2008 Jens Scherdin Andreas Meyburg Universität Bremen Juni 2008 Der Satz von Gérard Desargues Veranstaltung: Geometrie Seminarleiter: Dr. Reimund Albers Bearbeiter: Andreas Meyburg, Matrikel-Nr.: 2172110
