Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
|
|
|
- Babette Siegel
- vor 5 Jahren
- Abrufe
Transkript
1 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 7. Juni 03
2 Vorbemerkungen Bei diesen Blattern handelt es sich zur Zeit nur um eine begleitende Erganzung des Vorlesungsskriptes von Herrn Prof. Dr. Rannacher. Sie sind unvollstandig und viele Teile fehlen noch. Ich habe mich dennoch entschlossen, sie schon ins Netz zu stellen, damit hoffentlich einige Inkonsistenzen in der Notation aufgeklart werden konnen. Fur Hinweise auf Fehler bin ich immer dankbar. Bitte achten Sie aber immer darauf, dass das Datum Ihrer Ausgabe mit dem Im Internet ubereinstimmt. Mein Dank gilt auch Herrn David Stronczek fur seine Hilfe bei der Verfassung dieser Seiten.
3 Verzeichnis der Abkürzungen AWA Anfangswertaufgabe, s. Denition?? auf Seite?? BDF Backward dierencing formula, s. Beispiel.3 auf Seite 3 DGL Dierentialgleichung LMM Lineare Mehrschrittmethode, s. Denition.4 auf Seite 4 RKV Runge-Kutta-Verfahren
4 Inhaltsverzeichnis Explizite Einschrittmethoden und Konvergenz 4. Fehleranalyse Runge-Kutta-Verfahren Eingebettete Runge-Kutta-Verfahren Stetige Runge-Kutta-Verfahren Lineare Mehrschrittmethoden 3. Denition und Konsistenz Eigenschaften von Dierenzengleichungen Stabilitat und Konvergenz LMM fur steife Probleme
5 Kapitel Explizite Einschrittmethoden und Konvergenz Beispiel.. Gegeben sei die AWA u = u u(0) = Oensichtlich gilt u(t) = e t, jedoch erhalten wir fur h = mit der Eulerschen Polygonzugmethode folgendes Losung: y 0 = u 0 = y = y 0 + h 0 f(t 0, y 0 ) = y = 4 y 3 = 8... Man erkennt, dass der Fehler zunehmend anwachst. Diese Approximation der Losung lasst sich verbessern, indem man h verkleinert. Es stellt sicht jedoch die Frage, in welcher Art der (maximale) Fehler von der Schrittweite h abhangt. 4
6 . Fehleranalyse Bemerkung.. Bei Einschrittmethoden ist per denitionem jeder Schritt gleichartig. Daher ist es bei der Betrachtung von lokalen Eigenschaften grunds atzlich hinreichend, den ersten Schritt zu betrachten. Im folgenden werden also in der Regel Aussagen fur den Wert y abhangig von y 0 getroen, die sich dann auf den generellen Schritt von y n auf y n+ ubertragen. Definition.3. Sei u eine Losung der Dierentialgleichung u = f(t, u) zumindest auf dem Intervall [t n, t n+ ] der Lange h n = t n t n. Dann ist der Abschneidefehler deniert als τ n = u(t n) u(t n ) h n F ( h n ; t n, u(t n ), u(t n ) ). (.) Definition.4 (Konsistenzordnung). Die Einschrittmethode F(h; t, y) ist konsistent von Ordnung p mit der AWA, wenn fur den Abschneidefehler gilt: max n τ n ch p (.) Beispiel.5 (Euler-Verfahren). Um herauszunden, welche Konsistenzordnung das Euler-Verfahren hat, betrachten die wir die Tailor-Entwicklung der Losung am Punkt t n : u(t n ) = u(t n ) + h n u (t n ) + h nu (ξ) Daher reduziert sich der Abschneidefehler auf: τ n = u(t n) u(t n ) h n F(h; t n, u(t n )) = u(t n ) + h n f(t n, u n ) + h nu (ξ) u(t n ) h n f(t n ; u n ) = h nu (ξ) Fur u (ξ) gilt aber: u (ξ) = d dξ f(ξ, u(ξ)) = f(ξ, u(ξ)) + f(ξ, u(ξ)) ξ u u (ξ) }{{} =f(ξ,u(ξ)) Unter der Voraussetzung, dass f C auf einer kompakten Menge um den Graphen von u, ist dieser Term beschrankt. τ n ch n Das Eulerverfahren ist also konsistent von Ordnung. 5
7 Hilfssatz.6 (Diskrete Gronwallsche Ungleichung). Seien (w n ), (a n ) und (b n ) nicht negative, reele Zahlenfolgen mit w 0 b 0 und w n n a k w k + b n fur n. Falls b n monoton steigend ist, so gilt: ( n ) w n exp a k b n (.3) k= Beweis. Bitte uber die kontinuierliche Ungleichung Definition.7 (Diskrete Lipschitzbedingung). Eine Funktion F erfullt die diskrete Lipschitzbedingung, wenn es ein L > 0 gibt mit k=0 F(h; t, y) F(h; t, x) L x y (.4) Satz.8 (Diskrete Stabilitat). Wenn F(...) die Lipschitzbedingung erfullt, dann ist das Verfahren diskret stabil, d.h. fur beliebige Folgen (y n ) und (z n ) gilt y n z n e L(t t 0) ( y 0 z 0 + n h k (Ly) k (Lz) k ) Satz.9 (Konvergenz). Das Verfahren F(...) sei konsistent von Ordnung p und diskret stabil, ferner y 0 = u 0. Dann gilt: k= Das Verfahren konvergiert mit Ordnung p in der Form u(t n ) y n ce L(t n t 0 ) h p h = max h n n. Runge-Kutta-Verfahren Wir wollen nun Verfahren nden, mit denen wir Dierentialgleichungen numerisch losen konnen. Dazu bringen wir diese zunachst in eine andere Form: u (t) = f(t) u(t 0 ) = u 0 t u(t) = u 0 + f(s)ds t 0 Wir konnen das Losen von Dierentialgleichungen also als Quadraturaufgabe betrachten. Diese Uberlegung fuhrt zu einer Klasse von Verfahren zum Losen von Dierentialgleichungen, den Runge-Kutta-Verfahren. 6
8 Definition.0 (Explizites Runge-Kutta-Verfahren). i g i = y 0 + h b ij g j i =,..., r (.5a) j= k i = f(t 0 + ha i, g i ) i =,..., r (.5b) r y = y 0 + h c j k j (.5c) j= Anmerkung.. Die Zwischenwerte g i werden in typischen Implementationen nicht gesondert abgescpeichert, da man das Verfahren allein mit den Werten k i durchfuhren kann. Wir werden aber spater sehen, dass zur Diskussion die Werte g i durchaus nutzlich sein konnen. Aus den obigen Gleichungen lesen wir ab, dass g i eine approximation der Losung im Punkt t 0 +ha i darstellt. Definition. (Butcher-Tableau). Bei der Notation von Runge-Kutta-Verfahren ist es der Ubersichtlichkeit halber ublich, die Koezienten der Gleichungen (.5) in der folgenden Matrixform zu schreiben: 0 a b a 3 b 3 b a r b r b r b r,r c c c r c r (.6) Beispiel.3 (Die Eulersche Polygonzugmethode). Die Eulersche Polygonzugmethode besitzt folgendes Butcher-Schema: 0 Dieses fuhrt zur bereits bekannten Formel: y n+ = y n + h n f(t n, y n ) Beispiel.4 (Das modizierte Eulerverfahren). Das modizierte Eulerverfahren ist eine Abwandlung der Eulerschen Polygonzugmethode und besitzt folgendes Butcher-Schema: 0 0 7
9 Dieses fuhrt zur Formel: k = f(t n, y n ) k = f(t n + h n, y n + h n k ) y n+ = y n + h n k Beispiel.5 (Zweistuges Runge-Kutta-Verfahren). Das Heunsche Verfahren,.Ordnung: 0 k = f(t n, y n ) k = f(t n + h n, y n + h n k ) y n+ = y n + h n ( k + k ) Beispiel.6 (Dreistuges Runge-Kutta-Verfahren). 3.Ordnung: k = f(t n, y n ) k = f(t n + h n, y n + h nk ) k 3 = f(t n + h n, y n h n k + h n k ) y n+ = y n + h n ( 6 k k + 6 k 3) Beispiel.7 (Das klassische Runge-Kutta-Verfahren). 4.Ordnung:
10 k = f(t n, y n ) k = f(t n + h n, y n + h nk ) k 3 = f(t n + h n, y n + h nk ) k 4 = f(t n + h n, y n + h n k 3 ) y n+ = y n + h n ( 6 k + 6 k + 6 k k 4) Bemerkung.8 (Maximale Ordnungen fur explizite RKV). Die maximale Ordnung eines expliziten RKVs wird u.a. begrenzt durch die Anzahl der Stufen. Fur ein explizites RKV der Ordnung p benotigt man r Stufen, wobei p und r wie folgt zusammenhangen: p 4 5, r p p + p + p ? Fur p = 0 ist bisher nur ein Verfahren mit r = 7 bekannt. Moglicherweise gibt es ein Verfahren, dass mit weniger Stufen auskommt, ein Beweis fur die minimale Stufenanzahl ist zur Zeit noch nicht vorhanden. Da wir die exakte Losung einer DGL (i.a.) nicht kennen, konnen wir den Abschneidefehler i.d.r. nicht direkt berechnen. Deshalb suchen wir nach einer Moglichkeit, diesen zu schatzen. τ n+ = u(t n+ u(t n )) h n+ F(t, u(t n )) τ = u(t ) u(t 0 ) h F(t 0, u(t 0 )) = h (u(t ) y ) Unser Ziel ist es den Fehler u(t ) y durch ^y y zu approximieren. Dieses ^y konnen beispielsweise erhalten, indem wir das selbe Verfahren mit halber Schrittweite durchfuhren. Satz.9. Sei ^y das Ergebnis eines RKV der Ordnung p nach Schritten der Schrittweite h und y das Ergebnis nach einem Schritt der Schrittweite h. Dann gilt fur den Fehler: 9
11 u(t ) ^y = ^y y p + O(hp+ ) Ferner bekommt man eine Approximation ~y = y + y^ y mit p u(t ) ~y = O(h p+ ). Fur τ^ n bekommen wir damit eine Abschatzung der Form: ^ τ n = h ^y y p + O(hp+ ) Das heit fur h 0 konvergiert die Abschatzung gegen den Fehler. Beweis. Siehe Skript S. 6.. Eingebettete Runge-Kutta-Verfahren Alternativ zur Schatzung des Abschneidefehlers in Abschnitt.3. im Skript durch Verkleinerung der Schrittweite kann man auch Verfahren verschiedener Ordnung benutzen und deren Dierenz zur Schatzung des Abschneidefehlers zu benutzen. Ein besonders ezienter Weg, sich zwei Losungen mit verschiedener Ordnung zu verschaen sind die eingebetteten Runge-Kutta-Verfahren. Hier werden beide Losungen mit denselben Funktionsauswertungen berechnet, aber verschieden aufsummiert. Definition.0 (Eingebettete Runge-Kutta-Verfahren). Ein eingebettetes Runge- Kutta-Verfahren der Stufe r mit Konsistenzordnungen p und ^p berechnet zwei Losungen y und ^y mit denselben Funktionsauswertungen. Dazu werden zunachst Beitrage k i fur i =,..., r wie im normalen ERK der Stufe r berechnet. Die Funktionswerte am Ende des Zeitschritts ergeben sich dann als y n+ = y n + h c i k i ^y n+ = y n + h ^c i k i. (.7) Das Verfahren fur y habe im folgenden Konsistenzordnung p und das fur ^y die Konsistenzordnung ^p > p, zum Beispiel ^p = p +. 0
12 Definition.. Das Butcher-Tableau fur eingebettete Verfahren hat die Form 0 a b a 3 b 3 b a s b r b r b r,r c c c r c r ^c ^c ^c r ^c r Anmerkung.. Ein paar kurze Erlauterungen dazu: oberhalb der ersten Linie werden die Beitrage k i fur i =,..., r wie gewohnt berechnet. Dann berechnet man daraus die Losungen y n+ und^y n+ mit zwei verschiedenen Quadraturformeln. Anmerkung.3. Naturlich stellt sich die Frage, warum man nicht die Losung ^y n+ benutzt, wenn sie schon eine Ordnung besser ist. Bei der Anwendung des Verfahrens macht man das in der Tat so. Es bleibt aber zu beachten, dass die Abschatzung fur den Abbruchfehler nur fur die schlechtere Losung y n+ gilt. Anmerkung.4 (Adaptive Schrittweitensteuerung). Aufbauend auf den eingebetteten RKV lasst sich ein Verfahren mit adaptiver Schrittweitensteuerung ableiten, dass ^y y als Abschatzung fur den Fehler nutzt. Man geht dabei wie folgt vor: Vorgabe: ^y y TOL Berechne: ^y y = err = hτ. Falls err TOL, akzeptiere Zeitschritt.. Berechne h opt durch h opt = h ( ) TOL p+ err 3. Falls h opt < h: Wiederhole Zeitschritt mit h = h opt Benutze h = h opt im nachsten Zeitschritt... Stetige Runge-Kutta-Verfahren Die bisher vorgestellten RKV generieren Stutzpunkte zwischen denen wir dann linear interpolieren konnen. Wir wollen nun die Ordnung der Interpolation
13 erhohen, indem wir die g i benutzen um die Werte zwischen den Stutzpunkten zu berechnen. Wir mussen dabei beachten, dass die Fehler der g i i.d.r. von niedrigerer Ordnung sind. Es ist daher im Allgemeinen nicht hinreichend, diese Werte zu interpolieren. Stattdessen deniert man sich mit Hilfe der k i ein neues RKV, das in jedem Punkt ϑ [0, ] eine Approximation liefert. Definition.5. Ein stetiges RKV ist ein Verfahren vom Typ wie in Denition.0, bei dem die Koezienten c i durch stetige Funktionen c i (ϑ) auf dem Intervall [0, ] ersetzt werden. Damit wird Gleichung (.5c) ersetzt durch y(t 0 + ϑh) = y 0 + r i= c i (ϑ)k i. (.8) Hier darf die Stufenzahl r auch groer als r sein. Dann mussen zusatzliche Zwischenwerte k i generiert werden. Anmerkung.6. Falls r > r wahle k r+ = k = f(t n, y ) des nachsten Zeitschritts. Beispiel.7. Fur das klassische RKV mit 4 Stufen kann man eine stetige Interpolation mit r = r durch die Koezienten c (ϑ) = ϑ 3 ϑ + 3 ϑ3 c (ϑ) = c 3 (ϑ) = ϑ 3 ϑ3 c 4 (ϑ) = ϑ + 3 ϑ3 denieren. Fur dieses Verfahren ist der Fehler y(ϑ) u(ϑ) = O(h 3 ).
14 Kapitel Lineare Mehrschrittmethoden. Definition und Konsistenz Beispiel. (Adams-Bashforth-Formeln). Beispiel. (Adams-Moulton-Formeln). Beispiel.3. Backward dierencing formulas (BDF) oder Ruckwartsdierenzenformeln basieren zwar ebenfalls auf Lagrange-Interpolation in den Punkten t n R bis t n, benutzen aber keine Quadratur fur die rechte Seite, sondern die Ableitung des Interpolationspolynoms im Punkt t n. Seien L i (t) die Lagrange-Polynome fur die obigen Punkte. Wir machen den Ansatz y(t) = y n r L n r (t), wobei y n noch zu bestimmen ist. Nun fordern wir, dass y im Punkt t n die DGL lost, also y (t) = f(t n, y n ) = y n r L n r(t). Daraus ergeben sich die folgenden Schemata: R = y n y n = hf n (.) R = y n 4 3 y n + 3 y n = 3 hf n (.) R = 3 y n 8 y n + 9 y n y n 3 = 6 hf n (.3) R = 4 y n 48 5 y n y n 6 5 y n y n 4 = 5 hf n (.4) 3
15 Definition.4. Eine lineare Mehrschrittmethode (LMM) mit R Schritten ist ein Verfahren der Form α R r y n r = h β R r f n r, (.5) wobei f k = f(t k, y k ) und t k = t 0 + hk. Wir unterscheiden explizite (β R = 0) und implizite (β R 0) Methoden. Fur dieses Verfahren denieren wir das erste und das zweite charakteristische Polynom ρ(x) = α r x r σ(x) = β r x r. (.6) Anmerkung.5. Die LMM wurde oben fur konstante Schrittweite h deniert. Prinzipiell ist es auch moglich, die Methode mit variabler Schrittweite zu implementieren, doch beschranken wir uns fur die Analyse auf den konstanten Fall. Bemerkungen zur Schrittweitensteuerung nden sich spater in diesem Kapitel. Definition.6. Mit der LMM verbinden wir den linearen Dierenzenoperator (L h u)(t n ) = ( α R r u(t n k ) hβ R r f ( t n k, u(t n k ) )) (.7) und denieren fur eine stetige Funktion u den Abschneidefehler Hilfssatz.7. τ h (n) = h L hu(t n ). (.8) Definition.8. Eine LMM ist konsistent von Ordnung p, wenn fur all hinreichend regularen Funktionen u und alle relevanten n gilt: τ h (n) = O(h p ) (.9) Satz.9. Eine LMM ist konsistent von Ordnung p genau dann, wenn eine der folgenden aquivalenten Bedingungen erfullt ist: α r = 0 and ( αr r q qβ r r q ) = 0, q =,..., p (.0a) ρ(e h ) hσ(e h ) = O(h p+ ) h 0 (.0b) Beweis. 4
16 . Eigenschaften von Differenzengleichungen Definition.0. Eine Gleichung der Form α r y n+r = 0 (.) wird als homogene Dierenzengleichung bezeichnet. Eine Folge {y n } n=0,..., ist Losung der Dierenzengleichung, wenn die Gleichung fur alle n R erfullt ist. Die Folgenwerte y n konnen in R, C, R d oder C d liegen. Hilfssatz.. Die Losungen der Gleichung (.) mit y n C oder y n C bilden einen Vektorraum der Dimension R. Beweis. Da die Gleichung (.) linear und homogen ist, erf ullen fur zwei Losungsfolgen {y () } und {y () } oensichtlich auch ihre Summe und Vielfachen die Gleichung. Sobald die Startwerte y 0 bis y R gewahlt sind, sind alle weiteren Folgenglieder eindeutig bestimmt. Insbesondere gilt y 0 = y = = y R = 0 = y n = 0, n 0. Damit genugt es also, die ersten R Werte zu betrachten. Sind diese linear unabhangig, so sind es die gesamten Folgen, und umgekehrt. Es ist aber oensichtlich, dass diese Werte einen R-dimensionalen Vektorraum bilden. Definition.. Als charakteristisches Polynom der Dierenzengleichung (.) bezeichnen wir das Polynom χ(x) = α r x r. (.) Hilfssatz.3. Fur jede Nullstelle ξ des charakteristischen Polynoms χ(x) ist die Folge y n = ξ n eine Losung der Dierenzengleichung (.). Beweis. Einsetzen der Losung y n = ξ n in die Dierenzengleichung ergibt α r ξ n+r = ξ n R α r ξ r = ξ n χ(ξ) = 0. 5
17 Satz.4. Seien {ξ i } i=,...,ι die Nullstellen des charakteristischen Polynoms χ mit Vielfachheit ν i. Dann bilden die Folgen der Form y (i,k) n = n k ξ n i i =,..., ι; k =,..., ν i (.3) eine Basis fur den Raum der Losungen der Dierenzengleichung (.). Beweis. Zunachst bemerken wir, dass die Summe aus den Vielfachheiten der Nullstellen gerade den Grad des Polynoms ergibt, also R = ι ν i. i= Ferner wissen wir wegen Hilfssatz., dass R die Dimension des Losungsraums ist. Es wir zeigen, dass die Folgen {y (i,k) n } linear unabhangig sind. Dies ist zunachst klar fur die Folgen zu einem Index i. Es ist aber auch fur verschiedene Nullstellen klar, da fur n die Exponentialfunktion den Einu der Polynome immer anulliert. Es bleibt zu zeigen, dass die Folgen {y (i,k) n } tatsachlich Losungen der Dierenzengleichung sind. Fur k = 0 haben wir dies bereits im Hilfssatz.3 bewiesen. Exemplarisch fuhren wir hier den Beweis fur k = und eine doppelte Nullstelle ξ i durch. Gleichung (.) angewandt auf die Folge {nξ n i } ergibt α r (n + r)ξ n+r i = nξ n i α r ξ r i + ξ n+ i r= = nξ n i ρ(ξ i ) + ξ n+ i ρ (ξ i ) = 0. α r rξ r i Hierbei fallt gerade der Term mit α 0 weg, weil er mit r = 0 multipliziert wird. Korollar.5 (Wurzelkriterium). Alle Losungen {y n } der Dierenzengleichung (.) sind beschrankt fur n genau dann, wenn gilt: alle Nullstellen des charakteristischen Polynoms χ(x) liegen im abgeschlossenen Einheitskreis { z C z } und alle Nullstellen auf dem Rand des Einheitskreises sind einfach. Beweis. Nach Satz.4 konnen wir alle Losungen angeben. Aus ihrer Darstellung in Gleichung (.3) entnehmen wir, dass. Alle Losungen zu ξ i < fur n gegen null konvergieren 6
18 . Alle Losungen zu ξ i > fur n gegen unendlich konvergieren 3. Alle Losungen zu ξ i = fur n genau dann beschrankt bleiben, wenn ξ i einfach ist. Dies beweist die Aussage des Satzes..3 Stabilität und Konvergenz Bemerkung.6. Im Gegensatz zu Einschrittverfahren folgt bei linearen Mehrschrittmethoden die Konvergenz nicht unmittelbar aus der Konsistenz der Methode, wenn die rechte Seite der Dierentialgleichung der Lipschitz-Bedingung (??) genugt. Analog zur A-Stabilitat werden wir dies im folgenden anhand eines einfachen Modellproblems diskutieren und eine Stabilitatsbedingung herleiten. Bemerkung.7. Im folgenden untersuchen wir die Losung zu einem festen Zeitpunkt t mit immer kleiner werdender Schrittweite h. Dazu wahlen wir n Schritte der Schrittweite h = t/n und lassen dann n gegen unendlich gehen. Definition.8. Eine LMM ist nullstabil, wenn sie angewandt auf die triviale DGL u = 0 (.4) mit beliebigen Startwerten y 0 bis y R Losungen y n erzeugt, die zu jedem Zeitpunkt t > 0 beschrankt bleiben, wenn die Schrittweite h gegen null konvergiert. Beispiel.9.??Gegenbeispiel aus der Hausaufgabe??? Satz.0. Eine LMM ist genau dann nullstabil, wenn alle Nullstellen des ersten charakteristischen Polynoms ρ(x) aus Gleichung (.6) im Einheitskreis der komplexen Zahlenebene liegen und alle Nullstellen auf dem Rand des Einheitskreises einfach sind. Beweis. Die Anwendung der LMM auf die Gleichung (.4) ergibt die Dierenzengleichung α R r y n r = 0. Wir haben nun nachzuweisen, dass ihre Losungen fur festes t = hn beschrankt bleiben, wenn h 0. Wir sehen aber, dass obige Gleichung kein h enthalt. Daher mussen wir nun untersuchen, ob die Losungen y n fur n beschrankt bleiben. Durch Umsortieren der Summation erhalten wir eine Dierenzengleichung der Form (.). Aus Korollar.5 folgt dann die Aussage des Satzes. 7
19 Korollar.. Die Adams-Bashforth- und Adams-Moulton-Verfahren sind nullstabil. Beweis. Bei allen diesen Verfahren ist das erste Charakteristische Polynom ρ(x) = x R x R. Dieses hat die einfache Nullstelle ξ = und die R - fache Nullstelle 0. Satz.. Die BDF-Verfahren sind nullstabil fur R 6 und nicht nullstabil fur R 7..4 LMM für steife Probleme Definition.3. Das Stabilitatspolynom einer LMM ergibt sich analog zu den Einschrittverfahren aus der Anwendung der Methode auf die DGL u = λu. Wir erhalten fur die Losung die Dierenzengleichung ( αr r hλβ R r )y n r. (.5) Wir erhalten damit wie dort durch Einsetzen von z = hλ und den Ansatz y n = x n r(x, z) = ( αr r zβ R r )x R r. (.6) Anmerkung.4. Anstelle der einfachen Verstarkungsfunktion r(z) der Einschrittverfahren erhalten wir hier eine Funktion von zwei Variablen, dem Punkt z fur den wir Stabilitat zeigen wollen und der kunstlichen Variablen x aus der Verfahrensanalyse. Definition.5. Das Stabilitatsgebiet einer LMM ist die Menge der Punkte z C, fur die alle Losungensfolgen {y n } der Gleichung (.5) fur n beschrankt bleiben. Eine LMM heit A-stabil, wenn das Stabilitatsgebiet die linke Halbebene von C enthalt. Hilfssatz.6. Ein Punkt z C liegt im Stabilitatsgebiet einer LMM, wenn fur das die Nullstellen des Stabilitatspolynoms r(x, z) als Funktion von x das Wurzelkriterium in Korollar.5 gilt. Beweis. Der Beweis ist analog zu Satz.0. 8
20 Satz.7 (. Dahlquistschranke). Es gibt keine A-stabile LMM mit Ordnung p >. Unter den A-stabilen LMM der Ordnung hat die Trapezregel?? die kleinste Fehlerkonstante. Definition.8. Eine Methode heit A(α)-stabil, wenn ihr Stabilitatsgebiet den Sektor { } z C Rz < 0 Iz Rz tan α enthalt. Sie heit A(0)-stabil, wenn die negative reelle Achse im Stabilitatsgebiet enthalten ist. Anmerkung.9. Die Einfuhrung der A(0)-Stabilitat ist motiviert durch lineare Systeme der Form u = Au mit symmetrisch, positiv deniter Matrix A. In der Tat benotigt man dort, da alle Eigenwerte reell sind, nur Stabilitat auf der reellen Achse. Ebenso sind A(α)-stabile LMM geeignet fur lineare Probleme, bei denen hochfrequente Schwingungen (Iλ gro) schnell abklingen ( Rλ gro). In beiden Fallen sind fur die Anwendung auf nichtlineare Probleme entsprechende Eigenschaften der Jacobimatrix u f zu betrachten. 9
Numerik gewöhnlicher Differentialgleichungen. Prof. Dr. Guido Kanschat
 Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
Numerik gewöhnlicher Differentialgleichungen Prof. Dr. Guido Kanschat 19. Juni 2013 Vorbemerkungen Bei diesen Blättern handelt es sich zur Zeit nur um eine begleitende Ergänzung des Vorlesungsskriptes
10 Stabilität und steife Systeme
 Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
Numerik II 34 Stabilität und steife Systeme Inhalt. Absolute Stabilität. Was sind steife Differentialgleichungen?.3 Weitere Stabilitätsbegriffe Stabilität und steife Systeme TU Bergakademie Freiberg, SS
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen
 TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
TU Ilmenau Institut für Mathematik Übungsaufgaben zum Lehrgebiet Numerische Mathematik III Numerik gewöhnlicher Differentialgleichungen Datei: NM34.TEX Serie 6 Mehrschrittverfahren (MSV) 1. Die allgemeine
Adaptive Mehrschrittverfahren
 Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Adaptive Mehrschrittverfahren Moritz Neumann 21. März 2011 1 Inhaltsverzeichnis 1 Vorwort 3 2 Einführung 3 3 Adaptive Seuerung der Schrittweite und Ordnung 5 3.1 Adams-Verfahren................................
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
3. Lineare Mehrschrittverfahren 3.1 Begriffe
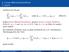 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Übungsblatt 10 Musterlösung
 Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Übungsblatt 0 Musterlösung Numerik gewöhnlicher Differentialgleichungen MA2304 - SS6 Aufgabe 45 Fehlerkonstante von MSV Betrachten Sie ein allgemeines lineares q Schrittverfahren α q j y i+ j = h β q j
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Seminar Gewöhnliche Dierentialgleichungen
 Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren
 Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
Kurze Einführung zu Stabilität bei Differentialgleichungen und Einschrittverfahren Was sind typische qualitative Aussagen bei gewöhnlichen Differentialgleichungen der Form x (t) = f(t, x)? (1) 1. Andere
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
6.6 Lineare Dierentialgleichungen n-ter Ordnung mit konstanten Koezienten
 6.6 Lineare Dierentialgleichungen n-ter Ordnung mit konstanten Koezienten Dieser Abschnitt ist ein Einschub. Gewöhnliche DGL werden im nächsten Semester behandelt. Unter einer linearen gewöhnlichen DGL
6.6 Lineare Dierentialgleichungen n-ter Ordnung mit konstanten Koezienten Dieser Abschnitt ist ein Einschub. Gewöhnliche DGL werden im nächsten Semester behandelt. Unter einer linearen gewöhnlichen DGL
Lösung - Serie 25. D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 25 1. Wie lautet die charakteristische Gleichung der Differentialgleichung y + 2y + y = 0? (a) λ 3 + 2λ + 1 = 0 (b) λ 3 + 2λ = 0 (c)
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden.
 Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
Lösungsvorschläge zur ersten Klausur Gewöhnliche Differenzialgleichungen am 20.6.2015 um 10 Uhr. Bearbeitungszeit beträgt zwei Stunden. Prof. Dr. Wolfgang Arendt Manuel Bernhard Sommersemester 2015 Achten
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren
 Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
Seminar: Numerik gewöhnlicher Differentinalgleichungen Diagonal implizite Runge-Kutta Verfahren Manuel Hofmann 4..00 Einleitung Ziel dieser Arbeit ist es den Begriff der S-Stabilität einzuführen und im.
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Lineare Differentialgleichungen n-ter Ordnung
 KAPITEL 5 Lineare Differentialgleichungen n-ter Ordnung 1 Veränderliche Koeffizienten Analog zu den linearen Dierentialgleichungen 2 Ordnung gilt: 75 76 5 LINEARE DIFFERENTIALGLEICHUNGEN n-ter ORDNUNG
KAPITEL 5 Lineare Differentialgleichungen n-ter Ordnung 1 Veränderliche Koeffizienten Analog zu den linearen Dierentialgleichungen 2 Ordnung gilt: 75 76 5 LINEARE DIFFERENTIALGLEICHUNGEN n-ter ORDNUNG
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Lösung - Schnellübung 13
 D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
D-MAVT/D-MATL Analysis II FS 7 Dr. Andreas Steiger Lösung - Schnellübung 3. Gegeben sei die Differentialgleichung y + λ 4 y + λ y = 0. Für welche Werte des reellen Parameters λ gibt es eine von Null verschiedene
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Zweite Prüfung zur Vorlesung
 Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Prof O Scherzer P Elbau, L Mindrinos Numerische Mathematik Fakultät für Mathematik Universität Wien 4 Oktober 23 Zweite Prüfung zur Vorlesung Numerische Mathematik Erlaubte Hilfsmittel: Schriftliche Unterlagen
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
4. Runge-Kutta-Verfahren 4.1 Konstruktion und Beispiele
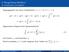 4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4. Konstruktion und Beispiele Ausgangspunkt wie immer (Substitution: s = t + τh, 0 τ ) y(t + h) = y(t) + [y(t + h) y(t)] = y(t) + = y(t) + h 0 y (t + τh) dτ. Approximiere Integral durch Quadraturformel
4 Funktionenfolgen und normierte Räume
 $Id: norm.tex,v 1.57 2018/06/08 16:27:08 hk Exp $ $Id: jordan.tex,v 1.34 2018/07/12 20:08:29 hk Exp $ 4 Funktionenfolgen und normierte Räume 4.7 Kompakte Mengen Am Ende der letzten Sitzung hatten wir zwei
$Id: norm.tex,v 1.57 2018/06/08 16:27:08 hk Exp $ $Id: jordan.tex,v 1.34 2018/07/12 20:08:29 hk Exp $ 4 Funktionenfolgen und normierte Räume 4.7 Kompakte Mengen Am Ende der letzten Sitzung hatten wir zwei
Wiederholung von Linearer Algebra und Differentialrechnung im R n
 Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT
 Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Prof. N. Hungerbühler ETH Zürich, Winter 6 Lösungen zur Prüfung Lineare Algebra I/II für D-MAVT. Hinweise zur Bewertung: Jede Aussage ist entweder wahr oder falsch; machen Sie ein Kreuzchen in das entsprechende
Kapitel 3 Der Fundamentalsatz der Algebra
 Kapitel 3 Der Fundamentalsatz der Algebra Dieser berühmte Satz wurde erstmals von C.F. Gauß 1801 in seiner Disseration bewiesen. Satz 3.1. Jedes nichtkonstante, komplexe Polynom n-ten Grades p(z) = n a
Kapitel 3 Der Fundamentalsatz der Algebra Dieser berühmte Satz wurde erstmals von C.F. Gauß 1801 in seiner Disseration bewiesen. Satz 3.1. Jedes nichtkonstante, komplexe Polynom n-ten Grades p(z) = n a
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Musterlösung Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
D-ITET, D-MATL Musterlösung Prüfung umerische Methoden, Sommer 01 Dr. Lars Kielhorn 1. a) z = exp(iϕ) = dz = i exp(iϕ) dϕ = c n [f] = 1 π f(exp(iϕ)) exp( iϕn) dϕ π 0 b) Allgemeine zusammengesetzte Trapezregel
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
8 Gewöhnliche Differentialgleichungen
 8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
8 Gewöhnliche Differentialgleichungen Beispiel: Radioaktiver Zerfall Sei m(t) die Menge radioaktiven Materials zur Zeit t. Der Zerfall des Materials geschieht proportional zur vorhandenen Menge mit dem
Zusatzmaterial zu Kapitel 6
 ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
ZU KAPITEL 62: METHODEN ZUR STABILITÄTSPRÜFUNG Zusatzmaterial zu Kapitel 6 Zu Kapitel 62: Methoden zur Stabilitätsprüfung Einleitung Bei der Feststellung der asymptotischen Stabilität (siehe Kapitel 63)
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Rheinisch-Westfälische Technische Hochschule. Gegeben seien eine gewöhnliche Dierentialgleichung (DGL) und ein Anfangswert. γ l K l.
 Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Rheinisch-Westfälische Technische Hochschule Institut für Geometrie und Praktische Mathematik Numerische Mathematik II Wintersemester 2009 Priv. Doz. Dr. Helmuth Jarausch Dr. KarlHeinz Brakhage Übung :
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
f f(x ɛξ) f(x) 0, d.h. f (x)ξ = 0 für alle ξ B 1 (0). Also f (x) = 0. In Koordinaten bedeutet dies gerade, dass in Extremstellen gilt: f(x) = 0.
 Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
Mehrdimensionale Dierenzialrechnung 9 Optimierung 9 Optimierung Definition Seien U R n oen, f : U R, x U x heiÿt lokales Maximum, falls eine Umgebung V U von x existiert mit y V : fx fy x heiÿt lokales
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
9 Numerische Verfahren für Anfangswertaufgaben
 Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
Numerik II 63 9 Numerische Verfahren für Anfangswertaufgaben Inhalt 9.1 Einige einfache Verfahren 9.2 Einschrittverfahren Definition und Eigenschaften 9.3 Runge-Kutta-Verfahren 9.4 Lineare Mehrschrittverfahren
8. Übungsblatt Aufgaben mit Lösungen
 8 Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Matrix Bestimmen Sie die allgemeine reelle Lösung des Differentialgleichungssystems u x = Aux für die A =, 9 indem Sie das System auf eine einzelne gewöhnliche
8 Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Matrix Bestimmen Sie die allgemeine reelle Lösung des Differentialgleichungssystems u x = Aux für die A =, 9 indem Sie das System auf eine einzelne gewöhnliche
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Rückblick auf die letzte Vorlesung
 Rückblick auf die letzte Vorlesung 1 Lineare autonome Differentialgleichungen 2 Bestimmung des Fundamentalsystems 3 Jordansche Normalform 4 Reelle Fundamentalsysteme Ausblick auf die heutige Vorlesung
Rückblick auf die letzte Vorlesung 1 Lineare autonome Differentialgleichungen 2 Bestimmung des Fundamentalsystems 3 Jordansche Normalform 4 Reelle Fundamentalsysteme Ausblick auf die heutige Vorlesung
Polynome und ihre Nullstellen
 Polynome und ihre Nullstellen 29. Juli 2017 Inhaltsverzeichnis 1 Einleitung 2 2 Explizite Berechnung der Nullstellen 2.1 Polynome vom Grad 0............................. 2.2 Polynome vom Grad 1.............................
Polynome und ihre Nullstellen 29. Juli 2017 Inhaltsverzeichnis 1 Einleitung 2 2 Explizite Berechnung der Nullstellen 2.1 Polynome vom Grad 0............................. 2.2 Polynome vom Grad 1.............................
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel;
 Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Kapitel Der Satz von Taylor. Taylor-Formel und Taylor-Reihe (Taylor-Polynom; Restglied; Integraldarstellung des Restgliedes; Lagrangesche Restgliedformel; die Klasse C ; reell analytische Funktionen) In
Numerik und Simulation in der Geoökologie
 1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Klausur zur Vordiplom-Prüfung
 Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
Technische Universität Hamburg-Harburg SS Arbeitsbereich Mathematik Dr. Jens-Peter M. Zemke Klausur zur Vordiplom-Prüfung Numerische Verfahren. Juli Sie haben Minuten Zeit zum Bearbeiten der Klausur. Bitte
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Fortgeschrittene Mathematik Raum und Funktionen
 Fortgeschrittene Mathematik Raum und Funktionen Thomas Zehrt Universität Basel WWZ Thomas Zehrt (Universität Basel WWZ) R n und Funktionen 1 / 33 Outline 1 Der n-dimensionale Raum 2 R 2 und die komplexen
Fortgeschrittene Mathematik Raum und Funktionen Thomas Zehrt Universität Basel WWZ Thomas Zehrt (Universität Basel WWZ) R n und Funktionen 1 / 33 Outline 1 Der n-dimensionale Raum 2 R 2 und die komplexen
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Gewöhnliche Dierentialgleichungen
 Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
Prof. Dr. Guido Sweers WS 28/29 Jan Gerdung, M.Sc. Gewöhnliche Dierentialgleichungen Übungsblatt 6 Die Lösungen müssen in den Übungsbriefkasten Gewöhnliche Dierentialgleichungen Raum 3 im MI) geworfen
y hom (x) = C e p(x) dx
 Gewöhnliche Differentialgleichungen F (x, y, y,..., y n ) = 0 Gleichung, die die Veränderliche x sowie die Funktion y = y(x) und ihre Ableitungen y,..., y n beinhaltet. Klassifiaktion: implizit F (...)
Gewöhnliche Differentialgleichungen F (x, y, y,..., y n ) = 0 Gleichung, die die Veränderliche x sowie die Funktion y = y(x) und ihre Ableitungen y,..., y n beinhaltet. Klassifiaktion: implizit F (...)
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
D-ITET Analysis II FS 13 Prof. Horst Knörrer. Musterlösung 1. 3xy 2 = 2 x 2. y y. 3 y y. 3 x v x + v = 2 3 v v.
 D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
D-ITET Analysis II FS 3 Prof. Horst Knörrer Musterlösung. a) Es gilt: dy d 3 + y 3 3y 3 y + y 3. Dies ist eine homogene Differentialgleichung, das heisst y hängt nur von y ab. Setze v : y y() v() y v +
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 22 3. Funktionen. Grenzwerte.
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 22 3. Funktionen. Grenzwerte.
Grundlagen der Numerischen Mathematik II
 J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
1/26. Integration. Numerische Mathematik 1 WS 2011/12
 1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
1/26 Integration Numerische Mathematik 1 WS 2011/12 Notation 2/26 Die Abbildung I b a : C([a, b]) R gegeben durch Ia b (f ) := beschreibt die Integration. b a f (x)dx, Um das Integral I(f ) zu approximieren
5. Funktional-Gleichung der Zetafunktion
 5. Funktional-Gleichung der Zetafunktion 5.. Satz (Poissonsche Summenformel. Sei f : R C eine stetig differenzierbare Funktion mit und sei f(x O( x und f (x O( x für x ˆf(t : f(xe πixt dx. die Fourier-Transformierte
5. Funktional-Gleichung der Zetafunktion 5.. Satz (Poissonsche Summenformel. Sei f : R C eine stetig differenzierbare Funktion mit und sei f(x O( x und f (x O( x für x ˆf(t : f(xe πixt dx. die Fourier-Transformierte
(a), für i = 1,..., n.
 .4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
.4 Extremwerte Definition Sei M R n eine Teilmenge, f : M R stetig, a M ein Punkt. f hat in a auf M ein relatives (oder lokales) Maximum bzw. ein relatives (oder lokales) Minimum, wenn es eine offene Umgebung
Dr. R. Käppeli D-ITET, D-MATL Sommer Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Sommer 217 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 9 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=1 Seiten) eigenhändig und handschriftlich
Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) = sin(πx) und geben die folgenden Stützstellen und Stützwerte vor:
 5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
5 Splineinterpolation Beispiel für eine periodische Spline-Interpolationsfunktion: Wir betrachten f(x) sin(πx) und geben die folgenden Stützstellen und Stützwerte vor: x i 3 f i Damit ist n 5, h Forderung
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Dr. R. Käppeli D-ITET, D-MATL Winter Numerische Methoden Punkte
 Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Dr. R. Käppeli D-ITET, D-MATL Winter 2018 Prüfung Numerische Methoden Wichtige Hinweise Die Prüfung dauert 90 Minuten. Erlaubte Hilfsmittel: 5 A4-Blätter doppelseitig (=10 Seiten) eigenhändig und handschriftlich
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Floquet Theorie II. 1 Einführung
 Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 18.10.2011 Sebastian Monschang 1 Einführung Auf den Ergebnissen des ersten Vortrags basierend werden wir in diesem Vortrag gewöhnliche lineare Differentialgleichungssysteme
Vortrag zum Seminar Gewöhnliche Differentialgleichungen, 18.10.2011 Sebastian Monschang 1 Einführung Auf den Ergebnissen des ersten Vortrags basierend werden wir in diesem Vortrag gewöhnliche lineare Differentialgleichungssysteme
Analysis 4. Lösungsvorschlag zum 12. Übungsblatt
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Andreas Geyer-Schulz SS 208. Juli 208 Analysis 4 Lösungsvorschlag zum 2. Übungsblatt Aufgabe 42 Wir untersuchen
Numerik gewöhnlicher Differentialgleichungen (MA2304) Modulprüfung F. Bornemann, C. Ludwig 14. August 2017
 Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Numerik gewöhnlicher Differentialgleichungen (MA234) Modulprüfung F. Bornemann, C. Ludwig 4. August 27 Aufgabe ( min) (a) Implementiere in Julia mit den Eingaben a, b, f und n die summatorische Trapez-Regel
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Übungen zur Vorlesung. Einführung in Dynamische Systeme. Musterlösungen zu Aufgabenblatt 1
 Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
Prof. Roland Gunesch Sommersemester 00 Übungen zur Vorlesung Einführung in Dnamische Ssteme Musterlösungen zu Aufgabenblatt Aufgabe : Sei A 0 4. a Bestimmen Sie für jeden Anfangswert 0 R das Verhalten
12 Gewöhnliche Differentialgleichungen
 12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
12 Gewöhnliche Differentialgleichungen 12.1 Der Satz von Picard-Lindelöf 12.1.1 Definition (Explizite Differentialgleichung erster Ordnung) Ω 1 R, Ω 2 R n seien offen und f : Ω 1 Ω 2 R n, (x,y) f (x,y)
Wann heit eine Menge reeller Zahlen beschrankt? oen? abgeschlossen? Was ist das Supremum (Inmum) Maximum (Minimum) einer Teilmenge
 1 1 Check-Liste Analysis 1.1 Mengen und Abbildungen Wann heit eine Menge reeller Zahlen beschrankt? oen? abgeschlossen? kompakt? Was ist das Supremum (Inmum) Maximum (Minimum) einer Teilmenge von R? Was
1 1 Check-Liste Analysis 1.1 Mengen und Abbildungen Wann heit eine Menge reeller Zahlen beschrankt? oen? abgeschlossen? kompakt? Was ist das Supremum (Inmum) Maximum (Minimum) einer Teilmenge von R? Was
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Aufgaben GDGL SS 1998
 Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
Aufgaben GDGL SS 1998 Frank Wübbeling 17. September 1998 Aufgabe 1: (4 Punkte) Stellen Sie eine Differentialgleichung 1. Ordnung auf für die Schar der Parabeln mit der x-achse als Achse und dem Ursprung
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
2 Der Weierstraßsche Produktsatz
 4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
