Mathematik für Ingenieure A III Wintersemester 2008
|
|
|
- Ilse Biermann
- vor 5 Jahren
- Abrufe
Transkript
1 1 / 48 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III
2 2 / 48 Wiederholung Potentialfelder, Stammfunktionen für Vektorwertige Abbildungen 1. Hauptsatz für Kurvenintegrale 2. Hauptsatz für Kurvenintegrale
3 Beispiel Berechnen Sie eine Stammfunktion für V 1 (x,y,z) V(x,y,z) = V 2 (x,y,z) := V 3 (x,y,z) auf dem Gebiet G = R 3! y 2 cosx 2ysinx + e 2z 2ye 2z 3 / 48
4 4 / 48 Beispiel Das Gebiet G = R 3 ist einfach zusammenhängend. Jacobimatrix von V ist: J V = J V = V 1 x V 2 x V 3 x V 1 y V 2 y V 3 y V 1 z V 2 z V 3 z y 2 sinx 2ycosx 0 2ycosx 2sinx 2e 2z 0 2e 2z 4ye 2z
5 5 / 48 Berechnung der Stammfunktion Es gibt eine Funktion f (x,y,z) mit f x f = = f y f z f x f y f z = 1. f x = y 2 cosx = f = y 2 sin x + c(y,z) y 2 cosx 2ysinx + e 2z 2ye 2z = V 2. f y = 2ysin x + c y (y,z) = 2ysinx + e 2z = c y (y,z) = e 2z = c(y,z) = ye 2z + d(z) 3. f z = ( y 2 sin x + ye 2z + d(z) ) z = 2ye2z + d (z) = 2ye 2z = d (z) = 0 = d(z) = d = const 4. f (x,y,z) = y 2 sin x + ye 2z + d
6 6 / 48 Flächen Integration auf Flächen
7 Flächen Wie stellt man formelmäßig eine Fläche im R 3 dar? Beispiel: Die Oberfläche einer Halbkugel mit Radius R Implizite Darstellung: x O = { y x 2 + y 2 + z 2 = R 2, z 0} = z x { y f (x,y,z) = 0, z 0} z 7 / 48
8 8 / 48 Flächen Graph einer Funktion: O ist der Graph der Funktion z = f (x,y) = R 2 x 2 y 2 auf der Menge D = {(x,y) R 2 x 2 + y 2 R 2 } O = { (Explizite Darstellung) x y f (x,y) (x,y) D}
9 Flächen Parameterdarstellung: Den Torus kann man nicht explizit darstellen. Jedem Punkt (x, y) entsprechen zwei z-koordinaten. Parameterdarstellung der Halbkugel: O = { r cos ϕ r sin ϕ R 2 r 2 0 r R, 0 ϕ < 2π} 9 / 48
10 10 / 48 Bereiche Für die Integration müssen die Definitionsbereiche der Parameterdarstellungen von Flächen einigermaßen regulär sein. Definition: Eine Teilmenge D R 2 heißt ein regulärer Bereich, wenn gilt - D ist abgeschlossen. - Der Rand D besteht aus einer stückweise glatten geschlossenen Kurve ohne Doppelpunkte. - Das Innere D von D ist ein Gebiet. Für die Integration sind auch noch Bereiche der Form D \ N zulässig, wo D ein regulärer Bereich und N eine Nullmenge ist.
11 11 / 48 Bereiche x- und y-projizierbare Mengen mit stetig differenzierbaren Randfunktionen x(y) < x(y) bzw. y(x) < y(x) sind reguläre Bereiche.
12 Flächen Definition: Eine Teilmenge S R 3 heißt eine Fläche, wenn es einen regulären Bereich D R 2 und eine stetige Abbildung x : D R 3 gibt, so dass S = { x(u,v) (u,v) D} x(u, v) heißt eine Parameterdarstellung von S. Bezeichnungen: x(u,v) = x 1 (u,v) x 2 (u,v) x 3 (u,v) oder x(u, v) = x(u, v) y(u, v) z(u, v) 12 / 48
13 13 / 48 Glatte Flächen Definition: Eine Fläche S = { x(u,v) R 3 (u,v) D} heißt eine glatte Fläche wenn sie eine Parameterdarstellung x(u, v) auf einem regulären Bereich D mit den folgenden Eigenschaften besitzt: 1. Es gibt ein Gebiet G D, so dass x(u,v) auf G stetig partiell differenzierbar ist. 2. Für je zwei beliebige Punkte (u,v) (u,v ) aus D gilt x(u,v) x(u,v ). 3. Für die Vektoren x u (u,v) = x 1 u (u,v) x 2 u (u,v) x 3 u (u,v) und x v (u,v) = und alle (u,v) D gilt x u (u,v) x v (u,v) 0. x 1 v (u,v) x 2 v (u,v) x 3 v (u,v)
14 14 / 48 Glatte Flächen Erläuterungen: zu 1. x muss auch in einer Umgebung des Rands von D stetig partiell differenzierbar sein. zu 2. Zwischen den Punkten aus D und denen der Fläche besteht eine eineindeutige Beziehung. Eine Fläche, die sich selbst durchschneidet, ist damit ausgeschlossen.
15 15 / 48 Glatte Flächen zu 3. Für festes v heißt die Kurve u x(u,v) die Parameterlinie v = const Für festes u heißt die Kurve v x(u,v) die Parameterlinie u = const x u (u 0,v 0 ) bzw. x v (u 0,v 0 ) sind Tangentialvektoren an die Parameterlinien v = const bzw. u = const im Punkt x(u 0,v 0 ) S.
16 Glatte Flächen zu 3. Die Eigenschaft x u (u,v) x v (u,v) 0 besagt, dass die Tangentialvektoren in jedem Punkt linear unabhängig sind. Die von den beiden Tangentialvektoren aufgespannte Ebene mit der Parameterdarstellung v(λ,µ) = λ x u (u 0,v 0 ) + µ x v (u 0,v 0 ) ist die Tangentialebene an die Fläche im Punkt x(u 0,v 0 ) S. 16 / 48
17 Glatte Flächen Der Vektor x u (u,v) x v (u,v) ist orthogonal zu x u (u,v) und zu x v (u,v) und zwar so, dass die drei Vektoren ein Rechtssystem bilden. Der normierte Vektor n(u,v) = x u(u,v) x v (u,v) x u (u,v) x v (u,v) heißt Flächennormale im Punkt x(u, v) S. 17 / 48
18 Stückweise glatte Flächen Rand einer glatten Fläche S: S := { x(u,v) (u,v) D} Eine stückweise glatte Fläche S ist die Vereinigung endlich vieler glatter Flächenstücke S i, von denen je zwei längs einem oder mehrerer gemeinsamer Randstücke aneinanderstoßen, aber sonst keine anderen Punkte gemeinsam haben. Der Rand S wird aus allen Randstücken gebildet, die nur zu einem der glatten Flächenstücke gehören. Ist S = /0, so heißt S geschlossen. 18 / 48
19 19 / 48 Beispiele zu Flächen Graphen: für (x,y) D x x = x(x,y) = 1 0 h x x y h(x, y), x y = 0 1 h y, x x x y = h x h y 1
20 20 / 48 Drehflächen Eine glatte Kurve ohne Doppelpunkte x(t) t 0 z(t) mit t 0 t t 1 und x(t) > 0 in der x-z- Ebene wird um die z-achse gedreht. Bei einer Drehung um den Winkel ϕ, 0 ϕ < 2π ergibt sich der Punkt cos ϕ sin ϕ 0 x(t) x(t)cos ϕ x(t,ϕ) = sin ϕ cos ϕ 0 0 = x(t)sin ϕ z(t) z(t)
21 21 / 48 Drehflächen x(t,ϕ) = x(t)cos ϕ x(t)sin ϕ z(t) Die Parameterlinien t = const heißen Breitenkreise, die Parameterlinien ϕ = const heißen Meridiane.
22 22 / 48 Drehflächen x(t,ϕ) = x(t)cos ϕ x(t)sin ϕ z(t), x t (t,ϕ) = x(t)cos ϕ x(t)sin ϕ z(t) x ϕ (t,ϕ) = x(t)sin ϕ x(t)cos ϕ 0, x t x ϕ = xżcos ϕ xżsin ϕ xẋ Die Voraussetzung x(t) > 0 ist erforderlich, damit die Regularitätsbedingung x t x ϕ = x 2 (ẋ 2 + ż 2 ) > 0 erfüllt ist.
23 23 / 48 Drehflächen Bei einer vollen Umdrehung fallen die Meridiane ϕ = 0 und ϕ = 2π zusammen. Die gesamte Drehfläche ist in diesem Fall nur stückweise glatt. Man setzt sie z.b. aus den beiden glatten Flächenstücken mit 0 ϕ π und π ϕ 2π zusammen.
24 24 / 48 Der Kegelstumpf Mantelfläche des Kegelstumpfs: x(t) = t, z(t) = b(1 t a ) a 0 t a. x(t,ϕ) = t cos ϕ t sin ϕ b(1 t a ) x t x ϕ =, a 0 t a, 0 ϕ 2π xżcos ϕ xżsin ϕ xẋ = b a t cos ϕ b a t sin ϕ t
25 25 / 48 Der Zylinder Mantelfläche des Zylinderstumpfs: x = r, z 0 z z 1 x(t,ϕ) = r cos ϕ r sin ϕ z x t x ϕ =, z 0 z z 1, 0 ϕ 2π xżcos ϕ xżsin ϕ xẋ = r cos ϕ r sin ϕ 0
26 26 / 48 Die Sphäre Oberfläche der Kugel mit Radius r: x(ψ) = r sin ψ, z(ψ) = r cos ψ 0 ψ π x(ψ,ϕ) = r sin ψ cos ϕ r sin ψ sin ϕ r cos ψ, 0 ψ π, 0 ϕ 2π x t x ϕ = xżcos ϕ xżsin ϕ xẋ = r 2 sin 2 ψ cos ϕ r 2 sin 2 ψ sin ϕ r sin ψ cos ϕ = (r sin ψ) x(ψ,ϕ)
27 27 / 48 Die Sphäre Das Vektorprodukt x t x ϕ = (r sin ψ) x(ψ,ϕ) ist an den Stellen ψ = 0 (Nordpol) und ψ = π (Südpol) gleich dem Nullvektor. Da die beiden Punkte eine Nullmenge darstellen, stört das nicht.
28 28 / 48 Der Torus Die Ringfläche entsteht durch Drehung des Kreises x(ψ) = R + r sin ψ, z(ψ) = r cos ψ 0 ψ 2π mit festen inneren und äußeren Radien r und R. x(ψ,ϕ) = (R + r sin ψ)cos ϕ (R + r sin ψ)sin ϕ r cos ψ, 0 ψ 2π, 0 ϕ 2π Der Torus ist eine stückweise glatte Fläche mit leerem Rand.
29 29 / 48 Die Wendelfläche Die Wendelfläche entsteht durch Schraubung einer Geraden, die die Schraubachse senkrecht schneidet. x(r,ϕ) = r cos ϕ r sin ϕ aϕ, r 0 r r 1, ϕ 0 ϕ ϕ 1
30 Das Vektorprodukt Für die Darstellung von Flächenintegralen benötigen wir einige Eigenschaften des Vektorprodukts, die im ersten Semester hergeleitet wurden. Definition: Für zwei Vektoren a = (a 1,a 2,a 3 ) und b = (b 1,b 2,b 3 ) heißt a b := das Vektorprodukt von a und b a 2 b 3 a 3 b 2 a 3 b 1 a 1 b 3 a 1 b 2 a 2 b 1 30 / 48
31 31 / 48 Rechenregeln (1) a a = 0 (2) (λ a) b = a (λ b) = λ( a b) (3) a und b sind genau dann linear abhängig, wenn a b = 0 (4) ( a + b) c a ( b + c) = a c + b c = a b + a c (5) a b = b a (6) Das Assoziativgesetz ist für das Vektorprodukt i.a. nicht erfüllt
32 32 / 48 Rechenregeln (7) a b ist orthogonal zu a und zu b (8) Sind a und b linear unabhängig, so bilden a, b und a b eine positiv orientierte Basis. (9) a b 2 = a 2 b 2 ( a b) 2 Für die Tangentialvektoren x u und x v einer Fläche heißen E := x u 2, F := x u x v und G := x v 2 die metrischen Fundamentalgrößen. Es ist daher x u x v = EG F 2
33 33 / 48 Geometrische Interpretation a und b seien linear unabhängig. a b = a b sin(α) = a b sin(α) a b ist die Fläche des durch a und b beschriebenen Parallelogramms.
34 34 / 48 Das Spatprodukt Für drei beliebige Vektoren a, b, c des R 3 heißt die reelle Zahl a ( b c) das Spatprodukt aus a, b und c Spat (oder Parallelepiped) Der Absolutbetrag a ( b c) ist das Volumen des Spats.
35 Der Flächeninhalt Wie berechnet man den Flächeninhalt einer glatten Fläche S = { x(u,v) (u,v) D}? Wir betrachten einen rechteckigen regulären Bereich D = {(u,v) a u b, c v d} Durch Zerlegungen der Intervalle [a, b] und [c, d] Z 1 : a = u 0 < u 1 <...u m = b Z 2 : c = v 0 < v 1 <...v n = d wird D in Teilrechtecke G ij = {(u,v) u i u u i+1, v j v v j+1 } unterteilt, denen die Flächenstücke S ij = { x(u,v) (u,v) G ij } entsprechen. 35 / 48
36 Der Flächeninhalt 36 / 48
37 37 / 48 Der Flächeninhalt Das Flächenstück S ij wird approximiert durch das entsprechende Teilstück der Tangentialfläche an S im Punkt x(u i,v j ) F ij = { v(s,t) = x + s x u + t x v ) 0 s u i+1 u i, 0 t v j+1 v j } wobei x, x u und x v jeweils an der Stelle (u i,v j ) ausgewertet werden:
38 38 / 48 Der Flächeninhalt Aus der Taylorentwicklung von x folgt, daß wegen x(u i + s,v j + t) v(s,t) = x(u i,v j ) + s x u (u i,v j ) + t x v (u i,v j ) die Fläche S ij für kleine Bereiche G ij gut durch F ij approximiert wird. Mit u i = u i+1 u i und v j = v j+1 v j ist F ij das von den Vektoren u i x u (u i,v j ) und v j x v (u i,v j ) aufgespannte Parallelogramm. Der Flächeninhalt von F ij ist daher gegeben durch F ij = ( u i x u (u i,v j )) ( v j x v (u i,v j )) = x u (u i,v j ) x v (u i,v j ) u i v j
39 39 / 48 Der Flächeninhalt Die Summe aller dieser Flächeninhalte ist ein Näherungswert für den Flächeninhalt von S, wobei die Näherung mit wachsender Feinheit der Zerlegung immer besser wird. Falls der Grenzwert existiert: lim x u (u i,v j ) x v (u i,v j ) u i v j = Z 1 0, Z 2 0 i,j x u (u,v) x v (u,v) d(u,v) stellt er den Flächeninhalt von S dar. D
40 Der Flächeninhalt Definition: Ist D R 2 ein regulärer Bereich und S = { x(u,v) (u,v) D} eine glatte Fläche, so existiert das Integral S ds := und heißt der Flächeninhalt von S. D x u (u,v) x v (u,v) d(u,v) 40 / 48
41 Der Flächeninhalt Anmerkungen 1. ds = x u (u,v) x v (u,v) d(u,v) nennen wir infinitesimales Flächenelement. 2. Mit den metrischen Fundamentalgrößen E := x u 2, F := x u x v und G := x v 2 lautet die Berechnungsformel für den Flächeninhalt ds := EG F 2 d(u,v) S D 3. Ist S eine stückweise glatte Fläche, die aus den glatten Flächenstücken S 1,S 2,...,S m zusammengesetzt ist, so definieren wir S ds := ds + ds ds S 1 S 2 S m 41 / 48
42 42 / 48 Beispiel: Oberfläche eines Graphen für (x,y) D x x = x(x,y) = 1 0 h x S x y h(x, y), x y = ds = D 0 1 h y, x x x y = 1 + h 2 x(x,y) + h 2 y(x,y)d(x,y) h x h y 1
43 Beispiel: Drehflächen Eine glatte Kurve ohne Doppelpunkte x(t) t 0 z(t) mit t 0 t t 1 und x(t) > 0 in der x-z- Ebene wird um die z-achse gedreht. 43 / 48
44 44 / 48 Beispiel: Drehflächen x(t,ϕ) = x(t)cos ϕ x(t)sin ϕ z(t), x t (t,ϕ) = x(t)cos ϕ x(t)sin ϕ z(t) x ϕ (t,ϕ) = x(t)sin ϕ x(t)cos ϕ 0, x t x ϕ = xżcos ϕ xżsin ϕ xẋ
45 45 / 48 Beispiel: Drehflächen Wegen x t x ϕ = x 2 (ẋ 2 + ż 2 ) = x ẋ 2 + ż 2 lautet die allgemeine Formel für den Flächeninhalt S ds = t1 ϕ1 t 0 ϕ 0 x(t) ẋ 2 (t) + ż 2 (t)dϕdt = t1 (ϕ 1 ϕ 0 ) x(t) ẋ 2 (t) + ż 2 (t)dt t 0 für 0 ϕ 0 < ϕ 1 2π.
46 46 / 48 Beispiel: Kugeloberfläche x(ψ,ϕ) = r sin ψ cos ϕ r sin ψ sin ϕ r cos ψ, 0 ψ π, 0 ϕ 2π
47 47 / 48 Beispiel: Kugeloberfläche x ψ x ϕ = wobei xżcos ϕ xżsin ϕ xẋ = r 2 sin 2 ψ cos ϕ r 2 sin 2 ψ sin ϕ r 2 sin ψ cos ψ = (r sin ψ) x(ψ,ϕ) (r sin ψ) x(ψ,ϕ) = r sin ψ x(ψ,ϕ) = r 2 sin ψ S ds = π 2π 0 0 π r 2 sin ψ dϕdψ = 2πr 2 sin ψ dψ = 4πr 2 0
48 48 / 48 Beispiel: Oberfläche eines Torus x(ψ,ϕ) = (R + r sin ψ)cos ϕ (R + r sin ψ)sin ϕ r cos ψ S, 0 ψ 2π, 0 ϕ 2π ds = 4π 2 rr
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 76 Mathematik für Ingenieure A III Wintersemester 28 J. Michael Fried Lehrstuhl Angewandte Mathematik III 12.11.28 2 / 76 Wiederholung Glatte Flächen Wiederholung Vektorprodukt Definition Flächeninhalt
1 / 76 Mathematik für Ingenieure A III Wintersemester 28 J. Michael Fried Lehrstuhl Angewandte Mathematik III 12.11.28 2 / 76 Wiederholung Glatte Flächen Wiederholung Vektorprodukt Definition Flächeninhalt
(u, v) z(u, v) u Φ(u, v) (v = const.) Parameterlinie v = const. v Φ(u, v) (u = const.) Parameterlinie u = const.
 13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
Oberflächenintegrale
 KAPITEL Oberflächenintegrale. Integration über Flächen im Raum.................. 36.2 Flächeninhalt.............................. 366.3 Oberflächenintegrale. und 2. Art.................. 369 Lernziele
KAPITEL Oberflächenintegrale. Integration über Flächen im Raum.................. 36.2 Flächeninhalt.............................. 366.3 Oberflächenintegrale. und 2. Art.................. 369 Lernziele
6.4 Oberflächenintegrale 1. und 2. Art
 6.4 Oberflächenintegrale. und. Art 6.4. Integration über Flächen im Raum Es gibt verschiedene Möglichkeiten der arstellung von Flächen im Raum:. explizite arstellung als Graph z = f(x, y), was aber eigentlich
6.4 Oberflächenintegrale. und. Art 6.4. Integration über Flächen im Raum Es gibt verschiedene Möglichkeiten der arstellung von Flächen im Raum:. explizite arstellung als Graph z = f(x, y), was aber eigentlich
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 35 Mathematik für Ingenieure A III Wintersemester 28 J. Michael Fried Lehrstuhl Angewandte Mathematik III 21.11.28 2 / 35 Wiederholung Divergenz und Rotation Gradient und Laplace-Operator Merkregeln
1 / 35 Mathematik für Ingenieure A III Wintersemester 28 J. Michael Fried Lehrstuhl Angewandte Mathematik III 21.11.28 2 / 35 Wiederholung Divergenz und Rotation Gradient und Laplace-Operator Merkregeln
Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form
 155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form. ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können.
 142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Höhere Mathematik Vorlesung 7
 Höhere Mathematik Vorlesung 7 Mai 2017 ii Phantasie ist wichtiger als Wissen, denn Wissen ist begrenzt. Albert Einstein 7 Flächenintegrale Flächen Reguläre Flächen: ei D R 2 regulär. Unter einer Fläche
Höhere Mathematik Vorlesung 7 Mai 2017 ii Phantasie ist wichtiger als Wissen, denn Wissen ist begrenzt. Albert Einstein 7 Flächenintegrale Flächen Reguläre Flächen: ei D R 2 regulär. Unter einer Fläche
Höhere Mathematik für Ingenieure 2
 Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt
 Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
Übungen zur Ingenieur-Mathematik III WS 2012/13 Blatt 9 19.12.2012 Aufgabe 35: Thema: Differenzierbarkeit a) Was bedeutet für eine Funktion f : R n R, dass f an der Stelle x 0 R n differenzierbar ist?
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Klausur HM II/III F 2003 HM II/III : 1
 Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
Klausur HM II/III F 3 HM II/III : Aufgabe : (7 Punkte) Untersuchen Sie die Funktion f : R R gegeben durch x 3 y 3 f(x, y) x + y sin, (x, y) (, ) x + y, (x, y) (, ) auf Stetigkeit und Differenzierbarkeit.
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Differentialgeometrische Eigenschaften von Kurven und Flächen
 Kapitel 5 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen
Kapitel 5 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen
Seite 1. sin 2 x dx. b) Berechnen Sie das Integral. e (t s)2 ds. (Nur Leibniz-Formel) c) Differenzieren Sie die Funktion f(t) = t. d dx ln(x + x3 ) dx
 Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
19.3 Oberflächenintegrale
 19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 11: e Prof. Dr. Erich Walter Farkas Mathematik I+II, 11. Linienintegrale 1 / 39 1 Ein einführendes Beispiel 2 3 Prof. Dr. Erich
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 11: e Prof. Dr. Erich Walter Farkas Mathematik I+II, 11. Linienintegrale 1 / 39 1 Ein einführendes Beispiel 2 3 Prof. Dr. Erich
Mehrfachintegrale 1-E1. Ma 2 Lubov Vassilevskaya
 Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Mehrfachintegrale 1-E1 1-E2 Mehrfachintegrale c Die Erweiterung des Integralbegriffs führt zu den Mehrfachintegralen, die in den naturwissenschaftlich-technischen Anwendungen u.a. bei der Berechnung der
Block I: Integration und Taylorentwicklung in 1D
 Wiederholungsübungen zur Ingenieur-Mathematik III WS 5/6 Blatt 3..6 Block I: Integration und Taylorentwicklung in D Aufgabe : Berechnen Sie die Integrale: a) π sin x cos x dx b) ( x) +x dx c) x e x dx
Wiederholungsübungen zur Ingenieur-Mathematik III WS 5/6 Blatt 3..6 Block I: Integration und Taylorentwicklung in D Aufgabe : Berechnen Sie die Integrale: a) π sin x cos x dx b) ( x) +x dx c) x e x dx
1. Juli F k x k (X), X D. k=1 (X) F. x 2 (X) F 3. x 1 F 2. F 1 (X). rot F (X) = F n (X) = F j x i. , 1 i, j 3
 . Juli 28 3 9 Vektoranalysis 9. Divergenz und otation Es sei D n offen und = [,..., n ] T sei stetig differenzierbares Vektorfeld. Unter der Divergenz des Vektorfeldes versteht man den Ausdruck div = n
. Juli 28 3 9 Vektoranalysis 9. Divergenz und otation Es sei D n offen und = [,..., n ] T sei stetig differenzierbares Vektorfeld. Unter der Divergenz des Vektorfeldes versteht man den Ausdruck div = n
16 Oberflächenintegrale
 16 Oberflächenintegrale Nachdem wir im vergangenen Abschnitt gesehen haben, wie man das Volumen eines dreidimensionalen Körpers z.b. das Volumen einer Kugel) mit Hilfe der Integralrechnung bestimmen kann,
16 Oberflächenintegrale Nachdem wir im vergangenen Abschnitt gesehen haben, wie man das Volumen eines dreidimensionalen Körpers z.b. das Volumen einer Kugel) mit Hilfe der Integralrechnung bestimmen kann,
Grundzüge der Vektoranalysis
 KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
KAPITEL 7 Grundzüge der Vektoranalysis 7. Satz von Green................................... 2 7.2 Satz von Stokes................................... 22 7.2. Zirkulation und Wirbelstärke..........................
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
Anleitungsaufgaben zu. Analysis III für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2011/12 Dr. K. Rothe Anleitungsaufgaben zu Analysis III für Studierende der Ingenieurwissenschaften Aufgabe 1: Für die folgenden Funktionen f : IR 2
Fachbereich Mathematik der Universität Hamburg WiSe 2011/12 Dr. K. Rothe Anleitungsaufgaben zu Analysis III für Studierende der Ingenieurwissenschaften Aufgabe 1: Für die folgenden Funktionen f : IR 2
5 5 5 Abbildung : Raumkurve Abbildung 5: Tangente t existiert nur dann, wenn _ ~x(t ) = ist. Ein Punkt mit f _x; _y; _zg = f; ; g heißt ein regulärer
 3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
Integralrechnung für Funktionen mehrerer Variabler
 Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 11. Juli 2016 Ableitungen im Höherdimensionalen Im Eindimensionalen war die Ableitung f (x 0 ) einer Funktion f : R R die
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 11. Juli 2016 Ableitungen im Höherdimensionalen Im Eindimensionalen war die Ableitung f (x 0 ) einer Funktion f : R R die
Schein-Klausur HM II F 2003 HM II : S-1
 Schein-Klausur HM II F 3 HM II : S- Aufgabe : Berechnen Sie die folgenden Grenzwerte: a) lim x ln ( + x) x b) lim (coshx) sin x Lösung: Wir verwenden in beiden Fällen die Regel von de l Hospital. a) Es
Schein-Klausur HM II F 3 HM II : S- Aufgabe : Berechnen Sie die folgenden Grenzwerte: a) lim x ln ( + x) x b) lim (coshx) sin x Lösung: Wir verwenden in beiden Fällen die Regel von de l Hospital. a) Es
31. Kurven in Ebene und Raum
 31. Kurven in Ebene und Raum Für ebene Kurven (also Kurven im R gibt es mehrere Darstellungsmöglichkeiten: implizite Darstellung : F (x, y = explizite Darstellung : y = f(x oder x = g(y Parameterdarstellung
31. Kurven in Ebene und Raum Für ebene Kurven (also Kurven im R gibt es mehrere Darstellungsmöglichkeiten: implizite Darstellung : F (x, y = explizite Darstellung : y = f(x oder x = g(y Parameterdarstellung
D-MAVT/D-MATL FS 2018 Dr. Andreas Steiger Analysis IILösung - Serie19. sind weder parallel noch stehen sie senkrecht aufeinander.
 -MAVT/-MATL FS 8 r. Andreas Steiger Analysis IILösung - Serie9. ie Fläche S sei einerseits durch die Parameterdarstellung (u, v) r(u, v) und andererseits durch die Gleichung f(x, y, z) = gegeben. Wir betrachten
-MAVT/-MATL FS 8 r. Andreas Steiger Analysis IILösung - Serie9. ie Fläche S sei einerseits durch die Parameterdarstellung (u, v) r(u, v) und andererseits durch die Gleichung f(x, y, z) = gegeben. Wir betrachten
Höhere Mathematik Vorlesung 4
 Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Mathematik für Anwender II
 Prof. Dr. H. Brenner Osnabrück SS 212 Mathematik für Anwender II Vorlesung 58 Der Satz von Green Wir betrachten eine kompakte eilmenge R 2, deren Rand R sich stückweise durch reguläre Kurven parametrisieren
Prof. Dr. H. Brenner Osnabrück SS 212 Mathematik für Anwender II Vorlesung 58 Der Satz von Green Wir betrachten eine kompakte eilmenge R 2, deren Rand R sich stückweise durch reguläre Kurven parametrisieren
Technische Universität München. Probeklausur Lösung SS 2012
 Technische Universität München Andreas Wörfel & Carla Zensen Ferienkurs Analysis für Physiker Probeklausur Lösung SS Aufgabe Differenzierbarkeit / Punkte: [4,, 3, 4] Es sei f(x, y) = sin(x3 + y 3 ) x +
Technische Universität München Andreas Wörfel & Carla Zensen Ferienkurs Analysis für Physiker Probeklausur Lösung SS Aufgabe Differenzierbarkeit / Punkte: [4,, 3, 4] Es sei f(x, y) = sin(x3 + y 3 ) x +
Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test
 Prof. C. Greiner, Dr. H. van Hees Wintersemester 2012/2013 Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test Aufgabe 1: Bruchrechnung Lösen Sie die folgenden Gleichungen nach x auf (a) x x 2 1
Prof. C. Greiner, Dr. H. van Hees Wintersemester 2012/2013 Übungen zur Theoretischen Physik 1 Lösungen zum Mathe-Test Aufgabe 1: Bruchrechnung Lösen Sie die folgenden Gleichungen nach x auf (a) x x 2 1
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
2.3 Gekrümmte Oberflächen
 2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
Mathematische Grundkenntnisse Selbsteinschätzungstest, Herbst 2009
 Mit diesem Test bieten wir Ihnen an, Ihr mathematisches Schulwissen abzurufen, zu überprüfen und allenfalls Lücken zu identifizieren. Die Teilnahme ist nicht verpflichtend und hat keine Konsequenzen. Der
Mit diesem Test bieten wir Ihnen an, Ihr mathematisches Schulwissen abzurufen, zu überprüfen und allenfalls Lücken zu identifizieren. Die Teilnahme ist nicht verpflichtend und hat keine Konsequenzen. Der
Wochenaufgaben: Teil 1
 Fachrichtung Mathematik Wochenaufgaben: Teil 1 Wiederholen Sie Kapitel 13 und Abschnitt 14.1. (Fernstudenten: Teil 3, A1, A3, A5.1 bzw. Kapitel 12 und Abschnitt 13.1. meines Skriptes). 1. Was ist eine
Fachrichtung Mathematik Wochenaufgaben: Teil 1 Wiederholen Sie Kapitel 13 und Abschnitt 14.1. (Fernstudenten: Teil 3, A1, A3, A5.1 bzw. Kapitel 12 und Abschnitt 13.1. meines Skriptes). 1. Was ist eine
b) Definieren Sie den Begriff Cauchy-Folge. c) Geben Sie zwei Beispiele für konvergente Folgen und deren jeweilige Grenzwerte an.
 Repetitorium zur Ingenieur-Mathematik I, WS 00/ Aufgabe : Bestimmen Sie das quadratische Polynom, auf dessen Graph die Punkte (, 4), (0, ), (, 7) liegen. Aufgabe : a) Wann ist eine Folge konvergent (Definition)?
Repetitorium zur Ingenieur-Mathematik I, WS 00/ Aufgabe : Bestimmen Sie das quadratische Polynom, auf dessen Graph die Punkte (, 4), (0, ), (, 7) liegen. Aufgabe : a) Wann ist eine Folge konvergent (Definition)?
Abbildung 10.1: Das Bild zu Beispiel 10.1
 Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. Simone Warzel Max Lein TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physik (Analysis 3) Wintersemester 29/2 Lösungsblatt 2 (27..29) Zentralübung 4. Parametrisierung einer
Prof. Dr. Simone Warzel Max Lein TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physik (Analysis 3) Wintersemester 29/2 Lösungsblatt 2 (27..29) Zentralübung 4. Parametrisierung einer
Angewandte Geometrie Semestralprüfung am 5. Juli 2005, Uhr
 Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Höhere Mathematik 3. Apl. Prof. Dr. Norbert Knarr. Wintersemester 2017/18. FB Mathematik
 Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2017/18 1. Integration von Funktionen in zwei Variablen 1.1. Integral auf Rechtecken Wir betrachten ein beschränktes Rechteck
Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2017/18 1. Integration von Funktionen in zwei Variablen 1.1. Integral auf Rechtecken Wir betrachten ein beschränktes Rechteck
5.6 Potential eines Gradientenfelds.
 die Zirkulation des Feldes v längs aufintegriert. 5.6 Potential eines Gradientenfelds. Die Ableitung einer skalaren Funktion ist der Gradient, ein Vektor bzw. vektorwertige Funktion (Vektorfeld). Wir untersuchen
die Zirkulation des Feldes v längs aufintegriert. 5.6 Potential eines Gradientenfelds. Die Ableitung einer skalaren Funktion ist der Gradient, ein Vektor bzw. vektorwertige Funktion (Vektorfeld). Wir untersuchen
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA94 Z4.. Parametrisierungsinvarianz des Oberflächenintegrals
Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA94 Z4.. Parametrisierungsinvarianz des Oberflächenintegrals
Prüfer: Dr. M. Lenz, Prof. Dr. M. Rumpf. Klausurdauer: 180 Minuten. Bitte Namen, Vornamen und Matrikel-Nr. einsetzen. Name:... Vorname:...
 Klausur zum Modul Ingenieurmathematik II (B22) 20. März 2014 für den Bachelorstudiengang Geodäsie und Geoinformation In der Klausur können 10 Punkte pro Aufgabe, also insgesamt 100 Punkte erreicht werden.
Klausur zum Modul Ingenieurmathematik II (B22) 20. März 2014 für den Bachelorstudiengang Geodäsie und Geoinformation In der Klausur können 10 Punkte pro Aufgabe, also insgesamt 100 Punkte erreicht werden.
Die Kugel. Mathematische Betrachtungen von Peter Franzke
 Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
PROBEPRÜFUNG MATHEMATIK I UND II
 PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
Mathematik I Herbstsemester 2018 Kapitel 5: Integralrechnung
 Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Kapitel 17 Skalar- und Vektorprodukt
 Kapitel 17 Skalar- und Vektorprodukt Mathematischer Vorkurs TU Dortmund Seite 1 / 22 Bisher hatten wir die Möglichkeit Vektoren des R n zu addieren und Vektoren mit rellen Zahlen zu multiplizieren. Man
Kapitel 17 Skalar- und Vektorprodukt Mathematischer Vorkurs TU Dortmund Seite 1 / 22 Bisher hatten wir die Möglichkeit Vektoren des R n zu addieren und Vektoren mit rellen Zahlen zu multiplizieren. Man
Kapitel I: Vektorrechnung 2: Vektoren im Raum
 WS 1/14 - Prof Dr Manfred Leitz 2 Vektoren im Raum A Grundbegriffe B Rechnen mit Vektoren C Der euklidische Betrag D Das euklidische Skalarprodukt E Vektorprodukt und Spatprodukt F Geraden und Ebenen im
WS 1/14 - Prof Dr Manfred Leitz 2 Vektoren im Raum A Grundbegriffe B Rechnen mit Vektoren C Der euklidische Betrag D Das euklidische Skalarprodukt E Vektorprodukt und Spatprodukt F Geraden und Ebenen im
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Linien- und Oberflächenintegrale
 Linien- und berflächenintegrale Bei den früheren eindimensionalen Integralen wurde in der Regel entlang eines Intervalls einer Koordinatenachse integriert. Bei einem Linienintegral wird der Integrationsweg
Linien- und berflächenintegrale Bei den früheren eindimensionalen Integralen wurde in der Regel entlang eines Intervalls einer Koordinatenachse integriert. Bei einem Linienintegral wird der Integrationsweg
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Lösungen zu Serie 8. F n ds = (0 + 0) dx dy = 0. (1 ( 1)) dx dy = 2
 D-EDW, D-HET, D-UY Mathematik II F Dr. Ana annas Lösungen zu erie 8. a) Wir berechnen den Fluss von F mittels Green F n ds + ) dx dy und die Zirkulation F T ds )) dx dy wobei Vol ) den Flächeninhalt des
D-EDW, D-HET, D-UY Mathematik II F Dr. Ana annas Lösungen zu erie 8. a) Wir berechnen den Fluss von F mittels Green F n ds + ) dx dy und die Zirkulation F T ds )) dx dy wobei Vol ) den Flächeninhalt des
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt. Mathematik II für Bauingenieure. (f) 4 sin x cos 5 x dx. 3 x e x2 dx (i) e 2x 1 dx.
 HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik II Mathematik II für Bauingenieure Wiederholungsaufgaben zur Prüfungsklausur im Juli 2007 1 Integralrechnung Aufgabe 1 : Berechnen Sie die folgenden
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik II Mathematik II für Bauingenieure Wiederholungsaufgaben zur Prüfungsklausur im Juli 2007 1 Integralrechnung Aufgabe 1 : Berechnen Sie die folgenden
Prüfung Modul A, Teil 2 (Mathematik 2) (Fernstudium Bauingenieurwesen)
 Name: Vorname: Matrikelnummer: TU Dresden, Fachrichtung Mathematik, Dr. N. Koksch 6. Februar 8 Prüfung Modul A, Teil (Mathematik ) (Fernstudium auingenieurwesen) ewertet werden nur solche Lösungsschritte,
Name: Vorname: Matrikelnummer: TU Dresden, Fachrichtung Mathematik, Dr. N. Koksch 6. Februar 8 Prüfung Modul A, Teil (Mathematik ) (Fernstudium auingenieurwesen) ewertet werden nur solche Lösungsschritte,
Mathematik II: Übungsblatt 01: Lösungen
 N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
6.2 Extremwertaufgaben mit Nebenbedingung
 6.. Extremwertaufgaben mit Nebenbedingung 87 6. Extremwertaufgaben mit Nebenbedingung Betrachten wir jetzt eine differenzierbare Funktion f:u R n R U offen in R n. Ist n = 3 und U eine glatte Fläche, dann
6.. Extremwertaufgaben mit Nebenbedingung 87 6. Extremwertaufgaben mit Nebenbedingung Betrachten wir jetzt eine differenzierbare Funktion f:u R n R U offen in R n. Ist n = 3 und U eine glatte Fläche, dann
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Flächen und ihre Krümmungen
 Flächen und ihre Krümmungen Teilnehmer: Levi Borodenko Anna Heinrich Jochen Jacobs Robert Jendersie Tanja Lappe Manuel Radatz Maximilian Rogge Käthe-Kollwitz-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
Flächen und ihre Krümmungen Teilnehmer: Levi Borodenko Anna Heinrich Jochen Jacobs Robert Jendersie Tanja Lappe Manuel Radatz Maximilian Rogge Käthe-Kollwitz-Oberschule, Berlin Käthe-Kollwitz-Oberschule,
Parametrisierung und Integralsätze
 Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Lösungsvorschlag Klausur MA9802
 Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Inhalt. Mathematik für Chemiker II Lineare Algebra. Vorlesung im Sommersemester Kurt Frischmuth. Rostock, April Juli 2015
 Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS Bauingenieurwesen. Dr. M. Voigt
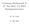 Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS auingenieurwesen Dr. M. Voigt 27. Mai 2013 II Inhaltsverzeichnis 7 Integralrechnung im R n 37 7.1 ereichsintegrale.................... 37 7.1.1 ebene ereichsintegrale.............
Vorlesung Mathematik II 27. Mai 2013, 2/2 SWS auingenieurwesen Dr. M. Voigt 27. Mai 2013 II Inhaltsverzeichnis 7 Integralrechnung im R n 37 7.1 ereichsintegrale.................... 37 7.1.1 ebene ereichsintegrale.............
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen
 Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat.
 1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 8. Übung WS 17/18: Woche vom
 Übungsaufgaben 8. Übung WS 17/18: Woche vom 27. 11. - 1. 12. 2017 Vektoranalysis: Differentialausdrücke in anderen Koordinaten 17.39, 17.43, 17.45 Skalare und Vektorfelder, grad, div, rot 19.1, 19.2 (a-d),
Übungsaufgaben 8. Übung WS 17/18: Woche vom 27. 11. - 1. 12. 2017 Vektoranalysis: Differentialausdrücke in anderen Koordinaten 17.39, 17.43, 17.45 Skalare und Vektorfelder, grad, div, rot 19.1, 19.2 (a-d),
Mathematische Einführung
 Lehrstuhl für Technische Elektrophysik Technische Universität München Übungen zu "Elektrizitätslehre" (Prof. Wachutka) Mathematische Einführung Die vorliegende Einführung in die Mathematik zur Vorlesung
Lehrstuhl für Technische Elektrophysik Technische Universität München Übungen zu "Elektrizitätslehre" (Prof. Wachutka) Mathematische Einführung Die vorliegende Einführung in die Mathematik zur Vorlesung
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n
![2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n](/thumbs/49/25862272.jpg) 2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
2. VEKTORANALYSIS 2.1 Kurven Definition: Ein Weg ist eine stetige Abbildung aus einem Intervall I = [a; b] R in den R n : f : I R n f ist in dem Fall ein Weg in R n. Das Bild f(t) des Weges wird als Kurve
Vektoranalysis Orientierte Flächenintegrale, Satz von Gauß, Satz von Stokes
 Vektoranalysis Orientierte Flächenintegrale, Satz von Gauß, Satz von Stokes Themen des Tutoriums am 03.06.2015: Wiederholung: Ein glattes Flächenstück ist eine Menge M R 3, die eine reguläre Parametrisierung
Vektoranalysis Orientierte Flächenintegrale, Satz von Gauß, Satz von Stokes Themen des Tutoriums am 03.06.2015: Wiederholung: Ein glattes Flächenstück ist eine Menge M R 3, die eine reguläre Parametrisierung
Übungsaufgaben zu den mathematischen Grundlagen von KM
 TUM, Institut für Informatik WS 2003/2004 Prof Dr Thomas Huckle Andreas Krahnke, MSc Dipl-Inf Markus Pögl Übungsaufgaben zu den mathematischen Grundlagen von KM 1 Bestimmen Sie die Darstellung von 1 4
TUM, Institut für Informatik WS 2003/2004 Prof Dr Thomas Huckle Andreas Krahnke, MSc Dipl-Inf Markus Pögl Übungsaufgaben zu den mathematischen Grundlagen von KM 1 Bestimmen Sie die Darstellung von 1 4
Analysis 2 - Übung 1
 Analysis - Übung 1 Felix Knorr 8 März 014 4 Gegeben sei die Polynomfunktion f(x, y xy 10x Man bestimme die Gleichungen ihrer Schnittkurven mit den senkrechten Ebenen x x 0 bzw y y 0 sowie die Höhenlinien
Analysis - Übung 1 Felix Knorr 8 März 014 4 Gegeben sei die Polynomfunktion f(x, y xy 10x Man bestimme die Gleichungen ihrer Schnittkurven mit den senkrechten Ebenen x x 0 bzw y y 0 sowie die Höhenlinien
Prüfungsklausur Mathematik II für Bauingenieure am
 HTWD, Fakultät Informatik/Mathematik Prof. Dr. M. Voigt Prüfungsklausur Mathematik II für Bauingenieure am 9.7.8 A Name, Vorname Matr. Nr. Sem. gr. Aufgabe 4 5 6 7 8 9 gesamt erreichbare P. 6 6 7 (5) (+5)
HTWD, Fakultät Informatik/Mathematik Prof. Dr. M. Voigt Prüfungsklausur Mathematik II für Bauingenieure am 9.7.8 A Name, Vorname Matr. Nr. Sem. gr. Aufgabe 4 5 6 7 8 9 gesamt erreichbare P. 6 6 7 (5) (+5)
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 12: Integralsätze von Gauss und Stokes Prof. Dr. Erich Walter Farkas Mathematik I+II, 12. Integralsätze 1 / 25 1 Gauss-scher Integralsatz
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 12: Integralsätze von Gauss und Stokes Prof. Dr. Erich Walter Farkas Mathematik I+II, 12. Integralsätze 1 / 25 1 Gauss-scher Integralsatz
Vorbereitungsaufgaben zur Klausur Mathematik I für Studierende des Studienganges Elektrotechnik und Informationssystemtechnik
 Vorbereitungsaufgaben zur Klausur Mathematik I für Studierende des Studienganges Elektrotechnik und Informationssystemtechnik (Aufgaben aus Klausuren). Bestimmen und skizzieren Sie in der Gaußschen Zahlenebene
Vorbereitungsaufgaben zur Klausur Mathematik I für Studierende des Studienganges Elektrotechnik und Informationssystemtechnik (Aufgaben aus Klausuren). Bestimmen und skizzieren Sie in der Gaußschen Zahlenebene
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
 Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Transformation mehrdimensionaler Integrale
 Transformation mehrdimensionaler Integrale Für eine bijektive, stetig differenzierbare Transformation g eines regulären Bereiches U R n mit det g (x), x U, gilt für stetige Funktionen f : f g det g du
Transformation mehrdimensionaler Integrale Für eine bijektive, stetig differenzierbare Transformation g eines regulären Bereiches U R n mit det g (x), x U, gilt für stetige Funktionen f : f g det g du
Übung 11: Lösungen. Technische Universität München SS 2004 Zentrum Mathematik Prof. Dr. K. Buchner
 Technische Universität München SS 4 Zentrum Mathematik 5.7.4 Prof. Dr. K. Buchner Dr. W. Aschbacher Analysis II Übung : Lösungen Aufgabe T 3 (Mehrdimensionale Integrale, (a Wir benutzen die verallgemeinerten
Technische Universität München SS 4 Zentrum Mathematik 5.7.4 Prof. Dr. K. Buchner Dr. W. Aschbacher Analysis II Übung : Lösungen Aufgabe T 3 (Mehrdimensionale Integrale, (a Wir benutzen die verallgemeinerten
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Serie 9: Satz von Stokes und Divergenzsatz
 D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas Serie 9: Satz von Stokes und Divergenzsatz Bemerkungen: Die Aufgaben der Serie 9 bilden den Fokus der Übungsgruppen vom 28./30. April. 1. Berechnen
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas Serie 9: Satz von Stokes und Divergenzsatz Bemerkungen: Die Aufgaben der Serie 9 bilden den Fokus der Übungsgruppen vom 28./30. April. 1. Berechnen
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Übungen zu Höhere Analysis und elementare Differentialgeometrie, WS 2015
 Übungen zu Höhere Analysis und elementare ifferentialgeometrie, WS 215 Ulisse Stefanelli 27. Januar 216 1 Wiederholung 1. Berechnen Sie die folgenden unbestimmten Integrale dx (arctan x) 3 (log x) 2 (2
Übungen zu Höhere Analysis und elementare ifferentialgeometrie, WS 215 Ulisse Stefanelli 27. Januar 216 1 Wiederholung 1. Berechnen Sie die folgenden unbestimmten Integrale dx (arctan x) 3 (log x) 2 (2
Technische Universität München Zentrum Mathematik. Übungsblatt 10
 Technische Universität München Zentrum Mathematik Mathematik 2 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt Hausaufgaben Aufgabe. Sei f : R 2 R gegeben durch x 2 y für (x, y)
Technische Universität München Zentrum Mathematik Mathematik 2 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt Hausaufgaben Aufgabe. Sei f : R 2 R gegeben durch x 2 y für (x, y)
Höhere Mathematik III. Variante A
 Prof. Dr. E. Triesch Höhere Mathematik III SoSe 2017 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur
Prof. Dr. E. Triesch Höhere Mathematik III SoSe 2017 Variante A Hinweise zur Bearbeitung: Benutzen Sie zur Beantwortung aller Aufgaben ausschließlich das in der Klausur ausgeteilte Papier! Es werden nur
Nachklausur zur Analysis 2, SoSe 2017
 BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 18.9.17 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis 2, SoSe 217 Aufgabe
01. Differentialrechnung in mehreren Variablen - 2. Teil
 01. Differentialrechnung in mehreren Variablen - 2. Teil Im folgenden werden die meisten Konzepte für Funktionen von 2 Variablen erklärt. In manchen Fällen können diese Konzepte unmittelbar auf Funktionen
01. Differentialrechnung in mehreren Variablen - 2. Teil Im folgenden werden die meisten Konzepte für Funktionen von 2 Variablen erklärt. In manchen Fällen können diese Konzepte unmittelbar auf Funktionen
Basisprüfung, Gruppe A Analysis I/II
 Offene Aufgaben. Jeder der folgenden sieben offenen Aufgaben ist eine einzelne thematisch verwandte Single Choice-Aufgabe vorangestellt. Beantworten Sie die Single Choice Aufgabe auf dem Antwortzettel.
Offene Aufgaben. Jeder der folgenden sieben offenen Aufgaben ist eine einzelne thematisch verwandte Single Choice-Aufgabe vorangestellt. Beantworten Sie die Single Choice Aufgabe auf dem Antwortzettel.
Übungsaufgaben zu Höherer Analysis, WS 2002/03. Aufgaben zu Doppelintegralen.
 Übungsaufgaben zu Höherer Analysis, WS 2002/03 Aufgaben zu Doppelintegralen. (A) Bestimmen Sie den Schwerpunkt des Gebietes 0 x π 2, 0 y cos x. (Antwort: s = ( π 2, π 8 )) (A2) Berechnen Sie die folgenden
Übungsaufgaben zu Höherer Analysis, WS 2002/03 Aufgaben zu Doppelintegralen. (A) Bestimmen Sie den Schwerpunkt des Gebietes 0 x π 2, 0 y cos x. (Antwort: s = ( π 2, π 8 )) (A2) Berechnen Sie die folgenden
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2 BIOL-B HST PHARM Prüfung zur Vorlesung Mathematik I/II. (8 Punkte) a) Mit Kürzen des Bruchs folgt ( ) x + sin(x) sin(x) cos(x) lim x sin(x) ( ) x = lim x sin(x) + cos(x)
Dr. A. Caspar ETH Zürich, August 2 BIOL-B HST PHARM Prüfung zur Vorlesung Mathematik I/II. (8 Punkte) a) Mit Kürzen des Bruchs folgt ( ) x + sin(x) sin(x) cos(x) lim x sin(x) ( ) x = lim x sin(x) + cos(x)
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Vorlesungsfolien Mathematik 3 WS 2010/11 UMIT. Einleitung
 Vorlesungsfolien Mathematik 3 WS 2010/11 Dr. Leonhard Wieser UMIT Einleitung Begriff Vektoranalysis: Kombination aus Linearer Algebra/Vektorrechnung mit Differential- und Integralrechnung Inhaltsangabe:
Vorlesungsfolien Mathematik 3 WS 2010/11 Dr. Leonhard Wieser UMIT Einleitung Begriff Vektoranalysis: Kombination aus Linearer Algebra/Vektorrechnung mit Differential- und Integralrechnung Inhaltsangabe:
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
Grundlagen der Mathematik (BSc Maschinenbau)
 Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Priv.-Doz. Dr. J. Ruppenthal Wuppertal, 5.9.7 Grundlagen der Mathematik (BSc Maschinenbau) Aufgabe. (6+8+6 Punkte) a) Zeigen Sie durch Induktion nach n N: n (k ) = n k= b) Stellen Sie die folgenden Mengen
Prüfungsklausur Höhere Mathematik II (22. Juli 2006) - Lösungen zum Theorieteil - für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM
 Prüfungsklausur Höhere Mathematik II (. Juli 6) für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM - Lösungen zum Theorieteil - Aufgabe 1: In der x-y-ebene seien die Mengen A {(x, y) : x } und
Prüfungsklausur Höhere Mathematik II (. Juli 6) für MB, EC, TeM, FWK, VT, KGB, BGi, WiW, GtB, Ma, WWT, ESM - Lösungen zum Theorieteil - Aufgabe 1: In der x-y-ebene seien die Mengen A {(x, y) : x } und
Aufgaben für die 14. Übung zur Vorlesung Mathematik 2 für Informatiker: Analysis Sommersemester 2010
 Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
KAPITEL 9. Doppelintegrale
 KAPITEL 9 Doppelintegrale 9.1 Doppelintegrale............................. 305 9.2 erechnung des Doppelintegrals................... 309 9.3 Transformation von Doppelintegralen................ 321 9.4 Zusammenfassung
KAPITEL 9 Doppelintegrale 9.1 Doppelintegrale............................. 305 9.2 erechnung des Doppelintegrals................... 309 9.3 Transformation von Doppelintegralen................ 321 9.4 Zusammenfassung
