Umwandlung elektrische Energie mit Leistungselektronik
|
|
|
- Daniel Hermann
- vor 7 Jahren
- Abrufe
Transkript
1 Umwandlung elektrische Energie mit Leistungselektronik Félix Rojas Technische Universität München Prof. Dr. Ing. Ralph Kennel. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Übung 2 Blockbetrieb
2 Gliederung Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
3 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
4 Darstellung der Ausgangsspannungen eines 2- Level Umrichters Motivation a Gleichrichter U d Umrichter b c V Gridrms Wir nehmen U d als Konstant. V umrichterrms
5 Ü1: Raumzeiger 2/44 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c
6 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={1, 0, 0} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2}
7 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={1, 1, 0} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2}
8 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={0, 1, 0} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2}
9 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={0, 1, 1} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2}
10 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={0, 0, 1} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2}
11 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={1, 0, 1} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2}
12 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={1, 1, 1} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2}
13 Funktionsweise 2- Level Umrichter mögliche Ausgangsspannungen {Sa, Sb, Sc}={0, 0, 0} U d /2 S a S b S c U d 0 U a0 a b c U d /2 S a S b S c {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2}
14 Ü1: Raumzeiger 11/44 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U c0 U a0 0 U b0 b U N0 Z Z N U bn Z U an U cn c U a0 U N0 U an = 0 U b0 U N0 U bn = 0 U c0 U N0 U cn = 0
15 Ü1: Raumzeiger 12/44 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U c0 U a0 0 U b0 b U N0 Z Z N U bn Z U an U cn c U N0 (t) = U a0(t)+u b0 (t)+u c0 (t) (U an (t)+u bn (t)+u cn (t)) 3
16 Ü1: Raumzeiger 12/44 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U c0 U a0 0 U b0 b U N0 Z Z N U bn Z U an U cn c U N0 (t) = U a0(t)+u b0 (t)+u c0 (t) (U an (t)+u bn (t)+u cn (t)) 3 U N0 = U a0+u b0 +U c0 (R (I a+i b +Ic)+L d dt (Ia+I b+i c)) 3
17 Ü1: Raumzeiger 12/44 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U c0 U a0 0 U b0 b U N0 Z Z N U bn Z U an U cn c U N0 (t) = U a0(t)+u b0 (t)+u c0 (t) (U an (t)+u bn (t)+u cn (t)) 3 U N0 = U a0+u b0 +U c0 (R (I a+i b +Ic)+L d dt (Ia+I b+i c)) 3 U N0 (t) = U a0(t)+u b0 (t)+u c0 (t) 3
18 Definition der Spannungen für Umrichter und Last symmetrische Belastung U d /2 S a S b S c U a0 U d 0 a b c U d /2 S a S b S c
19 Definition der Spannungen für Umrichter und Last symmetrische Belastung U d /2 S a S b S c U a0 U d 0 a b c U d /2 S a S b S c a U d U d /20 U d /2 U a0 U c0 U b0 U N0 b Z Z N Z U bn U an U cn c
20 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U d U d /20 U d /2 U a0 U c0 U b0 U N0 b Z Z U bn N Z U an U cn c U an (t) = Z Z+Z/2 U d = 2 3 U d
21 Ü1: Raumzeiger 14/44 Definition der Spannungen für Umrichter und Last symmetrische Belastung a U d U d /20 U d /2 U a0 U c0 U b0 U N0 b Z Z U bn N Z U an U cn c U an (t) = Z Z+Z/2 U d = 2 3 U d U bn (t) = U cn (t) = Z/2 Z+Z/2 U d = 1 3 U d Im Falle der aktiven Zeiger sind immer zwei Strnge parallel geschaltet, daher ist diese Spannungsverteilung immer gegeben.
22 Definition der Spannungen für Umrichter und Last symmetrische Belastung Die 8 Ausgangsspannungen des Umrichters sind gegeben mit: {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={ U d /2, U d /2, Ud/2} {U a0, U b0, U c0 }={U d /2, U d /2, Ud/2} Die common-mode Spannung des Umrichters ist: U N0 (t) = U a0 (t)+u b0 (t)+u c0 (t) 3 Für die aktiven Zeiger ist an der Last immer eine Spannungsverteilung von 2/3U d zu 1/3U d vorhanden.
23 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
24 Blockbetrieb eines 2-Level Umrichters Phasenspannungen U d /2 U a0 U d /2 U d /2 U b0 U d /2 U d /2 U c0 U d /2 Die Spannungen besitzen im Blockbetrieb nur zwei Spannungslevel und sind um 120 verschoben. Der Maximalwert entspricht der halben Zwischenkreisspannung.
25 Blockbetrieb eines 2-Level Umrichters verkettete Spannung U a0 U b0 U d /2 U d /2 U d U ab U d Der Maximalwert der verketteten Spannung entspricht der Zwischenkreisspannung, wobei diese 3 Spannungslevel besitzt.
26 Blockbetrieb eines 2-Level Umrichters verkettete Spannung für drei Phasen U c0 U d /2 U d /2 U b0 U b0 U d U ab U d U d U bc U d U d U ca U d
27 Blockbetrieb eines 2-Level Umrichters common mode Spannung U d /2 U a0 U d /2 U d /2 U b0 U d /2 U d /2 U c0 U d /2 U d /6 U d /6 U N0 Die common mode Spannung besitzt die dreifache Frequenz der Strangspannung mit einer Amplitude von U d /6.
28 Ü1: Raumzeiger 20/44 Blockbetrieb eines 2-Level Umrichters Strangspannung U d /2 U a0 U d /2 U d /6 U d /6 U N0 2U d /3 U d /3 U an Die Strangspannung besitzt 4 Spannungslevel und eine maximale Amplitude von 2U d /3
29 Blockbetrieb eines 2-Level Umrichters Strangspannung für drei Phasen U d /6 U d /6 U N0 2U d /3 U d /3 U an 2U d /3 U d /3 U bn 2U d /3 U d /3 U cn Analog zur Phasenspannungen zeigt auch die Strangspannung zwischen den 3 Phasen eine Phasenverschiebung von 120 Ü1: Raumzeiger 21/44
30 Blockbetrieb eines 2-Level Umrichters Darstellung von Phasen-, Strang-, verketteter- und common-mode Spannung U d /2 U a0 U d /2 U d U ab U d 2U d /3 U d /3 U an U d /6 U d /6 U N0 Da die common-mode Spannung ungleich Null ist, darf der Laststernpunkt nicht mit dem Umrichternullpunkt verbunden werden.
31 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
32 Ü1: Raumzeiger 23/44 Umrichterausgangsspannungen in Raumzeigerdarstellung Auflistung und Transformation der diskreten Spannungszeiger X α 1 X β = X a X 2 b X γ X c 2 2 2
33 Ü1: Raumzeiger 23/44 Umrichterausgangsspannungen in Raumzeigerdarstellung Auflistung und Transformation der diskreten Spannungszeiger X α 1 X β = X a X 2 b X γ X c S 1 = {S a, S b, S c }={1, 0, 0} S 2 = {S a, S b, S c }={1, 1, 0} S 3 = {S a, S b, S c }={0, 1, 0} S 4 = {S a, S b, S c }={0, 1, 1} S 5 = {S a, S b, S c }={0, 0, 1} S 6 = {S a, S b, S c }={1, 0, 1} S 0 = {S a, S b, S c }={0, 0, 0} S 7 = {S a, S b, S c }={1, 1, 1}
34 Ü1: Raumzeiger 23/44 Umrichterausgangsspannungen in Raumzeigerdarstellung Auflistung und Transformation der diskreten Spannungszeiger X α 1 X β = X a X 2 b X γ X c S 1 = {S a, S b, S c }={1, 0, 0} S 2 = {S a, S b, S c }={1, 1, 0} S 3 = {S a, S b, S c }={0, 1, 0} S 4 = {S a, S b, S c }={0, 1, 1} S 5 = {S a, S b, S c }={0, 0, 1} S 6 = {S a, S b, S c }={1, 0, 1} S 0 = {S a, S b, S c }={0, 0, 0} S 7 = {S a, S b, S c }={1, 1, 1} Beispielweise für S 1 ={1, 0, 0}: S α 1 1 S β = S γ S α S β = 2/3 0 S γ 1/3
35 Ü1: Raumzeiger 23/44 Umrichterausgangsspannungen in Raumzeigerdarstellung Auflistung und Transformation der diskreten Spannungszeiger X α 1 X β = X a X 2 b X γ X c S 1 = {S a, S b, S c }={1, 0, 0} S 2 = {S a, S b, S c }={1, 1, 0} S 3 = {S a, S b, S c }={0, 1, 0} S 4 = {S a, S b, S c }={0, 1, 1} S 5 = {S a, S b, S c }={0, 0, 1} S 6 = {S a, S b, S c }={1, 0, 1} S 0 = {S a, S b, S c }={0, 0, 0} S 7 = {S a, S b, S c }={1, 1, 1} Beispielweise für S 1 ={1, 0, 0}: S α 1 1 S β = S γ S α S β = 2/3 0 S γ 1/3 V 1 = S α eˆ α + S β eˆ β + S γ eˆ γ V 1 = 2/3eˆ α + 0eˆ β + 1/3eˆ γ V 1 = 2/3eˆ α + 1/3eˆ γ
36 Umrichterausgangsspannungen in Raumzeigerdarstellung Auflistung der 8 Spannungsvektoren Die γ Komponente kann vernachlässigt werden, da der Sternpunkt nicht verbunden ist. V 1 = 2/3eˆ α + 0eˆ β (1) V 2 = 1/3eˆ α + 3/3eˆ β (2) V 3 = 1/3eˆ α + 3/3eˆ β (3) V 4 = 2/3eˆ α + 0eˆ β (4) V 5 = 1/3eˆ α 3/3eˆ β (5) V 6 = 1/3eˆ α 3/3eˆ β (6) V 0 = 0 (7) V 7 = 0 (8) Die Zeiger V 1 V 6 werden als Aktivzeiger bezeichnet. Die Zeiger V 0 und V 7 sind Nullzeiger, weil sie die Last kurzschließen.
37 Umrichterausgangsspannungen in Raumzeigerdarstellung Grafische Darstellung der 8 Spannungsvektoren in αβ-koordinaten β V V V V 0,7 1 3 V α 3 3 V 5 V 6 Die aktiven Zeiger sind jeweils um 60 verschoben. Die Nullzeiger befinden sind im Ursprung.
38 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
39 RL Last im Blockbetrieb Beispiel 1 S a S b S c U d S a S b S c Z = R + jl L = 20[mH] R = 20[Ω] U d = a b c U bn Z N U cn Z U an Z
40 RL Last im Blockbetrieb Beispiel 1 S a S b S c U d S a S b S c U an (t) = RI a (t) + L d dt (I a(t)) Z = R + jl L = 20[mH] R = 20[Ω] U d = a b c U bn Z N U cn Z U an Z Die Sprungantwort ist für dieses System gegeben mit: I a (t) = UaN R ( 1 e R L (t t 0) ) + I a (t 0 )
41 Ü1: Raumzeiger 27/44 RL Last im Blockbetrieb Beispiel 1: Berechnung der Lastströme 2U d /3 U d /3 t 1 t 2 t 3 t 4 t 5 U an Wenn U an ist eine Schritt: Der Anfangswert jedes Intervalls entspricht dem Endwert des letzten Intervalls
42 RL Last im Blockbetrieb Beispiel 1: Berechnung der Lastströme 2U d /3 U d /3 t 1 t 2 t 3 t 4 t 5 U an Wenn U an ist eine Schritt: I a (t) = I a1 (t) = U d 3R (1 e R (t)) L + I a (0) für t [t 0,t 1 ] ( ) 1 e R L (t t 1) + I a (t 1 ) für t [t 1,t 2 ] I a2 (t) = 2U d 3R I a3 (t) = U d 3R (1 ) e R L (t t 2) + I a (t 2 ) für t [t 2,t 3 ] ( ) I a4 (t) = U d 3R 1 e R L (t t 3) + I a (t 3 ) für t [t 3,t 4 ] ( ) I a5 (t) = 2U d 3R 1 e R L (t t 4) + I a (t 4 ) für t [t 4,t 5 ] I a4 (t) = U d 3R ( 1 e R L (t t 5) ) + I a (t 5 ) für t [t 5,T ] Der Anfangswert jedes Intervalls entspricht dem Endwert des letzten Intervalls
43 RL Last im Blockbetrieb Beispiel 1: Simulation Ü1: Raumzeiger 28/44
44 Ü1: Raumzeiger 29/44 RL Last im Blockbetrieb Beispiel 1: Referenzspannungen und Phasenspannung V a0,v b0 und V c0 Referenzwerte U a0 in C: U a0 = (V a0ref >= 0) (Udc/2):( Udc/2);
45 Ü1: Raumzeiger 29/44 RL Last im Blockbetrieb Beispiel 1: Referenzspannungen und Phasenspannung V a0,v b0 und V c0 Referenzwerte U a0 in C: U a0 = (V a0ref >= 0) (Udc/2):( Udc/2); Spitzenwert von U a0 ist U d /2=380 2/2=268.7[V]
46 RL Last im Blockbetrieb Beispiel 1: Strangspannung und verkettete Spannung U ab : Spitzenwert U d =380 2=537.4[V]
47 RL Last im Blockbetrieb Beispiel 1: Strangspannung und verkettete Spannung U ab : Spitzenwert U d =380 2=537.4[V] U an : Spitzenwert 2 3 U d= =358.26[V] U an : Mittleres Level 1 3 U d = =179.13[V]
48 RL Last im Blockbetrieb Beispiel 1: Laststrom und Strangspannung I a(t)[a] und 0.15 U an (t)[v] Die Antwort des Strom in dem Teil n ist: ( I n(t) = K U d R 1 e R ) L (t tn) + I a(t n), mit: K = {± 1 3, ± 2 3 } Phasenstrom und Strangstrom sind identisch
49 RL Last im Blockbetrieb Beispiel 1: zeitliche Zuordnung der Raumzeiger U d /2 U d /2 U d /2 U d /2 U d /2 U d /2 V 6 V 1 V 2 V 3 V 4 V 5 U a0 U b0 U c0
50 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im transienten Zustand I b I a I c V 6 V 1 V 2 α-β Transformation
51 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im transienten Zustand I b I a I c V 6 V 1 V 2 α-β Transformation I α I β V 6 V 1 V 2
52 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im transienten Zustand I b I a I c V 6 V 1 V 2 α-β Transformation I α I β V 6 V 1 V 2
53 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im eingeschwungenen Zustand Ia I b I c V 6 V 1 V 2 V 3 V 4 V 5 α-β Transformation
54 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im eingeschwungenen Zustand Ia I b I c V 6 V 1 V 2 V 3 V 4 V 5 α-β Transformation I β I α V 6 V 1 V 2 V 3 V 4 V 5
55 RL Last im Blockbetrieb Beispiel 1: Stromraumzeigerdarstellung im eingeschwungenen Zustand Ia I b I c V 6 V 1 V 2 V 3 V 4 V 5 α-β Transformation I β I α V 6 V 1 V 2 V 3 V 4 V 5
56 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
57 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnen Sie den Effektivwert der Grundschwingung der verketten Spannung im Blockbetrieb. Gehen Sie davon aus, dass der Umrichter mit gespeist wird und die Zwischenkreisspannung konstant ist. U d - 5π 6 - π 6 π 6 5π 6 U d
58 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnen Sie den Effektivwert der Grundschwingung der verketten Spannung im Blockbetrieb. Gehen Sie davon aus, dass der Umrichter mit gespeist wird und die Zwischenkreisspannung konstant ist. U d - 5π 6 - π 6 π 6 5π 6 U d Fourierreihe: f(x) = a n cos(nx) + b n sin(nx) i=1 i=1 a n = 1 2π f(x) cos(nx)dx π 0 b n = 1 2π f(x) sin(nx)dx π 0
59 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnen Sie den Effektivwert der Grundschwingung der verketten Spannung im Blockbetrieb. Gehen Sie davon aus, dass der Umrichter mit gespeist wird und die Zwischenkreisspannung konstant ist. U d - 5π 6 - π 6 π 6 5π 6 U d Fourierreihe: f(x) = a n cos(nx) + b n sin(nx) i=1 i=1 a n = 1 2π f(x) cos(nx)dx π 0 b n = 1 2π f(x) sin(nx)dx π 0 Für ungerade Funktionen gilt a n = 0: x = ωt; ω = 2π T f(ωt) = b n sin(nωt) i=1 b n = 1 2π f(x) sin(nωt)dt π 0
60 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten b n = U d π 5π π ( U d ) sin(nωt)dωt + (U d ) sin(nωt)dωt 5π π 6 6-5π 6 - π 6 π 6 5π 6 U d
61 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten b n = - 5π 6 U d - π 6 π 5π π ( U d ) sin(nωt)dωt + (U d ) sin(nωt)dωt 5π π 6 6 b n = 2U d π 5π 6 π 6 sin(nωt)dωt π 6 5π 6 U d
62 Ü1: Raumzeiger 36/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten b n = - 5π 6 U d - π 6 π 5π π ( U d ) sin(nωt)dωt + (U d ) sin(nωt)dωt 5π π 6 6 b n = 2U d π 5π 6 π 6 sin(nωt)dωt π 6 5π 6 b n = 2U d nπ ( cos(nωt)) 5π 6π6 U d
63 Ü1: Raumzeiger 36/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten b n = - 5π 6 U d - π 6 π 5π π ( U d ) sin(nωt)dωt + (U d ) sin(nωt)dωt 5π π 6 6 b n = 2U d π 5π 6 π 6 sin(nωt)dωt π 6 5π 6 b n = 2U d nπ ( cos(nωt)) 5π 6π6 U d b n = 2U d nπ (cos(n π 6 ) cos(n 5π 6 ))
64 Ü1: Raumzeiger 36/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten b n = - 5π 6 U d - π 6 π 5π π ( U d ) sin(nωt)dωt + (U d ) sin(nωt)dωt 5π π 6 6 b n = 2U d π 5π 6 π 6 sin(nωt)dωt π 6 5π 6 b n = 2U d nπ ( cos(nωt)) 5π 6π6 U d b n = 2U d nπ (cos(n π 6 ) cos(n 5π 6 )) b n = 2U d nπ (cos(n(π 5π 6 )) cos(n 5π 6 ) }{{} g(n)
65 Ü1: Raumzeiger 37/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 )
66 Ü1: Raumzeiger 37/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 )
67 Ü1: Raumzeiger 37/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 ) ( g(n) = cos(n 5π 6 ) cos(nπ) ±1 ) 1 sin(nπ) sin(n 0 5π 6 )
68 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 ) ( g(n) = cos(n 5π 6 ) cos(nπ) ±1 ) 1 sin(nπ) sin(n 0 5π 6 ) { 2 cos(n 5π g(n) = 6 ) für ungerade n 0 für gerade n
69 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 ) ( g(n) = cos(n 5π 6 ) cos(nπ) ±1 ) 1 sin(nπ) sin(n 0 5π 6 ) { 2 cos(n 5π g(n) = 6 ) für ungerade n 0 für gerade n cos(n 0 5π 6 ) = 0
70 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 ) ( g(n) = cos(n 5π 6 ) cos(nπ) ±1 ) 1 sin(nπ) sin(n 0 5π 6 ) { 2 cos(n 5π g(n) = 6 ) für ungerade n 0 für gerade n cos(n 0 5π 6 ) = 0 5π n 0 6 = π I; I {1, 3, 5, 7, 9,...} 2
71 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten g(n) = cos(nπ) cos(n 5π 6 ) sin(nπ) sin(n 5π 6 ) cos(n 5π 6 ) g(n) = cos(n 5π 6 ) (cos(nπ) 1) sin(nπ) sin(n 5π 6 ) ( g(n) = cos(n 5π 6 ) cos(nπ) ±1 ) 1 sin(nπ) sin(n 0 5π 6 ) { 2 cos(n 5π g(n) = 6 ) für ungerade n 0 für gerade n cos(n 0 5π 6 ) = 0 5π n 0 6 = π I; I {1, 3, 5, 7, 9,...} 2 n 0 = 3 I; I {1, 3, 5, 7, 9,...} 5 n ist ganzzahlig und ungerade: n = {1,3,5,7,9,11,... }
72 Ü1: Raumzeiger 38/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten Dann: n 0 = 3 I; I = {5, 15, 25, 35, 45,...} 5 n 0 = {3, 9, 15, 21,...}
73 Ü1: Raumzeiger 38/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten Dann: n 0 = 3 I; I = {5, 15, 25, 35, 45,...} 5 n 0 = {3, 9, 15, 21,...} Dann: cos(n 0 5π 6 ) = 0; n 0
74 Ü1: Raumzeiger 38/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten Dann: n 0 = 3 I; I = {5, 15, 25, 35, 45,...} 5 n 0 = {3, 9, 15, 21,...} Dann: Dann: cos(n 0 5π 6 ) = 0; n 0 cos(n 5π 6 ) 0 ( n ungerade und n n 0 ) Jetzt ist n gegeben mit: n={1, 5, 7, 11, 13, 17, 19, 23, 25,...}
75 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten und grafische Darstellung cos(n 5π 6 ) = 0 für n = {3,9,15,21,...} 3 2 für n = {5,7,17,19...} 3 2 für n = {1,11,13,23,25...}
76 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten und grafische Darstellung cos(n 5π 6 ) = 0 für n = {3,9,15,21,...} 3 2 für n = {5,7,17,19...} g(n) = 2 cos(n 5π 6 ) = 3 2 für n = {1,11,13,23,25...} 0 für n = {3,9,15,21,...} 3 für n = {5,7,17,19...} 3 für n = {1,11,13,23,25...}
77 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten und grafische Darstellung cos(n 5π 6 ) = 0 für n = {3,9,15,21,...} 3 2 für n = {5,7,17,19...} g(n) = 2 cos(n 5π 6 ) = 3 2 für n = {1,11,13,23,25...} 0 für n = {3,9,15,21,...} 3 für n = {5,7,17,19...} 3 für n = {1,11,13,23,25...} b n = 2U d nπ (cos(n π 6 ) cos(n(π π 6 ))) }{{} g(n)
78 Ü1: Raumzeiger 39/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Berechnung der Fourierkoeffizienten und grafische Darstellung cos(n 5π 6 ) = 0 für n = {3,9,15,21,...} 3 2 für n = {5,7,17,19...} g(n) = 2 cos(n 5π 6 ) = 3 2 für n = {1,11,13,23,25...} 0 für n = {3,9,15,21,...} 3 für n = {5,7,17,19...} 3 für n = {1,11,13,23,25...} b n = 2U d nπ (cos(n π 6 ) cos(n(π π 6 ))) }{{} g(n) Dann: 0 für n = {3,9,15,21,...} b n = 2 3U d nπ für n = {5,7,17,19...} 2 3U d nπ für n = {1,11,13,23,25...} f(ωt) = b n sin(nωt) i=1
79 U d Spitzwert Fundamental (Großer als U d!): - 5π 6 - π 6 π 6 5π 6 b 1 = 2 3 π U d = U d Effektivwert Fundamental: U d b 1 = U d = 2π π U d
80 Ü1: Raumzeiger 40/44 U d Spitzwert Fundamental (Großer als U d!): - 5π 6 - π 6 π 6 5π 6 b 1 = 2 3 π U d = U d Effektivwert Fundamental: U d U d b 1 = U d = 2π π U d - 5π 6 - π 6 π 6 5π 6 Harmonischen: b 5 = 2 3 5π U d U d b 7 = 2 3 7π b 11 = π - 5π 6 - π 6 b 13 = π π 6 5π 6 U d f(ωt) = 2 ( 3 sin(ωt) + sin(5ωt) + sin(7ωt) ) +... π 5 7
81 U d - 5π 6 - π 6 π 6 5π 6 U d U d - 5π 6 - π 6 π 6 5π 6 U d f(ωt) = 2 ( 3 sin(ωt) sin(5ωt) sin(7ωt) + sin(11ωt) + sin(13ωt) )... π
82 Ü1: Raumzeiger 42/44 Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Beispiel 2: Stromgrundwelle und Strom in Raumzeigerdarstellung I Grundwelleαβ I αβ Für die Grundwellenspannung ergibt sich der Strom mit: I a(t) = 2 3 π (R 2 + (2π50L) 2 sin(ωt ϕ) ) I a(t) = 2 U d π (R 2 + (2π50L) 2 sin(ωt ϕ) ) I Grundewelleαβ = I αê α + I β ê β
83 Outline Darstellung der Ausgangsspannungen eines 2- Level Umrichters Blockbetrieb eines 2-Level Umrichters Umrichterausgangsspannungen in Raumzeigerdarstellung RL Last im Blockbetrieb Effektivwert und Spitzenwert der Ausgangsspannung im Blockbetrieb Zusammenfassung
84 Folgerung Die Spannungen an der Last besitzen mehr als zwei Spannungslevel Da die common mode Spannung ungleich Null ist darf der Sternpunkt nicht direkt verbunden werden Der Grundwellenspitzenwert der verketteten Spannung im Blockbetrieb ist grer als die maximale Zwischenkreisspannung Für eine RL-Last verhlt sich der Strom in Raumzeigerdarstellung linear, wobei die Stromtrajektorie verdreht ist.
85 Ü1: Raumzeiger 44/44 Übung für Zuhause Stellen Sie I α in Abhängigkeit von I β für das Zeitintervall [t 0, t 1 ] dar und zeigen Sie das es sich hierbei um eine lineare Funktion handelt.
86 Fragen Nächste Übung am um 09:45 Uhr
Umwandlung elektrischer Energie mit Leistungselektronik WS 2014
Umwandlung elektrischer Energie mit Leistungselektronik WS 2014 Übungsaufgaben Übung Raumzeiger: Gegeben ist folgende Durchflutung für die Wicklung a einer dreiphasigen Maschine. F a (θ mech, t) = α =
Blockbetrieb. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik. Arcisstraße 21 D München
Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eat@ei.tum.de Internet: http://www.eat.ei.tum.de Prof. Dr.-Ing. Ralph
3. Zeichnen Sie ein beliebiges Pulsmuster des Raumzeigers aus der vorherigen Aufgabe. Welche Freiheitsgrade bestehen bei der Wahl des Pulsmusters?
Ü bungsaufgabe RZM 1. Leiten Sie die Gleichungen für die Schaltzeiten t 1 und t für den dritten Sektor her.. Berechnen Sie die Schaltzeiten für folgenden Sollspannungszeiger U soll = u d (cos ( 5 π) 6
Raumzeiger. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik. Arcisstraße 21 D München
Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Arcisstraße 21 D 80333 München Email: eat@ei.tum.de Internet: http://www.eat.ei.tum.de Prof. Dr.-Ing. Ralph
Umwandlung elektrischer Energie mit Leistungselektronik
Umwandlung elektrischer Energie mit Leistungselektronik Félix Rojas Technische Universität München Prof. Dr. Ing. Ralph Kennel. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Übung 3
Umwandlung elektrischer Energie mit Leistungselektronik WS 2014
Umwandlung elektrischer Energie mit Leistungselektronik WS 2014 Übungsaufgaben Übung Raumzeiger: Gegeben ist folgende Durchflutung für die Wicklung a einer dreiphasigen Maschine. F a (θ mech, t) = α =
Umwandlung elektrischer Energie mit Leistungselektronik
Umwandlung elektrischer Energie mit Leistungselektronik Félix Rojas Technische Universität München Prof. Dr. Ing. Ralph Kennel. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Übung 4
Umwandlung elektrischer Energie mit Leistungselektronik
Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Prof. Dr.-Ing. Ralph Kennel Arcisstraße 1 Email: eat@ei.tum.de Tel.: +49 (0)89 89 858 D 80 München Internet:
2. Parallel- und Reihenschaltung. Resonanz
Themen: Parallel- und Reihenschaltungen RLC Darstellung auf komplexen Ebene Resonanzerscheinungen // Schwingkreise Leistung bei Resonanz Blindleistungskompensation 1 Reihenschaltung R, L, C R L C U L U
Aufgabe 1 Transiente Vorgänge
Aufgabe 1 Transiente Vorgänge S 2 i 1 i S 1 i 2 U 0 u C C L U 0 = 2 kv C = 500 pf Zum Zeitpunkt t 0 = 0 s wird der Schalter S 1 geschlossen, S 2 bleibt weiterhin in der eingezeichneten Position (Aufgabe
Apl. Prof. Dr. N. Knarr Höhere Mathematik III Musterlösung , 120min
Aufgabe 1 8 Punkte Es seien eine Kurve K R mit Parametrisierung C : [ π, π] R und ein Vektorfeld g : R R gegeben durch cos t 4y Ct :, gx, y : sin t 1 05 K 05 05 1 15 05 a 3 Punkte Berechnen Sie die Zirkulation
Leistungselektronik - Formelsammlung Seite 1 von 5. x(t)dt. x2 (t)dt
Leistungselektronik - Formelsammlung Seite von 5 allgemeine Formeln Spannung über einer Induktivität Strom durch Kondensator Zeitkonstante u L (t) = L di i C (t) = C du = L oder = C Berechnung des Mittelwertes
Lösung 04 Klassische Theoretische Physik I WS 15/16. c n = 1 T. c n,u e inωt + c n,u e inωt] c n e inωt = c 0 +
![Lösung 04 Klassische Theoretische Physik I WS 15/16. c n = 1 T. c n,u e inωt + c n,u e inωt] c n e inωt = c 0 +](/thumbs/57/39987542.jpg "Lösung 04 Klassische Theoretische Physik I WS 15/16. c n = 1 T. c n,u e inωt + c n,u e inωt] c n e inωt = c 0 +")
Karlsruher Institut für Technologie Institut für theoretische Festkörperphysik www.tfp.kit.edu Lösung 4 Klassische Theoretische Physik I WS 5/6 Prof. Dr. G. Schön 2 Punkte Sebastian Zanker, Daniel Mendler
Umwandlung elektrischer Energie mit Leistungselektronik
Umwandlung elektrischer Energie mit Leistungselektronik Félix Rojas Technische Universität München Prof. Dr. Ing. Ralph Kennel. Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Übung 5
7 Drehstromsteller. 7.1 Verbraucher mit zugänglichem Sternpunkt
7 Drehstromsteller Drehstromsteller werden zur verlustlosen Steuerung von Dreiphasensystemen eingesetzt. Die Frequenz wird nicht verändert. Sie werden im unteren Leistungsbereich zum Spannungsanlauf und
Grundlagen der Elektrotechnik 3. Übungsaufgaben
Campus Duisburg Grundlagen der Elektrotechnik 3 Nachrichtentechnische Systeme Prof. Dr.-Ing. Ingolf Willms Version Juli 08 Aufgabe 1: Man bestimme die Fourier-Reihenentwicklung für die folgende periodische
Elektrische Antriebe und Anlagen
Elektrische Antriebe und Anlagen Kapitel 8: selbstgeführte Wechselrichter 5.Jhrg KOHE KOHE 1 Wechsel-Umrichter Einführung: netzgeführte Direktumrichter f 0.5 f 2max 1 Umrichter mit Gleichspannungszwischenkreis
Fourier-Reihen und Fourier-Transformation
Fourier-Reihen und Fourier-Transformation Matthias Dreÿdoppel, Martin Koch, Bernhard Kreft 25. Juli 23 Einleitung Im Folgenden sollen dir und die Fouriertransformation erläutert und mit Beispielen unterlegt
NTB Druckdatum: ELA II. Zeitlicher Verlauf Wechselgrösse: Augenblickswert ändert sich periodisch und der zeitliche Mittelwert ist Null.
WECHSELSTROMLEHRE Wechselgrössen Zeitlicher Verlauf Wechselgrösse: Augenblickswert ändert sich periodisch und der zeitliche Mittelwert ist Null. Zeigerdarstellung Mittelwerte (Gleichwert, Gleichrichtwert
Elektrotechnik 3. Drehstrom Industrielle Stromversorgung Elektrische Maschinen / Antriebe. Studium Plus // WI-ET. SS 2016 Prof. Dr.
Elektrotechnik 3 Drehstrom Industrielle Stromversorgung Elektrische Maschinen / Antriebe Studium Plus // WI-ET SS 06 Prof. Dr. Sergej Kovalev Drehstromsystems Themen: Einführung Zeitverläufe Mathematische
Elektrische Antriebe und Anlagen
Elektrische Antriebe und Anlagen Kapitel 3: Grundlagen der Leistungselektronik 5.Jhrg KOHE 1 Bsp. Glühbirne Ziel: Helligkeitssteuerung einer Glühbirne. 1) Mit einstellbarem Vorwiderstand Spannungsteiler.
cos(kx) sin(nx)dx =?
3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
Serie 12 Musterlösung
Serie 2 Musterlösung ineare Algebra www.adams-science.org Klasse: Ea, Eb, Sb Datum: HS 7 In dieser Serie werden alle echnungen in der Basis und in SI-Einheiten durchgeführt. e ˆ cos(ω t) und e 2 ˆ sin(ω
Elektro- und Informationstechnik. Mathematik 1 - Übungsblatt 12 und nicht vergessen: Täglich einmal Scilab!
Mathematik 1 - Übungsblatt 12 und nicht vergessen: Täglich einmal Scilab! Aufgabe 1 (Zuordnung reeller Größen zu komplexen Größen) Der Vorteil der komplexen Rechnung gegenüber der reellen besteht darin,
Wärmeleitungsgleichung,
Fachbereich Mathematik der Universität Hamburg SoSe 2015 Dr. Hanna Peywand Kiani Wärmeleitungsgleichung, 05.06.2015 Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur die Mitarbeit während
3. Grundlagen des Drehstromsystems
Themen: Einführung Zeitverläufe Mathematische Beschreibung Drehstromschaltkreise Anwendungen Symmetrische und unsymmetrische Belastung Einführung Drehstrom - Dreiphasenwechselstrom: Wechselstrom und Drehstrom
18 Stromregelung selbstgeführter Wechselrichter
18 Stromregelung selbstgeführter Wechselrichter Übungsziele: Arbeitsweise von selbstgeführten B2-Brücken mit Phasenstromregelung Arbeitsweise von selbstgeführten B6-Brücken mit Phasenstromregelung Übungsdateien:
Elektrotechnik II Übung 3
Elektrotechnik II Übung 3 Prof. Dr. Göran Andersson FS 2011 http://www.eeh.ee.ethz.ch/ Feedback zur Übung 2 Übung 3-2 Ziel und Motivation der Übung 3 Ziele: 1. Praktische Realisierung eines PID-Reglers
Modellfall. Orthogonalität trigonometrischer Funktionen. Anwendungen: f : (0, L) R gegeben.
Modellfall Anwendungen: Fragen: Digitalisierung / digitale Darstellung von Funktionen, insbesondere für Ton- und Bilddaten Digitale Frequenzfilter Datenkompression: Abspeichern der unteren Frequenzen Lösung
Teil III. Fourieranalysis
Teil III Fourieranalysis 3 / 3 Fourierreihen Ziel: Zerlegung einer gegebenen Funktion in Schwingungen Konkret: f : (, L) R gegebene Funktion Gesucht: Darstellung der Form ( f (x) = a + a n cos ( n L x)
Fourier-Integrale: Ausgangsdaten und Transformierte sind jeweils Funktionen über der ganzen reellen Achse.
Fourier-Reihen Fourier-Transformation Die Fourier-Transformation ist eines der wichtigsten Instrumente zur Behandlung linearer Systeme, seien es gewöhnliche oder partielle lineare Differentialgleichungen
Apl. Prof. Dr. N. Knarr Höhere Mathematik III Musterlösung , 120min
Aufgabe (9 Punkte) Es sei die Fläche S R 3 gegeben durch S : { } (x, y, z) R 3 : 4z x + y 4, z. (a) ( Punkte) Geben Sie eine Parametrisierung für S an. (b) (4 Punkte) Berechnen Sie den Flächeninhalt von
Musterlösung Grundlagen der Elektrotechnik B
Prof. Dr.-Ing. Joachim Böcker Musterlösung Grundlagen der Elektrotechnik B 7.4.2 7.4.2 Musterlösung Grundlagen der Elektrotechnik B Seite von 4 Version vom 6. Mai 2 Aufgabe : Ausgleichsvorgang 2 Punkte).
Signale und Systeme Die Fourier-Reihe
Signale und Systeme Die Fourier-Reihe Zsolt Kollar BME HVT hvt.bme.hu 26. März 2012 Gliederung 1 Die kontinuierliche Fourier-Reihe Rekapitulation Berechnung der Koeffizienten Genauigkeit Spezielle Eigenschaften
FACHHOCHSCHULE Bielefeld 3. Juli 2001 Fachbereich Elektrotechnik
FACHHOCHSCHULE Bielefeld 3. Juli 2001 Fachbereich Elektrotechnik Professor Dr. Ing. habil. K. Hofer Klausur zu LEISTUNGSELEKTRONIK UND ANTRIEBE (LE) Bearbeitungsdauer: Hilfsmittel: 3.0 Zeitstunden Vorlesungsskriptum,
Uebungsserie 1.1 Harmonische Signale und Ihre Darstellung
28. September 2016 Elektrizitätslehre 3 Martin Weisenhorn Uebungsserie 1.1 Harmonische Signale und Ihre Darstellung Aufgabe 1. Die nachfolgende Grafik stellt das Oszillogramm zweier sinusförmiger Spannungen
10. Periodische Funktionen, Fourier Reihen
H.J. Oberle Analysis II SoSe 212 1. Periodische Funktionen, Fourier Reihen Jean Baptiste Joseph Fourier: Joseph Fourier wurde am 21.3.1768 bei Auxerre (Burgund) geboren und starb am 16.5.183 in Paris.
Lehrstuhl für Technische Elektrophysik TU München
Lehrstuhl für Technische Elektrophysik TU München Tutorübungen zu Elektromagnetische Felheorie 1, Prof. Wachutka, WS0809, Blatt 7 1. Aufgabe Ein Magnetfeld wird wie folgt in kartesischen Koordinaten definiert:
Anwendungen der Fourier-Entwicklung in der Elektrotechnik 1 / 22
Anwendungen der Fourier-Entwicklung in der Elektrotechnik 1 / Unser heutiges Ziel Reaktion eines Netzwerks auf ein periodisches Eingangssignal oder speziell Wie reagiert ein RC-Glied auf periodische Erregung?
Der Verlauf der magnetischen Kraftwirkung um einen Magneten wird mit Hilfe von magnetischen Feldlinien beschrieben.
Wechsel- und Drehstrom - KOMPAKT 1. Spannungserzeugung durch Induktion Das magnetische Feld Der Verlauf der magnetischen Kraftwirkung um einen Magneten wird mit Hilfe von magnetischen Feldlinien beschrieben.
Einführung in die Physik I. Schwingungen und Wellen 1
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Institut für Leistungselektronik und Elektrische Antriebe. Aufgabe 9
Institut für Leistungselektronik und Elektrische Antriebe Prof. Dr.-Ing. J. Roth-Stielow Aufgabe 9 Photovoltaik-Wechselrichter mit Leistungsmaximierung In dieser Aufgabe soll die Einspeisung von elektrischer
7.1 Überlagerung von Schwingungen, Fourier Zerlegung
Kapitel 7 Schwingungen und Wellen 7. Überlagerung von Schwingungen, Fourier Zerlegung Im Abschnitt über die Bewegungen einzelner Teilchen haben wir uns sehr intensiv mit den Harmonischen Schwingungen beschäftigt,
11 Fourier-Analysis Grundlegende Begriffe
11 Fourier-Analysis 11.1 Grundlegende Begriffe Definition: Eine Funktion f : R R (oder f : R C) heißt periodisch mit der Periode T (oder T-periodisch), falls f(t + T) = f(t) für alle t R. Ziel: Entwicklung
Musterloesung. Name:... Vorname:... Matr.-Nr.:...
Nachklausur Grundlagen der Elektrotechnik I-A 6. April 2004 Name:... Vorname:... Matr.-Nr.:... Bearbeitungszeit: 135 Minuten Trennen Sie den Aufgabensatz nicht auf. Benutzen Sie für die Lösung der Aufgaben
Schwache Formulierung der Poisson-Gleichung Finite Elemente Methoden Fouriermethoden für Wärmeleitungsgleichung
Department Mathematik der Universität Hamburg SoSe 29 Dr. Hanna Peywand Kiani Schwache Formulierung der Poisson-Gleichung Finite Elemente Methoden Fouriermethoden für Wärmeleitungsgleichung Die ins Netz
Apl. Prof. Dr. N. Knarr Musterlösung , 120min
Apl. Prof. Dr. N. Knarr Musterlösung 4.3.25, 2min Aufgabe ( Punkte) Es sei S := {(x, y, z) R 3 z = x 2 + y 2, z 2}. (a) (6 Punkte) Berechnen Sie den Flächeninhalt von S. (b) (4 Punkte) Berechnen Sie die
3.5 Vollgesteuerte 6-Puls-Brückenschaltung
.5 Vollgesteuerte -Puls-Brückenschaltung.5.1 Messungen an den vorgegebenen Schaltungen Schaltungen: ut1 ud ud ufd ud ud ifd Der arithmetischer Mittelwert der Gleichspannung, sowie Mittel- und Effektivwert
Grundlagen der Elektrotechnik 3
Campus Duisburg Grundlagen der Elektrotechnik 3 Fakultät für Ingenieurwissenschaften Abteilung Elektrotechnik und Informationstechnik Fachgebiet Allgemeine und Theoretische Elektrotechnik Bismarckstraße
Grundlagen der Elektrotechnik 3
Campus Duisburg Grundlagen der Elektrotechnik 3 Fakultät für Ingenieurwissenschaften Abteilung Elektrotechnik und Informationstechnik Fachgebiet Allgemeine und Theoretische Elektrotechnik Bismarckstraße
Konvergenz und Stetigkeit
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 12. Dezember 2007 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Aufgabe 7: Dreiphasiger Wechselrichter mit zeitdiskreter Schaltzustandsänderung
ufgabe 7: Dreiphasiger Wechselrichter mit zeitdiskreter Schaltzustandsänderung Im Rahmen der vorliegenden ufgabe wird der in Bild auf Seite 4 dargestellte dreiphasige Wechselrichter untersucht. Die an
Musterlösung Serie 2
D-ITET Analysis III WS 13 Prof. Dr. H. Knörrer Musterlösung Serie 1. Wir wenden die Methode der Separation der Variablen an. Wir schreiben u(x, t = X(xT (t und erhalten Daraus ergeben sich die Gleichungen
Leistungselektronik Grundlagen und Standardanwendungen. Übung 2: Netzgeführte Stromrichter
Lehrstuhl für Elektrische Antriebssysteme und Leistungselektronik Technische Universität München Arcisstraße 1 D 8333 München Email: eal@ei.tum.de Internet: http://www.eal.ei.tum.de Prof. Dr.-Ing. Ralph
Differenzengleichungen, Z - Transformation
Differenengleichungen, Z - Transformation In diesem Kapitel wollen wir eine weitere Transformation, die Z-Transformation behandeln. Mit Hilfe der Z-Transformation können lineare Differenengleichungen (DFG
Die Schaltung (M3) wird an einem symmetrischen Drehstromsystem betrieben. Die zeitlichen Verläufe der Spannungen werden damit beschrieben durch:
Aufgabe Ü Gegeben ist folgende Gleichrichterschaltung mit drei idealen Ventilen. An der Sekundärseite des Transformators liegt ein symmetrisches Dreiphasen-Wechselspannungssystem an. u s1 t u s t u V1
Übungsziel: Zusammensetzung der Stromrichterkomponenten zu Umrichterschaltungen.
Übungsziel: Zusammensetzung der Stromrichterkomponenten zu Umrichterschaltungen. Übungsdateien: SIMPLORER: u_umrdr.ssh; u_umrdr_m.ssh; u_umrdr_mf.mdx; u_umrdr_mf.day 19.1 Allgemeines Allgemein findet der
Name:...Vorname:... Seite 1 von 8. Hochschule München, FK 03 Grundlagen der Elektrotechnik WS 2008/2009
Name:...Vorname:... Seite 1 von 8 Hochschule München, FK 03 Grundlagen der Elektrotechnik WS 2008/2009 Matrikelnr.:... Hörsaal:...Platz:... Stud. Gruppe:... Zugelassene Hilfsmittel: beliebige eigene A
,Faltung. Heavisidefunktion σ (t), Diracimpuls δ (t) Anwendungen. 1) Rechteckimpuls. 2) Sprungfunktionen. 3) Schaltvorgänge
Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Diplomvorprüfung SS 2009 Grundlagen der Elektrotechnik Dauer: 90 Minuten
Diplomvorprüfung Grundlagen der Elektrotechnik Seite 1 von 7 Hochschule München Fakultät 03 Zugelassene Hilfsmittel: Taschenrechner, zwei Blatt DIN A4 eigene Aufzeichnungen Diplomvorprüfung SS 2009 Grundlagen
Johannes Veit. 8. Januar 2016
Finite im Ein Blick über den Tellerrand... mit FreeFem++ 8. Januar 2016 im 1 2 im 3 4 Gliederung 5 im 1 2 im 3 4 Gliederung 5 dem Einheitsquadrat Laplace - Gleichung: im u(x) = 0 Man betrachte das Problem
Konvergenz und Stetigkeit
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 10. Dezember 2008 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Rechenübungen zu Leistungselektronik
Ausarbeitung der Beispiele aus Rechenübungen zu eistungselektronik Teil B - Selbstgeführte Stromrichter Die hier angeführten Berechnungen könnten fehlerhaft sein Inhalt Beispiel 3 Beispiel 4 Beispiel 3
Übung 2: Spektrum periodischer Signale
ZHAW, SiSy, Rumc, Übung : Spektrum periodischer Signale Augabe Verschiedene Darstellungen der Fourierreihe. Betrachten Sie das periodische Signal s(t) = + sin(π t). a) Bestimmen Sie die A k - und B k -Koeizienten
A2.1: Gleichrichtung. Die Grafik zeigt das periodische Signal x(t). Legt man x(t) an den Eingang einer Nichtlinearität mit der Kennlinie
Abschnitt: 2.1 Allgemeine Beschreibung A2.1: Gleichrichtung Die Grafik zeigt das periodische Signal x(t). Legt man x(t) an den Eingang einer Nichtlinearität mit der Kennlinie so erhält man am Ausgang das
BERUFSAKADEMIE S T U T T G A R T University of Cooperative Education. Höhere Mathematik II. Übungen. Komplexe Zahlen. i e π + 1=
BERUFSAKADEMIE S T U T T G A R T University of Cooperative Education Höhere Mathematik II Übungen Komplexe Zahlen i e π + 0 8 R. Mohr FK Blatt Komplexe Zahlen I WS 004/ Aufgabe : Gegeben sind die komplexen
(2 π f C ) I eff Z = 25 V
Physik Induktion, Selbstinduktion, Wechselstrom, mechanische Schwingung ösungen 1. Eine Spule mit der Induktivität = 0,20 mh und ein Kondensator der Kapazität C = 30 µf werden in Reihe an eine Wechselspannung
Nerreter, Grundlagen der Elektrotechnik Carl Hanser Verlag München. 9 Nichtsinusförmige Größen
Nerreter, Grundlagen der Elektrotechnik Carl Hanser Verlag München 9 Nichtsinusförmige Größen Aufgabe 9.9 Die Klemmenspannung u(t) der zweipoligen Schaltung hat die Grundfrequenz f 1 = 100 Hz und wird
5. Fourier-Transformation
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fourier- und Laplace- Transformation
Übungsaufgaben zur Vorlesung Mathematik für Ingenieure Fourier- und Lalace- Transformation Teil : Lalace-Transformation Prof. Dr.-Ing. Norbert Hötner (nach einer Vorlage von Prof. Dr.-Ing. Torsten Benkner)
Klausur Grundlagen der Elektrotechnik B
Prof. Dr. Ing. Joachim Böcker Klausur Grundlagen der Elektrotechnik B 07.04.2009 Name: Matrikelnummer: Vorname: Studiengang: Aufgabe: (Punkte) 1 (16) 2 (23) 3 (22) 4 (21) 5 (18) Fachprüfung Leistungsnachweis
Aufgabe 1: Elektro-mechanischer Oszillator
37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
Inhaltsverzeichnis. 1 Reexions- und Brechungsgesetz. 1.1 Einführung
Inhaltsverzeichnis 1 Reexions- und Brechungsgesetz 1 1.1 Einführung...................................................... 1 1.2 Snelliussches Brechungsgesetz............................................
Elektro- und Informationstechnik. Mathematik 1 - Übungsblatt 12 Lösungsvorschläge
Mathematik - Übungsblatt Lösungsvorschläge Aufgabe (Zuordnung reeller Größen zu komplexen Größen) Der Vorteil der komplexen Rechnung gegenüber der reellen besteht darin, dass die erforderlichen Rechnungen
Name:...Vorname:... Seite 1 von 7. Matrikelnr.:... Hörsaal:...Platz:... Stud. Gruppe:...
Name:...Vorname:... Seite 1 von 7 FH München, FB 03 Grundlagen der Elektrotechnik SS 2006 Matrikelnr.:... Hörsaal:...Platz:... Stud. Gruppe:... Zugelassene Hilfsmittel: beliebige eigene A 1 2 3 4 Σ N Aufgabensteller:
Schaltungsanalyse Ergänzende Übungen zur Prüfungsvorbereitung - Teil 1
Schaltungsanalyse Ergänzende Übungen zur Prüfungsvorbereitung - Teil 1 1) DC Netzwerk - Verfahren R 1 U q R 2 R 3 R 4 I q A B U q = 6 V I q = 1 A R 1 = 6 R 2 = 6 R 3 = 6 R 4 = 2 2) Gesteuerte Quelle a)
Elektro- und Informationstechnik WS 2012/2013. Mathematik II - Übungsblatt 04 mit Lösungsvorschlägen. a 2, a 1, b 1,
Aufgabe 1 - Übungsblatt 04 mit Lösungsvorschlägen Berechnen Sie die Fourierkoeffizienten a 0, a 1, a 2, b 1, b 2 der im folgenden Diagramm dargestellte Rechteckspannung: Hinweis: Suchen Sie zunächst nach
Praktikum Grundlagen der Elektrotechnik
Fakultät für Elektrotechnik und Informationstechnik Institut für Informationstechnik Lehrgruppe Grundlagen der Elektrotechnik Praktikum Grundlagen der Elektrotechnik 1. Versuchsbezeichnung GET 10: Fourieranalyse
3.3 Das Abtasttheorem
17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
2 Grundlagen. 2.2 Gegenüberstellung Induktivität und Kapazität. 2.1 Gegenüberstellung der Grössen Translation > Rotation
1 Inhaltsverzeichnis 1 Inhaltsverzeichnis... 1 2 Grundlagen... 3 2.1 Gegenüberstellung der Grössen Translation > Rotation... 3 2.2 Gegenüberstellung Induktivität und Kapazität... 4 2.3 Zentrifugalkraft...
Lösung 07 Klassische Theoretische Physik I WS 15/16
Karlsruher Institut für Technologie Institut für theoretische Festkörperphysik www.tfp.kit.edu Lösung 7 Klassische Theoretische Physik I WS 5/6 Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler
Spannungszwischenkreisumrichter (Pulsumrichter)
Lehrveranstaltung Umwandlung elektrischer Energie mit Leistungselektronik Spannungszwischenkreisumrichter (Pulsumrichter) Prof. Dr. Ing. Ralph Kennel (ralph.kennel@tum.de) Technische Universität München
Im dargestellten Drehstomnetz sind folgende Impedanzen angeschlossen:
Aufgabe Ü3 Im dargestellten Drehstomnetz sind folgende Impedanzen angeschlossen: R = 1 Ω L1 W1 W4 I 1 R X C = 3 Ω X L = 2 3 Ω L2 W2 I 2 jx L -jx C = 13 V = 13 V e j120 L3 W3 W5 I 3 = 13 V e j120 N 1. Zeichnen
FOURIERREIHEN. a) Periodische Funktionen. 3) Rechteckschwingung. b) Stückweise stetige Funktionen. Skizze= Sägezahnschwingung
FOURIERREIHEN 1. Grundlagen a) Periodische Funtionen Beispiele: 1) f( x) = sin( x+ π / 3), T = 2 π /. 2) f( t) = cos( ωt+ ϕ), T = 2 π / ω. 3) Rechtecschwingung, 1< t < f() t =, f( t+ 2) = f() t 1, < t
4. Dämpfungsmodelle. 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. Elastodynamik 3.
4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
Einführung in die Laplace Transformation
Einführung in die aplace Transformation Peter Riegler 17. Oktober 2 Zusammenfassung Dieser Text gibt Ihnen eine kurze Einführung in das Werkzeug der aplace Transformation. Es zeigt Ihnen, wo und warum
Lehrstuhl für Technische Elektrophysik Technische Universität München
Lehrstuhl für Technische Elektrophysik Technische Universität München Tutorübungen zu "Elektromagnetische Feldtheorie II" (Prof. Wachutka) SS9 Blatt 1 Aufgabe: Ebene Wellen Im Vakuum, daß heißt die Leitfähigkeit
Aufgabe 1: Aufgabe 2: Berechnen Sie für den unten abgebildeten periodischen Spannungsverlauf. 1. den arithmetischen Mittelwert, 2.
Aufgabe 1: Berechnen Sie für den unten abgebildeten periodischen Spannungsverlauf 1. den arithmetischen Mittelwert, 2. den Effektivwert, 3. den Scheitelfaktor, 4. den Formfaktor. ū=5v, U = 6,45V, k s =
Experimentalphysik II Elektromagnetische Schwingungen und Wellen
Experimentalphysik II Elektromagnetische Schwingungen und Wellen Ferienkurs Sommersemester 2009 Martina Stadlmeier 10.09.2009 Inhaltsverzeichnis 1 Elektromagnetische Schwingungen 2 1.1 Energieumwandlung
Übungen zu Experimentalphysik 2
Physik Department, Technische Universität München, PD Dr. W. Schindler Übungen zu Experimentalphysik 2 SS 13 - Lösungen zu Übungsblatt 4 1 Schiefe Ebene im Magnetfeld In einem vertikalen, homogenen Magnetfeld
Höhere Antriebsleistungen durch separat gespeiste parallele Stränge
Themenvorschlag für FVA-AK Geregelte Antriebe Höhere Antriebsleistungen durch separat gespeiste parallele Stränge Kennwort : Parallelspeisung Prof. Dr.-Ing. Ralph M. Kennel Lehrstuhl für Elektrische Antriebssysteme
Feldorientierte Regelung
Dieter Gerling Audi-Forum elektrische Kleinantriebe im Fahrzeug Ingolstadt, 05.05.2014 Inhalt Grundlagen Feldorientierte Regelung am Beispiel Asynchronmaschine Feldorientierte Regelung am Beispiel Permanentmagnet-Maschine
Höhere Antriebsleistungen durch separat gespeiste parallele Stränge
Themenvorschlag für FVA-AK Geregelte Antriebe Höhere Antriebsleistungen durch separat gespeiste parallele Stränge Kennwort : Parallelspeisung Prof. Dr.-Ing. Ralph M. Kennel Lehrstuhl für Elektrische Antriebssysteme
1.2) Bestimmen Sie die Leistung, welche in Abhängigkeit der Frequenz ω am Widerstand abfällt und stellen Sie diesen Zusammenhang graphisch dar.
Übung /Grundgebiete der Elektrotechnik 3 (WS7/8 Frequenzabhängiges Übertragungsverhalten Dr. Alexander Schaum, Lehrstuhl für vernetzte elektronische Systeme Christian-Albrechts-Universität zu Kiel Aufgabe
Lehrfach: Grundlagen der Elektrotechnik Versuch: Drehstromnetzwerke
DSNW P_10_06.docx Lehrfach: Grundlagen der Elektrotechnik Versuch: Drehstromnetzwerke Oc Hochschule Zittau/Görlitz; Fakultät Elektrotechnik und Informatik Prof. Dr. techn. Stefan Kornhuber/Prof. Dr.-Ing.
1 Allgemeine Grundlagen
Allgemeine Grundlagen. Gleichstromkreis.. Stromdichte Die Stromdichte in einem stromdurchflossenen Leiter mit der Querschnittsfläche A ist definiert als: j d d :Stromelement :Flächenelement.. Die Grundelemente
Vom Zeit- zum Spektralbereich: Fourier-Analyse
Vom Zeit- zum Spektralbereich: Fourier-Analyse Ergebnis der Analyse Zerlegung eines beliebigen periodischen Signals in einem festen Zeitfenster in eine Summe von Sinoidalschwingungen Ermittlung der Amplituden
Lösungsvorschläge zur Klausur
Prüfung in Höhere Mathematik 3 5. September 3 Lösungsvorschläge zur Klausur für bau, ernen, fmt, IuI, mach, tema, umw, verf, geod und so weiter ; Aufgabe : Punkte Im R 3 wird eine Fläche T durch die Abbildung
Symmetrische Komponenten - Einführung
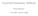Symmetrische Komponenten - Einführung Hannes Zinnbauer. Juni 2005 - gesetzt in L A TEX Inhaltsverzeichnis Theoretische Betrachtung 2 2 Beispiel 6 Theoretische Betrachtung Es wird gezeigt, daß sich jedes
FH Giessen-Friedberg StudiumPlus Dipl.-Ing. (FH) M. Beuler Grundlagen der Elektrotechnik Wechselstromtechnik
4 4. Wechselgrößen Nimmt eine Wechselgröße in bestimmten aufeinander folgenden Zeitabständen wieder denselben Augenblickswert an, nennt man sie periodische Wechselgröße. Allgemeine Darstellung periodischer