Inhalt der Vorlesung A1
|
|
|
- Richard Färber
- vor 7 Jahren
- Abrufe
Transkript
1 Inhal der Vorlesung A1 1. Einführung Mehode der Physik Physikalische Größen Übersich über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung von Teilchenbewegung Kinemaik: Quaniaive Erfassung Dynamik: Ursachen der Bewegung Energie, Arbei + Leisung Erhalungssäze: Impuls+Energieerhalung Drehbewegung Schwingungen, harmonischer Oszillaor B. Teilchensyseme 1
2 Der Aufbau eines Aoms Elemenareilchen, z.b. Elekron: besiz Masse m besiz keine Ausdehnung
3 1. Beschreibung von Bewegung Konzep des Massenpunks: Die Bewegung eines ausgedehnen, makroskopischen Körpers der Masse m im Raum kann so beschrieben werden, dass seine Masse als in einem Punk (späer: Schwerpunk) konzenrier gedach wird. Unser Raum und seine Srukur 3-dimensionaler Raum Vekorraum Punkraum Beziehung zwischen Punken im Raum wird durch Vekor eindeuig fesgeleg! 3
4 Physikalische Größen, die durch Särke und Richung beschrieben werden, nenn man Vekoren. Wahl eines Koordinaensysems eindeuige Feslegung eines Bezugssysems: Wahl eines Bezugspunks O Wahl von gericheen Orienierungslinien im Raum Posiion: Vekor von A zu B Massenpunk Vekor A AB B Verschiebung karesische Koordinaen z x r y, z ( x, y z) Der Vekor wird durch Angabe der Koordinaen x, y, z quaniaiv besimm. x r y 4
5 . Kinemaik In der Kinemaik wird versuch, einen Bewegungsvorgang quaniaiv zu erfassen. Dabei wird nich nach den Ursachen der Bewegung gefrag. zunächs: Beschränkung auf eindimensionale Bewegungen in der Praxis erreichbar durch geeignee Einschränkungen im Bewegungsablauf des Körpers. Beobachung: Bahnkurve x() Abhängigkei des Ores des Massenpunks von der Zei Charakerisische Größe: Annahme: gleichförmige Bewegung Ha ein Körper eine konsane Geschwindigkei, dann wird ihr Wer durch den Quoienen angegeben, oder symbolisch Geschwindigkei Geschwindigkei v s Weg Zei m s 5
6 . Kinemaik Da neben dem Berag auch die Richung wichig is, is die Geschwindigkei ein Vekor: v s x v x Jez wird allgemein der Fall einer beliebigen nich-konsanen Geschwindigkei behandel: 6
7 Der Or x veränder sich mi der Zei, x is also eine Funkion der Zei: x() Bei nich konsaner Geschwindigkei ergib sich im Weg-Zei-Diagramm eine beliebige Funkion: Bei konsaner Geschwindigkei ergib sich im Weg-Zei-Diagramm eine Gerade: x() x Geschwindigkei: v x Bahnkurve Definiion der momenanen zur Zei vorhandenen Geschwindigkei v(): v( ) lim x v Durchschnis- Geschwindigkei x( ) dx d x m s 7
8 Umgekehr kann man aus dem Verlauf der Geschwindigkei v() auch die Bahn berechnen. dx v ( ) dx v ( ) d x ( ) dx v ( ) d + C d Sei die Geschwindigkei konsan, also v() v cons., dann folg x( ) v d + C Wenn der Körper zum Zeipunk v d + C v + C am Or x() x war, dann folg sofor C x x ( ) v + x 8
9 Änder sich die Geschwindigkei v() mi der Zei, so biee sich eine weiere Größe zur Charakerisierung der Bewegung an, die Beschleunigung. Definiion der momenanen Beschleunigung in einer Dimension: dv d x m a( ) x d d s Aus der Beschleunigung können auch wieder rückwärs die Geschwindigkei und der Or berechne werden: v( ) a( τ + v τ1 τ ) d x( ) v( τ ) dτ + x a( ) d d 1 + v + x τ τ τ Die Anfangswere zur Zei sind: x und v Durch Angabe der Beschleunigung und der beiden Anfangsbedingungen is das Problem eindeuig fesgeleg! 9
10 Beispiel: Der senkreche Fall Auf der Erdoberfläche wirk die konsane Beschleunigung a m a g 9,81 s Nach 5s freier Fall is die Geschwindigkei (am Anfang is: v m/s): v a dτ a dτ g 49.5 m s und der zurückgelege Weg x : x τ1 1 a dτ dτ aτ1 dτ1 g 1.6 m 1
11 Versuch 1: Wurfparabel mi Wassersrahl Der Wassersrahl ri aus einer Düse horizonal mi einer Anfangsgeschwindigkei v aus, die konsan bleib, so daß der Weg linear mi der Zei zunimm: x v Verikal wirk die Graviaion, also is der Weg proporional zur Zei: z x Wassersrahl z z 1 g Beide unabhängigen Bewegungen zusammen ergeben die Wurfparabel. 11
12 Heben wir nun die Beschränkung auf eindimensionale Bewegungen auf! Im dreidimensionalen Raum haben wir den Orsvekor: x( ) r ( ) y( ) z( ) r () Bahnkurve 1
13 Die Durchschnisgeschwindigkei is wieder und die momenane Geschwindigkei: Die Ableiung eines Vekors erfolg durch Ableiung seiner Komponenen. v dr ( ) d r ( ) x v x ( ) y ( ) z ( ) v v v x y z Der Geschwindigkeisvekor v () lieg angenial zur Bahnkurve r (), also v v e Einheisvekor in Richung der Tangene e Der Berag der Geschwindigkei is dann gegeben durch v x + y + z ds d Die Beschleunigung is wieder die Änderung der Geschwindigkei pro Zei, jez aber als Vekor: a v dv d v v v x y z x y z 13
14 Beispiel: Der schiefe Wurf a a g g 9.81 m s v Die Inegraion eines Vekors erfolg durch Inegraion der Komponenen. a dτ + Die Geschwindigkei is dann In Komponenen ergib sich daher: v v + v g v a vx, vy, g + v + v z, 14
15 PHYSIK A WS 13/14 WS 14/15 15 Nochmalige Inegraion liefer den zeiabhängigen Orsvekor + d v r r ) ( ) ( τ τ τ τ d v g v v z y x r z y x + +,,, ) ( ,,, 1 ) ( ) ( ) ( ) ( z v g y v x v z y x r z y x In Komponenenschreibweise ergib sich dann für den Orsvekor erneu: Die Bewegungen enlang unerschiedlicher Raunrichungen laufen unabhängig voneinander ab!
16 Beispiel: z h v α α b b x In einem Brunnen sind zwei Wasserdüsen im Absand von b 8. m monier und um jeweils den Winkel α 7 geneig. Aus den Düsen ri das Wasser mi der Anfangsgeschwindigkei von v 1 m/s. In der Mie kreuzen sich die Wassersrahlen in einer Höhe h. Wie groß is diese Höhe h? 16
17 v Die Anfangsgeschwindigkei is in vekorieller Schreibweise v v cosα 3.4 v v x y z v sinα Die Zei, die das Wasser von der Düse bis zum Kreuzungspunk brauch, is b v x, Die Anfangskoordinaen des Wassersrahls sind r s m s Dann is der Bahnvekor im Kreuzungspunk r ( ) 1 v g x, + v z, 4.. m 4.81 Mi s ergib sich für den Kreuzungspunk der Wassersrahlen die Höhe h 4.81 m. 17
18 Versuch : Affenschuß Die Kanone wird in gerader Linie mi einem Lasersrahl auf das Plüschier ausgeriche. Beim Schuß fäll das Tier aber auch die Gummikugel und zwar um dieselbe Srecke. Kanone Laser Flugbahn der Kugel Fallweg des Tieres Ergebnis: Das Plüschier wird geroffen! 18
19 Beispiel : Gleichförmige Kreisbewegung r () r () Der zeiabhängige Orsvekor is dann cos( ω ) r ( ) ρ sin( ω ) Geschwindigkei Winkelgeschwindigkei : ω π f v( ) v r ( ) ρ v( ) sin( ω ) ω cos( ω ) ρ ω cons. Periode : T 1 f π ω Die Frequenz f gib die Anzahl der Umläufe pro Sekunde an. 19
20 Die Kreisbeschleunigung is a r ( ) cos( ω ) ρω sin( ω ) r () Die Kreisbeschleunigung seh senkrech auf der Geschwindigkei, sie weis immer zum Kreismielpunk (Zenripealbeschleunigung). Weierhin folg, daß die Kreisbeschleunigung proporional zum Quadra der Winkelgeschwindigkei is: a ρ ω ω
21 Inhal der Vorlesung A1 1. Einführung Mehode der Physik Physikalische Größen Übersich über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung von Teilchenbewegung Kinemaik: Quaniaive Erfassung Dynamik: Ursachen der Bewegung Energie, Arbei + Leisung Erhalungssäze: Impuls+Energieerhalung Drehbewegung Schwingungen, harmonischer Oszillaor B. Teilchensyseme 1
22 .3 Dynamik In der Dynamik werden die Ursachen der Bewegung hinerfrag. Vor allem bei der Behandlung von Soßprozessen is zur Charakerisierung des Einflusses eines Soßparners die Angabe von Masse und Geschwindigkei erforderlich Kombinaion zu einer neuen Größe Impuls p( ) p p p x y z ( ) ( ) ( ) mv ( ) v mv v x y z ( ) ( ) ( )
23 Dynamik wird ausgelös durch Wirkung von Kräfen. Beispiel: m S Ihre Einhei is: 1 kg m s - Newon 1 N Gewichskraf schwere Masse F ms g Dimension: Masse Länge / Zei F 1 F ges Kräfe sind Vekoren. Es gil das Superposiionsprinzip F F ges F 1 + F Oder allgemein F ges F 1 + F + + N F N F i i 1 3
24 Sir Isaac Newon Geboren: in Lincolnshire : Triniy College, Cambridge 1669: Ernennung zum Professor in Cambridge : Direkor des saalichen Münzames in London : Vorsiz der Royal Sociey Gesorben: in Kensingon, London
25 Principia:
26 Die PHYSIK drei Newon schen A WS 13/14 14/15 Axiome 6
27 Wesminser Abbey hp:// 7
28 .3.5 Die Newon schen Geseze Die Voraussezungen für die Güligkei der Newon schen Geseze sind durch Allagserfahrungen gegeben. z r() y m Die Zei is absolu und unveränderlich und häng nich von der Bewegung und dem Or ab. Es gib einen sog. absoluen Raum, d.h. ein absolu ruhendes Sysem, in dem alle Bewegungsabläufe safinden. Die Eigenschaf Masse eines Körpers is unabhängig vom Bewegungszusand. x 8
29 Die Newon schen Geseze 1. Gesez: Trägheisprinzip Ein Körper bleib in einem Inerialsysem in geradlinig gleichförmiger Bewegung, wenn keine Kraf auf ihn wirk. dv F a d. Gesez: Akionsprinzip Die zeiliche Änderung des Impulses is proporional zur äußeren Kraf, die auf den Körper wirk. Impuls: Kraf : p mv dp F d d( mv) d Falls die Masse m unabhängig von der Bewegung is, dann gil: F m a mv m r Kraf Masse Beschleunigung 3. Gesez: Reakionsprinzip Bei Wechselwirkung zweier Körper is die Kraf, die auf den ersen Körper wirk, umgekehr gleich der Kraf, die der zweie auf den ersen ausüb. acio reacio F F 1 F F 1 9
30 Diskussion der Newonschen Geseze 1. Newonsches Axiom: geradlinig v cons. gleichförmig Galileo Galilei Veranschaulichung, dass v cons. eine kräfefreie Bewegung bedeue. 3
31 1. Newonsches Axiom: v v cons., a Ein Sysem, in dem das 1. Newonsche Axiom gil, heiß Inerialsysem. Dabei wird nich zwischen Bezugssysemen mi v und v cons. unerschieden. 31
32 1. Newonsches Axiom: v cons. a 3
33 mcons. Newonsches Axiom F F m a mv m r Das. Newonsche Axiom ha mehrere Bedeuungen. Es kann als Definiion für die Kraf angesehen werden, so wie wir das hier gean haben. Darüber hinaus kann es als Definiion der (rägen) Masse dienen, falls mcons. Dann is die Masse das Verhälnis aus der Kraf F und der durch sie verursachen Beschleunigung a, d.h. m F / a. Die Masse is somi ein Maß für den Widersand, mi dem ein Körper der Veränderung seiner Geschwindigkei engegenwirk (Träghei). Bemerkungen: 1). Newonsches Axiom is Besimmungsgleichung für Bahnkurve. r a F( r, r, ) m dp d d( mv) d zweimalige Inegraion ergib ) Das. Newonsche Axiom beinhale 1. Axiom, da im Fall v cons. (und mcons.) sofor F folg. 33 r ()
34 Hinweis auf Erhalungsgrößen: Berachung des freien Teilchens 1. Konsequenz: m v cons. F d( mv) d vekorielle Beziehung. Konsequenz: Berachung in einer Dimension mx Muliplikaion mi Geschwindigkei mxx d d 1 m x d d 1 ( ) x m 1 m x cons. kineische Energie 34
35 . Newonsches Axiom F dp d mcons. d( mv) d m a mv m r Definiion der Masse: m Widersand eines Körpers gegenüber einer Geschwindigkeisänderung F F m a m 1 1 a m m 1 a a 1 Relaive Messung von Massen durch Vergleich der relaiven Beschleunigungen. Vorsich: Masse Gewich Gewichskraf!! Masse is eine skalare Größe, Gewich is eine vekorielle Größe! Die Masse is unabhängig davon, wo sich ein Körper befinde, im Gegensaz zur Gewichskraf. 35
36 . Newonsches Axiom Gewichskraf: Nahe der Erdoberfläche fallen alle Körper gleich schnell mi der Erdbeschleunigung g. g häng auf der Erde vom Or ab, im Miel is g 9.81m/s. Nur am selben Or gil daher: gcons. Gewichskraf (schwere) Masse Messung von Massen durch Gewichskräfe! äquivalene Verwendung der Begriffe! auf dem Mond gil jedoch: 1 g Mond g Die Ausrüsung des Asronauen Erde 6 mcons. is leicher auf dem Mond. ABER: Sie is nich leicher zu beschleunigen! 36
37 . Newonsches Axiom: Urkilogramm Deusches Normal: Bei der PTB in Braunschweig Masse: m(p 9. Ir 1. ) 1... kg Höhe Zylinder: h 39. mm Durchmesser: d 39. mm Diche: 1.5 g/cm 3 Wird alle 1 Jahre mi dem Pariser Urkilogramm verglichen!!! Ziel: Zurückführung auf bessere Größen. 37
38 3. Newonsches Axiom: Kräfe reen immer in Paaren auf. Beispiel: Freier Fall auf der Erdoberfläche Die Erde wird von der Masse m mi der Kraf G angezogen. mg m G G Masse m wird von der Erde mi der Kraf G angezogen. mg mg G mg 38
39 3. Newonsches Axiom: Kraf & Gegenkraf greifen an unerschiedlichen Körpern an!! 39
40 3. Newonsches Axiom: Pferdelogik: Das Pferd denk: Es gil sowieso acioreacio, d.h. wenn ich mich anfange zu bewegen, dann enseh sofor eine gleich große Gegenkraf, die die Bewegung verhinder! 4
41 Kräfe - Übersich über die verschiedenen Aren von Kräfen 41
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhal der Vorlesung A1 1. Einführung Mehode der Physik Physikalische Größen Übersich über die orgesehenen Themenbereiche. Teilchen A. Einelne Teilchen Beschreibung on
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhal der Vorlesung A1 1. Einführung Mehode der Physik Physikalische Größen Übersich über die orgesehenen Themenbereiche. Teilchen A. Einelne Teilchen Beschreibung on
Mechanik. 1 Kinematik
 Mechanik Kinemaik - Beschreibung der Bewegung eines Körpers durch Or, Geschwindigkei und Beschleunigung - Körper wird als Punkmasse (PM) beschrieben.. Modell der Punkmasse und Koordinaensseme (KS) Def.
Mechanik Kinemaik - Beschreibung der Bewegung eines Körpers durch Or, Geschwindigkei und Beschleunigung - Körper wird als Punkmasse (PM) beschrieben.. Modell der Punkmasse und Koordinaensseme (KS) Def.
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Basiswissen Physik 11. Jahrgangsstufe
 Basiswissen Physik 11. Jahrgangssufe 1. Einfache lineare Bewegungen a) Darsellung von Bewegungen im Koordinaensysem Unerscheide sorgfälig die in der Zei zurückgelege Srecke s() von der zur Zei eingenommenen
Basiswissen Physik 11. Jahrgangssufe 1. Einfache lineare Bewegungen a) Darsellung von Bewegungen im Koordinaensysem Unerscheide sorgfälig die in der Zei zurückgelege Srecke s() von der zur Zei eingenommenen
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Mathematik für Physiker I
 Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
1.1. Grundbegriffe zur Mechanik
 ... Die geradlinig gleichförmige Bewegung.. Grundbegriffe zur Mechanik Ein Körper beweg sich geradlinig und gleichförmig enlang der -Achse, wenn seine Geschwindigkei (eloci) 0 konsan bleib. Srecke Zeiabschni
... Die geradlinig gleichförmige Bewegung.. Grundbegriffe zur Mechanik Ein Körper beweg sich geradlinig und gleichförmig enlang der -Achse, wenn seine Geschwindigkei (eloci) 0 konsan bleib. Srecke Zeiabschni
(2) Kinematik. Vorlesung Animation und Simulation S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 () Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
() Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
Vorkurs Mathematik-Physik, Teil 6 c 2016 A. Kersch
 Vorkurs Mahemaik-Physik, Teil 6 c 6 A. Kersch Kinemaik In der Kinemaik geh es um die Frage: wie kann ich Bewegungen, also Bahnen von punkförmigen (Kinemaik der Translaion) oder ausgedehnen Körpern (Kinemaik
Vorkurs Mahemaik-Physik, Teil 6 c 6 A. Kersch Kinemaik In der Kinemaik geh es um die Frage: wie kann ich Bewegungen, also Bahnen von punkförmigen (Kinemaik der Translaion) oder ausgedehnen Körpern (Kinemaik
4. Quadratische Funktionen.
 4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
Ferienkurs Experimentalphysik 1
 Ferienkurs Experimenalphysik 1 1 Fakulä für Physik Technische Universiä München Bernd Kohler & Daniel Singh Bla 1 - Lösung WS 214/215 23.3.215 Ferienkurs Experimenalphysik 1 ( ) - leich ( ) - miel ( )
Ferienkurs Experimenalphysik 1 1 Fakulä für Physik Technische Universiä München Bernd Kohler & Daniel Singh Bla 1 - Lösung WS 214/215 23.3.215 Ferienkurs Experimenalphysik 1 ( ) - leich ( ) - miel ( )
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Inhalt der Vorlesung A1
 PHYSIK A WS 013/14 014/15 Inhal der Vorlesung A1. Teilhen A. Einzelne Teilhen Beshreibung von Teilhenbewegung Kinemaik: Quaniaive Erfassung Dynamik: Ursahen der Bewegung Kräfe Arbei + Leisung, Energie
PHYSIK A WS 013/14 014/15 Inhal der Vorlesung A1. Teilhen A. Einzelne Teilhen Beshreibung von Teilhenbewegung Kinemaik: Quaniaive Erfassung Dynamik: Ursahen der Bewegung Kräfe Arbei + Leisung, Energie
2. Kinematik. v = a = dx v = dt. 2.1 Ortskurven. x(t) v > 0. Kurve: Beschreibung der Bewegung von Massenpunkten. v = 0.
 . Kinemaik Beschreibun er Beweun on Massenpunken Kure: () > Definiion : : Zei [s] (,y,) : Posiion [m] s : urückeleer We [m] ( ) : Geschwinikei [m/s] a : Beschleuniun [m/s ] is Seiun er Kure: Allemein :
. Kinemaik Beschreibun er Beweun on Massenpunken Kure: () > Definiion : : Zei [s] (,y,) : Posiion [m] s : urückeleer We [m] ( ) : Geschwinikei [m/s] a : Beschleuniun [m/s ] is Seiun er Kure: Allemein :
Synopse der Vorlesung Physik I. Alexander Piel WS 2011/12
 Synopse der Vorlesung Physik I Aleander Piel WS 11/1 Disclaimer Die nachfolgenden Zusammensellungen und Kommenare sollen die Measrukur des Vorlesungssoffes erdeulichen sowie Begriffe und Mehoden ordnen.
Synopse der Vorlesung Physik I Aleander Piel WS 11/1 Disclaimer Die nachfolgenden Zusammensellungen und Kommenare sollen die Measrukur des Vorlesungssoffes erdeulichen sowie Begriffe und Mehoden ordnen.
Übungen zu Physik 1 für Maschinenwesen
 Physikdeparmen E13 WS 211/12 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peer Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körsgens, David Magerl, Markus Schindler, Moriz v. Sivers Vorlesung 1.11.211,
Physikdeparmen E13 WS 211/12 Übungen zu Physik 1 für Maschinenwesen Prof. Dr. Peer Müller-Buschbaum, Dr. Eva M. Herzig, Dr. Volker Körsgens, David Magerl, Markus Schindler, Moriz v. Sivers Vorlesung 1.11.211,
Einführung in die Physik I. Kinematik der Massenpunkte. O. von der Lühe und U. Landgraf
 Einfühung in die Phsik I Kinemaik de Massenpunke O. on de Lühe und U. Landgaf O und Geschwindigkei Wi beachen den O eines als punkfömig angenommenen Köpes im Raum als Funkion de Zei Eindimensionale Posiion
Einfühung in die Phsik I Kinemaik de Massenpunke O. on de Lühe und U. Landgaf O und Geschwindigkei Wi beachen den O eines als punkfömig angenommenen Köpes im Raum als Funkion de Zei Eindimensionale Posiion
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
II. Kinematik gradliniger Bewegungen
 II. Kinemaik gradliniger Bewegungen Kinemaik, von dem griechischen Verb kineo = ich bewege, nenn man den grundlegenden Zweig der Mechanik, der den zeilichen Ablauf einer Bewegung im Raum durch mahemaische
II. Kinemaik gradliniger Bewegungen Kinemaik, von dem griechischen Verb kineo = ich bewege, nenn man den grundlegenden Zweig der Mechanik, der den zeilichen Ablauf einer Bewegung im Raum durch mahemaische
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Aufgabe 1 (9 Punkte) Prüfungsklausur Technische Mechanik II
 echn. Mechanik & Fahrzeugdynamik M II Prof. Dr.-Ing. habil. Hon. Prof. (NUS) D. Besle 8. März Aufgabe (9 Punke) Ein Zahnrad 3 wird über eine Sange on einem Kolben 5 angerieben. Dieses Zahnrad greif in
echn. Mechanik & Fahrzeugdynamik M II Prof. Dr.-Ing. habil. Hon. Prof. (NUS) D. Besle 8. März Aufgabe (9 Punke) Ein Zahnrad 3 wird über eine Sange on einem Kolben 5 angerieben. Dieses Zahnrad greif in
1 Kinematik der geradlinigen Bewegung eines Punktes 1.1 Freier Fall; Geschwindigkeit, Fallzeit, kinematische Diagramme
 Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Grundbegriffe Geschwindigkeit und Beschleunigung. r = r dt
 Gundbegiffe Geschwindigkei und Beschleunigung Die Geschwindigkei eines Köpes is ein Maß fü seinen je Zeieinhei in eine besimmen Richung zuückgelegen Weg. Sie is, wie de O, ein Veko und definie duch die
Gundbegiffe Geschwindigkei und Beschleunigung Die Geschwindigkei eines Köpes is ein Maß fü seinen je Zeieinhei in eine besimmen Richung zuückgelegen Weg. Sie is, wie de O, ein Veko und definie duch die
INPUT-EVALUATION DER ZHW: PHYSIK SEITE 1. Serie 1
 INPUT-EVALUATIN DER ZHW: PHYSIK SEITE 1 Serie 1 1. Zwei Personen ziehen mi je 500 N an den Enden eines Seils. Das Seil ha eine Reissfesigkei von 600 N. Welche der vier folgenden Aussagen is physikalisch
INPUT-EVALUATIN DER ZHW: PHYSIK SEITE 1 Serie 1 1. Zwei Personen ziehen mi je 500 N an den Enden eines Seils. Das Seil ha eine Reissfesigkei von 600 N. Welche der vier folgenden Aussagen is physikalisch
2. Kinematik punktförmiger Körper
 . Kinemaik punkförmier Körper Beschleuniun: Körper werden als Massenpunke idealisier. Beweun im -dimensionalen Raum d( ) a( ) ɺ ( ) ɺɺ ( ) d Konenion: : Zei [s] (,y,) : Or [m] : Geschwindikei [m/s] a :
. Kinemaik punkförmier Körper Beschleuniun: Körper werden als Massenpunke idealisier. Beweun im -dimensionalen Raum d( ) a( ) ɺ ( ) ɺɺ ( ) d Konenion: : Zei [s] (,y,) : Or [m] : Geschwindikei [m/s] a :
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Physikaufgabe 104. arccos 1 2.
 Home Sarseie Impressum Konak Gäsebuch Aufgabe: Zeigen Sie an einem Beispiel, daß die Naurgeseze universell sind, d.h. unabhängig vom gewählen Bezugssysem gelen. Zeigen Sie ferner, daß die Raumkrümmung
Home Sarseie Impressum Konak Gäsebuch Aufgabe: Zeigen Sie an einem Beispiel, daß die Naurgeseze universell sind, d.h. unabhängig vom gewählen Bezugssysem gelen. Zeigen Sie ferner, daß die Raumkrümmung
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Kapitel 6: Ort, Geschwindigkeit und Beschleunigung als Funktion der Zeit
 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei 2 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei Einführung Lerninhal Einführung 3 Das Programm yzet erlaub es,
Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei 2 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei Einführung Lerninhal Einführung 3 Das Programm yzet erlaub es,
Die mit soviel Muhe und mathematischem Aufwand denierten kinematischen Grossen Ort ~r,
 2.5 Die fundamenalen Geseze der Mechanik 2.5.1 Einleiung Die mi soviel Muhe und mahemaischem Aufwand denieren kinemaischen Grossen Or ~r, Geschwindigkei ~v und Beschleunigung ~a beschreiben den Bewegungsablauf
2.5 Die fundamenalen Geseze der Mechanik 2.5.1 Einleiung Die mi soviel Muhe und mahemaischem Aufwand denieren kinemaischen Grossen Or ~r, Geschwindigkei ~v und Beschleunigung ~a beschreiben den Bewegungsablauf
Elektrodynamik II - Wechselstromkreise
 Physik A VL36 (18.1.13 Elekrodynamik II - Wechselspannung und Wechselsrom Wechselspnnung durch Indukion Drehsrom Schalungen mi Wechselsrom Kirchhoff sche h egeln Maschenregel bei Indukiviäen und Kapaziäen
Physik A VL36 (18.1.13 Elekrodynamik II - Wechselspannung und Wechselsrom Wechselspnnung durch Indukion Drehsrom Schalungen mi Wechselsrom Kirchhoff sche h egeln Maschenregel bei Indukiviäen und Kapaziäen
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Strömung im Rohr. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Physikalisches Grundpraktikum. 1 Aufgabenstellung 2
 Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Ein Ball wird unter einem Winkel α mit einer Anfangsgeschwindigkeit v 0. = 35 m/s vom Boden über eine Mauer der Höhe H = 10 m geworfen.
 Webinar: Dynamik Thema: Kinemaik eines Massenpunkes Aufabe: Schiefer Wurf Ein Ball wird uner einem Winkel α mi einer Anfanseschwindikei = 35 m/s vom Boden über eine Mauer der Höhe H = 10 m eworfen. H α
Webinar: Dynamik Thema: Kinemaik eines Massenpunkes Aufabe: Schiefer Wurf Ein Ball wird uner einem Winkel α mi einer Anfanseschwindikei = 35 m/s vom Boden über eine Mauer der Höhe H = 10 m eworfen. H α
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
5c Dynamik. Animation follows the laws of physics unless it is funnier otherwise. 1
 5c ynaik Aniaion foows he aws of physics uness i is funnier oherwise. 1 Zusaenfassung Newon 1+2 Grundegende Geseze der kassischen Mechanik werden durch die Newonschen Geseze beschrieben Trägheisprinzip,
5c ynaik Aniaion foows he aws of physics uness i is funnier oherwise. 1 Zusaenfassung Newon 1+2 Grundegende Geseze der kassischen Mechanik werden durch die Newonschen Geseze beschrieben Trägheisprinzip,
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Schwingungen. 1 Schwingung als periodischer Vorgang
 -I.D1- D Schwingungen 1 Schwingung als periodischer Vorgang 1.1 Definiion Voraussezungen für das Ensehen einer mechanischen Schwingung sind eine zur Gleichgewichslage gerichee rückreibende Kraf und die
-I.D1- D Schwingungen 1 Schwingung als periodischer Vorgang 1.1 Definiion Voraussezungen für das Ensehen einer mechanischen Schwingung sind eine zur Gleichgewichslage gerichee rückreibende Kraf und die
Inhalt der Vorlesung A1
 PHYSIK A WS 03/4 Inhal der Vorlesung A. Teilhen A. Einzelne Teilhen Beshreibung on Teilhenbewegung Kinemaik: Quaniaie Erfassung Dynamik: Ursahen der Bewegung Kräfe Arbei + Leisung, Energie Erhalungssäze:
PHYSIK A WS 03/4 Inhal der Vorlesung A. Teilhen A. Einzelne Teilhen Beshreibung on Teilhenbewegung Kinemaik: Quaniaie Erfassung Dynamik: Ursahen der Bewegung Kräfe Arbei + Leisung, Energie Erhalungssäze:
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
1.6 Energie 1.6.1 Arbeit und Leistung Wird ein Körper unter Wirkung der Kraft F längs eines Weges s verschoben, so wird dabei die Arbeit
 3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
 Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Hochschule Bremen Technische Physik (Kapitel 1) / Prof. Dr.-Ing. Dieter Kraus 1. Unter Naturwissenschaft versteht man
 . Einführung Aus der Neugierde des Menschen enwickele sich das Ineresse die ihn umgebende Wel zu ersehen. Um die Vielfal der Beobachungen (Ereignisse) zu ordnen haben sich unerschiedliche Herangehensweisen
. Einführung Aus der Neugierde des Menschen enwickele sich das Ineresse die ihn umgebende Wel zu ersehen. Um die Vielfal der Beobachungen (Ereignisse) zu ordnen haben sich unerschiedliche Herangehensweisen
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Bewegung. Einteilung der Mechanik. Kinematik. Bezugssystem. Modell Massepunkt. Geradlinig gleichförmige Bewegung
 Eineilung der Mechanik Kinemaik Mechanik Kinemaik Dynamik Lehre von den Bewegungen und ihren Gesezen, ohne Beachung der zu Grunde liegenden Ursachen Lehre von den Kräfen und deren Wirkungen und dami der
Eineilung der Mechanik Kinemaik Mechanik Kinemaik Dynamik Lehre von den Bewegungen und ihren Gesezen, ohne Beachung der zu Grunde liegenden Ursachen Lehre von den Kräfen und deren Wirkungen und dami der
2 Kinematik der Massenpunkte
 4 Kinemaik der Massenpunke Die Kinemaik is die Lehre on den Bewegungen der Körper (Griechisch: Kinema Bewegung). Dabei werden die Ursachen der Bewegungen, d.h. die beeiligen Kräfe, und die Wirkungen der
4 Kinemaik der Massenpunke Die Kinemaik is die Lehre on den Bewegungen der Körper (Griechisch: Kinema Bewegung). Dabei werden die Ursachen der Bewegungen, d.h. die beeiligen Kräfe, und die Wirkungen der
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Leseprobe. Dietmar Mende, Günter Simon. Physik. Gleichungen und Tabellen. ISBN (Buch): ISBN (E-Book):
 Lesepobe Diema Mende, Güne Simon Physik Gleichungen und Tabellen ISBN (Buch): 978-3-446-43754-8 ISBN (E-Book): 978-3-446-43861-3 Weiee Infomaionen ode Besellungen une hp://www.hanse-fachbuch.de/978-3-446-43754-8
Lesepobe Diema Mende, Güne Simon Physik Gleichungen und Tabellen ISBN (Buch): 978-3-446-43754-8 ISBN (E-Book): 978-3-446-43861-3 Weiee Infomaionen ode Besellungen une hp://www.hanse-fachbuch.de/978-3-446-43754-8
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Experimentalphysik E1
 Experimentalphysik E1 Newtonsche Axiome, Kräfte, Arbeit, Skalarprodukt, potentielle und kinetische Energie Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html
Experimentalphysik E1 Newtonsche Axiome, Kräfte, Arbeit, Skalarprodukt, potentielle und kinetische Energie Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html
Aufgabe 1 (7 Punkte) Prüfungsklausur Technische Mechanik II
 echn. Mechanik & Fahrzeugdynaik M II Prof. Dr.-Ing. habil. Hon. Prof. (NUS) D. Besle 7. März 05 Aufgabe (7 Punke) Das Rad (Radius r ) roll i der Winkelgeschwindigkei. I Punk A (Absand r / o Mielpunk) is
echn. Mechanik & Fahrzeugdynaik M II Prof. Dr.-Ing. habil. Hon. Prof. (NUS) D. Besle 7. März 05 Aufgabe (7 Punke) Das Rad (Radius r ) roll i der Winkelgeschwindigkei. I Punk A (Absand r / o Mielpunk) is
Numerische Behandlung von gewöhnlichen Differentialgleichungen Eine Einführung. Universität Hamburg SoSe07. K. Taubert
 Numerische Behandlung von gewöhnlichen Differenialgleichungen Eine Einführung Universiä Hamburg SoSe7 K. Tauber Besondere Aufgaben 6 UNSTETIGE-, SYMPLEKTISCHE- und ALGEBRO-DIFFERENTIALGLEICHUNGEN 6.1 Einführung
Numerische Behandlung von gewöhnlichen Differenialgleichungen Eine Einführung Universiä Hamburg SoSe7 K. Tauber Besondere Aufgaben 6 UNSTETIGE-, SYMPLEKTISCHE- und ALGEBRO-DIFFERENTIALGLEICHUNGEN 6.1 Einführung
Numerisches Programmieren
 Technische Universiä München WS 11/1 Insiu für Informaik Prof. Dr. Hans-Joachim Bungarz Michael Lieb, M. Sc. Dipl.-Inf. Chrisoph Riesinger Dipl.-Inf. Marin Schreiber Numerisches Programmieren 4. Programmieraufgabe:
Technische Universiä München WS 11/1 Insiu für Informaik Prof. Dr. Hans-Joachim Bungarz Michael Lieb, M. Sc. Dipl.-Inf. Chrisoph Riesinger Dipl.-Inf. Marin Schreiber Numerisches Programmieren 4. Programmieraufgabe:
Ladung (7. Klasse) - -
 Elekrischer Leier Einfacher elekrischer Srmkreis Pluspl Minuspl Ammdell Amkern mi Prnen und Neurnen Ladung (7. Klasse) Es gib zwei Aren vn Ladung: psiiv und negaiv Srmsärke (7. Klasse) Frmelbuchsabe: I
Elekrischer Leier Einfacher elekrischer Srmkreis Pluspl Minuspl Ammdell Amkern mi Prnen und Neurnen Ladung (7. Klasse) Es gib zwei Aren vn Ladung: psiiv und negaiv Srmsärke (7. Klasse) Frmelbuchsabe: I
mathphys-online Abschlussprüfung Berufliche Oberschule 2009 Mathematik 12 Technik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die reelle Funktion f( x)
 Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Inhalt Prof. Dr.-Ing. Barbara Hippauf Hochschule für Technik und Wirtschaft des Saarlandes; Physik, SS 2016
 Inhal.. 3. 4. 5. 6. 7. 8. Gekoppele Oszillaoren Gekoppele Oszillaoren, ifferenialgleichung Gekoppele Oszillaoren, Normalkoordinaen, Normalschwingungen Gekoppele Oszillaoren, Schwebungen Gekoppele Oszillaoren,
Inhal.. 3. 4. 5. 6. 7. 8. Gekoppele Oszillaoren Gekoppele Oszillaoren, ifferenialgleichung Gekoppele Oszillaoren, Normalkoordinaen, Normalschwingungen Gekoppele Oszillaoren, Schwebungen Gekoppele Oszillaoren,
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Lösungsblatt 8 zur Experimentalphysik I
 ösungsbla 8 zur xperimenalphysik I Sommersemeser 04 - Übungsbla 8 Aufgabe 8. eopolds ifaßsäule (Präsenzaufgabe) Der Künsler eopold Müßig möche für sein neuses Projek zwei drehbare ifaßsäulen aus Beon (ρ
ösungsbla 8 zur xperimenalphysik I Sommersemeser 04 - Übungsbla 8 Aufgabe 8. eopolds ifaßsäule (Präsenzaufgabe) Der Künsler eopold Müßig möche für sein neuses Projek zwei drehbare ifaßsäulen aus Beon (ρ
2. Grundlagen Schwingungslehre
 Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
1 Integrale von Funktionen in mehreren Variablen
 $Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
$Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Physik für Wirtschaftsingenieure
 Phsik fü Wischafsingenieue Chisophe Diemaie, Mahias Mändl ISBN 3-446-373-8 Lesepobe Weiee Infomaionen ode Besellungen une hp://www.hanse.de/3-446-373-8 sowie im Buchhandel Mechanik Bild. Bewegung eines
Phsik fü Wischafsingenieue Chisophe Diemaie, Mahias Mändl ISBN 3-446-373-8 Lesepobe Weiee Infomaionen ode Besellungen une hp://www.hanse.de/3-446-373-8 sowie im Buchhandel Mechanik Bild. Bewegung eines
Lösung Abiturprüfung 2000 Grundkurs (Baden-Württemberg)
 Lösung Abiurprüfung 2 Grundkurs (Baden-Würemberg) Analysis, Aufgabe I.1. a) ( x) = 1 [( x)3 9 ( x)]= 1 ( x3 + 9x)= 1 ( x3 9x) = ( x) Somi is (x ) punksymmerisch zum Ursprung. ( x) = 1 (x3 9x)= x(x 2 9)=
Lösung Abiurprüfung 2 Grundkurs (Baden-Würemberg) Analysis, Aufgabe I.1. a) ( x) = 1 [( x)3 9 ( x)]= 1 ( x3 + 9x)= 1 ( x3 9x) = ( x) Somi is (x ) punksymmerisch zum Ursprung. ( x) = 1 (x3 9x)= x(x 2 9)=
Ganzrationale Funktionenscharen. 4. Grades. Umfangreiche Aufgaben. Lösungen ohne CAS und GTR. Alle Methoden ganz ausführlich. Datei Nr.
 Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Regelungstechnik. Steuerung. Regelung. Beim Steuern bewirkt eine Eingangsgröße eine gewünschte Ausgangsgröße (Die nicht auf den Eingang zurückwirkt.
 Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Notizen zur Vorlesung über Kurven
 Noizen zur Vorlesung über Kurven Michel Krow, TU-Berlin krow@mh.tu-berlin.de November 6, 9 Definiion: Eine prmerisiere Kurve is eine seige Abbildung x : R I R n, wobei I ein (offenes, hlboffenes oder bgeschlossenes)
Noizen zur Vorlesung über Kurven Michel Krow, TU-Berlin krow@mh.tu-berlin.de November 6, 9 Definiion: Eine prmerisiere Kurve is eine seige Abbildung x : R I R n, wobei I ein (offenes, hlboffenes oder bgeschlossenes)
Kapitel II Bewegungen und Kräfte
 Kapiel II Bewegungen und Kräfe 3. Translaion und Roaion... 27 4. Soßprozesse... 35 5. Harmonische Schwingungen... 41 6. Gekoppele Schwingungen... 52 7. Gedämpfe und erzwungene Schwingungen... 59 8. Trägheismomen...
Kapiel II Bewegungen und Kräfe 3. Translaion und Roaion... 27 4. Soßprozesse... 35 5. Harmonische Schwingungen... 41 6. Gekoppele Schwingungen... 52 7. Gedämpfe und erzwungene Schwingungen... 59 8. Trägheismomen...
Übungen zur Experimentalphysik II Aufgabenblatt 3 - Lösung
 KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Friedhelm Kuypers Physik får Ingenieure und Naturwissenschaftler
 Friedhelm Kuypers Physik får Ingenieure und Naurwissenschafler Beachen Sie bie auch weiere ineressane Tiel zu diesem Thema Thomsen, C. Physik får Ingenieure får Dummies 011 ISBN: 978-3-57-706-8 Råsch,
Friedhelm Kuypers Physik får Ingenieure und Naurwissenschafler Beachen Sie bie auch weiere ineressane Tiel zu diesem Thema Thomsen, C. Physik får Ingenieure får Dummies 011 ISBN: 978-3-57-706-8 Råsch,
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
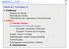
3. Dynamik. 3.1 Axiome. 3.2 Schwere und träge Masse. umgeformt: Ursachen der Bewegung: Kräfte. Die Einheit der Kraft ist Newton: [N] = [kg m/s 2 ]
![3. Dynamik. 3.1 Axiome. 3.2 Schwere und träge Masse. umgeformt: Ursachen der Bewegung: Kräfte. Die Einheit der Kraft ist Newton: [N] = [kg m/s 2 ] 3. Dynamik. 3.1 Axiome. 3.2 Schwere und träge Masse. umgeformt: Ursachen der Bewegung: Kräfte. Die Einheit der Kraft ist Newton: [N] = [kg m/s 2 ]](/thumbs/53/32967628.jpg) 3. Dnaik Ursachen der Bewegung: Kräfe 19 ugefor: = a 3.1 Axioe 1. Trägheisrinzi (lex ria) lex ria aus den Princiia von Isaac Newon, London 1687. Vor Newon (1643-177) auch schon forulier von Galilei Galileo
3. Dnaik Ursachen der Bewegung: Kräfe 19 ugefor: = a 3.1 Axioe 1. Trägheisrinzi (lex ria) lex ria aus den Princiia von Isaac Newon, London 1687. Vor Newon (1643-177) auch schon forulier von Galilei Galileo
Lösung - Serie 8. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe) 1. Was für eine Kurve stellt die Parametrisierung
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
Lösungen der Übungsaufgaben TM II Dynamik
 L Lösungen der Übungsaufgaben TM II Dynamik Einleiung und Grundlagen Aufgabe a) ẋ() A cos B sin, ẋ. () A 2 sin B 2 cos 2 x() b) ẋ() C sin, ẋ. () C 2 cos 2 x() c) ẋ Ce cos Ce sin, ẋ. Ce 2 2 cos 2 sin d)
L Lösungen der Übungsaufgaben TM II Dynamik Einleiung und Grundlagen Aufgabe a) ẋ() A cos B sin, ẋ. () A 2 sin B 2 cos 2 x() b) ẋ() C sin, ẋ. () C 2 cos 2 x() c) ẋ Ce cos Ce sin, ẋ. Ce 2 2 cos 2 sin d)
Schriftliche Abiturprüfung 2007 Sachsen-Anhalt Physik 13 n (Leistungskursniveau)
 Schrifliche Abiurprüfung 2007 Sachsen-Anhal Physik 13 n (Leisungskursniveau) Thema 2: Bewegungen in raviaionsfeldern 1 Eigenschafen des raviaionsfeldes Erläuern Sie den Feldbegriff anhand des raviaionsfeldes.
Schrifliche Abiurprüfung 2007 Sachsen-Anhal Physik 13 n (Leisungskursniveau) Thema 2: Bewegungen in raviaionsfeldern 1 Eigenschafen des raviaionsfeldes Erläuern Sie den Feldbegriff anhand des raviaionsfeldes.
Schwingungen g und Wellen II Wellen, Gedämpfte Schwingungen
 Physik A VL1 (7.11.1) Schwingngen g nd Wellen II Wellen, Gedämpfe Schwingngen Wellen Gedämpfe Schwingngen schwache Dämpfng aperiodischer Grenzfall Kriechfall 1 Ei Erinnerng: Beschreibng von Schwingngen
Physik A VL1 (7.11.1) Schwingngen g nd Wellen II Wellen, Gedämpfe Schwingngen Wellen Gedämpfe Schwingngen schwache Dämpfng aperiodischer Grenzfall Kriechfall 1 Ei Erinnerng: Beschreibng von Schwingngen
sin = cos = tan = Sinus und Cosinus im rechtwinkligen Dreieck Aufgabe: Berechnen Sie die fehlende Seitenlänge und den Winkel. Gegenkathete Hypotenuse
 Sinus und Cosinus im rechwinkligen Dreieck Ankahee Hpoenuse. Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Aufgabe: Berechnen Sie die fehlende Seienlänge und den Winkel.
Sinus und Cosinus im rechwinkligen Dreieck Ankahee Hpoenuse. Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Aufgabe: Berechnen Sie die fehlende Seienlänge und den Winkel.
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Aufgaben: 1. Gib eine Gleichung der Ebene E an, die durch A in Richtung von u und v verläuft.
 Prmeergleichung und Koordinenform einer Ebene Prmeergleichung und Koordinenform einer Ebene Die Lge einer Ebene E im Rum is durch drei Größen eindeuig fesgeleg: X. Einen Punk A, durch den die Ebene verläuf..
Prmeergleichung und Koordinenform einer Ebene Prmeergleichung und Koordinenform einer Ebene Die Lge einer Ebene E im Rum is durch drei Größen eindeuig fesgeleg: X. Einen Punk A, durch den die Ebene verläuf..
MATHEMATIK. Fachabituiprüfung 2013 zum Erwerb der Fachhochschulreife an. Fachoberschulen und Berufsoberschulen. Ausbildungsrichtung Technik
 Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
1 Grundwissen Elektrik
 1 Grundwissen Elekrik 1.1 Elekrisches Feld Elekrische Felder exisieren in der Umgebung von Ladungen. Die Feldrichung is dabei die Richung der Kraf auf eine posiive Probeladung. Die Feldlinien verlaufen
1 Grundwissen Elekrik 1.1 Elekrisches Feld Elekrische Felder exisieren in der Umgebung von Ladungen. Die Feldrichung is dabei die Richung der Kraf auf eine posiive Probeladung. Die Feldlinien verlaufen
1 Rasterelektronenmikroskop (vorbereitete Aufgabe, 1. Prüfungsteil)
 nur für den inernen Gebrauch Beispiel für eine mündliche Abiurprüfung im Fach Physik MündlicheAbiurprüfung Seie 1 von 6 Hilfsmiel: Zugelassener Taschenrechner, Wörerbuch der deuschen Rechschreibung. 1
nur für den inernen Gebrauch Beispiel für eine mündliche Abiurprüfung im Fach Physik MündlicheAbiurprüfung Seie 1 von 6 Hilfsmiel: Zugelassener Taschenrechner, Wörerbuch der deuschen Rechschreibung. 1
Sinus und Cosinus im rechtwinkligen Dreieck ( )
 Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
