3 Volumenintegrale und Transformationsformel
|
|
|
- Calvin Thomas
- vor 9 Jahren
- Abrufe
Transkript
1 3 Volumenintegrale und Transformationsformel Nachdem wir uns in den ersten beiden Kapiteln mit recht abstrakten Konstruktionen beschäftigt haben, wenden wir uns nun der Berechnung konkreter Lebesgue Integrale zu. Als erstes lernen wir den Satz von Fubini kennen, der es erlaubt, Integrale über R n auf Integrale über R zurückzuführen. Dann sehen wir uns das mehrdimensionale Analogon der Substitutionsregel die Transformationsformel an. In der Praxis ist die Transformationsformel oft nicht unmittelbar benutzbar, da die Transformationen Singularitäten aufweisen können (z.b. bei Polarkoordinaten. Andererseits liegen diese Singularitäten oft in Nullmengen und beeinflussen daher das Ergebnis einer Integration nicht. Wir diskutieren daher im dritten Abschnitt einige Methoden zum Nachweis, dass eine Menge eine Nullmenge ist. Schließlich ist der vierte Abschnitt einigen konkreten Beispielen gewidmet. 3.1 Der Satz von Fubini und seine Anwendungen Die Berechnung mehrdimensionaler Integrale oder der Volumina mehrdimensionaler Körper ist oft nicht leicht. Man versucht daher, die Berechnung mehrdimensionaler Integrale auf die Berechnung mehrerer Integrale in niedrigeren Dimensionen zu reduzieren. Das wichtigste Werkzeug dazu ist der folgende Satz, den wir aus Zeitgründen nicht beweisen werden. Sie finden einen Beweis z.b. in Bröcker, Analysis II, und in Bauer. Satz 3.1 (Satz von Fubini (a Sei f : R n+m R n R m [, ] messbar. Dann sind für jedes y R m und jedes x R n die Funktionen f y : f(,y : R n [, ] und f x : f(x, : R m [, ] messbar. Weiter sind die Funktionen F : R m [, ], y f y dλ n und G : R n [, ], x R n f x dλ m R m messbar, und es gilt R n+m fdλ n+m R m R n ( f(x,ydλ n (x dλ m (y R n ( f(x,ydλ m (y dλ n (x. R m (3.1 (b Ist f L 1 (R n+m, so sind die Funktionen f y bzw. f x für fast alle y R n bzw. x R n Lebesgue integrierbar. Weiter sind die fast überall definierten Funktionen F und G Lebesgue integrierbar, und es gilt wieder (3.1. 3
2 In Zukunft schreiben wir nur noch integrierbar statt Lebesgue integrierbar. Eine wichtige Anwendung dieses Satzes ist das folgende Prinzip von Cavalieri, das besagt, dass man das Volumen einer messbaren Teilmenge M des R n berechnen kann, indem man M in unendlich dünnen Schichten niedrigerer Dimension zerschneidet und die Volumina der Schichten aufintegriert. Satz 3. (Prinzip von Cavalieri Sei M R n+m messbar, und für y R m sei M y : {x R n : (x,y M}. Dann ist M y messbar, die Funktion y λ n (M y ist messbar, und es ist λ n+m (M λ n (M y dλ m (y. R m Beweis Wir wenden Satz 3.1 (a auf die Funktion χ M an und erhalten ( λ n+m (M χ M dλ n+m χ M (x,ydλ n (x dλ m (y R n+m R m R ( n χ My dλ n dλ m (y λ n (M y dλ m (y. R m R n R m Mit diesem Prinzip können wir testen, ob unsere naive Vorstellung aus der Analysis I, dass das Integral einer nichtnegativen Funktion die Fläche unter dem Graphen der Funktion beschreibt, gerechtfertigt war. Folgerung 3.3 Sei f : R n [, eine messbare Funktion. Dann ist die Menge { } M f : (x,t R n R 1 R n+1 : t < f(x messbar, und ihr Maß ist λ n+1 (M f fdλ n. R n Beweis Mit f sind auch die Funktionen R n R R, (x,t f(x und (x,t t messbar (HA. Daher ist auch H : R n R R, (x,t f(x t messbar, und folglich ist die Menge { } M f (x,t R n R : t und f(x t > { } (x,t R n R : t messbar. Für x R n ist } (M f x {t R : (x,t M f 31 { (x,t R n R : H(x,t > [,f(x }
3 und daher λ 1 ((M f x f(x. Mit Satz 3. ergibt sich also λ n+1 (M f λ 1 ((M f x dλ n (x f(xdλ n (x. R n R n Als eine Anwendung wollen wir das Volumen c n : λ n (B n der n dimensionalen Einheitskugel B n : {x R n : x 1} berechnen. Offenbar ist c 1 λ 1 ([ 1, 1], und aus der Schule wissen wir, dass wir c π erwarten sollten. Wir gehen nach dem Cavalierischen Prinzip vor und zerschneiden für n > 1 die Kugel B n in die Scheiben B n,s {x R n 1 : (x,s B n } {x R n 1 : x } 1 s 1 s B n 1 für s [ 1, 1] und B n,s sonst. Mit Folgerung 1.1 und Satz 3. erhalten wir c n 1 1 λ n 1 (B n,s ds 1 1 (1 s n 1 cn 1 ds c n (1 s n 1 ds. Damit ist die rekursive Berechnung von c n auf die Berechnung der Riemann Integrale I n : 1 1 (1 s n 1 ds zurückgeführt. Mit der Substitution s(t sint, t [ π I n π π π], folgt π (1 sin t n 1 cos t dt (cost n dt. π Diese Integrale berechnen wir rekursiv mit partieller Integration. Für n > 1 ist I n π/ π/ (cost n 1 cos t dt (sint(cost n 1 π/ π/ (sin t(n 1(cost n ( sin tdt π/ π/ π/ (n 1 (1 cos t(cost n dt (n 1I n (n 1I n. π/ Damit erhalten wir für n > 1 die Rekursionsformel I n n 1 I n n, und mit den bekannten Werten I π und I 1 finden wir I n (n 1(n n(n... 4 π (n 1(n ( n 1 π n(n n π 3
4 und I n+1 Hieraus ergibt sich n(n... 4 (n + 1(n n(n (n + 1 (n ( n + 1 n 1. woraus wir I n+1 I n π n + 1 und I n I n 1 π n, und analog c n I n c n 1 I n I n 1 c n π n c n πn 1 n! I c 1 πn 1 n! π πn n! c n+1 I n+1 I n c n 1 π n + 1 c n 1 (π n (n + 1 (n c 1 π n 1 n(n 1... c n+1 π n (n erhalten. Insbesondere ist also tatsächlich c π und c π. Mit Hilfe der Gammafunktion Γ : (, R, x t x 1 e t dt kann man die Formel für die Volumina c n einheitlich als c n πn/ Γ( n + 1 (3. schreiben. Dazu erinnern wir an die Rekursionsformel Γ(x + 1 xγ(x für x > und an die Identität Γ(1/ π (vgl. Tutorium Analysis II. Mit diesen Hinweisen sollten Sie (3. leicht bestätigen können. 3. Die Transformationsformel In diesem Abschnitt lernen wir das Analogon der eindimensionalen Substitutionsregel kennen, die wir uns zunächst noch einmal anschauen. Ist ϕ : [a, b] R 33
5 eine stetig differenzierbare und streng monoton wachsende Funktion und ist f : ϕ([a,b] R stetig, so ist b (f ϕ(tϕ (tdt ϕ(b a ϕ(a f(xdx bzw., als Lebesgue Integral geschrieben, (f ϕ(tϕ (tdt [a,b] ϕ([a,b] f(xdx. Ist dagegen ϕ monoton fallend, d.h. orientierungsumkehrend, so ist b ϕ(b ϕ(a (f ϕ(tϕ (tdt f(xdx f(xdx f(xdx. a ϕ(a ϕ(b ϕ([a,b] Diese beiden Identitäten lassen sich zu (f ϕ(t ϕ (t dt [a,b] ϕ([a,b] f(xdx (3.3 zusammenfassen, und das ist die Transformationsformel, die wir auf höhendimensionale Situationen verallgemeinern wollen. Wir werden dazu auch die Schreibweise f(xdx statt fdλ verwenden. Außerdem erinnern wir daran, dass B B eine bijektive Abbildung ϕ : U V zwischen offenen Mengen U und V im R n ein Diffeomorphismus heißt, wenn ϕ und ϕ 1 stetig differenzierbar sind. Satz 3.4 (Transformationsformel Seien U,V R n offen und ϕ : U V ein Diffeomorphismus. Dann ist eine Funktion f : V R genau dann über V integrierbar, wenn die Funktion (f ϕ detϕ : U R über U integrierbar ist. In diesem Fall ist ( f(ydy f ϕ(x detϕ (x dx. (3.4 V U Insbesondere gilt für jede messbare Teilmenge A U λ n (ϕ(a detϕ (x dx. (3.5 A Hier steht ϕ (x L(R n, R n für die Ableitung von ϕ : U V in x U. Vor dem Beweis von Satz 3.4 machen wir uns klar, was die Transformationsformel bedeutet. Der wesentliche Teil ist Formel (3.5, die angibt, wie sich das Volumen des Bildes einer messbaren Menge A unter ϕ berechnet. Ist insbesondere detϕ (x eine von x unabhängige Konstante c, so reduziert sich (3.5 auf λ n (ϕ(a cλ n (A. Die Konstante c ist also ein Verzerrungsfaktor, der angibt, wie sich das Volumen einer Menge bei Anwendung von ϕ ändert. Ist beispielsweise ϕ T U mit einer 34
6 linearen Abbildung T, so ist ϕ (x T und somit λ n (T(A dett λ n (A. Für U R n und A [, 1] n (Einheitswürfel im R n ergibt sich mit λ n (T([, 1] n dett eine anschauliche Bedeutung der Determinante als Volumen des Bildes des Einheitswürfels. Eine Menge der Gestalt T([, 1] n heißt auch Spat oder Parallelotop. Man kann sie schreiben als { n j1 x ja j : x j [, 1] für alle j}, wobei die a j die Bilder der kanonischen Basisvektoren unter T sind. Beweis der Transformationsformel 1. Schritt: Es genügt, (3.5 zu beweisen. Aus (3.5 erhält man unmittelbar (3.4 für die Funktion f χ ϕ(a, denn es ist ja χ ϕ(a ϕ χ A. Aus der Linearität des Integrals folgt damit (3.4 für den Fall, dass f eine nichtnegative Stufenfunktion ist. Für den allgemeinen Fall reicht es aus, nichtnegative Funktionen zu betrachten. Sei also f messbar. Nach Satz. gibt es eine monoton wachsende Folge (f k von Stufenfunktionen, die punktweise gegen f konvergiert. Aus dem Satz über monotone Kovergenz (Satz.11 folgt dann f(ydy lim f k (ydy lim f k (ϕ(x detϕ (x dx V k V U f k U ( ϕ(x detϕ (x dx, da auch die Folge (f k ϕ detϕ monoton wachsend ist und punktweise gegen (f ϕ detϕ konvergiert. Insbesondere sehen wir, dass (f ϕ det ϕ genau dann auf U integrierbar ist, wenn f auf V integrierbar ist. Es verbleibt, (3.5 zu zeigen.. Schritt: Es genügt, die Aussage für den Fall zu zeigen, dass jeder Punkt p U eine offene Umgebung W p U hat, so dass (3.5 für W p anstelle von U und für ϕ Wp anstelle von ϕ gilt. Für jeden Punkt p U gibt es einen Punkt q Q n und eine Kugel U r (q mit rationalem Radius so, dass p U r (q W p. Die Behauptung (3.5 gilt für jede der abzählbar vielen Mengen U r (q, und diese Mengen überdecken U. Wir haben also abzählbar viele Mengen (M k k 1 gefunden, für die (3.5 gilt und die U überdecken. Ist nun A U messbar, so schreiben wir A als disjunkte Vereinigung der Mengen A 1 : A M 1 und A k : (A M k \ (M 1... M k 1 für k. Aus der σ Additivität von λ n und aus Satz.6 folgt nun λ n (ϕ(a k1 λ n (ϕ(a k detϕ (x dx A k k1 A detϕ (x dx. 35
7 3. Schritt: (3.5 gilt, wenn ϕ eine Permutation der Koordinaten ist, d.h. wenn ϕ(x (x σ(1,...,x σ(n mit einer Bijektion σ : {1,...,n} {1,...,n}. In diesem Fall ist det ϕ (x 1, und (3.5 gilt offenbar für alle achsenparallelen Quader in R n. Nach dem Eindeutigkeitssatz für das Lebesgue Maß (Satz 1.18 folgt die Formel (3.5 für beliebiges messbares A. 4. Schritt: (3.5 gilt, falls n 1 und U ein Intervall ist. Wir benutzen wieder den Eindeutigkeitssatz (Satz Ist B V ein Intervall, so ist auch ϕ 1 (B U ein Intervall (da ϕ 1 stetig ist, und es ist λ(b ϕ (x dx ϕ 1 (B (Anwendung der Substitutionsregel (3.3 auf die Funktion f 1. Da B λ(b V und B ϕ (x dx ϕ 1 (B V nach Satz.6 Maße auf B(R definieren und diese auf allen beschränkten Intervallen übereinstimmen, stimmen sie nach Satz 1.18 überein. 5. Schritt: Gilt (3.5 für die Diffeomorphismen ϕ 1 : U 1 U und ϕ : U U 3, so gilt (3.5 auch für den Diffeomorphismus ϕ ϕ 1 : U 1 U 3. Aus Schritt 1 wissen wir, dass (3.5 die Formel (3.4 nach sich zieht. Nach der Kettenregel ist nun det ( (ϕ ϕ 1 (x det ( ϕ (ϕ 1 (x detϕ 1(x. (3.6 Wenden wir (3.5 auf ϕ und (3.4 auf ϕ 1 an, erhalten wir λ n ((ϕ ϕ 1 (A detϕ (y dy (nach (3.5 ϕ 1 (A ( detϕ ϕ 1 (x detϕ 1(x dx (nach (3.4 A det(ϕ ϕ 1 (x dx. (nach (3.6 A 6. Schritt Nun wird es ernst: Wir zeigen die lokale Aussage aus Schritt durch vollständige Induktion nach n. Der Induktionsanfang n 1 ist in Schritt 4 abgehandelt. Für den Induktionsschritt betrachten wir ϕ in einer Umgebung von p U. Wegen detϕ (p gibt es ein j mit ϕ 1 x j (p. Indem wir ϕ mit einer Koordinatenpermutation verknüpfen, dürfen wir nach Schritt 3 und 5 o.b.d.a. annehmen, dass j 1, d.h. dass ϕ 1 (p x 1 36
8 ist. Wir betrachten die Abbildung ψ : U R n, x (ϕ 1 (x,x,...,x n. Die Jabocimatrix von ψ in x (d.h. die Matrix von ψ (x bzgl. der natürlichen Basis des R n hat die Blockstruktur ϕ 1 x 1 (x I n 1 ist also insbesondere in x p invertierbar. Nach dem Satz über die Umkehrfunktion (Analysis II, Satz 1.5 dürfen wir nach einer gegebenenfalls erforderlichen Verkleinerung von U annehmen, dass ψ : U ψ(u ein Diffeomorphismus ist. Wir haben damit eine Zerlegung, ϕ ρ ψ : U V mit ρ ϕ ψ 1 : ψ(u V. Die erste Komponente von ρ ist dann gegeben durch ρ 1 (y (ϕ 1 ψ 1 (y (ψ 1 ψ 1 (y y 1. Nach Schritt 5 genügt es, die Behauptung für die Abbildungen ψ und ρ zu zeigen. Wir dürfen also annehmen, dass ϕ eine der Funktionen ψ oder ρ ist. Beiden Funktionen gemeinsam ist, dass es ein j gibt mit ϕ j (x x j für alle x U. Indem wir wieder geeignet permutieren, können wir nach Schritt 3 sogar ϕ 1 (x x 1 für alle x U annehmen. Wir können ϕ daher wie folgt schreiben: ( ϕ(t,x t,ϕ t (x mit (t,x R R n 1, wobei ϕ t : U t : { } { } x R n 1 : (t,x U V t : x R n 1 : (t,x V ein Diffeomorphismus ist. Die Jacobi Matrix J x (ϕ von ϕ in x (t,x hat die Struktur ( 1, J x (ϕ t so dass gilt detϕ (x det(ϕ t (x. (3.7 37
9 Für eine messbare Teilmenge A von U erhalten wir nun schrittweise ( λ n (ϕ(a λ n 1 ϕ(a t dt (Cavalieri R λ n 1 (ϕ t (A t dt (Definition von ϕ t R det(ϕ t (x dx dt (Induktionsannahme R A t χ At (x det(ϕ t (x dx dt R R n 1 χ A (x detϕ (x dx (Fubini und (3.7 R n det A ϕ (x dx. Wir halten noch eine wichtige Folgerung fest. Ist T L(R n eine Isometrie (d.h. wird T durch eine orthogonale Matrix dargestellt, so heißt die Abbildung x Tx eine Drehung des R n. Folgerung 3.5 (Drehungsinvarianz des Lebesgue-Maßes Für jede Drehung des R n und jede Borelmenge A R n gilt λ n (T(A λ n (A. Beweis Aus TT T I folgt (dett 1. Also ist dett 1, und die Behauptung folgt sofort aus (3.5. Diese Drehungsinvarianz ist nicht von vorherein klar, da wir ja das Lebesgue Maß basisabhängig konstruiert haben (nämlich zunächst auf Quadern, die parallel zu den Koordinatenachsen liegen. Weiter sei daran erinnert, dass wir die Translationsinvarianz des Lebesgue Maßes bereits in der Übung gezeigt haben. Zusammenfassend können wir feststellen, dass das Lebesgue Maß unter Abbildungen der Gestalt ϕ(x Tx + v mit einer linearen Isometrie T L(R n und einem Vektor v R n invariant ist. 3.3 Nullmengen Wir haben Nullmengen als Teilmengen von Borelmengen vom Lebesguemaß definiert. Wir wollen nun einige Kriterien kennenlernen, die es uns erlauben, gewisse Nullmengen schnell als solche zu erkennen. Dies ist z.b. bei Anwendungen der Transformationsformel nützlich, bei denen man aus dem Definitionsgebiet gewisse Nullmengen herausschneiden muss, um die Transformation zu einem Diffeomorphismus zu machen. In diesem Zusammenhang sei an Lemma 1.3 erinnert, das wir im Beweis des folgenden Satzes benutzen werden. Satz 3.6 Ist A R n eine Nullmenge und f : A R n Lipschitzstetig, so ist auch f(a eine Nullmenge. 38
10 Beweis Sei ε > und (W k k 1 eine Folge von Würfeln mit A k 1 W k und k1 λ n(w k < ε. Wir dürfen annehmen, dass jeder Würfel W k einen Punkt a k A enthält. Ist s k die Kantenlänge von W k, so ist λ n (W k s n k und x a k n sk für alle x W k (warum?. Da f Lipschitzstetig ist, gibt es ein L > so, dass f(x f(y L x y für alle x,y A. Insbesondere ist für alle x A W k f(x f(a k L x a k L n s k. Also liegt f(a W k in einer Kugel vom Radius L n s k und damit auch in einem Würfel Wk mit der Kantenlänge L n s k. Es ist also f(a k 1 f(a W k k 1 W k mit λ n ( W k k1 (L n s k n (L n n λ n (W k (L n n ε. k1 k1 Da ε > beliebig gewählt werden kann, ist f(a eine Nullmenge. Folgerung 3.7 Ist A Nullmenge in R n,u R n offen, A U und f : U R n stetig differenzierbar, so ist f(a eine Nullmenge in R n. Beweis Da U offen ist, ist U eine abzählbare Vereinigung von Quadern der Gestalt Q k [a k,b k ] mit a k,b k Q n (vgl. Beweis von Lemma 1.4. Als stetige Funktion ist f : U L(R n auf jedem der kompakten Quader Q k beschränkt, d.h. es gibt ein L k > mit f (x L k für alle x Q k. Nach Satz 1.19 aus Analysis II folgt f(y f(z L k y z für alle y,z Q k. Also ist f Qk Lipschitzstetig, und nach Satz 3.6 ist f(a Q k Nullmenge. Dann ist auch f(a k1 f(a Q k eine Nullmenge (Lemma 8.13 aus Ana II. Satz 3.6 und Folgerung 3.7 lassen sich nicht auf beliebige stetige Funktionen f verallgemeinern. Es gibt beispielsweise Kurven (sogenannte Peano Kurven, die ein ganzes Quadrat im R ausfüllen. Lemma 3.8 Jeder echte affine Unterraum A R n ist eine Nullmenge. 39
11 Beweis Wir verschieben A so, dass A, und drehen dann A so, dass A R n 1 {}. Nach Folgerung 3.5 und der Anmerkung danach dürfen wir also o.e.d.a. A R n 1 {} annehmen. Wir können A dann schreiben als A k1 ( [ k,k] n 1 {}, und aus λ n ([ k,k] n 1 {} und der σ Additivität folgt mit Lemma 1.17 (e, dass λ n (A. Folgerung 3.9 Ist A R n messbar und f : A R messbar, so ist der Graph { } Γ(f (x,f(x R n R : x A (3.8 eine Nullmenge in R n+1. Beweis Wir setzen f durch auf R n fort. Diese Fortsetzung ist messbar (warum?, und ihr Graph enthält den Graphen (3.8 als Teilmenge. Wir können daher A R n annehmen. Dann ist der Graph Γ(f {(x,y R n R : y f(x } als Nullstellenmenge einer messbaren Funktion messbar, und aus dem Cavalierischen Prinzip erhalten wir ( λ n+1 (Γ(f λ 1 {f(x} dλ n (x dλ n. R n R n 3.4 Koordinatentransformationen Oft lassen sich vorhandene Symmetrien dadurch ausnutzen, dass man Integrationsbereiche durch Koordinatentransformationen (d.h. durch eine geeignete Parametrisierung in Quader überführt, auf denen Integrale iterativ berechnet werden können. Aus der Fülle der möglichen Koordinatensysteme sehen wir uns hier nur sphärische Polarkoordinaten an und behandeln die Zylinderkoordinaten in der Übung. Polarkoordinaten in der Ebene. Der Übergang von Polar zu kartesischen Koordinaten in der Ebene wird beschrieben durch P : [, [, π] R, (r,ϕ (r cos ϕ,r sin ϕ. (3.9 Die Jacobimatrix von P in (r,ϕ ist gegeben durch ( cos ϕ r sin ϕ, sin ϕ r cosϕ und ihre Determinante ist gleich r. Man beachte, dass nur die Einschränkung von P auf die offene Menge (, (, π einen Diffeomorphismus auf die Menge R \ 4
12 ([, {} liefert (warum?. Um einen Diffeomorphismus zu erhalten, mussten wir also sowohl aus [, [, π] als auch aus R eine Nullmenge herausnehmen. Daher ist eine Funktion f : R R nach der Transformationsformel (Satz 3.4 genau dann integrierbar, wenn die Funktion ( (r,ϕ f P(r,ϕ detp (r,ϕ f(r cos ϕ,r sin ϕ r auf [, [, π] integrierbar ist (Nullmengen dürfen wir unberücksichtigt lassen, und es gilt in diesem Fall π fdλ f(x,ydλ (x,y f(r cos ϕ,r sin ϕrdρdr. (3.1 R R Wichtig ist, vor Anwendung der Transformationsformel zu prüfen, ob die Ausnahmemengen auf beiden Seiten Nullmengen sind. Beispiel 1 Als Anwendung von (3.1 berechnen wir das Integral R e x dx. Dazu betrachten wir die Funktion f : R R, (x,y e x y. Diese ist rotationssymmetrisch, und mit Polarkoordinaten, (3.1 und der Substitution s r erhalten wir π f(x,ydxdy e r rdϕdr π e r rdr π e s ds R π lim e s t π lim (1 t t e t π. Insbesondere ist also f integrierbar. Mit Fubini erhalten wir andererseits ( f(x,ydxdy e x e y dxdy e x dx e y dy R R R R R (, e x dx e y dy e dx x so dass schließlich R R R R e x dx π (3.11 folgt. Dieses Integral spielt in der Wahrscheinlichkeitstheorie eine zentrale Rolle. Beispiel : Die Beta Funktion. Die Identität (3.11 eröffnet uns einen weiteren Weg, um Γ(1/ zu berechnen. Mit der Substitution x t erhalten wir ( 1 Γ e t dt t e x x xdx 41 e x dx e x dx π.
13 Wir schauen uns noch an, was dieser Trick für allgemeinere Werte der Γ Funktion liefert. Mit der Substitution t x / bekommen wir Γ(u und hiermit finden wir t u 1 e t dt 1 u x (u 1 e x / xdx 1 u x u 1 e x / dx, Γ(uΓ(v u v Die Funktion u v u v π/ u v r u+v 1 e r / dr Γ(u + v π/ B : (, (, R, (u,v x u 1 e x / y v 1 e y / dxdy x u 1 y v 1 e (x +y / dxdy r u+v (cos ϕ u 1 (sin ϕ v 1 e r / r dϕdr π/ (cosϕ u 1 (sin ϕ v 1 dϕ. π/ (cosϕ u 1 (sin ϕ v 1 dϕ (cos ϕ u 1 (sin ϕ v 1 dϕ heißt Eulersche Betafunktion ; wir haben also gerade gesehen, dass B(u,v Γ(uΓ(v Γ(u + v. (3.1 Für u v 1 erhalten wir insbesondere B(1, 1 π/ dϕ π. Für die Berechnung des Volumens c n der n dimensionalen Einheitskugel hatten wir mit dem Cavalierischen Prinzip die Rekursionsformel c n c n 1 I n mit I n π/ π/ (cos t n dt π/ gefunden. Mit (3.1 ergibt sich nun direkt. und damit ( n + 1 (cos t n dt B, 1 ( n + 1 I n B, 1 Γ(n+1 Γ( 1 Γ( n+ π Γ(n+1 Γ( n+ c n c n 1 I n c n I n I n 1... c 1 I n I n 1...I π n 1 Γ( n+1 Γ( n+ Γ( n+1 Γ(n... Γ(3 Γ( π n 1 1 Γ(1 Γ( n+ π n Γ( n+. 4
14 Sphärische Polarkoordinaten im R n. Diese definieren wir rekursiv als P n : [, [, π] [,π] n R n, wobei ( P n (r,ϕ,θ 1,...,θ n sin θ n P n 1 (r,ϕ,θ 1,...,θ n 3,r cos θ n für n 3 und P wie in (3.9 festgelegt ist. Insbesondere haben wir für die Kugelkoordinaten im R 3 P 3 : [, [, π] [,π] R 3 mit P 3 (r,ϕ,θ ( sin θp (r,ϕ,r cos θ (r cos ϕ sin θ,r sin ϕ sin θ,r cos θ. Dabei misst r den Abstand zum Ursprung, ϕ den Längengrad und θ den Breitengrad. Mit θ : (θ 1,...,θ n und θ : (θ 1,...,θ n 3 können wir die Jacobimatrix von P n schreiben als ( sin θn J (r,ϕ,θ J (r,ϕ,θ (P n (P n 1 cos θ n P n 1 (r,ϕ,θ. cos θ n... r sin θ n Um davon die Determinante berechnen zu können, beachten wir, dass P n 1 (r,ϕ,θ rp n 1 (1,ϕ,θ (was man leicht durch Induktion bestätigt. Damit ist P n 1 r (r,ϕ,θ P n 1 (1,ϕ,θ r 1 P n 1 (r,ϕ,θ, und folglich stimmt die erste Spalte der Jacobimatrix von P n 1 mit r 1 P n 1 überein. Also ist die Determinante der (n 1 (n 1 Untermatrix, die man aus J (r,ϕ,θ (P n durch Streichen der ersten Spalte und letzten Zeile erhält, gleich r(cos θ n (sinθ n n ( 1 n det P n 1(r,ϕ,θ. Damit erhalten wir durch Entwicklung von det P n(r,ϕ,θ nach der letzten Zeile det P m(r,ϕ,θ r(sin θ n n detp n 1(r,ϕ,θ Induktiv folgt nun +( 1 n 1 r(cos θ n (sin θ n n ( 1 n detp n 1(r,ϕ,θ r(sin θ n n detp n 1 (r,ϕ,θ. detp n(r,ϕ,θ ( 1 n r n 1 (sin θ n n (sin θ n 3 n 3... (sin θ 1, 43
15 wenn man detp 3(r,ϕ,θ 1 r sin θ 1 berücksichtigt. Diskutieren Sie als Übung zunächst im Fall n 3 und dann im allgemeinen Fall, welche Nullmenge man aus [, [, π] [,π] n bzw. aus dem R n herausschneiden muss, damit die Einschränkung von P n ein Diffeomophismus wird. Als eine Anwendung wollen wir Integrale über rotationssymmetrischen Funktionen auf Kugelschalen berechnen. Satz 3.1 Sei I [, ein Intervall, K(I : {x R n : x I} die zugehörige Kugelschale und h : I R eine messbare Funktion. Dann ist die Funktion H : K(I R, x h( x genau dann integrierbar, wenn die Funktion I R, r r n 1 h(r integrierbar ist. In diesem Fall gilt Hdλ n nc n h(rr n 1 dr, (3.13 K(I wobei c n das Volumen der n dimensionalen Einheitskugel ist. Beweis Wir benutzen sphärische Polarkoordinaten im R n und beachten, dass K(I P n (I [, π] [,π] n ist. Da die Transformation P n außerhalb gewisser Nullmengen ein Diffeomorphismus ist, erhalten wir mit der Transformationsformel I K(I Hdλ n π π I π π I π π ( H P n (r,ϕ,θ det P n(r,ϕ,θ dθ 1...dθ n dϕdr h(rr n 1 (sin θ n n (sin θ n 3 n 3...(sin θ 1 dθ 1...dθ n dϕdr π π h(rr n 1 dr (sin θ n n dθ n... I π sin θ 1 dθ 1. (3.14 Um die Integrale über die θ j nicht explizit berechnen zu müssen, erinnern wir daran, dass das Integral Hdλ K(I n für I [, 1] und H 1 gerade das Volumen der n dimensionalen Einheitskugel liefert. Es ist also c n π π n 1 π r n 1 dr π (sin θ n n dθ n... (sin θ n n dθ n... π π sin θ 1 dθ 1 sin θ 1 dθ 1. (3.15 Ein Vergleich von (3.14 und (3.15 liefert (3.13, wobei die Aussage über die Existenz der Integrale ebenfalls aus Satz 3.4 folgt. 44
8 Beispiele von Koordinatentransformationen
 8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
8 Beispiele von Koordinatentransformationen Wir diskutieren nun diejenigen Koordinatentransformationen, die in der Praxis wirklich gebraucht werden (ebene und räumliche Polarkoordinaten sowie Zylinderkoordinaten).
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
9. Übung zur Maß- und Integrationstheorie, Lösungsskizze Aufgaben
 9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
9. Übung zur aß- und Integrationstheorie, Lösungsskizze Aufgaben A 50 (Eine Flächenberechnung mit dem Cavalierischen Prinzip). Es seien a, b > 0 und : { (x, y) R 2 : (x/a) 2 + (y/b) 2 1 }. (a) Skizzieren
Mathematik für Anwender II
 Prof. Dr. H. Brenner Osnabrück SS 2012 Mathematik für Anwender II Vorlesung 57 Die ransformationsformel für Integrale Wir kommen zur ransformationsformel für Integrale, wofür wir noch eine Bezeichnung
Prof. Dr. H. Brenner Osnabrück SS 2012 Mathematik für Anwender II Vorlesung 57 Die ransformationsformel für Integrale Wir kommen zur ransformationsformel für Integrale, wofür wir noch eine Bezeichnung
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
Integration über allgemeine Integrationsbereiche.
 Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA94 Z4.. Parametrisierungsinvarianz des Oberflächenintegrals
Prof. Dr. Michael Wolf Daniel Stilck França Stefan Huber Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik 4 für Physiker (Analysis 3) MA94 Z4.. Parametrisierungsinvarianz des Oberflächenintegrals
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
Lebesgue-Integral und L p -Räume
 Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
Lebesgue-Integral und L p -Räume Seminar Integraltransformationen, WS 2012/13 1 Treppenfunktionen Grundlage jedes Integralbegriffs ist das geometrisch definierte Integral von Treppenfunktionen. Für A R
10 Untermannigfaltigkeiten
 10. Untermannigfaltigkeiten 1 10 Untermannigfaltigkeiten Definition. Eine Menge M R n heißt k-dimensionale Untermannigfaltigkeit des R n, 1 k n, falls es zu jedem a M eine offene Umgebung U R n von a und
10. Untermannigfaltigkeiten 1 10 Untermannigfaltigkeiten Definition. Eine Menge M R n heißt k-dimensionale Untermannigfaltigkeit des R n, 1 k n, falls es zu jedem a M eine offene Umgebung U R n von a und
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
Transformation mehrdimensionaler Integrale
 Transformation mehrdimensionaler Integrale Für eine bijektive, stetig differenzierbare Transformation g eines regulären Bereiches U R n mit det g (x), x U, gilt für stetige Funktionen f : f g det g du
Transformation mehrdimensionaler Integrale Für eine bijektive, stetig differenzierbare Transformation g eines regulären Bereiches U R n mit det g (x), x U, gilt für stetige Funktionen f : f g det g du
Teil IV : Integration über Untermannigfaltigkeiten. 9 Untermannigfaltigkeiten von R n
 Teil IV : Integration über Untermannigfaltigkeiten In der Analysis II haben wir bereits Kurven in R n eine Länge zugeordnet (also ein eindimensionales Volumen ) und Funktionen über Kurven integriert. In
Teil IV : Integration über Untermannigfaltigkeiten In der Analysis II haben wir bereits Kurven in R n eine Länge zugeordnet (also ein eindimensionales Volumen ) und Funktionen über Kurven integriert. In
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
Parametrisierung und Integralsätze
 Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Abbildung 10.1: Das Bild zu Beispiel 10.1
 Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
46 Der Satz von Fubini
 46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
Das mehrdimensionale Riemann-Integral. 1. Volumenintegrale
 Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
3 Lebesgue-Integration im IR n
 33 3 Lebesgue-Integration im IR n 3.1 Vorbemerkung Zuerst eine heuristische Betrachtung: Wir betrachten eine nichtnegative stetige Funktion f(x, y, die über einem kompakten, also beschränkten und abgeschlossenen
33 3 Lebesgue-Integration im IR n 3.1 Vorbemerkung Zuerst eine heuristische Betrachtung: Wir betrachten eine nichtnegative stetige Funktion f(x, y, die über einem kompakten, also beschränkten und abgeschlossenen
Mathematik III. Vorlesung 68. Das Verhalten von Maßen bei linearen Abbildungen
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 68 Das Verhalten von Maßen bei linearen Abbildungen Lemma 68.1. Es sei V ein reeller Vektorraum und L :R n V eine bijektive lineare
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 68 Das Verhalten von Maßen bei linearen Abbildungen Lemma 68.1. Es sei V ein reeller Vektorraum und L :R n V eine bijektive lineare
Analysis III. Vorlesung 72. Korollar Es sei (M,A,µ) ein σ-endlicher Maßraum und v: M R n eine messbare Abbildung. Dann ist die Abbildung
 Prof. Dr. H. Brenner Osnabrück WS 15/16 Analysis III Vorlesung 7 Korollar 7.1. Es sei (,A,µ) ein σ-endlicher aßraum und v: R n eine messbare Abbildung. Dann ist die Abbildung bijektiv und maßtreu. ϕ v
Prof. Dr. H. Brenner Osnabrück WS 15/16 Analysis III Vorlesung 7 Korollar 7.1. Es sei (,A,µ) ein σ-endlicher aßraum und v: R n eine messbare Abbildung. Dann ist die Abbildung bijektiv und maßtreu. ϕ v
Analysis II. 8. Klausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Umkehrfunktion. g (y) = f (x) 1, x = g(y), Umkehrfunktion 1-1
 Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Das Volumen und die Oberfläche einer n-dimensionalen Kugel
 Das Volumen und die Oberfläche einer n-dimensionalen Kugel Alois Temmel 6. Februar 14 c 14, A. Temmel Inhaltsverzeichnis 1 Die Volumenformel 3 1.1 Die n-dimensionale Kugel.................... 3 1.1.1 Die
Das Volumen und die Oberfläche einer n-dimensionalen Kugel Alois Temmel 6. Februar 14 c 14, A. Temmel Inhaltsverzeichnis 1 Die Volumenformel 3 1.1 Die n-dimensionale Kugel.................... 3 1.1.1 Die
Kapitel 16 SATZ VON FUBINI UND DIE TRANSFORMATIONSFORMEL
 Kapitel 16 SAT VON FUBINI UND DIE TRANSFORMATIONSFORMEL Im folgenden sind X und Y metrische Räume, oder allgemeiner topologische Hausdor räume, und sind Radon-Integrale auf X bzw. Y. Fassung vom 24. Januar
Kapitel 16 SAT VON FUBINI UND DIE TRANSFORMATIONSFORMEL Im folgenden sind X und Y metrische Räume, oder allgemeiner topologische Hausdor räume, und sind Radon-Integrale auf X bzw. Y. Fassung vom 24. Januar
Das heißt, Γ ist der Graph einer Funktion von d 1 Veränderlichen.
 Kapitel 2 Der Gaußsche Satz Partielle Differentialgleichung sind typischerweise auf beschränkten Gebieten des R d, d 1, zu lösen. Dabei sind die Eigenschaften dieser Gebiete von Bedeutung, insbesondere
Kapitel 2 Der Gaußsche Satz Partielle Differentialgleichung sind typischerweise auf beschränkten Gebieten des R d, d 1, zu lösen. Dabei sind die Eigenschaften dieser Gebiete von Bedeutung, insbesondere
Integralrechnung für Funktionen mehrerer Variabler
 Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel. dt = lim. = lim = Weiters erhalten wir durch partielle Integration, dass
 Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel Zuerst wollen wir die Gamma-Funktion definieren, die eine Verallgemeinerung von n! ist. Dazu benötigen wir einige Resultate. Lemma.
Die Gamma-Funktion, das Produkt von Wallis und die Stirling sche Formel Zuerst wollen wir die Gamma-Funktion definieren, die eine Verallgemeinerung von n! ist. Dazu benötigen wir einige Resultate. Lemma.
Höhere Mathematik II für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
12 Der Gaußsche Integralsatz
 12. Der Gaußsche Integralsatz 1 12 Der Gaußsche Integralsatz Das Ziel dieses Abschnitts ist die folgende zentrale Aussage der mehrdimensionalen Analysis und der Theorie der partiellen Differentialgleichungen:
12. Der Gaußsche Integralsatz 1 12 Der Gaußsche Integralsatz Das Ziel dieses Abschnitts ist die folgende zentrale Aussage der mehrdimensionalen Analysis und der Theorie der partiellen Differentialgleichungen:
5 Die Transformationsformel
 $Id: transform.tex,v 1.6 1/1/11 15:47:59 hk Exp hk $ 5 Die Transformationsformel In der letzten Sitzung haben wir die Transformationsformel als n-dimensionale Erweiterung der bekannten Substitutionsregel
$Id: transform.tex,v 1.6 1/1/11 15:47:59 hk Exp hk $ 5 Die Transformationsformel In der letzten Sitzung haben wir die Transformationsformel als n-dimensionale Erweiterung der bekannten Substitutionsregel
1 Lösungsskizzen zu den Übungsaufgaben
 Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Lösungen zu den Hausaufgaben zur Analysis II
 Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
6 Integration auf Untermannigfaltigkeiten
 6 Integration auf Untermannigfaltigkeiten 6.1 annigfaltigkeiten. Eine k dimensionale C α annigfaltigkeit ist ein metrischer Raum mit einer Überdeckung {V : J} durch offene engen und Homöomorphismen ϕ :
6 Integration auf Untermannigfaltigkeiten 6.1 annigfaltigkeiten. Eine k dimensionale C α annigfaltigkeit ist ein metrischer Raum mit einer Überdeckung {V : J} durch offene engen und Homöomorphismen ϕ :
Analysis IV. Gruppenübungen
 Fachbereich Mathematik Prof. B. Farkas Martin Fuchssteiner Lisa Steiner TECHNISCHE UNIVESITÄT DAMSTADT ASS 6 7.7.26 Analysis IV 3. Übung mit Lösungshinweisen (G ) Berechnung einiger Volumina Gruppenübungen
Fachbereich Mathematik Prof. B. Farkas Martin Fuchssteiner Lisa Steiner TECHNISCHE UNIVESITÄT DAMSTADT ASS 6 7.7.26 Analysis IV 3. Übung mit Lösungshinweisen (G ) Berechnung einiger Volumina Gruppenübungen
Analysis 3 - Klausur - Lösung
 Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Implizite Funktionen. Ist für eine stetig differenzierbare Funktion f : R n R m R n. so lässt sich das Gleichungssystem
 Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
Implizite Funktionen Ist für eine stetig differenzierbare Funktion f : R n R m R n f (x, y ) = (0,..., 0) t, det f x (x, y ) 0, so lässt sich das Gleichungssystem f k (x 1,..., x n, y 1,..., y m ) = 0,
Analysis II - 2. Klausur
 Analysis II - 2. Klausur Sommersemester 25 Vorname: Name: Aufgabe Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 Aufgabe 7 Summe Analysis II - 2. Klausur 6.7.25 Aufgabe 6 Punkte Betrachten Sie die C
Analysis II - 2. Klausur Sommersemester 25 Vorname: Name: Aufgabe Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 Aufgabe 7 Summe Analysis II - 2. Klausur 6.7.25 Aufgabe 6 Punkte Betrachten Sie die C
10 Der Satz über implizite Funktionen und Umkehrfunktionen
 Vorlesung SS 9 Analsis Prof. Dr. Siegfried Echterhoff SATZ ÜBER IMPLIZITE FKT UND UMKEHRFKT Der Satz über implizite Funktionen und Umkehrfunktionen Motivation: Sei F : U R R eine differenzierbare Funktion
Vorlesung SS 9 Analsis Prof. Dr. Siegfried Echterhoff SATZ ÜBER IMPLIZITE FKT UND UMKEHRFKT Der Satz über implizite Funktionen und Umkehrfunktionen Motivation: Sei F : U R R eine differenzierbare Funktion
Meßbare Funktionen. Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen.
 Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Aufgaben. f : R 2 R, f(x, y) := y.
 11. Übung zur Maß- und Integrationstheorie, Lösungsskizze A 63 Untermannigfaltigkeiten von R 2 ). Aufgaben Skizzieren Sie grob die folgenden Mengen und begründen Sie, welche davon 1-dimensionale Untermannigfaltigkeiten
11. Übung zur Maß- und Integrationstheorie, Lösungsskizze A 63 Untermannigfaltigkeiten von R 2 ). Aufgaben Skizzieren Sie grob die folgenden Mengen und begründen Sie, welche davon 1-dimensionale Untermannigfaltigkeiten
Analysis III. Vorlesung 69. Integrierbare Funktionen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 69 Integrierbare Funktionen Wir führen nun das Lebesgue-Integral für messbare Funktionen auf einem aßraum ein. Dieser Integralbegriff
1 Eingebettete Untermannigfaltigkeiten des R d
 $Id: unter.tex,v 1.2 2014/04/14 13:19:35 hk Exp hk $ 1 Eingebettete Untermannigfaltigkeiten des R d In diesem einleitenden Paragraphen wollen wir Untermannigfaltigkeiten des R d studieren, diese sind die
$Id: unter.tex,v 1.2 2014/04/14 13:19:35 hk Exp hk $ 1 Eingebettete Untermannigfaltigkeiten des R d In diesem einleitenden Paragraphen wollen wir Untermannigfaltigkeiten des R d studieren, diese sind die
Mehrdimensionale Analysis
 KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Analysis II 14. Übungsblatt
 Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 01/13 F. Stoffers 04. Februar 013 Analysis II 14. Übungsblatt 1. Aufgabe (8 Punkte Man beweise: Die Gleichung z 3 + z + xy = 1 besitzt für jedes (x, y R genau
Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 01/13 F. Stoffers 04. Februar 013 Analysis II 14. Übungsblatt 1. Aufgabe (8 Punkte Man beweise: Die Gleichung z 3 + z + xy = 1 besitzt für jedes (x, y R genau
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
9 Integration von Differentialformen und der Satz von Stokes
 9 Integration von Differentialformen und der Satz von Stokes 9. Definition. Es sei ω = f dx... dx n eine n-form auf der offenen Menge U in R n. Wir definieren sofern das Integral rechts existiert: ω =
9 Integration von Differentialformen und der Satz von Stokes 9. Definition. Es sei ω = f dx... dx n eine n-form auf der offenen Menge U in R n. Wir definieren sofern das Integral rechts existiert: ω =
Topologie und Differentialrechnung mehrerer Veränderlicher, SS 2009 Modulprüfung/Abschlussklausur. Aufgabe Punkte
 Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen
 Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
30 Die Gammafunktion und die Stirlingsche Formel
 3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form
 155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
10 Der Integralsatz von Gauß
 10 Der Integralsatz von Gauß In diesem Abschnitt beweisen wir den Integralsatz von Gauß, die mehrdimensionale Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung. Aussage des Satzes
10 Der Integralsatz von Gauß In diesem Abschnitt beweisen wir den Integralsatz von Gauß, die mehrdimensionale Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung. Aussage des Satzes
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Übungen zur Ingenieur-Mathematik III WS 2011/12 Blatt N dl. y 3
 Übungen zur Ingenieur-Mathematik III WS / Blatt 9.. Aufgabe 5: Berechnen Sie das Integral K ( x y N dl über den Rand des Kreises K {(x, y x + y } einmal direkt mit Hilfe einer geeigneten Parametrisierung
Übungen zur Ingenieur-Mathematik III WS / Blatt 9.. Aufgabe 5: Berechnen Sie das Integral K ( x y N dl über den Rand des Kreises K {(x, y x + y } einmal direkt mit Hilfe einer geeigneten Parametrisierung
Analysis II. Vorlesung 52. Diffeomorphismen
 Prof. Dr. H. Brenner Osnabrück SS 2014 Analysis II Vorlesung 52 Diffeomorphismen Der Satz über die lokale Umkehrbarkeit gibt Anlass zu folgender Definition. Definition 52.1. EsseienV 1 undv 2 endlichdimensionalereellevektorräume
Prof. Dr. H. Brenner Osnabrück SS 2014 Analysis II Vorlesung 52 Diffeomorphismen Der Satz über die lokale Umkehrbarkeit gibt Anlass zu folgender Definition. Definition 52.1. EsseienV 1 undv 2 endlichdimensionalereellevektorräume
Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form. ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können.
 142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
Integralrechnung für GLET
 Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
11. Übungsblatt zur Mathematik II für MB
 Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 8.6.. Übungsblatt zur Mathematik für MB Aufgabe 5 ntervall im R egeben sei das ntervall { (x, y, z) R : π x π, y, z π}. Berechnen Sie x
Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 8.6.. Übungsblatt zur Mathematik für MB Aufgabe 5 ntervall im R egeben sei das ntervall { (x, y, z) R : π x π, y, z π}. Berechnen Sie x
Höhere Mathematik Vorlesung 4
 Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
1 Umkehrfunktionen und implizite Funktionen
 Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
B Lösungen. Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R 2 Berechnen Sie zur Abbildung. f(x, y) := x sin(xy) f : R 2 R,
 B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
Analysis I & II Lösung zur Basisprüfung
 FS 6 Aufgabe. [8 Punkte] (a) Bestimmen Sie den Grenzwert ( lim x x ). [ Punkte] log x (b) Beweisen Sie, dass folgende Reihe divergiert. n= + n + n + sin(n) n 3 + [ Punkte] (c) Finden Sie heraus, ob die
FS 6 Aufgabe. [8 Punkte] (a) Bestimmen Sie den Grenzwert ( lim x x ). [ Punkte] log x (b) Beweisen Sie, dass folgende Reihe divergiert. n= + n + n + sin(n) n 3 + [ Punkte] (c) Finden Sie heraus, ob die
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 4/5 r. Hanna Peywand Kiani 6..5 Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz,
Fachbereich Mathematik der Universität Hamburg WiSe 4/5 r. Hanna Peywand Kiani 6..5 Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz,
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
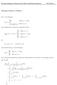 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Teil 8. Vektoranalysis
 Teil 8 Vektoranalysis 5 6 8. kalar- und Vektorfelder kalarfeld alternative chreibweisen: U = U(x, y, z) = U( r) R 3 P U(P ) R Visualisierung durch Niveaumengen oder Einschränkungen auf achsenparallele
Teil 8 Vektoranalysis 5 6 8. kalar- und Vektorfelder kalarfeld alternative chreibweisen: U = U(x, y, z) = U( r) R 3 P U(P ) R Visualisierung durch Niveaumengen oder Einschränkungen auf achsenparallele
3 Das n-dimensionale Integral
 3 as n-dimensionale ntegral Ziel: Wir wollen die ntegrationstheorie für f : R n R entwickeln. Wir wollen den nhalt (beziehungsweise das Maß M einer Punktmenge des R n definieren für eine möglichst große
3 as n-dimensionale ntegral Ziel: Wir wollen die ntegrationstheorie für f : R n R entwickeln. Wir wollen den nhalt (beziehungsweise das Maß M einer Punktmenge des R n definieren für eine möglichst große
Mathematik für Anwender II
 Prof. Dr. H. Brenner Osnabrück SS 212 Mathematik für Anwender II Vorlesung 58 Der Satz von Green Wir betrachten eine kompakte eilmenge R 2, deren Rand R sich stückweise durch reguläre Kurven parametrisieren
Prof. Dr. H. Brenner Osnabrück SS 212 Mathematik für Anwender II Vorlesung 58 Der Satz von Green Wir betrachten eine kompakte eilmenge R 2, deren Rand R sich stückweise durch reguläre Kurven parametrisieren
3 Messbare Funktionen
 3. Messbare Funktionen 1 3 Messbare Funktionen Sei (, A, µ) ein beliebiger Maßraum. Definition. ine Funktion f : R = [, + ] heißt messbar (bezüglich A), falls die Menge {f < c} = {x : f(x) < c} = f 1 ([,
3. Messbare Funktionen 1 3 Messbare Funktionen Sei (, A, µ) ein beliebiger Maßraum. Definition. ine Funktion f : R = [, + ] heißt messbar (bezüglich A), falls die Menge {f < c} = {x : f(x) < c} = f 1 ([,
4 Das Riemann-Integral im R n
 $Id: nintegral.tex,v 1.11 2012/11/27 14:07:09 hk Exp hk $ 4 Das Riemann-Integral im R n 4.3 Jordan-meßbare engen In der letzten Sitzung hatten wir schließlich das n-dimensionale Riemann-Integral auch auf
$Id: nintegral.tex,v 1.11 2012/11/27 14:07:09 hk Exp hk $ 4 Das Riemann-Integral im R n 4.3 Jordan-meßbare engen In der letzten Sitzung hatten wir schließlich das n-dimensionale Riemann-Integral auch auf
116 KAPITEL 15. INTEGRALSÄTZE
 116 APITEL 15. INTEGRALSÄTZE Aufgabe 15.1.3 (Verschwinden des Integrales über eine partielle Ableitung) Es sei U R n offen, ϕ C 0 (U; R). Dann ist für j = 1,..., n U ϕ x j dλ n = 0. Wir erinnern an die
116 APITEL 15. INTEGRALSÄTZE Aufgabe 15.1.3 (Verschwinden des Integrales über eine partielle Ableitung) Es sei U R n offen, ϕ C 0 (U; R). Dann ist für j = 1,..., n U ϕ x j dλ n = 0. Wir erinnern an die
Vorlesung: Analysis II für Ingenieure. Wintersemester 07/08. Michael Karow. Thema: Transformationsformel für Gebietsintegrale
 Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
1. Integrieren Sie die Funktion f(x, y, z) := xyz über die Kugel mit Zentrum im Ursprung und Radius 1. (2 Punkte) Hinweis: Verwenden Sie Symmetrien.
 1. Integrieren Sie die Funktion f(x, y, z) : xyz über die Kugel mit Zentrum im Ursprung und Radius 1. (2 Punkte) inweis: Verwenden Sie Symmetrien. Lösung: Betrachte den Diffeomorphismus j : B 1 () B 1
1. Integrieren Sie die Funktion f(x, y, z) : xyz über die Kugel mit Zentrum im Ursprung und Radius 1. (2 Punkte) inweis: Verwenden Sie Symmetrien. Lösung: Betrachte den Diffeomorphismus j : B 1 () B 1
2 Koordinatentransformationen
 Mathematik für Ingenieure III, WS 9/1 Montag 3.11 $Id: transform.tex,v 1.5 9/11/3 16:9: hk Exp $ Koordinatentransformationen. ie Transformationsformel In der letzten Sitzung hatten wir die Transformationsformel
Mathematik für Ingenieure III, WS 9/1 Montag 3.11 $Id: transform.tex,v 1.5 9/11/3 16:9: hk Exp $ Koordinatentransformationen. ie Transformationsformel In der letzten Sitzung hatten wir die Transformationsformel
Übungen zum Ferienkurs Analysis II 2014
 Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
2.2. Die Tangentialebene. Definition 2.12 (Tangentialebene). Sei S eine reguläre Fläche, sei p S. Dann heißt
 2.2. Die Tangentialebene. Definition 2.12 (Tangentialebene). Sei S eine reguläre Fläche, sei p S. Dann heißt { } T p S = X R 3 es gibt ein ε > 0 und eine glatte parametrisierte Kurve c : ( ε,ε) S mit c(0)
2.2. Die Tangentialebene. Definition 2.12 (Tangentialebene). Sei S eine reguläre Fläche, sei p S. Dann heißt { } T p S = X R 3 es gibt ein ε > 0 und eine glatte parametrisierte Kurve c : ( ε,ε) S mit c(0)
2 3 x3 17. x k dx = x k x k+1 k +1. Mit jeder weiteren partiellen Integration reduziert sich der Grad des Faktors x n, induktiv erhalten wir also
 Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
mit 0 < a < b um die z-achse entsteht.
 Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Alg. II SS 6 Blatt 8 13.6.6 Aufgabe 38: Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { (x, y, z) R 3 y, (x b) + z a } mit
Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Alg. II SS 6 Blatt 8 13.6.6 Aufgabe 38: Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { (x, y, z) R 3 y, (x b) + z a } mit
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Probeklausur zur Analysis II
 Probeklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 3. Februar 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Probeklausur zur Analysis II Prof. Dr. C. Löh/M. Blank 3. Februar 2012 Name: Matrikelnummer: Vorname: Übungsleiter: Diese Klausur besteht aus 8 Seiten. Bitte überprüfen Sie, ob Sie alle Seiten erhalten
Klausur zu Analysis II - Lösungen
 Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
Lösungen zu Koordinatentrafo und Integration im R n
 Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Serie 4: Gradient und Linearisierung
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
Nach Bogenlänge parametrisierte Kurven
 Nach Bogenlänge parametrisierte Kurven Eine orientierte Kurve ist eine Äquivalenzklasse von regulären parametrisierten Kurven bzgl. der orientierungserhaltenden Umparametrisierung als Äquivalenzrelation.
Nach Bogenlänge parametrisierte Kurven Eine orientierte Kurve ist eine Äquivalenzklasse von regulären parametrisierten Kurven bzgl. der orientierungserhaltenden Umparametrisierung als Äquivalenzrelation.
12. Übungsblatt zur Analysis II
 Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
Fachbereich Mathematik Prof. Dr. Steffen Roch Nada Sissouno Benno van den Berg WS 9/1 1.1.1 1. Übungsblatt zur Analysis II Gruppenübung Aufgabe G1 Kreuzen Sie die richtigen Aussagen an. Sei V C 1 (R n,
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
10 Der Satz von Fubini
 er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
1 Das Prinzip von Cavalieri
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
Kapitel 5 Untermannigfaltigkeiten. 5.1 Glatte Flächen in R 3
 Kapitel 5 Untermannigfaltigkeiten 5.1 Glatte Flächen in R 3 Bisher haben wir unter einem glatten Weg im R n stets eine differenzierbare Abbildung γ:i R n, definiert auf einem Intervall I R, verstanden.
Kapitel 5 Untermannigfaltigkeiten 5.1 Glatte Flächen in R 3 Bisher haben wir unter einem glatten Weg im R n stets eine differenzierbare Abbildung γ:i R n, definiert auf einem Intervall I R, verstanden.
VERTEILUNGEN VON FUNKTIONEN EINER ZUFALLSVARIABLEN
 KAPITEL 15 VETEILUNGEN VON FUNKTIONEN EINE ZUFALLSVAIABLEN In diesem Kapitel geht es darum, die Verteilungen für gewisse Funktionen von Zufallsvariablen zu bestimmen. Wir werden uns auf den Fall absolut
KAPITEL 15 VETEILUNGEN VON FUNKTIONEN EINE ZUFALLSVAIABLEN In diesem Kapitel geht es darum, die Verteilungen für gewisse Funktionen von Zufallsvariablen zu bestimmen. Wir werden uns auf den Fall absolut
Seite 1. sin 2 x dx. b) Berechnen Sie das Integral. e (t s)2 ds. (Nur Leibniz-Formel) c) Differenzieren Sie die Funktion f(t) = t. d dx ln(x + x3 ) dx
 Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
