Potentialtheorie. Vorbemerkung:
|
|
|
- Hannelore Goldschmidt
- vor 8 Jahren
- Abrufe
Transkript
1 Potentialtheorie Vorbemerkung: Die Erfassung dynamischer Kräfte, die durch Wasser- oder Luftströmungen an Bauwerken erzeugt werden, ist generell schwierig. Eine wirklich exakte Ermittlung ist nicht möglich. Es können eigentlich nur Abschätzungen vorgenommen werden. Im Gegensatz zum Konstruktiven Ingenieurbau, bei dem Kräfte oft als bekannt vorausgesetzt und lediglich in der Baukonstruktion verfolgt werden (Statik und Festigkeitslehre), besteht beim Konstruktiven Wasserbau eine wesentliche Aufgabe darin, Ansätze für dynamische (hydrodynamische) Kräfte zunächst zu formulieren. Zur Lösung wasserbaulicher Aufgaben gibt die theoretische Hydromechanik zwei Ansätze: Büsching, F.: Stauanlagenbau 2000/05.1
2 a. die Gleichungen von BERNOULLI und EULER für ideale, d.h., reibungsfrei gedachte, inkompressible Flüssigkeiten (mit dem wesentlichen Kennzeichen der Wirbelfreiheit) und b. die Gleichungen von NAVIER und STOKES für natürliche reibungsbehaftete Flüssigkeiten. Trotz der großen Erfolge der theoretischen und praktischen Strömungsforschung ist der Wasserbauingenieur bei vielen Problemen noch immer auf die Durchführung teilweise aufwendiger hydraulischer Modellversuche angewiesen. Dies gilt insbesondere bei dreidimensionalen Strömungen und bei komplizierten Randbedingungen. Für wirbelfrei ablaufende Strömungsvorgänge (z.b. Sickerströmungen), im Sinne einer ersten Näherung oder als Leitmodell zur Festlegung der Grenzen des eigentlichen hydraulischen Modells kann indessen als preiswertes Hilfsmittel ein Analogmodell verwendet werden, das auf der sog. Potentialtheorie basiert. Büsching, F.: Stauanlagenbau 2000/05.2
3 Die Potentialtheorie ist das mathematische Hilfsmittel, mit dem die Kontinuitätsgleichung (Satz von der Erhaltung der Masse (Q = A. v = konst.)) auf die Ebene (bzw. den Raum) übertragen werden kann. Damit ist die Möglichkeit gegeben, zwei- bzw. dreidimensionale Strömungsfelder zu beschreiben (im Gegensatz zur eindimensionalen Rohrhydraulik). Strömungsfeld: In einem räumlichen (bzw. ebenen) Strömungsfeld ist die Geschwindigkeit von den 3 (bzw. 2) Ortskoordinaten abhängig. Sie verändert sich mit dem Ort (vergl. konvektive Beschleunigung, Hydromechanik I). Die Behandlung soll hier auf das ebene Strömungsfeld beschränkt bleiben. Dieses wird als ein aus 2 Kurvenscharen bestehendes Netz dargestellt: Stromlinien und Äquipotentiallinien (kurz: Potentiallinien. (Tatsächlich bestände im Raum das Netz aus sog. Potential- und Stromfächen. Die Beschränkung auf eine zur Strömung parallele Ebene ist berechtigt, wenn die Geschwindigkeiten in allen auf einer Normalen zu dieser Ebene liegenden Punkten die gleiche ist). Büsching, F.: Stauanlagenbau 2000/05.3
4 Die mathematische Grundlage stellen die Laplace schen Potentialgleichungen 2 2 δ ϕ δ ϕ ϕ = + = 0 (Potentialfunktion) 2 2 δx δy und ψ = 2 2 δ ψ δ ψ + = 2 2 δx δy 0 (Stromfunktion) zusammen mit den Cauchy-Riemann schen Differentialgleichungen dar: v x δϕ = δx δψ, δy = v y = δϕ δψ = δy δx Näheres z.b. bei Böss, Paul (1938). Büsching, F.: Stauanlagenbau 2000/05.4
5 Die Lösung der Strömungsaufgabe besteht darin, die partiellen Differentialgleichungen den jeweiligen Randbedingungen anzupassen in der Art, dass das Strömungsfeld durch Kurvenscharen von Strom- und Potentiallinien als orthogonale Trajektorien beschrieben wird. Diese Aufgabe ist nun - trotz der dafür entwickelten Theorie der Konformen Abbildungen (vergl. Betz) - nur für wenige Sonderfälle geschlossen lösbar. Selbst Näherungslösungen sind in der Praxis kaum anwendbar. Die mathematischen Schwierigkeiten der Potentialtheorie können aber umgangen werden: Es wird die Tatsache ausgenutzt, dass sich oft unterschiedliche physikalische Prozesse mit gleichen Differentialgleichungen beschreiben lassen, d.h., dass diese eine gleiche mathematische Struktur aufweisen. Im vorliegenden Falle besteht eine Analogie zwischen der Potentialströmung und dem elektrischen Stromfeld in einem Leiter, der für den ebenen Fall ein dünnes Widerstandspapier sein kann, vergleiche weiter unten. Büsching, F.: Stauanlagenbau 2000/05.5
6 Vertikalschnitt durch eine Überfallströmung an einem scharfkantigen Wehr: Potentialnetz Büsching, F.: Stauanlagenbau 2000/05.6
7 Grundsätze der Potentialströmungen 1. Stromlinien sind Bahnlinien der Flüssigkeitsteilchen, Tangentenrichtungen geben die Richtung der Strömungsgeschwindigkeit an. 2. Jede Berandung eines Strömungsfeldes stellt selbst eine Stromlinie (Randstromlinie) dar. Die Aufgabe besteht im allgemeinen darin, bei vorgegebener Berandung zwischen den Randstromlinien das Strömungsfeld (unter Verwendung besonderer (verschiedener) Verfahren) durch weitere Stromlinien und Potentiallinien nach Geschwindigkeits- und Druckverhältnissen zu beschreiben. 3. Zwischen benachbarten Stromlinien eines Strömungsfeldes fließt jeweils die gleiche Teilmenge Q ab. Gesamtabfluss Q = n. Q mit n = Anzahl der Stromlinienabstände. Ein "Stromfaden" wird räumlich von einer Stromröhre umschlossen. Büsching, F.: Stauanlagenbau 2000/05.7
8 Entsprechend dem Satz von der Erhaltung der Masse (Kontinuitätsgleichung) wird die Strömungsgeschwindigkeit um so größer, je enger der Stromlinienabstand - und umgekehrt. 4. Wird der jeweilige Abstand der Stromlinien senkrecht zu den Stromlinien aufgetragen, so entstehen in der Ebene Potentialinien (im Raum: Potentialflächen). 5. Ein durch Strom- und (Äqui-) Potentiallinien darstellbares Strömungsfeld kann als die ebene Projektion einer räumlichen Fläche (Topographische Karte) gedeutet werden, in der die Stromlinien ψ = konst. = Fallinien und die Potentiallinien ϕ = konst. = Höhenschichtlinien sind. Zwischen Höhenschichtlinien besteht der Potentialunterschied dϕ, zwischen Fallinien besteht der Unterschied dψ. Die Strömungsgeschwindigkeit ist dann v = dϕ/ds mit s in Strömungsrichtung (= normal zur Potentiallinie). Büsching, F.: Stauanlagenbau 2000/05.8
9 6. Sowohl aus der Anwendung der Kontinuitätsgleichung mit Bezug auf den Abstand der Stromlinien als auch aus der Anwendung des Drallsatzes (v 1. r 1 = v 2. r 2 ) mit Bezug auf den Abstand der Potentiallinien folgt, dass die Strömungsgeschwindigkeit v den Maschenseiten ds umgekehrt proportional ist. In praktischen Fällen werden Strom- und Potentiallinienabstände gleichgesetzt, so dass sich ein Netz verzerrter Quadrate ergibt. Ist die Strömungsgeschwindigkeit an einer Stelle bekannt, kann die Geschwindigkeitsverteilung des Feldes aus der Geometrie ermittelt werden. 7. Strom- und Potentiallinien sind vertauschbar. Jedes Stromund Potentialliniennetz ist vierdeutig. (Z.B.: Quelle, Senke, rechts- oder linksdrehender Potentialwirbel). Büsching, F.: Stauanlagenbau 2000/05.9
10 Senke rechtsdrehend v = konst. r Potentialwirbel Quelle v = ± konst. r v = + konst. r linksdrehend Singulärer Punkt: r = 0 v Büsching, F.: Stauanlagenbau 2000/05.10
11 8. Potentialströmungen werden überlagert durch vektorielle Addition ihrer Strömungsgeschwindigkeiten. Neues Strömungsbild 9. Potentiallinien sind im allgemeinen nicht Linien gleichen Druckes (Folge aus 7.). Sie liefern durch das von ihnen bewirkte geodätische Gefälle Größe und Richtung der Geschwindigkeit. Nur bei Sickerströmungen sind Potentiallinien auch Linien gleichen Druckes. 10.Für den Fall, dass sich die Strömung infolge von Reibung und Trägheit von der Berandung ablöst (turbulente Wirbelzonen), ist eine Behandlung auf der Grundlage der Potentialtheorie selbstverständlich nicht mehr gerechtfertigt. Büsching, F.: Stauanlagenbau 2000/05.11
12 Büsching, F.: Stauanlagenbau 2000/05.12
13 Elektro-Analogie In Analogie zur Potentialströmung folgt der elektrische Strom in einem elektrischen Leiter der Richtung des Spannungsgefälles und die Stromlinien stehen senkrecht auf den Linien gleicher Spannung. Nach dem OHM' sehen Gesetz gilt (Spannung = Widerstand x Stromstärke) du Der Differentialquotient für den Strom lautet demnach: I = dr Der =OHM sche Widerstand des Leiters der Länge ds ist: dr = 1 c U 1 ds A mit c = Leitfähigkeitskonstante, A = Leiterquerschnitt und ds = Längenelement. = R I Büsching, F.: Stauanlagenbau 2000/05.13
14 Es ergibt sich die Analogie zwischen elektrischem Strom und der Strömung wie folgt: Der elektrische Strom: Strömung: du I = c A ds dϕ Q = A v = A ds Q ist analog I A ist analog A dϕ ds ist analog du ds c ist dabei eine unwesentliche Maßstabskonstante. Büsching, F.: Stauanlagenbau 2000/05.14
15 Zur Beschreibung einer ebenen Flüssigkeitsbewegung genügt eine beliebige zur Strömung parallele Ebene, da in allen auf einer Normalen zu dieser Ebene liegenden Punkten dieselbe Geschwindigkeit herrscht. Dementsprechend kann bei dem Elektro-Analogie-Verfahren ein flächenhafter Leiter verwendet werden, d.h., etwa ein Blech. Heute wird ein leitfähiges Papier (Widerstandspapier) verwendet. Linien gleicher Spannung werden als Äquipotentiallinien auf dem Modell eingemessen. Büsching, F.: Stauanlagenbau 2000/05.15
16 Zur Einmessung der Strom- oder Potentiallinien wird die WHEATSTONE sche WIDERSTANDSSCHALTUNG ( Brückenschaltung verwendet, die in der Elektrotechnik zur Messung von elektrischen (Ohm schen) Widerständen dient. Für den Fall dass 4 Widerstände in der gezeigten Formation zusammengeschaltet sind, ist keine Potentialdifferenz (Spannungsdifferenz) zwischen A und B messbar, wenn R 1 = R 2 R R 3 4 = Büsching, F.: Stauanlagenbau 2000/05.16
17 Das Modell entspricht dem einen aus 2 Widerständen R 1 + R 2 bestehenden Potentiometer, während R 3 + R 4 ein Messpotentiometer darstellt. Modell Büsching, F.: Stauanlagenbau 2000/05.17
18 Einmessung der Stromlinien zwischen zwei Randstromlinien: z.b. Flussufer. Büsching, F.: Stauanlagenbau 2000/05.18
19 Schema Modell eines Flussabschnittes mit einer Insel, deren Umströmung vorgegeben sei. Büsching, F.: Stauanlagenbau 2000/05.19
20 Büsching, F.: Stauanlagenbau 2000/05.20
21 Büsching, F.: Stauanlagenbau 2000/05.21
22 Büsching, F.: Stauanlagenbau 2000/05.22
23 Büsching, F.: Stauanlagenbau 2000/05.23
24 Elektro-Analog-Modelle: Unterströmung zweier unterschiedlicher Bauformen von Talsperrentiefschützen (mit und ohne Strahlleitblech). Büsching, F.: Stauanlagenbau 2000/05.24
25 Aufgabe: Aus dem im Grundriss dargestellten Fluss (Abfluss Q = 100 m 3 /s) sollen an der Stelle A 60 m 3 /s entnommen werden. Davon werden nach Gebrauch 30 m 3 /s bei B und 20 m 3 /s bei C wieder in den Fluss eingeleitet, während 10 m 3 /s anderweitig verwendet werden. A. Welche Gestalt hat das Stromlinienbild? B. Wie müssten die Elektroden eines Elektroanalogmodells angeordnet und geschaltet werden, mit dem das Stromlinienbild ermittelt werden kann? Büsching, F.: Stauanlagenbau 2000/05.25
26 Büsching, F.: Stauanlagenbau 2000/05.26
15 Eindimensionale Strömungen
 97 Durch Druckunterschiede entstehen Strömungen, die sich auf unterschiedliche Weise beschreiben lassen. Bei der Lagrange schen oder materiellen Beschreibung betrachtet man das einelne Fluidteilchen, das
97 Durch Druckunterschiede entstehen Strömungen, die sich auf unterschiedliche Weise beschreiben lassen. Bei der Lagrange schen oder materiellen Beschreibung betrachtet man das einelne Fluidteilchen, das
Strömung im Grundwasser II - Potentialströmungen
 Strömung im Grundwasser II - Potentialströmungen Matthias Willmann, Joaquin Jimenez-Martinez, Wolfgang Kinzelbach HS2016 / Grundwasser 1 / Potentialströmung 1 Potentialströmungen Potentialströmung: v Stationäre
Strömung im Grundwasser II - Potentialströmungen Matthias Willmann, Joaquin Jimenez-Martinez, Wolfgang Kinzelbach HS2016 / Grundwasser 1 / Potentialströmung 1 Potentialströmungen Potentialströmung: v Stationäre
2. Potentialströmungen
 2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
2. Potentialströmungen Bei der Umströmung schlanker Körper ist Reibung oft nur in einer dünnen Schicht um den Körper signifikant groß. Erinnerung: Strömung um ein zweidimensionales Tragflügelprofil: 1
Hydraulik für Bauingenieure
 Hydraulik für Bauingenieure Grundlagen und Anwendungen von Robert Freimann 1. Auflage Hydraulik für Bauingenieure Freimann schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser
Hydraulik für Bauingenieure Grundlagen und Anwendungen von Robert Freimann 1. Auflage Hydraulik für Bauingenieure Freimann schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser
Potentialströmung und Magnuseffekt
 Potentialströmung und Magnuseffekt (Zusammengefasst und ergänzt nach W Albring, Angewandte Strömungslehre, Verlag Theodor Steinkopff, Dresden, 3 Aufl 1966) Voraussetzungen Behandelt werden reibungs und
Potentialströmung und Magnuseffekt (Zusammengefasst und ergänzt nach W Albring, Angewandte Strömungslehre, Verlag Theodor Steinkopff, Dresden, 3 Aufl 1966) Voraussetzungen Behandelt werden reibungs und
Kontrollfragen. Hydrodynamik. Stephan Mertens. 6. Juli 2013 G N D O O
 Kontrollfragen Hydrodynamik Stephan Mertens 6. Juli 2013 UE R ICKE UNI VERSITÄT MAG G N VO D O TT O EBURG 1 Einführung und Motivation 1. Erläutern Sie die Lagrange sche und die Euler sche Darstellung
Kontrollfragen Hydrodynamik Stephan Mertens 6. Juli 2013 UE R ICKE UNI VERSITÄT MAG G N VO D O TT O EBURG 1 Einführung und Motivation 1. Erläutern Sie die Lagrange sche und die Euler sche Darstellung
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Definition Elektrisches Strömungsfeld in einem Zylinder eines Punktes einer Linie Elektrische Spannung und Widerstand Grenzbedingungen
 Definition Elektrisches Strömungsfeld in einem Zylinder eines Punktes einer Linie Elektrische Spannung und Widerstand Grenzbedingungen 1 Feldbegriff Feld räumliche Verteilung einer physikalischen Größe
Definition Elektrisches Strömungsfeld in einem Zylinder eines Punktes einer Linie Elektrische Spannung und Widerstand Grenzbedingungen 1 Feldbegriff Feld räumliche Verteilung einer physikalischen Größe
1.9. Hydrodynamik Volumenstrom und Massenstrom Die Strömungsgeschwindigkeit
 1.9.1. Volumenstrom und Massenstrom 1.9. Hydrodynamik Strömt eine Flüssigkeit durch ein Gefäss, so bezeichnet der Volumenstrom V an einer gegebenen Querschnittsfläche das durchgeströmte Volumen dv in der
1.9.1. Volumenstrom und Massenstrom 1.9. Hydrodynamik Strömt eine Flüssigkeit durch ein Gefäss, so bezeichnet der Volumenstrom V an einer gegebenen Querschnittsfläche das durchgeströmte Volumen dv in der
Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen
 Technische Universität München Department of Physics Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen Montag Daniel Jost Datum 2/8/212 Aufgabe 1: (a) Betrachten Sie eine Ladung, die im Ursprung
Technische Universität München Department of Physics Ferienkurs - Experimentalphysik 2 - Übungsblatt - Lösungen Montag Daniel Jost Datum 2/8/212 Aufgabe 1: (a) Betrachten Sie eine Ladung, die im Ursprung
Bernoulligleichung. umax. Bernoulligleichung. Stromfadenvorstellung. Bild 1: Stromfaden als Sonderform der Stromröhre
 Bernoulligleichung 1 Bernoulligleichung Stromfadenvorstellung Bild 1: Stromfaden als Sonderform der Stromröhre Im Arbeitsblatt Kontinuitätsgleichung wurde die Stromröhre eingeführt. Sie ist ein Bilanzgebiet
Bernoulligleichung 1 Bernoulligleichung Stromfadenvorstellung Bild 1: Stromfaden als Sonderform der Stromröhre Im Arbeitsblatt Kontinuitätsgleichung wurde die Stromröhre eingeführt. Sie ist ein Bilanzgebiet
PS II - Verständnistest
 Grundlagen der Elektrotechnik PS II - Verständnistest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 4 2 2 5 3 4 4 erreicht Aufgabe 8 9 10 11 Summe Punkte 3 3 3 2 35 erreicht Hinweise:
Grundlagen der Elektrotechnik PS II - Verständnistest 01.03.2011 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 4 2 2 5 3 4 4 erreicht Aufgabe 8 9 10 11 Summe Punkte 3 3 3 2 35 erreicht Hinweise:
Physik-Department. Ferienkurs zur Experimentalphysik 2 - Musterlösung
 Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
Physik-Department Ferienkurs zur Experimentalphysik 2 - Musterlösung Daniel Jost 27/08/13 Technische Universität München Aufgaben zur Magnetostatik Aufgabe 1 Bestimmen Sie das Magnetfeld eines unendlichen
= Dimension: = (Farad)
 Kapazität / Kondensator Ein Kondensator dient zur Speicherung elektrischer Ladung Die Speicherkapazität eines Kondensators wird mit der Größe 'Kapazität' bezeichnet Die Kapazität C ist definiert als: Dimension:
Kapazität / Kondensator Ein Kondensator dient zur Speicherung elektrischer Ladung Die Speicherkapazität eines Kondensators wird mit der Größe 'Kapazität' bezeichnet Die Kapazität C ist definiert als: Dimension:
Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz
 Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz Stephan Huber 19. August 2009 1 Nachtrag zum Drehmoment 1.1 Magnetischer Dipol Ein magnetischer Dipol erfährt
Ferienkurs Elektrodynamik - Drehmomente, Maxwellgleichungen, Stetigkeiten, Ohm, Induktion, Lenz Stephan Huber 19. August 2009 1 Nachtrag zum Drehmoment 1.1 Magnetischer Dipol Ein magnetischer Dipol erfährt
Praktikum Aerodynamik des Flugzeugs
 Praktikum Aerodynamik des Flugzeugs 1. Versuch: Sondenmessungen Betreuer: Dipl.-Ing. Anja Kölzsch Dipl.-Ing. Moritz Grawunder Ziel des heutigen Termins Einführung in die Strömungsmesstechnik Messung verschiedener
Praktikum Aerodynamik des Flugzeugs 1. Versuch: Sondenmessungen Betreuer: Dipl.-Ing. Anja Kölzsch Dipl.-Ing. Moritz Grawunder Ziel des heutigen Termins Einführung in die Strömungsmesstechnik Messung verschiedener
Spule, Kondensator und Widerstände
 Spule, Kondensator und Widerstände Schulversuchspraktikum WS 00 / 003 Jetzinger Anamaria Mat.Nr.: 975576 Inhaltsverzeichnis. Vorwissen der Schüler. Lernziele 3. Theoretische Grundlagen 3. Der elektrische
Spule, Kondensator und Widerstände Schulversuchspraktikum WS 00 / 003 Jetzinger Anamaria Mat.Nr.: 975576 Inhaltsverzeichnis. Vorwissen der Schüler. Lernziele 3. Theoretische Grundlagen 3. Der elektrische
Numerische Strömungssimulation
 Numerische Strömungssimulation Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 1. Teil Zusammenfassung
Numerische Strömungssimulation Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 1. Teil Zusammenfassung
10. Elektrodynamik Das elektrische Potential. ti 10.5 Magnetische Kraft und Felder 1051M Magnetische Kraft
 Inhalt 10. Elektrodynamik 10.3 Das elektrische Potential 10.4 Elektrisches Feld und Potential ti 10.5 Magnetische Kraft und Felder 1051M 10.5.1 Magnetische Kraft 10.3 Das elektrische Potential ti Wir hatten
Inhalt 10. Elektrodynamik 10.3 Das elektrische Potential 10.4 Elektrisches Feld und Potential ti 10.5 Magnetische Kraft und Felder 1051M 10.5.1 Magnetische Kraft 10.3 Das elektrische Potential ti Wir hatten
Rotation, Divergenz und das Drumherum
 Rotation, Divergenz und das Drumherum Eine Einführung in die elektromagnetische Feldtheorie Von Akad. Direktor i. R. Dr.-Ing. Gottlieb Strassacker Universität Fridericiana (TH) Karlsruhe 4., vollständig
Rotation, Divergenz und das Drumherum Eine Einführung in die elektromagnetische Feldtheorie Von Akad. Direktor i. R. Dr.-Ing. Gottlieb Strassacker Universität Fridericiana (TH) Karlsruhe 4., vollständig
Inhaltsverzeichnis. Kurz, G�nther Strà mungslehre, Optik, Elektrizit�tslehre, Magnetismus digitalisiert durch: IDS Basel Bern
 Inhaltsverzeichnis I Strömungslehre 11 1 Ruhende Flüssigkeiten (und Gase) - Hydrostatik 11 1.1 Charakterisierung von Flüssigkeiten 11 1.2 Druck - Definition und abgeleitete 11 1.3 Druckänderungen in ruhenden
Inhaltsverzeichnis I Strömungslehre 11 1 Ruhende Flüssigkeiten (und Gase) - Hydrostatik 11 1.1 Charakterisierung von Flüssigkeiten 11 1.2 Druck - Definition und abgeleitete 11 1.3 Druckänderungen in ruhenden
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 1. Teil Zusammenfassung 1. Teil
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 1. Teil Zusammenfassung 1. Teil
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 09. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 09. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 09. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 09. 06.
31 Die Potentialgleichung
 3 Die Potentialgleichung Die Potentialgleichung oder auch Poisson-Gleichung ist die lineare Gleichung zweiter Ordnung u = f in einem Gebiet R n. Im homogenen Fall f = 0 spricht man auch von der Laplace-
3 Die Potentialgleichung Die Potentialgleichung oder auch Poisson-Gleichung ist die lineare Gleichung zweiter Ordnung u = f in einem Gebiet R n. Im homogenen Fall f = 0 spricht man auch von der Laplace-
Vorlesung STRÖMUNGSLEHRE Zusammenfassung
 Lehrstuhl für Fluiddynamik und Strömungstechnik Vorlesung STRÖMUNGSLEHRE Zusammenfassung WS 008/009 Dr.-Ing. Jörg Franke Bewegung von Fluiden ( Flüssigkeiten und Gase) - Hydro- und Aerostatik > Druckverteilung
Lehrstuhl für Fluiddynamik und Strömungstechnik Vorlesung STRÖMUNGSLEHRE Zusammenfassung WS 008/009 Dr.-Ing. Jörg Franke Bewegung von Fluiden ( Flüssigkeiten und Gase) - Hydro- und Aerostatik > Druckverteilung
Elektrolytischer Trog
 Elektrotechnisches Grundlagen-Labor I Elektrolytischer Trog Versuch Nr. 10 Erforderliche Geräte Anzahl Bezeichnung, Daten GL-Nr. 1 elektrolytischer Trog mit Messeinrichtung 1 kleine Wanne zur κ-messung
Elektrotechnisches Grundlagen-Labor I Elektrolytischer Trog Versuch Nr. 10 Erforderliche Geräte Anzahl Bezeichnung, Daten GL-Nr. 1 elektrolytischer Trog mit Messeinrichtung 1 kleine Wanne zur κ-messung
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]
![3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P]](/thumbs/56/38171884.jpg) 3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
3.7 Gesetz von Biot-Savart und Ampèresches Gesetz [P] B = µ 0 I 4 π ds (r r ) r r 3 a) Beschreiben Sie die im Gesetz von Biot-Savart vorkommenden Größen (rechts vom Integral). b) Zeigen Sie, dass das Biot-Savartsche
Rotation, Divergenz und Gradient
 Gottlieb Strassacker, Roland Süße Rotation, Divergenz und Gradient Einführung in die elektromagnetische Feldtheorie 6. durchgesehene und ergänzte Auflage Mit 151 Abbildungen, 17 Tabellen und 70 Beispielen
Gottlieb Strassacker, Roland Süße Rotation, Divergenz und Gradient Einführung in die elektromagnetische Feldtheorie 6. durchgesehene und ergänzte Auflage Mit 151 Abbildungen, 17 Tabellen und 70 Beispielen
Grundlagen der Strömungsmechanik
 Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
Elektromagnetische Schwingkreise
 Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
VIII.1.4 Magnetisches Feld induziert durch einfache Ladungsströme
 V. Grundbegriffe und -ergebnisse der Magnetostatik 5 V..4 Magnetisches Feld induziert durch einfache Ladungsströme m Fall eines Ladungsstroms durch einen dünnen Draht vereinfacht sich das ntegral im Biot
V. Grundbegriffe und -ergebnisse der Magnetostatik 5 V..4 Magnetisches Feld induziert durch einfache Ladungsströme m Fall eines Ladungsstroms durch einen dünnen Draht vereinfacht sich das ntegral im Biot
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik
 D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
Einführung in die Strömungsmechanik
 Einführung in die Strömungsmechanik Rolf Radespiel Fluideigenschaften Grundlegende Prinzipien und Gleichungen Profile Windkanal und Druckmessungen BRAUNSCHWEIG, 5. JUNI 2002 Was versteht man unter Strömungsmechanik?
Einführung in die Strömungsmechanik Rolf Radespiel Fluideigenschaften Grundlegende Prinzipien und Gleichungen Profile Windkanal und Druckmessungen BRAUNSCHWEIG, 5. JUNI 2002 Was versteht man unter Strömungsmechanik?
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 02/2002 Laborunterlagen
 Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Institut für Elektrotechnik Übungen zu Elektrotechnik I Version 3.0, 0/00 7 Magnetismus 7. Grundlagen magnetischer Kreise Im folgenden wird die Vorgehensweise bei der Untersuchung eines magnetischen Kreises
Elektromagnetische Felder und Wellen: Lösung zur Klausur
 Elektromagnetische Felder und Wellen: zur Klausur 2014-2 1 Aufgabe 1 ( 7 Punkte) Eine ebene Welle der Form E = (E x, ie x, 0) exp{i(kz + ωt)} trifft aus dem Vakuum bei z = 0 auf ein Medium mit ε = 6 und
Elektromagnetische Felder und Wellen: zur Klausur 2014-2 1 Aufgabe 1 ( 7 Punkte) Eine ebene Welle der Form E = (E x, ie x, 0) exp{i(kz + ωt)} trifft aus dem Vakuum bei z = 0 auf ein Medium mit ε = 6 und
Grundlagen der Hydraulik
 Horst-W. Grollius Grundlagen der Hydraulik 7., aktualisierte Auflage 18 2 Physikalisches Basiswissen Bei der Bewegung des Kolbens 1umden Weg s 1 nach unten wird das Volumen V 1 ¼ A 1 s 1 verdr ngt, wodurch
Horst-W. Grollius Grundlagen der Hydraulik 7., aktualisierte Auflage 18 2 Physikalisches Basiswissen Bei der Bewegung des Kolbens 1umden Weg s 1 nach unten wird das Volumen V 1 ¼ A 1 s 1 verdr ngt, wodurch
PHYSIK. HYDROMECHANIK Statik, Dynamik, Kinematik der Flüssigkeiten ANGEWANDTE HYDROMECHANIK. HYDRAULIK Rohrleitung, Gerinne Eindimensionale Strömung
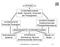 PHYSIK HYDROMECHANIK Statik, Dynamik, Kinematik der Flüssigkeiten HYDROSTATIK Ruhende Flüssigkeit HYDRODYNAMIK Dreidimensionale Flüssigkeitsbewegung ANGEWANDTE HYDROMECHANIK Hydrostatische Systeme HYDRAULIK
PHYSIK HYDROMECHANIK Statik, Dynamik, Kinematik der Flüssigkeiten HYDROSTATIK Ruhende Flüssigkeit HYDRODYNAMIK Dreidimensionale Flüssigkeitsbewegung ANGEWANDTE HYDROMECHANIK Hydrostatische Systeme HYDRAULIK
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
IK Induktion. Inhaltsverzeichnis. Sebastian Diebold, Moritz Stoll, Marcel Schmittfull. 25. April Einführung 2
 IK Induktion Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfelder....................... 2 2.2 Spule............................ 2
IK Induktion Blockpraktikum Frühjahr 2007 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Magnetfelder....................... 2 2.2 Spule............................ 2
ELEKTRISCHE SPANNUNGSQUELLEN
 Physikalisches Grundpraktikum I Versuch: (Versuch durchgeführt am 17.10.2000) ELEKTRISCHE SPANNUNGSQUELLEN Denk Adelheid 9955832 Ernst Dana Eva 9955579 Linz, am 22.10.2000 1 I. PHYSIKALISCHE GRUNDLAGEN
Physikalisches Grundpraktikum I Versuch: (Versuch durchgeführt am 17.10.2000) ELEKTRISCHE SPANNUNGSQUELLEN Denk Adelheid 9955832 Ernst Dana Eva 9955579 Linz, am 22.10.2000 1 I. PHYSIKALISCHE GRUNDLAGEN
Induktion. Die in Rot eingezeichnete Größe Lorentzkraft ist die Folge des Stromflusses im Magnetfeld.
 Induktion Die elektromagnetische Induktion ist der Umkehrprozess zu dem stromdurchflossenen Leiter, der ein Magnetfeld erzeugt. Bei der Induktion wird in einem Leiter, der sich in einem Magnetfeld bewegt,
Induktion Die elektromagnetische Induktion ist der Umkehrprozess zu dem stromdurchflossenen Leiter, der ein Magnetfeld erzeugt. Bei der Induktion wird in einem Leiter, der sich in einem Magnetfeld bewegt,
6.4.8 Induktion von Helmholtzspulen ******
 V648 6.4.8 ****** Motivation Das Induktionsgesetz von Faraday wird mit einer ruhenden Leiterschleife im zeitabhängigen B-Feld und mit einer bewegten Leiterschleife im stationären B-Feld untersucht. 2 Experiment
V648 6.4.8 ****** Motivation Das Induktionsgesetz von Faraday wird mit einer ruhenden Leiterschleife im zeitabhängigen B-Feld und mit einer bewegten Leiterschleife im stationären B-Feld untersucht. 2 Experiment
Sei Φ(x, y, z) ein skalares Feld, also eine Funktion, deren Wert in jedem Raumpunkt definiert ist.
 Beim Differenzieren von Vektoren im Zusammenhang mit den Kreisbewegungen haben wir bereits gesehen, dass ein Vektor als dreiwertige Funktion a(x, y, z) aufgefasst werden kann, die an jedem Punkt im dreidimensionalen
Beim Differenzieren von Vektoren im Zusammenhang mit den Kreisbewegungen haben wir bereits gesehen, dass ein Vektor als dreiwertige Funktion a(x, y, z) aufgefasst werden kann, die an jedem Punkt im dreidimensionalen
4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
 4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
Theoretische Physik II: Quantenmechanik
 Theoretische Physik II: Quantenmechanik Hans-Werner Hammer Marcel Schmidt ([email protected]) Wintersemester 2016/17 Probeklausur 12./13. Januar 2017 Name: Matrikelnummer: Studiengang:
Theoretische Physik II: Quantenmechanik Hans-Werner Hammer Marcel Schmidt ([email protected]) Wintersemester 2016/17 Probeklausur 12./13. Januar 2017 Name: Matrikelnummer: Studiengang:
2. Elektrostatik und Ströme
 2. Elektrostatik und Ströme 2.1. elektrische Ladung, ionische Lösungen Wir haben letztes Semester angeschnitten, dass die meisten Wechselwirkungen elektrischer Natur sind. Jetzt wollen wir elektrische
2. Elektrostatik und Ströme 2.1. elektrische Ladung, ionische Lösungen Wir haben letztes Semester angeschnitten, dass die meisten Wechselwirkungen elektrischer Natur sind. Jetzt wollen wir elektrische
Die Parallelschaltung elektrischer Widerstände
 Kapitel 5 Die Parallelschaltung elektrischer Widerstände Wie verteilt sich eigentlich der elektrische Strom an einem Knoten? Wodurch wird festgelegt, durch welche Teile einer verzweigten Schaltung viel
Kapitel 5 Die Parallelschaltung elektrischer Widerstände Wie verteilt sich eigentlich der elektrische Strom an einem Knoten? Wodurch wird festgelegt, durch welche Teile einer verzweigten Schaltung viel
Schaltungen mit mehreren Widerständen
 Grundlagen der Elektrotechnik: WIDERSTANDSSCHALTUNGEN Seite 1 Schaltungen mit mehreren Widerständen 1) Parallelschaltung von Widerständen In der rechten Schaltung ist eine Spannungsquelle mit U=22V und
Grundlagen der Elektrotechnik: WIDERSTANDSSCHALTUNGEN Seite 1 Schaltungen mit mehreren Widerständen 1) Parallelschaltung von Widerständen In der rechten Schaltung ist eine Spannungsquelle mit U=22V und
Elektrizitätslehre und Magnetismus
 Elektrizitätslehre und Magnetismus Othmar Marti 12. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 12. 06.
Elektrizitätslehre und Magnetismus Othmar Marti 12. 06. 2008 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Physik Klassische und Relativistische Mechanik 12. 06.
PN 2 Einführung in die Experimentalphysik für Chemiker
 PN 2 Einführung in die Experimentalphysik für Chemiker 2. Vorlesung 25.4.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
PN 2 Einführung in die Experimentalphysik für Chemiker 2. Vorlesung 25.4.08 Evelyn Plötz, Thomas Schmierer, Gunnar Spieß, Peter Gilch Lehrstuhl für BioMolekulare Optik Department für Physik Ludwig-Maximilians-Universität
Experimentelle Hydromechanik Wehrüberfall und Ausfluss am Planschütz
 UNIVERSITÄT DER BUNDESWEHR MÜNCHEN Fakultät für Bauingenieur- und Vermessungswesen Institut für Wasserwesen Dr.-Ing. H. Kulisch Universitätsprofessor Dr.-Ing. Andreas Malcherek Hydromechanik und Wasserbau
UNIVERSITÄT DER BUNDESWEHR MÜNCHEN Fakultät für Bauingenieur- und Vermessungswesen Institut für Wasserwesen Dr.-Ing. H. Kulisch Universitätsprofessor Dr.-Ing. Andreas Malcherek Hydromechanik und Wasserbau
Physik. Abiturwiederholung. Das Elektrische Feld
 Das Elektrische Feld Strom Strom ist bewegte Ladung, die Stromstärke ergibt sich also als Veränderung der Ladung nach der Zeit, also durch die Ableitung. Somit kann man die Ladung als Fläche betrachten,
Das Elektrische Feld Strom Strom ist bewegte Ladung, die Stromstärke ergibt sich also als Veränderung der Ladung nach der Zeit, also durch die Ableitung. Somit kann man die Ladung als Fläche betrachten,
Praktikum II TR: Transformator
 Praktikum II TR: Transformator Betreuer: Dr. Torsten Hehl Hanno Rein [email protected] Florian Jessen [email protected] 30. März 2004 Made with L A TEX and Gnuplot Praktikum
Praktikum II TR: Transformator Betreuer: Dr. Torsten Hehl Hanno Rein [email protected] Florian Jessen [email protected] 30. März 2004 Made with L A TEX and Gnuplot Praktikum
V. Ähnlichkeitsgesetze und dimensionslose Kennwerte
 V. Ähnlichkeitsgesetze und dimensionslose Kennwerte Die Entwicklung großer hydraulischer Strömungsmaschinen wird am Modell durchgeführt. Weitere Beispiel: Ausnahme: Autos, Flugzeuge, Schiffe Kleine Maschinen,
V. Ähnlichkeitsgesetze und dimensionslose Kennwerte Die Entwicklung großer hydraulischer Strömungsmaschinen wird am Modell durchgeführt. Weitere Beispiel: Ausnahme: Autos, Flugzeuge, Schiffe Kleine Maschinen,
Numerische Strömungsberechnungen mit NX Herausforderungen und Lösungen bei Durchströmungs- und Umströmungs-Vorgängen
 CAE Herbsttagung 2013 Numerische Strömungsberechnungen mit NX Herausforderungen und Lösungen bei Durchströmungs- und Umströmungs-Vorgängen Prof. Dr.-Ing. Alexander Steinmann Dr. Binde Ingenieure Design
CAE Herbsttagung 2013 Numerische Strömungsberechnungen mit NX Herausforderungen und Lösungen bei Durchströmungs- und Umströmungs-Vorgängen Prof. Dr.-Ing. Alexander Steinmann Dr. Binde Ingenieure Design
3.5.6 Geschwindigkeitsprofil (Hagen-Poiseuille) ******
 3.5.6 ****** 1 Motivation Bei der Strömung einer viskosen Flüssigkeit durch ein Rohr ergibt sich ein parabolisches Geschwindigkeitsprofil. 2 Experiment Abbildung 1: Versuchsaufbau zum Der Versuchsaufbau
3.5.6 ****** 1 Motivation Bei der Strömung einer viskosen Flüssigkeit durch ein Rohr ergibt sich ein parabolisches Geschwindigkeitsprofil. 2 Experiment Abbildung 1: Versuchsaufbau zum Der Versuchsaufbau
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
PS II - Verständnistest 24.02.2010
 Grundlagen der Elektrotechnik PS II - Verständnistest 24.02.2010 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 3 4 2 2 1 5 2 erreicht Aufgabe 8 9 10 11 12 Summe Punkte 4 2 3 3 4 35 erreicht Hinweise:
Grundlagen der Elektrotechnik PS II - Verständnistest 24.02.2010 Name, Vorname Matr. Nr. Aufgabe 1 2 3 4 5 6 7 Punkte 3 4 2 2 1 5 2 erreicht Aufgabe 8 9 10 11 12 Summe Punkte 4 2 3 3 4 35 erreicht Hinweise:
Widerstände. Schulversuchspraktikum WS 2000/2001 Redl Günther und 7.Klasse. Inhaltsverzeichnis:
 Schulversuchspraktikum WS 2000/2001 Redl Günther 9655337 Widerstände 3. und 7.Klasse Inhaltsverzeichnis: 1) Vorraussetzungen 2) Lernziele 3) Verwendete Quellen 4) Ohmsches Gesetz 5) Spezifischer Widerstand
Schulversuchspraktikum WS 2000/2001 Redl Günther 9655337 Widerstände 3. und 7.Klasse Inhaltsverzeichnis: 1) Vorraussetzungen 2) Lernziele 3) Verwendete Quellen 4) Ohmsches Gesetz 5) Spezifischer Widerstand
5 Der Gaußsche und Stokes sche Integralsatz
 HM III = MATH III FT 2013 50 5 Der Gaußsche und Stokes sche Integralsatz Der Gaußsche Integralsatz umgangssprachlich am eispiel strömender Flüssigkeiten: Die Flüssigkeitsmenge, die durch die Oberfläche
HM III = MATH III FT 2013 50 5 Der Gaußsche und Stokes sche Integralsatz Der Gaußsche Integralsatz umgangssprachlich am eispiel strömender Flüssigkeiten: Die Flüssigkeitsmenge, die durch die Oberfläche
Aufgabe 1 ( 3 Punkte)
 Elektromagnetische Felder und Wellen: Klausur 2016-2 1 Aufgabe 1 ( 3 Punkte) Welche elektrische Feldstärke benötigt man, um ein Elektron (Masse m e, Ladung q = e) im Schwerefeld der Erde schweben zu lassen?
Elektromagnetische Felder und Wellen: Klausur 2016-2 1 Aufgabe 1 ( 3 Punkte) Welche elektrische Feldstärke benötigt man, um ein Elektron (Masse m e, Ladung q = e) im Schwerefeld der Erde schweben zu lassen?
Technische Universität München Zentrum Mathematik. Übungsblatt 11
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Lineare Quellen. Martin Schlup. 7. Februar 2014
 Lineare Quellen Martin Schlup 7. Februar 204. Ideale Quellen Ideale Quellen sind Modelle mit Eigenschaften, die in Wirklichkeit nur näherungsweise realisiert werden können. Ideale Quellen sind z. B. in
Lineare Quellen Martin Schlup 7. Februar 204. Ideale Quellen Ideale Quellen sind Modelle mit Eigenschaften, die in Wirklichkeit nur näherungsweise realisiert werden können. Ideale Quellen sind z. B. in
Theoretischen Physik II SS 2007 Klausur II - Aufgaben und Lösungen
 Theoretischen Physik II SS 007 Klausur II - Aufgaben und Lösungen Aufgabe Hohlleiter Gegeben sei ein in z-richtung unendlich langer, gerader Hohlleiter (Innenradius R/3, Außenradius R), der einen Stromfaden
Theoretischen Physik II SS 007 Klausur II - Aufgaben und Lösungen Aufgabe Hohlleiter Gegeben sei ein in z-richtung unendlich langer, gerader Hohlleiter (Innenradius R/3, Außenradius R), der einen Stromfaden
Magnetische Induktion Φ = Der magnetische Fluss Φ durch eine Fläche A ist definiert als
 E8 Magnetische Induktion Die Induktionsspannung wird in Abhängigkeit von Magnetfeldgrößen und Induktionsspulenarten untersucht und die Messergebnisse mit den theoretischen Voraussagen verglichen.. heoretische
E8 Magnetische Induktion Die Induktionsspannung wird in Abhängigkeit von Magnetfeldgrößen und Induktionsspulenarten untersucht und die Messergebnisse mit den theoretischen Voraussagen verglichen.. heoretische
I. Bezeichnungen und Begriffe
 UniversitätPOsnabrück Fachbereich Physik Vorlesung Elektronik 1 Dr. W. Bodenberger 1. Einige Bezeichnungen und Begriffe I. Bezeichnungen und Begriffe Spannung: Bezeichnung: u Signalspannung U Versorgungsspannung
UniversitätPOsnabrück Fachbereich Physik Vorlesung Elektronik 1 Dr. W. Bodenberger 1. Einige Bezeichnungen und Begriffe I. Bezeichnungen und Begriffe Spannung: Bezeichnung: u Signalspannung U Versorgungsspannung
Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018)
 Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) 4.1 Begriff
Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) 4.1 Begriff
Aufgabenkatalog ET2 - v12.2. σ 1 σ 2
 2 Strömungsfeld 2.1 Geschichtetes Medium Gegeben ist ein geschichteter Widerstand (Länge 2a) mit quadratischen Platten der Kantenlänge a, der vom Strom durchflossen wird. Der Zwischenraum habe wie eingezeichnet
2 Strömungsfeld 2.1 Geschichtetes Medium Gegeben ist ein geschichteter Widerstand (Länge 2a) mit quadratischen Platten der Kantenlänge a, der vom Strom durchflossen wird. Der Zwischenraum habe wie eingezeichnet
12.1 Fluideigenschaften
 79 Als Fluide bezeichnet man Kontinua mit leicht verschieblichen Teilen. Im Unterschied zu festen Körpern setzen sie langsamen Formänderungen ohne Volumenänderung nur geringen Widerstand entgegen. Entsprechend
79 Als Fluide bezeichnet man Kontinua mit leicht verschieblichen Teilen. Im Unterschied zu festen Körpern setzen sie langsamen Formänderungen ohne Volumenänderung nur geringen Widerstand entgegen. Entsprechend
Vorbereitung zum Versuch
 Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
Vorbereitung zum Versuch elektrische Messverfahren Armin Burgmeier (347488) Gruppe 5 2. Dezember 2007 Messungen an Widerständen. Innenwiderstand eines µa-multizets Die Schaltung wird nach Schaltbild (siehe
Physik I im Studiengang Elektrotechnik
 hysik I im Studiengang Elektrotechnik - Mechanik deformierbarer Körper - rof. Dr. Ulrich Hahn WS 015/016 Deformation Starrer Körper: Kraftwirkung Translation alle Massenpunkte: gleiches Rotation alle Massenpunkte:
hysik I im Studiengang Elektrotechnik - Mechanik deformierbarer Körper - rof. Dr. Ulrich Hahn WS 015/016 Deformation Starrer Körper: Kraftwirkung Translation alle Massenpunkte: gleiches Rotation alle Massenpunkte:
Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG
 3 G8_Physik_2011_Ph11_Loe Seite 1 von 7 Ph 11-1 Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG 1) a) b) - - + + + c) In einem Homogenen elektrischen Feld nimmt das Potential in etwa linear. D.h. Es sinkt
3 G8_Physik_2011_Ph11_Loe Seite 1 von 7 Ph 11-1 Physik G8-Abitur 2011 Aufgabenteil Ph 11 LÖSUNG 1) a) b) - - + + + c) In einem Homogenen elektrischen Feld nimmt das Potential in etwa linear. D.h. Es sinkt
3.4 Magnetfelder. µ im Magnetfeld Æ B ein Drehmoment. M = Æ µ Æ B.
 - 151-3.4 Magnetfelder 3.4.1 Grundlagen Während die Wechselwirkungen zwischen statischen elektrischen Ladungen sich durch das Coulomb'sche Gesetz, resp. ein elektrisches Feld beschreiben lassen, treten
- 151-3.4 Magnetfelder 3.4.1 Grundlagen Während die Wechselwirkungen zwischen statischen elektrischen Ladungen sich durch das Coulomb'sche Gesetz, resp. ein elektrisches Feld beschreiben lassen, treten
2 Das elektrostatische Feld
 Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts
 9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
Kapitel 1. Kleinsignalparameter
 Kapitel 1 Kleinsignalparameter Der Name analoge Schaltung drückt aus, dass das Ausgangssignal dieser Schaltung immer stufenlos dem Eingangssignal folgt, d. h. in irgendeiner Form eine Proportionalität
Kapitel 1 Kleinsignalparameter Der Name analoge Schaltung drückt aus, dass das Ausgangssignal dieser Schaltung immer stufenlos dem Eingangssignal folgt, d. h. in irgendeiner Form eine Proportionalität
Höhere Mathematik für Ingenieure
 Burg/Haf/Wille Höhere Mathematik für Ingenieure Band IV Vektoranalysis und Funktionentheorie Von Prof. Dr. rer. nat. Herbert Haf und Prof. Dr. rer. nat. Friedrich Wille Universität Kassel, Gesamthochschule
Burg/Haf/Wille Höhere Mathematik für Ingenieure Band IV Vektoranalysis und Funktionentheorie Von Prof. Dr. rer. nat. Herbert Haf und Prof. Dr. rer. nat. Friedrich Wille Universität Kassel, Gesamthochschule
10.1 Ampère sches Gesetz und einfache Stromverteilungen
 1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
1 Magnetostatik Solange keine Verwechslungen auftreten, werden wir in diesem und in den folgenden Kapiteln vom magnetischen Feld B an Stelle der magnetischen Induktion bzw. der magnetischen Flußdichte
3 Lineare Differentialgleichungen
 3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde. Sommersemester VL #19 am
 Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 007 VL #9 am 30.05.007 Vladimir Dyakonov Leistungsbeträge 00 W menschlicher Grundumsatz 00 kw PKW-Leistung
Einführung in die Physik II für Studierende der Naturwissenschaften und Zahnheilkunde Sommersemester 007 VL #9 am 30.05.007 Vladimir Dyakonov Leistungsbeträge 00 W menschlicher Grundumsatz 00 kw PKW-Leistung
Pfui Teufel, ein widerlicher Österreicherwitz! So etwas könnte sich tatsächlich zugetragen haben. Begründung: Antwort richtig nur mit Begründung!
 Musterprüfung: 1. Was ist ein Faradayscher Käfig? 2. Millikan fand auf einem Öltröpfchen eine Ladung Q von 8 10-19 C. Wie gross war die Ladung des Öltröpfchens wahrscheinlich auf vier signifikante Ziffern
Musterprüfung: 1. Was ist ein Faradayscher Käfig? 2. Millikan fand auf einem Öltröpfchen eine Ladung Q von 8 10-19 C. Wie gross war die Ladung des Öltröpfchens wahrscheinlich auf vier signifikante Ziffern
Exakte Differentialgleichungen
 Exakte Differentialgleichungen M. Vock Universität Heidelberg Seminar Mathematische Modellierung am 11.11.2008 Gliederung Differentialgleichungen eine erste Begegnung Definition Gewöhnliche DGL Die exakte
Exakte Differentialgleichungen M. Vock Universität Heidelberg Seminar Mathematische Modellierung am 11.11.2008 Gliederung Differentialgleichungen eine erste Begegnung Definition Gewöhnliche DGL Die exakte
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 12: Integralsätze von Gauss und Stokes Prof. Dr. Erich Walter Farkas Mathematik I+II, 12. Integralsätze 1 / 25 1 Gauss-scher Integralsatz
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 12: Integralsätze von Gauss und Stokes Prof. Dr. Erich Walter Farkas Mathematik I+II, 12. Integralsätze 1 / 25 1 Gauss-scher Integralsatz
11.2. Lineare Differentialgleichungen erster Ordnung
 112 Lineare Differentialgleichungen erster Ordnung Dynamische Entwicklung von Populationen Entwickelt sich eine bestimmte Größe, zb die einer Population oder eines einzelnen Organismus, nicht nur proportional
112 Lineare Differentialgleichungen erster Ordnung Dynamische Entwicklung von Populationen Entwickelt sich eine bestimmte Größe, zb die einer Population oder eines einzelnen Organismus, nicht nur proportional
Elektrizitätslehre 2.
 Elektrizitätslehre. Energieumwandlung (Arbeit) im elektrischen Feld Bewegung einer Ladung gegen die Feldstärke: E s Endposition s Anfangsposition g W F Hub s r F Hub r Fq FHub Eq W qes W ist unabhängig
Elektrizitätslehre. Energieumwandlung (Arbeit) im elektrischen Feld Bewegung einer Ladung gegen die Feldstärke: E s Endposition s Anfangsposition g W F Hub s r F Hub r Fq FHub Eq W qes W ist unabhängig
3. Polarographie. Hamann / Vielstich Prinzip: Voltammetrische Messungen an einer tropfenden Quecksilberelektrode (Heyrowsky 1925)
 3. Polarographie Hamann / Vielstich 1.2.1 Prinzip: Voltammetrische Messungen an einer tropfenden Quecksilberelektrode (Heyrowsky 1925) Warum Quecksilber? Flüssiges Metall: jeder Tropfen hat eine neue reine
3. Polarographie Hamann / Vielstich 1.2.1 Prinzip: Voltammetrische Messungen an einer tropfenden Quecksilberelektrode (Heyrowsky 1925) Warum Quecksilber? Flüssiges Metall: jeder Tropfen hat eine neue reine
IE3. Modul Elektrizitätslehre. Induktion
 IE3 Modul Elektrizitätslehre Induktion In diesem Experiment wird das Phänomen der Induktion untersucht. Bei der Induktion handelt es sich um einen der faszinierendsten Effekte der Elektrizitätslehre. Die
IE3 Modul Elektrizitätslehre Induktion In diesem Experiment wird das Phänomen der Induktion untersucht. Bei der Induktion handelt es sich um einen der faszinierendsten Effekte der Elektrizitätslehre. Die
Divergenz und Rotation von Vektorfeldern
 Divergenz und Rotation von Vektorfeldern Mit Hilfe des Nabla-Operators können nun zwei weitere wichtige elementare Operationen definiert werden, welche formal der Bildung des Skalarproduktes bzw. des äußeren
Divergenz und Rotation von Vektorfeldern Mit Hilfe des Nabla-Operators können nun zwei weitere wichtige elementare Operationen definiert werden, welche formal der Bildung des Skalarproduktes bzw. des äußeren
Physikalische Grundlagen der Aerodynamik
 Physikalische Grundlagen der Aerodynamik Andreas Dillmann 2 2.1 Grundgleichungen der Strömungsmechanik 2.1.1 Erhaltungssätze Physikalische Grundlage der Strömungsmechanik ist die Anwendung der Newtonschen
Physikalische Grundlagen der Aerodynamik Andreas Dillmann 2 2.1 Grundgleichungen der Strömungsmechanik 2.1.1 Erhaltungssätze Physikalische Grundlage der Strömungsmechanik ist die Anwendung der Newtonschen
2 Grundgrößen und -gesetze der Elektrodynamik
 Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
Grundgrößen und -gesetze der Elektrodynamik. Grundgrößen der Elektrodynamik.. Ladung und die dreidimensionale δ-distribution Ladung Q, q Ladungen treten in zwei Variationen auf: positiv und negativ Einheit:
4. Veranstaltung. 16. November 2012
 4. Veranstaltung 16. November 2012 Heute Wiederholung Beschreibung von Bewegung Ursache von Bewegung Prinzip von Elektromotor und Generator Motor Generator Elektrischer Strom Elektrischer Strom Magnetkraft
4. Veranstaltung 16. November 2012 Heute Wiederholung Beschreibung von Bewegung Ursache von Bewegung Prinzip von Elektromotor und Generator Motor Generator Elektrischer Strom Elektrischer Strom Magnetkraft
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Schulinterner Lehrplan Qualifikationsphase Q1. Präambel
 Präambel Dieses Curriculum stellt keinen Maximallehrplan dar, sondern will als offenes Curriculum die Möglichkeit bieten, auf die didaktischen und pädagogischen Notwendigkeiten der Qualifikationsphase
Präambel Dieses Curriculum stellt keinen Maximallehrplan dar, sondern will als offenes Curriculum die Möglichkeit bieten, auf die didaktischen und pädagogischen Notwendigkeiten der Qualifikationsphase
Materialien WS 2014/15 Dozent: Dr. Andreas Will.
 Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will [email protected] Reynoldszahl
Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will [email protected] Reynoldszahl
Biophysik für Pharmazeuten
 Transportprozesse II. III. Diffusion (Volumentransport) (Stofftransport) Biophysik für Pharmazeuten 11. 4. 016. Transportprozesse Elektrischer Strom en I. Elektrischer Strom (el. Ladungstransport) IV.
Transportprozesse II. III. Diffusion (Volumentransport) (Stofftransport) Biophysik für Pharmazeuten 11. 4. 016. Transportprozesse Elektrischer Strom en I. Elektrischer Strom (el. Ladungstransport) IV.
Differentialgleichungen 2. Ordnung
 Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
Differentialgleichungen 2. Ordnung 1-E1 1-E2 Einführendes Beispiel Freier Fall Viele Geschichten ranken sich um den schiefen Turm von Pisa: Der Legende nach hat der aus Pisa stammende Galileo Galilei bei
