4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
|
|
|
- Ingrid Kruse
- vor 7 Jahren
- Abrufe
Transkript
1 4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich, so wird der Körper verzerrt: Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich. Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
2 4. Verzerrungen Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
3 4. Verzerrungen 4.1 Verschiebung und Verzerrung 4.2 Verzerrungstransformation 4.3 Messung der Verzerrungen Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
4 4.1 Verschiebung und Verzerrung Verschiebung: Die Verschiebung der Punkte des Körpers wird durch einen ortsabhängigen Verschiebungsvektor u(p) beschrieben: x P ' =x P +u( x P, y P ) y P ' =y P +v( x P, y P ) y F x(p ' )= x(p)+u(p) P u P' x Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
5 4.1 Verschiebung und Verzerrung Verzerrung: Ein kleines Element des Körpers erfährt eine Translation, eine Rotation und eine Verzerrung. Die Verzerrung führt zu einer Änderung der Form des Elementes: Längenänderungen werden durch Dehnungen beschrieben. P Winkeländerungen werden durch Scherungen beschrieben. P' Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
6 4.1 Verschiebung und Verzerrung Zusammenhang zwischen Verschiebung und Verzerrung: Betrachtet werden drei Punkte P, Q und R auf dem Körper, die so gewählt sind, dass die Strecken PQ und PR parallel zu den Achsen des Koordinatensystems sind. Δy R P R' α P' Δx y Q β x Q' Die Punkte werden durch die Verschiebung auf die Punkte P', Q' und R' abgebildet. Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
7 4.1 Verschiebung und Verzerrung Koordinaten: Unverformt: P : ( x P, y P ) Q : ( x P +Δ x, y P ) R : ( x P, y P +Δ y ) Verformt: P ' : ( x P ', y P ' )=( x P +u( x P, y P ),y P +v ( x P, y P )) Q ' : ( x Q ', y Q ' )=( x P +Δ x+u( x P +Δ x, y P ), y P +v( x P +Δ x, y P )) R ' : ( x R ', y R ' )=( x P +u( x P, y P +Δ y), y P +Δ y+v ( x P, y P +Δ y)) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
8 4.1 Verschiebung und Verzerrung In der Umgebung von Punkt P gilt für die Verschiebungen: u( x P +Δ x, y P )=u( x P, y P )+ u x Δ x v(x P +Δ x,y P )=v( x P,y P )+ v x Δ x u( x P, y P +Δ y)=u( x P, y P )+ u y Δ y v(x P,y P +Δ y)=v (x P, y P )+ v y Δ y Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
9 4.1 Verschiebung und Verzerrung Daraus folgt für die Koordinaten im verformten Zustand: x P ' =x P +u( x P, y P ), y P ' =y P +v( x P, y P ) x Q ' =x P +Δ x +u(x P, y P )+ u x Δ x=x P '+Δ x + u x Δ x y Q ' =y P +v (x P, y P )+ v x Δ x=y P '+ v x Δ x x R ' =x P +u( x P, y P )+ u y Δ y=x P '+ u y Δ y y R' =y P +Δ y+v ( x P, y P )+ v y Δ y=y P '+Δ y+ v y Δ y Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
10 4.1 Verschiebung und Verzerrung Längenänderungen: Länge der Strecke P'Q' : P ' Q ' = ( x Q ' x P ' ) 2 +(y Q ' y P ' ) 2 = ( u 1+ ) 2 + ( v ) 2 Δ x x x Für kleine Verzerrungen gilt: ( v x ) 2 1 Damit folgt: P ' Q ' ( 1+ u x ) Δ x Mit PQ =Δ x gilt für die Dehnung: P ' Q ' PQ ϵ x = = u PQ x Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
11 4.1 Verschiebung und Verzerrung Entsprechend folgt: P ' R ' PR ϵ y = = v PR y Winkeländerung: Für die Änderung des Winkels QPR gilt: Für kleine Winkeländerungen gilt: γ xy =α+β α tan (α)= x R ' x P ' y R ' y P ' = u y Δ y ( v 1+ ) y Δ y u y Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
12 4.1 Verschiebung und Verzerrung Damit gilt für die Scherung: Ergebnis: β tan(β)= y Q ' y P ' = x Q ' x P ' v x Δ x ( 1+ u x ) Δ x v x γ xy = u y + v x Wenn die Verschiebungsgradienten klein sind, gilt für die Verzerrungen: ϵ x = u x, ϵ y= v y, γ xy= u y + v x Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
13 4.1 Verschiebung und Verzerrung Beispiel: Gegeben sind die Verschiebungen u( x, y)=a x+b y v( x,y)=c x+d y Die Verzerrungen berechnen sich zu ϵ x = u x =a, ϵ y= v y =d γ xy = u y + v x =b+c y b d 1 D A = A' D' C B 1 a + b B' c a C' c + d x Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
14 4.2 Verzerrungstransformation Die bisher gefundenen Dehnungen geben an, wie sich die Längen von Strecken entlang der Koordinatenachsen ändern. Die bisher gefundene Scherung beschreibt die Änderung des Winkels zwischen zwei Strecken entlang der beiden Koordinatenachsen. Nun sollen die Dehnungen für beliebig orientierte Strecken und die Scherung für zwei beliebige senkrecht aufeinander stehende Strecken berechnet werden. Die Aufgabe lässt sich durch Umrechnung der Verzerrungen in ein gedrehtes Koordinatensystem lösen. Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
15 4.2 Verzerrungstransformation Drehung des Koordinatensystems: Koordinaten von Punkt P: η y P x=r cos(α), y=r sin(α) ξ=r cos(β), η=r sin(β) r β ξ Mit β = α ϕ folgt: α ϕ x ξ=r cos(α ϕ)=r cos(α)cos(ϕ)+ r sin(α)sin(ϕ) =x cos(ϕ)+y sin(ϕ) η=r sin(α ϕ)=r sin(α)cos(ϕ) r cos(α)sin(ϕ) =y cos(ϕ) x sin(ϕ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
16 4.2 Verzerrungstransformation Die Umrechnung vom gedrehten in das ursprüngliche Koordinatensystem erfolgt mit dem Winkel -ϕ. Damit lauten die Transformationsgleichungen für die Koordinaten: ξ = x cos(ϕ) + y sin(ϕ) η = x sin(ϕ) + y cos(ϕ), Die Komponenten des Verschiebungsvektors berechnen sich aus den Differenzen der Koordinaten. Sie transformieren sich daher wie die Koordinaten: u ξ = u cos(ϕ) + v sin(ϕ) v η = u sin(ϕ) + v cos(ϕ) x = ξ cos(ϕ) ηsin(ϕ) y = ξ sin(ϕ) + η cos(ϕ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
17 4.2 Verzerrungstransformation Ableitungen der Verschiebungen: Zur Berechnung der Verzerrungen im gedrehten System werden die Ableitungen der Verschiebungen im gedrehten System nach ξ und η benötigt: u ξ ξ = u ξ x x ξ + u ξ y y ξ = ( u x + ( u y cos(ϕ)+ v x sin(ϕ) ) cos(ϕ) cos(ϕ)+ v y sin(ϕ) ) sin(ϕ) = u x cos2 (ϕ)+ ( u y + v ) v sin(ϕ)cos(ϕ)+ x y sin2 (ϕ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
18 4.2 Verzerrungstransformation Entsprechend folgt: u ξ η = u y cos2 (ϕ) ( u x v y ) sin(ϕ)cos(ϕ) v x sin2 (ϕ) v η ξ = u y sin 2 (ϕ) ( u x v ) v sin(ϕ)cos(ϕ)+ y x cos2 (ϕ) v η η = u x sin 2 (ϕ) ( u y + v x ) sin(ϕ)cos(ϕ)+ v y cos2 (ϕ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
19 4.2 Verzerrungstransformation Verzerrungen im gedrehten Koordinatensystem: Mit den Beziehungen für die Ableitungen im gedrehten Koordinatensystem und für die Verzerrungen im Ausgangssystem folgt: ϵ ξ = u ξ ξ =ϵ x cos2 (ϕ)+γ xy sin(ϕ)cos(ϕ)+ϵ y sin 2 (ϕ) ϵ η = v η η =ϵ x sin2 (ϕ) γ xy sin(ϕ)cos(ϕ)+ϵ y cos 2 (ϕ) γ ξ η = u ξ η + v η ξ =γ xy (cos 2 (ϕ) sin 2 (ϕ)) 2 ( ϵ x ϵ y ) sin(ϕ)cos(ϕ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
20 4.2 Verzerrungstransformation Mit den trigonometrischen Beziehungen folgt: 2 sin(ϕ)cos(ϕ)=sin(2 ϕ), 2 cos 2 (ϕ)=1+cos(2 ϕ), 2 sin 2 (ϕ)=1 cos(2 ϕ) ϵ ξ = 1 2 ( ϵ x +ϵ y ) ( ϵ x ϵ y ) cos(2ϕ) + γ xy 2 sin(2 ϕ) ϵ η = 1 2 ( ϵ x +ϵ y ) 1 2 ( ϵ x ϵ y ) cos(2ϕ) γ xy sin(2 ϕ) 2 γ ξ η = 1 γ 2 2 ( ϵ x ϵ y )sin(2 ϕ) + xy cos(2 ϕ) 2 Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
21 4.2 Verzerrungstransformation Bemerkungen: Die Dehnung ε ξ beschreibt die Längenänderung einer Strecke, die mit der x-achse den Winkel ϕ einschließt. Die Verzerrungen ε x, ε y und ε xy = γ xy /2 transformieren sich genauso wie die Spannungen. Sie werden als Tensorverzerrungen bezeichnet. Im Gegensatz dazu heißen die Verzerrungen ε x, ε y und γ xy Ingenieurverzerrungen. Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
22 4.2 Verzerrungstransformation Beispiel: Gegeben: ϵ x =1, , ϵ y = 5, , γ xy = 7, Gesucht: Dehnung in Richtung ϕ = 30 Lösung: 1 2 ( ϵ x +ϵ y )=2, , 1 2 ( ϵ x ϵ y )=7, γ xy 2 = 3, ϵ ξ =2, , cos(60 ) 3, sin(60 ) =6, Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
23 4.2 Verzerrungstransformation Hauptachsen: Wie bei den Spannungen gibt es zwei senkrecht aufeinander stehende Richtungen, für die die Dehnungen Extremwerte annehmen und die Scherung verschwindet. Diese Richtungen heißen Hauptdehnungsrichtungen. Der rechte Winkel zwischen Linien entlang der Hauptdehnungsrichtungen wird durch die Verzerrung nicht verändert. Die Hauptdehnungsrichtungen berechnen sich zu tan(2 ϕ E )= 2ϵ xy ϵ x ϵ = γ xy y ϵ x ϵ y Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
24 4.2 Verzerrungstransformation Die zugehörigen Dehnungen sind die Hauptdehnungen. Wie bei den Spannungen folgt für die Hauptdehnungen: ϵ 1/ 2 = ϵ x +ϵ y 2 ± ( ϵ ϵ 2 x y ) 2 +ϵ 2 xy Bei Verwendung von Ingenieurverzerrungen gilt: ϵ 1/ 2 = ϵ x +ϵ y 2 ± ( ϵ ϵ 2 x y ) γ 2 xy Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
25 4.3 Messung der Verzerrungen Dehnungen lassen sich mit Dehnungsmessstreifen (DMS) messen, die auf die Oberfläche des Bauteils geklebt werden. Dabei wird ausgenutzt, dass die Änderung des elektrischen Widerstands eines DMS proportional zu seiner Längenänderung ist. Zur vollständigen Bestimmung des Verzerrungszustands an einem Punkt sind drei DMS nötig, die die Dehnungen in drei unterschiedlichen Richtungen messen. Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
26 4.3 Messung der Verzerrungen b γ β α a c x Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
27 4.3 Messung der Verzerrungen Auswertung der Messung: Aus der Messung seien die drei Dehnungen ε a, ε b und ε c bekannt, die zu den ab der x-achse gemessenen Winkeln α, β und γ gehören. Für die Dehnungen gilt: ϵ a = 1 2 ( ϵ x +ϵ y )+ 1 2 ( ϵ x ϵ y ) cos(2 α)+ 1 2 γ xy sin(2α) ϵ b = 1 2 ( ϵ x +ϵ y )+ 1 2 ( ϵ x ϵ y ) cos(2β)+ 1 2 γ xy sin(2β) ϵ c = 1 2 ( ϵ x +ϵ y )+ 1 2 ( ϵ x ϵ y ) cos(2 γ)+ 1 2 γ xy sin(2 γ) Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
28 4.3 Messung der Verzerrungen Die gesuchten Größen ε x, ε y und γ xy sind Lösung des linearen Gleichungssystems (1+cos(2α)) ϵ x + (1 cos(2α) )ϵ y + sin(2 α) γ xy = 2ϵ a (1+cos(2 β)) ϵ x + (1 cos(2β)) ϵ y + sin(2β) γ xy = 2ϵ b (1+cos(2 γ))ϵ x + (1 cos(2 γ)) ϵ y + sin(2 γ) γ xy = 2 ϵ c Für α = 0, β = 45 und γ = 90 lautet das Gleichungssystem 2 ϵ x = 2 ϵ a ϵ x + ϵ y + γ xy = 2ϵ b 2ϵ y = 2 ϵ c ϵ x =ϵ a γ xy =2ϵ b ϵ a ϵ c ϵ y =ϵ c Prof. Dr. Wandinger 2. Ebene Elastizitätstheorie TM
2. Momentanpol. Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: y A ), v Py. =v Ay
 ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
3D-Transformationen. Kapitel Translation Skalierung
 Kapitel 13 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Kapitel 13 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Geometrie. 1 Vektorielle analytische Geometrie der Ebene, Kegelschnitte
 Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
KREISFUNKTIONEN. Allgemeines
 KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
 Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
2. Räumliche Bewegung
 2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
Kinematik des starren Körpers
 Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher Umlaufsinn!
 Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 5. Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 5. Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
3. Mathematikschulaufgabe
 Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
1. Kinematik. Untersucht wird die Bewegung eines Punktes P in Bezug auf zwei Bezugssysteme: Bezugssystem Oxyz ist ruhend:
 Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
3. Erhaltungsgrößen und die Newton schen Axiome
 Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Übungen zur T1: Theoretische Mechanik, SoSe13 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physik.uni-muenchen.de 3. Erhaltungsgrößen und die Newton schen Axiome Übung 3.1:
Analytische Geometrie Seite 1 von 6. Die Addition von Vektoren kann veranschaulicht werden durch das Aneinanderhängen von Pfeilen.
 Analytische Geometrie Seite 1 von 6 1. Wichtige Formeln AB bezeichnet den Vektor, der die Verschiebung beschreibt, durch die der Punkt A auf den Punkt B verschoben wird. Der Vektor, durch den die Verschiebung
Analytische Geometrie Seite 1 von 6 1. Wichtige Formeln AB bezeichnet den Vektor, der die Verschiebung beschreibt, durch die der Punkt A auf den Punkt B verschoben wird. Der Vektor, durch den die Verschiebung
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Repräsentation und Transformation von geometrischen Objekten
 Repräsentation und Transformation von geometrischen Objekten Inhalt: Grundlagen Überblick Einfache Transformationen in der Ebene Homogene Koordinaten Einfache Transformationen in der Ebene mit homogenen
Repräsentation und Transformation von geometrischen Objekten Inhalt: Grundlagen Überblick Einfache Transformationen in der Ebene Homogene Koordinaten Einfache Transformationen in der Ebene mit homogenen
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
1. Unterteilung von allgemeinen Dreiecken in rechtwinklige
 Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
Übungen zur Analysis II Blatt 27 - Lösungen
 Prof. Dr. Torsten Wedhorn SoSe 22 Daniel Wortmann Übungen zur Analysis II Blatt 27 - Lösungen Aufgabe 5: 6+6+6* Punkte Bestimme alle lokalen Extrema der folgenden Funktionen: a b c* f : R 3 R g : R 2 R
Prof. Dr. Torsten Wedhorn SoSe 22 Daniel Wortmann Übungen zur Analysis II Blatt 27 - Lösungen Aufgabe 5: 6+6+6* Punkte Bestimme alle lokalen Extrema der folgenden Funktionen: a b c* f : R 3 R g : R 2 R
Eine Methode zur Positionsberechnung aus Relativmessungen. Von Eckhardt Schön, Erfurt
 Eine Methode zur Positionsberechnung aus Relativmessungen Von Eckhardt Schön, Erfurt Mit 4 Abbildungen Die Bewegung der Sterne und Planeten vollzieht sich für einen irdischen Beobachter scheinbar an einer
Eine Methode zur Positionsberechnung aus Relativmessungen Von Eckhardt Schön, Erfurt Mit 4 Abbildungen Die Bewegung der Sterne und Planeten vollzieht sich für einen irdischen Beobachter scheinbar an einer
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
 Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
 1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
Trigonometrie. Schülerzirkel Mathematik Schülerseminar
 Schülerzirkel Mathematik Schülerseminar Trigonometrie Im Schülerseminar für Schülerinnen und Schüler der Klassenstufen 8 10 wurde die Trigonometrie innerhalb der Einheit über komplexe Zahlen behandelt,
Schülerzirkel Mathematik Schülerseminar Trigonometrie Im Schülerseminar für Schülerinnen und Schüler der Klassenstufen 8 10 wurde die Trigonometrie innerhalb der Einheit über komplexe Zahlen behandelt,
KORREKTURANLEITUNGEN zum Testheft A1
 Projekt Standardisierte schriftliche Reifeprüfung in Mathematik KORREKTURANLEITUNGEN zum Testheft A1 A1 Zahlen N Z Q R 0,03-6 π 3 10-3 1 Bemerkung: Die Aufgabe gilt nur dann als richtig gelöst, wenn alle
Projekt Standardisierte schriftliche Reifeprüfung in Mathematik KORREKTURANLEITUNGEN zum Testheft A1 A1 Zahlen N Z Q R 0,03-6 π 3 10-3 1 Bemerkung: Die Aufgabe gilt nur dann als richtig gelöst, wenn alle
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Grundsätzliches Produkte Anwendungen in der Geometrie. Vektorrechnung. Fakultät Grundlagen. Juli 2015
 Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
1 Vorlesungen: und Vektor Rechnung: 1.Teil
 1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
3. Übungsblatt Aufgaben mit Lösungen
 . Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
. Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
Trigonometrie - Zusammenfassende Übungen Raumgeometrie Vorbereitung auf die Abschlussprüfung
 1.0 Das Quadrat ABCD mit der Seitenlänge a cm ist Grundfläche eines Würfels mit der Deckfläche EFGH, wobei E über A, F über B usw. liegen. Zur Grundfläche ABCD parallele Ebenen schneiden die Würfelkanten
1.0 Das Quadrat ABCD mit der Seitenlänge a cm ist Grundfläche eines Würfels mit der Deckfläche EFGH, wobei E über A, F über B usw. liegen. Zur Grundfläche ABCD parallele Ebenen schneiden die Würfelkanten
Mathematik II für Inf und WInf
 Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation
 Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
1. Mathematikschulaufgabe
 1.0 Gegeben ist die Funktion f: y = 1 ( ) 1 x + in G= x. 1.1 Tabellarisiere f für x = [ -1; 7 ] mit x = 1 sowie für x =,5 und x =,5. 1. Zeichne den Graphen von f. Für die Zeichnung: 1 LE = 1 cm - 1 x 8-1
1.0 Gegeben ist die Funktion f: y = 1 ( ) 1 x + in G= x. 1.1 Tabellarisiere f für x = [ -1; 7 ] mit x = 1 sowie für x =,5 und x =,5. 1. Zeichne den Graphen von f. Für die Zeichnung: 1 LE = 1 cm - 1 x 8-1
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
3. Zentrales ebenes Kräftesystem
 3. Zentrales ebenes Kräftesystem Eine ruppe von Kräften, die an einem starren Körper angreifen, bilden ein zentrales Kräftesystem, wenn sich die Wirkungslinien aller Kräfte in einem Punkt schneiden. f
3. Zentrales ebenes Kräftesystem Eine ruppe von Kräften, die an einem starren Körper angreifen, bilden ein zentrales Kräftesystem, wenn sich die Wirkungslinien aller Kräfte in einem Punkt schneiden. f
Analytische Geometrie, Vektorund Matrixrechnung
 Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Aufgabe 1: Elektro-mechanischer Oszillator
 37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
Vektoren. Kapitel 3. 3.1 Skalare, Vektoren, Tensoren. 3.2 Vektoren
 Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
Kapitel 3 Vektoren 31 Skalare, Vektoren, Tensoren Viele physikalische Größen lassen sich bei bekannter Maßeinheit durch Angabe ihres Betrages als reelle Zahl vollständig angeben Solche Größen nennt man
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
 (Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
Grundwissen 10. Überblick: Gradmaß rπ Länge eines Bogens zum Mittelpunktswinkels α: b = α
 Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Lineare (affine) Abbildung
 Lineare affine Aildung A e 2 a e Wir üerziehen die Eene neen dem vertrauten Quadrat-Gitternetz, das durch die Basisvektoren e und e 2 festgelegt ist, mit einem Parallelogramm-Gitternetz, dessen Maschen
Lineare affine Aildung A e 2 a e Wir üerziehen die Eene neen dem vertrauten Quadrat-Gitternetz, das durch die Basisvektoren e und e 2 festgelegt ist, mit einem Parallelogramm-Gitternetz, dessen Maschen
1. Einfache ebene Tragwerke
 Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
4. Mathematikschulaufgabe
 .0 Berechne folgende Terme:.. x + 4 = x =. (y x) (x + y) =.0 Schreibe ohne Klammern und vereinfache soweit wie möglich:. (x + ) (x 4) =. (0,4x + y) (0,4x y) + (y) =. Ermittle den Extremwert durch Termumformung.
.0 Berechne folgende Terme:.. x + 4 = x =. (y x) (x + y) =.0 Schreibe ohne Klammern und vereinfache soweit wie möglich:. (x + ) (x 4) =. (0,4x + y) (0,4x y) + (y) =. Ermittle den Extremwert durch Termumformung.
Aus Kapitel 4 Technische Mechanik Aufgaben
 6 Aufgaben Kap. 4 Aus Kapitel 4 Aufgaben 4. Zugproben duktiler Werkstoffe reißen im Zugversuch regelmäßig mit einer größtenteils um 45 zur Kraftrichtung geneigten Bruchfläche. F F 3. Mohr scher Spannungskreis:
6 Aufgaben Kap. 4 Aus Kapitel 4 Aufgaben 4. Zugproben duktiler Werkstoffe reißen im Zugversuch regelmäßig mit einer größtenteils um 45 zur Kraftrichtung geneigten Bruchfläche. F F 3. Mohr scher Spannungskreis:
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Vektorrechnung in der Physik und Drehbewegungen
 Vektorrechnung in der Physik und Drehbewegungen 26. November 2008 Vektoren Vektoren sind bestimmt durch a) Betrag und b) Richtung Beispiel Darstellung in 3 Dimensionen: x k = y z Vektor in kartesischen
Vektorrechnung in der Physik und Drehbewegungen 26. November 2008 Vektoren Vektoren sind bestimmt durch a) Betrag und b) Richtung Beispiel Darstellung in 3 Dimensionen: x k = y z Vektor in kartesischen
1 Analytische Geometrie
 Analytische Geometrie. Grundlagen, Begriffe, Schreibweisen Achsenkreuz Die Achsen heißen in dieser Darstellung x und -Achse. Punkte Punkte werden weiterhin mit großen, lateinischen Buchstaben bezeichnet
Analytische Geometrie. Grundlagen, Begriffe, Schreibweisen Achsenkreuz Die Achsen heißen in dieser Darstellung x und -Achse. Punkte Punkte werden weiterhin mit großen, lateinischen Buchstaben bezeichnet
6. Orbits und die Runge-Lenz Vektor
 Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
mentor Lernhilfe: Mathematik 10. Klasse Baumann
 mentor Lernhilfe: Mathematik 10. Klasse Geometrie: Winkelfunktionen, Trigonometrie, Additionstheoreme, Vektorrechnung von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 10. Klasse Baumann schnell
mentor Lernhilfe: Mathematik 10. Klasse Geometrie: Winkelfunktionen, Trigonometrie, Additionstheoreme, Vektorrechnung von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 10. Klasse Baumann schnell
mentor Lernhilfe: Mathematik 7. Klasse Baumann
 mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
1. Eindimensionale Bewegung
 1. Eindimensionale Bewegung Die Gesamtheit aller Orte, die ein Punkt während seiner Bewegung einnimmt, wird als Bahnkurve oder Bahn bezeichnet. Bei einer eindimensionalen Bewegung bewegt sich der Punkt
1. Eindimensionale Bewegung Die Gesamtheit aller Orte, die ein Punkt während seiner Bewegung einnimmt, wird als Bahnkurve oder Bahn bezeichnet. Bei einer eindimensionalen Bewegung bewegt sich der Punkt
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
Komplexe Zahlen und konforme Abbildungen
 Kapitel 1 Komplexe Zahlen und konforme Abbildungen 1.0 Geometrie der komplexen Zahlen Die Menge C der komplexen Zahlen, lässt sich mithilfe der bijektiven Abbildung C := {x + iy : x,y R}, C z = x + iy
Kapitel 1 Komplexe Zahlen und konforme Abbildungen 1.0 Geometrie der komplexen Zahlen Die Menge C der komplexen Zahlen, lässt sich mithilfe der bijektiven Abbildung C := {x + iy : x,y R}, C z = x + iy
7.3 Lorentz Transformation
 26 KAPITEL 7. SPEZIELLE RELATIVITÄTSTHEORIE 7.3 Lorent Transformation In diesem Abschnitt sollen die Transformationen im 4-dimensionalen Minkowski Raum betrachtet werden. Dabei wollen wir uns auf solche
26 KAPITEL 7. SPEZIELLE RELATIVITÄTSTHEORIE 7.3 Lorent Transformation In diesem Abschnitt sollen die Transformationen im 4-dimensionalen Minkowski Raum betrachtet werden. Dabei wollen wir uns auf solche
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Der Punkt von Fermat 1
 Der Punkt von Fermat 1 Geometrie Der Punkt von Fermat Autor: Peter Andree Inhaltsverzeichnis 9 Der Punkt von Fermat 1 9.1 Die Aufgabe von Fermat an Torricelli................... 1 9.2 Der klassische, analytische
Der Punkt von Fermat 1 Geometrie Der Punkt von Fermat Autor: Peter Andree Inhaltsverzeichnis 9 Der Punkt von Fermat 1 9.1 Die Aufgabe von Fermat an Torricelli................... 1 9.2 Der klassische, analytische
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
VIII.1.4 Magnetisches Feld induziert durch einfache Ladungsströme
 V. Grundbegriffe und -ergebnisse der Magnetostatik 5 V..4 Magnetisches Feld induziert durch einfache Ladungsströme m Fall eines Ladungsstroms durch einen dünnen Draht vereinfacht sich das ntegral im Biot
V. Grundbegriffe und -ergebnisse der Magnetostatik 5 V..4 Magnetisches Feld induziert durch einfache Ladungsströme m Fall eines Ladungsstroms durch einen dünnen Draht vereinfacht sich das ntegral im Biot
4. Die ebene Platte. 4.1 Schallabstrahlung von Platten 4.2 Biegeschwingungen von Platten. Prof. Dr. Wandinger 4. Schallabstrahlung Akustik 4.
 4. Die ebene Platte 4.1 Schallabstrahlung von Platten 4.2 Biegeschwingungen von Platten Prof. Dr. Wandinger 4. Schallabstrahlung Akustik 4.4-1 Schallabstrahlung einer unendlichen ebenen Platte: Betrachtet
4. Die ebene Platte 4.1 Schallabstrahlung von Platten 4.2 Biegeschwingungen von Platten Prof. Dr. Wandinger 4. Schallabstrahlung Akustik 4.4-1 Schallabstrahlung einer unendlichen ebenen Platte: Betrachtet
Mathematik I Pflichtteil - Nachtermin Aufgabe P 1. Klasse: Platzziffer: Punkte:
 Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Informationsblatt für den Einstieg ins 2. Mathematikjahr AHS Kursleiter: Manfred Gurtner
 Informationsblatt für den Einstieg ins 2. Mathematikjahr AHS Kursleiter: Manfred Gurtner Stoff für den Einstufungstest Mathematik in das 2. Jahr AHS 1) Gleichungen/ Gleichungssysteme/ Terme Lineare Gleichungen
Informationsblatt für den Einstieg ins 2. Mathematikjahr AHS Kursleiter: Manfred Gurtner Stoff für den Einstufungstest Mathematik in das 2. Jahr AHS 1) Gleichungen/ Gleichungssysteme/ Terme Lineare Gleichungen
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen 7. Juni 201 *Aufgabe 1. Gegeben seien fx, y = xy 2 8e x+y und P = 1, 2. Der Gradient von f ist genau an der Stelle P Null. a Untersuchen Sie mit Hilfe der Hesse-Matrix,
Tutorium Mathematik II, M Lösungen 7. Juni 201 *Aufgabe 1. Gegeben seien fx, y = xy 2 8e x+y und P = 1, 2. Der Gradient von f ist genau an der Stelle P Null. a Untersuchen Sie mit Hilfe der Hesse-Matrix,
Kapitel 3: Geometrische Transformationen
 [ Computeranimation ] Kapitel 3: Geometrische Transformationen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 3. Geometrische Transformationen
[ Computeranimation ] Kapitel 3: Geometrische Transformationen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 3. Geometrische Transformationen
2.4 Stoßvorgänge. Lösungen
 .4 Stoßvorgänge Lösungen Aufgabe 1: a) Geschwindigkeit und Winkel: Für die Wurfhöhe gilt: H = v 0 g sin Die zugehörige x-koordinate ist: x 1 = v 0 g sincos Aus diesen beiden Gleichungen lässt sich die
.4 Stoßvorgänge Lösungen Aufgabe 1: a) Geschwindigkeit und Winkel: Für die Wurfhöhe gilt: H = v 0 g sin Die zugehörige x-koordinate ist: x 1 = v 0 g sincos Aus diesen beiden Gleichungen lässt sich die
2. Aufgabe Vereinfachen Sie die folgenden Ausdrücke so, dass möglichst wenige Multiplikationen ausgeführt werden müssen!
 Studiengang: PT/LOT/PVHT Semester: WS 9/ lgebra Serie: 2 Thema: Matrizen, Determinanten. ufgabe Gegeben sind die Matrizen = µ 2 3 2 µ 3 2 4, B = 2 Berechnen Sie: a) 2 + 3B b) B 2 c) B T d) B T e) T B f)
Studiengang: PT/LOT/PVHT Semester: WS 9/ lgebra Serie: 2 Thema: Matrizen, Determinanten. ufgabe Gegeben sind die Matrizen = µ 2 3 2 µ 3 2 4, B = 2 Berechnen Sie: a) 2 + 3B b) B 2 c) B T d) B T e) T B f)
Exzentrischer Stoß. Der genaue zeitliche Verlauf der Kraft ist nicht bekannt. Prof. Dr. Wandinger 4. Exzentrischer Stoß Dynamik 2 4-1
 Exzentrischer Stoß Allgemeine Stoßvorgänge zwischen zwei Körpern in der Ebene können mit Hilfe des integrierten Impulssatzes und des integrierten Drallsatzes behandelt werden. Während des Stoßes treten
Exzentrischer Stoß Allgemeine Stoßvorgänge zwischen zwei Körpern in der Ebene können mit Hilfe des integrierten Impulssatzes und des integrierten Drallsatzes behandelt werden. Während des Stoßes treten
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Mechanische Spannung und Elastizität
 Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
11 Üben X Affine Funktionen 1.01
 Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
d 2 b 2 c 2 d 3 b 3 c 3 , D a 1 d 1 c 1 v 3 Definiton (Verbindungsvektor): Zwei Punkte A(a 1 a 2 a 3 ) und B(b 1 b 2 b 3 ) legen den Vektor b 1 a 1
 2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
1. Bewegungsgleichung
 1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
B Lösungen. Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R 2 Berechnen Sie zur Abbildung. f(x, y) := x sin(xy) f : R 2 R,
 B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
Kinetik des starren Körpers
 Technische Mechanik II Kinetik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes 2.
Technische Mechanik II Kinetik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes 2.
Lösung zur Übung 2. Lösung durch Ausrechnen Die Funktion lässt sich durch die Doppelwinkelfunktion des Sinus ausdrücken.
 Lösung zur Übung Aufgabe 5 Berechnen Sie die kleinste Periode folgender Funktionen a) y(x) = sin(x) cos(x) Lösung durch Ausrechnen Die Funktion lässt sich durch die Doppelwinkelfunktion des Sinus ausdrücken.
Lösung zur Übung Aufgabe 5 Berechnen Sie die kleinste Periode folgender Funktionen a) y(x) = sin(x) cos(x) Lösung durch Ausrechnen Die Funktion lässt sich durch die Doppelwinkelfunktion des Sinus ausdrücken.
Musterlösung Lineare Algebra und Geometrie Herbstsemester 2015, Aufgabenblatt 6
 Musterlösung Lineare Algebra und Geometrie Herbstsemester 015, Aufgabenblatt 6 Aufgabenblatt 6 40 Punkte Aufgabe 1 (Bandornamente) Ordne die sechs Bandornamente rechts den sieben Klassen zu. Zu jeder Klasse
Musterlösung Lineare Algebra und Geometrie Herbstsemester 015, Aufgabenblatt 6 Aufgabenblatt 6 40 Punkte Aufgabe 1 (Bandornamente) Ordne die sechs Bandornamente rechts den sieben Klassen zu. Zu jeder Klasse
& sind die Vektorkomponenten von und sind die Vektorkoordinaten von. A x. a) Der Betrag eines Vektors
 Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Wiederholungsblatt Elementargeometrie LÖSUNGSSKIZZE
 Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Übungen zu Partielle Differentialgleichungen, WS 2016
 Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Trigonometrische Funktionen
 Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Trigonometrie am rechtwinkligen Dreieck
 1. Geschichtliches Trigonometrie am rechtwinkligen Dreieck Die Trigonometrie ein Teilgebiet der Geometrie, welches sich mit Dreiecken beschäftigt. Sie entstand vor allem aus der frühen stronomie 1, hat
1. Geschichtliches Trigonometrie am rechtwinkligen Dreieck Die Trigonometrie ein Teilgebiet der Geometrie, welches sich mit Dreiecken beschäftigt. Sie entstand vor allem aus der frühen stronomie 1, hat
2. Räumliche Bewegung
 2. Räumliche Bewegung Wenn die Bahn des Massenpunkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort im Raum zu bestimmen. Es muss ein Ortsvektor angegeben werden. Prof.
2. Räumliche Bewegung Wenn die Bahn des Massenpunkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort im Raum zu bestimmen. Es muss ein Ortsvektor angegeben werden. Prof.
Arbeitsblatt Geometrie / Trigonometrie
 Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung
 Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung Udo Backhaus 14. Dezember 2004 1 Prinzip Die Messung der Astronomischen Einheit durch Kontaktzeitmessungen beim Venustransit
Kontaktzeitmessungen beim Venustransit und die Ableitung der Sonnenentfernung Udo Backhaus 14. Dezember 2004 1 Prinzip Die Messung der Astronomischen Einheit durch Kontaktzeitmessungen beim Venustransit
Drehung um einen Punkt um Winkel α.
 Drehung um einen Punkt um Winkel α. Sei A R 2 und α R. Drehung um A um Winkel α ist eine Abbildung D A (α) : R 2 R 2 welche wie folgt definiert ist: D A (α) = T A D 0 (α) T ( A), wobei die Abbildung D
Drehung um einen Punkt um Winkel α. Sei A R 2 und α R. Drehung um A um Winkel α ist eine Abbildung D A (α) : R 2 R 2 welche wie folgt definiert ist: D A (α) = T A D 0 (α) T ( A), wobei die Abbildung D
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Das Skalarprodukt zweier Vektoren
 Beim Skalarprodukt zweier Vektoren werden die Vektoren so multipliziert, dass sich ein Skalar eine Zahl ergibt. Die Berechnung des Skalarproduktes ist ziemlich einfach, aber die weiteren Eigenschaften
Beim Skalarprodukt zweier Vektoren werden die Vektoren so multipliziert, dass sich ein Skalar eine Zahl ergibt. Die Berechnung des Skalarproduktes ist ziemlich einfach, aber die weiteren Eigenschaften
Trägheitsmomente starrer Körper
 Trägheitsmomente starrer Körper Mit Hilfe von Drehschwingungen sollen für einen Würfel und einen Quader die Trägheitsmomente für verschiedene Drehachsen durch den Schwerpunkt gemessen werden. Das zugehörige
Trägheitsmomente starrer Körper Mit Hilfe von Drehschwingungen sollen für einen Würfel und einen Quader die Trägheitsmomente für verschiedene Drehachsen durch den Schwerpunkt gemessen werden. Das zugehörige
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 2016 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 12. PD
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 2016 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 12. PD
Elektromagnetische Felder und Wellen. Klausur Herbst Aufgabe 1 (5 Punkte) Aufgabe 2 (3 Punkte) Aufgabe 3 (5 Punkte) Aufgabe 4 (12 Punkte) Kern
 Elektromagnetische Felder und Wellen Klausur Herbst 2000 Aufgabe 1 (5 Punkte) Ein magnetischer Dipol hat das Moment m = m e z. Wie groß ist Feld B auf der z- Achse bei z = a, wenn sich der Dipol auf der
Elektromagnetische Felder und Wellen Klausur Herbst 2000 Aufgabe 1 (5 Punkte) Ein magnetischer Dipol hat das Moment m = m e z. Wie groß ist Feld B auf der z- Achse bei z = a, wenn sich der Dipol auf der
Lösung zum Parabolspiegel
 Lösung zum Parabolspiegel y s 1 s 2 Offensichtlich muss s = s 1 + s 2 unabhängig vom Achsenabstand y bzw. über die Parabelgleichung auch unabhängig von x sein. f F x s = s 1 + s 2 = f x + y 2 + (f x) 2
Lösung zum Parabolspiegel y s 1 s 2 Offensichtlich muss s = s 1 + s 2 unabhängig vom Achsenabstand y bzw. über die Parabelgleichung auch unabhängig von x sein. f F x s = s 1 + s 2 = f x + y 2 + (f x) 2
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
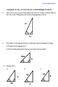 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Stoffgesetze Spannungszustand
 16. 9.4 Stoffgesete Spannungsustand Belastungen ereugen in elastischen Bauteilen einen Spannungsustand, der sowohl vom Ort als auch von der Orientierung (Winkel) des betrachteten Schnittes beüglich der
16. 9.4 Stoffgesete Spannungsustand Belastungen ereugen in elastischen Bauteilen einen Spannungsustand, der sowohl vom Ort als auch von der Orientierung (Winkel) des betrachteten Schnittes beüglich der
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
Theoretische Physik I Mechanik Blatt 1
 PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
