2.3 Symmetrien und Erhaltungssätze
|
|
|
- Daniel Til Braun
- vor 7 Jahren
- Abrufe
Transkript
1 2 Analytsche Mechan 23 Symmetren un Erhaltungssätze 231 Konstanten / Integrale er Bewegung De Lagrange-Glechung ermöglcht ene rete un enhetlche Herletung er wchtgsten Erhaltungssätze Man ann aus er Lagrange-Glechung ret zegen, ass ür s verallgemenerte Koornaten 2s 1 Konstanten er Bewegung exsteren müssen: Wr haben s verallgemenerte Koornaten q un s verallgemenerte Geschwngeten q, also nsgesamt 2s ynmsche Varablen Be er Integraton er s Bewegungsglechungen zweter Ornung erhalten wr 2s Integratonsonstanten C, e aus en Anangsbengungen bestmmt weren Außerem benötgen wr 2s Anangsbengungen, h wr benötgen e Koornaten un Geschwngeten zur Zet t 0: q 0 q (0,C 1,,C 2s ), q 0 q (0,C 1,,C 2s ) Aus esen 2s Bewegungsglechungen weren sowe 2s Anangsbengungen erhalten wr e 2s Integratonsonstanten un amt e Koornaten un Geschwngeten als Funton er Zet, h heßen Integral er Bewegung oer Konstante er Bewegung oer Erhaltungsgröße Dese Größen bleben onstant ür alle Bahnen, welche e Bewegungsglechungen erüllen 232 Integrable Systeme En System mt s Frehetsgraen st ntegrabel, wenn es unabhängge Konstanten F (q, q,t)c, 1,,s gbt Damt legen alle Bahnurven enes ntegrablen Systems au ener s-mensonalen Hpyerläche m 2s-mensonalen Raum (q, q ) Bespel: en enmensonaler harmonscher Oszllator mt er Lagrange-Funton L T V m 2 ẋ2 m 2 ω2 x 2 erüllt e Glechung ẋ x m(ẍ + ω2 x)0 De Lösung lautet x(t) Asn(ωt + ϕ 0 ) ẋ(t) Aω cos(ωt + ϕ 0 ) q q (t,c 1,,C 2s ), q q (t,c 1,,C 2s ) Darn tauchen e 2s Integratonsonstanten au Es st grunsätzlch möglch, eses System aus 2s Glechungen zu nverteren, h e Integratonsonstanten als Funton er Koornaten un Gesschwngeten arzustellen, c c (q 1,q s, q 1, q s,t), 1,,2s) Es exsteren somt 2s Größen, welche zwar ormal von en Koornaten un Geschwngeten abhängen, aber onstant, h zetlch unveränerlch sn Denton: Größen F, ür e glt F 0 Abblung 215: Bahnurve es 1D harmonschen Oszllators m Phasenraum Des entsprcht er Parameterarstellung ener Ellpse, we n Abb 215 argestellt Der 1D harmonsche Oszllator bewegt sch somt au ener Bahnurve mt enem enzgen Frehetsgra Das System bestzt en Integral er Bewegung, e Energe E(x,ẋ)T +V 22
2 2 Analytsche Mechan 233 Bsp: Translaton n er Zet Da n en Bewegungsglechungen enes geschlossenen Systems e Zet ncht explzt erschent, müssen wr e glechen Resultate erhalten, wenn wr en Ursprung er Zetachse um enen Betrag t 0 verscheben Man ann eshalb mmer ene er Integratonsonstanten urch ene Verschebung er Zetachse elmneren Das enachste Bespel st e Funton q(t)at + b Abblung 216: Verschebung er Zetachse 234 Koornatentransormaton Ene Koornatentransormaton (Punttransormaton) enert en Übergang von enem Satz Koornaten {q } zu enem zweten Satz {Q }, wobe e Form er Abhängget zunächst belebg se, außer ass e neuen Koornaten ncht von en Geschwngeten q er alten abhängen sollen Loal am Punt P önnen wr se lnearseren; M(P) Q 1 Q 1 q q 1 Q q 1 Q q Dese Bezehung st (am Punt P) umehrbar, alls e Jacob-Determnante J an esem Punt ncht veschwnet, J Det Q 1 Q 1 q q 1 Q q 1 Q q 0 Her önnen wr e Integratonsonstante b elmneren, nem wr e Zetachse verscheben: h q(t t t 0 )a(t +t 0 )+b at + at 0 + b, q(t )at, allst 0 b a P q2 P Q2 Q1 ach er Wahl es Ursprungs er Zetachse bleben somt 2s unabhängge Glechungen un 2s 1 Integratonsonstanten un e Zet als unabhängge Varable Wr önnen nun ese Glechungen statt als Bestmmungsglechungen ür e Varablen q, q auch als Bestmmungsglechungen ür e 2s 1 Integratonsonstanten un e Zet auassen Dann wr oenschtlch ass e Integratonsonstanten unabhängg von er Zet sn, h es sn Konstanten, resp Integrale er Bewegung In enem System mt velen Frehetsgraen net man eshalb ene grosse Zahl von Konstanten er Bewegung Allerngs spelen ncht alle ene wchtge Rolle Wr suteren n er Folge e wchtgsten, welche sch ret aus Symmetreegenschaten es Raumes, resp er Zet ableten lassen Dese Größen weren als Erhaltungsgrößen bezechnet q1 Abblung 217: Kooratentransormaton Seen nun q un Q e Koornaten es selben Puntes P Für enen Punt P, er gegenüber P nntesmal verschoben st, önnen wr e neuen Kooranten schreben als Q Q(q + δq )Q(P)+Mδq + O(δq 2 ) Falls e Inverse er Matrx M exstert, önnen wr ese Glechung loal nverteren, q q(p)+m 1 δq δq Q (P ) Q(P) 23
3 2 Analytsche Mechan 235 Fehlene Formnvaranz er Bewegungsglechungen Wenn wr ene Koornatentransormaton vornehmen, so ann sch e Form er Glechungen änern So lauten e ewton schen Bewegungsglechungen n 2D ür artessche Koornaten mẍ V x mÿ V y Hätte e ewton sche Glechung n en Polaroornaten r,ϕ e gleche Form we n en artesschen Koornaten, so würe se lauten m r V r m ϕ V ϕ Dass es so ncht orret sen ann, zegt berets ene enache Dmensonsanalyse Deses Problem stellt sch allgemen bem Übergang n en Koornatensystem, welches en Interalsystem st De orrete Form erhält man, nem man zb mt Hle es Prnzps von Alembert Enacher st es, von er Lagrange-Glechung auszugehen We wr m Kaptel 236 zegen weren, st ese ormnvarant Abblung 218: Transormaton von artesschen zu polaren Koornaten Wr benötgen aür e Transormatonsglechungen ür e Koornaten x r cosϕ y r snϕ un ür e Geschwngeten ẋ ṙ cosϕ r snϕ ϕ ẏ ṙ snϕ + r cosϕ ϕ De netsche Energe n en neuen Koornaten st T m 2 (ẋ2 + ẏ 2 ) m 2 (ṙ2 + r 2 ϕ 2 ) Wr verwenen e Lagrange-Glechung n er Form T T ṙ r V V ṙ r Wenn wr berücschtgen, ass as Potenzal ncht von en Geschwngeten abhängt, verenacht sch es zu T ṙ T r V r Wr setzen en Ausruc ür e netsche Energe en un erhalten T T ṙ r m( r r ϕ2 ) V r ür e raale Koornate Für en Spezalall enes Zentralratproblems (h V / φ 0) erhalten wr ür e Wneloornate mr(r ϕ 2ṙ ϕ)0 236 Formnvaranz er Lagrangeunton Wr untersuchen jetzt e Frage er Formnvaranz ür e Lagrangeunton: n artesschen Koornaten lautet e Lagrange-Glechung zweter Art q q 0 Ist se ormnvarant, so muss se n en transormerten Koornaten emnach L L 0 Q Q lauten Dazu betrachten wr e Geschwngeten er neuen Koornaten un entwceln ese n en Alten: Q Somt st Q q Q q Q q q + Q t 24
4 2 Analytsche Mechan un q Q q Q (24) Wr betrachten nun e neue Lagrange-Funton L, e wr urch Ersetzen von q (Q ) aus er alten erhalten: L (Q, Q,t)L (q (Q,t), q (Q, Q,t),t) Für e Lagrange-Glechung benötgen wr e partellen Abletungen nach Q j un Q j q + q (25) Q j q Q j q Q j un Q j q + q (26) q Q j q Q j De Punttransormaton st geschwngetsunabhängg; somt st q Q j 0 un Glechung (26) verenacht sch zu Q j q q Q j q q Q j Im zweten Schrtt haben wr e Bezehung (24) verwenet Wr benötgen jetzt e totale Zetabletung eses Ausrucs L q + q (27) Q j q Q j q Q j De Lagrange-Glechung ür e neuen Koornaten erhalten wr aus er Derenz von 27 un 25: L L Q j Q j q + q q Q j q Q j q + q q Q j q Q j q 0, q q Q j a er Ausruc n Klammern verschwnet Damt olgt aus 0 q q auch h L L 0, Q Q De Lagrange-Glechung st nvarant unter Puntoornatentransormatonen Wenn se n enem Koornatensystem erüllt sn, so sn se es auch n jeem aneren Koornatensystem Des st ene er wchtgsten Motvatonen ür e Anwenung es Lagrange-Formalsmus: Se erlaubt enem, n belebgen Koornatensystemen (auch n beschleungten), e Bewegungsglechungen abzuleten 237 Vralsatz Wr betrachten e Größe G p r un hre zetlche Änerung G p ṙ +ṗ r Der erste Term st gerae as Doppelte er netschen Energe, er zwete ann, gemäß ewton s Theorem, geschreben weren als Prout aus Kräten un Vetoren, p ṙ +ṗ r 2T +F r Wr blen as zetlche Mttel über ene Zet τ: 1 τ G τ 0 1 τ [G(τ) G(0)] 2T + F r (28) 25
5 2 Analytsche Mechan Für en gebunenes System sn Orte un Impulse beschränt un somt st G(t) enlch Insbesonere glt es ür G(τ) un G(0) Damt wr lm G τ 1 τ G 0 τ 0 Damt olgt aus Glechung 28 er Vralsatz: T 1 2 F r Anwenung: Zentralratproblem mt enem r Potenzal: Das Potenzal se V (r)αr De Krat st somt F V (r) αr 2 r Somt st as Prout F r αr V (r) un e netsche Energe gemäß Vralsatz wr T V 2 Wchtge Spezalälle sn er harmonsche Oszllator mt 2 un somt T V 1/r Potenzal mt 1 un somt T 1 2V 238 Ähnlchetstransormaton Wr betrachten ene neue Lagrangeunton L, e wr aus er alten Funton L urch Salerung mt enem onstanten Fator γ erhalten haben: L (q,t)γl (q,t) Aus em Verglech er entsprechenen Lagrange- Glechungen γ L L 0 q q q q ür jees st erschtlch, ass bee Lagrange- Funtonen e gleche Bewegung beschreben Wr wollen uns ese wchtge Egenschat er Lagrangeunton zu nutze machen, um Egenschaten er Lösung er Telchenbewegung zu nen, ohne explzt e Bewegungsglechung lösen zu müssen Wr untersuchen Systeme, ür e e potenzelle Energy V ene homogene Funton vom Gra K er Koornaten q st: V (αq 1,,αq )α K V (q 1,,q ) un α onstant Wr eneren jetzt ene Ähnlchetstransormaton urch e Salenunton q αq t βt, wobe wr e Konstante β noch bestmmen müssen Damt erhalten wr q t α β q T α2 β 2 T Ṽ α K V Damt st e neue Lagrangeunton L T Ṽ α2 β 2 T αk V Se beschrebt somt as gleche mechansche System wenn γ α2 β 2 αk Somt muss er Salerungsator ür e Zet olgener Bengung gehorchen: β α 1 K/2 α δ Deser Zusammenhang zwschen er Salerung von Längen un Zeten charatersert e Art es physalschen Systems: 26
6 2 Analytsche Mechan K physalsches System 2 harmonscher Oszllator 1 Telchen m Gravtatonsel -1 Zentralratproblem 239 Echnvaranz δ Beschrebung 0 τ unabhängg von er Auslenung: Ampltue un Frequenz sn ncht geoppelt 1/2 τ 2 z: Wurparabel 3/2 τ 2 3 : 3 Keplersches Gesetz Zwe Lagrange-Funtonen L un L, eren Derenz als totale zetlche Abletung ener Funton χ(q,t) geschreben weren ann, L L + χ(q,t), beschreben e gleche Dynam De Transormaton bezechnet man als loale Echtransormaton: Se ann an jeem Ort unterschelch sen Allerng ar χ nur vom Ort, aber ncht von er Geschwnget abhängen Bewes: Wr schreben en Derenzterm als χ(q χ,t) q + χ q t Damt wr er erste Term er Lagrange-Glechung q un er zwete + χ q q + χ q q q Zusammen erhalten wr L q q + χ q q 0 q q Des st analog zur Eletroynam: Dort waren e Bewegungsglechungen nvarant unter ener Transormaton er Potenzale: A A A + χ Φ Φ Φ χ t 2310 Kanonsche Krat un anonscher Impuls Wr betrachten ene Lagrange-Funton L T V, be er nur er Potenzal-Term V von en Koornaten q abhängt Dann st (T V ) V q q q De Abletung enes Potenzals nach ener generalserten Koornate ann als ene generalserte Krat verstanen weren Umgeehrt hängt nur e netsche Energe von en Geschwngeten ab, h (T V ) T q q q Es legt eshalb nahe, p q T q als enen generalserten Impuls zu nterpreteren Da er urch Abletung nach q aus L entsteht, gehört er zur Koornate q un wr auch als anonscher Impuls bezechnet Damt erhalten e Lagrange- Glechungen ene ewton-ähnlche Form: ṗ q Bespel 1 : Frees Telchen De Lagrange-Funton enes reen Telchens st L T 1 2 m ṙ 2 27
7 2 Analytsche Mechan Der anonsche Impuls hat somt e Komponenten p x ẋ mẋ p y ẏ mẏ p z ż mż Der anonsche Impuls entsprcht her also em Stanarmpuls Bespel 2 : Penel Für en Penel er Länge mt Auslenung ϕ lautet e Lagrange-Funton L m 2 2 ϕ 2 + mgcosϕ Der entsprechene anonsche Impuls st somt p ϕ ϕ m2 ϕ We ene Dmensonsanalyse pϕ gm 2 s zegt, st es ncht glech em nematschen Impuls mv m ϕ, sonern glech em Drehmpuls L m 2 ϕ Bespel 3 : Telchen m eletromagnetschen Fel Für en Telchen m eletromagnetschen Fel wr e Lagrange-Funton L T qφ + qv A Damt wr er anonsche Impuls p v mv + q A, h er wecht vom nematschen Impuls mv ab, un zwar um as Prout aus Laung un Vetorpotenzal Er st amt ncht echnvarant! Allgemen st er anonsche Impuls glech em nematschen Impuls alls e Bewegung n enem geschwngetsunabhänggen Potenzal stattnet Des st zb ncht er Fall ür gelaene Telchen n enem Magnetel Dort erhält man en anonschen Impuls als p mv + qa aus em nematschen Impuls Umgeehrt erhält man en nematschen Impuls als mv p qa 2311 Zylsche Koornaten un Erhaltungsgrößen Wenn ene Lagrange-Funton L ene Koornate q ncht enthällt, sonern nur q, nennt man q ene zylsche Koornate Für ene solche Varable reuzert sch hre Lagrange-Glechung zu q p 0 Damt st er anonsche Impuls p ene Konstante er Bewegung un blebt erhalten Wenn L ncht von q abhängt, beeutet es, ass e Lagrangeunton sch unter er Koornatentransormaton q q q + a ncht änert, h L (q,t)l (q,t) Das System st somt translatonsnvarant bezüglch eser Koornate un er zugehörge anonsche Impuls st ene Erhaltungsgröße Für en vollstäng translatonsnvarantes System glt V const un amt sn alle q zylsch Als Konsequenz erhalten wr e Impulserhaltung De Erhaltung es Gesamtmpules P olgt, wenn as Potenzal nur von en relatven Koornatenq q j abhängt un ncht von en Schwerpuntsoornaten q Des entsprcht em Träghetsgesetz von Galle un ewton 28
8 2 Analytsche Mechan 2312 Knetsche Energe als quaratsche Form Wr betrachten mt Telchen un generalserten Koornaten Dann st e netsche Energe T ene quaratsche Funton er verallgemenerten Geschwngeten q : T,l A l q q l (29) alls e Koornatentransormaton von en artesschen Koornaten x (q 1,,q ) ncht explzt zetabhängg st, x (q 1,,q ) t 0 1,,3 Solch en System nennt man auch sleronom Bewes: ẋ x q q a q Damt önnen wr e netsche Energe umschreben T m ẋ m l 3 l A l q q l, m a q 1 2 m a a l 2 a q a q l l q q l wobe e Matrxelemente A l enert sn als A l m a a l un e a urch e Koornatentransormaton: a x q Damt haben wr gezegt, ass e netsche Energe quaratsch n en generalserten Koornaten st, alls e Koornatentransormaton zetunabhängg st 2313 Energeerhaltung Für en abgeschlossenes System sn verscheene Zetpunte äquvalent, h en Punt er Zetachse st gegenüber en anern ausgezechnet Man sagt, e Zet se homogen Damt ann auch e Lagrange-Funton ncht explzt von er Zet abhängen, t 0 De totale zetlche Abletung ener solchen Funton st L q q + q q (210) Wr benutzen e Lagrange-Glechung n er Form q q Wenn wr ese n Gl 210 ensetzen, erhalten wr L q q + q q q q Wr schreben as um zu q L 0 q Aners ausgerüct st e Größe H q q L (211) n enem geschlossenen sleronomen System ene Konstante Man bezechnet se als Energeunton es Systems Se st oenschtlch av, h e 29
9 2 Analytsche Mechan gesamte Energe ergbt sch als Summe er Energen von solerten Telsystemen Laut Glechung (29) st e netsche Energe enes sleronomen Systems ene homogene quaratsche Größe er Geschwngeten q : T Somt st un,l A l q q l T q q l (A l + A l ) l T q q q l q (A l + A l )2T l De potenzelle Energe st unabhängg von en Geschwngeten, V q 0 Damt wr er erste Term er Energeunton (211) (T V ) T q q q q q 2T q De Energeunton wr amt H 2T L T +V un entsprcht amt unserer Erwartung ür e gesamte Energe enes Systems 2314 Gesamtmpuls En zwete Erhaltungsgröße olgt aus er Homogentät es Raumes: alle Punte m Raum sn äquvalent Des glt nur n er Abwesenhet enes äußeren Potenzals Im Gegensatz zur Homogentät er Zet önnen wr jetzt ncht schleßen, ass L ene explzte Ortsabhängget bestzt, a be enem -Körperproblem vele Ortsoornaten berücschtgt weren müssen Se ührt aber azu, ass e Lagrange-Funton Abblung 219: Verschebung es Koornatensystems unter Verschebungen aller Koornaten onstant blebt Se st somt ncht von en Koornaten r, r j abhängg, sonern nur von en Derenzen c j r r j : L (r r j )L (r r j)l (c j ) Mathematsch lässt sch e Homogentät es Raumes am besten urch Betrachtung nntesmaler Verschebungen es Koornatensystems um δr erassen Wr entwceln e Änerung er Lagrange- Funton urch ese Verschebung n ene Taylorrehe 0 δl a r a δr a δr a r a Her sn e δr a e Komponenten von δr un wr verwenen e Abürzung r x y z Da er Verschebungsvetor δr belebg st, muss 0 (212) a r a gelten Zusammen mt er Lagrange-Glechung q q 30
10 2 Analytsche Mechan oer r a v a erhalten wr a v a e P 0 Oenbar st n enem mechanschen System er Vetor P a v a ene Erhaltungsgröße; er wr als Gesamtmpuls es Systems bezechnet Der Gesamtmpuls enes Systems von Telchen st mmer glech er Summe er Impulse er enzelnen Telchen, unabhängg avon, ob se n Wechselwrung treten oer ncht Glechung (212) hat ene enache physalsche Beeutung: Da nur as Potenzal von en Koornaten abhängt, stellt e Abletung von L nach en Koornaten (212) e gesamte au as System wrene Krat ar Dese verschwnet n enem homogenen Raum ohne äußere Feler cht mmer st er Raum vollstäng homogen, zb wenn e Lagrange-Funton urch as Potenzal von ener enzelnen Koornate abhängt, V V (q ) In esem Fall önnen wr mmer noch Erhaltungssätze ür enzelne Komponenten es Impulses herleten Falls q j n er Lagrange-Funton ncht vorommt, so olgt aus er entsprechenen Lagrange- Glechung 0 p const, q q q h er zugehörge Impuls stellt ene Erhaltungsgröße ar Für enzelne Telchen st es oenbar e enachere Herletung er Impulserhaltung De oben urchgeührte Herletung blebt aber auch be Systemen von Telchen gültg, wo as Potenzal von sämtlchen Koornaten (zb über e Abstäne c j ) abhängt 2315 Drehmpuls In glecher Wese önnen wr be er Herletung er Drehmpulserhaltung verahren Wr verwenen abe e Isotrope es Raums, h e Tatsache, ass n Abwesenhet enes externen Feles alle Raumrchtungen glechwertg sn Damt ar sch e Lagrange-Funton ncht änern, wenn wr as Koornatensystem rehen De Drehung ann ausgeührt weren mt Hle er Transormatonsglechungen δr δϕ r δṙ δϕ ṙ Her stellt δϕ δϕn ene nntesmale Drehung um en Wnel ϕ um e Achsen ar Wr betrachten we üblch en abgeschlossenes mechansches System ohne Rebung De Änerung n er Lagrangeunton st δl L (r 1 + δr 1,r 2 + δr 2,,r + δr, ṙ 1 + δṙ 1,ṙ 2 + δṙ 2,,ṙ + δṙ ) L (r 1,r 2,,r,ṙ 1,ṙ 2,,ṙ ) δr + r ṙ δṙ 0 Wr müssen esmal auch e Änerung er Geschwngeten berücschtgen, a ese urch ene Rotaton ebenalls transormert weren Wr verwenen p ṙ un erhalten 0 δϕ ṗ r ṗ (δϕ r )+ p (δϕ r ) p (δϕ ṙ ) (r p )δϕ L 31
11 2 Analytsche Mechan mt em Gesamtrehmpuls L (r p ) Da e Drehung δϕ belebg st, muss gelten L r p const De Rotatonsnvaranz ann urch en äußeres Fel, zb e Gravtaton, engeschränt weren Angenommen, as äußere Fel bestzt ene Symmetreachse (Gravtaton: z-achse), ann blebt nur e Projeton es Drehmpulses au ese Achse erhalten, h au L n n L Besspel 1 : Gravtaton De potenzelle Energe V mgz st rotatonsnvarant um e z-achse Damt blebt erhalten L z e z r p Bespel 2 : Zentralrat Her st as Potenzal V A r Es blebt somt nvarant gegenüber Drehungen um ene belebge Achse urch en Ursprung Damt bleben alle Komponenten von L erhalten Das Potenzal st jeoch ncht translatonsnvarant, so ass er Impuls ncht erhalten blebt 2316 Das oether-theorem Wr betrachten ene Koornatentransormaton ür jee generalserte Koornate q De Transormaton soll ene ontnuerlche Abblung mt enem Parameter α sen: q q h (q 1,,q,α,t) Für α 0 soll se e entsche Abblung arstellen, q h (q 1,,q,α 0,t) Außerem soll h nach α stetg erenzerbar un nverterbar sen Bespele ür solche Abblungen sn e Translaton r r r + αa un e Rotaton um e z-achse: x y z cosα snα 0 snα cosα Wenn jetzt e Lagrange-Funton L x y z (213) L ( q, q,t,α)l (h (q,α,t),ḣ (q,α,t),t) sch nur um ene Echtransormaton L ( q, q,t,α)l (q, q,t)+ χ( q,α,t) von L unterscheet, ann st olgenen Funton ene Konstante: I α (q, q,t) Bewes: q q ( q,t,α) χ( q,α,t) α0 α0 De been Lagrange-Funtonen sn, abgesehen von er Echtransormaton entsch, alls e Abhängget von α verschwnet, h α L ( q, q,t,α) χ( q,α,t) 0 (214) sen De Lagrangeunton L n en neuen Koornaten q erhalten wr zb nem wr n er ursprünglchen Lagrangeunton L e alten Koornaten q urch e neuen ausrücen: L ( q, q,t,α)l (q( q,t,α), q( q,t,α),t) 32
12 2 Analytsche Mechan Damt önnen wr e Änerung er Lagrangeunton mt α schreben als e partelle Abletung nach α, wobe e Varablen q un q estgehalten weren: 2317 Anwenungsbespele Impulserhaltung Das Potenzal (Gravtaton) se nur von z abhängg, q q + q q q + q q q q q Des glt ür alle Werte von α Insbesonere önnen wr α 0 setzen Damt erhalten wr ür e Änerung (214) L ( q, q,t,α) α χ( q,α,t) q q χ( q,α,t) Damt st as oether-theorem bewesen Es α0 0 vernüpt ontnuerlche Symmetren er Lagrange-Funton mt Erhaltungsgrößen glt aher ncht be sreten Symmetren, zb Raumspegelungen Aus er Symmetre olgt e Erhaltungsgröße, e Umehrung glt ncht Der Erhaltungssatz, er zu ener zylschen Koornate q gehört, st en Spezalall: Dann st e Lagrange-Funton nvarant unter ener Translaton er entsprechenen Koornate Ene weterer wchtger Spezalall st er, ass e Echunton χ verschwnet Dann st e Erhaltungsgröße I α (q, q,t) q q ( q,t,α) α0 L (x,z,ẋ,ż) m 2 (ẋ2 + ż 2 ) V (z) Somt ann as System belebg n x-rchtung verschoben weren, h x st zylsch, x x + α x De Echunton χ verschwnet n esem Fall Damt erhalten wr ür e zugehörge Erhaltungsgröße q I α (x,z,ẋ,ż) q x α0 ẋ mẋ, also e Impulserhaltung ür e x-komponente, n Überenstmmung mt er Dsusson m Zusammenhang mt zylschen Koornaten Drehmpuls De Lagrangeunton L (r,ṙ) m 2 (ẋ2 + ẏ 2 + ż 2 ) V (x 2 + y 2,z) st unter Rotatonen um e z-achse nvarant De Rotaton st gegeben urch e Koornatentransormaton (213) un ergbt e transomerte Funton L (r,ṙ,α) m 2 (ẋ 2 +ẏ 2 +ż 2 ) V (x 2 +y 2,z ) st oenbar nvarant Mt x(x,α) y(y,α) x snα + y cosα y nen wr e Erhaltungsgröße x cosα y snα x ẋ y + ẏ ( x)m(ẋy ẏx) L z, h e z-komponente es Drehmpulses 33
13 2 Analytsche Mechan Wr önnen e Rechnung auch n symmetreangepassten Koornaten urchühren, h n Zylneroornaten Damt wr e Lagrangeunton L (r,ṙ) m 2 (ṙ2 + r 2 ϕ 2 + ż 2 ) V (r 2,z) Darn taucht e Wneloornate ϕ nur als Abletung au Somt st e Lagrangeunton unter zetunabhänggen Rotatonen ϕ ϕ ϕ + α nvarant Damt wr ϕ (ϕ α) ene Erhaltungsgröße mr 2 ϕ L z 2318 Galle-Invaranz un Schwerpunt Wr betrachten zwe Inertalsysteme, welche sch relatv zu enaner mt er onstanten Geschwngetv bewegen, h zwschen hren Koornaten gbt es olgene Bezehung: r r +vt t t Man bezechnet es als Galle-Transormaton Des entsprcht em Grenzall nerger Geschwnget er Lorentz-Transormaton De netsche Energe m -Koornatensystem st Her st T 1 2 m (v +v) 2 T +m v v T + M m m v 2 m r v Mv2 t e Gesamtmasse es Systems Damt erhalten wr e neue Lagrangeunton aus er alten: L L + χ(r,t) urch ene Echtransormaton χ(r,t)m r v Mv2 t Aus em oether-theorem önnen wr somt re Erhaltungsgrößen gewnnen, nem wr e Geschwngeten v n e re Raumrchtungen als Parameter α verwenen Dann erhalten wr mt β x,y,z: I vβ t m r v + 1 ẋ β v β 2 Mv2 t m ẋ β t m x β Mv β t const De Schwerpuntsoornate R st urch R 1 M m r enert Aus em oether-theorem olgt amt Her st Pt MR Mvt MR 0 const P m ẋ β er Impuls es Gesamtsystems Des beeutet, ass sch er Schwerpunt geralng un glechörmg bewegt, 1 R(t)R 0 + M P v t Mt ener Transormaton n en bewegtes Bezugsystem mt er Geschwnget v 1 M P wr R zu ener Erhaltungsgröße Deses ausgezechnete Bezugsystem heßt auch Schwerpuntsystem 2319 Zusammenassung Wr haben amt olgenen Symmetren Erhaltungsgrößen n enem mechanschen System 34
14 2 Analytsche Mechan Translatonsnvaranz Gesamtmpulserhaltung (vetorell) Rotatonsnvaranz um e Achse n Gesamtrehmpulserhaltung ür e entsprechene Komponente Galle-Invaranz Frehet es Ursprungs, bzw Schwerpuntssystem (vetorell) Translatonsnvaranz n er Zet Energeerhaltung (salar) Im reen Raum haben wr amt nsgesamt 10 Erhaltungsgrößen: 6 Schwerpuntsntegrale, 3 Drehmpuls- un en Energentegral, e mt 10 ontnuerlchen Größen n Zusammenhang stehen 24 Zentralratproblem un Keplerproblem Wr betrachten zwe Massenpunte m 1,m 2 m Raum, e auenaner ene Krat ausüben, e n Rchtung es Relatvabstanr r 1 r 2 zegt un nur vom Abstan r abhängt Solch en Zentralratproblem st onvervatv, mt enem rotatonsymmetrschen Potenzal V (r) De Lagrangeunton st urch gegeben L m 1 2 ṙ m 1 2 ṙ 2 2 V ( r 1 r 2 ) (215) Wegen er Translatonsnvaranz m Raum st er Gesamtmpuls erhalten Mt er Galle-Invaranz transormeren wr ns Schwerpuntsystem R m 1r 1 + m 2 r 2 m 1 + m 2 (216) r 1 R + m 2 r (217) M r 2 R m 1 r (218) M mt M m 1 + m 2 De transormert Lagrange- Funton lautet ann L m 1 Ṙ m M 2 m 2 ṙ + Ṙ m 1 2 M 2 ṙ V (219) (r) M Ṙ 2 + µ 2 2 ṙ 2 V (r), (220) wobe wr e reuzerte Masse µ µ m 1m 2 m 1 + m 2 (221) un e Gesamtmasse M m 1 + m 2 engeührt haben R zylsch Schwerpuntsmpuls P M Ṙ const Im Schwerpuntsystem glt auch noch e Erhaltung es Drehmpules Da L r p const (222) rl r(r p)0 (223) 35
Kapitel 5. Symmetrien und Erhaltungsgrößen. 5.1 Symmetrietransformationen
 Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
18. Vorlesung Sommersemester
 8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Dynamik starrer Körper
 Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Kreisel. koerperfestes KS. z y. raumfestes KS. Starrer Körper: System von Massepunkten m i, deren Abstände r i r j untereinander konstant sind.
 Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Methoden der innerbetrieblichen Leistungsverrechnung
 Methoden der nnerbetreblchen Lestungsverrechnung In der nnerbetreblchen Lestungsverrechnung werden de Gemenosten der Hlfsostenstellen auf de Hauptostenstellen übertragen. Grundlage dafür snd de von den
Methoden der nnerbetreblchen Lestungsverrechnung In der nnerbetreblchen Lestungsverrechnung werden de Gemenosten der Hlfsostenstellen auf de Hauptostenstellen übertragen. Grundlage dafür snd de von den
1 Mehrdimensionale Analysis
 1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
Geld- und Finanzmärkte
 Gel- un Fnanzmärkte Prof. Dr. Volker Clausen akroökonomk 1 Sommersemester 2008 Fole 1 Gel- un Fnanzmärkte 4.1 De Gelnachfrage 4.2 De Bestmmung es Znssatzes I 4.3 De Bestmmung es Znssatzes II 4.4 Zwe alternatve
Gel- un Fnanzmärkte Prof. Dr. Volker Clausen akroökonomk 1 Sommersemester 2008 Fole 1 Gel- un Fnanzmärkte 4.1 De Gelnachfrage 4.2 De Bestmmung es Znssatzes I 4.3 De Bestmmung es Znssatzes II 4.4 Zwe alternatve
12 LK Ph / Gr Elektrische Leistung im Wechselstromkreis 1/5 31.01.2007. ω Additionstheorem: 2 sin 2 2
 1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
3. Lineare Algebra (Teil 2)
 Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Anwendungsmöglichkeiten von Lernverfahren
 Künstlche Neuronale Netze Lernen n neuronalen Netzen 2 / 30 Anwendungsmöglcheten von Lernverfahren Prnzpelle Möglcheten Verbndungsorentert 1 Hnzufügen neuer Verbndungen 2 Löschen bestehender Verbndungen
Künstlche Neuronale Netze Lernen n neuronalen Netzen 2 / 30 Anwendungsmöglcheten von Lernverfahren Prnzpelle Möglcheten Verbndungsorentert 1 Hnzufügen neuer Verbndungen 2 Löschen bestehender Verbndungen
NSt. Der Wert für: x= +1 liegt, erkennbar an dem zugehörigen Funktionswert, der gesuchten Nullstelle näher.
 PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
Prof. Dr.-Ing. P. Eberhard, Prof. Dr.-Ing. M. Hanss SS 2016 A 1.1
 Insttut für Technsche und Num. Mechan Technsche Mechan IV Prof. Dr.-Ing. P. Eberhard, Prof. Dr.-Ing. M. Hanss SS 16 A 1.1 Aufgabe 1: En mechansches Sstem wrd durch folgende lnearserte Bewegungsglechungen
Insttut für Technsche und Num. Mechan Technsche Mechan IV Prof. Dr.-Ing. P. Eberhard, Prof. Dr.-Ing. M. Hanss SS 16 A 1.1 Aufgabe 1: En mechansches Sstem wrd durch folgende lnearserte Bewegungsglechungen
Aufgabe 8 (Gewinnmaximierung bei vollständiger Konkurrenz):
 LÖSUNG AUFGABE 8 ZUR INDUSTRIEÖKONOMIK SEITE 1 VON 6 Aufgabe 8 (Gewnnmaxmerung be vollständger Konkurrenz): Betrachtet wrd en Unternehmen, das ausschleßlch das Gut x produzert. De m Unternehmen verwendete
LÖSUNG AUFGABE 8 ZUR INDUSTRIEÖKONOMIK SEITE 1 VON 6 Aufgabe 8 (Gewnnmaxmerung be vollständger Konkurrenz): Betrachtet wrd en Unternehmen, das ausschleßlch das Gut x produzert. De m Unternehmen verwendete
3 Vorlesung: Lagrange Mechanik I. 3.1 Zwangsbedingungen. Beispiele (nach Kuypers)
 3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
Physik A VL11 ( )
 Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Konkave und Konvexe Funktionen
 Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Hamiltonsche Mechanik
 Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
1 Definition und Grundbegriffe
 1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
Für jeden reinen, ideal kristallisierten Stoff ist die Entropie am absoluten Nullpunkt gleich
 Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
12 UMPU Tests ( UMP unbiased )
 89 1 UMPU Tests ( UMP unbased ) Nach Bemerkung 11.8(b) exstert m Allgemenen ken zwesetger UMP- Test zu enem Nveau α. Deshalb Enschränkung auf unverfälschte Tests: ϕ Φ α heßt unverfälscht (unbased) zum
89 1 UMPU Tests ( UMP unbased ) Nach Bemerkung 11.8(b) exstert m Allgemenen ken zwesetger UMP- Test zu enem Nveau α. Deshalb Enschränkung auf unverfälschte Tests: ϕ Φ α heßt unverfälscht (unbased) zum
Methoden zur Bewertung von Credit Default Swaps
 Methoen zur Bewertung von Cret Default Swas Dr. Walter Gruber ( PLUS GmbH); Sylva Lause (Sarasse Hannover) Inhalt Enführung... Moell er Dscounte Sreas... 3 Moell er Ajuste Sreas... 4 Moell von JPMorgan...
Methoen zur Bewertung von Cret Default Swas Dr. Walter Gruber ( PLUS GmbH); Sylva Lause (Sarasse Hannover) Inhalt Enführung... Moell er Dscounte Sreas... 3 Moell er Ajuste Sreas... 4 Moell von JPMorgan...
MOD-01 LAGRANGE FORMALISMUS -- TEIL 1
 MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
3.3 Lineare Abbildungen und Matrizen
 33 LINEARE ABBILDUNGEN UND MATRIZEN 87 33 Lneare Abbldungen und Matrzen Wr wollen jetzt de numersche Behandlung lnearer Abbldungen zwschen Vektorräumen beschreben be der vorgegebene Basen de Hauptrolle
33 LINEARE ABBILDUNGEN UND MATRIZEN 87 33 Lneare Abbldungen und Matrzen Wr wollen jetzt de numersche Behandlung lnearer Abbldungen zwschen Vektorräumen beschreben be der vorgegebene Basen de Hauptrolle
5. Gruppenübung zur Vorlesung. Höhere Mathematik 1. Wintersemester 2012/2013
 O. Alaya, S. Demrel M. Fetzer, B. Krnn M. Wed 5. Gruppenübung zur Vorlesung Höhere Mathematk Wntersemester /3 Dr. M. Künzer Prof. Dr. M. Stroppel Lösungshnwese zu den Hausaufgaben: Aufgabe H 6. Darstellungen
O. Alaya, S. Demrel M. Fetzer, B. Krnn M. Wed 5. Gruppenübung zur Vorlesung Höhere Mathematk Wntersemester /3 Dr. M. Künzer Prof. Dr. M. Stroppel Lösungshnwese zu den Hausaufgaben: Aufgabe H 6. Darstellungen
Netzwerkstrukturen. Entfernung in Kilometer:
 Netzwerkstrukturen 1) Nehmen wr an, n enem Neubaugebet soll für 10.000 Haushalte en Telefonnetz nstallert werden. Herzu muss von jedem Haushalt en Kabel zur nächstgelegenen Vermttlungsstelle gezogen werden.
Netzwerkstrukturen 1) Nehmen wr an, n enem Neubaugebet soll für 10.000 Haushalte en Telefonnetz nstallert werden. Herzu muss von jedem Haushalt en Kabel zur nächstgelegenen Vermttlungsstelle gezogen werden.
Flußnetzwerke - Strukturbildung in der natürlichen Umwelt -
 Flußnetzwerke - Strukturbldung n der natürlchen Umwelt - Volkhard Nordmeer, Claus Zeger und Hans Joachm Schlchtng Unverstät - Gesamthochschule Essen Das wohl bekannteste und größte exsterende natürlche
Flußnetzwerke - Strukturbldung n der natürlchen Umwelt - Volkhard Nordmeer, Claus Zeger und Hans Joachm Schlchtng Unverstät - Gesamthochschule Essen Das wohl bekannteste und größte exsterende natürlche
4. Energie, Arbeit, Leistung, Impuls
 34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
p : Impuls in Ns v : Geschwindigkeit in m/s
 -I.C9-4 Impuls 4. Impuls und Kraftstoß 4.. Impuls De Bewegung enes Körpers wrd bespelswese durch de Geschwndgket beschreben. Um de Bewegung enes Körpers zu ändern braucht man ene Kraft (Abb.). Dese führt
-I.C9-4 Impuls 4. Impuls und Kraftstoß 4.. Impuls De Bewegung enes Körpers wrd bespelswese durch de Geschwndgket beschreben. Um de Bewegung enes Körpers zu ändern braucht man ene Kraft (Abb.). Dese führt
8. MARKOVKETTEN 127. Abbildung 8.1: Reduzible und periodische Markovkette. p ji IIP[X n 1 = j] = [(IIP[X n 1 = j]) j E P ] i. j=0
![8. MARKOVKETTEN 127. Abbildung 8.1: Reduzible und periodische Markovkette. p ji IIP[X n 1 = j] = [(IIP[X n 1 = j]) j E P ] i. j=0 8. MARKOVKETTEN 127. Abbildung 8.1: Reduzible und periodische Markovkette. p ji IIP[X n 1 = j] = [(IIP[X n 1 = j]) j E P ] i. j=0](/thumbs/52/30042483.jpg) 8. MARKOVKETTEN 17 8. Marovetten Abbldung 8.1: Reduzble und perodsche Marovette 8.1. Homogene Marovetten n dsreter Zet En Prozess {X n : n IIN} hesst homogene Marovette (n dsreter Zet) mt (abzählbarem)
8. MARKOVKETTEN 17 8. Marovetten Abbldung 8.1: Reduzble und perodsche Marovette 8.1. Homogene Marovetten n dsreter Zet En Prozess {X n : n IIN} hesst homogene Marovette (n dsreter Zet) mt (abzählbarem)
1 = Gl.(12.7) Der Vergleich mit Gl. (12.3) zeigt, dass für die laminare Rohrströmung die Rohrreibungszahl
 0. STRÖMUNG INKOMPRESSIBLER FLUIDE IN ROHRLEITUNGEN Enführung Vorlesung Strömungslehre Prof. Dr.-Ing. Chrstan Olver Pascheret C. O. Pascheret Insttute of Flud Mechancs and Acoustcs olver.pascheret@tu-berln.de
0. STRÖMUNG INKOMPRESSIBLER FLUIDE IN ROHRLEITUNGEN Enführung Vorlesung Strömungslehre Prof. Dr.-Ing. Chrstan Olver Pascheret C. O. Pascheret Insttute of Flud Mechancs and Acoustcs olver.pascheret@tu-berln.de
Daten sind in Tabellenform gegeben durch die Eingabe von FORMELN können mit diesen Daten automatisierte Berechnungen durchgeführt werden.
 Ene kurze Enführung n EXCEL Daten snd n Tabellenform gegeben durch de Engabe von FORMELN können mt desen Daten automatserte Berechnungen durchgeführt werden. Menüleste Symbolleste Bearbetungszele aktve
Ene kurze Enführung n EXCEL Daten snd n Tabellenform gegeben durch de Engabe von FORMELN können mt desen Daten automatserte Berechnungen durchgeführt werden. Menüleste Symbolleste Bearbetungszele aktve
Seminar Analysis und Geometrie Professor Dr. Martin Schmidt - Markus Knopf - Jörg Zentgraf. - Fixpunktsatz von Schauder -
 Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
2. Nullstellensuche. Eines der ältesten numerischen Probleme stellt die Bestimmung der Nullstellen einer Funktion f(x) = 0 dar.
 . Nullstellensuche Enes der ältesten numerschen Probleme stellt de Bestmmung der Nullstellen ener Funkton = dar. =c +c =c +c +c =Σc =c - sn 3 Für ene Gerade st das Problem trval, de Wurzel ener quadratschen
. Nullstellensuche Enes der ältesten numerschen Probleme stellt de Bestmmung der Nullstellen ener Funkton = dar. =c +c =c +c +c =Σc =c - sn 3 Für ene Gerade st das Problem trval, de Wurzel ener quadratschen
KAPITEL 8. Rekorde Satz von Rényi Der folgende Satz beschreibt die gemeinsame Verteilung der Zufallsvariablen ξ 1, ξ 2,...
 KAPITEL 8 Rekore Seen X, X 2,... unabhängge un entsch vertelte Zufallsvarablen mt stetger Vertelungsfunkton F. Wr setzen M n = max{x,..., X n }. Defnton 8.0.. Wr sagen, ass zum Zetpunkt n N en Rekor aufgestellt
KAPITEL 8 Rekore Seen X, X 2,... unabhängge un entsch vertelte Zufallsvarablen mt stetger Vertelungsfunkton F. Wr setzen M n = max{x,..., X n }. Defnton 8.0.. Wr sagen, ass zum Zetpunkt n N en Rekor aufgestellt
Der Satz von COOK (1971)
 Der Satz von COOK (1971) Voraussetzung: Das Konzept der -Band-Turng-Maschne (TM) 1.) Notatonen: Ene momentane Beschrebung (mb) ener Konfguraton ener TM st en -Tupel ( α1, α2,..., α ) mt α = xqy, falls
Der Satz von COOK (1971) Voraussetzung: Das Konzept der -Band-Turng-Maschne (TM) 1.) Notatonen: Ene momentane Beschrebung (mb) ener Konfguraton ener TM st en -Tupel ( α1, α2,..., α ) mt α = xqy, falls
Kapitel 1. Grundlagen der Fehleranalyse
 Kaptel Grundlagen der Fehleranalyse B... (Fehlerarten): Von den Fehlerquellen ausgehend unterscheden wr dre unterschedlche Fehlerarten: () Engangsehler Dese entstehen durch a) Modellerungsehler (Z.B. wenn
Kaptel Grundlagen der Fehleranalyse B... (Fehlerarten): Von den Fehlerquellen ausgehend unterscheden wr dre unterschedlche Fehlerarten: () Engangsehler Dese entstehen durch a) Modellerungsehler (Z.B. wenn
Lagrangesche Mechanik
 Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
1.6 Energie 1.6.1 Arbeit und Leistung Wird ein Körper unter Wirkung der Kraft F längs eines Weges s verschoben, so wird dabei die Arbeit
 3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
3.6 Energe.6. Arbe und Lesung Wrd en Körper uner Wrkung der Kraf F längs enes Weges s verschoben, so wrd dabe de Arbe W = F s Arbe = Kraf Weg verrche. In deser enfachen Form gülg, wenn folgende Voraussezungen
9. Der starre Körper; Rotation I
 Mechank De stae Köpe; Rotaton I 9. De stae Köpe; Rotaton I 9.. Enletung bshe: (Systeme on) Punktmassen jetzt: Betachtung ausgedehnte Köpe, übe de de Masse glechmäßg etelt st (kene Atome). Köpe soll sch
Mechank De stae Köpe; Rotaton I 9. De stae Köpe; Rotaton I 9.. Enletung bshe: (Systeme on) Punktmassen jetzt: Betachtung ausgedehnte Köpe, übe de de Masse glechmäßg etelt st (kene Atome). Köpe soll sch
Statistik und Wahrscheinlichkeit
 Regeln der Wahrschenlchketsrechnung tatstk und Wahrschenlchket Regeln der Wahrschenlchketsrechnung Relatve Häufgket n nt := Eregnsalgebra Eregnsraum oder scheres Eregns und n := 00 Wahrschenlchket Eregnsse
Regeln der Wahrschenlchketsrechnung tatstk und Wahrschenlchket Regeln der Wahrschenlchketsrechnung Relatve Häufgket n nt := Eregnsalgebra Eregnsraum oder scheres Eregns und n := 00 Wahrschenlchket Eregnsse
1. Runde 2010. Aufgaben und Lösungen. Bundeswettbewerb Mathematik
 Bundeswettbewerb Mathemat Wssenschaftszentrum Postfach 2 14 48 53144 Bonn Fon: 228-9 59 15-2 Fax: 228-9 59 15-29 e-mal: nfo@bundeswettbewerb-mathemat.de www.bundeswettbewerb-mathemat.de Korreturommsson
Bundeswettbewerb Mathemat Wssenschaftszentrum Postfach 2 14 48 53144 Bonn Fon: 228-9 59 15-2 Fax: 228-9 59 15-29 e-mal: nfo@bundeswettbewerb-mathemat.de www.bundeswettbewerb-mathemat.de Korreturommsson
6. Elektrische Wechselgrössen
 Grundlagen der Elektrotechnk GE 2 [Buch GE 2: Seten 72-14] Grundbegrffe Wechselgrössen Perodsche Wechselgrössen Lnearer und quadratscher Mttelwert Der Effektvwert Bezugspfele Verallgemenerte Zetfunktonen
Grundlagen der Elektrotechnk GE 2 [Buch GE 2: Seten 72-14] Grundbegrffe Wechselgrössen Perodsche Wechselgrössen Lnearer und quadratscher Mttelwert Der Effektvwert Bezugspfele Verallgemenerte Zetfunktonen
Andreas Schulz. 18. Juni Lokal- orthogonale Koordinatesysteme Math. Hilfsmittel: Antisymmetrischer Tensor: Kreuzprodukt, Spatprodukt,
 Tutorum zur G2 Srker - SS3 Mathematscher Notfallkoffer : Dfferentaloperatoren und Integraton n allgemenen, krummlng-orthogonalen Korrdnatensystemen Andreas Schulz 8. Jun 23 Inhaltsverzechns Bevor es losgeht...
Tutorum zur G2 Srker - SS3 Mathematscher Notfallkoffer : Dfferentaloperatoren und Integraton n allgemenen, krummlng-orthogonalen Korrdnatensystemen Andreas Schulz 8. Jun 23 Inhaltsverzechns Bevor es losgeht...
3.1 Grundlagen der Multivariaten Modellierung
 Semnar: Quanttatves Rskomanagement Multvarate Moelle I Prof: Hanspeter.Schml Betreuung: Jula Esenberg Zhou,Yng 3. Multvarate Moelle I Fnanzelle Rskomoelle für en Absatzmarkt oer für Kretrsken sn grunsätzlch
Semnar: Quanttatves Rskomanagement Multvarate Moelle I Prof: Hanspeter.Schml Betreuung: Jula Esenberg Zhou,Yng 3. Multvarate Moelle I Fnanzelle Rskomoelle für en Absatzmarkt oer für Kretrsken sn grunsätzlch
Erwartungswert, Varianz, Standardabweichung
 RS 24.2.2005 Erwartungswert_Varanz_.mcd 4) Erwartungswert Erwartungswert, Varanz, Standardabwechung Be jedem Glücksspel nteresseren den Speler vor allem de Gewnnchancen. 1. Bespel: Setzen auf 1. Dutzend
RS 24.2.2005 Erwartungswert_Varanz_.mcd 4) Erwartungswert Erwartungswert, Varanz, Standardabwechung Be jedem Glücksspel nteresseren den Speler vor allem de Gewnnchancen. 1. Bespel: Setzen auf 1. Dutzend
Spiele und Codes. Rafael Mechtel
 Spele und Codes Rafael Mechtel Koderungstheore Worum es geht Über enen Kanal werden Informatonen Übertragen. De Informatonen werden dabe n Worte über enem Alphabet Q übertragen, d.h. als Tupel w = (w,,
Spele und Codes Rafael Mechtel Koderungstheore Worum es geht Über enen Kanal werden Informatonen Übertragen. De Informatonen werden dabe n Worte über enem Alphabet Q übertragen, d.h. als Tupel w = (w,,
50 Matrixnormen und Eigenwertabschätzungen
 50 Matrxnormen und Egenwertabschätzungen 501 Motvaton De Berechnung der Egenwerte ener Matrx st aufwändg (vgl Kaptel 45, Kaptel 51) Kann man de Egenwerte ener Matrx mt gerngem Aufwand abschätzen? Des spelt
50 Matrxnormen und Egenwertabschätzungen 501 Motvaton De Berechnung der Egenwerte ener Matrx st aufwändg (vgl Kaptel 45, Kaptel 51) Kann man de Egenwerte ener Matrx mt gerngem Aufwand abschätzen? Des spelt
4. Musterlösung. Problem 1: Kreuzende Schnitte **
 Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
3.2 Die Kennzeichnung von Partikeln 3.2.1 Partikelmerkmale
 3. De Kennzechnung von Patkeln 3..1 Patkelmekmale De Kennzechnung von Patkeln efolgt duch bestmmte, an dem Patkel mess bae und deses endeutg beschebende physka lsche Gößen (z.b. Masse, Volumen, chaaktestsche
3. De Kennzechnung von Patkeln 3..1 Patkelmekmale De Kennzechnung von Patkeln efolgt duch bestmmte, an dem Patkel mess bae und deses endeutg beschebende physka lsche Gößen (z.b. Masse, Volumen, chaaktestsche
Auswertung univariater Datenmengen - deskriptiv
 Auswertung unvarater Datenmengen - desrptv Bblografe Prof. Dr. Küc; Statst, Vorlesungssrpt Abschntt 6.. Bleymüller/Gehlert/Gülcher; Statst für Wrtschaftswssenschaftler Verlag Vahlen Bleymüller/Gehlert;
Auswertung unvarater Datenmengen - desrptv Bblografe Prof. Dr. Küc; Statst, Vorlesungssrpt Abschntt 6.. Bleymüller/Gehlert/Gülcher; Statst für Wrtschaftswssenschaftler Verlag Vahlen Bleymüller/Gehlert;
Unter der Drehgruppe verstehen wir diegruppe der homogenen linearen Transformationen
 Darstellunstheore der SO() und SU() Powtschnk Alexander. Defnton Darstellun Ene Darstellun ener Gruppe G st homomorphe Abbldun von deser Gruppe auf ene Gruppe nchtsnulärer lnearer Operatoren auf enem Vektorraum
Darstellunstheore der SO() und SU() Powtschnk Alexander. Defnton Darstellun Ene Darstellun ener Gruppe G st homomorphe Abbldun von deser Gruppe auf ene Gruppe nchtsnulärer lnearer Operatoren auf enem Vektorraum
Z Z, kurz { } Zählt die Reihenfolge der Buchstaben (ja/nein) Daraus ergeben sich wiederum vier Möglichkeiten, Wörter der Länge k zu bilden.
 Kombnator. Problemstellung Ausgangspunt be ombnatorschen Fragestellungen st mmer ene endlche Menge M, aus deren Elementen man endlche Zusammenstellungen von Elementen aus M bldet. Formal gesprochen bedeutet
Kombnator. Problemstellung Ausgangspunt be ombnatorschen Fragestellungen st mmer ene endlche Menge M, aus deren Elementen man endlche Zusammenstellungen von Elementen aus M bldet. Formal gesprochen bedeutet
Hydrosystemanalyse: Finite-Elemente-Methode (FEM)
 Hydrosystemanalyse: Prof. Dr.-Ing. habl. Olaf Koldtz 1 Helmholtz Centre for Envronmental Research UFZ, Lepzg 2 Technsche Unverstät Dresden TUD, Dresden Dresden, 03. Jul 2015 1/31 Prof. Dr.-Ing. habl. Olaf
Hydrosystemanalyse: Prof. Dr.-Ing. habl. Olaf Koldtz 1 Helmholtz Centre for Envronmental Research UFZ, Lepzg 2 Technsche Unverstät Dresden TUD, Dresden Dresden, 03. Jul 2015 1/31 Prof. Dr.-Ing. habl. Olaf
Nullstellen Suchen und Optimierung
 Nullstellen Suchen und Optmerung Typsche Probleme: De optmale Bahnkurve De Mnmerung des Erwartungswertes ür den Hamltonan Wr möchten ene Funkton mnmeren oder mameren solch en Problem wrd Optmerung genannt!
Nullstellen Suchen und Optmerung Typsche Probleme: De optmale Bahnkurve De Mnmerung des Erwartungswertes ür den Hamltonan Wr möchten ene Funkton mnmeren oder mameren solch en Problem wrd Optmerung genannt!
Einführung in die Wahrscheinlichkeitsrechnung. Wahrscheinlichkeitsrechnung. Übersicht. Wahrscheinlichkeitsrechnung. bedinge Wahrscheinlichkeit
 Enführung n de bednge Wahrschenlchket Laplace-Wahrschenlchket p 0.56??? Zufallsexperment Randwahrschenlchket Überscht Was st Wahrschenlchket? Rechenregeln Der Multplkatonssatz Axomatsche Herletung Unabhänggket
Enführung n de bednge Wahrschenlchket Laplace-Wahrschenlchket p 0.56??? Zufallsexperment Randwahrschenlchket Überscht Was st Wahrschenlchket? Rechenregeln Der Multplkatonssatz Axomatsche Herletung Unabhänggket
Kreditrisikomodellierung und Risikogewichte im Neuen Baseler Accord
 1 Kredtrskomodellerung und Rskogewchte m Neuen Baseler Accord erschenen n: Zetschrft für das gesamte Kredtwesen (ZfgK), 54. Jahrgang, 2001, S. 1004-1005. Prvatdozent Dr. Hans Rau-Bredow, Lehrstuhl für
1 Kredtrskomodellerung und Rskogewchte m Neuen Baseler Accord erschenen n: Zetschrft für das gesamte Kredtwesen (ZfgK), 54. Jahrgang, 2001, S. 1004-1005. Prvatdozent Dr. Hans Rau-Bredow, Lehrstuhl für
Versicherungstechnischer Umgang mit Risiko
 Verscherungstechnscher Umgang mt Rsko. Denstlestung Verscherung: Schadensdeckung von für de enzelne Person ncht tragbaren Schäden durch den fnanzellen Ausglech n der Zet und m Kollektv. Des st möglch über
Verscherungstechnscher Umgang mt Rsko. Denstlestung Verscherung: Schadensdeckung von für de enzelne Person ncht tragbaren Schäden durch den fnanzellen Ausglech n der Zet und m Kollektv. Des st möglch über
Proseminar Spieltheorie SS 2006 Ausarbeitung zum Vortrag Allgemeine Zwei-Personenspiele am Vortragender: Florian Leiner
 Prosemnar Speltheore SS 2006 Ausarbetung zum Vortrag Allgemene Zwe-Personenspele am 06.07.2006 Vortragender: Floran Lener Der Vortrag basert auf dem entsprechenden Kaptel wo-person general-sum games aus
Prosemnar Speltheore SS 2006 Ausarbetung zum Vortrag Allgemene Zwe-Personenspele am 06.07.2006 Vortragender: Floran Lener Der Vortrag basert auf dem entsprechenden Kaptel wo-person general-sum games aus
Polygonalisierung einer Kugel. Verfahren für die Polygonalisierung einer Kugel. Eldar Sultanow, Universität Potsdam, sultanow@gmail.com.
 Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Verfahren für de Polygonalserung ener Kugel Eldar Sultanow, Unverstät Potsdam, sultanow@gmal.com Abstract Ene Kugel kann durch mathematsche Funktonen beschreben werden. Man sprcht n desem Falle von ener
Was erwarten wir als Ergebnis von freien Verhandlungen in einer Gruppe mit Koalitionsmöglichkeiten?
 Prof. Dr. Fredel Bolle 1 Prof. Dr. Fredel Bolle Vorlesung 1 Defnton: Kooperatves Spel En ooperatves Spel Γ st en Tupel (N,V), wobe der N = {1,...,m} mt m > 1 de Menge der Speler bezechnet und Was erwarten
Prof. Dr. Fredel Bolle 1 Prof. Dr. Fredel Bolle Vorlesung 1 Defnton: Kooperatves Spel En ooperatves Spel Γ st en Tupel (N,V), wobe der N = {1,...,m} mt m > 1 de Menge der Speler bezechnet und Was erwarten
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 2 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 7: (B. Fredmans Urnenmodell)
6. Hilbertraum und lineare Operatoren (mathematische Grundlagen QM)
 6. Hlbertraum und lneare Operatoren (mathematsche Grundlagen QM) 6.1 Hlbertraum Raum = mathematsches Konstrukt: Vektorraum a) Der lneare komplexe Raum st de Menge von mathematschen Objekten mt folgenden
6. Hlbertraum und lneare Operatoren (mathematsche Grundlagen QM) 6.1 Hlbertraum Raum = mathematsches Konstrukt: Vektorraum a) Der lneare komplexe Raum st de Menge von mathematschen Objekten mt folgenden
6. Modelle mit binären abhängigen Variablen
 6. Modelle mt bnären abhänggen Varablen 6.1 Lneare Wahrschenlchketsmodelle Qualtatve Varablen: Bnäre Varablen: Dese Varablen haben genau zwe möglche Kategoren und nehmen deshalb genau zwe Werte an, nämlch
6. Modelle mt bnären abhänggen Varablen 6.1 Lneare Wahrschenlchketsmodelle Qualtatve Varablen: Bnäre Varablen: Dese Varablen haben genau zwe möglche Kategoren und nehmen deshalb genau zwe Werte an, nämlch
FORMELSAMMLUNG STATISTIK (I)
 Statst I / B. Zegler Formelsammlng FORMELSAMMLUG STATISTIK (I) Statstsche Formeln, Defntonen nd Erläterngen A a X n qaltatves Mermal Mermalsasprägng qanttatves Mermal Mermalswert Anzahl der statstschen
Statst I / B. Zegler Formelsammlng FORMELSAMMLUG STATISTIK (I) Statstsche Formeln, Defntonen nd Erläterngen A a X n qaltatves Mermal Mermalsasprägng qanttatves Mermal Mermalswert Anzahl der statstschen
Diskrete Mathematik 1 WS 2008/09
 Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
5 Integralsätze am Beispiel der Gravitation
 5 INTEGRALSÄTZE AM BEISPIEL DER GRAVITATION 1 5 Integralsätze am Bespel der Gravtaton 5.1 Integralsatz von Stokes Im letzten Kaptel haben wr de Rotaton enes Vektorfeldes engeführt und Lnenntegrale betrachtet.
5 INTEGRALSÄTZE AM BEISPIEL DER GRAVITATION 1 5 Integralsätze am Bespel der Gravtaton 5.1 Integralsatz von Stokes Im letzten Kaptel haben wr de Rotaton enes Vektorfeldes engeführt und Lnenntegrale betrachtet.
Vermessungskunde für Bauingenieure und Geodäten
 Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Lehrstuhl für Empirische Wirtschaftsforschung und Ökonometrie Dr. Roland Füss Statistik II: Schließende Statistik SS 2007
 Lehrstuhl für Emprsche Wrtschaftsforschung und Ökonometre Dr Roland Füss Statstk II: Schleßende Statstk SS 007 5 Mehrdmensonale Zufallsvarablen Be velen Problemstellungen st ene solerte Betrachtung enzelnen
Lehrstuhl für Emprsche Wrtschaftsforschung und Ökonometre Dr Roland Füss Statstk II: Schleßende Statstk SS 007 5 Mehrdmensonale Zufallsvarablen Be velen Problemstellungen st ene solerte Betrachtung enzelnen
Auswertung univariater Datenmengen - deskriptiv
 Auswertung unvarater Datenmengen - desrptv Bblografe Prof. Dr. Küc; Statst, Vorlesungssrpt Abschntt 6.. Bleymüller/Gehlert/Gülcher; Statst für Wrtschaftswssenschaftler Verlag Vahlen Bleymüller/Gehlert;
Auswertung unvarater Datenmengen - desrptv Bblografe Prof. Dr. Küc; Statst, Vorlesungssrpt Abschntt 6.. Bleymüller/Gehlert/Gülcher; Statst für Wrtschaftswssenschaftler Verlag Vahlen Bleymüller/Gehlert;
Vorlesung 1. Prof. Dr. Klaus Röder Lehrstuhl für BWL, insb. Finanzdienstleistungen Universität Regensburg. Prof. Dr. Klaus Röder Folie 1
 Vorlesung Entschedungslehre h SS 205 Prof. Dr. Klaus Röder Lehrstuhl für BWL, nsb. Fnanzdenstlestungen Unverstät Regensburg Prof. Dr. Klaus Röder Fole Organsatorsches Relevante Informatonen önnen Se stets
Vorlesung Entschedungslehre h SS 205 Prof. Dr. Klaus Röder Lehrstuhl für BWL, nsb. Fnanzdenstlestungen Unverstät Regensburg Prof. Dr. Klaus Röder Fole Organsatorsches Relevante Informatonen önnen Se stets
1 BWL 4 Tutorium V vom 15.05.02
 1 BWL 4 Tutorum V vom 15.05.02 1.1 Der Tlgungsfaktor Der Tlgungsfaktor st der Kehrwert des Endwertfaktors (EWF). EW F (n; ) = (1 + )n 1 T F (n; ) = 1 BWL 4 TUTORIUM V VOM 15.05.02 (1 ) n 1 Mt dem Tlgungsfaktor(TF)
1 BWL 4 Tutorum V vom 15.05.02 1.1 Der Tlgungsfaktor Der Tlgungsfaktor st der Kehrwert des Endwertfaktors (EWF). EW F (n; ) = (1 + )n 1 T F (n; ) = 1 BWL 4 TUTORIUM V VOM 15.05.02 (1 ) n 1 Mt dem Tlgungsfaktor(TF)
Bilderbuch zur Vorlesung Experimentalphysik -1. Struktur der Materie. Verhalten von Materie und Strahlung. Wintersemester 2012/13
 Fragestellung der Physk Blderbuch zur Vorlesung Expermentalphysk - Struktur der Matere Verhalten von Matere und Strahlung Wntersemester / Prof. Dr. Hanspeter Helm Un-Freburg quanttatve Beobachtung (Messung)
Fragestellung der Physk Blderbuch zur Vorlesung Expermentalphysk - Struktur der Matere Verhalten von Matere und Strahlung Wntersemester / Prof. Dr. Hanspeter Helm Un-Freburg quanttatve Beobachtung (Messung)
Nernstscher Verteilungssatz
 Insttut für Physkalsche Cheme Grundpraktkum 7. NERNSTSCHER VERTEILUNGSSATZ Stand 03/11/2006 Nernstscher Vertelungssatz 1. Versuchsplatz Komponenten: - Schedetrchter - Büretten - Rührer - Bechergläser 2.
Insttut für Physkalsche Cheme Grundpraktkum 7. NERNSTSCHER VERTEILUNGSSATZ Stand 03/11/2006 Nernstscher Vertelungssatz 1. Versuchsplatz Komponenten: - Schedetrchter - Büretten - Rührer - Bechergläser 2.
Beschreibende Statistik Mittelwert
 Beschrebende Statstk Mttelwert Unter dem arthmetschen Mttel (Mttelwert) x von n Zahlen verstehen wr: x = n = x = n (x +x +...+x n ) Desen Mttelwert untersuchen wr etwas genauer.. Zege für n = 3: (x x )
Beschrebende Statstk Mttelwert Unter dem arthmetschen Mttel (Mttelwert) x von n Zahlen verstehen wr: x = n = x = n (x +x +...+x n ) Desen Mttelwert untersuchen wr etwas genauer.. Zege für n = 3: (x x )
Wir betrachten in diesem Abschnitt Matrixspiele in der Maximierungsform, also endliche 2 Personen Nullsummenspiele der Gestalt
 Kaptel 3 Zwe Personen Spele 3.1 Matrxspele 3.2 Matrxspele n gemschten Strategen 3.3 B Matrxspele und quadratsche Programme 3.4 B Matrxspele und lneare Komplementartätsprobleme 3.1 Matrxspele Wr betrachten
Kaptel 3 Zwe Personen Spele 3.1 Matrxspele 3.2 Matrxspele n gemschten Strategen 3.3 B Matrxspele und quadratsche Programme 3.4 B Matrxspele und lneare Komplementartätsprobleme 3.1 Matrxspele Wr betrachten
Ko- und kontravariante Darstellung
 Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Zweck... 2. Geltungsbereich... 2. I. Generelles zur Risikoquantifizierung im SST... 2. I.1 Analytisches Modell... 3. I.1.1 Vollversion...
 WEGLEITUNG zum SST-Martrso-Stanarmoell Ausgabe vom 23. Dezember 2015 Inhaltsverzechns Zwec... 2 Geltungsberech... 2 I. Generelles zur Rsoquantfzerung m SST... 2 I.1 Analytsches Moell... 3 I.1.1 Vollverson...
WEGLEITUNG zum SST-Martrso-Stanarmoell Ausgabe vom 23. Dezember 2015 Inhaltsverzechns Zwec... 2 Geltungsberech... 2 I. Generelles zur Rsoquantfzerung m SST... 2 I.1 Analytsches Moell... 3 I.1.1 Vollverson...
13.Selbstinduktion; Induktivität
 13Sebstndukton; Induktvtät 131 Sebstndukton be En- und Ausschatvorgängen Versuch 1: Be geschossenem Schater S wrd der Wderstand R 1 so groß gewäht, dass de Gühämpchen G 1 und G 2 gech he euchten Somt snd
13Sebstndukton; Induktvtät 131 Sebstndukton be En- und Ausschatvorgängen Versuch 1: Be geschossenem Schater S wrd der Wderstand R 1 so groß gewäht, dass de Gühämpchen G 1 und G 2 gech he euchten Somt snd
Ordnungsstatistiken und Quantile
 KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
KAPITEL Ordugsstatste ud Quatle Um robuste Lage- ud Streuugsparameter eführe zu öe, beötge wr Ordugsstatste ud Quatle... Ordugsstatste ud Quatle Defto... Se (x,..., x R ee Stchprobe. Wr öe de Elemete der
Zufallsvariable, Wahrscheinlichkeitsverteilungen und Erwartungswert
 R. Brnkmann http://brnkmann-du.de Sete..8 Zufallsvarable, Wahrschenlchketsvertelungen und Erwartungswert Enführungsbespel: Zwe Würfel (en blauer und en grüner) werden 4 mal zusammen geworfen. De Häufgketen
R. Brnkmann http://brnkmann-du.de Sete..8 Zufallsvarable, Wahrschenlchketsvertelungen und Erwartungswert Enführungsbespel: Zwe Würfel (en blauer und en grüner) werden 4 mal zusammen geworfen. De Häufgketen
6.5. Rückgewinnung des Zeitvorgangs: Rolle der Pole und Nullstellen
 196 6.5. Rückgewnnung des Zetvorgangs: Rolle der Pole und Nullstellen We n 6.2. und 6.. gezegt wurde, st de Übertragungsfunkton G( enes lnearen zetnvaranten Systems mt n unabhänggen Spechern ene gebrochen
196 6.5. Rückgewnnung des Zetvorgangs: Rolle der Pole und Nullstellen We n 6.2. und 6.. gezegt wurde, st de Übertragungsfunkton G( enes lnearen zetnvaranten Systems mt n unabhänggen Spechern ene gebrochen
Boost-Schaltwandler für Blitzgeräte
 jean-claude.feltes@educaton.lu 1 Boost-Schaltwandler für Bltzgeräte In Bltzgeräten wrd en Schaltwandler benutzt um den Bltzkondensator auf ene Spannung von engen 100V zu laden. Oft werden dazu Sperrwandler
jean-claude.feltes@educaton.lu 1 Boost-Schaltwandler für Bltzgeräte In Bltzgeräten wrd en Schaltwandler benutzt um den Bltzkondensator auf ene Spannung von engen 100V zu laden. Oft werden dazu Sperrwandler
Normalisierung. 8. Expressionsdaten: Normalisierung. Normalisierung
 ormalserung 8. Expressonsaten: ormalserung 1. Bologsche Frage. Expermentelles Desgn 3. Mcroarray-Experment 4. Blanalyse 5. ormalserung 6. Statstsche Analyse 7. Bologsche Verfkaton an Interpretaton Globale
ormalserung 8. Expressonsaten: ormalserung 1. Bologsche Frage. Expermentelles Desgn 3. Mcroarray-Experment 4. Blanalyse 5. ormalserung 6. Statstsche Analyse 7. Bologsche Verfkaton an Interpretaton Globale
Universität Karlsruhe (TH)
 Unverstät Karlsruhe (TH) Forschungsunverstät gegründet 825 Parallele Algorthmen I Augaben und Lösungen Pro. Dr. Walter F. Tchy Dr. Vctor Pankratus Davd Meder Augabe () Gegeben se en N-elementger Zahlenvektor
Unverstät Karlsruhe (TH) Forschungsunverstät gegründet 825 Parallele Algorthmen I Augaben und Lösungen Pro. Dr. Walter F. Tchy Dr. Vctor Pankratus Davd Meder Augabe () Gegeben se en N-elementger Zahlenvektor
Übungen zur Vorlesung Physikalische Chemie 2 (B. Sc.) Lösungsvorschlag zu Blatt 6
 Übungen zur Vorlesung Physkalsche Chee B. Sc. ösungsvorschlag zu Blatt 6 Prof. Dr. Norbert Happ Jens Träger Wnterseester 7/8.. 7 Aufgabe De Wellenfunkton des haronschen Oszllators hat de For Ψ v N v H
Übungen zur Vorlesung Physkalsche Chee B. Sc. ösungsvorschlag zu Blatt 6 Prof. Dr. Norbert Happ Jens Träger Wnterseester 7/8.. 7 Aufgabe De Wellenfunkton des haronschen Oszllators hat de For Ψ v N v H
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
binäre Suchbäume Informatik I 6. Kapitel binäre Suchbäume binäre Suchbäume Rainer Schrader 4. Juni 2008 O(n) im worst-case Wir haben bisher behandelt:
 Informatk I 6. Kaptel Raner Schrader Zentrum für Angewandte Informatk Köln 4. Jun 008 Wr haben bsher behandelt: Suchen n Lsten (lnear und verkettet) Suchen mttels Hashfunktonen jewels unter der Annahme,
Informatk I 6. Kaptel Raner Schrader Zentrum für Angewandte Informatk Köln 4. Jun 008 Wr haben bsher behandelt: Suchen n Lsten (lnear und verkettet) Suchen mttels Hashfunktonen jewels unter der Annahme,
d da B A Die gesamte Erscheinung der magnetischen Feldlinien bezeichnet man als magnetischen Fluss. = 1 V s = 1 Wb
 S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
S N De amte Erschenng der magnetschen Feldlnen bezechnet man als magnetschen Flss. = V s = Wb Kraftflssdchte oder magnetsche ndkton B. B d da B = Wb/m = T Für homogene Magnetfelder, we se m nneren von
Klasse : Name1 : Name 2 : Datum : Nachweis des Hookeschen Gesetzes und Bestimmung der Federkonstanten
 Versuch r. 1: achwes des Hook schen Gesetzes und Bestmmung der Federkonstanten achwes des Hookeschen Gesetzes und Bestmmung der Federkonstanten Klasse : ame1 : ame 2 : Versuchszel: In der Technk erfüllen
Versuch r. 1: achwes des Hook schen Gesetzes und Bestmmung der Federkonstanten achwes des Hookeschen Gesetzes und Bestmmung der Federkonstanten Klasse : ame1 : ame 2 : Versuchszel: In der Technk erfüllen
R R R R R. Beim Herausziehen des Weicheisenkerns steigt die Stromstärke.
 . Selbstndukton Spule mt Wechesenkern Wrd en Wechesenkern n ene stromdurchflossene Spule hnengeschoben, so snkt vorübergehend de Stromstärke I. Erklärung: Das Esen erhöht de Flussdchte B und damt den magnetschen
. Selbstndukton Spule mt Wechesenkern Wrd en Wechesenkern n ene stromdurchflossene Spule hnengeschoben, so snkt vorübergehend de Stromstärke I. Erklärung: Das Esen erhöht de Flussdchte B und damt den magnetschen
Erzeugung mit einer rotierenden flachen Spule
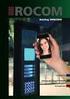 2. Snuförmge Wechelpannung De elektromagnetche Indukton t ene der Grundlagen unerer technchen Zvlaton. Der Strom, der au der Steckdoe kommt, t bekanntlch en Wecheltrom. De hn verurachende Wechelpannung
2. Snuförmge Wechelpannung De elektromagnetche Indukton t ene der Grundlagen unerer technchen Zvlaton. Der Strom, der au der Steckdoe kommt, t bekanntlch en Wecheltrom. De hn verurachende Wechelpannung
3.6 Molekulare Dynamik
 3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
nonparametrische Tests werden auch verteilungsfreie Tests genannt, da sie keine spezielle Verteilung der Daten in der Population voraussetzen
 arametrsche vs. nonparametrsche Testverfahren Verfahren zur Analyse nomnalskalerten Daten Thomas Schäfer SS 009 1 arametrsche vs. nonparametrsche Testverfahren nonparametrsche Tests werden auch vertelungsfree
arametrsche vs. nonparametrsche Testverfahren Verfahren zur Analyse nomnalskalerten Daten Thomas Schäfer SS 009 1 arametrsche vs. nonparametrsche Testverfahren nonparametrsche Tests werden auch vertelungsfree
Zur Erinnerung. Stichworte aus der 9. Vorlesung: Einteilung von Stößen:
 Zu nneung tchwote aus de 9. Volesung: ntelung von tößen: kn, kn kn,, kn, Q Q = 0 elastsche töße de umme de nneen nege de Telchen (chwngung und Rotaton) blebt unveändet, Q > 0 unelastsche töße knetsche
Zu nneung tchwote aus de 9. Volesung: ntelung von tößen: kn, kn kn,, kn, Q Q = 0 elastsche töße de umme de nneen nege de Telchen (chwngung und Rotaton) blebt unveändet, Q > 0 unelastsche töße knetsche
Im Wöhlerdiagramm wird die Lebensdauer (Lastwechsel oder Laufzeit) eines Bauteils in Abhängigkeit von der Belastung dargestellt.
 Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Webull & Wöhler 0 CRGRAPH Wöhlerdagramm Im Wöhlerdagramm wrd de Lebesdauer ( oder Laufzet) ees Bautels Abhägget vo der Belastug dargestellt. Kurzetfestget Beaspruchug Zetfestget auerfestget 0 5 3 4 6 0
Wärmeübertragung. Grundsätzlich sind drei verschiedene Möglichkeiten der Wärmeübertragung möglich: Wärmeleitung, Konvektion und Strahlung:
 ämeübetgung Unte ämeübetgung vesteht mn sämtlche Eschenungen, e enen äumlchen nspot von äme umfssen. De ämeübegng efolgt mme ufgun enes empetugefälles, un zw mme von e höheen zu neeen empetu (.Huptstz).
ämeübetgung Unte ämeübetgung vesteht mn sämtlche Eschenungen, e enen äumlchen nspot von äme umfssen. De ämeübegng efolgt mme ufgun enes empetugefälles, un zw mme von e höheen zu neeen empetu (.Huptstz).
Während der Zeit dt fließe durch den Querschnitt eines Leiters die Ladung dq es herrscht die Stromstärke
 Elektrztätslehre Glechstrom 26. Glechstrom 26.. Stromstärke Während der Zet dt fleße durch den Querschntt enes Leters de Ladung dq es herrscht de Stromstärke dq dt () Maßenhet: As C [ ] A S s s De Maßenhet
Elektrztätslehre Glechstrom 26. Glechstrom 26.. Stromstärke Während der Zet dt fleße durch den Querschntt enes Leters de Ladung dq es herrscht de Stromstärke dq dt () Maßenhet: As C [ ] A S s s De Maßenhet
Funktionsgleichungen folgende Funktionsgleichungen aus der Vorlesung erhält. = e
 Andere Darstellungsformen für de Ausfall- bzw. Überlebens-Wahrschenlchket der Webull-Vertelung snd we folgt: Ausfallwahrschenlchket: F ( t ) Überlebenswahrschenlchket: ( t ) = R = e e t t Dabe haben de
Andere Darstellungsformen für de Ausfall- bzw. Überlebens-Wahrschenlchket der Webull-Vertelung snd we folgt: Ausfallwahrschenlchket: F ( t ) Überlebenswahrschenlchket: ( t ) = R = e e t t Dabe haben de
