Modellieren mit AMPL
|
|
|
- Eduard Straub
- vor 6 Jahren
- Abrufe
Transkript
1 Modellieren mit AMPL Elisabeth Gassner Mathematische Modelle in den Wirtschaftswissenschaften Prof. R. E. Burkard 27. April 2007 E. Gassner (Mathematische Modelle) AMPL 27. April / 21
2 Überblick AMPL - Algebraic modeling language for mathematical programming Algebraische Schreibweise eine linearen Programms: min x s.t. n c j x j j=1 n a ij x j b i j=1 x j 0 i = 1,..., m j = 1,..., n Ziel: Übergabe eines Modells und der Daten an einen Solver und Ausgabe einer Optimallösung. E. Gassner (Mathematische Modelle) AMPL 27. April / 21
3 Überblick Eigenschaften von AMPL: AMPL ist eine Modelliersparche, die es ermöglicht, ein Optimierungsmodell in kompakter Form darzustellen. AMPL löst das Optimierungsproblem nicht selbst sondern übergibt es einem Solver (z.b. CPLEX, minos, etc.) Das Modell und die Daten sind getrennt (file.mod, file.dat) Das Modellfile enthält Deklaration der Datenparameter und Variablen, die Zielfunktion und die Nebenbedingungen. Das Datenfile enthält die aktuellen Werte der Parameter. E. Gassner (Mathematische Modelle) AMPL 27. April / 21
4 Überblick Verfügbarkeit: Freie Studentenversion von AMPL auf Online-Version In der Windows-Version wird Solver mit zip-file mitgeliefert, für Unix/Linux muss CPLEX getrennt downgeloadet werden. E. Gassner (Mathematische Modelle) AMPL 27. April / 21
5 Beispiel 1: Produktionsplanung Eine Stahlfabrik muss den Produktionsplan für eine Woche zusammenstellen. Die Fabrik kann Produkt A oder Produkt B herstellen. Die Produkte werden in folgenden Raten gefertigt: Der Verkaufspreis beträgt Tonnen pro Stunde: Produkt A 200 Produkt B 140 Profit pro Tonne: Produkt A 25 Produkt B 30 Aufgrund von Kapazitätsbeschränkungen müssen folgende Grenzen eingehalten werden: Maximal in Tonnen: Produkt A 6000 Produkt B 4000 Wieviel Tonnen von Produkt A und B sollen produziert werden, wenn 40 Arbeitsstunden zur Verfügung stehen und als Ziel der gesamte Verkaufserlös maximiert werden soll? E. Gassner (Mathematische Modelle) AMPL 27. April / 21
6 Beispiel 1: Produktionsplanung (Fs.) Entscheidungsvariablen: x A (Tonnen von Produkt A), x B (Tonnen von Produkt B) max s.t. 25x A + 30x B x A x B 40 0 x A x B 4000 E. Gassner (Mathematische Modelle) AMPL 27. April / 21
7 Beispiel 1: Produktionsplanung (Fs.) Trennung von Modell und Daten! production.mod set PROD; param rate {PROD} >0; param profit {PROD}; param schranke {PROD}; param arbeitszeit; var menge {PROD}; #Produkte #Produktionsrate für jedes Produkt #Profit pro Tonne für jedes Produkt #obere Schranke für jedes Produkt #Arbeitsstunden pro Woche #Produktionsmenge für jedes Produkt maximize Gesamtprofit: sum {p in PROD} profit[p] * menge[p]; subject to Zeit: sum {p in PROD} (1/rate[p]) * menge[p] <= arbeitszeit; subject to Schranken {p in PROD}: menge[p] <= schranke[p]; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
8 Beispiel 1: Produktionsplanung (Fs.) production.dat set PROD := ProduktA ProduktB; param arbeitszeit := 40; param: rate profit schranke := ProduktA ProduktB ; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
9 Beispiel 1: Produktionsplanung (Fs.) production.run model production.mod; data production.dat; option solver cplex; #option solver cplexamp; solve; display menge; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
10 Starten von AMPL Starten von AMPL Windows: MS-DOS Fenster: Doppelklick auf ampl.exe MS-DOS Fenster öffnet sich mit ampl: Scrolling-Window Utility: Doppelklick auf sw.exe Fenster öffnet sich mit sw: sw: ampl ampl: Linux/Unix: Konsole ampl Lösen eines Optimierungsproblems mit AMPL include filename.run; Beenden von AMPL mit quit; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
11 Output von AMPL ILOG AMPL 9.100, licensed to university-graz. AMPL Version (Linux e.24smp) ILOG CPLEX 9.100, licensed to university-graz, options: e m b q CPLEX 9.1.0: optimal solution; objective dual simplex iterations (0 in phase I) menge [*] := ProduktA 6000 ProduktB 1400 ; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
12 Die Modelldatei (1) Definition von Mengen, Parametern und Variablen Mengen: set MENGENNAME; Parameter: param PARAMETERNAME >= lb, <= ub; Indizierter Parameter: param PARAMETERNAME {MENGE} >= lb, <= ub; #oder param PARAMETERNAME {MENGE1, MENGE2} >= lb, <= ub; Variablen: var VARIABLENNAME >= lb, <= ub; #oder var VARIABLENNAME {j in MENGE} >= lb, <= ub; #oder var VARIABLENNAME {i in MENGE1, j in MENGE2} # optional binary oder integer E. Gassner (Mathematische Modelle) AMPL 27. April / 21
13 Die Modelldatei (2) Definition der Zielfunktion: maximize/minimize ZIELNAME: Funktion; Nebenbedingungen: eine Bedingung: subject to NAME: Restriktion; mehrere Bedingungen: subject to NAME {j in Menge}: Restriktion; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
14 Die Datendatei Mengen: set MENGENNAME := M1 M2 M3 M4; set MENGENNAME := by 2; #oder Parameter: param PARAMETERNAME := 40; Einfach indizierter Parameter: param PARAMETERNAME:= M1 p1 M2 p2; #einfach indiziert param: PARAMETERNAME1 PARAMETERNAME2 := M1 p1 p2 M2 p3 p4; #mehrere Parameter E. Gassner (Mathematische Modelle) AMPL 27. April / 21
15 Die Datendatei (2) Mehrfach indizierte Parameter: param PARAMETERNAME:= [M1,*] N1 a N2 b [M2,*] N1 c N2 d; #doppelt indiziert param PARAMETERNAME: N1 N2:= M1 a b M2 c d; #einfache Schreibweise param PARAMETERNAME:= [A1,*,*] C1 C2 C3 B1 a b c B2 d e f [A2,*,*] C1 C2 C3 B1 g h i B2 j k l; #Parameter mit 3 Indizes E. Gassner (Mathematische Modelle) AMPL 27. April / 21
16 Die Run-Datei reset; model DATEINAME.mod; data DATEINAME.dat; option solver cplex; #option solver cplexamp; solve; display VARIABLE1, VARIABLE2; #Output am Bildschirm display VARIABLE3 > OUTPUT.txt; #Output in Datei OUTPUT.txt E. Gassner (Mathematische Modelle) AMPL 27. April / 21
17 Einige Grundsätze und Fehlerquellen Wählen Sie aussagekräftige Namen. Variablen und Nebenbedingungen dürfen nicht den gleichen Namen tragen. Dokumentieren Sie das Modell. Alles nach dem Symbol # wird ignoriert. Jede Zeile muss mit Strichpunkt enden. Jede Variable muss mit var definiert sein. E. Gassner (Mathematische Modelle) AMPL 27. April / 21
18 Beispiel 2: Zuordnungsproblem Ein Unternehmen besitzt 3 Lager und 4 Fabriken. Die Ressourcen für die Produktion in den Fabriken müssen von den Lagern zugeliefert werden. Die Lager verfügen über folgende Kapazitäten Lager 1: 250, Lager 2: 800, Lager 3: 760 und die Fabriken haben folgenden Bedarf Fabrik 1: 300, Fabrik 2: 320, Fabrik 3: 800, Fabrik 4: 390 Die Transportkosten pro gelieferter Einheit sind linear von der Distanz abhängig: Fabrik 1 Fabrik 2 Fabrik 3 Fabrik 4 Lager Lager Lager Bestimmen Sie einen zulässigen Transportplan, der die Gesamtkosten minimiert. E. Gassner (Mathematische Modelle) AMPL 27. April / 21
19 Beispiel 2: Zuordnungsproblem zuordnung.mod param anzahlfabriken; #Anzahl der Fabriken param anzahllager; #Anzahl der Lager set fabriken:=1..anzahlfabriken; #Menge aller Fabriken set lager:=1..anzahllager; #Menge der Lager param cost{i in lager, j in fabriken}; #Kosten von Lager i zu Fabrik j param kapazitaet {i in lager}; #Kapazitaet von Lager i param bedarf {j in fabriken}; #Bedarf von Fabrik j var transport {i in lager, j in fabriken} >=0; #Transportierte Menge von Lager i zu Fabrik j E. Gassner (Mathematische Modelle) AMPL 27. April / 21
20 Beispiel 2: Zuordnungsproblem zuordnung.mod (Fs.) minimize Kosten: sum{i in lager, j in fabriken} cost[i,j] * transport[i,j]; subject to Lagerkapazitaet {i in lager}: sum{j in fabriken} transport[i,j] <= kapazitaet[i]; #Gesamttransport ab Lager i subject to Fabriksbedarf {j in fabriken}: sum{i in lager} transport[i,j] >= bedarf[j]; #Gesamttransport zu Fabrik j E. Gassner (Mathematische Modelle) AMPL 27. April / 21
21 Beispiel 2: Zuordnungsproblem zuordnung.dat param anzahlfabriken := 4; param anzahllager :=3; param kapazitaet:= ; param bedarf:= ; param cost: := ; E. Gassner (Mathematische Modelle) AMPL 27. April / 21
maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];
![maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j]; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];](/thumbs/64/50698761.jpg) AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
Optimierung für Nichtmathematiker
 Technische Universität Chemnitz Chemnitz, 19.10.2009 Prof. Dr. C. Helmberg, A. Lau Optimierung für Nichtmathematiker Übung 2 Einführung in die Modellierungssprache AMPL 1. Wir betrachten zunächst das Mozartproblem
Technische Universität Chemnitz Chemnitz, 19.10.2009 Prof. Dr. C. Helmberg, A. Lau Optimierung für Nichtmathematiker Übung 2 Einführung in die Modellierungssprache AMPL 1. Wir betrachten zunächst das Mozartproblem
Kapitel 4. Mathematische Optimierungsmodelle. Einführung in AMPL (1) Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin
 Kapitel 4 Mathematische Optimierungsmodelle Einführung in AMPL () Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin Optimierungssysteme Version. / SS 200 Modellierungssysteme Sind
Kapitel 4 Mathematische Optimierungsmodelle Einführung in AMPL () Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin Optimierungssysteme Version. / SS 200 Modellierungssysteme Sind
Rechnerpraktikum zur Nichtlinearen Optimierung
 Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Einführung in Softwaretools zur Nichtlinearen Optimierung
 Einführung in Softwaretools zur Nichtlinearen Optimierung 3. April 2017 5. April 2017 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl
Einführung in Softwaretools zur Nichtlinearen Optimierung 3. April 2017 5. April 2017 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Eine kurze Beschreibung zu AMPL und CPLEX
 Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Veranstaltung und Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen. Uwe Suhl Veronika Waue SS 2008
 Veranstaltung 10033025 und 101053 Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen Uwe Suhl Veronika Waue SS 2008 Organisatorisches Veronika Waue Sprechstunde Mi.11h-12h (R214) E-mail: veronika@waue.net
Veranstaltung 10033025 und 101053 Übung: Optimierungssysteme Modelle, Software, Praxisanwendungen Uwe Suhl Veronika Waue SS 2008 Organisatorisches Veronika Waue Sprechstunde Mi.11h-12h (R214) E-mail: veronika@waue.net
Computer Science Department - High Performance and Web Computing Group. Optimierungsprobleme
 Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
6. Softwarewerkzeuge für die Lineare Programmierung
 6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
LPL - Linear Programming Language
 LPL - Linear Programming Language Ein Matrix-Generator Tony Hürlimann 26.04.2004 LPL-Einführung 1 Agenda (0) 1. Grundelemente eines Modells 2. Erstellung eines LPL-Programms 3. Beispiel "kommune.lpl" 4.
LPL - Linear Programming Language Ein Matrix-Generator Tony Hürlimann 26.04.2004 LPL-Einführung 1 Agenda (0) 1. Grundelemente eines Modells 2. Erstellung eines LPL-Programms 3. Beispiel "kommune.lpl" 4.
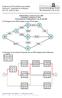
Als Instanz für das p-median Problem wählen wir das Netzwerk von Abbildung 1-1 des Buches auf Seite 6.
 Übung zum p-median Problem Prof. Dr. R. Vahrenkamp, Universität Kassel Als Instanz für das p-median Problem wählen wir das Netzwerk von Abbildung 1-1 des Buches auf Seite 6. Abbildung1 1: Ausschnitt aus
Übung zum p-median Problem Prof. Dr. R. Vahrenkamp, Universität Kassel Als Instanz für das p-median Problem wählen wir das Netzwerk von Abbildung 1-1 des Buches auf Seite 6. Abbildung1 1: Ausschnitt aus
LINGO: Eine kleine Einführung
 LINGO: Eine kleine Einführung Jun.-Prof.Dr. T. Nieberg Lineare und Ganzzahlige Optimierung, WS 2009/10 LINDO/LINGO ist ein Software-Paket, mit dessen Hilfe (ganzzahlige) lineare Programme schnell und einfach
LINGO: Eine kleine Einführung Jun.-Prof.Dr. T. Nieberg Lineare und Ganzzahlige Optimierung, WS 2009/10 LINDO/LINGO ist ein Software-Paket, mit dessen Hilfe (ganzzahlige) lineare Programme schnell und einfach
Inhalt. 8.1 Motivation. 8.2 Optimierung ohne Nebenbedingungen. 8.3 Optimierung unter Nebenbedingungen. 8.4 Lineare Programmierung
 8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
AMPL Eine kurze Einführung
 AMPL Eine kurze Einführung Sebastian Lohse Juni 2006 Beispiel Modellierung Mengen Parameter Dateneingabe Anzeige Analyse Optionen Script-Files Historisches um 1985 implementiert und seither stetig weiterentwickelt
AMPL Eine kurze Einführung Sebastian Lohse Juni 2006 Beispiel Modellierung Mengen Parameter Dateneingabe Anzeige Analyse Optionen Script-Files Historisches um 1985 implementiert und seither stetig weiterentwickelt
AMPL Eine kurze Einführung
 AMPL Eine kurze Einführung Sebastian Lohse, Maria Pilecka März 2014 1 / 54 Einleitung Modellierung Allgemeines Mengen Parameter, Variablen, Modell Weiterführende Konzepte Dateneingabe Anzeige Daten- und
AMPL Eine kurze Einführung Sebastian Lohse, Maria Pilecka März 2014 1 / 54 Einleitung Modellierung Allgemeines Mengen Parameter, Variablen, Modell Weiterführende Konzepte Dateneingabe Anzeige Daten- und
LinOpt - Tool zur Visualisierung eines multikriteriellen Optimierungsproblems
 LinOpt Tool zur Visualisierung eines multikriteriellen Optimierungsproblems Erstellt von Michael Berklmeir, Michael Haarnagell, Stefan Kraus, Stephan Roser im Rahmen einer Seminararbeit am Lehrstuhl für
LinOpt Tool zur Visualisierung eines multikriteriellen Optimierungsproblems Erstellt von Michael Berklmeir, Michael Haarnagell, Stefan Kraus, Stephan Roser im Rahmen einer Seminararbeit am Lehrstuhl für
Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung
 Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung Sascha Kurz Jörg Rambau 24. November 2009 2 Aufgabe 3.1. Ein in m Depots gelagertes homogenes
Mathematische Grundlagen für Wirtschaftswissenschaftler Übungsaufgaben aus Kapitel 3 - Lineare Optimierung Sascha Kurz Jörg Rambau 24. November 2009 2 Aufgabe 3.1. Ein in m Depots gelagertes homogenes
Unimodularität. Kapitel 1. Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206
 Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Optimierung für Wirtschaftsinformatiker: Lineare Programme
 Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Einführung in Xpress-Mosel
 Einführung in Xpress-Mosel Matthias Silbernagl Computerblockpraktikum zur linearen Optimierung Gliederung 1 Mosel-Grundlagen 1.1 Xpress im Überblick Inhaltsverzeichnis 1 Mosel-Grundlagen 1 1.1 Xpress im
Einführung in Xpress-Mosel Matthias Silbernagl Computerblockpraktikum zur linearen Optimierung Gliederung 1 Mosel-Grundlagen 1.1 Xpress im Überblick Inhaltsverzeichnis 1 Mosel-Grundlagen 1 1.1 Xpress im
1 Lineare Optimierung, Simplex-Verfahren
 1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
1. Hausaufgabenblatt (16.04./ )
 Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
Lehrstuhl Ingenieurmathematik Modul: (Wirtschaftsingenieurwesen/Betriebswirtschaftslehre/Informatik) Sommersemester 2014 1. Hausaufgabenblatt (16.04./23.04.2015) Aufgabe H 1.1 Lösen Sie die linearen Gleichungssysteme
Operations Research für Logistik
 Operations Research für Logistik Lineare Optimierung (170.202) Ao. Univ. - Prof. Norbert SEIFTER Dipl. - Ing. Stefanie VOLLAND Sommersemester 2012 Lehrstuhl Industrielogistik Lineare Optimierung Inhalte:
Operations Research für Logistik Lineare Optimierung (170.202) Ao. Univ. - Prof. Norbert SEIFTER Dipl. - Ing. Stefanie VOLLAND Sommersemester 2012 Lehrstuhl Industrielogistik Lineare Optimierung Inhalte:
Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge)
 Beispiel: Produktionsplanung Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge) Produktionskapazität Ressourcenmenge bei als fest angenommenem
Beispiel: Produktionsplanung Maximiere Gesamtgewinn aus verschiedenen Produkten unter Restriktionen an Produktmenge (Lagermenge, Transportmenge) Produktionskapazität Ressourcenmenge bei als fest angenommenem
Lineare Optimierung und ganzzahlige lineare Optimierung
 Definition 1: Problem LP: Lineare Optimierung und ganzzahlige lineare Optimierung geg.: m, n N, A Z m n, b Z m, c Z n ges.: x R n 0 mit c T x max Beispiel 1: (Gewinnmaximierung) Ax b Gerät Abteilung 1
Definition 1: Problem LP: Lineare Optimierung und ganzzahlige lineare Optimierung geg.: m, n N, A Z m n, b Z m, c Z n ges.: x R n 0 mit c T x max Beispiel 1: (Gewinnmaximierung) Ax b Gerät Abteilung 1
N ---> INFEASIBILTY SOLVE TIME 00:00:00 ITER 1 MEMORY USED 0.0%
 Aufgabe 2.1: MODEL Beispiel1.1.; = /1 2 3/; i= /1:3/; x{}; PARAMETER A{i,}= /: 1 2 3 : 1 2 3 0 2 1-8 7 3 4 2 1 /; b{i}=[8 5-1]; Zielfunktionswert{}=[2-1 -3]; NB{i}: SUM{} A*x
Aufgabe 2.1: MODEL Beispiel1.1.; = /1 2 3/; i= /1:3/; x{}; PARAMETER A{i,}= /: 1 2 3 : 1 2 3 0 2 1-8 7 3 4 2 1 /; b{i}=[8 5-1]; Zielfunktionswert{}=[2-1 -3]; NB{i}: SUM{} A*x
Kap. 4.3: Das Dualitätstheorem der linearen Optimierung
 Kap. 4.3: Das Dualitätstheorem der linearen Optimierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 18. VO A&D WS 08/09 18.12.2008 1 Literatur
Kap. 4.3: Das Dualitätstheorem der linearen Optimierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 18. VO A&D WS 08/09 18.12.2008 1 Literatur
Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel:
 Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel: Eine Firma produziert die Produkte P 1, P 2,..., P q aus den Rohstoffen R 1, R 2,..., R m. Dabei stehen b j Einheiten
Kapitel 7 : Lineare Programmierung Die Simplexmethode (G.B.Dantzig, 1947) Beispiel: Eine Firma produziert die Produkte P 1, P 2,..., P q aus den Rohstoffen R 1, R 2,..., R m. Dabei stehen b j Einheiten
3.2.5 Dualität der linearen Optimierung I
 3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
3..5 Dualität der linearen Optimierung I Jedem linearen Programm in Standardform kann ein sogenanntes duales Programm zugeordnet werden. Es entsteht dadurch, daß man von einem Minimierungsproblem zu einem
Kapitel 2. Mathematische Optimierungsmodelle. Lineare Optimierung. Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin
 Kapitel 2 Mathematische Optimierungsmodelle Lineare Optimierung Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin Optimierungssysteme Version 1.1 / SS 2008 Mathematische Optimierungsmodelle
Kapitel 2 Mathematische Optimierungsmodelle Lineare Optimierung Uwe H. Suhl Lehrstuhl für Wirtschaftsinformatik Freie Universität Berlin Optimierungssysteme Version 1.1 / SS 2008 Mathematische Optimierungsmodelle
Optimierungsworkshop: Beispiele und Übungen
 Optimierungsworkshop: Beispiele und Übungen Teil 1: Lineare Modelle Aufgabe 1 (Gürtelbeispiel) Ein Unternehmen stellt 2 Gürteltypen A und B mit einem Deckungsbeitrag von 2,00 bzw. 1,50 je Stück her. Ein
Optimierungsworkshop: Beispiele und Übungen Teil 1: Lineare Modelle Aufgabe 1 (Gürtelbeispiel) Ein Unternehmen stellt 2 Gürteltypen A und B mit einem Deckungsbeitrag von 2,00 bzw. 1,50 je Stück her. Ein
Abbildung 1: Graphische Lösung der ersten Übungsaufgabe
 Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Lösungen zu den Übungsaufgaben im Kapitel 1 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier 1. Lösen Sie die folgende lineare Optimierungsaufgabe
Optimierung I. Dr. Ulf Lorenz F2.413
 Optimierung I Dr. Ulf Lorenz F2.413 flulo@upb.de Organisation Dozent: Dr. Ulf Lorenz F2.413 Fürstenallee 11 email: flulo@upb.de WWW: http://www.upb.de/cs/flulo (hier auch aktuelle Infos + Ü-Zettel) Vorlesungen:
Optimierung I Dr. Ulf Lorenz F2.413 flulo@upb.de Organisation Dozent: Dr. Ulf Lorenz F2.413 Fürstenallee 11 email: flulo@upb.de WWW: http://www.upb.de/cs/flulo (hier auch aktuelle Infos + Ü-Zettel) Vorlesungen:
Modelle und Methoden der Linearen Optimierung (Die Thesen zur Vorlesung 1)
 (Die Thesen zur Vorlesung 1) das Thema der Vorlesung Grundlagen der Methode der linearen Optimierung (Grundlegende Annahmen der linearen Programmierung) Prof. Dr. Michal Fendek Institut für Operations
(Die Thesen zur Vorlesung 1) das Thema der Vorlesung Grundlagen der Methode der linearen Optimierung (Grundlegende Annahmen der linearen Programmierung) Prof. Dr. Michal Fendek Institut für Operations
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA Mögliche Fälle für Z Etschberger - WS2016 1 Z =, d.h., es existiert keine zulässige (x 1, x 2 )-Kombination. 2
Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA Mögliche Fälle für Z Etschberger - WS2016 1 Z =, d.h., es existiert keine zulässige (x 1, x 2 )-Kombination. 2
Optimization in Business Applications: 2. Modeling principles
 Optimization in Business Applications: 2. Modeling principles IGS Course Dynamic Intelligent Systems Part 2 Universität Paderborn, June July 2010 Leena Suhl www.dsor.de Prof. Dr. Leena Suhl, suhl@dsor.de
Optimization in Business Applications: 2. Modeling principles IGS Course Dynamic Intelligent Systems Part 2 Universität Paderborn, June July 2010 Leena Suhl www.dsor.de Prof. Dr. Leena Suhl, suhl@dsor.de
Substitutionsverfahren
 Substitutionsverfahren 1 Motivation Wir stehen vor folgendem Problem: In unserem Betrieb kann unsere einzige Maschine Produkt A in zwei Stunden und Produkt B in einer Stunde produzieren. Die Maschine läuft
Substitutionsverfahren 1 Motivation Wir stehen vor folgendem Problem: In unserem Betrieb kann unsere einzige Maschine Produkt A in zwei Stunden und Produkt B in einer Stunde produzieren. Die Maschine läuft
Modelle und Methoden der Linearen Optimierung (Die Thesen zur Vorlesung 1_Fallstudie)
 (Die Thesen zur Vorlesung 1_Fallstudie) das Thema der Vorlesung Grundlagen der Methode der linearen Optimierung (Lineares Optimierungsmodell der Wahl der Produktionsstrategie des ) Prof. Dr. Michal Fendek
(Die Thesen zur Vorlesung 1_Fallstudie) das Thema der Vorlesung Grundlagen der Methode der linearen Optimierung (Lineares Optimierungsmodell der Wahl der Produktionsstrategie des ) Prof. Dr. Michal Fendek
GAMS (General Algebraic Modeling System)
 GAMS (General Algebraic Modeling System) Crash-Kurs Dortmund, Januar 1999 Prof. Dr. Heinz-Michael Winkels, Fachbereich Wirtschaft FH Dortmund Emil-Figge-Str. 44, D44227-Dortmund, TEL.: (0231)755-4966,
GAMS (General Algebraic Modeling System) Crash-Kurs Dortmund, Januar 1999 Prof. Dr. Heinz-Michael Winkels, Fachbereich Wirtschaft FH Dortmund Emil-Figge-Str. 44, D44227-Dortmund, TEL.: (0231)755-4966,
Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester 2007/2008
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Klausur zur Vorlesung Einführung in das Operations Research im Wintersemester
Optimierung I, SS 2008
 Aufgabe. ca. 4 Punkte Technische Universität München Zentrum Mathematik Prof. Dr. P. Gritzmann, Dipl.-Math. M. Ritter, Dipl.-Inf. Dipl.-Math. S. Borgwardt Optimierung I, SS 2008 Übungsblatt Um gegen die
Aufgabe. ca. 4 Punkte Technische Universität München Zentrum Mathematik Prof. Dr. P. Gritzmann, Dipl.-Math. M. Ritter, Dipl.-Inf. Dipl.-Math. S. Borgwardt Optimierung I, SS 2008 Übungsblatt Um gegen die
Optimale Steuerung 1 Prozessoptimierung 1
 Optimale Steuerung 1 Prozessoptimierung 1 Kapitel 2: Lineare Optimierung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Lineare Algebra (Mathematische Grundlagen) 2 Beispiel: Produktionsplanung
Optimale Steuerung 1 Prozessoptimierung 1 Kapitel 2: Lineare Optimierung Prof. Dr.-Ing. Pu Li Fachgebiet Simulation und Optimale Prozesse (SOP) Lineare Algebra (Mathematische Grundlagen) 2 Beispiel: Produktionsplanung
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Lineare Optimierung. Volker Kaibel Fakultät für Mathematik Institut für Mathematische Optimierung Otto-von-Guericke Universität Magdeburg
 Lineare Optimierung Volker Kaibel Fakultät für Mathematik Institut für Mathematische Optimierung Otto-von-Guericke Universität Magdeburg VL 1: Einführung 10. April 2007 Überblick Optimierung unter Nebenbedingungen
Lineare Optimierung Volker Kaibel Fakultät für Mathematik Institut für Mathematische Optimierung Otto-von-Guericke Universität Magdeburg VL 1: Einführung 10. April 2007 Überblick Optimierung unter Nebenbedingungen
Optimierung. Optimierung. Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung Fabian Kuhn
 Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Rechnerpraktikum zur Optimierung III
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 2007 Teil I Rechnerpraktikum zur Optimierung III P1. Durchhängenes Seil Die senkrechten
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. M. Ulbrich Dipl.-Math. Florian Lindemann Sommersemester 2007 Teil I Rechnerpraktikum zur Optimierung III P1. Durchhängenes Seil Die senkrechten
Einführung in MATLAB + MATLAB Simulink. Dipl.-Inf. Markus Appel
 Einführung in MATLAB + MATLAB Simulink Dipl.-Inf. Markus Appel mappel@informatik.hu-berlin.de 28.10.2016 Was ist MATLAB? ein universelles Algebra-Programm zur Lösung mathematischer Probleme grafische Darstellung
Einführung in MATLAB + MATLAB Simulink Dipl.-Inf. Markus Appel mappel@informatik.hu-berlin.de 28.10.2016 Was ist MATLAB? ein universelles Algebra-Programm zur Lösung mathematischer Probleme grafische Darstellung
PuLP ein Python LP-Modellierer
 PuLP ein Python LP-Modellierer How to use PuLP Dr. Klaus Ladner Institut für Statistik und Operations Research 1. Dezember 2016 Was ist PuLP? Ein LP-Modellierer CBC (COIN-OR Branch und Cut) Solver PuLP
PuLP ein Python LP-Modellierer How to use PuLP Dr. Klaus Ladner Institut für Statistik und Operations Research 1. Dezember 2016 Was ist PuLP? Ein LP-Modellierer CBC (COIN-OR Branch und Cut) Solver PuLP
Einführung in Softwaretools zur nichtlinearen Optimierung (WS 2016/17)
 Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Einführung in Softwaretools zur nichtlinearen
Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung, M1 Sebastian Garreis, M. Sc. (hons) Johannes Haubner, M. Sc. Einführung in Softwaretools zur nichtlinearen
Kombinatorische Optimierung
 Kombinatorische Optimierung Juniorprof. Dr. Henning Meyerhenke PARALLELES RECHNEN INSTITUT FÜR THEORETISCHE INFORMATIK, FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales
Kombinatorische Optimierung Juniorprof. Dr. Henning Meyerhenke PARALLELES RECHNEN INSTITUT FÜR THEORETISCHE INFORMATIK, FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales
Probeklausur Optimierung
 Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
10.2 Dualitätstheorie Operations Research. In der Standardform eines Maximierungsproblem: b e ) mit ( w) + a ej ) x j + x g = ( b g + g G
 48 0 Operations Research In der Standardform eines Maximierungsproblem: Max ( w) mit ( w) + u. d. N. z + x l + n ( a gj + j= g G e E n d j x j = z 0 j= n a l j x j = b l für alle l L j= x g n + a gj x
48 0 Operations Research In der Standardform eines Maximierungsproblem: Max ( w) mit ( w) + u. d. N. z + x l + n ( a gj + j= g G e E n d j x j = z 0 j= n a l j x j = b l für alle l L j= x g n + a gj x
1. Transport- und Zuordnungsprobleme
 1. Transport- und Zuordnungsprobleme Themen 1. Transport- und Zuordnungsprobleme Themen: Analyse der Problemstruktur Spezielle Varianten des Simplexalgorithmus für Transport- und Zuordnungsprobleme Bezug
1. Transport- und Zuordnungsprobleme Themen 1. Transport- und Zuordnungsprobleme Themen: Analyse der Problemstruktur Spezielle Varianten des Simplexalgorithmus für Transport- und Zuordnungsprobleme Bezug
Optimierung I Sommersemester 2017
 Optimierung I Sommersemester 2017 Dr. Dominique Andres Übungsblatt 6 (Abgabe: 16. Mai 2017) Hausaufgabe 30. Welche der folgenden linearen Programme sind unzulässig, unbeschränkt bzw. haben eine Optimallösung?
Optimierung I Sommersemester 2017 Dr. Dominique Andres Übungsblatt 6 (Abgabe: 16. Mai 2017) Hausaufgabe 30. Welche der folgenden linearen Programme sind unzulässig, unbeschränkt bzw. haben eine Optimallösung?
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung
 Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Klausurrepetitorium ABWL
 Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel 3 - Lineare Optimierung
 Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel - Lineare Optimierung Sascha Kurz Jörg Rambau 8. August Lösung Aufgabe.. Da es sich um ein homogenes
Mathematische Grundlagen für Wirtschaftswissenschaftler Lösungshinweise zu den Übungsaufgaben aus Kapitel - Lineare Optimierung Sascha Kurz Jörg Rambau 8. August Lösung Aufgabe.. Da es sich um ein homogenes
1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme. Duales Problem. a i u i + i=1. j=1
 1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme Duales Problem Lemma 1.4. Das zum Transportproblem duale Problem lautet: max unter den Nebenbedingungen m a i u i + i=1
1. Transport- und Zuordnungsprobleme Optimierungsalgorithmus für Transportprobleme Duales Problem Lemma 1.4. Das zum Transportproblem duale Problem lautet: max unter den Nebenbedingungen m a i u i + i=1
Einführung. Kapitel 1. Peter Becker (H-BRS) Operations Research I Sommersemester 2015 14 / 298
 Kapitel 1 Einführung Peter Becker (H-BRS) Operations Research I Sommersemester 2015 14 / 298 Inhalt Inhalt 1 Einführung Was ist Operations Research? Planungsprozess im OR Peter Becker (H-BRS) Operations
Kapitel 1 Einführung Peter Becker (H-BRS) Operations Research I Sommersemester 2015 14 / 298 Inhalt Inhalt 1 Einführung Was ist Operations Research? Planungsprozess im OR Peter Becker (H-BRS) Operations
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse
 Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Fachbereich Wirtschaftswissenschaften Professur f. Quantitativen Methoden Prof. Dr. Dietrich Ohse Diplomprüfung / Sommersemester 24 Quantitative Methoden der BWL Musterlösung der Prüfungsklausur vom. Juli
Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
 Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
Leibniz Universität Hannover Wirtschaftswissenschaftliche Fakultät Institut für Produktionswirtschaft Prof. Dr. Stefan Helber Sitzplatznr.: Klausur zur Vorlesung Operations Research im Wintersemester 2009/10
Technische Universität München. Grundlagen der konvexen Optimierung
 Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung Grundlagen der konveen Optimierung Michael Ulbrich April 2012 Gliederung der Vorlesung 1. Einführung Konvee
Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische Optimierung Grundlagen der konveen Optimierung Michael Ulbrich April 2012 Gliederung der Vorlesung 1. Einführung Konvee
Ganzzahlige OR-Methoden: Operations Research II a. Übungsblatt 1
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dr. Eva-Maria Sprengel Ganzzahlige OR-Methoden: Operations Research II a Übungsblatt 1 Aufgabe 1 a) Erläutern Sie bitte die allgemeine
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dr. Eva-Maria Sprengel Ganzzahlige OR-Methoden: Operations Research II a Übungsblatt 1 Aufgabe 1 a) Erläutern Sie bitte die allgemeine
Managemententscheidungsunterstützungssysteme
 tzungsssteme (Die Thesen zur Vorlesung 6) das Thema der Vorlesung Die Anwendung der Methoden der Mehrkriterienoptimierung bei der Lösung der ökonomischen Entscheidungsprobleme (Teil ) Prof. Dr. Michal
tzungsssteme (Die Thesen zur Vorlesung 6) das Thema der Vorlesung Die Anwendung der Methoden der Mehrkriterienoptimierung bei der Lösung der ökonomischen Entscheidungsprobleme (Teil ) Prof. Dr. Michal
Produktionsplanung und Lineare Optimierung im Rahmen des Projekts Mathematik und Ökonomie 12./13. November 2003 in Düsseldorf.
 Übungsaufgaben Aufgabe 1a Medikamentenmischung Ein Pharmaziehersteller möchte ein neues Medikament auf den Markt bringen. Das Medikament kann aus vier verschiedenen Komponenten (K1 K4) zusammengestellt
Übungsaufgaben Aufgabe 1a Medikamentenmischung Ein Pharmaziehersteller möchte ein neues Medikament auf den Markt bringen. Das Medikament kann aus vier verschiedenen Komponenten (K1 K4) zusammengestellt
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
a) Warum sind Kosten bzw. Tarife für Transportdienstleistungen unterhalb einer Komplettladung in der Praxis üblicherweise mengendegressiv?
 Aufgabe 1 (12 Punkte) a) Warum sind Kosten bzw. Tarife für Transportdienstleistungen unterhalb einer Komplettladung in der Praxis üblicherweise mengendegressiv? b) Welchen Nachteil hat die Weitergabe mengendegressiver
Aufgabe 1 (12 Punkte) a) Warum sind Kosten bzw. Tarife für Transportdienstleistungen unterhalb einer Komplettladung in der Praxis üblicherweise mengendegressiv? b) Welchen Nachteil hat die Weitergabe mengendegressiver
Math. II, Numerik, Uebung 2, Termin Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen
 Math. II, Numerik, Uebung 2, Termin 25.10.2012 1-Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen ALLGEMEINES Detaillierter Bewertungsbogen auf der Rückseite des Deckblatts 1. Nur Verfahren der angewandten
Math. II, Numerik, Uebung 2, Termin 25.10.2012 1-Eigenvektoren, 2-Eigenwerte, 3-Simplex, 4-Zwei-Phasen ALLGEMEINES Detaillierter Bewertungsbogen auf der Rückseite des Deckblatts 1. Nur Verfahren der angewandten
1.2 Das Lösen von linearen Problemen mit Hilfe eines Computerprogramms.
 1.2 Das Lösen von linearen Problemen mit Hilfe eines Computerprogramms. An Hand eines Beispiels werden wir ein lineares Problem mit Hilfe eines Computerprogramms lösen. Das hier angewandte Programm ist
1.2 Das Lösen von linearen Problemen mit Hilfe eines Computerprogramms. An Hand eines Beispiels werden wir ein lineares Problem mit Hilfe eines Computerprogramms lösen. Das hier angewandte Programm ist
Verfahren des Operations Research
 Verfahren des Operations Research Blatt 1 (WS 2017/18) wird bearbeitet am 23.10.2017 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Verfahren des Operations Research Blatt 1 (WS 2017/18) wird bearbeitet am 23.10.2017 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Ganzzahlige OR-Methoden: Operations Research II a. Übungsblatt 12
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dr. Eva-Maria Sprengel Ganzzahlige OR-Methoden: Operations Research II a Übungsblatt 12 Aufgabe 37 Auf einem Güterumschlagplatz werden
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dr. Eva-Maria Sprengel Ganzzahlige OR-Methoden: Operations Research II a Übungsblatt 12 Aufgabe 37 Auf einem Güterumschlagplatz werden
Betriebliche Optimierung
 Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 22 1 Das Travelling Salesperson Problem
Betriebliche Optimierung Joachim Schauer Institut für Statistik und OR Uni Graz Joachim Schauer ( Institut für Statistik und OR Uni Graz Betriebliche ) Optimierung 1 / 22 1 Das Travelling Salesperson Problem
Lineare Optimierung Ergänzungskurs
 Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Lineare Optimierung Ergänzungskurs Wintersemester 2015/16 Julia Lange, M.Sc. Literatur Werner, F.; Sotskov, Y.N. (2006): Mathematics of Economics and Business; Routledge; London Bemerkungen Diese Unterlagen
Betriebswirtschaftliche Optimierung
 Institut für Statistik und OR Uni Graz 1 Das Travelling Salesperson Problem 2 Das Travelling Salesperson Problem Zentrales Problem der Routenplanung Unzählige wissenschaftliche Artikel theoretischer sowie
Institut für Statistik und OR Uni Graz 1 Das Travelling Salesperson Problem 2 Das Travelling Salesperson Problem Zentrales Problem der Routenplanung Unzählige wissenschaftliche Artikel theoretischer sowie
Prüfungsklausur Operations Research,
 HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Prüfungsklausur Operations Research, 10.7.2008 A Name, Vorname Matr. Nr. Aufgabe 1 : In drei Porzellanwerken W 1, W 2 und W 3 werden Speiseservice hergestellt,
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Prüfungsklausur Operations Research, 10.7.2008 A Name, Vorname Matr. Nr. Aufgabe 1 : In drei Porzellanwerken W 1, W 2 und W 3 werden Speiseservice hergestellt,
1.4 Aufgaben. 2002/2003
 .4 Aufgaben. 00/003 Aufgabe. Eine Firma stellt zwei Sorten A und B einer Meterware her. Pro Meter entstehen folgende Kosten und Erlöse in Euro: Rohstoffkosten Bearbeitungskosten Verkaufserlös A 6 3 5 B
.4 Aufgaben. 00/003 Aufgabe. Eine Firma stellt zwei Sorten A und B einer Meterware her. Pro Meter entstehen folgende Kosten und Erlöse in Euro: Rohstoffkosten Bearbeitungskosten Verkaufserlös A 6 3 5 B
Dateneingabe und Transformation Übersicht
 Dateneingabe und Transformation Übersicht 2.0 Allgemeine 2.1 Eingabe über die 2.2 2.3 Eingabe eines externen ASCII-Files 2.4 Varianten der INPUT-Anweisung, Formatierungselemente 2.5 Ein- und Ausgabe von
Dateneingabe und Transformation Übersicht 2.0 Allgemeine 2.1 Eingabe über die 2.2 2.3 Eingabe eines externen ASCII-Files 2.4 Varianten der INPUT-Anweisung, Formatierungselemente 2.5 Ein- und Ausgabe von
RUHR - UNIVERSITÄT BOCHUM KLAUSUR. Name. Vorname. Teilnehmer-Nr. Zur Beachtung. Bitte nicht ausfüllen
 RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 6.2.997 (WS 97/98) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
RUHR - UNIVERSITÄT BOCHUM Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen L i n e a r e A l g e b r a 6.2.997 (WS 97/98) Name Vorname Teilnehmer-Nr. Zur Beachtung Die Klausur umfaßt
Dualitätssätze der linearen Optimierung
 Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009
 Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009 Daten Modelle Steuerung Wilfried Grossmann Teil 3: Steuerung Mathematische Modelle werden häufig dazu verwendet um ein optimales Verhalten zu bestimmen
Einführung in die Wirtschaftsinformatik VO WS 2008 / 2009 Daten Modelle Steuerung Wilfried Grossmann Teil 3: Steuerung Mathematische Modelle werden häufig dazu verwendet um ein optimales Verhalten zu bestimmen
Lineare Optimierung. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet.
 Lineare Optimierung Dr. Bommhardt. Das ervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Gleichungen und Ungleichungen n der Wirtschaft sind häufig
Lineare Optimierung Dr. Bommhardt. Das ervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Gleichungen und Ungleichungen n der Wirtschaft sind häufig
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 2008/09 Blatt 3 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung P9. Installation
TU München Lehrstuhl Mathematische Optimierung Prof. Dr. Michael Ulbrich Dipl.-Math. Florian Lindemann Wintersemester 2008/09 Blatt 3 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung P9. Installation
FK WMS: Wirtschaftsmathematik 2, Einheit 7/8
 FK WMS: Wirtschaftsmathematik 2, Einheit 7/8 Markus Sinnl 1 markus.sinnl@univie.ac.at http://homepage.univie.ac.at/markus.sinnl basierend auf Folien von Dr. Ivana Ljubic, Mag. Christian Spreitzer und Mag.
FK WMS: Wirtschaftsmathematik 2, Einheit 7/8 Markus Sinnl 1 markus.sinnl@univie.ac.at http://homepage.univie.ac.at/markus.sinnl basierend auf Folien von Dr. Ivana Ljubic, Mag. Christian Spreitzer und Mag.
Erzielte Bonuspunkte aus der Vorklausur:
 Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen Wintersemester 2013/2014 24.2.2014 Name Vorname Matrikelnummer Teilnehmer-Nr. Unterschrift Erzielte Bonuspunkte aus der Vorklausur:
Fakultät für Wirtschaftswissenschaft KLAUSUR Mathematik für Ökonomen Wintersemester 2013/2014 24.2.2014 Name Vorname Matrikelnummer Teilnehmer-Nr. Unterschrift Erzielte Bonuspunkte aus der Vorklausur:
ist ein Polyeder. c) Sei F eine Seite von P. Wann ist f 1 (F ) eine Seite von f 1 (P )? Begründen Sie Ihre Antwort. x 1. x = max{ x i i N n }.
 alteklausuraufgaben 1 LinOpt Klausur Sommersemester 05 Aufgabe 1 a) Definieren Sie den Begriff der konischen Hülle. b) Sei S R n. Zeigen Sie: Cone S = Lin S x S : x Cone (S \ {x}). Aufgabe 2 a) Definieren
alteklausuraufgaben 1 LinOpt Klausur Sommersemester 05 Aufgabe 1 a) Definieren Sie den Begriff der konischen Hülle. b) Sei S R n. Zeigen Sie: Cone S = Lin S x S : x Cone (S \ {x}). Aufgabe 2 a) Definieren
Verfahren des Operations Research
 Verfahren des Operations Research Blatt 1 (WS 2018/19) wird bearbeitet am 31.10.2018 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Verfahren des Operations Research Blatt 1 (WS 2018/19) wird bearbeitet am 31.10.2018 1. Ein Rohstoff kann zu drei Gütern G 1, G 2 und G 3 verarbeitet werden. Man benötigt für G 1 60 kg/stk, für G 2 80
Fachakademie für Wirtschaft der FHM A2: Lineare Optimierung und das Simplexverfahren
 A2.1 Lineare Optimierung mit dem Simplexverfahren Wenn ein Unternehmen ermitteln möchte, wie viele Mengeneinheiten von verschiedenen Produkten zu produzieren sind, damit bei gegebenen Verkaufspreisen der
A2.1 Lineare Optimierung mit dem Simplexverfahren Wenn ein Unternehmen ermitteln möchte, wie viele Mengeneinheiten von verschiedenen Produkten zu produzieren sind, damit bei gegebenen Verkaufspreisen der
III. Transportaufgaben 1. Problemstellung 2. Analyse 3. Bestimmung der Startecke 4. Eckenaustausch 5. Umladeprobleme 6. Zuordnungsprobleme
 III. Transportaufgaben 1. Problemstellung 2. Analyse 3. Bestimmung der Startecke 4. Eckenaustausch 5. Umladeprobleme 6. Zuordnungsprobleme H. Weber, FHW, OR SS07, Teil 6, Seite 1 1. Problemstellung Wir
III. Transportaufgaben 1. Problemstellung 2. Analyse 3. Bestimmung der Startecke 4. Eckenaustausch 5. Umladeprobleme 6. Zuordnungsprobleme H. Weber, FHW, OR SS07, Teil 6, Seite 1 1. Problemstellung Wir
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Beispiel: Graphische Darstellung Zulässigkeitsbereich Ungleichung (1) mit
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Beispiel: Graphische Darstellung Zulässigkeitsbereich Ungleichung (1) mit
Aussage: richtig falsch
 Aufgabe 1 (15 Minuten) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an! Stimmt Ihre Bewertung einer Aussage so gibt es einen Punkt.
Aufgabe 1 (15 Minuten) Folgende Aussagen sind entweder richtig oder falsch! Kreuzen Sie jeweils direkt hinter der Aussage eines der Kästchen an! Stimmt Ihre Bewertung einer Aussage so gibt es einen Punkt.
Automatiche Teameinteilung für PSE
 Automatiche Teameinteilung für PSE Einführung ILP-Modellierung LEHRSTUHL PROGRAMMIERPARADIGMEN 0 7.12.2016 - PSE/TSE WS 2016/17 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft LEHRSTUHL PROGRAMMIERPARADIGMEN
Automatiche Teameinteilung für PSE Einführung ILP-Modellierung LEHRSTUHL PROGRAMMIERPARADIGMEN 0 7.12.2016 - PSE/TSE WS 2016/17 KIT Die Forschungsuniversität in der Helmholtz-Gemeinschaft LEHRSTUHL PROGRAMMIERPARADIGMEN
Algorithmen I - Tutorium 28 Nr. 12
 Algorithmen I - Tutorium 28 Nr. 12 20.07.2017: Spaß mit Dynamischer und Linearer Programmierung Marc Leinweber marc.leinweber@student.kit.edu INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR. JÖRN
Algorithmen I - Tutorium 28 Nr. 12 20.07.2017: Spaß mit Dynamischer und Linearer Programmierung Marc Leinweber marc.leinweber@student.kit.edu INSTITUT FÜR THEORETISCHE INFORMATIK (ITI), PROF. DR. JÖRN
14.4 Warum die Methode der Lagrange-Multiplikatoren funktioniert
 14 Optimierung unter Nebenbedingungen 14.4 Warum die Methode der Lagrange-Multiplikatoren funktioniert [1] Lösen sie die folgenden Probleme, indem Sie diese auf ein univariates Problem zurückführen. Zeigen
14 Optimierung unter Nebenbedingungen 14.4 Warum die Methode der Lagrange-Multiplikatoren funktioniert [1] Lösen sie die folgenden Probleme, indem Sie diese auf ein univariates Problem zurückführen. Zeigen
1 Zahlenmengen und einige mathematische Symbole
 1 Zahlenmengen und einige mathematische Symbole Inhalt 1.1 Vorbemerkung................................................... 3 1.2 Zahlenmengen................................................... 4 1.3 Summenzeichen..................................................
1 Zahlenmengen und einige mathematische Symbole Inhalt 1.1 Vorbemerkung................................................... 3 1.2 Zahlenmengen................................................... 4 1.3 Summenzeichen..................................................
Rechnerpraktikum zur Nichtlinearen Optimierung
 Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Rechnerpraktikum zur Nichtlinearen Optimierung 9. März 2016 11. März 2016 Sebastian Garreis, B. Sc. Philipp Jarde, M. Sc. Technische Universität München Fakultät für Mathematik Lehrstuhl für Mathematische
Compilerbau 12. Übungsblatt, Sommersemester 2015 Abgabetermin:
 12 12. Übungsblatt, Sommersemester 2015 Abgabetermin: 14.07.2015 Aufgabe 32 Übersetzen Sie den arithmetischen Ausdruck a*-(b+c) in 3-Adress-Code. Aufgabe 33 Entwickeln Sie für die folgende Teilgrammatik
12 12. Übungsblatt, Sommersemester 2015 Abgabetermin: 14.07.2015 Aufgabe 32 Übersetzen Sie den arithmetischen Ausdruck a*-(b+c) in 3-Adress-Code. Aufgabe 33 Entwickeln Sie für die folgende Teilgrammatik
Sattelpunkt-Interpretation
 Sattelpunkt-Interpretation Vinzenz Lang 14. Mai 2010 Die Sattelpunkt-Interpretation befasst sich mit der Interpretation der Lagrange- Dualität. Sie wird im weiteren Verlauf des Seminars nicht noch einmal
Sattelpunkt-Interpretation Vinzenz Lang 14. Mai 2010 Die Sattelpunkt-Interpretation befasst sich mit der Interpretation der Lagrange- Dualität. Sie wird im weiteren Verlauf des Seminars nicht noch einmal
