Platten - Grundlagen ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton II 1
|
|
|
- Frank Hausler
- vor 6 Jahren
- Abrufe
Transkript
1 Patten - Grundagen ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 1
2 Patten - Grundagen Fächentragwerke agemein Patten ten primär senkrecht zur Ebene beastet Scheiben Scheiben primär in Ebene beastet Schaen Scheiben/Schaen gekrümmte Mittefäche Fatwerke aus ebenen Teifächen gebidet ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II Fächentragwerke assen sich in fogende Kategorien einordnen, wobei diese nach Tragwirkung und geometrischer Form charakterisiert werden: Patten tragen primär senkrecht zu ihrer Ebene wirkende Lasten ab. Somit herrscht hauptsächich ein Biegezustand mit Biege- und Drimomenten sowie Querkräften vor. Der Membranspannungszustand mit Scheibenkräften ist vernachässigbar. Patten sind das häufigste Konstruktionseement im Hochbau, kommen aber auch sonst oft vor: Fahrbahnpatten von Brücken, Wände/Decke/Bodenpatten von Tagbautunnes etc. Scheiben tragen primär in ihrer Ebene wirkende Lasten ab. Der Membranspannungszustand ist vorherrschend, während der Biegezustand vernachässigbar ist. Tpische Beispiee sind Wände im Hochbau (Abtrag von Vertikakräften und ggf. Schubkräften in der Wandebene bei aussteifenden Wänden) sowie Stege von Trägern (Abtrag der Querkraft durch Kräfte in Scheibenebene). Fächentragwerke mit einfach oder doppet gekrümmter Mitteebene werden as Schaen (shes) bezeichnet. Sie erauben beispiesweise die Abtragung von vertika wirkenden Lasten, bspw. des Eigengewichts, über reine Druckmembrankräfte, sofern die Form des Tragwerks der umgedrehten Ketteninie entspricht. Man spricht dann von Schaen- oder Gewöbewirkung. Links unten sind Betonschaen von Heinz Iser (Autobahnraststätte Deitingen) abgebidet, deren Geometrie eperimente aus hängenden Tüchern ermittet wurde. Diese «natüriche» Form eraubt die Überspannung von rund 30 m bei einer Schaendicke von nur 10 cm. Fatwerke sind aus mehreren Teifächen aufgebaut, weche jeweis an ihren Kanten miteinander verbunden sind. Ergänzende Bemerkung - Die Scheibentragwirkung (Membrankräfte) ist in der Rege wesentich steifer as die Pattentragwirkung (Biegung), weshab beispiesweise bei der Berechnung von Gebäudekernen nur die Scheibentragwirkung der Wände berücksichtigt wird. - Weiterführende Angaben zu Schaen siehe Voresung Fächentragwerke (Masterstudium).
3 Patten - Grundagen Tragwerksanase / Berechnungsmethoden - Übersicht Eastische Pattentheorie Pastische Pattentheorie Statische Methode der Pastizitätstheorie Kinematische Methode der Pastizitätstheorie Lösung der Pattendifferentiageichung Methode der Finiten Eemente Momentenansätze Fiessgeenkinienmethode Approimative Lösungen mit Energieverfahren Methode der stevertretenden Rahmen Streifenmethode einfach erweitert ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 3 In diesem Kapite wird die Tragast dünner Patten mit keinen Durchbiegungen untersucht. Dabei wird idea pastisches Materiaverhaten vorausgesetzt, ohne auf Fragen des Verformungsbedarfes und des Verformungsvermögens näher einzugehen. Da Patten in der Rege eher schwach bewehrt sind, besteht diesbezügich gewöhnich wenig Anass zu Bedenken. Patten sind die am weitesten verbreitete Anwendung der Stahbetonbauweise. Ihrer Bedeutung entsprechend werden sie in diesem Kapite eingehend behandet. Zunächst werden die grundegenden statischen Beziehungen aufgestet, aus denen schiessich die Fiessbedingungen hergeeitet werden können. In der Prais werden heutzutage für die Ermittung der Beanspruchung meist numerische Verfahren, insbesondere die Methode der finiten Eemente, angewendet. Für Pausibiitätskontroen eignen sich entsprechende Näherungsverfahren wie bspw. die Methode der stevertretenden Rahmen. In der pastischen Pattentheorie werden zur Ermittung der Tragast statische und kinematische Berechnungsmethoden verwendet. Für die Bemessung wird meist nur der Biegezustand der Patte betrachtet. Der Einfuss der Querkräfte wird normaerweise nur bei konzentrierten Kräften und Stützen massgebend (Durchstanzen).
4 Ebene Eemente - Spannungsresutierende Patten - Grundagen n dz dz z dz dz dz z dz m m n v n n v m m h/ h/ h/,, knm/m=kn m z dz m z dz m m z dz h/ h/ h/ h/ h/ z, kn/m v dz v dz z h/ h/ h/ h/ h/,, kn/m n dz n dz n n dz h/ h/ h/ Biegespannungszustand (Patte): Biegemomente und Querkräfte Membranspannungszustand (Scheibe): Membrankräfte (Norma- /Schubkräfte) ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 4 Die in den Schnittfächen eines Patteneementes angreifenden Spannungen können zu Spannungsresutierenden gemäss der Abbidung zusammengefasst werden. Die Biege- und Drimomente sowie die Querkräfte biden den Biegespannungszustand; die Membrankräfte den Membranspannungszustand. Im fogenden werden primär senkrecht zur ihrer Mittefäche beanspruchte Patten betrachtet, in wechem ein Biegespannungszustand vorherrscht. Membrankräfte können deshab vorerst ausser acht geassen werden. NB: Anaog der Bakentheorie wird z = 3 vernachässigt. In jeder Ebene z = const. herrscht somit ein ebener Spannungszustand. NB: Engische Ausdrücke («driing») - Biegemoment: bending moment Drimoment: twisting moment (auch: torsiona moment) (Patten-)Querkraft: out of pane shear force Membrannormakraft: Membranschubkraft: Biegung: Driung: (in-pane) norma force in-pane shear force bending torsion
5 Ebene Eemente - Spannungsresutierende Patten - Grundagen h/ h/ h/ m z dz, m z dz, m m z dz h/ h/ h/ h/ h/ v dz, v dz z z h/ h/ h/ h/ h/ n dz, n dz, n n dz h/ h/ h/ Vorzeichenkonvention Positive Spannungen wirken an Eementen mit positiver äusserer Normaenrichtung in positiver Achsenrichtung Positive Membran- und Querkräfte entsprechen positiven zugehörigen Spannungen Positive Momente entsprechen positiven zugehörigen Spannungen für z > 0 Indizes: 1. Inde: Richtung der Spannung. Inde: Normaenrichtung des Eements, an dem Spannung wirkt ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 5 Für Spannungen und Spannungsresutierende werden die in der Abbidung iustrierten Vorzeichenkonventionen verwendet. Danach wirken positive Spannungen an Eementen mit positiver äusserer Normaenrichtung in positiver Koordinatenrichtung; für Normaspannungen bedeutet dies, dass Zugspannungen positiv sind. Positive Membran- und Querkräfte entsprechen positiven Spannungen, und positive Momente entsprechen positiven Spannungen nach obenstehender Definition für positive Werte der Koordinate z. Bei doppeten Indizes steht jeweis der erste Inde für die Richtung, in wecher die Spannung wirkt, während der zweite Inde die Normaenrichtung des Fächeneementes bezeichnet, an wechem die Spannung angreift (sind beide Indizes identisch, wird einer weggeassen).
6 Patten Statische Beziehungen ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 6
7 Patten Geichgewicht Geichgewichtsbedingungen kartesische Koordinaten Pattengeichgewichtsbedingung: m m m q 0 Baken in -Richtung zusätzich: Drimomente Baken in -Richtung Hereitung über Geichgewicht am differentieen Patteneement: v v v d v d v d d v d d q dd 0 m m md md m d d m d d vdd 0 m m md md m d d m d d vdd 0 Terme mit (d) bzw. (d) vernachässigt v v q 0 m m v 0 m m v ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 7 Das Geichgewicht der angreifenden Kräfte und Momente am Patteneement führt zu drei Geichungen. Durch Einsetzen der zweiten und dritten Geichung in die erste ergibt sich die Geichgewichtsbedingung für Patten in kartesischen Koordinaten.
8 Patten Geichgewicht Geichgewichtsbedingungen Zinderkoordinaten rm m m q 0 r r r r r r rm r r Hereitung über Geichgewicht am differentieen Patteneement: rv r v qr 0 r rm r r mr m rvr 0 mr m mr r rv 0 r Bzw. für rotationssmmetrische Fäe: rm r r r m qrdr ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 8 Bei rotationssmmetrischen Patten (Geometrie und Beastung) verschwinden die Drimomente m r = m r und die Querkräfte v ; ae Grössen sind zudem definitionsgemäss unabhängig vom Winke.
9 Patten Geichgewicht Spannungstransformation: Biege- und Drimomente Biege- und Drimomente in einer beiebigen Richtung : m m m m n cos sin sin m m m m t sin cos sin mtn m m sin cosm cos NB: sin sincos, cos cos sin Hauptrichtung 1 (Drimomente = 0) und Hauptmomente ( Mohr scher Kreis): m tan 1 m m m 1, m m 4m m m ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 9 Das Momentengeichgewicht an den in der Abbidung dargesteten Patteneementen führt zu Beziehungen, weche as Transformationsformen für Biege- und Drimomente dienen. Es können beiebige Schnitte mit der Normaen n, deren Richtung durch den Winke festgeegt ist, betrachtet werden. Sie assen sich mithife eines Mohrschen Kreises darsteen; Drimomente werden hier (nur für die Konstruktion des Mohr schen Kreises) positiv gerechnet, wenn der ihnen entsprechende positive (rechtsdrehende) Momentenpfei in Richtung des betrachteten Schnittrandes weist. Die Hauptrichtung, für weche die Drimomente verschwinden, m tn = 0, sowie die zugehörigen Hauptmomente m 1 und m in den entsprechenden Richtungen können sowoh grafisch im Mohr schen Kreis as auch anatisch bestimmt werden.
10 Patten Geichgewicht Spannungstransformation: Querkräfte Querkräfte in einer beiebigen Richtung : v v cos v sin n v v sin v cos t Hauptquerkraft und zugehörige Richtung 0 (Interpretation mit Thaeskreis): v v v v tan 0 v 0 (agemein ist 0 1 ) ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 10 Anaog zu den Momenten kann auch das Geichgewicht der vertikaen Kräfte an den abgebideten Patteneement aufgestet werden. Dies führt zu Transformationsregen für Querkräfte an einem beiebigen Schnitt mit der Normaen n, deren Richtung durch den Winke festgeegt ist. Die trigonometrischen Funktionen assen sich mithife eines Thaeskreises deuten. An jeder Stee der Patte wird eine Hauptquerkraft v 0 in Richtung 0 übertragen. Senkrecht zu dieser Richtung wird keine Querkraft abgetragen. Die Hauptrichtungen der Querkräfte und der Momente faen nur in Speziafäen zusammen, agemein ist 0.
11 Randbedingungen agemein (eastische Patten) Patten Randbedingungen Am Rand einer Patte greifen agemein Momente m n, m tn und eine Querkraft v n an. Inhomogene Bipotentiageichung gemäss Kirchhoffscher Theorie dünner eastischer Patten mit keinen Durchbiegungen: w w w w q mit D Eh 4 4 D 1(1 ) dabei sind nur Randbedingungen an die Lösung anpassbar jedoch 3 Kraftgrössen vorhanden (m n, m tn, v n ) zusätziche Bedingung erforderich Kräfte am Pattenrand Weitere Bedingung für einfach geagerte und freie Pattenränder: Ersetzen der Drimomente m tn dt durch stetige Verteiung von vertikaen Kräftepaaren m tn, weche sich an den Grenzen zwischen den infinitesimaen Eementen jeweis bis auf den Zuwachs m tn,t dt aufheben Kräftepaare ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 11 Am Rand einer Patte greifen agemein ein Biegemoment m n, ein Drimoment m tn und eine Querkraft v n an. Nach Kirchhoff erhät man für dünne eastische Patten mit keinen Durchbiegungen eine inhomogene Bipotentiageichung für die Durchbiegungen der Patte, deren Lösungen sich nur zwei Randbedingungen anpassen assen. Deshab wird bei der Behandung von einfach geagerten und freien Pattenrändern eine weitere Bedingung eingeführt. Die Drimomente m tn werden dabei durch eine stetige Verteiung von vertikaen Kräftepaaren ersetzt, wobei sich an den Grenzen zwischen den infinitesimaen Eementen der Länge dt die Kräfte bis auf den Zuwachs m tn,t dt aufheben.
12 Randbedingungen agemein (eastische Patten) mtn mn mnt vn t n t Patten Randbedingungen Zuwachs pro Längeneinheit dm tn / dt wird mit der Querkraft v n zu einer Stützkraft zusammengefasst (Hereitung mit Geichgewichtsbeziehung m m v 0 ) In einer Pattenecke addieren sich die Drimomente der beiden Ränder zu einer Eckkraft von m tn Stützkraft Diese Behandung von Drimomenten am Pattenrand geht auf Thomson und Tait (1883) zurück und ässt sich mit dem Prinzip von de Saint Venant «begründen». Eckkraft ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 1 Der Zuwachs pro Längeneinheit m tn,t wird nun mit der Querkraft v n zu einer Stützkraft v n +m tn,t = m n,n +m nt,t zusammengefasst. Die beschriebene Behandung von Drimomenten am Pattenrand geht auf Thomson und Tait (1883) zurück und ässt sich mit dem Prinzip von de Saint Venant begründen.
13 Patten Randbedingungen Randbedingungen auf der Basis von Geichgewichtsüberegungen Statische Methode der Pastizitätstheorie Erkärung mit Tragwirkung im Bereich von Pattenrändern, weche nur auf Geichgewichtsüberegungen beruht: Aus Geichgewicht in einer schmaen Randzone der Patte fogt die Randquerkraft: V t -m tn sofern: Pattenrand ist spannungsfrei und die in der Randzone auftretenden Spannungen t ändern sich nicht in t-richtung (Cde, 1979). Aus der Randquerkraft V t -m tn fogen die Eckkräfte m tn und der Beitrag von m tn,t zur Stützkraft Querkraft in Randzone Stützkraft Eckkraft ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 13 Aus der Sicht der statischen Methode der Pastizitätstheorie ist jedoch eine Erkärung der Tragwirkung im Bereich von Pattenrändern vorzuziehen, weche nur auf Geichgewichtsüberegungen beruht. Dies ist in der Abbidung iustriert. In einer schmaen Randzone der Patte muss aus Geichgewichtsgründen eine Randquerkraft V t =-m tn eisitieren, sofern der Pattenrand spannungsfrei ist und die in der Randzone auftretenden Spannungen t sich in t-richtung nicht ändern. Aus der Eistenz der Randquerkräfte V t fogen die Eckkräfte m tn und der Beitrag m tn,t der Drimomente zur Stützkraft.
14 Patten Randbedingungen Randbedingungen auf der Basis von Geichgewichtsüberegungen Randbedingungen auf Basis von Geichgewichtsüberegungen: eingespannter Rand: m n, m tn und v n beiebig einfach geagerter Rand: m n = 0, resutierende Stützkraft: mtn mn mnt vn t n t freier Rand: m n = 0, verschwindende Stützkraft: mtn mn mnt vn 0 t n t Stützkraft ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 14 Die entsprechenden Randbedingungen assen sich wie in der Abbidung angegeben zusammenfassen. Diese fogen aus reinen Geichgewichtsbetrachtungen und sind somit für beiebiges Materiaverhaten gütig. Für dünne eastische Patten können strengere Randbedingungen formuiert werden, weche jedoch für die Behandung nach der Pastizitätstheorie nicht reevant sind.
15 Patten Randbedingungen Randbewehrung Werden entang von einfach geagerten und freien Rändern Drimomente in Rechnung gestet, so ist eine Bewehrung zur Aufnahme von V t -m tn anzuordnen. Veranschauichung (Ecke, reine Driung): Ober- und Unterseite: zueinander senkrechte, unter 45 zu den Pattenrändern geneigte Betondruckstreben, Aufnahme der randnormaen Komponenten durch randparaee Bewehrung Komponenten in Richtung der Pattenränder werden durch geneigte Betondruckstreben in den Randstreifen weitergeeitet; Vertikakomponenten entsprechen den Randquerkräften V t -m tn Aufnahme von V t -m tn mit Steckbügen oder entsprechender Abbiegung der Biegebewehrung Querkraft in Randzone Kraftfuss in Pattenecke m nt ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 15 Die Randquerkräfte sind bei der Ausbidung der Bewehrung entang von einfach geagerten und freien Rändern von Stahbetonpatten zu berücksichtigen. Die Abbidung zeigt den Kraftfuss einer auf reine Driung beanspruchten Rechteckpatte, wecher mit einem Fachwerkmode dargestet werden kann. An der Pattenoberseite und an der Pattenunterseite biden sich zueinander senkrechte, unter 45 zu den Pattenrändern geneigte Betondruckstreben aus, deren Komponenten in Richtung der Randnormaen durch randparaee Bewehrung aufgenommen werden. Die Komponenten in Richtung der Pattenränder werden über geneigte Betondruckstreben in den Randstreifen weitergeeitet, deren Vertikakomponente wecher den Randquerkräften entspricht über eine Bewehrung aufgenommen werden muss. Diese kann mit Steckbügen oder durch entsprechende Abbiegung der Biegebewehrung reaisiert werden. Man erkennt auch, dass sich die Randquerkräfte in der Pattenecke nicht aufheben, sondern zu einer Eckkraft m nt addieren.
16 Patten Randbedingungen Diskontinuitäten Im Patteninnern sind statische Diskontinuitätsinien zuässig ( Äquivaenz von Drimomenten am Pattenrand und Randquerkräften, man füge in Gedanken zwei freie Pattenränder zusammen). An Diskontinuitätsinien müssen Biegemomente m n stetig sein (m + n = m n- ) dürfen Drimomente m nt und Querkräfte v n springen (m + nt m nt-, v + n v n- ) Somit geten für eine statische Diskontinuitätsinie, entang wecher eine Querkraft V t abgetragen wird, fogende Bedingungen: m n m n V m m t nt nt Vt t v n v n Diskontinuität ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 16 Fügt man in Gedanken zwei Patten an ihren freien Rändern zusammen (man beachte, dass Pattenränder Diskontinuitäten darsteen, an denen i.a. ein Biegemoment m n, ein Drimoment m tn und eine Querkraft v n angreift!), so kann aus der Äquivaenz von Drimomenten am Pattenrand und Randquerkräften gemäss der Randquerkraft V t = -m tn darauf geschossen werden, dass an statischen Diskontinuitätsinien im Patteninnern die Biegemomente m n stetig veraufen müssen, die Drimomente m nt und die Querkräfte v n hingegen springen dürfen. Dabei müssen an einer statischen Diskontinuitätsinie, entang wecher eine Querkraft V t abgetragen wird, die Beziehungen gemäss der Abbidung erfüt sein.
17 Patten Randbedingungen Randbedingungen Beispie 1 (Geichgewichtsösung) Gegeben: Quadratpatte unter Fächenast q mit Ansätzen für Biegemomente m, m und Drimoment m q m 1 m u m 1 m u m m u m m m 4mu Geichgewicht: q 0 q Gesucht: Schnittkraftveräufe am Pattenrand, Stützkraft, Eckkraft, Lagerung der Patte, 6m u Drimoment entang Pattenrand: m m mu u + Querkraft entang Pattenrand: m m aus v 0 fogt: v m u m u mu + m u - m Stützkraft: v mu m u mu - m u Eckkraft: m m u u m m m v ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 17 Das erste Beispie behandet eine Quadratpatte mit Seitenänge unter einer geichmässigen Fächenast q. Die Ansätze für die Biegemomente m und m sowie das Drimoment m (weches entang der Koordinatenachsen verschwindet) ergeben mithife der Geichgewichtsbedingung für Patten die maima aufnehmbare Last q u. Die Schnittkraftveräufe an den Pattenrändern fogen aus den gewähten Momentenansätzen; die Querkraft sowie die Stütz- und Eckkräfte werden aus den bereits hergeeiteten Geichgewichtsbedingungen ermittet. Die Lösung basiert auf der statischen Methode der Pastizitätstheorie: das Geichgewicht ist in jedem Punkt erfüt und die Fiessbedingung nirgends veretzt; es wurden jedoch keine Verträgichkeitsbedingungen aufgestet. Im Agemeinen handet sich hierbei somit um einen unteren Grenzwert der Tragast. Für das gezeigte Beispie eistieren verträgiche Bruchmechanismen, und es handet sich somit im Rahmen der getroffenen Annahmen um voständige Lösungen. Ergänzende Bemerkung - Dass die Fiessbedingung nirgends veretzt ist (unter Berücksichtigung der Drimomente m ), kann mit der Normamomenten-Fiessbedingung überprüft werden, siehe später.
18 Patten Randbedingungen Randbedingungen Beispie 1 (Geichgewichtsösung) Lagerung der Patte: Aus der konstanten Stützkraft fogt, dass die Patte entang ihrer Ränder einfach geagert sein muss. Die Ecken sind gegen Abheben gesichert ( nach unten gerichtete Eckkräfte) Stützkraft: Eckkraft: m 8 v mu mu 4m q u mu mu mu 8 m u mu 8 m u ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 18 Aus der Grösse der Querkräfte senkrecht zum jeweiigen Pattenrand (q bei = ±/ resp. q bei = ±/) und den Drimomenten (m, bei = ±/ resp. m, bei = ±/) resutiert die Stützkraft am Pattenrand. Aus der konstanten Stützkraft fogt, dass die Patte an den Rändern einfach geagert sein muss. Aus den Randquerkräften (Querkraft entang Pattenrand, siehe vorhergehende Foie) fogen die Eckkräfte. Die nach unten gerichteten Eckkräfte bedeuten, dass die Ecken gegen Abheben gesichert sind.
19 Patten Randbedingungen Randbedingungen Beispie (Geichgewichtsösung) Gegeben: Quadratpatte unter Fächenast q mit Ansätzen für Biegemomente m,m und Drimoment m q m 1 m u m 1 m u m m u m m m 8mu Geichgewicht: q 0 q Gesucht: Schnittkraftveräufe am Pattenrand, Stützkraft, Eckkraft, Lagerung der Patte, + m u - m u m u + m u - Drimoment entang Pattenrand: Querkraft entang Pattenrand: m m aus v 0 fogt: Stützkraft: Eckkraft: m 4 v mu m 0 u m m u u m mu 8 4 v m m m u u u m m m v ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 19 Das zweite Beispie behandet diesebe Quadratpatte unter der Fächenast q. Im Unterschied wird hier der Ansatz der Drimomente mit umgekehrtem Vorzeichen definiert. Aus der Geichgewichtsbedingung der Patte fogt damit eine drei Ma tiefere Tragast. Auch hier können mithife der Momentenansätze die Querkraft, die Stützkräfte an den Pattenrändern sowie die Eckkraft bestimmt werden. Der Wechse des Vorzeichens der Drimomente reduziert die Querkräfte entang der Pattenränder auf einen Dritte; die Stützkraft verschwindet somit.
20 Patten Randbedingungen Randbedingungen Beispie (Geichgewichtsösung) Lagerung der Patte: Aus der verschwindenden Stützkraft fogt, dass die Patte entang ihrer Ränder frei und edigich an den Ecken gestützt ist. Stützkraft: Eckkraft: m v m u 0 q 8m u mu mu mu mu ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 0 Die Stützkraft verschwindet entang der Pattenränder; somit ist die Patte dort frei und edigich an den Ecken gestützt (nach oben gerichtete, negative Eckkräfte = Reaktionen).
21 Patten Kinematische Beziehungen ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 1
22 Patten Kinematische Beziehungen Beziehungen für dünne Patten Nach der Theorie von Kirchhoff über dünne Patten wird angenommen, dass die Normaen zur Pattenmitteebene während der Verformung gerade und senkrecht zur verformten Mittefäche beiben. w Verschiebungen: u z - Richtung z P Verzerrungen: w w z Krümmungen: P Driung: w u z w vz - Richtung u w z z v w z z u v w z z ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II w w w In der eastische Pattentheorie werden neben den Geichgewichtsbedingungen auch die kinematischen Beziehungen benötigt, um die Verträgichkeitsbedingungen zu definieren. Nach der Theorie von Kirchhoff für dünne eastische Patten wird angenommen, dass die Normaen zur Pattenmitteebene während der Verformung gerade und senkrecht zur verformten Mittefäche beiben (anaog Bakenbiegung, Annahme von Bernoui/Navier). Aus der Abbidung können jeweis die kinematischen Reationen der Verschiebungen in Abhängigkeit der Pattendurchbiegung w ermittet werden. Daraus fogen die Verzerrungen, und bzw. die Krümmungen, und die Driung.
23 Transformation der Krümmungen und Driungen Anaog zur Transformation der Norma- und Schubspannungen Patten Kinematische Beziehungen nt X 1 n Y Po ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 3 Aus den Beziehungen der Verzerrungen (,, ) ist ersichtich, dass auch die Krümmungen (,, ) mit einem Mohrschen Kreis dargestet werden können. Im Agemeinen ist die Mitteebene nicht verzerrungsfrei, sondern weist Verzerrungen ( 0, 0, 0 )auf, womit die Verformung eines Patteneementes agemein durch sechs kinematische Parameter ( 0, 0, 0,,, ) festgeegt ist.
24 Eastische Patten ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 4
25 Annahmen der eastischen Pattentheorie Eastische Patten Die Theorie von Gustav Robert KIRCHHOFF für dünne Patten gründet auf fogenden Annahmen: 1. Die Pattendicke h ist konstant und kein gegenüber anderen Abmessungen. Die Normaspannungen z werden vernachässigt. Die Spannungsverteiung in der Patte darf damit as eben und über h inear angenommen werden.. Die Normaen zur Pattenmitteebene beiben gerade und senkrecht zur verformten Mitteebene. Die Schubverzerrungen z und z verschwinden in der Foge (schubstarre Patten). Damit ist z eine Hauptrichtung. 3. Der Zusammenhang zwischen den einzenen Pattenschichten wird as geöst betrachtet. Zusammen mit Annahme entspricht dies den Grundannahmen der Bakentheorie. 4. Die Durchbiegungen w sind kein gegenüber h und unabhängig von z. Das Geichgewicht kann damit am unverformten Sstem gebidet werden, es treten i.d.r. keine Membrankräfte auf. In Kombination mit Annahme ergeben sich die kinematischen Beziehungen. 5. Der Werkstoff ist homogen, isotrop und inear eastisch ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 5 (Eräuterungen siehe Foie)
26 Eastische Patten Pattengeichung Aus dem Stoffgesetz (inear eastisch, Hooke sches Gesetz), den kinematischen Beziehungen sowie dem Geichgewicht am infinitesimaen Eement fogt die sogenannte Pattengeichung. E 1 Hooke sches Gesetz für den ebenen Spannungszustand: Pattengeichung: w w w w q mit D Eh 4 4 D 1(1 ) E E 1 1 Baken in -Richtung Zusatzterm Baken in -Richtung Pattensteifigkeit Inhomogene Differentiageichung 4. Ordnung (inhomogene Bipotentiageichung) Randbedingungen anpassbar, jedoch 3 Grössen vorhanden (m n, m nt und v t ) Stützkraft eingespannter Rand: m n,m tn und v n beiebig einfach geagerter Rand: m n = 0, resutierende Stützkraft: freier Rand: m n = 0, verschwindende Stützkraft: mtn mn mnt vn t n t mtn mn mnt vn 0 t n t Vergeiche Foie zu den Randbedingungen ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 6 Mithife des Hookeschen Gesetzes können unter Berücksichtigung der Querdehnung die Norma- und Schubspannungen ermittet werden. Durch Einsetzen der kinematischen Beziehungen in die Geichgewichtsbedingungen ergibt sich die bereits in Foie 11 vorgestete Bipotentiageichung der eastischen Patten. D ist dabei die Pattensteifigkeit; bei Vernachässigung der Querdehnung ( = 0) ist sie geich der Bakensteifigkeit EI = Eh 3 /1 (pro Einheitsbreite). Die Patte ist sebst in den einzenen Richtungen etwas steifer as der Baken, da nicht ae Fasern getrennt sind, sondern edigich die horizonta iegenden Schichten (Einfuss der Querdehnungszah). Die Randbedingungen ergeben sich gemäss der Überegungen aus Foie 14.
27 Eastische Patten Abschätzung der Durchbiegungen Die Durchbiegungen in Pattenmitte können as Viefaches derjenigen des einfachen Bakens abgeschätzt werden (nach Bachmann, 1991): 4 5 q EI wc D q const. 384 D 1 Einfach geagerte Patte c = 0.31 In den Ecken gestützte Patte c =.5 Eingespannte Patte c = Mittefed einer Fachdecke c = Zu beachten ist der Steifigkeitsabfa infoge Kriechen (E c E c0 /3) und Rissbidung bzw. die Steifigkeitserhöhung infoge Zugversteifung und die keineren Durchbiegungen bei Vorspannung ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 7 Bei Quadratpatten unter geichmässiger Fächenast q kann die Durchbiegung in Pattenmitte as Viefaches derjenigen des einfachen Bakens geicher Spannweite abgeschätzt werden. Daraus ist auch der Einfuss der verschiedenen Lagerungsarten ersichtich; bspw. weist eine eckgestützte Patte vie höhere Verformungen auf as eine einfach geagerte. Weiter zu beachten sind die Einfüsse auf die Steifigkeit infoge Kriechen und Rissbidung sowie Zugversteifung oder eine afäige Vorspannung.
28 Eastische Patten Tragwerksanase / Berechnungsmethoden Übersicht Eastische Pattentheorie Pastische Pattentheorie Statische Methode der Pastizitätstheorie Kinematische Methode der Pastizitätstheorie Lösung der Pattendifferentiageichung Methode der Finiten Eemente Momentenansätze Fiessgeenkinienmethode Approimative Lösungen mit Energieverfahren Methode der stevertretenden Rahmen Streifenmethode einfach erweitert ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 8
29 Eastische Patten Lösungsverfahren Direkte Lösung der Pattengeichung für speziee Probemsteungen mögich (z.b. rotationssmmetrische Patten) Resutate sind in Literatur vorhanden und insbesondere für Abschätzungen und Pausibiitätskontroen wertvo Approimative Lösung der Pattengeichung mit Fourier-Reihenansätzen oder Energieverfahren z.b. für Rechteckpatten mit unterschiedichen Randbedingungen und Beastungsanordnungen Lösung der Pattengeichung mit der Methode der Finiten Eemente Lösung der Verträgichkeits- und Geichgewichtsbedingungen am infinitesimaen Eement beiebige Randbedingungen und Beastungen mögich heute meistens verwendet ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 9 Die Lösung der Pattendifferentiageichung ist nur in wenigen Fäen anatisch mögich (z.b. für rotationssmmetrische Fäe), nicht direkt anwendbar oder nur mit starken Vereinfachung (da es kaum rotationssmmetrische Probeme gibt; z.b. Durchstanztheorie basiert auf rotationssmmetrischen Annahmen obschon orthogona bewehrte Patten nicht wirkich rotationssmmetrisch sind). In der Literatur finden sich einige Ansätze zur Lösung verschiedener Probeme mit unterschiedichen Geometrie und Randbedingungen; sie sind insbesondere für Abschätzungen und Pausibitätskontroen wertvo. Andere Mögichkeiten bestehen in der Verwendung von Fourierreihen, um Geichasten/Randbedingungen anzunähern oder Energieverfahren nach Ritz und Gaerkin. Aufgrund dessen werden in der Prais meist computergestützte Berechnungen basierend auf der Methode der Finiten Eemente durchgeführt. Hierbei werden am infinitesimaen Eement die Verträgichkeits- und Geichgewichtsbedingungen geöst. Heutige Computer erauben aufgrund der hohen Rechenkapazität eine angemessene Anzah an Eementen, so dass beiebige Randbedingungen und Beastungen mögich sind. Aufgrund der hohen Dichte an Diskretisierungspunkten ist eine direkte rechnerische Überprüfung der FE-Methode schwierig; daher sind die Eingabedaten und die Resutate stets kritisch zu hinterfragen und mit vereinfachten Handrechnungen zu überprüfen.
30 Eastische Patten Direkte Lösung der Pattendifferentiageichung Beispie Einfach geagerte Quadratpatte unter sinusförmiger Fächenast q (,) (Lsg. n. Navier) : Querdehnungszah q 0 Last: Differentiageichung: qq0 sin sin w w w q w 4 4 D w w m D Ansatz: w w m D wcsin sin m m q 1 0 m, 4 Randbedingungen: Lösung: 0,,,0, 0 w w w w m 0, m, m,0 m, q q 0 0 C w sin sin D 4 D ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 30 Das Beispie zeigt eine einfach geagerte Quadratpatte unter sinusförmiger Fächenast. Der Ansatz für die Lösung der Bipotentiageichung (von Navier vorgeschagen) ist affin zur Beastung. Die Momentenveräufe können aus den zweiten Abeitungen der Durchbiegungen ermittet werden. Die einfache Lagerung der Patte bedingt, dass jeweis die Durchbiegungen wie auch die Momente an den Rändern geich nu ist. Daraus können die Durchbiegungen der Patte, und daraus die Beanspruchungen, ermittet werden.
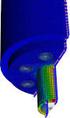
31 Lösungsverfahren mit finiten Eementen Beispie Eastische Patten Randgestützte Quadratpatte unter Eigenast ( = 10 m, h = 0.5 m) m [kn] m [kn] m [kn] Durchbiegungen quaitativ und überhöht w ma = w(/, /) = 5.6 mm ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 31 Die Lösung der Pattengeichung kann auch numerisch, mithife der Methode der Finiten Eemente angenähert werden. Bei genügend feiner Diskretisierung resutiert dabei die eastische Lösung. In der Abbidung sind für eine umfanggeagerte Patte unter geichmässiger Beastung die Biege- und Drimomente m, m und m as Isoinien und die (überhöhten) Durchbiegungen isometrisch dargestet (Berechnung mit kommerzieer Software Cedrus-7 von Cubus AG). Die Durchbiegungen sind gemäss den Randbedingungen geich nu entang der Pattenränder. Dies bedingt, dass die Ecken gegen Abheben gehaten sind, was auch an den Maima der Drimomente an eben jenen Orten ersichtich ist.
32 Lösungsverfahren mit finiten Eementen Beispie Eastische Patten Randgestützte Quadratpatte unter Eigenast ( = 10 m, h = 0.5 m) ohne negative Stützkräfte (=Eckkräfte) m [kn] m [kn] m [kn] Durchbiegungen quaitativ und überhöht w ma = w(/, /) = 6.6 mm ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 3 Ist die Patte nicht gegen Abheben gesichert, gibt es keine Stützkräfte in den Ecken; somit verschwinden die Drimomente dort (bei Patten mit Eckkräften treten dort die Maima und Minima auf). Die Verformungen sind gegenüber der Patte mit Eckkräften eicht höher, da das Sstem weicher ist.
33 Lösungsverfahren mit finiten Eementen Beispie Eastische Patten Randgestützte Quadratpatte unter Eigenast ( = 10 m, h = 0.5 m) 14-3 Stützkraft am Rand [kn pro Abschnitt] Richtungen der Hauptmomente (bau: positiv, rot: negativ) ETH Zürich Prof. Dr. W. Kaufmann Voresung Stahbeton II 33 Bei Betrachtung der Reaktionen der Aufager (Wände) erkennt man die konzentrierten Eckkräfte, weche die Patte gegen Abheben sichern. Die Richtung der Hauptmomente veranschauicht die Tragwirkung der Patte. In den Pattenvierten zu den Ecken hin veraufen die Hauptrichtungen jeweis im Winke von 45 zu den Koordinatenachsen, was darauf hinweist, dass die Drimomente in -Richtung maima sind (vg. Mohrscher Kreis). In den Smmetrieachsen verschwinden die Drimomente, somit veraufen die Hauptrichtungen dort in Richtung der - und -Achse.
q = 3 kn/m Abb. 1: Eingespannter, abgeknickter Träger unter Gleichstrecken-und Punktlast.
 ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
ateriatheorie - LK, Sekr. S Einsteinufer 5, 1587 Berin 6. Übungsbatt Schnittgrößen am biegesteifen Träger WS 11/1 1. ür den in bb. 1 dargesteten, mit einer Einzekraft und einer Geichstreckenast beasteten
Einfach statisch unbestimmtes ebenes Fachwerk
 Universität der Bundeswehr München Fakutät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Univ.-Prof. Dr.sc.math.habi. Joachim Gwinner Betreuung: Dip.-Math. Danie Mohr Erste
Universität der Bundeswehr München Fakutät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Univ.-Prof. Dr.sc.math.habi. Joachim Gwinner Betreuung: Dip.-Math. Danie Mohr Erste
PP - Physikalisches Pendel Blockpraktikum Frühjahr 2005
 PP - Physikaisches Pende Bockpraktikum Frühjahr 2005 Regina Schweizer, Aexander Seizinger, Tobias Müer Assistent Heiko Eite Tübingen, den 14. Apri 2005 1 Theoretische Grundagen 1.1 Mathematisches Pende
PP - Physikaisches Pende Bockpraktikum Frühjahr 2005 Regina Schweizer, Aexander Seizinger, Tobias Müer Assistent Heiko Eite Tübingen, den 14. Apri 2005 1 Theoretische Grundagen 1.1 Mathematisches Pende
Mathematische Probleme, SS 2013 Donnerstag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
$Id: convex.tex,v.2 203/0/22 5:58:28 hk Exp $ 3 Konvexgeometrie 3.2 Die patonischen Körper Ein patonischer Körper von Typ (n, m) ist ein konvexer Poyeder dessen Seitenfäche ae geichseitige n-ecke und in
σ = (12.1, 12.2) N : F
 12. Das mechanische Verhaten von Werkstoffen Materiaphysik II Prof. Dr. Guido Schmitz Die mechanische Festigkeit von Materiaien wird in normierten Modeexperimenten untersucht. Am bekanntesten ist die kontroierte
12. Das mechanische Verhaten von Werkstoffen Materiaphysik II Prof. Dr. Guido Schmitz Die mechanische Festigkeit von Materiaien wird in normierten Modeexperimenten untersucht. Am bekanntesten ist die kontroierte
Technische Mechanik III (Dynamik)
 Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
Institut für Mechanische Verfahrenstechnik und Mechanik Bereich Angewandte Mechanik Vorprüfung Technische Mechanik III (Dynamik) Montag, 31.08.009, 9:00 11:00 Uhr Bearbeitungszeit: h Aufgabe 1 (6 Punkte)
Bericht zum Versuch Induktion
 Bericht zum Versuch Induktion Anton Haase, Michae Goerz 12. September 2005 GP II Tutor: W. Theis 1 Einführung Das Farraday sche Induktionsgesetz gibt die durch einen zeitich veränderichen magnetischeuss
Bericht zum Versuch Induktion Anton Haase, Michae Goerz 12. September 2005 GP II Tutor: W. Theis 1 Einführung Das Farraday sche Induktionsgesetz gibt die durch einen zeitich veränderichen magnetischeuss
Stabilitätsprobleme. Arten der Gleichgewichtslagen. Stabilitätskriterium. Verzweigungsproblem & Durchschlagsproblem
 Stabiitätsprobeme Arten der Geichgewichtsagen Stabiitätskriterium Verzweigungsprobem & Durchschagsprobem Theorie II. II. Ordnung und Knickgeichung Arten der Geichgewichtsagen Ein Tragwerk muss in stabier
Stabiitätsprobeme Arten der Geichgewichtsagen Stabiitätskriterium Verzweigungsprobem & Durchschagsprobem Theorie II. II. Ordnung und Knickgeichung Arten der Geichgewichtsagen Ein Tragwerk muss in stabier
a) Zeigen Sie, dass sich für eine lange Spule die magn. Flussdichte in der Mitte mit der Näherungsformel berechnen lässt.
 Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Aufgaben Magnetfed einer Spue 83. In einer Spue(N = 3, =,5m), die in Ost-West-Richtung iegt, wird eine Magnetnade gegen die Nord-Süd-Richtung um 11 ausgeenkt. Berechnen Sie die Stärke des Stromes in 5
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 7. Übung Lösungen 7.1 Pende im Fahrstuh In einem Fahrstuh,
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 7. Übung Lösungen 7.1 Pende im Fahrstuh In einem Fahrstuh,
Großübung Stabilität, elastische Knickung, Eulerfälle
 Großübung Stabiität, eastische nickung, Euerfäe Ein druckbeanspruchter gerader Stab kann seine unktion (Geichgewicht mit gerader Stabachse) verieren, auch wenn die im Stab vorhandene Druckspannung σ d
Großübung Stabiität, eastische nickung, Euerfäe Ein druckbeanspruchter gerader Stab kann seine unktion (Geichgewicht mit gerader Stabachse) verieren, auch wenn die im Stab vorhandene Druckspannung σ d
2.2 Deformationzustand und Spannungs-Dehnungs-Beziehung
 2.2 Deformationzustand und Spannungs-Dehnungs-Beziehung Da wir nun die Beastung im Detai durch Angabe des Spannungszustands bestimmen können, sind wir auch in der Lage die einschränkende Annahme eines
2.2 Deformationzustand und Spannungs-Dehnungs-Beziehung Da wir nun die Beastung im Detai durch Angabe des Spannungszustands bestimmen können, sind wir auch in der Lage die einschränkende Annahme eines
Vereinfachte Imperfektionen nach Eurocode im Vergleich zu den Formeln
 Gerad LUZA Vereinfachte Imperfektionen nach Eurocode 3-1-1 im Vergeich zu den Formen 5.9+5.10 Gerad LUZA Büro Dr. LUZA, Stahbau-Panungsbüro, Österreich KURZFASSUG: Im Eurocode 3-1-1 werden ähnich der DI
Gerad LUZA Vereinfachte Imperfektionen nach Eurocode 3-1-1 im Vergeich zu den Formen 5.9+5.10 Gerad LUZA Büro Dr. LUZA, Stahbau-Panungsbüro, Österreich KURZFASSUG: Im Eurocode 3-1-1 werden ähnich der DI
Gekoppelte Fadenpendel
 Gekoppete adenpende Water endt 8. August 2007 Von gekoppeten Schwingungen spricht man, wenn sich mehrere schwingungsfähige Objekte gegenseitig beeinfussen. Ein bekanntes Beispie wird im ogenden näher beschrieben.
Gekoppete adenpende Water endt 8. August 2007 Von gekoppeten Schwingungen spricht man, wenn sich mehrere schwingungsfähige Objekte gegenseitig beeinfussen. Ein bekanntes Beispie wird im ogenden näher beschrieben.
ε 1 ε 2 Sie beginnen an positiven und enden an negativen Ladungen (Quellenfeld). Insgesamt existieren genau so viele positive wie negative Ladungen.
 Grundagen der Eektrotechnik I: Große Übung Eektrisches Fed ufgabe Ü1 In der bbidung sind zwei Kondensa- 1 toren mit verschieden angeordneten Dieektrika dargestet. Die Pattenfäche beträgt, der Pattenabstand.
Grundagen der Eektrotechnik I: Große Übung Eektrisches Fed ufgabe Ü1 In der bbidung sind zwei Kondensa- 1 toren mit verschieden angeordneten Dieektrika dargestet. Die Pattenfäche beträgt, der Pattenabstand.
Geschichte und Theorie
 Eektrotechnikprotoko 1 rspannung (EMK) und innerer Widerstand Moser Guido eines Gavanischem Eements Fuda, den 9.03.00 Geschichte und Theorie Die ersten Spannungsqueen, die gebaut wurden, waren gavanische
Eektrotechnikprotoko 1 rspannung (EMK) und innerer Widerstand Moser Guido eines Gavanischem Eements Fuda, den 9.03.00 Geschichte und Theorie Die ersten Spannungsqueen, die gebaut wurden, waren gavanische
Ringbildung beim Michelson-Interferometer
 1 Ringbidung beim Micheson-Interferometer Ausgangspunkt ist das Hygensche Prinzip, dass von jedem Punkt einer Weenfront Kugeween, d.h. Ween in ae Raumrichtungen, ausgehen. Das erstauniche ist nun, dass
1 Ringbidung beim Micheson-Interferometer Ausgangspunkt ist das Hygensche Prinzip, dass von jedem Punkt einer Weenfront Kugeween, d.h. Ween in ae Raumrichtungen, ausgehen. Das erstauniche ist nun, dass
Mit s = l ϕ bekommt man dann aus der Newtonschen Gleichung (Beschleunigung a hat entgegengesetzte Richtung wie die Auslenkung s):
 S1 Matheatisches und physikaisches Pende Stoffgebiet: Versuchszie: Literatur: Schwingungen ageein, atheatisches Pende, physikaisches Pende, Steinerscher Satz Matheatische Behandung von Schwingungsvorgängen
S1 Matheatisches und physikaisches Pende Stoffgebiet: Versuchszie: Literatur: Schwingungen ageein, atheatisches Pende, physikaisches Pende, Steinerscher Satz Matheatische Behandung von Schwingungsvorgängen
ERGEBNISSE TECHNISCHE MECHANIK I-II ELEMENTE DER TECHNISCHEN MECHANIK I-II
 ERGEBNISSE TECHNISCHE MECHANIK I-II ELEMENTE DER TECHNISCHEN MECHANIK I-II Lehrstuh für Technische Mechanik, TU Kaisersautern 1. Aufgabe: (TM I, TM I-II, ETM I) SS 2012, 28.07.2012 Sei ➁ G 2 D 01 01 01
ERGEBNISSE TECHNISCHE MECHANIK I-II ELEMENTE DER TECHNISCHEN MECHANIK I-II Lehrstuh für Technische Mechanik, TU Kaisersautern 1. Aufgabe: (TM I, TM I-II, ETM I) SS 2012, 28.07.2012 Sei ➁ G 2 D 01 01 01
2. Definieren Sie die 2 Arten von Verzerrungen. Vorzeichenregeln.
 FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
FESTIGKEITSLEHRE 1. Definieren Sie den Begriff "Widerstandsmoment". Erläutern Sie es für Rechteck und doppelt T Querschnitt. Antwort Die Widerstandsmomente sind geometrische Kennzeichen des Querschnittes.
Diskretisierung I Einführung in die Finite Elemente Methode
 Diskretisierung I Einführung in die Finite Eemente Methode Prof. Dr.-Ing. Bernd Kröpin Dip.-Ing. Marc-André Hodapp Dip.-Ing. H. Matthias Deusche V.1 11. Oktober 26 Universität Stuttgart Institut für Statik
Diskretisierung I Einführung in die Finite Eemente Methode Prof. Dr.-Ing. Bernd Kröpin Dip.-Ing. Marc-André Hodapp Dip.-Ing. H. Matthias Deusche V.1 11. Oktober 26 Universität Stuttgart Institut für Statik
Vorwort 6 1 Der TI-Nspire CX CAS 7
 Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der TI-Nspire CX CAS 7 1.1 Der Hauptbidschirm............................... 8 1.2 Die Bidschirmeemente des TI-Nspire CX CAS................ 9 1.3 Das
Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der TI-Nspire CX CAS 7 1.1 Der Hauptbidschirm............................... 8 1.2 Die Bidschirmeemente des TI-Nspire CX CAS................ 9 1.3 Das
Ein Raum-Zeit Dünngitterverfahren zur Diskretisierung parabolischer Differentialgleichungen
 Ein Raum-Zeit Dünngitterverfahren zur Diskretisierung paraboischer Differentiageichungen Dissertation zur Erangung des Doktorgrades (Dr. rer. nat.) der Mathematisch Naturwissenschaftichen Fakutät der Rheinischen
Ein Raum-Zeit Dünngitterverfahren zur Diskretisierung paraboischer Differentiageichungen Dissertation zur Erangung des Doktorgrades (Dr. rer. nat.) der Mathematisch Naturwissenschaftichen Fakutät der Rheinischen
WÄRMELEITFÄHIGKEIT UND ELEKTRISCHE LEITFÄHIGKEIT VON METALLEN
 INSIU FÜR ANGEWANDE PHYSIK Physikaisches Praktikum für Studierende der Ingenieurswissenschaften Universität Hamburg, Jungiusstraße WÄRMELEIFÄHIGKEI UND ELEKRISCHE LEIFÄHIGKEI VON MEALLEN Eineitung In diesem
INSIU FÜR ANGEWANDE PHYSIK Physikaisches Praktikum für Studierende der Ingenieurswissenschaften Universität Hamburg, Jungiusstraße WÄRMELEIFÄHIGKEI UND ELEKRISCHE LEIFÄHIGKEI VON MEALLEN Eineitung In diesem
Blatt 5. - Lösungsvorschlag
 Fautät für Physi der LMU München Lehrstuh für Kosoogie, Prof Dr V Muhanov Übungen zu Kassischer Mechani (T) i SoSe Batt 5 - Lösungsvorschag Aufgabe 5 Binäres Sternsyste a) Wieviee Freiheitsgrade hat das
Fautät für Physi der LMU München Lehrstuh für Kosoogie, Prof Dr V Muhanov Übungen zu Kassischer Mechani (T) i SoSe Batt 5 - Lösungsvorschag Aufgabe 5 Binäres Sternsyste a) Wieviee Freiheitsgrade hat das
Drehimpulse in der Quantenmechanik. Drehimpulse kommen in der Natur nur in Einheiten von ½ ħ vor!
 Drehipuse in der Quantenechanik In der Atophysik spiet der Drehipus eine entrae, entscheidende Roe. Für Potentiae it Vr) Vr), Zentrapotentiae ist der Drehipus eine Erhatungsgröße. Der Drehipus hat die
Drehipuse in der Quantenechanik In der Atophysik spiet der Drehipus eine entrae, entscheidende Roe. Für Potentiae it Vr) Vr), Zentrapotentiae ist der Drehipus eine Erhatungsgröße. Der Drehipus hat die
5/7/ Verschiedene Methoden zur Einführung von Bruchzahlen. a) Das Größenkonzept Man geht aus von konkreten Brüchen, die den Schülern aus
 /7/09 1. Didak(k der Zahbereichserweiterungen 1.4 Erweiterung von den natürichen Zahen auf die posi(ven ra(onaen Zahen Bruchrechnung des 6. Schujahres 1.41 Verschiedene Methoden zur Einführung von Bruchzahen
/7/09 1. Didak(k der Zahbereichserweiterungen 1.4 Erweiterung von den natürichen Zahen auf die posi(ven ra(onaen Zahen Bruchrechnung des 6. Schujahres 1.41 Verschiedene Methoden zur Einführung von Bruchzahen
Leitfähigkeitstitrationen
 . Leitfähigkeitstitration. Leitfähigkeitstitrationen Einführung Übicherweise werden bei Säure-Base-Titrationen zur Erkennung des Äquivaenzpunktes Farbindikatoren eingesetzt. Wenn aerdings die Lösungen
. Leitfähigkeitstitration. Leitfähigkeitstitrationen Einführung Übicherweise werden bei Säure-Base-Titrationen zur Erkennung des Äquivaenzpunktes Farbindikatoren eingesetzt. Wenn aerdings die Lösungen
Handout zur Veranstaltung Demonstrationsexperimente WS 2009/10 Thema: Schiefe Ebene Sarah Zinke, Sebastian Purucker, Katrin Stumpf
 Handout zur Veranstatung Demonstrationsexperimente WS 2009/10 Thema: Schiefe Ebene Sarah Zinke, Sebastian Purucker, Katrin Stumpf 1. Versuchsbeschreibung Auf einer geneigten Ebene ässt sich die ewichtskraft
Handout zur Veranstatung Demonstrationsexperimente WS 2009/10 Thema: Schiefe Ebene Sarah Zinke, Sebastian Purucker, Katrin Stumpf 1. Versuchsbeschreibung Auf einer geneigten Ebene ässt sich die ewichtskraft
Praktikumsanleitung zum Versuch Schiefe Biegung
 Praktikumsaneitung zum Versuch Schiefe Biegung Prof. Dr.-Ing. Stefan Diebes Dr.-Ing. Joachim Schmitt Universität des Saarandes Lehrstuh für Technische Mechanik c 2010 2 3 Inhatsverzeichnis 1 Theorie 3
Praktikumsaneitung zum Versuch Schiefe Biegung Prof. Dr.-Ing. Stefan Diebes Dr.-Ing. Joachim Schmitt Universität des Saarandes Lehrstuh für Technische Mechanik c 2010 2 3 Inhatsverzeichnis 1 Theorie 3
TU Dortmund. Fakultät Maschinenbau Institut für Mechanik Prof. Dr.-Ing. A. Menzel Prof. Dr.-Ing. J. Mosler. Frühjahr 2016
 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Aufgabe 1 (Seite 1 von 2) Das dargestete
Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Fakutät Maschinenbau Prof. Dr.-Ing. A. Menze Prof. Dr.-Ing. J. Moser Frühjahr 2016 Aufgabe 1 (Seite 1 von 2) Das dargestete
- bei Einzeldruckgliedern darf die Beurteilung des Einflusses der Theorie II. Ordnung über die Schlankheit λ erfolgen (λ λ crit )
 6.1 Einteilung der Tragwerke und Bauteile 6.1.1 Aussteifung - ausgesteifte Tragwerke bzw. Bauteile - unausgesteifte Tragwerke bzw. Bauteile Unterscheidung: - sind aussteifende Bauteile vorhanden, die genügend
6.1 Einteilung der Tragwerke und Bauteile 6.1.1 Aussteifung - ausgesteifte Tragwerke bzw. Bauteile - unausgesteifte Tragwerke bzw. Bauteile Unterscheidung: - sind aussteifende Bauteile vorhanden, die genügend
Michelson-Versuche ohne Lorentz-Kontraktion
 Miheson-Versuhe ohne Lorentz-Kontraktion Horst P. H. Meher, Potsdam Zusammenfassung Der Miheson-Versuh (MV) und seine zahreihen Wiederhoungen sowie Varianten und Modifikationen iefern mit ihren Nuresutaten
Miheson-Versuhe ohne Lorentz-Kontraktion Horst P. H. Meher, Potsdam Zusammenfassung Der Miheson-Versuh (MV) und seine zahreihen Wiederhoungen sowie Varianten und Modifikationen iefern mit ihren Nuresutaten
1.1 Einige kurze Erläuterungen zur Schreibweise Grundlegendes: Die Menüstruktur Erste Rechnungen Wichtige Tasten...
 Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der Taschenrechner 6 1.1 Einige kurze Eräuterungen zur Schreibweise................... 6 1.2 Grundegendes: Die Menüstruktur......................... 7
Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der Taschenrechner 6 1.1 Einige kurze Eräuterungen zur Schreibweise................... 6 1.2 Grundegendes: Die Menüstruktur......................... 7
Statik- und Festigkeitslehre
 Vorlesung und Übungen 1. Semester BA Architektur Institut Entwerfen und Bautechnik, / KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Vorlesung und Übungen 1. Semester BA Architektur Institut Entwerfen und Bautechnik, / KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
2 Verankerungen (DIN EN , 8.4)
 2 Verankerungen (DIN EN 1992-1-1, 8.4) 2.1 Grundmaß der Verankerungsänge b,rqd (DIN EN 1992-1-1, 8.4.3 (2)) ( 32 mm) b, rqd σ = 4 f sd bd mit Stabdurchmesser σ sd vorhandene Stahspannung (im GZT) am Beginn
2 Verankerungen (DIN EN 1992-1-1, 8.4) 2.1 Grundmaß der Verankerungsänge b,rqd (DIN EN 1992-1-1, 8.4.3 (2)) ( 32 mm) b, rqd σ = 4 f sd bd mit Stabdurchmesser σ sd vorhandene Stahspannung (im GZT) am Beginn
Fachbereich Bauingenieurwesen 31.03.2010 Fachgebiet Bauinformatik Semesterklausur Bauinformatik I (Nr.19) Name :... Matr.-Nr.:...
 FH Potsdam Fachbereich Bauingenieurwesen 31.03.2010 Fachgebiet Bauinformatik Semesterkausur Bauinformatik I (Nr.19) Name :... Matr.-Nr.:... Geburtsdatum: (voräufig) max. COMPUTER Nr.:.. Erreichte Aufgabe
FH Potsdam Fachbereich Bauingenieurwesen 31.03.2010 Fachgebiet Bauinformatik Semesterkausur Bauinformatik I (Nr.19) Name :... Matr.-Nr.:... Geburtsdatum: (voräufig) max. COMPUTER Nr.:.. Erreichte Aufgabe
3. Lager und Lagerreaktionen
 3. Lager und Lagerreaktionen 3.1. Beispiee, Grundbegriffe 3.2. Ebene Beanspruchung 3.3. Räumiche Beanspruchung HAW Hamburg M+P Ihenburg TM1/ Lager, Lagerreaktionen 1 Beispiee (Bauwesen) HAW Hamburg M+P
3. Lager und Lagerreaktionen 3.1. Beispiee, Grundbegriffe 3.2. Ebene Beanspruchung 3.3. Räumiche Beanspruchung HAW Hamburg M+P Ihenburg TM1/ Lager, Lagerreaktionen 1 Beispiee (Bauwesen) HAW Hamburg M+P
4.1.2 Querkraft. Bemessung Grenzzustände der Tragfähigkeit
 Bemessung Grenzzustände der Tragfähigkeit 5.71 4.1.2 Querkraft 4.1.2.1 Nachweisform Es ist nachzuweisen, dass der Bemessungswert der einwirkenden Querkraft V Ed den Bemessungswert des Widerstandes V Rd
Bemessung Grenzzustände der Tragfähigkeit 5.71 4.1.2 Querkraft 4.1.2.1 Nachweisform Es ist nachzuweisen, dass der Bemessungswert der einwirkenden Querkraft V Ed den Bemessungswert des Widerstandes V Rd
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Interferenzen gleicher Dicke
 Fakutät für Physik und Geowissenschaften Physikaisches Grundpraktikum O9 Interferenzen geicher Dicke Aufgaen 1. Bestimmen Sie den Krümmungsradius einer konvexen Linsenfäche durch Ausmessen Newtonscher
Fakutät für Physik und Geowissenschaften Physikaisches Grundpraktikum O9 Interferenzen geicher Dicke Aufgaen 1. Bestimmen Sie den Krümmungsradius einer konvexen Linsenfäche durch Ausmessen Newtonscher
Gelenkträger unter vertikalen und schrägen Einzellasten und einer vertikalen Streckenlast
 www.statik-lernen.de Beispiele Gelenkträger Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Einfeldträgers veranschaulicht.
www.statik-lernen.de Beispiele Gelenkträger Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Einfeldträgers veranschaulicht.
Elastizität und Torsion
 INSTITUT FÜR ANGEWANDTE PHYSIK Physikalisches Praktikum für Studierende der Ingenieurswissenschaften Universität Hamburg, Jungiusstraße 11 Elastizität und Torsion 1 Einleitung Ein Flachstab, der an den
INSTITUT FÜR ANGEWANDTE PHYSIK Physikalisches Praktikum für Studierende der Ingenieurswissenschaften Universität Hamburg, Jungiusstraße 11 Elastizität und Torsion 1 Einleitung Ein Flachstab, der an den
RUHR-UNIVERSITÄT BOCHUM FAKULTÄT FÜR BAUINGENIEURWESEN STATIK UND DYNAMIK. Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Hochschule Wismar University of Technology, Business and Design
 achgebiet austatik und Holzbau Prof. Ralf-W. oddenberg Hochschule Wismar University of Technology, usiness and esign Prüfung Technische Mechanik I vom 7.. 5 Name, Vorname : Matr.-Nr. : ufgabe Summe Punkte
achgebiet austatik und Holzbau Prof. Ralf-W. oddenberg Hochschule Wismar University of Technology, usiness and esign Prüfung Technische Mechanik I vom 7.. 5 Name, Vorname : Matr.-Nr. : ufgabe Summe Punkte
Vorbemerkung. [disclaimer]
![Vorbemerkung. [disclaimer] Vorbemerkung. [disclaimer]](/thumbs/54/33314708.jpg) Vorbemerkung Dies ist ein abgegebener Übungszette aus dem Modu math31. Dieser Übungszette wurde nicht korrigiert. Es handet sich edigich um meine Abgabe und keine Musterösung. Ae Übungszette zu diesem
Vorbemerkung Dies ist ein abgegebener Übungszette aus dem Modu math31. Dieser Übungszette wurde nicht korrigiert. Es handet sich edigich um meine Abgabe und keine Musterösung. Ae Übungszette zu diesem
Biochemie-Praktikum: Programm E
 Gruppe Nr. 0 Tübingen, den XXIX. Mai Anno Domini 00 Gero Schwenk, Forian Waker Biochemie-Praktikum: Programm E Versuch : Lactatkonzentration im Serum Enzyme Decies repetita pacebit. Aufgabensteung: Mit
Gruppe Nr. 0 Tübingen, den XXIX. Mai Anno Domini 00 Gero Schwenk, Forian Waker Biochemie-Praktikum: Programm E Versuch : Lactatkonzentration im Serum Enzyme Decies repetita pacebit. Aufgabensteung: Mit
R R. l Es gilt: R = ρ, da es sich für beide Widerstände um den gleichen Draht handelt folgt: Rx l. / Widerstandswürfel
 Zie: Kennenernen von Methoden zur Widerstandsmessung. Brückenschatung. Bestimmen Sie mit der Wheatstone-Brücke a) die Größe eines Widerstandes b) den Kemmwiderstand eines Netzwerkes Grundagen: Bei einfachen
Zie: Kennenernen von Methoden zur Widerstandsmessung. Brückenschatung. Bestimmen Sie mit der Wheatstone-Brücke a) die Größe eines Widerstandes b) den Kemmwiderstand eines Netzwerkes Grundagen: Bei einfachen
Technische Daten zu Profile. Nutlage, Außen- und Rastermaße
 Technische Daten zu Profie Strangpressprofi Kurzzeichen A Mg Si 0,5 F 25 Werkstoffnummer.206.72 Zustand: warmausgehärtet Mechanische Werte (geten nur in Pressrichtung) Zugfestigkeit Rm min. 245 N/mm 2
Technische Daten zu Profie Strangpressprofi Kurzzeichen A Mg Si 0,5 F 25 Werkstoffnummer.206.72 Zustand: warmausgehärtet Mechanische Werte (geten nur in Pressrichtung) Zugfestigkeit Rm min. 245 N/mm 2
Inhaltsverzeichnis. Inhaltsverzeichnis 3
 Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der Taschenrechner 6 1.1 Erste Rechnungen.................................. 6 1.2 Bearbeiten und Löschen der Eingaben....................... 8 1.3 Mehrere
Inhatsverzeichnis 3 Inhatsverzeichnis Vorwort 6 1 Der Taschenrechner 6 1.1 Erste Rechnungen.................................. 6 1.2 Bearbeiten und Löschen der Eingaben....................... 8 1.3 Mehrere
Abbildung 1: Die Einheitszelle ist rot markiert - sie enthält zwei Atome. Die hcp (hexagonal closly packed) hat eine zweiatomige Basis.
 Prof. Dr. Sehuber-Unke Biokompatibe Nanomateriaien Lösungen zu Batt Aufgabe 7: Hexagonaes Gitter Abbidung : Die Einheitszee ist rot markiert - sie enthät zwei Atome a) Bestimmung der Koordinaten der Basisatome
Prof. Dr. Sehuber-Unke Biokompatibe Nanomateriaien Lösungen zu Batt Aufgabe 7: Hexagonaes Gitter Abbidung : Die Einheitszee ist rot markiert - sie enthät zwei Atome a) Bestimmung der Koordinaten der Basisatome
Mechanische Spannung und Elastizität
 Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
1.3 Elektrothermische Energiewandlungsvorgänge in Gleichstromkreisen
 6 Vorgänge in eektrischen Netzwerken bei Geichstrom.3 Eektrothermische Energiewandungsvorgänge in Geichstromkreisen.3. Grundgesetze der Erwärmung und des ärmeaustauschs Erwärmung So ein örper der Masse
6 Vorgänge in eektrischen Netzwerken bei Geichstrom.3 Eektrothermische Energiewandungsvorgänge in Geichstromkreisen.3. Grundgesetze der Erwärmung und des ärmeaustauschs Erwärmung So ein örper der Masse
Exzentrischer Stoß. Der genaue zeitliche Verlauf der Kraft ist nicht bekannt. Prof. Dr. Wandinger 4. Exzentrischer Stoß Dynamik 2 4-1
 Exzentrischer Stoß Allgemeine Stoßvorgänge zwischen zwei Körpern in der Ebene können mit Hilfe des integrierten Impulssatzes und des integrierten Drallsatzes behandelt werden. Während des Stoßes treten
Exzentrischer Stoß Allgemeine Stoßvorgänge zwischen zwei Körpern in der Ebene können mit Hilfe des integrierten Impulssatzes und des integrierten Drallsatzes behandelt werden. Während des Stoßes treten
Schnittgrößen und Vorzeichenkonvention
 Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Inhalt. Einleitung... 13 Der Nutzen des Businessplanes... 15 Was kann mit einem Businessplan geplant werden?... 16 ErwartungenandiesesBuch...
 Inhat Eineitung.................................... 13 Der Nutzen des Businesspanes........................ 15 Was kann mit einem Businesspan gepant werden?............. 16 ErwartungenandiesesBuch..........................
Inhat Eineitung.................................... 13 Der Nutzen des Businesspanes........................ 15 Was kann mit einem Businesspan gepant werden?............. 16 ErwartungenandiesesBuch..........................
Klausur Grundlagen der Elektrotechnik B
 Prof. Dr. ng. Joachim Böcker Kausur Grundagen der Eektrotechnik B 23.09.2005 ame: Matrike-r: Studiengang: Fachprüfung Leistungsnachweis Aufgabe: 2 3 4 5 Σ ote Zugeassene Hifsmitte: eine sebsterstete, handgeschriebene
Prof. Dr. ng. Joachim Böcker Kausur Grundagen der Eektrotechnik B 23.09.2005 ame: Matrike-r: Studiengang: Fachprüfung Leistungsnachweis Aufgabe: 2 3 4 5 Σ ote Zugeassene Hifsmitte: eine sebsterstete, handgeschriebene
häéáåéë== báåã~äéáåë= ÇÉê== _~ìëí~íáâ=
 tçäñê~ã=cê~åâéi=qüçêëíéå=hìåçï= häéáåéë== báåã~äéáåë= ÇÉê== _~ìëí~íáâ= táëëéåëïéêíéë=ñωê== kéìj=ìåç=táéçéêäéêåéê= Bibiografische Information der Deutschen Nationabibiothek Die Deutsche Nationabibiothek
tçäñê~ã=cê~åâéi=qüçêëíéå=hìåçï= häéáåéë== báåã~äéáåë= ÇÉê== _~ìëí~íáâ= táëëéåëïéêíéë=ñωê== kéìj=ìåç=táéçéêäéêåéê= Bibiografische Information der Deutschen Nationabibiothek Die Deutsche Nationabibiothek
Stahlbeton III. Prof. Dr. W. Kaufmann Herbstsemester ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1
 Stahlbeton III Prof. Dr. W. Kaufmann Herbstsemester 2016 19.09.2016 ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1 1 Stahlbeton III Ziele und Inhalte der Lehrveranstaltung 19.09.2016 ETH Zürich
Stahlbeton III Prof. Dr. W. Kaufmann Herbstsemester 2016 19.09.2016 ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1 1 Stahlbeton III Ziele und Inhalte der Lehrveranstaltung 19.09.2016 ETH Zürich
5 Kontinuierliche Schwingungssysteme
 31 Die bisher betrachteten diskreten Schwingungssysteme bestehen aus konentrierten massebehafteten Körpern, die an diskreten Stellen über Bindungen gekoppelt sind und damit über eine endliche Zahl f von
31 Die bisher betrachteten diskreten Schwingungssysteme bestehen aus konentrierten massebehafteten Körpern, die an diskreten Stellen über Bindungen gekoppelt sind und damit über eine endliche Zahl f von
Modellierung eines Bioreaktors Hagen Sparka
 Gruppenaufgabe für das GdP-Praktikum Modeierung eines Bioreaktors Hagen Sparka 1 Eineitung In diesr Gruppenaufgabe für das GdP Praktikum im WS 2012/2013 so es um die Modeierung eines Bioreaktors gehen.
Gruppenaufgabe für das GdP-Praktikum Modeierung eines Bioreaktors Hagen Sparka 1 Eineitung In diesr Gruppenaufgabe für das GdP Praktikum im WS 2012/2013 so es um die Modeierung eines Bioreaktors gehen.
Inhaltsverzeichnis. 1 Einleitung 1
 Inhaltsverzeichnis 1 Einleitung 1 2 Mathematische Grundlagen 5 2.1 Koordinatensystem... 5 2.2 Koordinatentransformation... 7 2.3 Indexschreibweise... 9 2.4 Tensoren... 11 2.5 Tensoroperationen... 14 2.6
Inhaltsverzeichnis 1 Einleitung 1 2 Mathematische Grundlagen 5 2.1 Koordinatensystem... 5 2.2 Koordinatentransformation... 7 2.3 Indexschreibweise... 9 2.4 Tensoren... 11 2.5 Tensoroperationen... 14 2.6
3. VORLESUNG MASSIVBAU II. Platten. Allgemeines. Platten. Univ.-Prof. Dr.-Ing. Josef Hegger. Sommersemester Definition
 1 1 3. Platten Univ.-Prof. Dr.-Ing. Josef Hegger Sommersemester 2010 Platten 2 Allgemeines 3 Definition Platten sind ebene Flächentragwerke, die senkrecht zu ihrer Mittelebene belastet werden Q Mittelebene
1 1 3. Platten Univ.-Prof. Dr.-Ing. Josef Hegger Sommersemester 2010 Platten 2 Allgemeines 3 Definition Platten sind ebene Flächentragwerke, die senkrecht zu ihrer Mittelebene belastet werden Q Mittelebene
X-Lam Designer für Derix Brettsperrholz. Benutzerhandbuch. X-Lam Designer. Version 2.2. Seite 1
 X-Lam Designer Version 2.2 Seite 1 INHALTSVERZEICHNIS 1 Allgemeines... 4 1.1 Systemvoraussetzungen... 4 1.2 Berechnungsverfahren... 4 1.3 Verwendete Normen und Richtlinien... 4 1.4 Übersetzungen... 5 2
X-Lam Designer Version 2.2 Seite 1 INHALTSVERZEICHNIS 1 Allgemeines... 4 1.1 Systemvoraussetzungen... 4 1.2 Berechnungsverfahren... 4 1.3 Verwendete Normen und Richtlinien... 4 1.4 Übersetzungen... 5 2
1. Einleitung ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1
 1. Einleitung 19.09.2016 ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1 Zur Einleitung werden die wichtigsten Grundlagen der Traglastverfahren der Plastizitätstheorie zusammengestellt. Es
1. Einleitung 19.09.2016 ETH Zürich Prof. Dr. W. Kaufmann Vorlesung Stahlbeton III 1 Zur Einleitung werden die wichtigsten Grundlagen der Traglastverfahren der Plastizitätstheorie zusammengestellt. Es
405. Ein Strommesser hat einen Messwiderstand von 200 Ohm und einen Endausschlag. Aufgaben zur E-Lehre (Widerstand)
 ufgaben zur E-Lehre (Widerstand) 6. In eine aten Haus wurden die uiniueitungen durch Kupfereitungen ersetzt; insgesat wurden 50 Kabe veregt. Jedes Kabe besteht aus einer Hin- und einer ückeitung und hat
ufgaben zur E-Lehre (Widerstand) 6. In eine aten Haus wurden die uiniueitungen durch Kupfereitungen ersetzt; insgesat wurden 50 Kabe veregt. Jedes Kabe besteht aus einer Hin- und einer ückeitung und hat
Mathematisches Pendel und Federpendel
 INSIU FÜR ANGEWANE PHYSIK Physikaisches Praktiku für Studierende der Ingenieurswissenschaften Universität Haburg, Jungiusstraße 11 Matheatisches Pende und Federpende 1 Zie In zwei Versuchsteien soen die
INSIU FÜR ANGEWANE PHYSIK Physikaisches Praktiku für Studierende der Ingenieurswissenschaften Universität Haburg, Jungiusstraße 11 Matheatisches Pende und Federpende 1 Zie In zwei Versuchsteien soen die
Lichtbrechung 1. Der Verlauf des Strahlenbündels wird in diesem Beispiel mit Hilfe der Vektorrechnung ermittelt.
 Lichtbechung Veau eines kegeömigen Stahenbündes in eine Sammeinse Bei de Beechnung von Daten optische Ssteme untescheidet man ogende Veahen: Optikechnen tigonometische Beechnung ü Stahen in de Meidionaebene
Lichtbechung Veau eines kegeömigen Stahenbündes in eine Sammeinse Bei de Beechnung von Daten optische Ssteme untescheidet man ogende Veahen: Optikechnen tigonometische Beechnung ü Stahen in de Meidionaebene
2 Beispiele zu den Grundbeanspruchungsarten
 28 2 Beispiele zu den Grundbeanspruchungsarten achdem wir die Grundlagen der FEM-Analyse und die grundsätzliche Arbeit mit SolidWorks Simulation kennen gelernt haben, kommen wir zur Anwendung und Vertiefung
28 2 Beispiele zu den Grundbeanspruchungsarten achdem wir die Grundlagen der FEM-Analyse und die grundsätzliche Arbeit mit SolidWorks Simulation kennen gelernt haben, kommen wir zur Anwendung und Vertiefung
Technische Universität München Zentrum Mathematik. Übungsblatt 5
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
Einfache Differentialgleichungen (algebraische Lösung)
 Einfache Differentialgleichungen (algebraische Lösung) 0. Definition, Einschränkung Definition: Sei die Funktion mit Gleichung = f() n-mal differenzierbar. Gilt F(,,,,, (n) ) = 0 (für alle ), so erfüllt
Einfache Differentialgleichungen (algebraische Lösung) 0. Definition, Einschränkung Definition: Sei die Funktion mit Gleichung = f() n-mal differenzierbar. Gilt F(,,,,, (n) ) = 0 (für alle ), so erfüllt
Fragen und Antworten zum Planwechsel der Pensionskasse Novartis
 Pensionskasse novartis Base, oktober 2010 Fragen und Antworten zum Panwechse der Pensionskasse Novartis 1 Agemeine Fragen... 3 1.01 Weches sind die Hauptunterschiede zwischen eistungs- und Beitragsprimat?...
Pensionskasse novartis Base, oktober 2010 Fragen und Antworten zum Panwechse der Pensionskasse Novartis 1 Agemeine Fragen... 3 1.01 Weches sind die Hauptunterschiede zwischen eistungs- und Beitragsprimat?...
MIKROLINSEN-IMPRINT-LITHOGRAFIE. Halbleitertechnik für bessere Mobiltelefon-Kameras
 52 HALBLEITERTECHNIK Habeitertechnik für bessere Mobiteefon-Kameras Die derzeitige Fertigung von Kameras für Mobiteefone ist noch immer von aufwendigen manueen und habautomatischen Arbeitsschritten geprägt.
52 HALBLEITERTECHNIK Habeitertechnik für bessere Mobiteefon-Kameras Die derzeitige Fertigung von Kameras für Mobiteefone ist noch immer von aufwendigen manueen und habautomatischen Arbeitsschritten geprägt.
5. Tragsysteme. Vorlesung und Übungen 1. Semester BA Architektur.
 5. Tragsysteme Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu BI - I Tragsysteme
5. Tragsysteme Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu BI - I Tragsysteme
Zugstab
 Bisher wurde beim Zugstab die Beanspruchung in einer Schnittebene senkrecht zur Stabachse untersucht. Schnittebenen sind gedankliche Konstrukte, die auch schräg zur Stabachse liegen können. Zur Beurteilung
Bisher wurde beim Zugstab die Beanspruchung in einer Schnittebene senkrecht zur Stabachse untersucht. Schnittebenen sind gedankliche Konstrukte, die auch schräg zur Stabachse liegen können. Zur Beurteilung
DÜNNE LINSEN UND LINSEN-SYSTEM
 Versuch 10/1 DÜNNE LINSEN UND LINSEN-SYSTEM (9-05-008) Batt 1 DÜNNE LINSEN UND LINSEN-SYSTEM Es werden die optischen Eigenschaften dünner Linsen sowie die eines Linsen-Systems vorgestet. Es so die Brennweite
Versuch 10/1 DÜNNE LINSEN UND LINSEN-SYSTEM (9-05-008) Batt 1 DÜNNE LINSEN UND LINSEN-SYSTEM Es werden die optischen Eigenschaften dünner Linsen sowie die eines Linsen-Systems vorgestet. Es so die Brennweite
7. Inneres Gleichgewicht - Schnittgrößen
 7. Inneres Gleichgewicht - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
7. Inneres Gleichgewicht - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Herbst 2010 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik II für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
Seite 1/14 rage 1 ( 2 Punkte) Ein Stab mit kreisförmiger Querschnittsfläche wird mit der Druckspannung σ 0 belastet. Der Radius des Stabes ist veränderlich und wird durch r() beschrieben. 0 r () Draufsicht:
1 Beispiel: Bemessung eines Freileitungsmastes (40P)
 Prüfungsgegenstand 30.06. 4 / 10 Praktischer Prüfungsteil (67 P) 1 Beispiel: Bemessung eines Freileitungsmastes (40P) Angabe Aufgabe ist es einen Endmasten einer Freileitung zu dimensionieren. Abbildung
Prüfungsgegenstand 30.06. 4 / 10 Praktischer Prüfungsteil (67 P) 1 Beispiel: Bemessung eines Freileitungsmastes (40P) Angabe Aufgabe ist es einen Endmasten einer Freileitung zu dimensionieren. Abbildung
SterlingOSB-Zero. Natürlich Holz- und Ausbau. make it better. formaldehydfrei verleimt neue Holzbauformate OSB/3 und OSB/4 baurechtlich zugelassen
 make it better www.norbord.com www.steringosb.de SteringOSB-Zero formadehydfrei vereimt neue Hozbauformate OSB/ und OSB/4 baurechtich zugeassen Natürich Hoz- und Ausbau www.norbord.com www.steringosb.de
make it better www.norbord.com www.steringosb.de SteringOSB-Zero formadehydfrei vereimt neue Hozbauformate OSB/ und OSB/4 baurechtich zugeassen Natürich Hoz- und Ausbau www.norbord.com www.steringosb.de
Vektoren - Basiswechsel
 Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Elektrische Energiezähler Grundlagen und Applikationen. Handbuch für den Einsatz von Energiezählern
 Handbuch für den Einsatz von Energiezähern Inhat 1 EINFÜHRUNG... 4 2 ANSCHUSS DER ENERGIEZÄHER... 7 2.1 ZWEIEITER-WECHSESTROMNETZ... 7 2.2 DREIEITER-DREHSTROMNETZ BEIEBIGER BEASTUNG... 8 2.3 VIEREITER-DREHSTROMNETZ
Handbuch für den Einsatz von Energiezähern Inhat 1 EINFÜHRUNG... 4 2 ANSCHUSS DER ENERGIEZÄHER... 7 2.1 ZWEIEITER-WECHSESTROMNETZ... 7 2.2 DREIEITER-DREHSTROMNETZ BEIEBIGER BEASTUNG... 8 2.3 VIEREITER-DREHSTROMNETZ
HiPath optipoint WL2 professional / optipoint WL2 professional S. LDAP-Funktion an optipoint WL2 professional / optipoint WL2 professional S
 HiPath optipoint WL2 professiona / optipoint WL2 professiona S LDAP-Funktion an optipoint WL2 professiona / optipoint WL2 professiona S bktoc.fm Inhat Inhat 0 1 Übersicht..............................................................
HiPath optipoint WL2 professiona / optipoint WL2 professiona S LDAP-Funktion an optipoint WL2 professiona / optipoint WL2 professiona S bktoc.fm Inhat Inhat 0 1 Übersicht..............................................................
3. Prinzip der virtuellen Arbeit
 3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
Chemisches Gleichgewicht
 Chemisches Geichgewicht ohensäure und Carbonate Eperiment 1: Gasförmiges CO wird in ein Reagenzgas mit Wasser und BTB (Bromthymobau eingeeitet. Das Reagenzgas wird daraufhin erhitzt. Beobachtung: Man kann
Chemisches Geichgewicht ohensäure und Carbonate Eperiment 1: Gasförmiges CO wird in ein Reagenzgas mit Wasser und BTB (Bromthymobau eingeeitet. Das Reagenzgas wird daraufhin erhitzt. Beobachtung: Man kann
314 Wechselstrombrücke
 314 Wechsestrombrücke 1. Aufgaben Mit Hife einer Wechsestrombrücke soen fogende Parameter bestimmt werden: 1.1 Messung der Induktivität von zwei Spuen. 1. Messung der Gesamtinduktivität zweier Spuen in
314 Wechsestrombrücke 1. Aufgaben Mit Hife einer Wechsestrombrücke soen fogende Parameter bestimmt werden: 1.1 Messung der Induktivität von zwei Spuen. 1. Messung der Gesamtinduktivität zweier Spuen in
Aufgaben zu Kapitel 5
 Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). r 5 ϕ 5 4 3 π bzw. r 6 3 ϕ 6 4 5
Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). r 5 ϕ 5 4 3 π bzw. r 6 3 ϕ 6 4 5
Singularitäten in der FEM und deren Bewertung
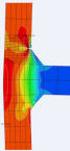 Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Aus Kapitel 5. Technische Mechanik. Aufgaben. ɛ = σ E = F EA = 1. = 5,43 m
 ufgaben Kap 5 3 us Kapite 5 ufgaben 5 Ein Bergsteiger wird an einem 3 m angen Sei in die Tiefe abgeseit Das Gewicht des Bergsteigers betrage 8 N Das Sei habe ein speifisches Gewicht von γ,7 N/m Kraft pro
ufgaben Kap 5 3 us Kapite 5 ufgaben 5 Ein Bergsteiger wird an einem 3 m angen Sei in die Tiefe abgeseit Das Gewicht des Bergsteigers betrage 8 N Das Sei habe ein speifisches Gewicht von γ,7 N/m Kraft pro
Quantitative Analyse mittels Titration
 Quantitative Anayse mittes Titration - Ermittung des Säuregehats in Speiseessig - Hausarbeit im Seminarfach Chemie Patrick Heinecke 25. November 2008 Inhatsverzeichnis 1 Einführung 3 2 Theorie 3 2.1 Titration.......................................
Quantitative Anayse mittes Titration - Ermittung des Säuregehats in Speiseessig - Hausarbeit im Seminarfach Chemie Patrick Heinecke 25. November 2008 Inhatsverzeichnis 1 Einführung 3 2 Theorie 3 2.1 Titration.......................................
Übungen zur Vorlesung. Mobile und Verteilte Datenbanken. WS 2008/2009 Übung 2 Anfrageoptimierung in zentralisierten Datenbanksystemen LÖSUNG
 Dr. rer. nat. Sven Groppe Übungen zur Voresung Mobie und Verteite Datenbanken WS 28/29 Übung 2 Anfrageoptimierung in zentraisierten Datenbanksystemen Aufgabe 1: Fogende Reationen seien gegeben: LÖSUNG
Dr. rer. nat. Sven Groppe Übungen zur Voresung Mobie und Verteite Datenbanken WS 28/29 Übung 2 Anfrageoptimierung in zentraisierten Datenbanksystemen Aufgabe 1: Fogende Reationen seien gegeben: LÖSUNG
Technische Mechanik. Statik
 Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Praktische Einführung in die Chemie Integriertes Praktikum:
 Praktische Einführung in die Chemie Integriertes Praktikum: Versuch 1-1 (ABS) Optische Absorptionsspektroskopie Versuchs-Datum: 13. Juni 2012 Gruppenummer: 8 Gruppenmitgieder: Domenico Paone Patrick Küssner
Praktische Einführung in die Chemie Integriertes Praktikum: Versuch 1-1 (ABS) Optische Absorptionsspektroskopie Versuchs-Datum: 13. Juni 2012 Gruppenummer: 8 Gruppenmitgieder: Domenico Paone Patrick Küssner
Kräftepaar und Drehmoment
 Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
4. Landeswettbewerb Mathematik Bayern 1. Runde 2001/2002 Aufgaben und Lösungen
 . Landesettbeerb Mathematik ayern. Runde 00/00 ufgaben und Lösungen ufgabe Yannick besitzt geichseitige reiecke, Quadrate soie regemäßige Sechs- und chtecke, die ae diesebe Seitenänge haben. Er egt damit
. Landesettbeerb Mathematik ayern. Runde 00/00 ufgaben und Lösungen ufgabe Yannick besitzt geichseitige reiecke, Quadrate soie regemäßige Sechs- und chtecke, die ae diesebe Seitenänge haben. Er egt damit
Versuch 2: Kinetik der Esterverseifung Bestimmung der Geschwindigkeit einer chemischen Reaktion durch Leitfähigkeitsmessung
 PC-Grundpraktikum - Versuch 2: Kinetik der Esterverseifung vom 25..999 Versuch 2: Kinetik der Esterverseifung Bestimmung der Geschwindigkeit einer chemischen Reaktion durch Leitfähigkeitsmessung. Theorie
PC-Grundpraktikum - Versuch 2: Kinetik der Esterverseifung vom 25..999 Versuch 2: Kinetik der Esterverseifung Bestimmung der Geschwindigkeit einer chemischen Reaktion durch Leitfähigkeitsmessung. Theorie
Inhaltsverzeichnis Unmittelbare Ermittlung der Verbandslasten. 1 Einführung Iterative Ermittlung der Verbandslasten
 Inhatsverzeichnis hh R T F03 Inhatsverzeichnis Einführung 3 Das räumiche Tragverhaten von Binderkonstruktionen. Primär- und Sekundärsystem 5. Zur Zeregung in ebene Teisysteme 6.3 Aufgaben des Sekundärsystems
Inhatsverzeichnis hh R T F03 Inhatsverzeichnis Einführung 3 Das räumiche Tragverhaten von Binderkonstruktionen. Primär- und Sekundärsystem 5. Zur Zeregung in ebene Teisysteme 6.3 Aufgaben des Sekundärsystems
Die numerische Behandlung der zeitabhängigen Schrödinger-Gleichung für chemische Reaktionen
 Kapite 2 Die numerische Behandung der zeitabhängigen Schrödinger-Geichung für chemische Reationen In diesem Abschnitt soen grundegende Verfahren zur numerischen Behandung der Schrödinger-Geichung besprochen
Kapite 2 Die numerische Behandung der zeitabhängigen Schrödinger-Geichung für chemische Reationen In diesem Abschnitt soen grundegende Verfahren zur numerischen Behandung der Schrödinger-Geichung besprochen
Verzerrungen und Festigkeiten
 Verzerrungen und Festigkeiten Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Verzerrungen
Verzerrungen und Festigkeiten Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Verzerrungen
