10 Ideale Quantengase
|
|
|
- Hinrich Winter
- vor 5 Jahren
- Abrufe
Transkript
1 1 Ideale Quantengase Bei tiefen Temperaturen T und/oder hohen Dichten N zeigen ideale Gase Abweichungen vom klassischen erhalten P = Nk B T. Diese werden aber nicht wie bei der vdw- Gleichung durch Wechselwirkung der Gasteilchen verursacht, sondern sind Quanteneffekte wechselwirkungsfreier Teilchen. Daher der Name ideale Quantengase. 1.1 Produktform der großkanonischen Zustandssumme Die in Abschnitt 9. beschriebenen Probleme beim Abzählen der Mikrozustände bei tiefen Temperaturen lassen sich mit der großkanonischen Gesamtheit bewältigen Besetzungszahlen In Kapitel 9 nummerierte der Index i die unterscheidbaren Teilchen durch, i = 1,...,N. Dagegen kennzeichnet er jetzt die Einteilchenzustände i = 1,...,, die von diesen Teilchen besetzt werden können. Waren dort k i σ der Wellenvektor und ǫ σ i die Energie des i-ten Teilchens im N-Teilchen- Mikrozustand σ, ǫ σ i = m k iσ, 99 so sind jetzt k i bzw. ǫ i die entsprechenden Größen des i-ten Einteilchenzustands im vorgegebenen olumen egal ob dieser von Teilchen besetzt ist oder nicht, ǫ i = m k i. 3 Da die gleichartigen Teilchen Atome, Moleküle, Elektronen, etc. eines Quantengases nicht unterscheidbar sind, ist ein Mikrozustand σ vollständig charakterisiert durch den Satz {n σ 1,nσ,...} der Besetzungszahlen nσ i aller Einteilchenzustände i = 1,,3,.... Teilchenzahl N σ und Energie E σ im Mikrozustand σ sind jetzt gegeben durch N σ = n σ i, E σ = n σ i ǫ i. 31 Während in der kanonischen Gesamtheit alle Mikrozustände dieselbe Teilchenzahl haben, N σ = N für alle σ, gilt in der großkanonischen Gesamtheit N σ =,1,,
2 Mit Gl. 31 wird aus der großkanonischen Zustandssumme aus Gl. 58 ΞT,,µ σ mit der Abkürzung e [E σ µn σ ]/k B T = σ = σ e nσ i [ǫ i µ]/k B T e [ǫ i µ]/k B T σ n i }{{},3 x i T,,µ µ ǫi x i T,,µ := exp. 33 k B T Bei der Summation über alle Mikrozustände σ durchläuft die Besetzungszahl n i jedes Einteilchen-Zustands i jeweils unabhängig von allen übrigen j alle erlaubten Werte, nmax n max [ nmax ΞT,,µ =... x i T,,µ n i x i T,,µ ]. n 34 n 1 = n = n= 1.1. Bose-Einstein- und Fermi-Dirac-Statistik Bezüglich der maximal möglichen Besetzungszahl n max eines jeden Einteilchenzustands i gibt es in der Natur zwei Arten von Teilchensorten. 1. Bosonen gehorchen der Bose-Einstein-Statistik, BE : n max =. In diesem Fall können also beliebig viele gleichartige Teilchen den gleichen Einteilchenzustand i besetzen. Beispiele sind He-Atome genauer: 4 He, H -, O - und N -Moleküle, aber auch die Photonen der Hohlraumstrahlung. Damit Ξ endlich bleibt, muß jetzt gelten x i < 1 µ < ǫ i für alle i, s. Gl. 33. Dann gilt n= xn i = 1 1 x i, und wir erhalten Ξ BE T,,µ = n= x n i = 1 1 x i T,,µ = 1 1 e. 35 [µ ǫ i]/k B T. Fermionen gehorchen der Fermi-Dirac-Statistik, FD : n max = 1. Jeder Einteilchenzustand i kann jetzt nur einfach besetzt oder unbesetzt sein. Beispiele für Fermionen sind 3 He-Atome, Elektronen etwa die Leitungselektronen im Metall oder die Elektronen in einem weißen Zwergstern der Astrophysik, sowie Protonen. Jetzt folgt Ξ FD T,,µ = 1 n= x n i = [ ] 1+x i T,,µ = [ ] 1+e [µ ǫ i]/k B T. 36 Bem.: Fermionen sind alleteilchen mit halbzahligem Spin s { 1, 3,...}, Bosonen jene mit ganzzahligem Spin s {, 1,...} Spin-Statistik-Theorem der Quantenfeldtheorie. 68
3 1.1.3 ergleich mit der Maxwell-Boltzmann-Statistik Zum ergleich mit diesen exakten Ergebnissen wollen wir aus den klassischen kanonischen Zustandssummen, zunächst für unterscheidbare Teilchen berechnet, und dann mit einem Faktor 1/N! näherungsweise für Ununterscheidbarkeit korrigiert, eine ähnliche Produktform der großkanonischen Zustandssumme gewinnen. Dabei finden Besetzungszahlen n σ i und das Resultat 34 keine erwendung. ielmehr gilt jetzt N= Ξ MB T,,µ = N= 1 N! z MBT, N e µn/k BT, 37 mit der kanonischen Einteilchen-Zustandssumme z MB T, = e ǫ i/k B T, [ N [ 1 N Ξ MB T,,µ = e µ/k BT e ǫ i/k B T] 1 = x i T,,µ]. 38 N! N! Wegen 1 N= N! un = e u folgt schließlich Ξ MB T,,µ = e x it,,µ = N= e xit,,µ = e expµ ǫ i k B T Zusammenfassung Diese insgesamt drei Fälle können also auf einfache Weise zusammengefaßt werden, ΞT,,µ = Φ x i T,,µ, Φx = e x MB, 1 BE, 1 x 1+x FD. 31 Man beachte, daß für x 1 in allen drei Fällen gilt Φx 1+x. Für das große thd. Potential ΩT,,µ ergibt sich ΩT,,µ k B T lnξt,,µ k B T lnφ x i T,,µ. 311 Die Bedeutung des chemischen Potentials µ wird in Abschnitt 1. genauer:?? geklärt. In Abschnitt 1.3 genauer: 1.3. werden wir ΩT,, µ auswerten. Bemerkung: Dieser Ausdruck läßt sich nur im Fall MB in geschlossener Form auswerten, L 3 Ω MB T,,µ = k B T x i T,,µ k B T dk4πk π e [µ k /m]/k B T = k B T [ πmkb T BT 8π 3eµ/k 69 ] 3/. 31
4 Dieses Resultat ergibt sich aber schneller direkt aus Gl. 37, [ ] Ξ MB T,,µ = exp e µ/kbt z MB T,, 313 mit z MB T, = und dem Ausdruck 79 für die thermische Wellenlänge λt, λt 3 [ ] 3/ Ω MB T,,µ k B T lnξ MB T,,µ = k B Te µ/k πmkb T BT. 314 π Die partiellen Ableitungen hiervon ergeben nach Gl. 61 die Funktionen ST,, µ, PT,, µ und NT,, µ. Umkehrung der letzteren liefert insbesondere das chemische Potential des klassischen idealen Gases, N µ MB T,,N = k B T ln λt Thermische Besetzungszahlen der Einteilchenzustände 1..1 Definition und Berechnung Im Gegensatz zu ΩT,, µ lassen sich die mittleren thermischen Besetzungszahlen N i T,,µ := σ n σ i p σ = σ n σ i 1 Ξ e[ Eσ+µNσ]/k BT der Einteilchenzustände i = 1,, 3,... in geschlossener Form berechnen. Ihre Summe N i ist gleich der Gesamtteilchenzahl N = Ω NT,,µ = µ k BT lnφx i = k B T i = 1,,3, µ T,, Φ x i x i Φx i µ = Φ x i Φx i x i, 317 wobei x i T,,µ = exp µ ǫ i k B benutzt wurde. Es liegt also nahe, zu identifizieren T N i T,,µ = Φ x i Φx i x i 318 strenge Herleitung in Abschnitt Die thermische Besetzungszahl hängt also bei gegebenen T und µ von nur über die Energie ǫ = ǫ i des Einteilchenzustands ab, N i T,,µ = NT,ǫ i,µ. 319 M.a.W.: Hat ein Einteilchenzustand i die Energie ǫ i = ǫ, so hat bei gegebenen Werten von T und µ seine thermische Besetzungszahl N i T,,µ den Wert e ǫ µ/k BT MB, NT,ǫ,µ = 1 BE 3. e ǫ µ/k BT 1 FD 7
5 1.. Graphische Deutung Wir schreiben auch NT,ǫ,µ =: Ñ T ǫ µ, Ñ T u = e u/k BT 1 e u/k BT 1 MB, BE. FD 31 Wir betrachten ein Modell-System mit den tiefsten Einteilchen-Energien etwa in me: ǫ 1 ǫ ǫ 3 ǫ 4 ǫ 5 ǫ 6 ǫ Diese seien der Einfachheit halber nicht entartet. Zeichne nach rechts eine ǫ-achse, etwa von ǫ = bis ǫ = 1. Trage die Werte der Tabelle als vertikale Linien nach oben ein. Zeichne nach oben eine Achse für die thermischen Besetzungszahlen BZ N i T,,µ ÑT ǫ i µ, 3 etwa von N = bis N =. 1. Fall: MB-Statistik Zeichne für k B T die Kurven ÑMB T ǫ µ ein, und zwar jeweils für µ =, µ = ǫ 3 und µ = ǫ 3. Lies jeweils die BZen der Einteilchenzustaände ab. Bem. 1: Jetzt hat ein Einteilchen-Zustand mit ǫ i = µ die BZ N i = 1. Bem. : Da die Summe aller BZen N i die Gesamtteilchenzahl N des Systems ergibt, N i T,,µ = NT,,µ µ = µt,,n, 33 erkennen wir hier die Rolle des chemische Potentials µ als Normierungsparameter.. Fall: BE-Statistik Bem.: Jetzt muß µ < ǫ 1 = sein. Im Grenzfall µ ǫ 1 geht die BZ N 1 T,,µ gegen Bose-Einstein-Kondensation. 3. Fall: FD-Statistik 71
6 1..3 Einteilchenenergien ǫ i als formal unabhängige ariable Um Gl. 318 in Strenge herzuleiten, betrachten wir vorübergehend statt des olumens die Folge {ǫ i } i N der Einteilchenenergien als unabhängig vorgegebene ariable, ΞT,,µ σ = σ = σ e [µnσ Eσ]/k BT exp j=1 exp j=1 n σ j n σ j µ ǫ j k B T µ ǫ j k B T =: ξ T,{ǫ i },µ. 34 ǫi=ǫi Für die neue Funktion ξt,{ǫ i },µ, in der die Besetzungszahlen n σ i nicht als ariable, sondern, ebenso wie die Konstante k B, als Parameter aufzufassen sind, gilt einerseits k B T ǫ i lnξt,{ǫ j },µ = k B T ǫ i ξ ξ = k BT ξ = σ = σ σ n σ 1 i ξ ǫ i j=1 exp j=1 exp n σ j n σ j µ ǫ j k B T µ ǫ j k B T n σ i p σ = N i 35 und andererseits, mit x j T,ǫ j,µ := exp µ ǫ j k B T, k B T lnξ T,{ǫ j },µ k B T ǫ i ǫ i Damit ist Gl. 318 in Strenge bewiesen. lnφ x j j=1 k B T lnφ x i = k B T Φ x i x i = Φ x i ǫ i Φ x i ǫ i Φ x i x i.36 7
7 1.3 Fugazität Definition und Wertebereich Wir drücken das chemische Potential µ durch die sog. Fugazität θ aus, θ := e µ/k BT µ = k B T lnθ. 37 Dann sind die thermischen Besetzungszahlen der Einteilchenzustände gegeben durch θe ǫ/k BT MB, NT,ǫ,µ = 1 θ 1 e ǫ/k BT 1 θe ǫ/kbt BE θe ǫ/k BT FD Die Energien ǫ der Einteilchenzustände seien der Größe nach geordnet, mit = ǫ 1 < ǫ ǫ 3 ǫ Da N i generell nicht negativ und im Fall FD nicht größer als 1 werden kann, folgt für den maximal möglichen Wertebereich von θ bzw. µ Im Fall MB gilt nach Gl. 315 BE: θ 1 < µ, FD: θ < + < µ < +, 33 MB: θ N λt3 < + < µ < Bem.: Im Grenzfall θ 1 also µ verschwinden nach Gl. 38 die Unterschiede der idealen Quantengase BE bzw. FD vom klassischen idealen Gas MB. Mit wachsendem θ > werden dagegen Quanteneffekte immer deutlicher. Man spricht von wachsender Entartung des idealen Gases. Maximale Entartung tritt im Fall BE bereits bei θ = +1 auf, während im Fall FD θ beliebig groß werden kann. 73
8 1.3. Das Potential ΩT,, µ als Integral Aus Gl. 311 erhalten wir mit x i T,,µ = θe ǫ i /k B T ΩT,,µ = ±k B T i ln 1 θe ǫ i/k B T BE FD. 33 Für großes olumen NλT 3 wird, mit p 3 = k 3 = π L 3 = π 3, gemäß fǫ i g π 3 p d 3 pf m g = s mit der Spinentartung g = s+1 aus der Summe wieder ein Integral, 8 ΩT,,µ = ±g k BT π 3 Wegen Ω = P folgt sofort Mit dθ dµ d dµ eµ/k BT = θ k B T = ±g k BT λt 3 4π π 3/ dp4πp ln 1 θe p /mk B T dxx ln 1 θe x. 334 }{{} I±θ PT,,µ = g k BT λt 3 4 π I±θ. 335 folgt weiter für N = Ω µ T, NT,,µ = θ Ω k B T θ T, 4 = g π θ d λt 3 dθ I±θ 4 = g π dxx θe x. 336 λt 3 1 θe x Bevor wir diese Integrale systematisch untersuchen Abschnitt wollen wir zuerst eine allgemeine Beziehung zwischen Druck P und Energie U herleiten. 8 Ist die Bedingung NλT 3 nicht erfüllt, so wird diese Integraldarstellung beim Bose-Gas unzureichend, s. Abschnitt Dann ist Gl. 336 zu ersetzen durch Gl
9 1.3.3 Beziehung zwischen Energie U und Druck P Die Funktion UT,,µ erhalten wir aus UT,,µ = ǫ i N i T,,µ = ǫ i θe ǫ i/k B T 1 θe ǫ i/k B T. 337 Mit ǫ i = k i /m = p i /m wird daraus für λt3 wieder ein Integral, U = g π 3 = 4π 3 π 3/k BTg λt 3 = 4 π k B Tg dp4πp p m θe p /mk B T 1 θe p /mk B T dx x3 3 }{{} ux { 3 [ ] uv λt 3 = 4 3 [ ] k B Tg uv π λt 3 x θe x } 1 θe {{ x } v x [ dx x }{{} u x Im letzten Schritt haben wir Gl. 335 eingesetzt. Weiterhin gilt [ ] uv } ±ln 1 θe x] } {{ } vx + 3 P. 338 [ x 3 = ± 3 ln 1 θe x] x 3 = ± lim x 3 θe x x 3 lim x 3 ln 1 θ1 x =. 339 Im Fall FD unteres Z verschwinden beide Limites offensichtlich für alle möglichen Werte θ. Dasselbe gilt im Fall BE oberes Z; θ 1, denn für den einzigen problematischen Wert θ = 1 haben wir den Limes x 3 lim x 3 lnx = lim x 3 x3 lnx =. 34 Im Fall ǫ i = k i /m gilt also allgemein die Beziehung U = 3 P. 341 Im Fall anderer Dispersionsrelationen, etwa ǫ i = k i beim Photonengas der Hohlraumstrahlung, besteht dagegen in der Regel ein anderer Zusammenhang zwischen U und P. 75
10 1.3.4 Die Polylogarithmen Für ξ < 1 wird der Polylogarithmus der Ordnung l definiert durch ξ k Li l ξ := kl. 34 Allgemein gilt offenbar die Ableitungsregel k=1 Li l ξ = ξ d dξ Li l+1ξ. 343 Für l {, 1,,...} sind diese Funktionen rational. Insbesondere gilt Li ξ = ξ 1 ξ, Li 1ξ = ln1 ξ, lim l Li l ξ = ξ. 344 All diese Funktionen lassen sich analytisch fortsetzen auf das Intervall < ξ < 1. Sie sind sms, haben bei ξ = ihre einzige Nullstelle und die Ableitung Li l = 1. Für l > 1 gilt außerdem Li l 1 = ζl, mit der Riemannschen Zetafunktion ζx, Li 1 1 =, Li 3/ 1 = ζ 3 =.614, Li 5/1 = ζ 5 = SKIZZE mit l {,1, 3, 5, } Wegen ln1 u = u k k=1 für u < 1 gilt für das Integral aus Gl. 334 k 4 I±θ = 4 dxx k ±θe x π π k k=1 = 4 π k=1 ±θ k k dxx e kx = k=1 ±θ k k 5/ = Li 5/ ±θ. 346 Folglich ist in Gl π θ d dθ I±θ = θ d dθ Li 5/±θ = θli 5/ ±θ = Li 3/±θ, und mit Gln. 335 und 336 ergibt sich PT,,µ = ±g k BT λt 3 Li 5/±θ, 347 NT,,µ = ±g Wir sehen also: Die Funktionen Li 3/ ξ und Li 5/ ξ beschreiben für < ξ ein Fermigas mit Fugazität θ = ξ und für ξ < 1 ein Bosegas mit Fugazität θ = +ξ. 76 λt 3 Li 3/±θ. 348
11 1.4 Zustandsgleichungen Ziel dieses Abschnitts ist es, das chemische Potential µ bzw. die Fugazität θ zugunsten der Teilchenzahl N zu eliminieren, um die thermische und kalorische Zustandsgleichung, also die Funktionen PT,,N und UT,,N = 3 PT,,N zu gewinnen Formale Elimination des chemischen Potentials Durch formales Auflösen von Gl. 348 nach θ, θt,,n = ±Li 1 3/ ± NλT3, 349 g und Einsetzen in Gl. 347 ergibt sich im Prinzip die thermische Zustandsgleichung, PT,,N = ±g k BT λt Li 3 5/ Li 1 3/ ± NλT3 g = ±P N τ 5/ Li 5/ Li 1 3/ Dabei haben wir zu gegebener Teilchendichte ρ = N durch τ := g /3 mk B π T ρ /3 = einen dimensionslosen Temperatur-Parameter eingeführt. ±τ 3/, P ρ = π g 3/ m ρ5/3. 35 g / λt 3 N Im klassischen Grenzfall τ, τ 3/ gilt Li 5/ Li 1 3/ ±τ 3/ ±τ 3/, also PT,,N P N τ = Nk B T. 35 DieFunktion±τ 5/ Li 5/ Li 1 3/ ±τ 3/ istimfallfdunteresorzeichen füralleτ, im Fall BE dagegen nur für τ 3/ ζ 3, also τ.5 definiert. Ihr Graph läßt sich in diesembereichleichtauswertetabellenderfunktionenli 3/ xundli 5/ xkonstruieren. SKIZZE! Für τ <.5 ist Gl. 348 im Fall BE zu ersetzen durch Gl. 383 in Abschnitt 1.4.4, da dann der niedrigste Einteilchen-Zustand makroskopisch besetzt wird und folglich der Übergang von Summe zu Integral in Gl. 334 nicht zulässig ist. nicht ex- Um analytische Ausdrücke zu erhalten, obwohl die Umkehrfunktion Li 1 3/ plizit bekannt ist, betrachten wir verschiedene interessante Grenzfälle separat. 77
12 1.4. Schwache Entartung Mit der Reihe 34 für Li 5/ x und dem Inversen der entsprechenden Reihe für Li 3/ x ergibt sich die für τ > ζ 3 /3 =.5 konvergente Entwicklung ±τ 5/ Li 5/ Li 1 3/ ±τ 3/ = τ [1 τ 3/ 5/ 3 1 ] τ , 353 5/ 8 da die Entwicklung von Li 1 3/ x um x = den Konvergenzradius r = ζ3 hat. Also gilt PT,,N = P N τ [1 τ 3/ }{{} 5/ 3 1 ] τ / 8 Nk B T τ > Wir sehen: Beim Bosegas ist gegenüber dem klassischen idealen Gas der Druck erniedrigt. Beim Fermigas ist er dagegen infolge des Pauli-erbots erhöht. Dies ist entscheidend für das Gleichgewicht der weißen Zwergsterne in der Astrophysik Das Fermi-Gas bei tiefen Temperaturen Im Fall θ 1 bzw. µ k B T gilt im Fall FD für die Besetzungszahlen Gl. 31 N FD T,ǫ,µ 1 e ǫ µ/k BT +1 { 1 falls ǫ < µ kb T, falls ǫ > µ+k B T. 355 Dann sind also so gut wie alle Zustände i mit ǫ i < µ k B T vollständig besetzt, während so gut wie alle mit ǫ i > µ+k B T leer sind. In dem kleinen Energieintervall ǫ µ < k B T nimmt dann N FD T,ǫ,µ von 1 auf ab. Entsprechend hat die Ableitung 1 k B T eǫ µ/k BT ǫ N FDT,ǫ,µ = [ e ǫ µ/k BT +1 ] 356 bei ǫ = µ ein scharfes Minimum und ist außerhalb dieses Intervalls praktisch gleich null. Diese besonderen Eigenschaften der Funktion N FD T,ǫ,µ werden wir ausnutzen. A Maximale Entartung: Nullpunktsdruck Zuerst betrachten wir aber den einfachen Extremfall θ e µ/kbt + also T, 1 { 1 falls ǫ < µ, N FD T=,ǫ,µ = 357 e ǫ µ/k BT +1 T= falls ǫ > µ. 78
13 Jetzt sind alle Einteilchenzustände i mit ǫ i < µ vollständig also mit je einem Teilchen besetzt, während alle mit ǫ i > µ unbesetzt sind. Die höchste besetzte Einteilchenenergie, ǫ F p F m = µ, 358 heißt die Fermi-Energie des Systems. Die Teilchenzahl N ist jetzt direkt berechenbar, N,,µ = N FD,ǫ i,µ = g ǫ i <µ π 3 pf dp4πp 1 = g π 4π p 3 F Die Fermi-Energie ist also eine reine Funktion der Teilchendichte N, ǫ F p F m = 1 [ 3 π 3 N ] /3 6π /3 N /3. = 36 m 4π g m g Bem.: Für die dimensionslose Temperatur aus Gl. 351 gilt τ = 16 1/3 k B T 9π ǫ F =.87 k BT ǫ F. 361 Für die Gesamtenergie ergibt sich entsprechend als Funktion von T =, und N U,,N = g π 3 pf dp4πp p m = g 3 π 4πp F 3 5 p F m = 3 5 Nǫ F. 36 Sie ist also infolge des Pauli-Prinzips ganz wesentlich verschieden von größer als null. Dies gilt insbesondere für den Nullpunktsdruck, P,,N U 3 = N 5 ǫ F. 363 B Starke Entartung: Sommerfeld-Entwicklung In Anhang A leiten wir unter Ausnutzung der erwähnten besonderen Eigenschaften der Funktion N FD T,ǫ,µ folgende Enwicklung für große aber endliche θ 1 her, Li 5/ θ = 8 [ ] 15 π lnθ5/ 1+ 5π 8 lnθ 7π4 384 lnθ 4 +Olnθ Mit Li 3/ ξ = ξ d dξ Li 5/ξ erhalten wir daraus Li 3/ θ = 4 3 π lnθ3/ [ 1+ π 8 lnθ + 7π4 64 lnθ 4 +Olnθ 6 ]
14 Durch Inversion der Reihe für Li 3/ θ findet man schließlich Anhang A PT,,N = 5 ǫ N F [1+ 5π kb T 9π 4 kb T 4 ] ǫ F 96 ǫ F k B T ǫ F, 366 UT,,N = 3 [ ] 5 ǫ FN Insbesondere erhalten wir die molare spezifische Wärme bei tiefen Temperaturen, c v T,v 1 n U T,N = 3 5 N Ak B [ 5π mit der Sommerfeld-Konstante γ = N A π k B ǫ F N /3. Mit τ = 16 9π 1/3k BT ǫ F 6 k B T ] kb T 3, +... = γt +O 368 ǫ F ǫ F bringen wir Gl. 354 zum ergleich mit Gl. 366 auf die Form N [ kb T PT,,N = ǫ F / ǫf 1/ ǫf 3 ] ǫ F 5/ 9π k B T k B T k B T ǫ F Das Bose-Gas bei tiefen Temperaturen A Sonderbehandlung des tiefsten Einteilchenzustands Die Gesamt-Teilchenzahl eines Bose-Gases, NT,,µ = g N BE T,ǫ i,µ, 37 ist die Summe der thermischen Besetzungszahlen der Einteilchenzustände, N BE T,ǫ,µ = 1 e ǫ µ/k BT Das chemische Potential µ darf nicht größer sein als die kleinste Einteilchenenergie ǫ 1, da sonst N BE negative Werte annehmen würde. Wir wählen ǫ 1 =. 37 Dann muß also µ sein, und für die Fugazität θ := e µ/k BT folgt θ
15 Starke Entartung entspricht nun dem Grenzfall θ 1. Dabei kann die Besetzungszahl θ N 1 T,,µ gn BE T,ǫ 1,µ = g 1 θ 374 des tiefsten Einteilchenzustands im Gegensatz zu allen höheren Einteilchenzuständen makroskopisch werden. Wir spalten sie daher von der Summe 37 ab, θ NT,,µ = g 1 θ +N et,,µ. 375 Die Restsumme aller übrigen Besetzungszahlen läßt sich wieder als Integral schreiben N e T,,µ = g N BE T,ǫ i,µ = g dp4πp θ π 3 p e p /mk BT θ. 376 i= Die untere Grenze p k, mit < p < π, trägt dem Ausschluß des Terms i = 1 aus L der Summe Rechnung. Der genaue Wert von p ist eine komplizierte Funktion von T und θ. Wir werden jedoch zeigen, daß es auf ihn gar nicht ankommt. Dazu betrachten wir zunächst den Fall θ < 1. Die Funktion im Integranden, fp = p e p /mk B T, 377 θ verschwindet bei p = und für p. Die Bedingung f p = führt auf die Gleichung 1 x = θe x, x := p mk B T. 378 Wegen θ < 1 besitzt sie genau eine Lösung ˆx, mit < ˆx < 1. Der Integrand hat also genau ein Maximum bei ˆp = mk B Tˆx. 379 ˆx kann zwar klein aber nicht null sein. Wird also bei vorgegebener Temperatur T > das Gasvolumen = L 3 hinreichend groß gewählt, so gilt p < π L ˆp. 38 Demnach ist die genaue Wahl der unteren Integrationsgrenze ganz unwichtig. Wir können sogar p = wählen, N e T,,µ = g π 3 dp4πp θ e p /mk B T θ = g λt 3 Li 3/θ. 381 Diese Wahl ist aber auch im Fall θ = 1 zulässig. Dann liegt zwar das Maximum der Funktion fp bei ˆp =. Sie ist aber erst bei p =.5mk B T π L auf die Hälfte abgesunken. x =.5 ist die positive Lösung von x = e x
16 Nach Gl. 375 gilt also θ NT,,θ = g +g } 1 θ {{} λt Li 3/θ. 383 } 3 {{} N 1 θ N et,,θ Ähnliche Argumente führen von den Gln. 33, 334 und 335, mit P = Ω, auf PT,,θ = g k [ ] BT ln1 θ +g k BT } {{} λt Li 5/θ [Wegen θ = N 1 1 g N 1 +g N 1 gilt hier 1 ln1 θ = 1 ln N 1 g < 1 ln N, was im thd. Limes g verschwindet.] Zu untersuchen ist dabei anstatt von Gl. 376 aus Gl. 334 das Integral g k BT π 3 p dp4πp ln 1 θe p /mk B T. 385 B Einstein-Kondensation Es ist illustrativ, NT,,θ bei festem T und als Funktion von θ [,1] zu skizzieren. Wählen wir die Masse m = kg von 4 He-Atomen g = 1, sowie die Werte T = 1 K und =.665m 3, so wird, mit λt = π /πmk B T 1/, aus Gl. 383 NT,,θ = θ 1 θ }{{} N 1 +Li 3/ θ 1 1 }{{}. 386 N e Beide Summanden auf der rechten Seite steigen mit θ, beginnend mit dem Wert null bei θ =, monoton an. Für θ < ist der zweite Term extrem dominierend. Dann übernimmt jedoch plötzlich der erste Term die Führung, da er für θ 1 divergiert, während der zweite Term nur den endlichen Wert erreicht. SKIZZE Satyendranath Bose 1894 Calcutta 1974 Calcutta. 8
17 Wollen wir dagegen zu vorgegebener Teilchenzahl N = 1 mit =.665m 3 die Fugazität θ als Funktion der Temperatur T bestimmen, so stoßen wir auf die Gleichung Für T 1 = 4 K wird daraus 1 = θ 1 θ }{{} N 1 T + 1K 3/Li3/ θ N e } {{ } 1 = θ 1 θ +8 Li 3/θ Wegen g 3/.797 = liegt die Lösung sehr nahe bei θ =.797, da gegenüber dem zweiten Term in extrem starkem Maße vernachlässigbar ist. In diesem Fall gilt also N 1 = = 3.93 N, N e = 8 Li 3/ = 1 = N. 389 Für T =.5 K ergibt sich die Gleichung 1 = θ 1 θ Li 3/θ Jetzt muß Li 3/ θ 1 =.53 = Li /.99945, also ζ sein. Dann ist also der Term θ 1817 gegenüber N = 1 θ 1 immer noch völlig vernachlässigbar, N 1 N, N e N. 391 Für die nur geringfügig tiefere Temperatur T 3 =.4 K ergibt sich dagegen 1 = θ 1 θ Li 3/θ Jetzt ist der zweite Term, selbst im günstigsten Fall mit θ = 1, deutlich kleiner als N, Li 3/ = < Es muß also θ 1 θ = sein. Das geht nur, wenn θ extrem nahe bei 1 liegt, sodaß mit hoher Genauigkeit gilt Li 3/ θ.61. Dann folgt N 1 = , N e = Zusammenfassung: Während bei T =.5 K die Besetzungszahl des tiefsten Einteilchenzustands praktisch gleich null ist, nimmt sie bei T =.4 K einen makroskopischen Wert an. Die makroskopische Besetzung dieses Einteilchenzustands wird als Einstein- Kondensation bezeichnet. 83
18 Mit sinkender Temperatur T setzt Einstein-Kondensation also dann bei T = T c ein, wenn Li 3/ θ bereits sehr nahe an den Wert Li 3/ 1 ζ 3 herangekommen ist, N e aber gerade noch nicht merklich unter den Hochtemperatur-Wert N abgesunken ist. Daraus folgt die Bestimmungsgleichung für die kritische Temperatur T c = T c N = N e g λt c 3 ζ3 = N 395 π N /3 [ζ 3 = g]/3 mk B 4π [6π ζ 3 ]3/ ǫ F k B. 396 Für T > T c ist also N e = N; für T < T c darf man in Gl. 383 Li 3/ θ = Li 3/ 1 setzen, T 3/ N e T,,N = g λt 3 ζ3 N T c T < T c. 397 DieZahlderGasteilchenimtiefstenEinteilchenzustandistN 1 T,,N = N N e T,,N. SKIZZE C Druck, Energie und Spezifische Wärme Der Druck P ergibt sich für T < T c aus Gl. 384, indem wir den konstanten Wert θ = 1 einsetzen, PT,,N = Nk BT c ζ 5 ζ 3 T T c 5/ T T c. 398 Für T T c gilt die Entwicklung 354. Mit τ 3/ NλT3 g = ζ 3 λt3 λt c 3 ζ3 Tc 3/ 399 T finden wir zum ergleich PT,,N = Nk [ BT c T ζ3 3/ Tc 1/ ζ 3 Tc ] T c 5/ T 3 3 5/ T T > T c. 4 84
19 1.5 Photonen und Phononen Wir betrachten nun zwei physikalisch sehr unterschiedliche Systeme, deren statistische Behandlungen in mathematischer Hinsicht jedoch sehr ähnlich sind. Das eine System ist das elektromagnetische Strahlungsfeld, das sich im thd. Gleichgewicht in einem evakuierten Hohlraum einstellt, dessen Wände auf einer gegebenen Temperatur T gehalten werden. Das andere sind die Gitterschwingungen eines Kristalls, ebenfalls im thd. Gleichgewicht bei gegebener Temperatur T. Wir werden sehen, daß sich beide Systeme als ideale Bose-Gase mit chemischem Potential µ = interpretieren lassen Klassische Schwingungsmoden Die elektromagnetischen Felder Er, t und Br, t im Hohlraum, sowie das diskrete Auslenkungsfeld ur l,t im Kristall hier als einatomig angenommen, l = 1,,3,...,N, wobei N die Gesamtzahl der Atome im Kristall ist können ebene Wellen ausbilden, Er,t,Br,t e ik r ω kt, ur l,t e ik r l ω k t. 41 Die Wellenvektoren k müssen im olumen des Hohlraums bzw. des Kristalls periodische Randbedingungen erfüllen, { } π k M := α L xe x +α y e y +α z e z α x,α y,α z Z. 4 ImFallderGitterschwingungenwerdenwegenderdiskretenOrtsvariabler l nurk-ektoren der ersten Brillouin-Zone gebraucht, Phononen: k BZ M. 43 Die zu einem bestimmten k-ektor gehörende Schwingungskreis-frequenz ω k ist durch die jeweilige Dispersionsrelation gegeben, ω k = ωk. 44 Wir wollen dies am einfachen Modell der linearen Kette N Punktmassen m, durch N Schraubenfedern mit Federkonstante D zu einem Ring mit Umfang L = Na verbunden erläutern. Ist u l die Auslenkung der l-ten Masse aus ihrer Gleichgewichtslage x l und p l = m u l ihr Impuls, so lautet die klassische Hamiltonfunktion der Kette, Hu 1,...,u N ;p 1,...,p N = N l=1 { p l m + D } u l+1 u l
20 Bildet man auf geschickte Weise N Linearkombinationen Q k die sog. Normalkoordinaten aus den N Koordinaten u 1,...,u N, so wird H in N unabhängige Summanden entkoppelt, H = k BZ { P } { k m + mω k Q k, BZ =,± π L,±4π L,...,±Nπ L }, 46 wobei P k der zu Q k kanonisch konjugierte Impuls ist. Man beachte, daß die Wellenzahlen ± Nπ einander äquivalent sind, also tatsächlich genau N unabhängige Terme vorliegen. L Als Dispersionsrelation ergibt sich in diesem Fall 4D ω k = sin ka. 47 m ω k istdiekreisfrequenzeinerwelle, diesichmitwellenzahlkentlangderketteausbreitet, u l t ux l,t = acoskx l ω k t+bsinkx l ω k t. 48 Durch die neuen Koordinaten wird diese Schwingungsmode dargestellt als Q k t = Acosω k t+bsinω k t, Q j t = j k. 49 Tatsächlich liefert Gl. 46 die kanonischen Bewegungsgleichungen Q k H P k = P k m, P k H = mωk Q Q k Qk = ωk Q k. 41 k Die Kette aus N gekoppelten Atomen entspricht also N unabhängigen harmonischen Oszillatoren. Ist nur einer dieser Oszillatoren aktiv, so schwingen alle Atome mit derselben Frequenz ω k aber mit verschiedenen Phasenverschiebungen und, bei mehratomigen Einheitszellen, auch verschiedenen Amplituden. Das System befindet sich dann in einer bestimmten Schwingungsmode, auch Eigenschwingung genannt Schwingungsquanten Klassisch können diese Oszillatoren mit beliebigen Energiewerten E k schwingen. Quantenmechanisch sind nur diskrete Werte möglich, E n k = n+ 1 ω k n =,1,, Dabei können verschiedene Moden zugleich angeregt sein. Ihre Energien addieren sich... Es gibt also N unabhängige Einteilchenzustände Oszillatoren mit Energien ǫ k = ω k k BZ, die jeweils mit beliebig vielen Quanten Phononen besetzt werden können: Ideales Bosegas. 86
21 Ganz ähnlich ist es bei der Hohlraumstrahlung. Als wichtigster Unterschied ist jetzt die Zahl der Oszillatoren unbegrenzt. Der ideale Charakter des Photonen-Gases resultiert aus der Superpositionsmöglichkeit elektromagnetischer Wellen. In beiden Fällen handelt es sich um Systeme mit gegebenem olumen im Kontakt mit einem Wärmebad vorgegebener Temperatur T. Die Teilchenzahl N ist zwar nicht vorgegeben aber auch nicht als dritte unabhängige ariable frei wählbar. ielmehr stellt diese sich im thd. Gleichgewicht als Funktion NT, der beiden genannten unabhängigen ariablen ein. Das thd. Gleichgewicht ist bestimmt durch das Minimum der Helmholtzschen Freien Energie F. Wir schließen daraus, daß das chemische Potential null sein muß, µ =. Andernfalls könnte F nämlich durch Änderung der Teilchenzahl weiter abgesenkt werden, F N T, = µ. 41 Diese Argumentation setzt voraus, daß es in der Umgebung der Gleichgewichtszustände mit N = NT, Nicht-Gleichgewichtszustände gibt, auf die die Funktion FT, analytisch fortsetzbar ist; gehemmtes Gleichgewicht. Wegen µ = haben wir also N k T, = gn BE T, ω k,, N BE T, ω, = 1 e ω/k BT Da µ = von vorneherein bekannt ist, brauchen wir nicht mehr NT,,µ nach µ aufzulösen, um in PT,, µ einzusetzen, sondern können direkt berechnen: UT, = k PT, 1 ΩT, = k BT ln = g k BT π 3 ǫ k N k T, = g π 3 kmax k dk4πk ln kmax dk4πk ω k e ω k/k BT 1, e ω k/k B T 1 e ω k/k B T. 415 Jetzt müssen wir beide Integrale berechnen, da die Beziehung U = 3 P nur im Fall der Dispersionsrelation ω k = k /m für massive Teilchen gilt, s. etwa Gl
22 1.5.3 Hohlraumstrahlung Photonen Spin s = 1 haben die Dispersionsrelation bzw. Anzahl der Spineinstellungen ǫ k ω k = c k ck = hν, g =. 416 Klassisch gibt es g = unabhängige Polarisationen, nämlich links- und rechtszirkular, die quantenmechanisch den Einstellungen des Spins in oder gegen Ausbreitungsrichtung entsprechen. Daß der Spin s = 1 hier nur zwei statt s+1 = 3 Einstellungen hat, ist ein relativistischer Effekt. Da es für k keine obere Grenze k max gibt, erhalten wir UT, = dk4πk ck π 3 e ck/k BT 1 = 8π dνν hν c 3 e hν/k BT 1 = mit dem Planckschen Strahlungsgesetz uν,t = 8πh ν 3 c 3 e hν/k BT 1 für die spektrale Energiedichte uν, T der Hohlraumstrahlung. dνuν,t, Integration über alle Frequenzen ergibt die räumliche Energiedichte ut := UT, = dνuν,t = 8πh kb T 4 dx x3 c 3 h e x 1 = at Mit dem Integral dx x3 = π4 e x 1 15 ergibt sich a = 8π5 kb 4 15ch 3. 4 Anders als uν,t und ut ist die Intensität IT der aus einem kleinen Loch in der Hohlraumwand pro Fläche austretenden Strahlung direkt meßbar, IT = c 4 ut = dνiν,t = σt 4, σ = π5 kb 4 15c h3. 41 Dies ist das Stefan-Boltzmann-Gesetz und σ ist die gleichnamige Konstante. Partielle Integration vgl. Abschnitt ergibt aus Gl. 415 den Strahlungsdruck, PT, k BT dk4πk ln 1 e ck/k BT π 3 8π k BT kb T 3 dxx ln1 e x π 3 c = 8π k BT 4 dx x3 1 hc 3 3 e x 1 = 1 ut. 4 3 Für die Hohlraumstrahlung gilt also nicht U = 3 P, sondern U = 3P. 88
23 1.5.4 Das Debye-Modell der Gitterschwingungen Das Debye-Modell für die Phononen eines einatomigen dreidimensionalen 3D Kristalls beruht auf der, etwa gegenüber Gl. 47, idealisierten Dispersionsrelation ω k = c k ck, g = 3, 43 mit einer frequenzunabhängigen Schallgeschwindigkeit c. Der Faktor g = 3 kommt daher, daß es in 3D zu jedem k-ektor je drei verschiedene Schwingungsmoden gibt: eine longitudinale und zwei transversale. Die Anzahl der k-ektoren in der ersten Brillouin-Zone ist gleich der Gesamtzahl N der Atome des einatomigen Kristalls, N = k BZ = π 3 kd dk4πk = π 3 4π 3 k3 D = 6π k3 D. 44 Die maximale Debye- Wellenzahl k max = k D ist also gegeben durch k D = 6π N 1/3. 45 Jetzt ergibt Gl. 414 für die Energie mit π = h UT, = 3 π 3 kd = 1π k BT 4 hc 3 dk4πk ck e ck/k BT 1 xd dx x3 e x 1, x D := ck D k B T =: T D T. 46 Da k D, anders als x D, nicht von der Temperatur abhängt, findet man die spezifische Wärme am einfachsten durch Differentiation des ersten Integrals in Gl. 46, C T, = U T kd = 3 dk4πk ck π 3 T e ck/k BT 1 T 3 xd x 4 e x = 9Nk B dx T D e x Für hohe Temperaturen x D 1, e x 1+x finden wir das Dulong-Petit-Gesetz, T 3 xd C T, 9Nk B dxx 1+x 3Nk B T T D. 48 T D Bei tiefen Temperaturen kann in Gl. 46 die obere Grenze durch ersetzt werden, C T, = 1π4 T 3 5 Nk B T T D. 49 T D Dies ist das Debyesche T 3 -Gesetz. [Metalle bei T T D,T F : C T = γ +AT...] 89
9.6 Photonen und Phononen
 9.6 Photonen und Phononen Wir betrachten nun zwei physialisch sehr unterschiedliche Systeme, deren statistische Behandlungen in mathematischer Hinsicht jedoch sehr ähnlich sind. Das eine System ist das
9.6 Photonen und Phononen Wir betrachten nun zwei physialisch sehr unterschiedliche Systeme, deren statistische Behandlungen in mathematischer Hinsicht jedoch sehr ähnlich sind. Das eine System ist das
9.1 Berechnung der großkanonischen Zustandssumme
 9 Ideale Quantengase Bei tiefen Temperaturen T und/oder hohen Dichten N zeigen ideale Gase Abweichungen vom klassischen erhalten P = N. Diese werden aber nicht wie bei der vdw- Gleichung durch Wechselwirkung
9 Ideale Quantengase Bei tiefen Temperaturen T und/oder hohen Dichten N zeigen ideale Gase Abweichungen vom klassischen erhalten P = N. Diese werden aber nicht wie bei der vdw- Gleichung durch Wechselwirkung
9.1 Berechnung der großkanonischen Zustandssumme
 9 Ideale Quantengase Bei tiefen Temperaturen T und/oder hohen Dichten N zeigen ideale Gase Abweichungen vom klassischen erhalten P = N. Diese werden aber nicht wie bei der vdw- Gleichung durch Wechselwirkung
9 Ideale Quantengase Bei tiefen Temperaturen T und/oder hohen Dichten N zeigen ideale Gase Abweichungen vom klassischen erhalten P = N. Diese werden aber nicht wie bei der vdw- Gleichung durch Wechselwirkung
8 Das klassische ideale Gas
 8 Das klassische ideale Gas 8.1 Unterscheidbare Atome Gleichartige Atome (etwa zwei He-Atome) sind in der Quantenmechanik grundsätzlich nicht unterscheidbar. Wir wollen dies jedoch zunächst ignorieren,
8 Das klassische ideale Gas 8.1 Unterscheidbare Atome Gleichartige Atome (etwa zwei He-Atome) sind in der Quantenmechanik grundsätzlich nicht unterscheidbar. Wir wollen dies jedoch zunächst ignorieren,
13.5 Photonen und Phononen
 Woche 11 13.5 Photonen und Phononen Teilchen mit linearem Dispersionsgesetz: E = c p, c - Ausbreitungsgeschwindigkeit (Licht- oder Schallgeschwindigkeit). 13.5.1 Photonen Quantisierung der Eigenschwingungen
Woche 11 13.5 Photonen und Phononen Teilchen mit linearem Dispersionsgesetz: E = c p, c - Ausbreitungsgeschwindigkeit (Licht- oder Schallgeschwindigkeit). 13.5.1 Photonen Quantisierung der Eigenschwingungen
Klausur-Musterlösungen
 Klausur-Musterlösungen 9.7.4 Theoretische Physik IV: Statistische Physik Prof. Dr. G. Alber Dr. O. Zobay. Der in Abb. dargestellte Kreisprozess wird mit einem elektromagnetischen Feld ausgeführt. Abb..
Klausur-Musterlösungen 9.7.4 Theoretische Physik IV: Statistische Physik Prof. Dr. G. Alber Dr. O. Zobay. Der in Abb. dargestellte Kreisprozess wird mit einem elektromagnetischen Feld ausgeführt. Abb..
Moderne Theoretische Physik IIIa WS 18/19
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik IIIa WS 8/9 Prof. Dr. Alexander Mirlin Lösungen zu Blatt 7 Dr. Stefan Rex Besprechung: 9..9.
Proseminar: Theoretische Physik. und Astroteilchenphysik. Fermi- und Bose Gase. Thermodynamisches Gleichgewicht
 Proseminar: Theoretische Physik und Astroteilchenphysik Thermodynamisches Gleichgewicht Fermi- und Bose Gase Inhalt 1. Entropie 2. 2ter Hauptsatz der Thermodynamik 3. Verteilungsfunktion 1. Bosonen und
Proseminar: Theoretische Physik und Astroteilchenphysik Thermodynamisches Gleichgewicht Fermi- und Bose Gase Inhalt 1. Entropie 2. 2ter Hauptsatz der Thermodynamik 3. Verteilungsfunktion 1. Bosonen und
Vorlesung Statistische Mechanik: N-Teilchensystem
 Virialentwicklung Die Berechnung der Zustandssumme bei realen Gasen ist nicht mehr exakt durchführbar. Eine Möglichkeit, die Wechselwirkung in realen Gasen systematisch mitzunehmen ist, eine Entwicklung
Virialentwicklung Die Berechnung der Zustandssumme bei realen Gasen ist nicht mehr exakt durchführbar. Eine Möglichkeit, die Wechselwirkung in realen Gasen systematisch mitzunehmen ist, eine Entwicklung
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Übungen zu Moderne Theoretischen Physik III SS Maxwell-Boltzmann-Gas: großkanonisches Ensemble (5+5+5=15 Punkte, schriftlich)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zu Moderne Theoretischen Physik III SS 016 Prof. Dr. A. Shnirman Blatt 6 PD Dr. B. Narozhny, P. Schad Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zu Moderne Theoretischen Physik III SS 016 Prof. Dr. A. Shnirman Blatt 6 PD Dr. B. Narozhny, P. Schad Lösungsvorschlag
Theorie der Wärme Musterlösung 11.
 Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Seminar für Fragen der Festkörpertheorie. P.N. Racec
 Seminar für Fragen der Festkörpertheorie P.N. Racec WS2003/2004 2 Contents Spezialthemen in Festkörperphysik 5. Fermi-Dirac Verteilungsfunktion........................ 6.2 Bose-Einstein Verteilungsfunktion.......................
Seminar für Fragen der Festkörpertheorie P.N. Racec WS2003/2004 2 Contents Spezialthemen in Festkörperphysik 5. Fermi-Dirac Verteilungsfunktion........................ 6.2 Bose-Einstein Verteilungsfunktion.......................
Gitterschwingungen in Festkörpern
 in Festkörpern Gitterschwingungen Wie bei den Molekülen wollen wir im folgenden die Dynamik der Festkörper, also Schwingungen des Kristallgitters behandeln Erklärung, Beschreibung Elastische Eigenschaften
in Festkörpern Gitterschwingungen Wie bei den Molekülen wollen wir im folgenden die Dynamik der Festkörper, also Schwingungen des Kristallgitters behandeln Erklärung, Beschreibung Elastische Eigenschaften
Klausur zur Statistischen Physik SS 2013
 Klausur zur Statistischen Physik SS 2013 Prof. Dr. M. Rohlfing Die folgenden Angaben bitte deutlich in Blockschrift ausfüllen: Name, Vorname: geb. am: in: Matrikel-Nr.: Übungsgruppenleiter: Aufgabe maximale
Klausur zur Statistischen Physik SS 2013 Prof. Dr. M. Rohlfing Die folgenden Angaben bitte deutlich in Blockschrift ausfüllen: Name, Vorname: geb. am: in: Matrikel-Nr.: Übungsgruppenleiter: Aufgabe maximale
Erreichte Punktzahlen: Die Bearbeitungszeit beträgt 3 Stunden.
 Fakultät für Physik der LMU München Prof. Ilka Brunner Michael Kay Vorlesung T4, WS11/12 Klausur am 18. Februar 2012 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Fakultät für Physik der LMU München Prof. Ilka Brunner Michael Kay Vorlesung T4, WS11/12 Klausur am 18. Februar 2012 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Fermi-Dirac-Verteilung
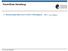 Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k B T + 6.7.23 Michael Buballa Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k
Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k B T + 6.7.23 Michael Buballa Fermi-Dirac-Verteilung Besetzungsfunktion pro innerem Freiheitsgrad: n(ε) = e (ε µ)/k
Grundlagen der Quantentheorie
 Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
6.2 Schwarzer Strahler, Plancksche Strahlungsformel
 6. Schwarzer Strahler, Plancsche Strahlungsformel Sehr nappe Herleitung der Plancschen Strahlungsformel Ziel: Berechnung der Energieverteilung der Strahlung im thermischen Gleichgewicht bei der Temperatur
6. Schwarzer Strahler, Plancsche Strahlungsformel Sehr nappe Herleitung der Plancschen Strahlungsformel Ziel: Berechnung der Energieverteilung der Strahlung im thermischen Gleichgewicht bei der Temperatur
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 3 Lösungsvorschlag
 T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 3 Lösungsvorschlag 1. Extremwerte unter Nebenbedingungen In der Vorlesung wurden die mittleren Besetzungszahlen für verschiedene
T4p: Thermodynamik und Statistische Physik Prof. Dr. H. Ruhl Übungsblatt 3 Lösungsvorschlag 1. Extremwerte unter Nebenbedingungen In der Vorlesung wurden die mittleren Besetzungszahlen für verschiedene
5 Bose-Einstein-Kondensation. Suprafluidität
 Prof. Dr. A. Muramatsu Fortgeschrittene Quantentheorie WS / 9 5 Bose-Einstein-Kondensation. Suprafluidität Wie im Fall der Fermionen betrachten wir in diesem Kapitel zunächst nicht wechselwirkende Bosonen.
Prof. Dr. A. Muramatsu Fortgeschrittene Quantentheorie WS / 9 5 Bose-Einstein-Kondensation. Suprafluidität Wie im Fall der Fermionen betrachten wir in diesem Kapitel zunächst nicht wechselwirkende Bosonen.
Statistische Mechanik
 David H. Trevena Statistische Mechanik Eine Einführung '«WO«.»vmo i; Übersetzt von Thomas Filk VCH Weinheim New York Basel Cambridge Tokyo Inhaltsverzeichnis Vorwort von H. N. V. Temperley Vorwort des
David H. Trevena Statistische Mechanik Eine Einführung '«WO«.»vmo i; Übersetzt von Thomas Filk VCH Weinheim New York Basel Cambridge Tokyo Inhaltsverzeichnis Vorwort von H. N. V. Temperley Vorwort des
Ferienkurs Experimentalphysik 4
 Ferienkurs Experimentalphysik 4 Vorlesung 5 Quantenstatistik Florian Lippert & Andreas Trautner 31.08.2012 Inhaltsverzeichnis 1 Quantenstatistik 1 1.1 Vorüberlegungen............................... 1 1.2
Ferienkurs Experimentalphysik 4 Vorlesung 5 Quantenstatistik Florian Lippert & Andreas Trautner 31.08.2012 Inhaltsverzeichnis 1 Quantenstatistik 1 1.1 Vorüberlegungen............................... 1 1.2
T2 Quantenmechanik Lösungen 2
 T2 Quantenmechanik Lösungen 2 LMU München, WS 17/18 2.1. Lichtelektrischer Effekt Prof. D. Lüst / Dr. A. Schmidt-May version: 12. 11. Ultraviolettes Licht der Wellenlänge 1 falle auf eine Metalloberfläche,
T2 Quantenmechanik Lösungen 2 LMU München, WS 17/18 2.1. Lichtelektrischer Effekt Prof. D. Lüst / Dr. A. Schmidt-May version: 12. 11. Ultraviolettes Licht der Wellenlänge 1 falle auf eine Metalloberfläche,
Repetitorium QM 1 - Tag 5
 Thermodynamik und 4. März 2016 Inhaltsverzeichnis 1 Thermodynamik Hauptsätze der Thermodynamik 2 Zustandsgrößen Thermodynamik Hauptsätze der Thermodynamik Ziel: Beschreibung des makroskopischen Gleichgewichtszustandes
Thermodynamik und 4. März 2016 Inhaltsverzeichnis 1 Thermodynamik Hauptsätze der Thermodynamik 2 Zustandsgrößen Thermodynamik Hauptsätze der Thermodynamik Ziel: Beschreibung des makroskopischen Gleichgewichtszustandes
Vorbereitung. (1) bzw. diskreten Wellenzahlen. λ n = 2L n. k n = nπ L
 Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Physikalisches Fortgeschrittenenpraktikum Gitterschwingungen Vorbereitung Armin Burgmeier Robert Schittny 1 Theoretische Grundlagen Im Versuch Gitterschwingungen werden die Schwingungen von Atomen in einem
Opto-elektronische. Materialeigenschaften VL # 3
 Opto-elektronische Materialeigenschaften VL # 3 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Experimental Physics VI, Julius-Maximilians-University of Würzburg und Bayerisches Zentrum für Angewandte
Opto-elektronische Materialeigenschaften VL # 3 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Experimental Physics VI, Julius-Maximilians-University of Würzburg und Bayerisches Zentrum für Angewandte
Seminar: Quantenoptik und nichtlineare Optik Quantisierung des elektromagnetischen Strahlungsfeldes und die Dipolnäherung
 Seminar: Quantenoptik und nichtlineare Optik Quantisierung des elektromagnetischen Strahlungsfeldes und die Dipolnäherung 10. November 2010 Physik Institut für Angewandte Physik Jörg Hoppe 1 Inhalt Motivation
Seminar: Quantenoptik und nichtlineare Optik Quantisierung des elektromagnetischen Strahlungsfeldes und die Dipolnäherung 10. November 2010 Physik Institut für Angewandte Physik Jörg Hoppe 1 Inhalt Motivation
10.6 Mehratomige ideale Gase
 10.6 Mehratomige ideale Gase Wir wenden uns jetzt dem Problem molekularer idealer Quantengase zu. 10.6.1 Quantenmechanik der starren Hantel Eine starre Hantel aus zwei Punktmassen m 1 und m 2, die durch
10.6 Mehratomige ideale Gase Wir wenden uns jetzt dem Problem molekularer idealer Quantengase zu. 10.6.1 Quantenmechanik der starren Hantel Eine starre Hantel aus zwei Punktmassen m 1 und m 2, die durch
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin WS 6/7 Fachbereich Physik 4..6 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 7: Dichtematrix, Variationsprinzip Aufgabe (5 Punkte) Betrachten Sie ein Gas
Freie Universität Berlin WS 6/7 Fachbereich Physik 4..6 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 7: Dichtematrix, Variationsprinzip Aufgabe (5 Punkte) Betrachten Sie ein Gas
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 6
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 6
X.4 Elektromagnetische Wellen im Vakuum
 X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
X.4 Elektromagnetische Wellen im Vakuum 173 X.4 Elektromagnetische Wellen im Vakuum In Abwesenheit von Quellen, ρ el. = 0 j el. = 0, nehmen die Bewegungsgleichungen (X.9) (X.11) für die elektromagnetischen
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik
 Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik begleitend zur Vorlesung Statistische Mechanik und Thermodynamik WS 2006/2007 Prof. Dr. Dieter W. Heermann erstellt
Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik begleitend zur Vorlesung Statistische Mechanik und Thermodynamik WS 2006/2007 Prof. Dr. Dieter W. Heermann erstellt
E 3. Ergänzungen zu Kapitel 3
 E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
Übungen zu Moderne Theoretischen Physik III SS Curie-Paramagnetismus ( =30 Punkte, schriftlich)
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Übungen zu Moderne heoretischen Physik III SS 06 Prof. Dr. A. Shnirman Blatt 5 PD Dr. B. Narozhny, P. Schad Lösungsvorschlag.
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Übungen zu Moderne heoretischen Physik III SS 06 Prof. Dr. A. Shnirman Blatt 5 PD Dr. B. Narozhny, P. Schad Lösungsvorschlag.
WKB-Methode. Jan Kirschbaum
 WKB-Methode Jan Kirschbaum Westfälische Wilhelms-Universität Münster Fachbereich Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie 1 Einleitung Die WKB-Methode, unabhängig und fast
WKB-Methode Jan Kirschbaum Westfälische Wilhelms-Universität Münster Fachbereich Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie 1 Einleitung Die WKB-Methode, unabhängig und fast
Nachklausur zur Vorlesung Theoretische Physik in zwei Semestern II. Musterlösungen
 UNIVERSITÄT ZU KÖLN Institut für Theoretische Physik Wintersemester 005/006 Nachklausur zur Vorlesung Theoretische Physik in zwei Semestern II Musterlösungen 1. Welche experimentellen Tatsachen weisen
UNIVERSITÄT ZU KÖLN Institut für Theoretische Physik Wintersemester 005/006 Nachklausur zur Vorlesung Theoretische Physik in zwei Semestern II Musterlösungen 1. Welche experimentellen Tatsachen weisen
Erreichte Punktzahlen: Die Bearbeitungszeit beträgt 3 Stunden.
 Fakultät für Physik der LMU München Prof. Ilka Brunner Dr. Andres Collinucci Vorlesung T4, WS10/11 Klausur am 16. Februar 2011 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Fakultät für Physik der LMU München Prof. Ilka Brunner Dr. Andres Collinucci Vorlesung T4, WS10/11 Klausur am 16. Februar 2011 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Statistik und Thermodynamik
 Klaus Goeke Statistik und Thermodynamik Eine Einführung für Bachelor und Master STUDIUM VIEWEG+ TEUBNER Inhaltsverzeichnis I Grundlagen der Statistik und Thermodynamik 1 1 Einleitung 3 2 Grundlagen der
Klaus Goeke Statistik und Thermodynamik Eine Einführung für Bachelor und Master STUDIUM VIEWEG+ TEUBNER Inhaltsverzeichnis I Grundlagen der Statistik und Thermodynamik 1 1 Einleitung 3 2 Grundlagen der
Übungen zu Moderne Theoretischen Physik III SS Maxwell-Verteilung: (30 Punkte, schriftlich)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zu Moderne Theoretischen Physik III SS 06 Prof. Dr. A. Shnirman Blatt 4 PD Dr. B. arozhny, P. Schad Lösungsvorschlag.
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zu Moderne Theoretischen Physik III SS 06 Prof. Dr. A. Shnirman Blatt 4 PD Dr. B. arozhny, P. Schad Lösungsvorschlag.
Wellen und Dipolstrahlung
 Wellen und Dipolstrahlung Florian Hrubesch 25. März 2010 Inhaltsverzeichnis 1 Photoeffekt 1 2 Comptoneffekt 3 3 Bragg Streuung 4 4 Strahlungsgesetze 5 1 Photoeffekt Der Photoeffekt wurde erstmals 1839
Wellen und Dipolstrahlung Florian Hrubesch 25. März 2010 Inhaltsverzeichnis 1 Photoeffekt 1 2 Comptoneffekt 3 3 Bragg Streuung 4 4 Strahlungsgesetze 5 1 Photoeffekt Der Photoeffekt wurde erstmals 1839
Inhalt. Vorwort v. Liste der wichtigsten verwendeten Symbole und Abkürzungen xiii. Einleitung 1
 Inhalt Vorwort v Liste der wichtigsten verwendeten Symbole und Abkürzungen xiii Einleitung 1 1 Grundlagen der Statistischen Physik 5 1.1 Zustände in der Quantenmechanik 5 1.1.1 Zustände, Observable, Erwartungswerte
Inhalt Vorwort v Liste der wichtigsten verwendeten Symbole und Abkürzungen xiii Einleitung 1 1 Grundlagen der Statistischen Physik 5 1.1 Zustände in der Quantenmechanik 5 1.1.1 Zustände, Observable, Erwartungswerte
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
1 Innere Rotation von Alkanen
 Physikalische Chemie II Lösung 1 25. November 216 1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e
Physikalische Chemie II Lösung 1 25. November 216 1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e
Zusätzliche Aspekte der Absorbtion und Emission von Photonen
 Vorlesung 9 Zusätzliche Aspekte der Absorbtion und Emission von Photonen Plancksche Verteilung und thermisches Gleichgewicht: Wir betrachten ein Medium aus Atomen. Die Atome wechselwirken nicht direkt
Vorlesung 9 Zusätzliche Aspekte der Absorbtion und Emission von Photonen Plancksche Verteilung und thermisches Gleichgewicht: Wir betrachten ein Medium aus Atomen. Die Atome wechselwirken nicht direkt
2. Max Planck und das Wirkungsquantum h
 2. Max Planck und das Wirkungsquantum h Frequenzverteilung eines schwarzen Strahlers Am 6. Dezember 1900, dem 'Geburtsdatum' der modernen Physik, hatte Max Planck endlich die Antwort auf eine Frage gefunden,
2. Max Planck und das Wirkungsquantum h Frequenzverteilung eines schwarzen Strahlers Am 6. Dezember 1900, dem 'Geburtsdatum' der modernen Physik, hatte Max Planck endlich die Antwort auf eine Frage gefunden,
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Übungen zur Theoretischen Physik F SS Ideales Boltzmann-Gas: ( =25 Punkte, schriftlich)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS 2016 Prof. Dr. A. Shnirman Blatt 2 Dr. B. Narozhny, Dipl.-Phys. P. Schad Lösungsvorschlag
UniversitätQ Osnabrück Fachbereich Physik Dr. W. Bodenberger
 UniversitätQ Osnabrück Fachbereich Physik Dr. W. Bodenberger Statistik der Elektronen und Löcher in Halbleitern Die klassische Theorie der Leitungselektronen in Metallen ist nicht anwendbar auf die Elektronen
UniversitätQ Osnabrück Fachbereich Physik Dr. W. Bodenberger Statistik der Elektronen und Löcher in Halbleitern Die klassische Theorie der Leitungselektronen in Metallen ist nicht anwendbar auf die Elektronen
(a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle?
 FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
Physik IV Übung 4
 Physik IV 0 - Übung 4 8. März 0. Fermi-Bose-Boltzmann Verteilung Ein ideales Gas befinde sich in einer Box mit Volumen V = L 3. Das Gas besteht entweder aus Teilchen, die die Bose-Einstein oder Fermi-Dirac
Physik IV 0 - Übung 4 8. März 0. Fermi-Bose-Boltzmann Verteilung Ein ideales Gas befinde sich in einer Box mit Volumen V = L 3. Das Gas besteht entweder aus Teilchen, die die Bose-Einstein oder Fermi-Dirac
Elektrodynamik (T3p)
 Zusatzaufgaben zur Vorlesung Elektrodynamik (T3p) SoSe 5 Beachten Sie, dass die nachfolgenden Aufgaben nur als zusätzliche Übung und nicht als potenzielle Klausuraufgaben angesehen werden sollten! Aufgabe
Zusatzaufgaben zur Vorlesung Elektrodynamik (T3p) SoSe 5 Beachten Sie, dass die nachfolgenden Aufgaben nur als zusätzliche Übung und nicht als potenzielle Klausuraufgaben angesehen werden sollten! Aufgabe
1) Brillouin-Streuung zur Ermittlung der Schallgeschwindigkeit
 Übungen zu Materialwissenschaften II Prof. Alexander Holleitner Übungsleiter: Eric Parzinger / Jens Repp Kontakt: eric.parzinger@wsi.tum.de / jens.repp@wsi.tum.de Blatt 3, Besprechung: 7. und 14.5.214
Übungen zu Materialwissenschaften II Prof. Alexander Holleitner Übungsleiter: Eric Parzinger / Jens Repp Kontakt: eric.parzinger@wsi.tum.de / jens.repp@wsi.tum.de Blatt 3, Besprechung: 7. und 14.5.214
Quantisierung des elektromagnetischen Feldes
 18. Juni 2008 1 Energiewerte Maxwell-Gleichungen Wellengleichung Lagrange-Funktion Hamilton-Funktion 1 Kanonische Helmholtzsche freie Energie Innere Energie Übersicht Behandelt wird die im Vakuum. Das
18. Juni 2008 1 Energiewerte Maxwell-Gleichungen Wellengleichung Lagrange-Funktion Hamilton-Funktion 1 Kanonische Helmholtzsche freie Energie Innere Energie Übersicht Behandelt wird die im Vakuum. Das
Klausur zur T1 (Klassische Mechanik)
 Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Vorlesung 17. Quantisierung des elektromagnetischen Feldes
 Vorlesung 17 Quantisierung des elektromagnetischen Feldes Wir wissen, dass man das elektromagnetische Feld als Wellen oder auch als Teilchen die Photonen beschreiben kann. Die Verbindung zwischen Wellen
Vorlesung 17 Quantisierung des elektromagnetischen Feldes Wir wissen, dass man das elektromagnetische Feld als Wellen oder auch als Teilchen die Photonen beschreiben kann. Die Verbindung zwischen Wellen
Bose-Einstein Kondensation und Fermigase. 1924/25 Theorie: S.Bose, A.Einstein Experiment: E.Cornell, C.Wieman, W.Ketterle
 Bose-Einstein Kondensation und Fermigase 1924/25 Theorie: S.Bose, A.Einstein 1995 Experiment: E.Cornell, C.Wieman, W.Ketterle Bose-Einstein Kondensation und Fermigase Theorie Quantengase und Grundzüge
Bose-Einstein Kondensation und Fermigase 1924/25 Theorie: S.Bose, A.Einstein 1995 Experiment: E.Cornell, C.Wieman, W.Ketterle Bose-Einstein Kondensation und Fermigase Theorie Quantengase und Grundzüge
Kapitel 5. Kanonisches Ensemble. 5.1 Herleitung 1; E 1 =? 2; E 2 =?
 Kapitel 5 Kanonisches Ensemble 5.1 Herleitung Abgesehen von der Legendre-Transformation S(E,, N) F (T,, N) besteht noch eine weitere Möglichkeit, die freie Energie zu berechnen, und zwar wiederum mittels
Kapitel 5 Kanonisches Ensemble 5.1 Herleitung Abgesehen von der Legendre-Transformation S(E,, N) F (T,, N) besteht noch eine weitere Möglichkeit, die freie Energie zu berechnen, und zwar wiederum mittels
4.4 Die Potentialgleichung
 Beispiel 29. f(z) = exp( 1 ) H(C {}) z 1 w : z n = log w + 2πin, n N lim z n = n f(z n ) = exp(log w + 2πin) = w + exp(2πin) }{{} =1 In jeder Umgebung von Null nimmt f jeden Wert w (unendlich oft) an wesentliche
Beispiel 29. f(z) = exp( 1 ) H(C {}) z 1 w : z n = log w + 2πin, n N lim z n = n f(z n ) = exp(log w + 2πin) = w + exp(2πin) }{{} =1 In jeder Umgebung von Null nimmt f jeden Wert w (unendlich oft) an wesentliche
Stirling sche Näherungsformel
 Stirling sche Näherungsformel ln(n!) N ln(n) N für N 6.5.22 Michael Buballa Stirling sche Näherungsformel ln(n!) = N ln(k) k= N dx ln(x) = (x ln(x) x) N = N ln(n) N 6.5.22 Michael Buballa Stirling sche
Stirling sche Näherungsformel ln(n!) N ln(n) N für N 6.5.22 Michael Buballa Stirling sche Näherungsformel ln(n!) = N ln(k) k= N dx ln(x) = (x ln(x) x) N = N ln(n) N 6.5.22 Michael Buballa Stirling sche
1.4 Streuung an Kristallen
 34 Theoretische Festkörperphysik Prof. Heermann.4 Streuung an Kristallen.4. Elastische Streuung Wir betrachten etwa die folgende Situation. Zunächst spezifizieren wir den Anfangszustand des Kristalls durch
34 Theoretische Festkörperphysik Prof. Heermann.4 Streuung an Kristallen.4. Elastische Streuung Wir betrachten etwa die folgende Situation. Zunächst spezifizieren wir den Anfangszustand des Kristalls durch
Ferienkurs Theoretische Mechanik 2009 Hamilton Formalismus und gekoppelte Systeme
 Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Vorlesung 21. Identische Teilchen und das Pauli-Prinzip
 Vorlesung 1 Identische Teilchen und das Pauli-Prinzip Identische Teilchen: Jede Art von Teilchen in der Natur definieren wir durch ihre Eigenschaften, z.b. Massen, Spins, Ladungen usw. Das bedeutet, dass
Vorlesung 1 Identische Teilchen und das Pauli-Prinzip Identische Teilchen: Jede Art von Teilchen in der Natur definieren wir durch ihre Eigenschaften, z.b. Massen, Spins, Ladungen usw. Das bedeutet, dass
Physik IV - Schriftliche Sessionsprüfung Sommer 2009
 Physik IV - Schriftliche Sessionsprüfung Sommer 2009 9:00 11:00, Samstag, 8. August 2009, HG F1 & HG F3 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt SECHS Aufgaben auf VIER SEITEN. Es können insgesamt
Physik IV - Schriftliche Sessionsprüfung Sommer 2009 9:00 11:00, Samstag, 8. August 2009, HG F1 & HG F3 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt SECHS Aufgaben auf VIER SEITEN. Es können insgesamt
Notizen zur statistischen Physik
 Notizen zur statistischen Physik Kim Boström Begriffe der hermodynamik System: Gedanklich und im Prinzip operativ abtrennbarer eil der Welt. Physik ist das Studium der Eigenschaften von Systemen. Umgebung:
Notizen zur statistischen Physik Kim Boström Begriffe der hermodynamik System: Gedanklich und im Prinzip operativ abtrennbarer eil der Welt. Physik ist das Studium der Eigenschaften von Systemen. Umgebung:
M. 59 Perle auf rotierendem Draht (F 2018)
 M. 59 Perle auf rotierendem Draht (F 8) Eine Perle der Masse m bewegt sich reibungslos auf einem mit konstanter Winkelgeschwindigkeit ω um die z-achse rotierenden Draht. Für die Belange dieser Aufgabe
M. 59 Perle auf rotierendem Draht (F 8) Eine Perle der Masse m bewegt sich reibungslos auf einem mit konstanter Winkelgeschwindigkeit ω um die z-achse rotierenden Draht. Für die Belange dieser Aufgabe
V. Optik in Halbleiterbauelementen
 V.1: Einführung V. Optik in Halbleiterbauelementen 1. Kontakt 1. 3.. 1. Kontakt Abb. VI.1: Spontane Emission an einem pn-übergang Rekombination in der LED: - statistisch auftretender Prozess - Energie
V.1: Einführung V. Optik in Halbleiterbauelementen 1. Kontakt 1. 3.. 1. Kontakt Abb. VI.1: Spontane Emission an einem pn-übergang Rekombination in der LED: - statistisch auftretender Prozess - Energie
Thermodynamische Grundlagen
 Kapitel 1 Thermodynamische Grundlagen 1.1 Einige thermodynamische Relationen Die statistische Mechanik beschreibt die Eigenschaften und das Verhalten physikalischer Systeme, die aus einer großen Anzahl
Kapitel 1 Thermodynamische Grundlagen 1.1 Einige thermodynamische Relationen Die statistische Mechanik beschreibt die Eigenschaften und das Verhalten physikalischer Systeme, die aus einer großen Anzahl
Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e [
 Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
Erreichte Punktzahlen: Die Bearbeitungszeit beträgt 3 Stunden.
 Fakultät für Physik der LMU München Prof. Ilka Brunner Vorlesung T4p, WS08/09 Klausur am 11. Februar 2009 Name: Matrikelnummer: Erreichte Punktzahlen: 1.1 1.2 1.3 2.1 2.2 2.3 2.4 Hinweise Die Bearbeitungszeit
Fakultät für Physik der LMU München Prof. Ilka Brunner Vorlesung T4p, WS08/09 Klausur am 11. Februar 2009 Name: Matrikelnummer: Erreichte Punktzahlen: 1.1 1.2 1.3 2.1 2.2 2.3 2.4 Hinweise Die Bearbeitungszeit
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Welche Zustände sind denn eigentlich besetzt?
 elche Zustände sind denn eigentlich besetzt? elche Zustände sind denn eigentlich besetzt? ( 0 ) 12 9 -im Prinzip sollte das Ganze ähnlich wie beim Atom erfolgen 6 - Besetzung von unten nach oben 3 -...wie
elche Zustände sind denn eigentlich besetzt? elche Zustände sind denn eigentlich besetzt? ( 0 ) 12 9 -im Prinzip sollte das Ganze ähnlich wie beim Atom erfolgen 6 - Besetzung von unten nach oben 3 -...wie
4.6 Stöße mit Phononen
 Physik der kondensierten Materie WS 00/0 05..00 ii) Wie viele mögliche k-vektoren gibt es in der ersten Brillouinzone? Wir betrachten eine Kette mit N Atomen unter periodischen Randbedingungen, d.h. für
Physik der kondensierten Materie WS 00/0 05..00 ii) Wie viele mögliche k-vektoren gibt es in der ersten Brillouinzone? Wir betrachten eine Kette mit N Atomen unter periodischen Randbedingungen, d.h. für
Berechnung der Leitfähigkeit ( ) Anzahl der Ladungsträger im Leitungsband
 8.1 Berechnung der eitfähigkeit Quantitativ wird die eitfähigkeit σ berechnet durch: adung des Elektrons Beweglichkeit der adungsträger im eitungsband ( ) σ = e µ n + µ p n Anzahl der adungsträger im eitungsband
8.1 Berechnung der eitfähigkeit Quantitativ wird die eitfähigkeit σ berechnet durch: adung des Elektrons Beweglichkeit der adungsträger im eitungsband ( ) σ = e µ n + µ p n Anzahl der adungsträger im eitungsband
1.3. DAS COULOMBSCHE GESETZ, ELEKTROSTATISCHES FELD 9
 8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
Statistische Thermodynamik I Lösungen zur Serie 11
 Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
1 Innere Rotation von Alkanen
 1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e hω/2k BT = a 0 x n e hωn+ 1 2 /k BT e hωn/kbt = e
1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e hω/2k BT = a 0 x n e hωn+ 1 2 /k BT e hωn/kbt = e
Statistische Mechanik
 Kapitel 7 Statistische Mechanik 7.1 Lagrange-Multiplikatoren Fkt fx). Bedingung eines Maximums oder Minimums) df = f x)dx = 0. Fkt von n Variablen: fx 1,x 2,...,x n ). Bedingung des Maximums: Sei df x)
Kapitel 7 Statistische Mechanik 7.1 Lagrange-Multiplikatoren Fkt fx). Bedingung eines Maximums oder Minimums) df = f x)dx = 0. Fkt von n Variablen: fx 1,x 2,...,x n ). Bedingung des Maximums: Sei df x)
Auswahl von Prüfungsfragen für die Prüfungen im September 2011
 Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Auswahl von Prüfungsfragen für die Prüfungen im September 2011 Was ist / sind / bedeutet / verstehen Sie unter... Wie nennt man / lautet / Wann spricht man von / Definieren Sie... Die anschließenden Fragen
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
 Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
,Faltung. Heavisidefunktion σ (t), Diracimpuls δ (t) Anwendungen. 1) Rechteckimpuls. 2) Sprungfunktionen. 3) Schaltvorgänge
 Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
1-D photonische Kristalle
 1-D photonische Kristalle Berechnung der Dispersionsrelation und der Zustandsdichte für elektromagnetische Wellen Antonius Dorda 15.03.09 Inhaltsverzeichnis 1 Einleitung 2 2 Herleitung der Relationen 2
1-D photonische Kristalle Berechnung der Dispersionsrelation und der Zustandsdichte für elektromagnetische Wellen Antonius Dorda 15.03.09 Inhaltsverzeichnis 1 Einleitung 2 2 Herleitung der Relationen 2
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 4 Lösung. P + a )
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
Theoretische Physik F: Zwischenklausur SS 12
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie heoretische Physik F: Zwischenklausur SS 1 Prof. Dr. Jörg Schmalian Lösungen Dr. Igor Gornyi esprechung 18.05.01 1. Quickies:
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie heoretische Physik F: Zwischenklausur SS 1 Prof. Dr. Jörg Schmalian Lösungen Dr. Igor Gornyi esprechung 18.05.01 1. Quickies:
Elektrodynamik eines Plasmas
 Elektrodynamik eines Plasmas Elektrodynamik eines Plasmas Klassifikation von Plasmen Klassisches Plasma / Quantenplasma nicht-relativistisches / relativistisches Plasma Schwach / stark wechselwirkendes
Elektrodynamik eines Plasmas Elektrodynamik eines Plasmas Klassifikation von Plasmen Klassisches Plasma / Quantenplasma nicht-relativistisches / relativistisches Plasma Schwach / stark wechselwirkendes
e βεa = 1 β eα Z 1 (β,v ), über die allgemeine Beziehung e αn Z (kl) N (β,v )
 Im Limes e α lautet das großkanonische Potential XII.29) Ωβ,,α)= ln ± e α βεa β β eα a a e βεa = β eα Z β, ), XII.62) mit Z β, ) der kanonischen Zustandssumme für ein Teilchen. Der ergleich mit der allgemeinen
Im Limes e α lautet das großkanonische Potential XII.29) Ωβ,,α)= ln ± e α βεa β β eα a a e βεa = β eα Z β, ), XII.62) mit Z β, ) der kanonischen Zustandssumme für ein Teilchen. Der ergleich mit der allgemeinen
Übungen zu Theoretische Physik IV
 Physikalisches Institut Übungsblatt 4 Universität Bonn 02. November 2012 Theoretische Physik WS 12/13 Übungen zu Theoretische Physik IV Priv.-Doz. Dr. Stefan Förste http://www.th.physik.uni-bonn.de/people/forste/exercises/ws1213/tp4
Physikalisches Institut Übungsblatt 4 Universität Bonn 02. November 2012 Theoretische Physik WS 12/13 Übungen zu Theoretische Physik IV Priv.-Doz. Dr. Stefan Förste http://www.th.physik.uni-bonn.de/people/forste/exercises/ws1213/tp4
11. April Institut für Theoretische Physik. Das Toda-Gitter: periodische Lösungen. Daniel Westerfeld. Motivation. Vorbereitungen.
 Toda- Institut für Theoretische Physik 11. April 2012 Überblick Toda- 1 2 3 Toda- Toda- Betrachte eindimensionale Kette N identischer Teilchen. Wechselwirkung nur zwischen Nachbarn = Bewegungsgleichung:
Toda- Institut für Theoretische Physik 11. April 2012 Überblick Toda- 1 2 3 Toda- Toda- Betrachte eindimensionale Kette N identischer Teilchen. Wechselwirkung nur zwischen Nachbarn = Bewegungsgleichung:
Übungsblatt 6 ( ) mit Lösungen
 1) Wellengleichung Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 014/15 Übungsblatt 6 (09.01.015) mit Lösungen Eine Welle, die sich in positiver x-richtung mit der Geschwindigkeit
1) Wellengleichung Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 014/15 Übungsblatt 6 (09.01.015) mit Lösungen Eine Welle, die sich in positiver x-richtung mit der Geschwindigkeit
UNIVERSITÄT LEIPZIG INSTITUT FÜR THEORETISCHE PHYSIK
 UNIVERSITÄT LEIPZIG INSTITUT FÜR THEORETISCHE PHYSIK Quantenmechanik II Übungsblatt 10 Solutions 7. Wenn die zeitabhängige Störung periodisch in der Zeit ist, V = αx cos(ωt), mit einer Zahl α und einem
UNIVERSITÄT LEIPZIG INSTITUT FÜR THEORETISCHE PHYSIK Quantenmechanik II Übungsblatt 10 Solutions 7. Wenn die zeitabhängige Störung periodisch in der Zeit ist, V = αx cos(ωt), mit einer Zahl α und einem
Kapitel 3. Statistische Definition der Entropie. 3.1 Ensemble aus vielen Teilchen
 Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
