Formelsammlung Analysis
|
|
|
- Uwe Lehmann
- vor 7 Jahren
- Abrufe
Transkript
1 Formelsammlung Analysis Klemens Fersch. August 0 Inhaltsverzeichnis Analysis. Grenzwert - Stetigkeit Grenzwert von f(x) für x gegen x Grenzwert von f(x) für x gegen Unendlich Stetigkeit Rechenregeln Differentialrechnung Definition Ableitung - Monotonie - Extremwerte Graph der. Ableitung Ableitung - Krümmung - Wendepunkte Graph der. Ableitung Ableitung der Grundfunktionen Ableitungsregeln Tangenten- und Normalengleichung Newtonsches Iterationsverfahren Integralrechnung Definition Integration der Grundfunktionen Integrationsregeln Graph der Stammfunktion Kurvendiskussion Ganzrationale Funktion Gebrochenrationale Funktion Exponentialfunktion (Basis e) Logarithmusfunktion (Basis e) Aufstellen von Funktionsgleichungen Ganzrationale Funktion
2 Analysis. Grenzwert - Stetigkeit.. Grenzwert von f(x) für x gegen x0 (x ) f (x) = (x + )(x ) f (x) = ln(x ) + f (x) = e x + VA x = x = HA y = 0 HA y = VA x = Linksseitiger Grenzwert (LGW) von f(x) geht gegen eine Konstante (konvergiert) f(x) = a oder f(x) = a x x 0 x x < 0 Rechtsseitiger Grenzwert (RGW) von f(x) geht gegen eine Konstante (konvergiert) f(x) = a oder f(x) = a x x + 0 x x > 0 Grenzwert von f(x) existiert linksseitige Grenzwert = rechtsseitige Grenzwert f(x) = f(x) = a x x 0 x x + 0 f(x) = a x x 0 Linksseitiger Grenzwert von f(x) geht gegen Unendlich (bestimmt divergiert) f(x) = ± x x 0 Rechtsseitiger Grenzwert von f(x) geht gegen Unendlich (bestimmt divergiert) f(x) = ± x x + 0 vertikale Asymptote - Polstelle an der Stelle x = x 0 (x ) f (x) = D = R \ {; } (x + )(x ) Linksseitiger Grenzwert von f(x) für x gegen x f(x), 99 0, 95, 999 0, 9, , 9, , 7 (x ) x (x + )(x ) = x (x + ) = Rechtsseitiger Grenzwert von f(x) für x gegen x + f(x), 0 0, 89, 00 0, 9, 000 0,, , (x ) x + (x + )(x ) = x + (x + ) = f(x) = Stetig behebare Definitionslücke x Linksseitiger Grenzwert von f(x) für x gegen - x f(x) (x ), 0 00 x, (x + )(x ) =, x, , (x + ) = Rechtsseitiger Grenzwert von f(x) für x gegen - x + f(x), 99 00, , , , (x ) x + (x + )(x ) = x + (x + ) = ln(x ) + = x + Vertikale Asymptote (Polstelle): x = Interaktive Inhalte: hier klicken
3 Analysis Grenzwert - Stetigkeit.. Grenzwert von f(x) für x gegen Unendlich Grenzwert von f(x) geht gegen eine Konstante (konvergiert) f(x) = a x ± horizontale Asymptote y = a Grenzwert von f(x) geht gegen Unendlich (bestimmt divergiert) f(x) = ± x ± Funktion: f (x) = x Grenzwert von f(x) für x gegen und gegen - x f(x) x f(x) x = [ ] = x = [ ( ) ] = (x ) f (x) = (x + )(x ) D = R \ {; } Grenzwert von f(x) für x gegen und gegen - x f(x) 0 x f(x) 0 0 0, , , , , , , , , , 0000 f (x) = (x ) (x + )(x ) = x x x = x( x ) x ( x 8 x ) x ± x( x ) x ( x 8 = x ) x ± Horizontale Asymptote: y = 0 f (x) = ln(x ) + ln(x ) + = f (x) = e x + ex + = x ex + = Horizontale Asymptote: y = x x = x ± x = 0 Interaktive Inhalte: hier klicken.. Stetigkeit stetig { x, x f (x) = x, x > unstetig { x, x f (x) = x, x > stetig behebar (x ) f (x) = (x + )(x ) x =
4 Grenzwert - Stetigkeit Ein Funktion ist an der Stelle x 0 stetig, wenn der linksseitige GW = rechtsseitige GW = Funktionswert f(x) f(x) = f(x) = f(x 0 ) x x 0 x x + 0 Stetige Funktionen - Ganzrationale Funktionen - Exponentialfunktionen - Sinus- und Kosinusfunktion Stetige Funktionen, bei denen die Unstetigkeitsstellen aus dem Definitionsbereich ausgeschlossen sind: - Gebrochenrationale Funktionen - Logarithmusfunktionen - Tangensfunktion Abschnittsweise definierte Funktionen müssen an den Schnittstellen auf Stetigkeit untersucht werden. Stetig behebare Definitionslücke x 0 - linksseitige GW = rechtsseitige GW f(x) = f(x) x x 0 x x + 0 { x, x f (x) = x, x > LGW: x = x RGW: x = x + FW: f () = = LGW = RGW = FW ist stetig { an der Stelle x 0 = x, x f (x) = x, x > LGW: x = x RGW: x = x + FW: f () = = LGW RGW FW ist unstetig an der Stelle x 0 = f (x) = (x ) (x + )(x ) = (x + ) f (x) stetig in D RGW: x + (x + ) = LGW: x (x + ) = RGW = LGW stetig behebare Definitionslücke: x 0 = Stetige Fortsetzung von f (x) f (x) = D = R \ {} (x + ) D = R \ {; } Interaktive Inhalte: hier klicken.. Rechenregeln Wichtige Grenzwerte a x = 0 x 0 a x = ex = ln x = x 0 + a x 0 x = a x = 0 x ex = 0 ln x = x = 0 x 0 7 x = ex = ln x = x x 0 x = x = 0 x ex = 0 ln x = Rechenregeln f(x) = f g(x) = g x x 0 x x 0 (f(x) + g(x)) = f(x) + g(x) = f + g x x 0 x x 0 x x 0 (f(x) g(x)) = f(x) g(x) = f g x x 0 x x 0 x x 0 (f(x) g(x)) = f(x) g(x) = f g x x 0 x x 0 x x 0 f(x) g(x) 0 x x 0 g(x) = f(x) x x 0 g(x) = f x x 0 g x ± x x( x 8 x ) = 0 Zähler: x ± x = 0 Nenner: 8 x ± x = 0 0 = x ± x ± x = 0 Zähler durch Nenner: = 0 x( 0 0) = x ±
5 Grenzwert - Stetigkeit Unbestimmte Ausdrücke Typ : f(x) g(x) = 0 0 Regel von L Hospital Typ : f(x) g(x) = ± ± Zähler und Nenner getrennt ableiten, bis man den Grenzwert berechnen kann. f(x) g(x) = f (x) g (x) = f (x) g (x)... Typ : f(x) g(x) = 0 ± - Umformen in Typ oder und danach L Hospital Typ : (f(x) g(x)) = - Brüche auf gemeinsamen Hauptnenner bringen - Faktorisieren Typ : 0 0 sin x x 0 x = cos x = cos 0 = x 0 Typ : x e = x x e = x e = = 0 Typ : 0 x x e x = e = x e = 0 x ln x x x ln x = x 0 + x 0 + = x 0 x + = x = 0 x Typ : x x = x(x ) = ( x 0 x ) x = = x x 0 x Wichtige unbestimmte Ausdrücke x n e x = 0 x n ln x = e x x n = ln x x n = 0 x 5 e x = 0 x ln x = e x x = ln x x = 0 5
6 Analysis Differentialrechnung. Differentialrechnung.. Definition Sekantensteigung Tangentensteigung f(x) = x P P y x f(x) = x P (x; f(x)) x y Sekantensteigung Eine Grade schneidet eine Funktion in den Punkten P (x 0 ; f(x 0 )) und P (x; f(x)). Steigung der Sekante an der Stelle x 0 m = y x = f(x) f(x 0) x x 0 x = h x = x 0 + h m = f(x 0 + h) f(x 0 ) h Sekantensteigung = Differenzenquotient = Mittlere Änderungsgrate Für kleine h ist die Sekantensteigung Tangentensteiung m f (x 0 ) f(x) = x Die Sekantensteiung m durch die Punkte P (0.5; 0, 5) P (, 5;, 5) f(x) f(x0) m = x x 0, 5 0, 5 m =, 5 0, 5 = Die Sekantensteiung m an der Stelle x 0 = 0, 5 und h = f(x0 + h) f(x0) m = h f(0, 5 + ) f(0, 5) m =.5 0, 5 m = = Die Sekantensteigung m an der Stelle x 0 = 0, 5 und h = 0, 00 f(x0 + h) f(x0) m = h f(0, 5 + 0, 00) f(0, 5) m = 0, 00 0, 500 0, 5 m = =, 00 0, 00 m f (0, 5) =. Ableitung - Differentialqoutient Die Ableitung von f(x) ist die Steigung des Graphen der Funktion f(x) an der Stelle x 0. f f(x) f(x 0 ) (x) = x x 0 x x 0 x = x 0 + h f f(x 0 + h) f(x 0 ) (x) = h 0 h. Ableitung = Steigung der Tangente = Steigung der Funktion f(x)=lokale (momentane) Änderungsrate Die Ableitung von f(x) an einer beliebigen Stelle x f f(x + h) f(x) (x) = h 0 h Die. Ableitung von f(x) = x an der Stelle x 0 = 0, 5 f (0, 5 + h) 0, 5 () = h 0 h f 0, 5 + h + h 0, 5 () = h 0 h f h( + h) () = h 0 h f () = + h = h 0 Die Ableitung von f(x) = x an einer beliebigen Stelle x f (x) = h 0 (x + h) x h f x + hx + h x (x) = h 0 h f h(x+h) (x) = h 0 h f (x) = x f (0, 5) = = h 0 x + h = x
7 Analysis Differentialrechnung.Ableitung Die Ableitung der. Ableitung ist die.ableitung. Die.Ableitung gibt die Krümmung einer Funktion f(x) an der Stelle x 0 an. f (x) = x + x + x f (x) = x + x + f (x) = x + Interaktive Inhalte: hier klicken... Ableitung - Monotonie - Extremwerte f (x) = x x f (x) = x x HP(-/) HT sms smf sms TP(/-) HT HT smf smf sms TEP(0/-) TP(,5/,75) HT sms - streng monoton steigend; smf - streng monoton fallend; VZW - Vorzeichenwechsel; NST - Nullstelle ; HP - Hochpunkt (Maximum); TP - Tiefpunkt (Minimum) ; HT - horizontale Tangente; TEP - Terrassenpunkt; Steigung von f(x 0 ) an der Stelle x 0 m = f (x 0 ) Funktion f (x) = x x. Ableitungen f (x) = x = Steigung an der Stelle x = m = f () = 7 8 Steigung an der Stelle x = f () = 8 (x + )(x ) Stelle x 0 an der f(x 0 ) die Steigung m besitzt f (x) = m Bei horizontalen Tangenten ist die Steigung Null. f (x) = 0. Ableitungen f (x) = x Horizontale Tangente x = 0 / + x = / : x = x = ± x = x = 7
8 Differentialrechnung Monotonieverhalten monoton steigend f (x) 0 streng monoton steigend sms f (x) > 0 monoton fallend f (x) 0 streng monoton fallend smf f (x) < 0 Monotonieverhalten an der Stelle x = m = f () = 7 8 > 0 sms Monotonieverhalten an der Stelle x = f () = 8 < 0 smf Das Monotonieverhalten kann sich nur an den Extremstellen und an den Rändern des Definitionbereich (Definitionslücken) ändern. Extremwerte und das Monotonieverhalten Extremwerte sind Hochpunkte (Maxima) bzw. Tiefpunkte (Minima) der Funktion. In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Zur Unterscheidung werden die Nullstellen in die Vorzeichentabelle eintragen. Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. (Hinreichende Bedingung) Hochpunkt (HP) Monotonoieverhalten ändert sich von streng monoton steigend (sms) nach streng monoton fallend (smf). Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus. x < x < x f (x) + 0 Graph sms HP smf Tiefpunkt (TP) Monotonoieverhalten ändert sich von streng monoton fallend (smf) nach streng monoton steigend (sms). Vorzeichenwechsel (VZW) der.ableitung f (x) von Minus nach Plus. x < x < x f (x) 0 + Graph smf TP sms Terrassenpunkt (TEP) Monotonoieverhalten ändert sich nicht. Kein Vorzeichenwechsel (VZW) der.ableitung. x < x < x f (x) Graph sms TEP sms x < x < x f (x) 0 Graph smf TEP smf Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. Funktion f (x) = x x. Ableitungen f (x) = x = (x + )(x ) f (x) = x = 0 x = 0 / + x = / : x = x = ± x = x = Vorzeichentabelle von f (x) x < < x < < x f (x) Graph sms HP smf T P sms Hochpunkt:(/) Tiefpunkt:(/ ) Monotonieverhalten x ] ; [ ]; [ f (x) > 0 sms x ] ; [ f (x) < 0 smf Funktion f (x) = x x. Ableitungen f (x) = x (x ) x (x ) = ( x x ) x (x ) = x x (x ) Zaehler = 0 x (x ) = 0 x = 0 x = 0 x = 0 / + x = x 0 = 0; -fache Nullstelle x = ; -fache Nullstelle Nullstellen des Nenners aus f(x) übernehmenx = f (x) x < 0 < x < < x < < x Graph smf T EP smf smf HP sms TEP(0/0) TP( / ) 8 Monotonieverhalten x ] ; 0[ ]0; [ ] ; [ f (x) < 0 smf x ] ; [ f (x) > 0 sms 8
9 Analysis Differentialrechnung Extremwerte und die.ableitung In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) > 0(LK) Tiefpunkt (Minimum) bei x 0 f (x 0 ) < 0(RK) Hochpunkt (Maximum) bei x 0 f (x 0 ) = 0 f (x 0 ) 0 Terrassenpunkt Funktion f (x) = x x. Ableitungen f (x) = x =. Ableitungen f (x) = x f (x) = x = 0 x = 0 / + x = / : (x + )(x ) x = x = ± x = x = f () = < 0 HP(/) f () = > 0 TP(/ ) Interaktive Inhalte: hier klicken.. Graph der. Ableitung Funktion f (x) = x, 5x HP sms smf sms HT Funktion f (x) = 0,5x x smf smf sms TP HT HT TP HT TEP Ableitung f (x) = x.5 Ableitung f (x) = x,5x (x ) f (x) > 0 NST TP f (x) < 0 f (x) > 0 NST f (x) < 0 HP+NST NST f (x) > 0 f (x) < 0 sms - streng monoton steigend; smf - streng monoton fallend; VZW - Vorzeichenwechsel; NST - Nullstelle ; HP - Hochpunkt (Maximum); TP - Tiefpunkt (Minimum) ; HT - horizontale Tangente; TEP - Terrassenpunkt; VA - vertikale Asymptote; HA - horizontale Asymptote; LK - Linkskrümmung; RK - Rechtskrümmung; WP - Wendepunkt; 9
10 Analysis Differentialrechnung Funktion -. Ableitung f (x) Funktion f(x) Ableitung f (x) Extremwert NST f (x) = 0 HT NST f (x) = 0 HP NST und VZW von + nach TP NST und VZW von nach + TEP WP sms smf NST ohne VZW Extremwert f (x) > 0 (positiv) f (x) < 0 (negativ) VA VA f (x) = ± x x 0 HA HA (x) = 0 x ± f (x) = x, 5x f (x) = x.5 f (x) f (x) Extremwert: x = NST x = HP:x = VZW von + nach - x = WP: x = 0 Extremwert: x = 0 sms: x < f(x) > 0 x < Interaktive Inhalte: Graph (JS) - Graph -... Ableitung - Krümmung - Wendepunkte f (x) = x x f (x) = x x LK RK WP(0/0) LK HT LK TEP(0/-) RK VZW - Vorzeichenwechsel; NST - Nullstelle ; HT - horizontale Tangente; TEP - Terrassenpunkt; VA - vertikale Asymptote; HA - horizontale Asymptote; LK - Linkskrümmung; RK - Rechtskrümmung; WP - Wendepunkt; Krümmung von f(x 0 ) an der Stelle x 0 Rechtskrümmung RK f (x) < 0 Linkskrümmung LK f (x) > 0 Das Krümmungsverhalten kann sich nur an den Nullstellen der. Ableitung und an den Rändern des Definitionbereichs (Definitionslücken) ändern. 0
11 Differentialrechnung Wendepunkte und das Krümmungsverhalten Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Zur Unterscheidung zwischen Wendepunkt und Flachpunkt werden die Nullstellen in die Vorzeichentabelle eintragen. (Hinreichende Bedingung) Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. Wendepunkt (WP) Das Krümmungsverhalten ändert sich von rechtsgekrümmt (RK) nach linksgekrümmt (LK) oder von linksgekrümmt nach rechtsgekrümmt. Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus oder von Minus nach Plus. x < x < x x < x < x f (x) + 0 f (x) 0 + Graph LK WP RK Graph RK WP LK Flachpunkt (FP) Krümmungsverhalten ändert sich nicht Kein Vorzeichenwechsel (VZW) der.ableitung x < x < x x < x < x f (x) f (x) 0 Graph LK FP LK Graph RK FP RK Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. Funktion f (x) = x x f (x) = x. Ableitungen f (x) = x f (x) = x = 0 x = 0 x < 0 < x f (x) 0 + Graph RK WP LK WP(0/0) x ]0; [ f (x) > 0 LK x ] ; 0[ f (x) < 0 RK Funktion f (x) = x f (x) == x x (x ). Ableitungen f (x) = (x x + )x (x ) Zähler =0 x(x x + ) = 0 x = 0 x x + = 0 x x + = 0 x / = + ± ( ) x / = + ± Diskriminante negativ keine Lösung x 9 = 0; -fache Nullstelle Nullstelle des Nenners aus f(x) übernehmen x 0 = ; -fache Nullstelle x < 0 < x < < x f (x) Graph RK WP LK RK WP(0/ ) kein WP x = x ] ; 0[ ]; [ f (x) > 0 LK x ]0; [ f (x) < 0 RK Wendepunkte und die.ableitung Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) 0 Wendepunkt Funktion f (x) = x x. Ableitungen f (x) = x =. Ableitungen f (x) = x. Ableitungen f (x) = f (x) = x = 0 x = 0 f (0) = 0 Wp(0/0) (x + )(x ) Interaktive Inhalte: hier klicken
12 Analysis Differentialrechnung..5 Graph der. Ableitung f (x) = x x f (x) = x x LK RK WP(0/0) LK HT LK TEP(0/-) RK. Ableitung f (x) = x. Ableitung f (x) = x x +x (x ) f (x) > 0 f (x) > 0 f (x) > 0 f (x) < 0 f (x) < 0 sms - streng monoton steigend; smf - streng monoton fallend; VZW - Vorzeichenwechsel; NST - Nullstelle ; HP - Hochpunkt (Maximum); TP - Tiefpunkt (Minimum) ; HT - horizontale Tangente; TEP - Terrassenpunkt; VA - vertikale Asymptote; HA - horizontale Asymptote; LK - Linkskrümmung; RK - Rechtskrümmung; WP - Wendepunkt; Funktion -. Ableitung f (x) Funktion f(x). Ableitung f (x) WP NST f (x) = 0 mit VZW LK f (x) > 0 RK f (x) < 0 TEP NST mit VZW VA VA HA HA Interaktive Inhalte: Graph (JS) - Graph -
13 Differentialrechnung.. Ableitung der Grundfunktionen Polynomfunktion f (x) = x n f (x) = nx n Die Ableitungen bildet man durch:exponent vorziehen und vom Exponenten abziehen f (x) = x f (x) = f (x) = ax n f (x) = nax n f (x) = ax f (x) = a Konstanter Faktor a bleibt erhalten f (x) = a f (x) = 0 (f(x) ± g(x)) = f (x) ± g (x) Bei Summen wird jeder Summand einzeln abgeleitet f (x) = x 5 f (x) = 5x 5 = 5x f (x) = 8x 5 f (x) = 8 5x 5 = 0x f (x) = x f (x) = f (x) = 5 f (x) = 0 f 5 (x) = x 5 + x + x + f 5 (x) = 5x + x + f 5 (x) = 0x + x Exponentialfunktion Basis e f (x) = e x f (x) = e x f (x) = ae x f (x) = ae x f (x) = ae x + b f (x) = ae x f (x) = e x + f (x) = e x Logarithmusfunktion Basis e f (x) = ln x f (x) = x f (x) = a ln x f (x) = a x f (x) = a ln x + b f (x) = a x f (x) = ln x + 5 f (x) = x Exponentialfunktion allgemein f (x) = a x f (x) = a x ln a f (x) = x f (x) = x ln Logarithmusfunktion allgemein f (x) = log a x f (x) = x ln a f (x) = log x f (x) = x ln Trigonometrische Funktionen f (x) = sin x f (x) = cos x f (x) = cos x f (x) = sin x f (x) = tan x f (x) = cos x f (x) = x + sin x f (x) = x + cos x Interaktive Inhalte: hier klicken..7 Ableitungsregeln Ableiten von Summen und Differenzen (f(x) ± g(x)) = f (x) ± g (x) f (x) = x 5 + x + x + f (x) = 5x + x + f (x) = 0x + x f (x) = x + sin x f (x) = x + cos x
14 Differentialrechnung Ableiten mit konstantem Faktor (c f(x)) = c f (x) f (x) = 5e x + ln x f (x) = 5e x + x f (x) = 5 cos x + sin x f (x) = 5 sin x + cos x Kettenregel (f(g(x))) = f (g(x)) g (x) äußere Funktion f() ableiten innere Funktion g(x) unabgeleitet abschreiben mit der Ableitung der inneren Funktion g(x) multiplizieren (nachdifferenzieren) f (x) = e x äußere Funktion: e (..) innnere Funktion: x f (x) = e x = e x f (x) = sin 5x äußere Funktion: sin(..) innnere Funktion: 5x f (x) = cos 5x 5 = 5 cos 5x f (x) = 5e x äußere Funktion: e innnere Funktion: x f (x) = 5e x 9x = 5x e x f (x) = (x x) 7 äußere Funktion: (...) 7 innnere Funktion: x x f (x) = 7(x x) (x ) = (x 7)(x x) Produktregel (f(x) g(x)) = f (x) g(x) + f(x) g (x). Faktor f(x) ableiten mal. Faktor g(x) unabgeleitet plus. Faktor f(x) unabgeleitet mal. Faktor g(x) abgeleitet f (x) = x e x f (x) = x e x + x e x f (x) = xe x ( + x) f (x) = (x x + ) e x f (x) = ( x ) e x + (x x + ) e x f (x) = e x (x + x x + ) f (x) = e x (x x ) Quotientenregel ( ) f(x) = f (x) g(x) f(x) g (x) g(x) (g(x)) Zähler f(x) ableiten mal Nenner g(x) unabgeleitet minus Zähler f(x) unabgeleitet mal Nenner g(x) abgeleitet durch Nenner g(x) im Quadrat f (x) = x f (x) = x (x ) x x (x ) f (x) = x (x x) x f (x) = x +x (x ) f (x) = x(x ) x f (x) = (x ) x f (x) = x + x
15 Differentialrechnung..8 Tangenten- und Normalengleichung Tangentengleichung Tangente an der Stelle x 0 : g(x) = f (x 0 )(x x 0 ) + f(x 0 ) oder y 0 = f(x 0 ) m t = f (x 0 ) Geradengleichung: y = m x + t m t, x 0, y 0 einsetzen und nach t auflösen t = y 0 m t x 0 m t, t einsetzen y = m t x + t Funktion f (x) = x f (x) = x Tangente an der Stelle x 0 = f( ) = f ( ) = g(x) = f (x 0)(x x 0) + f(x 0) g(x) = f ( )(x ) + f( ) g(x) = (x ) + g(x) = x + g(x) = x Normalengleichung Normale an der Stelle x 0 : g(x) = f (x 0 ) (x x 0) + f(x 0 ) oder y 0 = f(x 0 ) m t = f (x 0 ) Steigung der Normalen m n = m t Geradengleichung: y = m x + t m n, x 0, y 0 einsetzen und nach t auflösen Funktion f (x) = x f (x) = x Normale an der Stelle x 0 = f( ) = f ( ) = g(x) = f (x 0 (x x0) + f(x0) ) g(x) = (x ) + f( ) f ( ) g(x) = (x ) + g(x) = x + + g(x) = x + t = y 0 m n x 0 m n, t einsetzen y = m n x + t Interaktive Inhalte: Graph (JS) - Graph - hier klicken 5
16 Differentialrechnung..9 Newtonsches Iterationsverfahren Nullstelle einer Funktion mit dem Newtonsches Iterationsverfahren x n+ = x n f(x n) f (x n ) Startwert x 0 wählen x = x 0 f(x 0) f (x 0 ) x = x f(x ) f (x )... Funktion f (x) = x f (x) = x x n+ = x n f(xn) f (x n) Startwert: x 0 = f() = f () = x = f() f () x = x =, 5 f(, 5) = f (, 5) = x =, 5 f(, 5) f (, 5) x = x =, 05 f(, 05) = f (, 05) = x =, 05 x =, 05 x =, 00 f(, 05) f (, 05) Interaktive Inhalte: hier klicken
17 Integralrechnung. Integralrechnung.. Definition f (x) = 0, 5x +, 5x f (x) = x x A > 0 A > 0 A < 0 A < 0 Hauptsatz der Integralrechnung F (x) = f(x) Die Ableitung von F (x) ist f(x) F (x) ist Stammfunktion von f(x) Die Menge aller Stammfunktionen erhält man durch das Addieren einer Konstanten c. f (x) = ax n F (x) = n+ axn+ + c F (x) = x + F (x) = x F (x) ist Stammfunktion von f(x) = x F (x) = x + F (x) = x F (x) ist Stammfunktion von f(x) = x Die Menge aller Stammfunktionen von f(x) = x F (x) = x + c Unbestimmtes Integral F (x) = f (x) dx = F (x) + c Die Stammfunktion zu einer Funktion f(x) ist das unbestimmte Integral. f (x) = x F (x) = x dx = x+ + c F (x) = x + c F (x) = ( x + x + 5) dx = x + x + 5x + c 7
18 Integralrechnung Bestimmtes Integral Flächenbilanz A = b a f (x) dx = [F (x)] b a = F (b) F (a) A ist der Flächeninhalt unter einer Kurve der Funktion f(x) im Integrationsbereich von a bis b. Fläche oberhalb der x-achse A > 0 Fläche unterhalb der x-achse A < 0 Flächen unterhalb und oberhalb der x-achse Summe der Teilflächen Fläche zwischen dem Graphen und der x-achse - Nullstellen berechnen - Flächen zwischen den Nullstellen berechnen - Beträge der Flächen addieren Funktion f (x) = x + x Stammfunktion F (x) = x + x Fläche unterhalb der x-achse A < 0 0 ( A = x + ) [ x dx = x + ] 0 x = ( 0 + 0) ( () + ()) = (0) ( ) = Fläche oberhalb der x-achse A > 0 ( A = 0 x + ) [ x dx = x + ] x 0 = ( + ) ( 0 + 0) = ( ) (0) = Fläche unterhalb und oberhalb der x-achse Summe der Teilflächen (Flächenbilanz) ( A = x + ) [ x dx = x + ] x = ( + ) ( () + ()) = ( ) ( ) = A = A + A = ( ) + = f (x) = x x = x(x + )(x ) Nullstellen: x = x = 0 x = A = 0 ( x x ) dx = [ x x ] 0 = ( 0 0 ) ( () () ) = (0) () = A = 0 ( x x ) dx = [ x x ] ) = ( ) ( = () (0) = Fläche zwischen dem Graphen und der x-achse: A = A + A = + = 8 Integralfunktion F (x) = x k f (t) dt = [F (t)] x k = F (x) F (k) Jede Integralfunktion hat mindestens eine Nullstelle. F (k) = 0 F (x) = x ( t + t ) dt = [ t + t ] x = ( x + x ) ( () + () ) = x + x F () = 0 Interaktive Inhalte: hier klicken hier klicken.. Integration der Grundfunktionen Polynomfunktion F (x) = x n dx = n+ xn+ + c Zum Exponenten addieren, durch den Exponenten dividieren F (x) = x dx = x + c F (x) = ax n dx = a n+ xn+ + c Konstanter Faktor a bleibt erhalten F (x) = a dx = ax + c f(x) + g(x) dx = f(x) dx + g(x)dx Bei Summen wird jeder Summand einzeln integriert F (x) = dx = x + c F (x) = ( x + x + 5) dx = F (x) = x+ + x+ + 5x + c F (x) = x + x + 5x + c 8
19 Integralrechnung Exponentialfunktion Basis e F (x) = e x dx = e x + c F (x) = ae x dx = ae x + c F (x) = ae x + b dx = ae x + bx + c F (x) = e x + dx = e x + x + c Logarithmusfunktion Basis e F (x) = ln x dx = x ln x x + c F (x) = a ln x dx = a(x ln x x) + c F (x) = a ln x + b dx == a(x ln x x) + bx + c F (x) = 7 ln x + dx == 7(x ln x x) + x + c Rationale Funktion mit linearer Funktion im Nenner F (x) = x dx = ln x + c F (x) = F (x) = ax+b dx = a ln ax + b + c x+ dx = ln x + + c F (x) = dx = ln x + + c x+ Trigonometrische Funktionen F (x) = sin x dx = cos x + c F (x) = cos x dx = sin x + c Interaktive Inhalte: hier klicken.. Integrationsregeln Integration von Summen und Differenzen f(x)dx + g(x)dx = f(x) + g(x)dx Integration mit konstanten Faktor c f(x)dx = c f(x)dx Integration mit vertauschten Grenzen b f(x) dx = a a b f(x) dx Integrationsgrenzen zusammenfassen b f(x) dx + c f(x)dx = c a b a f(x) dx Ableitung des Nenners im Zähler f (x) f(x) dx = ln f(x) + c x x x +5 dx = ln x + c x +5x dx = ln x + 5x + c 9
20 Analysis Integralrechnung Innere Funktion ist abgeleiteter Faktor g (x)f(g(x)) dx = F (x) + c x(x ) dx = 5 (x ) 5 + c xe x dx = e x + c x sin(x ) dx = cos(x ) + c (x x)e x x dx = e x x + c Innere Funktion ist eine lineare Funktion f(ax + b) dx = a F (x) + c (x ) dx = (x 5 )5 + c = (x 0 )5 + c e x dx = ex + c cos(x ) dx = sin(x ) + c dx = ln 5x + + c 5x+ 5.. Graph der Stammfunktion Funktion f (x) = x.5 Funktion f (x) = x,5x (x ) f(x) > 0 f(x) > 0 NST NST TP f(x) < 0 f(x) < 0 HP+NST NST f(x) > 0 f(x) < 0 Stammfunktion F (x) = x, 5x + c HT HP sms smf sms NST NST F 0(x) = F (x) = x, 5x F (x) = x, 5x F (x) = x, 5x x, 5x + TP TP HT Stammfunktion F (x) = 0,5x x + c HT smf smf sms TP TEP F (x) = 0,5x x F (x) = 0,5x F 0(x) = 0,5x x + x F (x) = 0,5x x sms - streng monoton steigend; smf - streng monoton fallend; VZW - Vorzeichenwechsel; NST - Nullstelle ; HP - Hochpunkt (Maximum); TP - Tiefpunkt (Minimum) ; HT - horizontale Tangente; TEP - Terrassenpunkt; VA - vertikale Asymptote; HA - horizontale Asymptote; LK - Linkskrümmung; RK - Rechtskrümmung; WP - Wendepunkt; HT 0
21 Integralrechnung Zu jeder Funktion f(x) gibt es eine Menge von Stammfunktionen F(x), die um c in y-richtung verschoben sind. Funktion f(x) NST f(x) = 0 VZW von + nach VZW von nach + NST ohne VZW Extremwert f(x) > 0 (positiv) f(x) < 0 (negativ) Stammfunktion F (x) Extremwert (HT) HP TP TEP WP sms smf f (x) = x.5 F (x) = x.5 dx = x.5x + c F (x) = x, 5x + F (x) = x, 5x F (x) = x, 5x F 0(x) = x, 5x f (x) F (x) NST x = Extremwert: x = VZW von + nach - x = HP:x = Extremwert: x = 0 WP: x = 0 f(x) > 0 x < sms: x < Interaktive Inhalte: Graph (JS) - Graph -
22 Kurvendiskussion. Kurvendiskussion.. Ganzrationale Funktion f (x) =, 5 x + 5 x f (x) = (x ) f (x) = x + x + f (x) = 0, x(x + )(x ) f 5(x) = 0, 0(x + ) (x ) f (x) = (x + ) f 7(x) = 0, 05(x )(x ) f 8(x) = x (x ) Formen der Polynomfunktion - ganzrationalen Funktion Summendarstellung der Polynomfunktion f(x) = a n x n + a n x n + a n x n... + a x + a 0 oder f(x) = ax n + bx n + cx n... Die höchste Potenz (n) gibt den Grad der Polynomfunktion an. Produktdarstellung (faktorisierte Form) der Polynomfunktion Ist der Grad des Polynoms gleich der Anzahl der (reellen)nullstellen, kann man die Funktion in faktorisierter Form schreiben. f(x) = a(x x )(x x )(x x )... Nullstellen: x, x, x... Linearfaktoren: (x x ), (x x )... a=koeffizient der höchsten Potenz Grad : Lineare Funktion f(x) = ax + b Grad : Quadratische Funktion f(x) = ax + bx + c f(x) = a(x x )(x x ) Grad : Kubische Funktion f(x) = ax + bx + cx + d f(x) = a(x x )(x x )(x x ) Grad : Biquadratische Funktionen f(x) = ax + bx + cx + dx + e f(x) = a(x x )(x x )(x x )(x x ) Grad 5: f(x) = ax 5 + bx + cx + dx + ex + f f(x) = a(x x )(x x )(x x )(x x )(x x 5 ) Summen- in Produktdarstellung f (x) = x + 5x = x(x ) f (x) = x + x + = (x + ) (x ) f (x) = 0 x x = 0 5 x( 0 x ) = 0 5 x = 0 0 x = 0 5 x = x = Grad der Funktion = Anzahl der Nullstellen = Faktorisierte Form: f (x) = 0, x(x + )(x ) f 7(x) = 0 x x + = 0 5 u = x u = x 0 u u + = 0 5 u / = + ± ( ) u = u = x = x = ± x = x = x = x = ± x = x = Faktorisierte Form: f 7 (x) = (x + )(x )(x + )(x ) 0 Produkt- in Summendarstellung f (x) = (x )(x )(x ) = (x ) f (x) = x x x 8 f 5 (x) = 0, x(x + )(x ) = 0, x x 5 f (x) = (x + ) = x + x + x + x + f 7(x) = 0, 05(x )(x ) = 0, 05x x + 5 f 8(x) = x (x ) = x x
23 Kurvendiskussion Definitions- und Wertebereich Definitionsbereich D = R Wertebereich - höchster Exponent ungerade: W = R - höchster Exponent gerade: W = [absoluter Tiefpunkt; [ W =] ;absoluter Hochpunkt] f (x) = x + 5x absoluter Hochpunkt: (/5) höchster Exponent (gerade) D = R W =], 5[ f (x) = x + x + höchster Exponent (ungerade Zahl) D = R W = R f 5 (x) = 0, x x D = R W = R 5 f 7(x) = 0, 05x x + 5 absoluter Tiefpunkt aus der Kurvendiskussion D = R W = [, [ 5 Symmetrie Punktsymmetrie zum Ursprung: f ( x) = f (x) f (x) hat nur ungerade Exponenten Achsensymmetrie zur y-achse: f ( x) = f (x) f (x) hat nur gerade Exponenten f ( x) = ( x) + 5 ( x) keine Symmetrie zur y-achse und zum Ursprung f ( x) = ( x) + ( x) + keine Symmetrie zur y-achse und zum Ursprung f (x) = 0, x x 5 f ( x) = 0, ( x) ( x) 5 f ( x) = ( 0, x x) 5 f ( x) = f (x) Symmetrie zum Ursprung f 7(x) = 0, 05x x + 5 f 7 ( x) = 0 ( x) ( x) + 5 f 7 ( x) = 0 x x + 5 f 7 ( x) = f (x) Symmetrie zur y-achse
24 Kurvendiskussion Schnittpunkte mit der x-achse - Nullstellen Funktionsterm gleich Null setzen und die Gleichung lösen. ( siehe Algebra-Gleichungen) f (x) = 0 ax n + bx n + cx n... = 0 höchster Exponent ungerade Anzahl der Nullstellen Grad des Polynoms höchster Exponent gerade 0 Anzahl der Nullstellen Grad des Polynoms Faktorisierte Polynomfunktion Nullstellen aus faktorisierten Polynom ablesen. a(x x )(x x )(x x )... = 0 Nullstellen: x, x, x... Nullstellen aus faktorisierten Polynom ablesen. f (x) = (x ) x = -fache Nullstelle f 5(x) = 0, 0(x + ) (x ) x = -fache Nullstelle x = -fache Nullstelle Funktionsterm gleich Null setzen. f (x) = x + 5x = 0 x( x + 5) = 0 x = 0 x + 5 = 0 x + 5 = 0 x = x = 0 x = Faktorisierte Form: f (x) = x(x ) f (x) = x + x + = 0 Nullstelle für Polynmomdivision erraten:x = ( x +x + ) : (x + ) = x + x + ( x x ) x +x + (x +x) x + (x +) 0 x + x + = 0 x / = ± ( ) x = x = ( ) Faktorisierte Form: f (x) = (x + ) (x ) f (x) = 0 x x = 0 5 x( 0 x ) = 0 5 x = 0 x = x = 0 x = 0 5 Grad der Funktion = Anzahl der Nullstellen = Faktorisierte Form: f 5 (x) = 0, x(x + )(x ) f 7(x) = 0 x x + = 0 5 u = x u = x 0 u u + = 0 5 u / = + ± ( ) u = u = x = x = ± x = x = x = x = ± x = x = Faktorisierte Form: f 7 (x) = (x + )(x )(x + )(x ) 0
25 Kurvendiskussion Graph oberhalb/unterhalb der x-achse Bei ganzrationalen Funktionen kann sich das Vorzeichen nur an den Nullstellen ändern. Einen beliebigen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen des Funktionswerts in die Tabelle eintragen. Vorzeichentabelle mit f(x) x < x < x f(x) + 0 Graph oberhalb 0 unterhalb + f(x)>0 Graph oberhalb der x-achse - f(x)<0 Graph unterhalb der x-achse f (x) = x + 5x x < 0 < x < < x f(x) x ]0; [ f(x) > 0 oberhalb der x-achse x ] ; 0[ ]; [ f(x) < 0 unterhalb der x-achse f (x) = x + x + x < < x < < x f(x) x ] ; [ ] ; [ f(x) > 0 oberhalb der x-achse x ]; [ f(x) < 0 unterhalb der x-achse Faktorisierte Form: f 5 (x) = 0, x(x + )(x ) Nullstellen:x = 0 x = x = 5 < f 5( 5) =, 5 x < < x < 0 < x < < x f(x) x ] ; 0[ ]; [ f(x) > 0 oberhalb der x-achse x ] ; [ ]0; [ f(x) < 0 unterhalb der x-achse Grenzwert - Verhalten im Unendlichen f(x) = a n x n + a n x n + a n x n... + a x + a 0 f(x) = ± f(x) = ± x Das Vorzeichen des Glieds mit der höchsten Potenz und der Grad des Polynoms bestimmen das Vorzeichen des Grenzwerts. Grenzwert gegen plus Unendlich a n Grad Grenzwert + gerade an n = + ungerade an n = - gerade an n = - ungerade an n = Grenzwert gegen minus Unendlich a n Grad Grenzwert + gerade x an ( )n = + ungerade x an ( )n = - gerade x an ( )n = - ungerade x an ( )n = f (x) = x + 5x Glied mit der höchsten Potenz: x f (x) = [ ] = x f (x) = [ ( ) ] = f (x) = x + x + Glied mit der höchsten Potenz: x f (x) = [ ] = x f (x) = [ ( ) ] = 5
26 Kurvendiskussion Ableitung f(x) = a n x n + a n x n... + a x + a x + a 0 Die Ableitungen bildet man durch: Exponent vorziehen und vom Exponenten abziehen. Die erste Ableitung f (x) gibt die Steigung der Funktion an der Stelle x an. Die zweite Ableitung f (x) gibt die Krümmung der Funktion an der Stelle x an. f (x) = x + 5x = x(x ) f (x) = x + 5 f (x) = f (x) = 0 f (x) = x + x + = (x + ) (x ) f (x) = x + = (x + )(x ) f (x) = x = x f (x) = f (x) = a n n x n +a n (n ) x n...+a x +a f (x) = ax n f (x) = nax n Grad : Lineare Funktion f(x) = ax + b f (x) = a Grad : Quadratische Funktion f(x) = ax + bx + c f (x) = ax + b Grad : Kubische Funktion f(x) = ax + bx + cx + d f (x) = ax + bx + c Grad : Biquadratische Funktionen f(x) = ax + bx + cx + dx + e f (x) = ax + bx + cx + d Extremwerte und die.ableitung In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) > 0(LK) Tiefpunkt (Minimum) bei x 0 f (x 0 ) < 0(RK) Hochpunkt (Maximum) bei x 0 f (x 0 ) = 0 f (x 0 ) 0 Terrassenpunkt f (x) = x + 5 = 0 x + 5 = 0 / 5 x = 5 / : ( ) x = 5 x = f () < 0 Hochpunkt: (/5) f (x) = x + = 0 x + = 0 / x = / : ( ) x = x = ± x = x = f ( ) = > 0 Tiefpunkt: ( /0) f () = f () < 0 Hochpunkt: (/)
27 Kurvendiskussion Extremwerte und das Monotonieverhalten Extremwerte sind Hochpunkte (Maxima) bzw. Tiefpunkte (Minima) der Funktion. In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Zur Unterscheidung werden die Nullstellen in die Vorzeichentabelle eintragen. Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. (Hinreichende Bedingung) Hochpunkt (HP) Monotonoieverhalten ändert sich von streng monoton steigend (sms) nach streng monoton fallend (smf). Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus. x < x < x f (x) + 0 Graph sms HP smf Tiefpunkt (TP) Monotonoieverhalten ändert sich von streng monoton fallend (smf) nach streng monoton steigend (sms). Vorzeichenwechsel (VZW) der.ableitung f (x) von Minus nach Plus. x < x < x f (x) 0 + Graph smf TP sms f (x) = x + 5 x < < x f (x) + 0 streng monoton steigend x ] ; [ f (x) > 0 streng monoton fallend x ]; [ f (x) < 0 f (x) = x + x < < x < < x f (x) streng monoton steigend x ] ; [ f (x) > 0 streng monoton fallend x ] ; [ ]; [ f (x) < 0 Terrassenpunkt (TEP) Monotonoieverhalten ändert sich nicht. Kein Vorzeichenwechsel (VZW) der.ableitung. x < x < x x < x < x f (x) f (x) 0 Graph sms TEP sms Graph smf TEP smf Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. Wendepunkte und.ableitung Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) 0 Wendepunkt f (x) = 0 kein Wendepunkt f (x) = x = 0 x = 0 f (0) = f (0) 0 Wendepunkt: (0/) 7
28 Kurvendiskussion Wendepunkte und das Krümmungsverhalten Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Zur Unterscheidung zwischen Wendepunkt und Flachpunkt werden die Nullstellen in die Vorzeichentabelle eintragen. (Hinreichende Bedingung) Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. Wendepunkt (WP) Das Krümmungsverhalten ändert sich von rechtsgekrümmt (RK) nach linksgekrümmt (LK) oder von linksgekrümmt nach rechtsgekrümmt. Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus oder von Minus nach Plus. x < x < x x < x < x f (x) + 0 f (x) 0 + Graph LK WP RK Graph RK WP LK Flachpunkt (FP) Krümmungsverhalten ändert sich nicht Kein Vorzeichenwechsel (VZW) der.ableitung x < x < x x < x < x f (x) f (x) 0 Graph LK FP LK Graph RK FP RK Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. f (x) = x x < 0 < x f (x) + 0 x ] ; 0[ f (x) > 0 linksgekrümmt x ]0; [ f (x) < 0 rechtsgekrümmt Stammfunktion von f(x) Stammfunktionen bildet man durch: zum Exponent addieren, durch den Exponenten dividieren. f (x) = ax n F (x) = n+ axn+ + c Unbestimmtes Integral: F (x) = f (x) dx = F (x) + c F (x) = ( x + 5x)dx = 5 x + x + c F (x) = ( x + x + ) dx = x + x + x + c Bestimmtes Integral A = x x f (x) dx = [F (x)] x x = F (x ) F (x ) A = ( 0 x + 5x ) dx = [ 5 x + x] 0 = ( 5 + ) ( ) = ( ) (0) = A = ( x + x + ) dx = [ x + x + x ] = ( + + ) ( ( ) + ( ) + ( ) ) = () ( ) = Interaktive Inhalte: Graph (JS) - Graph - Kurvendiskussion - 8
29 Kurvendiskussion.. Gebrochenrationale Funktion f (x) = x + x = x = f (x) = x +x+ x f (x) = x x x =, 5 y = 0 y = x = y = x + Formen der gebrochenrationalen Funktion Summendarstellung der gebrochenrationale Funktion f(x) = Z(x) N(x) = a nx n + a n x n + a n x n... + a x + a x + a 0 b m x m + b m x m + b m x m... + b x + b x + b 0 Zählerpolynom vom Grad n Z(x) = a n x n +a n x n +a n x n...+a x +a x +a 0 Nennerpolynom vom Grad m: N(x) = b m x m + b m x m + b m x m... + b x + b x + b 0 f (x) = x + x + x Zählerpolynom:Z(x) = x + x + Zählergrad: Nennerpolynom:N(x) = x Nennergrad: Faktorisierte Form: f (x) = (x+) (x+)(x) f (x) = x x Funktion nach der Polynomdivision: f (x) = x + + x Produktdarstellung (faktorisierte Form) der gebrochenrationale Funktion f(x) = a (x z )(x z )(x z )... (x n )(x n )(x n )... z, z, z... Nullstellen des Zählers n, n, n... Nullstellen des Nenners Definitions- und Wertebereich Definitionsbereich: Nullstellen des Nennerpolynoms ausschließen. Nennerpolynom: N(x) = 0 n, n, n... Nullstellen des Nenners (Definitionslücken) D = R \ {n 0, n, n..} (siehe Algebra - Gleichungen) Wertebereich: Bestimmung nur nach Kurvendiskussion möglich. f (x) = (x + ) D = R \ {} f (x) = x + x + x Nenner Null setzen x = 0 x = 0 / + x = ± x = x = D = R \ {; } Symmetrie Punktsymmetrie zum Ursprung: f ( x) = f (x) Achsensymmetrie zur y-achse: f ( x) = f (x) 9
30 Kurvendiskussion Schnittpunkte mit der x-achse - Nullstellen Zählerpolynom gleich Null setzen. Zählerpolynom: Z(x) = 0 z, z, z... Nullstellen des Zählers (siehe Algebra - Gleichungen) f (x) = x + x + x Zählerpolynom gleich Null setzen: x + x + = 0 x / = ± x / = ± 0 x = x = x = ; -fache Nullstelle Verhalten im Unendlichen - Grenzwert - Asymptoten Zählergrad>Nennergrad f(x) = ± x f(x) = ± Das Vorzeichen der Glieder mit der höchsten Potenzen und der Grad der höchsten Exponenten, bestimmen das Vorzeichen des Grenzwerts. Grenzwert gegen plus Unendlich a n b m ( )n ( ) = ± m Grenzwert gegen minus Unendlich a n x b m ( )n ( ) = ± m Zählergrad=Nennergrad+ x ± f (x) = ± Polynomdivision - schiefe Asymptote Zählergrad=Nennergrad f (x) = a n x ± b m horizontale Asymptote y = a n b m Zählergrad<Nennergrad f (x) = 0 x ± horizontale Asymptote y = 0 Zählergrad < Nennergrad x ± x + = 0 Horizontale Asymptote: y = 0 Zählergrad = Nennergrad x + x + = x = Horizontale Asymptote: y = x ± Zählergrad = Nennergrad+ f (x) = x x ( ) = ( ) x oder ( ) = ( ) x ( x ) x( = x ) x x ( x ) = x( x ) P olynomdivision : (x ) : (x ) = x + (x x) x ( x ) f (x) = x + + x Schiefe Asymptote: y = x + 0
31 Kurvendiskussion Verhalten an den Definitionslücken - Grenzwert - Asymptoten D = R \ {x 0, x..} x 0, x.. sind Definitionslücken von f(x) f(x) = x x 0 Vertikale Asymptote: x = x 0 x + (x + ) = x (x + ) = Vertikale Asymptote (Polstelle): x = (x + ) x + (x + )(x ) = (x + ) x (x + )(x ) = Vertikale Asymptote (Polstelle): x = (x + ) x + (x + )(x ) = (x + ) x (x + )(x ) = Vertikale Asymptote (Polstelle): x = Ableitung Die Ableitungen bildet man durch die Quotientenregel, f (x) = Z (x) N(x) Z(x) N (x) (N(x)) Die erste Ableitung f (x) gibt die Steigung der Funktion an der Stelle x an. Die zweite Ableitung f (x) gibt die Krümmung der Funktion an der Stelle x an. f (x) = 0 (x+) (x+) = 0 (x+) = (x+) = (x+) f (x) = 0 (x +x+) ( ) (x+) (x +x+) = 0 (x) (x +x+) x+ = (x +x+) x+ (x +x+) = (x + ) = (x + ) = (x + ) f (x) = x +x+ x f (x) = (x+) (x ) (x +x+) x (x ) = (x +x 8x 8) (x +x +x) (x ) = x 0x 8 (x ) Extremwerte und die. Ableitung In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) > 0(LK) Tiefpunkt (Minimum) bei x 0 f (x 0 ) < 0(RK) Hochpunkt (Maximum) bei x 0 f (x 0 ) = 0 f (x 0 ) 0 Terrassenpunkt f (x) = x 0x 8 x 8x + = 0 x 0x 8 = 0 x / = +0 ± ( 0) () ( 8) () x / = +0 ± x / = 0 ± x = 0 + x = 0 x = x = f () = > 0 Tiefpunkt: (/ ) f ( ) = f ( ) < 0 Hochpunkt: ( /0)
32 Kurvendiskussion Extremwerte und das Monotonieverhalten Extremwerte sind Hochpunkte (Maxima) bzw. Tiefpunkte (Minima) der Funktion. In den Extremwerten hat f(x) eine horizontale Tangente (HT). f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). In diesen Nullstellen (x 0, x..) kann die Funktion einen Hochpunkt, Tiefpunkt oder Terrassenpunkt (Sattelpunkt) besitzen. Zur Unterscheidung werden die Nullstellen in die Vorzeichentabelle eintragen. Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. (Hinreichende Bedingung) Hochpunkt (HP) Monotonoieverhalten ändert sich von streng monoton steigend (sms) nach streng monoton fallend (smf). Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus. x < x < x f (x) + 0 Graph sms HP smf Tiefpunkt (TP) Monotonoieverhalten ändert sich von streng monoton fallend (smf) nach streng monoton steigend (sms). Vorzeichenwechsel (VZW) der.ableitung f (x) von Minus nach Plus. x < x < x f (x) 0 + Graph smf TP sms (x+) f (x) = Zaehler = 0 keine Lösung Nullstellen des Nenners aus f(x) übernehmen x = ; -fache Nullstelle x < < x f (x) 0 x ] ; [ ] ; [f (x) < 0 smf Terrassenpunkt (TEP) Monotonoieverhalten ändert sich nicht. Kein Vorzeichenwechsel (VZW) der.ableitung. x < x < x x < x < x f (x) f (x) 0 Graph sms TEP sms Graph smf TEP smf Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. Wendepunkt und die.ableitung Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Einsetzen der Nullstellen x 0, x.. in die. Ableitung (Hinreichende Bedingung) f (x 0 ) 0 Wendepunkt
33 Kurvendiskussion Wendepunkte und das Krümmungsverhalten Im Wendepunkt und im Flachpunkt ist das Krümmungsverhalten gleich Null. f (x) = 0 (Notwendige Bedingung) Die Nullstellen der. Ableitung bestimmen (x 0, x..). Zur Unterscheidung zwischen Wendepunkt und Flachpunkt werden die Nullstellen in die Vorzeichentabelle eintragen. (Hinreichende Bedingung) Einen Wert kleiner bzw. größer als die Nullstelle wählen und das Vorzeichen von f (x) in die Tabelle eintragen. Wendepunkt (WP) Das Krümmungsverhalten ändert sich von rechtsgekrümmt (RK) nach linksgekrümmt (LK) oder von linksgekrümmt nach rechtsgekrümmt. Vorzeichenwechsel (VZW) der.ableitung f (x) von Plus nach Minus oder von Minus nach Plus. x < x < x x < x < x f (x) + 0 f (x) 0 + Graph LK WP RK Graph RK WP LK Flachpunkt (FP) Krümmungsverhalten ändert sich nicht Kein Vorzeichenwechsel (VZW) der.ableitung x < x < x x < x < x f (x) f (x) 0 Graph LK FP LK Graph RK FP RK Die Ränder des Definitionsbereichs (Definitionslücken) müssen in die Tabelle mit eingetragen werden. Kruemmung f (x) = (x + ) Zaehler = 0 keine Lösung Nullstelle des Nenners aus f(x) übernehmen x = ; -fache Nullstelle x < < x f (x) 0 + x ] ; [ f (x) > 0 linksgekrümmt x ] ; [ f (x) < 0 rechtsgekrümmt Interaktive Inhalte: Graph (JS) - Graph - Kurvendiskussion -.. Exponentialfunktion (Basis e) y = y = 0 y = y = y = 0 f (x) = e x f (x) = e x+ f (x) = e x + f (x) = e x f 5(x) = e x + Formen der Exponentialfunktion Exponentialfunktion f(x) = e x Allgemeine Exponentialfunktion f(x) = ae b(x c) + d (siehe Funktionen - Exponentialfunktion) f (x) = e x+ f (x) = e x f 5(x) = e x +
34 Kurvendiskussion Definitions- und Wertebereich f(x) = e x D = R W = R + f(x) = ae b(x c) + d D = R a > 0 W = [d; [ a < 0 W =] ; d] f (x) = e x+ D = R W = [; [ f (x) = e x D = R R + f 5(x) = e x + D = R W =] ; ] Schnittpunkte mit der x-achse - Nullstellen f(x) = e x f(x) = ae (b(x c)) + d ae b(x c) + d = 0 ae b(x c) = d e b(x c) = d a d a > 0 b(x c) = ln x = ln ( ) d a b d a e x > 0 keine Nullstellen / : a / ln ( ) d a + c / d 0 keine Nullstellen / : b / + c f (x) = e x+ e (x+) = 0 e (x+) = 0 / + e (x+) = + / : e (x+) = / ln x + = ln () / x = f (x) = e x + e x + = 0 / e x = < 0 keine Nullstellen Grenzwert - Asymptoten f(x) = e x ex = + x ex = 0 horizontale Asymptote y=0 f(x) = ae b(x c) + d aeb(x c) + d Schrittweise Berechnung für b > 0 und a > 0: b( c) = e = a +d = b( c) = x x e = 0 a 0 + d = d HA: y = d a b Grenzwert + Asymptote + + aeb(x c) + d = keine - + aeb(x c) + d = keine + - aeb(x c) + d = d y = d - - aeb(x c) + d = d y = d a b Grenzwert Asymptote + + x aeb(x c) + d = d - + x aeb(x c) + d = d + - x aeb(x c) + d = - - x aeb(x c) + d = y = d y = d keine keine f (x) = e x+ ex+ + = ex+ = x ex+ e = x 0 = x ex+ = ( + ) = HA : y = f (x) = e x e x = 0 HA : y = 0 x e x = + f 5(x) = e x + e x + = HA : y = x e x + = + = x e = 0 Ableitung f (x) = e x f (x) = e x f (x) = e x Ableitung mit der Kettenregel f (x) = e bx f (x) = be bx f (x) = b e bx f (x) = ae b(x c) + d f (x) = a be b(x c) f (x) = a b e b(x c) f (x) = e x+ f (x) = e x+ f (x) = e x+ f (x) = e x f (x) = e x f (x) = e x f 5(x) = e x + f 5(x) = e x f (x) = e x + f (x) = e x f (x) = e x
35 Kurvendiskussion Monotonieverhalten f (x) = e x f (x) = e x e x > 0 streng monoton steigend f(x) = ae b(x c) + d f (x) = a be b(x c) e b(x c) > 0 a b > 0 streng monoton steigend (sms) a b < 0 streng monoton fallend (smf) a b Monotonieverhalten + + sms - + smf + - smf - - sms f (x) = e x+ > 0 sms f (x) = e x < 0 smf f 5(x) = e x > 0 sms f (x) = e x > 0 sms Ableitung f (x) = e x f (x) = e x Ableitung mit Kettenregel f (x) = e ax f (x) = ae ax f (x) = ae b(x c) + d f (x) = a be b(x c) f (x) = e x+ f (x) = e x+ f (x) = e x f (x) = e x f 5(x) = e x + f 5(x) = e x Krümmungsverhalten f (x) = e x f (x) = e x e x > 0 linksgekrümmt (LK) f(x) = ae b(x c) + d f (x) = a b e b(x c) e b(x c) > 0 a > 0 linksgekrümmt (LK) a < 0 rechtsgekrümmt (RK) f f f (x) = e x+ > 0 LK (x) = e x > 0 LK 5 (x) = e x < 0 RK f (x) = e x > 0 LK Stammfunktion von f(x) - unbestimmtes Integral f (x) = e x F (x) = e x + k f (x) = ae b(x c) F (x) = a b eb(x c) + k f (x) = e x+ F (x) = e x+ x + c f (x) = e x F (x) = e x + c f 5(x) = e x + F 5(x) = e x + x + c f (x) = e x + F (x) = e x + x + c = e x + x + c Interaktive Inhalte: Graph (JS) - Graph - 5
36 Kurvendiskussion.. Logarithmusfunktion (Basis e) x = x = 0 x = 0 x = f (x) = ln(x) f (x) = ln(x) + f (x) = ln(x + ) + f (x) = ln( x) + f 5(x) = ln(x ) + f (x) = 0, 5 ln(x + ) Formen der Logarithmusfunktion Logarithmusfunktion f(x) = ln x Allgemeine Logarithmusfunktion f(x) = a ln(b(x c)) + d (siehe Funktionen - Logarithmusfunktion) f (x) = ln(x) f (x) = ln(x) + f (x) = ln(x + ) + f (x) = ln( x) + f 5(x) = ln(x ) + f (x) = 0, 5 ln(x + ) Definitions- und Wertebereich f(x) = ln x W = R D = R + f(x) = a ln b(x c) + d W = R Definitionsbereich: bx c > 0 b > 0 D =]c; [ b < 0 D =] ; c[ f (x) = ln(x) D = R + f (x) = ln(x) + D = R + f (x) = ln(x + ) + D =] ; [ f (x) = ln( x) + D = R f 5(x) = ln(x ) + D =]; [ f (x) = 0, 5 ln(x + ) D =] ; [ Schnittpunkte mit der x-achse - Nullstellen f(x) = ln(x) ln(x) = 0 /e x = e 0 x = f(x) = a ln(b(x c)) + d a ln(b(x c)) + d = 0 / d a ln(b(x c)) = d / : a ln(b(x c)) = d /e a b(x c) = e ( d a ) / : b / + c d e( a ) x = + c b f (x) = ln(x + ) + ln (x + ) + = 0 ln (x + ) + = 0 / ln (x + ) = /e.. x + = e / x = e x =, 95 f (x) = 0, 5 ln(x + ) ln (x + ) = 0 ln (x + ) = 0 / + ln (x + ) = + / : ln (x + ) = /e.. x + = e / x = e x =, 98
37 Kurvendiskussion Grenzwert - Asymptoten f(x) = ln(x) ln(x) = vertikale Asymptote: x = 0 x 0 + ln(x) = f(x) = a ln(b(x c)) + d Schrittweise Berechnung für b > 0 und a > 0: b( c) = ln = b(c+ c) = 0 + ln 0+ = x c + x 0 + a ( ) + d = VA: x = c + x 0 a b Grenzwert ± Asymptote keine + + a ln b(x c) + d = - + a ln b(x c) + d = + - a ln b(x c) + d = x - - a ln b(x c) + d = x a + d = a b Grenzwert c Asymptote x + + a ln b(x c) + d = x c a ln b(x c) + d = x c a ln b(x c) + d = x c - - a ln b(x c) + d = x c = c = c = c = c f 5(x) = ln(x ) + D =]; [ ln(x ) + = ln = ln(x ) + = ln(x ) + x + ) = 0 + x +(+ ( ) = x + ln 0+ = x + ln(x ) + = V A : x = x + f (x) = ln( x) + D = R ln( x) + = x ln( x) + = V A : x = 0 x 0 + = Ableitung f (x) = ln(x) f (x) = x = x f (x) = x = x Ketten- und Quotientenregel : f (x) = ln bx f (x) = x = x f (x) = b bx = x f (x) = a ln(b(x c)) + d f (x) = a b b(x c) f a b (x) = (b(x c)) f (x) = ln(x) + f (x) = x = x f (x) = x = x f (x) = ln(x + ) + f (x) = = (x + ) x + f (x) = (x + ) = (x + ) f (x) = ln( x) + f (x) = x = x f (x) = x = x f 5(x) = ln(x ) + f 5 (x) = = (x ) (x ) f 5 (x) = (x ) = (x ) Monotonieverhalten f (x) = ln(x) f (x) = x = x streng monoton steigend D = R+ x f (x) = a ln(b(x c)) + d f (x) = a b b(x c) b(x c) > 0 a b Monotonieverhalten + + sms - + smf + - smf - - sms f (x) = x > 0 sms f (x) = x + > 0 sms f 5 (x) = (x ) < 0 smf 7
38 Kurvendiskussion Krümmungsverhalten f (x) = ln(x) x f (x) = x = x < 0 rechtsgekrümmt (RK) f (x) = a ln(b(x c)) + d f (x) = (b(x c)) > 0 a > 0 rechtsgekrümmt (RK) a < 0 linkssgekrümmt (LK) a b (b(x c)) f (x) = x = x < 0 RK f (x) = (x + ) = (x + ) < 0 RK f 5 (x) = (x ) = (x ) > 0 LK Stammfunktion von f(x) - unbestimmtes Integral f (x) = ln(x) F (x) = x ln(x) x + c Interaktive Inhalte: Graph (JS) - Graph - 8
Kurvendiskussion Ganzrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Gebrochenrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Gebrochenrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 7. September 0 Inhaltsverzeichnis Gebrochenrationale Funktion Gebrochen rationale Funktion Zählergrad < Nennergrad
Kurvendiskussion Gebrochenrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 7. September 0 Inhaltsverzeichnis Gebrochenrationale Funktion Gebrochen rationale Funktion Zählergrad < Nennergrad
2 x = 4. f(x) = ± f(x) = 1. x = x 0. (x 4) (x + 2)(x 4) x 4 + f(x) 1 6. x 2 + (x + 2)(x 4) = 3, , (x 4) (x + 2)(x 4) =
 (x ) f (x) = (x + )(x ) f (x) = (x ) + f (x) = e x + x = x = y = 0 y = x = f(x) = a f(x) = a x x 0 x x < 0 f(x) = a f(x) = a x x + 0 x x > 0 = f(x) = f(x) = a x x 0 x x + 0 f(x) = a x x 0 f(x) = ± x x
(x ) f (x) = (x + )(x ) f (x) = (x ) + f (x) = e x + x = x = y = 0 y = x = f(x) = a f(x) = a x x 0 x x < 0 f(x) = a f(x) = a x x + 0 x x > 0 = f(x) = f(x) = a x x 0 x x + 0 f(x) = a x x 0 f(x) = ± x x
Zusammenfassung der Kurvendiskussion
 Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
GF MA Differentialrechnung A2
 Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen
 Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
GRENZWERTE BEI GEBROCHENRATIONALEN FUNKTIONEN
 GRENZWERTE BEI GEBROCHENRATIONALEN FUNKTIONEN Graph von f mit Epsilonstreifen und Asymptoten.5.5 y-achse 0.5 6 0 8 6 0 6 8 0 6 0.5.5 -Achse Inhaltsverzeichnis Kapitel Inhalt Seite Einführung Der Grenzwertbegriff.
GRENZWERTE BEI GEBROCHENRATIONALEN FUNKTIONEN Graph von f mit Epsilonstreifen und Asymptoten.5.5 y-achse 0.5 6 0 8 6 0 6 8 0 6 0.5.5 -Achse Inhaltsverzeichnis Kapitel Inhalt Seite Einführung Der Grenzwertbegriff.
Die gebrochenrationale Funktion
 Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Aufgaben für Analysis in der Oberstufe. Robert Rothhardt
 Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
1 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 11
 Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Inhalt A Differenzialrechnung 8 Grundlagen 8 Funktionen 8 Differenzenquotient und Änderungsrate 9 Ableitung 2 Ableitungsregeln 2 Potenzregel 2 Konstantenregel 3 Summenregel 4 Produktregel 4 Quotientenregel
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
LÖSUNGEN Kurvendiskussion
 M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
(Unvollständige) Zusammenfassung Analysis Grundkurs
 (Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
(Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
Grundfunktion Wendepunkt Extrempunkt Nullstelle 1. Ableitung Extrempunkt Nullstelle - 2. Ableitung Nullstelle - -
 KURVENDISKUSSION Vorüberlegungen Die Kurvendiskussion ist ein wichtiges Teilgebiet der Mathematik, das speziell für die Matura von großer Bedeutung ist. Dabei untersucht man einen Graphen auf dessen geometrische
KURVENDISKUSSION Vorüberlegungen Die Kurvendiskussion ist ein wichtiges Teilgebiet der Mathematik, das speziell für die Matura von großer Bedeutung ist. Dabei untersucht man einen Graphen auf dessen geometrische
Gebrochen-rationale Funktionen
 Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
Mathematik Abitur Zusammenfassung Marius Buila
 Mathematik Abitur Zusammenfassung Marius Buila 1.Analysis 1.1 Grundlagen: Ableitung f (u) ist Steigung in Punkt P (u/f(u)) auf K f(x) = a * x r f (x) = a * r * x r-1 Tangentengleichung: y= f (u) * (x-u)
Mathematik Abitur Zusammenfassung Marius Buila 1.Analysis 1.1 Grundlagen: Ableitung f (u) ist Steigung in Punkt P (u/f(u)) auf K f(x) = a * x r f (x) = a * r * x r-1 Tangentengleichung: y= f (u) * (x-u)
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I
 Michael Buhlmann Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I Einleitung: Eine gebrochen rationale Funktion (Polynom) f: D f -> R (mit maximaler Definitionsbereich D f)
Michael Buhlmann Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I Einleitung: Eine gebrochen rationale Funktion (Polynom) f: D f -> R (mit maximaler Definitionsbereich D f)
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Lösungshinweise und Tipps Die Lösungshinweise beziehen sich auf die konkrete Aufgabenstellung, während die von Fall zu Fall beigefügten
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Lösungshinweise und Tipps Die Lösungshinweise beziehen sich auf die konkrete Aufgabenstellung, während die von Fall zu Fall beigefügten
Oberstufenmathematik leicht gemacht
 Peter Dörsam Oberstufenmathematik leicht gemacht Band 1: Differential- und Integralrechnung 5. überarbeitete Auflage mit zahlreichen Abbildungen und Beispielaufgaben PD-Verlag Heidenau Inhaltsverzeichnis
Peter Dörsam Oberstufenmathematik leicht gemacht Band 1: Differential- und Integralrechnung 5. überarbeitete Auflage mit zahlreichen Abbildungen und Beispielaufgaben PD-Verlag Heidenau Inhaltsverzeichnis
Gebrochenrationale Funktionen Ü bungsaufgaben vor Kurzarbeit
 Gebrochenrationale Funktionen Ü bungsaufgaben vor Kurzarbeit Diskutieren Sie die Funktionen: a.) f(x) = 1 + x 5 x 2 1 b.) f(x) = x 4 + 5 x+2 c.) f(x) = x3 +2x 2 +x+2 x+2 Lösung: a.) An der Summenform des
Gebrochenrationale Funktionen Ü bungsaufgaben vor Kurzarbeit Diskutieren Sie die Funktionen: a.) f(x) = 1 + x 5 x 2 1 b.) f(x) = x 4 + 5 x+2 c.) f(x) = x3 +2x 2 +x+2 x+2 Lösung: a.) An der Summenform des
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 12. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
Übungsaufgaben zur Kurvendiskussion
 SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf. SBP Mathe Grundkurs 2
 SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
5 Gebrochen-rationale Funktionen
 5 Gebrochen-rationale Funktionen 5. Definition: Eine Funktion f, deren Term f(x) als Bruch Z(x) N(x) von zwei Polynomfunktion Z(x) und N(x) geschrieben werden kann und deren Nennergrad größer als 0 ist,
5 Gebrochen-rationale Funktionen 5. Definition: Eine Funktion f, deren Term f(x) als Bruch Z(x) N(x) von zwei Polynomfunktion Z(x) und N(x) geschrieben werden kann und deren Nennergrad größer als 0 ist,
Aufgaben zur e- und ln-funktion
 Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
Diskussion einzelner Funktionen
 Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
1 Q12: Lösungen bsv 2.2
 Q: Lösungen bsv... 3. 4. Graphisches Bestimmen einer Integralfunktion a) Nullstellen (laut Graph): x = 0; x = VZT x < 0 x = 0 0 < x < x > f(x) - 0 + 0 - G Io TIP HOP b) Aus der Abbildung ergibt sich: VZT
Q: Lösungen bsv... 3. 4. Graphisches Bestimmen einer Integralfunktion a) Nullstellen (laut Graph): x = 0; x = VZT x < 0 x = 0 0 < x < x > f(x) - 0 + 0 - G Io TIP HOP b) Aus der Abbildung ergibt sich: VZT
Mathematik Semester 3 / Arbeitsblatt f (x) = x x 3 4 x. 5 x 3 20 x. x 2 1
 9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
Einführung in die Algebra
 1 Einführung in die Algebra 1.1 Wichtige Formeln Formel Symbol Definition Wert Bedingungen n Fakultät n! k = 1 2 3 n n N Binomialkoeffizient Binomische Formeln Binomischer Lehrsatz Potenzen ( ) n k Definition
1 Einführung in die Algebra 1.1 Wichtige Formeln Formel Symbol Definition Wert Bedingungen n Fakultät n! k = 1 2 3 n n N Binomialkoeffizient Binomische Formeln Binomischer Lehrsatz Potenzen ( ) n k Definition
Kurvendiskussion von Polynomfunktionen
 Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Analysis.
 Analysis www.schulmathe.npage.de Inhaltsverzeichnis 1 Zahlenfolgen 4 1.1 Bildungsvorschriften für Zahlenfolgen..................... 5 1.2 Monotonie von Zahlenfolgen.......................... 5 1.3 Arithmetische
Analysis www.schulmathe.npage.de Inhaltsverzeichnis 1 Zahlenfolgen 4 1.1 Bildungsvorschriften für Zahlenfolgen..................... 5 1.2 Monotonie von Zahlenfolgen.......................... 5 1.3 Arithmetische
und geben Sie die Gleichungen und Art aller Asymptoten an. an, bestimmen Sie die Koordinaten der Achsenschnittpunkte von G f auflösen x x 2 2 ( 2/ 0)
 Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
3.6 Verhalten an den Polstellen
 44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
1.2 Einfache Eigenschaften von Funktionen
 1.2 Einfache Eigenschaften von Funktionen 1.2.1 Nullstellen Seien A und B Teilmengen von R und f : A B f : Df Wf eine Funktion. Eine Nullstelle der Funktion f ist ein 2 D f, für das f ( = 0 ist. (Eine
1.2 Einfache Eigenschaften von Funktionen 1.2.1 Nullstellen Seien A und B Teilmengen von R und f : A B f : Df Wf eine Funktion. Eine Nullstelle der Funktion f ist ein 2 D f, für das f ( = 0 ist. (Eine
Mathematik 12. Jahrgangsstufe - Hausaufgaben
 Version:. November Mathematik. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Integralrechnung.5 Kurvendiskussion und Integralrechnung................... Flächenberechnung. Stammfunktionen..................................
Version:. November Mathematik. Jahrgangsstufe - Hausaufgaben Inhaltsverzeichnis Integralrechnung.5 Kurvendiskussion und Integralrechnung................... Flächenberechnung. Stammfunktionen..................................
FH Gießen-Friedberg, Sommersemester 2010 Skript 9 Diskrete Mathematik (Informatik) 30. April 2010 Prof. Dr. Hans-Rudolf Metz.
 FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
2015, MNZ. Jürgen Schmidt. Vorkurs. Mathematik. Ableiten. Tag WS 2015/16
 Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Grundkurs Höhere Mathematik I (für naturwissenschaftliche. Studiengänge) Beispiele
 Grundkurs Höhere Mathematik I (für naturwissenschaftliche Studiengänge) Beispiele Prof. Dr. Udo Hebisch Diese Beispielsammlung ergänzt das Vorlesungsskript und wird ständig erweitert. 1 DETERMINANTEN 1
Grundkurs Höhere Mathematik I (für naturwissenschaftliche Studiengänge) Beispiele Prof. Dr. Udo Hebisch Diese Beispielsammlung ergänzt das Vorlesungsskript und wird ständig erweitert. 1 DETERMINANTEN 1
Basistext Kurvendiskussion
 Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Stichwortverzeichnis. Stichwortverzeichnis
 Stichwortverzeichnis Die Ergänzungen (A) und (B) hinter einem Eintrag bedeuten: (A) Dieser Eintrag tritt in einer Aufgabe auf. (B) Dieser Eintrag tritt in einem Beispiel auf. 1 1. Hauptsatz der Differential-
Stichwortverzeichnis Die Ergänzungen (A) und (B) hinter einem Eintrag bedeuten: (A) Dieser Eintrag tritt in einer Aufgabe auf. (B) Dieser Eintrag tritt in einem Beispiel auf. 1 1. Hauptsatz der Differential-
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Aufgaben zur e-funktion
 Aufgaben zur e-funktion 1.0 Gegeben ist die reelle Funktion f(x) = 2x 2x e 1 x2 mit x R (Abitur 2000 AII). 1.1 Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion f und bestimmen Sie die Nullstellen
Aufgaben zur e-funktion 1.0 Gegeben ist die reelle Funktion f(x) = 2x 2x e 1 x2 mit x R (Abitur 2000 AII). 1.1 Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion f und bestimmen Sie die Nullstellen
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
3 Funktionen diskutieren
 3 Funktionen diskutieren 3.1 Polynomfunktionen Siehe dazu die Abschnitte 8.6 11 in der Formelsammlung. 1. f x = 1 3 x3 x 2. f x = 1 27 x 3 3 x 2 24 x + 26 mit f 1 = 0 3. f x = 1 4 x4 2 x 2 4. f x = 1 4
3 Funktionen diskutieren 3.1 Polynomfunktionen Siehe dazu die Abschnitte 8.6 11 in der Formelsammlung. 1. f x = 1 3 x3 x 2. f x = 1 27 x 3 3 x 2 24 x + 26 mit f 1 = 0 3. f x = 1 4 x4 2 x 2 4. f x = 1 4
Tiefpunkt = relatives Minimum hinreichende Bedingung:
 R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Zusammenfassung Abitursstoff Mathematik
 Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Zusammenfassung Mathematik 2012 Claudia Fabricius
 Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
x 1 keinen rechtsseitigen Grenzwert x 0+ besitzen. (Analog existiert der linksseitige Grenzwert nicht.)
 Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur 11. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
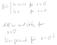 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
(Quelle Abitur BW 2004) Gegeben sind die Schaubilder der Funktion mit, ihrer Ableitungsfunktion, einer Stammfunktion von und der Funktion mit.
 Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
2 Differenzialrechnung für Funktionen einer Variablen
 2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Lösungen zu Grundwissensaufgaben 11. Jahrgangstufe Teil 1
 Lösungen zu Grundwissensaufgaben. Jahrgangstufe Teil. Eigenschaften gebrochen-rationaler Funktionen Umformungen DD ff NS GW ff(xx) xx + (xx )(xx + ) + xx² + xx xx(xx + ) xx + xx + xx + xx + RR\{ } xx xx
Lösungen zu Grundwissensaufgaben. Jahrgangstufe Teil. Eigenschaften gebrochen-rationaler Funktionen Umformungen DD ff NS GW ff(xx) xx + (xx )(xx + ) + xx² + xx xx(xx + ) xx + xx + xx + xx + RR\{ } xx xx
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[
![Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[ Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[](/thumbs/76/73058958.jpg) Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
1.4 Schaubild von Schaubild von Schaubild von 1., /
 Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
LMU MÜNCHEN. Mathematik für Studierende der Biologie Wintersemester 2016/17. GRUNDLAGENTUTORIUM 5 - Lösungen. Anmerkung
 LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
LMU MÜNCHEN Mathematik für Studierende der Biologie Wintersemester 2016/17 GRUNDLAGENTUTORIUM 5 - Lösungen Anmerkung Es handelt sich hierbei um eine Musterlösung so wie es von Ihnen in einer Klausur erwartet
Mathematik LK M2, 2. KA Eigenschaften ganzr. Funktionen Lösung
 Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Polynome. Ein Term der Form. mit n und a 0 heißt Polynom. Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms.
 Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Funktionen. Mathematik-Repetitorium
 Funktionen 4.1 Funktionen einer reellen Veränderlichen 4.2 Eigenschaften von Funktionen 4.3 Die elementaren Funktionen 4.4 Grenzwerte von Funktionen, Stetigkeit Funktionen 1 4. Funktionen Funktionen 2
Funktionen 4.1 Funktionen einer reellen Veränderlichen 4.2 Eigenschaften von Funktionen 4.3 Die elementaren Funktionen 4.4 Grenzwerte von Funktionen, Stetigkeit Funktionen 1 4. Funktionen Funktionen 2
Abiturprüfung Mathematik 13 Technik A II - Lösung mit CAS
 GS.6.6 - m6_3t-a_lsg_cas_gs.pdf Abiturprüfung 6 - Mathematik 3 Technik A II - Lösung mit CAS Teilaufgabe Gegeben ist die Funktion f mit ( x ) mit der Definitionsmenge D ( x ) ( x 3) f IR \ { ; 3 }. Teilaufgabe.
GS.6.6 - m6_3t-a_lsg_cas_gs.pdf Abiturprüfung 6 - Mathematik 3 Technik A II - Lösung mit CAS Teilaufgabe Gegeben ist die Funktion f mit ( x ) mit der Definitionsmenge D ( x ) ( x 3) f IR \ { ; 3 }. Teilaufgabe.
Mathematik 1 Bachelorstudiengang Maschinenbau
 Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
