B.7 Kurzzusammenfassung zum Thema Kurvendiskussion
|
|
|
- Roland Kristian Hofmeister
- vor 7 Jahren
- Abrufe
Transkript
1 B.7 Kurzzusammenfassung zum Thema Kurvendiskussion B.7.a Übersicht Charakteristische Punkte/Verläufe einer Kurve Eine Funktion bzw. Gleichung wird üblicherweise auf folgende charakteristische Punkte analysiert: a) Nullstellen (Schnittpunkt mit der x-achse) b) Extremstellen: - Unterscheidung von lokalen bzw. relativen Extrema absoluten bzw. globalen Extrema - Arten von Extremwerten werden unterschieden: Maxima Minima c) Sattelstellen: Sonderfall bei dem die Steigung in einem Punkt zwar Null ist aber dennoch kein Extrempunkt vorliegt (siehe unten) d) Wendestellen e) Polstellen Asymptoten B.7.b Nullstellen Die Schnittpunkte mit der x-achse des Funktions-/Gleichungsgraphen sind gesucht. Beispiel: f(x)=x 4 +9x 3 +6x +74x+4 -> Abspaltung von Linearfaktoren: f(x)=(x+4)(x+3)(x+)(x+) Aus der rechten Darstellung der Funktion sind direkt die Nullstellen erkennbar: Folgende x-werte sind Nullstellen von f(x) (f(x)=): x Nullstellen ={-4;-3;-;-/} Das Auffinden der Nullstellen für ein Polynom 4. Ordnung in der Form x 4 +9x 3 +6x +74x+4 kann sich hier recht kompliziert gestalten. Da der höchstwertige Koeffizient ungleich ist ( auch nicht alle Koeffizienten ganzzahlig durch teilbar sind), sind nicht alle rationalen Nullstellen notwendigerweise ganzzahlige Teiler von 4. Praktisch muss man bei einem Polynom 4.Grades Nullstellen durch probieren finden (ggf. durch Anwendung des Zwischenwertsatzes ). Die Nullstellen des Restpolynoms.Ordnung kann man dann mittels pq-formel oder binomische Ergänzung bestimmen.. Zwischenwertsatz: Wenn f(x) im Intervall [a;b] stetig ist, f(a)> f(b)< ist, so muss es einen Wert c im Intervall [a;b] geben mit f(c)=
2 Die Nullstellen der Funktion sind in folgendem Graphen gekennzeichnet: f(x)=(x+4)(x+3)(x+)(x+)=x^4+9x^3+6x^+74x B.7.c Extremstellen Sattelstellen Vorbemerkung: Für die folgenden Betrachtungen wird davon ausgegangen, daß die benötigten Ableitung für den Definitionsbereich der Ausgangsfunktion existieren. Dies muß nicht zwangsläufig der Fall sein (vergl. Abschnitt Vorgehen, wenn die Definitionsmenge von f (x) kleiner ist als die von f(x) ). Vor der formalen Definition sollen zunächst die Extremstellen der unter B.7.b bereits behandelte Funktion f(x) der Funktion g(x)=-f(x) betrachtet werden.
3 f(x)=(x+4)(x+3)(x+)(x+)=x^4+9x^3+6x^+74x+4 lokales bzw. relatives Maximum (f (a )=) Umgebung, in der das lokale Maximum ein Maximum ist ( ) Umgebung, in der das lokale Minimum ein Minimum ist ) - - lokales bzw. relatives Minimum (f (a )=) globales bzw. absolutes Minimum (f (a )=) a -3 a - a - f (x)=8x^3+7x^+x Die stetige Funktion f(x) weist Extremstellen für x={a ;a ;a } auf. Das absolute Minimum für x=a ist ein globales bzw. absolutes Minimum, weil es kein x D gibt für das f(x) kleiner ist als f(a ). Die lokalen bzw. relativen Extremstellen sind nur in den gekennzeichneten Umgebungen (Intervallen) Extremstellen. Die Steigung dy/dx von f(x) an den Extremstellen ist. Der Graph der. Ableitung schneidet die x-achse für x={a ;a ;a }. 3
4 Ist (a;f(a)) ein Minimum weist f(x) links vom Minimum eine fallende Monotonie rechts davon eine steigende Monotonie auf. D.h., daß f (x) links von x=a in diesem Fall negativ (<) ist rechts davon positiv (x>) ist. Wenn dies der Fall ist, dann ist f (a)>. Ist (a;f(a)) ein Maximum weist f(x) links vom Minimum eine steigende Monotonie rechts davon eine fallende Monotonie auf (gilt nur in der weiter unten definierten Umgebung). D.h., daß f (x) links von x=a in diesem Fall positiv (>) ist rechts davon negativ (x<) ist. Wenn dies der Fall ist, dann ist f (a)<. In der folgenden Abbildung sind f(x), f (x) f (x) dargestellt. f(x)=(x+4)(x+3)(x+)(x+)=x^4+9x^3+6x^+74x+4 f (x)=8x^3+7x^+x+74 f (x)=4x^+4x+ Maximum: f (x=a )= f (x=a )< - Minimum: f (x=a )= f (x=a )> - Minimum: f (x=a )= f (x=a )> a -3 a - a - Wenn man f(x) an der x-achse spiegelt (Multiplikation mit -: g(x)=-f(x)) erhält man für die x- Werte, die bei f(x) ein Minimum aufweisen ein Maximum umgekehrt. D.h. g(x) weist ein globales Maximum, ein lokales Maximum lokales Minimum auf. g(x)=-(x+4)(x+3)(x+)(x+)=-x^4-9x^3-6x^-74x-4 g (x)=-8x^3-7x^-x-74 g (x)=-4x^-4x- globales bzw. absolutes Maximum (f (a )=) a 4
5 Nach dieser anschaulichen Betrachtung von Extremstellen sollen diese nun mathematisch beschrieben werden: a) Definition absolutes (globales) Extremum: gegeben: f( x) D R, W R a D f(a) ist ein absolutes (globales) Maximum wenn folgendes gilt: fa ( ) fx ( ) für alle x D f(a) ist ein absolutes (globales) Minimum wenn folgendes gilt: fa ( ) fx ( ) für alle x D Globale Maxima Minima werden auch als Extremwerte bezeichnet. Weitere Bedingung siehe Punkt c! b) Definition relatives (lokales) Extremum: f(a) ist ein relatives (lokales) Maximum wenn in der Umgebung U(a) Ua ( ) D folgendes gilt: fa ( ) fx ( ) für alle f(a) ist ein relatives (lokales) Minimum wenn in der Umgebung U(a) Ua ( ) D folgendes gilt: fa ( ) fx ( ) für alle Weitere Bedingung siehe Punkt c! c) Ein Extremum liegt nur dann vor wenn f(x) zu beiden Seiten von x=a eine entgegengesetzte Monotonie aufweist - d.h.: - f (a)= - f (a) ist nicht selbst ein Extremum (hinreichend Bedingung: f ( a) ) (vergleiche auch Sattelstelle - Punkt e) d) Definition Umgebung: Eine Menge Ua ( ) D heißt Umgebung der reellen Zahl a, wenn es ein offenes Intervall (b;c) gibt, das a enthält mit abc,, D. (Achtung: z.b.: D=[;4] -> U(a=4) existiert nicht, weil es kein offenes Intervall gibt, das a=4 enthält) e) Definition Sattelstelle: Eine Sattelstelle liegt dann vor wenn - f(x) bei x=a eine waagerechte Tangente hat (also f (a)=) - f(x) zu beiden Seiten von x=a die gleiche Monotonie aufweist bzw. f (a) ein Extremwert von f (x) ist. Die Funktion h(x)=x 3 weist bei x=a= eine Sattelstelle auf: h ()= h () ist ein Extremwert von h (x): h ()= h () 3 h(x)=x^3-3 h (x)=3x^ h (x)=6x h (x)=6 - - Sattelstelle: h ()=, h ()=, h ()
6 Ist die erste Ableitung einer Funktion/Gleichung für x=a mit a D gleich, so liegt hier also entweder ein Sattelpunkt oder ein Extremum vor. Ein Sattelpunkt liegt dann vor, wenn die.ableitung für x=a ein Extremum aufweist. Wenn die. Ableitung für x=a ebenfalls gleich ist so kann man nun iterativ/rekursiv überprüfen, ob die. Ableitung für x=a ein Extremum oder einen Sattelpunkt aufweist. Dies soll an folgendem Beispiel exemplarisch gezeigt werden: Untersuchung von ix ( ) = x 7 auf Extremwerte bzw. Sattelstellen für x=: Tabelle : Analyse, ob ix ( ) = x 7 bei x= eine Sattelstelle oder eine Extremstelle aufweist Schritt Ableitung Folgerung. Ableitung: i ()= i(x) weist für x= eine Sattelstelle oder ein i ( x) = 7x 6 Extremum auf. Ableitung: i ()= i (x) weist für x= eine Sattelstelle oder ein i ( x) = 4x Extremum auf 3 3. Ableitung: i ()= i (x) weist für x= eine Sattelstelle oder i ( x) = x 4 ein Extremum auf 4 4. Ableitung: i ()= i (x) weist für x= eine Sattelstelle oder i ( x) = 84x 3 ein Extremum auf. Ableitung: i ()= i (x) weist für x= eine Sattelstelle oder i ( x) = x ein Extremum auf 6 6. Ableitung: i ()= i (x) weist für x= eine Sattelstelle oder i ( x) = 3x ein Extremum auf 7 7. Ableitung: i ()> i (x) (6. Ableitung) ist bei x= monoton i ( x) = 3 steigend => i (x) (. Ableitung) weist für x= ein Minimum auf 8 4. Ableitung da.ableitung Extremum => 4.Ableitung Sattelstelle (monoton steigend) 9 3. Ableitung da 4.Ableitung Sattelstelle (monoton steigend) => 3.Ableitung Minimum. Ableitung da 3.Ableitung Extremum =>.Ableitung Sattelstelle (monoton steigend). Ableitung da.ableitung Sattelstelle (monoton steigend) =>.Ableitung Minimum Ausgangsfunktion da.ableitung Extremum => Ausgangsfunktion Sattelstelle (monoton steigend) Aus den Rechenschritten ist auch ersichtlich, daß die Funktion j(x)=7x 6 für x= ein Minimum hat. Die Analyse des kritischen Punkts (x=;y=) von i(x) ist nach diesem Verfahren recht aufwendig. Generell muß in jedem Fall die. Ableitung gebildet werden, um zeigen zu können, ob der 6
7 kritische Punkt ein Minimum, Maximum oder eventuell ein Sattelpunkt ist. In den meisten Fällen ist aber die.ableitung bereits ungleich damit ein Extremum eindeutig identifiziert. In der folgenden Abbildung ist ein Entscheidungsdiagramm für die Untersuchung von f(x) auf ein Minimum, Maximum eine Sattelstelle dargestellt. f (x=a)=? ja f (x=a)>? nein f (x=a)<? nein nein f(x=a) ist kein Extremum keine Sattelstelle ja f(x=a) ist ein Minimum ja f(x=a) ist ein Maximum 4 Möglichkeiten: ) f (x=a) Maximum => f(x=a) Sattelstelle monoton fallend ) f (x=a) Minimum => f(x=a) Sattelstelle monoton steigend 3) f (x=a) Sattelstelle monoton fallend => f(x=a) Maximum 4) f (x=a) Sattelstelle monoton steigend => f(x=a) Minimum nächster Schritt: rekursives Überprüfen von f (x=a) auf ein Extremum alternatives Verfahren zur Klassifikation eines kritischen Punktes Das oben behandelte Verfahren zur Analyse von Extrem- Sattelstellen hat Nachteile: a) wenn die. Ableitung für x=a Null ist, dann müssen rekursiv die nächst höhere(n) Ableitungen überprüft werden => aufwendig b) wenn bereits die. Ableitung ein komplizierter algebraischer Ausdruck ist, dann wird die. Ableitung oftmals noch komplizierter (z.b. durch Anwendung der Produkt-, Quotienten- oder Kettenregel) c) die Ableitungen f (a) f (a) existieren unter Umständen nicht - siehe Punkt Vorgehen, wenn die Definitionsmenge von f (x) kleiner ist als die von f (x) Als Alternative kann man auch - wenn f (x=a)= ist - f (x) oder f(x) in der Umgebung von x=a überprüfen. Dies soll nun für die 4 zu unterscheidenen Fälle gezeigt werden. Es ist jedesmal eine Beispielfunktion gewählt worden, um die Kriterien nochmal anschaulich überprüfen zu können. Die magenta-farbenen Linien kennzeichnen die gewählten x-werte in der Umgebung von x=a (a=- in den Beispielen). 7
8 Überprüfung von f(x) in der Überprüfung von f (x) in der kritischer Punkt von f(x) ist f(x)>f(a) für x< a x U( a) f (x)< für x < a Minimum f(x)>f(a) für x> a f (x)> für x > a 8 f(x)=(x+)^+ f (x)=(x+) x<a x>a -8 x - a=- x + a a
9 Überprüfung von f(x) in der Überprüfung von f (x) in der kritischer Punkt von f(x) ist f(x)<f(a) für x< a x U( a) f (x)> für x < a Maximum f(x)<f(a) für x> a f (x)< für x > a 8 f(x)=-(x+)^+ f (x)=-(x+) x<a x>a -8 x - a=- x + a a
10 Überprüfung von f(x) in der Überprüfung von f (x) in der kritischer Punkt von f(x) ist f(x)<f(a) für x< a x U( a) f(x)>f(a) für x> a f (x)> für f (x)> für x < a x > a Sattelstelle monoton steigend 8 f(x)=(x+)^3+ f (x)=3(x+)^ x<a x>a -8 x - a=- x + a a
11 Überprüfung von f(x) in der Überprüfung von f (x) in der kritischer Punkt von f(x) ist f(x)>f(a) für x< a x U( a) f(x)<f(a) für x> a f (x)< für f (x)< für x < a x > a Sattelstelle monoton fallend 8 f(x)=-(x+)^3+ f (x)=-3(x+)^ x<a x>a -8 x - a=- x + a a Die Beobachtungen für die 4 Flälle sind in folgender Tabelle nochmal zusammen gefaßt: Überprüfung von f(x) in der Überprüfung von f (x) in der kritischer Punkt von f(x) ist f(x)>f(a) für x< a x U( a) f (x)< für x < a Minimum f(x)>f(a) für x> a f (x)> für x > a f(x)<f(a) für x< a x U( a) f (x)> für x < a Maximum f(x)<f(a) für x> a f (x)< für x > a f(x)<f(a) für x< a x U( a) f(x)>f(a) für x> a f (x)> für f (x)> für x < a x > a Sattelstelle monoton steigend f(x)>f(a) für x< a x U( a) f(x)<f(a) für x> a f (x)< für f (x)< für x < a x > a Sattelstelle monoton fallend Nun stellt sich natürlich die Frage wie groß die Umgebung U(a) um x=a gewählt werden darf. Im Intervall (x a- ;x a+ ), das die Umgebung U(a) begrenzt, muß folgendes gelten: - f (x) darf keine weitere Nullstelle als f (a) aufweisen
12 - f (x) muß im gesamten Intervall stetig sein. Man kann sich in dieser Umgebung willkürlich je einen x-wert für x<a einen x-wert für x>a auswählen. Anschließend kann man nun einfach die Funktionswerte von f(x) bzw. f (x) bestimmen nach o.a. Tabelle den kritischen Punkt klassifizieren. Aufgabe : Untersuchen Sie die Funktion fx ( ) = x 7 auf Extrempunkte Sattelpunkte! Untersuchen Sie hierzu die Werte der.ableitung in der Umgebung von Nullstellen von f (x)! Vorgehen, wenn die Definitionsmenge von f (x) kleiner ist als die von f(x) Dieser Fall kann am besten an Hand eines Beispiels erklärt werden: Beispiel: kx ( ) = x = x für x < x für x k(x)= x =sqrt(x^) k (x)= x /x=sqrt(x^)/x Aus dem Graphen ist direkt ersichtlich, daß k(x) für x= ein Minimum hat k (x) hier nicht definiert ist. Mathematisch kann man wie folgt vorgehen: Aufgabe : a) Überprüfen Sie mathematisch, ob k(x)= x an der möglichen kritischen Stelle in den Intervallen ( ; ) ( ; ) stetig ist! b) Wenn k(x) hier stetig ist: Überprüfen Sie nach der Tabelle alternatives Verfahren zur Klassifikation eines kritischen Punktes ob ein Minimum oder ein Maximum vorliegt. Hierbei die Bedingungen für die Wahl der Umgebung beachten! Überprüfung von f(x) in der kritischer Punkt von f(x) ist f(x)>f(a) für x< a f(x)>f(a) für x > a Minimum f(x)<f(a) für x< a f(x)<f(a) für x > a Maximum
13 B.7.d Wendestellen Eine Wendestelle liegt dort vor, - wo der Zuwachs der Steigung der Tangenten von f(x) sich umkehrt bzw. - f (x) eine Extremstelle aufweist. D.h., bei der Bestimmung von Wendestellen muß f (x) auf kritische Stellen überprüft werden (siehe Abschnitt B.7.c). Die Wendestellen sollen anhand der bekannten Funktion fx ( ) = x 4 + 9x 3 + 6x + 74x + 4 diskutiert werden. f(x)=(x+4)(x+3)(x+)(x+)=x^4+9x^3+6x^+74x+4 f (x)=8x^3+7x^+x+74 f (x)=4x^+4x+ - - Wendestelle: f(x=a3): Umkehrung Steigungs- Zuwachs der Tangenten f (x=a 3 ): Maximum f (x=a 3 )= Wendestelle: f(x=a4): Umkehr Steigungs-Zuwachs der Tangenten f (x=a 3 ): Minimum f (x=a 3 )= a 3-3 a - a 4 - Sattelpunkte sind grsätzlich auch Wendepunkte. Der Graph von f(x) ändert am Wendepunkt seine Krümmung. Die Krümmung von f(x) ist in diesem Fall wie folgt: konvex ( nach oben geöffnet ): in den Intervallen (- ;a 3 ) (a 4 ; ) konkav ( nach unten geöffnet ): im Intervall (a 3 ;a 4 ) B.7.e Polstellen - vertikale Asymptoten Polstellen liegen immer dann vor, wenn eine der folgenden Bedingungen zutrifft: lim fx ( ) = ± x a lim x a - lim x a + fx ( ) fx ( ) = = ± ± 3
14 Bekannte Beispiele für Funktionen mit Polstellen sind: a) rationale Funktionen: Polstellen liegen bei den x-werten vor, die Definitionslücken bilden, weil der Nenner Null wird - z.b. lx ( ) = Polstelle für x= x= x ( x ) l(x)=/(x(x-)) b) Logarithmusfunktion: Beispiel mx ( ) = log x m(x)=log_(x)
15 B.7.e Horizontale Asymptoten Im Gegensatz zur Definition von vertikalen Asymptoten läßt man bei horizontalen Asymptoten die Veränderliche x gegen ± streben. Wenn f(x) für x gegen ± gegen einen fixen Wert L strebt, so strebt f(x) asymptotisch gegen die waagerechte Gerade y=l. Also: Die Gerade y=l ist eine horizontale Asymptote der Funktion y=f(x) wenn eine der folgenden Bedingungen erfüllt ist: lim fx ( ) = L lim fx ( ) = L x x Dies soll wieder anhand des obiben Beispiels von l(x) betrachtet werden: lim fx ( ) = x ± Soll eine rationalen Funktionen mit einem Nennerpolynom vom Grad n> analysiert werden, so ist folgender grlegende Satz von Bedeutung: für r>: lim --- = lim x r = ± x ± x r x ± Wenn man eine rationale Funktion untersucht, so streben sowohl der Zähler als auch der Nenner gegen ±. Damit ist der Quotient aus Zähler Nenner erst einmal nicht offensichtlich. Expemplarisch soll hier die Funktion r(x) betrachtet werden: 3x x rx ( ) = x gesucht: lim rx ( ) + 4x + x ± Um eine rationale Funktion auf horizontale Asymptoten zu untersuchen, muß man eine algebraische Umformung vornehmen kann hierauf nun die Grenzwertsätze anwenden: a) man teile sowohl das Zähler- als auch das Nennerpolynom durch x n, wobei n der Grad des Nennerpolynoms ist (eine Division durch wäre nicht erlaubt - da x jedoch sehr große/kleine Werte, die ungleich Null sind, annimmt, ist dies kein Problem) lim rx ( ) 3x x x lim x = = lim x ± x ± x + 4x + x ± x x b) man wende die Grenzwertsätze an ermittele damit den Grenzwert: lim 3 lim -- lim ---- x lim rx ( ) x x ± x ± x x ± x lim = = = = -- x ± x ± lim lim 4 -- lim x x x ± x ± x x ± x Folgerungen: es können 3 Fälle für rationale Funktionen unterschieden werden: ) Grad des Zählerpolynoms größer als Grad des Nennerpolynoms: lim rx ( ) = ± x ± ) Grad des Zählerpolynoms kleiner als Grad des Nennerpolynoms: lim rx ( ) = x ± z max 3) Grad des Zählerpolynoms ist gleich dem Grad des Nennerpolynoms: lim rx ( ) = , x ± n max wobei z max bzw. n max die höchstwertigen Koeffizienten des Zähler- bzw. Nennerpolynoms sind.
16 Aufgabe 3: a) Untersuchen Sie qx ( ) = x auf horizontale Asymptoten! 3x b) Untersuchen Sie sx ( ) = x + x auf horizontale Asymptoten! formen Sie s(x) nach der 3.binomischen For- x Tip: Multiplizieren Sie s(x) mit x x + + x mel um! B.7.f Asymptoten im Unendlichen Eine weitere Kurvencharakteristik ist, wenn lim fx ( ) = ± - also für x gegen oder x ± die Funktion gegen oder strebt. Es soll nun noch das Verhalten einer rationalen Funktion noch genauer betrachet werden. Wie bereits festgestellt, strebt der Funktionswert gegen ± für x ± wenn der Grad des Zählerpolynoms größer ist als der Grad des Nennerpolynoms. Der Graph nähert sich in diesem Fall asymptotisch einem Graphen a(x). Diesen Graphen a(x) erhält man, indem man das Zählerdurch das Nennerpolynom so lange dividiert bis der Grad des Restpolynoms kleiner ist als der des Nennerpolynoms. 3x 3 x Beispiel: ex ( ) = x gesucht: lim ex ( ) + 4x + x ± ( 3x 3 x ) : ( x + 4x + ) = 3x x x x x 3 --x x x x lim ex ( ) lim --x = + lim = lim --x x ± x ± x ± x + 4x + x ± 3 7 Für x ± nähert sich e(x) also asymptotisch dem Graphen ax ( ) = --x -----, der natürlich wiederum selbst gegen ± strebt. B.7.g Zusammenfassung 3 --x x x + 4x + Wenn man eine Funktion auf die in Kapitel B.7.a bis B.7.f behandelten Charakteristiken untersucht, dann kann man mit den Erkenntnissen den Graphen an den charakteristischen Stellen skizzieren. Dies soll anhand von Beispielen praktiziert werden. 6
17 Aufgabe 4: Der Graph der Funktion sieht wie folgt aus: wx ( ) = x a ( x b) ( x c) Parameter a, bc, R w(x)=(x-a)/((x-b)(x-c)) a) Bestimmen Sie aus dem Graphen die Parameter a,b c! b) Bestimmen Sie mathematisch - die Nullstellen von w(x) - die Extremstellen von w(x) - die Polstellen - die waagerechten Asymptoten 3x( x a) c) Untersuchen Sie w( x) = 3x w( x) = auf waagerechte Asymptoten! ( x b) ( x c) d) Untersuchen Sie w3( x) 3x 3x ( x a) = wx ( ) = auf Asymptoten für x ±! ( x b) ( x c) Allgemeine Anmerkung Die Darstellungen in diesem Skript zum Thema Kurvendiskussion gelten sowohl für Funktionen als auch allgemein für implizite Gleichungen deren Ableitungen. Übungen: siehe Aufgabenblatt 8 7
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer
 von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer Überblick Tangentensteigung einer Funktion Extremstellen Sattelstellen Extremstellen: notwendige und hinreichende Bedingung lokale bzw. relative und absolute
von Prof. Dr. Ing. Dirk Rabe Hochschule Emden/Leer Überblick Tangentensteigung einer Funktion Extremstellen Sattelstellen Extremstellen: notwendige und hinreichende Bedingung lokale bzw. relative und absolute
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
GF MA Differentialrechnung A2
 Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Die gebrochenrationale Funktion
 Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Basistext Kurvendiskussion
 Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Polynome. Ein Term der Form. mit n und a 0 heißt Polynom. Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms.
 Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 12. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur 11. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 06. Dezember 06 Höhere Mathematik I für Ingenieurinnen und Ingenieure Beispiele zur. Übung In
Eigenschaften von Funktionen
 Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
4.3 Differentialrechnung III
 4. Differentialrechnung III Inhaltsverzeichnis Extremalpunkte Wendepunkte 5 Zusammenfassung 7 4 Kurvendiskussion 8 Diff rechnung III 6..6 Theorie und Übungen Differentialrechnung III-Spezielle Punkte auf
4. Differentialrechnung III Inhaltsverzeichnis Extremalpunkte Wendepunkte 5 Zusammenfassung 7 4 Kurvendiskussion 8 Diff rechnung III 6..6 Theorie und Übungen Differentialrechnung III-Spezielle Punkte auf
Funktionen untersuchen
 Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Funktionen untersuchen Mögliche Fragestellungen Definition: lokale und globale Extrema Monotonie und Extrema Notwendige Bedingung für Extrema Hinreichende Kriterien, Vergleich Krümmungsverhalten Neumann/Rodner
Zusammenfassung Mathematik 2012 Claudia Fabricius
 Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[
![Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[ Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[](/thumbs/76/73058958.jpg) Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Kurvendiskussion von Polynomfunktionen
 Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
bestimmt werden. Allein die Regel (5.4) würde wegen g(x) = 2, folglich erhalten wir den korrekten lim
 bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
Analysis f(x) = x 2 1. (x D f )
 Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
Tiefpunkt = relatives Minimum hinreichende Bedingung:
 R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 0.0.01 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Differentialrechnung. Mathematik W14. Christina Sickinger. Berufsreifeprüfung. v 1 Christina Sickinger Mathematik W14 1 / 79
 Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Analysis 8.
 Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Kurvendiskussion von Funktionsscharen
 Kurvendiskussion von Funktionsscharen Die Untersuchung von Funktionsscharen unterscheidet sich nicht von der Untersuchung von normalen Funktionen. Einzig die Bestimmung der Ortskurven von Extremstellen
Kurvendiskussion von Funktionsscharen Die Untersuchung von Funktionsscharen unterscheidet sich nicht von der Untersuchung von normalen Funktionen. Einzig die Bestimmung der Ortskurven von Extremstellen
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Kapitel 5: Differentialrechnung
 Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
4.2 Differentialrechnung III
 4. Differentialrechnung III Inhaltsverzeichnis 1 Überblick Extremal- und Wendepunkte Monotonie und erste Ableitung 3 Krümmung und zweite Ableitung 6 4 Extremalpunkte 7 5 Wendepunkte 1 6 Anwendungsaufgaben
4. Differentialrechnung III Inhaltsverzeichnis 1 Überblick Extremal- und Wendepunkte Monotonie und erste Ableitung 3 Krümmung und zweite Ableitung 6 4 Extremalpunkte 7 5 Wendepunkte 1 6 Anwendungsaufgaben
Wirtschaftsmathematik
 Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Da der Nenner immer positiv ist, folgt. g (x) > 0 2x(2 x) > 0 0 < x < 2 g (x) < 0 2x(2 x) < 0 x < 0 oder x > 2
 Da der Nenner immer positiv ist, folgt g (x) > 0 x( x) > 0 0 < x < g (x) < 0 x( x) < 0 x < 0 oder x > Also ist g auf (0,) streng monoton wachsend sowie auf (,0) und auf (, ) strengmonotonfallend.außerdemistg
Da der Nenner immer positiv ist, folgt g (x) > 0 x( x) > 0 0 < x < g (x) < 0 x( x) < 0 x < 0 oder x > Also ist g auf (0,) streng monoton wachsend sowie auf (,0) und auf (, ) strengmonotonfallend.außerdemistg
3.6 Verhalten an den Polstellen
 44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
44 Kapitel 3. Gebrochen-rationale Funktionen Beispiel 3.5.3. f(x) = 2x2 + 5 2x 1 f(0) = 2 02 + 5 2 0 1 = 5 1 = 5 3.6 Verhalten an den Polstellen Die Polstellen teilen den Graph in mehrere Teile. Da der
1 Polynome III: Analysis
 1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
Gebrochen-rationale Funktionen
 Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
Definition Eine gebrochen-rationale Funktion ist eine Funktion, bei der sich im Zähler und Nenner eine ganzrationale Funktion (Polynom) befindet: Eigenschaften f(x) = g(x) h(x) Echt gebrochen-rationale
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
Zusammenfassung der Kurvendiskussion
 Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Anwendungen der Differentialrechnung
 KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
KAPITEL 3 Anwendungen der Differentialrechnung 3.1 Lokale Maxima und Minima Definition 16: Sei f : D R eine Funktion von n Veränderlichen. Ein Punkt x heißt lokale oder relative Maximalstelle bzw. Minimalstelle
Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I
 Michael Buhlmann Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I Einleitung: Eine gebrochen rationale Funktion (Polynom) f: D f -> R (mit maximaler Definitionsbereich D f)
Michael Buhlmann Mathematik-Aufgabenpool > Kurvendiskussion gebrochen rationaler Funktionen I Einleitung: Eine gebrochen rationale Funktion (Polynom) f: D f -> R (mit maximaler Definitionsbereich D f)
Abb lokales Maximum und Minimum
 .13 Lokale Extrema, Monotonie und Konvexität Wir kommen nun zu den ersten Anwendungen der Dierentialrechnung. Zwischen den Eigenschaten einer Funktion, dem Verlau des zugehörigen Graphen und den Ableitungen
.13 Lokale Extrema, Monotonie und Konvexität Wir kommen nun zu den ersten Anwendungen der Dierentialrechnung. Zwischen den Eigenschaten einer Funktion, dem Verlau des zugehörigen Graphen und den Ableitungen
Algebra. Roger Burkhardt Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft
 Algebra Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft FS 2010 Roger Burkhardt roger.burkhardt@fhnw.ch Algebra
Algebra Roger Burkhardt roger.burkhardt@fhnw.ch Fachhochschule Nordwestschweiz Hochschule für Technik Institut für Geistes- und Naturwissenschaft FS 2010 Roger Burkhardt roger.burkhardt@fhnw.ch Algebra
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
3.2 Funktionsuntersuchungen mittels Differentialrechnung
 3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Übungsaufgaben zur Kurvendiskussion
 SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
6 Die Bedeutung der Ableitung
 6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
Lösung Semesterendprüfung
 MAE Mathematik: Analysis für Ingenieure Herbstsemester 07 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Aufgabe : Lösung Semesterendprüfung a) Wir verwenden die Def. 4 der Vorlesung für die Implikation,
MAE Mathematik: Analysis für Ingenieure Herbstsemester 07 Dr. Christoph Kirsch ZHAW Winterthur Aufgabe : Aufgabe : Lösung Semesterendprüfung a) Wir verwenden die Def. 4 der Vorlesung für die Implikation,
2 Differenzialrechnung für Funktionen einer Variablen
 2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Analysis 7. f(x) = 4 x (x R)
 Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung
 TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
TU Bergakademie Freiberg Sommersemester Dr. Gunter Semmler Dr. Anja Kohl Höhere Mathematik II für BWIW, BNC, BAI, BGIP, GTB, Ma Hausaufgaben zum Übungsblatt 5 - Lösung Differentialrechnung für Funktionen
2015, MNZ. Jürgen Schmidt. Vorkurs. Mathematik. Ableiten. Tag WS 2015/16
 Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
3.3 Linkskurve, Rechtskurve Wendepunkte
 166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
Kurvendiskussion Ganzrationale Funktion Aufgaben und Lösungen
 Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Kurvendiskussion Ganzrationale Funktion Aufgaben und http://www.fersch.de Klemens Fersch 9. August 0 Inhaltsverzeichnis Ganzrationale Funktion Quadratische Funktionen f x) = ax + bx + c 8. Aufgaben...................................................
Mathematik LK M2, 2. KA Eigenschaften ganzr. Funktionen Lösung
 Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Aufgabe 1: Grenzwerte 2 x 3 1.1 Berechne unter Anwendung der 3( +12 x 10 Grenzwertsätze für Funktionen: lim x 3 x 3 +2 x+10 2 x 2 x 3 +12 x 10 1+ 6 lim x 3 x 3 +2 x+10 = lim x 10 3) 2 x 2 x 2 3 x 3( 1
Lösungen Kapitel A: Funktionen
 Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
Lösungen Kapitel A: Funktionen Arbeitsblatt 01: Abhängigkeiten entstehen a) Zu Beginn des Tages befinden sich 10 Besucher am Strand. Bis um 4 Uhr nachts haben alle den Strand verlassen. Um 6 Uhr sind bereits
5 Gebrochen rationale Funktionen
 c 003, Thomas Barmetler FOS, 11 Jahrgangsstufe (technisch) 5 Gebrochen rationale Funktionen Unter einer gebrochen rationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen Dabei
c 003, Thomas Barmetler FOS, 11 Jahrgangsstufe (technisch) 5 Gebrochen rationale Funktionen Unter einer gebrochen rationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen Dabei
Extrema gebrochen rationaler Funktionen
 Übungen zum Thema: Extrema gebrochen rationaler Funktionen Hier angewandte Lösungsmethode: Grenzwertmethode Versionsnummer: Version in Arbeit vom 6.09.007 / 19.00 Uhr Finde lokale Extrema der gebrochen
Übungen zum Thema: Extrema gebrochen rationaler Funktionen Hier angewandte Lösungsmethode: Grenzwertmethode Versionsnummer: Version in Arbeit vom 6.09.007 / 19.00 Uhr Finde lokale Extrema der gebrochen
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Aufgabe zum Thema: Gebrochen - rationale Funktionen
 Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
durch folgende Einschränkungen bestimmt:
 1 von 11 27.04.2008 16:00 Kurvendiskussion aus Wikipedia, der freien Enzyklopädie Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften,
1 von 11 27.04.2008 16:00 Kurvendiskussion aus Wikipedia, der freien Enzyklopädie Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen Eigenschaften,
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
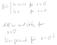 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Kurvendiskussion einer ganzrationalen Funktion
 Kurvendiskussion einer ganzrationalen Funktion Lernzuflucht 24. November 20 L A TEX M. Neumann Folgende Funktion soll in einer Kurvendiskussion bearbeitet werden: f(x) = x 4 2x 2 ; D = R () Diese Funktion
Kurvendiskussion einer ganzrationalen Funktion Lernzuflucht 24. November 20 L A TEX M. Neumann Folgende Funktion soll in einer Kurvendiskussion bearbeitet werden: f(x) = x 4 2x 2 ; D = R () Diese Funktion
13 Polynome und Nullstellen
 60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
60 II. Differentialrechnung 13 Polynome und Nullstellen Lernziele: Resultat: Zwischenwertsatz Methoden: Raten von Nullstellen, Euklidischer Algorithmus, Horner-Schema Kompetenzen: Bestimmung von Nullstellen
Mathe- Multiple-Choice-Test für Wirtschaftsinformatiker
 REELLE FUNKTIONEN 1 Was muss aufgeführt werden, wenn man eine reelle Funktion angibt? a) Ihre Funktionsvorschrift und ihren Wertebereich. Ihre Funktionsvorschrift und ihren Definitionsbereich. c) Den Wertebereich
REELLE FUNKTIONEN 1 Was muss aufgeführt werden, wenn man eine reelle Funktion angibt? a) Ihre Funktionsvorschrift und ihren Wertebereich. Ihre Funktionsvorschrift und ihren Definitionsbereich. c) Den Wertebereich
e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme sin(x+y) = cos(x) sin(y)+sin(x) cos(y). und f. Für eine reelle Zahl x R gilt e ix = 1.
 8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
C. Eicher Analysis Study Center ETH Zürich HS Extremwerte
 C. Eicher Analysis Study Center ETH Zürich HS 05 Extremwerte Gelöste Aufgabenbeispiele:. Bestimme die lokalen und globalen Extrema der Funktion f(x) = x x + x auf dem Intervall [ 4, ]. a. Bestimmung der
C. Eicher Analysis Study Center ETH Zürich HS 05 Extremwerte Gelöste Aufgabenbeispiele:. Bestimme die lokalen und globalen Extrema der Funktion f(x) = x x + x auf dem Intervall [ 4, ]. a. Bestimmung der
, a n 2. p(x) = a n x n + a n 1. x n a 2 x 2 + a 1 x + a 0. reelles Polynom in der Variablen x vom Grad n. Man schreibt deg p(x) = n
 . Graphen gebrochen rationaler Funktionen ==================================================================. Verhalten in der Umgebung der Definitionslücken ------------------------------------------------------------------------------------------------------------------
. Graphen gebrochen rationaler Funktionen ==================================================================. Verhalten in der Umgebung der Definitionslücken ------------------------------------------------------------------------------------------------------------------
Mathematik für Studierende der Biologie Wintersemester 2017/18. Grundlagentutorium 4 Lösungen
 Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Mathematik für Studierende der Biologie Wintersemester 207/8 Grundlagentutorium 4 Lösungen Sebastian Groß Termin Mittwochs 5:45 7:45 Großer Hörsaal Biozentrum (B00.09) E-Mail gross@bio.lmu.de Sprechzeiten
Funktionstypen und ihre Schaubilder 1
 Funktionstypen und ihre Schaubilder 1 Funktionen können Nullstellen, Extremstellen, Sattelstellen, Wendestellen, Polstellen bzw. deren Schaubilder (Kurven) können Schnittpunkte mit der x-achse, Extrempunkte
Funktionstypen und ihre Schaubilder 1 Funktionen können Nullstellen, Extremstellen, Sattelstellen, Wendestellen, Polstellen bzw. deren Schaubilder (Kurven) können Schnittpunkte mit der x-achse, Extrempunkte
BKO WFH11 - Material Vertretung-Mathematik Übungsaufgaben Differentialrechnung einschließlich Wendepunkte 68
 Übungsaufgaben Differentialrechnung einschließlich Wendepunkte 68 Aufgabe Terme umformen, Gleichungen lösen und Polynomdivision 1 Gegeben ist f mit f ( x ) = ( x + 2 ) ( x - 5 ) ; x IR. 2 Gegeben ist f
Übungsaufgaben Differentialrechnung einschließlich Wendepunkte 68 Aufgabe Terme umformen, Gleichungen lösen und Polynomdivision 1 Gegeben ist f mit f ( x ) = ( x + 2 ) ( x - 5 ) ; x IR. 2 Gegeben ist f
Gebrochen-Rationale Funktionen
 Gebrochen-Rationale Funktionen Bernhard Scheideler Albrecht-Dürer-Gymnasium Hagen Hilfen zur Analysis (Q1) 20. Januar 2012 Inhalt: Die Diskussion einer gebrochen-rationalen Funktion wird an einem Beispiel
Gebrochen-Rationale Funktionen Bernhard Scheideler Albrecht-Dürer-Gymnasium Hagen Hilfen zur Analysis (Q1) 20. Januar 2012 Inhalt: Die Diskussion einer gebrochen-rationalen Funktion wird an einem Beispiel
3 Gebrochen-rationale Funktionen
 3 Gebrochen-rationale Funktionen In diesem Kapitel werden wir die Kurvendiskussion von gebrochen-rationalen Funktionen besprechen. Prinzipiell sind die zu behandelnden Aspekte die gleichen wie bei der
3 Gebrochen-rationale Funktionen In diesem Kapitel werden wir die Kurvendiskussion von gebrochen-rationalen Funktionen besprechen. Prinzipiell sind die zu behandelnden Aspekte die gleichen wie bei der
Differentiation und Taylorentwicklung. Thomas Fehm
 Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
assume(type::real) //Definiert die Definitionsmenge über die reele a) f:=x->1/2*x^3-4*x^2+8*x // Definition einer Funktion mit der Variable "x".
 Wochenplan zu Wendestellen; Kurvendiskussion und Tangenten reset() //Entleert sämtliche Speicher! A1 assume(type::real) //Definiert die Definitionsmenge über die reele R a) f:=x->1/*x^-*x^+8*x // Definition
Wochenplan zu Wendestellen; Kurvendiskussion und Tangenten reset() //Entleert sämtliche Speicher! A1 assume(type::real) //Definiert die Definitionsmenge über die reele R a) f:=x->1/*x^-*x^+8*x // Definition
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
x 1 keinen rechtsseitigen Grenzwert x 0+ besitzen. (Analog existiert der linksseitige Grenzwert nicht.)
 Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Aufgaben zur e- und ln-funktion
 Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN. 3. Übung/Lösung Mathematik für Studierende der Biologie
 LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anreas Herz, Dr. Stefan Häusler email: haeusler@biologie.uni-muenchen.e Department Biologie II Telefon: 089-80-74800 Großhaernerstr. Fax:
LUDWIG-MAXIMILIANS-UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR BIOLOGIE Prof. Anreas Herz, Dr. Stefan Häusler email: haeusler@biologie.uni-muenchen.e Department Biologie II Telefon: 089-80-74800 Großhaernerstr. Fax:
(Unvollständige) Zusammenfassung Analysis Grundkurs
 (Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
(Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
