Übungen zu Moderne Theoretischen Physik III SS Curie-Paramagnetismus ( =30 Punkte, schriftlich)
|
|
|
- Kathrin Steinmann
- vor 7 Jahren
- Abrufe
Transkript
1 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Übungen zu Moderne heoretischen Physik III SS 06 Prof. Dr. A. Shnirman Blatt 5 PD Dr. B. Narozhny, P. Schad Lösungsvorschlag. Curie-Paramagnetismus Punkte, schriftlich amiltonoperator der Spin-J-eilchen mit Magnetfeld in z-richtung: Ĥ µ N Ĵ i µ N Ĵz. a Die Mikrozustände sind charakterisiert durch {α} {m, m, m 3,..., m N } mit Quantenzahlen m i { J, J +,..., J, J}. Die zugehörigen Energien sind E α µ N m i. i Wir bestimmen die kanonische Zustandssumme. Für unabhängige Spins faktorisiert die Zustandssumme mit Spin-Spin-Wechselwirkung ist das im Allgemeinen nicht mehr der Fall: Z tr e βĥ {α} e βeα {α} N e βµm i N +J m i J e βµm i Z N, 3 Die einzelnen Zustandssummen sind alle identisch, Z i Z, es reicht deshalb die Zustandssumme eines Spins Z zu berechnen. Dazu schreiben wir die Summe als geometrische Reihe: Z +J m J e βµm e βµj J+µ µ J e βµ p e βµj eβµj+ e βµ 4 Für den Spezialfall J kann man mit der Formel x x cosh x das evtl. bekannte Ergebnis Z cosh µ ableiten. Aus der Zustandssumme erhalten wir die freie Energie: J+µ k F, k B ln Z Nk B ln Z Nk B ln B µ J + µ Nk B ln ln µ. 5
2 b Die Entropie können wir aus der freien Energie berechnen: S F finden wir J+µ k S k B N ln B k µ B N J + µ J + µ coth k B + k B N µ µ coth k B N [ ln J+µ µ + µ coth µ. Mit Gl. 5 ] J + µ J + coth Man kann überprüfen, dass diese Entropie für 0 verschwindet, in Übereinstimmung mit dem dritten auptsatz. Die Magnetisierung erhalten wir aus M α. Es ist M x M y 0, nur F α die Komponente in Richtung des äußeren Magnetfelds ist ungleich null: M M z µn J + µ J + coth coth µ Die Magnetisierung M µn m kann auch über eine Ableitung, m Z, Z βµ direkt aus der Zustandssumme berechnet werden. Für die Wärmekapazität c S µ c Nk B µ erhalten wir manche erme kürzen sich 6 7 J +. 8 J+µ Für die Wärmekapazität c M verwenden wir das auf Blatt, Aufgabe 3 hermodyn. Antwortfunktionen erhaltene Zwischenergebnis Gl. 38 des Lösungsvorschlags zu Blatt c M c S M χ. 9 Um diese Relation zu erhalten wurde das totale Differentiale dm, benutzt, um ds, als Differential ds, M zu schreiben Alternativ diese Relation auch mit den auf Blatt, Aufgabe 3, gezeigten Identitäten erhalten werden. Wichtig ist hier, c M so auszudrücken, dass wir die oben abgeleiteten Ergebnisse S, und M, benutzen können. Die Magnetisierung M, Gl. 7, hängt nur vom Verhältnis µ k B ab, deshalb gibt es einen einfachen Zusammenhang der Ableitungen nach und : M M χ M χ. 0 Wir brauchen also noch S. Auch im Fall von S, gibt es einen Zusammenhang zwischen den Ableitungen: S S c.
3 Wir setzen jetzt 0 und in 9 ein und finden c M c c 0 Das ist das erwartete Ergebnis, da die Energie, Gl., direkt mit der Magnetisierung zusammenhängt. Bei fester Magnetisierung kann sich auch die Energie des Systems nicht ändern, deshalb erwarten wir c M 0. c Kleine Felder µ/k B : Wir nähern coth x + x. Aus Gl. 7 erhalten wir x 3 damit M µn µ 6k B J + JJ + Nµ 3k B Für die Nullfeld-Suszeptibilität erhalten wir daraus das bekannte Curie-Gesetz M χ lim C JJ + Nµ mit C k B Große Magnetfelder µ /k B : wir nähern coth x ± für 0, damit 3 M µnjsign. 5 Für große Felder ist das Spin-System gesättigt, alle Spins sind entlang des äußeren Feldes ausgerichtet.. Reißverschlußmodell eines DNA-Moleküls 0+00 Punkte, schriftlich a Die Mikrozustände sind eindeutig festgelegt durch die Anzahl p offener Bindugnen: {α} {p} mit p 0,,,..., N. Die Energie eines Mikrozustands ist E α E p N pω. Wir berechnen die Zustandssumme, die sich mit der geschlossenen Formel für geometrische Reihen vereinfachen lässt: Z α e βeα e βn pω e βnω e βω p e βnω eβωn e βω 6 und damit b Die mittlere Zahl p offener Bindungen ist Z e βωn. 7 eβω p Z p α e βeα Z α p e βn pω 8 Der Mittelwert p kann als Ableitung der Zustandssumme dargestellt werden. Dazu erweitern wir mit ±N: p Z p Ne βn pω + N Z e βn pω Z Z βω + N 9
4 Jetzt verwenden wir das Ergebnis 7 aus a, p Z und erhalten Ne βωn + eβω e βωn e βω e βω p + N Ne βωn e βωn + eβω + N, e βω N e βωn + e βω. 0 Was passiert mit dem Anteil offener Bindungen p im Grenzfall N? Das N Verhalten hängt vom Vorzeichen von Ω ab, für positives Ω folgt e βωn 0, für negatives Ω ist e βωn e βωn 0. Damit { p lim N N, Ω > 0 0, Ω < Ensemble harmonischer Oszillatoren Punkte N unabhängige und unterscheidbare -dimensionale harmonische Oszillatoren: N p i m + mω x i. In der ersten Version des Aufgabenblatts ist im Potentialterm ein Fehler passiert, es müsste mω x i statt mωx i heißen korrigiertes Aufgabenblatt ist online. a Mikrokanonisches Ensemble im klassischen Fall: die Zustände sind charakterisiert durch Koordinaten x i und Impulse p i. Wie in der Vorlesung diskutiert ist die Entropie des mikrokanonischen Ensembles gegeben durch S k B ln ΩE weil für N- dimensionale Kugeln bei großen N der größte Anteil des Volumens an der Oberfläche sitzt. Wir bestimmen zunächst das Phasenraumvolumen ΩE: ΩE π N dx dx... dx n dp dp... dp N ΘE x i, p i 3 Wir vereinheitlichen die Variablen durch folgende Substitutionen q i { m i, i,..., N m p i N, i N +,..., N. 4 Damit wird die amiltonfunktion zu N q i, und wir sehen, dass das Integral in 3 einem Integral über eine N-dimensionale Kugel mit Radius E entspricht. Das Volumen einer n-dimensionalen Kugel ist V n πn/ R n und Γn/+ n/!. Γn/+ Damit erhalten wir ΩE π ω N dq dq... dq N ΘE N q i } {{ } πn E N N! E N N! ω N. 5
5 Wir setzen dieses Ergebnis in die Entropie ein und verwenden die Stirlingformel ln N! N ln N N: SE, V, N k B ln ΩE k B N ln E N ω + k BN. 6 Interessanterweise hängt die Entropie nicht vom Volumen ab. Die Erklärung dafür steckt im Potentialterm, der effektiv das Volumen der eilchen einschränkt. Man kann die Entropie auch mit S k B ln ΣE E und Σ dω oder ohne E de ausrechnen, im Limes N sind die Ergebnisse identisch. Das Ergebnis sieht auch etwas komplizierter aus, wenn man in 3 nicht mit π normiert. Im mikrokanonischen Ensemble ist die emperatur definiert als S E V,N. Mit 6 finden wir E k B N. 7 Die emperatur ist also gerade die Energie des Systems geteilt durch die Anzahl der Oszillatoren. b Kanonisches Ensemble im klassischen Fall: Statt dem Phasenraumvolumen suchen wir das Zustandsintegral: Z dx π N dx... dx n dp dp... dp n e βx i,p i N N dp e β π N m p dx e β m ω x }{{}}{{} πm β N/ und damit Z kb ω π βmω N/ Wir berechnen die gesuchten thermodynamischen Größen: F k B ln Z F Nk B ln k B ω S F N. 8 9 S Nk B ln k B ω + k BN 30 U F + S U Nk B 3 c V S U V,N c V Nk B 3 V,N Um die Entropien aus der mikrokanonischen, Gl. 6, und der kanonischen, Gl. 30, Rechnung zu vergleichen verwenden wir U Nk B E in 30: S Nk B ln E N ω + k BN. 33 Das stimmt mit dem Ergebnis 6 erhalten für N überein.
6 c Kanonisches Ensemble im quantenmechanischen Fall: Der amiltonoperator der -dimensionalen Oszillatoren ist Ĥ N ω ˆn i Die Zustände sind charakterisiert durch die Besetzungszahlen der harmonischen Oszillatoren {α} {n,..., n N }, die Energien sind E α i ωn i +. Die kanonische Zustandssumme faktorisiert ungekoppelte Oszillatoren, wir berechnen zunächst die Zustanssumme eines einzelnen harmonischen Oszillators mit der geometrischen Reihe: Z tr e βĥ n 0 e β ωn+/ e β ω/ e. 35 β ω ω Damit erhalten wir Z α e βeα Z N ω N. 36 Wir berechnen wieder die thermodynamischen Größen: F Nk B ln ω 37 S Nk B ln ω ω ω + Nk B coth 38 U N ω ω coth 39 ω c V Nk B ω 40 Grenzfälle: : Für hohe emperaturen findet man die klassischen Ergebnisse: U Nk B, c V Nk B. 4 0: Die quantenmechanischen harmonischen Oszillatoren haben eine Nullpunktsenergie: U ωn. 4 Die endliche Nullpunktsenergie äußert sich als Energielücke in der spezifischen Wärme: ω c V Nk B e ω k B mit einer Energielücke ω. N e /k B, 43
Theoretische Physik F: Zwischenklausur SS 12
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie heoretische Physik F: Zwischenklausur SS 1 Prof. Dr. Jörg Schmalian Lösungen Dr. Igor Gornyi esprechung 18.05.01 1. Quickies:
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie heoretische Physik F: Zwischenklausur SS 1 Prof. Dr. Jörg Schmalian Lösungen Dr. Igor Gornyi esprechung 18.05.01 1. Quickies:
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet
 Freie Universität Berlin WS 2006/2007 Fachbereich Physik 26.01.2007 Statistische Physik - heorie der Wärme PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet Aufgabe 1 6 Punkte) Ein ferromagnetisches System
Freie Universität Berlin WS 2006/2007 Fachbereich Physik 26.01.2007 Statistische Physik - heorie der Wärme PD Dr. M. Falcke) Übungsblatt 12: Ferromagnet Aufgabe 1 6 Punkte) Ein ferromagnetisches System
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 6
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 6
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Prof. Dr. U. Schollwöck Sommersemester 2013
 Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Theoretische Physik 25. Juli 2013 Thermodynamik und statistische Physik (T4) Klausur Prof. Dr. U. Schollwöck Sommersemester 2013 Matrikelnummer: Aufgabe 1 2 3 4 5 6 Summe Punkte Note: WICHTIG! Schreiben
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 4 Lösung. P + a )
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter ogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 4 Lösung. van der Waals Gas, Adiabatengleichung
Übungen zur Theoretischen Physik F SS 08. ds + dv + dn = TdS pdv + µdn. w α ln(w α )
 Universität Karlsruhe Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physi F SS 08 Prof. Dr. P. Wölfle Musterlösung Dr. M. Greiter Blatt 12 1. Alle thermodynamischen Zustandgrössen,
Universität Karlsruhe Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physi F SS 08 Prof. Dr. P. Wölfle Musterlösung Dr. M. Greiter Blatt 12 1. Alle thermodynamischen Zustandgrössen,
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 7 Prof. Dr. Alexander Mirlin Musterlösung: Blatt
Theorie der Wärme Musterlösung 11.
 Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Theorie der Wärme Musterlösung. FS 05 Prof. Thomas Gehrmann Übung. Edelgas im Schwerefeld Berechne den Erwartungswert der Energie eines monoatomaren idealen Gases z. B. eines Edelgases in einem zylindrischen
Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik
 Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik begleitend zur Vorlesung Statistische Mechanik und Thermodynamik WS 2006/2007 Prof. Dr. Dieter W. Heermann erstellt
Ruprecht-Karls-Universität Heidelberg Vorbereitung zur Diplomprüfung Theoretische Physik begleitend zur Vorlesung Statistische Mechanik und Thermodynamik WS 2006/2007 Prof. Dr. Dieter W. Heermann erstellt
Erreichte Punktzahlen: Die Bearbeitungszeit beträgt 3 Stunden.
 Fakultät für Physik der LMU München Prof. Ilka Brunner Michael Kay Vorlesung T4, WS11/12 Klausur am 18. Februar 2012 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Fakultät für Physik der LMU München Prof. Ilka Brunner Michael Kay Vorlesung T4, WS11/12 Klausur am 18. Februar 2012 Name: Matrikelnummer: Erreichte Punktzahlen: 1 2 3 4 5 6 Hinweise Die Bearbeitungszeit
Vorlesung Statistische Mechanik: N-Teilchensystem
 Virialentwicklung Die Berechnung der Zustandssumme bei realen Gasen ist nicht mehr exakt durchführbar. Eine Möglichkeit, die Wechselwirkung in realen Gasen systematisch mitzunehmen ist, eine Entwicklung
Virialentwicklung Die Berechnung der Zustandssumme bei realen Gasen ist nicht mehr exakt durchführbar. Eine Möglichkeit, die Wechselwirkung in realen Gasen systematisch mitzunehmen ist, eine Entwicklung
Kapitel 3. Statistische Definition der Entropie. 3.1 Ensemble aus vielen Teilchen
 Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
Kapitel 3 Statistische Definition der Entropie 3.1 Ensemble aus vielen Teilchen Die Überlegungen dieses Abschnitts werden für klassische Teilchen formuliert, gelten sinngemäß aber genauso auch für Quantensysteme.
Erreichte Punktzahlen: Die Bearbeitungszeit beträgt 3 Stunden.
 Fakultät für Physik der LMU München Prof. Ilka Brunner Vorlesung T4p, WS08/09 Klausur am 11. Februar 2009 Name: Matrikelnummer: Erreichte Punktzahlen: 1.1 1.2 1.3 2.1 2.2 2.3 2.4 Hinweise Die Bearbeitungszeit
Fakultät für Physik der LMU München Prof. Ilka Brunner Vorlesung T4p, WS08/09 Klausur am 11. Februar 2009 Name: Matrikelnummer: Erreichte Punktzahlen: 1.1 1.2 1.3 2.1 2.2 2.3 2.4 Hinweise Die Bearbeitungszeit
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F Statistische Mechanik) SS 17 Prof. Dr. Alexander Mirlin Blatt 2 PD Dr. Igor Gornyi,
Notizen zur statistischen Physik
 Notizen zur statistischen Physik Kim Boström Begriffe der hermodynamik System: Gedanklich und im Prinzip operativ abtrennbarer eil der Welt. Physik ist das Studium der Eigenschaften von Systemen. Umgebung:
Notizen zur statistischen Physik Kim Boström Begriffe der hermodynamik System: Gedanklich und im Prinzip operativ abtrennbarer eil der Welt. Physik ist das Studium der Eigenschaften von Systemen. Umgebung:
8 Das klassische ideale Gas
 8 Das klassische ideale Gas 8.1 Unterscheidbare Atome Gleichartige Atome (etwa zwei He-Atome) sind in der Quantenmechanik grundsätzlich nicht unterscheidbar. Wir wollen dies jedoch zunächst ignorieren,
8 Das klassische ideale Gas 8.1 Unterscheidbare Atome Gleichartige Atome (etwa zwei He-Atome) sind in der Quantenmechanik grundsätzlich nicht unterscheidbar. Wir wollen dies jedoch zunächst ignorieren,
Übungen zur Theoretischen Physik F SS 12
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS Prof. Dr. Jörg Schmalian Blatt 8: Lösungen Dr. Igor Gornyi Besprechung 5.6.. Landauscher
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Theoretischen Physik F SS Prof. Dr. Jörg Schmalian Blatt 8: Lösungen Dr. Igor Gornyi Besprechung 5.6.. Landauscher
Statistische Thermodynamik I Lösungen zur Serie 11
 Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
Theorie der Kondensierten Materie I WS 2016/2017
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie I WS 216/217 Prof Dr A Shnirman Blatt 5 PD Dr B Narozhny MSc T Ludwig Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie I WS 216/217 Prof Dr A Shnirman Blatt 5 PD Dr B Narozhny MSc T Ludwig Lösungsvorschlag
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 18. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 18. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 18. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 18. 06.
Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie
 Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
Sommer-Semester 2011 Moderne Theoretische Physik III Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Di 09:45-11:15, Lehmann HS 022, Geb 30.22 Do 09:45-11:15,
ẋ = v 0 (t t 1 ). x(t) = x 1 + v 0 (t t 1 ). t 1 t 2 (x 2 x 1 ) 2 (t 2 t 1 ) 2. m (x 2 x 1 ) 2. dtl = = m x 2 x 1
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 1 Prof Dr Alexander Shnirman Blatt 7 Dr Boris Narozhny, Dr Holger Schmi 25521 1 Die
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 1 Prof Dr Alexander Shnirman Blatt 7 Dr Boris Narozhny, Dr Holger Schmi 25521 1 Die
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin WS 6/7 Fachbereich Physik 4..6 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 7: Dichtematrix, Variationsprinzip Aufgabe (5 Punkte) Betrachten Sie ein Gas
Freie Universität Berlin WS 6/7 Fachbereich Physik 4..6 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 7: Dichtematrix, Variationsprinzip Aufgabe (5 Punkte) Betrachten Sie ein Gas
Winter-Semester 2017/18. Moderne Theoretische Physik IIIa. Statistische Physik
 Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Winter-Semester 2017/18 Moderne Theoretische Physik IIIa Statistische Physik Dozent: Alexander Shnirman Institut für Theorie der Kondensierten Materie Do 11:30-13:00, Lehmann Raum 022, Geb 30.22 http://www.tkm.kit.edu/lehre/
Vorlesung Statistische Mechanik: Ising-Modell
 Ising-Modell Vorlesung Statistische Mechanik: Ising-Modell Das Ising Modell besteht auser einer Anzahl von Spins, die wir mit s i bezeichnen wollen. Jeder der N Spins kann den Wert ±1 annehmen. Die Spins
Ising-Modell Vorlesung Statistische Mechanik: Ising-Modell Das Ising Modell besteht auser einer Anzahl von Spins, die wir mit s i bezeichnen wollen. Jeder der N Spins kann den Wert ±1 annehmen. Die Spins
10.6 Mehratomige ideale Gase
 10.6 Mehratomige ideale Gase Wir wenden uns jetzt dem Problem molekularer idealer Quantengase zu. 10.6.1 Quantenmechanik der starren Hantel Eine starre Hantel aus zwei Punktmassen m 1 und m 2, die durch
10.6 Mehratomige ideale Gase Wir wenden uns jetzt dem Problem molekularer idealer Quantengase zu. 10.6.1 Quantenmechanik der starren Hantel Eine starre Hantel aus zwei Punktmassen m 1 und m 2, die durch
Theorie der Kondensierten Materie I WS 2016/2017
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie I WS 216/217 Prof. Dr. A. Shnirman Blatt 6 PD Dr. B. Narozhny, M.Sc. T. Ludwig Lösungsvorschlag
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theorie der Kondensierten Materie I WS 216/217 Prof. Dr. A. Shnirman Blatt 6 PD Dr. B. Narozhny, M.Sc. T. Ludwig Lösungsvorschlag
Übungen zur Klassischen Theoretischen Physik III (Theorie C Elektrodynamik) WS 12-13
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt Dr.
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt Dr.
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Quantentheorie für Nanoingenieure Klausur Lösung
 07. April 011 PD Dr. H. Kohler Quantentheorie für Nanoingenieure Klausur Lösung K1. Ja Nein Fragen (8P) Jede richtige Antwort liefert einen Punkt, jede falsche Antwort liefert einen Minuspunkt. Eine nicht
07. April 011 PD Dr. H. Kohler Quantentheorie für Nanoingenieure Klausur Lösung K1. Ja Nein Fragen (8P) Jede richtige Antwort liefert einen Punkt, jede falsche Antwort liefert einen Minuspunkt. Eine nicht
Moderne Theoretische Physik III (Theorie F Statistische Mechanik) SS 17
 Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F tatistische Mechanik) 17 Prof Dr lexander Mirlin Musterlösung zu latt 3 PD Dr Igor
Karlsruher Institut für echnologie Institut für heorie der Kondensierten Materie Moderne heoretische Physik III (heorie F tatistische Mechanik) 17 Prof Dr lexander Mirlin Musterlösung zu latt 3 PD Dr Igor
3.7 Das magnetische Feld in Materie
 15 KAPITEL 3. MAGNETOSTATIK 3.7 Das magnetische Feld in Materie Wie wir in den vorangegangenen Kapiteln bereits gesehen haben, wird die magnetische Induktionsdichte B durch ein Vektorpotenzial A charakterisiert,
15 KAPITEL 3. MAGNETOSTATIK 3.7 Das magnetische Feld in Materie Wie wir in den vorangegangenen Kapiteln bereits gesehen haben, wird die magnetische Induktionsdichte B durch ein Vektorpotenzial A charakterisiert,
Grundlagen der Physik 2 Schwingungen und Wärmelehre
 Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Grundlagen der Physik 2 Schwingungen und Wärmelehre Othmar Marti othmar.marti@uni-ulm.de Institut für Experimentelle Physik 14. 06. 2007 Othmar Marti (Universität Ulm) Schwingungen und Wärmelehre 14. 06.
Thermodynamik und Statistische Physik
 Thermoynamik un Statistische Physik (Kompenium Herausgegeben von Jeffrey Kelling Felix Lemke Stefan Majewsky Stan: 14. Februar 2009 1 Inhaltsverzeichnis Statistische Operatoren 3 Zustäne 3 Darstellung
Thermoynamik un Statistische Physik (Kompenium Herausgegeben von Jeffrey Kelling Felix Lemke Stefan Majewsky Stan: 14. Februar 2009 1 Inhaltsverzeichnis Statistische Operatoren 3 Zustäne 3 Darstellung
Das ferromagnetische Curie Weiss Modell 1
 Das ferromagnetische Curie Weiss Modell 1 Vorbemerkung In der Statistischen Physik können magnetische Materialien als System von miteinander wechselwirkender Elementarmagneten, sogenannter Spins, beschrieben
Das ferromagnetische Curie Weiss Modell 1 Vorbemerkung In der Statistischen Physik können magnetische Materialien als System von miteinander wechselwirkender Elementarmagneten, sogenannter Spins, beschrieben
Probeklausur STATISTISCHE PHYSIK PLUS
 DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
DEPARTMENT FÜR PHYSIK, LMU Statistische Physik für Bachelor Plus WS 2011/12 Probeklausur STATISTISCHE PHYSIK PLUS NAME:... MATRIKEL NR.:... Bitte beachten: Schreiben Sie Ihren Namen auf jedes Blatt; Schreiben
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin WS 2006/2007 Fachbereich Physik 0..2006 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 3: Zentraler Grenzwertsatz, Mikrokanonisches Ensemble, Entropie Aufgabe
Freie Universität Berlin WS 2006/2007 Fachbereich Physik 0..2006 Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke) Übungsblatt 3: Zentraler Grenzwertsatz, Mikrokanonisches Ensemble, Entropie Aufgabe
1) Brillouin-Streuung zur Ermittlung der Schallgeschwindigkeit
 Übungen zu Materialwissenschaften II Prof. Alexander Holleitner Übungsleiter: Eric Parzinger / Jens Repp Kontakt: eric.parzinger@wsi.tum.de / jens.repp@wsi.tum.de Blatt 3, Besprechung: 7. und 14.5.214
Übungen zu Materialwissenschaften II Prof. Alexander Holleitner Übungsleiter: Eric Parzinger / Jens Repp Kontakt: eric.parzinger@wsi.tum.de / jens.repp@wsi.tum.de Blatt 3, Besprechung: 7. und 14.5.214
Klassische Theoretische Physik III WS 2014/ Elektromagnetische Induktion: (3+3+4=10 Punkte)
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik III WS 014/015 Prof Dr A Shnirman Blatt 8 Dr B Narozhny Lösungen 1 Elektromagnetische Induktion:
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik III WS 014/015 Prof Dr A Shnirman Blatt 8 Dr B Narozhny Lösungen 1 Elektromagnetische Induktion:
Moderne Theoretische Physik WS 2013/2014
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik WS 23/24 Prof. Dr. A. Shnirman Blatt 2:Lösungen Dr. B. Narozhny Besprechung 8..23. Gauß scher
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Moderne Theoretische Physik WS 23/24 Prof. Dr. A. Shnirman Blatt 2:Lösungen Dr. B. Narozhny Besprechung 8..23. Gauß scher
Blatt 11.4: Deltafunktion und Fourierreihen
 Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
Seminar zur Theorie der Atome, Kerne und kondensierten Materie. Kohärente Zustände des harmonischen Oszillators. Thomas Biekötter
 Seminar zur Theorie der Atome, Kerne und kondensierten Materie Kohärente Zustände des harmonischen Oszillators Thomas Biekötter 16.11.011 QUANTENMECHANISCHER HARMONISCHER OSZILLATOR 1 Klassischer harmonischer
Seminar zur Theorie der Atome, Kerne und kondensierten Materie Kohärente Zustände des harmonischen Oszillators Thomas Biekötter 16.11.011 QUANTENMECHANISCHER HARMONISCHER OSZILLATOR 1 Klassischer harmonischer
Aufgabe 1: Elektro-mechanischer Oszillator
 37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
37. Internationale Physik-Olympiade Singapur 6 Lösungen zur zweiten Runde R. Reindl Aufgabe : Elektro-mechanischer Oszillator Formeln zum Plattenkondensator mit der Plattenfläche S, dem Plattenabstand
E 3. Ergänzungen zu Kapitel 3
 E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
E 3. Ergänzungen zu Kapitel 3 1 E 3.1 Kritisches Verhalten des van der Waals Gases 2 E 3.2 Kritisches Verhalten des Ising Spin-1/2 Modells 3 E 3.3 Theorie von Lee und Yang 4 E 3.4 Skalenhypothese nach
1 Innere Rotation von Alkanen
 Physikalische Chemie II Lösung 1 25. November 216 1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e
Physikalische Chemie II Lösung 1 25. November 216 1 Innere Rotation von Alkanen a Unter Verwendung der Energieniveaus des harmonischen Oszillators schreibt sich die Zustandssumme Q = g n e εn/kbt = = e
u v w v = 1 w u w u v schon in der Mathematik gesehen?
 Die Kettenregel für die Thermodynamik Ziel ist die in der Thermodynamik benutzten Differentiationsregeln die auf den ersten Blick nicht denen aus der Mathematik ähneln doch als dieselben zu beschreiben
Die Kettenregel für die Thermodynamik Ziel ist die in der Thermodynamik benutzten Differentiationsregeln die auf den ersten Blick nicht denen aus der Mathematik ähneln doch als dieselben zu beschreiben
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
(a) Transformation auf die generalisierten Koordinaten (= Kugelkoordinaten): ẏ = l cos(θ) θ sin(ϕ) + l sin(θ) cos(ϕ) ϕ.
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Molekulare Bioinformatik
 Molekulare Bioinformatik Wintersemester 2013/2014 Prof. Thomas Martinetz Institut für Neuro- und Bioinformatik Universität zu Luebeck 14.01.2014 1 Molekulare Bioinformatik - Vorlesung 11 Wiederholung Wir
Molekulare Bioinformatik Wintersemester 2013/2014 Prof. Thomas Martinetz Institut für Neuro- und Bioinformatik Universität zu Luebeck 14.01.2014 1 Molekulare Bioinformatik - Vorlesung 11 Wiederholung Wir
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
Symplektische Geometrie
 Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
5 Bose-Einstein-Kondensation. Suprafluidität
 Prof. Dr. A. Muramatsu Fortgeschrittene Quantentheorie WS / 9 5 Bose-Einstein-Kondensation. Suprafluidität Wie im Fall der Fermionen betrachten wir in diesem Kapitel zunächst nicht wechselwirkende Bosonen.
Prof. Dr. A. Muramatsu Fortgeschrittene Quantentheorie WS / 9 5 Bose-Einstein-Kondensation. Suprafluidität Wie im Fall der Fermionen betrachten wir in diesem Kapitel zunächst nicht wechselwirkende Bosonen.
Die ausgefrorene freie Energie des Sherrington Kirkpatrick Modells 1
 Die ausgefrorene freie Energie des Sherrington Kirkpatrick Modells Vorbemerkung In der Statistischen hysik können magnetische Materialien als System von miteinander wechselwirkender Elementarmagneten,
Die ausgefrorene freie Energie des Sherrington Kirkpatrick Modells Vorbemerkung In der Statistischen hysik können magnetische Materialien als System von miteinander wechselwirkender Elementarmagneten,
Theorie der Phasenübergänge: Eine Einführung
 Michael Kastner, SS06, Universität Bayreuth heorie der Phasenübergänge: Eine Einführung Übersicht: Ein Phasenübergang ist ein Phänomen aus der physikalischen Disziplin der Statistischen Physik bzw. der
Michael Kastner, SS06, Universität Bayreuth heorie der Phasenübergänge: Eine Einführung Übersicht: Ein Phasenübergang ist ein Phänomen aus der physikalischen Disziplin der Statistischen Physik bzw. der
Klausur zur T1 (Klassische Mechanik)
 Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Klausur zur T1 (Klassische Mechanik) WS 2006/07 Bearbeitungsdauer: 120 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
IV.2 Kanonische Transformationen
 IV.2 Kanonische Transformationen 79 IV.2 Kanonische Transformationen IV.2.1 Phasenraum-Funktionen Die verallgemeinerten Koordinaten q a t) und die dazu konjugierten Impulse p a t) bestimmen den Bewegungszustand
IV.2 Kanonische Transformationen 79 IV.2 Kanonische Transformationen IV.2.1 Phasenraum-Funktionen Die verallgemeinerten Koordinaten q a t) und die dazu konjugierten Impulse p a t) bestimmen den Bewegungszustand
Statistik und Thermodynamik
 Klaus Goeke Statistik und Thermodynamik Eine Einführung für Bachelor und Master STUDIUM VIEWEG+ TEUBNER Inhaltsverzeichnis I Grundlagen der Statistik und Thermodynamik 1 1 Einleitung 3 2 Grundlagen der
Klaus Goeke Statistik und Thermodynamik Eine Einführung für Bachelor und Master STUDIUM VIEWEG+ TEUBNER Inhaltsverzeichnis I Grundlagen der Statistik und Thermodynamik 1 1 Einleitung 3 2 Grundlagen der
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
Theorie von Phasenübergängen Die Landau-Theorie
 Seminar: Theorie der Teilchen und Felder Theorie von Phasenübergängen Die Landau-Theorie Bastian Brandt 1 1 bastianbrandt@uni-muenster.de Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Die Landau-Theorie
Seminar: Theorie der Teilchen und Felder Theorie von Phasenübergängen Die Landau-Theorie Bastian Brandt 1 1 bastianbrandt@uni-muenster.de Inhaltsverzeichnis 2 Inhaltsverzeichnis 1 Einleitung 3 2 Die Landau-Theorie
Lernhilfe zur Diplomprüfung Thermodynamik
 Lernhilfe zur Diplomprüfung Thermodynamik Diese Zusammenfassung wurde für die Vorbereitung auf meine Diplomprüfung erstellt. Bei Fehlern bitte ich um Korrekturhinweise. Inhaltsverzeichnis I Thermodynamik
Lernhilfe zur Diplomprüfung Thermodynamik Diese Zusammenfassung wurde für die Vorbereitung auf meine Diplomprüfung erstellt. Bei Fehlern bitte ich um Korrekturhinweise. Inhaltsverzeichnis I Thermodynamik
Seminar für Fragen der Festkörpertheorie. P.N. Racec
 Seminar für Fragen der Festkörpertheorie P.N. Racec WS2003/2004 2 Contents Spezialthemen in Festkörperphysik 5. Fermi-Dirac Verteilungsfunktion........................ 6.2 Bose-Einstein Verteilungsfunktion.......................
Seminar für Fragen der Festkörpertheorie P.N. Racec WS2003/2004 2 Contents Spezialthemen in Festkörperphysik 5. Fermi-Dirac Verteilungsfunktion........................ 6.2 Bose-Einstein Verteilungsfunktion.......................
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
1 Massenwirkungsgesetz
 1 Massenwirkungsgesetz Zeige: Bei konstantem Druck und konstanter emperatur gilt für chemische Reaktionen der Art a 1 A 1 + a A + : : : a L A L b 1 B 1 + b B + : : : b R B R : K c (A i ) ai c (B j ) bj
1 Massenwirkungsgesetz Zeige: Bei konstantem Druck und konstanter emperatur gilt für chemische Reaktionen der Art a 1 A 1 + a A + : : : a L A L b 1 B 1 + b B + : : : b R B R : K c (A i ) ai c (B j ) bj
Klausur zur Statistischen Physik SS 2013
 Klausur zur Statistischen Physik SS 2013 Prof. Dr. M. Rohlfing Die folgenden Angaben bitte deutlich in Blockschrift ausfüllen: Name, Vorname: geb. am: in: Matrikel-Nr.: Übungsgruppenleiter: Aufgabe maximale
Klausur zur Statistischen Physik SS 2013 Prof. Dr. M. Rohlfing Die folgenden Angaben bitte deutlich in Blockschrift ausfüllen: Name, Vorname: geb. am: in: Matrikel-Nr.: Übungsgruppenleiter: Aufgabe maximale
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Beschreibung von Phasenübergängen und kritischen Phänomenen im Rahmen von Thermodynamik und statistischer Physik
 Seminar zur heorie der eilchen und Felder Beschreibung on Phasenübergängen und kritischen Phänomenen im Rahmen on hermodynamik und statistischer Physik Steffen Decking 07.03.013 Inhaltserzeichnis 1. Einleitung
Seminar zur heorie der eilchen und Felder Beschreibung on Phasenübergängen und kritischen Phänomenen im Rahmen on hermodynamik und statistischer Physik Steffen Decking 07.03.013 Inhaltserzeichnis 1. Einleitung
Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge zu Übungsblatt 4
 TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
TUM, Zentrum Mathematik Lehrstuhl für Mathematische Physik WS 3/4 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weidner Tutoraufgaben: Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge
Blatt 1. Kinematik- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Statistische Physik - Theorie der Wärme (PD Dr. M. Falcke)
 Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Freie Universität Berlin W 006/007 Fachbereich Physik 8..006 tatistische Physik - heorie der Wärme (PD Dr. M. Falcke) Übungsblatt 9: hermodynamische Identitäten, hermische/kalorische Zustandsgleichung,
Differentialformen. Lie-Ableitung von Differentialformen und Poincaré-Formel. Differentialform dp dx und ihre Invarianz bzgl. Hamiltonischer Flüsse.
 Differentialformen Plan Zuerst lineare Algebra: Schiefsymmetrische Formen im R n. Dann Differentialformen: Invarianz bzgl. Diffeomorphismen (und sogar beliebigen glatten Abbildungen). Äußere Ableitung.
Differentialformen Plan Zuerst lineare Algebra: Schiefsymmetrische Formen im R n. Dann Differentialformen: Invarianz bzgl. Diffeomorphismen (und sogar beliebigen glatten Abbildungen). Äußere Ableitung.
Aufgabe 4 3. Hauptsatz* Beschreiben Sie in einem Satz die Aussage des dritten Hauptsatzes der Thermodynamik.
 E-Ep: Experimentalphysik Prof. J. Lipfert SS 018 Übungsblatt 5 Thermodynamik 5 Das 5. Übungsblatt wird in der Zentralübung am Dienstag den 15. Mai von 1-14 Uhr im großen Physikhörsaal besprochen. Aufgaben,
E-Ep: Experimentalphysik Prof. J. Lipfert SS 018 Übungsblatt 5 Thermodynamik 5 Das 5. Übungsblatt wird in der Zentralübung am Dienstag den 15. Mai von 1-14 Uhr im großen Physikhörsaal besprochen. Aufgaben,
Kapitel 5. Kanonisches Ensemble. 5.1 Herleitung 1; E 1 =? 2; E 2 =?
 Kapitel 5 Kanonisches Ensemble 5.1 Herleitung Abgesehen von der Legendre-Transformation S(E,, N) F (T,, N) besteht noch eine weitere Möglichkeit, die freie Energie zu berechnen, und zwar wiederum mittels
Kapitel 5 Kanonisches Ensemble 5.1 Herleitung Abgesehen von der Legendre-Transformation S(E,, N) F (T,, N) besteht noch eine weitere Möglichkeit, die freie Energie zu berechnen, und zwar wiederum mittels
Thermodynamik und Statistische Physik
 hermodynamik und Statistische Physik Matthias Vojta Institut für heoretische Physik U Dresden, WS 0/3 hermodynamik Nullter Hauptsatz Für jedes thermodynamische System existiert eine intensive Zustandsgröße
hermodynamik und Statistische Physik Matthias Vojta Institut für heoretische Physik U Dresden, WS 0/3 hermodynamik Nullter Hauptsatz Für jedes thermodynamische System existiert eine intensive Zustandsgröße
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
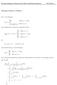 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Abbildung 10.1: Das Bild zu Beispiel 10.1
 Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Seminar zur Theorie der Teilchen und Felder Phasenübergänge und kritische Phänomene. Landau-Theorie. für Phasenübergänge 2.
 Seminar zur Theorie der Teilchen und Felder Phasenübergänge und kritische Phänomene Landau-Theorie für Phasenübergänge 2. Ordnung Semir Vrana 0.05.202 INHALTSVERZEICHNIS Inhaltsverzeichnis Einleitung 2
Seminar zur Theorie der Teilchen und Felder Phasenübergänge und kritische Phänomene Landau-Theorie für Phasenübergänge 2. Ordnung Semir Vrana 0.05.202 INHALTSVERZEICHNIS Inhaltsverzeichnis Einleitung 2
(dφ) 2 + (dz) 2. φ 2 dφ mit z=z(φ).
 PD Dr. S. Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt 5 WS 8/9.. 8. Strecke auf Zylinder. Bestimmen Sie die kürzeste Verbindung zwischen zwei Punkten auf Pkt.) dem Zylinder.
PD Dr. S. Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt 5 WS 8/9.. 8. Strecke auf Zylinder. Bestimmen Sie die kürzeste Verbindung zwischen zwei Punkten auf Pkt.) dem Zylinder.
Blatt 05.2: Green sche Funktionen
 Fakultät für Physik T: Klassische Mechanik, SoSe 05 Dozent: Jan von Delft Übungen: Katharina Stadler, Frauke Schwarz, Dennis Schimmel, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5t/
Fakultät für Physik T: Klassische Mechanik, SoSe 05 Dozent: Jan von Delft Übungen: Katharina Stadler, Frauke Schwarz, Dennis Schimmel, Lukas Weidinger http://homepages.physik.uni-muenchen.de/~vondelft/lehre/5t/
Seminar zur Theorie der Teilchen und Felder Supersymmetrie
 Alexander Hock a-hock@gmx.net Seminar zur Theorie der Teilchen und Felder Supersymmetrie Datum des Vortrags: 28.05.2014 Betreuer: Prof. Dr. J. Heitger Westfälische Wilhelms-Universität Münster, Deutschland
Alexander Hock a-hock@gmx.net Seminar zur Theorie der Teilchen und Felder Supersymmetrie Datum des Vortrags: 28.05.2014 Betreuer: Prof. Dr. J. Heitger Westfälische Wilhelms-Universität Münster, Deutschland
TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1. Dr. M. Herrich SS 2017
 TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1 Prof. Dr. K. Eppler Institut für Numerische Mathematik Dr. M. Herrich SS 2017 Aufgabe 1 Übungen zur Vorlesung Mathematik II 4. Übung,
TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1 Prof. Dr. K. Eppler Institut für Numerische Mathematik Dr. M. Herrich SS 2017 Aufgabe 1 Übungen zur Vorlesung Mathematik II 4. Übung,
Übungen zur Klassischen Theoretischen Physik III (Theorie C Elektrodynamik) WS 12-13
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt 4: Lösungen
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Übungen zur Klassischen Theoretischen Physik III Theorie C Elektrodynamik WS 2-3 Prof. Dr. Alexander Mirlin Blatt 4: Lösungen
Kapitel 4. Thermodynamisches Gleichgewicht zwischen zwei Systemen. 4.1 Systeme im thermischen Kontakt 1; E 1 =? 2; E 2 =?
 Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Ferienkurs Experimentalphysik Übung 2 - Musterlösung
 Ferienkurs Experimentalphysik 4 00 Übung - Musterlösung Kopplung von Drehimpulsen und spektroskopische Notation (*) Vervollständigen Sie untenstehende Tabelle mit den fehlenden Werten der Quantenzahlen.
Ferienkurs Experimentalphysik 4 00 Übung - Musterlösung Kopplung von Drehimpulsen und spektroskopische Notation (*) Vervollständigen Sie untenstehende Tabelle mit den fehlenden Werten der Quantenzahlen.
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 11 1 Hamiltonsche Mechanik, kanonische Transformationen und Hamilton-Jacobi-Theorie Wie die Lagrangesche Mechanik
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 11 1 Hamiltonsche Mechanik, kanonische Transformationen und Hamilton-Jacobi-Theorie Wie die Lagrangesche Mechanik
Moderne Theoretische Physik III
 Moderne Theoretische Physik III Statistische Physik Alexander Mirlin SS 205 Inhaltsverzeichnis Übersicht vi Inhalt............................................ vi Literatur..........................................
Moderne Theoretische Physik III Statistische Physik Alexander Mirlin SS 205 Inhaltsverzeichnis Übersicht vi Inhalt............................................ vi Literatur..........................................
Thermodynamik un Statistische Mechanik
 Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik un Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispiele n und Aufgaben mit ausführlichen
Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik un Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispiele n und Aufgaben mit ausführlichen
Blatt 05.3: Green sche Funktionen
 Fakultät für Physik T: Klassische Mechanik, SoSe 06 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_6/t_theor_mechanik/
Fakultät für Physik T: Klassische Mechanik, SoSe 06 Dozent: Jan von Delft Übungen: Benedikt Bruognolo, Sebastian Huber, Katharina Stadler, Lukas Weidinger http://www.physik.uni-muenchen.de/lehre/vorlesungen/sose_6/t_theor_mechanik/
[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration
![[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration [A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration](/thumbs/66/55829074.jpg) 1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
Klassische Theoretische Physik: Elektrodynamik
 Klassische Theoretische Physik: Elektrodynamik Kaustuv Basu (Deutsche Übersetzung: Jens Erler) Argelander-Institut für Astronomie Auf dem Hügel 71 kbasu@astro.uni-bonn.de Website: www.astro.uni-bonn.de/tp-l
Klassische Theoretische Physik: Elektrodynamik Kaustuv Basu (Deutsche Übersetzung: Jens Erler) Argelander-Institut für Astronomie Auf dem Hügel 71 kbasu@astro.uni-bonn.de Website: www.astro.uni-bonn.de/tp-l
10. und 11. Vorlesung Sommersemester
 10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
Wahrscheinlichkeitsrechnung und Statistik
 5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
Musterlösungen zu Blatt 14
 Musterlösungen zu Blatt 4 Aufgabe 79 Sei F eine Stammfunktion von f (eistiert, da f stetig ist). Dann ist b() a() f(t)dt = F (b()) F (a()) nach dem Hauptsatz der Differential- und Integralrechnung. Man
Musterlösungen zu Blatt 4 Aufgabe 79 Sei F eine Stammfunktion von f (eistiert, da f stetig ist). Dann ist b() a() f(t)dt = F (b()) F (a()) nach dem Hauptsatz der Differential- und Integralrechnung. Man
Thermodynamik und Statistische Mechanik
 Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik und Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispielen und Aufgaben mit ausführlichen
Theoretische Physik Band 9 Walter Greiner Ludwig Neise Horst Stöcker Thermodynamik und Statistische Mechanik Ein Lehr- und Übungsbuch Mit zahlreichen Abbildungen, Beispielen und Aufgaben mit ausführlichen
Institut für Theorie der Kondensierten Materie. Universität Karlsruhe
 Theorie F: Statistische Physik P. Wölfle Institut für Theorie der Kondensierten Materie Universität Karlsruhe http://www-tkm.physik.uni-karlsruhe.de Vorlesung SS 200 und SS 2007 Ausarbeitung: Daniel Hermann
Theorie F: Statistische Physik P. Wölfle Institut für Theorie der Kondensierten Materie Universität Karlsruhe http://www-tkm.physik.uni-karlsruhe.de Vorlesung SS 200 und SS 2007 Ausarbeitung: Daniel Hermann
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
7 Zwei- und Dreidimensionale Probleme in kartesischen Koordinaten
 7 Zwei- und Dreidimensionale Probleme in kartesischen Koordinaten 7.1 Das Teilchen im -Dimensionalen Kasten Slide 119 Das Teilchen im Kasten Das Teilchen soll sich zwischen = 0 und = L und = 0 und = L
7 Zwei- und Dreidimensionale Probleme in kartesischen Koordinaten 7.1 Das Teilchen im -Dimensionalen Kasten Slide 119 Das Teilchen im Kasten Das Teilchen soll sich zwischen = 0 und = L und = 0 und = L
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5 Fehlerfortpflanzung
 5 Fehlerfortpflanzung Diese Lektion folgt D.S. Sivia, Data Analysis: A Bayesian Tutorial, Oxford University Press, Chapter 3.6. Lernziele Lektion 5 Sie wissen, wie man Wahrscheinlichkeitsverteilungen von
5 Fehlerfortpflanzung Diese Lektion folgt D.S. Sivia, Data Analysis: A Bayesian Tutorial, Oxford University Press, Chapter 3.6. Lernziele Lektion 5 Sie wissen, wie man Wahrscheinlichkeitsverteilungen von
