Zusatzmaterial zur Mathematik I für E-Techniker Übung 7
|
|
|
- Benjamin Schmitt
- vor 7 Jahren
- Abrufe
Transkript
1 Mathemati I für E-Technier C. Erdmann WS 0/, Universität Rostoc, 7. Vorlesungswoche Zusatzmaterial zur Mathemati I für E-Technier Übung 7 Loale Etrema, Satz von Rolle, Mittelwertsatz Man sagt, in liegt ein loales Maimum, wenn fy f für alle y aus einer Umgebung U von gilt analog: loales Minimum. Notwendige Bedingung für loale Etrema: Liegt in ein loales Maimum/Minimum der differenzierbaren Funtion f, dann gilt f 0. Satz von Rolle: Sei < a < b < und f : [a, b] R eine stetige Funtion mit fa fb. Die Funtion f sei in ]a, b[ differenzierbar. Dann eistiert ein ξ ]a, b[ mit f ξ 0. Folgerung Mittelwertsatz: Sei < a < b < und f : [a, b] R eine stetige Funtion, die in ]a, b[ differenzierbar ist. Dann eistiert ein ξ ]a, b[, so dass fb fa b a f ξ. Das Monotonieverhalten wird durch die Ableitung bestimmt: f 0 ist äquivalent dazu, dass f monoton wächst f 0 äquivalent dazu, dass f monoton fällt. Hinreichende Bedingung für loale Etrema: Konveität Ist f :]a, b[ R zweimal differenzierbar und gilt f 0, so besitzt f ein loales Minimum in ]a, b[, falls außerdem f > 0 anlog f < 0 für Maima. Ist f :]a, b[ R differenzierbar und gilt neben f 0 auch noch f 0 lins von und f 0 rechts von, so liegt in ein loales Minimum vor analog für Maima. Sei D R ein Intervall. Eine Funtion f : D R heißt onve, falls, D λ R 0 < λ < fλ + λ λf + λf. f heißt onav, falls f onve. Satz: Sei D R ein offenes Intervall, f : D R zweimal differenzierbar. Dann gilt Bernoulli- L Hospitalsche Regel f onve D : f 0 Seien f :]a, b[ R, g :]a, b[ R a < b zwei differenzierbare Funtionen. Sei g 0 für alle f ]a, b[, und es gelte f 0 g bzw. f g. Eistiert λ b b b b b g auch als uneigentlicher Grenzwert, so gilt f b g Eine entsprechende Aussage gilt für a. Taylor-Formel, Taylor-Reihen, Taylor-Polynome λ b f g. Satz [Taylor-Formel]: Sei I R ein Intervall und f : I R eine n + -mal stetig differenzierbare Funtion. Dann gilt für alle, 0 I die Taylorsche Formel f oder n 0 f R n+ mit dem Restglied R n+ : t n f n+ t dt! n! 0 R n+ : Definition: Es heißt T f,0,n n 0n+ n! 0 0 θ n f n+ 0 + θ 0 dθ. f 0! 0 das n -te Taylorpolynom von f bei 0.
2 Satz [Lagrange sche Form des Restgliedes]: Sei f : [a, b] R. Für n 0 eistiere die n -te Ableitung f n : [a, b] R, welche stetig sei. Weiterhin eistiere die n + -te Ableitung f n+ : ]a, b[ R im Inneren. Dann eistiert für beliebige, 0 [a, b] mit 0 ein ξ zwischen und 0 oder alternativ ein θ ]0, [, so dass die Taylorsche Formel f n 0 f 0! 0 + R n+ mit dem Restglied R n+ : f n+ ξ 0n+ n +! oder R n+ : f n+ 0 + θ 0 0 n+ gilt. R n+ heißt Lagrange sches Restglied. n +! Definition [Taylor-Reihe]: Ist eine Funtion f : [a, b] R beliebig oft stetig differenzierbar und 0 [a, b], dann heißt die Potenzreihe f 0 T f,0 : 0! 0 die Taylor-Reihe oder Taylor-Entwiclung von f um den Entwiclungspunt 0. Der Konvergenzradius muss nicht > 0 sein und auf dem Konvergenzintervall muss T f,0 auch nicht unbedingt gegen f onvergieren, sondern tut dies nur dann, wenn das Restglied für n gegen 0 onvergiert. Satz [Abelscher Grenzwertsatz]: Ist c n n N0 eine reelle Zahlenfolge und onvergiert c n, dann on- vergiert die Potenzreihe f : c n n gleichmäßig auf [0, ]. n0 Satz: n Für alle < und sogar gilt ln + n. Logarithmus-Reihe n n Für alle gilt arctan n n+ n +. Arcus-Tangens-Reihe n0 Sei α R. Für alle < gilt dann + α α n. Binomische Reihe n n Zusatzaufgaben mit Lösungen n0 Aufgabe 7.. Bestimme die Ableitung der folgenden Funtionen jeweils mittels des Satzes über die Ableitung der Umehrfuntion: a f arcsin b f arccos c f arccot Lösung zu Aufgabe 7.. a Offensichtlich ist f d sin und sin cos. Somit gilt d f cos arcsin. Wobei die letzte Gleichheit aus der Tatsache folgt, dass für y arcsin gilt dass cosy sin y. b Offensichtlich ist f d cos und cos sin. Somit gilt d f sin arccos. Wobei die letzte Gleichheit aus der Tatsache folgt, dass für y arccos gilt dass siny cos y. c Offensichtlich ist f d cos cot und d sin sin cot. Somit gilt f + cotarccot +.
3 Aufgabe 7.. i Bestimmen Sie die Intervalle, in denen die folgenden Funtionen monoton fallend, bzw. monoton wachsend sind! ii Bestimmen Sie mit Hilfe von i die loalen Etrema der Funtionen! iii Bestimmen Sie die Intervalle, in denen die folgenden Funtionen onav, bzw. onve sind! iv Bestimmen Sie die Wendestellen der Funtionen! a f b f sin cos c f e 55 Lösung zu Aufgabe 7.. a Die ersten beiden Ableitungen lauten f f i Zur Untersucheung der Monotonie setzen wir die. Ableitung 0 und erhalten , 5 ± 5 5 ±, somit als ritische Stellen und. Da f stetig ist, önnen wir uns bei der weiteren Untersuchung der Monotonie auf die drei Intervalle,,, und, beschränen. Aufgrund der Stetigeit önnen wir den ZWS anwenden und uns jeweils auf beliebige Vertreter der Intervalle beschränen. f 000 > 0 f ist monoton wachsend in, f 5 < 0 f ist monoton fallend in, f 000 > 0 f ist monoton wachsend in, ii Aufgrund des Übergangs der Monotoniearten önnen wir nun schließen, dass bei eine loale Maimalstelle und bei eine loale Minimalstelle vorliegt. Dabei handelt es sich aber nicht um globale Etremstellen, da f, f. iii Zur Untersuchung der Konveität setzen wir die.ableitung 0 und erhalten Da f stetig ist, önnen wir uns bei der weiteren Untersuchung der Konveität auf die beiden Intervalle, 5 und 5, beschränen. Aufgrund der Stetigeit önnen wir den ZWS anwenden und uns auf jeweilige Vertreter der Intervalle beschränen. f 000 < 0 f ist onav in, 5 f 000 > 0 f ist onve in 5, iv Aufgrund des Wechsels bei der Konveität liegt bei 5 b Die ersten beiden Ableitungen lauten f cos sin cos, eine Wendestelle vor. f cos sin i Zur Untersucheung der Monotonie setzen wir die. Ableitung 0 und erhalten 0 cos cos, { somit als ritische Punte +π } Z. Da f stetig und π -periodisch ist, önnen wir uns bei der weiteren Untersuchung der Monotonie auf die vier Intervalle π, π, π, π, π, 5π und
4 5π, 7π beschränen. Aufgrund der Stetigeit önnen wir den ZWS anwenden und uns jeweils auf beliebige Vertreter der Intervalle beschränen. f 0 > 0 f ist monoton wachsend in 8 π 8 + π, f π 8 + π < 0 f ist monoton fallend in 8 + π, 8 + π f 8 + 5π π > 0 f ist monoton wachsend in, f π 8 + 5π < 0 f ist monoton fallend in, 8 + 7π, Z, Z, Z, Z { ii Aufgrund des Übergangs der Monotoniearten önnen wir nun schließen, dass bei +π } Z jeweils { eine loale Maimalstelle und bei +π } Z jeweils eine loale Minimalstelle vorliegt. Dabei ist jede loale Etremstelle zugleich auch globale Etremstelle, da f π -periodisch ist. iii Zur Untersuchung der Konveität setzen wir die.ableitung 0 und erhalten { } π 0 cos sin Z. Da f stetig und π -periodisch ist, önnen wir uns bei der weiteren Untersuchung der Konveität auf die vier Intervalle 0, π, π, π, π, π und π, π beschränen. Aufgrund der Stetigeit önnen wir den ZWS anwenden und uns auf jeweilige Vertreter der Intervalle beschränen. f π π + π < 0 f ist onav in,, Z f π + π + π > 0 f ist onve in,, Z f 5π + π + π < 0 f ist onav in,, Z f 7π + π + π > 0 f ist onve in,, Z c iv Aufgrund des Wechsels bei der Konveität liegen bei { π Z} jeweils Wendestellen vor. Es ergeben sich für die erste und zweite Ableitung der Funtion f e 8 + 7, f e. i Es ist e > 0 für alle R und als nach oben geöffnete Parabel ist { 0 für [ 7, 8] > 0 für R \ [ 7, 8]. Demnach ist f monoton fallend in [ 7, 8] denn dort ist die Ableitung nichtpositiv und monoton wachsend in ], 7] bzw. in [8, [ denn dort ist die Ableitung nichtnegativ. ii Wiederum ist e > 0 für alle R und als nach oben geöffnete Parabel ist [ ] 0 für, [ ]. > 0 für R \, [ Demnach ist f onav in ] ] in, bzw. in ], ], [ denn dort ist die zweite Ableitung nichtpositiv und onve denn dort ist die zweite Ableitung nichtnegativ. iii Aus dem Monotonieverhalten der Funtion folgt: Bei 7 besitzt f ein loales Maimum mit Wert f 7 8e. Bei 8 besitzt f ein loales Minimum mit Wert f8 7e 6. Weitere loale Etremstellen besitzt die Funtion nicht, da alle Punte des Definitionsintervalls innere Punte sind und f 0 genau dann, wenn { 7, 8}.
5 Da f und f 0 > 7e6 f8, folgt: Die Funtion f besitzt in 8 ein globales Minimum mit Wert f8 7e 6. Die Funtion f besitzt eine weiteren globalen Etremstellen. iv Aus dem Wölbungsverhalten der Funtion folgt: Bei und besitzt f Wendepunte. Die Funtion besitzt eine weiteren Wendepunte, { da alle Punte des } Definitionsintervalls innere Punte sind und f 0 genau dann, wenn,. Aufgabe 7.. a Man bestimme die loalen und globalen Etrema der Funtion f + + +, [, ] b Sind die folgenden Funtionen in der Umgebung von 0 0 onav oder onve? f 7 + g arctan + Lösung zu Aufgabe 7.. a Die ersten beiden Ableitungen sind gegeben durch f + + f 6 +. Setzen wir die erste Ableitung Null, so erhalten wir die ritischen Punte f + + 0, ± 9 9, ± Somit beommen wir als Kandidaten für loale Etrema und. Wegen f 6 < 0, f > 0 handelt es sich bei um ein loale Maimumstelle und bei Weiterhin handelt es sich wirlich nur um loale Etremstellen, da um eine loale Minimumstelle. f ±. ± b Um zu erennen, ob eine -mal stetig differenzierbare Funtion onve oder onav ist, önnen wir die. Ableitung bilden. Diese lauten f 6 > 0 und g g + g < 0 Dementsprechend ist die Funtion f bei 0 0 onve und die Funtion g bei 0 0 onav. Aufgabe 7.. a Man beweise die Ungleichung < ln + < + für > 0. Hinweis: Man wende den Mittelwertsatz der Differentialrechnung auf f ln + an. b Zeigen Sie durch vollständige Indution, dass f! + die -te Ableitung der Funtion f ln + ist. 5
6 Lösung zu Aufgabe 7.. a Sei a 0 und b. Offenbar ist f ln + stetig in [a; b] und differenzierbar in a, b. Daher eistiert nach dem Mittelwertsatz ein ξ a, b 0, mit Weil ξ 0, folgt daraus, dass sowie b IA: fb fa b a ln + d ln + d ln + ln + + ξ. + ξ > +, + ξ <. + + IS: + IV: Es gelte f! + für ein. IB: zu zeigen: f +! + Beweis der IB: f + d+ ln + d + d d ln + d d d! + d! + I.V.! + Aufgabe 7.5. An den Ecen einer rechtwinligen Platte mit den Seiten a und b seien gleichgroße Quadrate ausgeschnitten. Aus der verbleibenden reuzförmigen Figur werde eine offene Schachtel hergestellt, deren Höhe gleich der Seitenlänge der ausgechnittenen Quadrate ist. Man bestimme diejenige Seitenlänge der Quadrate, für welche die Schachtel das größte Volumen hat! Lösung zu Aufgabe 7.5. Die zu maimierende Funtion ist gegeben durch f Höhe Länge Breite a b ab a b + a + b + ab. Leiten wir diese zweimal ab, so folgt f a + b + ab, f a + b. Setzen wir nun die erste Ableitung gleich Null, so ergeben sich als Lösung f a + b + ab 0 ab a + b + 0 a + b a + b, ± ab a + b, ± a ab + b 6 6. Offensichtlich ist f > 0 für > a+b und f < 0 für < a+b. Da 6 6 a+b a ab + b 6 6 < a+b 6 liegt in ein loales Maimum vor. Aufgabe 7.6. Welcher Punt auf dem Graphen der Funtion f + hat zu ; den minimalsten Abstand? Lösung zu Aufgabe 7.6. Für das Quadrat der Distanzfuntion gilt dist
7 Um das Minimum zu finden bilden wir die.ableitung und erhalten dist + +. Dies setzen wir 0 und erhalten mittels quadratischer Lösungsformel, ± ± 7. Logischerweise entfällt die negative Lösung und es beibt 7 als Lösung übrig. Dies ist wirlich ein Minimum, denn es gilt dist 6 +, dist 7 > 0 Aufgabe 7.7. Es soll ein Tunnel mit möglichst großen Umfang entstehen. Dabei setzt sich der Tunnelquerschnitt aus einem Rechtec mit aufgesetztem Halbreis zusammen. Der Flächeninhalt soll als onstant angenommen werden. Wie groß ist das Rechtec zu wählen? Lösung zu Aufgabe 7.7. Der Flächeninhalt ist gegeben durch und der Umfang durch A Aa, r a r + r π Ua, r r + a + rπ. Die Formel für den Flächeninhalt stellen wir nach a um und erhalten a A r rπ. Dies setzen wir in die Funtion für den Umfang ein und erhalten Ua, r Ur r + A r rπ + rπ r + A r + rπ. Dies leiten wir nach r ab und setzen die Ableitung 0, also U r A r + π 0. Somit lautet die Lösung A r + π. Dementsprechend hat das Rechtec Seitenlängen von A + π und A A + π A + π π. Aufgabe 7.8. Unter allen Rechtecen von gegebenen Unfang l ist dasjenige mit maimalem Flächeninhalt zu bestimmen. Lösung zu Aufgabe 7.8. Der Flächeninhalt eines Rechteces ist durch gegeben, der Umfang durch Aa, b ab Ua, b l a + b. Da der Umfang gegeben ist, stellen wir einfach nach der Seite a um und setzen das Ergebnis in die Formel für den Flächeninhalt ein. Dann bestimmen wir davon die Ableitung und setzen diese 0. Ab lb b, dab db l b 0 b l 7
8 Also erhalten wir insgesamt, dass a b l. Das Ergebnis ist also immer ein Quadrat. Dass es sich wirlich um ein Maimum handelt folgt aus d Ab < 0. db Aufgabe 7.9. Welche Punte, y der Hyperbel y haben vom Punt ; 0 die leinste Entfernung? Lösung zu Aufgabe 7.9. Die Distanzfuntion ist offensichtlich durch dist gegeben. Leiten wir diese ab und setzen dies dann 0, dann erhalten wir ddist d 0. Setzen wir dies ein, so erhalten wir für die y -Koordinate y ± 5 folgt aus ddist > 0. d. Dass es sich wirlich um ein Minimum handelt Aufgabe 7.0. Sei f : + + e. a Berechnen Sie für den Graphen dieser Funtion f die Koordinaten der Schnittpunte mit den Koordinatenachsen und die Koordinaten der Etrem- und Wendepunte! b In welchen Intervallen ist f onve bzw. onav? c Sizzieren Sie den Graphen von f im Intervall [, 8]. Geben Sie alle für diese Darstellung verwendeten Eigenschaften an und begründen Sie diese! Lösung zu Aufgabe 7.0. Zu ersteinmal berechnen wir die ersten Ableitungen von f : f e + f e f e + a Der Schnittpunt mit der Ordinate y-achse ist durch 0, f0 0, gegeben. Der Schnittpunt mit der Abzisse -Achse ist als Lösung der Gleichung f 0 definiert: f + + }{{} + Somit ist der Schnittpunt eigentlich handelt es sich um einen Berührungspunt durch, 0 gegeben. Um eine Menge von Stellen zu erhalten, die als Etremstellen in Frage ommen ritische Stellen, setzen wir die. Ableitung Null: f }{{} e + 0 }{{} >0 + Demnach ommen als ritische Stellen, ± in Frage. Um die Art des Etremums zu bestimmen, setzen wir in die. Ableitung ein und erhalten e }{{} >0 0. f e e < 0, f e + e > 0. Daher liegt im Punt, f, e ein loales Maimum und bei, 0 ein loales Minimum vor. Um die Menge der Kandidaten zu bestimmen, die als Wendepunte in Frage ommen, setzen wir die. Ableitung Null f e }{{} }{{} >0 R + 0 8
9 Somit ommen, ± als Kandidaten für die Wendestellen in Frage. Damit dies auch wirlich der Fall ist, setzen wir in die. Ableitung ein und erhalten f ± 0. Somit liegen bei +, e und, + + e + jeweils Wendepunte vor. b Um das Krümmungsverhalten von f zu untersuchen, betrachten wir die Ergebnisse aus der ersten Teilaufgabe genauer und studieren die zweite Ableitung. Als ritische Punte haben wir, ± berechnet. Weil f eine C R Funtion ist, ann sich nur an diesen beiden Stellen das Krümmungsverhalten ändern. Da bei eine loale Maimumstelle vorliegt, muss die Funtion im Intervall, + onav sein. Da wir auch schon verifiziert hatten, dass bei, Wendestellen liegen und sich dort das Krümmungsverhalten ändert, folgt, dass f in den Intervallen, und +, onve sein muss. c Die Begründung der Sizze ist offensichtlich und steht in den beiden vorangegangenen Aufgabenteilen. Aufgabe 7.. Man beweise mittels vollständiger Indution die LEIBNIZsche Produtregel n f g n n f n g 0 Lösung zu Aufgabe 7.. IA: n d d f g f g 0 + f 0 g IS: n n + IV: Es gelte f g j j j 0 f j g für alle j n. IB: zu zeigen: f g n+ n+ 0 f n+ g n+ f g 0 9
10 Beweis der IB: f g n+ I.V. n + n d f g n d n d d n f n g n n f n+ g + f n g + n n n f n+ g n + f n g + n 0 n n f n+ g + f n+ g + n+ 0 n n+ n + f n+ g + f n+ g + fg n+ n+ n + f n+ g. f n+ g + fg n+ Aufgabe 7.. Mit Hilfe des Mittelwertsatzes der Differentialrechnung beweise man die Ungleichung e + R. Lösung zu Aufgabe 7.. Sei a 0 und b >. Offenbar ist f ln + stetig in [a, b] und differenzierbar in a, b. Daher eistiert nach dem Mittelwertsatz ein ξ a, b 0, für, 0 dreht sich das Intervall natürlich um, jedoch ändert das nichts an der Vorgehensweise mit fb fa b a ln + + ξ. Weil ξ 0, folgt daraus, dass ln + + ξ +, sowie ln + >. + ξ Da die Eponentialfuntion streng monoton wachsend ist, ändert sich die Relation beim eponieren nicht und es folgt + e >. Da die Eponentialfuntion auf R positiv bleibt, gilt weiter + 0 e. Alternativ ann man den Mittelwertsatz auch diret auf e im Intervall 0, anwenden. Aufgabe 7.. Sie sollen möglichst materialsparend zylindrische Konservendosen produzieren. Wie müssen Sie den Durchmesser und die Höhe des Zylinders einstellen, damit Sie möglichst wenig Blech verbrauchen minimale Oberfläche, um ein vorgegebenes Dosenvolumen von genau einem Liter zu erreichen. Lösung zu Aufgabe 7.. Sei die Stäre des Blechs durch die Konstante a > 0 gegeben wir nehmen vereinfacht an, dass das Blech überall gleich star ist. Dann ist das Volumen durch V r π h 0
11 gegeben. Die Oberfläche ist durch A r + a π + h π r + a gegeben. Da das Volumen ein Liter betragen soll, setzen wir dies in die Gleichung für das Volumen ein und formen nach h um: h r π. Dies setzen wir in die Gleichung für die Oberfläche ein, welche wir minimieren wollen und erhalten Ar r + a π + r + a r πr + πar + a π + r + a r Um hiervon das Minimum zu finden, bilden wir die erste Ableitung und setzen diese Null: r Ar, a πr + πa r a r 0 πr + aπr r a 0 Da diese Gleichung ohne Computer schwer zu lösen ist, vernachlässigen wir die Materialstäre und setzen a 0. Wir erhalten dann als Lösungen r 0 und r. Offensichtlich scheidet r 0 als Lösung schonmal aus. Wegen π r Ar, a π + r + a r, r A π, 0 π + 8π < 0. liegt dort eine loale Minimumstelle vor. Die Höhe der Ummantelung der Dose ist dementsprechend durch h π π π π π π gegeben. Die Einheit von r und h ist jeweils Dezimeter, da l dm. Aufgabe 7.. Für welche Punte P der Parabel y p ist das vom Berührungspunt P bis zur Leitlinie, der Geraden p, betrachtete Stüc der Tangente in P ein Minimum? Lösung zu Aufgabe 7.. Wir betrachten das Problem für p > 0 und somit 0, da wir das Problem ansonsten an der -Achse spiegeln önnten. Weiterhin genügt es nur einen der beiden Äste der Parabel zu betrachten, da es sich bezüglich der y -Achse ebenfalls um ein symmetrisches Problem handelt. Der Punt P hat somit die Koordinaten P P, p P. Die Steigung der Tangente t m + n an diesem Punt ist durch p p m pp P gegeben. Der absolute Anteil n ist wegen p t P p + n p P durch n p P pp pp pp pp gegeben. Somit lautet die Tangentengleichung Der Schnittpunt mit der Leitline ist wegen t t p p + P. P p p + P, P p P
12 durch S p, gegeben. Nun berechnen wir den Abstand der beiden Punte P und S und minimieren diesen. A P P + p pp p + p + P P P + p P + p + pp p + P P + p P + p + pp P + p P + p + pp P + p P P + p P + p 8 P P + p P + p + pp + p + p 8 P d d P A P P + p + p p 8 P P + p P + p P + p P + p pp 8 P p. Die beiden negativen Lösungen scheiden aus, da wegen p > 0 auch 0 sein muss. Wegen d d P A P + p P, d d P A p > 0 p, p liegt dort auch ein loales Minimum vor. Die Koordinaten der Punte lauten also P Symmetrie P p, p. Für p 0 ist nichts zu zeigen, da die Parabel dann zu einem Punt degeneriert. und wegen der Aufgabe 7.5. Berechnen Sie nach geeigneter Umformung mit der Regel von L Hospital Bernoulli-L Hospital a ln b c sin d π tan e + a für a R. π Lösung zu Aufgabe 7.5. a Wegen 0 und ln folgt nach Anwendung der Regel von L Hospital 0 ln 0 ln 0 Regel von L Hospital b Aufgrund der Stetigeit der Eponentialfuntion folgt nun sofort 0 ep ln ep ln 0 0 c Durch zweimalige Anwendung der Regel von L Hospital ergibt sich 0 sin sin 0 sin wegen 0 sin 0 und 0 cos sin. d Wiederum durch Anwenden der Regel von L Hospital ergibt sich π π tan π π cot 0 ep0. cos sin + cos sin 0 cos + cos sin 0 0 π sin.
13 e Es gilt zunächst + a e ln+ a e ln+ a. Wegen 0 und ln + a ist die Regel von L Hospital anwendbar, so dass aufgrund von ln + a t 0 ln + t a ln + 0 a ln 0 ln + a Regel von L Hospital + a a a Aus der Stetigeit der Eponentialfuntion folgt + a e a. Aufgabe 7.6. Bestimmen Sie folgende Grenzwerte: a 0 ln + d 0 e a e b g 0 + sin b e ln e e h cot 0 lg c 0 0 f 0 sin cot i ln ln j m 0 e 0 + n +0 sin arctan l cot sin +0 Lösung zu Aufgabe 7.6. a b c d e f g ln ln e e e e lg ln0 0 ln0 e a e b ae a be b a b sin cos cos sin sin 0 sin 0 cos sin 0 + cos 6 5
14 h cos 0 sin 0 cos sin sin cos sin cos 0 sin + cos sin cos 0 sin + cos + cos sin cos cos + sin 0 cos + cos sin sin cos i j l m n wobei die letzte Gleichheit aus folgt. und daher undefiniert. 0 wobei die letzte Gleicheit aus folgt. ep ln, ln + 0 ln 0 0 lnln ln 0 arctan arctan sin cos ep sin ln sin cos sin sin tan ± 0 + sin cos sin 0 e e 0 e 0 cos, sin tan 0 cos 0 e + e 0 0 sin ep sin ln, 0 wobei die letzte Gleichheit aus folgt. 0 sin ln cos 0 ln ln e e e 0 cos ln ln 0
15 Aufgabe 7.7. Man entwicle die Funtion f ln + in eine Taylor-Reihe nach Potenzen von. Lösung zu Aufgabe 7.7. Für die ersten beiden Ableitungen gilt f +, f 0 0, f +, f 0. Mittels Indution lässt sich zeigen, dass f n n n! und daher f n 0 n n!. Für das Taylorpolynom folgt + n n n! T n n n! n n. Der Konvergenzradius beträgt R. n n Aufgabe 7.8. Man entwicle die Funtion f cosh in eine Taylorreihe an der Stelle 0 0 a diret durch die Berechnung der Ableitungen, b unter Verwendung der Taylor-Reihe für e. Man bestimme insbesondere das Restglied und zeige, dass dies für n gegen Null strebt! Lösung zu Aufgabe 7.8. Die n -te Ableitung von cosh ist durch d n d n cosh { sinh falls n cosh gegeben. Somit gilt für die Taylorreihe an der Stelle 0 0 T cosh,0 n0 falls n n n!. Andererseits gilt cosh e + e n0 n n! + n0 n n! n + n n0 n! n0 n n!. Für das N + -te Restglied nach Lagrange und festes R, Θ 0, gilt R N+ { sinhθ N+ N+!, N coshθ N+ N+!, N e Θ N+ N +! e N+ N+ e N eθ eθ 0. N + N+ N + Für das N + -te Restglied nach Cauchy und festes R, Θ 0, gilt { sinhθ N+ Θ N, N R N+ N! e Θ N+ e Θ e N coshθ N+ Θ N, N N! N N N! wobei wir beide male die Ungleichung n e n < n! benutzt haben. e Θ e N N 0, N
ANALYSIS I. Lösung der Klausur vom 25/02/14. Aufgabe 1
 ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
ANALYSIS I Lösung der Klausur vom 5//4 Aufgabe (a) Das Monotonieriterium für Folgen besagt, dass monoton wachsende nach oben beschränte Folgen (a n ) R onvergent sind. Entsprechendes gilt für monoton fallende
Technische Universität München Zentrum Mathematik. Übungsblatt 5
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 5 Hausaufgaben Aufgabe 5. Bestimmen Sie folgende Grenzwerte. Benutzen
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:
![1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen: 1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:](/thumbs/53/30982501.jpg) Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Mathematik Übungsblatt - Lösung. b) x=2
 Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Sommersemester 204 Technische Informatik Bachelor IT2 Vorlesung Mathematik 2 Mathematik 2 4. Übungsblatt - Lösung Differentialrechnung
Tutorium Mathematik I M WM Lösungen
 Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Analysis I Lösung von Serie 9
 FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
Vorkurs Mathematik für Ingenieur Innen WS 2018/2019 Übung 7
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieur Innen WS 018/019 Übung 7 Aufgabe 1 : Etremwerte Der Ellipse + y = 1 ist ein Rechteck mit Seitenlängen p, q, dessen Seiten parallel
Vorkurs Mathematik für Ingenieure WS 2015/2016 Übung 6
 Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik für Ingenieure WS 015/016 Übung 6 Aufgabe 1 : Differentialrechnung (a Berechnen Sie die Ableitung nachstehender Funktionen an der Stelle 0 und
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Diskussion einzelner Funktionen
 Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Aufgabe 1. Version A Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Analysis I, WiSe 013/14, 04.0.014 (Ise 1 Aufgabe 1. Version A Multiple Choice (4 Punte. Kreuzen Sie die richtige(n Antwort(en an. a Welche der folgenden Aussagen über Folgen sind sinnvoll und wahr? jede
Aufgabe 51. Gegeben ist die Preis-Absatz-Funktion. p W R C! R C mit p.x/ D 20 2x :
 Aufgabe 5 Differentialrechnung: Preiselastizität (DIFF0.4) Gegeben ist die Preis-Absatz-Funktion p W R C! R C mit p./ D 0 : Dabei steht R C für die nachgefragte Menge und p R C für den Preis. Bestimmen
Aufgabe 5 Differentialrechnung: Preiselastizität (DIFF0.4) Gegeben ist die Preis-Absatz-Funktion p W R C! R C mit p./ D 0 : Dabei steht R C für die nachgefragte Menge und p R C für den Preis. Bestimmen
Analysis II 13. Übungsblatt
 Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 22/3 F. Stoffers 28. Januar 23 Analysis II 3. Übungsblatt. Aufgabe 4322 Punte a Sei U R n offen und f : R n R m eine stetig Fréchet-differenzierbare Abbildung.
Jun.-Prof. PD Dr. D. Mugnolo Wintersemester 22/3 F. Stoffers 28. Januar 23 Analysis II 3. Übungsblatt. Aufgabe 4322 Punte a Sei U R n offen und f : R n R m eine stetig Fréchet-differenzierbare Abbildung.
Probeklausur zur Analysis für Informatiker
 Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Zusammenfassung: Differenzialrechnung 2
 LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
VI. Iterationsverfahren
 VI. Iterationsverahren To ininity and beyond Falls eine direte Lösung des Problems nicht möglich oder ineizient ist. 6.. Fipuntgleichungen 6... Problemstellung: Iterationsuntion Iteration: R Startwert,
VI. Iterationsverahren To ininity and beyond Falls eine direte Lösung des Problems nicht möglich oder ineizient ist. 6.. Fipuntgleichungen 6... Problemstellung: Iterationsuntion Iteration: R Startwert,
Mathematik zum Mitnehmen
 Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 5. x 1 2x 3 = lim 6x
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
Klausur zur Vorlesung Analysis 1 (240003) 1. Termin: Aufgaben und Lösungen
 Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
2.6 Lokale Extrema und Mittelwertsatz
 2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Vorlesung Mathematik für Ingenieure 1 (Wintersemester 2008/09)
 Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
existiert (endlich oder unendlich). f x h f x Dableitbar, wenn sie in jedem Punkt aus E ableitbar ist. f x h f x ':, ' lim
 Ableitbare Funktionen. Ableitungen De. Sei die Funktion : D und Dein Häuungspunkt. Die Funktion ist genau dann an der Stelle eistiert und endlich ist. Die Funktion hat genau dann an der Stelle Grenzwert
Ableitbare Funktionen. Ableitungen De. Sei die Funktion : D und Dein Häuungspunkt. Die Funktion ist genau dann an der Stelle eistiert und endlich ist. Die Funktion hat genau dann an der Stelle Grenzwert
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
dx nf(x 0). dx f(n 1) (x 0 ) = dn
 4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 11. Übungsblatt. { wachsend fallend
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 8/9 Aufgabe Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 8/9 Aufgabe Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
Abgabe: KW 11. Aufgabe 2-0a: Berechnen Sie die Grenzwerte der Funktionen. x 2 x. lim. lim
 . Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
. Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Ferienkurs Analysis 1
 TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
Serie 4: Flächeninhalt und Integration
 D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
5. Übung zur Analysis II
 Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Julius-Maximilians-Universität Würzburg Institut für Mathemati Prof. Dr. H. Pabel Christian Lageman, Martin Lamprecht, Ralf Winler Würzburg, den. Juni 006 5. Übung zur Analysis II Sommersemester 006 Lösungshinweise.)
Höhere Mathematik I für die Fachrichtung Physik. Lösungsvorschläge zum 12. Übungsblatt
 Institut für Analysis WS07/8 Prof. Dr. Dirk Hundertmark 6..08 Dr. Michal Je Höhere Mathematik I für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe 68: a Es sei c irgendeine Zahl zwischen
Institut für Analysis WS07/8 Prof. Dr. Dirk Hundertmark 6..08 Dr. Michal Je Höhere Mathematik I für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt Aufgabe 68: a Es sei c irgendeine Zahl zwischen
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Übungsaufgaben zur Analysis
 Serie Übungsaufgaben zur Analysis. Multiplizieren Sie folgende Klammern aus: ( + 3y)( + 4a + 4b) (a b )( + 3y 4) (3 + )(7 + y) + (a + b)(3 + ). Multiplizieren Sie folgende Klammern aus: 6a( 3a + 5b c)
Serie Übungsaufgaben zur Analysis. Multiplizieren Sie folgende Klammern aus: ( + 3y)( + 4a + 4b) (a b )( + 3y 4) (3 + )(7 + y) + (a + b)(3 + ). Multiplizieren Sie folgende Klammern aus: 6a( 3a + 5b c)
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt. < 0 für alle t > 1. tan(x) tan(0) x 0
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
100 und (a) Wie gross ist die Konzentration des Medikaments zu Beginn des Experiments (für t = 0), bzw. nach 5 Stunden (für t = 5)?
 Mathematik I für Naturwissenschaften Dr. Christine Zehrt 18.10.18 Übung 5 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 22. Oktober 2018 in den Übungsstunden Sei f() = 1 f(1+h) f(1) und g(h)
Mathematik I für Naturwissenschaften Dr. Christine Zehrt 18.10.18 Übung 5 (für Pharma/Geo/Bio) Uni Basel Besprechung der Lösungen: 22. Oktober 2018 in den Übungsstunden Sei f() = 1 f(1+h) f(1) und g(h)
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
ARBEITSUNTERLAGEN. zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES
 ARBEITSUNTERLAGEN zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES Vorbemerkung Ziel des Propädeutikums ist es, die Schulmathematik wieder ins Gedächtnis zu rufen und eine gemeinsame Grundlage für die
ARBEITSUNTERLAGEN zum STARTERKURS an der UNIVERSITÄT DES SAARLANDES Vorbemerkung Ziel des Propädeutikums ist es, die Schulmathematik wieder ins Gedächtnis zu rufen und eine gemeinsame Grundlage für die
Satz von Taylor, Taylor-Reihen
 Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Michael Hott, M. Sc. WS 05/06 08.0.06 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum 9. Übungsblatt
Thema 5 Differentiation
 Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
1. Aufgabe 8 Punkte. f (x) = (x 2 + 1) e x2. Es gilt. f (x) = 2xe x2 + ( x ) e x2 ( 2x) = 2x 3 e x2.
 1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
1. Aufgabe 8 Punkte Geben Sie die Bereiche, auf denen die Funktion f : R R mit f (x) = (x + 1) e x monoton wachsend oder fallend ist, an, und untersuchen Sie die Funktion auf lokale und globale Extrema.
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
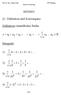 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
6 Weiterer Ausbau der Differentialrechnung
 6 Weiterer Ausbau der Differentialrechnung 6.1 Mittelwertsätze, Extremwerte, Satz von Taylor Motivation: Wie wählt man Höhe und Durchmesser einer Konservendose, so dass bei festem Volumen V möglichst wenig
6 Weiterer Ausbau der Differentialrechnung 6.1 Mittelwertsätze, Extremwerte, Satz von Taylor Motivation: Wie wählt man Höhe und Durchmesser einer Konservendose, so dass bei festem Volumen V möglichst wenig
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
19.2 Mittelwertsatz der Differentialrechnung
 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
23 Konvexe Funktionen und Ungleichungen
 23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
3.2 Funktionsuntersuchungen mittels Differentialrechnung
 3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 4. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 9 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu en Hausaufgaben: Aufgabe H. a)
P. Engel, T. Pfrommer S. Poppitz, Dr. I. Rybak 4. Gruppenübung zur Vorlesung Höhere Mathematik Sommersemester 9 Prof. Dr. M. Stroppel Prof. Dr. N. Knarr Lösungshinweise zu en Hausaufgaben: Aufgabe H. a)
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 115
 5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
3 Grenzwert und Stetigkeit 1
 3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
y f(t)dt in eine Taylorreihe um (0,0). Für welche (x,y) konvergiert diese Reihe gegen F(x,y)? x 5! x7 7! +... = 2 3! x ! x !
 Wolfgang Erben (1. Januar 016) WS 01 Analysis Aufgabe 1. (6 Punkte) Gegeben sei die Funktion f () sinh sin a) Zeigen Sie, dass f () für alle 0 durch eine Potenzreihe um 0 dargestellt werden kann. Geben
Wolfgang Erben (1. Januar 016) WS 01 Analysis Aufgabe 1. (6 Punkte) Gegeben sei die Funktion f () sinh sin a) Zeigen Sie, dass f () für alle 0 durch eine Potenzreihe um 0 dargestellt werden kann. Geben
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK
 ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
Beispiele zur Taylorentwicklung
 Beispiele zur Taylorentwiclung Nun ein paar Augaben, die mit der Taylorentwiclung zu tun haben. In diesem Zusammenhang sollte man au jeden Fall die Formel ür die Taylorentwiclung und das Restglied nach
Beispiele zur Taylorentwiclung Nun ein paar Augaben, die mit der Taylorentwiclung zu tun haben. In diesem Zusammenhang sollte man au jeden Fall die Formel ür die Taylorentwiclung und das Restglied nach
Modulprüfung Analysis I für Ingenieurwissenschaften
 Technische Universität Berlin WiSe 4/5 Fakultät II Institut für Mathematik 20. Februar 205 Doz.: Fackeldey, Guillemard, Penn-Karras Ass.: Beßlich, Winkert Modulprüfung Analysis I für Ingenieurwissenschaften
Technische Universität Berlin WiSe 4/5 Fakultät II Institut für Mathematik 20. Februar 205 Doz.: Fackeldey, Guillemard, Penn-Karras Ass.: Beßlich, Winkert Modulprüfung Analysis I für Ingenieurwissenschaften
Prüfungklausur HM 1 (Ing), Lösungshinweise
 Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Aufgabe : a Welche komplexen Zahlen erfüllen die Gleichung z + i z =? Skizzieren Sie die Lösungsmenge in der Gaussschen Zahlenebene. 6 Punkte b Für welche komplexen Zahlen z gilt (z + i = 8 e π i? Die
Lösung - Serie 2. D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Welche der folgenden Funktionen ( 1, 1) R sind strikt monoton wachsend?
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
Aufgaben e-funktion. Gegeben sind die Funktionen f k (x) = x+k e x. a) Leite g(x) = 1 x k e x. ab.
 Aufgaben e-funktion 7 6 5 4 3-3 - - 3 u 4 - Gegeben sind die Funktionen f k () = +k e. a) Leite g() = k e ab. b) Die Graphen von f und f 3, die -Achse und die Gerade = u (u > 0) begrenzen die Fläche A(u).
Aufgaben e-funktion 7 6 5 4 3-3 - - 3 u 4 - Gegeben sind die Funktionen f k () = +k e. a) Leite g() = k e ab. b) Die Graphen von f und f 3, die -Achse und die Gerade = u (u > 0) begrenzen die Fläche A(u).
6 Die Bedeutung der Ableitung
 6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
1 Differentialrechnung
 BT/MT SS 6 Mathematik II Klausurvorbereitung www.eah-jena.de/~puhl Thema: Üben, üben und nochmals üben!!! Differentialrechnung Aufgabe Differenzieren Sie folgende Funktionen: a y = ln( b f( = a a + c f(
BT/MT SS 6 Mathematik II Klausurvorbereitung www.eah-jena.de/~puhl Thema: Üben, üben und nochmals üben!!! Differentialrechnung Aufgabe Differenzieren Sie folgende Funktionen: a y = ln( b f( = a a + c f(
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Analysis I. 7. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 7. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine surjektive Abbildung f: L M. () Ein archimedisch
Funktionen mehrerer Variabler
 Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Funktionen mehrerer Variabler Fakultät Grundlagen Juli 2015 Fakultät Grundlagen Funktionen mehrerer Variabler Übersicht Funktionsbegriff 1 Funktionsbegriff Beispiele Darstellung Schnitte 2 Partielle Ableitungen
Wesentliche Sätze (Analysis 1 für Lehramt)
 Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
Wesentliche Sätze (Analysis für Lehramt) Inhaltsverzeichnis Alexander Schmalstieg TU Dortmund, Wintersemester 203/204 Wichtige Formeln 2 Folgen 2 3 Maxima und Suprema 3 4 Gleichmäßige Konvergenz 3 5 Funtionen
Vorlesung Mathematik WS 08/09. Friedel Bolle. Vorbemerkung
 Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Mathematik M 1/Di WS 2001/02 1. Sei f : D R eine Funktion mit nichtleerem Definitionsbereich D. Sei a D. f heißt stetig in a, falls gilt
 Mathematik M 1/Di WS 2001/02 1 b) Stetigkeit Sei f : D R eine Funktion mit nichtleerem Definitionsbereich D Sei a D f heißt stetig in a, falls gilt lim f() = f(a) a f heißt stetig auf D, wenn f in jedem
Mathematik M 1/Di WS 2001/02 1 b) Stetigkeit Sei f : D R eine Funktion mit nichtleerem Definitionsbereich D Sei a D f heißt stetig in a, falls gilt lim f() = f(a) a f heißt stetig auf D, wenn f in jedem
Serie 6 - Funktionen II + Differentialrechnung
 Analysis D-BAUG Dr. Meike Akvel HS 05 Serie 6 - Funktionen II + Differentialrechnung. a) Sei Lösung 3, falls < 0, f : R R, f) c +, falls 0, + 8, falls >. Bestimmen Sie c R un R, so ass f überall stetig
Analysis D-BAUG Dr. Meike Akvel HS 05 Serie 6 - Funktionen II + Differentialrechnung. a) Sei Lösung 3, falls < 0, f : R R, f) c +, falls 0, + 8, falls >. Bestimmen Sie c R un R, so ass f überall stetig
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Mathematik IT 3 (Analysis)
 Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Mathematik IT (Analysis) für die Studiengänge Informatik, IMT und ebusiness im Wintersemester 0/04 Geben Sie
Lehrstuhl Mathematik, insbesondere Numerische und Angewandte Mathematik Prof. Dr. L. Cromme Mathematik IT (Analysis) für die Studiengänge Informatik, IMT und ebusiness im Wintersemester 0/04 Geben Sie
Kapitel VII Untersuchung von Funktionen mittels Ableitungen (Lösungen)
 Kapitel VII Untersuchung von Funktionen mittels Ableitungen (Lösungen) 7 cos sin 7 a) b a b b a a b a ln ln ln b) 8 sin cos sin ) ( lnsin π π π π π c) + + + ln 7 a) + e e e e b) ) + + ( + + 7 a) + + +
Kapitel VII Untersuchung von Funktionen mittels Ableitungen (Lösungen) 7 cos sin 7 a) b a b b a a b a ln ln ln b) 8 sin cos sin ) ( lnsin π π π π π c) + + + ln 7 a) + e e e e b) ) + + ( + + 7 a) + + +
Klausur - Analysis 1
 Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Kapitel 5 Differential- und Integralrechnung in einer Variablen
 Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
( 0 ( x) d) Die Funktionsgleichung der Funktion 1 lautet: f( Für x 2 = 0 : Wähle die Werte -1 und 1. Überprüfe x1 = 1,
 Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Lösungsskizzen Mathematik für Informatiker 5. Aufl. Kapitel 15 Peter Hartmann
 Verständnisfragen 1. Ist f : D und 0 D, so ist der Differenzenquotient eine Abbildung von D\ 0. Warum muss hier 0 aus dem Definitionsbereich herausgenommen werden? Weil sonst der Nenner 0 werden kann..
Verständnisfragen 1. Ist f : D und 0 D, so ist der Differenzenquotient eine Abbildung von D\ 0. Warum muss hier 0 aus dem Definitionsbereich herausgenommen werden? Weil sonst der Nenner 0 werden kann..
