Modellbildung und Simulation SS2011 Lineare Iterationsverfahren
|
|
|
- Heinrich Salzmann
- vor 6 Jahren
- Abrufe
Transkript
1 restart; with(plots): with(linearalgebra): Modellbildung und Simulation SS2 Lineare Iterationsverfahren Hilfsfunktionen: Bilder malen bild malt einen Vektor als stueckweise lineare Funktion ueber dem Einheitsintervall. Der Parameter p_options ist eine Liste von Plot-Optionen, z.b. [color=blue,thickness= 2] bild := proc(u::vector,p_options::list(equation)) local i,m; m := Dimension(u)+; plot([[,],seq([i/m,u[i]], i=..m-),[,]],style=line,op (p_options)) (.) bild(randomvector(,generator=-....),[]);
2 bilder malt eine Liste von Bildern wie oben in ein Diagramm farben := proc(i::posint) return [RED,BLUE,GREEN,BLACK][(i-) mod 4 +] (.2) bilder := proc(l::list(vector)) display([seq(bild(l[i], [color=farben(i), title=sprintf("%d / %d", i, nops(l)), titlefont=[helvetica,24], thickness=2]), i=..nops(l))], insequence=true); (.3)
3 bilder([seq(randomvector(,generator=-....),i=..3)]); / 3 Residuum zum Differenzenstern Hier ist die Matrix A ausprogrammiert; wir brauchen sie nur in der Form (x,b) -> b - Ax, berechnen also das Residuum von Ax=b: residuum := proc(x::vector,b::vector)::vector; local i,m,hh,ax; m := Dimension(x)+; if m=2 then Ax := Vector(,8*x[]) else hh := /m^2; Ax := Vector(m-); Ax[] := (2*x[] - x[2])/hh;
4 for i from 2 to m-2 do Ax[i] := (2*x[i]-x[i-]-x[i+])/hh; end do; Ax[m-] := (2*x[m-] - x[m-2])/hh; end if; return b - Ax; (2.) Jacobi-Verfahren Ein Schritt des (mit Faktor gedaempften) Jacobi-Verfahrens:. Die Parameter und werden durchgereicht, das Ergebnis ist die Sequenz, die wieder als Parameter von jacobi auftreten kann. Das erlaubt die Hintereinanderausfuehrung von j Iterationen mittels jacobi@@j. Wenn man nur an der Iterierten interessiert ist, schreibt man halt jacobi(x,b,alpha) []. jacobi := proc(x::vector,b::vector,alpha::numeric)::vector, Vector,numeric; local r,hh; r := residuum(x,b); hh :=./(Dimension(x)+)^2; return x + alpha/(2/hh)*r, b, alpha (3.)
5 Eigenvektoren von A und damit der Jacobi-Iteration: Wir wissen: der Vektor mit Komponenten ist Eigenvektor von A zum Eigenwert, mithin Eigenvektor der Iterationsmatrix M des Jacobi-Verfahrens zum Eigenwert. eigv := proc(m::posint, k::posint)::vector; return Vector(m-, i->evalf(sin(i*k*pi/m))) (4.) bilder([seq(eigv(32,k),k=..3)]);
6 / 3 Beispiele fuer Konvergenz des Jacobi-Verfahrens Wir legen die Zahl der Teilintervalle fest (hier beliebig; spaeter beim Mehrgitter muss es eine Zweierpotenz sein): m_ex := 32; (5.) Wir waehlen einen der Eigenvektoren als Startloesung, was auch der Startfehler e := eigv(m_ex,): bild(e,[thickness=2]); ist...
7 ... weil wir als rechte Seite waehlen: b := Vector(Dimension(e),); (5.2) So sieht das Residuum am Anfang aus: bild(residuum(e, b),[thickness=2]);
8 Und das ist das Ergebnis der ersten Jacobi-Iterationen (also bis ): b, )[],j=..)]);
9 / Diesen Prozess automatisieren wir: diese Prozedur erzeigt ein Bild mit der Startloesung ersten nj Iterierten. konvbild := proc(e::vector, alpha::numeric, nj::posint) local x, s, j, b_null; x := e; s := x; b_null := Vector(Dimension(e),); for j from to nj do x := jacobi(x, b_null, alpha)[]; s := s, x; end do; bilder([s]) und den (5.3)
10 Nochmal mit dem Startvektor von vorhin: konvbild(e,.5,); / Ein zweites Beispiel aus der Mitte des Spektrums: eneu := eigv(m_ex,round(m_ex/2)): konvbild(eneu,.5,);
11 / Und beide zusammen: konvbild(e+eneu,.5,);
12 / Auch ein zufaelliger Startwert laeuft schnell in Richtung "renitenteste Fehleranteile": konvbild(randomvector(m_ex+),.5,);
13 / Mehrgitterverfahren Nun bauen wir uns ein einfaches Mehrgitterverfahren (das waere fuer dieses Modellproblem mit seiner Tridiagonalmatrix nicht noetig, aber man sieht daran das Prinzip) Restriktion der rechten Seite auf das -Gitter Hier triviale Restriktion: die Komponenten mit ungeradem Index wegwerfen. Der Parameter b_fein muss die Laenge mit einem haben, das Ergebnis hat die Laenge. restriktion := proc(b_fein::vector)::vector; local m_grob; m_grob := (Dimension(b_fein)+)/2; Vector(m_grob-, i -> b_fein[2*i]) (6..)
14 Prolongation der Korrektur auf das -Gitter Hier lineare Interploation: Komponenten mit geradem (Feingitter-)Index bekommen den entsprechenden Grobgitterwert, die ungeraden werden linear aus ihren Nachbarwerten interpoliert: prolongation := proc(x_grob::vector)::vector; local x_fein,m_grob,i; m_grob := Dimension(x_grob)+; x_fein := Vector(2*m_grob-, ); for i from to m_grob- do x_fein[2*i] := x_grob[i]; x_fein[2*i-] := x_fein[2*i-]+x_grob[i]/2; x_fein[2*i+] := x_fein[2*i+]+x_grob[i]/2; end do; x_fein; (6.2.) Test fuer Prolongation und Restriktion Ein Beispielvektor: x_ex := eigv(4,); (6.3.)
15 Linear interpoliert... prolongation(x_ex); (6.3.2)... sieht man (spaetestens auf den zwieten Blick), dass man nichts sieht: bild(prolongation(x_ex),[thickness=2]); Es gilt hier: Restriktion nach Prolobgation gibt die Identitaet: restriktion(prolongation(x_ex)); (6.3.3)
16 (6.3.3) Das Mehrgitterverfahren Nun koennen wir alles zusammenbauen. Die Parameter: x: Startvektor, also b: rechte Seite l: Anzahl der Vergroeberungsschritte (die Laenge von x und b soll mit einem sein). nu, nu2: zahl der Vor- bzw. Nachglaettungen Das eigentliche Ergebnis ist der Vektor Parameter (ausser x) einfach durchgereicht. Als Glaetter wird das Jacobi-Verfahren mit wie bei der Prozedur jacobi werden die uebrigen verwendet. mg := proc(x::vector, b::vector, l::nonnegint, nu::nonnegint, nu2::nonnegint):: Vector,Vector,nonnegint,nonnegint,nonnegint; local i, xneu, xg, tmp; xneu:= (jacobi@@nu)(x,b,.5)[]; if l> then xneu := xneu + prolongation( mg(vector((dimension(x)-)/2,), restriktion(residuum(xneu,b)), l-, nu, nu2)[] ); end if; (jacobi@@nu2)(xneu, b,.5)[], b, l, nu, nu2 (6.4.)
17 Beispielrechnungen Fuer l_max Vergroeberungen... l_max := 5;...brauchen wir mindestens soviele Teilintervalle: m_ex := 2^(l_max+); (6.5.) Nun nehmen wir wieder (wie bei der Jacobi-Iteration) einen beliebigen Startwert und als rechte Seite: e := eigv(m_ex,): b := Vector(Dimension(e),): Damit sind verschiedene Experimente moeglich: Mit l= bekommt man mit einem Aufruf einfach Jacobi-Schritte ausgefuehrt. Mit zunehmendem l werden die niederfrequenten Anteile des Fehlers immer besser gedaempft..... bis zum groesstmoeglichen l=l_max Dazu lassen wir uns analog zum Jacobi-Verfahren Bilder malen: konvbild_mg := proc(e::vector, l::nonnegint, nu::nonnegint, nu2::nonnegint, nj::posint) local x, s, j, b_null; x := e; s := x; b_null := Vector(Dimension(e),); for j from to nj do x := mg(x, b_null, l, nu, nu2)[]; s := s, x; end do; bilder([s]) (6.5.2)
18 Der ganz normale Jacobi-Verfahren: konvbild_mg(e,,,, ); / Und die Mehrgitteridee im Einsatz (je 2 Vor- und Nachglaettungsschritte - unter Vernachlaessigung des Grobgitteraufwandes entspricht ein mg also 4 jacobi) konvbild_mg(e, l_max, 2, 2, );
19 /
Teil XV. Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
 Teil XV Mehrgitterverfahren zur Lösung linearer Gleichungssysteme T. Neckel Einführung in die wissenschaftliche Programmierung IN8008 Wintersemester 2017/2018 387 Konzept von Teil XV: Mehrgitterverfahren
Teil XV Mehrgitterverfahren zur Lösung linearer Gleichungssysteme T. Neckel Einführung in die wissenschaftliche Programmierung IN8008 Wintersemester 2017/2018 387 Konzept von Teil XV: Mehrgitterverfahren
Sortieren. Maple sortiert; Unordnung schaffen. > restart;
 restart; Sortieren Maple sortiert; Unordnung schaffen Vorbemerkung: Maple kann schon selber sortieren. Dazu erzeugen wir erstmal eine unsortierte Liste: > r := rand(1..100): > l := [seq(r(), i=1..10)];
restart; Sortieren Maple sortiert; Unordnung schaffen Vorbemerkung: Maple kann schon selber sortieren. Dazu erzeugen wir erstmal eine unsortierte Liste: > r := rand(1..100): > l := [seq(r(), i=1..10)];
Modellbildung und Simulation, SS 2011 Blatt 5: Inverses Pendel
 restart; with(detools): with(linearalgebra): with(plots): with(plottools): Modellbildung und Simulation, SS 2011 Blatt 5: Inverses Pendel Beispielgroessen Zahlenwerte im Beispiel (Wagenmasse, Stabmasse,
restart; with(detools): with(linearalgebra): with(plots): with(plottools): Modellbildung und Simulation, SS 2011 Blatt 5: Inverses Pendel Beispielgroessen Zahlenwerte im Beispiel (Wagenmasse, Stabmasse,
D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys. Serie 13
 D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys Serie 13 1. Um einen Tisch sitzen 7 Zwerge. Vor jedem steht ein Becher mit Milch. Einer der Zwerge verteilt seine Milch gleichmässig auf alle
D-INFK Lineare Algebra HS 2014 Roman Glebov Marc Pollefeys Serie 13 1. Um einen Tisch sitzen 7 Zwerge. Vor jedem steht ein Becher mit Milch. Einer der Zwerge verteilt seine Milch gleichmässig auf alle
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme
 Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
11. Gruppenübung zur Linearen Algebra I
 11. Gruppenübung zur Linearen Algebra I > restart; > with(linalg): Warning, new definition for norm Warning, new definition for trace Aufgabe 1: Zuerst derfinieren wir uns die Hilfsfunktion linindep, um
11. Gruppenübung zur Linearen Algebra I > restart; > with(linalg): Warning, new definition for norm Warning, new definition for trace Aufgabe 1: Zuerst derfinieren wir uns die Hilfsfunktion linindep, um
6a. Iterative Verfahren: Nullstellen und Optima. Besser, schneller, höher, weiter!
 6a. Iterative Verfahren: Nullstellen und Optima Besser, schneller, höher, weiter! Part-II - Reserve Page 1 of 15 Konjugierte Richtungen Anstelle der Residuen oder negativen Gradienten r (i) suchen wir
6a. Iterative Verfahren: Nullstellen und Optima Besser, schneller, höher, weiter! Part-II - Reserve Page 1 of 15 Konjugierte Richtungen Anstelle der Residuen oder negativen Gradienten r (i) suchen wir
8. Vorlesung, 5. April Numerische Methoden I. Eigenwerte und Eigenvektoren
 8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
8. Vorlesung, 5. April 2017 170 004 Numerische Methoden I Eigenwerte und Eigenvektoren 1 Eigenwerte und Eigenvektoren Gegeben ist eine n n-matrix A. Gesucht sind ein vom Nullvektor verschiedener Vektor
5 Suchmaschinen Page Rank. Page Rank. Information Retrieval und Text Mining FH Bonn-Rhein-Sieg, SS Suchmaschinen Page Rank
 Page Rank Google versucht die Bedeutung von Seiten durch den sogenannten Page Rank zu ermitteln. A C Page Rank basiert auf der Verweisstruktur des Webs. Das Web wird als großer gerichteter Graph betrachtet.
Page Rank Google versucht die Bedeutung von Seiten durch den sogenannten Page Rank zu ermitteln. A C Page Rank basiert auf der Verweisstruktur des Webs. Das Web wird als großer gerichteter Graph betrachtet.
Kapitel 3. Iterative Verfahren für LGS. 3.1 Der Banach sche Fixpunktsatz. Definition 3.1:
 Kapitel 3 Iterative Verfahren für LGS 3 Der Banach sche Fixpunktsatz Sei A R n n invertierbar und das LGS A x b gegeben Ein iteratives Verfahren besteht aus einer Berechnungsvorschrift x (j+) F ( x (j))
Kapitel 3 Iterative Verfahren für LGS 3 Der Banach sche Fixpunktsatz Sei A R n n invertierbar und das LGS A x b gegeben Ein iteratives Verfahren besteht aus einer Berechnungsvorschrift x (j+) F ( x (j))
13 Beispiel: Poisson-Gleichung
 13 Beispiel: Poisson-Gleichung Etwas komplizierter wird die Simulation, wenn wir mehr als eine Raumdimension haben während sich im Eindimensionalen die Unbekannten einfach der Reihe nach in eine Liste
13 Beispiel: Poisson-Gleichung Etwas komplizierter wird die Simulation, wenn wir mehr als eine Raumdimension haben während sich im Eindimensionalen die Unbekannten einfach der Reihe nach in eine Liste
Iterative Löser: Einführung
 Iterative Löser: Einführung Im vergangenen Semester wurden folgende Löser für LGS betrachtet: LU-Zerlegung (mit und ohne Pivotisierung) QR-Zerlegung (Householder und Givens) Lösung beliebiger, regulärer,
Iterative Löser: Einführung Im vergangenen Semester wurden folgende Löser für LGS betrachtet: LU-Zerlegung (mit und ohne Pivotisierung) QR-Zerlegung (Householder und Givens) Lösung beliebiger, regulärer,
PCG Verfahren. B ist symmetrisch positiv definit. Eine Matrix-Vektor-Multiplikation mit B hat geringen Aufwand
 PCG Verfahren Zur Verbesserung des Konvergenzverhaltens des CG-Verfahrens, wird in der Praxis oft ein geeigneter Vorkonditionierer konstruiert. Vorraussetzungen an einen Vorkonditionierer B sind: B ist
PCG Verfahren Zur Verbesserung des Konvergenzverhaltens des CG-Verfahrens, wird in der Praxis oft ein geeigneter Vorkonditionierer konstruiert. Vorraussetzungen an einen Vorkonditionierer B sind: B ist
Glättung durch iterative Verfahren
 Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Lineare Iterationsverfahren: Definitionen
 Lineare Iterationsverfahren: Definitionen 1. Ein Lösungsverfahren zur Berechnung von Ax = b heißt iterativ, falls ausgehend von einem Startwert x eine Folge x k von Iterierten bestimmt wird. 2. Ein Iterationsverfahren
Lineare Iterationsverfahren: Definitionen 1. Ein Lösungsverfahren zur Berechnung von Ax = b heißt iterativ, falls ausgehend von einem Startwert x eine Folge x k von Iterierten bestimmt wird. 2. Ein Iterationsverfahren
12. Gruppenübung zur Linearen Algebra I
 2. Gruppenübung zur Linearen Algebra I > restart; > with(linalg): Warning, new definition for norm Warning, new definition for trace Zuerst definieren wir uns die Hilfsfunktion linindep (vgl.. Übung),
2. Gruppenübung zur Linearen Algebra I > restart; > with(linalg): Warning, new definition for norm Warning, new definition for trace Zuerst definieren wir uns die Hilfsfunktion linindep (vgl.. Übung),
2.3 Chaos und Lyapunov-Exponent. d dx f(x) λ = lim n n . (1) Programm. k=0. PROGRAM lyapunov ...
 2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
2.3 Chaos und Lyapunov-Exponent... PROGRAM lyapunov REAL*8 1 λ = lim n n :: a,x,fly n k=0 ln d dx f(x). (1) x=xk DO it=1,itmax+ivor! Schleife Iterationen x=a*x*(1.-x)! log. Abbildung IF(it.GT.ivor.and.ABS(x-.5).GT.1.E-30)
Name: Matr.-Nr.: 2. Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: b a 2 3a 1
 Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Name: Matr.-Nr.: 2 Aufgabe 1. Gegeben sei das folgende lineare Gleichungssystem: 1 1 0 2 b 1 1 2 4 1 1 4 6 x = 1 1. 2 2 2a 2 3a 1 (a) Bringen Sie das lineare Gleichungssystem auf Treppenform. (b) Für welche
Praktikum Wissenschaftliches Rechnen 7. Aufgabenblatt
 Institut für Wissenschaftliches Rechnen Technische Universität Braunschweig Prof. Hermann G. Matthies, Ph. D. Dipl.-inform. Oliver Kayser-Herold Praktikum Wissenschaftliches Rechnen 7. Aufgabenblatt Die
Institut für Wissenschaftliches Rechnen Technische Universität Braunschweig Prof. Hermann G. Matthies, Ph. D. Dipl.-inform. Oliver Kayser-Herold Praktikum Wissenschaftliches Rechnen 7. Aufgabenblatt Die
Teil XV. Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
 Teil XV Mehrgitterverfahren zur Lösung linearer Gleichungssysteme IN8008, Wintersemester 2014/2015 376 Wiederholung: Relaxationsverfahren Direkte Lösung des LGS ist viel zu teuer; Daher wird versucht,
Teil XV Mehrgitterverfahren zur Lösung linearer Gleichungssysteme IN8008, Wintersemester 2014/2015 376 Wiederholung: Relaxationsverfahren Direkte Lösung des LGS ist viel zu teuer; Daher wird versucht,
Blatt 12. g := # f eingeschränkt auf den Einheitskreis
 Blatt 12 Aufgabe 46 restart; with(plots): with(vectorcalculus): BasisFormat(false): f := (x, y) - 4*x^2-3*x*y; param := t - ( cos(t), sin(t) ); g := (f@param)(t); # f eingeschränkt auf den Einheitskreis
Blatt 12 Aufgabe 46 restart; with(plots): with(vectorcalculus): BasisFormat(false): f := (x, y) - 4*x^2-3*x*y; param := t - ( cos(t), sin(t) ); g := (f@param)(t); # f eingeschränkt auf den Einheitskreis
Collatz-Folge. falls a i ungerade.
 14 Klausurtraining Heute gibt s nichts Neues mehr wir machen nochmal einen Streifzug durch die behandelten Themen unter besonderer Berücksichtigung von Aufgaben in der Art, wie sie in Klausuraufgaben vorzukommen
14 Klausurtraining Heute gibt s nichts Neues mehr wir machen nochmal einen Streifzug durch die behandelten Themen unter besonderer Berücksichtigung von Aufgaben in der Art, wie sie in Klausuraufgaben vorzukommen
Einführung in die Programmierung (MA8003)
 Theorie 2.2: Schleifen, Vektorisierung, bedingte Ausführung Dr. Lorenz John Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik M2 05.10.2016 Numerische Mathematik M2
Theorie 2.2: Schleifen, Vektorisierung, bedingte Ausführung Dr. Lorenz John Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik M2 05.10.2016 Numerische Mathematik M2
Computergrafik SS 2016 Oliver Vornberger. Vorlesung vom Kapitel 11: Fraktale
 Computergrafik SS 2016 Oliver Vornberger Vorlesung vom 03.05.2016 Kapitel 11: Fraktale 1 Selbstähnlichkeit 2 Koch'sche Schneeflocke a+(x-a) cos(60 ) - (y-b) sin(60 ) b+(y-b) cos(60 ) + (x-a) sin(60 ) a,b
Computergrafik SS 2016 Oliver Vornberger Vorlesung vom 03.05.2016 Kapitel 11: Fraktale 1 Selbstähnlichkeit 2 Koch'sche Schneeflocke a+(x-a) cos(60 ) - (y-b) sin(60 ) b+(y-b) cos(60 ) + (x-a) sin(60 ) a,b
Algorithmus der Vektoriteration
 TU Ilmenau Institut für Mathematik FG Numerische Mathematik und Informationsverarbeitung PD Dr. W. Neundorf Datei: pb ewp.tex Praktikumsbeispiele zum Lehrgebiet WR II, Numerische Mathematik und CAS Serie
TU Ilmenau Institut für Mathematik FG Numerische Mathematik und Informationsverarbeitung PD Dr. W. Neundorf Datei: pb ewp.tex Praktikumsbeispiele zum Lehrgebiet WR II, Numerische Mathematik und CAS Serie
MATLAB Ferienkurs WS 2010/2011
 MATLAB Ferienkurs WS 2010/2011 Teil 4 von 6 Andreas Klimke, Matthias Wohlmuth Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik Basier auf Kursunterlagen von Boris
MATLAB Ferienkurs WS 2010/2011 Teil 4 von 6 Andreas Klimke, Matthias Wohlmuth Technische Universität München Fakultät Mathematik, Lehrstuhl für Numerische Mathematik Basier auf Kursunterlagen von Boris
Musterlösung. Aufgaben zu Iterative Lösung Linearer Gleichungssysteme. Vordiplomskurs Numerische Methoden Sommer 2008
 Musterlösung Aufgaben zu Iterative Lösung Linearer Gleichungssysteme Vordiplomskurs Numerische Methoden Sommer 8. Betrachte das Gleichungssystem Ax b mit ( ( 3 A, b. 6 8 a Konvergiert das Jacobi Verfahren
Musterlösung Aufgaben zu Iterative Lösung Linearer Gleichungssysteme Vordiplomskurs Numerische Methoden Sommer 8. Betrachte das Gleichungssystem Ax b mit ( ( 3 A, b. 6 8 a Konvergiert das Jacobi Verfahren
Kapitel 3. Konvergenz von Folgen und Reihen
 Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Kapitel 3. Konvergenz von Folgen und Reihen 3.1. Normierte Vektorräume Definition: Sei V ein Vektorraum (oder linearer Raum) über (dem Körper) R. Eine Abbildung : V [0, ) heißt Norm auf V, falls die folgenden
Einführung in die numerische Mathematik
 Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Prof. Dr. M. Günther K. Gausling, M.Sc. C. Hendricks, M.Sc. Sommersemester 4 Bergische Universität Wuppertal Fachbereich C Mathematik und Naturwissenschaften Angewandte Mathematik / Numerische Analysis
Sommersemester 2017 Blatt 1 von 6 Studiengänge: RMM Masterstudiengang Sem. 1 und Wiederholer
 HOCHSCHULE ESSLINGEN Sommersemester 07 Blatt von 6 Studiengänge: RMM Masterstudiengang Sem. und Wiederholer Prüfungsfach: Hilfsmittel: Modellbildung und Simulation Literatur, Manuskript; keine Taschenrechner
HOCHSCHULE ESSLINGEN Sommersemester 07 Blatt von 6 Studiengänge: RMM Masterstudiengang Sem. und Wiederholer Prüfungsfach: Hilfsmittel: Modellbildung und Simulation Literatur, Manuskript; keine Taschenrechner
Eigenwerte. Vorlesung Computergestützte Mathematik zur Linearen Algebra. Lehrstuhl für Angewandte Mathematik Sommersemester 2009
 Eigenwerte Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2009 25. Juni + 2.+9. Juli 2009 Grundlagen Definition Ist für A C n,n, Ax = λx
Eigenwerte Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Sommersemester 2009 25. Juni + 2.+9. Juli 2009 Grundlagen Definition Ist für A C n,n, Ax = λx
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 4. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 17. März 2016 Lineare Gleichungssysteme 1 Wiederholung: Normen, Jacobi-Matrix,
Lineare Gleichungssysteme 4. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 17. März 2016 Lineare Gleichungssysteme 1 Wiederholung: Normen, Jacobi-Matrix,
Iterative Lösung dünnbesetzter Gleichungssysteme
 Iterative Lösung dünnbesetzter Gleichungssysteme Stefan Lang Interdisziplinäres Zentrum für Wissenschaftliches Rechnen Universität Heidelberg INF 368, Raum 532 D-69120 Heidelberg phone: 06221/54-8264 email:
Iterative Lösung dünnbesetzter Gleichungssysteme Stefan Lang Interdisziplinäres Zentrum für Wissenschaftliches Rechnen Universität Heidelberg INF 368, Raum 532 D-69120 Heidelberg phone: 06221/54-8264 email:
Kapitel 6. Iterationsverfahren für lineare Gleichungssysteme
 Kapitel 6 Iterationsverfahren für lineare Gleichungssysteme Falls n sehr groß ist und falls die Matrix A dünn besetzt ist (sparse), dann wählt man zur Lösung von Ax = b im Allgemeinen iterative Verfahren.
Kapitel 6 Iterationsverfahren für lineare Gleichungssysteme Falls n sehr groß ist und falls die Matrix A dünn besetzt ist (sparse), dann wählt man zur Lösung von Ax = b im Allgemeinen iterative Verfahren.
Jacobi- und Gauß-Seidel-Verfahren, Jacobi-Relaxationsverfahren
 Universität Hamburg SS 2005 Proseminar Numerik Leitung: Prof. W. Hofmann Vortrag von Markus Stürzekarn zum Thema: Jacobi- und Gauß-Seidel-Verfahren, Jacobi-Relaxationsverfahren Gegeben sei ein lineares
Universität Hamburg SS 2005 Proseminar Numerik Leitung: Prof. W. Hofmann Vortrag von Markus Stürzekarn zum Thema: Jacobi- und Gauß-Seidel-Verfahren, Jacobi-Relaxationsverfahren Gegeben sei ein lineares
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme
 Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Begleitmaterial zur Vorlesung Numerik linearer Gleichungssysteme Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik 1
Maple-Test zur LVA 'Computermathematik', SS Gruppe weiß
 Maple-Test zur LVA 'Computermathematik', SS 2011 Gruppe weiß *** ANMERKUNGEN UND LÖSUNGSHINWEISE *** Aufgabe Punkte ---------------------------------- 1 / 2 2 / 3 3 / 3 4 / 5 5 / 6 6 / 4 7 / 3 8 / 4 ------------------------------------
Maple-Test zur LVA 'Computermathematik', SS 2011 Gruppe weiß *** ANMERKUNGEN UND LÖSUNGSHINWEISE *** Aufgabe Punkte ---------------------------------- 1 / 2 2 / 3 3 / 3 4 / 5 5 / 6 6 / 4 7 / 3 8 / 4 ------------------------------------
Lineare Schieberegisterfolgen
 Lineare Schieberegisterfolgen Sei K ein endlicher Körper. Man nehme zwei Vektoren x 0 a0 x n 1, a n 1 K n n 1 x n := a i x i und betrachte die lineare Abbildung : K n K n, die durch i=0, berechne x 0 x
Lineare Schieberegisterfolgen Sei K ein endlicher Körper. Man nehme zwei Vektoren x 0 a0 x n 1, a n 1 K n n 1 x n := a i x i und betrachte die lineare Abbildung : K n K n, die durch i=0, berechne x 0 x
Schleifeninvarianten. Dezimal zu Binär
 Schleifeninvarianten Mit vollstandiger Induktion lasst sich auch die Korrektheit von Algorithmen nachweisen. Will man die Werte verfolgen, die die Variablen beim Ablauf eines Algorithmus annehmen, dann
Schleifeninvarianten Mit vollstandiger Induktion lasst sich auch die Korrektheit von Algorithmen nachweisen. Will man die Werte verfolgen, die die Variablen beim Ablauf eines Algorithmus annehmen, dann
Übungsblatt 5 Musterlösung
 MSE SS7 Übungsblatt 5 Musterlösung Lösung 6 (Vergleich von direkten und iterativen Verfahren: Teil ) Aufwand Jacobi-Verfahren: Das Jacobi Verfahren lässt sich als x (k+) = x (k) +D (b Ax (k) ) x (k+) =
MSE SS7 Übungsblatt 5 Musterlösung Lösung 6 (Vergleich von direkten und iterativen Verfahren: Teil ) Aufwand Jacobi-Verfahren: Das Jacobi Verfahren lässt sich als x (k+) = x (k) +D (b Ax (k) ) x (k+) =
Iterative Verfahren, Splittingmethoden
 Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
Iterative Verfahren, Splittingmethoden Theodor Müller 19. April 2005 Sei ein lineares Gleichungssystem der Form Ax = b b C n, A C n n ( ) gegeben. Es sind direkte Verfahren bekannt, die ein solches Gleichungssystem
Rechenoperationen mit Folgen. Rekursion und Iteration.
 Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Rechenoperationen mit Folgen. Die Menge aller Folgen in V bildet einen Vektorraum, V N, für den die Addition und skalare Multiplikation wie folgt definiert sind. (a n ) n N + (b n ) n N := (a n + b n )
Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen
 www.dlr.de Folie 1 > STAB Workshop, 12.11.2013 > Marcel Wallraff, Tobias Leicht 12.11.2013 Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen Marcel Wallraff, Tobias
www.dlr.de Folie 1 > STAB Workshop, 12.11.2013 > Marcel Wallraff, Tobias Leicht 12.11.2013 Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen Marcel Wallraff, Tobias
Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt
 TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
2. Geben Sie für das Jacobi-Verfahren eine scharfe a-priori Abschätzung für den Fehler. x (10) x p
 Wiederholungsaufgaben Algorithmische Mathematik Sommersemester Prof. Dr. Beuchler Markus Burkow Übungsaufgaben Aufgabe. (Jacobi-Verfahren) Gegeben sei das lineare Gleichungssystem Ax b = für A =, b = 3.
Wiederholungsaufgaben Algorithmische Mathematik Sommersemester Prof. Dr. Beuchler Markus Burkow Übungsaufgaben Aufgabe. (Jacobi-Verfahren) Gegeben sei das lineare Gleichungssystem Ax b = für A =, b = 3.
Matrix-Potenzen und größter Eigenwert
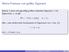 Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
Matrix-Potenzen und größter Eigenwert Besitzt A einen betragsmäßig größten einfachen Eigenwert λ mit Eigenvektor v, so gilt A n x = λ n (cv + o(1)), n, falls x eine nichttriviale Komponente im Eigenraum
Universität Tübingen Tübingen, den Mathematisches Institut D. Mansour, J. Seyrich
 Universität Tübingen Tübingen, den 03.07.2013 Mathematisches Institut D. Mansour, J. Seyrich Probeklausur zu Algorithmen der Numerischen Mathematik SS 2013 ID Nummer: 1 Name:.........................................
Universität Tübingen Tübingen, den 03.07.2013 Mathematisches Institut D. Mansour, J. Seyrich Probeklausur zu Algorithmen der Numerischen Mathematik SS 2013 ID Nummer: 1 Name:.........................................
2. Lineare Gleichungssysteme: direkte und iterative Lösungsverfahren
 2. Lineare Gleichungssysteme: direkte und iterative Lösungsverfahren Problem (P2): Löse Ax = b, A R n und b R. 2.1 Satz: Die folgenden Aussagen sind äquivalent: (i) Ax = b ist für jedes b eindeutig lösbar;
2. Lineare Gleichungssysteme: direkte und iterative Lösungsverfahren Problem (P2): Löse Ax = b, A R n und b R. 2.1 Satz: Die folgenden Aussagen sind äquivalent: (i) Ax = b ist für jedes b eindeutig lösbar;
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Mehrgitterverfahren. Bachelorarbeit. Fakultät für Mathematik Ruhr-Universität Bochum
 Mehrgitterverfahren Bachelorarbeit Fakultät für Mathematik Ruhr-Universität Bochum Hrik Flaskühler Bochum, September 202 Inhaltsverzeichnis Einleitung 2 Numerische Behandlung partieller Differentialgleichungen
Mehrgitterverfahren Bachelorarbeit Fakultät für Mathematik Ruhr-Universität Bochum Hrik Flaskühler Bochum, September 202 Inhaltsverzeichnis Einleitung 2 Numerische Behandlung partieller Differentialgleichungen
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 11 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig
Numerische Lineare Algebra Vorlesung 11 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig
Der CG-Algorithmus (Zusammenfassung)
 Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Arbeit: Page, Brin, Motwani, Winograd (1998). Ziel: Maß für absolute
 3.4 PageRank Arbeit: Page, Brin, Motwani, Winograd (1998). Ziel: Maß für absolute Wichtigkeit von Webseiten; nicht Relevanz bezüglich Benutzeranfrage. Anfrageunabhängiges Ranking. Ausgangspunkt: Eingangsgrad.
3.4 PageRank Arbeit: Page, Brin, Motwani, Winograd (1998). Ziel: Maß für absolute Wichtigkeit von Webseiten; nicht Relevanz bezüglich Benutzeranfrage. Anfrageunabhängiges Ranking. Ausgangspunkt: Eingangsgrad.
Übungen zur Linearen Algebra II, Sommersemester Test, , Gruppe A: Lösung
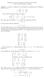 Aufgabe. (5 Punkte) Matrix A C 3 3 : Übungen zur Linearen Algebra II, Sommersemester 0. Test, 9.5.0, Gruppe A: Lösung Bestimmen Sie alle Eigenwerte und Eigenräume der folgenden 8 A 9 6 3 9 Lösung: Charakteristisches
Aufgabe. (5 Punkte) Matrix A C 3 3 : Übungen zur Linearen Algebra II, Sommersemester 0. Test, 9.5.0, Gruppe A: Lösung Bestimmen Sie alle Eigenwerte und Eigenräume der folgenden 8 A 9 6 3 9 Lösung: Charakteristisches
6. Übungsblatt zur Mathematik II für Inf, WInf
 Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 5. 9. Mai 6. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G (Standardskalarprodukt Sei v, e R und es
Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 5. 9. Mai 6. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G (Standardskalarprodukt Sei v, e R und es
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Diplomarbeit. Ein paralleles graphenbasiertes algebraisches Mehrgitterverfahren
 Diplomarbeit Ein paralleles graphenbasiertes algebraisches Mehrgitterverfahren Angefertigt am Institut für Numerische Simulation Vorgelegt der Mathematisch-Naturwissenschaftlichen akultät der Rheinischen
Diplomarbeit Ein paralleles graphenbasiertes algebraisches Mehrgitterverfahren Angefertigt am Institut für Numerische Simulation Vorgelegt der Mathematisch-Naturwissenschaftlichen akultät der Rheinischen
KAPITEL 1. Einleitung
 KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
Banach scher Fixpunktsatz. 1) D ist abgeschlossen und konvex; 2) f ist selbstabbildend, d.h. f(d) D;
 Institut für Geometrie und Praktische Mathematik Höhere Mathematik IV (für Elektrotechniker und Technische Informatiker) - Numerik - SS 2007 Dr. S. Börm, Dr. M. Larin Banach scher Fixpunktsatz Gegeben
Institut für Geometrie und Praktische Mathematik Höhere Mathematik IV (für Elektrotechniker und Technische Informatiker) - Numerik - SS 2007 Dr. S. Börm, Dr. M. Larin Banach scher Fixpunktsatz Gegeben
Numerische Mathematik für Ingenieure (SoSe 2013)
 Numerische Mathematik für Ingenieure (SoSe 2013) PD Dr(USA) Maria Charina Auszüge aus Vorlesungsfolien von Prof Joachim Stöckler werden verwendet Für die Bereitstellung dieses Materials und der Tex-Files
Numerische Mathematik für Ingenieure (SoSe 2013) PD Dr(USA) Maria Charina Auszüge aus Vorlesungsfolien von Prof Joachim Stöckler werden verwendet Für die Bereitstellung dieses Materials und der Tex-Files
Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang. Institut für Geometrie und Praktische Mathematik RWTH Aachen
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Beispiellösung Serie 7
 D-MAVT FS 2014 K. Nipp A. Hiltebrand NUMERISCHE MATHEMATIK Beispiellösung Serie 7 1. a) Exakt: 0.005 1 1 1 0.005 1 ( 1 0 200-199 L = 200 1 Rückwärts einsetzen Lz = b : z 1 = 0.5, z 2 = 1 100 = 99 Rx =
D-MAVT FS 2014 K. Nipp A. Hiltebrand NUMERISCHE MATHEMATIK Beispiellösung Serie 7 1. a) Exakt: 0.005 1 1 1 0.005 1 ( 1 0 200-199 L = 200 1 Rückwärts einsetzen Lz = b : z 1 = 0.5, z 2 = 1 100 = 99 Rx =
1.) Matrix einer linearen Abbildung
 1.) Matrix einer linearen Abbildung Aufgaben: 7 restart; with(linearalgebra): Definitionen MATH: Seien und Vektorräume über dem Körper mit Basen und. Wir wollen eine bequeme Art finden, eine lineare Abbildung
1.) Matrix einer linearen Abbildung Aufgaben: 7 restart; with(linearalgebra): Definitionen MATH: Seien und Vektorräume über dem Körper mit Basen und. Wir wollen eine bequeme Art finden, eine lineare Abbildung
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
III Das Symmetrische Eigenwertproblem (SEP)
 III Das Symmetrische Eigenwertproblem (SEP) III3 Algorithmen für symmetrische tridiagonale Eigenwertprobleme Sei im folgenden a b A = b a b b n a n b n b n a n R n n, zb nach Householder- oder Lanczos(im
III Das Symmetrische Eigenwertproblem (SEP) III3 Algorithmen für symmetrische tridiagonale Eigenwertprobleme Sei im folgenden a b A = b a b b n a n b n b n a n R n n, zb nach Householder- oder Lanczos(im
Algorithmik kontinuierlicher Systeme
 Algorithmik kontinuierlicher Systeme Iterative Verfahren (2/2) Ziel dieser Vorlesung Wie schnell können wir Gleichungssysteme lösen? O(n 3 ) LR- oder QR-Zerlegung: Immer anwendbar Standardverfahren Aber:
Algorithmik kontinuierlicher Systeme Iterative Verfahren (2/2) Ziel dieser Vorlesung Wie schnell können wir Gleichungssysteme lösen? O(n 3 ) LR- oder QR-Zerlegung: Immer anwendbar Standardverfahren Aber:
Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen
 Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen Institut für Aerodynamik und Strömungstechnik DLR 10.11.2011 1 / 24 Übersicht Motivation DG-Verfahren Gleichungen p-mehrgitter Voraussetzungen
Entwicklung von p-mehrgitter-verfahren für turbulente Strömungen Institut für Aerodynamik und Strömungstechnik DLR 10.11.2011 1 / 24 Übersicht Motivation DG-Verfahren Gleichungen p-mehrgitter Voraussetzungen
Wiederhole die obigen Themen! Wir stellen Fragen im Testat!
 1.) Wiederholung: Stetigkeit: Definition und elementare Eigenschaften, Anwendungen von Stetigkeit: Zwischenwertsatz, Intervallschachtelung, Extrema, Grenzwerte und Stetigkeit, Beispiele und erste Theorie
1.) Wiederholung: Stetigkeit: Definition und elementare Eigenschaften, Anwendungen von Stetigkeit: Zwischenwertsatz, Intervallschachtelung, Extrema, Grenzwerte und Stetigkeit, Beispiele und erste Theorie
Einführung in die Programmierung II. 9. Dynamische Datenstrukturen: Binärbäume
 -1- Einführung in die Programmierung II 9. Dynamische Datenstrukturen: Binärbäume Thomas Huckle, Stefan Zimmer 20. 6. 2007 Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen
-1- Einführung in die Programmierung II 9. Dynamische Datenstrukturen: Binärbäume Thomas Huckle, Stefan Zimmer 20. 6. 2007 Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen
Kapitel 2: Lineare Gleichungssysteme. 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen
 Kapitel 2: Lineare Gleichungssysteme 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen B(n, m) : Ω {0,...,255}, n = 1,...,N, m = 1,...,M. dig. Camera Realisierung
Kapitel 2: Lineare Gleichungssysteme 2.1 Motivation: Bildverarbeitung Sei B = (B(n, m)) ein N M stochastisches Feld mit ZVen B(n, m) : Ω {0,...,255}, n = 1,...,N, m = 1,...,M. dig. Camera Realisierung
c i u i. (10.2) x = i
 Kapitel 0 Von Mises Wielandt Verfahren Im Folgenden wollen wir uns ausschließlich auf reelle, symmetrischen Matrizen der Ordnung n beschränken. Wie im letzten Kapitel diskutiert, sind für solche Matrizen
Kapitel 0 Von Mises Wielandt Verfahren Im Folgenden wollen wir uns ausschließlich auf reelle, symmetrischen Matrizen der Ordnung n beschränken. Wie im letzten Kapitel diskutiert, sind für solche Matrizen
Kapitel 4. Raumkurven. 4.1 Graphische Darstellung
 Kapitel 4 Raumkurven 4.1 Graphische Darstellung Für die Darstellung von Raumkurven existiert in MAPLE der Befehl spacecurve aus der Bibliothek plots. Diesem Befehl lassen sich noch einige Parameter mitgeben.
Kapitel 4 Raumkurven 4.1 Graphische Darstellung Für die Darstellung von Raumkurven existiert in MAPLE der Befehl spacecurve aus der Bibliothek plots. Diesem Befehl lassen sich noch einige Parameter mitgeben.
Einführung in Maple. Kontoerstellung: Einloggen am Rechner und Start von Maple: Allgemeine Eingaben in Maple:
 Einführung in Maple Herzlich willkommen zum Maplepraktikum für Lehramtsstudierende! Um Ihnen den Einstieg etwas zu erleichtern, erklären wir hier ein paar grundlegende Dinge im Umgang mit Maple. Sie werden
Einführung in Maple Herzlich willkommen zum Maplepraktikum für Lehramtsstudierende! Um Ihnen den Einstieg etwas zu erleichtern, erklären wir hier ein paar grundlegende Dinge im Umgang mit Maple. Sie werden
Übungsblatt 5 Musterlösung
 MSE Mathe 4 SS Übungsblatt Musterlösung Lösung (Solution) Siehe MATLAB Codes function [x_new, it, rho] = jacobi (A, x_start, b, TOL, it_max) 3 % Set up all the quantities used during iteration 4 % Diagonal
MSE Mathe 4 SS Übungsblatt Musterlösung Lösung (Solution) Siehe MATLAB Codes function [x_new, it, rho] = jacobi (A, x_start, b, TOL, it_max) 3 % Set up all the quantities used during iteration 4 % Diagonal
Numerische Methoden 6. Übungsblatt
 Karlsruher Institut für Technologie (KIT) SS 202 Institut für Analysis Prof. Dr. Michael Plu Dipl.-Math.techn. Rainer Mandel Nuerische Methoden 6. Übungsblatt Aufgabe 3: Newton-Verfahren I Ziel dieser
Karlsruher Institut für Technologie (KIT) SS 202 Institut für Analysis Prof. Dr. Michael Plu Dipl.-Math.techn. Rainer Mandel Nuerische Methoden 6. Übungsblatt Aufgabe 3: Newton-Verfahren I Ziel dieser
9. Rekursion. 1 falls n 1 n (n 1)!, andernfalls. Experiment: Die Türme von Hanoi. Links Mitte Rechts. Mathematische Rekursion
 Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
Experiment: Die Türme von Hanoi. Rekursion Mathematische Rekursion, Terminierung, der Aufrufstapel, Beispiele, Rekursion vs. Iteration Links Mitte Rechts Mathematische Rekursion Viele mathematische Funktionen
18.4 Das Newton-Verfahren
 18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
18.4 Das Newton-Verfahren Ziel: Wir suchen die Nullstellen einer Funktion f : D R n, D R n : f(x) = 0 Wir kennen bereits die Fixpunktiteration x k+1 := Φ(x k ) mit Startwert x 0 und Iterationsvorschrift
5.3.5 Abstiegs & Gradientenverfahren
 5.3 Iterative Lösungsverfahren für lineare Gleichungssysteme 5.3.5 Abstiegs & Gradientenverfahren Die bisher kennengelernten Iterationsverfahren zur Approximation von linearen Gleichungssystemen haben
5.3 Iterative Lösungsverfahren für lineare Gleichungssysteme 5.3.5 Abstiegs & Gradientenverfahren Die bisher kennengelernten Iterationsverfahren zur Approximation von linearen Gleichungssystemen haben
Kapitel 5 Iterative Verfahren für LGS
 Kapitel 5 Iterative Verfahren für LGS Einführung Matrixnormen Splitting Verfahren Mehrgitter (Multigrid) Verfahren Gradientenverfahren Vorkonditionierung CG-Verfahren Abbruch von iterativen Verfahren Zusammenfassung
Kapitel 5 Iterative Verfahren für LGS Einführung Matrixnormen Splitting Verfahren Mehrgitter (Multigrid) Verfahren Gradientenverfahren Vorkonditionierung CG-Verfahren Abbruch von iterativen Verfahren Zusammenfassung
4.6 Berechnung von Eigenwerten
 4.6 Berechnung von Eigenwerten Neben der Festlegung auf den betragsgrößten Eigenwert hat die Potenzmethode den Nachteil sehr langsamer Konvergenz, falls die Eigenwerte nicht hinreichend separiert sind.
4.6 Berechnung von Eigenwerten Neben der Festlegung auf den betragsgrößten Eigenwert hat die Potenzmethode den Nachteil sehr langsamer Konvergenz, falls die Eigenwerte nicht hinreichend separiert sind.
Ferienakademie. Ferienakademie
 Scientific Computing in Computer Science, Technische Universita t Mu nchen Commercial: Ferienakademie Programm 2016 Ferienakademie Ferienakademie 18. 30.09. 2016 Sarntal (Südtirol) Sarntal / Südtirol Sonntag,
Scientific Computing in Computer Science, Technische Universita t Mu nchen Commercial: Ferienakademie Programm 2016 Ferienakademie Ferienakademie 18. 30.09. 2016 Sarntal (Südtirol) Sarntal / Südtirol Sonntag,
Satz. Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus?
 Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus? Seien [F] B und [F] B die Darstellungsmatrizen von F bezüglich zweier Basen B und B. Weiter sei T die
Wie wirkt sich ein Basiswechsel auf die Darstellungsmatrix einer linearen Abbildung F : V n V n aus? Seien [F] B und [F] B die Darstellungsmatrizen von F bezüglich zweier Basen B und B. Weiter sei T die
Klausur zu Grundlagen der Computermathematik
 Prof. Dr. Klaus Höllig. März 11 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A n x/ A n
Prof. Dr. Klaus Höllig. März 11 Klausur zu Grundlagen der Computermathematik en Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. a Die Folge A n x/ A n
Übungsaufgaben Lösungen
 Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Achterbahnzahlen oder Das 3n+1 Problem
 Informationsblatt für die Lehrkraft Multiplikation Achterbahnzahlen oder Das 3n+1 Problem Beitrag zu "Werkstattunterricht Multiplikation" Allgemeine Didaktik - Seminar SS95 Autor: Markus Furter Langgrütstr.
Informationsblatt für die Lehrkraft Multiplikation Achterbahnzahlen oder Das 3n+1 Problem Beitrag zu "Werkstattunterricht Multiplikation" Allgemeine Didaktik - Seminar SS95 Autor: Markus Furter Langgrütstr.
Einführung in die Programmierung für NF. Rückgabewerte, Fallunterscheidung, Schleifen
 Einführung in die Programmierung für NF Rückgabewerte, Fallunterscheidung, Schleifen FUNKTIONEN UND PROZEDUREN 3 EBNF, Fallunterscheidung, Schleifen 2 Funk=on und Prozedur Methoden bestehen aus Funk=onen
Einführung in die Programmierung für NF Rückgabewerte, Fallunterscheidung, Schleifen FUNKTIONEN UND PROZEDUREN 3 EBNF, Fallunterscheidung, Schleifen 2 Funk=on und Prozedur Methoden bestehen aus Funk=onen
Kapitel 2. Zahlenbereiche
 Kapitel 2. Zahlenbereiche 2.3. Reelle Zahlen Erweiterung des Zahlenbereichs der natürlichen Zahlen Ganze Zahlen Z := {..., 3, 2, 1, 0, 1, 2, 3,... } = N {0} N. Rationale Zahlen Q := { m n m Z, n N }. Beachte:
Kapitel 2. Zahlenbereiche 2.3. Reelle Zahlen Erweiterung des Zahlenbereichs der natürlichen Zahlen Ganze Zahlen Z := {..., 3, 2, 1, 0, 1, 2, 3,... } = N {0} N. Rationale Zahlen Q := { m n m Z, n N }. Beachte:
Übungsblatt 12 Musterlösung
 NumLinAlg WS56 Übungsblatt 2 Musterlösung Lösung 44 (QR-Algorithmus mit Wilkinson-Shift und Deflation) a)+b) Die QR-Iteration zur Berechnung aller Eigenwerte einer Matrix A kann wie folgt implementiert
NumLinAlg WS56 Übungsblatt 2 Musterlösung Lösung 44 (QR-Algorithmus mit Wilkinson-Shift und Deflation) a)+b) Die QR-Iteration zur Berechnung aller Eigenwerte einer Matrix A kann wie folgt implementiert
Allgemeine Hinweise zur Klausur
 Semestralklausur Numerisches Programmieren, WS 2009/10, 27.02.2010 Name, Vorname, Matrikelnummer: Seite 1/17 Unterschrift: Bearbeitungszeit: 110 Minuten. Allgemeine Hinweise zur Klausur Hilfsmittel: Ein
Semestralklausur Numerisches Programmieren, WS 2009/10, 27.02.2010 Name, Vorname, Matrikelnummer: Seite 1/17 Unterschrift: Bearbeitungszeit: 110 Minuten. Allgemeine Hinweise zur Klausur Hilfsmittel: Ein
3. Lineare Gleichungssysteme
 3. Lineare Gleichungssysteme 1 3.1. Problemstellung 2 3.2. Direkte Verfahren 3 3.3. Normen und Fehleranalyse 4 3.4. Iterative Verfahren 5 3.5. Konvergenz von linearen Iterationsverfahren 6 3.6. Gradienten-Verfahren
3. Lineare Gleichungssysteme 1 3.1. Problemstellung 2 3.2. Direkte Verfahren 3 3.3. Normen und Fehleranalyse 4 3.4. Iterative Verfahren 5 3.5. Konvergenz von linearen Iterationsverfahren 6 3.6. Gradienten-Verfahren
Zwei-Level-Verfahren zur Lösung Linearer Gleichungssysteme mit nichtsingulärer unsymmetrischer M-Matrix
 Zwei-Level-Verfahren zur Lösung Linearer Gleichungssysteme mit nichtsingulärer unsymmetrischer M-Matrix Diplomarbeit von Florian Goßler Technische Universität Berlin Fakultät II - Institut für Mathematik
Zwei-Level-Verfahren zur Lösung Linearer Gleichungssysteme mit nichtsingulärer unsymmetrischer M-Matrix Diplomarbeit von Florian Goßler Technische Universität Berlin Fakultät II - Institut für Mathematik
Angewandte Strömungssimulation
 ngewandte Strömungssimulation 8. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung uswertung Parameter und Kennzahlen
ngewandte Strömungssimulation 8. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung uswertung Parameter und Kennzahlen
Binärbäume: Beispiel
 Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen wir uns jetzt Binärbäume an Ein Binärbaum wird rekursiv definiert: Er ist leer oder besteht aus einem Knoten (die Wurzel des
Binärbäume Als Beispiel für eine interessantere dynamische Datenstruktur sehen wir uns jetzt Binärbäume an Ein Binärbaum wird rekursiv definiert: Er ist leer oder besteht aus einem Knoten (die Wurzel des
D-ITET, D-MATL Numerische Methoden FS 2014 Dr. R. Käppeli M. Sprecher. Musterlösung 5
 D-ITET, D-MATL Numerische Methoden FS 2014 Dr. R. Käppeli M. Sprecher Musterlösung 5 1. a) function [m1,m2,r]=circle_linear_fit(x,y) n=100; A=[2*x 2*y ones(n,1)]; b=x.^2+y.^2; l=a\b; m1=l(1); m2=l(2);
D-ITET, D-MATL Numerische Methoden FS 2014 Dr. R. Käppeli M. Sprecher Musterlösung 5 1. a) function [m1,m2,r]=circle_linear_fit(x,y) n=100; A=[2*x 2*y ones(n,1)]; b=x.^2+y.^2; l=a\b; m1=l(1); m2=l(2);
Numerische Mathematik
 Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
