Einflussfunktionen und finite Elemente
|
|
|
- Peter Knopp
- vor 5 Jahren
- Abrufe
Transkript
1 Einflussfunktionen und finite Elemente F. Hartmann Institut für Baustatik und Baudynamik Universität Kassel 16. Juni 2009
2 Messen = Bewegen
3 Was kommt bei der Last an?
4
5 Zu jeder Schnittgröße gehört eine Schaukel.
6 Y Y Z Z X X Y Y Z Z X X
7
8 Eisenbahn auf Brücke
9 Thesen Mechanik ist Kinematik. Zu jeder Zahl gehört eine Bewegung. Jede Zahl ist eine Energie. u(x) 1 = Ω G(y, x) p(y) dy (Betti)
10 Der zentrale Satz Ein FE-Programm berechnet alle Werte mittels Einflussfunktionen. Einflussfunktionen = Look-Up functions = Tabellen
11 Spannung in einem Punkt
12 Verbessertes Netz
13
14 Konsequenz Mit falschen Einflussfunktionen erhält man falsche Werte. Also müssen die Einflussfunktionen verbessert werden!
15 Einflussfunktionen sind normale Lastfälle.
16 Wie kann man Einflussfunktionen verbessern?
17 Adaptive Verfeinerung des Netzes
18 Strategie
19 Verbesserte Strategie In einem Punkt x soll die Spannung möglichst genau sein! Fehlermaß im Element σ(x) σ h (x) u u h G 1 G h 1 η = η u η G = Fehler in u Fehler in G 1 K u = f K u G =f G Lastfall Einflussfunktion
20
21
22 Goal oriented refinement
23
24 Etwas Theorie: Funktionale l J(u) = u(x) = 0 l J(u) = N(x) = J(u) = 1 σ xx dω = Ω Ω Zu jedem Funktional gehört eine Bewegung. 0 Ω G 0 (y, x) p(y) dy G 1 (y, x) p(y) dy G Σ (y, x) p(y) dω y J(.) G(y, x) G h (y, x) J h (.) (Riesz) und es gilt u h V h : J(u h ) = J h (u) J(.) V
25 FEM = Approximation von Funktionalen Lehrbücher: FE = Interpolation mit Hütchenfunktionen u h (x) = i u i ϕ i (x) Alternativ: FE = Approximation von Funktionalen J(u h ) = u h (x i ) = G h (y, x i ) p(y) dω y ( der Daumen auf dem Keilriemen ) Ω
26 Die ganze Mathematik steckt in drei Zeilen...
27 Unendlich große Energie Kann man den Daumendruck (= Einzelkraft) überhaupt mit finiten Elementen darstellen? Die meisten Einflussfunktionen haben unendlich große Energie! Wie will man den Abstand zum Punkt klein machen?
28 Membran und Einzelkraft Z Y X
29 Unendlich große Energie auch bei Scheiben
30 Funktionale, Knoten und Gausspunkte
31 Fast alle Daten im Ausdruck und auf dem Bildschirm stammen von schlecht gestellten Problemen ( ill posed problems )! (?) Die Singularitäten der Einflussfunktionen in den Knoten und Gausspunkten sind viel größer als die Singularitäten auf den Rändern!
32 Modellanpassung Änderungen von Steifigkeiten Grobes Modell - feines Modell: Abschätzungen Optimierung
33 Wann ist fein fein genug?
34 Lokale Änderungen haben globale Effekte
35 Änderungen in den Steifigkeiten
36 Der Trick
37 Geänderte Einflussfunktion G G c Globale Analyse (Der ganze Koffer) J(u c u) = l 0 [G c (y, x) G(y, x)] p(y) dy (Betti) Lokale Analyse [x 1, x 2 ] (nur der Ziegelstein) J(u c u) = x2 EI w c G dy = EI x 1 EI x2 x 1 M c M G EI dy Die lokale Analyse misst die Änderung über die virtuelle innere Energie.
38
39
40 Vereinfachung ,5 3 2,5 2 1,5 1 0, J(u c u) = d(u, G c ) = d(u, G) d(u, G c G) d(u, G)
41 Retrofitting structures
42 Retrofitting structures J(u h c u h ) d(g h, u h )
43 Inklusionen
44 Zusammenfassung Mechanik ist angewandte Kinematik Zu jeder Zahl gehört eine Bewegung, eine Einflussfunktion FE = eingeschränkte Kinematik = ungenaue Einflussfunktionen = ungenaue Ergebnisse Goal oriented refinement = gezielte Anpassung des Netz Sensitvitätsanalyse mit Einflussfunktionen
45 Literatur Bangerth W, Rannacher R. (2003) Adaptive Finite Element Methods for Differential Equations. Birkhäuser Verlag Braack M, Ern A (2003) A posteriori control of modeling errors and discretization errors, Multiscale Model. Simul. 1: Ern A, Guermond J-L (2004) Theory and Practice of Finite Elements, Springer-Verlag Hartmann F, Katz C. (2007) Structural Analysis with Finite Elements, 2nd ed., Springer-Verlag (Diplomarbeiten, Doktorarbeiten, Programme zu dem Thema)
Statik mit finiten Elementen
 Statik mit finiten Elementen Fachgebiet Baustatik Prof. Dr.-Ing. Friedel Hartmann 28.02.2003 Universität Kassel 1 Was sind finite Elemente? Knotenkräfte gibt es die? Der äquivalente Lastfall Einflussfunktionen
Statik mit finiten Elementen Fachgebiet Baustatik Prof. Dr.-Ing. Friedel Hartmann 28.02.2003 Universität Kassel 1 Was sind finite Elemente? Knotenkräfte gibt es die? Der äquivalente Lastfall Einflussfunktionen
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
Dipl.-Ing. Christoph Erath 10. November FVM-BEM Kopplung. Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln?
 Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt
 Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht Partielle Differentialgleichungen, Approximation der Lösung Finite Elemente, lineare und höhere Ansatzfunktionen Dünn
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht Partielle Differentialgleichungen, Approximation der Lösung Finite Elemente, lineare und höhere Ansatzfunktionen Dünn
16 A-posteriori-Fehlerabschätzungen
 Numerik partieller Differentialgleichungen 16 A-posteriori-Fehlerabschätzungen Die A-priori-Fehlerabschätzungen u u h # c h p u H m (Ω) aus 15 haben folgende praktische Nachteile: Die Konstante c und die
Numerik partieller Differentialgleichungen 16 A-posteriori-Fehlerabschätzungen Die A-priori-Fehlerabschätzungen u u h # c h p u H m (Ω) aus 15 haben folgende praktische Nachteile: Die Konstante c und die
3. Das Prinzip der virtuellen Arbeit
 3.1 Stab 3.2 Scheibe 3. Das Prinzip der virtuellen Arbeit Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.3-1 3.1 Stab Herleitung des Prinzips der virtuellen Arbeit: Am Stab greifen als äußere
3.1 Stab 3.2 Scheibe 3. Das Prinzip der virtuellen Arbeit Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.3-1 3.1 Stab Herleitung des Prinzips der virtuellen Arbeit: Am Stab greifen als äußere
Johannes Veit. 8. Januar 2016
 Finite im Ein Blick über den Tellerrand... mit FreeFem++ 8. Januar 2016 im 1 2 im 3 4 Gliederung 5 im 1 2 im 3 4 Gliederung 5 dem Einheitsquadrat Laplace - Gleichung: im u(x) = 0 Man betrachte das Problem
Finite im Ein Blick über den Tellerrand... mit FreeFem++ 8. Januar 2016 im 1 2 im 3 4 Gliederung 5 im 1 2 im 3 4 Gliederung 5 dem Einheitsquadrat Laplace - Gleichung: im u(x) = 0 Man betrachte das Problem
Finite Elemente Methoden (aus der Sicht des Mathematikers)
 Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht: Partielle Differentialgleichungen, Approximation der Lösung, Finite Elemente, lineare und höhere Ansatzfunktionen, Dünn
Finite Elemente Methoden (aus der Sicht des Mathematikers) Alfred Schmidt Übersicht: Partielle Differentialgleichungen, Approximation der Lösung, Finite Elemente, lineare und höhere Ansatzfunktionen, Dünn
Kapitel 9 Räumlicher Spannungszustand
 Kapitel 9 Räumlicher Spannungszustand 9 9 9 Räumlicher Spannungszustand 9.1 Problemdefinition... 297 9.2 Die Grundgleichungen des räumlichen Problems... 297 9.2.1 Die Feldgleichungen des räumlichen Problems...
Kapitel 9 Räumlicher Spannungszustand 9 9 9 Räumlicher Spannungszustand 9.1 Problemdefinition... 297 9.2 Die Grundgleichungen des räumlichen Problems... 297 9.2.1 Die Feldgleichungen des räumlichen Problems...
Finite Elemente I Konvergenzaussagen
 Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Fehlerschätzer und adaptive Verfahren
 Fehlerschätzer und adaptive Verfahren Kurzzusammenfassung D. MATERNA F.-J. BARTHOLD Universität Dortmund / Fakultät Bauwesen Lehrstuhl Numerische Methoden und Informationsverarbeitung Prof. Dr.-Ing. habil.
Fehlerschätzer und adaptive Verfahren Kurzzusammenfassung D. MATERNA F.-J. BARTHOLD Universität Dortmund / Fakultät Bauwesen Lehrstuhl Numerische Methoden und Informationsverarbeitung Prof. Dr.-Ing. habil.
6. Adaptive Finite-Element-Methoden
 6. Adaptive Finite-Element-Methoden Adaptive Finite-Element-Methoden werden eingesetzt, um die FE-Lösung lokal oder global zu verbessern. Dieses Thema ist Gegenstand der heutigen Vorlesung. 6.1 Herleitung
6. Adaptive Finite-Element-Methoden Adaptive Finite-Element-Methoden werden eingesetzt, um die FE-Lösung lokal oder global zu verbessern. Dieses Thema ist Gegenstand der heutigen Vorlesung. 6.1 Herleitung
3. Prinzip der virtuellen Arbeit
 3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
3. Prinzip der virtuellen rbeit Mit dem Satz von Castigliano können erschiebungen für Freiheitsgrade berechnet werden, an denen Lasten angreifen. Dabei werden nicht immer alle Terme der Formänderungsenergie
Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1.
 Der Satz von Betti oder warum Statik nicht statisch ist. Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1. (1) Bevor
Der Satz von Betti oder warum Statik nicht statisch ist. Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1. (1) Bevor
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18)
 Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18) Lösung 18.1: Die Aufgabe wird nach der im Beispiel des Abschnitt 18.1.5 demonstrierten Strategie für die Lösung
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 5 (Kapitel 18) Lösung 18.1: Die Aufgabe wird nach der im Beispiel des Abschnitt 18.1.5 demonstrierten Strategie für die Lösung
Sensitivitätsanalyse mit Einflussfunktionen
 Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 2 Sensitivitätsanalyse mit Einflussfunktionen von Oliver Carl Bearbeitungszeit: 13. Mai 24 bis 4. August
Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 2 Sensitivitätsanalyse mit Einflussfunktionen von Oliver Carl Bearbeitungszeit: 13. Mai 24 bis 4. August
CAD-FEM-MKS, CAD FEM MKS. von der dreidimensionalen Konstruktionszeichnung zum guten mechanischen Simulationsmodell
 CAD-FEM-MKS, 24.11.16 CAD FEM MKS von der dreidimensionalen Konstruktionszeichnung zum guten mechanischen Simulationsmodell der erste Schritt zum digitalen Zwilling im Rahmen von Industrie 4.0 Bocholt,
CAD-FEM-MKS, 24.11.16 CAD FEM MKS von der dreidimensionalen Konstruktionszeichnung zum guten mechanischen Simulationsmodell der erste Schritt zum digitalen Zwilling im Rahmen von Industrie 4.0 Bocholt,
Baustatik II und III (PO 2013)
 Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Finite Elemente Modellierung
 Finite Elemente Modellierung Modellerstellung Diskretisierung des Kontinuums Methode der Finite Elemente Anwendungsbeispiele der FEM Zugstab: Kraftmethode Zugstab: Energiemethode Zugstab: Ansatzfunktion
Finite Elemente Modellierung Modellerstellung Diskretisierung des Kontinuums Methode der Finite Elemente Anwendungsbeispiele der FEM Zugstab: Kraftmethode Zugstab: Energiemethode Zugstab: Ansatzfunktion
10 Der Integralsatz von Gauß
 10 Der Integralsatz von Gauß In diesem Abschnitt beweisen wir den Integralsatz von Gauß, die mehrdimensionale Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung. Aussage des Satzes
10 Der Integralsatz von Gauß In diesem Abschnitt beweisen wir den Integralsatz von Gauß, die mehrdimensionale Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung. Aussage des Satzes
Kleines Einmaleins der Baustatik
 IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Buchvorstellung Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher
IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Buchvorstellung Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher Einstieg I Ein einfacher
WINFEM. User s Manual. Thomas Grätsch, Friedel Hartmann
 WINFEM User s Manual Thomas Grätsch, Friedel Hartmann 1 Vorbemerkungen WINFEM ist ein auf der Methode der finiten Elemente basierendes Programm zur linear elastischen Berechnung von Scheiben für den ebenen
WINFEM User s Manual Thomas Grätsch, Friedel Hartmann 1 Vorbemerkungen WINFEM ist ein auf der Methode der finiten Elemente basierendes Programm zur linear elastischen Berechnung von Scheiben für den ebenen
Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem
 Institute of Structural Engineering Page 1 Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem Institute of Structural Engineering Page 2 Lernziele: Sie können Stabilitätsprobleme
Institute of Structural Engineering Page 1 Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem Institute of Structural Engineering Page 2 Lernziele: Sie können Stabilitätsprobleme
Entwicklung einer hp-fast-multipole-
 Entwicklung einer hp-fast-multipole- Boundary-Elemente-Methode Übersicht: 1. Motivation 2. Theoretische Grundlagen a) Boundary-Elemente-Methode b) Fast-Multipole-Methode 3. Erweiterungen a) Elementordnung
Entwicklung einer hp-fast-multipole- Boundary-Elemente-Methode Übersicht: 1. Motivation 2. Theoretische Grundlagen a) Boundary-Elemente-Methode b) Fast-Multipole-Methode 3. Erweiterungen a) Elementordnung
Einführung. Vita Rutka. Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009
 Einführung Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009 Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung,
Einführung Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009 Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung,
Angewandte Mathematik am Rechner 1
 Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 5 Grundlagen Analysis Kontinuierliche Mengen Vollständige Mengen Folgen Iterative Berechnungen Grenzwert:
Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 5 Grundlagen Analysis Kontinuierliche Mengen Vollständige Mengen Folgen Iterative Berechnungen Grenzwert:
Numerische Methoden I FEM/REM
 Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 06.0.206 Zusammenfassung 8. Vorlesung. Schiefwinklige Scheibenelemente Numerischer
Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 06.0.206 Zusammenfassung 8. Vorlesung. Schiefwinklige Scheibenelemente Numerischer
Algorithmische Geometrie: Einstimmung
 Algorithmische Geometrie: Einstimmung Nico Düvelmeyer WS 2009/2010, 20.10.2009 Überblick 1 Organisatorisches 2 Fachgebiet Typische Untersuchungsgegenstände Typische Anwendungsgebiete 3 Inhalte der Vorlesung
Algorithmische Geometrie: Einstimmung Nico Düvelmeyer WS 2009/2010, 20.10.2009 Überblick 1 Organisatorisches 2 Fachgebiet Typische Untersuchungsgegenstände Typische Anwendungsgebiete 3 Inhalte der Vorlesung
Optimierung der Geometrie eines Kühlkörpers
 Johann Jakob Preuß Jan Michael Schulte Institut für Numerische und Angewandte Mathematik Westfälische Wilhelms-Universität Münster Abschlusspräsentation, 2. Februar 2009 Inhaltsverzeichnis 1 Modellierung
Johann Jakob Preuß Jan Michael Schulte Institut für Numerische und Angewandte Mathematik Westfälische Wilhelms-Universität Münster Abschlusspräsentation, 2. Februar 2009 Inhaltsverzeichnis 1 Modellierung
Finite Element Analyse (FEA) (Solver & Post-Processing)
 Finite Element Analyse (FEA) (Solver & Post-Processing) Vortrag im Rahmen des 3D Druck ProSeminars 2016 Lars Lamberti Gliederung Solver Zuverlässigkeit und Genauigkeit Genauigkeitssteigerung Post-Processing
Finite Element Analyse (FEA) (Solver & Post-Processing) Vortrag im Rahmen des 3D Druck ProSeminars 2016 Lars Lamberti Gliederung Solver Zuverlässigkeit und Genauigkeit Genauigkeitssteigerung Post-Processing
Numerische Verfahren zur Lösung der Monge-Ampère-Gleichung, Teil II
 für zur Lösung der Monge-Ampère-Gleichung, Teil II Andreas Platen Institut für Geometrie und Praktische Mathematik RWTH Aachen Seminar zur Approximationstheorie im Wintersemester 2009/2010 1 / 27 Gliederung
für zur Lösung der Monge-Ampère-Gleichung, Teil II Andreas Platen Institut für Geometrie und Praktische Mathematik RWTH Aachen Seminar zur Approximationstheorie im Wintersemester 2009/2010 1 / 27 Gliederung
Finite-Elemente-Simulation und Optimierung in der frühen Entwicklungsphase. Isabel Braun 19. April 2018
 Finite-Elemente-Simulation und Optimierung in der frühen Entwicklungsphase Isabel Braun 19. April 2018 Inhalt Konventioneller und verbesserter Entwurfsprozess Grundlagen der Strukturoptimierung Topologieoptimierung
Finite-Elemente-Simulation und Optimierung in der frühen Entwicklungsphase Isabel Braun 19. April 2018 Inhalt Konventioneller und verbesserter Entwurfsprozess Grundlagen der Strukturoptimierung Topologieoptimierung
Modellieren in der Angewandten Geologie II. Sebastian Bauer
 Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Projekt 3. Verbesserte Berechnung von lokalen Zielgrößen mit der Methode der finiten Elemente unter Verwendung von Grundlösungen
 Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 4 Bauingenieurwesen Projekt 3 Verbesserte Berechnung von lokalen Zielgrößen mit der Methode der finiten Elemente unter Verwendung von Grundlösungen
Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 4 Bauingenieurwesen Projekt 3 Verbesserte Berechnung von lokalen Zielgrößen mit der Methode der finiten Elemente unter Verwendung von Grundlösungen
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Lösungen zu Mathematik I/II. ( Punkte) a) Wir führen Polynomdivision durch und erhalten (x 3 5) : (x ) = x +x+ 4 x. Also ist g(x) die Asymptote von f(x)
Dr. A. Caspar ETH Zürich, August BIOL-B GES+T PHARM Lösungen zu Mathematik I/II. ( Punkte) a) Wir führen Polynomdivision durch und erhalten (x 3 5) : (x ) = x +x+ 4 x. Also ist g(x) die Asymptote von f(x)
Thorsten Kunow. Modellfehler und Greensche Funktionen in der Statik
 Thorsten Kunow Modellfehler und Greensche Funktionen in der Statik Universität Kassel Fachgebiet Baustatik Dissertation 28 Diese Arbeit wurde vom Fachbereich Bauingenieurwesen der Universität Kassel als
Thorsten Kunow Modellfehler und Greensche Funktionen in der Statik Universität Kassel Fachgebiet Baustatik Dissertation 28 Diese Arbeit wurde vom Fachbereich Bauingenieurwesen der Universität Kassel als
FEM-Anwendungen in der maritimen Branche
 Familie STRAK, 2009-10-15 FEM-Anwendungen in der maritimen Branche Ronald Horn - FEM GmbH Vita Dr. Ronald Horn seit 10/08 S.M.I.L.E.-FEM GmbH, Heikendorf Geschäftsführer 04/08-09/08 Lindenau GmbH, Schiffswerft
Familie STRAK, 2009-10-15 FEM-Anwendungen in der maritimen Branche Ronald Horn - FEM GmbH Vita Dr. Ronald Horn seit 10/08 S.M.I.L.E.-FEM GmbH, Heikendorf Geschäftsführer 04/08-09/08 Lindenau GmbH, Schiffswerft
Modellierung elastischer Materialien Variationsformulierung Galerkin-Approximation FreeFem++ Ausblick: Lineare Thermoelastiz. Lineare Elastizität
 Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Lineare Elastizität Dominik Woznica Universität des Saarlandes 05.02.2016 Gliederung 1 Modellierung elastischer Materialien 2 Variationsformulierung 3 Galerkin-Approximation 4 FreeFem++ 5 Ausblick: Lineare
Diskontinuierliche Galerkin-Analyse für die lineare Elastizität. CES-Seminararbeit. Vorgelegt von: Siamak Mirzagholipour. Matr.Nr.:
 Diskontinuierliche Galerkin-Analyse für die lineare Elastizität CES-Seminararbeit Vorgelegt von: Siamak Mirzagholipour Matr.Nr.: 284442 Betreuer: M. Sc. Hamid Reza Bayat November 2015 1 Inhaltsverzeichnis
Diskontinuierliche Galerkin-Analyse für die lineare Elastizität CES-Seminararbeit Vorgelegt von: Siamak Mirzagholipour Matr.Nr.: 284442 Betreuer: M. Sc. Hamid Reza Bayat November 2015 1 Inhaltsverzeichnis
Die Formelsprache der Nichtstandardanalysis (NSA) und das Axiom vom idealen Punkt. Antje Rogalla Freie Universität Berlin
 Die Formelsprache der Nichtstandardanalysis (NSA) und das Axiom vom idealen Punkt Antje Rogalla Freie Universität Berlin 31.10.2012 1 Inhaltsverzeichnis 1 Einleitung 3 2 Die Formelsprache der NSA 4 3 Das
Die Formelsprache der Nichtstandardanalysis (NSA) und das Axiom vom idealen Punkt Antje Rogalla Freie Universität Berlin 31.10.2012 1 Inhaltsverzeichnis 1 Einleitung 3 2 Die Formelsprache der NSA 4 3 Das
Inverse und implizite Funktionen
 Kapitel 8 Inverse und implizite Funktionen Josef Leydold Mathematik für VW WS 2017/18 8 Inverse und implizite Funktionen 1 / 21 Inverse Funktion Sei f : D f R n W f R m, x y = f(x). Eine Funktion f 1 :
Kapitel 8 Inverse und implizite Funktionen Josef Leydold Mathematik für VW WS 2017/18 8 Inverse und implizite Funktionen 1 / 21 Inverse Funktion Sei f : D f R n W f R m, x y = f(x). Eine Funktion f 1 :
Kapitel 5: Einfaktorielle Varianzanalyse
 Rasch, Friese, Hofmann & Naumann (006). Quantitative Methoden. Band (. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Rasch, Friese, Hofmann & Naumann (006). Quantitative Methoden. Band (. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Finite Elemente am Beispiel der Poissongleichung
 am Beispiel der Poissongleichung Roland Tomasi 11.12.2013 Inhalt 1 2 3 Poissongleichung Sei R n ein Gebiet mit abschnittsweise glattem Rand und f L 2 (). Wir suchen u : R, so dass u = f in, u = 0 Physikalische
am Beispiel der Poissongleichung Roland Tomasi 11.12.2013 Inhalt 1 2 3 Poissongleichung Sei R n ein Gebiet mit abschnittsweise glattem Rand und f L 2 (). Wir suchen u : R, so dass u = f in, u = 0 Physikalische
Praktikum. Vita Rutka. Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik WS 2007
 Praktikum Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik WS 2007 Block 1 jeder Anfang ist eindimensional Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches
Praktikum Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik WS 2007 Block 1 jeder Anfang ist eindimensional Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode
 Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Bionik Wirtschaftszentrum. Bionische Optimierung bei der Konstruktion technischer Bauteile in der Automobilindustrie
 Bionik Wirtschaftszentrum B-I-C Bremen, BIOKON, IBZ, Kompetenznetz Biomimetrik, VDI, DBU 8. und 9. April 2008, Osnabrück Bionische Optimierung bei der Konstruktion technischer Bauteile in der Automobilindustrie
Bionik Wirtschaftszentrum B-I-C Bremen, BIOKON, IBZ, Kompetenznetz Biomimetrik, VDI, DBU 8. und 9. April 2008, Osnabrück Bionische Optimierung bei der Konstruktion technischer Bauteile in der Automobilindustrie
Kleines Einmaleins der
 Wolfram Franke, Thorsten Kunow Kleines Einmaleins der Baustatik Wissenswertes für Neu- und Wiederlerner ULB Darmstadt Illlllllllllllllllllllll 16544701 kassel univershy Grundwissen 1 1.1 Statik sehen 1
Wolfram Franke, Thorsten Kunow Kleines Einmaleins der Baustatik Wissenswertes für Neu- und Wiederlerner ULB Darmstadt Illlllllllllllllllllllll 16544701 kassel univershy Grundwissen 1 1.1 Statik sehen 1
Partielle Differentialgleichungen Kapitel 7
 Partielle Differentialgleichungen Kapitel 7 Intermezzo zu Distributionen Die Physik hat der Mathematik die Dirac-δ-Funktion gebracht. Diese δ-funktion soll folgende Eigenschaften haben: n δ (x ϕ (x dx
Partielle Differentialgleichungen Kapitel 7 Intermezzo zu Distributionen Die Physik hat der Mathematik die Dirac-δ-Funktion gebracht. Diese δ-funktion soll folgende Eigenschaften haben: n δ (x ϕ (x dx
Beitrag AM zum Lehrveranstaltungsplan SoSe 2010 (Stand: 30. November 2009)
 Beitrag AM zum Lehrveranstaltungsplan SoSe 2010 (Stand: 30. November 2009) A. Mathematik I. BACHELOR (MATHEMATIK, WIRTSCHAFTSMATHEMATIK, MATHEMATIK LEHRAMT AN GYMNASIEN UND LEHRAMT AN BERUFLICHEN SCHULEN)
Beitrag AM zum Lehrveranstaltungsplan SoSe 2010 (Stand: 30. November 2009) A. Mathematik I. BACHELOR (MATHEMATIK, WIRTSCHAFTSMATHEMATIK, MATHEMATIK LEHRAMT AN GYMNASIEN UND LEHRAMT AN BERUFLICHEN SCHULEN)
Thema für eine Diplomarbeit Gemischte Finite-Elemente-Methoden für konvektionsdominante elliptische Randwertprobleme
 Gemischte Finite-Elemente-Methoden für konvektionsdominante elliptische Randwertprobleme Ziel: Numerische Diskretisierung und Lösung des elliptischen Randwertproblems div(a(x) u) + b(x)u = f in Ω, u =
Gemischte Finite-Elemente-Methoden für konvektionsdominante elliptische Randwertprobleme Ziel: Numerische Diskretisierung und Lösung des elliptischen Randwertproblems div(a(x) u) + b(x)u = f in Ω, u =
Baustatik III SS Platten
 Baustatik III SS 016 3. Platten 3.1 Scheiben und Platten 3. Annahmen der Kirchhoffschen Platentheorie 3.3 Schnittgrößen in Platten 3.4 Praktische Methoden zur Bestimmung der Schnittgrößen in Platten 3.4.1
Baustatik III SS 016 3. Platten 3.1 Scheiben und Platten 3. Annahmen der Kirchhoffschen Platentheorie 3.3 Schnittgrößen in Platten 3.4 Praktische Methoden zur Bestimmung der Schnittgrößen in Platten 3.4.1
Diplomarbeit I. Sensitivitätsanalyse
 Diplomarbeit I Sensitivitätsanalyse an ebenen und räumlichen Rahmen von Walid Kh. A. Al Otaibi wk 1985@hotmail.com Bearbeitungszeit: 1. Februar 29 bis 7. April 29 Betreuer: Prof. Dr.-Ing. F. Hartmann 2.
Diplomarbeit I Sensitivitätsanalyse an ebenen und räumlichen Rahmen von Walid Kh. A. Al Otaibi wk 1985@hotmail.com Bearbeitungszeit: 1. Februar 29 bis 7. April 29 Betreuer: Prof. Dr.-Ing. F. Hartmann 2.
Institut für Angewandte und Experimentelle Mechanik. Anwendungsfach Adaptive Strukturen. Prof. Dr.-Ing. Michael Hanss. Pfaffenwaldring 9, 3.
 Institut für Angewandte und Experimentelle Mechanik Pfaffenwaldring 9, 3. OG Institutsdirektor: Stellvertreter: Anwendungsfach Adaptive Strukturen o.prof. Dr.-Ing.habil. Lothar Gaul Prof. Dr.-Ing. Arnold
Institut für Angewandte und Experimentelle Mechanik Pfaffenwaldring 9, 3. OG Institutsdirektor: Stellvertreter: Anwendungsfach Adaptive Strukturen o.prof. Dr.-Ing.habil. Lothar Gaul Prof. Dr.-Ing. Arnold
Approximation flächenhaft harmonischer Funktionen mittels bikubisch finiter Elemente
 . Session 6: Theoretische Geodäsie Approximation flächenhaft harmonischer Funktionen mittels bikubisch finiter Elemente 1 Jessica Franken Institut für Geodäsie und Geoinformation Professur für Theoretische
. Session 6: Theoretische Geodäsie Approximation flächenhaft harmonischer Funktionen mittels bikubisch finiter Elemente 1 Jessica Franken Institut für Geodäsie und Geoinformation Professur für Theoretische
BlendaX Grundlagen der Computergrafik
 BlendaX Grundlagen der Computergrafik Beleuchtungsmodelle (Reflection Models) 16.11.2007 BlendaX Grundlagen der Computergrafik 1 Rendering von Polygonen Der Renderingprozess lässt sich grob in folgende
BlendaX Grundlagen der Computergrafik Beleuchtungsmodelle (Reflection Models) 16.11.2007 BlendaX Grundlagen der Computergrafik 1 Rendering von Polygonen Der Renderingprozess lässt sich grob in folgende
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
Bildsegmentierung mit Snakes und aktiven Konturen
 Bildsegmentierung mit Snakes und aktiven Konturen 5. Dezember 2005 Vortrag zum Seminar Bildsegmentierung und Computer Vision Übersicht 1 2 Definition der Snake Innere Energie S(c) 3 Statisches Optimierungsproblem
Bildsegmentierung mit Snakes und aktiven Konturen 5. Dezember 2005 Vortrag zum Seminar Bildsegmentierung und Computer Vision Übersicht 1 2 Definition der Snake Innere Energie S(c) 3 Statisches Optimierungsproblem
Wiederholung einiger Rechenregeln
 Wiederholung einiger Rechenregeln 1 Ableitungsrechenregeln 1. Potenzfunktion Potenzregel) 2. Produktregel f x) x b df x) bx b 1 h x) f x) g x) dh x) df x) g x) + f x) dg x) hx) x c + a) b x) dh x) cx c
Wiederholung einiger Rechenregeln 1 Ableitungsrechenregeln 1. Potenzfunktion Potenzregel) 2. Produktregel f x) x b df x) bx b 1 h x) f x) g x) dh x) df x) g x) + f x) dg x) hx) x c + a) b x) dh x) cx c
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 19. März AUFGABE 1 (16 Punkte)
 KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 9. März 2 AUFGABE (6 Punkte) Der Stab 2 in Abb. mit l =,5 m ist in gelenkig gelagert und in 2 abgestützt. In wirkt die Kraft F = 5. N. a) Man bestimme die Reaktionen
Inverse Problems In Medical Imaging
 Inverse Problems In Medical Imaging 07.05.18 Simon Krug physics654: Seminar Medical Imaging University of Bonn Inverse Problems Problem solving Inverse problems Noise Object and Image Radon transform Silent
Inverse Problems In Medical Imaging 07.05.18 Simon Krug physics654: Seminar Medical Imaging University of Bonn Inverse Problems Problem solving Inverse problems Noise Object and Image Radon transform Silent
Baustatik 2. Semestrale am Aufgabe 2 (3 Punkte) (Biegemoment u. Krümmung infolge T) (Normalkraft u. Dehnung infolge T s ) (Senkfeder)
 Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Protokoll E 3 - Wheatstonesche Messbrücke
 Protokoll E 3 - Wheatstonesche Messbrücke Martin Braunschweig 10.06.2004 Andreas Bück 1 Aufgabenstellung 1. Der ohmsche Widerstand einer Widerstandskombination ist in einer Wheatstoneschen Brückenschaltung
Protokoll E 3 - Wheatstonesche Messbrücke Martin Braunschweig 10.06.2004 Andreas Bück 1 Aufgabenstellung 1. Der ohmsche Widerstand einer Widerstandskombination ist in einer Wheatstoneschen Brückenschaltung
Inhaltsverzeichnis. Raimond Dallmann. Baustatik 1. Berechnung statisch bestimmter Tragwerke ISBN:
 Inhaltsverzeichnis Raimond Dallmann Baustatik 1 Berechnung statisch bestimmter Tragwerke ISBN: 978-3-446-42319-0 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42319-0 sowie
Inhaltsverzeichnis Raimond Dallmann Baustatik 1 Berechnung statisch bestimmter Tragwerke ISBN: 978-3-446-42319-0 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42319-0 sowie
Exakte Differentialgleichungen
 Exakte Differentialgleichungen M. Vock Universität Heidelberg Seminar Mathematische Modellierung am 11.11.2008 Gliederung Differentialgleichungen eine erste Begegnung Definition Gewöhnliche DGL Die exakte
Exakte Differentialgleichungen M. Vock Universität Heidelberg Seminar Mathematische Modellierung am 11.11.2008 Gliederung Differentialgleichungen eine erste Begegnung Definition Gewöhnliche DGL Die exakte
Anwendungsfach: Adaptive Strukturen. Lehrveranstaltungen:
 Anwendungsfach: Adaptive Strukturen Lehrveranstaltungen: - Smart Structures (SS, 2V, 1Ü) Brad Beadle, Ph.D. - Finite Elemente Methode (WS, 2V, 2Ü) Dr. Wagner - Boundary Element Methods (SS, 3V, 1Ü) Prof.
Anwendungsfach: Adaptive Strukturen Lehrveranstaltungen: - Smart Structures (SS, 2V, 1Ü) Brad Beadle, Ph.D. - Finite Elemente Methode (WS, 2V, 2Ü) Dr. Wagner - Boundary Element Methods (SS, 3V, 1Ü) Prof.
Hodge Theorie. Viktoria Vilenska. Seminar über Kählermannigfaltigkeiten WS 2007/08 Veranstalter: Prof. Dr. Lorenz Schwachhöfer
 Hodge Theorie Viktoria Vilenska Seminar über Kählermannigfaltigkeiten WS 2007/08 Veranstalter: Prof. Dr. Lorenz Schwachhöfer 1 Inhaltsverzeichnis 1 Einführung des Hodge -Operators 3 2 Hodge Theorie auf
Hodge Theorie Viktoria Vilenska Seminar über Kählermannigfaltigkeiten WS 2007/08 Veranstalter: Prof. Dr. Lorenz Schwachhöfer 1 Inhaltsverzeichnis 1 Einführung des Hodge -Operators 3 2 Hodge Theorie auf
4. Das Verfahren von Galerkin
 4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
Institut für Entwicklung. Mechatronischer Systeme. 2. Swiss VPE Symposium, 14. April 2011, Hochschule für Technik Rapperswil 1
 Virtuelle Prototypen am Beispiel von Luftfahrt- und Elektromobilgetrieben Josef Althaus NTB Buchs 2. Swiss VPE Symposium, 14. April 2011, Hochschule für Technik Rapperswil 1 Warum virtuelle Prototypen?
Virtuelle Prototypen am Beispiel von Luftfahrt- und Elektromobilgetrieben Josef Althaus NTB Buchs 2. Swiss VPE Symposium, 14. April 2011, Hochschule für Technik Rapperswil 1 Warum virtuelle Prototypen?
Kapitel 10 Stabilitätsprobleme
 Institute of Structural Engineering Page 1 Kapitel 10 Stabilitätsprobleme Institute of Structural Engineering Page 2 Lernziele: Was ist Stabilität und wann ist ein Sstem stabil Stabilitätsprobleme klassifizieren
Institute of Structural Engineering Page 1 Kapitel 10 Stabilitätsprobleme Institute of Structural Engineering Page 2 Lernziele: Was ist Stabilität und wann ist ein Sstem stabil Stabilitätsprobleme klassifizieren
Mathematik I Herbstsemester 2018 Kapitel 2: Stetigkeit
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 33 2. Stetigkeit Reelle Zahlenfolgen Grenzwert einer Folge Grenzwert einer Funktion Stetigkeit einer Funktion
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 33 2. Stetigkeit Reelle Zahlenfolgen Grenzwert einer Folge Grenzwert einer Funktion Stetigkeit einer Funktion
Baustatik II. Kapitel IV. Einflusslinien für statisch unbestimmte Systeme. Institute of Structural Engineering Seite 1
 Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
Optimale Steuerung Studieren geht über Probieren
 Studieren geht über Probieren Antrittsvorlesung 23. Oktober 2008 Danksagungen Hans Josef Pesch Fredi Tröltzsch Karl Kunisch Martin Bernauer Frank Schmidt Gerd Wachsmuth Wegweiser Einmal von A nach B bitte!
Studieren geht über Probieren Antrittsvorlesung 23. Oktober 2008 Danksagungen Hans Josef Pesch Fredi Tröltzsch Karl Kunisch Martin Bernauer Frank Schmidt Gerd Wachsmuth Wegweiser Einmal von A nach B bitte!
Higher order lower bounds on eigenvalues of symmetric elliptic operators
 Higher order lower bounds on eigenvalues of symmetric elliptic operators Tomáš Vejchodský (vejchod@math.cas.cz) Institute of Mathematics Czech Academy of Sciences INSTITUTEofMATHEMATICS Czech Academy of
Higher order lower bounds on eigenvalues of symmetric elliptic operators Tomáš Vejchodský (vejchod@math.cas.cz) Institute of Mathematics Czech Academy of Sciences INSTITUTEofMATHEMATICS Czech Academy of
Berechnung von Einflussfunktionen mit der Methode der finiten Elemente
 Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 1 Berechnung von Einflussfunktionen mit der Methode der finiten Elemente von Thorsten Panke Bearbeitungszeit:
Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 1 Berechnung von Einflussfunktionen mit der Methode der finiten Elemente von Thorsten Panke Bearbeitungszeit:
Grundlagen der Objektmodellierung
 Grundlagen der Objektmodellierung Daniel Göhring 30.10.2006 Gliederung Grundlagen der Wahrscheinlichkeitsrechnung Begriffe zur Umweltmodellierung Bayesfilter Zusammenfassung Grundlagen der Wahrscheinlichkeitsrechnung
Grundlagen der Objektmodellierung Daniel Göhring 30.10.2006 Gliederung Grundlagen der Wahrscheinlichkeitsrechnung Begriffe zur Umweltmodellierung Bayesfilter Zusammenfassung Grundlagen der Wahrscheinlichkeitsrechnung
Adaptivität II - Theorie
 Adaptivität II - Theorie Hubertus Bromberger, Manuel Nesensohn, Johannes Reinhardt, Johannes Schnur 8. November 2007 Fazit des ersten Vortrages Ein geeignet verfeinertes Gitter ermöglicht massive Einsparung
Adaptivität II - Theorie Hubertus Bromberger, Manuel Nesensohn, Johannes Reinhardt, Johannes Schnur 8. November 2007 Fazit des ersten Vortrages Ein geeignet verfeinertes Gitter ermöglicht massive Einsparung
Kapitel 5: Einfaktorielle Varianzanalyse
 Rasch, Friese, Hofmann & Naumann (010). Quantitative Methoden. Band (3. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Rasch, Friese, Hofmann & Naumann (010). Quantitative Methoden. Band (3. Auflage). Heidelberg: Springer. Kapitel 5: Einfaktorielle Varianzanalyse Berechnen der Teststärke a priori bzw. Stichprobenumfangsplanung
Hinreichende Bedingungen für Optimalsteuerungsprobleme mit nichtglatten Zuständen
 Hinreichende Bedingungen für Optimalsteuerungsprobleme mit nichtglatten Zuständen Ricki Rosendahl Schwerpunkt Optimierung und Approximation Department Mathematik - Universität Hamburg Hamburg, 10. April
Hinreichende Bedingungen für Optimalsteuerungsprobleme mit nichtglatten Zuständen Ricki Rosendahl Schwerpunkt Optimierung und Approximation Department Mathematik - Universität Hamburg Hamburg, 10. April
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:...
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
Probabilistische, strukturmechanische Untersuchung von Rotorscheiben unter Berücksichtigung geometrischer Streuungen
 Probabilistische, strukturmechanische Untersuchung von Rotorscheiben unter Berücksichtigung geometrischer Streuungen I. Reuter, M. Voigt, K. Vogeler - Technische Universität Dresden T. Weiß, H. Schlums
Probabilistische, strukturmechanische Untersuchung von Rotorscheiben unter Berücksichtigung geometrischer Streuungen I. Reuter, M. Voigt, K. Vogeler - Technische Universität Dresden T. Weiß, H. Schlums
Studienschwerpunkt Numerische Mathematik
 Studienschwerpunkt Numerische Mathematik Ralf Hiptmair Seminar for Applied Mathematics, ETH Zürich Wahlfachvorstellung SS 25 R.Hiptmair (SAM, ETH Zürich) Numerische Mathematik SS 25 / 3 Vorlesungsangebot
Studienschwerpunkt Numerische Mathematik Ralf Hiptmair Seminar for Applied Mathematics, ETH Zürich Wahlfachvorstellung SS 25 R.Hiptmair (SAM, ETH Zürich) Numerische Mathematik SS 25 / 3 Vorlesungsangebot
Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes
 IMW - Institutsmitteilung Nr. 8 (00) 117 Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes Dzik, S.; Wolny, S.; Siemieniec, A. In dieser Abhandlung werden die
IMW - Institutsmitteilung Nr. 8 (00) 117 Das Problem der inneren Kräfte in den Zugbändern der Tragkonstruktion des Schachtfördergefäßes Dzik, S.; Wolny, S.; Siemieniec, A. In dieser Abhandlung werden die
Anwendung von FEMAG-Script: Mehrkriterielle Optimierung - Algorithmus, Umsetzung und Beispiele
 FEMAG-Anwendertreffen am 2. und 3. Dezember 2010 Anwendung von FEMAG-Script: Mehrkriterielle Optimierung - Algorithmus, Umsetzung und Beispiele Jens Krotsch, Bernhard Piepenbreier Lehrstuhl für Elektrische
FEMAG-Anwendertreffen am 2. und 3. Dezember 2010 Anwendung von FEMAG-Script: Mehrkriterielle Optimierung - Algorithmus, Umsetzung und Beispiele Jens Krotsch, Bernhard Piepenbreier Lehrstuhl für Elektrische
Der Taylorsche Satz Herleitung und Anwendungen
 Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
Der Taylorsche Satz Herleitung und Anwendungen Joachim Schneider Juni 2004 Zusammenfassung Es wird ein enfacher Beweis des Taylorsche Satz über die lokale Approximierbarkeit hinreichend glatter Funktionen
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Umkehrfunktion. g (y) = f (x) 1, x = g(y), Umkehrfunktion 1-1
 Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Balkentragwerke mit dem FEM-System MEANS V10 berechnen. Homepage: Telefon:
 Balkentragwerke mit dem FEM-System MEANS V10 berechnen Homepage: www.femcad.de Email: info@femcad.de Telefon: 07844 98 641 Kapitel 14: Balkentragwerke mit MEANS V10 berechnen 1 Kapitel 14: Balkentragwerke
Balkentragwerke mit dem FEM-System MEANS V10 berechnen Homepage: www.femcad.de Email: info@femcad.de Telefon: 07844 98 641 Kapitel 14: Balkentragwerke mit MEANS V10 berechnen 1 Kapitel 14: Balkentragwerke
7. Übung zur Numerik partieller Differentialgleichungen I
 MATHEMATISCHES INSTITUT Sommersemester 2018 DER UNIVERSITÄT ZU KÖLN Prof. Dr. A. Klawonn J. Knepper, M. Sc. M. Kühn, M. Sc. 29. Mai 2018 7. Übung zur Numerik partieller Differentialgleichungen I Hinweis:
MATHEMATISCHES INSTITUT Sommersemester 2018 DER UNIVERSITÄT ZU KÖLN Prof. Dr. A. Klawonn J. Knepper, M. Sc. M. Kühn, M. Sc. 29. Mai 2018 7. Übung zur Numerik partieller Differentialgleichungen I Hinweis:
12. Die Galois Gruppe einer auflösbaren Gleichung.
 12. Die Galois Gruppe einer auflösbaren Gleichung. Wir wollen zeigen, dass die Gleichung p(x) = x 5 6x + 2 = 0 nicht auflösbar ist. Hierfür brauchen wir zunächst neue Definitionen, die mit dem Begriff
12. Die Galois Gruppe einer auflösbaren Gleichung. Wir wollen zeigen, dass die Gleichung p(x) = x 5 6x + 2 = 0 nicht auflösbar ist. Hierfür brauchen wir zunächst neue Definitionen, die mit dem Begriff
Eine objektorientierte Programmierumgebung für differentialgeometrische Berechnungen in MuPAD
 1 Eine objektorientierte Programmierumgebung für differentialgeometrische Berechnungen in MuPAD Studienarbeit von WOLFGANG GLOBKE Betreuer: Dipl. Inf. Marcus Hausdorf Dr. Werner Seiler Institut für Algorithmen
1 Eine objektorientierte Programmierumgebung für differentialgeometrische Berechnungen in MuPAD Studienarbeit von WOLFGANG GLOBKE Betreuer: Dipl. Inf. Marcus Hausdorf Dr. Werner Seiler Institut für Algorithmen
Übung 3: Balkenstruktur Nachbesprechung
 Folie 4-1 Übung 3: Balkenstruktur Nachbesprechung Übung 3: Balkenstruktur Nachbesprechung Punkt auf Linie setzen: Punkt gehört nicht zur Linie Linie hier aufbrechen, oder von Anfang an zwei Linien zeichnen
Folie 4-1 Übung 3: Balkenstruktur Nachbesprechung Übung 3: Balkenstruktur Nachbesprechung Punkt auf Linie setzen: Punkt gehört nicht zur Linie Linie hier aufbrechen, oder von Anfang an zwei Linien zeichnen
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz Dr P C Kunstmann Dipl-Math M Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive Komplexe
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz Dr P C Kunstmann Dipl-Math M Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie inklusive Komplexe
FEM Isoparametric Concept
 FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
FEM Isoparametric Concept home/lehre/vl-mhs--e/cover_sheet.tex. p./26 Table of contents. Interpolation Functions for the Finite Elements 2. Finite Element Types 3. Geometry 4. Interpolation Approach Function
Potential und Spannung
 Potential und Spannung Arbeit bei Ladungsverschiebung: Beim Verschieben einer Ladung q im elektrischen Feld E( r) entlang dem Weg C wird Arbeit geleistet: W el = F C d s = q E d s Vorzeichen: W el > 0
Potential und Spannung Arbeit bei Ladungsverschiebung: Beim Verschieben einer Ladung q im elektrischen Feld E( r) entlang dem Weg C wird Arbeit geleistet: W el = F C d s = q E d s Vorzeichen: W el > 0
H.J. Oberle Analysis II SoSe Interpolation
 HJ Oberle Analysis II SoSe 2012 7 Interpolation 71 Allgemeine Problemstellung Interpolation ist die Kunst, zwischen den Zeilen einer Tabelle zu lesen (Rutishauser) Von f : R R seien Funktionswerte (x j,
HJ Oberle Analysis II SoSe 2012 7 Interpolation 71 Allgemeine Problemstellung Interpolation ist die Kunst, zwischen den Zeilen einer Tabelle zu lesen (Rutishauser) Von f : R R seien Funktionswerte (x j,
Singularitäten in der FEM und deren Bewertung
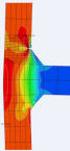 Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
5. Ebene Probleme. 5.1 Ebener Spannungszustand 5.2 Ebener Verzerrungszustand Höhere Festigkeitslehre Prof. Dr.
 5. Ebene Probleme 5.1 Ebener Spannungszustand 5.2 Ebener Verzerrungszustand 1.5-1 Definition: Bei einem ebenen Spannungszustand ist eine Hauptspannung null. Das Koordinatensystem kann so gewählt werden,
5. Ebene Probleme 5.1 Ebener Spannungszustand 5.2 Ebener Verzerrungszustand 1.5-1 Definition: Bei einem ebenen Spannungszustand ist eine Hauptspannung null. Das Koordinatensystem kann so gewählt werden,
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
