Finite Elemente Modellierung
|
|
|
- Liane Böhmer
- vor 6 Jahren
- Abrufe
Transkript
1 Finite Elemente Modellierung Modellerstellung Diskretisierung des Kontinuums Methode der Finite Elemente Anwendungsbeispiele der FEM Zugstab: Kraftmethode Zugstab: Energiemethode Zugstab: Ansatzfunktion
2 FEM Wesentliche Schritte für eine Berechnung: Aufstellung eines hinreichend genauen Modells Mathematisch korrekte Bearbeitung des Modells Richtige Interpretation der Ergebnisse
3 1. Geometrie: Modellerstellung Beschreibung des Raumes, in dem der physikalische Prozess abläuft Übernahme der Geometrie in das Berechnungsmodell, so dass alle wesentlichen Effekte, die von der Geometrie abhängen, berücksichtigbar sind Setzt Erfahrung voraus (zu grob, zu fein)
4 Modellerstellung 2. Werkstoffeigenschaften: Gesamtheit der Gesetze der Stoffe, aus denen sich die betrachtete Struktur zusammensetzt Oft stark vereinfachte Modelle der komplexen atomaren oder molekularen Vorgänge in den Stoffen
5 3. Randbedingungen: Modellerstellung Alle Einflüsse der Umgebung auf das zu berechnende Bauelement Wirkung meist auf die Oberfläche oder den Rand des zu untersuchenden Gebietes Zwei Arten von Randbedingungen: physikalische Grössen, Änderung dieser physikalischen Grössen
6 Diskretisierung Beispiele von Kontinua: a) 1-D: Schnur, Faden b) 2-D: Platte, c) 3-D: Würfel
7 Diskretisierung Beispiele diskreter Strukturen: a) 1-D: Zugstab unterlast, b) 2-D: ebenes Getriebe, c) 3-D: räumliches Fachwerk unter Last
8 Grundidee der FEM Ein reales Bauteil wird aus einfachen Teilen (Elementen) zusammengesetzt, deren Verhalten bekannt ist. Dies bezeichnet man als Diskretisierung des Kontinuums. Das Verhalten des Bauteils unter Belastung ist die Summe des Verhaltens seiner Elemente
9 Diskretisierung des Kontinuums Diskretisierung einer ebenen Platte: a) regelmässiges Netz 8x6, b) regelmässiges Netz 16x12, c) lokal modifiziertes Netz, 47 Viereckelemente, d) unregelmässiges Netz, 18 Drei- und Viereckelemente
10 Elementformen Elementformen kommerzieller Programmsysteme: a) 1-dimensional (Stab), b) 2-dimensional, c) 3- dimensional
11 Ansatzfunktionen
12 Ansatzfunktionen Die Funktion ist auf dem ganzen Element definiert Jede Funktion ist einem Knoten des Elements zugeordnet An diesem Knoten habe die Funktion den Wert 1, an anderen Knoten verschwindet sie Die Summe der Näherungsfunktionen auf einem Element ist 1 An gemeinsamen Flächen oder Kanten haben die Näherungsfunktionen der jeweiligen Knoten gemeinsame Werte
13 Ansatzfunktionen 2-D Ansatzfunktionen und darstellbare Funktionsverläufe: a) linear, b) quadratisch, c) kubisch
14 Finites Element: FEM Ein Finites Element ist ein durch endlich viele Knoten beschriebener Teilbereich des Kontinuums mit einer dazu passenden Ansatzfunktion
15 Methode der FE Elementeinteilung einer Platte mit Einzellast und Einspannung
16 Methode der FE Ersatzfedermodell: a) unverzerrtes und verzerrtes Modell, b) Ersatzfedern der Elementsteifigkeit
17 Methode der FE Zusammenbau der Gesamtsteifigkeit aus den Elementbeiträgen
18 Methode der FE Berechnete Verformungen der Platte a) 6x8 QUAD4- Elemente, b) 6x8 QUAD8-Elemente, c) 12x16 QUAD4- Elemente, d) 12x16 QUAD8-Elemente
19 Methode der FE Modell Element- Typ Anzahl Knoten Anzahl Elemente Verschiebung Krafteinleitungs knoten Rechenzeit a QUAD ,1420 0,51 b QUAD ,1867 1,02 c QUAD ,1749 1,45 d QUAD ,2191 3,67
20 Anwendungsgebiete der FEM
21 Anwendungsgebiete der FEM
22 Zugstab: Kraftmethode Elementare Gleichungen:
23 Zugstab: Kraftmethode Verlängerung eines Stabes unter Last a) Ausgangslänge, b) Verlängerungerung durch Kraft F: es gilt
24 Zugstab: Kraftmethode Definition der Steifigkeit: Steifigkeit k ist der Quotient aus Kraft F und Verlängerung l
25 Zugstab: Kraftmethode An den Enden E 1, E 2 wirken die Kräfte F 1, F 2 in x-richtung Es stellen sich die Verschiebungen u 1 und u 2 ein
26 Zugstab: Kraftmethode Gedankenexperiment: E 1 wird festgehalten (u 1 =0), Verschiebung bei E 2 sei u 2 sei K ij = (Kraft F i auf Stabende i) / (Verschiebung u J des Endes E J ) so ergibt sich:
27 Zugstab: Kraftmethode Um das Ende E 2 um u 2 zu verschieben (E 1 fest), ist die Kraft F 2 erforderlich: Bei dieser Verschiebung tritt am Ende E1 eine Lager-, Einspann- oder Reaktionskraft auf:
28 Somit wird Zugstab: Kraftmethode Entsprechend gilt bei der Verschiebung u 1 am Ende E 1 bei u 2 =0:
29 Zugstab: Kraftmethode Allgemeiner Fall: Verschiebungen u 1 und u 2 an den Enden Die Kräfte berechnen sich aus den Steifigkeiten:
30 Zugstab:Kraftmethode Für die beiden Gleichungen wählt man eine Matrixdarstellung; F elem ist der Element Kraftvektor mit den Komponenten F 1 und F 2, u elem ist der Element-Verschiebungsvektor mit den Komponenten u 1 und u 2
31 Zugstab:Kraftmethode Diese Matrix heißt Elementsteifigkeitsmatrix des 1-dimensionalen, 2-knotigen Zugstabes (1-D ROD2-Element). Die meisten Elementmatrizen sind symmetrisch. Das lineare Gleichungssystem K elem u elem = F elem ist nur lösbar, wenn der Stab mindestens an einem Ende gelagert wird (sonst Det K elem = 0).
32 Zugstab: Energiemethode Bestimmung der Steifigkeit mit Hilfe des Energieerhaltungssatzes Erhaltung der gespeicherten elastischen Dehnungsenergie des Zugstabes Die an den Enden wirkenden Kräfte leisten die äußere Arbeit:
33 Zugstab:Energiemethode Elastische Energiedichte: Gespeicherte elastische Energie:
34 Zugstab: Energiemethode Mit der Dehnung Ergibt sich: Matrixschreibweise: Daraus kann die Steifigkeitsmatrix berechnet werden.
35 Zugstab: Ansatzfunktion Die Verschiebung u(x) längs des Zugstabes wird linear interpoliert aus den Verschiebungen der beiden Enden E 1 und E 2 Die Enden werden als Knoten bezeichnet (K 1, K 2 )
36 Zugstab: Ansatzfunktion
37 Zugstab: Ansatzfunktion Ansatzfunktionen h 1 (x)= (1-x/l), h 2 = x/l Somit ist u(x) = u 1 h 1 (x) + u 2 h 2 (x) Matrixform: Interpolationsmatrix H :
38 Zugstab: Ansatzfunktion Dehnung als Ableitung der Verschiebung: Matrixschreibweise: B heißt Verzerrungs-Verschiebungs- Transformationsmatrix
39 Zugstab: Ansatzfunktion Elastische Energiedichte in Matrixform:
40 Zugstab: Ansatzfunktion Diese Beziehung stellt die Dichte der inneren elastischen Energie als Funktion der Verschiebung des den Stab definierenden Knotens dar. Dazu wurde das folgende Matrizenprodukt benötigt:
41 Zugstab: Ansatzfunktion Elastische Gesamtenergie erhält man durch Integration über das Volumen; Im vorliegenden Fall (elastischer Zugstab mit konstanter Spannung und Dehnung entspricht die Integration über das Volumen der Multiplikation mit dem Volumen
42 Zugstab: Ansatzfunktion Daraus ergibt sich die Steifigkeitsmatrix K elem
Inhaltsverzeichnis Einleitung Mathematische Grundlagen
 Inhaltsverzeichnis 1 Einleitung 1.1 Vorgehensweise bei der FEM... 3 1.2 Verschiedene Elementtypen... 5 1.3 Beispiele zur Finite-Elemente-Methode... 10 1.3.1 Beispiel zu nichtlinearen Problemen... 10 1.3.2
Inhaltsverzeichnis 1 Einleitung 1.1 Vorgehensweise bei der FEM... 3 1.2 Verschiedene Elementtypen... 5 1.3 Beispiele zur Finite-Elemente-Methode... 10 1.3.1 Beispiel zu nichtlinearen Problemen... 10 1.3.2
Modellieren in der Angewandten Geologie II. Sebastian Bauer
 Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Die Finite-Elemente-Methode. Anwendungsbereiche Soft- und Hardwarevoraussetzungen Programmierbarkeit
 Die Finite-Elemente-Methode Anwendungsbereiche Soft- und Hardwarevoraussetzungen Programmierbarkeit Inhalt Die Finite-Elemente-Methode Was ist das und wofür? Die Idee mit den Elementen Anwendung der FEM
Die Finite-Elemente-Methode Anwendungsbereiche Soft- und Hardwarevoraussetzungen Programmierbarkeit Inhalt Die Finite-Elemente-Methode Was ist das und wofür? Die Idee mit den Elementen Anwendung der FEM
Einführung FEM, 1D - Beispiel
 Einführung FEM, D - Beispiel home/eichel/lehre/mhs/fem_intro/deckblatt.tex. p./6 Inhaltsverzeichnis D Beispiel - Finite Elemente Methode. D Aufbau Geometrie 2. Bilanzgleichungen 3. Herleitung der Finiten
Einführung FEM, D - Beispiel home/eichel/lehre/mhs/fem_intro/deckblatt.tex. p./6 Inhaltsverzeichnis D Beispiel - Finite Elemente Methode. D Aufbau Geometrie 2. Bilanzgleichungen 3. Herleitung der Finiten
FEM isoparametrisches Konzept
 FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
FEM isoparametrisches Konzept /home/lehre/vl-mhs-/folien/vorlesung/5_fem_isopara/deckblatt.tex Seite von 25. p./25 Inhaltsverzeichnis. Interpolationsfunktion für die finiten Elemente 2. Finite-Element-Typen
3. Das Gleichungssystem
 Lagerung: Damit das Fachwerk Kräfte aufnehmen kann, muss es gelagert werden, Die Lagerung muss so beschaffen sein, dass keine Starrkörperbewegungen oder Mechanismen mehr möglich sind. Die Verschiebungen
Lagerung: Damit das Fachwerk Kräfte aufnehmen kann, muss es gelagert werden, Die Lagerung muss so beschaffen sein, dass keine Starrkörperbewegungen oder Mechanismen mehr möglich sind. Die Verschiebungen
Fachwerksberechnung mit FEM I (Theorie)
 HTBL-Kapfenberg achwerksberechnung mit EM Seite 1 lorian Grabner fi.do@gmx.net achwerksberechnung mit EM I (Theorie) Mathematische / achliche Inhalte in Stichworten: inite Elemente Methode Kurzzusammenfassung
HTBL-Kapfenberg achwerksberechnung mit EM Seite 1 lorian Grabner fi.do@gmx.net achwerksberechnung mit EM I (Theorie) Mathematische / achliche Inhalte in Stichworten: inite Elemente Methode Kurzzusammenfassung
Kolloquium zur Bachelorarbeit Alain-B. Nsiama-Leyame 567830 Bachelorstudiengang Produktentwicklung und Produktion WS 2015 / 2016
 Strukturanalyse einer mittels Rapid-Prototyping gefertigten Pelton-Turbinenschaufel - grundlegende Festigkeitsanalysen sowie Überlegungen zu Materialkennwerten Kolloquium zur Bachelorarbeit Alain-B. Nsiama-Leyame
Strukturanalyse einer mittels Rapid-Prototyping gefertigten Pelton-Turbinenschaufel - grundlegende Festigkeitsanalysen sowie Überlegungen zu Materialkennwerten Kolloquium zur Bachelorarbeit Alain-B. Nsiama-Leyame
3. Isoparametrische Elemente
 3. Isoparametrische lemente Mit dem einfachen Rechteckelement lassen sich nur Probleme mit einer sehr einfachen Geometrie berechnen. Vielseitigere lemente lassen sich formulieren, wenn neben den Verschiebungen
3. Isoparametrische lemente Mit dem einfachen Rechteckelement lassen sich nur Probleme mit einer sehr einfachen Geometrie berechnen. Vielseitigere lemente lassen sich formulieren, wenn neben den Verschiebungen
1. Zug und Druck in Stäben
 1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
Klausurlösung Einführung in Numerische Methoden und FEM Universität Siegen, Department Maschinenbau,
 Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
Universität Siegen, Department Maschinenbau, 7.7. Aufgabe y 3 l 3 3 F l l x Das dargestellte Fachwerk soll statisch mit Hilfe der FEM untersucht werden. Die Knoten und Elemente sind in der Abbildung nummeriert.
2. Gauß-Integration. Prof. Dr. Wandinger 4. Scheibenelemente FEM 4.2-1
 Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
Die analytische Integration der Steifigkeitsmatrix für das Rechteckelement ist recht mühsam. Für Polynome gibt es eine einfachere Methode zur Berechnung von Integralen, ohne dass die Stammfunktion benötigt
Finite-Elemente-Methode
 Finite-Elemente-Methode Rechnergestützte Einführung von Peter Steinke 1. Auflage Finite-Elemente-Methode Steinke schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Springer 2012 Verlag
Finite-Elemente-Methode Rechnergestützte Einführung von Peter Steinke 1. Auflage Finite-Elemente-Methode Steinke schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Springer 2012 Verlag
Das Geheimnis. der Kaffeetasse
 Das Geheimnis der Kaffeetasse Uttendorf 2005 Lutz Justen Überblick Der Kaffeetasseneffekt was ist das? Einige (nicht-numerische!) Experimente Modellierung: Lineare Elastizitätsgleichung Numerik: FEM Testrechnungen
Das Geheimnis der Kaffeetasse Uttendorf 2005 Lutz Justen Überblick Der Kaffeetasseneffekt was ist das? Einige (nicht-numerische!) Experimente Modellierung: Lineare Elastizitätsgleichung Numerik: FEM Testrechnungen
4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
 4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
2 BAUELEMENTE SPANENDER WERKZEUGMASCHINEN 2.1 Verhalten und Analyse von Werkzeugmaschinen
 2 BAUELEMENTE SPANENDER WERKZEUGMASCHINEN 2.1 Verhalten und Analyse von Werkzeugmaschinen 2.1.1 Statisches Verhalten 2.1.2 Dynamisches Verhalten 2.1.3 Modalanalyse 2.1.4 Thermisches Verhalten 2.1.5 Beschreibung
2 BAUELEMENTE SPANENDER WERKZEUGMASCHINEN 2.1 Verhalten und Analyse von Werkzeugmaschinen 2.1.1 Statisches Verhalten 2.1.2 Dynamisches Verhalten 2.1.3 Modalanalyse 2.1.4 Thermisches Verhalten 2.1.5 Beschreibung
Finite-Elemente-Methoden im Stahlbau
 Rolf Kindmann Matthias Kraus Finite-Elemente-Methoden im Stahlbau ICENTENN Ernst & Sohn Inhaltsverzeichnis 1 Einleitung und Übersicht 1 1.1 Erforderliche Nachweise und Nachweisverfahren 1 1.2 Verfahren
Rolf Kindmann Matthias Kraus Finite-Elemente-Methoden im Stahlbau ICENTENN Ernst & Sohn Inhaltsverzeichnis 1 Einleitung und Übersicht 1 1.1 Erforderliche Nachweise und Nachweisverfahren 1 1.2 Verfahren
Otto-von-Guericke-Universität Magdeburg Lehrstuhl Mikrosystemtechnik
 Mechanische Eigenschaften Die Matrix der Verzerrungen ε ij und die Matrix der mechanischen Spannungen σ ij bilden einen Tensor 2. Stufe und werden durch den Tensor 4. Stufe der elastischen Koeffizienten
Mechanische Eigenschaften Die Matrix der Verzerrungen ε ij und die Matrix der mechanischen Spannungen σ ij bilden einen Tensor 2. Stufe und werden durch den Tensor 4. Stufe der elastischen Koeffizienten
Prof. Dr.-Ing. Christopher Bode. Finite-Elemente-Methode
 Prof. Dr.-Ing. Christopher Bode Finite-Elemente-Methode Kapitel 1: Einleitung BEUTH Hochschule für Technik Berlin Prof. Dr.-Ing. C. Bode 2 Was ist FEM? Die FEM ist ein mathematisches Verfahren zur Lösung
Prof. Dr.-Ing. Christopher Bode Finite-Elemente-Methode Kapitel 1: Einleitung BEUTH Hochschule für Technik Berlin Prof. Dr.-Ing. C. Bode 2 Was ist FEM? Die FEM ist ein mathematisches Verfahren zur Lösung
3. Das Prinzip der virtuellen Arbeit
 3.1 Stab 3.2 Scheibe 3. Das Prinzip der virtuellen Arbeit Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.3-1 3.1 Stab Herleitung des Prinzips der virtuellen Arbeit: Am Stab greifen als äußere
3.1 Stab 3.2 Scheibe 3. Das Prinzip der virtuellen Arbeit Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.3-1 3.1 Stab Herleitung des Prinzips der virtuellen Arbeit: Am Stab greifen als äußere
Computational Biology: Bioelektromagnetismus und Biomechanik
 Computational Biology: Bioelektromagnetismus und Biomechanik Biomechanik III Gliederung Wiederholung: Biomechanik II Spannungsanalyse Materialgleichungen Bewegungsgleichungen Biomechanik III Statische
Computational Biology: Bioelektromagnetismus und Biomechanik Biomechanik III Gliederung Wiederholung: Biomechanik II Spannungsanalyse Materialgleichungen Bewegungsgleichungen Biomechanik III Statische
8. Qualitätsbetrachtung
 sbetrachtung Jedes Berechnungsmodell ist nur so gut wie seine Eingabedaten! 1 8.1 Eindimensionale Elemente 1-dimensionale Elemente (Länge) o Stabelement Zug-/Druckstab o Balkenelement allgemeiner 3-D elastischer
sbetrachtung Jedes Berechnungsmodell ist nur so gut wie seine Eingabedaten! 1 8.1 Eindimensionale Elemente 1-dimensionale Elemente (Länge) o Stabelement Zug-/Druckstab o Balkenelement allgemeiner 3-D elastischer
Inhaltsverzeichnis. 2 Anwendungsfelder und Software Problemklassen Kommerzielle Software 12
 Bernd Klein FEM Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen- und Fahrzeugbau 8., verbesserte und erweiterte Auflage Mit 230 Abbildungen, 12 Fallstudien und 20 Übungsaufgaben STUDIUM
Bernd Klein FEM Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen- und Fahrzeugbau 8., verbesserte und erweiterte Auflage Mit 230 Abbildungen, 12 Fallstudien und 20 Übungsaufgaben STUDIUM
Einführung in die Finite Elemente Methode für Bauingenieure
 Diethard Thieme Einführung in die Finite Elemente Methode für Bauingenieure 3., überarbeitete Auflage mit 145 Abbildungen, 71 Tafeln und 53 Berechnungsbeispielen Shaker Verlag Aachen 2008 Bibliografische
Diethard Thieme Einführung in die Finite Elemente Methode für Bauingenieure 3., überarbeitete Auflage mit 145 Abbildungen, 71 Tafeln und 53 Berechnungsbeispielen Shaker Verlag Aachen 2008 Bibliografische
Praktikum Nichtlineare FEM
 Praktikum Nichtlineare FEM Einführung FEM II - Einführung 1 Mario.Lindner@MB.TU-Chemnitz.DE Ziele des Praktikums Überblick über die Berechnung nichtlinearer Strukturen Umgang mit der kommerziellen FEM-Software
Praktikum Nichtlineare FEM Einführung FEM II - Einführung 1 Mario.Lindner@MB.TU-Chemnitz.DE Ziele des Praktikums Überblick über die Berechnung nichtlinearer Strukturen Umgang mit der kommerziellen FEM-Software
Übungsaufgaben Systemmodellierung WT 2015
 Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
FEM. Finite Elemente Methode. Diese Unterlagen dienen gemäß 53, 54 URG ausschließlich der Ausbildung an der Hochschule Bremen.
 FEM Finite Elemente Methode Diese Unterlagen dienen gemäß 53, 54 URG ausschließlich der Ausbildung an der Hochschule Bremen. Vorlesung FEM INHALT 1.Einleitung 1.1.Historischer Überblick über die Finite
FEM Finite Elemente Methode Diese Unterlagen dienen gemäß 53, 54 URG ausschließlich der Ausbildung an der Hochschule Bremen. Vorlesung FEM INHALT 1.Einleitung 1.1.Historischer Überblick über die Finite
Besteht eine Matrix nur aus einer Spalte (Zeile), so spricht man auch von einem Spaltenvektor (Zeilenvektor)
 Matrizenrechnung. Matrizen Matrizen sind bereits im Kapitel Lineare Gleichungssysteme aufgetreten. Unter einer (m n) -Matrix A verstehen wir ein rechteckiges Zahlenschema mit m Zeilen und n Spalten. Der.
Matrizenrechnung. Matrizen Matrizen sind bereits im Kapitel Lineare Gleichungssysteme aufgetreten. Unter einer (m n) -Matrix A verstehen wir ein rechteckiges Zahlenschema mit m Zeilen und n Spalten. Der.
In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N. Wenn (mit einem n > 1)
 34 Determinanten In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N Wenn (mit einem n > 1) a 11 a 12 a 1n a 21 a 22 a 2n A =, (1)
34 Determinanten In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N Wenn (mit einem n > 1) a 11 a 12 a 1n a 21 a 22 a 2n A =, (1)
8 Extremwerte reellwertiger Funktionen
 8 Extremwerte reellwertiger Funktionen 34 8 Extremwerte reellwertiger Funktionen Wir wollen nun auch Extremwerte reellwertiger Funktionen untersuchen. Definition Es sei U R n eine offene Menge, f : U R
8 Extremwerte reellwertiger Funktionen 34 8 Extremwerte reellwertiger Funktionen Wir wollen nun auch Extremwerte reellwertiger Funktionen untersuchen. Definition Es sei U R n eine offene Menge, f : U R
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
Einführung. Vita Rutka. Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009
 Einführung Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009 Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung,
Einführung Vita Rutka Universität Konstanz Fachbereich Mathematik & Statistik AG Numerik SS 2009 Was ist FEM? Die Finite-Elemente-Methode (FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung,
3 Matrizenrechnung. 3. November
 3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
Extremwerte von Funktionen mehrerer reeller Variabler
 Extremwerte von Funktionen mehrerer reeller Variabler Bei der Bestimmung der Extrema von (differenzierbaren) Funktionen f : R n R ist es sinnvoll, zuerst jene Stellen zu bestimmen, an denen überhaupt ein
Extremwerte von Funktionen mehrerer reeller Variabler Bei der Bestimmung der Extrema von (differenzierbaren) Funktionen f : R n R ist es sinnvoll, zuerst jene Stellen zu bestimmen, an denen überhaupt ein
Lernmodul 2 Modelle des Raumes
 Folie 1 von 21 Lernmodul 2 Modelle des Raumes Bildnachweis: www. tagesschau.de Folie 2 von 21 Modelle des Raumes Übersicht Motivation Was ist Raum? Formalismus und Invarianz Metrischer Raum/Euklidischer
Folie 1 von 21 Lernmodul 2 Modelle des Raumes Bildnachweis: www. tagesschau.de Folie 2 von 21 Modelle des Raumes Übersicht Motivation Was ist Raum? Formalismus und Invarianz Metrischer Raum/Euklidischer
Finite Elemente Programmsystem MEANS V10 für Windows
 Finite Elemente Programmsystem MEANS V10 für Windows Statik Dynamik Formoptimierung Beulen und Temperatur Geometrisch nichtlineare und plastische Verformungen Kontaktbedingungen mit Aufprall Umfangreiche
Finite Elemente Programmsystem MEANS V10 für Windows Statik Dynamik Formoptimierung Beulen und Temperatur Geometrisch nichtlineare und plastische Verformungen Kontaktbedingungen mit Aufprall Umfangreiche
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Info-Sheet Materialdaten
 Aufbereitung eines Werkstoffdatensatzes zur Berechnung von Schweißverzügen und Eigenspannungen Schweißstruktursimulationen basieren auf gekoppelten thermo-mechanischen Simulationen unter Berücksichtigung
Aufbereitung eines Werkstoffdatensatzes zur Berechnung von Schweißverzügen und Eigenspannungen Schweißstruktursimulationen basieren auf gekoppelten thermo-mechanischen Simulationen unter Berücksichtigung
Die Finite Elemente Methode (FEM) gibt es seit über 50 Jahren
 Die Finite Elemente Methode (FEM) gibt es seit über 50 Jahren Aber es gibt bis heute kein Regelwerk oder allgemein gültige Vorschriften/Normen für die Anwendung von FEM-Analysen! Es gibt nur sehr vereinzelt
Die Finite Elemente Methode (FEM) gibt es seit über 50 Jahren Aber es gibt bis heute kein Regelwerk oder allgemein gültige Vorschriften/Normen für die Anwendung von FEM-Analysen! Es gibt nur sehr vereinzelt
Fachwerkelemente sind an ihren Enden durch reibungsfreie Gelenke miteinander verbunden
 47 8 achwerke achwerke sind Tragwerkstrukturen aus geraden Stäben. Sie finden ihren Einsatz überall dort, wo große Distanzen zu überbrücken sind. Durch ihren Aufbau vermeiden sie Momentenbelastungen und
47 8 achwerke achwerke sind Tragwerkstrukturen aus geraden Stäben. Sie finden ihren Einsatz überall dort, wo große Distanzen zu überbrücken sind. Durch ihren Aufbau vermeiden sie Momentenbelastungen und
CAE, 1.3 Übersicht Computerunterstützte Produktentwicklung
 1 Einleitung und Übersicht 1.1 Begrüßung 1.2 Aktuelle Marktstudie PLM-, CAD-, CAE-Systeme 1.3 Übersicht CAE (Computerunterstützte Produktentwicklung) 1 2 Die Finite Elemente Methode 2.1 Das Prinzip der
1 Einleitung und Übersicht 1.1 Begrüßung 1.2 Aktuelle Marktstudie PLM-, CAD-, CAE-Systeme 1.3 Übersicht CAE (Computerunterstützte Produktentwicklung) 1 2 Die Finite Elemente Methode 2.1 Das Prinzip der
Mechanische Spannung und Elastizität
 Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
Mechanische Spannung und Elastizität Wirken unterschiedliche Kräfte auf einen ausgedehnten Körper an unterschiedlichen Orten, dann erfährt der Körper eine mechanische Spannung. F 1 F Wir definieren die
Finite Elemente in der Baustatik
 Horst Werkle Finite Elemente in der Baustatik Statik und Dynamik der Stab- und Flachentragwerke 3., aktualisierte und erweiterte Auflage mit 305 Abbildungen und 43 Tabellen vieweg IX Inhaltsverzeichnis
Horst Werkle Finite Elemente in der Baustatik Statik und Dynamik der Stab- und Flachentragwerke 3., aktualisierte und erweiterte Auflage mit 305 Abbildungen und 43 Tabellen vieweg IX Inhaltsverzeichnis
 Statik I Ergänzungen zum Vorlesungsskript Dr.-Ing. Stephan Salber Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Statik I Vorlesungs- und Übungsmaterial Vorlesung Benutzername: Vorlesungsskript
Statik I Ergänzungen zum Vorlesungsskript Dr.-Ing. Stephan Salber Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Statik I Vorlesungs- und Übungsmaterial Vorlesung Benutzername: Vorlesungsskript
2.4 Elastische Lagerung elastische Bettung
 38 2 Stabtragwerke 2.4 Elastische Lagerung elastische Bettung 2.4.1 Elastisch gebetteter Fundamentbalken Neben der starren oder verschieblichen Lagerung kommen in der Praxis noch zahlreiche Systeme vor,
38 2 Stabtragwerke 2.4 Elastische Lagerung elastische Bettung 2.4.1 Elastisch gebetteter Fundamentbalken Neben der starren oder verschieblichen Lagerung kommen in der Praxis noch zahlreiche Systeme vor,
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Lineare Algebra: Determinanten und Eigenwerte
 : und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
BAUMECHANIK I Prof. Dr.-Ing. Christian Barth
 BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
BAUMECHANIK I Umfang V/Ü/P (ECTS) 2/2/0 (5) 2/2/0 2/2/0 2/2/0-2*/2*/0 - Diplom 5. 6. 7. 8. 9. 10. Definitionen und Klassifizierungen Kräfte und Kraftarten, Vektor, Vektorsysteme Darstellung vektorieller
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
FINITE ELEMENT METHODE ZUSAMMENFASSUNG MOTIVATION/GRUNDGEDANKE: ALLGEMEINES ZU FEM: AUFBAU EINER FEM STRUKTUR. Finite Element Methode Zusammenfassung
 1 von 5 FINITE ELEMENT METHODE ZUSAMMENFASSUNG MOTIVATION/GRUNDGEDANKE: Mathematisch: Ein numerisches Verfahren zur Lösung von partiellen Differentialgleichungen, welche in ein algebraisches Gleichungssystem
1 von 5 FINITE ELEMENT METHODE ZUSAMMENFASSUNG MOTIVATION/GRUNDGEDANKE: Mathematisch: Ein numerisches Verfahren zur Lösung von partiellen Differentialgleichungen, welche in ein algebraisches Gleichungssystem
Praktikum CA-Techniken FT 2016
 Praktikum CA-Techniken FT 2016 Professur für Fahrzeugtechnik Juni 2016 1 Einleitung Die Bearbeitung dieses Praktikums soll von jedem Studenten eigenständig durchgeführt werden. Die Anmeldung für das Praktikum
Praktikum CA-Techniken FT 2016 Professur für Fahrzeugtechnik Juni 2016 1 Einleitung Die Bearbeitung dieses Praktikums soll von jedem Studenten eigenständig durchgeführt werden. Die Anmeldung für das Praktikum
Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am (bitte deutlich schreiben!)
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
Inhaltsverzeichnis 1 Matrizenrechnung 2 Grundgleichungen der Elastizitätstheorie 3 Finite-Element-Methode für Stabwerke
 IX Inhaltsverzeichnis 1 Matrizenrechnung... 1 1.1 Matrizen und Vektoren... 1 1.2 Matrizenalgebra... 3 1.2.1 Addition und Subtraktion... 3 1.2.2 Multiplikation... 4 1.2.3 Matrizeninversion... 6 1.3 Gleichungssysteme...
IX Inhaltsverzeichnis 1 Matrizenrechnung... 1 1.1 Matrizen und Vektoren... 1 1.2 Matrizenalgebra... 3 1.2.1 Addition und Subtraktion... 3 1.2.2 Multiplikation... 4 1.2.3 Matrizeninversion... 6 1.3 Gleichungssysteme...
Elastizität Hooke sches Gesetz
 Elastizität Hooke sches Gesetz Im linearen (elastischen) Bereich gilt: Die Spannung ist proportional zur Dehnung F E A E l l Die Proportionalitätskonstante heißt: Elastizitätsmodul. Das makroskopische
Elastizität Hooke sches Gesetz Im linearen (elastischen) Bereich gilt: Die Spannung ist proportional zur Dehnung F E A E l l Die Proportionalitätskonstante heißt: Elastizitätsmodul. Das makroskopische
3 FEM-Anwendungspraxis 3.1 Modellierungstechniken
 3 FEM-Anwendungspraxis 3.1 Modellierungstechniken 1 Arten der Modellgenerierung Direkte (manuelle) Generierung (Direct modeling): Der Anwender selbst erzeugt die Knoten und Elemente ohne zuvor die Geometrie
3 FEM-Anwendungspraxis 3.1 Modellierungstechniken 1 Arten der Modellgenerierung Direkte (manuelle) Generierung (Direct modeling): Der Anwender selbst erzeugt die Knoten und Elemente ohne zuvor die Geometrie
Mathematischer Vorkurs für Physiker WS 2009/10
 TU München Prof. Dr. P. Vogl, Dr. S. Schlicht Mathematischer Vorkurs für Physiker WS 29/ Vorlesung 9, Freitag vormittag Linienintegrale und Potential Wir betrachten einen Massenpunkt, auf den die konstante
TU München Prof. Dr. P. Vogl, Dr. S. Schlicht Mathematischer Vorkurs für Physiker WS 29/ Vorlesung 9, Freitag vormittag Linienintegrale und Potential Wir betrachten einen Massenpunkt, auf den die konstante
Vektorielle Addition von Kräften
 Vektorielle Addition von Kräften (Begleitende schriftliche Zusammenfassung zum Online-Video) Was wir bisher betrachtet haben: (a) Kräfte wirken entlang derselben Wirkungslinie (parallel oder antiparallel)
Vektorielle Addition von Kräften (Begleitende schriftliche Zusammenfassung zum Online-Video) Was wir bisher betrachtet haben: (a) Kräfte wirken entlang derselben Wirkungslinie (parallel oder antiparallel)
9.2 Invertierbare Matrizen
 34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Entwicklung einer netzbasierten Methodik zur Modellierung von Prozessen der Verdunstungskühlung
 Institut für Energietechnik - Professur für Technische Thermodynamik Entwicklung einer netzbasierten Methodik zur Modellierung von Prozessen der Verdunstungskühlung Tobias Schulze 13.11.2012, DBFZ Leipzig
Institut für Energietechnik - Professur für Technische Thermodynamik Entwicklung einer netzbasierten Methodik zur Modellierung von Prozessen der Verdunstungskühlung Tobias Schulze 13.11.2012, DBFZ Leipzig
Inhalt. 1 Rechenoperationen Gleichungen und Ungleichungen... 86
 Inhalt 1 Rechenoperationen.................................. 13 1.1 Grundbegriffe der Mengenlehre und Logik............................. 13 1.1.0 Vorbemerkung.................................................
Inhalt 1 Rechenoperationen.................................. 13 1.1 Grundbegriffe der Mengenlehre und Logik............................. 13 1.1.0 Vorbemerkung.................................................
Inhalt. 1. Einführung in die Informatik. 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele.
 1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
1. Einführung in die Informatik Inhalt 2. Algorithmen Definition, Eigenschaften, Entwurf Darstellung von Algorithmen Beispiele Peter Sobe 1 Einführende Beispiele 2. Algorithmen Täglich werden Verarbeitungsvorschriften
Methode der f initen Elemente
 r Methode der f initen Elemente Eine Einführung unter besonderer Berücksichtigung der Rechenpraxis Von Dr. sc. math. Hans Rudolf Schwarz ord. Professor an der Universität Zürich 3., neubearbeitete Auflage
r Methode der f initen Elemente Eine Einführung unter besonderer Berücksichtigung der Rechenpraxis Von Dr. sc. math. Hans Rudolf Schwarz ord. Professor an der Universität Zürich 3., neubearbeitete Auflage
Finite Elemente. Klaus Knothe Heribert Wessels. Eine Einführung für Ingenieure. Springer
 Klaus Knothe Heribert Wessels Finite Elemente Eine Einführung für Ingenieure Dritte, überarbeitete und erweiterte Auflage mit 344 Abbildungen Springer Inhaltsverzeichnis 1 Einleitung 1 1.1 Beispiele aus
Klaus Knothe Heribert Wessels Finite Elemente Eine Einführung für Ingenieure Dritte, überarbeitete und erweiterte Auflage mit 344 Abbildungen Springer Inhaltsverzeichnis 1 Einleitung 1 1.1 Beispiele aus
Modell der Punktmasse
 Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Kinematik Die Kinematik (kinema, griech., Bewegung) ist die Lehre von der Bewegung von Punkten und Körpern im Raum, beschrieben durch die Größen Weg (Änderung der Ortskoordinate) s, Geschwindigkeit v und
Landesabitur 2007 Beispielaufgaben 2005_M-LK_A 7. Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 1.
 I. Thema und Aufgabenstellung Lineare Algebra / Analytische Geometrie Aufgaben Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 3. Achse 2. Achse 1. Achse Die Sonne scheint
I. Thema und Aufgabenstellung Lineare Algebra / Analytische Geometrie Aufgaben Eine quadratische Pyramide (Grundkante 4 und Höhe 6) steht neben einer Stufe. 3. Achse 2. Achse 1. Achse Die Sonne scheint
CES-Softwareentwicklungspraktikum Projekt: Elastische zweidimensionale Tragwerksberechnung
 CES-Softwareentwicklungspraktikum Projekt: Elastische zweidimensionale Tragwerksberechnung Dipl.-Ing. M. Nicolai, Dipl. Phys. Eva Schlauch, Dipl. Phys. Roland Siegbert, Chair for Computational Analysis
CES-Softwareentwicklungspraktikum Projekt: Elastische zweidimensionale Tragwerksberechnung Dipl.-Ing. M. Nicolai, Dipl. Phys. Eva Schlauch, Dipl. Phys. Roland Siegbert, Chair for Computational Analysis
Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011)
 M. Sc. Frank Gimbel Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011) 1 Motivation Ziel ist es, ein gegebenes lineares Gleichungssystem der Form Ax = b (1) mit x, b R n und A R n n zu lösen.
M. Sc. Frank Gimbel Beginn der Vorlesung zur Numerik I (Wintersemester 2010/2011) 1 Motivation Ziel ist es, ein gegebenes lineares Gleichungssystem der Form Ax = b (1) mit x, b R n und A R n n zu lösen.
Prinzip der virtuellen Verschiebung
 1 Elektrostatik 52 Prinzip der virtuellen Verschiebung Wir verwenden hier das Prinzip der virtuellen Verschiebung (PVV) zur Berechnung der Kraft auf einen Körper im elektrostatischen Feld. Beim PVV wird
1 Elektrostatik 52 Prinzip der virtuellen Verschiebung Wir verwenden hier das Prinzip der virtuellen Verschiebung (PVV) zur Berechnung der Kraft auf einen Körper im elektrostatischen Feld. Beim PVV wird
8.2 Invertierbare Matrizen
 38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Der CG-Algorithmus (Zusammenfassung)
 Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
Der CG-Algorithmus (Zusammenfassung) Michael Karow Juli 2008 1 Zweck, Herkunft, Terminologie des CG-Algorithmus Zweck: Numerische Berechnung der Lösung x des linearen Gleichungssystems Ax = b für eine
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Eine statische Analyse des Wilson-Elements
 Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 1 Eine statische Analyse des Wilson-Elements von Oliver Carl Bearbeitungszeit: 17. Dezember 2002 bis 12.
Prof. Dr.-Ing. Friedel Hartmann Fachgebiet Baustatik Fachbereich 14 Bauingenieurwesen Diplomarbeit 1 Eine statische Analyse des Wilson-Elements von Oliver Carl Bearbeitungszeit: 17. Dezember 2002 bis 12.
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Numerische Methoden I FEM/REM
 Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Finite Elemente in der Baustatik
 Horst Werkle Finite Elemente in der Baustatik Statik und Dynamik der Stab- und Flächentragwerke Mit 208 Abbildungen, 36 Tabellen und zahlreichen Beispielen 2., überarbeitete und erweiterte Auflage vieweg
Horst Werkle Finite Elemente in der Baustatik Statik und Dynamik der Stab- und Flächentragwerke Mit 208 Abbildungen, 36 Tabellen und zahlreichen Beispielen 2., überarbeitete und erweiterte Auflage vieweg
Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr E Schörner WS / Blatt 6 Übungen zur Vorlesung Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag Wir verwenden das Unterraumkriterium,
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr E Schörner WS / Blatt 6 Übungen zur Vorlesung Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag Wir verwenden das Unterraumkriterium,
Lineare Differenzengleichungen
 Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung
Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 08/09 K 2. Aufgabe 1 (5 Punkte)
 Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
Institut für Technische und Num. Mechanik Technische Mechanik III Prof. Dr.-Ing. Prof. E. h. P. Eberhard WS 8/9 K 6. Februar 9 Klausur in Technische Mechanik III Nachname Vorname Aufgabe (5 Punkte) Der
Institut für Strömungsmechanik und Elektron. Rechnen im Bauwesen der Universität Hannover
 ! H W B - Bibliothek!nv.-Nr. p Institut für Strömungsmechanik und Elektron. Rechnen im Bauwesen der Universität Hannover BERICHT NR. 24/1987 Technische Universität Darmslacit Bibliothek Wasser und Umwelt
! H W B - Bibliothek!nv.-Nr. p Institut für Strömungsmechanik und Elektron. Rechnen im Bauwesen der Universität Hannover BERICHT NR. 24/1987 Technische Universität Darmslacit Bibliothek Wasser und Umwelt
Fehlerfortpflanzung. M. Schlup. 27. Mai 2011
 Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Matrizen, Determinanten, lineare Gleichungssysteme
 Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Matrizen, Determinanten, lineare Gleichungssysteme 1 Matrizen Definition 1. Eine Matrix A vom Typ m n (oder eine m n Matrix, A R m n oder A C m n ) ist ein rechteckiges Zahlenschema mit m Zeilen und n
Numerische Simulation des Absturzes eines Fachwerkträgers der Neuen Messe Stuttgart anhand von FE-Modellen
 Numerische Simulation des Absturzes eines Fachwerkträgers der Neuen Messe Stuttgart anhand von FE-Modellen Seminararbeit im Rahmen des Seminars Virtual Lab Michael Graumann 09. November 2010 i Gliederung
Numerische Simulation des Absturzes eines Fachwerkträgers der Neuen Messe Stuttgart anhand von FE-Modellen Seminararbeit im Rahmen des Seminars Virtual Lab Michael Graumann 09. November 2010 i Gliederung
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
Fit für die Prüfung Elektrotechnik Effektives Lernen mit Beispielen und ausführlichen Lösungen
 Jan Luiken ter Haseborg Christian Schuster Manfred Kasper Fit für die Prüfung Elektrotechnik Effektives Lernen mit Beispielen und ausführlichen Lösungen 18 1 Elektrische Gleichstromnetzwerke det(a 2 )
Jan Luiken ter Haseborg Christian Schuster Manfred Kasper Fit für die Prüfung Elektrotechnik Effektives Lernen mit Beispielen und ausführlichen Lösungen 18 1 Elektrische Gleichstromnetzwerke det(a 2 )
Singularitäten in der FEM und deren Bewertung
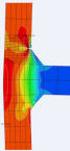 Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Singularitäten in der FEM und deren Bewertung Jeder FEM-Anwender wird früher oder später mit Spannungssingularitäten konfrontiert werden, sich dessen aber nicht unbedingt im Klaren sein. Dafür gibt es
Strömungen in Wasser und Luft
 Strömungen in Wasser und Luft Strömungssimulationen im UZWR Daniel Nolte März 2009 Mathematische Strömungsmodelle Navier Stokes Gleichungen (Massenerhaltung, Impulserhaltung, Energieerhaltung) ρ + (ρ U)
Strömungen in Wasser und Luft Strömungssimulationen im UZWR Daniel Nolte März 2009 Mathematische Strömungsmodelle Navier Stokes Gleichungen (Massenerhaltung, Impulserhaltung, Energieerhaltung) ρ + (ρ U)
Matrizen und Drehungen
 Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
Teil I Physikalische Grundlagen...1. Lernziel...1
 Inhaltsverzeichnis Teil I Physikalische Grundlagen...1 Lernziel...1 1 Temperaturfelder und Wärmeübertragung...1 1.1 Einleitung... 1 1.2 Stationäre und instationäre Wärmeübertragung...2 1.3 Lineare und
Inhaltsverzeichnis Teil I Physikalische Grundlagen...1 Lernziel...1 1 Temperaturfelder und Wärmeübertragung...1 1.1 Einleitung... 1 1.2 Stationäre und instationäre Wärmeübertragung...2 1.3 Lineare und
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode
 Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Numerische Qualität von FEM-Analysen Vergleich der h- und p-methode Dr. Stefan Reul, PRETECH GmbH 2. Norddeutsches Simulationsforum 27. Mai 2010 All rights reserved Copyright per DIN 34 Seite 1 Diskussionspunkte»
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
2 Das elektrostatische Feld
 Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
Das elektrostatische Feld Das elektrostatische Feld wird durch ruhende elektrische Ladungen verursacht, d.h. es fließt kein Strom. Auf die ruhenden Ladungen wirken Coulomb-Kräfte, die über das Coulombsche
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski. Serie 9
 D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Alexander Dabrowski Serie 9 Best Before: 24.5/25.5, in den Übungsgruppen (2 wochen) Koordinatoren: Alexander Dabrowski, HG G 52.1, alexander.dabrowski@sam.math.ethz.ch
ERLÄUTERUNGEN ZUM KRAFTGRÖßENVERFAHREN An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.
 FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
2.1.2 Konkretisierte Unterrichtsvorhaben auf der Basis des Lehrwerks
 2.1.2 Konkretisierte Unterrichtsv auf der Basis des Lehrwerks Einführungsphase 1 Buch: Bigalke, Dr. A., Köhler, Dr. N.: Mathematik Gymnasiale Oberstufe Nordrhein-Westfalen Einführungsphase, Berlin 2014,
2.1.2 Konkretisierte Unterrichtsv auf der Basis des Lehrwerks Einführungsphase 1 Buch: Bigalke, Dr. A., Köhler, Dr. N.: Mathematik Gymnasiale Oberstufe Nordrhein-Westfalen Einführungsphase, Berlin 2014,
LEHRPLAN FÜR DAS ERGÄNZUNGSFACH ANWENDUNGEN DER MATHEMATIK
 LEHRPLAN FÜR DAS ERGÄNZUNGSFACH ANWENDUNGEN DER MATHEMATIK A. Stundendotation Klasse 1. 2. 3. 4. Wochenstunden 4 (1) Beitrag des Faches zur gymnasialen Bildung Der Unterricht im Ergänzungsfach Anwendungen
LEHRPLAN FÜR DAS ERGÄNZUNGSFACH ANWENDUNGEN DER MATHEMATIK A. Stundendotation Klasse 1. 2. 3. 4. Wochenstunden 4 (1) Beitrag des Faches zur gymnasialen Bildung Der Unterricht im Ergänzungsfach Anwendungen
$Id: integral.tex,v /05/05 14:57:29 hk Exp hk $ ln(1 + t) 2 = ln 2 ln 3 + ln 2 = ln
 $Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
$Id: integral.tex,v.5 2009/05/05 4:57:29 hk Exp hk $ 2 Integralrechnung 2.3 Die Integrationsregeln Wir wollen noch eine letzte kleine Anmerkung zur Substitutionsregel machen. Der letzte Schritt bei der
Klausurvorbereitung CM2 Lösungsvorschläge
 Klausurvorbereitung CM2 Lösungsvorschläge 1 Praktische Modellierung und Berechnung 1.1 Beispiele für Wissens- und Verständnis-Fragen 1.) Erklären Sie die Begriffe Solid Modeling und Direkte Generierung!
Klausurvorbereitung CM2 Lösungsvorschläge 1 Praktische Modellierung und Berechnung 1.1 Beispiele für Wissens- und Verständnis-Fragen 1.) Erklären Sie die Begriffe Solid Modeling und Direkte Generierung!
