Baudynamik (Master) SS 2017
|
|
|
- Evagret Wagner
- vor 5 Jahren
- Abrufe
Transkript
1 Baudynamik (Master) SS 7 3. Schwingungen mit zwei und mehr Freiheitsgraden 3. Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.. Einige Prinzipien der Mechanik 3.. Herleitung der Schwingungsgleichungen 3. Ungedämpfte freie Schwingungen 3.. Eigenfrequenzen und Eigenformen 3.. Eigenschaften der Eigenfrequenzen und Eigenformen 3..3 Modalmatrix und modale Transformation 3..4 Näherungsverfahren zur Berechnung der Eigenfrequenzen Rayleigh-Verfahren für diskrete Systeme Rayleigh-Verfahren für kontinuierliche Systeme Ritz-Verfahren für kontinuierliche Systeme
2 Baudynamik (Master) SS Gedämpfte freie Schwingungen 3.3. Eigenwertproblem 3.3. Modale Dämpfung und Rayleigh-Dämpfung 3.4 Ungedämpfte erzwungene Schwingungen 3.4. Direkte Lösungsmethode 3.4. Methode der Modaltransformation 3.5 Gedämpfte erzwungene Schwingungen 3.5. Direkte Lösungsmethode 3.5. Methode der Modaltransformation 3.6 Modale Reduktion und Vergleich der Methoden 3.6. Modale Reduktion 3.6. Vergleich der direkten Methode und der modalen Methode
3 Baudynamik (Master) SS 7 3. Schwingungen mit zwei und mehr Freiheitsgraden 3. Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.. Einige Prinzipien der Mechanik 3.. Herleitung der Schwingungsgleichungen 3
4 Baudynamik (Master) SS Einige Prinzipien der Mechanik Quelle der Bilder: 4
5 Newtonsches Gesetz, d Alembertsches Prinzip.). Newtonsches Gesetz Isaac Newton ( ) F ma.) d Alembertsche Trägheitskraft Jean-Baptiste le Rond d Alembert ( ) F F T FT ma 5 Dynamisches Gleichgewicht, Prinzip der d Alembertschen Trägheitskräfte, d Alembertsches Prinzip d Alembertsche Trägheitskraft
6 d Alembertsches Prinzip d Alembertsches Prinzip lautet eigentlich: ( F ma) r r : virtuelle Verrückung 6
7 Lagrangesche Gleichung 3.) Lagrangesche Gleichung Joseph-Louis de Lagrange ( ) Lq (, q, t) E E i i k p f d L L dt q i qi i L q Leonhard Euler ( ) L : Lagrangesche Funktion qi : verallgemeinerte Koordinaten t : Zeit Ek : kinetische Energie E : potentielle Energie p i : verallgemeinerte Kräfte Euler-Lagrangesche Gleichung 7
8 Hamiltonsches Prinzip 4.) Hamiltonsches Prinzip William Rowan Hamilton ( ) p i L q n i i : verallgemeinerte Impulse Legendre-Transformation: H q p L E E i i k p q i H p i, p i : Hamiltonsche Funktion H q Hamiltonsche Gleichungen, kanonische Gleichungen q, p : kanonische Variablen i i Adrien-Marie Legendre ( ) i 8
9 Legendre Adrien-Marie Legendre ( ) (Französischer Mathematiker) Louis Legendre (75 797) (Französischer Politiker) Beide wurden für etwa Jahre verwechselt (bis 5)! 9
10 Baudynamik (Master) SS Herleitung der Schwingungsgleichungen
11 Herleitung der Schwingungsgleichungen Methoden zur Herleitung der Schwingungsgleichungen:.) Einmassenschwinger, einfache Systeme. Newtonsches Gesetz.) Zwei- und Mehrmassenschwinger, komplizierte Systeme Nachgiebigkeitsmethode Steifigkeitsmethode Lagrangesche Gleichungen Hamiltonsches Prinzip
12 Herleitung der Schwingungsgleichungen Beispiel : Herleitung mit der Nachgiebigkeitsmethode m m F T F T w w d Alembertsche Trägheitskräfte: F mw FT mw T Gesamte Durchbiegungen: w F F T T w F F T T
13 Herleitung der Schwingungsgleichungen Schwingungsgleichungen: mw mw w mw mw w m m w w m m w w m w w m w w δmw w δ m M m Nachgiebigkeitsmatrix, Flexibilitätsmatrix Massenmatrix w w w Verschiebungsvektor 3
14 Herleitung der Schwingungsgleichungen Nachgiebigkeitsmatrix: l l : 3 3 l 3 l 3 6EI 3EI l 5l 3 6EI 48EI l / : l l 3 5l 3 6EI 48EI l l 3 6EI 4EI δ 3 l EI 5 4
15 Herleitung der Schwingungsgleichungen Beispiel : Herleitung mit der Steifigkeitsmethode m m F T F T w w F F k d Alembertsche Trägheitskräfte: F mw FT mw T k k Rückstellkräfte: F w k w k F w k w k k 5
16 Herleitung der Schwingungsgleichungen Dynamisches Gleichgewicht: F T F T F F F T F T F w w F w k w k mw w k w k m w k k w m w k k w m w K k k k k Steifigkeitsmatrix K w+mw M m m Massenmatrix w w w Verschiebungsvektor 6
17 Herleitung der Schwingungsgleichungen Bestimmung der Steifigkeitsmatrix:.) Methode K δ =I K=δ.) Methode δ K= δ k = k k = k k k k 5, k 7 7 7
18 Herleitung der Schwingungsgleichungen k k = k k = k k k 6 5, k 7 7 8
19 Herleitung der Schwingungsgleichungen Beispiel 3: Lagrangesche Gleichung Kinetische Energie: Ek mx mx Potentielle Energie: Ep cx c x x Lagrangesche Funktion: L Ek Ep m x m x c x c x x q x, q x 9
20 Herleitung der Schwingungsgleichungen L q L q L x L x mx mx d dt d dt L x L x mx mx L cx cx x( ) x L x c x x mx c c x cx mx cxcx cc cx m x c c x m x K x+m x=
21 Herleitung der Schwingungsgleichungen Beispiel 4: Hamiltonsches Prinzip Impulse: p mx, p mx Kinetische Energie: Ek mx mx p p m m Potentielle Energie: E p cx c xx Hamiltonsche Funktion: H E k E p p p c x c m m x x q x, q x
22 Herleitung der Schwingungsgleichungen q i H p p cq m c q q H p H p H p i x x m m m p p m p p m H cx c x x q H c x x q p i H q H p cx c x x q H p c x x q i
23 Herleitung der Schwingungsgleichungen mx c c x cx mx cxcx cc cx m x c c x m x K x+m x= 3
24 Baudynamik (Master) SS 7 3. Ungedämpfte freie Schwingungen 3.. Eigenfrequenzen und Eigenformen 4
25 3.. Eigenfrequenzen und Eigenformen Zwei Freiheitsgrade: x+x oder x x : Nachgiebigkeitsmatrix, Flexibilitätsmatrix : Steifigkeitsmatrix : Massenmatrix Lösungsansatz: x Acos( t ) 5
26 Eigenfrequenzen und Eigenformen Eigengleichungen: oder I A M A : Nachgiebigkeitsmatrix, Flexibilitätsmatrix : Steifigkeitsmatrix : Massenmatrix : Einheitsmatrix : Eigenfrequenzen : Eingenvektoren, Eigenformen 6
27 Eigenfrequenzen und Eigenformen Bedingung für nicht-triviale Lösungen: Det I oder M Det Charakteristische Gleichung für die Eigenfrequenzen Eigenfrequenzen :, ( ) Eigenvektoren : A, A 7
28 Bemerkungen: Eigenfrequenzen und Eigenformen M A M A Eigenfrequenzen und Eigenformen sind wichtige dynamische Systemeigenschaften. Die Eigenfrequenzen sind die Eigenwerte des Eigenwertproblems. Die Eigenvektoren werden häufig als Eigenformen oder Eigenmoden bezeichnet. 8
29 Homogene Lösung Lösung: x=a c cos( t ) A c cos( t ) Insgesamt 4 Unbekannten aus 4 Anfangsbedingungen (pro Masse Anfangsbedingungen)! x () () () = x x x v, () x() x x = x () v 9
30 Bemerkungen zu Freiheitsgraden Methode der konzentrierten Massen Kontinuierliches System: Unendlich viele Freiheitsgrade m, m,..., mn i wx ( ) ai( t) i( x) Methode der verallgemeinerten Koordinaten n Diskretes System: Endlich viele Freiheitsgrade 3
31 Bemerkungen zu Freiheitsgraden Die Anzahl der Freiheitsgrade ist im Allgemeinen nicht gleich der Anzahl der Massen. Die Anzahl der Freiheitsgrade ist abhängig von der Annahme (dehnstarr, dehnbar, etc.). Die Anzahl der Freiheitsgrade ist unabhängig von der statischen Unbestimmtheit und der geometrischen Unbestimmtheit. Je mehr Freiheitsgrade, desto genauer sind die Ergebnisse, desto aufwendiger ist die dynamische Berechnung. 3
32 Eigenfrequenzen und Eigenformen n Freiheitsgrade: x x x Acos( t ) M A Det M Eigenfrequenzen :,,..., n Eigenvektoren : A, A,..., An 3
33 Homogene Lösung Lösung: x=ac cos( t ) A c cos( t )... A c cos( t ) n n n n Insgesamt xn Unbekannten aus xn Anfangsbedingungen (pro Masse Anfangsbedingungen)! x v x v x () =, x () = x v n n 33
34 Baudynamik (Master) SS 7 3. Ungedämpfte freie Schwingungen 3.. Eigenschaften der Eigenfrequenzen und Eigenformen 34
35 Eigenschaften der Eigenfrequenzen und Eigenformen Die Berechnung der Nullstellen der charakteristischen Gleichung bei großen Matrizen (größer als 3x3) ist meistens sehr aufwendig. Daher werden häufig numerische Näherungsverfahren angewendet. Dazu gehören numerische Methoden für symmetrische Matrizen und dünnbesetzte große Matrizen: Potenzmethode Inverse Iteration Lanczos-Verfahren Arnoldi-Verfahren Jacobi-Verfahren Jacobi-Davidson-Verfahren Satz für die Eigenfrequenzen: Wenn M und K reell, symmetrisch und positiv definit sind, dann existieren n positive reelle Eigenfrequenzen (n = Anzahl der Freiheitsgrade). Wenn M reell, symmetrisch und positiv definit, und K reell, symmetrisch und semi-positiv definit ist, dann existieren n nichtnegative Eigenfrequenzen (n = Anzahl der Freiheitsgrade). 35
36 Eigenschaften der Eigenfrequenzen und Eigenformen Eine Matrix ist positiv definit, falls ihre quadratische Form positiv ist, d.h. T xkx Eine Matrix ist semi-positiv definit, falls ihre quadratische Form nicht negativ ist, d.h. T xkx 36
37 Eigenschaften der Eigenfrequenzen und Eigenformen Eigenschaften der Eigenformen: Die Elemente der Eigenvektoren A i sind nicht unabhängig voneinander und können nicht eindeutig bestimmt werden. A i können nur für ihre Verhältnisse oder mit einer Normierung bestimmt werden. Häufig verwendete Normierungen:.) A oder A (Ingenieurnormierung) i ni T im MAiM T ik KAiK.) A (Massennormiert, wichtig für Modalanalyse) 3.) A (Steifigkeitsnormiert, manchmal numerisch vorteilhaft) Umrechnung: A i A im = A T i M A i 37
38 Eigenschaften der Eigenfrequenzen und Eigenformen Orthogonalität: T.) Ai MA j ( i j). Orthogonalität T.) Ai KA j ( i j). Orthogonalität Physikalische Bedeutung: Schwingt ein System in einer bestimmten Eigenform, leisten seine Trägheitskräfte keine Arbeit auf andere Eigenformen. Seine Energie kann also nicht auf andere Eigenformen übertragen werden. Die Orthogonalitätseigenschaft der Eigenvektoren wird häufig bei iterativen Bestimmungen der Eigenvektoren ausgenutzt. 38
39 Baudynamik (Master) SS 7 3. Ungedämpfte freie Schwingungen 3..3 Modalmatrix und modale Transformation 39
40 Modalmatrix Eigenmatrix oder Modalmatrix: A A A A A A A A A A A A n n,,..., n n n nn (hier : A i A im!) A A T i T i MA (Massennormiert) MA i j (Orthogonalität) T M I M A i T T T Ai i M Ai Ai Ai i Ai Ai T T T Ai jm A j Ai A j j Ai A j i 4 T K
41 Modale Transformation Modaltransformation: x= q q q x : Physikalische Koordinaten q: Modale Koordinaten T T q q q q I Entkoppelte Differentialgleichungen! q x= q Rücktransformation 4
42 q ω q q c t q ω q Modale Transformation q cos( ) q c cos( t ) Insgesamt n Unbekannten aus n Anfangsbedingungen (pro Masse )! ( ) Φ x() Φ x; q() Φ x() Φ v Beachte: T - T Φ MΦ= I Φ = Φ M Alternativ: Die Anpassung der Anfangsbedingungen kann auch nach der Rücktransformation durchgeführt werden! 4
43 Modalanalyse Die Methode der modalen Transformation wird häufig auch als Modalanalyse bezeichnet. Die grundlegende Idee der Modalanalyse besteht darin, Schwingungen von Mehrfreiheitsgradsystemen als Superposition der Schwingungen von mehreren Einfreiheitsgradsystemen darzustellen. 43
44 Baudynamik (Master) SS 7 3. Ungedämpfte freie Schwingungen 3..4 Näherungsverfahren zur Berechnung der Eigenfrequenzen Rayleigh-Verfahren für diskrete Systeme Rayleigh-Verfahren für kontinuierliche Systeme Ritz-Verfahren für kontinuierliche Systeme 44
45 Rayleigh und Ritz Lord Rayleigh ( ) Walter Ritz ( ) Quelle: 45
46 Rayleigh-Verfahren für diskrete Systeme Potentielle Energie: Kinetische Energie: E E p k kx mx E E p k T xkx T xmx E E p,max k,max T AKA T AMA E E p k AKA T t x Acos( t ) cos ( ) sin ( t ) T AMA Energieerhaltung: E p,max E k,max T AKA T AMA Rayleigh-Quotient 46
47 Rayleigh-Verfahren für diskrete Systeme Bemerkungen: Falls der exakte Eigenvektor A verwendet wird, dann erhält man auch die exakte Eigenfrequenz. Falls nur eine Näherungslösung für den Eigenvektor verwendet wird, dann erhält man eine Näherungslösung für die Eigenfrequenz: i AKA AMA Man kann zeigen, dass die Näherungslösung für die Eigenfrequenz immer größer als die exakte Eigenfrequenz ist: T i T i i i, exakt Das Rayleigh-Verfahren wird überwiegend für die. (niedrigste) Eigenfrequenz verwendet. Als Näherungslösung für den Eigenvektor kann die statische Lösung verwendet werden. i i 47
48 Rayleigh-Verfahren für kontinuierliche Systeme l M Formänderungsenergie: Ep U dx EI( x) w( x, t) dx EI( x) l Kinetische Energie: Ek m( x) w( x, t) dx l cos ( ) ( ) ( ) Ep U t EI x W x dx l Ek sin ( t) m( x) W( x) dx l w W( x)cos( t) E p,max E k,max l l EI( x) W ( x) dx mx ( ) W( x) dx 48 Rayleigh-Quotient
49 Rayleigh-Verfahren für kontinuierliche Systeme Bemerkungen: Falls die exakte Biegelinie W(x) verwendet wird, dann erhält man auch die exakte Eigenfrequenz. Falls nur eine Näherungslösung für die Biegelinie verwendet wird, dann erhält man auch nur eine Näherungslösung für die Eigenfrequenz: l EI( x) W ( x) dx i l mx ( ) W ( x) dx Man kann zeigen, dass die Näherungslösung für die Eigenfrequenz immer größer als die exakte Eigenfrequenz ist: i i, exakt Das Rayleigh-Verfahren wird überwiegend für die. (niedrigste) Eigenfrequenz verwendet. Als Näherungslösung für die Biegelinie kann die statische Biegelinie verwendet werden. Je weniger die Näherungslösung von der exakten Biegelinie abweicht, desto genauer ist die abgeschätzte Eigenfrequenz im Rayleigh-Verfahren. Die Näherungslösung für die Biegelinie soll mindestens die geometrischen Randbedingungen erfüllen. 49
50 Ritz-Verfahren für kontinuierliche Systeme Das Ritz-Verfahren ist eine Erweiterung des Rayleigh-Verfahrens (daher auch als Rayleigh-Ritz- Verfahren bekannt), indem man einen mehrgliederigen Ansatz macht: W( x) aii( x) n i a i werden als verallgemeinerte Koordinaten und i (x) werden als Ritz-Basisfunktionen oder Formfunktionen bezeichnet. n entspricht der Anzahl der Freiheitsgrade. Mit der Energiebetrachtung erhält man nun den Rayleigh-Quotienten: Ra ( ) Damit der Fehler minimal bleibt, muss gelten: i l i i i n l n EI( x) a ( x) dx mx ( ) aii( x) dx i Ra ( i ) U U E U U E ai E ai E ai ai E ai U E 5
51 Ritz-Verfahren für kontinuierliche Systeme U a i E a i n l a EI( x) ( x) ( x) dx k a j j i ij j j j n l a m( x) ( x) ( x) dx m a j j i ij j j j n n Daraus ergibt sich: n j k m a ij ij j Oder in Matrizenschreibweise: K M a 5
52 Ritz-Verfahren für kontinuierliche Systeme Die verallgemeinerte Steifigkeitsmatrix K und die verallgemeinerte Massenmatrix M können aus den folgenden Gleichungen bestimmt werden: l k EI( x) ( x) ( x) dx ij i j l m m( x) ( x) ( x) dx ij i j 5
53 Ritz-Verfahren für kontinuierliche Systeme Bemerkungen: Falls nur ein Glied im Ritz-Ansatz verwendet wird, dann ergibt sich als Sonderfall das Rayleigh- Verfahren. Das Rayleigh-Verfahren ist nur für die. (niedrigste) Eigenfrequenz geeignet, während das Ritz- Verfahren auch für höhere Frequenzen geeignet ist. Man kann zeigen, dass die Eigenfrequenzen aus dem Ritz-Verfahren immer größer als die exakten Werte sind: i i, exakt Je mehr Glieder verwendet werden, desto genauer sind die Ergebnisse, desto aufwendiger ist die Berechnung. Der Ritz-Ansatz muss mindestens die geometrischen Randbedingungen erfüllen. Wird das Ritz-Verfahren nicht auf die gesamte Struktur, sondern nur auf ein Element angewendet, dann ist das Ritz-Verfahren identisch mit der finiten Elemente Methode (FEM). 53
54 FEM wx ( ) a a a a x x ( x) 3 l l a a EI, ml, a 4 a 3 x x ( x) x l l x x 3 ( x) 3 l l ( x) x x x l l 4 x/ l
55 FEM Eigenschaften der Formfunktionen: (), () () () 3 4 (), () () () 3 4 () l, () l () l () l 3 4 () l, () l () l () l 4 3 l k EI ( x) ( x) dx ij i j K EI l 6 6 l l 6 4l 6 l 6 6 l l 6 l 6 4l l m m ( x) ( x) dx ij i j 56 l 54 3l m l 4l 3l 3l M l 56 l 3l 3l l 4l 55
56 Baudynamik (Master) SS Gedämpfte freie Schwingungen 3.3. Eigenwertproblem 56
57 Eigenwertproblem Kx Dx Mx [ K D M] A x Ae t Det( K D M) Komplex konjugierte Eigenwerte: n an a a + + i (j,,..., n) j j d, j 57
58 Bemerkungen: Eigenwertproblem Die Eigenwertberechnung bei gedämpften Systemen ist im Allgemeinen sehr aufwendig. Falls j positiv (schwache Dämpfung) ist, dann hat man eine gedämpfte Schwingung mit abklingenden Amplituden. Falls i negativ (starke Dämpfung) ist, dann hat man keine Schwingung (Kriechbewegung). D ist im Allgemeinen symmetrisch. Die Modalmatrix kann die Steifigkeitsmatrix K, aber nicht die Dämpfungsmatrix D diagonalisieren. D.h., eine Entkoppelung der Schwingungsgleichungen ist durch eine Modaltransformation bei gedämpften Schwingungen im Allgemeinen nicht möglich. Nur durch spezielle Annahmen für die Dämpfung (modale Dämpfung und Rayleigh-Dämpfung, siehe später) können die Schwingungsgleichungen durch eine Modaltransformation entkoppelt werden. 58
59 Eigenwertproblem Kx Dx Mx Kq Dq Mq x Φq Τ Τ Τ Kq D q Mq diagonal i. A. nicht diagonal diagonal Entkoppelung der Gleichungen i. A. nicht möglich! Dämpfung: Stahlbeton: 5% Stahl: etwa %-% 59 Τ Τ Τ K modale Steifigkeitsmatrix M: modale Massenmatrix D: modale Dämpfungsmatrix
60 Baudynamik (Master) SS Gedämpfte freie Schwingungen 3.3. Modale Dämpfung und Rayleigh-Dämpfung 6
61 Modale Dämpfung Ungedämpft: Gedämpft: q q ω q dq ω Modale Dämpfung! q D d D Modale Dämpfung! q D q ω q q D q ω q Modale Dämpfung: In jeder modalen Gleichung wird ein Dämpfungsterm addiert! 6
62 Modale Dämpfung Lösung: t q c e t cos( ) t q c e t cos( ) Insgesamt n Unbekannten aus n Anfangsbedingungen (pro Masse )! q ( ) Φ x() Φ x; q() Φ x() Φ v Rücktransformation: x Φq Alternativ: Die Anpassung der Anfangsbedingungen kann auch nach der Rücktransformation durchgeführt werden! 6
63 Rayleigh-Dämpfung Rayleigh-Dämpfung: (Proportionale Dämpfung, Bequemlichkeitshypothese) D M K Kq Kx Dx Mx (M K) q M q x Φq T Φ KΦq ω T ( Φ MΦ I T Φ KΦ)q d ω T Φ MΦq I q dq ω q 63
64 Rayleigh-Dämpfung D d D Im Modalraum ist die modale Dämpfung also identisch mit der Rayleigh-Dämpfung! D j j j D D ( D D) ( ) Lösung: i q c e t cos( t ), ( i,,...,n) i i i i Insgesamt n Unbekannten aus n Anfangsbedingungen (pro Masse )! q ( ) Φ x() Φ x; q() Φ x() Φ v Rücktransformation: x Φq 64
65 Baudynamik (Master) SS Ungedämpfte erzwungene Schwingungen 3.4. Direkte Lösungsmethode 3.4. Methode der Modaltransformation 65
66 Direkte Lösungsmethode x x F Harmonischer Lastvektor: Gesamtlösung: F() t Fcos( t) x() t x () t x () t h p Homogene Lösung: siehe freie Schwingungen!: Partikularlösung: Ansatz vom Typ der rechten Seite x K p dyn () t x cos( t ) x p p Dynamische Steifigkeitsmatrix ( ) H( ) K K M dyn F xp Kdyn F dyn Dynamische Nachgiebigkeitsmatrix Wird häufig auch als Frequenzgangmatrix H oder Übertragungsmatrix bezeichnet. 66
67 Methode der Modaltransformation x x F x q q q=f F() t Fcos( t) Harmonische Erregung q q = F T T T q+ q F q q q h p x q Rücktransformation 67
68 Methode der Modaltransformation Homogene Lösung: siehe freie Schwingungen!: Partikularlösung: Ansatz vom Typ der rechten Seite q () t q p cos( t ) q + q F p T p q ip A T im i F T T T n T M M M M nm nm im im xp A A A A A A F = A A F n i i dyn 68
69 Baudynamik (Master) SS Gedämpfte erzwungene Schwingungen 3.5. Direkte Lösungsmethode 3.5. Methode der Modaltransformation 69
70 Direkte Lösungsmethode: Homogene Lösung x Dx x h h h vgl.: Gedämpfte freie Schwingungen! x () h t Bemerkung: Die homogene Lösung bei gedämpften Systemen klingt mit der Zeit rasch ab, so dass nach kurzer Zeit (im eingeschwungenen Zustand) nur die Partikularlösung maßgebend bleibt. 7
71 Direkte Lösungsmethode: Partikularlösung x Dx x F p p p F() t F i t e x p () t x i t pe i p D- x F id xp F K dyn Dynamische Steifigkeitsmatrix xp KdynF dyn Dynamische Nachgiebigkeitsmatrix i ( ) H( ) K K+ M M dyn Wird häufig auch als Frequenzgangmatrix H oder Übertragungsmatrix bezeichnet. 7
72 Methode der Modaltransformation x Dx xf q Dq+ q F x q T qdq+ q F F() t Fcos( t) T F * * q+dq+ q F F () t F cos( t) * * q D q q F t * i + ii i + i i i cos( ) q / +( D / ) q + q ( F / ) cos( t) * i i i i i i i i (vgl. gedämpfter Einmassenschwinger!) 7
73 Methode der Modaltransformation q h () t q t V F t * ip () i ( i / i )cos( i ) Partikularlösung Di tan( i), V i i i i 4Dii x h () t q h q p () t F A * T i im F q=q h q p V x () t A A F cos( t ) n T i p im im i i i x q Rücktransformation 73
74 Baudynamik (Master) SS Modale Reduktion und Vergleich der Methoden 3.6. Modale Reduktion 3.6. Vergleich der direkten Methode und der modalen Methode 74
75 Modale Reduktion Die Lösung einer Schwingung ist die gewichtete Superposition der Eigenschwingungen (Eigenformen, Eigenmoden). Daher wird die Methode der Modaltransformation auch als Methode der Modalsuperposition oder Modalsuperpositionsmethode bezeichnet. Niedrige Eigenformen leisten größere Beiträge und höhere Eigenformen haben kleinere Beiträge. x q A A A A A () t q q NqN NqN nqn Wichtig! Weniger wichtig! x AqAq ANqN ( NN) q Modale Reduktion Große Rechenaufwandsreduzierung falls N<<n! 75
76 Modale Reduktion Modale Reduktion reduziert den Rechenaufwand, aber wie bestimmt man die Grenze N? Faustregel: Frequenzband der Erregung:, Obergrenze der Eigenfrequenzen:,5 i min max max 76
77 Vergleich der direkten Methode und der modalen Methode Direkte Methode Modale Methode Dämpfung Beliebig. Beliebig. Entkoppelung Nein. Ja, nur mit Annahme (modal oder Rayleigh). Aufwand Groß, da K dyn für jede Anregungsfrequenz neu zu berechnen und zu invertieren ist. Klein, wenn Entkoppelung oder modale Reduktion (N<<n). Genauigkeit Hoch. Hoch wenn keine modale Reduktion. Niedrig bei modaler Reduktion. Linearität Empfehlung Anwendbar auch bei Nichtlinearität. Bei Stoß (schmallbandig) (direkte Zeit-Integration) Nur anwendbar bei Linearität. Bei Erdbeben, Wind (breitbandig) 77
Baudynamik (Master) SS 2014
 Baudynamik (Master) SS 14 3. Schwingungen mit zwei und mehr Freiheitsgraden 3.1 Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.1.1 Einige Prinzipien der Mechanik 3.1. Herleitung
Baudynamik (Master) SS 14 3. Schwingungen mit zwei und mehr Freiheitsgraden 3.1 Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.1.1 Einige Prinzipien der Mechanik 3.1. Herleitung
Baudynamik (Master) SS Beispiele: Ungedämpfte freie Schwingungen
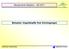 Baudynamik (Master) SS 7 Beispiee: Ungedämpfte freie Schwingungen Ungedämpfte freie Schwingungen Beispie : Eigenfrequenzen und Eigenformen m m m m, m m m Steifigkeitsmatrix: K= k 7 5 5 6 k 48EI Massenmatrix:
Baudynamik (Master) SS 7 Beispiee: Ungedämpfte freie Schwingungen Ungedämpfte freie Schwingungen Beispie : Eigenfrequenzen und Eigenformen m m m m, m m m Steifigkeitsmatrix: K= k 7 5 5 6 k 48EI Massenmatrix:
3. Erzwungene Schwingungen
 3. Erzwungene Schwingungen 3.1 Grundlagen 3.2 Tilger 3.3 Kragbalken 3.4 Fahrbahnanregung 3.3-1 3.1 Grundlagen Untersucht wird die Antwort des Systems auf eine Anregung mit harmonischem Zeitverlauf. Bewegungsgleichung:
3. Erzwungene Schwingungen 3.1 Grundlagen 3.2 Tilger 3.3 Kragbalken 3.4 Fahrbahnanregung 3.3-1 3.1 Grundlagen Untersucht wird die Antwort des Systems auf eine Anregung mit harmonischem Zeitverlauf. Bewegungsgleichung:
6 Systeme mit mehreren Freiheitsgraden
 6 Systeme mit mehreren Freiheitsgraden 6.. Steifigkeitsformulierung 6. Formulierung der Bewegungsgleichung 6.. Gleichgewichtsformulierung Die Freiheitsgrade sind die horizontalen Verschiebungen und u auf
6 Systeme mit mehreren Freiheitsgraden 6.. Steifigkeitsformulierung 6. Formulierung der Bewegungsgleichung 6.. Gleichgewichtsformulierung Die Freiheitsgrade sind die horizontalen Verschiebungen und u auf
2. Schwingungen eines Einmassenschwingers
 Baudynamik (Master) SS 2017 2. Schwingungen eines Einmassenschwingers 2.1 Freie Schwingungen 2.1.1 Freie ungedämpfte Schwingungen 2.1.2 Federzahlen und Federschaltungen 2.1.3 Freie gedämpfte Schwingungen
Baudynamik (Master) SS 2017 2. Schwingungen eines Einmassenschwingers 2.1 Freie Schwingungen 2.1.1 Freie ungedämpfte Schwingungen 2.1.2 Federzahlen und Federschaltungen 2.1.3 Freie gedämpfte Schwingungen
4 Erzwungene Schwingungen konservativer Schwingungssysteme
 23 4 Erzwungene Schwingungen konservativer Schwingungssysteme Die allgemeine Lösung einer inhomogenen linearen Schwingungsgleichung findet man durch Überlagerung der homogenen Lösung (freie Schwingungen)
23 4 Erzwungene Schwingungen konservativer Schwingungssysteme Die allgemeine Lösung einer inhomogenen linearen Schwingungsgleichung findet man durch Überlagerung der homogenen Lösung (freie Schwingungen)
3. Fluid-Struktur-Kopplung
 3. Fluid-Struktur-Kopplung Bei einer schwingenden Struktur muss die Normalkomponente der Schallschnelle mit der Normalkomponente der Geschwindigkeit an der Oberfläche der Struktur übereinstimmen. Dadurch
3. Fluid-Struktur-Kopplung Bei einer schwingenden Struktur muss die Normalkomponente der Schallschnelle mit der Normalkomponente der Geschwindigkeit an der Oberfläche der Struktur übereinstimmen. Dadurch
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Baudynamik (Master) SS 2018
 Baudynamk (Master) SS 8 3. Schwngungen mt zwe und mehr Frehetsgraden 3. Enge Prnzpen der Mechank und Herletung der Schwngungsglechungen 3.. Enge Prnzpen der Mechank 3.. Herletung der Schwngungsglechungen
Baudynamk (Master) SS 8 3. Schwngungen mt zwe und mehr Frehetsgraden 3. Enge Prnzpen der Mechank und Herletung der Schwngungsglechungen 3.. Enge Prnzpen der Mechank 3.. Herletung der Schwngungsglechungen
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
6 Eigenlösungen der eindimensionalen Wellengleichung
 39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
1. Aufgabe: (ca. 14% der Gesamtpunkte)
 Institut für Mechanik Prof. Dr.-Ing. habil. P. Betsch Prof. Dr.-Ing. habil. Th. Seelig Prüfung in Baudynamik 23. Juli 2018 1. Aufgabe: (ca. 14% der Gesamtpunkte) a) Geben Sie Amplitude, Frequenz und Phasenverschiebung
Institut für Mechanik Prof. Dr.-Ing. habil. P. Betsch Prof. Dr.-Ing. habil. Th. Seelig Prüfung in Baudynamik 23. Juli 2018 1. Aufgabe: (ca. 14% der Gesamtpunkte) a) Geben Sie Amplitude, Frequenz und Phasenverschiebung
10 Erzwungene Schwingungen durch inhomogene Randbedingungen
 63 10 Erzwungene Schwingungen durch inhomogene Randbedingungen Schwingungen eines kontinuierlichen Systems lassen sich nicht nur durch verteilte Kräfte, sondern auch durch zeitveränderliche Bindungen an
63 10 Erzwungene Schwingungen durch inhomogene Randbedingungen Schwingungen eines kontinuierlichen Systems lassen sich nicht nur durch verteilte Kräfte, sondern auch durch zeitveränderliche Bindungen an
Kapitel 7 Generalisierte Koordinaten und dynamische Antwortrechnung
 Kapitel 7 Generalisierte Koordinaten und dynamische Antwortrechnung In Kap. 4 wurden am Beispiel von Zwei- und Mehrmassenschwingern dynamische Antwortrechnungen durchgeführt. Dabei zeigte sich, dass bei
Kapitel 7 Generalisierte Koordinaten und dynamische Antwortrechnung In Kap. 4 wurden am Beispiel von Zwei- und Mehrmassenschwingern dynamische Antwortrechnungen durchgeführt. Dabei zeigte sich, dass bei
Teilstrukturen
 5. Teilstrukturen Die Berechnung von komplexen trukturen lässt sich oft vereinfachen, wenn die truktur in Teilstrukturen unterteilt wird. Die Teilstrukturen hängen an den Anschlusspunkten zusammen. Für
5. Teilstrukturen Die Berechnung von komplexen trukturen lässt sich oft vereinfachen, wenn die truktur in Teilstrukturen unterteilt wird. Die Teilstrukturen hängen an den Anschlusspunkten zusammen. Für
Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem
 Institute of Structural Engineering Page 1 Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem Institute of Structural Engineering Page 2 Lernziele: Sie können Stabilitätsprobleme
Institute of Structural Engineering Page 1 Kapitel 12 Berechnung nach Theorie 2. Ordnung DSM & das Eigenwertproblem Institute of Structural Engineering Page 2 Lernziele: Sie können Stabilitätsprobleme
9 Erzwungene Schwingungen durch verteilte Kräfte
 57 9 Erzwungene Schwingungen durch verteilte Kräfte Wirken auf ein kontinuierliches System verteilte zeitveränderliche Kräften bzw. Momente, entstehen erzwungene Schwingungen. In diesem Fall sind die partiellen
57 9 Erzwungene Schwingungen durch verteilte Kräfte Wirken auf ein kontinuierliches System verteilte zeitveränderliche Kräften bzw. Momente, entstehen erzwungene Schwingungen. In diesem Fall sind die partiellen
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik
 D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik
 D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
3. Modalanalyse. Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen.
 3. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Bei der rechnerischen Modalanalyse muss ein Eigenwertproblem
3. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Bei der rechnerischen Modalanalyse muss ein Eigenwertproblem
4. Einführung in die Baudynamik
 Baustatik III SS 2017 4. Einführung in die Baudynamik 4.1 Allgemeine Vorbemerkungen 4.1.1 Bedeutungen der Baudynamik 4.1.2 Grundbegriffe und Klassifizierung 4.1.3 Modellierung der Bauwerksschwingungen
Baustatik III SS 2017 4. Einführung in die Baudynamik 4.1 Allgemeine Vorbemerkungen 4.1.1 Bedeutungen der Baudynamik 4.1.2 Grundbegriffe und Klassifizierung 4.1.3 Modellierung der Bauwerksschwingungen
8 Freie Schwingungen kontinuierlicher Systeme
 51 Freie Schwingungen sind Lösungen der partiellen Differentialgleichung gegebene Anfangs- und Randbedingungen. Das Vorgehen ist die eindimensionale Wellengleichung und die Balkenbiegung einheitlich und
51 Freie Schwingungen sind Lösungen der partiellen Differentialgleichung gegebene Anfangs- und Randbedingungen. Das Vorgehen ist die eindimensionale Wellengleichung und die Balkenbiegung einheitlich und
2. Modalanalyse. Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen.
 2. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Die experimentelle Modalanalyse von Flugzeugen erfolgt
2. Modalanalyse Die Ermittlung der Eigenschwingungen wird als Modalanalyse bezeichnet. Die Modalanalyse kann experimentell oder rechnerisch erfolgen. Die experimentelle Modalanalyse von Flugzeugen erfolgt
11.4. Lineare Differentialgleichungen höherer Ordnung
 4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4 Lineare Differentialgleichungen höherer Ordnung Bei vielen geometrischen, physikalischen und technischen Problemen hat man nicht nur eine Funktion (in einer Variablen) und ihre Ableitung zueinander in
4. Transiente Analyse
 4. Transiente Analyse Bei der transienten Analyse wird der zeitliche Verlauf der Antwort auf eine zeitlich veränderliche Last bestimmt. Die zu lösende Bewegungsgleichung lautet: [ M ] [ü ]+[ D ] [ u ]+
4. Transiente Analyse Bei der transienten Analyse wird der zeitliche Verlauf der Antwort auf eine zeitlich veränderliche Last bestimmt. Die zu lösende Bewegungsgleichung lautet: [ M ] [ü ]+[ D ] [ u ]+
Ausblick. 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen. Prof. Dr. Wandinger 5. Ausblick FEM 5-1
 Ausblick 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen Prof. Dr. Wandinger 5. Ausblick FEM 5-1 1. Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen
Ausblick 1. Lineare dynamische Analysen 2. Nichtlineare Analysen 3. Weitere Anwendungen Prof. Dr. Wandinger 5. Ausblick FEM 5-1 1. Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen
MATRIZEN. und Determinanten. und ihre Anwendung in Technik und Ökonomie. von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing.
 MATRIZEN und Determinanten und ihre Anwendung in Technik und Ökonomie von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing. Henry Stahl 5., neubearbeitete Auflage Mit 63 Bildern und 133 Beispielen und Lösungen
MATRIZEN und Determinanten und ihre Anwendung in Technik und Ökonomie von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing. Henry Stahl 5., neubearbeitete Auflage Mit 63 Bildern und 133 Beispielen und Lösungen
Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss. Aufgabensammlung mit Kurzlösungen
 Prof. Dr.-Ing. Prof. E.h. P. Eberhard / Prof. Dr.-Ing. M. Hanss SS 17 Ü1 Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss Aufgabensammlung mit Kurzlösungen Sommersemester 017 Prof. Dr.-Ing.
Prof. Dr.-Ing. Prof. E.h. P. Eberhard / Prof. Dr.-Ing. M. Hanss SS 17 Ü1 Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss Aufgabensammlung mit Kurzlösungen Sommersemester 017 Prof. Dr.-Ing.
Baudynamik und Zustandsanalyse
 Baudynamik und Zustandsanalyse Eine Einführung in die Baudynamik mit Mathematica Das vorliegende Skript wurde im Original mit dem Programmsystem MATHEMATICA von WOLFRAM-Research [http://www.wolfram.com]
Baudynamik und Zustandsanalyse Eine Einführung in die Baudynamik mit Mathematica Das vorliegende Skript wurde im Original mit dem Programmsystem MATHEMATICA von WOLFRAM-Research [http://www.wolfram.com]
Klassische Theoretische Physik II. V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch. Klausur 1 Lösung. 27. Juli 2015, Uhr
 KIT SS 05 Klassische Theoretische Physik II V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch Klausur Lösung 7. Juli 05, 6-8 Uhr Aufgabe : Kurzfragen (+4++3=0 Punkte) (a) Zwangsbedingungen beschreiben Einschränkungen
KIT SS 05 Klassische Theoretische Physik II V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch Klausur Lösung 7. Juli 05, 6-8 Uhr Aufgabe : Kurzfragen (+4++3=0 Punkte) (a) Zwangsbedingungen beschreiben Einschränkungen
4. Ausblick. 4.1 Lineare dynamische Analysen 4.2 Nichtlineare Analysen 4.3 Weitere Anwendungen Höhere Festigkeitslehre 3.
 4. Ausblick 4.1 Lineare dynamische Analysen 4.2 Nichtlineare Analysen 4.3 Weitere Anwendungen 3.4-1 4.1 Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen Analysen hängen die Knotenpunktsverschiebungen
4. Ausblick 4.1 Lineare dynamische Analysen 4.2 Nichtlineare Analysen 4.3 Weitere Anwendungen 3.4-1 4.1 Lineare dynamische Analysen Beschleunigungen: Bei linearen dynamischen Analysen hängen die Knotenpunktsverschiebungen
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
2. Einmassenschwinger. Inhalt:
 . Einmassenschwinger Inhalt:.1 Bewegungsdifferentialgleichung. Eigenschwingung.3 Harmonische Anregung.4 Schwingungsisolation.5 Stossartige Belastung.6 Allgemeine Belastung.7 Nichtlineare Systeme.8 Dämpfungsarten
. Einmassenschwinger Inhalt:.1 Bewegungsdifferentialgleichung. Eigenschwingung.3 Harmonische Anregung.4 Schwingungsisolation.5 Stossartige Belastung.6 Allgemeine Belastung.7 Nichtlineare Systeme.8 Dämpfungsarten
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
3. Erzwungene gedämpfte Schwingungen
 3. Erzwungene gedämpfte Schwingungen 3.1 Schwingungsgleichung 3.2 Unwuchtanregung 3.3 Weganregung 3.4 Komplexe Darstellung 2.3-1 3.1 Schwingungsgleichung F(t) m Bei einer erzwungenen gedämpften Schwingung
3. Erzwungene gedämpfte Schwingungen 3.1 Schwingungsgleichung 3.2 Unwuchtanregung 3.3 Weganregung 3.4 Komplexe Darstellung 2.3-1 3.1 Schwingungsgleichung F(t) m Bei einer erzwungenen gedämpften Schwingung
4. Dämpfungsmodelle. 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. Elastodynamik 3.
 4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
a) Wir nutzen den Drallsatz für die Rolle und horizontale Komponente des Schwerpunktsatzes, für kleine Auslenkungen: Abb.
 Tutoriumsaufgaben. Aufgabe a) Wir nutzen den Drallsatz für die olle und horizontale Komponente des Schwerpunktsatzes, für kleine Auslenkungen: Θ S φ = M(t) rs + cos(φ) F c + F H () m x = S + F H F c Gl.
Tutoriumsaufgaben. Aufgabe a) Wir nutzen den Drallsatz für die olle und horizontale Komponente des Schwerpunktsatzes, für kleine Auslenkungen: Θ S φ = M(t) rs + cos(φ) F c + F H () m x = S + F H F c Gl.
k = 1, 2,..., n (4.44) J k ϕ
 236 4 Torsionsschwinger und Längsschwinger ( J1 J2) M J M J2/ J1= 02, 10 0,5 8 1 + 6 2 max 4 5 2 10 2 bezogenes Moment 0 Bild 45 1 2 5 10 relatives Spiel ctϕ S/ M10 Maximales Moment infolge Spiel im Antrieb
236 4 Torsionsschwinger und Längsschwinger ( J1 J2) M J M J2/ J1= 02, 10 0,5 8 1 + 6 2 max 4 5 2 10 2 bezogenes Moment 0 Bild 45 1 2 5 10 relatives Spiel ctϕ S/ M10 Maximales Moment infolge Spiel im Antrieb
6. Lineare DGL-Systeme erster Ordnung
 HJ Oberle Differentialgleichungen I WiSe 22/3 6 Lineare DGL-Systeme erster Ordnung A Allgemeines Wir betrachten ein lineares DGL System erster Ordnung y (t = A(t y(t + b(t (6 und setzen voraus, dass die
HJ Oberle Differentialgleichungen I WiSe 22/3 6 Lineare DGL-Systeme erster Ordnung A Allgemeines Wir betrachten ein lineares DGL System erster Ordnung y (t = A(t y(t + b(t (6 und setzen voraus, dass die
2. Lagrange-Gleichungen
 2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
2. Lagrange-Gleichungen Mit dem Prinzip der virtuellen Leistung lassen sich die Bewegungsgleichungen für komplexe Systeme einfach aufstellen. Aus dem Prinzip der virtuellen Leistung lassen sich die Lagrange-Gleichungen
8. Periodische Bewegungen
 8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
Theoretische Physik I/II
 Theoretische Physik I/II Prof. Dr. M. Bleicher Institut für Theoretische Physik J. W. Goethe-Universität Frankfurt Aufgabenzettel XI 27. Juni 2011 http://th.physik.uni-frankfurt.de/ baeuchle/tut Lösungen
Theoretische Physik I/II Prof. Dr. M. Bleicher Institut für Theoretische Physik J. W. Goethe-Universität Frankfurt Aufgabenzettel XI 27. Juni 2011 http://th.physik.uni-frankfurt.de/ baeuchle/tut Lösungen
Hochschule Düsseldorf University of Applied Sciences. 05. Januar 2017 HSD. Physik. Schwingungen II
 Physik Schwingungen II Ort, Geschwindigkeit, Beschleunigung x(t) = cos! 0 t v(t) =ẋ(t) =! 0 sin! 0 t t a(t) =ẍ(t) =! 2 0 cos! 0 t Energie In einem mechanischen System ist die Gesamtenergie immer gleich
Physik Schwingungen II Ort, Geschwindigkeit, Beschleunigung x(t) = cos! 0 t v(t) =ẋ(t) =! 0 sin! 0 t t a(t) =ẍ(t) =! 2 0 cos! 0 t Energie In einem mechanischen System ist die Gesamtenergie immer gleich
3 Freie Koppelschwingungen konservativer Schwingungssysteme
 17 3 Freie Koppelschwingungen onservativer Schwingungssysteme Das Eigenschwingungsverhalten ungedämpfter Systeme ohne äußere Erregung ann durch trigonometrische Funtionen beschrieben werden, deren Frequenzen
17 3 Freie Koppelschwingungen onservativer Schwingungssysteme Das Eigenschwingungsverhalten ungedämpfter Systeme ohne äußere Erregung ann durch trigonometrische Funtionen beschrieben werden, deren Frequenzen
51 Numerische Berechnung von Eigenwerten und Eigenvektoren
 5 Numerische Berechnung von Eigenwerten und Eigenvektoren 5. Motivation Die Berechnung der Eigenwerte einer Matrix A IR n n als Lösungen der charakteristischen Gleichung (vgl. Kapitel 45) ist für n 5 unpraktikabel,
5 Numerische Berechnung von Eigenwerten und Eigenvektoren 5. Motivation Die Berechnung der Eigenwerte einer Matrix A IR n n als Lösungen der charakteristischen Gleichung (vgl. Kapitel 45) ist für n 5 unpraktikabel,
Baudynamik. Jan Höffgen 18. Februar Koordinatensysteme 2
 Baudynamik Jan Höffgen 8. Februar 204 Inhaltsverzeichnis Koordinatensysteme 2 2 Bewegungsgleichungen 2 2. Allgemeines................................................ 2 2.2 Synthetische Methode nach d Alembert................................
Baudynamik Jan Höffgen 8. Februar 204 Inhaltsverzeichnis Koordinatensysteme 2 2 Bewegungsgleichungen 2 2. Allgemeines................................................ 2 2.2 Synthetische Methode nach d Alembert................................
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
1 Lagrange-Formalismus
 Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Lagrange-Formalismus SS 4 In der gestrigen Vorlesung haben wir die Beschreibung eines physikalischen Systems mit Hilfe der Newton schen Axiome kennen gelernt. Oft ist es aber nicht so einfach die Kraftbilanz
Lineare Systeme mit einem Freiheitsgrad
 Höhere Technische Mechanik Lineare Systeme mit einem Freiheitsgrad Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/200 Übersicht. Grundlagen der Analytischen
Höhere Technische Mechanik Lineare Systeme mit einem Freiheitsgrad Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/200 Übersicht. Grundlagen der Analytischen
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 6 Eigenwerte
2. Freie Schwingungen
 2. Freie Schwingungen Die einfachsten schwingungsfähigen Systeme sind lineare Systeme: Die Rückstellkräfte sind proportional zur Auslenkung. Die Dämpfungskräfte sind proportional zur Geschwindigkeit. Bei
2. Freie Schwingungen Die einfachsten schwingungsfähigen Systeme sind lineare Systeme: Die Rückstellkräfte sind proportional zur Auslenkung. Die Dämpfungskräfte sind proportional zur Geschwindigkeit. Bei
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 12/13/14) Dozent: J. von Delft Übungen: B. Kubala Nachklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2008 (1. Oktober
4. Hamiltonformalismus
 4. Hamiltonormalismus Für die praktische Lösung von Problemen bietet der Hamiltonormalismus meist keinen Vorteil gegenüber dem Lagrangeormalismus. Allerdings bietet der Hamiltonormalismus einen direkten
4. Hamiltonormalismus Für die praktische Lösung von Problemen bietet der Hamiltonormalismus meist keinen Vorteil gegenüber dem Lagrangeormalismus. Allerdings bietet der Hamiltonormalismus einen direkten
9. Periodische Bewegungen
 Inhalt 9.1 Schwingungen 9.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 9.1.4 Erzwungene Schwingung 9.1 Schwingungen 9.1 Schwingungen Schwingung Zustand y wiederholt sich in bestimmten Zeitabständen
Inhalt 9.1 Schwingungen 9.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 9.1.4 Erzwungene Schwingung 9.1 Schwingungen 9.1 Schwingungen Schwingung Zustand y wiederholt sich in bestimmten Zeitabständen
Systeme gewöhnlicher Di erentialgleichungen. Ordnung
 Systeme gewöhnlicher Di erentialgleichungen. Ordnung Systeme. Ordnung De nition Für eine gegebene n n-matrix A(x) =(a ij (x)) n i,j=, deren Elemente Funktionen von x sind und einer gegebenen rechten Seite
Systeme gewöhnlicher Di erentialgleichungen. Ordnung Systeme. Ordnung De nition Für eine gegebene n n-matrix A(x) =(a ij (x)) n i,j=, deren Elemente Funktionen von x sind und einer gegebenen rechten Seite
Theoretische Physik 1 Mechanik
 Technische Universität München Fakultät für Physik Ferienkurs Theoretische Physik 1 Mechanik Skript zu Vorlesung 3: Lagrange-Formalismus, Systeme von Schwingungen gehalten von: Markus Krottenmüller & Markus
Technische Universität München Fakultät für Physik Ferienkurs Theoretische Physik 1 Mechanik Skript zu Vorlesung 3: Lagrange-Formalismus, Systeme von Schwingungen gehalten von: Markus Krottenmüller & Markus
5. Fourier-Transformation
 5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
1. Einführung. Baudynamik (Master) SS 2017
 Baudynamik (Master) SS 2017 1. Einführung 1.1 Bedeutungen der Baudynamik 1.2 Grundbegriffe und Klassifizierung 1.3 Modellierung der Bauwerksschwingungen LEHRSTUHL FÜR BAUSTATIK 1 Baudynamik (Master) SS
Baudynamik (Master) SS 2017 1. Einführung 1.1 Bedeutungen der Baudynamik 1.2 Grundbegriffe und Klassifizierung 1.3 Modellierung der Bauwerksschwingungen LEHRSTUHL FÜR BAUSTATIK 1 Baudynamik (Master) SS
Maschinendynamik. Klausur Frühjahr Name: Matrikel-Nr.:
 Maschinendynamik Klausur Frühjahr 2009 Name: Matrikel-Nr.: Punkte Aufgabe 1 Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 erreichte Punkte mögliche Punkte 60 Maschinendynamik Klausur Frühjahr 2009
Maschinendynamik Klausur Frühjahr 2009 Name: Matrikel-Nr.: Punkte Aufgabe 1 Aufgabe 2 Aufgabe 3 Aufgabe 4 Aufgabe 5 Aufgabe 6 erreichte Punkte mögliche Punkte 60 Maschinendynamik Klausur Frühjahr 2009
Analytische Mechanik in a Nutshell. Karsten Kirchgessner Dezember Januar 2008
 Analytische Mechanik in a Nutshell Karsten Kirchgessner Dezember 2007 - Januar 2008 Inhaltsverzeichnis 1 Definitionen und Basisüberlegungen 1 2 Schlussfolgerungen aus dem d Alembert schen Prinzip 2 2.1
Analytische Mechanik in a Nutshell Karsten Kirchgessner Dezember 2007 - Januar 2008 Inhaltsverzeichnis 1 Definitionen und Basisüberlegungen 1 2 Schlussfolgerungen aus dem d Alembert schen Prinzip 2 2.1
7. Gekoppelte Harmonische Schwingungen
 7. Gekoppelte Harmonische Schwingungen Ausgehend von einer allgemeinen Lagrange-Funktion wollen wir in harmonischer Näherung die Eigenrequenzen und Eigenschwingungen eines Systems mit vielen Freiheitsgraden
7. Gekoppelte Harmonische Schwingungen Ausgehend von einer allgemeinen Lagrange-Funktion wollen wir in harmonischer Näherung die Eigenrequenzen und Eigenschwingungen eines Systems mit vielen Freiheitsgraden
Lagrangesche Mechanik. Ari Wugalter 22. September 2009
 Lagrangesche Mechanik. September 009 Teil II. Lagrangesche Mechanik. Einführung in die Lagrange-Regeln.Art.. Generalisierte Koordinaten, Freiheitsgrade und Zwangsbedingungen In der Newtonschen Mechanik
Lagrangesche Mechanik. September 009 Teil II. Lagrangesche Mechanik. Einführung in die Lagrange-Regeln.Art.. Generalisierte Koordinaten, Freiheitsgrade und Zwangsbedingungen In der Newtonschen Mechanik
Name: Gruppe: Matrikel-Nummer: Aufgabe Punkte
 T1: Klassische Mechanik, SoSe2007 Prof. Dr. Jan von Delft Theresienstr. 37, Zi. 420 Dr. Vitaly N. Golovach vitaly.golovach@physik.lmu.de Endklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2007 (28.
T1: Klassische Mechanik, SoSe2007 Prof. Dr. Jan von Delft Theresienstr. 37, Zi. 420 Dr. Vitaly N. Golovach vitaly.golovach@physik.lmu.de Endklausur zur Vorlesung T1: Theoretische Mechanik, SoSe 2007 (28.
Übungen zu Theoretischer Mechanik (T1)
 Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. Viatcheslav Mukhanov Sommersemester 08 Übungen zu Theoretischer Mechanik T Übungsblatt 8, Besprechung ab 04.06.08 Aufgabe 8. Lineare
Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. Viatcheslav Mukhanov Sommersemester 08 Übungen zu Theoretischer Mechanik T Übungsblatt 8, Besprechung ab 04.06.08 Aufgabe 8. Lineare
F R. = Dx. M a = Dx. Ungedämpfte freie Schwingungen Beispiel Federpendel (a) in Ruhe (b) gespannt: Auslenkung x Rückstellkraft der Feder
 6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
f = f = f = Institut für Technische und Num. Mechanik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P März 2018
 Institut für Technische und Num. Mechanik Maschinendynamik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P 1 20. März 2018 Prüfung in Maschinendynamik Nachname, Vorname Aufgabe 1 (6 Punkte) Bestimmen
Institut für Technische und Num. Mechanik Maschinendynamik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P 1 20. März 2018 Prüfung in Maschinendynamik Nachname, Vorname Aufgabe 1 (6 Punkte) Bestimmen
Anwendung: gedämpfter harmonischer Oszillator (ohne Antrieb) Exponentialansatz: Eigenwertproblem: Charakteristisches Polynom: Zwischenbemerkung:
 Anwendung: gedämpfter harmonischer Oszillator (ohne Antrieb) Exponentialansatz: Eigenwertproblem: Charakteristisches Polynom: Zwischenbemerkung: (3q.6) folgt auch direkt, wenn ein exp-ansatz für x(t),
Anwendung: gedämpfter harmonischer Oszillator (ohne Antrieb) Exponentialansatz: Eigenwertproblem: Charakteristisches Polynom: Zwischenbemerkung: (3q.6) folgt auch direkt, wenn ein exp-ansatz für x(t),
4 Plattenschwingungen
 Elastodynamik Bewegungsgleichung Die Bewegungsgleichung für die homogene Kirchhoff-Platte lautet w x w x y w y h w B t = p B Dabei ist wx, y,t die Verschiebung in z- Richtung, p x, y,t der auf die Platte
Elastodynamik Bewegungsgleichung Die Bewegungsgleichung für die homogene Kirchhoff-Platte lautet w x w x y w y h w B t = p B Dabei ist wx, y,t die Verschiebung in z- Richtung, p x, y,t der auf die Platte
Hamilton-Systeme. J. Struckmeier
 Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Theoretische Physik I bei Prof. A. Rosch
 Vorlesungsmitschrift Theoretische Physik I bei Prof. A. Rosch von M. & O. Filla 08. Dezember 2016 Wiederholung der Lagrange Gleichungen Wir wissen, dass für unsere Funktionale S gilt: S = δs = 0 t 0 Lx,
Vorlesungsmitschrift Theoretische Physik I bei Prof. A. Rosch von M. & O. Filla 08. Dezember 2016 Wiederholung der Lagrange Gleichungen Wir wissen, dass für unsere Funktionale S gilt: S = δs = 0 t 0 Lx,
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Begleitmaterial zur Vorlesung Numerik II
 Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
Begleitmaterial zur Vorlesung Numerik II Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial Numerik II 1 / 35 Inhalte der Numerik
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Name: Gruppe: Matrikel-Nummer:
 Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Theoretische Physik 1 (Theoretische Mechanik) SS08, Studienziel Bachelor (170 1/13/14) Dozent: J. von Delft Übungen: B. Kubala Klausur zur Vorlesung T1: Theoretische Mechanik, SoSe 008 (3. Juli 007) Bearbeitungszeit:
Ferienkurs Theoretische Mechanik 2009 Hamilton Formalismus und gekoppelte Systeme
 Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Eine DG ist eine Gleichung, die Ableitungen der gesuchten Funktion enthält.
 C7 Differentgleichungen (DG) (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel C7 weicht ab vom Altland-Delft-Text] C7.1 Was ist eine DG, wozu wird sie gebraucht?
C7 Differentgleichungen (DG) (enthalten Ableitungen der gesuchten Funktionen) [Stoffgliederung im Skript für Kapitel C7 weicht ab vom Altland-Delft-Text] C7.1 Was ist eine DG, wozu wird sie gebraucht?
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Klausur zu Theoretische Physik 2 Klassische Mechanik
 Klausur zu Theoretische Physik 2 Klassische Mechanik 1. August 216 Prof. Marc Wagner Goethe-Universität Frankfurt am Main Institut für Theoretische Physik 5 Aufgaben mit insgesamt 25 Punkten. Die Klausur
Klausur zu Theoretische Physik 2 Klassische Mechanik 1. August 216 Prof. Marc Wagner Goethe-Universität Frankfurt am Main Institut für Theoretische Physik 5 Aufgaben mit insgesamt 25 Punkten. Die Klausur
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
2. Fourier-Transformation
 2. Fourier-Transformation Die Fourier-Transformation ist ein wichtiges Hilfsmittel für die dynamische Analyse linearer Systeme: Die Fourier-Transformierte der Antwort ist gleich dem Produkt der Fourier-Transformierten
2. Fourier-Transformation Die Fourier-Transformation ist ein wichtiges Hilfsmittel für die dynamische Analyse linearer Systeme: Die Fourier-Transformierte der Antwort ist gleich dem Produkt der Fourier-Transformierten
I) MATRIZEN. 1) Speichern geometrischer Daten: Punkte, Vektoren. j - te Variable (Spalte), j = 1,2,3,..., n
 I) MATRIZEN Motivation: 1) Speichern geometrischer Daten: Punkte, Vektoren. 2) Lineare Gleichungen y1 = a11x1+ a12x2 + a13x3 y2 = a21x1+ a22x2 + a23x3... Koeffizienten a ij i - te Gleichung (Zeile), i
I) MATRIZEN Motivation: 1) Speichern geometrischer Daten: Punkte, Vektoren. 2) Lineare Gleichungen y1 = a11x1+ a12x2 + a13x3 y2 = a21x1+ a22x2 + a23x3... Koeffizienten a ij i - te Gleichung (Zeile), i
Lösung der harmonischen Oszillator-Gleichung
 Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
Lösung der harmonischen Oszillator-Gleichung Lucas Kunz 8. Dezember 016 Inhaltsverzeichnis 1 Physikalische Herleitung 1.1 Gravitation................................... 1. Reibung.....................................
WS 2014/15 FINITE-ELEMENT-METHODE JUN.-PROF. D. JUHRE
 Approximation der äußeren virtuellen Arbeit Die virtuelle Arbeit der äußeren Lasten lässt sich als Funktion der vorgeschriebenen Knotenlasten N i 1 und der vorgeschriebenen Streckenlast p 1 ξ 1 angeben.
Approximation der äußeren virtuellen Arbeit Die virtuelle Arbeit der äußeren Lasten lässt sich als Funktion der vorgeschriebenen Knotenlasten N i 1 und der vorgeschriebenen Streckenlast p 1 ξ 1 angeben.
Seite 1. sin 2 x dx. b) Berechnen Sie das Integral. e (t s)2 ds. (Nur Leibniz-Formel) c) Differenzieren Sie die Funktion f(t) = t. d dx ln(x + x3 ) dx
 Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Differentialformen in Natur und Technik. Geometrie Hamiltonscher Systeme
 Differentialformen in Natur und Technik. Geometrie Hamiltonscher Systeme Florian Krämer 27.1.2009 Anwendungen in der Physik Phasen- und Zustandsraum Hamiltonsche Systeme Integralinvarianten Anwendungen
Differentialformen in Natur und Technik. Geometrie Hamiltonscher Systeme Florian Krämer 27.1.2009 Anwendungen in der Physik Phasen- und Zustandsraum Hamiltonsche Systeme Integralinvarianten Anwendungen
2. Finite Elemente. Die Methode der finiten Elemente ist ein spezielles Bubnow-Galerkin-Verfahren:
 2. Finite lemente Die Methode der finiten lemente ist ein spezielles Bubnow-Galerkin-Verfahren: Zur Lösung der Gleichung K [ ~ u,u]+d [ ~ u, u]+m [ ~ u, ü]=l[ ~ u ] ~ u wird folgender Ansatz gemacht: u=
2. Finite lemente Die Methode der finiten lemente ist ein spezielles Bubnow-Galerkin-Verfahren: Zur Lösung der Gleichung K [ ~ u,u]+d [ ~ u, u]+m [ ~ u, ü]=l[ ~ u ] ~ u wird folgender Ansatz gemacht: u=
Baudynamik und Zustandsanalyse
 Baudynamik und Zustandsanalyse Eine Einführung in die Baudynamik mit Mathematica Das vorliegende Skript wurde im Original mit dem Programmsystem MATHEMATICA von WOLFRAM-Research [http://www.wolfram.com]
Baudynamik und Zustandsanalyse Eine Einführung in die Baudynamik mit Mathematica Das vorliegende Skript wurde im Original mit dem Programmsystem MATHEMATICA von WOLFRAM-Research [http://www.wolfram.com]
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
Ferienkurs Theoretische Physik: Mechanik Blatt 4 - Lösung Technische Universität München 1 Fakultät für Physik 1 Zwei Kugeln und der Satz von Steiner Nehmen Sie zwei Kugeln mit identischem Radius R und
