Programmierung Eine Einführung in die Informatik mit Standard ML Musterlösungen für ausgewählte Aufgaben. 1 Schnellkurs. Gert Smolka.
|
|
|
- Martina Irma Egger
- vor 8 Jahren
- Abrufe
Transkript
1 Programmierung Eine Einführung in die Informatik mit Standard ML Musterlösungen für ausgewählte Aufgaben Gert Smolka Vorbemerkungen a) Ich danke den Assistenten der Vorlesungen in Saarbrücken für ihre Beiträge zu den Musterlösungen. b) Musterlösungen für die Kapitel 8 16 sind in Vorbereitung. 1 Schnellkurs Aufgabe 1.1 Betrachten Sie das folgende Programm: val = 7+4 val y = *(-1) val z = ~*(y-2) Welche Bezeichner, Konstanten, Operatoren und Schlüsselwörter kommen in dem Programm vor? An welche Werte bindet das Programm die vorkommenden Bezeichner? Lösung 1.1 Bezeichner:,y,z Konstanten: 7, 4, 1, 2 Operatoren: +,,, Schlüsselwörter: val,=, (, ) Bindungen : =11, y= 110, z= 1188 Aufgabe 1.2 Deklarieren Sie eine Prozedur p :, die für das Ergebnis 2 2 liefert. Identifizieren Sie das Argumentmuster, die Argumentvariable und den Rumpf Ihrer Prozedurdeklaration. Lösung 1.2 fun p (:) = 2**- Argumentmuster: Argumentvariable: Rumpf: ( : ) 2 Aufgabe 1.3 (Signum) Schreiben Sie eine Prozedur signum :, die für negative Argumente 1, für positive Argumente 1, und für 0 das Ergebnis 0 liefert. Lösung 1.3 (Signum) fun signum (:) = if <0 then ~1 else if >0 then 1 else 0
2 Aufgabe 1.4 Schreiben Sie eine Prozedur hoch17 :, die zu einer Zahldie Potenz 17 berechnet. Dabei sollen möglichst wenig Multiplikationen verwendet werden. Schreiben Sie die Prozedur auf zwei Arten: Mit einer Hilfsprozedur und mit lokalen Deklarationen. Lösung 1.4 Mit Hilfsprozedur: fun q (:) = * fun hoch17 (:) = * q (q (q (q ))) Mit lokalen Deklarationen: fun hoch17 (:) = let val a = * val b = a*a val c = b*b val d = c*c in *d end Aufgabe 1.5 a) Geben Sie ein Tupel mit 3 Positionen und nur einer Komponente an. b) Geben Sie einen Tupelausdruck an, der den Typ (bool ( unit)) hat. c) Geben Sie ein Paar an, dessen erste Komponente ein Paar und dessen zweite Komponente ein Tripel ist. Lösung 1.5 a) (1, 1, 1) b) (1,(true,(1,()))) c) ((1, false),((),(), true)) Aufgabe 1.7 Schreiben Sie eine Prozedur ma :, die zu drei Zahlen die größte liefert, auf zwei Arten: a) Benutzen Sie keine Hilfsprozedur und drei Konditionale. b) Benutzen Sie eine Hilfsprozedur und insgesamt nur ein Konditional. Lösung 1.7 a) fun ma (:, y:, z:) = if >y then if >z then else z else if y>z then y else z b) fun ma (:, y:) = if >y then else y fun ma (:, y:, z:) = ma (, ma (y,z)) c) Aus (b) erhält man eine Lösung mit 2 Konditionalen, indem man ma direkt bestimmt und das Ergebnis der geschachtelte Anwendung von ma mit einer lokalen Deklaration verfügbar macht (da es zweimal verwendet wird). fun ma (:, y:, z:) = let val k = if y < z then z else y in if < k then k else end
3 Aufgabe 1.10 Schreiben Sie eine Prozedur teilbar : bool, die für(,y) testet, obdurchy ohne Rest teilbar ist. Lösung 1.10 fun teilbar (:, y:) = ( mod y = 0) Aufgabe 1.11 (Zeitangaben) Oft gibt man eine Zeitdauer im HMS-Format mit Stunden, Minuten und Sekunden an. Beispielsweise ist 2h5m26s eine hervorragende Zeit für einen Marathonlauf. a) Schreiben Sie eine Prozedur sec :, die vom HMS-Format in Sekunden umrechnet. Beispielsweise soll sec(1, 1, 6) die Zahl 3666 liefern. b) Schreiben Sie eine Prozedur hms :, die eine in Sekunden angegebene Zeit in das HMS-Format umrechnet. Beispielsweise soll hms 3666 das Tupel (1, 1, 6) liefern. Berechnen Sie die Komponenten des Tupels mithilfe lokaler Deklarationen. Lösung 1.11 (Zeitangaben) a) fun sec (h:, m:, s:) = 3600*h + 60*m + s b) fun hms (s:) = let val h = s div 3600 val m = (s mod 3600) div 60 val s = s mod 60 in (h,m,s ) end Aufgabe 1.12 Sei die folgende rekursive Prozedurdeklaration gegeben: fun f(n:, a:) : = if n=0 then a else f(n-1, a*n) a) Geben Sie die Rekursionsfolge für den Aufruff(3, 1) an. b) Geben Sie ein verkürztes Ausführungsprotokoll für den Ausdruck f(3, 1) an. c) Geben Sie ein detailliertes Ausführungsprotokoll für den Ausdruck f(3, 1) an. Halten Sie sich dabei an das Beispiel in Abbildung 1.1 (Buch S. 14). Wenn es mehrere direkt ausführbare Teilausdrücke gibt, soll immer der am weitesten links stehende zuerst ausgeführt werden. Sie sollten insgesamt 18 Ausführungsschritte bekommen. Lösung 1.12 a) Rekursionsfolge: f(3, 1) f(2, 3) f(1, 6) f(0, 6) b) verkürztes Ausführungsprotokoll: f(3, 1)=f(2, 3) =f(1, 6) =f(0, 6) = 6
4 c) detailliertes Ausführungsprotokoll: f(3, 1)=if 3=0then 1 elsef(3 1, 1 3) = if false then 1 elsef(3 1, 1 3) =f(3 1, 1 3) =f(2, 1 3) =f(2, 3) = if 2=0then 3 elsef(2 1, 3 2) = if false then 3 elsef(2 1, 3 2) =f(2 1, 3 2) =f(1, 3 2) =f(1, 6) = if 1=0then 6 elsef(1 1, 6 1) = if false then 6 elsef(1 1, 6 1) =f(1 1, 6 1) =f(0, 6 1) =f(0, 6) = if 0=0then 6 elsef(0 1, 6 0) = if true then 6 elsef(0 1, 6 0) = 6 Aufgabe 1.14 Der ganzzahlige Quotient div y lässt sich aus durch wiederholtes Subtrahieren vony bestimmen. Schreiben Sie eine rekursive Prozedur mydiv :, die für 0undy 1 das Ergebnis div y liefert. Geben Sie zunächst Rekursionsgleichungen für div y an. Lösung 1.14 Rekursionsgleichungen: Prozedur: y = 0 für<y y = 1+ sonst y y fun mydiv (:, y:) : = if <y then 0 else 1+mydiv(-y,y) Aufgabe 1.17 (Quersumme) Schreiben Sie eine rekursive Prozedur quer :, die die Quersumme einer ganzen Zahl berechnet. Die Quersumme einer Zahl ist die Summe ihrer Dezimalziffern. Beispielsweise hat die Zahl 3754 die Quersumme 19. Geben Sie zunächst die Rekursionsgleichungen für quer an. Verwenden Sie Restbestimmung modulo 10, um die letzte Ziffer einer Zahl zu bestimmen.
5 Lösung 1.17 (Quersumme) Rekursionsgleichungen: quer = quer( ) quer 0 = 0 quer = ( mod 10)+quer 10 für<0 für>0 Prozedur: fun quer (:) : = if <0 then quer(~) else if =0 then 0 else mod 10 + quer( div 10) Aufgabe 1.23 (Reversion) Unter der Reversion rev n einer natürlichen Zahl n wollen wir die natürliche Zahl verstehen, die man durch Spiegeln der Dezimaldarstellung von n erhält. Beispielsweise soll rev 1234 = 4321, rev 76 = 67 und rev 1200 = 21 gelten. a) Schreiben Sie zunächst eine endrekursive Prozedur rev :, die zu zwei natürlichen Zahlen m und n die Zahl liefert, die sich ergibt, wenn man die reversierte Dezimaldarstellung von n rechts an die Dezimaldarstellung von m anfügt. Beispielsweise soll rev (65, 73) = 6537 und rev (0, 12300) = 321 gelten. Die Arbeitsweise von rev ergibt sich aus dem verkürzten Ausführungsprotokoll rev (65, 73)=rev (653, 7)=rev (6537, 0)=6537. b) Schreiben Sie mithilfe der Prozedur rev eine Prozedur rev, die natürliche Zahlen reversiert. c) Machen Sie sich klar, dass die entscheidende Idee bei der Konstruktion des Reversionsalgorithmus die Einführung einer Hilfsfunktion mit einem Akku ist. Überzeugen Sie sich davon, dass Sie rev nicht ohne Weiteres durch Rekursionsgleichungen bestimmen können. Lösung 1.23 (Reversion) a) fun rev (m:, n:) : = if n=0 then m else rev (m*10 + n mod 10,n div 10) b) fun rev (n:) = rev (0,n) c) Mit zwei Hilfsfunktionen (Potenz und Stelligkeit (Aufgabe 1.16)) kann man Rekursionsgleichungen für rev angeben. revn=n revn=(n mod 10) 10 (stell n) 1 + rev n 10 fürn<10 für 10 2 Programmiersprachliches Aufgabe 2.1 Geben Sie die Baumdarstellungen der folgenden durch Zeichendarstellungen beschriebenen Phrasen an. a) * -> bool b) if <3 then 3 else p 3
6 c) let val = 2+y in -y end d) fun p(:,n:):=if n>0then *p(,n-1)else 1 Lösung 2.1 c) d) Programm val + let 2 y y p () : n fun : > n 0 if 1 p () n 1 Aufgabe 2.2 Geben Sie die Baumdarstellungen der folgenden durch Zeichendarstellungen beschriebenen Phrasen an. a) +3*f -4 b) c) 1+2*-y*3+4 d) *(*)*->* Lösung 2.2 c) d) y 3 Aufgabe 2.4 Welche Bindungen berechnet das folgende Programm? fun f (:bool) = if then 1 else 0 val = 5*7 fun g (z:) = f(z<)< val = g 5 Lösung 2.4 f :=(fun f = if then 1 else 0, bool, []) g :=(fun g z= f(z< )<, bool, [f :=(fun f = if then 1 else 0, bool, []), := 35]) := true Aufgabe 2.6 Betrachten Sie das folgende Programm: val = 3+2 fun f (y:) = +y fun g (y:) : = if y< then 0 else y+g(y-1)
7 a) Geben Sie die Umgebung an, die die Ausführung des Programms in der Umgebung [] liefert ( 2.7.4). b) Geben Sie die Umgebung an, in der der Rumpf der Prozedurf bei der Ausführung des Aufrufsf7ausgeführt wird ( 2.7.2). c) Geben Sie die Umgebung an, in der der Rumpf der Prozedurg bei der Ausführung des Aufrufsg 13 ausgeführt wird ( 2.7.2). Lösung 2.6 a) [ := 5, f :=(fun f y= + y,, [ := 5]) g :=(fun g y= if y< then 0 else y+ g(y 1),, [ := 5])] b) [ := 5, f :=(fun f y= + y,, [ := 5]), y := 7] c) [ := 5, g :=(fun g y= if y< then 0 else y+ g(y 1),, [ := 5]), y := 13] Aufgabe 2.7 Geben Sie einen geschlossenen Ausdruck an, der eine Prozedur beschreibt, die zu das Ergebnis 2 liefert. Geben Sie die Tripeldarstellung der durch Ihren Ausdruck beschriebenen Prozedur an. Hinweis: Verwenden Sie einen Let-Ausdruck. Lösung 2.7 Ausdruck: let fun f (:) = * in f end Tripeldarstellung: (fun f =,, []) 3 Höherstufige Prozeduren Aufgabe 3.2 Deklarieren Sie zwei Prozeduren, die die Operation div (ganzzahlige Division) kartesisch und kaskadiert darstellen. Lösung 3.2 fun divkar (:, y:) = div y fun divkas (:) (y:) = div y Aufgabe 3.3 Geben Sie die Baumdarstellung des Ausdrucks mul y + mul (y + 2) * 5 an. Überprüfen Sie die Richtigkeit Ihrer Darstellung mit einem Interpreter. Lösung y 5 mul + mul y 2
8 Aufgabe 3.4 Geben Sie die Baumdarstellungen der folgenden Typen an: a) real bool b) bool Lösung 3.4 b) bool Aufgabe 3.5 Geben Sie zu den folgenden Abstraktionen semantisch äquivalente Ausdrücke an, die ohne die Verwendung von Abstraktionen gebildet sind. a) fn( : ) b) fn( : ) fn(y : ) + y Hilfe: Verwenden Sie Let-Ausdrücke und Prozedurdeklarationen. Lösung 3.5 b) let fun f ( : )(y : )=+ y in f end Aufgabe 3.6 Geben Sie die Tripeldarstellung der Prozedur an, zu der der folgende Ausdruck auswertet: (fn (:) => fn (b:bool) => if b then else 7) (2+3) Lösung 3.6 (fn b if b then else 7, bool, [ := 5]) Aufgabe 3.7 Geben Sie die Tripeldarstellung der Prozedur an, zu der der folgende Ausdruck auswertet: let val a = 7 fun f (:) = a + fun g (:) (y:) : = g (f ) y in g (f 5) end Lösung 3.7 (fn y g(f )y,, [f :=(fun f = a+,, [a := 7]), g :=(fun g y= g(f )y,, [f :=(fun f = a+,, [a := 7])]), := 12])
9 Aufgabe 3.8 Deklarieren Sie eine Prozedur power :, die zuundn 0die Potenz n liefert, wie folgt: a) Mit einer kaskadierten Deklaration. b) Mit einer Deklaration mit val und Abstraktionen. Lösung 3.8 a) fun power (:) (n:) : = if n=0 then 1 else * power (n-1) b) val rec power : -> = fn (:) => fn (n:) => if n=0 then 1 else * power (n-1) Aufgabe 3.10 Deklarieren Sie mithilfe der höherstufigen Prozedur sum eine Prozedur sum :( ), die fürk 0die Gleichung sum fmk=0+f(m+1) +f(m+k) erfüllt. Die Prozedur sum soll nicht rekursiv sein. Lösung 3.10 fun sum (f:->) (m:) = sum (fn (i:) => f(m+i)) Aufgabe 3.11 Geben Sie die Baumdarstellung des folgenden Typs an: ( bool ) Lösung 3.11 b) Aufgabe 3.12 Geben Sie geschlossene Abstraktionen an, die die folgenden Typen haben: a) ( bool) bool b) ( real) (bool ) bool real Die Abstraktionen sollen nur mit Prozeduranwendungen, Tupeln und Bezeichnern gebildet werden. Konstanten und Operatoren sollen nicht verwendet werden. Lösung 3.12 c) fn f:->bool => fn g:bool->real => fn : => g(f )
10 Aufgabe 3.13 Schreiben Sie zwei Prozeduren cas :( ) car :( ) sodass cas zur kartesischen Darstellung einer zweistelligen Operation die kaskadierte Darstellung und car zur kaskadierten Darstellung die kartesische Darstellung liefert. Erproben Sie cas und car mit Prozeduren, die das Maimum zweier Zahlen liefern: fun macas (:) (y:) = if <y then y else fun macar (:, y:) = if <y then y else val macas = cas macar val macar = car macas Wenn Sie cas und car richtig geschrieben haben, verhält sich macas genauso wie macas und macar genauso wie macar. Hinweis: Die Aufgabe hat eine sehr einfache Lösung. Lösung 3.13 fun cas (p:*->) (:) (y:) = p(,y) fun car (p:->->) (:, y:) = p y Aufgabe 3.15 Geben Sie eine Abstraktion e an, sodass die Ausführung des Ausdrucks first e für alledivergiert. Lösung 3.15 fn _ => false Aufgabe 3.17 Deklarieren Sie mit iter eine Prozedur fac, die zun 0dien-te Fakultätn! liefert. Lösung 3.17 fun fac (n:) : = #2(iter n (0,1) (fn (k:, a:) => (k+1, a*(k+1)))) alternativ: fun fac (n:) : = #1(iter n (1,n) (fn (a:, k:) => (a*k, k-1))) Aufgabe 3.20 Deklarieren Sie polymorphe Prozeduren wie folgt: cas : car : αβγ.(α β γ) α β γ αβγ.(α β γ) α β γ Ihre Prozeduren sollen nicht rekursiv sein. Machen Sie sich klar, dass die angegebenen Typschemen das Verhalten der Prozeduren eindeutig festlegen. Lösung 3.20 fun cas f y = f(,y) fun car f (,y) = f y Aufgabe 3.21 Dieter Schlau ist ganz begeistert von polymorphen Prozeduren. Er deklariert die Prozedur
11 fun a pif (:bool, y: a, z: a) = if then y else z valαpif : bool *α*α α und behauptet, dass man statt eines Konditionals stets die Prozedur pif verwenden kann: if e 1 then e 2 else e 3 pif(e 1, e 2, e 3 ) Was übersieht Dieter? Denken Sie an rekursive Prozeduren und daran, dass der Ausdruck, der das Argument einer Prozeduranwendung beschreibt, vor dem Aufruf der Prozedur ausgeführt wird. Lösung 3.21 Das Problem mit pif haben wir bereits in Aufgabe 1.25 kennengelernt. Betrachten Sie die folgenden Prozeduren: fun p n = if n>0 then p(n-1) else 0 fun q n = pif(n>0,q(n-1),0) Während p für alle Argumente n den Wert 0 liefert, divergiert q für alle n. Aufgabe 3.22 Geben Sie ein Typschema für den Bezeichner f an, sodass der Ausdruck (f 1, f 1.0) wohlgetypt ist. Lösung 3.22 α.α α Aufgabe 3.23 Warum gibt es keinen Typent, sodass die Abstraktion fn f : t (f 1, f 1.0) wohlgetypt ist? Lösung 3.23 Die Argumentvariable f wird in Standard ML monomorph getypt. Aufgabe 3.24 (Let und Abstraktionen) Dieter Schlau ist begeistert. Scheinbar kann man Let-Ausdrücke mit Val-Deklarationen auf Abstraktion und Applikation zurückführen: let val = e in e end (fn : t e )e Auf der Heimfahrt von der Uni kommen ihm jedoch Zweifel an seiner Entdeckung, da ihm plötzlich einfällt, dass Argumentvariablen nicht polymorph getypt werden können. Können Sie ein Beispiel angeben, das zeigt, dass Dieters Zweifel berechtigt sind? Hilfe: Geben Sie einen semantisch zulässigen Let-Ausdruck an, dessen Übersetzung gemäß des obigen Schemas scheitert, da Sie keinen passenden Typ t für die Argumentvariable finden können. Lösung 3.24 (Let und Abstraktionen) let val id = fn => in (id 1,id 1.0) end
12 Aufgabe 3.27 Geben Sie Deklarationen an, die monomorph getypte Bezeichner wie folgt deklarieren: a : unit bool b : unit ( unit) (real unit) c : d : bool e : real f : real real g : ( ) bool Verzichten Sie dabei auf eplizite Typangaben und verwenden Sie keine Operator- und Prozeduranwendungen. Lösung 3.27 fun c = if true then else 1 Aufgabe 3.29 Deklarieren Sie eine Identitätsprozedur a ideq : a a, deren Typschema auf Typen mit Gleichheit eingeschränkt ist. Verzichten Sie dabei auf eplizite Typangaben. Lösung 3.29 fun ideq = #1(, = ) Aufgabe 3.30 Betrachten Sie den Ausdruck (fn => (fn y => (fn => y) ) y) a) Geben Sie die Baumdarstellung des Ausdrucks an. b) Markieren Sie die definierenden Bezeichnerauftreten durch Überstreichen. c) Stellen Sie die leikalischen Bindungen durch Pfeile dar. d) Geben Sie alle Bezeichner an, die in dem Ausdruck frei auftreten. e) Bereinigen Sie den Ausdruck durch Indizieren der gebundenen Bezeichnerauftreten. Lösung 3.30 a) y fn fn fn b) (fn => (fn y => (fn => y) ) y) c) y y (fn => (fn y => (fn => y) ) y) d), y
13 e) (fn 1 => (fn y 1 => (fn 2 => y 1 ) 1 ) y) Aufgabe 3.32 Betrachten Sie die bereinigte Deklaration fun f (, y) = (fn z => (fn u => (fn v => u) z) y) a) Geben Sie die Baumdarstellung der Deklaration an. b) Stellen Sie die leikalischen Bindungen der Deklaration durch Pfeile dar. c) Geben Sie die statischen Bezeichnerbindungen an, die durch die semantische Analyse bestimmt werden. d) Geben Sie eine möglichst einfache, semantisch äquivalente Deklaration an, die ohne Abstraktionen gebildet ist. Lösung 3.32 a) fun f () y fn z fn y u fn z b) v u fun f (, y) = (fn z => (fn u => (fn v => u) z) y) c) f : αβ.α β β :α y :β z :α u :β v :α d) fun f (, y) = y Aufgabe 3.37 Deklarieren Sie mit iterup eine Prozedur a) power, die zuundndie Potenz n liefert. b) fac, die zun 0dien-te Fakultätn! liefert. c) sum, die zuf undndie Summe 0+f 1...+fn liefert. d) iter, die zun,s undf dasselbe Ergebnis liefert wie iter n s f. Lösung 3.37 fun sum f n = iterup 1 n 0 (fn(i,a)=>a+f i)
14 Aufgabe 3.38 Deklarieren Sie mithilfe der Prozedur iter eine Prozedur a) iterup, die zum,n,s undf dasselbe Ergebnis wie iterup m n s f liefert. b) iterdn, die zun,m,s undf dasselbe Ergebnis wie iterdn n m s f liefert. Lösung 3.38 fun iterup m n s f = #2(iter (n-m+1) (m,s) (fn (k,a) => (k+1,f(k,a)))) 4 Listen und Strings Aufgabe 4.2 Betrachten Sie den Ausdruck 3::4::nil. a) Geben Sie die Baumdarstellung des Ausdrucks an. b) Geben Sie die Baumdarstellung der beschriebenen Liste an. c) Geben Sie die beschriebene Liste mit [...] an. Lösung 4.2 a) b) :: 1 :: nil :: 3 :: 4 nil :: 1 :: 2 :: 3 :: 4 nil c) [1, 2, 3, 4] Aufgabe 4.9 Schreiben Sie mithilfe von foldl eine polymorphe Prozedur member : a a list bool, die testet, ob ein Wert als Element in einer Liste vorkommt. Lösung 4.9 fun member = foldl (fn (y,b) => =y orelse b) false Aufgabe 4.12 Deklarieren Sie die Faltungsprozedur foldr mithilfe der Faltungsprozedur foldl. Verwenden Sie dabei keine weitere rekursive Hilfsprozedur. Lösung 4.12 fun foldr f s s = foldl f s (foldl op:: nil s) oder kürzer: fun foldr f s = foldl f s o foldl op:: nil Aufgabe 4.13 Deklarieren Sie die Faltungsprozedur foldl mithilfe der Faltungsprozedur foldr. Gehen Sie wie folgt vor: a) Deklarieren Sie append mithilfe von foldr. b) Deklarieren Sie rev mithilfe von foldr und append.
15 c) Deklarieren Sie foldl mithilfe von foldr und rev. d) Deklarieren Sie foldl nur mithilfe von foldr. Lösung 4.13 b) fun rev s = foldr (fn (,ys) => append(ys,[])) nil s Aufgabe 4.15 (Last) Deklarieren Sie eine Prozedur last : α list α, die das Element an der letzten Position einer Liste liefert. Wenn die Liste leer ist, soll die Ausnahme Empty geworfen werden. Lösung 4.15 (Last) fun last s = hd (rev s) Aufgabe 4.16 (Ma) Schreiben Sie mit foldl eine Prozedur ma : list, die das größte Element einer Liste liefert. Wenn die Liste leer ist, soll die Ausnahme Empty geworfen werden. Verwenden Sie die vordefinierte Prozedur Int.ma :. Lösung 4.16 (Ma) fun ma s = foldl Int.ma (hd s) (tl s) Aufgabe 4.17 (Take und Drop) Schreiben Sie zwei polymorphe Prozeduren take und drop, die gemäßαlist α list getypt sind und die folgende Spezifikation erfüllen: a) take(s, n) liefert die erstennelemente der Liste s. Fallsn<0oder s <ngilt, soll die Ausnahme Subscript geworfen werden. b) drop(s, n) liefert die Liste, die man auss erhält, wenn man die erstennelemente weglässt. Falls n < 0 oder s < n gilt, soll die Ausnahme Subscript geworfen werden. Hinweis: Verwenden Sie orelse und die Prozeduren hd, tl und null. Lösung 4.17 (Take und Drop) a) fun take(s,n) = if n=0 then nil else if n<0 orelse null s then raise Subscript else hd s :: take(tl s, n-1) b) fun drop(s,n) = if n=0 then s else if n<0 orelse null s then raise Subscript else drop(tl s, n-1) Aufgabe 4.19 Entscheiden Sie für jeden der folgenden Werte, ob er das Muster (, y :: _ ::z, (u, 3)) trifft. Geben Sie bei einem Treffer die Bindungen für die Variablen des Musters an. a) (7, [1], (3, 3)) b) ([1, 2], [3, 4, 5], (11, 3)) Lösung 4.19
16 a) Das Muster wird nicht getroffen. b) :=[1, 2],y := 3,z:=[5],u:= 11 Aufgabe 4.22 Schreiben Sie eine Prozedur reverse : string string, die Strings reversiert (z.b. reverse "hut"="tuh"). Lösung 4.22 fun reverse s = implode (rev (eplode s)) oder kürzer: val reverse = implode o rev o eplode Aufgabe 4.23 Schreiben Sie eine Prozedur isdigit : char bool, die mithilfe der Prozedur ord testet, ob ein Zeichen eine der Ziffern 0,...,9 ist. Nützen Sie dabei aus, dass ord die Ziffern durch aufeinander folgende Zahlen darstellt. Lösung 4.23 fun isdigit c = ord c >= ord #"0" andalso ord c <= ord #"9" 5 Sortieren Aufgabe 5.4 Schreiben Sie eine Prozedur issort : list list, die eine Liste sortiert und dabei Mehrfachauftreten von Elementen eliminiert. Beispielsweise soll für [3, 1, 3, 1, 0] die Liste[0, 1, 3] geliefert werden. Lösung 5.4 fun sinsert (,nil) = [] sinsert (,y::yr) = case Int.compare(,y) of LESS => ::y::yr EQUAL => y::yr _ => y::sinsert(,yr) val issort = foldl sinsert nil Aufgabe 5.7 Deklarieren Sie eine Prozedur PairCompare :( ) ( ) order die die leikalische Ordnung für Paare des Typs darstellt. Zum Beispiel soll [(3, 4), (3, 5), (4, 0)] gemäß dieser Ordnung sortiert sein. Lösung 5.7 fun PairCompare ((, ),(y,y )) = case Int.compare(,y) of EQUAL => Int.compare(,y ) v => v Aufgabe 5.14 (Striktes Sortieren durch Mischen)
17 a) Schreiben Sie eine polymorphe Prozedur smerge, die zwei strikt sortierte Listen zu einer strikt sortierten Liste kombiniert. Beispielsweise soll gelten: smerge Int.compare([1, 3], [2, 3]) =[1, 2, 3]. b) Schreiben Sie eine polymorphe Prozedur ssort, die Listen strikt sortiert. Beispielsweise soll ssort Int.compare[5, 3, 2, 5] =[2, 3, 5] gelten. c) Machen Sie sich klar, dass es sich bei ssort Int.compare um eine Prozedur handelt, die zu einer Liste s die eindeutig bestimmte strikt sortierte Liste liefert, die dieselbe Menge wie s darstellt. Lösung 5.14 (Striktes Sortieren durch Mischen) a) fun smerge _ (nil,ys) = ys smerge _ (s,nil) = s smerge compare (::r,y::yr) = case compare(,y) of LESS => ::smerge compare (r,y::yr) EQUAL => ::smerge compare (r,yr) GREATER => y::smerge compare (::r,yr) b) fun ssort compare = let fun ssort nil = nil ssort [] = [] ssort s = let val (ys,zs) = split s in smerge compare (ssort ys,ssort zs) end in ssort end 6 Konstruktoren und Ausnahmen Aufgabe 6.1 Deklarieren Sie eine Prozedur variant : shape, die die Variantennummer eines geometrischen Objekts liefert. Beispielsweise soll variant(square 3.0) = 2 gelten. Lösung 6.1 fun variant (Circle _) = 1 variant (Square _) = 2 variant (Triangle _) = 3 Aufgabe 6.7 Deklarieren Sie eine Prozedur check : ep ep bool, die für zwei Ausdrückeeunde testet, obeein Teilausdruck vone ist. Lösung 6.7 fun check e e = e=e orelse case e of A(e1,e2) => check e e1 orelse check e e2 M(e1,e2) => check e e1 orelse check e e2 _ => false Aufgabe 6.8 Schreiben Sie eine Prozedur instantiate : env ep ep, die zu einer UmgebungV und einem Ausdruckeden Ausdruck liefert, den man auseerhält, indem man die inevorkommenden Variablen gemäßv durch Konstanten ersetzt. Beispielsweise soll
18 für die in deklarierte Umgebung env und den Ausdruck A(V "", V "y") der Ausdruck A(C 5, C 3) geliefert werden. Orientieren Sie sich an der Prozedur eval. Lösung 6.8 fun instantiate env (V s) = C(env s) instantiate env (A(e,e )) = A(instantiate env e,instantiate env e ) instantiate env (M(e,e )) = M(instantiate env e,instantiate env e ) instantiate env e = e Aufgabe 6.13 Führen Sie zweistellige Sequenzialisierungen (e 1 ;e 2 ) auf Abstraktionen und Applikationen zurück. Lösung 6.13 (fn _ e 2 )e 1 7 Bäume Aufgabe 7.1 Schreiben Sie eine Prozedur compound : tree bool, die testet, ob ein Baum zusammengesetzt ist. Lösung 7.1 fun compound (T[]) = false compound _ = true Aufgabe 7.3 Geben Sie Ausdrücke an, die Bäume mit den unten gezeigten grafischen Darstellungen beschreiben. Dabei können Sie die Bezeichner t1 = T[] und t2 = T[t1, t1, t1] verwenden. Lösung 7.3 T[T[t1]] T[T[t1, t1], T[t1]] T[t2, t1, t1, t2] Aufgabe 7.4 Sei die grafische Darstellung eines Baums gegeben. Nehmen Sie an, dass die Darstellungn 1Kanten enthält und beantworten Sie die folgenden Fragen: a) Wie viele Knoten enthält die Darstellung mindestens/höchstens? b) Wie viele Blätter enthält die Darstellung mindestens/höchstens? c) Wie viele innere Knoten enthält die Darstellung mindestens/höchstens? Lösung 7.4 a) Ein Baum mitnkanten hat eaktn+1 Knoten b) Die Darstellung enthält mindestens 1 und höchstensnblätter c) Aus b) folgt, dass es mindestens 1 und höchstensninnere Knoten gibt
19 Aufgabe 7.7 Ordnen Sie die folgenden Bäume gemäß der leikalischen Ordnung an: t1, t2, t3, T[T[t1]], T[t1,T[T[t1]]], T[T[T[T[t1]]]]. Lösung 7.7 t1<t2< T[t1, T[T[t1]]]<T[T[t1]]<t3<T[T[T[T[t1]]]] Aufgabe 7.9 Geben Sie einen Baum mit 5 Knoten an, der genau zwei Teilbäume hat. Wie viele solche Bäume gibt es? Lösung 7.9 folgt aus: Der einzige Baum mit 5 Knoten, der genau zwei Teilbäume hat, sieht wie Aufgabe 7.11 Schreiben Sie eine Prozedur tree : tree, die fürn 0 binäre Bäume wie folgt liefert: n=0 n=1 n=2 n=3 Achten Sie darauf, dass die identischen Unterbäume der zweistelligen Teilbäume jeweils nur einmal berechnet werden. Das sorgt dafür, dass Ihre Prozedur auch für n = 1000 schnell ein Ergebnis liefert. Verwenden Sie die Prozedur iter aus 3.4. Lösung 7.11 fun tree n = iter n (T[]) (fn t => T[t,t]) Aufgabe 7.13 Betrachten Sie die grafische Darstellung des Baumst3 in Abbildung a) Geben Sie die Adresse der Wurzel an. b) Geben Sie die Adressen der inneren Knoten an (es gibt genau 4). c) Geben Sie die Adressen der Auftreten des Teilbaumst2 an. Lösung 7.13 a) [] b) [],[1],[1, 1],[2],[3] c) [1, 1],[3] Aufgabe 7.15 Schreiben Sie Prozeduren des Typs tree list bool wie folgt: a) node testet, ob eine Adresse einen Knoten eines Baums bezeichnet. b) root testet, ob eine Adresse die Wurzel eines Baums bezeichnet. c) inner testet, ob eine Adresse einen inneren Knoten eines Baums bezeichnet. d) leaf testet, ob eine Adresse ein Blatt eines Baums bezeichnet. Lösung 7.15
20 fun node t s = (ast t s;true) handle Subscript => false fun root (T _) (s: list) = null s fun inner t s = compound (ast t s) handle Subscript => false fun leaf t s = compound (ast t s) = false handle Subscript => false Aufgabe 7.23 Schreiben Sie die oben angegebene Prozedur size so um, dass sie ohne map auskommt. Hilfe: Erledigen Sie die rekursive Anwendung von size in der Verknüpfungsprozedur für foldl. Lösung 7.23 fun size (T ts) = foldl (fn (t,s) => size t + s) 1 ts Hinweis : Aufgabe 7.27 hat ein Beispiel im Buch Aufgabe 7.32 Schreiben Sie eine Prozedur post : tree tree, die zu einem Baum und einer Postnummer den entsprechenden Teilbaum liefert. Realisieren Sie die Agenda von post mit der folgenden Typdeklaration: datatype a entry = I of a F of a Lösung 7.32 datatype a entry = I of a F of a fun lift (T ts) = map I ts fun post nil _ = raise Subscript post (F t::_) 0 = t post (F _::tr) k = post tr (k-1) post (I t::tr) k = post (lift F t :: tr) k fun post t = post [I t] Aufgabe 7.33 Geben Sie die Prä- und die Postlinearisierung des Baums T[T[],T[T[]],T[T[],T[]]] an. Lösung 7.33 Prälinearisierung: [3, 0, 1, 0, 2, 0, 0] Postlinearisierung: [0, 0, 1, 0, 0, 2, 3] Aufgabe 7.34 Gibt es Listen über N, die gemäß der Prä- oder Postlinearisierung keine Bäume darstellen? Lösung 7.34 Ja. Beispielsweise stellt die Liste[1] weder gemäß der Prä- noch Postlinearisierung einen Baum dar. Aufgabe 7.37 Deklarieren Sie eine Prozedur direct : tree tree, die zu einem Baum einen gerichteten Baum liefert, der die gleiche Menge darstellt. Verwenden Sie die polymorphe Sortierprozedur aus Aufgabe 5.14 auf S. 107 und die Vergleichsprozedur comparetree aus Lösung 7.37 fun direct (T ts) = T(ssort comparetree (map direct ts)) Aufgabe 7.42 Schreiben Sie Prozeduren leftmost, rightmost : α ltr α, die das linkeste beziehungsweise rechteste Blatt eines Baums liefern.
21 Lösung 7.42 fun rightmost (L(a,nil)) = a rightmost (L(a,ts)) = rightmost (last ts) Aufgabe 7.49 Schreiben Sie eine Prozedur find :(α bool) α ltr α option, die zu einer Prozedur und einem Baum die gemäß der Präordnung erste Marke des Baums liefert, für die die Prozedur true liefert. Orientieren Sie sich an der Prozedur prest aus Lösung 7.49 fun find p nil = NONE find p (L(,ts)::es) = if p then SOME else find p (ts@es) fun find p t = find p [t] Aufgabe 7.54 Die Grenze eines markierten Baums ist die Liste der Marken seiner Blätter, in der Ordnung ihres Auftretens von links nach rechts und mit Mehrfachauftreten. Die Grenze des Baums t3 ( 7.9) ist [2, 7, 7, 4, 2, 7, 7]. Schreiben Sie eine Prozedur frontier :α ltr α list, die die Grenze eines Baums liefert. Lösung 7.54 fun frontier (L(,nil)) = [] frontier (L(,ts)) = List.concat (map frontier ts)
1. Probeklausur zu Programmierung 1 (WS 07/08)
 Fachschaft Informatikstudiengänge Fachrichtung 6.2 Informatik Das Team der Bremser 1. Probeklausur zu Programmierung 1 (WS 07/08) http://fsinfo.cs.uni-sb.de Name Matrikelnummer Bitte öffnen Sie das Klausurheft
Fachschaft Informatikstudiengänge Fachrichtung 6.2 Informatik Das Team der Bremser 1. Probeklausur zu Programmierung 1 (WS 07/08) http://fsinfo.cs.uni-sb.de Name Matrikelnummer Bitte öffnen Sie das Klausurheft
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 2 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 8.11.2011 Dieses Blatt behandelt
Klausur Programmierung WS 2002/03
 Klausur Programmierung WS 2002/03 Prof. Dr. Gert Smolka, Dipl. Inf. Thorsten Brunklaus 14. Dezember 2002 Leo Schlau 45 Vor- und Nachname Sitz-Nr. 4711 007 Matrikelnummer Code Bitte öffnen Sie das Klausurheft
Klausur Programmierung WS 2002/03 Prof. Dr. Gert Smolka, Dipl. Inf. Thorsten Brunklaus 14. Dezember 2002 Leo Schlau 45 Vor- und Nachname Sitz-Nr. 4711 007 Matrikelnummer Code Bitte öffnen Sie das Klausurheft
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Funktionale Programmierung
 Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
Funktionale Programmierung Jörg Kreiker Uni Kassel und SMA Solar Technology AG Wintersemester 2011/2012 2 Teil II Typen mit Werten und Ausdruck, sogar listenweise 3 Haskell Programme Programm Module ein
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK
 TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 4 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 21.11.2011 Dieses Blatt behandelt
TECHNISCHE UNIVERSITÄT MÜNCHEN FAKULTÄT FÜR INFORMATIK WS 11/12 Einführung in die Informatik II Übungsblatt 4 Univ.-Prof. Dr. Andrey Rybalchenko, M.Sc. Ruslán Ledesma Garza 21.11.2011 Dieses Blatt behandelt
Kapiteltests zum Leitprogramm Binäre Suchbäume
 Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Kapiteltests zum Leitprogramm Binäre Suchbäume Björn Steffen Timur Erdag überarbeitet von Christina Class Binäre Suchbäume Kapiteltests für das ETH-Leitprogramm Adressaten und Institutionen Das Leitprogramm
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Excel Funktionen durch eigene Funktionen erweitern.
 Excel Funktionen durch eigene Funktionen erweitern. Excel bietet eine große Anzahl an Funktionen für viele Anwendungsbereiche an. Doch es kommt hin und wieder vor, dass man die eine oder andere Funktion
Excel Funktionen durch eigene Funktionen erweitern. Excel bietet eine große Anzahl an Funktionen für viele Anwendungsbereiche an. Doch es kommt hin und wieder vor, dass man die eine oder andere Funktion
Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 4 (Kapitel 4)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 4 (Kapitel 4) Hinweis: Dieses Übungsblatt enthält
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 4 (Kapitel 4) Hinweis: Dieses Übungsblatt enthält
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
1. Probeklausur zur Programmierung I
 DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6.2 Informatik Tutoren der Vorlesung 1. Probeklausur zur Programmierung I Name: Matrikelnummer: Bitte öffnen Sie das Klausurheft erst dann, wenn Sie dazu aufgefordert
DEPENDABLE SYSTEMS AND SOFTWARE Fachrichtung 6.2 Informatik Tutoren der Vorlesung 1. Probeklausur zur Programmierung I Name: Matrikelnummer: Bitte öffnen Sie das Klausurheft erst dann, wenn Sie dazu aufgefordert
2.11 Kontextfreie Grammatiken und Parsebäume
 2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
2.11 Kontextfreie Grammatiken und Parsebäume Beispiel: Beispiel (Teil 3): Beweis für L(G) L: Alle Strings aus L der Länge 0 und 2 sind auch in L(G). Als Induktionsannahme gehen wir davon aus, dass alle
Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 1 (Kapitel 1)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 1 (Kapitel 1) Hinweis: Dieses Übungsblatt enthält
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 1 (Kapitel 1) Hinweis: Dieses Übungsblatt enthält
Funktionale Programmierung mit Haskell
 Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Funktionale Programmierung mit Haskell Dr. Michael Savorić Hohenstaufen-Gymnasium (HSG) Kaiserslautern Version 20120622 Überblick Wichtige Eigenschaften Einführungsbeispiele Listenerzeugung und Beispiel
Binäre Bäume Darstellung und Traversierung
 Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail fb641378@inf.tu-dresden.de Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Binäre Bäume Darstellung und Traversierung Name Frank Bollwig Matrikel-Nr. 2770085 E-Mail fb641378@inf.tu-dresden.de Datum 15. November 2001 0. Vorbemerkungen... 3 1. Terminologie binärer Bäume... 4 2.
Algorithmik II. a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge 20, 28, 35, 31, 9, 4, 13, 17, 37, 25 ein.
 Aufgabe 10 Binäre Bäume a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge, 28, 35, 31, 9, 4,, 17, 37, 25 ein. 1. Einfügen von : 3. Einfugen von 35: 2. Einfügen von 28: 28 28 10. Einfügen
Aufgabe 10 Binäre Bäume a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge, 28, 35, 31, 9, 4,, 17, 37, 25 ein. 1. Einfügen von : 3. Einfugen von 35: 2. Einfügen von 28: 28 28 10. Einfügen
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Folge 19 - Bäume. 19.1 Binärbäume - Allgemeines. Grundlagen: Ulrich Helmich: Informatik 2 mit BlueJ - Ein Kurs für die Stufe 12
 Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Grundlagen: Folge 19 - Bäume 19.1 Binärbäume - Allgemeines Unter Bäumen versteht man in der Informatik Datenstrukturen, bei denen jedes Element mindestens zwei Nachfolger hat. Bereits in der Folge 17 haben
Funktionale Programmierung ALP I. Funktionen höherer Ordnung. Teil 2 SS 2013. Prof. Dr. Margarita Esponda. Prof. Dr.
 ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
ALP I Funktionen höherer Ordnung Teil 2 SS 2013 Funktionen höherer Ordnung Nehmen wir an, wir möchten alle Zahlen innerhalb einer Liste miteinander addieren addall:: (Num a) => [a -> a addall [ = 0 addall
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Typdeklarationen. Es gibt in Haskell bereits primitive Typen:
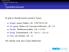 Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Typdeklarationen Es gibt in bereits primitive Typen: Integer: ganze Zahlen, z.b. 1289736781236 Int: ganze Zahlen mit Computerarithmetik, z.b. 123 Double: Fließkommazahlen, z.b. 3.14159 String: Zeichenketten,
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?
![Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Fragen. f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))?](/thumbs/24/4200701.jpg) Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Fragen f [ ] = [ ] f (x : y : ys) = x y : f ys f (x : xs) = f (x : x : xs) Wozu evaluiert f [1, 2, 3] (Abkürzung für f (1 : 2 : 3 : [ ]))? Wozu evaluiert [f [ ], f [ ]]? Weiteres Beispiel: f [ ] y = [
Idee: Wenn wir beim Kopfknoten zwei Referenzen verfolgen können, sind die Teillisten kürzer. kopf Eine Datenstruktur mit Schlüsselwerten 1 bis 10
 Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Programmierung 1 Probeklausur zur Vorklausur
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 05.12.2015 Programmierung 1 Probeklausur zur Vorklausur Matrikelnummer: Bitte öffnen Sie das Klausurheft
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 05.12.2015 Programmierung 1 Probeklausur zur Vorklausur Matrikelnummer: Bitte öffnen Sie das Klausurheft
368 4 Algorithmen und Datenstrukturen
 Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
Kap04.fm Seite 368 Dienstag, 7. September 2010 1:51 13 368 4 Algorithmen und Datenstrukturen Java-Klassen Die ist die Klasse Object, ein Pfeil von Klasse A nach Klasse B bedeutet Bextends A, d.h. B ist
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen:
 Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Ein- und Ausgabe Zweite Möglichkeit: Ausgabe direkt auf dem Bildschirm durchführen: fun p r i n t T r e e printa t = c a s e t o f Leaf a => ( p r i n t Leaf ; printa a ) Node ( l, a, r ) => ( p r i n
Wir basteln einen Jahreskalender mit MS Excel.
 Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
Wir basteln einen Jahreskalender mit MS Excel. In meinen Seminaren werde ich hin und wieder nach einem Excel-Jahreskalender gefragt. Im Internet findet man natürlich eine ganze Reihe mehr oder weniger
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
4. AUSSAGENLOGIK: SYNTAX. Der Unterschied zwischen Objektsprache und Metasprache lässt sich folgendermaßen charakterisieren:
 4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
4. AUSSAGENLOGIK: SYNTAX 4.1 Objektsprache und Metasprache 4.2 Gebrauch und Erwähnung 4.3 Metavariablen: Verallgemeinerndes Sprechen über Ausdrücke von AL 4.4 Die Sprache der Aussagenlogik 4.5 Terminologie
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen, Bäume)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen,
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2015/16) Wiederholungstutorium Lösungsblatt 15 (Linearer Speicher, Listen,
Statuten in leichter Sprache
 Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Statuten in leichter Sprache Zweck vom Verein Artikel 1: Zivil-Gesetz-Buch Es gibt einen Verein der selbstbestimmung.ch heisst. Der Verein ist so aufgebaut, wie es im Zivil-Gesetz-Buch steht. Im Zivil-Gesetz-Buch
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Bevor lineare Gleichungen gelöst werden, ein paar wichtige Begriffe, die im Zusammenhang von linearen Gleichungen oft auftauchen.
 R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
R. Brinkmann http://brinkmann-du.de Seite 1 13.0.010 Lineare Gleichungen Werden zwei Terme durch ein Gleichheitszeichen miteinander verbunden, so entsteht eine Gleichung. Enthält die Gleichung die Variable
Programmierung und Modellierung
 Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Programmierung und Modellierung Terme, Suchbäume und Pattern Matching Martin Wirsing in Zusammenarbeit mit Moritz Hammer SS 2009 2 Inhalt Kap. 7 Benutzerdefinierte Datentypen 7. Binärer Suchbaum 8. Anwendung:
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at
 Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Inhalt SWP Funktionale Programme (2. Teil) Einfache Ausdrücke Datentypen Rekursive funktionale Sprache Franz Wotawa Institut für Softwaretechnologie wotawa@ist.tugraz.at Interpreter für funktionale Sprache
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
Eine Logikschaltung zur Addition zweier Zahlen
 Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Eine Logikschaltung zur Addition zweier Zahlen Grundlegender Ansatz für die Umsetzung arithmetischer Operationen als elektronische Schaltung ist die Darstellung von Zahlen im Binärsystem. Eine Logikschaltung
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 7 (Kapitel 7)
 Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 7 (Kapitel 7) Hinweis: Dieses Übungsblatt enthält
Fachrichtung 6.2 Informatik Universität des Saarlandes Tutorenteam der Vorlesung Programmierung 1 Programmierung 1 (Wintersemester 2012/13) Lösungsblatt 7 (Kapitel 7) Hinweis: Dieses Übungsblatt enthält
Übungen zu C++ Kapitel 1
 Übungen zu C++ Kapitel 1 Aufgabe 1 Ergänze den Text. a) Die sechs logischen Einheiten eines Computers sind Eingabe-Einheit, Ausgabe-Einheit, RAM, ALU, CPU, Plattenspeicher. b) Die Programme, welche Hochsprachenprogramme
Übungen zu C++ Kapitel 1 Aufgabe 1 Ergänze den Text. a) Die sechs logischen Einheiten eines Computers sind Eingabe-Einheit, Ausgabe-Einheit, RAM, ALU, CPU, Plattenspeicher. b) Die Programme, welche Hochsprachenprogramme
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 1. Semester ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN
 ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
ARBEITSBLATT 3 RECHNEN MIT GANZEN ZAHLEN Wir wollen nun die Rechengesetze der natürlichen Zahlen auf die Zahlenmenge der ganzen Zahlen erweitern und zwar so, dass sie zu keinem Widerspruch mit bisher geltenden
Erstellen einer digitalen Signatur für Adobe-Formulare
 Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
Erstellen einer digitalen Signatur für Adobe-Formulare (Hubert Straub 24.07.13) Die beiden Probleme beim Versenden digitaler Dokumente sind einmal die Prüfung der Authentizität des Absenders (was meist
3. LINEARE GLEICHUNGSSYSTEME
 176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
176 3. LINEARE GLEICHUNGSSYSTEME 90 Vitamin-C-Gehalt verschiedener Säfte 18,0 mg 35,0 mg 12,5 mg 1. a) 100 ml + 50 ml + 50 ml = 41,75 mg 100 ml 100 ml 100 ml b) : Menge an Kirschsaft in ml y: Menge an
Prüfziffern. Man versucht, solche Fehler zu erkennen, indem man der Zahl eine weitere Ziffern, die sog. Prüfziffern, hinzufügt.
 Prüfziffern Bei der Erfassung von langen Zahlen können Fehler auftreten: Ziffern werden weggelassen oder hinzugefügt, zwei benachbarte Ziffern werden vertauscht, eine Ziffer wird falsch übernommen, usw..
Prüfziffern Bei der Erfassung von langen Zahlen können Fehler auftreten: Ziffern werden weggelassen oder hinzugefügt, zwei benachbarte Ziffern werden vertauscht, eine Ziffer wird falsch übernommen, usw..
4. BEZIEHUNGEN ZWISCHEN TABELLEN
 4. BEZIEHUNGEN ZWISCHEN TABELLEN Zwischen Tabellen können in MS Access Beziehungen bestehen. Durch das Verwenden von Tabellen, die zueinander in Beziehung stehen, können Sie Folgendes erreichen: Die Größe
4. BEZIEHUNGEN ZWISCHEN TABELLEN Zwischen Tabellen können in MS Access Beziehungen bestehen. Durch das Verwenden von Tabellen, die zueinander in Beziehung stehen, können Sie Folgendes erreichen: Die Größe
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
5 DATEN. 5.1. Variablen. Variablen können beliebige Werte zugewiesen und im Gegensatz zu
 Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Kapitel I: Registrierung im Portal
 Kapitel I: Registrierung im Portal Um zu unserem Portal zu gelangen, rufen Sie bitte die folgende Internetseite auf: www.arag-forderungsmanagement.de Bei Ihrem ersten Besuch des ARAG Portals ist es notwendig,
Kapitel I: Registrierung im Portal Um zu unserem Portal zu gelangen, rufen Sie bitte die folgende Internetseite auf: www.arag-forderungsmanagement.de Bei Ihrem ersten Besuch des ARAG Portals ist es notwendig,
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Quadratische Gleichungen
 Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Mathematische Grundlagen der Kryptographie. 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe. Stefan Brandstädter Jennifer Karstens
 Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Probleme beim Arbeiten mit Variablen, Termen und Gleichungen
 Probleme beim Arbeiten mit Variablen, Termen und Gleichungen Tage des Unterrichts in Mathematik, Naturwissenschaften und Technik Rostock 2010 Prof. Dr. Hans-Dieter Sill, Universität Rostock, http://www.math.uni-rostock.de/~sill/
Probleme beim Arbeiten mit Variablen, Termen und Gleichungen Tage des Unterrichts in Mathematik, Naturwissenschaften und Technik Rostock 2010 Prof. Dr. Hans-Dieter Sill, Universität Rostock, http://www.math.uni-rostock.de/~sill/
Java Einführung Operatoren Kapitel 2 und 3
 Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
Java Einführung Operatoren Kapitel 2 und 3 Inhalt dieser Einheit Operatoren (unär, binär, ternär) Rangfolge der Operatoren Zuweisungsoperatoren Vergleichsoperatoren Logische Operatoren 2 Operatoren Abhängig
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Übungsblatt 3: Algorithmen in Java & Grammatiken
 Humboldt-Universität zu Berlin Grundlagen der Programmierung (Vorlesung von Prof. Bothe) Institut für Informatik WS 15/16 Übungsblatt 3: Algorithmen in Java & Grammatiken Abgabe: bis 9:00 Uhr am 30.11.2015
Humboldt-Universität zu Berlin Grundlagen der Programmierung (Vorlesung von Prof. Bothe) Institut für Informatik WS 15/16 Übungsblatt 3: Algorithmen in Java & Grammatiken Abgabe: bis 9:00 Uhr am 30.11.2015
Teile und Herrsche Teil 2
 Teile und Herrsche Teil 2 binär Suchen und schnell Multiplizieren Markus Fleck Manuel Mauky Hochschule Zittau/Görlitz 19. April 2009 Suchen in langen Listen (0, 1, 2, 7, 8, 9, 9, 13, 13, 14, 14, 14, 16,
Teile und Herrsche Teil 2 binär Suchen und schnell Multiplizieren Markus Fleck Manuel Mauky Hochschule Zittau/Görlitz 19. April 2009 Suchen in langen Listen (0, 1, 2, 7, 8, 9, 9, 13, 13, 14, 14, 14, 16,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer
 Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Fachdidaktik der Informatik 18.12.08 Jörg Depner, Kathrin Gaißer Klassendiagramme Ein Klassendiagramm dient in der objektorientierten Softwareentwicklung zur Darstellung von Klassen und den Beziehungen,
Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung: Lösungsvorschlag
 Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Ludwig-Maximilians-Universität München WS 2015/16 Institut für Informatik Übungsblatt 13 Prof. Dr. R. Hennicker, A. Klarl Übungen zu Einführung in die Informatik: Programmierung und Software-Entwicklung:
Vorkurs C++ Programmierung
 Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Widerrufsbelehrung der Free-Linked GmbH. Stand: Juni 2014
 Widerrufsbelehrung der Stand: Juni 2014 www.free-linked.de www.buddy-watcher.de Inhaltsverzeichnis Widerrufsbelehrung Verträge für die Lieferung von Waren... 3 Muster-Widerrufsformular... 5 2 Widerrufsbelehrung
Widerrufsbelehrung der Stand: Juni 2014 www.free-linked.de www.buddy-watcher.de Inhaltsverzeichnis Widerrufsbelehrung Verträge für die Lieferung von Waren... 3 Muster-Widerrufsformular... 5 2 Widerrufsbelehrung
Einführung in die Programmierung
 Name, Vorname Matrikelnummer Probeklausur zur Vorlesung Einführung in die Programmierung WS 2008/09 Dauer: 2 Stunden Hinweise: Schreiben Sie Ihren Namen und Ihre Matrikelnummer auf dieses Deckblatt und
Name, Vorname Matrikelnummer Probeklausur zur Vorlesung Einführung in die Programmierung WS 2008/09 Dauer: 2 Stunden Hinweise: Schreiben Sie Ihren Namen und Ihre Matrikelnummer auf dieses Deckblatt und
Grundlagen der Programmierung 2. Bäume
 Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Grundlagen der Programmierung 2 Bäume Prof. Dr. Manfred Schmidt-Schauÿ Künstliche Intelligenz und Softwaretechnologie 24. Mai 2006 Graphen Graph: Menge von Knoten undzugehörige (gerichtete oder ungerichtete)
Aufgabe 1 Berechne den Gesamtwiderstand dieses einfachen Netzwerkes. Lösung Innerhalb dieser Schaltung sind alle Widerstände in Reihe geschaltet.
 Widerstandsnetzwerke - Grundlagen Diese Aufgaben dienen zur Übung und Wiederholung. Versucht die Aufgaben selbständig zu lösen und verwendet die Lösungen nur zur Überprüfung eurer Ergebnisse oder wenn
Widerstandsnetzwerke - Grundlagen Diese Aufgaben dienen zur Übung und Wiederholung. Versucht die Aufgaben selbständig zu lösen und verwendet die Lösungen nur zur Überprüfung eurer Ergebnisse oder wenn
Algorithmen & Datenstrukturen 1. Klausur
 Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
2 Lineare Gleichungen mit zwei Variablen
 2 Lineare Gleichungen mit zwei Variablen Die Klasse 9 c möchte ihr Klassenzimmer mit Postern ausschmücken. Dafür nimmt sie 30, aus der Klassenkasse. In Klasse 7 wurden lineare Gleichungen mit einer Variablen
2 Lineare Gleichungen mit zwei Variablen Die Klasse 9 c möchte ihr Klassenzimmer mit Postern ausschmücken. Dafür nimmt sie 30, aus der Klassenkasse. In Klasse 7 wurden lineare Gleichungen mit einer Variablen
BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG
 Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
Frist berechnen BERECHNUNG DER FRIST ZUR STELLUNGNAHME DES BETRIEBSRATES BEI KÜNDIGUNG Sie erwägen die Kündigung eines Mitarbeiters und Ihr Unternehmen hat einen Betriebsrat? Dann müssen Sie die Kündigung
Das Leitbild vom Verein WIR
 Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
Das Leitbild vom Verein WIR Dieses Zeichen ist ein Gütesiegel. Texte mit diesem Gütesiegel sind leicht verständlich. Leicht Lesen gibt es in drei Stufen. B1: leicht verständlich A2: noch leichter verständlich
SCHRITT 1: Öffnen des Bildes und Auswahl der Option»Drucken«im Menü»Datei«...2. SCHRITT 2: Angeben des Papierformat im Dialog»Drucklayout«...
 Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
Drucken - Druckformat Frage Wie passt man Bilder beim Drucken an bestimmte Papierformate an? Antwort Das Drucken von Bildern ist mit der Druckfunktion von Capture NX sehr einfach. Hier erklären wir, wie
LISP. Eine Einführung
 LISP Eine Einführung 5. OBERFLÄCHLICHES Übersicht 2 5.1 Verschiedenes zum letzten Aufgabenblatt 5.2 Geschwister und Komponenten oder wie finde ich was 5.3 on-click-methoden und on-change-methoden 5.1 Musterlösung
LISP Eine Einführung 5. OBERFLÄCHLICHES Übersicht 2 5.1 Verschiedenes zum letzten Aufgabenblatt 5.2 Geschwister und Komponenten oder wie finde ich was 5.3 on-click-methoden und on-change-methoden 5.1 Musterlösung
Codierungsverfahren SS 2011. Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur
 Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Reed-Solomon-Codes zur Mehrblock-Bündelfehler-Korrektur Wie die zyklischen BCH-Codes zur Mehrbitfehler-Korrektur eignen sich auch die sehr verwandten Reed-Solomon-Codes (= RS-Codes) zur Mehrbitfehler-Korrektur.
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
der Eingabe! Haben Sie das Ergebnis? Auf diesen schwarzen Punkt kommen wir noch zu sprechen.
 Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
Medizintechnik MATHCAD Kapitel. Einfache Rechnungen mit MATHCAD ohne Variablendefinition In diesem kleinen Kapitel wollen wir die ersten Schritte mit MATHCAD tun und folgende Aufgaben lösen: 8 a: 5 =?
SEP 114. Design by Contract
 Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Design by Contract SEP 114 Design by Contract Teile das zu entwickelnde Programm in kleine Einheiten (Klassen, Methoden), die unabhängig voneinander entwickelt und überprüft werden können. Einheiten mit
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Kapitel 6. Konstruktortypen und Ausnahmen. 6.1 Varianten und Konstruktoren
 Kapitel 6 Konstruktortypen und Ausnahmen Wir lernen jetzt, wie man mithilfe von Konstruktoren neue Typen deklariert. Mit Konstruktortypen lassen sich Mengen von geordneten Bäumen beschreiben. Außerdem
Kapitel 6 Konstruktortypen und Ausnahmen Wir lernen jetzt, wie man mithilfe von Konstruktoren neue Typen deklariert. Mit Konstruktortypen lassen sich Mengen von geordneten Bäumen beschreiben. Außerdem
Suchmaschinen. Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6
 Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
Universität Augsburg, Institut für Informatik SS 2014 Prof. Dr. W. Kießling 23. Mai 2014 Dr. M. Endres, F. Wenzel Lösungsblatt 6 Aufgabe 1: Pareto mit SV-Semantik Suchmaschinen Pareto Definition: x < P
3.2 Binäre Suche. Usr/local/www/ifi/fk/menschen/schmid/folien/infovk.ppt 1
 3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
3.2 Binäre Suche Beispiel 6.5.1: Intervallschachtelung (oder binäre Suche) (Hier ist n die Anzahl der Elemente im Feld!) Ein Feld A: array (1..n) of Integer sei gegeben. Das Feld sei sortiert, d.h.: A(i)
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Datenaufbereitung in SPSS. Daten zusammenfügen
 Daten zusammenfügen I. Fälle hinzufügen Diese Schritte müssen Sie unternehmen, wenn die Daten in unterschiedlichen Dateien sind; wenn also die Daten von unterschiedlichen Personen in unterschiedlichen
Daten zusammenfügen I. Fälle hinzufügen Diese Schritte müssen Sie unternehmen, wenn die Daten in unterschiedlichen Dateien sind; wenn also die Daten von unterschiedlichen Personen in unterschiedlichen
