Strömung realer inkompressibler Fluide
|
|
|
- Gisela Biermann
- vor 8 Jahren
- Abrufe
Transkript
1 4 STRÖMUNG REALER INKOMPRESSIBLER FLUIDE 4.1 EIGENSCHAFTEN REALER FLUIDE Fluidreibung und Viskosität Wesentlichstes Merkmal realer Fluide ist die Fluidreibung. Sie wurde erstmals von I. Newton (engl. Mathem. & Phys. 17.Jh) untersucht (Newtonsche Fluidreibung). Fluidreibung beruht auf zwischenmolekularen Anziehungkräften (van-der- Waals-schen Zähigkeitskräften), die sich der freien Verschiebung der Teilchen entgegenstellen. Diese Kräfte sind im Gegensatz zu den Reibungskräften der Festkörper-Reibung unabhängig vom Pressdruck (in diesem Fall Fluiddruck). Die Fluidreibung ist direkt proportional der Differenzgeschwindigkeit zwischen den Fluidteilchen, d.h. dem Geschwindigkeits- oder Schergefälle senkrecht zur Strömung ( v/ z). Bewegt man nämlich eine ebene Platte über einem Fluid im Abstand ( z) von einer zweiten ruhenden Platte mit der Differenzgeschwindigkeit ( c), so benötigt man dafür eine Kraft (F R ), die als Reibungs- oder Scherkraft bezeichnet wird und dem Newtonschen Fluidreibungsgesetz folgt. z bewegte Platte F R v= v F R = η A v/ z z v z=0 =0 (4.1) ruhende Platte Der Proportionalitätsfaktor (η) ist eine stoffspezifische Konstante und heißt dynamische Viskosität (Zähigkeit; Maßeinheit: N s/m² bzw. Pa s). Fluide, die dieser Gesetzmäßigkeit (η=konst.) unterliegen, werden Newtonsche Fluide genannt. Zu ihnen zählen alle tropfbaren Flüssigkeiten und alle Gase. Wichtigste Randbedingung ist die Haftbedingung an der Wand [v z=0 = 0]. Sie besagt, daß die Relativgeschwindigkeit der Strömung zur Wand direkt an der Wand Null ist. Die Strömung haftet also an der Wand. Wie alle Stoffkonstanten ist die Viskosität abhängig von Druck und Temperatur. Die Druckabhängigkeit von Flüssigkeiten ist jedoch oft vernachlässigbar gering (solange p < 100 bar). dyn. Viskosität Gase und Dämpfe Flüssigkeiten Temperatur strö1-kap4.doc/
2 Den Quotienten aus Scherkraft (F R ) und Reibungsfläche (A) bezeichnet man als Scher- oder Schubspannung (t) τ = η v/ z 4.2 In der Strömungstechnik wird die Viskosität oft auf die Dichte des Stoffes bezogen und erhält dann den Namen kinematische Viskosität (n) (Maßeinheit enthält nur kinemat. Größen). ν = η / ρ (m²/s) Ähnlichkeitsgesetze (Kennzahlen) Die Beschreibung der komplizierten Gesetzmäßigkeiten realer Fluide bedurfte und bedarf auch heute noch der experimentellen Untersuchung in Laborversuchen, oft im verkleinerten Maßstab (Modell). Um die dabei gewonnenen Erkenntnisse verallgemeinern zu können und physikalische Gesetzmäßigkeiten abzuleiten, haben sich die sogenannten Ähnlichkeitskennzahlen als sehr praktisch erwiesen. Sie bezeichnen als dimensionslose Kennzahlen die Randbedingungen (Kräfte, Zustandsgrößen, Stoffeigenschaften, Geometrien etc.), deren Verhältnis konstant sein muß, damit Versuchsergebnisse von einem Modellfall übertragbar sind. geometrische Ähnlichkeit Alle Modelle müssen möglichst vollständige geometrische Ähnlichkeit aufweisen, d.h. ihre wichtigen Abmessungen müssen den gleichen Maßstab aufweisen wie die sog. Großausführung. Die Geometrien von Modell (Strömung 1) und Großausführung (Strömung 2) müssen folgende Bedingungen bezügl. einer charakteristischen Länge (l) erfüllen: Längen: Fläche: Volumen: Rauhigkeit: d 1 = l 1 ; A 1 = l² 1 ; V 1 = l³ 1 ; k 1 = k d 2 l 2 A 2 l² 2 V 2 l³ 2 l 1 l 2 physikalische Ähnlichkeit Reynolds-Zahl Die in der Strömungstechnik realer Fluide wichtigste Ähnlichkeit ist die Reynolds sche Ähnlichkeit, benannt nach Osborn Reynolds (engl. Phys. 19.Jh.), der als erster Reibungsphänomene in Flüssigkeiten näher untersuchte und zu der Erkenntnis gelangte, daß diese unter folgenden Bedingungen ähnlich sind. Das Verhältnis von Trägheitskraft (F T ) und Reibungskraft (F R ), welches später als Reynoldszahl (Re) bezeichnet wurde, ist konstant. Daraus ergibt sich folgende Gleichung: Re = F T = m a = ρ A z ( v/ t) = ρ z² = z² strö1-kap4.doc/
3 F R η A v/ z η A v/ z η t ν t mit der geometrischen Ähnlichkeit z l und t l/v folgt: Re = v l 4.5 ν Das bedeutet, die Reynoldszahl ist das Verhältnis einer charakteristischen Geschwindigkeit (v) multipliziert mit einer charakteristischen Länge (l bzw d) und der kinematische Viskosität (ν). Die dritte allgemeine Kraft in Strömungen, die Druckkraft (F P ) hat demzufolge keine Auswirkung auf das Reibungsverhalten. Froude-Zahl Die Froude Zahl (W.Froude; engl. Ing. 19.Jh) kennzeichnet als zweite in der Strömungstechnik gebräuchliche Kennzahl die in bewegten Fluiden mit einer freien Oberfläche (Abwasserkanäle, Flüsse etc.) wichtige Ähnlichkeit, die sich aus dem Verhältnis von Trägheitskraft (F T ) und Schwerkraft (F G ) ergibt. Aus historischen Gründen wurde zusätzlich die Quadratwurzel in die Formel übernommen, die jedoch an dem Kräfteverhältnis nichts ändert. m a v l Fr = (nach Umstellung a =, Erweiterung mit der Länge l und Ersetzen von = v m g t t Fr = v l g t l = v g l 4.6 Mach-Zahl Als dritte Ähnlichkeitsbeziehung soll die Mach-Zahl erläutert werden. Sie ist das Verhältnis von Strömungsgeschwindigkeit (v) und Schallgeschwindigkeit (a) und gilt als Prüfkriterium, welches aussagt, ob eine Strömung noch als inkompressibel betrachtet werden kann. Ma = v/a 4.7 Die Schallgeschwindigkeit selbst ist als stoffspezifische Konstante druck- und temperaturabhängig. Unter Atmosphärenbedingungen (T=15 C; p=1 bar) ergibt sich für die technisch wichtigsten Fluide Luft und Wasser: a Luft = 340 m/s a Wasser = 1455 m/s Die Dichteänderung in einem strömenden kompressiblen Fluid (Gas) wird nämlich durch den dynamischen Druck ( p= ρ 0 /2 v² ) und die Schallgeschwindigkeit (a² = p/ ρ) bestimmt. strö1-kap4.doc/
4 Substituiert man in Gleichung 4.7 die Geschwindigkeiten >a< und >v< so ergibt sich folgende Beziehung ½ Ma² ρ/ρ Für technische Berechnungen gilt allgemein eine Machzahl von Ma = 0,3 als Grenze für die Gültigkeit der Gesetze für inkompressible Fluide. Der Fehler ( ρ/ρ 0 ) ist dabei nach Gl. 4.8 kleiner als 5%. 4.2 STRÖMUNGSFORMEN UND STRÖMUNGSGRENZSCHICHT In technische Strömungen sind zwei grundsätzlich verschiedene Strömungsformen zu beobachten, - die Schichtenströmung, die als laminare Strömung bezeichnet wird und - die Wirbelströmung, die als turbulente Strömung bezeichnet wird. Welche der beiden Formen sich in einer Strömung ausbilden hängt in erster Linie von der Strömungsgeschwindigkeit, aber auch von den übrigen geometrischen und physikalischen Randbedingungen ab. Laminare Strömungen existieren nur bei relativ geringen Strömungsgeschwindigkeiten und hohen kinem. Zähigkeiten. Sobald die Geschwindigkeit über ein gewisses Maß steigt, wird fast jede reale Strömung turbulent. Den Strömungsumschlag von der laminaren zur turbulenten Bewegung hat O. Reynolds in seinem Farbfadenversuch (Bild 3.1) gezeigt. Innenströmung In vollständig umrandeten und gefüllten Systemen (gerade Rohrleitungen oder Kanäle) ist das Umschlagkriterium die kritische Reynoldszahl. Aus seinen umfangreichen Versuchen konnte Reynolds folgende noch heute gebräuchliche allgemeingültige Aussage ableiten: Re = v d < laminare Strömung 4.9 ν Re = v d > ν turbulente Strömung wobei der Innedurchmesser d für die charakteristische Länge l steht Allerdings gilt die Aussage Re Krit =2320 nach heutiger Kenntnis nicht mehr als festes Grenzkriterium. Sondern vielmehr existiert ein Grenzbereich, in welchem die Turbulenz einer Strömung langsam ansteigt. Der Wert Re=2320 ist dabei die unterste beobachtete Grenze des Umschlags. Die obere Grenze für laminare Innenströmungen liegt bei ca. Re=10 4. strö1-kap4.doc/
5 Umströmung Bei der äußeren Umströmung eines Körpers ist der Umschlag von laminarer in turbulente Strömung noch weniger einheitlich als bei Innenströmungen. Er ereignet sich je nach Körpergeometrie in einem breiten Reynoldszahl-Bereich. z.b. bei Kugeln gilt: 10 5 < Re= v d < 10 6 ν (d=außendurchmesser) Strömung mit freier Oberfläche In offenen Gerinnen wird neben der Differenzierung laminar-turbulent noch unterschieden, ob die Strömung gleichförmig ist (konstante Wasserteife (l t ) oder ins Schießen gerät (in Strömungsrichtung abnehmende Wassertiefe und zunehmende Geschwindigkeit). Es gilt: v Fr = gl < 1 gleichförmig strömende Bewegung (geringes Gefälle) 4.10 > 1 schießende Bewegung (großes Gefälle) wobei die hydraulische Wasserteife l t nur in Rechteckkanälen gleich der Wasserstandshöhe h ist. In anders geformten Gerinnen ergibt sich l t als Verhältnis von Querschnittsfläche A und Spiegelbreite der freien Oberfläche l t = A/ b Sp Grenzschichttheorie Die heute gebräuchliche physikalische Erklärung über die Entstehung und Entwicklung von Turbulenzerscheinungen und Reibungsdruckverlusten gelang Ludwig Prandtl (dt. Phys. 20.Jh.) mit der Grenzschichttheorie. Darin unterscheidet Prandtl zwischen zwei Strömungsbereichen: -einer relativ dünnen wandnahen Strömungsschicht (Grenzschicht), in welcher aufgrund der Wandreibung sehr starke Geschwindigkeitsgradienten ( v/ z) auftreten, - und einem weitgehend ungestörten Außenbereich (Außenströmung), in welchem näherungsweise die Gesetze der idealen Potentialströmungen gelten. In Newtonschen Fluiden mit relativ geringer Viskosität ist die Fluidreibung fast ausschließlich in der Grenzschicht wirksam. Die Grenzschicht weist weiterhin folgende Eigenschaften auf, die für das Strömungsverhalten realer Fluide ganz entscheidend sind: In der Grenzschicht gilt das Newtonsche Reibungsgesetz (Gl Wandreibung). Jede Grenzschichtströmung beginnt laminar (Einlauf- oder Anlaufströmung genannt). strö1-kap4.doc/
6 Die Grenzschichtdicke steigt mit der Lauflänge (s) und der Geschwindigkeit der Außenströmung (v ). Nach dem Erreichen einer bestimmten Grenzschichtdicke findet in der Grenzschicht der Strömungsumschlag von laminar in turbulent statt (Bild 4.1). Die Turbulenzbewegung in der Grenzschicht wird durch Impulsaustausch (Fluidreibung und teilelastische Stöße der Fluidteilchen) auf die Hauptströmung übertragen, die dadurch ihrerseits turbulent wird (Mischbewegung). Grenzschichten können sich insgesamt ablösen und werden von Rückströmungen hinterströmt, wenn die angrenzende Wandkontur eine starke Richtungsänderung erfährt (Wirbelablösung). Berechnung der Grenzschichtdicke Die Ausdehnung einer Grenzschicht hängt - wie oben erwähnt - von der Lauflänge (s) und der Strömungsgeschwindigkeit in der Hauptströmung (v ) ab und läßt sich aus den folgenden empirischen Näherungsformeln bestimmen. laminar: δ L = 5 (ν s L / v ) 1/ a turbulent: δ T = 0,37 (ν s T 4 / v ) 1/ b Der Umschlagpunkt mit der Lauflänge (s krit ) ist durch die kritische Reynoldszahl der Hauptstömung Re krit festgelegt. Re krit = v s krit 5 x 10 5 ν Turbulenz und Turbulenzgrad Turbulenzbewegungen lassen sich mathematisch nur sehr schwer exakt beschreiben, da sie stochastischer d.h zufallsbedingter Natur sind. Sie können lediglich mit Hilfe statistischer Methoden näherungsweise erfaßt werden (z.b. Mittelwert-Schwankungswert-Methode: v=v m +v >Momentangeschwindigkeit = mittlere Geschwindigkeit+Geschwindigkeitsschwankung<). Trägt man die Messwerte einer Geschwindigkeitsmessung in einer turbulenten Strömung als Funktion der Zeit auf, so ergibt sich folgendes Bild. v (Geschwindigkeit Mittelwert v m strö1-kap4.doc/
7 v Schwankungsgeschwindigkeit t (zeit) Zur Lösung der meisten technischen Probleme und für die damit verbundenen Berechnungen ist eine detaillierte mathematische Erfassung der Strömungsturbulenzen auch gar nicht erforderlich. Das gilt auch für den Rahmen dieser Vorlesung. Befaßt man sich jedoch mit der Computer-Simulation von komplizierten Strömungsvorgängen, d.h. der numerischen Lösung der dreidimensionalen differentiellen Bewegungsgleichungen, so müssen geeignete statistische Turbulenzmodelle einbezogen werden. Zur meßtechnischen Feststellung von Turbulenzen verwendet man i.a. Hitzdrahtanemometer (Meßinstument mit feinem beheizten Draht dessen Temperaturänderung in der Strömung ein Maß für die Geschwindigkeitsschwankung ist), mit dem man die Strömungsschwankungen >v < richtungsunabhängig in allen 3-Raumdimensionen erfassen kann. Als Maß zur Beurteilung und zum Vergleich gemessener Turbulenzen wird folgende Größe als Turbulenzgrad (Tu) definiert. Tu = 2 ( v' ) v m m wobei v' 2 m 1 = n n 1 v' wobei >v ²< die zeitlichen Schwankungswerte der momentanen Geschwindigkeit >v< in den drei Dimensionen x,y,z darstellen. In technischen Strömungen nimmt der Turbulenzgrad etwa folgende Größenordnungen an: - voll ausgeprägte Turbulenz: Tu = turbulenzarme Strömung: Tu = 10-4 ( z.b. Windkanal) Umschlag laminar-turbulent: Tu = 10-3 Trotz der stochastischen Natur der dreidimensionalen Turbulenzen bleibt die Hauptströmungsrichtung meistens dominant. Die mittlere Strömungsgeschwindigkeit (v m ) dieser Hauptrichtung wird an jedem Ort wie in laminaren oder idealen Strömungen durch einem Vektor dargestellt, so daß auch reale turbulente Strömungen grundsätzlich mit dem Stromfadenmodell beschrieben werden können. strö1-kap4.doc/
8 4.2.3 Geschwindigkeitsverteilung in Rohren und Kanälen In Rohren und Kanälen mit symmetrischem Querschnitt bilden sich typische Geschwindigkeitsprofile aus (Bild 4.2). Sie leiten sich aus dem Reibungsverhalten und der Haftbedingung an der Wand ab. laminare Strömung Die Geschwindigkeitsverteilung in laminaren Strömungen läßt sich aus dem Kräftegleichgewicht zwischen den Druck- und Reibungskräften an einem differentiellen Strömungselement analytisch ableiten (siehe Anhang zu Kap 4). Es gilt für jeden Ort des Querschnittes im Abstand (r ) von der Rohrachse v ( r ) = K (r 0 ² - r²) Gesetz von Stokes 4.14 Dieses ist die Gleichung einer Parabel mit den Grenzen Maximalgeschwindigkeit in Rohrmitte v max = K r 0 ² Minimalgeschwindigkeit an der Rohrwand v min = 0 In Rohren mit Kreisquerschnitt (runde Rohre) ist das Strömungsprofil somit eine rotationssymmetrische Parabel (Paraboloid). Definiert man weiterhin eine mittlere Geschwindigkeit (v mit ), die sich aus der Durchflußgleichung (v mit = V/A) errechnet, so läßt sich diese aus der Volumengleichheit von einem Zylinder und dem Paraboloid mit gleicher Grundfläche (A) ermitteln. Es gilt: v mit = V/A = ½ v max 4.15 turbulente Strömung Das Geschwindigkeitsprofil turbulenter Strömungen verläuft in der wandnahen Grenzschicht viel steiler und im turbulenten mittleren Strömungsbereich viel flacher als das Profil laminarer Strömungen. Nach Auswertung umfangreicher Versuche haben Prandtl und sein Mitarbeiter Nikuradse folgenden exponentiellen Zusammenhang gefunden. v ( r) = K v mit (1 - r/r 0 ) n 4.16 mit der Konstanten K= ½ (n+1)(n+2) und dem Exponenten n = f (Re) (n ist Funktion der Reynoldszahl). Die Maximalgeschwindigkeit der turbulenten Strömung ist dabei etwa um den Faktor F=1,2 größer als die durchflußäquivalente mittlere Geschwindigkeit. v max 1,2 v mit 4.17 strö1-kap4.doc/
9 4.3 ERWEITERTE ENERGIEGLEICHUNG UND DRUCKVERLUST Reibung verursacht stets eine Umwandlung von kinetischer Energie in Wärme. Dieser Vorgang heißt Energie-Dissipation. Neben der Reibung trägt auch die Turbulenz mit ihrem Impulsaustausch zur Dissipation bei. Dissipation mindert also die verfügbare Transportenergie des Systems und wird daher als Energieverlust bezeichnet. Reale Strömungen sind immer verlustbehaftet. Bezieht man den Energieverlust nun in die Energiegleichung von Bernoulli für ideale Strömungen ein, so ergibt sich folgende erweiterte Energiegleichung für die Strömung realer Fluide bezogen auf zwei beliebige Querschnitte 1 und 2 (vgl. Bild 3.2 d und Gl. 3.6). Diese Gleichung läßt sich in drei Varianten ausdrücken, die durch einfache mathematische Umformung ineinander überführt werden können. Energieform (J/kg): g z 1 + p 1 + v 1 ² = g z 2 + p 2 + v 2 ² + Y V 4.18 a ρ 2 ρ 2 mit Y V spez. massebezogener Energieverlust Druckform (N/m²) ρ g z 1 + p 1 + ρ v 1 ² = ρ g z 2 + p 2 + ρ v 2 ² + Dp V 4.18 b 2 2 mit p Verl = ρ Y V Druckverlust Höhenform (m): z 1 + p 1 + v 1 ² = z 2 + p 2 + v 2 ² + h V 4.18 c g ρ 2 g g ρ 2 g mit h V = Y V / g Verlusthöhe Jede der drei Gleichungen bezeichnet natürlich weiterhin einen Energieverlust, wobei sich der Druckverlust auf die Druckenergie bezieht und die Verlusthöhe auf die potentielle Lageenergie der Ortshöhe. Den Verlauf des verfügbaren Energiepotentials (Druck+Geschwindigkeit+Lage) entlang der Strömung nennt man Energielinie. Sie ergibt sich aus dem Anfangspotential abzüglich der Energieverluste (siehe Bild 4.3) Da in Fluidtransportsystemen (Rohre, Kanäle etc.) der Energieverlust wegen der Kontinuitätsbedingung meist als Druckverlust auftritt und gemessen wird, ist diese Bezeichnung am gebräuchlichsten. Man spricht daher im allgemeinen von Strömungsdruckverlust. Die Bestimmung und Berechnung von Druckverlusten ist eine der wichtigsten ingenieurtechnische Aufgaben innerhalb der Strömungstechnik. Sie wird im folgenden Kapitel 5 ausführlich behandelt. strö1-kap4.doc/
10 4.4 STRÖMUNG MIT ENERGIEZUFUHR Damit technische Strömungen im Dauerbetrieb aufrecht erhalten werden können, muß ihnen kontinuierlich Energie zugeführt werden, da das Energiepotential der realen Strömung - wie gezeigt - durch Reibungs- und Turbulenzverluste ständig verringert wird. Die Aufgabe der erforderlichen Energiezufuhr übernehmen die Strömungsmaschinen. In Strömungsmaschinen (Pumpen,Turbinen, Ventilatoren oder Strahltriebwerken) kann der Strömung aber nicht nur Energie zugeführt sondern auch entzogen werden. Welche Vorgänge im einzelnen eine Rolle spielen, ist Gegenstand der Vorlesung Teil 2 ( Strömungsmaschinen ). Im Rahmen der Energiebilanz nach der Bernoullischen Energiegleichung (Gl a-c) sind für Strömungen mit Energiezufuhr bzw. -abfuhr lediglich zusätzliche Gleichungsterme zu addieren (Y zu; ; Y ab ). Energiegleichung: g z e + p e + v e² + Y zu = g z a + p a + v a ² + Y V + Y ab 4.19 ρ 2 ρ 2 Der Term ( Y zu ) repräsentieren die Netto-Energiezufuhr als Strömungsenergie. Die tatsächlich aufzubringende Brutto-Energie in Form von mechanischer oder elektrischer Energie erhält man durch Division mit dem Maschinenwirkungsgrad (η zu ). Sie ist entsprechend größer als die Netto-Energiezufuhr. Der Term ( Y ab ) bezeichnet die Brutto-Energieentnahme. Sie ist mit dem Maschinenwirkungsgrad (η ab )zu multiplizieren, um die der Strömung entzogene Netto-Nutzenergie zu ermitteln. Maschinenwirkungsgrade von Strömungsmaschinen liegen i.a. zwischen η= 0,6 bis η= 0,9. strö1-kap4.doc/
Klausur Strömungsmechanik 1 WS 2009/2010
 Klausur Strömungsmechanik 1 WS 2009/2010 03. März 2010, Beginn 15:00 Uhr Prüfungszeit: 90 Minuten Zugelassene Hilfsmittel sind: Taschenrechner (nicht programmierbar) TFD-Formelsammlung (ohne handschriftliche
Klausur Strömungsmechanik 1 WS 2009/2010 03. März 2010, Beginn 15:00 Uhr Prüfungszeit: 90 Minuten Zugelassene Hilfsmittel sind: Taschenrechner (nicht programmierbar) TFD-Formelsammlung (ohne handschriftliche
I. Mechanik. I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen. Physik für Mediziner 1
 I. Mechanik I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen Physik für Mediziner Stromdichte Stromstärke = durch einen Querschnitt (senkrecht zur Flussrichtung) fließende Menge pro Zeit ( Menge
I. Mechanik I.4 Fluid-Dynamik: Strömungen in Flüssigkeiten und Gasen Physik für Mediziner Stromdichte Stromstärke = durch einen Querschnitt (senkrecht zur Flussrichtung) fließende Menge pro Zeit ( Menge
lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.)
 lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.) Temperaturgrenzschicht Geschwindigkeitsgrenzschicht Vergleich von Geschwindigkeits- und Temperaturgrenzschicht laminare
lokaler und globaler konvektiver Wärmeübergang (Oberflächentemperatur T s = const.) Temperaturgrenzschicht Geschwindigkeitsgrenzschicht Vergleich von Geschwindigkeits- und Temperaturgrenzschicht laminare
10.3.1 Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 2320)
 0.3-0.3 Rohrströmung 0.3. Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 30) Bei laminarer Rohrströmung läßt sich der Reibungsverlust theoretisch berechnen, as bei der turbulenten Strömung
0.3-0.3 Rohrströmung 0.3. Druckverlust in Rohrleitungen bei laminarer Strömung (Re < 30) Bei laminarer Rohrströmung läßt sich der Reibungsverlust theoretisch berechnen, as bei der turbulenten Strömung
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Physik I TU Dortmund WS2017/18 Gudrun Hiller Shaukat Khan Kapitel 7
 1 Ergänzungen zur Hydrodynamik Fluide = Flüssigkeiten oder Gase - ideale Fluide - reale Fluide mit "innerer Reibung", ausgedrückt durch die sog. Viskosität Strömungen von Flüssigkeiten, d.h. räumliche
1 Ergänzungen zur Hydrodynamik Fluide = Flüssigkeiten oder Gase - ideale Fluide - reale Fluide mit "innerer Reibung", ausgedrückt durch die sog. Viskosität Strömungen von Flüssigkeiten, d.h. räumliche
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
Physik für Biologen und Zahnmediziner Kapitel 8: Hydrodynamik, Grenzflächen Dr. Daniel Bick 01. Dezember 2017 Daniel Bick Physik für Biologen und Zahnmediziner 01. Dezember 2017 1 / 33 Übersicht 1 Mechanik
σ ½ 7 10-8 cm = 7 10-10 m σ ½ 1 nm
 Zahlenbeispiele mittlere freie Weglänge: Λ = 1 / (σ n B ) mittlere Zeit zwischen Stößen τ = Λ / < v > Gas: Stickstoff Druck: 1 bar = 10 5 Pa Dichte n = 3 10 19 cm -3 σ = 45 10-16 cm 2 σ ½ 7 10-8 cm = 7
Zahlenbeispiele mittlere freie Weglänge: Λ = 1 / (σ n B ) mittlere Zeit zwischen Stößen τ = Λ / < v > Gas: Stickstoff Druck: 1 bar = 10 5 Pa Dichte n = 3 10 19 cm -3 σ = 45 10-16 cm 2 σ ½ 7 10-8 cm = 7
Hydrodynamik y II - Viskosität
 Physik A VL9 (..0) Hydrodynamik y II - Viskosität Die Viskosität ität Das Gesetz on Hagen-Poiseuille Die Stokes sche Reibung Die Reynolds-Zahl Viskose Fluide Viskosität bisher: Kräfte zwischen dem strömenden
Physik A VL9 (..0) Hydrodynamik y II - Viskosität Die Viskosität ität Das Gesetz on Hagen-Poiseuille Die Stokes sche Reibung Die Reynolds-Zahl Viskose Fluide Viskosität bisher: Kräfte zwischen dem strömenden
Versuch 1. Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch)
 Versuch 1 Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und Raumfahrt Georg-August-Universität
Versuch 1 Bestimmung des Umschlagpunktes laminar-turbulent bei einer Rohrströmung (Reynoldsversuch) Strömungsmechanisches Praktikum des Deutschen Zentrums für Luft- und Raumfahrt Georg-August-Universität
3. Strömungstechnische Grundlagen
 - 1-3. Strömungstechnische Grundlagen Die Strömungstechnik befasst sich mit den Gesetzen der Bewegung von Flüssigkeiten und Gasen. Da die meisten dieser Gesetze gleichermaßen für Flüssigkeiten und Gase
- 1-3. Strömungstechnische Grundlagen Die Strömungstechnik befasst sich mit den Gesetzen der Bewegung von Flüssigkeiten und Gasen. Da die meisten dieser Gesetze gleichermaßen für Flüssigkeiten und Gase
3.4. Oberflächenspannung und Kapillarität
 3.4. Oberflächenspannung und Kapillarität Aus dem Experiment: Flüssigkeitsfaden, Moleküle der Flüssigkeit zeigen Zusammenhalt. Eigenschaften kondensierter Materie: Zwischen den Molekülen herrschen starke
3.4. Oberflächenspannung und Kapillarität Aus dem Experiment: Flüssigkeitsfaden, Moleküle der Flüssigkeit zeigen Zusammenhalt. Eigenschaften kondensierter Materie: Zwischen den Molekülen herrschen starke
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas. Thermodynamik
 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Physik I Mechanik und Thermodynamik
 Physik I Mechanik und Thermodynamik 1 Einführung: 1.1 Was ist Physik? 1.2 Experiment - Modell - Theorie 1.3 Geschichte der Physik 1.4 Physik und andere Wissenschaften 1.5 Maßsysteme 1.6 Messfehler und
Physik I Mechanik und Thermodynamik 1 Einführung: 1.1 Was ist Physik? 1.2 Experiment - Modell - Theorie 1.3 Geschichte der Physik 1.4 Physik und andere Wissenschaften 1.5 Maßsysteme 1.6 Messfehler und
Vergleich von experimentellen Ergebnissen mit realen Konfigurationen
 Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Ähnlichkeitstheorie Vergleich von experimentellen Ergebnissen mit realen Konfigurationen Verringerung der Anzahl der physikalischen Größen ( Anzahl der Experimente) Experimentelle Ergebnisse sind unabhängig
Zusammenfassung 23.10.2006, 0. Einführung
 Zusammenfassung 23.10.2006, 0. Einführung - Umrechnung der gebräuchlichen Einheiten - Teilung/Vervielfachung von Einheiten - Kenngrößen des reinen Wassers (z.b. Dichte 1000 kg/m 3 ) Zusammenfassung 30.10.2006,
Zusammenfassung 23.10.2006, 0. Einführung - Umrechnung der gebräuchlichen Einheiten - Teilung/Vervielfachung von Einheiten - Kenngrößen des reinen Wassers (z.b. Dichte 1000 kg/m 3 ) Zusammenfassung 30.10.2006,
Prüfungsfrage Strömung der Flüssigkeiten. Fluideigenschaften. Strömungslehre. HYDROSTATIK keine Bewegung
 016.11.18. Prüfungsfrage Strömung der Flüssigkeiten Typen der Flüssigkeitsströmung. Die Reynolds-Zahl. Die Viskosität. Die Gesetzmäßigkeiten der Flüssigkeitsströmung: die Gleichung der Kontinuität, das
016.11.18. Prüfungsfrage Strömung der Flüssigkeiten Typen der Flüssigkeitsströmung. Die Reynolds-Zahl. Die Viskosität. Die Gesetzmäßigkeiten der Flüssigkeitsströmung: die Gleichung der Kontinuität, das
NTB Druckdatum: SC. typische Zeitkonstante für die Wärmeleitungsgleichung Beispiel
 SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
SCIENTIFIC COMPUTING Die eindimensionale Wärmeleitungsgleichung (WLG) Begriffe Temperatur Spezifische Wärmekapazität Wärmefluss Wärmeleitkoeffizient Fourier'sche Gesetz Spezifische Wärmeleistung Mass für
Materialien WS 2014/15 Dozent: Dr. Andreas Will.
 Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will will@tu-cottbus.de Reynoldszahl
Master Umweltingenieur, 1. Semester, Modul 42439,, 420607, VL, Do. 11:30-13:00, R. 3.21 420608, UE, Do. 13:45-15:15, R. 3.17 Materialien WS 2014/15 Dozent: Dr. Andreas Will will@tu-cottbus.de Reynoldszahl
Theoriefragen für das Labortestat und die Prüfung Fluidmechanik II
 Theoriefragen für das Labortestat und die Prüfung Fluidmechanik II 1) Wie stellt sich der Druck p E im Austrittsquerschnitt beim Austritt eines Gases aus einem Kessel durch eine stetig konvergente Mündung,
Theoriefragen für das Labortestat und die Prüfung Fluidmechanik II 1) Wie stellt sich der Druck p E im Austrittsquerschnitt beim Austritt eines Gases aus einem Kessel durch eine stetig konvergente Mündung,
Einführung in die Technische Strömungslehre
 Einführung in die Technische Strömungslehre Bearbeitet von Gerd Junge 1. Auflage 2011. Buch. 288 S. Hardcover ISBN 978 3 446 42300 8 Format (B x L): 16,7 x 240,3 cm Gewicht: 546 g Weitere Fachgebiete >
Einführung in die Technische Strömungslehre Bearbeitet von Gerd Junge 1. Auflage 2011. Buch. 288 S. Hardcover ISBN 978 3 446 42300 8 Format (B x L): 16,7 x 240,3 cm Gewicht: 546 g Weitere Fachgebiete >
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
4 Freie Konvektion Vertikale Platte. Freie Konvektion entsteht durch Dichteunterschiede infolge eines Temperaturgradienten.
 4 Freie Konvektion Freie Konvektion entsteht durch Dichteunterschiede infolge eines Temperaturgradienten. 4. Vertikale Platte Wärmeabgabe einer senkrechten beheizten Platte Thermische Grenzschichtdicke
4 Freie Konvektion Freie Konvektion entsteht durch Dichteunterschiede infolge eines Temperaturgradienten. 4. Vertikale Platte Wärmeabgabe einer senkrechten beheizten Platte Thermische Grenzschichtdicke
14. Strömende Flüssigkeiten und Gase
 14. Strömende Flüssigkeiten und Gase 14.1. orbemerkungen Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien erschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
14. Strömende Flüssigkeiten und Gase 14.1. orbemerkungen Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien erschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
3.5.6 Geschwindigkeitsprofil (Hagen-Poiseuille) ******
 3.5.6 ****** 1 Motivation Bei der Strömung einer viskosen Flüssigkeit durch ein Rohr ergibt sich ein parabolisches Geschwindigkeitsprofil. 2 Experiment Abbildung 1: Versuchsaufbau zum Der Versuchsaufbau
3.5.6 ****** 1 Motivation Bei der Strömung einer viskosen Flüssigkeit durch ein Rohr ergibt sich ein parabolisches Geschwindigkeitsprofil. 2 Experiment Abbildung 1: Versuchsaufbau zum Der Versuchsaufbau
... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre ρ L0
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 03. 08. 007 1. Aufgabe (10 Punkte) Ein mit elium gefüllter Ballon (Volumen V 0 für z = 0) steigt in einer Atmosphäre mit der Gaskonstante R
...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 03. 08. 007 1. Aufgabe (10 Punkte) Ein mit elium gefüllter Ballon (Volumen V 0 für z = 0) steigt in einer Atmosphäre mit der Gaskonstante R
Strömungen. Kapitel 10
 Kapitel 10 Strömungen In Kapitel 9 behandelten wir die statistische Bewegung einzelner Moleküle in einem Gas, aber noch keine makroskopische Bewegung des Mediums. Der Mittelwert der Impulse aller Teilchen
Kapitel 10 Strömungen In Kapitel 9 behandelten wir die statistische Bewegung einzelner Moleküle in einem Gas, aber noch keine makroskopische Bewegung des Mediums. Der Mittelwert der Impulse aller Teilchen
Zugfestigkeit (4)
 3..1. Zugfestigkeit (4) ui 1,6 1,4 1, 1,0 n = 000 min -1 Z = 0,45 bar Z = 0,00 bar Messung berechnet 0,8 0,6 0,4 ui u,i ptot,0 p u 1, a v 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 ' u,i q [ - ] ptot,0 pkrit ptot,0
3..1. Zugfestigkeit (4) ui 1,6 1,4 1, 1,0 n = 000 min -1 Z = 0,45 bar Z = 0,00 bar Messung berechnet 0,8 0,6 0,4 ui u,i ptot,0 p u 1, a v 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 ' u,i q [ - ] ptot,0 pkrit ptot,0
Physikalisches Praktikum I
 Fachbereich Physik Physikalisches Praktikum I Name: Kugelfallviskosimeter Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Dieser Fragebogen muss von
Fachbereich Physik Physikalisches Praktikum I Name: Kugelfallviskosimeter Matrikelnummer: Fachrichtung: Mitarbeiter/in: Assistent/in: Versuchsdatum: Gruppennummer: Endtestat: Dieser Fragebogen muss von
Vorlesung STRÖMUNGSLEHRE Zusammenfassung
 Lehrstuhl für Fluiddynamik und Strömungstechnik Vorlesung STRÖMUNGSLEHRE Zusammenfassung WS 008/009 Dr.-Ing. Jörg Franke Bewegung von Fluiden ( Flüssigkeiten und Gase) - Hydro- und Aerostatik > Druckverteilung
Lehrstuhl für Fluiddynamik und Strömungstechnik Vorlesung STRÖMUNGSLEHRE Zusammenfassung WS 008/009 Dr.-Ing. Jörg Franke Bewegung von Fluiden ( Flüssigkeiten und Gase) - Hydro- und Aerostatik > Druckverteilung
12.1 Fluideigenschaften
 79 Als Fluide bezeichnet man Kontinua mit leicht verschieblichen Teilen. Im Unterschied zu festen Körpern setzen sie langsamen Formänderungen ohne Volumenänderung nur geringen Widerstand entgegen. Entsprechend
79 Als Fluide bezeichnet man Kontinua mit leicht verschieblichen Teilen. Im Unterschied zu festen Körpern setzen sie langsamen Formänderungen ohne Volumenänderung nur geringen Widerstand entgegen. Entsprechend
1. Die Wellengleichung
 1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
Physikalisches Grundpraktikum
 Ernst-Moritz-Arndt-Universität Greifswald / Institut für Physik Physikalisches Grundpraktikum Praktikum für Mediziner M1 Viskose Strömung durch Kapillaren Name: Versuchsgruppe: Datum: Mitarbeiter der Versuchsgruppe:
Ernst-Moritz-Arndt-Universität Greifswald / Institut für Physik Physikalisches Grundpraktikum Praktikum für Mediziner M1 Viskose Strömung durch Kapillaren Name: Versuchsgruppe: Datum: Mitarbeiter der Versuchsgruppe:
KLAUSUR STRÖMUNGSLEHRE. Studium Maschinenbau. und
 Univ.-Prof. Dr.-Ing. Wolfram Frank 01.10.2002 Lehrstuhl für Fluiddynamik und Strömungstechnik Aufgabe Name:... Vorname:... (Punkte) 1)... Matr.-Nr.:... HS I / HS II / IP / WI 2)... 3)... Beurteilung:...
Univ.-Prof. Dr.-Ing. Wolfram Frank 01.10.2002 Lehrstuhl für Fluiddynamik und Strömungstechnik Aufgabe Name:... Vorname:... (Punkte) 1)... Matr.-Nr.:... HS I / HS II / IP / WI 2)... 3)... Beurteilung:...
Fragen zur Prüfungsvorbereitung Strömungsmechanik II. Stand Sommersemester 2009
 Fragen zur Prüfungsvorbereitung Strömungsmechanik II Stand Sommersemester 2009 Allgemein Sicherer Umgang in der für die im Vorlesungsrahmen benötigte Tensorrechnung. Insbesondere Kenntnis der einzelnen
Fragen zur Prüfungsvorbereitung Strömungsmechanik II Stand Sommersemester 2009 Allgemein Sicherer Umgang in der für die im Vorlesungsrahmen benötigte Tensorrechnung. Insbesondere Kenntnis der einzelnen
Grundlagen der Strömungsmechanik
 Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
Franz Durst Grundlagen der Strömungsmechanik Eine Einführung in die Theorie der Strömungen von Fluiden Mit 349 Abbildungen, davon 8 farbig QA Springer Inhaltsverzeichnis Bedeutung und Entwicklung der Strömungsmechanik
KLAUSUR STRÖMUNGSLEHRE. Studium Maschinenbau. und
 Univ.-Prof. Dr.-Ing. Wolfram Frank 14.10.2005 Lehrstuhl für Fluiddynamik und Strömungstechnik Aufgabe Name:... Matr.-Nr.:... Vorname:... HS I / HS II / IP / WI (Punkte) Frage 1)... Frage 2)... Beurteilung:...
Univ.-Prof. Dr.-Ing. Wolfram Frank 14.10.2005 Lehrstuhl für Fluiddynamik und Strömungstechnik Aufgabe Name:... Matr.-Nr.:... Vorname:... HS I / HS II / IP / WI (Punkte) Frage 1)... Frage 2)... Beurteilung:...
Technische Strömungsmechanik I
 Technische Strömungsmechanik I Lehrbuch Autoren: Prof. Dr.-Ing. habil. Gert Naue, Merseburg (federführender Autor) Prof. Dr. sc. teehn. Friedrich Liepe, Köthen Doz. Dr.-Ing. habil. Hans-Joachim Mascheck,
Technische Strömungsmechanik I Lehrbuch Autoren: Prof. Dr.-Ing. habil. Gert Naue, Merseburg (federführender Autor) Prof. Dr. sc. teehn. Friedrich Liepe, Köthen Doz. Dr.-Ing. habil. Hans-Joachim Mascheck,
Technische Strömungsmechanik für Studium und Praxis
 Albert Jogwich Martin Jogwich Technische Strömungsmechanik für Studium und Praxis 2. Auflage
Albert Jogwich Martin Jogwich Technische Strömungsmechanik für Studium und Praxis 2. Auflage
Vakuum und Gastheorie
 Vakuum und Gastheorie Jan Krieger 9. März 2005 1 INHALTSVERZEICHNIS 0.1 Formelsammlung.................................... 2 0.1.1 mittlere freie Weglänge in idealen Gasen................... 3 0.1.2 Strömungsleitwerte
Vakuum und Gastheorie Jan Krieger 9. März 2005 1 INHALTSVERZEICHNIS 0.1 Formelsammlung.................................... 2 0.1.1 mittlere freie Weglänge in idealen Gasen................... 3 0.1.2 Strömungsleitwerte
Praktikum Aerodynamik des Flugzeugs
 Praktikum Aerodynamik des Flugzeugs 1. Versuch: Sondenmessungen Betreuer: Dipl.-Ing. Anja Kölzsch Dipl.-Ing. Moritz Grawunder Ziel des heutigen Termins Einführung in die Strömungsmesstechnik Messung verschiedener
Praktikum Aerodynamik des Flugzeugs 1. Versuch: Sondenmessungen Betreuer: Dipl.-Ing. Anja Kölzsch Dipl.-Ing. Moritz Grawunder Ziel des heutigen Termins Einführung in die Strömungsmesstechnik Messung verschiedener
Strömende Flüssigkeiten und Gase
 Strömende Flüssigkeiten und Gase Laminare und turbulente Strömungen Bei laminar strömenden Flüssigkeiten oder Gasen bewegen sich diese in Schichten, die sich nicht miteinander vermischen. Es treten keine
Strömende Flüssigkeiten und Gase Laminare und turbulente Strömungen Bei laminar strömenden Flüssigkeiten oder Gasen bewegen sich diese in Schichten, die sich nicht miteinander vermischen. Es treten keine
df Druck p 1.5 Fluide: Mechanik der Flüssigkeiten und Gase 1.5.1 Ruhende Flüssigkeiten und Gase 1.5.1.1 Druck
 .5 Fluide: Mechanik der Flüssigkeiten und Gase Wir haben im Kaitel Mechanik bisher behandelt: ) Masseunkte ) Feste Körer (Starre Körer, elastische Körer siehe Vorl. techn. Mechanik!) Feste Körer haben
.5 Fluide: Mechanik der Flüssigkeiten und Gase Wir haben im Kaitel Mechanik bisher behandelt: ) Masseunkte ) Feste Körer (Starre Körer, elastische Körer siehe Vorl. techn. Mechanik!) Feste Körer haben
Hydrodynamik Kontinuitätsgleichung. Massenerhaltung: ρ. Massenfluss. inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms : v
 Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
c S sin 2 1 2 c c p sin 4 4.8 Kugelumströmung 4.8.1 Ideale reibungsfreie Umströmung der Kugel (Potentialströmung) Geschwindigkeit auf der Oberfläche
 4.7 Kugelumströmung... 4.7. Ideale reibungsfreie Umströmung der Kugel (Potentialströmung)... 4.7. Reibungsbehaftete Umströmung der Kugel... 4.8 Zylinderumströmung... 4.9 Rohrströmung... 5 4.9. Laminare
4.7 Kugelumströmung... 4.7. Ideale reibungsfreie Umströmung der Kugel (Potentialströmung)... 4.7. Reibungsbehaftete Umströmung der Kugel... 4.8 Zylinderumströmung... 4.9 Rohrströmung... 5 4.9. Laminare
Grundlagen der Hydromechanik
 Berichte aus der Umweltwissenschaft Rainer Helmig, Holger Class Grundlagen der Hydromechanik / Shaker Verlag Aachen 2005 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis Abbildungsverzeichnis Tabellenverzeichnis
Berichte aus der Umweltwissenschaft Rainer Helmig, Holger Class Grundlagen der Hydromechanik / Shaker Verlag Aachen 2005 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis Abbildungsverzeichnis Tabellenverzeichnis
Tutorium Hydromechanik I + II
 Tutorium Hydromechanik I + II WS 2015/2016 Session 3 Prof. Dr. rer. nat. M. Koch 1 Aufgabe 13 (Klausuraufgabe am 07.10.2012) Der bekannte Bergsteiger Reinhold Messner befindet sich mal wieder auf Himalaya
Tutorium Hydromechanik I + II WS 2015/2016 Session 3 Prof. Dr. rer. nat. M. Koch 1 Aufgabe 13 (Klausuraufgabe am 07.10.2012) Der bekannte Bergsteiger Reinhold Messner befindet sich mal wieder auf Himalaya
Versuch V1 - Viskosität, Flammpunkt, Dichte
 Versuch V1 - Viskosität, Flammpunkt, Dichte 1.1 Bestimmung der Viskosität Grundlagen Die Viskosität eines Fluids ist eine Stoffeigenschaft, die durch den molekularen Impulsaustausch der einzelnen Fluidpartikel
Versuch V1 - Viskosität, Flammpunkt, Dichte 1.1 Bestimmung der Viskosität Grundlagen Die Viskosität eines Fluids ist eine Stoffeigenschaft, die durch den molekularen Impulsaustausch der einzelnen Fluidpartikel
Klausur. Strömungsmechanik
 Strömungsmechanik Klausur Strömungsmechanik. Juli 007 Name, Vorname: Matrikelnummer: Fachrichtung: Unterschrift: Bewertung: Aufgabe : Aufgabe : Aufgabe 3: Aufgabe 4: Gesamtpunktzahl: Klausur Strömungsmechanik
Strömungsmechanik Klausur Strömungsmechanik. Juli 007 Name, Vorname: Matrikelnummer: Fachrichtung: Unterschrift: Bewertung: Aufgabe : Aufgabe : Aufgabe 3: Aufgabe 4: Gesamtpunktzahl: Klausur Strömungsmechanik
Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide
 Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
Daniel Janocha Aus der Reihe: e-fellows.net stipendiaten-wissen e-fellows.net (Hrsg.) Band 1064 Schwache Lösung der Stokes-Gleichungen für nicht-newton'sche Fluide Weak solution of the Stokes equations
Klausur Strömungsmechanik II u x + v. y = 0. ρ u u x + v u ) ρ c p. x + v T ) v ; ρ = ρ ; x = x u ρ L ; ȳ = y L ; u ; v = λ λ Konti:
 ...... Name, Matr.-Nr, Unterschrift Klausur Strömungsmechanik II 05. 08. 011 1. Aufgabe a Konti: Impuls: Energie: u x + v = 0 ρ u u x + v u ρ c p u T x + v T = η u = λ T dimensionslose Größen: ū = u u
...... Name, Matr.-Nr, Unterschrift Klausur Strömungsmechanik II 05. 08. 011 1. Aufgabe a Konti: Impuls: Energie: u x + v = 0 ρ u u x + v u ρ c p u T x + v T = η u = λ T dimensionslose Größen: ū = u u
Thermodynamik (Wärmelehre) III kinetische Gastheorie
 Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
laminare Grenzschichten Wofür Grenzschichttheorie?
 laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
Hydraulische Auslegung von Erdwärmesondenanlagen - Grundlage für effiziente Planung und Ausführung
 Hydraulische Auslegung von Erdwärmesondenanlagen - Grundlage für effiziente Planung und Ausführung Christoph Rosinski, Franz Josef Zapp GEFGA mbh, Gesellschaft zur Entwicklung und Förderung von Geothermen
Hydraulische Auslegung von Erdwärmesondenanlagen - Grundlage für effiziente Planung und Ausführung Christoph Rosinski, Franz Josef Zapp GEFGA mbh, Gesellschaft zur Entwicklung und Förderung von Geothermen
Bernoulligleichung. umax. Bernoulligleichung. Stromfadenvorstellung. Bild 1: Stromfaden als Sonderform der Stromröhre
 Bernoulligleichung 1 Bernoulligleichung Stromfadenvorstellung Bild 1: Stromfaden als Sonderform der Stromröhre Im Arbeitsblatt Kontinuitätsgleichung wurde die Stromröhre eingeführt. Sie ist ein Bilanzgebiet
Bernoulligleichung 1 Bernoulligleichung Stromfadenvorstellung Bild 1: Stromfaden als Sonderform der Stromröhre Im Arbeitsblatt Kontinuitätsgleichung wurde die Stromröhre eingeführt. Sie ist ein Bilanzgebiet
Relativistische Punktmechanik
 KAPITEL II Relativistische Punktmechanik Der Formalismus des vorigen Kapitels wird nun angewandt, um die charakteristischen Größen und Funktionen zur Beschreibung der Bewegung eines freien relativistischen
KAPITEL II Relativistische Punktmechanik Der Formalismus des vorigen Kapitels wird nun angewandt, um die charakteristischen Größen und Funktionen zur Beschreibung der Bewegung eines freien relativistischen
Ergänzungsübungen zur Physik für Ingenieure (Maschinenbau) (WS 13/14)
 Ergänzungsübungen zur Physik für Ingenieure (Maschinenbau) (WS 13/14) Prof. W. Meyer Übungsgruppenleiter: A. Berlin & J. Herick (NB 2/28) Ergänzung J Hydrodynamik In der Hydrodynamik beschreibt man die
Ergänzungsübungen zur Physik für Ingenieure (Maschinenbau) (WS 13/14) Prof. W. Meyer Übungsgruppenleiter: A. Berlin & J. Herick (NB 2/28) Ergänzung J Hydrodynamik In der Hydrodynamik beschreibt man die
Leibniz Universität Hannover Institut für Turbomaschinen und Fluid-Dynamik Prof. Dr.-Ing. J. Seume. Klausur Herbst Strömungsmechanik I
 Leibniz Universität Hannover Institut für Turbomaschinen und Fluid-Dynamik Prof. Dr.-Ing. J. Seume Klausur Herbst 008 Strömungsmechanik I Bearbeitungsdauer: 90 min zugelassene Hilfsmittel: - Taschenrechner
Leibniz Universität Hannover Institut für Turbomaschinen und Fluid-Dynamik Prof. Dr.-Ing. J. Seume Klausur Herbst 008 Strömungsmechanik I Bearbeitungsdauer: 90 min zugelassene Hilfsmittel: - Taschenrechner
Einfluß des Strömungszustandes (laminar / turbulent) im Wärmeträgerrohr auf den Kollektorwirkungsgradfaktor eines Finnenabsorbers
 Einfluß des Strömungszustandes (laminar / turbulent) im Wärmeträgerrohr auf den Kollektorwirkungsgradfaktor eines Finnenabsorbers Dipl. Ing. Robert Hausner, Arbeitsgemeinschaft ERNEUERBARE ENERGIE, A-8200
Einfluß des Strömungszustandes (laminar / turbulent) im Wärmeträgerrohr auf den Kollektorwirkungsgradfaktor eines Finnenabsorbers Dipl. Ing. Robert Hausner, Arbeitsgemeinschaft ERNEUERBARE ENERGIE, A-8200
Die Förderhöhe einer Pumpe errechnet sich wie folgt: Sie setzt sich also zusammen aus: dem zu überwindenden Höhenunterschied
 Zum Verständnis der folgenden Kapitel werden wir zuerst die in dieser Broschüre verwendeten Fachbegriffe der definieren und erläutern. Im Stichwortverzeichnis finden Sie diese Begriffe alphabetisch geordnet
Zum Verständnis der folgenden Kapitel werden wir zuerst die in dieser Broschüre verwendeten Fachbegriffe der definieren und erläutern. Im Stichwortverzeichnis finden Sie diese Begriffe alphabetisch geordnet
Freie Konvektion und Wärmeübertragung
 Ulrich Müller/ Peter Ehrhard Freie Konvektion und Wärmeübertragung C. F. Müller Verlag, Heidelberg Freie Konvektion und Wärmeübertragung Inhaltsverzeichnis 1 Einführung 1 1 Konvektion in offenen Systemen
Ulrich Müller/ Peter Ehrhard Freie Konvektion und Wärmeübertragung C. F. Müller Verlag, Heidelberg Freie Konvektion und Wärmeübertragung Inhaltsverzeichnis 1 Einführung 1 1 Konvektion in offenen Systemen
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 2. Das reale Gas. Das reale Gas
 Prof. Dr. Norbert Hampp 1/9 2. Das reale Gas Das reale Gas Für die Beschreibung des realen Gases werden die Gasteilchen betrachtet als - massebehaftet - kugelförmig mit Durchmesser d - Wechselwirkungen
Prof. Dr. Norbert Hampp 1/9 2. Das reale Gas Das reale Gas Für die Beschreibung des realen Gases werden die Gasteilchen betrachtet als - massebehaftet - kugelförmig mit Durchmesser d - Wechselwirkungen
Fluidmechanik. Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen. -Laborübung- 3. Semester. Namen: Datum: Abgabe:
 Strömungsanlage 1 Fachhochschule Trier Studiengang Lebensmitteltechnik Fluidmechanik -Laborübung-. Semester Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen Namen: Datum: Abgabe:
Strömungsanlage 1 Fachhochschule Trier Studiengang Lebensmitteltechnik Fluidmechanik -Laborübung-. Semester Thema Erfassung der Druckverluste in verschiedenen Rohrleitungselementen Namen: Datum: Abgabe:
Heinz Herwig. Strömungsmechanik. Einführung in die Physik von technischen Strömungen Mit 83 Abbildungen und 13 Tabellen STUDIUM VIEWEG+ TEUBNER
 Heinz Herwig Strömungsmechanik Einführung in die Physik von technischen Strömungen Mit 83 Abbildungen und 13 Tabellen STUDIUM VIEWEG+ TEUBNER vii 0 Das methodische Konzept dieses Buches 1 A Einführung
Heinz Herwig Strömungsmechanik Einführung in die Physik von technischen Strömungen Mit 83 Abbildungen und 13 Tabellen STUDIUM VIEWEG+ TEUBNER vii 0 Das methodische Konzept dieses Buches 1 A Einführung
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 9: Turbulente Strömungen, Grenzflächen, Schwingungen Dr. Daniel Bick 30. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 30. November 2016
Physik für Biologen und Zahnmediziner Kapitel 9: Turbulente Strömungen, Grenzflächen, Schwingungen Dr. Daniel Bick 30. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 30. November 2016
Klausur Strömungslehre a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes.
 ......... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 20. 08. 2004 1. Aufgabe (11 Punkte) a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes. b) Nennen
......... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 20. 08. 2004 1. Aufgabe (11 Punkte) a) Beschreiben Sie kurz in Worten das Prinzip des hydrostatischen Auftriebs nach Archimedes. b) Nennen
Eigenschaften der Fluide
 W. Heller, 2011 PT Kapitel 2 Eigenschaften der Fluide Aggregatzustand fest flüssig gasförmig Festkörper Flüssigkeiten Gase Fluide Wechselwirkung der Fluid- Moleküle dominiert durch intermolekulares Potential
W. Heller, 2011 PT Kapitel 2 Eigenschaften der Fluide Aggregatzustand fest flüssig gasförmig Festkörper Flüssigkeiten Gase Fluide Wechselwirkung der Fluid- Moleküle dominiert durch intermolekulares Potential
3. Innere Reibung von Flüssigkeiten
 IR1 3. Innere Reibung von Flüssigkeiten 3.1 Einleitung Zwischen den Molekülen in Flüssigkeiten wirken anziehende Van der Waals Kräfte oder wie im Falle des Wassers Kräfte, die von sogenannten Wasserstoffbrückenbindungen
IR1 3. Innere Reibung von Flüssigkeiten 3.1 Einleitung Zwischen den Molekülen in Flüssigkeiten wirken anziehende Van der Waals Kräfte oder wie im Falle des Wassers Kräfte, die von sogenannten Wasserstoffbrückenbindungen
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 9: Turbulente Strömungen, Grenzflächen, Schwingungen Dr. Daniel Bick 30. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 30. November 2016
Physik für Biologen und Zahnmediziner Kapitel 9: Turbulente Strömungen, Grenzflächen, Schwingungen Dr. Daniel Bick 30. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 30. November 2016
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts
 9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
9.4 Stationäre kompressible Strömungen in Rohren oder Kanälen konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes Element
3 Erzwungene Konvektion 1
 3 Erzwungene Konvektion 3. Grunlagen er Konvektion a) erzwungene Konvektion (Strömung angetrieben urch Pumpe oer Gebläse) b) freie Konvektion (Dichteunterschiee aufgrun von Temperaturunterschieen) c) Konensation
3 Erzwungene Konvektion 3. Grunlagen er Konvektion a) erzwungene Konvektion (Strömung angetrieben urch Pumpe oer Gebläse) b) freie Konvektion (Dichteunterschiee aufgrun von Temperaturunterschieen) c) Konensation
Physikalisches Praktikum
 Physikalisches Praktikum Viskosität von Flüssigkeiten Laborbericht Korrigierte Version 9.Juni 2002 Andreas Hettler Inhalt Kapitel I Begriffserklärungen 5 Viskosität 5 Stokes sches
Physikalisches Praktikum Viskosität von Flüssigkeiten Laborbericht Korrigierte Version 9.Juni 2002 Andreas Hettler Inhalt Kapitel I Begriffserklärungen 5 Viskosität 5 Stokes sches
Inhaltsverzeichnis. Gerd Junge. Einführung in die Technische Strömungslehre ISBN: Weitere Informationen oder Bestellungen unter
 Inhaltsverzeichnis Gerd Junge Einführung in die Technische Strömungslehre ISBN: 978-3-446-42300-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42300-8 sowie im Buchhandel.
Inhaltsverzeichnis Gerd Junge Einführung in die Technische Strömungslehre ISBN: 978-3-446-42300-8 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42300-8 sowie im Buchhandel.
... (Name, Matr.-Nr, Unterschrift) Klausur Technische Strömungslehre
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Technische Strömungslehre 16. 3. 006 1. Aufgabe (6 Punkte) Eine starre, mit Luft im Umgebungszustand gefüllte Boje hat die Form eines Kegels (Höhe h 0, Radius
...... (Name, Matr.-Nr, Unterschrift) Klausur Technische Strömungslehre 16. 3. 006 1. Aufgabe (6 Punkte) Eine starre, mit Luft im Umgebungszustand gefüllte Boje hat die Form eines Kegels (Höhe h 0, Radius
Mechanik der Flüssigkeiten und Gase
 BIBLIOTHEK DES TECHNIKERS UXMT Mechanik der Flüssigkeiten und Gase Technische Physik von Horst Herr VERLAG EUROPA-LEHRMITTEL Nourney, Vollmer GmbH & Co. KLEINER WERTH 50 POSTFACH 201815 5600 WUPPERTAL
BIBLIOTHEK DES TECHNIKERS UXMT Mechanik der Flüssigkeiten und Gase Technische Physik von Horst Herr VERLAG EUROPA-LEHRMITTEL Nourney, Vollmer GmbH & Co. KLEINER WERTH 50 POSTFACH 201815 5600 WUPPERTAL
3. Grenzschichtströmungen Grenzschichtablösung
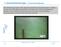 3. Grenzschichtströmungen - 3. Grenzschichtablösung Eine Strömung ist nicht in der Lage sehr schnellen Konturänderungen zu folgen, da dies sehr hohe Beschleunigungen und daher sehr hohe Druckgradienten
3. Grenzschichtströmungen - 3. Grenzschichtablösung Eine Strömung ist nicht in der Lage sehr schnellen Konturänderungen zu folgen, da dies sehr hohe Beschleunigungen und daher sehr hohe Druckgradienten
Dr.-Ing. habil. Jörg Wollnack 18.12.2008 GHY.1. Hydraulische Systeme
 GHY.1 Hydraulische Systeme GHY.2 Hydraulische Motoren GHY.3 p i const, p i Fi i F F 1 2 1 2 F 1 2 F 1 2 Hydraulische Presse I GHY.4 Energieerhaltungssatz S + s S + s 01 1 02 2 S F ds F ds 1 1 2 2 S 01
GHY.1 Hydraulische Systeme GHY.2 Hydraulische Motoren GHY.3 p i const, p i Fi i F F 1 2 1 2 F 1 2 F 1 2 Hydraulische Presse I GHY.4 Energieerhaltungssatz S + s S + s 01 1 02 2 S F ds F ds 1 1 2 2 S 01
Grundpraktikum der Physik. Versuch 05. Viskosität von Flüssigkeiten. Durchführung am 09.11.2007. Gruppe D12 Betreuer: Anne Kröske
 Grundpraktikum der Physik Versuch 05 Viskosität von Flüssigkeiten Durchführung am 09.11.2007 Gruppe D12 Betreuer: Anne Kröske Nadine Kremer nadine.kremer@uni-ulm.de Rainer Pfeiffer rainer.pfeiffer@uni-ulm.de
Grundpraktikum der Physik Versuch 05 Viskosität von Flüssigkeiten Durchführung am 09.11.2007 Gruppe D12 Betreuer: Anne Kröske Nadine Kremer nadine.kremer@uni-ulm.de Rainer Pfeiffer rainer.pfeiffer@uni-ulm.de
Abb.1 Zur Veranschaulichung: Scherung eines Fluids zwischen zwei Platten
 Viskosität Die innere Reibung von Fluiden wird durch ihre dynamische Viskosität η beschrieben. Die dynamische Viskosität η eines Fluids stellt dessen Widerstand gegen einen erzwungenen, irreversiblen Ortswechsel
Viskosität Die innere Reibung von Fluiden wird durch ihre dynamische Viskosität η beschrieben. Die dynamische Viskosität η eines Fluids stellt dessen Widerstand gegen einen erzwungenen, irreversiblen Ortswechsel
Fahrzeug- und Windradaerodynamik
 Fahrzeug- und Windradaerodynamik Geometrisch einfache Körper Dr.-Ing. A. Henze, Prof. Dr.-Ing. W. Schröder Institute of Aerodynamics, RWTH Aachen University Versuchsbedingungen für große Re-Zahlen braucht
Fahrzeug- und Windradaerodynamik Geometrisch einfache Körper Dr.-Ing. A. Henze, Prof. Dr.-Ing. W. Schröder Institute of Aerodynamics, RWTH Aachen University Versuchsbedingungen für große Re-Zahlen braucht
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume. Klausur Frühjahr Strömungsmechanik I. Name Vorname Matr.
 Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 2002 Strömungsmechanik I Bearbeitungsdauer: 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 2002 Strömungsmechanik I Bearbeitungsdauer: 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
laminare Grenzschichten Wofür Grenzschichttheorie?
 laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
laminare Grenzschichten Wofür Grenzschichttheorie? mit der Potentialtheorie können nur Druckverteilungen berechnet werden Auftriebskraft Die Widerstandskräfte können nicht berechnet werden. Reibungskräfte
ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben
![ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben ETH-Aufnahmeprüfung Herbst Physik U 1. Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben](/thumbs/64/51931310.jpg) ETH-Aufnahmeprüfung Herbst 2015 Physik Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben U 1 V a) Betrachten Sie den angegebenen Stromkreis: berechnen Sie die Werte, die von den Messgeräten (Ampere-
ETH-Aufnahmeprüfung Herbst 2015 Physik Aufgabe 1 [4 pt + 4 pt]: zwei unabhängige Teilaufgaben U 1 V a) Betrachten Sie den angegebenen Stromkreis: berechnen Sie die Werte, die von den Messgeräten (Ampere-
6. Welche der folgenden Anordnungen von vier gleich großen ohmschen Widerständen besitzt den kleinsten Gesamtwiderstand?
 1 1. Welche der folgenden Formulierungen entspricht dem ersten Newton schen Axiom (Trägheitsprinzip)? Ein Körper verharrt in Ruhe oder bewegt sich mit konstanter gleichförmiger Geschwindigkeit, wenn die
1 1. Welche der folgenden Formulierungen entspricht dem ersten Newton schen Axiom (Trägheitsprinzip)? Ein Körper verharrt in Ruhe oder bewegt sich mit konstanter gleichförmiger Geschwindigkeit, wenn die
VORLESUNGEN. Numerische. Diplomarbeit. Strömungsmechanik Kolleg
 VORLESUNGEN Strömungslehre 5 Angewandte Strömungsmechanik Math. Methoden der Strömungslehre 6 Numerische Strömungsmechanik 7 Trainings-Kurs 8 Diplomarbeit Strömungsmechanik Kolleg Mathematische Methoden
VORLESUNGEN Strömungslehre 5 Angewandte Strömungsmechanik Math. Methoden der Strömungslehre 6 Numerische Strömungsmechanik 7 Trainings-Kurs 8 Diplomarbeit Strömungsmechanik Kolleg Mathematische Methoden
Grundpraktikum M6 innere Reibung
 Grundpraktikum M6 innere Reibung Julien Kluge 1. Juni 2015 Student: Julien Kluge (564513) Partner: Emily Albert (564536) Betreuer: Pascal Rustige Raum: 215 Messplatz: 2 INHALTSVERZEICHNIS 1 ABSTRACT Inhaltsverzeichnis
Grundpraktikum M6 innere Reibung Julien Kluge 1. Juni 2015 Student: Julien Kluge (564513) Partner: Emily Albert (564536) Betreuer: Pascal Rustige Raum: 215 Messplatz: 2 INHALTSVERZEICHNIS 1 ABSTRACT Inhaltsverzeichnis
Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018)
 Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) 4.1 Begriff
Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) Versuch 4 Messung der dynamischen Viskosität mit dem Rotationsviskosimeter (Grundlagen DIN 53018) 4.1 Begriff
Klausur Strömungsmechanik II
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungsmechanik II 16. 08. 018 1. Aufgabe (14 Punkte) Das Kräftegleichgewicht in einer ausgebildeten, laminaren Rohrströmung unter Gravitationseinfluss wird
...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungsmechanik II 16. 08. 018 1. Aufgabe (14 Punkte) Das Kräftegleichgewicht in einer ausgebildeten, laminaren Rohrströmung unter Gravitationseinfluss wird
25. Vorlesung Sommersemester
 25. Vorlesung Sommersemester 1 Dynamik der Flüssigkeiten Als Beispiel für die Mechanik der Kontinua soll hier noch auf die Bewegung von Flüssigkeiten, eingegangen werden. Traditionell unterscheidet man
25. Vorlesung Sommersemester 1 Dynamik der Flüssigkeiten Als Beispiel für die Mechanik der Kontinua soll hier noch auf die Bewegung von Flüssigkeiten, eingegangen werden. Traditionell unterscheidet man
Strömungsmechanik. YJ Springer. Heinz Herwig. Eine Einführung in die Physik und die mathematische Modellierung von Strömungen
 Heinz Herwig Strömungsmechanik Eine Einführung in die Physik und die mathematische Modellierung von Strömungen 2., neu bearbeitete und erweiterte Auflage Mit 100 Abbildungen und 48 Tabellen YJ Springer
Heinz Herwig Strömungsmechanik Eine Einführung in die Physik und die mathematische Modellierung von Strömungen 2., neu bearbeitete und erweiterte Auflage Mit 100 Abbildungen und 48 Tabellen YJ Springer
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume. Klausur Frühjahr Strömungsmechanik I. Name Vorname Matr.
 Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 003 Strömungsmechanik I Bearbeitungsdauer: PO 000 : 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
Universität Hannover Institut für Strömungsmaschinen Prof. Dr.-Ing. J.Seume Klausur Frühjahr 003 Strömungsmechanik I Bearbeitungsdauer: PO 000 : 90 min zugelassene Hilfsmittel: Taschenrechner Formelsammlung-IfS,
Technische Strömungslehre Formelsammlung
 Formelammlung Strömunglehre Seite von 4 Tehnihe Strömunglehre Formelammlung Komreibilität K von Flüigkeiten E FL V V K E Fl Komreibilität von Gaen V Bei Gaen entriht E V Ga vonϑ C ;, 35bar für den Normzutand
Formelammlung Strömunglehre Seite von 4 Tehnihe Strömunglehre Formelammlung Komreibilität K von Flüigkeiten E FL V V K E Fl Komreibilität von Gaen V Bei Gaen entriht E V Ga vonϑ C ;, 35bar für den Normzutand
Stationäre Rohrströmung ohne Reibung. 2002 Büsching, F.: Hydromechanik 07.1
 Stationäre Rohrströmung ohne Reibung. 00 Büsching, F.: Hydromechanik 07.1 Stationäre Rohrströmung mit Reibung. 00 Büsching, F.: Hydromechanik 07. FLIEßVORGANG REALER FLÜSSIGKEITEN: 1. Laminare und turbulente
Stationäre Rohrströmung ohne Reibung. 00 Büsching, F.: Hydromechanik 07.1 Stationäre Rohrströmung mit Reibung. 00 Büsching, F.: Hydromechanik 07. FLIEßVORGANG REALER FLÜSSIGKEITEN: 1. Laminare und turbulente
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze
 Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
Symmetrie von Naturgesetzen - Galilei-Transformationen und die Invarianz der Newton schen Gesetze Symmetrie (Physik) (aus Wikipedia, der freien Enzyklopädie) Symmetrie ist ein grundlegendes Konzept der
4.1.4 Stationäre kompressible Strömungen in Rohren oder Kanälen
 4.1.4 Stationäre kompressible Strömungen in Rohren oder Kanälen 4.1.4-1 konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes
4.1.4 Stationäre kompressible Strömungen in Rohren oder Kanälen 4.1.4-1 konstanten Querschnitts Die Strömung tritt mit dem Zustand 1 in die Rohrleitung ein. Für ein aus der Rohrstrecke herausgeschnittenes
Klausur Strömungslehre
 ...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 10. 3. 2005 1. Aufgabe (6 Punkte) Ein Heißluftballon mit ideal schlaffer Hülle hat beim Start ein Luftvolumen V 0. Während er in die Atmosphäre
...... (Name, Matr.-Nr, Unterschrift) Klausur Strömungslehre 10. 3. 2005 1. Aufgabe (6 Punkte) Ein Heißluftballon mit ideal schlaffer Hülle hat beim Start ein Luftvolumen V 0. Während er in die Atmosphäre
Julius-Maximilians-Universität Würzburg. Lehrstuhl für Physik und ihre Didaktik
 Julius-Maximilians-Universität Würzburg Lehrstuhl für Physik und ihre Didaktik Erste Staatprüfung für ein Lehramt an Gymnasien Schriftliche Hausarbeit Schülerwindkanal Aufbau, Charakterisierung und Experimente
Julius-Maximilians-Universität Würzburg Lehrstuhl für Physik und ihre Didaktik Erste Staatprüfung für ein Lehramt an Gymnasien Schriftliche Hausarbeit Schülerwindkanal Aufbau, Charakterisierung und Experimente
Physik 1 für Chemiker und Biologen 9. Vorlesung
 Physik 1 für Chemiker und Biologen 9. Vorlesung 19.12.2016 "I am an old man now, and when I die and go to heaven there are two matters on which I hope for enlightenment. One is quantum electrodynamics,
Physik 1 für Chemiker und Biologen 9. Vorlesung 19.12.2016 "I am an old man now, and when I die and go to heaven there are two matters on which I hope for enlightenment. One is quantum electrodynamics,
Dynamik der Atmosphäre. Einige Phänomene
 Dynamik der Atmosphäre Einige Phänomene Extratropische Zyklone L L L = 1000 km U = 10 m/sec Tropische Zyklon, Hurrikan, Taifun L L = 500 km U = 50 m/sec Cumulonimbuswolke L L = 10-50 km U = 10-20 m/sec
Dynamik der Atmosphäre Einige Phänomene Extratropische Zyklone L L L = 1000 km U = 10 m/sec Tropische Zyklon, Hurrikan, Taifun L L = 500 km U = 50 m/sec Cumulonimbuswolke L L = 10-50 km U = 10-20 m/sec
